Introduction

In the chemistry of ruthenium, the coordination chemistry of complexes containing N-heterocyclic derivatives is one of the most studied aspects. The wide interest is this field originates from the very rich redox chemistry and photophysics of these compounds. Even small changes in the coordination environment around the ruthenium can play a key role in altering the redox properties of the complexes, and thus, complexation of ruthenium by various ligands is very interesting and has been widely studied [1–4].

The η6-arene–ruthenium complexes play a vital role in organometallic chemistry [5–7]. The arene–ruthenium halide compounds are key starting materials for the formation of a wide range of neutral and cationic ligand derivatives [8–11]. The half-sandwich arene–ruthenium complexes may serve as excellent catalyst precursors for hydrogenation and for ring-opening metathesis polymerization. Some studies of arene–ruthenium complexes have shown that they can inhibit cancer cell growth [12–15].

The triazolopyrimidine ligands are interesting due to their biological activity. The triazolopyrimidine derivatives are examples of purine mimics, and 7-hydroxy-5-methyl[1,2,4]triazolo[1,5-a]pyrimidine (Hmtp) Hmtp is a good representative of these derivatives.

The complexes reported in this paper combine our interest in ruthenium coordination compounds and complexes containing Hmtp or pyrimidine. I present the synthesis, crystal, molecular and electronic structures, and the spectroscopic characterization of these new half-sandwich ruthenium(II) complexes.

Experimental

The starting material [(C6H6)RuCl2]2 was synthesized according to the literature procedure [16, 17]. All other reagents were commercially available and were used without further purification.

Synthesis of the complexes

A mixture of [(C6H6)RuCl2]2 (0.25 g; 5 × 10−4 mol) and 5-methyl-7-hydroxy-1,2,4-triazolo-[1,5-α]pyrimidine or pyrimidine (7 × 10−4 mol) in methanol (50 cm−3) was refluxed for 3 h, cooled and filtered. Crystals suitable for X-ray crystal analysis were obtained by slow evaporation of the filtrate.

Complex 1

[(C6H6)RuCl2(Hmtp)], Yield 82%. IR (KBr): 3,410 (νOH), 3,214 (νCH), 3,120 (νCH), 3,062 (νCH), 1,720 (νring), 1,636 (νCN), 1,490 (νC=C), 1,435 (νring + νCH), 1,325 (δCH), 1,142 (δCH), 898 (γCH), 529 (νRu–N). UV–VIS (acetonitrile, λ [nm] (logε)): 445.0 (1.37), 337.2 (1.96), 272.3 (3.22), 233.7 (3.18) sh, 213.3 (3.77). 1H NMR: (CDCl3, ppm): 8.36 (s, OH), 7.54 (s, H2), 7.02 (s, H6), 5.89 (s, C6H6), 2.38 (s, CH3).

Complex 2

[(C6H6)RuCl2(C4H4N2)], Yield 87%. IR (KBr): 3,071 (νCH), 1,582 (νCN), 1,505 (νC=C), 1,435 (νring + νCH), 1,399 (δCH), 1,140 (δCH), 828 (γCH), 451 (νRu–N). UV–VIS (methanol, λ [nm] (logε)): 409.9 (1.46), 302.1 (1.98), 270.9 (2.76), 231.3 (3.12) sh, 212.6 (3.62). 1H NMR: (CDCl3, ppm): 9.27 (s, H2), 8.79 (s, H4,6), 7.39 (s, H5), 5.76 (s, C6H6).

Physical measurements

Infrared spectra were recorded on a Nicolet Magna 560 spectrophotometer in the spectral range 4,000/400 cm−1 using KBr pellets. Electronic spectra were measured on a Lab Alliance UV–VIS 8,500 spectrophotometer in the range of 600–180 nm in methanol solution. 1H NMR spectra were obtained at room temperature in CDCl3 using a Bruker 400 spectrometer.

DFT calculations

The calculations were carried out using the Gaussian09 [18, 19] program. The DFT/B3LYP [20] method was used for the geometry optimization and electronic structure determination, and electronic spectra were calculated by the TD–DFT [21] method. The calculations were performed using the DZVP basis set [22, 23] with f functions with exponents 1.94722036 and 0.748930908 on ruthenium, and polarization functions for all other atoms: 6-31 g(2d,p)—chlorine, 6-31 g**—carbon, nitrogen and 6-31 g(d,p)—hydrogen. The PCM solvent model was used in the Gaussian calculations with acetonitrile as the solvent. GaussSum 2.2 [24] was used to calculate group contributions to the molecular orbitals and to prepare the partial density of states (DOS) and overlap population density of states (OPDOS) spectra. The contribution of a group to a molecular orbital was calculated using Mulliken population analysis. The PDOS and OPDOS spectra were created by convoluting the molecular orbital information with Gaussian curves of unit height and FWHM of 0.3 eV.

Crystal structure determination and refinement

Red crystals of [(C6H6)RuCl2(Hmtp)] and [(C6H6)RuCl2(C4H4N2)] were mounted in turn on an Xcalibur, Atlas, Gemini ultra Oxford Diffraction automatic diffractometer, equipped with a CCD detector and used for data collection. X-ray intensity data were collected with graphite monochromated MoK α radiation (λ = 0.71073 Å) at temperature 295.0(2) K, with ω scan mode. Ewald sphere reflections were collected up to 2θ = 50.10° and 57.54° for complexes 1 and 2, respectively. The unit cell parameters were determined from least-squares refinement of the setting angles of 13,309 and 12,292 strongest reflections. Details concerning crystal data and refinement are gathered in Table 1. During the data reduction, the decay correction coefficients were taken into account. Lorentz, polarization and numerical absorption corrections were applied. The structures were solved by the Patterson method. All the non-hydrogen atoms were refined anisotropically using full-matrix, least-squares technique on F2. All the hydrogen atoms were found from difference Fourier synthesis after four cycles of anisotropic refinement and refined as “riding” on the adjacent atoms with individual isotropic temperature factor equal 1.2 times the value of equivalent temperature factor of the parent atom, with geometry idealization after each cycle. The Olex2 [25] program was used for all the calculations. Atomic scattering factors were those incorporated into the computer programs.

Table 1 Crystal data and structure refinement details of [(C6H6)RuCl2(Hmtp)].CH3OH (1) and [(C6H6)RuCl2(C4H4N2)] (2)
Full size table

Results and discussion

The half-sandwich complexes were obtained by the reaction of [(C6H6)RuCl2]2 with Hmtp or pyrimidine in methanol solutions. In the IR spectrum of complex 1, the ring C=C and C=N stretching modes of the Hmtp ligand are present at 1,720 and 1,636 cm−1, and for complex 2, the pyrimidine C=C and C=N stretches are found at 1,582 cm−1. The stretching modes of the C–H are observed at 3,214, 3,120, 3,062 and 3,071 cm−1, for complexes 1 and 2, respectively. The phenyl ring C–H bend mode is visible in the bands with maxima at 1,490, 1,435, 1,325 cm−1 in 1, and 1,505, 1,435, 1,398 cm−1 in 2. The methyl group (Hmtp) C–H bend mode has a maximum at 1,142 cm−1. The twist mode of benzene C–H is at 898 and 896 cm−1 for compounds 1 and 2, respectively. The stretching frequency of the Ru–N bond is at 529 cm−1 in complex 1 and 451 cm−1 in 2. In the 1H NMR spectra of the complexes, the protons of the C6H6 ligands appear as a singlet at 5.89 and 5.76 ppm, respectively, for complexes 1 and 2. The OH proton of Hmtp appears at 8.36 ppm.

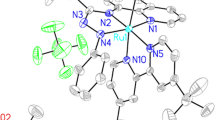
Crystal structures

The complexes 1 and 2 crystallize in the monoclinic space groups C2/c and P21/c, respectively. The molecular structures of the compounds are shown in Fig. 1. Selected bond lengths and angles are listed in Table 2. The complexes adopt a distorted piano-stool type of geometry with the ruthenium atom π-bonded with the benzene ring with an average Ru–C distance of 2.1595(3) Å in 1 and 2.182(5) Å in compound 2, while the distance between the ruthenium atom and the centroid of the benzene ring is 1.418 and 1.675 Å for complexes 1 and 2, respectively. The ruthenium atom is also directly coordinated with one of the nitrogen atoms of the Hmtp or pyrimidine ligand with a normal distance. The Ru–Cl bond lengths are also normal and comparable with other ruthenium(II) half-sandwich complexes. The angles between the nitrogen heteroaromatic ligands and chlorine ligands in the complexes 1 and 2 are close to those observed in the ruthenium–arene compounds [26]. In the structures of both complexes, inter- and intramolecular weak hydrogen bonds exist and these are [27] collected in Table 3.

Fig. 1
figure 1

ORTEP drawing of [(C6H6)RuCl2(Hmtp)] and [(C6H6)RuCl2(C4H4N2)] with 50% probability displacement ellipsoids

Full size image
Table 2 Selected bond lengths [Å] and angles [°] for [(C6H6)RuCl2(Hmtp)] (1) and [(C6H6)RuCl2(C4H4N2)] (2) with the optimized geometry values
Full size table
Table 3 Hydrogen bonds for [(C6H6)RuCl2(Hmtp)] (1) and [(C6H6)RuCl2(C4H4N2)] (2) (Å and o)
Full size table

Geometry and electronic structure

To form an insight into the electronic structures and bonding properties of the complexes 1 and 2, the DFT calculations were carried out. Before calculation of electronic structures of the complexes, their geometries were optimized in singlet states using the DFT method with the B3LYP functional. From the data collected in Table 2, one may see that the majority of differences between the experimental and calculated geometries are found in the benzene ligand. The largest differences were found for the ruthenium–benzene carbon distances. The calculated Ru–benzene centroid distance is 1.722 Å in 1 and 1.725 Å in 2. The maximum differences in the bond distances are found between Ru(1) and C(8) being 0.104 Å in 1 and 0.068 Å in 2. For the optimized angles, the maximum differences from the experimental values are in Cl(1)–Ru(1)–Cl(2) and Cl(1)–Ru(1)–C(9) being 4.73 and 4.99°, respectively, for the complex of Hmtp and in Cl(1)–Ru(1)–C(7) and Cl(2)–Ru(1)–C(9) being 7.13 and 7.61°, respectively, for the complex with pyrimidine.

The formal charge of ruthenium is +2 in both complexes. The calculated charge on the ruthenium atom, obtained from natural population analysis, is approximately 0.2 in compound 1 and 0.18 in complex 2. The natural atomic orbital d occupancies are as follows: d xy 1.42, d xz 1.25, d yz 1.31, \( d_{{x^{2} - y^{2} }} \) 1.27 and \( d_{{z^{2} }} \) 1.70 in compound 1 and d xy 1.56, d xz 1.79, d yz 1.34, \( d_{{x^{2} - y^{2} }} \) 1.16 and \( d_{{z^{2} }} \) 1.10 in 2. The charge on the chlorine ligands is equal to –0.38 and those on the Hmtp and pyrimidine nitrogen donor atoms are –0.47 and –0.42, respectively. This is a result of charge donation from the ligands to the metal centre. The conclusion confirms the second-order perturbation analysis from NBO. The stabilization energy calculated in this analysis shows that the lone pairs localized on the chlorine ligand and nitrogen of Hmtp ligand donate the charge to the ruthenium d orbitals, and the stabilization energy (ΔE ij ) is 764.61 and 138.09 kcal/mol, respectively. The values of stabilization energy of charge donation from the Cl and N-pyrimidine donors in complex 2 are 301.71 kcal/mol and 180.36 kcal/mol, respectively. The stabilization energy associated with the charge donation from ruthenium to the N-donor ligands is small, averaging to 6.38 kcal/mol for complex 1 and 3.59 kcal/mol for compound 2. The stabilization energy of the charge donation from the benzene ring to the antibonding d orbitals is 372.33 kcal/mol for complex 1 and 525.09 for 2, and the back donation charge from ruthenium to the benzene ring stabilizes molecules 1 and 2 by 87.99 and 87.87 kcal/mol, respectively.

The atomic charge calculations can give description of the location of the electron density of the compounds. Since the electron distribution is not apparent from the partial atomic charges, Fig. 2 shows the plots of the electrostatic potentials for the complexes 1 and 2. The isoelectronic contours are plot at 0.005 a.u. (3.1 kcal/mol). The colour code of these maps is in the range of 0.05 a.u. (deepest red) to −0.005 a.u. (deepest blue), where blue indicates the strongest attraction and red indicates the strongest repulsion. Regions of negative V(r) are usually associated with the lone pairs of electronegative atoms. The negative potential in the complexes 1 and 2 encompasses the chloride atoms, hydroxyl group and heteroaromatic nitrogen.

Fig. 2
figure 2

Electrostatic potential (ESP) surfaces of complexes 1 and 2. ESP surface is shown both in space (with positive and negative regions shown in red and blue, respectively) and mapped on electron densities (isovalue = 0.005) of the molecule (ESP colour scale is such that δ+ → δ− in the direction red → blue). (Color figure online)

Full size image

In the frontier region, neighbouring orbitals may show quasi-degeneracy of the energetic levels. In such cases, consideration of only the HOMO and LUMO may not yield a realistic description of the frontier orbitals. For this reason, the partial density of states (DOS) and overlap population density of states (OPDOS) in terms of Mulliken population analysis were calculated using the GaussSum program. They provide a pictorial representation of the MO compositions and their contributions to chemical bonding. The DOS and OPDOS diagrams are shown in Fig. 3. The DOS plot mainly presents the composition of the fragment orbitals contributing to the molecular orbitals. The OPDOS can enable us to ascertain the bonding, non-bonding and antibonding characteristics with respect to the particular fragments. A positive value in the OPDOS plot means a bonding interaction, while a negative value represents an antibonding interaction, and a near zero value indicates a non-bonding interaction.

Fig. 3
figure 3

The density of states (DOS) and overlap partial density of states (OPDOS) diagrams for [(C6H6)RuCl2(Hmtp)] (1) and [(C6H6)RuCl2(C4H4N2)] (2)

Full size image

As can be seen from the OPDOS plot, the chloride ligands have significant antibonding character in the HOMO and HOMO-1 molecular orbitals. The interactions of the benzene ligand with the Ru(II) d orbitals have positive values in the energy range adequate to the HOMO and HOMO-1 molecular orbitals, and in lower occupied orbitals, the interaction has antibonding character. In the frontier occupied and virtual molecular orbitals, the values of the interaction between ruthenium and the Hmtp or pyrimidine ligands are small, which indicates that these ligands are weak π-acceptors. This conclusion is confirmed on the one hand by the stabilization energy mentioned above and on the other hand by the proportion of the Ru(II) and N-heteroaromatic ligands in the frontier molecular orbitals and Mayer bond orders. For example, in the HOMO, HOMO-1 and HOMO-2, the d ruthenium orbitals contribute 35, 30 and 27% in complex 1 and 38, 31, 35% in 2, and the Hmtp and pyrimidine ligands only 1, 3, 5% and 2, 2, 3%, respectively. On the other hand, HOMO-3 in complex 1 and HOMO-10 in 2 are localized on the Hmtp (94%) and pyrimidine (94%) fragments. Furthermore, the Mayer bond orders for Ru–N(1) of 0.71 for complex 1 and 0.79 for 2 show the weakness of this bond compared with the Ru–Cl (1.75) bond. The bond between the benzene ring and ruthenium is slightly more covalent in complex 2 (0.90–0.78) than in the complex with Hmtp (0.85–0.71). In the two lowest virtual orbitals, an interaction of the ruthenium d orbital (LUMO 54%; LUMO + 1 45%, 55% for 1 and 2, respectively) with benzene π orbitals (31%, 19% in 1 and 23, 27% in 2) is visible. Additionally, the d ruthenium (22, 27% for 1; 26, 20% for 2) and π benzene (71, 69%; 77, 71%) orbitals play a significant role in the LUMO + 4 and LUMO + 5 molecular orbitals. The LUMO + 2 (97%) is localized on the Hmtp fragment in complex 2, while the LUMO (96%) and LUMO + 3 (96%) are localized on the pyrimidine moiety.

The energy decomposition analysis of the complexes, based on the work of Morokuma [28–30], and the extended transition state (ETS) partitioning scheme of Ziegler [31, 32] have been carried out using the ADF program (Release 2008) [33] at the level of B3LYP/TZP. The binding energy of each compound was calculated as the difference between the energy of the geometry optimized complexes and the energies of the optimized free ligands Hmtp and pyrimidine and the [(C6H6)RuCl2] fragment. The general theoretical background on the bond energy decomposition scheme has been reviewed [34]. In Table 4, are listed the results of energy decomposition analysis calculated for the complexes in the gas phase and in methanol solvent. As one can see, the kinetic and Coulomb (steric and orbital interaction) energies play an important role for the [(C6H6)RuCl2]–Hmtp binding in solution, and in the case of complex 2, the kinetic energy plays the dominant role. The calculated bonding energies for the two compounds are close to each other, which suggests similarities in π-accepting properties of the Hmtp and pyrimidine ligands.

Table 4 Energy decomposition analysis for complexes [(C6H6)RuCl2(Hmtp)] and [(C6H6)RuCl2(C4H4N2)] in the [(C6H6)RuCl2] fragment and the Hmtp, pyrimidine ligands (energies in kcal.mol−1)
Full size table

Electronic spectrum

The UV–Vis spectra of the complexes displayed bands with maxima at 445, 337, 272, 234 and 213 nm for [(C6H6)RuCl2(Hmtp)] and 410, 302, 271, 231 and 213 nm for [(C6H6)RuCl2(C4H4N2)]. The assignments of the calculated transitions to the experimental bands are based on the criteria of energy and oscillator strength of the calculated transitions. In the description of the electronic transitions, only the main components of the molecular orbitals are taken into consideration.

The two asymmetric and broad experimental bands in the visible region of the electronic spectra of the complexes 1 and 2 are assigned to the transitions between the HOMO, HOMO-1, HOMO-2 and LUMO, LUMO + 1 and LUMO + 2 molecular orbitals. As the HOMO, HOMO-1, HOMO-2 and LUMO + 1, LUMO + 2 are composed of the d ruthenium orbitals with admixture of π–benzene, the transitions are of Ligand Field type (d → d). The LUMOs are localized on the Hmtp and pyrimidine ligands, respectively, in complexes 1 or 2, and Metal–Ligand Charge Transfer transitions are associated with these. The bands observed at 272 and 271 nm have been attributed to the Metal–Ligand and Ligand–Metal Charge Transfer transitions (d → π*benzene/Hmtp/pyrimidine/Cl; π*Hmtp/pyrimidine → d). In this energy region, the transitions between the HOMO-3 → LUMO + 1 (92% in both complexes), HOMO-3 → LUMO (93%) and HOMO-2 → LUMO + 3 (88%) were calculated. The highest energy bands with maxima at 213 nm and 213 nm are attributed to transitions of the Ligand–Ligand Charge Transfer type (π → π*C=N).

Based on the pseudooctahedral geometry of these and taking into account the d–d transitions assigned to 1A1 → 1T1 and 1A1 → 1T2 in octahedral symmetry (or 1A1 → 1A2/B1/B2 in lower symmetry fields as C2v), the ligand field parameters 10Dq can be estimated to 2,9847 and 27,158 cm−1 for the complexes 1 and 2, respectively. Racah’s parameters for complexes 1 and 2 are B = 598, 544 cm−1; C = 2,380, 2,166 cm−1, respectively, and the nephelauxetic parameters have values β55 = 0.83 and 0.76, respectively. The differences in these parameters are in accordance with the covalence (Mayer bond orders) of these complexes.

The emission characteristics of complex 1 have been examined in acetonitrile solution (1 × 10−3mol/dm3) at room temperature. Excitation at 370 nm gave an intense unsymmetrical emission peak with maximum at 480 nm. The unsymmetrical structure of the luminescence spectrum suggests that more than one state is involved in the luminescence process. Hence, the luminescence is of IL/MLCT origin in this system.

Conclusion

From the reactions between [(C6H6)RuCl2]2 and 7-hydroxy-5-methyl-[1,2,4]triazolo[1,5-a]pyrimidine or pyrimidine in methanol, two new half-sandwich ruthenium(II) complexes were obtained. Both complexes are neutral. The molecular structures of the compounds were determined by X-ray crystallography, and the spectroscopic properties were studied. Based on the crystal structures, computational studies were made to determine the electronic structures and UV–Vis spectra of the complexes. The results indicate that the Hmtp and pyrimidine ligands have similar π-acceptor properties, being rather weak π-acceptors.

Appendix A. Supplementary data

CCDC 755383 and CCDC 757130 contain the supplementary crystallographic data for complexes [(C6H6)RuCl2(Hmtp)] and [(C6H6)RuCl2(C4H4N2)], respectively. These data can be obtained free of charge from http://www.ccdc.cam.ac.uk/conts/retrieving.html, or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: (+44) 1223-336-033; or e-mail: deposit@ccdc.cam.ac.uk.

The Gaussian09 calculations were carried out in Wrocław Centre for Networking and Supercomputing, WCSS, Wrocław, Poland.