Introduction

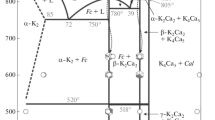
Aurichalcite (Zn,Cu2+)5(CO3)2(OH)6 is usually found as a secondary mineral in copper and zinc deposits. In nature the mineral appears as aggregates or tufts of light blue to green needles/blades [1–4]. The aurichalcite composition shows variation in the Cu:Zn ratio [5]. The aurichalcite mineral can be confused with other related minerals, such as rosasite because of their similar appearance. Rosasite minerals including glaukosphaerite, kolwezite and mcguinnessite show larger crystals. Other related hydroxy carbonate minerals are nullaginite and pokrovskite [6–9]. Aurichalcite is related to hydrozincite, Zn5(CO3)2(OH)6 and the minerals are formed under similar conditions when copper is present in solution [10, 11]. The crystal structure of aurichalcite was solved by Harding et al. [12]. The structure consists of double layers of closely packed oxygen layers parallel to (100). Within this double layer are the octahedral M1 and the tetragonally elongated M2 sites. On the opposite sides of this double layer are the tetrahedral M3 site and the trigonal bipyramidal site, M4. The layers are attached together on one side by hydrogen bonding between the hydroxyl groups and oxygen from a carbonate group, while on the other side there is metal–oxygen bonding. Aurichalcite is used in industry as a catalyst precursor for hydrogenation processes and a number of studies have consequently been focussed on the study of aurichalcite [13–15].

Spectroscopic investigations like NIR, IR and Raman spectroscopy show evidence of variable composition in natural minerals. For example, in aurichalcite, rosasite group of minerals, the effect of structural cation substitution (Ca2+, Cu2+, Fe2+, Cd2+and Zn2+) has been observed [5–9, 16]. The naturally occurring hydroxyl-bearing zinc and copper carbonates are represented by the following five minerals according to the status of the species [2]:

$$ \begin{aligned} {{{\text{hydrozincite}}}} & {{{\text{Zn}}_{{\text{5}}} {\text{(CO}}_{{\text{3}}} {\text{)}}_{{\text{2}}} {\text{(OH)}}_{{\text{6}}} }} \\ {{{\text{aurichalcite}}}} & {{{\text{(Zn,Cu)}}_{{\text{5}}} {\text{(CO}}_{{\text{3}}} {\text{)}}_{{\text{2}}} {\text{(OH)}}_{{\text{6}}} }} \\ {{{\text{malachite}}}} & {{{\text{Cu}}_{{\text{2}}} {\text{(CO}}_{{\text{3}}} {\text{)(OH)}}_{{\text{2}}} }} \\ {{{\text{rosasite}}}} & {{{\text{(Cu,Zn)}}_{{\text{2}}} {\text{(CO}}_{{\text{3}}} {\text{)(OH)}}_{{\text{2}}} }} \\ {{{\text{azurite}}}} & {{{\text{Cu}}_{{\text{3}}} {\text{(CO}}_{{\text{3}}} {\text{)}}_{{\text{2}}} {\text{(OH)}}_{{\text{2}}} }} \\ \end{aligned} $$

The catalytic activity of copper–zinc oxides is known to depend on the catalyst precursor. The use of aurichalcite in synthesising these catalyst precursors rests with the thermal decomposition of the aurichalcite to prepare mixed oxides which are mixed at the atomic level rather than the particle scale. This aspect is investigated in the present work through the study of the spectral properties of synthetic aurichalcite by varying the Cu:Zn ratio. The significance of the hydroxy carbonates precursor phases of Cu–ZnO catalysts was first highlighted by Herman et al. [17] and later extended to malachite and aurichalcite [18, 19]. Many have focussed on catalysts containing only copper and zinc oxide, the two components of greatest catalytic significance for hydrogenation [20–22]. Subsequently, many studies have researched Cu–ZnO/Al2O3 (CZA) catalysts [23–25] with Cu, Zn and Al in various selected proportions. The work described by Stone and Waller [26] on Cu–ZnO and alumina-supported Cu–ZnO as catalysts for the reverse shift reaction shows Cu:Zn ratios varying between Cu-rich and Zn-rich compositions.

Synthetic hydroxyl carbonates of Cu and Zn have potential use as catalysts or catalyst precursors. The Cu:Zn ratio specifies carbonate minerals, for example, malachite, rosasite or aurichalcite. Optimum ratio of Cu:Zn is an important component in biological and other systems. The behaviour of structural cations can be studied by means of electronic spectra and band shifts are expected for both Cu2+ ion and carbonate ions.

Divalent copper has a d9 configuration. The Cu2+ ion has one free ion term, 2D. In octahedral crystal field, this term splits into ground 2E and excited 2T states. The splitting of both 2E and 2T states is the effect of site distortion for Cu2+ ion that occupies Jahn–Teller sites in many copper complexes [27–31]. For Cu2+ the number of bands observable is four and three in rhombic and tetragonal fields, respectively [32]. The energies of the three bands in tetragonal field are related to 2B1 → 2A1, 2B1 → 2B2 and 2B1 → 2E transitions. In this article, we discuss the spectral properties of synthetic aurichalcite, with variable Cu:Zn ratio, using UV–Vis and NIR spectroscopy, having in mind the thermal treatment of aurichalcite produces Cu–ZnO catalysts.

Experimental

Synthesis of aurichalcite

The mineral (Zn,Cu2+)5(CO3)2(OH)6 was synthesised with different ratios of Cu to Zn. Williams inferred from studies of natural aurichalcite minerals that the highest ratio of Cu to Zn in aurichalcite is 1:3 [11]. A common formula for natural aurichalcite is Cu1.25Zn3.75(CO3)2(OH)6. In this work, aurichalcites were synthesised with ratios of 1:9, 1:4, 1:3, 2:3 and 1:1.

Synthesis of ideal products was modelled on the procedure by Fujita et al. [33]. A solution of metal ions (M2+) was prepared by mixing appropriate concentrations of 1.5 M Cu(NO3)2 and Zn(NO3)2 corresponding to the metal concentrations desired in the products. Synthesis of the lower copper concentrations of aurichalcite (Cu < 50%) was carried out by adding dropwise 100 cm3 of a 1.5 M M2+ solution via a peristaltic pump to 1,000 cm3 of 0.2 M \( {\text{HCO}}^{ - }_{3} \) solution at 338 K. The relatively sensitive nature of aurichalcite to acidic (pH < 6) conditions precluded the use of the depleting methods mentioned in the literature [34] in order to obtain optimum yields of high phase purity aurichalcite. As such, a stream of saturated sodium bicarbonate was added at a quasi-constant rate in order to maintain a pH = 7.15; the samples were then aged for 30 min at 338 K under constant stirring. Aged samples were vacuum filtered and washed with hot, degassed and demineralised water. Samples were then dried overnight at 373 K.

The minerals were analysed by XRD for phase identification [35] and scanning electron microscopy (SEM) was employed for composition analysis. The chemical composition was obtained through EDX measurements.

X-ray diffraction

Powder X-ray diffraction analyses were performed on a Phillips X-ray diffractometer (radius: 173.0 mm). Incident X-ray radiation was produced from a long-fine focused C-Tech PW1050 Co X-ray tube, operating at 40 kV and 32 mA. The incident beam passed through a 1° divergence slit, a 15 mm fixed mask and a 1° fixed anti scatter slit. After interaction with the sample, the diffracted beam was detected by a proportional detector with a 0.2 mm receiving slit fitted to a graphite post-diffraction monochrometer. The detector was set in scanning mode, with an active length of 2.022 mm. Samples were analysed utilising Bragg–Brentano 1° geometry over a range of 3–75° 2θ with a step size of 0.02° 2θ, with each step measured for 200 s.

UV–Vis spectroscopy

A Varian Cary 3 UV–Visible spectrophotometer, equipped with Diffuse Reflectance Accessory (DRA) was employed to record the electronic spectra of the samples in the region between 200 and 900 nm. This technique allows the study of the reflectance spectra of the samples in powder form. The DRA consists of a 73-mm diameter-integrating sphere, featuring an inbuilt high performance photomultiplier. Sample was mounted on coarse filter paper (#1), by resuspending the sample and submerging the filter paper into the suspension. Initially, a base line was recorded using two pressed polytetrafluoroethylene (PTFE) reference disks. Next, the sample was mounted flat over the sample port and the reflectance spectrum of the sample, relative to the reference disks, was collected by the integrating sphere. By placing the sample flat any specular components of reflectance should be directed out of the DRA entrance port, as the angle of incidence is 0°. The diffuse reflectance measurements were converted into absorption (arbitrary units) using the Kubelka–Munk function \( ({\text{f}}({\text{R}}_{\infty}) = (1 - {\text{R}}_{\infty})^{2}/2{\text{R}}_{\infty}). \) Data manipulation was performed using Microsoft Excel.

Near-infrared (NIR) and mid-infrared spectroscopy

NIR spectra were collected on a Nicolet Nexus FT-IR spectrometer with a Nicolet Near-IR Fibreport accessory (Madison, Wisconsin). A white light source was used, with a quartz beam splitter and TEC NIR InGaAs detector. Spectra were obtained from 13,000 to 4,000 cm−1 (0.77–2.50) by the co-addition of 64 scans at a spectral resolution of 8 cm−1. A mirror velocity of 1.266 m s−1 was used. The spectra were transformed using the Kubelka–Munk algorithm to provide spectra for comparison with published absorption spectra.

Infrared spectra were obtained using a Nicolet Nexus 870 FT-IR spectrometer with a smart endurance single-bounce diamond ATR cell. Spectra over the 4,000–525 cm−1 range were obtained by the co-addition of 64 scans with a resolution of 4 cm−1 and a mirror velocity of 0.6329 cm s−1. Spectra were co-added to improve the signal to noise ratio.

Spectral manipulation, such as baseline adjustment, smoothing and normalisation were performed using the Spectracalc software package GRAMS (Galactic Industries Corporation, NH, USA). Band component analysis was undertaken using the Jandel ‘Peakfit’ software package which enabled the type of fitting function to be selected and allows specific parameters to be fixed or varied accordingly. Band fitting was done using a Lorentz–Gauss cross-product function with the minimum number of component bands used for the fitting process. The Gauss–Lorentz ratio was maintained at values greater than 0.7 and fitting was undertaken until reproducible results were obtained with squared correlations of r 2 greater than 0.995.

Results and discussion

X-ray diffraction and EDX analysis

The X-ray diffraction patterns for the synthesised aurichalcite together with two reference patterns are shown in Fig. 1. The XRD patterns for Cu/Zn aurichalcite from 0.1/0.9, 0.25/0.75, 0.4/0.6 and 0.5/0.5 are shown. No minor impurities are observed. EDX analyses show that the average chemical composition corresponds to the formula given in Fig. 1.

Fig. 1
figure 1

X-ray diffraction patterns of synthetic aurichalcite together with standard reference materials

Full size image

UV–Vis spectroscopy

Reflectance spectra of carbonate minerals in the visible (Vis) and near-infrared (NIR) spectral regions show various features which are caused by multiphonon absorptions of the fundamental internal and lattice vibrational modes of the carbonate radical and OH units, and by electronic transitions in the unfilled d-shells of the transition metal cations [36, 37]. We have examined five samples of aurichalcite in which Cu:Zn ratios are in the range from 1:9 to 2:3. UV–Vis–NIR reflectance spectra are shown in Figs. 2 and 3 as plots of the Kubelka–Munk function (proportional to absorption) versus wavelength/wavenumber. The spectra in the UV–Vis region are shown in the Fig. 2a–e for the samples with Cu:Zn ratio of 1:9, 1:4, 1:3, 2:3 and 1:1. The Cu–ZnO catalysts with variable Cu:Zn (CZ) ratio between Zn-rich and Cu-rich compositions show an absorption edge at ∼400 nm (25,000 cm−1) attributable to ZnO and a broad diagnostic band at 775 nm (12,900 cm−1) related to the electronic transitions of Cu2+ ions in a distorted octahedral symmetry [5]. For the mixture of CZ with ratio of 2:3, both these absorptions are well resolved (Fig. 2d).

Fig. 2
figure 2

(a–e) UV–Visible spectra of synthetic aurichalcite with CZ ratios of 1:9, 1:4, 1:3. 2:3, 1:1

Full size image
Fig. 3
figure 3

(a–e) NIR spectra of synthetic aurichalcite with CZ ratios of 1:9, 1:4, 1:3. 2:3, 1:1

Full size image

Copper atoms occupy Jahn–Teller distorted sites in many minerals including, aurichalcite, rosasite and smithsonite [5, 9, 38]. In many compounds three bands, one in the visible region around 600–700 nm (16,665–14,285 cm−1) and two in the near-infrared at 800–900 nm and 1,100–1,200 nm (12,500–11,110 and 9,090–8,330 cm−1) have been reported [28, 32, 39, 40] for Cu2+ ion in a distorted octahedral coordination. A report on the characterization of Cu/ZnO/Al2O3 catalysts shows one weak broad band at 800 nm (12,500 cm−1) for Cu(II) ions in a distorted octahedral symmetry [41]. The spectra in the Fig. 2a–e, show a broad absorption at 775 nm (12,900 cm−1) for all the five copper containing precursors from Cu:Zn ratio of 1:9, 1:4, 1:3, 2:3 to 1:1. This feature is characteristic of Cu(II) ion and is assigned to the 2B1 → 2B2 transition and the first band observed in the near-infrared (Fig. 3c) around 7,600 cm−1 (1,315 nm ) to the 2B1 → 2A1 transition. Third band expected for copper ion in the visible is hidden by edge absorptions on either side of the turning points at 500 nm (20,000 cm−1) in the UV–Vis spectrum. The strong band at ∼300 nm (33,330 cm−1) is related to charge transfer transitions involving \( {\text{Cu}}^{{{\text{2+}}}}-{\text{O}}^{{{\text{2}}-}}-{\text{Cu}}^{{{\text{2 + }}}} \) species [42, 43]. The effect of Zn on Cu is observed in the extreme UV spectrum of Cu–ZnO catalyst for CZ ratio variation from 1:9, 1:4, 1:3, 2:3 to 1:1. The UV edge absorption derived (Fig. 2a) by CZ ratio of 1:9 resolved into a band (Fig. 2d) at 240 nm (41,665 cm−1) for CZ ratio of 2:3. This band may be assigned to the charge transfer transition, O2− → Cu2+ [42].

Near-infrared (NIR) spectroscopy

Carbonate minerals display absorption features from near-infrared to mid-infrared regions. Bands in NIR may be due to overtones of carbonate ion and hydroxyl units, in addition to the electronic transitions of the transition metal cations. The electronic bands are observed from 13,000 to 7,000 cm−1 (0.77–1.43 μm) and overtone bands from 7,000 to 4,000 cm−1 (1.43–2.50 μm). The substitution of Zn by copper in copper–zinc hydroxy carbonates provides characteristic bands with variable positions. Transition metal ion complexes, for example, carbonate minerals that include Cu(II)/Cu(II)and Fe(II) provide absorption features in the 13,000–7,000 cm−1 (0.77–1.43 μm) region. For carbonates several strong bands occur from 7,000 to 300 cm−1 (1.43–33.33 μm) due to the vibrations of the carbonate ion and OH units [36, 37].

The near-infrared spectra of synthetic aurichalcite for five compositions with varying Cu:Zn ratio, are shown in Fig. 3a–e. These spectra exhibit three distinct groups of bands. The first group consists of bands due to both electronic and vibronic transitions in the high wavenumber region of 9,000–5,500 cm−1 (1.11–1.82 μm). The second and third groups from 5,500 to 4,500 cm−1 (1.82–2.22 μm) and 4,500 to 4,000 cm−1 (2.22–2.50 μm) are concerned with the overtones and combinations of vibrational modes of carbonate ion. The complexity of these band systems is resolved by the application of band component analysis, in particular, the bands in the higher energy side of the spectrum from 9,000 to 5,500 cm−1 (1.11–1.82 μm), where overlapping OH stretching bands and d–d transition band of Cu2+ occur. The spectra show a number of bands with increase in intensity from 9,000 to 4,000 cm−1 (1.11–2.50 μm). Four bands are well resolved in the first group around 7,600, 7,000, 6,700 and 6,200 cm−1 (1.32, 1.43, 1.49 and 1.61 μm). The first band is the d–d transition of Cu(II) and the latter, three bands are the overtones of the OH-stretching vibrational modes observed in the infrared from 3,400 to 3,200 cm−1 (Fig. 4). The report of the Raman spectrum of aurichalcite by Bouchard and Smith [44] shows a broad band for OH at 3,331 cm−1. The effect of Zn on Cu is shown in the spectra (Fig. 3a, b), where Cu(II) band appeared at 7,586 and 7,580 cm−1 (1,318 and 1,319 nm) with weak in intensity for Cu:Zn ratio of 1:9 and 1:4. As concentration of Cu increases, the Cu2+ band becomes strong (Fig. 3c–e). The substitution of Cu(II) for Zn(II) in zinc–copper hydroxyl carbonates produces characteristic features with variable band positions and intensities because of the ratio of Cu to Zn may not be same in all the samples. For example, minerals of aurichalcite show variable band positions due compositional variations [5]. The carbonate stretching region of synthesized aurichalcite shows five bands around 5,200, 5,000, 4,800, 4,400 and 4,200 cm−1 (1.92, 2.00, 2.08, 2.27 and 2.38 μm). The assignments of bands are made to the overtones and combination modes of carbonate groups and compared with the calculated values from the fundamental modes observed in IR. The assignments of the bands for a selected set of three Cu:Zn ratios (1:3, 2:3 and 1:1) are tabulated and compared with three natural minerals of aurichalcite whose composition is similar. The shift of both Cu(II) and carbonate bands to lower wavenumbers when compared to natural minerals might be the effect of other cation impurities like Ca, Mg in the minerals. The weak band located near 5,400 cm−1 (1.85 μm) may be attributed to traces of adsorbed water in synthetic aurichalcite.

Fig. 4
figure 4

Infrared spectra in the region of 2,700–3,700 cm−1 synthetic aurichalcite with CZ ratios of 1:9, 1:4, 1:3. 2:3, 1:1

Full size image

Mid-IR spectroscopy

The infrared spectra of OH-stretching region of the five synthetic samples of aurichalcite are shown in Fig. 4 while the spectra of carbonate stretching region is shown in two parts (Figs. 5 and 6) from 1,650 to 1,150 and 1,150 to 650 cm−1. There are two main bands in the spectra of OH-stretching region from 3,400 to 3,200 cm−1. The compositional variation of CZ shows variation in band position and intensity in each spectrum and the two bands are attributed to the OH-stretching vibrations. The weak band at 2,860–2,880 cm−1 shows traces of adsorbed water in synthetic samples. A single band 3,338 cm−1 was observed for aurichalcite mineral from Durango. This might be compared with 3,348 cm−1 for Arizona aurichalcite and 3,355 cm−1 for the Chihuahua mineral [16]. Band positions appearing differently in the hydroxyl stretching region of natural and synthetic aurichalcites are related to the variation of the hydrogen bond distances between the OH-units and the oxygens of adjacent carbonate units [45] (Table 1).

Fig. 5
figure 5

Infrared spectra in the 1,150–1,650 cm−1 region of synthetic aurichalcite with CZ ratios of 1:9, 1:4, 1:3. 2:3, 1:1

Full size image
Fig. 6
figure 6

Infrared spectra in the 650–1,150 cm−1 region of synthetic aurichalcite with CZ ratios of 1:9, 1:4, 1:3. 2:3, 1:1

Full size image
Table 1 Assignments of UV–Visible and NIR bands of synthetic and natural aurichalcite minerals
Full size table

A broad band profile shown in carbonate stretching region from 1,650 to 1,150 cm−1 is attributed to the ν3 (CO3)2− antisymmetric stretching modes. For CZ ratio of 1:9, two broad bands are observed at ∼1,500 and 1,400 cm−1 and appear as four component bands at 1,518, 1,483, 1,398 and 1,349 cm−1 (Fig. 5). For increase of Cu concentration, four individual bands are resolved at 1,565, 1,508, 1,408 and 1,357 cm−1 for Cu:Zn ratio = 1/3. The bands become sharp for Cu:Zn ratio = 2/3 and 1/1. The band positions and intensity of the ν3 vibrational modes of carbonate ion depends on the ratio of CZ. Spectra in the second part of the carbonate stretching region 1,150–650 cm−1 are depicted in Fig. 6. The low wavenumber of the carbonate stretching region is a complex profile and is resolved into a number of bands. The ν2 bending modes for carbonates vary between 824 and 833 cm−1. On either side of this sharp band, two other modes at ∼1,050 and 740 cm−1 are ν1 symmetric stretching vibration and ν4 bending modes (CO3)2− ion. The observation of multiple bands in symmetric stretching and bending regions confirms the reduction of symmetry from D 3h to C 2v /C s for (CO3)2− ion in aurichalcite. Raman spectroscopic study of aurichalcite reported by Frost et al. [16] shows the ranges of vibrational modes for carbonate ion are (ν1 = 1,072–1,060 cm−1, ν2 = 850–800 cm−1, ν3 = 1,500–1,300 cm−1 and ν4 = 750–720 cm−1. The analysis of IR data is in harmony with the reported Raman spectra of aurichalcite minerals.

Conclusions

The catalyst activity of copper–zinc oxides is known to depend on the catalyst precursor. For example, such copper–zinc oxides can be used as photocatalysts for the wet photocatalytic oxidation of recalcitrant organics in potentially potable water and aqueous media. These oxide mixtures also have biological activity and may be used for the removal of biological organisms from potentially potable water. The use of aurichalcite in synthesising these catalysts precursors rests with the thermal decomposition of the aurichalcite to prepare mixed oxides which are mixed at the atomic level rather than the particle scale.

Aurichalcite was synthesized by varying Cu:Zn ratio between the range 1:9 and 2:3. Characterization of aurichalcite shows two broad bands in the electronic spectrum at ∼7,600 and 12,900 cm−1 (1,315 and 775 nm) for Cu2+ ion in a distorted octahedral symmetry. The effect of increasing the Cu:Zn ratio results in increased intensity and band position in the electronic spectrum due to increasing molar ratio of Cu2+.

The shifts of Cu(II) and carbonate bands to lower wavenumbers of synthetic minerals, when compared with natural minerals might be the result of other cation impurities like Fe2+, Ca, Mg in the natural minerals which negate these shifts. A weak band near 5,400 cm−1 (1.85 μm) indicates traces of adsorbed water in synthetic aurichalcite. The band positions and intensity of the ν3 vibrational modes of carbonate ion depends on the ratio of CZ. The bands become sharp for Cu:Zn ratio = 2/3 and 1/1. Compositional variations are controlled by Cu:Zn ratio. The analysis of IR data agrees closely with the reported Raman spectra of aurichalcite minerals. The spectra of synthetic aurichalcite may be used as a basis to analyse the spectra of natural hydroxy-carbonates in particular, Cu–Zn carbonates.