1 Introduction

Viscous fingering in a porous medium is a process that occurs within a wide range of flow processes, including CO\(_2\) storage, enhanced oil recovery, and geothermal energy systems. The porous rocks that are relevant for these applications have often undergone fracturing processes, and fractures generally extend throughout the entire reservoir (Berkowitz 2002). These fractures impose a structural constraint on fluid flow and transport through the domain, and this paper targets the interplay between unstable miscible fingering and channeling through fractures that are more permeable than the surrounding rock matrix.

When a less viscous fluid displaces a more viscous fluid, hydrodynamical instabilities are induced that may cause viscous fingering (Homsy 1987). Miscible viscous fingering in a homogeneous medium has been extensively studied using a variety of different methods, including linear stability analysis (Tan and Homsy 1986, 1987), numerical simulations (Nijjer et al. 2018; Zimmerman and Homsy 1991, 1992; Christie 1989), and laboratory experiments (Kopf-Sill and Homsy 1988; Bacri et al. 1992; Petitjeans et al. 1999; Chui et al. 2015). These studies have characterized the evolution of the viscous fingering from the initialization to the later stages. The onset of viscous fingers can be predicted by the wave number with the highest growth rate from linear stability analysis. As the instabilities grow, the flow is governed by different mechanisms such as splitting, merging, or shielding (Homsy 1987). The exact behavior of the displacement front is determined by the parameter regime, and the viscous instabilities depend on a wide range of factors, including gravity (Manickam and Homsy 1995), miscibility (Fu et al. 2017), anisotropic dispersion (Yortsos and Zeybek 1988), mixing (Jha et al. 2011), and reactions (De Wit 2004).

Porous media found in geological formations are in general not homogeneous, but vary on a wide range of length scales, from the pore scale to the reservoir scale. De Wit and Homsy (1997a, b) and Nicolaides et al. (2015) considered different randomly varying permeability fields and found that the preferential flow paths given by the permeability field are competing with the unstable flow paths from the viscous fingering. By applying a method similar to critical path analysis, Tang et al. (2020) found a relation between preferential flow paths and viscous fingering in three dimensional pore networks. More structured permeability fields have also been studied, with the main focus on layered porous media. When the flow is predominantly aligned with the permeable layers, the heterogeneities tend to cause channeling through the domain (Nijjer et al. 2019; Sajjadi and Azaiez 2013; Shahnazari et al. 2018).

When fractures are present in a porous medium, the fractures can act as preferential flow paths due to high-permeability contrasts with the rock matrix. Fractures can give rise to complicated flow and transport patterns through a porous medium, and they present challenges to modeling (Neuman 2005), upscaling (Nissen et al. 2018), and discretization (Flemisch et al. 2018), which are further complicated by fracture geometries (Berge et al. 2019). These challenges have received considerable attention the last two decades; for an overview, we refer the reader to the textbooks by Dietrich et al. (2005) and Sahimi (2011), and the recent review of studies that included field observations, laboratory experiments and predictive modeling by Viswanathan et al. (2022). For a detailed discussion on different mathematical models of fracture flow see the benchmark study by Berre et al. (2021). Fractures can be represented in models in various ways, however, when studying the dynamics between fractures and viscous fingering it warrants an explicit representation of fractures to capture the intricate effects of fracture geometry. A popular class of conceptual models for fractured porous medium that explicitly represents fractures in the domain are the discrete-fracture-matrix (DFM) models. An efficient approach for representing DFM models is to consider fractures as lower-dimensional inclusions in the rock matrix due to their large aspect ratios (Martin et al. 2005; Karimi-Fard et al. 2003). This approach has lead to the development of accompanying discretization strategies; see, e.g., (Flemisch et al. 2018; Nordbotten et al. 2019; Reichenberger et al. 2006).

Fracture networks are known to create preferential flow paths through the interplay of different mechanism, such as capillary and viscous fingering (Yang et al. 2019). Fracture network geometry is also known to affect the channeling (Hyman 2020), and fracture roughness has been found to increase in the dispersion (Dejam et al. 2018). Budek et al. (2015) show experimental and numerical results for viscous fingering in microchannels that behave similar to fracture networks, however, they do not consider flow in the material between the channels that would represent the rock matrix. Zhang et al. (1998) include fluid flow in both fractures and rock matrix in their numerical experiments of radial flow, and investigate how the viscous fingering in immiscible displacement is affected by various fracture network parameters. Fracture geometry is also found to be an important and can enhance or limit transport (Gudala and Govindarajan 2021). Both experimental (Zare Vamerzani et al. 2021) and numerical (Rokhforouz and Akhlaghi Amiri 2018) studies find fracture orientation to be an important factor for the sweep efficiency.

The current paper considers miscible flow in both the rock matrix and fractures and addresses three key questions: (i) what factors related to the fracture flow are most important when studying the effect on the viscous instabilities, (ii) how does the interplay between the viscous instabilities and fractures affect the flow patters in the rock matrix, and (iii) how does different fracture geometries affect the answer to question (i) and (ii). To address these questions, we exploit recent advancements within modeling and simulation tools that focus on flow and transport in fractured porous media. We employ a DFM model, and by state-of-the-art numerical simulations characterize unstable miscible displacement through various fracture network geometries. This modeling approach is necessitated by the high and discontinuous permeability contrasts between fractures and rock matrix as well as the complexity of the random fracture networks investigated in this study. Furthermore, to obtain simulations that extend up to the point of viscous fingering shutdown, we employ adaptive strategies. It is worth noting that the intricacies of implementing these adaptive strategies within the framework of DFM models can be challenging. As a result, we make our implementation open source to facilitate further research and exploration in this field.

The remaining manuscript is laid out as follows. In Sect. 2, we present the governing equations for miscible viscous flow in a fractured porous media. Special attention is given to the mixed-dimensional DFM model. In Sect. 2.3, the equations are represented in dimensionless form, and we discuss the three new dimensionless numbers that appear due to the fractures, and in Sect. 3, we discuss the numerical method. The results given in Sect. 4 are divided into three subsection, one for each fracture geometry considered, and finally, we give concluding remarks.

2 Governing Equations

Fig. 1
figure 1

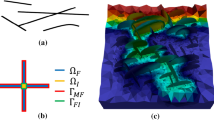
A schematic representation of the problem setup. a A domain of length L and width H. The rock matrix is denoted by \(\Omega _m\) and contains two fractures denoted by \(\Omega _f\). The transversal distance between the fractures is given by W. The porous medium is initially filled by a fluid of viscosity \(\mu _d\) and displaced by a fluid of viscosity \(\mu _u\). b Conceptual figure of a fracture. The rock matrix, \(\Omega _m\), has two boundaries, \(\Gamma ^+\) and \(\Gamma ^-\), associated with the fracture, \(\Omega _f\). Note that \(\Gamma ^+\), \(\Gamma ^-\) and \(\Omega _f\) all coincide geometrically, but are separated in the illustration for a better visualization

Full size image

A schematic illustration of the problem setup is shown in Fig. 1. We consider two incompressible fluids with different viscosities \(\mu _u \le \mu _d\), in a periodic fractured porous media. The two fluids are completely miscible and can therefore be modeled as a single-phase fluid with two components. The fractures, denoted by \(\Omega _f\), are considered as one-dimensional (1D) inclusions, embedded in a surrounding two-dimensional (2D) rock matrix denoted by \(\Omega _m\). Throughout this paper we use subscripts “f” and “m” when it is necessary to distinguish fracture and rock matrix values, respectively. The intersection between the rock matrix domain boundary and the fractures defines one interface on each side of the fracture, which we call the positive and negative interface, \(\partial \Omega _m\cap \Omega _f = \{\Gamma ^+,\Gamma ^-\}\). We denote the unit normal vector on \(\Gamma ^\pm\) that points outward from \(\Omega _m\) by \(\varvec{\nu }^\pm\), as depicted in Fig. 1b.

The viscosity of the mixed fluid is assumed to depend exponentially on the mass ratio, c, of the two components, \(\mu = \mu _de^{-Rc}\), with \(R = \ln \mu _d / \mu _u\), and the fluid follows Darcy’s law both in the rock matrix and in the fractures. The rock matrix has a constant scalar permeability \(k_m\), the porosity \(\phi _m\) is constant, and the diffusivity, \(D_m\), is assumed isotropic and independent of the component concentration. Thus, the governing equations in the rock matrix domain \(\Omega _m\) are given by

$$\begin{aligned} \begin{aligned} \varvec{u}_m = -\frac{k_m}{\mu (c_m)}\nabla p_m, \quad \nabla \cdot \varvec{u}_m = 0 \\ \frac{\partial \phi _mc_m}{\partial t} + \nabla \cdot (c_m\varvec{u}_m - D_m\nabla c_m) = 0 \end{aligned} \qquad \text {in}\ \Omega _m, \end{aligned}$$
(1)

in addition to the boundary conditions. The first line of Eq. (1) consists of Darcy’s law, and mass conservation for an incompressible fluid. The second line describes the advective and diffusive mass transport of the components.

2.1 Fracture Flow

Recall that the governing equations are written for some intermediate scale, large compared to the pore size and fracture aperture, but small compared to the extension of the fractures. This motivates a reduction in dimensionality where the fractures are represented as lower-dimensional. For details on the derivation of the reduced dimensional models, we refer the reader to Martin et al. (2005), Flemisch et al. (2018), Schwenck et al. (2015).

The fluid flow in the fractures is governed by Darcy’s law and mass conservation. Assuming a lower-dimensional representation of the fractures, it is natural to consider flow rate through the fracture per unit length. This flow rate tangential to the fractures is then given by

$$\begin{aligned} \varvec{u}_f = -\frac{a k_f}{\mu (c_f)}\nabla _{||} p_f \quad \text {in}\ \Omega _f, \end{aligned}$$
(2)

where \(\nabla _{||}p_f\) is the pressure gradient in the tangential direction of the fracture, a is the fracture aperture, and \(k_f\) is the fracture permeability. The value \(a k_f\) is the effective fracture permeability, and this structure of the effective permeability is valid for fractures that have an aperture a and are filled by a porous material (e.g., gouge) with permeability \(k_f\). However, it can also be associated with the permeability of open fractures through the cubic law (see, e.g., Jaeger et al. 2007).

Mass conservation in the fractures can be formulated as

$$\begin{aligned} \nabla _{||} \cdot \varvec{u}_f - [\![\lambda ]\!] = 0 \quad \text {in}\ \Omega _f, \end{aligned}$$
(3)

where \(\nabla _{||}\) is the del-operator in tangential direction, and the term \([\![\lambda ]\!] = \lambda ^+ + \lambda ^-\) is the sum of the fluid fluxes flowing from the rock matrix to fracture, defined by a Darcy type relation (see, e.g., Martin et al. 2005):

$$\begin{aligned} \varvec{u}_m^\pm \cdot \varvec{\nu }^\pm = \lambda ^\pm =-\frac{k_f}{\mu (c^\pm )}\frac{(p_f - \text {tr}^\pm (p_m))}{a/2} \quad \text {on}\ \Gamma ^\pm , \end{aligned}$$
(4)

where \(\text {tr}^\pm (\cdot )\) is the trace operator restricted to the positive or negative interface and \(c^\pm\) is the upwind value on the interface:

$$\begin{aligned} c^\pm = {\left\{ \begin{array}{ll} \text {tr}^\pm (c_m) &{}\text {if}\ \lambda > 0\\ c_f &{}\text {if}\ \lambda \le 0. \end{array}\right. } \end{aligned}$$
(5)

The coupling condition in Eq. (4) represents a constitutive law that takes a Darcy-like structure. The law can be derived by assuming Darcy flow in the fracture and continuity of fluid flux and pressure on the interface between the fracture and the rock matrix and integrating over the fracture aperture. This coupling condition has seen widespread use (Berre et al. 2019) and is consistent with formal upscaling of highly permeable fractures (Dugstad and Kumar 2022). For immiscible two-phase flow, the coupling condition above may not be sufficient to capture the capillary effects (Brenner et al. 2018).

The transport equation of the concentration in the fractures, \(c_f\), is derived in a similar manner as the pressure equation. We denote the sum of the advective and diffusive flux from the rock matrix domain by \(\lambda _c\) and write the conservation equation in the fracture as

$$\begin{aligned} \frac{\partial a\phi _f c_f}{\partial t} + \nabla _{||} \cdot (c_f\varvec{u}_f - D_fa\nabla _{||} c_f) - [\![\lambda _c]\!] = 0 \quad \text {in}\ \Omega _f, \end{aligned}$$

where \(\phi _f\) and \(D_f\) are the fracture porosity and diffusivity, respectively. The total flux between the domains is given by

$$\begin{aligned} \lambda _c^\pm = c^\pm \lambda ^\pm -\frac{D_f}{a/2}(c_f - \text {tr}^\pm (c_m)) \quad \text {on}\ \Gamma ^\pm . \end{aligned}$$
(6)

The intersection of two or more fractures is a 0D point. The intersections are treated in a similar way as fractures, i.e., they are embedded 0D inclusions in the 1D fractures. Thus, we assume a complete mixing of the upstream concentrations at the intersections.

2.2 Boundary and Initial Conditions

We consider flow that is periodic in the y-direction:

$$\begin{aligned} \begin{aligned} p(x, 0, t)&= p(x, H, t),&\varvec{u}(x, 0, t)&= \varvec{u}(x, H, t),\\ c(x, 0, t)&= c(x, H, t),&D\nabla c(x, 0, t)&= D\nabla c(x, H, t). \end{aligned} \end{aligned}$$

A constant flux, \(U_m\), is enforced at the upstream boundary of the rock matrix:

$$\begin{aligned} \varvec{u}_m(X_u, y, t)\cdot \varvec{\nu } = -U_m, \quad \ (X_u, y)\in \partial \Omega _m, \end{aligned}$$
(7)

where \(X_u\) is the x-position of the upstream boundary and \(\varvec{\nu }\) is the outer normal vector. The upstream flux on the fracture boundary,

$$\begin{aligned} \varvec{u}_f(0, y, t)\cdot \varvec{\nu } = -U_f = -\frac{k_fa}{k_m}U_m, \quad (X_u, y)\in \partial \Omega _f, \end{aligned}$$
(8)

is chosen such that the initial pressure drops for the test case with parallel fractures only varies in the x-direction. A fixed pressure is given at the downstream boundary that is located at x-coordinate \(X_d\):

$$\begin{aligned} p_\alpha (X_d, y, t) = 0, \quad [X_d, y]\in \partial \Omega _\alpha ,\quad \alpha \in \{m,f\}. \end{aligned}$$

The initial condition is given by an almost sharp interface and a small perturbation centered at \(x=0\),

$$\begin{aligned} c_\alpha (x, y, t=0) = \frac{1}{2}+\frac{1}{2}\text {erf}\left( -\frac{x}{\sqrt{t_0}}\right) +U(x,y)\exp \left( -\frac{x^2}{t_0}\right) ,\quad \alpha \in \{m, f\} \end{aligned}$$

where \(\text {erf}(\cdot )\) is the error function, \(U(x,y)\in [0,10^{-4}]\) is a uniformly random perturbation added to initialize the viscous instabilities, and \(t_0=10^{-5}\) is chosen to aid the numerical scheme at early times. We have chosen the initial random perturbation to compare our implementation to previous studies of homogeneous porous media, e.g., Nijjer et al. (2018). The fractures introduced in the current work represent heterogeneities that will initiate the viscous fingering; however, we keep the random initial perturbation in the test cases presented in this paper to obtain the results of a homogeneous porous media when the permeability ratio approaches 1.

2.3 Dimensionless Equations

The characteristic length scale for our problem is given by the width of the domain H as shown in Fig. 1. The characteristic velocity is chosen as the matrix injection flux \(U_m\), while the characteristic viscosity is \(\mu _d\). By following classical results from the study of viscous fingering (see, e.g., Tan and Homsy (1986)), the Péclet number is defined by \({\textit{Pe}}= \frac{U_mH}{D}\), the characteristic time by \(T = \frac{\phi _m H}{U_m}\), and the characteristic pressure by \(P = \frac{\mu _d U_mH}{k_m}\). The dimensionless variables are denoted by a hat \(\hat{\cdot }\), that by a rescaling of Eq. (1) gives the dimensionless equations defined in the rock matrix:

$$\begin{aligned} \begin{aligned} \hat{{\varvec{u}}}_m = -\frac{1}{\hat{\mu }(c_m)}\nabla \hat{p}_m, \quad \nabla \cdot \hat{{\varvec{u}}}_m = 0\\ \frac{\partial c_m}{\partial \hat{t}} + \nabla \cdot c_m\hat{{\varvec{u}}}_m - \frac{1}{{\textit{Pe}}}\Delta c_m = 0 \end{aligned} \qquad \text {in}\ \hat{\Omega }_m. \end{aligned}$$
(9)

Similarly, in the fractured domain, the flux is rescaled by the characteristic fracture flux \(HU_m\). We will assume that the fractures are filled with a material that has the same porosity and diffusivity as the rock matrix, i.e., \(\phi _f = \phi _m\), \(D_f = D_m\). This assumption on the diffusion in the fractures is not valid in general, in fact, both the porosity and the diffusivity are expected to be different between the fractures and the rock matrix in a real reservoir. The porosity in a high-permeable fracture will typically be larger than in the surrounding rock matrix allowing for a larger fluid volume in the fractures than what we assume. Thus, our assumption of equal porosity is a reasonable lower bound on the pore-volume available in highly permeable fractures. We are also interested in the case of highly permeable fractures where advection dominates over diffusion in the fractures and the fracture diffusion is expected to play a minor role. This gives the dimensionless equations:

$$\begin{aligned} \begin{aligned} \hat{{\varvec{u}}}_f = -\frac{{\mathcal{K}\mathcal{A}}}{{\hat{\mu }}(c_f)}\nabla _{||} \hat{p}_f, \quad {\nabla }_{||} \cdot \hat{{\varvec{u}}}_f -[\![\hat{\lambda }]\!]= 0 \\ \frac{{\mathcal {A}}\partial c_f}{\partial \hat{t}} + \nabla _{||} \cdot c_f{\hat{{\varvec{u}}}}_f - \frac{{\mathcal {A}}}{{\textit{Pe}}}\Delta _{||} c_f - [\![\hat{\lambda }_c]\!] = 0 \end{aligned} \qquad&\text {in}\ \hat{\Omega }_f, \end{aligned}$$
(10)

where we have defined the dimensionless numbers

$$\begin{aligned} \mathcal K = \frac{k_f}{k_m}, \quad \mathcal A = \frac{a}{H}. \end{aligned}$$
(11)

The permeability ratio, \(\mathcal K\), defines the ratio of the permeability in the fractures and rock matrix, while the second dimensionless number, \(\mathcal A\), is the dimensionless aperture which represents the ratio of the width of the fractures and the characteristic width of the domain that is related to the Péclet number.

The dimensionless coupling equations are obtained by rescaling Eqs. (4) and (6):

$$\begin{aligned} \begin{aligned} \hat{\lambda }^\pm = -\frac{\mathcal {K}}{\mathcal {A}\hat{\mu }(c^\pm )} \frac{{\hat{p}}_f - \text {tr}(\hat{p}_m)}{1 / 2},\quad \hat{\lambda }_c^{\pm } = c^\pm \hat{\lambda }^\pm - \frac{1}{{\mathcal {A}}{\textit{Pe}}} \frac{c_f - \text {tr}(c_m)}{1 / 2} \end{aligned} \quad \text {on}\ \hat{\Gamma }^\pm . \end{aligned}$$
(12)

To summarize, the dimensionless variables are

$$\begin{aligned} \begin{aligned} \hat{{\varvec{x}}}&= \frac{1}{H}\varvec{x}, \quad&\hat{t}&= \frac{U_m}{\phi _m H} t, \quad&\hat{\mu }&= \frac{1}{\mu _d}\mu , \quad&\hat{\lambda }&= \frac{1}{U_m}\lambda \\ \hat{{\varvec{u}}}_m&= \frac{1}{U_m}\varvec{u}_m, \quad&\hat{{\varvec{u}}}_f&= \frac{1}{HU_m}\varvec{u}_f, \quad&\hat{p}_m&= \frac{k_m}{{\mu _{d}}U_{m}H}p_m, \quad&\hat{p}_f&= \frac{k_m}{{\mu _{d}}U_{m}H}p_f. \end{aligned} \end{aligned}$$

From the dimensionless Eqs. (9)–(12), we obtain that the dimensionless numbers governing the behavior of this system:

$$\begin{aligned} {\textit{Pe}}= \frac{U_{m}H}{D},\quad R = \ln \left( \frac{\mu _d}{\mu _u}\right) ,\quad \mathcal {K} = \frac{k_{f}}{k_{m}},\quad \mathcal {A} = \frac{a}{H},\quad N = \frac{H}{W}. \end{aligned}$$
(13)

In addition, we have here introduced the dimensionless number, N, that represents the fracture density in a vertical slice of the domain. While the fracture density, N, to some extent describe the fracture network geometry, it does not describe it fully. The details of the fracture geometry is given in Sect. 4.

2.4 Quantitative Measures

As a quantitative measure of the global solution, we use the mixing length \(h(\hat{t})\) and the number of fingers in the domain \(n(\hat{t})\). The mixing length is defined as the length where the two fluids have spread:

$$\begin{aligned} h(\hat{t}) = \max (\hat{x}|_{c(\hat{x}, \hat{y}, \hat{t})>0.01 }) - \min (\hat{x}|_{c(\hat{x}, \hat{y}, \hat{t})<0.99}). \end{aligned}$$
(14)

The second quantitative measure, the number of fingers, is calculated as

$$\begin{aligned} n(\hat{t}) = \frac{1}{h(\hat{t})}\int _{\min (\hat{x}_{\hat{x}, \hat{y}, \hat{t})<0.99})}^{\max (\hat{x}|_{c(\hat{x}, \hat{y}, \hat{t})>0.01 })} \eta (x){\text {d}}\!x, \end{aligned}$$

where \(\eta (x)\) is the number of local maxima in a vertical slice.

3 Numerical Methods

The numerical schemes used for studying fingering phenomena in porous media are typically higher order schemes (Riaz et al. 2006; Nijjer et al. 2019; De Wit and Homsy 1997a; Sajjadi and Azaiez 2013). While these methods are superior on regular domains, they are challenging to employ in domains with complex fracture geometries, which is one of the main concerns in this paper. Further, the higher order schemes usually require a smooth permeability field, while the contrast between the fractures and rock matrix permeability represents a discontinuity. The final case presented in this paper necessitates the use of numerical schemes that can handle complex unstructured fracture network geometries; hence, in this paper, we use a finite-volume scheme that, in addition to handling discontinuities in the permeability field, is easy to implement for the lower-dimensional fractures. The reduction in the dimension of the fractures allows us to simulate on layers that are orders of magnitude thinner than the domain width without needing an extensive grid refinement around the fractures, which makes it feasible to run long time simulations. In this section, the discretization is presented, as well as details about the mesh adaptivity and the implementation.

Each subdomain, \(\hat{\Omega }_m\) and \(\hat{\Omega }_f\), is partitioned into a set of non-overlapping cells that defines one mesh of the 2D domain and one mesh of the 1D domain. The 2D mesh is a logical Cartesian mesh, and we use a 1D mesh with cells that conform to the faces of the 2D mesh.

3.1 Spatial and Temporal Discretization

The system of Eqs. (9)–(12) is approximated using a finite-volume discretization. The flux from the rock matrix to the fracture domain, defined in Eq. (12), is included as a Neumann boundary in the rock matrix and a source term in the fractures. For details on the mixed-dimensional coupling, we refer the interested reader to (Keilegavlen et al. 2021). As the discretizations of the rock matrix domain and the fracture domain are equivalent, we drop the domain subscript m and f when we describe the discretization in the following subsections.

3.1.1 Pressure Equation

To discretize the pressure equation, Darcy’s law is substituted into the mass conservation equation and integrated over a cell L. By applying the divergence theorem we obtain:

$$\begin{aligned} \int _{\partial L} \frac{k}{\hat{\mu }(c)}\nabla \hat{p} \cdot \varvec{\nu } {\text {d}}\,\!S - \int _L Q{\text {d}}\,\!V = 0, \end{aligned}$$
(15)

where the term Q is a source term, and \(\varvec{\nu }\) is the outwards pointing normal vector of \(\partial L\). Note also that the permeability in the rock matrix for the dimensionless equation is 1 while it is \({\mathcal{K}\mathcal{A}}\) in the fractures. Further, the source term is zero in the rock matrix, and \(Q=[\![\hat{\lambda }]\!]\) in the fractures. The integral of the source term over the cell is approximated by multiplying the cell-centered value of the source by the cell volume. To discretize the flux term, let \(\sigma\) be the face between cell L and cell R (referred to as left and right cell). The fluid flux across the face is approximated as

$$\begin{aligned} \int _\sigma \frac{k}{\hat{\mu }(c)}\nabla \hat{p} \cdot \varvec{\nu } {\text {d}}\,\!S\approx F_{LR} =\frac{T_{\sigma }}{\hat{\mu }(c_{\sigma })} (\hat{p}_L-\hat{p}_R), \end{aligned}$$
(16)

where \(T_\sigma\) is the transmissibility and \(\hat{p}_i\) is the cell center pressure of cell \(i\in \{L, R\}\). All numerical simulations in this paper are run on a Cartesian grid, and we use the Two-Point Flux Approximation (TPFA) to calculate the transmissibility. In TPFA, the transmissibility is calculated as the harmonic average of the half-transmissibilities:

$$\begin{aligned} T_{\sigma } = \frac{T_{\sigma L}T_{\sigma R}}{T_{\sigma L}+T_{\sigma R}},\quad T_{\sigma i} = \frac{|\sigma |k\varvec{d}_{\sigma i} \cdot \varvec{\nu }_{\sigma i}}{\varvec{d}_{\sigma i}\cdot \varvec{d}_{\sigma i}}, \quad i\in \{L, R\}, \end{aligned}$$

where \(|\sigma |\) is the area of the face, \(\varvec{d}_{\sigma i}\) is the vector pointing from the cell center of cell i to the face center of face \(\sigma\), and \(\varvec{\nu }_{\sigma i}\) is the normal vector of face \(\sigma\) pointing outwards of cell i. The concentration on the face, \(c_{\sigma }\), is taken as the upwind value of the concentration:

$$\begin{aligned} c_{\sigma } = \text {up}(c, \hat{p}_L, \hat{p}_R) = {\left\{ \begin{array}{ll} c_L, &{}\text {if}\ \hat{p}_L-\hat{p}_R > 0\\ c_R, &{}\text {if}\ \hat{p}_L-\hat{p}_R \le 0, \end{array}\right. } \end{aligned}$$
(17)

for the cell center concentrations \(c_L\) and \(c_R\).

3.1.2 Transport Equation

A similar approach is used for the transport equation where we first integrate over a cell L:

$$\begin{aligned} \int _L \frac{\partial \phi c}{\partial \hat{t}}{\text {d}}\,\!V - \int _{\partial L} (c\hat{{\varvec{u}}} - D\nabla c)\cdot \varvec{\nu } {\text {d}}\,\!S - \int _L Q_c{\text {d}}\,\!V = 0, \end{aligned}$$
(18)

where \(Q_c = 0\), \(\phi =1\) in the rock matrix and \(Q_c = [\![\hat{\lambda }_c]\!]\), \(\phi =\mathcal A\) in the fractures (for the dimensionless equation). The diffusive flux \(\int _{\partial L}D\nabla c\cdot \varvec{\nu } {\text {d}}\,\!S\) is approximated by the TPFA scheme, equivalent to Eq. (16) (\(D=1/{\textit{Pe}}\) in \(\hat{\Omega }_m\) and \(D=\mathcal A/{\textit{Pe}}\) in \(\hat{\Omega }_f\)). The advective flux across the face \(\sigma\) is approximated by

$$\begin{aligned} \int _{\sigma } c\hat{{\varvec{u}}}\cdot \varvec{\nu }{\text {d}}\,\!S \approx c_{\sigma } F_{LR}, \end{aligned}$$
(19)

where \(F_{LR}\) is the flux defined by Eq. (16) and \(c_{\sigma }\) is the upwind value as defined by Eq. (17). For the time derivative of Eq. (18) the second-order Crack–Nicholson scheme is used.

3.1.3 Coupling Equations

To discretize the coupling Eq. (12) a discrete trace operator in the rock matrix must be defined. The TPFA scheme allows for the reconstruction of the pressure/concentration on the faces of the cells from the half-transmissibilities, and we employ this reconstruction as the trace operator. To evaluate the viscosity on the interface, we use the upstream value of the concentration in the rock matrix and in the fracture.

3.1.4 Linearization and Time Stepping

The coupling between the transport equation, the pressure equation and the concentration dependent viscosity results in a discrete nonlinear system of equations. The nonlinear system is linearized by Newton’s method, and the Jacobian is obtained by forward-mode Automatic Differentiation (Neidinger 2010).

The initial time-step size is set to \(\Delta \hat{t}_0 = 10^{-5}\), and the time-step size is incremented by a constant factor after each time step until it reaches the maximum time-step size, \(\Delta \hat{t}_{\max } = 10^{-2}\). The increment factor is 1.2 if the Newton scheme converges in less than 3 iterations, 1.1 if the Newton scheme converges in less than 7 iterations, and there is no time-step size increment if the Newton iteration takes more than or equal 7 iterations. If the Newton iteration fails, the time step is halved and the iteration restarted.

3.2 Mesh Adaptivity

The initial condition contains a sharp concentration front, and linear stability analysis shows that many small fingers (the number related to the most stable wave number) will appear at the onset of the viscous fingering (Tan and Homsy 1986). Thus, a very fine mesh is needed to resolve the initiation of these fingers accurately. In the simulations, in this paper, we use an initial mesh with a cell length \(\sim 0.002\). At the shutdown of the viscous fingering, the finger length is typically of order 100, and even higher for the cases with high-permeability contrast. If the initial mesh size is kept for the whole simulations, this would result on the order of \(10^7\) cells. Thus, in order to simulate for a long time scale, \(\hat{t} > 10\), adaptivity of the mesh is needed to achieve acceptable run-times. We employ three adaptive strategies to make the runtimes feasible. The first adaptive strategy is to extend the simulation domain when the viscous fingers grow to close to the domain boundary. In the simulations, the domain is extended if the viscous fingers are closer to the domain boundary than 20% of the current domain length. The second adaptive strategy employed is to coarsen the mesh size when the fine mesh is no longer needed; as the concentration front diffuses, the displacement front smoothens out which allows for a coarser mesh. In the numerical simulations, the mesh is coarsened when the extension of the grid causes the number of cells to exceed 600 000. When the domain is coarsened, we also double the maximum allowed time-step size in the temporal discretization. The final adaptive strategy is to shift the domain downstream if the distance from the upstream boundary to the concentration front (\(\min (\hat{x}|_{c(\hat{x},\hat{y},\hat{t})<0.99))}\)) is longer than 30% of the domain length. We have compared the solutions of several simulations using the adaptive strategies to the solutions on a fine mesh and not found any notable discrepancies between the solutions that have a significant impact on either the qualitative structure of the fingers, nor the measurables defined in Sect. 2.4

3.3 Implementation and Software

The implementation is done in the open-source software PorePy (Keilegavlen et al. 2021), and we have validated our numerical method by comparing the initial fingering in a domain without fractures to both linear stability analysis and to the evolution of the viscous and late time regimes described in the numerical simulations by Nijjer et al. (2018). The mixed-dimensional coupling between the fractures and rock matrix has been applied in PorePy for both flow and transport in several papers (Nordbotten et al. 2019; Stefansson et al. 2018; Fumagalli and Keilegavlen 2019). In recent work, we have also validated the modeling approach and computer implementation against laboratory experiments and found excellent match between the physical experiment and numerical simulations (Both et al. 2023). To solve the resulting linear system, the direct solver UMFPACK is used (Davis 2004), and Paraview (Ayachit 2015) has been applied for postprocessing and visualization of the results. To facilitate reproducibility, the run-scripts used in the simulations reported below are available at GitHubFootnote 1 and archived on Zenondo (Berge 2023). In addition, the results of the simulations are also archived on Zenondo (Berge et al. 2023)

4 Numerical Simulations

In the following subsections, we study the three different characteristic fracture network geometries illustrated in Fig. 2. The fracture networks are chosen to illustrate a wide range of different flow dynamics and interactions between the fracture and rock matrix. The following test case with only fractures parallel to the flow directions is equivalent to a layered porous media where the width of the high-permeability layer (the fracture) is several orders of magnitude smaller than the width of the low-permeability layer (the matrix). Compared to the parallel fractures, the brick network and random network have a complex geometry with intersecting fractures, fractures of finite size and fractures not aligned with the flow direction.

Fig. 2
figure 2

Schematics of the fracture networks studied in the numerical simulations. The characteristic width W is indicated by the double arrow. The principle direction of flow is from left to right

Full size image

4.1 Parallel Fractures

To understand the effect fractures have on viscous fingering, we first investigate the geometrically simple case of fractures parallel to the flow direction. The key question we study is how the dimensionless numbers \(\mathcal K\), \(\mathcal A\) and N in Eq. (13), which are introduced by the addition of fractures, affect the viscous fingering compared to a homogeneous porous medium.

All simulations in this subsection are run in a moving frame of reference by a change of variables:

$$\begin{aligned} \tilde{x} = \hat{x} - \hat{t},\ \tilde{\varvec{u}} = \hat{{\varvec{u}}} - \varvec{i}, \end{aligned}$$

where \(\varvec{i}\) is the unit basis vector in the \(\hat{x}\)-direction. The initial dimensionless size of the computational domain is set to \(L / H = 2\).

4.1.1 Influence of Permeability Ratio and Dimensionless Aperture

We investigate how the viscous fingering is affected by the permeability ratio and dimensionless aperture by fixing the Péclet number to 1000 and the log viscosity ratio to \(R=2\). The domain contains a single fracture located in the middle of the domain. The permeability ratio is varied between \(\mathcal K=1.1\) and \(\mathcal K=10^3\), and the dimensionless aperture is varied between \(\mathcal A = 10^{-2}\) and \(\mathcal A = 10^{-4}\).

Initially, the concentration is transversely homogeneous with a sharp concentration front at \(x=0\). The diffusion across the concentration front dominates and the transport equation in the fracture and the rock matrix decouples and reduces to a pure diffusive transport. Thus, at early times, the mixing length that scales as \(h\sim \sqrt{\hat{t}/{\textit{Pe}}}\). The difference in permeability between the fracture and the rock matrix causes an advective growth of the mixing length, \(h=O\left( (\mathcal K-1)\hat{t}\right)\), that outgrows the diffusive initial regime. In all simulations, an initial finger develops around the fracture that outgrows any fingers caused solely by the viscous instabilities. Figure 3 shows the continued evolution of the concentration front that is typical for the cases where the permeability ratio is less than 10. In these cases, we observe that the viscous fingers exhibit growth patterns similar to those observed in homogeneous domains within the rock matrix, away from the fractures. Following the initiation of viscous fingers in the rock matrix, the viscous fingers in the rock matrix compete with the finger aligned with the fracture before undergoing coarsening and merging processes, eventually leaving only a single dominant finger in the domain.

Fig. 3
figure 3

Evolution of the concentration field for the parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A, N\} = \{1000, 2, 10, 10^{-3}, 1\}\). The white line indicates the position of the fracture. Note the increasing aspect ratio in the figures

Full size image

For all parameter ranges investigated in this study, a common observation is the initial growth of a finger aligned with the fracture and the final regime with a single propagating finger. However, there are variations in the behavior of the simulations during intermediate times. Particularly, for cases with the largest permeability ratio, we observe that the viscous fingers in the rock matrix do not exhibit significant growth. Instead, the flow transitions directly from a diffusive regime to the dominance of a single propagating finger. This is illustrated in Fig. 4 that shows snapshots of the concentration profiles of all simulations at time \(\hat{t}=3\). We have divided the flow into three qualitative regimes, indicated by the different background shades of gray, which we will elaborate on in the following paragraphs.

For small permeability ratio and small dimensionless aperture, the viscous fingering dominates over the fracture flow, indicated by the lightest shade (bottom left). In these simulations, the viscous fingering in the rock matrix has displaced the finger aligned with the fracture. For the largest permeability ratios and highest dimensionless apertures, the finger aligned with the fracture suppresses the growth of the viscous fingers, and we observe no viscous fingering in the rock matrix except the one aligned with the fracture, indicated by the darkest shade (upper right). In the intermediate parameter regime, the dominant finger aligned with the fracture is competing with the viscous fingering in the rock matrix (indicated by the intermediate shade). The fingers that develops in the rock matrix transition the flow to a regime where the viscous fingers dominates over the fracture.

In general, the qualitative classification into these three regimes is not stable through the whole simulation, but may transition from one regime to another. For the parameters, we have studied that we have only observed the fluid flow evolve from a more fracture dominated flow to a more viscous fingering dominated flow as a function of time.

Fig. 4
figure 4

Domain with a horizontal fracture shown as a white line. The figure shows the concentration for \(\hat{t}=3\), for different permeability ratios and dimensionless apertures. The other parameters are fixed to \((R, {\textit{Pe}}, N) = (2, 1000, 1)\). The different background shades of gray indicate different qualitative regimes. Note that the simulation domains are much larger than shown in the figures

Full size image

The effect of the fracture can also be seen in the quantitative measures plotted in Fig. 5, which plot the mixing length for varying permeability ratios and dimensionless aperture. Even for the smallest permeability ratio of the simulations, \(\mathcal K=1.1\), the number of fingers is reduced by almost an order of magnitude compared to the case without fractures at \(\hat{t}\approx 1\). As the viscous fingering develops, we can also observe the transition from a fracture-dominated flow to a viscous dominated flow in the quantitative measures as an increase in the number of fingers.

Fig. 5
figure 5

Evolution of the quantitative measures for a domain with a single fracture parallel to the flow direction. The Péclet number, log viscosity ratio and fracture density are \(\{Pe, R, N\} = \{1000, 2, 1\}\). The dotted black line represents measures from a simulation without any fractures. The left column shows the mixing length and number of fingers for different permeability ratios \(\mathcal K\) and fixed dimensionless aperture \(\mathcal A=10^{-3}\). The right column shows the mixing length and number of fingers for fixed permeability ratio \(\mathcal K=10\) and different dimensionless aperture \(\mathcal A\)

Full size image

As inferred from Figs. 4 and 5, the quantity \({\mathcal{K}\mathcal{A}}\) both scales the fluid flux in the fracture and also to first order describes the qualitative structure of the solution. The dimensionless number \({\mathcal{K}\mathcal{A}}\) represents the ratio of the volumetric flux in the fractures to the volumetric flux in the rock matrix, and we expect it to be important when describing the behavior of the flow. Figure 6 plots the mixing length and number of fingers for the volumetric flux ratio varying from \(\mathcal K\mathcal A=10^{-3}\) to \(\mathcal K\mathcal A = 1\). For each value of the volumetric flux ratio, the permeability and aperture are varied three orders of magnitude. Due to the initial conditions, the fluid flux between the rock matrix and the fracture is initially zero and the equations in the rock matrix is decoupled from the equations in the fractures. Thus, the dimensionless advective velocity in the fracture is \(\mathcal K\). In Fig. 6, cases with equal permeability ratio have the same line type, and in the figure, it can be seen that the mixing length for small \(\hat{t}\) is independent of \(\mathcal A\) and only vary with the permeability ratio \(\mathcal K\). When the concentration front in the fracture outgrows that in the rock matrix, two fluxes occur. First, there is a diffusive flux from the forward finger in the fracture to the rock matrix due to the concentration gradient. Second, an advective flux arises from pressure differences-higher pressure in the fracture ahead of the concentration front and lower pressure just behind it, driven by the viscosity ratio. This pressure difference increases as the finger lengthens, reducing the growth rate of the mixing length, as depicted in Fig. 6. The advective flux from a leading finger is also observed in studies by Budek et al. (2015), which investigated viscous fingering in connected microchannels. The mixing length’s growth rate slows until it reaches equilibrium between the fracture’s volumetric flux and exchange with the rock matrix. Figure 6 illustrates this as the convergence of mixing length in simulations with the same volumetric flux ratio, \({\mathcal{K}\mathcal{A}}\) (lines of the same color).

Fig. 6
figure 6

Evolution of the concentration field for a domain with a single fracture parallel to the flow direction. The Péclet number, log viscosity ratio and fracture density are \(\{Pe, R, N\} = \{1000, 2, 1\}\). The dotted black line is a simulation without any fractures. The colors show the volumetric flux ratio \(\mathcal K\mathcal A\), and the line style the value of \(\mathcal K\). Left figure shows the mixing length and right figure shows the number of fingers. The small irregularities for the case \(\mathcal K=10^3\), \({\mathcal{K}\mathcal{A}}=1\) are due to the coarsening of the mesh; however, we have no reason to believe that this affects the general conclusions

Full size image

From the mixing length and the number of fingers plotted in Figs. 5 and 6, we conclude that increasing the permeability ratio, \(\mathcal K\), or the dimensionless aperture, \(\mathcal A\), increases the mixing length and decreases the number of fingers by up to several orders of magnitude. The effect of the fractures on the quantitative measures is largest before the advective regime of the viscous fingering in the homogeneous case, \(\hat{t} \sim 1\), for the current parameters. At early times, the mixing length is only dependent on the permeability ratio, but when the fracture interacts with the rock matrix, the behavior of the flow changes and the governing parameter of the fracture is the volumetric flux ratio \({\mathcal{K}\mathcal{A}}\). Thus, at intermediate to late stages, the permeability contrast can vary three orders of magnitude but will not significantly affect the qualitative or quantitative measures if the volumetric flux ratio is fixed.

4.1.2 Influence of the Fracture Density

In the previous subsection, the width between the fractures was equal to the characteristic width H. In this section, we increase the fracture density in the domain, which leaves less space for viscous fingers within the rock matrix. In all simulations, in this subsection, the parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{1000, 2, 10, 10^{-3}\}\) are fixed, and the fracture density is varied from 1 to 5. The fractures are evenly spaced in the domain.

Fig. 7
figure 7

Evolution of the concentration field for the case with fractures parallel to the principle flow directions. The parameters used in the simulations are \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{1000, 2, 10, 10^{-3}\}\). a–d Color maps of the concentration field for \(N = 3\) at different times. Note the increasing aspect ratio in the figures. e The mixing length and number of fingers for different fracture density. The dotted lines show the evolution for the homogeneous case without fractures

Full size image

Figure 7 shows the time evolution of the concentration field for the case \(N=3\). All other values of N show the same qualitative behavior where the flow goes through three distinct regimes. In the first regime, there are stable propagating fingers aligned with the fractures. In the second regime, there is viscous fingering across the whole domain, and in the final regime, there is a single propagating finger. In the following, we discuss each regime in detail.

Initially, a finger forms around each fracture, which quickly outgrows the diffusive front. Mass exchange from fracture to matrix then slows finger growth, leading to close-to-square-root mixing length growth, as seen in Fig. 7. For the cases with \(N=1\) and \(N=2\), fractures are spaced sufficiently apart for viscous fingers to develop in the rock matrix between fractures, slightly increasing the number of fingers around \(\hat{t}\sim 1\). When the viscous fingering starts in the rock matrix the fingers aligned with the fractures are disturbed and the viscous fingering behaves as for an homogeneous medium. For the cases with \(N \ge 3\), no viscous fingers are observed in the rock matrix before the second regime characterized by the viscous fingering across the fracture geometry. This transition occurs when the previous stable displacement with one finger coinciding with each fracture becomes unstable, and the viscous fingers interact across the fractures. This is evident in Fig. 7 as a sudden drop in the number of fingers and an increase in mixing length growth rate. The continued evolution of the new viscous fingering behaves similar to the viscous fingering in the homogeneous case, with tip splitting, shielding, and finger coarsening until only one finger is left in the domain. This behavior resembles observations in layered porous media (Nijjer et al. 2019) characterized by viscous fingering across highly permeable layers.

4.1.3 Influence of the Péclet Number and the Log Viscosity Ratio

To study how the fractured domain is affected by the Péclet number and log viscosity ratio, we consider a domain with a single horizontal fracture that is centered in the domain. The permeability ratio and dimensionless aperture are fixed to \(\mathcal K = 10\) and \(\mathcal A = 10^{-3}\). Two sets of simulations are run. In the first set, the Péclet number is varied, \({\textit{Pe}}= 100, 500, 1000, 2000, 4000\), and the log viscosity ratio is fixed to \(R = 2\). In the second set, the log viscosity ratio is varied, \(R = 1, 2, 3, 4\), and the Péclet number is fixed to 1000.

Fig. 8
figure 8

The mixing length (top row) and the number of fingers (bottom row) for the test case with fractures parallel to the principal flow direction. The parameters \(\{{\mathcal {K}}, {\mathcal {A}}, N\} = \{10, 10^{-3}, 1\}\) are fixed. The transparent lines show the values from simulations without fractures. Two sets of simulations are run. In the first set (left column), the log viscosity ratio is varied, while \({\textit{Pe}}= 1000\) is fixed. In the second set (middle column), the Péclet number is varied, while \(R=2\) is fixed. The right column shows all simulations with rescaled length and time

Full size image

Figure 8 shows the mixing length and number of fingers for all the cases. As we have seen in Sect. 4.1.1, a single finger forms along the fracture and this finger causes the early time (\(\hat t\sim 10^{-3}\)) difference in mixing length. At this time, both the mixing length and number of fingers are independent of the Péclet number and log viscosity ratio. For times \(10^{-2}\lesssim \hat{t}\lesssim 10^1\) increasing the log viscosity ratio or the Péclet number increases the mixing length. The onset of viscous fingers in the rock matrix between the fractures can be seen as the increase in the number of fingers. We observe more viscous fingers at an earlier time in the matrix for higher Péclet numbers.

After the transition to a advective regime of the viscous fingering in the homogeneous case at \(\hat{t}\sim 1\), the mixing length in the homogeneous domain grows linearly and faster than the fractured case until they coincide. Eventually, in the final stages of all simulations, both fractured and homogeneous cases exhibit a single propagating finger, behaving qualitatively and quantitatively as in a homogeneous domain. Nijjer et al. (2018) shows that for late times, \(\hat{t}\sim {\textit{Pe}}\), the mixing length for a homogeneous domain scales as \(h\sim R{\textit{Pe}}\). In the right column of Fig. 8, we apply this scaling to the fracture case and show that after the shutdown of the viscous fingering, the mixing length and the number of fingers collapses onto this late time scaling. This is equivalent to the observation in Sects. 4.1.1 and 4.1.2 where simulations with dimensionless volumetric flux ratios \(\mathcal K\mathcal A\le 10^{-2}\) approached the behavior of the homogeneous case for times \(\hat{t}\sim {\textit{Pe}}\).

From the simulations in this subsection with a permeability ratio, \(\mathcal K = 10^1\), and dimensionless aperture, \(\mathcal A = 10^{-3}\), we can conclude that the influence of the fractures is most important up to the onset of the viscous fingers in the rock matrix, and the effect of the fracture is negligible at late times, \(\hat{t}\sim {\textit{Pe}}\).

4.2 Brick Shaped Fracture Networks

In the previous subsection, we learned important lessons about the importance of the volumetric flux ratio when describing the effects fractures have on viscous fingering. In this section, we consider variants of the brick shaped fracture network depicted in Fig. 2b to investigate further how the permeability ratio and dimensionless aperture affect the flow paths for a more complex geometry. The length of the bricks in \(\hat{x}\)-direction is twice the width of the bricks in \(\hat{y}\)-direction.

4.2.1 Influence of the Permeability Ratio and Dimensionless Aperture

Fig. 9
figure 9

Domain with a brick pattern, the fractures are shown as white lines. The figure shows the concentration for \(\hat{t}=3\), for different permeability ratios and dimensionless apertures. The other parameters are fixed to \(\{R, {\textit{Pe}}, N\} = \{2, 500, 1\}\). The different background shades of gray indicate different qualitative regimes. Note that the simulation domains are much larger than shown in the figures

Full size image
Fig. 10
figure 10

Evolution of the concentration field for the brick shaped fracture network. The other parameters are fixed to \(\{Pe, R, N\} = \{500, 2, 1\}\) for varying \(\mathcal K\) and \({\mathcal{K}\mathcal{A}}\). The dotted black line is a simulation without any fractures. The colors show the volumetric flux ratio \(\mathcal K\mathcal A\), and the line style the value of \(\mathcal K\). The left figure shows the mixing length, and the right figure shows the number of fingers

Full size image

In the simulations in this section, the Péclet number is fixed to \({\textit{Pe}}= 500\), the log viscosity ratio to \(R = 2\), and \(N=1\). Note that N is the fracture density in a vertical slice of the domain, thus, the brick network has two sets of discontinuous horizontal lines as seen in Fig. 9.

The general trend in the simulations is equivalent for all simulations. A finger develops around the horizontal fracture, and when the horizontal fracture ends, the finger continues through the rock matrix until it reaches the next horizontal fracture. The exception is for the highest volumetric flux ratios \(\mathcal K\mathcal A \ge 10^0\) where the fluid continues through the vertical fractures when the horizontal fractures end. This can be observed in Fig. 9, displaying snapshots of the concentration profile at \(\hat{t} = 3\) for all simulations. The first observation we make is that there are almost no viscous fingers in any of the parameter combinations. Only for the smallest volumetric flux ratios do a few fingers emerge in the rock matrix between the fractures (lightest shade in the lower-left corner of the figure). The vertical fractures are perpendicular to the principle flow direction which causes the intricate zig–zag patterns in the rock matrix domain for the volumetric flux ratios \({\mathcal{K}\mathcal{A}}\ge 1\).

It is striking how simulations with fixed volumetric flux ratio \(\mathcal K \mathcal A\) (diagonals in Fig. 9) are remarkably similar, even for cases with three orders of magnitude difference in permeability ratio. The quantitative measures for the same volumetric flux ratio also collapse at intermediate to late times, as can be seen in Fig. 10. The dependence on the volumetric flux ratio is equivalent to the behavior observed for the parallel fractures in Sect. 4.1. At early times, the flow is determined by the permeability ratio (lines with the same line style in Fig. 10), however, as the viscous fingers grow, the dynamics of the matrix-fracture interaction changes and becomes independent of the permeability contrast. At times \(\hat{t} >0.1\), it is the volumetric flux ratio \(\mathcal K \mathcal A\) that governs the fluid flow for the parameter range in this study, but the exact transition time varies between simulations. This is shown in Fig. 10 where it can be seen that simulations with equal volumetric flux ratio \(\mathcal K \mathcal A\) (lines with same color) have an almost equal mixing length and number of fingers.

Finally, we observe that due to the zig–zag pattern of the fracture network, the mixing length for the highest permeability ratios (seen in Fig. 10) is reduced by up to an order of magnitude compared to the parallel fractures (seen in Fig. 6). The fluid flow also has a different qualitative behavior as seen by comparing the darkest regions (upper right corner) of Figs. 4 and 9.

4.2.2 Influence of the Fracture Density

In the previous subsection, the transversal distance between the fractures was equal the characteristic width H. In this section, we increase the fracture density in the domain, which leaves less space for viscous fingers within the rock matrix. In all simulations, in this section, the parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{500, 2, 10, 10^{-3}\}\) are fixed, and the fracture density is varied from \(N = 1\) to \(N = 5\).

Fig. 11
figure 11

Evolution of the concentration field for the brick shaped fractures. The parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{500, 2, 10, 10^{-3}\}\) are fixed, while the fracture density is varied. a–d Color maps of the concentration field for \(N=3\) at different times. Note the increasing aspect ratio in the figures. e The mixing length and number of fingers for different fracture densities

Full size image

Figure 11 shows the time evolution of the case \(N = 3\). The other simulations behave in a qualitative similar manner. In the simulation, a finger is initiated along each fracture as can be seen in subfigure (a). When the horizontal fractures end, the fingers continue through the rock matrix instead of following the fracture network around the block. When the trailing displacement front in the rock matrix reaches the next set of bricks located at \(\hat{x} = 0.5\), a new set of fingers is initiated along the second set of horizontal fractures. The new set of fingers and old set of fingers (six in total) continue to grow, and we do not observe any other fingers in the domain and the displacement is stable with the six propagating fingers growing longer (as seen in subfigure (b)). At times \(\hat{t} \approx 10\), the fingers that are aligned with the fractures become unstable and start to compete. The viscous fingers then behaves similar to the viscous instabilities in the homogeneous case with merging, tip splitting and shielding until all fingers have merge to a single finger (c). The merging of the fingers is clearly seen in subfigure (e) as the sudden drop in the number of fingers at time \(\hat{t}\approx 20\) and as an increase in the growth rate of the mixing length h.

4.3 Random Fractured Networks

The random fracture networks are generated by creating two sets of fractures, one horizontal set and one vertical set. The fractures in both sets are generated from two random variables, the coordinate of the starting point of the fractures and the fracture length. The starting point follows a uniform distribution in the domain. The fracture lengths are uniformly distributed in the intervals [0, 5] and [0, 1] in \(\hat{x}\)- and \(\hat{y}\)-direction, respectively. Due to the periodicity of the boundary, the vertical fractures with a starting point \(\hat{y}_s\) and length \(\Delta \hat{y} > 1-\hat{y}_s\) are wrapped around the periodic boundary and extend a length \(\Delta \hat{y} - (1-\hat{y}_s)\) from the bottom boundary. To avoid arbitrary close fractures, all fractures are snapped to a coarse Cartesian grid with dimensionless resolution 0.1.

4.3.1 Influence of the Volumetric Flux Ratio

To study the influence of the volumetric flux ratio, a suite of simulations is set up with the parameters \(\{{\textit{Pe}}, R, \mathcal A\} = \{500, 2, 10^{-3}\}\) fixed while the permeability ratio and fracture density are varied. For the random network, significant variations in the quantitative measures are observed among each realization of the fracture network. To account for this variability, five simulations were conducted for each parameter set.

Fig. 12
figure 12

Domain with a random fracture network, the fractures are shown as white lines. The figure shows the concentration for \(\hat{t}=12\), for different volumetric flux ratios and fracture density. The other parameters are fixed to \(\{R, {\textit{Pe}}, \mathcal A\} = \{2, 500, 10^{-3}\}\). Note that the simulation domains are much larger than shown in the figures

Full size image

Figure 12 shows a contour plot of one of the simulations for each parameter set. It is only when the volumetric flux ratio \({\mathcal{K}\mathcal{A}}=1\) that the primary fluid pathway occurs through the vertical fractures that connect the horizontal fractures; otherwise, the finger aligned with a fracture enters the rock matrix when the horizontal fracture ends. This qualitative behavior, observed in Fig. 12 for the evolution of the concentration, is also seen in the case of the brick shaped network. Figure 13 depicts the mixing length and the number of fingers for simulations conducted with two different values of \(N = {1, 3}\). The variance of the quantitative measures between each simulation is largest for the case of the highest volumetric flux ratio (\(\mathcal K\mathcal A=1\)). Note that some simulations for \(\mathcal K\mathcal A=1, N=3\) was ended earlier than \(\hat{t}=100\) when the adaptivity caused a domain size domain larger than 2 500 (\(h\sim 200\)) due to computational demands. Based on these observations, we propose that \({\mathcal{K}\mathcal{A}}=1\) serves as a threshold value, where the flow behavior is governed by the fracture geometry for values above this threshold.

Fig. 13
figure 13

Finger length h and number of fingers n for varying \({\mathcal{K}\mathcal{A}}\) and N for the random fracture network. The solid lines are the median of the individual simulations (represented by the transparent lines). The remaining parameters in the simulations are \(\{{\textit{Pe}}, R, \mathcal A\} = \{500, 2, 10^{-3}\}\)

Full size image

A few of the generated fracture networks for the case \(N=1\) did not have a horizontal fracture that crossed the initial diffusion front. In these cases, the concentration front evolved diffusively until it reached a horizontal fracture. After the first horizontal fracture was reached, the evolution continued as for the simulations with an initial fracture crossing the concentration front. In Fig. 13, this can be best seen in the plot of the mixing length. Further, the zig–zag evolution of the mixing length is caused by the leading finger reaching the end of the connected horizontal fracture. Because the fracture networks for \(N=3\) are more connected with longer chains of connected fractures and shorter distances between unconnected fractures, these jumps and plateaus in mixing length are smaller.

4.3.2 Influence of the Fracture Density

We set up a suite of simulations to investigate the impact of the fracture density for the random network. In these simulations, the parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{500, 2, 10, 10^{-3}\}\) are fixed while the fracture density N is varied. In this parameter regime, where the volumetric flux ratio is \({\mathcal{K}\mathcal{A}} = 10^{-2}\), the variation between different random fracture networks was in Sect. 4.3.1 shown to be small, and one simulation for each value of N is used in this section.

Figure 14 shows the evolution of the mixing length and the number of fingers of the simulations. In these simulations, we do observe a finger that is initiated along each horizontal fracture that cross the initial concentration front at \(\hat{x} = 0\). The initial fingers follow the horizontal fractures until they end, and we observe the viscous fingers to some extent follow new horizontal fractures they reach. However, we only observe the initiation of new fingers when the concentration front in the rock matrix reaches a new horizontal fracture for \(\hat{t} \lesssim 1\). We believe that when the concentration front reaches a new horizontal fracture after this time, then, the viscous fingers already developed suppresses the initiation of new fingers.

For both the brick shaped networks and the networks with parallel fractures, varying the fracture density alters the fluid flow both qualitatively and quantitatively. However, the alteration is mainly due to the repeated structure of these networks causing a stable finger to form around each horizontal fracture. Such a repeated structure is not present in the random network, and the clear transition from fingers propagating along fractures to viscous fingering across fractures that were present for the structured networks does not appear for the random networks. The randomness of the fracture network causes instabilities between the initial fingers aligned with the fractures and does not allow them to grow at equal rates as was seen in the structured networks.

Fig. 14
figure 14

Evolution of the concentration field for the random fracture networks. The parameters \(\{{\textit{Pe}}, R, \mathcal K, \mathcal A\} = \{500, 2, 10, 10^{-3}\}\) are fixed. a–d Color maps of the concentration field for the case \(N=3\) at different times. Note that the increasing aspect ratio in the figures. e The mixing length and number of fingers for different values of N

Full size image

5 Discussion and Concluding Remarks

This paper focuses on investigating the influence of highly permeable fractures on miscible viscous fingering in porous media using numerical simulations. We introduce three dimensionless numbers that characterize the fractures: the permeability ratio between fracture and rock matrix, the dimensionless fracture aperture, and the fracture density. Through extensive numerical simulations, we examine how these dimensionless numbers impact fluid flow for various fracture geometries. Our findings reveal that the volumetric flux ratio, which is the product of the permeability ratio and the dimensionless aperture, is the most critical parameter for describing the influence of fractures on fluid flow. This quantity represents the volume ratio of fluid flowing through the fractures compared to the fluid flowing through the rock matrix.

When fractures are present in an otherwise homogeneous domain, the early time qualitative effects observed in this paper are similar across all fracture geometries and parameter ranges. In the presence of a permeability contrast between the fractures and rock matrix, fingers aligned with the fractures always form. These fracture-induced fingers outgrow any other viscous instabilities occurring in the rock matrix, even for moderate permeability contrasts. The fracture-induced fingers significantly shield the viscous fingering process within the rock matrix, thereby stabilizing the initial fingering behavior. However, the subsequent evolution of viscous fingering strongly depends on the volumetric flux ratio, leading us to classify the flow into two distinct qualitative regimes.

In the first regime, characterized by a small volumetric flux ratio (\({\mathcal{K}\mathcal{A}}<10^{-1}\)), the stable propagation of the fingers aligned with the fracture geometry is disrupted by viscous instabilities. These instabilities can arise from the competition between fingers aligned with different fractures or from the formation of fingers in the rock matrix between fractures. In this regime, the geometry of the fracture networks does not significantly influence the flow behavior once the viscous instabilities have emerged. Instead, the fluid behavior resembles that of a homogeneous domain, with the shutdown of viscous fingering occurring at a time scale \(\hat{t}\sim {\textit{Pe}}\), where a single finger propagates independently of the fracture geometry. However, we find that the fracture geometry plays a crucial role before the onset of viscous fingering in the rock matrix, determining when the transition to a regime dominated by viscous effects occurs.

When the volumetric flux ratio is sufficiently large, the fluid flow transitions to the second regime, where the flow is dominated by the fractures. For the fracture geometries examined in this paper, the transition to a fracture-dominated flow occurs at a volumetric flux ratio of approximately \({\mathcal{K}\mathcal{A}}\sim 10^{-1}-10^0\) depending on the fracture geometry. In this regime, only channeling along the fractures is observed, while the displacement front in the rock matrix remains stable. In these cases, the flow paths are entirely determined by the fracture network. All investigated geometries exhibit a similar transition from unstable flow to flow dominated by the fractures as the volumetric flux ratio increases. However, the interplay between viscous instabilities and fracture geometry results in fundamentally different flow paths within the various fractured porous media. We find that the geometry of the fracture network is particularly crucial in the transition regime leading to the fracture-dominated regime. During the transition regime, the connections between fractures aligned with the flow direction by transversal fractures become important, giving rise to intricate interactions between the fracture network geometry and fluid flow.

In our modeling approach, we employ a DFM model where the fractures are represented as lower-dimensional objects. A limitation of this model is that it cannot capture viscous fingering within the fractures. If we define the fracture Péclet number as \({\textit{Pe}}_f=U_f/D = \mathcal K\mathcal A {\textit{Pe}}\), we do expect viscous fingering within the fractures for the highest volumetric flux ratios used within this study. The assumptions on the coupling conditions for the pressure and the concentration to be transversal homogeneous will in these cases fail. In our study, we have also assumed equal porosity and diffusivity in the rock matrix and the fractures. Hence, the results of this paper cannot be interpreted directly for physical systems where this is not applicable.

In this study, we investigate homogeneous fracture aperture, however in nature, the fractures will have spatially varying aperture and permeability. In the 2D domains considered in this paper, we expect heterogeneities in the fractures to play a minor role when the heterogeneities are small compared to the permeability ratio between the fractures and the rock matrix. This is because the 1D structure of the fractures does not allow for the aperture differences to create preferentially flow paths within individual fractures. However, for the interconnected fracture networks, the heterogeneities may create preferential flow paths through the networks similar to the preferential flow paths seen through the case with random fracture network presented in Sect. 4.3. The 2D domain can represent a thin geological layer with vertical fractures; however, in full 3D geometries, spatial variation of the fracture aperture has been shown in both experiments and simulations to influence the fingering patterns within fracture planes (Yang et al. 2019). In full 3D geometries, we still believe equivalent transitions from a viscous dominated flow to a fracture-dominated flow will occur and that the governing parameter of the transition will be the volumetric flux ratio \({\mathcal{K}\mathcal{A}}\). However, as we have seen in this paper, the geometry of the fracture network affects the exact numerical values of the transition between flow regimes, and the additional degree of freedom in 3D likely gives rise to an even richer interplay between the fracture geometry and the viscous instabilities.

In conclusion, the examples in this paper show the complex interplay between fracture geometry and unstable flow. While regimes where, respectively, fracture flow and viscous fingering dominates can be identified, there are important cross-over regimes where no such assumptions on the fluid flow structure applies. The effect of fractures on the viscous fingering in the rock matrix is largest at intermediate time scales and the fluid flow transition into a shutdown of the viscous fingering on the same time scale as for viscous fingering in a homogeneous domain.