Investigating Microstructure–Property Relationships of Nonwovens by Model-Based Virtual Material Testing

Abstract

Quantifying the relationship between geometric descriptors of microstructure and effective properties like permeability is essential for understanding and improving the behavior of porous materials. In this paper, we employ a previously developed stochastic model to investigate microstructure–property relationships of nonwovens. First, we show the capability of the model to generate a wide variety of realistic nonwovens by varying the model parameters. By computing various geometric descriptors, we investigate the relationship between model parameters and microstructure morphology and, in this way, assess the range of structures which may be described by our model. In a second step, we perform virtual materials testing based on the simulation of a wide range of nonwovens. For these 3D structures, we compute geometric descriptors and perform numerical simulations to obtain values for permeability as an effective material property. We then examine and quantify the relationship between microstructure morphology and permeability by fitting parametric regression formulas to the obtained data set, including but not limited to formulas from the literature. We show that for structures which are captured by our model, predictive power may be improved by allowing for slightly more complex formulas.

1 Article Highlights

• We utilize a stochastic microstructure model to generate a large database of virtual yet realistic samples of nonwovens.

• We investigate the relationship between geometric descriptors of 3D microstructure and effective properties.

• Incorporating various geometric descriptors into prediction formulas for permeability improves their performance.

2 Introduction

Fiber-based materials, especially nonwovens, play an important role in a wide variety of applications like gas-diffusion layers in fuel cell technology (Schulz et al. 2007), filtration (Geerling et al. 2020), printing paper (Chinga-Carrasco 2009), and hygiene products (Kroutilova et al. 2020). In different applications, various material properties are crucial for the performance of the final product and thus, must be optimized during design and production of the fiber mats. Aside from the properties of the fiber material, the geometric structure of the fiber systems is directly linked to many effective properties like wettability or diffusivity. Using modern tomographic imaging techniques, the 3D microstructure of existing nonwovens can be investigated and used as an input for numerical simulations to determine effective properties (Soltani et al. 2014). However, while tomographic imaging and numerical simulations alone may provide some insight into advanced properties which may not be accessible to experimental investigation, they are still limited in the range of feasible structures: changing the properties of the nonwovens necessitates changes to the production process and is thus costly and time-consuming.

By instead using a stochastic model for the 3D microstructure of nonwovens, a huge variety of virtual but realistic structures can be easily generated on the computer and still be used for numerical simulations. By this so-called virtual materials testing, relationships between the 3D geometry and effective properties can be investigated at a low cost and the development of new materials with improved properties can be accelerated (Huang et al. 2017; Schneider 2017; Venkateshan et al. 2016). Moreover, quantitative functional relationships between microstructure and effective properties can be obtained from this kind of data, as has already been shown in the literature. For example, in Prifling et al. (2021) such relationships were determined on structures derived from artificial models with no direct reference to measured image data for real existing materials. On the other hand, for fiber-based materials, functional relationships based on extensive experimental studies have been derived in Jackson and James (1986). However, the latter investigations focused on the solid volume fraction and fiber diameter as the main contributing factors. When performing investigations based on simulated data of fiber systems, a larger number of geometric descriptors can be calculated and a more comprehensive view of the relationship between microstructure and effective properties can be obtained.

Model-based approaches as described above or as discussed in Soltani et al. (2017) are primarily motivated by the shortcomings of real-world methods. In order to investigate relationships between manufacturing, microstructure, and effective properties of porous materials through physical experimentation, it is necessary to produce a large number of samples. This step alone would already require immense time and financial resources. Furthermore, manufacturing processes are often rigid and varying individual production parameters is not always trivial. While it is possible in theory to produce the necessary number of samples, it would not be feasible. Even if the necessary number of samples was available, determining all properties of interest through experimentation could prove problematic for many reasons, e.g., if the resolution of a sensor is not high enough or if a material sample is not stable enough to perform the experiment.

Based on the flexible stochastic model for the 3D structure of nonwovens which was developed and validated in Weber et al. (2023), we present a simulation study to investigate the relationship between geometric descriptors and effective properties of nonwovens, where we focus on the permeability as the effective property of interest. The present work illustrates the full process of virtual materials testing by fitting the microstructure model to measured data, simulating structures matching the properties of measured structure and subsequently analyzing various scenarios of novel, yet realistic structures using established numerical methods. At less than 10 min per simulated and analyzed structure, the proposed method allows for a fast and automated investigation of a huge number of samples.

We lay the foundation for our study by drawing a large number of virtual yet realistic microstructures from the model proposed in Weber et al. (2023). While this model was initially fitted to through air bonded nonwovens, it may be equally suitable for other types of nonwovens. By considering a wide range of different parameter sets for the model, we manage to obtain realistic structures with significantly varying properties. On these structures, we compute geometric descriptors and, by numerical simulations, permeability.

First, we investigate the relationship between model parameters and geometric descriptors by systematically varying the values of selected parameters. Not surprisingly, varying parameters which directly control the porosity of the resulting structures leads to a huge variation in a wide range of geometric descriptors. Varying other model parameters that control the shape and arrangement of fibers, we are able to adjust some selected geometric descriptors. Joint variation of multiple model parameters leads to drastic differences in the resulting structures which we investigate in a second step.

The major part of this paper is dedicated to investigating the relationship between geometric descriptors and permeability as illustrated in Fig. 1. In particular, we fit parametric regression formulas for predicting the permeability from geometric descriptors. We discuss the performance of various approaches, partly taken from the literature and partly developed for this study. Finally, we discuss the results and outline possibilities for further research.

Fig. 1

Overview of the framework for virtual materials testing. Virtual but realistic structures are simulated using the presented stochastic model. Then, geometric descriptors and permeability are computed for these structures. Functional relationships are established to predict permeability from geometric descriptors

3 Methods

In the following, we will outline the methods applied throughout the present paper. In particular, we will give a short summary of the model proposed in Weber et al. (2023) and discuss how we choose model parameters for virtual materials testing. Moreover, we describe the geometric descriptors that are used for the investigation of microstructure–property relationships and show how permeability is numerically computed on the simulated structures. Finally, we discuss how parametric regression formulas are fitted for the prediction of permeability from geometric descriptors.

3.1 Stochastic Model for Nonwoven Fiber Systems

For the present study, we will employ a spatial stochastic model developed in previous works (Weber et al. 2023), which was designed to represent nonwoven fiber systems. It is based on assuming fibers with a circular cross section of constant diameter $d > 0$ and by representing the centerlines of single fibers by polygonal tracks with constant segment length. This is the centerline of a fiber considered as a sequence of (random) points $\ldots , P_{-1}, P_0, P_1, P_2, \ldots \in \mathbb {R}^3$ with $|P_{n+1} - P_n| = c$ for all $n \in \mathbb {Z}$ and some constant $c >0$. Furthermore, it is assumed that $\left\{ P_n, n \in \mathbb {Z}\right\}$ forms a stationary, reversible third-order Markov chain (Raftery 1985). The transition function, which determines the distribution of $P_n$ conditional on $P_{n-1}, P_{n-2}, P_{n-3}$ is constructed by modeling the joint distribution of the random vector $(P_1, \ldots , P_4)$. Due to stationarity, this fully determines the transition function of the given third-order Markov chain.

For modeling the joint distribution of $(P_1, \ldots , P_4)$, the z-coordinates and the (x, y)-coordinates of $P_i = (X_i, Y_i, Z_i)$ for $i = 1, \ldots , 4$ are independently modeled. More precisely, $Z_4$ is assumed to be independent of $Z_1$ conditional on $Z_2, Z_3$, i.e., $\left\{ Z_n, n \in \mathbb {Z}\right\}$ forms a second-order Markov chain and, for simplicity of notation, the joint distribution of $(Z_1, Z_2, Z_3)$ is considered. This, in turn, is equivalent to modeling the distribution of $(Z_1, Z_2 - Z_1, Z_3 - Z_2)$. In the model proposed in Weber et al. (2023), a copula approach is used to model this distribution. It consists of modeling the marginal distributions of $Z_1$ and $Z_2 - Z_1$ (which has the same distribution as $Z_3 - Z_2$) by generalized normal distributions. Then, in a second step, the correlation structure is modeled by a pair-copula approach, using Clayton copulas for the joint distribution of $(Z_3 - Z_2, Z_1)$ and the joint distribution of $(Z_2 - Z_1, Z_1)$, and a Student’s t copula for the joint distribution of $(Z_3 - Z_2, Z_2 - Z_1)$ conditional on $Z_1$.

For modeling the sequence of random vectors $(X_1, Y_1), \ldots , (X_4, Y_4)$, the angle A between $(X_3, Y_3) - (X_2, Y_2)$ and $(X_2, Y_2) - (X_1, Y_1)$, and the angle B between $(X_4, Y_4) - (X_3, Y_3)$ and $(X_3, Y_3) - (X_2, Y_2)$ are considered. They determine the values of $(X_1, Y_1), \ldots , (X_4, Y_4)$ up to rigid transformations and the joint distribution of (A, B) is sufficient to describe the transition function of $(X_1, Y_1), \ldots , (X_4, Y_4)$. The joint distribution of (A, B) is again modeled by a copula approach where the (identical) marginal distributions of A and B are modeled by a generalized normal distribution and the correlation structure of (A, B) is modeled using a Student’s t copula, see (Weber et al. 2023). Note that for example, the curl of fibers is largely determined by the distribution and correlation of the angles A and B. Higher values of the scale parameter $\alpha _A$ generally correspond to stronger curl, whereas higher values of $\rho _{(A, B)}$ lead to less changes in direction.

Table 1 gives an overview of the 14 parameters of the model, which will be varied for the present study. They will be denoted by $P = (p_1, \ldots , p_{14})$ in the following. Additional parameters are the extent of the structure in x- and y-direction, which are fixed to 5 mm, and the length of individual segments of the polygonal tracks, fixed to 50$\upmu$m.

Note that, in the given model, individual fibers are simulated independently of each other and thus may overlap. This does not seem to significantly affect the permeability and most of the considered geometric descriptors. For more details and a validation of the used model, see (Weber et al. 2023).

3.2 Simulated Structures

By systematic variation of the parameters $P = (p_1, \ldots , p_{14})$ of the model described in Sect. 3.1, we obtain a wide range of realistic, yet novel, nonwoven structures. The range of chosen parameters is based on two sets of model parameters $P^1 = (p^1_1, \ldots , p^1_{14}), P^2 = (p^2_1, \ldots , p^2_{14})$ which were obtained in Weber et al. (2023) by fitting the model to measured data of two different through air bonded nonwovens, where some further bounds for the model parameters must be taken into account, see Table 1.

Table 1 Overview of the model parameters which will be varied for the present study

For the different aspects of the current study, we consider three different scenarios creating the following sets of structures:

• Scenario I The first set is obtained by keeping all parameters fixed with the exception of one single model parameter, which is systematically varied. Each of the 14 parameters was varied in 10 steps between specifically chosen minimum and maximum values, see Table 1. By this method, we created two subsets of structures, for which all (but the varied) parameters were chosen to equal $P^1$ or $P^2$, respectively. In total, this resulted in $280 = 14 \cdot 10 \cdot 2$ cases, for each of which 3 structures were simulated, resulting in 840 structures.

• Scenario II The second set of structures was created by randomly varying all model parameters at the same time. This means that, except for the fiber diameter, which was kept fixed, each entry $p_i$ of the parameter vector $P = (p_1, \ldots , p_{14})$ was independently drawn from a specific (truncated) normal distribution which was chosen such that the mean value was given by $\mu = (p^1_i + p^2_i) / 2$, and the standard deviation by $\sigma = |p^1_i - p^2_i| / (2 \Phi _{0.75})$, where $\Phi _{0.75}$ denotes the 0.75-quantile of the standard normal distribution. Thus, the value of $p_i$ belongs to the interval $(p^1_i,p^2_i)$ with probability 0.5. The normal distributions were truncated to observe the parameter bounds shown in Table 1. For each of 500 parameter vectors chosen in this way, 3 structures were simulated, resulting in 1500 structures.

• Scenario III The third set of structures is a small dataset showcasing the effect of fiber diameter d and fiber density $D_L$ on permeability. Note that the porosity $\varepsilon$ introduced in Sect. 3.3 below can be approximately expressed by

  $$\begin{aligned} \varepsilon \approx 1 - a D_L d^2 \end{aligned}$$

  (1)

  for some constant $a > 0$. Thus, different combinations of fiber density and fiber diameter can lead to the same value of porosity but hugely different values of permeability. To investigate this behavior, all model parameters were kept fixed, except for the fiber diameter and fiber density. Seven different target values for porosity $\varepsilon$ between 0.9 and 1 were chosen and for each target value, 5 different combinations of fiber diameter and fiber density leading to the specific value of porosity, were considered. For each combination, 3 structures were simulated, resulting in 105 structures.

In the lateral direction, all structures were simulated in a window of size $5 \times {\text{5}}\,{\text{mm}}$, which turned out to be sufficiently large. For each sample, the simulation of the structure took about 10 s, the computation of the geometric descriptors terminated after about 62 s and the numerical simulation of the permeability took about 380 s on a standard desktop computer equipped with an Intel Core i7–7700K and 32GB of RAM.

3.3 Geometric Descriptors

In the following, we introduce the geometric descriptors on which further analysis of microstructure–property relationships is based. Most descriptors are similar to those used in Prifling et al. (2023), where a more detailed discussion can be found. Recall that for the computation of the descriptors we may use the representation of a structure as set of polygonal tracks as well as voxel image.

Porosity Probably, the most fundamental geometric descriptor when it comes to any kind of porous material is the porosity $\varepsilon \in [0,1]$, or the solid volume fraction $1 - \varepsilon$. We estimate porosity from voxel images by simply counting the number of voxels belonging to the void space and dividing by the total number of voxels.

Tortuosity The notion of tortuosity is often considered when investigating transport phenomena. While there exists a wide variety of different specifications of tortuosity (Holzer et al. 2023; Ghanbarian et al. 2013), we only consider the geodesic tortuosity $\tau \ge 1$, which is based purely on geometric information and does not involve numerical simulations. It is related to the windedness of the shortest transportation paths. While in general, tortuosity is a second-order tensor, it is enough for us to consider a scalar because we are only interested in the through direction of nonwoven, perpendicular to the plane that the fibers are oriented almost parallel to. We compute the tortuosity by considering the voxelized structures and defining a transport direction, in our case, from $z = 0$ to $z = z_{max}$. For each target voxel on the plane through $z = z_{\rm max}$, we compute the shortest path from the opposite side to that voxel through the pore space using Dijkstra’s algorithm (Jungnickel 2008) on the voxel grid. Note that, Dijkstra’s algorithm is a greedy algorithm iteratively finding shortest paths in a weighted graph. The voxel-based tortuosity is then computed as the ratio of the length of the shortest path and the thickness $z_{\rm max}$ of the structure. For the present study, the mean geodesic tortuosity $\mu (\tau )$ and its standard deviation $\sigma (\tau )$ are considered which are estimated from the tortuosity values for all target voxels from a given structure.

Constrictivity A further directly transport-related property is the constrictivity $\beta \in [0,1]$ which measures bottleneck effects along transportation pathways. Again, we define the transport direction from $z = 0$ to $z = z_{max}$. Then, the constrictivity $\beta$ is defined as the ratio $\beta = \frac{r_{min}}{r_{max}}$ of two characteristic pore radii $r_{min}$ and $r_{max}$, where $r_{max}$ is the maximum radius such that 50% of pore space can be covered in (overlapping) spheres of that radius. These spheres are not allowed to penetrate into the solid phase, i.e., the fibers. Similarly, $r_{min}$ is the maximum radius of spheres which can intrude from the plane at $z = 0$ into the structure and fill 50% of pore space. This concept may be viewed as a digital version of mercury intrusion porosimetry.

Specific surface area The specific surface area S is the (mean) area of the solid-pore interface per unit volume. It is estimated by computing the total surface area within a given sampling window and dividing it by the window’s volume. In the case of fiber systems, the specific surface area is directly related to the porosity, the fiber diameter and the curl and overlap of fibers.

Chord length distribution Chords are straight lines in a given direction fully contained in the pore space which start and end at the pore-solid interface or the boundary of the sampling window. The distribution of the length C of such segments is called chord length distribution. In this work, we consider chords in z-direction and estimate the chord length distribution by collecting all possible chords within the voxelized structure. Note that other definitions use other notions of ‘‘random chord” and essentially lead to a length-weighted distribution of chord lengths. In the following, we consider the mean chord length $\mu (C)$.

Mean spherical contact distance The average distance from a randomly selected point within the pore space to the nearest point within the solid phase (i.e., to the nearest fiber) is called mean spherical contact distance, In the following, it will be denoted by $\mu (H)$. We estimate it by randomly choosing a large number of points within the pore space and averaging over their distances to the nearest fiber, computed directly on the polygonal track data.

The geometric descriptors stated above are determined for all simulated structures of Scenarios I, II and III. The obtained results are stored in a database, which contains the values of model parameters used for the simulation of a given structure, along with the corresponding values computed for geometric descriptors and permeability, where the computation of permeability is explained in the next section.

3.4 Computation of Permeability

In general, the permeability $\kappa$ is a 3 × 3 tensor corresponding to the 3 spatial directions. Furthermore, it is a material property. For nonwoven, fibers tend to be oriented strongly anisotropically nearly in a plane, and only the through-direction perpendicular to that plane is measured. By our convention for modelled structures, the through-direction is the z-direction. With this in mind, a scalar permeability $\kappa$, the (3, 3) entry of the above-mentioned tensor, is computed for the through-direction (or z-direction) based on appropriately rearranging Darcy’s law

$$\begin{aligned} \frac{Q}{A} = \bar{u} = \frac{\kappa }{\mu } \cdot \frac{\Delta P}{L}. \end{aligned}$$

(2)

Here, Q is the flow rate, A the area perpendicular to the flow direction over which the flow rate occurs, i.e., in the x-y plane, $\bar{u}$ is the (macroscopic) flow velocity, $\Delta P$ is the pressure drop, L is the thickness of the nonwoven, i.e., length in the z-direction, and $\mu$ is the dynamic viscosity of the fluid, that contains the kinematic viscosity of the fluid and its density. The permeability $\kappa$ identifies the proportionality between the pressure drop and flow velocity.

Darcy’s crucial observation was that the permeability is determined by the geometry of the pore space alone and thus is a constant for porous materials. The viscosity $\mu$ and media thickness L are fluid and material parameters, respectively, that must be fixed and known in order to compute $\kappa$. Darcy’s law, see Eq. (2), is valid under some assumptions on the representativeness of the material and parameters of the flow, i.e., that the fluid is incompressible, Newtonian and flowing rather slowly, corresponding to a moderate pressure drop. In real experiments, u and $\Delta P$ are measured, and the proportionality only holds for small pressure drops and velocities, but independently of the fluid viscosity $\mu$ and experimental value $\Delta P$. For faster flows and higher pressure drops, there exists a generalization of Darcy’s law called Forchheimer’s law. The latter uses two material constants which can also be determined by computer simulations, but is not considered here.

In the computational experiments, the permeability for the nonwoven models is determined using the FlowDict module of the GeoDict software (Linden et al. 2018; Becker et al. 2023). The flow solver code was validated against previous code versions that in turn were validated against experimental data in Glatt et al. (2009). For a given $\Delta P$, the approach is to solve a large linear system of equations resulting from a discretization of the Stokes equations, see Eqs, (3)–(5), on the microstructure where the pressure p and the x-, y-, and z-components of the (local, interstitial) velocity vector u at each pore space voxel of the binary image are the unknowns. Then, the local velocities get averaged to find the macroscopic or superficial $\bar{u}$ (Wiegmann 2007). For the sake of concreteness, the simulations assume that the pressure drop is 0.02 Pa and that the dynamic viscosity $\mu = 1.834 \cdot 10^{-5}$ i.e., that the pore space is filled with air at $20\,{^\circ }{\text{C}}$. The resulting permeability is independent of the choice of pressure drop and viscosity as it should be analytically due to the dropping of the intertia term of the Navier-Stokes equations, up to the accuracy of the numerical computations. Note some symbols conflict with other definitions in this paper, but are chosen in this section to be consistent with existing literature.

Each simulated structure is initially given as a set of polygonal tracks (fibers) within a fixed bounding cuboid $W = [0, x_{\rm max}] \times [0, y_{\rm max}] \times [0, z_{\rm max}]$ and equipped with a fiber diameter d. However, for the numerical flow simulations, a conversion into (binary) voxel images is done by the software. The voxel length h must be chosen small enough to resolve the fiber diameter, and so that the results of the flow simulation do not depend on it as would be the case for too large voxel sizes. For highly porous fibrous materials, as in the case under consideration here, voxel length $h = d /10$ is sufficient. These binary images also form the base for the computation of some of the geometric descriptors.

Finally, to compute the permeability in the z-direction we add an inlet of the length $l_{in}$ and an outlet of the length $l_{\rm out}$ to the domain to allow for the flow to be uniform far in front and behind the nonwoven, and thus to be able to use periodic boundary conditions for the velocity in all three spatial directions as well as periodic boundary conditions for the pressure.

Under the assumption of slow, viscous, steady-state incompressible flow through the nonwoven, the Reynolds number is zero, and the time-derivative as well as the inertial term in the Navier–Stokes equations can neglected. This means we can use the steady state incompressible Stokes equations with periodic boundary conditions on the domain and no-slip boundary conditions, see Eq. (5), on the fiber surfaces

$$\begin{aligned} -\mu \Delta \textbf{u} + \nabla p= & {} \textbf{f} \text{ in } \Omega \setminus G, \end{aligned}$$

(3)

$$\begin{aligned} \nabla \cdot \textbf{u}= & {} 0 \text{ in } \Omega \setminus G, \end{aligned}$$

(4)

$$\begin{aligned} \textbf{u}= & {} 0 \text{ on } \partial G, \end{aligned}$$

(5)

where G is the volume that is occupied by fibers, $\Omega$ is the computational box $\left[ 0,x_{\rm max}\right] \times \left[ 0,y_{\rm max}\right] \times \left[ -l_{in},z_{\rm max}+l_{\rm out}\right]$, and $\partial G$ is the surface of G. $\textbf{u}$ is the periodic velocity vector with components, u, v and w. $\textbf{f} = (0,0,c)$ is a constant body force vector where c is derived from the desired pressure drop $\Delta P$ and the length of the computational domain in the z-direction, and p is the periodic pressure. That pressure can be made physical by adding the linear function that is independent of x and y and assumes the values $\Delta P$ at the inlet boundary and 0 at the outlet boundary. The latter choice removes the non-uniqueness of the pressure resulting from the periodic boundary conditions and lets us see the computed pressure as the difference from the atmospheric pressure at the outlet of the simulation domain. Figure 2 illustrates this behavior. It clarifies also the fact that L is only the thickness of the nonwoven media and does not include the inlet and outlet, as longer or slightly shorter inlets and outlets would not change the behavior of the flow.

Fig. 2

The physical pressure resulting from a simulation with inlet and outlet. There is no pressure loss in the empty space before and behind the nonwoven, and the slight deviation from linear over the nonwoven is typical for highly porous and uniform porous materials

The linear systems of equations resulting from the discretization of Eqs. (3)–(5) are solved in Becker et al. (2023) using the LIR approach from Linden et al. (2014, 2015) with improved discretization of the no-slip boundary conditions (following Harlow and Welch 1965) and greater efficiency than were proposed in Wiegmann (2007).

3.5 Fitting of Parametric Regression Formulas

For the prediction of permeability from geometric descriptors, we consider different parametric regression formulas which will be discussed in Sect. 4.2 below. For fitting and evaluation of the prediction formulas, we use the data obtained for structures from Scenario II, where we split it into a subset for fitting the formulas and a (smaller) subset for evaluating their performance. Fitting of the formulas is performed by means of SciPy’s (Virtanen et al. 2020) built-in methods for least-squares optimization using the Levenberg-Marquardt algorithm. Note that the values of permeability obtained for the structures from Scenario II are within a much tighter range than, e.g., those considered in Prifling et al. (2021). Nevertheless, they span two orders of magnitude, such that the behavior for large values of permeability would disproportionately influence the fit of the formulas. Thus, we apply a log-transform prior to fitting.

To assess the quality of the fit, we use the mean absolute percentage error (MAPE), which is given by

$$\textrm{MAPE} = \frac{100}{k} \sum _{j=1}^{k} \left| \frac{\hat{y_j} - y_j}{y_j}\right| ,$$

and the coefficient of determination $R^2$ given by

$$R^2 = 1 - \frac{\sum _{j=1}^{k}(y_j - \hat{y}_j)^2}{\sum _{j=1}^{k}(y_j - \bar{y})^2} \,,$$

where $y_1, \ldots , y_k$ is the ground truth data, $\hat{y}_1, \ldots , \hat{y}_k$ are the corresponding predictions and $\bar{y} = \frac{1}{k} \sum _{j=1}^{k} y_j$ is the mean of the ground truth data. The values of MAPE and $R^2$ are computed on (not log-transformed) test data which has not been used for fitting. However, note that the least-squares fit essentially optimizes the $R^2$-value for the log-transformed data.

4 Results

For each structure generated in Scenarios I, II and III as outlined in Sect. 3.2, we computed the geometric descriptors described above as well as the corresponding permeability. In the following, we present the results of the statistical analysis of this data. This includes the investigation of microstructure–property relationships, where we consider various parametric regression formulas for the prediction of permeability from a range of geometric descriptors and discuss their performance.

Recall that for each specification of model parameters, 3 structures were generated which vary with respect to geometric descriptors and permeability. For structures of Scenario II, the coefficient of variation for the numerically computed values of permeability is equal to 60.10 when considering the full set of simulated structures. However, the mean coefficient of variation when considering each specification of model parameters individually is only equal to 3.06, indicating that structures which were simulated using the same specification of model parameters are rather similar.

Fig. 3

Examples of simulated structures of Scenario II. The top left structure exhibits a very low tortuosity, the top right and bottom structures have a low and high constrictivity, respectively

4.1 Statistical Analysis of Simulated Fiber Systems

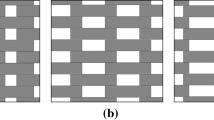
In a first step, we illustrate the range of feasible structures and investigate some basic relationships between model parameters and geometric descriptors resp. permeability. Structures of Scenario II, which were simulated using randomly chosen model parameters as discussed above, exhibit a wide range of values for many geometric descriptors, see Fig. 3, which shows cutouts of 3 simulated structures of Scenario II. This can be made more precise by histograms of geometric descriptors and permeability computed for each of the simulated structures of Scenario II, see Fig. 4. It can be clearly seen that none of these histograms can be modeled by a Gaussian distribution.

Fig. 4

Histograms of geometric descriptors and permeability computed for structures of Scenario II

Furthermore, we may use the data of Scenario III to investigate the fiber diameter, fiber density, and permeability. Recall that the volume fraction of fibers (i.e., $1 - \varepsilon$) is roughly a function of the squared fiber diameter while fiber density has a linear effect, see Eq. (1). As expected, increasing the fiber diameter while decreasing the fiber density to keep the porosity fixed has a positive effect on permeability, see Fig. 5.

Fig. 5

Relationship between permeability, porosity, and fiber diameter. As expected, for given porosity, permeability is low when the structure is composed of a huge number of thin fibers as compared to a smaller number of thicker fibers. Each dot corresponds to a structure of Scenario III

Finally, to investigate the influence of single model parameters on geometric descriptors, we consider structures of Scenario I. Figure 6 shows this kind of relationships for selected pairs of model parameters and descriptors. As expected, increasing the fiber density changes many geometric descriptors, including the mean chord length. But other parameters also influence the morphology of the fiber systems. The value of $\beta _A$ which influences the curvature of fibers projected onto the x–y-plane has a strong influence on the constrictivity of the resulting structures. The dependence of geometric descriptors on other parameters is more complex and the effect of some model parameters on the morphology of the fiber systems may not be captured by the geometric descriptors stated in Sect. 3.3.

Fig. 6

Relationships between selected pairs of model parameters and geometric descriptors, for structures of Scenario I. For each pair, we used the model parameters $P^1 = (p^1_1, \ldots , p^1_{14})$ (blue dots) and $P^2 = (p^2_1, \ldots , p^2_{14})$ (orange dots), which were obtained in Weber et al. (2023) by fitting the model to measured data of two different nonwovens, and varied only one single parameter. Left: Constrictivity vs shape parameter of the distribution of A. Center: Mean spherical contact distance vs parameter $\alpha$ of the copula corresponding to $(Z_2 - Z_1, Z_1)$. Right: Mean chord length vs fiber density

4.2 Quantitative Microstructure–Property Relationships

In this section we consider various parametric regression formulas which express permeability in term of geometric descriptors of the simulated fiber systems. In this context, we first analyze the correlation between different geometric descriptors and permeability. Figure 7 shows these correlations based on data of Scenario II. Note that various geometric descriptors are strongly correlated with permeability. As expected, porosity and permeability are positively correlated whereas mean geodesic tortuosity and permeability are negatively correlated. Moreover, most geometric descriptors are highly correlated with porosity, i.e., suggesting that a large amount of information about the morphology of the fiber systems is contained in a single geometric descriptor.

Fig. 7

Correlation between geometric descriptors and permeability, based on data of Scenario II

However, besides porosity, the other geometric descriptors considered in this paper deliver further (refined) morphological information. Figure 8 shows scatter plots of various pairs of descriptors obtained for structures of Scenario II. As expected, the porosity $\varepsilon$ has a huge impact on the permeability, but other properties play an important role as well. E.g., the standard deviation of tortuosity together with the mean chord length seem to be highly correlated with permeability.

Fig. 8

Relationship between selected pairs of geometric descriptors and permeability (color of dots) for structures of Scenario II. Left: Porosity vs constrictivity. Center: Mean chord length vs specific surface area. Right: Standard deviation of tortuosity vs mean chord length

Based on the data of Scenario II, we fitted different regression formulas to predict the permeability $\kappa$ from geometric descriptors. In the following, we will discuss these formulas and their goodness of fit. Note that some formulas which were proposed in the literature, specifically for fibrous porous media, predict the quantity $\kappa /d^2$ instead of $\kappa$ (Jackson and James 1986). However, as the fiber diameter d was not varied for the structures of Scenario II, we will ignore the fiber diameter and fit formulas to directly predict $\kappa$.

While some prediction formulas are designed observing physical units, others are solely targeted to obtain the best numerical values at the cost of a limited interpretability. As a baseline formula which does not preserve meaningful units, we consider the equation

$$\begin{aligned} \hat{\kappa }_1 = c_1 \varepsilon ^{c_2}, \end{aligned}$$

(6)

which represents one of the most simple relationships between porosity and permeability. Based on the data of Scenario II, we obtain the fitted parameters $c_1 = {3.85\times 10^{-8}}$ and $c_2 = 61.07$.

Additionally incorporating constrictivity $\beta$ and specific surface area S, the following formula was introduced in Neumann et al. (2020), which preserves the physical units:

$$\begin{aligned} \hat{\kappa }_2 = c_1 \varepsilon ^{c_2} \beta ^{c_3} S^{-2} \mu (\tau )^{c_4}, \end{aligned}$$

(7)

where fitting led to the parameters $c_1 = {5.03 \times 10^{-12}}, c_2 = -24.88, c_3 = 0.13$ and $c_4 = 59.51$. Furthermore, a slightly simplified version of Eq. (7) given by

$$\begin{aligned} \hat{\kappa }_3 = c_1 \varepsilon ^{c_2} S^{-2} \mu (\tau )^{c_4} \end{aligned}$$

(8)

was considered in Röding et al. (2020). Then, the fitted parameters are $c_1 = {4.96\times 10^{-12}}, c_2 = -24.17$ and $c_3 = 59.91$. Deviating from pure power-law type formulas as described above, in Prifling et al. (2021) still another formula was introduced, which is based on the same descriptors as Eq. (7):

$$\begin{aligned} \hat{\kappa }_4 = c_1 \varepsilon ^{c_2 + c_3 \beta } S^{-2} \mu (\tau )^{c_4} \end{aligned}$$

(9)

with fitted parameters $c_1 = {4.80\times 10^{-12}}, c_2 = -8.08, c_3 = -23.06$ and $c_4 = 55.68$.

Again ignoring physical units, we consider the following slight modification of Eq. (7) which allows for a flexible choice of the exponent of S:

$$\begin{aligned} \hat{\kappa }_5 = c_1 \varepsilon ^{c_2} S^{c_3} \mu (\tau )^{c_4}, \end{aligned}$$

(10)

where fitting leads to the parameters $c_1 = {2.29\times 10^{-10}},\, c_2 = 4.41,\, c_3 = -1.15$ and $c_4 = -13.50$. Adding the constrictivity $\beta$ as a variable leads to the formula

$$\begin{aligned} \hat{\kappa }_6 = c_1 \varepsilon ^{c_2} \beta ^{c_3} S^{c_4} \mu (\tau )^{c_5} \end{aligned}$$

(11)

with fitted parameters $c_1 = {5.07\times 10^{-10}},\, c_2 = 4.21,\, c_3 = 1.01,\, c_4 = -1.00$ and $c_5 = -29.72$. Alternatively, one may ignore the specific surface area, leading to

$$\begin{aligned} \hat{\kappa }_7 = c_1 \varepsilon ^{c_2} \beta ^{c_3} \mu (\tau )^{c_4} \end{aligned}$$

(12)

with fitted parameters $c_1 = {5.04\times 10^{-8}},\, c_2 = 33.21,\, c_3 = 1.88,\, c_4 = -118.69.$

Finally, we consider a power-law type formula incorporating a wider range of geometric descriptors to investigate the theoretically achievable predictive power of these types of relationships, where fitting the formula

$$\begin{aligned} \hat{\kappa }_8 = c_1 \varepsilon ^{c_2} \beta ^{c_3} S^{c_4} \mu (\tau )^{c_5} \sigma (\tau )^{c_6} \mu (C)^{c_7} \mu (H)^{c_8} \end{aligned}$$

(13)

leads to the parameters $c_1 = {5.08\times 10^{-8}},\, c_2 = 12.18,\, c_3 = -2.21,\, c_4 = -0.67,\, c_5 = 101.67,\, c_6 = 1.05,\, c_7 = 1.56$ and $c_8 = 0.51$.

A visual impression of the predictive power of Eqs. (6)–(13) can be obtained from Fig. 9. Visually, all prediction formulas perform reasonably well, which is corroborated by the values of $R^2$ and $\textrm{MAPE}$ shown in Table 2. However, there is a clear trend for most prediction formulas showing a better fit for lower values of permeability. As the fits were performed on log-transformed data, this is probably due to the fact that only few structures exhibit the higher values of permeability while a huge amount of data are present for lower values. Especially, when considering Eq. (13), it becomes clear that the prediction can be improved significantly when considering further geometric descriptors as compared to, e.g., Eq. (6), which is solely based on the porosity $\varepsilon$.

Fig. 9

Permeability predicted by the parametric formulas given in Eqs. (6)–(13), against the ground-truth permeability computed by the methods described in Sect. 3.4. Each dot corresponds to one structure from the test dataset of Scenario II

Table 2 Performance metrics of the fitted prediction formulas computed on the test dataset

5 Conclusion

For the efficient development of improved functional materials, understanding the relationship between easy to manipulate geometric descriptors of their 3D morphology and desired material properties is important. Traditional experimental setups for the investigation of these relationships are expensive and time-consuming and, furthermore, some important aspects may not be accurately measured. By using a stochastic microstructure model combined with numerical simulations, virtual materials testing may be performed to investigate these relationships. Compared to real experiments, our approach based on modeling and simulation is cheap and time-efficient at less than 10 min per simulated and analyzed structure on a regular desktop computer. It can be used to generate a huge database of virtual but realistic structures for which all the desired geometric descriptors and effective properties can be easily computed. From this data, a thorough understanding of the relationship between 3D morphology and effective properties of nonwovens can be obtained. Using this knowledge, the production process may be optimized by targeting solely geometric descriptors which are easier to manipulate than the effective material properties.

In this paper, we showed the full process of virtual materials testing by fitting the microstructure model to measured data, simulating structures matching the properties of measured structure and subsequently analyzing various scenarios of novel, yet realistic structures using established numerical methods. Precisely, we employed a stochastic model for nonwoven fiber materials to generate a large set of different structures and computed various geometric descriptors for each simulated structure. Furthermore, through numerical simulations, we computed permeability. To exemplify the approach of virtual materials testing, we then deduced parametric regression formulas to describe the relationship between 3D morphology and permeability. We used different types of formulas found in the literature as well as some custom-designed formulas and were able to show that permeability does not only depend on porosity, but very much on other geometric descriptors as well.

Our approach enables material scientists and designers to make fast predictions about a material’s effective properties based purely on easy-to-measure geometric descriptors. Using the prediction formulas considered in this paper, it might also be easier to design or modify a material in order to achieve a desired permeability, as it becomes clear how individual descriptors factor into the permeability of the material. For real-world production processes, this means that instead of finding the right production parameters to obtain the desired material properties, it is only necessary to optimize the process to get 3D morphologies with the right geometric descriptors. If the relationship between production parameters and geometric descriptors of the material is known to the manufacturer, the entire pipeline of the material’s design can be done virtually.

The methods shown in this paper can easily be extended to the full permeability tensor or other properties like diffusivity or wettability. Further work could use the large amount of virtual samples as training data for a machine learning based approach that could establish a fast and more precise, yet less interpretable link between geometric descriptors and effective properties of fiber-based materials.

Utilized Numerical Tools

The python programming language was used to implement the model, simulate the structures, compute geometric descriptors, fit parametric formulas and prepare most of the figures for this manuscript. Notably, the following libraries were used: NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), a slightly modified version of pyvinecopulib (Vinecopulib 2023), Numba (Lam et al. 2015) for accelerated execution and Matplotlib (Hunter 2007) and seaborn (Waskom 2021) for creating most of the figures.

GeoDict (Becker et al. 2023) was used to numerically compute the permeability and for 3D rendering of selected structures.