Convective Drying of Porous Media: Comparison of Phase-Field Simulations with Microfluidic Experiments

Abstract

Convective drying of porous media is central to many engineering applications, ranging from spray drying over water management in fuel cells to food drying. To improve these processes, a deep understanding of drying phenomena in porous media is crucial. Therefore, detailed simulation of multiphase flows with phase change is of great importance to investigate the complex processes involved in drying porous media. While many studies aim to access the phenomena solely by simulations, here we succeed to compare comprehensively simulations with an experimental methodology based on microfluidic multiphase flow studies in engineered porous media. In this contribution, we propose a Navier–Stokes Cahn–Hilliard model coupled with balance equations for heat and moisture to simulate the two-phase flow with phase change. The phase distribution of the two fluids air and water is modeled by the Phase-Field equation. Comparisons with experiments are rare in the literature and usually involve very simple cases. We compare our simulation with convective drying experiments of porous media. Experimentally, the interface propagation of the water–air interface was visualized in detail during drying in a structured microfluidic cell made from PDMS. The drying pattern and the drying time in the experiment are very well reproduced by our simulation. This validation will enable the application for the presented Navier–Stokes Cahn–Hilliard model in more complex cases focused more on applications, e.g., in the field of fibrous materials.

1 Introduction

Drying of porous materials, such as food, pharmaceuticals and textiles, is a vital process in several engineering fields, including materials manufacturing, chemical engineering and food production. Improving current techniques and developing new materials to meet these needs is crucial, but trial and error experimentation can be inefficient and costly. To overcome this problem, numerical modeling is often used to simulate the drying process in porous materials. However, this can be difficult as it involves simulating intertwined heat and mass transfer over a wide range of scales, from nanometers to meters.

Several numerical models have been developed to address the complex drying processes in porous materials. These models can be divided into two categories: macro-scale models and pore-scale models. Macro-scale models treat the porous materials as a continuum and consider volume-averaged or homogenized properties, making them useful for large-scale problems (Bear 2018; Blunt 2017). However, they have a limitation. They depend on constitutive transport correlations with adjustable transport parameters which allow to take the microstructure of the porous material into account (Ashari et al. 2010; van Genuchten 1980; Maier et al. 2023). These correlations are often empirical. Therefore, their ability to provide insight into the fundamental physics of the drying process is limited, making them less effective for material development. Pore-scale models, on the other hand, account for heat and mass transfer in the microscale geometry of porous materials, providing local velocities, local mass transfer rates and pressures of interest. Consequently, pore-scale models can be used to determine constitutive relationships for continuum-scale models. Consequently, microscale simulations are a prerequisite for the further development and parameterization of macro-scale models. However, a trustworthy validation of the microscale models is of great importance since they are the foundation for macro-scale models. Microfluidic experiments offer a new possibility to validate microscale simulations. These experiments facilitate an in situ observation of the interfaces and flow phenomena in the artificial porous media and allow a direct comparison to the simulation (Kunz et al. 2016; von Wolff et al. 2021; Yin et al. 2019; Yiotis et al. 2021).

To model the complex task of drying porous media on pore-scale, advanced multiphase models are necessary. There are various methods for simulating multiphase transport, such as particle-based methods like Lattice Boltzmann and Smoothed Particle Hydrodynamics, continuum lagrangian type methods like Front Tracking, Moving Mesh and eulerian type methods such as Volume of Fluid, Level-Set, and Phase Field (Kunz et al. 2016; Qin et al. 2019; Wörner 2012). In this contribution we consider the Cahn Hilliard Phase-Field method to model the drying of porous media. Recently, the Cahn Hilliard Phase-Field method has taken an important stance in modeling multiphase flow, most likely due to its mass conservation and its intuitive way of modeling the surface tension force and wettability (Yue 2020; Yue et al. 2006).

Only a small number of publications consider the modeling of multiphase flow with phase change being Phase-Field models. Most of the publications consider boiling phase change, where phase change is driven by the temperature gradient and takes place at the boiling temperature of the considered fluid. Wang et al. present a Phase-Field model to simulate boiling phase change which is implemented in an in-house code using the temperature gradient in the interface to model the phase change rate (Wang et al. 2021). Jafari et al. simulate the vapor bubble growth in microchannels with a Phase-Field model, which is implemented in the commercial software COMSOL Multiphysics™ (Jafari & Okutucu-Özyurt 2016). The authors model the phase change with a kinetic approach, as proposed by Lee in the context of Volume of Fluid, to model the phase change (Lee 2002). The kinetic parameter is fitted to experiments. Badillo (Badillo 2012) proposes a Phase-Field model to simulate the boiling phase change, which can be seen as a Level-Set model and not Phase-Field model in a classical sense (Wang et al. 2021).

In contrast to boiling phase change, evaporation takes places at a temperature below the boiling point of the evaporating fluid. In evaporation, the driving force of the phase change is the concentration gradient of the vapor mass fraction. To the best knowledge of the authors, only Safari, Sugimoto, Quin and Fei considered evaporative phase change Phase Field (Fei et al. 2022; Qin et al. 2019; Safari et al. 2014; Sugimoto et al. 2021). All works employed the Lattice Boltzmann method. Safari and Sugimoto simulated the evaporation of a sessile droplet. Fei and Quin simulated the evaporation of water in synthetic porous media.

In addition to modeling the phase change computationally, evaporation from porous networks can be observed experimentally with the aid of a microfluidic model. Microfluidics has emerged as an increasingly common and useful tool to investigate phenomena on the microscale. Thanks to easy observability and good control over the process, a wide range of applications is possible with microfluidic devices (Convery and Gadegaard 2019). Among the most notable applications are replicas of systems as complex as human lungs on a microfluidic platform (Huh et al. 2010). More often, however, the quasi-2D nature of microfluidic models is used to view an artificial cross section of otherwise optically dense objects, usually porous systems (Zhao et al. 2019). Other applications include fluid–fluid displacement, showcasing the strength of microfluidic models to visualize multiphase phenomena in pore networks (Kalde et al. 2022a, b). Similar models were used previously to support and validate simulations on convective drying in porous media (Qin et al. 2019; Wu et al. 2017).

In this contribution we present a Phase-Field model to simulate evaporation. To the best knowledge of the authors this contribution is the first work presenting the simulation of evaporation in porous media with an eulerian Phase-Field model. Then, we compare model predictions to a microfluidic experiment to validate the model and further investigate the convective evaporation of water in artificial porous media.

2 Numerical and Experimental Methods

2.1 Numerical Model

2.1.1 Description of the Phase-Field Model

In the following, we describe the Phase-Field model to simulate evaporation. The model accounts for non-isothermal evaporation and models the humidity balance, which is the driving force in non-boiling phase change.

The foundation of phase-field theory lies in the principle of minimizing free energy. Since a physical system always tends to minimize its free energy, the phase-field equation is derived from the free energy formulation. Van der Waals postulated the following form of the free energy density (Jamet & Misbah 2008)

$$f={f}^{0}+\lambda {\nabla }^{2}C.$$

(1)

${f}^{0}$ is the local free energy density, represented by the Ginzburg–Landau functional, a double well potential functional, as shown in Fig. 1a. For an immiscible system, as considered in this contribution, ${f}^{0}$ has two minima ${C}_{eq,0}$ and ${C}_{eq,1}$. The Phase-Field variable $C$ describes the distribution of the liquid phase $L$ and the gas phase $G$ in an immiscible system. Here, the local free energy density ${f}^{0}$ has two distinct minima for order parameter $C,$ where ${C}_{eq,0}=0$ and ${C}_{eq,1}=1$. The second term accounts for the influence of local spatial gradient of $C$ on the free energy density and is scaled by the homogeneous mixing energy coefficient $\lambda$, which balances the influence of the nonlocal part of the free energy density. Further details regarding the selection of $\lambda$ is provided later.

Fig. 1

a Double well potential of the local free energy density. b Variation of the order parameter $C$ over a planar interface

Next the chemical potential is formulated based on the free energy density. The free energy of a system is:

$$F={\int }_{V}fdV.$$

(2)

The chemical potential can be derived using variational procedure with the variational derivative of $F$ to $C$. The chemical potential of an immiscible system is:

$$\frac{\delta F}{\delta C}=\mu =\lambda {\varepsilon }^{-2}C\left({C}^{2}-1\right)-\lambda {\nabla }^{2}C.$$

(3)

$\varepsilon$ is the capillary length and scales the width of the diffusive interface, where the order parameter C varies from ${C}_{eq,0}$ to ${C}_{eq,1}$. The system’s equilibrium state can be determined by solving $\mu \left(C\right)=0$. The solution of the one-dimensional equation results in a Phase-Field variable $C$ profile along the $x$ direction, perpendicular to the interface. The $C$ profile exhibits a tangent hyperbolical variation from 0 to 1 over the interface, as depicted in Fig. 1b. It can be shown that the thickness of the diffusive interface is ${L}_{IP}=4.164\cdot \varepsilon$ (Cai 2016). The interface thickness is defined from 0.05 to 0.95 C (Jacqmin 1999).

Since the nonlocal contribution of the free energy density is formally directly related to the surface tension (Kahl & Enders 2000; Vinš et al. 2014)

$$\lambda =\sigma \varepsilon 6\sqrt{2}.$$

(4)

In this contribution, $\lambda$ is a constant, since very small temperature gradients are expected, due to the slow evaporation; and hence, the surface tension $\sigma$ is assumed to be constant. In situations with steep temperature gradients, $\lambda$ must be dependent on temperature to account for Marangoni effects.

Cahn and Hilliard derived based on the chemical potential formulation (3) a fourth order transport equation, which describes the phase distribution in an immiscible system. The famous convective Cahn–Hilliard equation (Jacqmin 1999) is then:

$$\frac{\partial C}{\partial t}+\nabla \cdot \left({\varvec{u}}C\right)=\nabla \cdot \left(M\nabla \mu \right)-\frac{{\dot{m}}^{\prime\prime\prime}}{{\rho }_{L}}$$

(5)

where ${\varvec{u}}$ and ${\rho }_{L}$ are the velocity density of the liquid phase, respectively. The mobility $M$ is a diffusion parameter which controls how quickly the phases equilibrate, the choice of $M$ is described in the following. ${\dot{m}}^{\prime\prime\prime}$ is the evaporation rate, which is discussed later in more detail.

The parameters $M$ and $\varepsilon$ are the crucial parameters of the Cahn–Hilliard equation. In this contribution, $M$ and $\varepsilon$ are not selected with the intention of modeling the physical microscopic diffusive interface, as the length scale of the real interface is on the order of angstrom to nanometer (Hopp-Hirschler 2017). This would result in an impractical computational cost. Instead, $M$ and $\varepsilon$ are chosen in such a way that the diffusive interface is represented on a coarser scale, which reduces computational expenses while still capturing the essential physical phenomena. Therefore, the choice of the capillary width $\varepsilon$ is made in accordance with reference length scale ${L}_{c}$, which is characteristic of a certain interfacial flow problem under consideration. The Cahn Number $Cn$ characterizes the ratio of $\varepsilon$ to ${L}_{C}$. If $Cn$ is chosen such that $Cn=[0.01; 0.04]$, the simulated interfacial flow phenomena get insensitive to $\varepsilon$ (Cai 2016; Ding et al. 2007; Jamshidi et al. 2019). The mobility $M$ determines the interface dynamics. Jacqmin and Magaletti et al. showed, $M {\text{O}}({\upvarepsilon }^{2})$ ensures that the Cahn–Hilliard diffusion approaches zero as $\varepsilon$ goes to zero (Jacqmin 1999; Magaletti et al. 2013). Thus, the conventional sharp interface model could be recovered. Consequently, we chose $Cn=[0.02;0.04]$ and $M=\alpha \cdot {\varepsilon }^{2}$. $\alpha$ is a tuning parameter chosen between 0.1 and 10 to fit the interfacial dynamics to the experimental data, if available (Jamshidi et al. 2019). When considered evaporation in porous media, the interface dynamics is magnitudes faster than the evaporation process; therefore, the interfacial dynamics due not influences the drying. As a result, $\alpha$ was selected to ensure a stable simulation, prioritizing a reasonably large timestep for the time integrator.

To model the wettability of the solid surfaces, a wetting boundary condition is needed. With the assumption of the wall free energy being at local equilibrium, one derives a wetting boundary condition to take into account the solid surface wettability as follows:

$${\varvec{n}}\cdot \nabla C=\frac{\sqrt{2}}{\varepsilon }{\text{cos}}\theta \sqrt{\frac{1}{4}{C}^{2}{\left(1-C\right)}^{2}}.$$

(6)

where ${\varvec{n}}$ and $\theta$ are the normal vector to the solid surface and the equilibrium contact angle, respectively. For the detailed derivation we refer to (Ding & Spelt 2007). We assume a constant contact angle without a spatial change in the simulation domain.

For the evaporation rate, a constitutive equation must be derived. Employing a mass balance at the phase interface within the conventional sharp interface formulation as discussed in (Hardt et al. 2008; Safari et al. 2014; Wang et al. 2021), the area-related evaporation rate can be derived:

$${\dot{m}}^{\prime\prime}=\frac{{\rho }_{G}{D}_{DG}}{1-{Y}_{V}}\nabla {Y}_{V}\cdot {{\varvec{n}}}_{L}$$

(7)

where ${D}_{DG}$, ${Y}_{V}$ and ${\rho }_{G}$ are the binary diffusion coefficient, vapor mass fraction and density of the gaseous phase, respectively. In this context, there is no vapor mass fraction present in the liquid phase, resulting in a zero gradient. According to Safari and Hardt (Hardt et al. 2008; Safari et al. 2014), the normal vector of the phase boundary results in

$${{\varvec{n}}}_{L}=\frac{\nabla C}{|\nabla C|}.$$

(8)

With the local interface volume

$${\int }_{\Omega }\left|\nabla C\right|d\Omega =1$$

(9)

the evaporation rate can be smoothed over the diffusive interface, to obtain an evaporation rate suitable for the diffusive interface formulation, as shown in Fig. 2. The area-related evaporation gives the volumetric evaporation rate (Safari et al. 2013)

Fig. 2

Schematic representation of the profile of $C$ for a sharp interface, with the area-related evaporation rate and the diffusive interface with the volumetric evaporation rate

$${\dot{m}}^{\prime\prime\prime}=\frac{{\rho }_{G}{D}_{DG}}{1-{Y}_{D}}\nabla {Y}_{V}\cdot \nabla C.$$

(10)

The two-phase flow hydrodynamics for immiscible, incompressible Newtonian fluids can be described by the two-phase Navier–Stokes equations in single-field formulation (Abels et al. 2011):

$$\rho \left(\frac{\partial {\varvec{u}}}{\partial t}+\left({\varvec{u}} \cdot \nabla \right){\varvec{u}}\right)=-\nabla p+\left(\eta \left(\nabla {\varvec{u}}+{\left(\nabla {\varvec{u}}\right)}^{T}\right)\right)-\mu \nabla C$$

(11)

where ${\varvec{u}}$, $p$, $\rho$ and $\eta$ are velocity, pressure, density and the dynamic viscosity of the fluid, respectively. $-\mu \nabla C$ models the surface tension force in potential form (Jacqmin 1999). For phase change, we obtain the non-divergence free continuity equation

$$\nabla \cdot {\varvec{u}}={\dot{m}}^{\prime\prime\prime}\left(\frac{1}{{\rho }_{G}}-\frac{1}{{\rho }_{L}}\right).$$

(12)

For the detailed derivation we refer to Hardt et al. (2008), Sadeghi et al. (2016). The density and the viscosity are arithmetically interpolated with the Phase-Field variable C:

$$\rho ={\rho }_{{\text{L}}}C+{\rho }_{{\text{G}}}(1-C)$$

(13)

$$\eta ={\eta }_{{\text{L}}}C+{\eta }_{{\text{G}}}(1-C)$$

(14)

The model assumes a constant viscosity (${\eta }_{{\text{L}}}, {\eta }_{{\text{G}}})$ and density $\left({\rho }_{{\text{L}}}, {\rho }_{{\text{G}}}\right)$ for each phase which is independent of the temperature.

According to Li et al. (2017) the temperature balance is obtained under the assumptions that the heat dissipation due to viscous friction and pressure fluctuations due to mechanical equilibrium at the interface can be neglected:

$$\rho {c}_{p}\frac{\partial T}{\partial t}+\rho {c}_{p}{\varvec{u}} \cdot \nabla T=\nabla \cdot \left(k\nabla T\right)-{\dot{m}}^{\prime\prime\prime}{h}_{LD}$$

(15)

where $T$, $k$, ${h}_{LD}$ and ${c}_{p}$ are the temperature, heat conductivity, evaporation enthalpy and the heat capacity, respectively. The heat capacity and conductivity are arithmetically interpolated with the Phase-Field variable$C$, as the viscosity and the density changes in the heat capacity and conductivity due to temperature gradients are not considered in this model.

$$k={k}_{L}C+{k}_{G}(1-C)$$

(16)

$${c}_{p}={c}_{p,L}C+{c}_{p,G}(1-C)$$

(17)

To simulate the vapor mass fraction field ${Y}_{V}$, the vapor species transport equation must be solved. The continuity equation of the vapor species inside an incompressible gas flow in the absence of chemical reactions is expressed as follows:

$$\frac{\partial {Y}_{V}}{\partial t}+{\varvec{u}} \cdot \nabla {Y}_{V}=\nabla \cdot \left({D}_{LG}\nabla {Y}_{V}\right)+a\frac{\left({Y}_{V}-{Y}_{LV}\right)}{{Y}_{LV}}$$

(18)

$$ {\text{with}}\;a\left( C \right) = \left\{ {\begin{array}{ll} {10^{5}} \hfill &\quad {{\text{if}}\;C > 0.95} \hfill \\ 0 \hfill &\quad {{\text{otherwise}}} \hfill \\ \end{array} } \right. . $$

(19)

The source term on the right-hand side of equation was added to ensure equilibrium conditions of the humidity at the interface of the liquid phase and to fulfill zero gradient of the vapor mass fraction in the liquid phase. The corresponding assumption is that the saturation pressure of the species under consideration is always present at the interface. The kinetic parameter $a(C)$ is not from experimental data, instead it is big enough to always ensure equilibria ${Y}_{V}={Y}_{LV}$. The dependence on $C$ ensures, that the evaporation only occurs in the interface. Emphasizing, this limits the model to slow drying, where the equilibrium assumption holds. The choice of $a$ was carefully validated, by comparing to analytical solution (compare Supporting Information Sect. 5.1). Wolf et al. used a similar approach to model successfully the precipitation with a Cahn–Hilliard Navier Stokes Model (von Wolff et al. 2021).

The Clausius–Clapeyron equation is used to calculate the value of the saturation vapor pressure of water ${p}_{D}$:

$${p}_{D}={p}_{{\text{amb}}} exp\left[-\frac{{h}_{LD}{{\text{MW}}}_{{{\text{H}}}_{2}{\text{O}}}}{R}\left(\frac{1}{{T}_{I}}-\frac{1}{{T}_{{\text{sat}}}}\right)\right]$$

(20)

${{\text{MW}}}_{{{\text{H}}}_{2}{\text{O}}}$ is the molecular weight of water, ${p}_{{\text{amb}}}$ is the ambient pressure, ${T}_{{\text{sat}}}$ is the boiling temperature, and $R$ is the universal gas constant. With ${p}_{D}$ is the equilibrium mass fraction of water ${X}_{LD}=\frac{{p}_{D}}{{p}_{{\text{amb}}}}$ can be calculated, this gives then the specific mass fraction ${Y}_{LD}=\frac{{X}_{D}{MW}_{{H}_{2}O}}{{\sum }_{i}{X}_{i}{MW}_{i}}$, the index $i$ refers to the components of air. We assume a constant pressure ${p}_{{\text{amb}}}.$ In the context of porous media, the saturation pressure above the fluid interface of the curved interface can potentially be influenced by the high curvature of the interface—a phenomena known as Kelvin effect (Adamson and Gast 1997). Employing the Kelvin equation, we determined the change in the saturation pressure taking into account the contact angle and pore size (compare Supporting Information 5.4). Our analysis leads us to the conclusion that the pores in the microfluidic system under consideration are adequately large, rendering any potential influence on saturation pressure practically negligible. We propose that in future studies, the Kelvin effect can be readily incorporated into Eq. (20).

All simulations are performed with the fluids water and air. The fluid parameters are shown in Table 1.

Table 1 Fluid parameters of the simulations

2.1.2 Pseudo Three-Dimensional Model

Microfluidic experiments often involve the study of three-dimensional structures, but due to the small and uniform depth of the microchannels, it is computationally more efficient to solve the problem in two dimensions while accounting for effects from the depth direction. One effect to consider is the viscous resistance from the top and bottom walls of the micromodel, which can significantly affect the flow behavior. To account for this effect, it is common to assume a parabolic velocity field in the depth direction and integrate the Navier–Stokes equation over the depth. This integration results in an additional resistance term that takes into account the viscous resistance from the top and bottom walls of the microchannel (Kunz et al. 2016):

$${f}_{visc}=-\frac{12 \eta }{{h}^{2}}{\varvec{u}}$$

(21)

The other effect to consider is the change in interface shape due to the presence of top and bottom walls. For the extra curvature in the third dimension, the following relation is obtained (Yin et al. 2019):

$$\kappa =-\frac{2}{h}cos\theta $$

(22)

The corrected pseudo three-dimensional model is derived from the well-known Continuous Surface Force Formulation, denoted as ${f}_{CSF}=\sigma \kappa \delta \overrightarrow{n}$. In the context of diffusive interface methods $\overrightarrow{n}$ is defined as $\frac{\nabla C}{\left|\nabla C\right|}$ and $\delta$ as $\left|\nabla C\right|$. The corrected pseudo three-dimensional model becomes:

$$\rho \left(\frac{\partial {\varvec{u}}}{\partial t}+\left({\varvec{u}} \cdot \nabla \right){\varvec{u}}\right)=-\nabla p+\left(\eta \left(\nabla {\varvec{u}}+{\left(\nabla {\varvec{u}}\right)}^{T}\right)\right)-\sigma \frac{2}{h}cos\theta \nabla C-\frac{12 \eta }{{h}^{2}}{\varvec{u}}-\mu \nabla C$$

(23)

To the best knowledge of the authors this is the first proposed corrected two-dimensional Cahn Hilliard Navier–Stokes model to simulate microfluidic experiments.

2.1.3 Numerical Implementation

The model was implemented in COMSOL Multiphysics™ (V5.6), which is a robust commercial finite element software. The PDE Module with linear elements was used to implement the Cahn–Hilliard equation and the temperature and humidity balance. To solve the flow field, the built-in Navier–Stokes Solver with stabilized Finite Elements P1 + P1 was utilized. For time integration, a second order BDF scheme with adaptive time-stepping with a damped Newton algorithm was used. The system of linear equations was solved using the PARADISO Solver (Alappat et al. 2020). A triangular mesh was used for spatial discretization, with the maximum mesh resolution chosen such that the interface was resolved by at least four elements to ensure mesh convergence.

2.2 Microfluidic Experiments

Master structures were 3D-printed on a Nanoscribe Photonic GT + professional in IP-S photoresist. Residual resin was removed by immersing them in propylene glycol monomethyl acetate (PEGMEA, Sigma Aldrich) and post-curing was done for at least 6 h under UV light (365 nm). Polydimethylsiloxane (PDMS; SYLGARD184 Silicone Elastomer Kit, Dow Chemicals) was mixed in a 10 to 1 ratio of elastomer base to hardener by weight and poured over the master structure. After degassing under vacuum and curing in a 55 °C oven for at least 4 h, PDMS replicas of the masters were obtained and removed from the mold. Holes to attach tubings were punched using biopsy punches (1.2 mm diameter). The PDMS channels were cleaned with isopropanol (> 99% purity, Sigma Aldrich) in an Elmasonic xtra TT ultrasonic bath. Glass slides were coated with 0.5 g of PDMS, degassed in a vacuum and cured in a 55 °C oven for at least 4 h. The channels were bonded to the PDMS-coated glass slides by activating both surfaces with oxygen plasma in a Diener Zepto plasma oven for 1 min at 50 W and pressing the channel onto the PDMS-coated glass slide. Figure 3 shows an illustrative PDMS Micromodel.

Fig. 3

PDMS Micromodel with a gas flow of 5 ml/min

They were then stored for at least 48 h at room temperature prior to use to ensure the contact angle of PDMS reverts back to around 100° (compare SI Sect. 5.2).

2.2.1 Evaporation Experiments

The channels were placed onto a heating stage set to the desired temperature and FEP tubing (inner diameter 1/32″, outer diameter 1/16″) was connected to an Elveflow microfluidic flow controller OB1 MK4. At the channel outlet, a humidity sensor (UFT75-ST1) was connected as shown in Fig. 4. To control the gas flow more precisely, a rotameter (Supelco 23,325 0–110 ml/min with needle valve) was attached between the flow controller and the channel.

Fig. 4

Experimental setup of the drying experiments

The chip was placed onto an inverted microscope (Leica DMIL LED) equipped with a heating stage (okolab H601-K-frame glass flat with okolab H401-T-Penny temperature controller). The temperature of the heating stage was set to 40 °C. For a typical experiment, the chip was filled with deionized water from the water inlet. To remove residual air trapped in the structure, all other valves were closed and a pressure of 300–500 mbar was applied to force the air through the permeable PDMS housing. After the entire chip was filled with water, the pressure was reduced and the gas inlet and outlet valves were opened again. While applying a small pressure of 10–30 mbar on the water inlet, gas was slowly flushed through the gas channel to remove water from the gas channel, valves and tubing. When water remained only in the pillar array of the chip, all pressures were reduced to 0 mbar and the water inlet was removed, to prevent hydrostatic pressure from the tubing to influence the result. A defined gas flow rate was set by applying a pressure and monitoring the flow rate with the rotameter. Evaporation of water from the pillar array was observed and recorded with a Basler ace 2.3 MP microscope camera at 25 fps using the Basler video recording software v1.0.0.9258. Humidity data were recorded from the humidity sensor with the software Sentax 1.6.0.1. When all of the water was evaporated, all pressures were set to 0 mbar.

2.2.2 Data evaluation

The recorded videos were converted into an image series with one image per second. These were then evaluated using a custom MATLAB (V R2020b) script. For each measurement, a mask of the channel was created using the last frame of the image series with the photo editing software GIMP v2.10.12, where the pillars as well as the outer boundaries of the chip and the water inlet were masked off. The mask was added to each binarized image from the experiment and the phase boundary was detected using edge detection. Artifacts were filtered and the area of regions enclosed by the phase boundary was determined. Conversion from pixel units to µm was done and the volume of water for all points in time was determined. The values were normalized to the initial state at the beginning of the experiment; and the thus, obtained saturation was plotted over time (compare Fig. 6a).

3 Results

3.1 Validation of the Pseudo Three-Dimensional Simulation

In order to validate the accuracy of the proposed model in accounting for the third dimension, we performed simulations of the drainage of a non-wetting rectangular duct ($400 \upmu m \times 40 \upmu m \times 40 \upmu m)$ initially filled with air, similar to the study by Yin et al. (2019). The contact angle was set to $\theta$ = 140°, and both a fully resolved three-dimensional simulation and a reduced two-dimensional simulation with the simplifications described in Sect. 2.1.2. were conducted also a two-dimensional model without the additional terms described in Sect. 2.1.2. was simulated. A constant inlet pressure of ${p}_{in}$ = 5700 Pa was applied and ${L}_{c}=40$ μm, $Cn=0.0025$ and $\alpha =2$ were chosen for the simulation. The water saturation over time was determined through volume and surface integration, and the phase distribution after 0.0035 s and the saturation over time are shown in Fig. 5.

Fig. 5

a Comparison of the liquid saturation in a duct between a fully resolved, pseudo three-dimensional and a two-dimensional model. b Comparison of the phase distribution after 0.0035 s of the fully resolved three dimensional and the pseudo three-dimensional model

Figure 5 demonstrates the good agreement between the proposed simplified model and the fully resolved model. The two-dimensional model, which does not account for the effects in the third dimension drains significantly faster than the fully resolved and the pseudo three-dimensional model. This shows that the simplifications made for model reduction are effective in reproducing the behavior of the fully resolved model. Specifically, for the simple geometry considered in our study, the corrected two-dimensional model was able to recover the behavior of the three-dimensional model. While this may not be the case for more complex geometries, the corrected two-dimensional model is still useful for reducing computational cost and will be utilized in the next section to simulate the microfluidic experiment.

3.2 Simulation of Drying in Porous Structure

The geometries used in the simulation and the experiment were identical, as shown in Fig. 3. The computational domain is shown with the corresponding boundary and initial conditions in Fig. 6.

Fig. 6

Computational domain with initial and boundary condition to simulate the drying in a microfluidic model. The fluid parameters of water and air at 40 °C are given in Table 1

The simulation domain’s length, excluding the inflow channel, is $2\cdot {10}^{-3} {\text{m}}$. The depth of the microfluidic channel in the third dimension is $h=100 \cdot {10}^{-6} {\text{m}}$. With the depth information the additional viscous resistance and capillary force was calculated, to account for the third dimension, as described in Sect. 2.1.2. To replicate the constant flow rate observed in the experiment a constant inlet velocity of ${{\varvec{u}}}_{in}=3.3 \frac{{\text{m}}}{{\text{s}}}$ was calculated with the dimensions of the rectangular air inlet ($100 \cdot {10}^{-6} {\text{m}} \times 250\cdot {10}^{-6} {\text{m}})$ and the density of dry air at 40 °C. A constant inlet velocity ${{\varvec{u}}}_{in}$ as Dirichlet boundary condition on the left-hand side of the purge flow channel was used. A Dirichlet boundary condition was imposed at the inlet for the vapor mass fraction, with a value of ${Y}_{V}=0.$ Since the experiment was conducted on a heated microscopy stage and the evaporation process is slow, a constant temperature of ${T}_{Surf}=313.15 {\text{K}}$, was assumed at the PDMS interface. Equation (6) governing the wetting boundary condition was calibrated using a static contact angle of $\theta =100^\circ .$ This angle was determined through measurements in the micromodel used in the experiment, specifically under conditions of a stationary fluid distribution in the microfluidic system and the absence of purge-gas flow, thereby precluding any evaporation. A fluctuating contact angle inside of the microfluidic device caused by impurities and surface roughness was consequently disregarded. The simulation’s parameters were selected as ${L}_{c}=50$ μm, $Cn$ = 0.0025 and $\alpha =0.08$.

Figure 7 shows the results of the drying simulation of the PDMS micromodel at 145 s.

Fig. 7

Images of the simulation at 145 s: a Phase distribution; b Interface area; c Vapor mass fraction field; d Temperature field; e Velocity field; f Pressure field

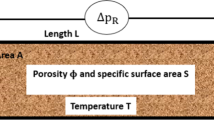
The first pore to drain in the Micromodel is the largest one. The phase transition takes place at the interface, which means that the coolest interface is the one closest to the channel, where the greatest humidity gradient can be observed. The curvature of the interface and the surface tension result in a pressure differential between the phases $\Delta p \approx -1700 {\text{Pa}}$, the capillary pressure.

3.3 Mesh resolution study

The phase-field method relies on critical parameters, $Cn$ and the Number of cells resolving the interface ${N}_{c}$. These parameters play a crucial role in determining the level of detail achievable in capturing local features at the gas–liquid–solid contact region. Decreasing $Cn$ enhances the accuracy of local feature representation, although it comes at the cost of a potentially significant increase in computational expenses. This is because a sufficient number of ${N}_{c}$ mesh cells is required to resolve the diffuse interface, and the total number of mesh cells scales quadratically as ${\left(\frac{{N}_{c}}{Cn}\right)}^{2}$ in 2D simulations. To assess the adequacy of interface resolution, a parameter study was conducted. Three different Cahn Numbers $Cn=[0.0025, 0.004, 0.0055]$ and three different ${N}_{c}=[2, 4, 6]$ where investigated, while keeping the other simulation parameters constant. The water saturation decrease over time is used as quantitative comparison. The parameter study is shown in Fig. 8.

Fig. 8

Mesh resolution study on the drying time for three different Cahn Numbers with ${N}_{c}=4$ (left) and three different Nc at $Cn=0.04$ (right)

The mesh resolution study reveals that for the considered process, the Cahn Number $Cn=0.04$ and a mesh resolution of ${N}_{c}=4$ is sufficient. However, the presented simulations in the following chapters are obtained with $Cn=0.0025$ and ${N}_{c}=4$.

3.4 Discussion of Experimental Results

To gain further insights into the drying of porous media and to attempt to validate the simulation, we performed microfluidic experiments in a microchannel that is geometrically identical to the simulated system. Finding suitable parameters such as temperature, gas flow and surface properties was done in parallel with the simulation, to ensure that a stable simulation as well as reproducible experiments could be obtained. The final parameters were a temperature of 40 °C and a gas flow of 5 ml/min with a measured surface contact angle of 100° (compare Supporting Information 5.2).

In the experiments, similar parameters were identified that influence the evaporation behavior. Mainly, the temperature and gas flow rate changed the evaporation dynamics, as would be expected. At higher gas flow, additionally, the pressure in the chip increased. This could be observed easily, as the phase boundary was pushed back in the initial stages of the experiment much faster than would be possible by evaporation. Thus, the water inlet channel was closed for further experiments, to prevent any flushing of the water out of the channel. Residual hydrostatic pressure on the water inlet also influences the patterns, thus for the final experiments, the water inlet tubing was removed after filling the chip and the inlet was closed with glue or tape to prevent leakage.

With the final setup, microfluidic evaporation experiments were standardized and reproducible, enabling a comparison between the simulated and experimental results.

3.5 Comparison of Simulation and Experiment

Figure 9 illustrates the comparison of the simulation and the experiment of the drying in the microfluidic device.

Fig. 9

Comparison of the simulated phase distribution (black phase) and phase distribution in the experiment

During the initial stages of evaporation, the phase pattern observed in the simulation and experiment agree closely, with both showing the largest pore draining first. However, in later stages, the phase pattern differs due to the increased prominence of effects such as stick–slip and contact line pinning, caused by surface roughness in the microfluidic channel becoming more pronounced as the surface-to-volume ratio increases for smaller fluid clusters. As the simulation does not account for surface roughness, the results differ from the experiment. This is also emphasized by the fact, that even in reproductions of the experiments, small deviations were observed in the later stages of drying (Fig. 9). This is mainly due to slight differences of the surface between different manufactured channels, as, e.g., small dust particles can get trapped on the surface of the PDMS, which then influence the surface roughness and evaporation behavior. These small factors are not accounted for in the simulation.

Furthermore, the computed evaporation rate is approximately 15% slower than that observed in the experiment, as shown in Fig. 10, which displays the water saturation decrease over time. Several factors could contribute to this difference. For instance, the air–water interface, where the phase change occurs, has a significant impact on evaporation. As the simulation does not resolve the third dimension in detail, the increase in interface area due to curvature in the third dimension is not taken into account, potentially leading to slower evaporation in the simulation due to a smaller interface area.

Fig. 10

Measured liquid saturation in the experiment versus the drying time with standard deviation and Simulated liquid saturation versus the drying time

Additionally, the dry air flow field in the experiment may differ from that in the simulation due to impurities such as dust particles, surface roughness, and other factors that could induce small eddies, thereby enhancing mass transfer. These factors are not modeled in the simulation, which could account for the slower evaporation rate. Finally, corner and film flows are also not modeled in the simulation, which could further contribute to differences between the simulation and experiment. In conclusion, the simulation reasonably captures the drying process of the microfluidic device.

4 Conclusion

Our contribution presents a novel pore-scale model to simulate drying from first principles. To accommodate three-dimensional microfluidic experiments in a two-dimensional simulation, we proposed a dimension-reduced Cahn–Hilliard Navier–Stokes model. To validate the model, we provided four different tests, as shown in detail in Sect. 3.1 and the Supporting Information. The proposed drying model enables simulations of drying below saturation temperature, which is commonly encountered in numerous natural and technological processes. The model is limited to slow evaporation, as it assumes equilibrium conditions for humidity at the liquid phase interface and neglects Marangoni effects.

We conducted both simulations and experiments on drying in a microfluidic model, and the proposed model was able to qualitatively reproduce the complex drying process observed in the experiment. We found good agreement between the simulation and experiment for the phase distribution during evaporation but observed that the drying dynamics were approximately 15% slower in the simulation than in the experiment. This discrepancy may be attributed to the smaller interface area in the simulation, but further investigations are required to confirm this hypothesis. In future studies, the model can be extended to account for Marangoni effects by introducing temperature-dependent surface tension, and additional species transport equations can be included to explore reactive transport with evaporation.

Furthermore, the numerical pore-scale model can be used to determine constitutive correlations like capillary pressure—saturation curves and interfacial-area—saturation curves, by volume averaging. These correlations can be employed to parameterize an up-scaled continuum model, as suggested by Lu et al. (2020). They accomplished this through pore-network simulations. The up-scaled continuum model enables parameter studies and process scale simulations.

Our study demonstrates the reliability of the model, which offers possibilities for investigating the drying of porous media in various technical applications, such as gas-diffusion layers, textiles, and coatings. The model enables the evaluation of the influence of the porous media’s structure and process parameters. Moreover, the model provides new opportunities for bridging the scales from micro to macro by parametrizing process or macroscopic models for drying.