1 Introduction

Fibres and foam-like media are both classified as fibrous porous media [e.g. Tadrist et al. (2004) and Woudberg et al. (2021)]. There are numerous applications for fibres in industry that make use of filtration processes, transport in biological systems, acoustic properties, compact heat exchangers, technology in fuel cells, paper production, fibrous beds for manufacturing processes and many other mechanical, biological and chemical systems (Soltani et al. 2014; Stylianopoulos et al. 2008; Tahir and Tafreshi 2009). An example is coalescing filters which make use of fibres, such as glass fibres, as a filter medium and remove droplets of liquid aerosols and other air streams and include applications in dehumidification, filtration of cabin air, automotive engine crank case ventilation and metal working (Manzo et al. 2016). The popularity of fibres in such systems are accredited to their mechanical strength, flexible structure, large specific surface area, low weight, high heat transfer coefficients and high permeability, as well as their high porosities (Tahir and Tafreshi 2009; Tamayol and Bahrami 2010). The study of transport properties and morphological parameters of fibres are therefore an important and necessary contribution towards the effective operation of fibres in all these various fields of application. Foam-like media, referring to ceramic and metal foams, also cover a wide range of applications in industry. A few examples include uses in compact heat sinks for power electronics, catalytic beds, air-cooled condensers, multi-functional heat exchangers, cryogenics, combustion chambers and other applications requiring effective heat transfer characteristics (Mancin et al. 2010). Foams have similar properties to fibres that make them attractive to use in gas filters, heat exchangers, porous burners and catalyst supports, namely their mechanical strength, large specific surface areas and high porosities which lead to good chemical resistance, enhanced heat and mass transfer properties and low pressure drops (Inayat et al. 2011). Edouard et al. (2008) noted that the specific surface area is important for many industrial systems because it is responsible for the high performance and successful design of reactors. They stated that \(S_{v} > 2000 \, \text {m}^{-1}\) for foam matrices, even at very low densities, and that compact heat exchangers generally require that \(S_{v} > 700 \, \text {m}^{-1}\), where \(S_{v}\) denotes the specific surface area.

Experimental studies of the permeability of porous media is most often performed by measuring the pressure drop of a fluid through the specific porous medium and using the Darcy–Forchheimer equation to determine the permeability values, given by

$$\begin{aligned} \frac{\Delta p}{L} = \frac{\mu }{K} \, q + \frac{\rho }{K_\textrm{F}} \, q^{2} , \end{aligned}$$
(1)

where \(\Delta p/L\) is the pressure gradient, \(\mu\) is the dynamic viscosity of the fluid, \(\rho\) is the fluid density, K and \(K_\textrm{F}\) are the permeability coefficients of the Darcy and Forchheimer flow regimes, respectively. In this study both K and \(K_\textrm{F}\) will be considered. The most frequently used correlation between the permeability and the average pore-scale parameters of a porous medium is the Ergun equation (Ergun 1952). This equation is based on flow through granular media, although some authors in the literature have proposed different versions of the Ergun equation for other types of porous media, e.g. foams, as briefly summarized by Moreira and Coury (2004). Most of these versions, however, involve an empirical adjustment to the coefficients in the Ergun equation, as done by Dietrich et al. (2009).

There are numerous models that predict the Darcy permeability of fibre structures and a few authors have also compared some of these models to one another and experimental data [e.g. Jackson and James (1986), Tamayol and Bahrami (2009) and Zhang et al. (2020)]. Tamayol and Bahrami (2011) identified three main categories of fibre-like media: fibres with 1D (one-dimensional), 2D (two-dimensional) and 3D (three-dimensional) fibre arrangements. For unidirectional fibrous porous media, the 1D fibre arrangement is divided into flow parallel and perpendicular to the axes of the fibres. For fibres randomly distributed in a plane, the 2D layered fibre arrangement is divided into in-plane and through plane flow and the 3D arrangement describes fibres that are randomly distributed in space. A few of these models, primarily for 2D and 3D flow, available in the literature will be utilized in this study for comparative analysis.

Tomadakis and Robertson (2005) determined an expression for predicting the Darcy permeability of 2D and 3D fibre media by employing electrical conduction principles, given by

$$\begin{aligned} \frac{K}{a^{2}} = \frac{\epsilon }{8 \ln {\epsilon ^{2}}} \cdot \frac{(\epsilon - \epsilon _{p})^{\alpha + 2}}{(1 - \epsilon _{p})^{\alpha } \left[ (\alpha + 1) \epsilon - \epsilon _{p} \right] ^{2}} , \end{aligned}$$
(2)

where a denotes the fibre radius, \(\epsilon\) the porosity, \(\epsilon _{p}\) denotes the percolation threshold and \(\alpha\) a constant. For 2D in-plane flow, \(\epsilon _{p} = 0.11\) and \(\alpha = 0.521\), for 2D through plane flow, \(\epsilon _{p} = 0.11\) and \(\alpha = 0.785\) and for 3D flow \(\epsilon _{p} = 0.037\) and \(\alpha = 0.661\). Van Doormal and Pharoah (2009) presented simulated correlations for 2D in-plane and through plane Darcy permeabilities of fibre type media, given by

$$\begin{aligned} \frac{K}{a^{2}} = 0.26 \frac{\epsilon ^{3.6}}{1 - \epsilon } , \end{aligned}$$
(3)

and

$$\begin{aligned} \frac{K}{a^{2}} = 0.28 \frac{\epsilon ^{4.3}}{1 - \epsilon } , \end{aligned}$$
(4)

respectively. Tamayol and Bahrami (2011) studied the transverse Darcy permeability of fibre type media, both theoretically and experimentally, providing equations for unidirectional aligned fibres for different arrays, 2D mats and cubic structures (i.e. 1D, 2D and 3D fibre arrangements, respectively). The expression for the dimensionless Darcy permeability of the 2D fibre media is given by

$$\begin{aligned} \frac{K}{b^{2}} = 0.008 \sqrt{\epsilon } \left[ \left( \frac{\pi }{4(1 - \epsilon )} \right) ^{2} - 2 \frac{\pi }{4(1 - \epsilon )} + 1 \right] , \end{aligned}$$
(5)

and the expression for the 3D fibre media is

$$\begin{aligned} \frac{K}{b^{2}} = 0.08 \frac{(S - b)^{4}}{S^{2} b^{2} \epsilon ^{0.3}} , \end{aligned}$$
(6)

where the ratio of S and b can be calculated from

$$\begin{aligned} 1 - \epsilon = \frac{3 \pi }{4} \cdot \frac{b^{2}}{S^{2}} - \sqrt{2} \cdot \frac{b^{3}}{S^{3}} , \end{aligned}$$
(7)

with b denoting the fibre diameter of the fibre type media considered, such that \(b = 2a\). In all the equations provided by Tamayol and Bahrami (2011), they used the solid volume fraction instead of porosity. In Eqs. (5)–(7), the solid volume fractions were replaced with \(1 - \epsilon\) for consistency purposes in this study. Very few studies on the Forchheimer permeability coefficient for fibre type media were found in the literature. Tamayol et al. (2012) presented numerical correlations for their definition of the Forchheimer coefficient, which, in this study, may be defined as F where \(K_\textrm{F} = \sqrt{K}/F\), for different fibre arrangements.

Equations for predicting the permeability of foam-like materials are also available in the literature. Such equations acquired from Dietrich et al. (2009) and Giani et al. (2006) will specifically be used for comparison purposes in this study. Dietrich et al. (2009) provided experimental results for the pressure drop of different ceramic foams and furthermore used the results to obtain coefficients for an Ergun-type equation. They provided correlations between the permeability coefficients and the hydraulic diameter. Dietrich et al. (2009) furthermore presented the specific surface area in terms of the hydraulic diameter and provided an expression for the specific surface area proposed by Buciuman and Kraushaar-Czarnetzki (2003). From all the information provided, the permeability coefficients could be determined in this study in terms of the pore diameter, denoted by \(d_\textrm{p}\), and the porosity. The resulting equations are given by

$$\begin{aligned} \frac{K}{d_\textrm{p}^{2}} = 0.018 \frac{\epsilon ^{3}}{\sqrt{1 - \epsilon }} \left( 1 - \sqrt{\frac{1 - \epsilon }{2.59}} \right) ^{-2} , \end{aligned}$$
(8)

and

$$\begin{aligned} \frac{K_\textrm{F}}{d_\textrm{p}} = 0.96 \frac{\epsilon ^{3}}{(1 - \epsilon )^{0.25}} \left( 1 - \sqrt{\frac{1 - \epsilon }{2.59}} \right) ^{-1} . \end{aligned}$$
(9)

Giani et al. (2006) investigated the pressure drop and mass-transfer properties of metallic foams. They have determined an expression for the pressure drop in terms of the porosity and pore diameter, for both the Darcy and Forchheimer flow regimes. Only the Forchheimer coefficient will be given in this study and utilized due to the Darcy coefficient yielding predictions that are different in trend than most other predictions for the Darcy permeability. The dimensionless Forchheimer coefficient is given by

$$\begin{aligned} \frac{K_\textrm{F}}{d_\textrm{p}} = 2.30 \left( 1 - \sqrt{\frac{4}{3 \pi } (1 - \epsilon )} \right) ^{4} . \end{aligned}$$
(10)

Some specific foam models used by various authors to study the parameters of foams have been discussed briefly by Maré and Woudberg (2019) and more extensively by Maré (2020). A summary of the expressions for the specific surface area obtained using these foam models will be given [as also provided by Maré (2020)]. Reference to the specific surface area of fibres together with experimental measurements thereof are provided by Sullivan (1942). No equations for predicting the specific surface area of fibre type media could however be found in the literature by the present authors.

Fig. 1
figure 1

Isotropic geometric models for foam-like porous media

Full size image

The cubic unit cell model, shown in Fig. 1a, was proposed by Lu et al. (1998), who investigated the use of open-celled foams in heat transfer applications. Giani et al. (2006) also used the cubic unit cell model to study the mass-transfer properties of open-celled foams. They presented expressions for the specific surface area in terms of the pore diameter \(d_\textrm{p}\) and the strut diameter b based on the cubic unit cell model geometry. The latter two linear dimensions are indicated in Fig. 1a. The resulting expressions are given by

$$\begin{aligned} S_{v} = \frac{2}{d_\textrm{p}} \sqrt{3 \pi (1 - \epsilon )} , \end{aligned}$$
(11)

and

$$\begin{aligned} S_{v} = \frac{4}{b} (1 - \epsilon ) . \end{aligned}$$
(12)

Lacroix et al. (2007) conducted a study to obtain the pressure drop for SiC foams by also utilizing the cubic unit cell geometry. They investigated the pressure drop predictions using an Ergun-type equation and merely made use of the model geometry to determine the specific surface area in order to find correlations among other parameters necessary for the pressure drop predictions. Lacroix et al. (2007) also presented Eq. (12) to predict the specific surface area using the cubic unit cell model. Based on work done by Lacroix et al. (2007), an approach for determining the specific surface area in terms of the pore diameter was considered by Maré (2020), where the total volume of a unit cell is given by \((d_\textrm{p} + b)^{3}\), as opposed to the approach based on the work of Giani et al. (2006) who defined the total volume as \(d_\textrm{p}^{3}\), and the expression obtained was:

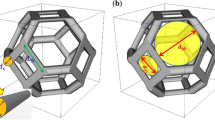
$$\begin{aligned} S_{v} = \frac{2}{d_\textrm{p}} \left[ \sqrt{3 \pi (1 - \epsilon )} - 2 (1 - \epsilon ) \right] . \end{aligned}$$
(13)

Mass transfer and pressure drop properties of open-cell foams were also investigated by Garrido et al. (2008). They made use of specific surface area predictions obtained from both the cubic unit cell and the tetrakaidecahedron models in order to determine mass transfer coefficients. Experimental specific surface area values were furthermore obtained which were compared to the model predictions. A schematic representation of the tetrakaidecahedron model is shown in Fig. 1b. This model resembles a truncated octahedron, having eight hexagonal faces and six square faces (Buciuman and Kraushaar-Czarnetzki 2003). The struts are furthermore triangular prisms with the edge width of the strut being l, as indicated in Fig. 1b, and not cylinders as in the case of the cubic unit cell model. Giani et al. (2006) observed an overestimation of the specific surface area predicted by the cubic unit cell and tetrakaidecahedron models, and also mentioned that the overestimation could be due to the assumption of constant thickness of struts in the geometric models, whereas ceramic foams tend to have accumulation of solid material around the nodes. Gibson and Ashby (1988) considered different polyhedra in which the structures of foams could be modelled and concluded that the tetrakaidecahedron yielded the most consistent agreement with observed properties. Some geometric relationships were furthermore derived by Gibson and Ashby (1988) for the tetrakaidecahedron unit cell. These results were also used by Richardson et al. (2000), who studied and measured the pressure drop of flow through ceramic foams and derived a specific surface area equation from the tetrakaidecahedron model. The expression they determined for the specific surface area in terms of the pore diameter is given by

$$\begin{aligned} S_{v} = \frac{12.979}{d_\textrm{p}} \sqrt{1 - \epsilon } \left( 1 - 0.971 \sqrt{1 - \epsilon } \right) . \end{aligned}$$
(14)

In Maré (2020), it was however noted that the coefficient in Eq. (14), i.e. 12.979, should be 5.621 and that it is possible that there was a mistake made in the calculation of the coefficient in the expression of Richardson et al. (2000). Buciuman and Kraushaar-Czarnetzki (2003) also made use of the tetrakaidecahedron model. They presented the expressions for the specific surface area in terms of the face diameter, which is the sum of the strut and pore diameters. Using the geometry of a tetrakaidecahedron model unit cell, as defined by Buciuman and Kraushaar-Czarnetzki (2003), an expression for the specific surface area in terms of the pore diameter was determined by Maré (2020) and is given by

$$\begin{aligned} S_{v} = \frac{4.82 \sqrt{1 - \epsilon } - 2.99 (1 - \epsilon )}{d_\textrm{p}} . \end{aligned}$$
(15)

Inayat et al. (2011) investigated specific surface area predictions based on various model geometries and compared it to experimental data. The model geometries which they considered were the cubic unit cell model, the dodecahedron model and the tetrakaidecahedron model. They determined that the tetrakaidecahedron geometry was the most suitable model for describing foam structures and also made adjustments to the strut geometry of the model in order to accommodate the changes in strut morphologies at different porosities. Huu et al. (2009) modelled solid foams using a geometric approach involving the pentagonal dodecahedron due to the dodecahedron structure having such a close resemblance to a foam cell. Huu et al. (2009) differentiated between the dodecahedron model with triangular struts for high porosities (\(\epsilon > 0.9\)) and the dodecahedron model with cylindrical struts for lower porosities (\(\epsilon < 0.9\)). They furthermore made a distinction between “slim” and “fat” struts, where “slim” struts have triangular nodes (where the struts connect) that resemble foams of very high porosities (\(\epsilon > 0.9\)) and “fat” struts are more rounded at the edges of the nodes and resemble foams of lower porosities (\(\epsilon < 0.9\)). In Fig. 1c, a schematic representation of the dodecahedron model with triangular “slim” strut geometry is shown, where l is the triangular edge width similar to that of the tetrakaidecahedron model. For the dodecahedron with cylindrical struts, b denotes the diameter of the cylinders. Huu et al. (2009) furthermore provided expressions for the specific surface area from which predictions in terms of the pore diameter could be deduced. The expression for the specific surface area of the dodecahedron model with triangular “slim” struts is given by

$$\begin{aligned} S_{v} = \frac{60 \, k_{1}}{\sqrt{5} \, \phi ^{3} \sqrt{3 - \phi } \, d_\textrm{p}} \left( 1 - \frac{1}{2} \sqrt{\frac{2}{3}} \, k_{1} \right) ^{2} , \end{aligned}$$
(16)

where \(k_{1}\) can be determined from the following expression:

$$\begin{aligned} - \, \frac{\sqrt{10}}{3 \phi ^{4}} k_{1}^{3} + \frac{\sqrt{15}}{\phi ^{4}} k_{1}^{2} - (1 - \epsilon ) = 0 . \end{aligned}$$
(17)

Similarly, the specific surface area of the dodecahedron model with cylindrical “fat” struts can be expressed as

$$\begin{aligned} S_{v}&= \frac{20 \, \pi \, k_{2}}{\sqrt{5} \, \phi ^{3} \sqrt{3 - \phi } \, d_\textrm{p}} \left( 1 - \frac{1}{2} \sqrt{\frac{2}{3}} \, k_{2} \right) ^{2} + \frac{\left( 1 - \frac{1}{2} \, \sqrt{\frac{2}{3}} \, k_{2} \right) }{\phi \, \sqrt{3 - \phi }} \nonumber \\&\quad \times \left[ \frac{12 \, \pi \, k_{2} \, \left( 1 - \frac{1}{2} \, \sqrt{\frac{2}{3}} \, k_{2}\right) }{\sqrt{5} \, \phi \, \sqrt{3 - \phi } \, d_\textrm{p}} + \frac{\sqrt{15} \, \sin ^{2}\left( \frac{\pi }{5} \right) \, \left( 1 - \frac{1}{2} \, \sqrt{\frac{2}{3}} \, k_{2}\right) ^{2}}{2 \, (3 - \phi ) \, d_\textrm{p}} \right] \, , \end{aligned}$$
(18)

where \(k_{2}\) can be determined from:

$$\begin{aligned}&\left[ \frac{2 \sqrt{10}}{12 \phi ^{4}} - \frac{\sqrt{5} \pi }{2 \phi ^{4}} \sqrt{\frac{2}{3}} \right] k_{2}^{3} + \frac{\sqrt{5} \pi }{\phi ^{4}} k_{2}^{2} + \frac{12 \, k_{2}}{\sqrt{5} \, \phi ^{4}} \, \left[ \frac{5 \, \phi }{4 \, \sqrt{3 - \phi }} - \frac{\pi \, \phi ^{2}}{4 \, (3 - \phi )} \right] \nonumber \\&\quad \times \left( 1 - \frac{1}{2} \, \sqrt{\frac{2}{3}} \, k_{2} \right) ^{2} + \frac{5 \, \sin ^{2}\left( \frac{\pi }{5}\right) }{4 \, \sqrt{15} \, (3 - \phi ) \, \phi ^{2}} \, \sqrt{\frac{1}{4} - \frac{\sin ^{2}\left( \frac{\pi }{5}\right) \, \phi ^{2}}{9 - 3 \, \phi }} \nonumber \\&\quad \times \left( 1 - \frac{1}{2} \, \sqrt{\frac{2}{3}} \, k_{2} \right) ^{3} - (1 - \epsilon ) = 0. \end{aligned}$$
(19)

In Eqs. (16)–(19), \(\phi\) denotes the golden ratio, equal to the value of \(\left( 1 + \sqrt{5}\right) /2\). The expression for the specific surface area of the tetrakaidecahedron model, obtained from Richardson et al. (2000) and given by Eq. (14) with the corrected coefficient, will be used for comparison with other specific surface area predictions later in this study. This is due to the study performed by Maré (2020), who determined that this expression correlated the best with the experimental data obtained from Dietrich et al. (2009) and Garrido et al. (2008) from all the model predictions considered. This is substantiated by the findings of Inayat et al. (2011), as previously mentioned.

The representative unit cell (RUC) modelling approach was first presented by Du Plessis and Masliyah (1988) for foam-like media and was further developed to account for granular and fibre-porous media by Du Plessis and Masliyah (1991), Du Plessis (1991), Du Plessis and Van der Westhuizen (1993), and Du Plessis (1994). The geometric models obtained from this modelling approach will be the main focus of this study due to its simple rectangular geometry that can easily be adapted to accommodate changes to its morphological structure, such as compression, as well as its reported success in providing accurate model predictions for various porous media parameters. Woudberg (2017) identified three main categories of fibre-like media and presented 1D, 2D and 3D RUC models accordingly. The three-strut (or foam) RUC model was furthermore developed by Crosnier et al. (2006) and Woudberg and Du Plessis (2016) and a two-strut RUC model was proposed by Van Heyningen (2014). The 2D and two-strut RUC models, as well as the 3D and three-strut RUC models, respectively, resemble one another in structure, but different modelling approaches have been used to obtain the permeability coefficient predictions of these models. The two-strut and three-strut RUC model permeability coefficients were obtained by applying the assumption of double piece-wise parallel plate flow through the two and three duct sections of these models respectively, whereas the 2D and 3D RUC permeability coefficients were obtained by applying weights to the permeability expressions obtained from the 1D RUC model for transverse flow and the 1D RUC model for parallel flow. A schematic representation of all the RUC models mentioned above is shown in Fig. 2.

Fig. 2
figure 2

RUC models

Full size image

In Fig. 2 the parameters \(U_\textrm{o}\), \(U_\textrm{s}\) and \(U_\textrm{f}\) represent the total volume, solid volume and fluid (or void) volume of the RUC model, respectively. d denotes the cell or face diameter of the RUC model, \(d_\textrm{p}\) once again denotes the pore diameter and the strut diameter \(d_\textrm{s}\) is defined such that \(d_\textrm{s}^{2} = \frac{\pi }{4} b^{2}\) for the 1D, 2D, two-strut and 3D RUC models and \(d_\textrm{s}^{2} = b^{2}\) for the three-strut RUC model. The strut diameter is calculated in this manner due to the 1D, 2D, two-strut and 3D RUC models being used to geometrically represent fibre materials. In the literature, fibres are usually approximated to be cylindrical in shape and the fibre diameter is therefore defined as the diameter of a circle. This is implemented as done by Woudberg (2017) for the 2D and 3D RUC models, where the cross-sectional area of a rectangular strut, as shown in Fig. 2, is set equal to the cross-sectional area of a cylindrical strut (i.e. the area of a square is set equal to the area of a circle with diameter b). The three-strut RUC model is generally used to represent foam materials, where strut diameters vary in shape and are not necessarily regarded as cylindrical. As a result of this b is therefore defined as the side-length of the square strut as represented in Fig. 2c by \(d_\textrm{s}\). The three-strut RUC model will, however, also be used in this study in a comparison involving fibre type media in order to compare its performance with the 3D RUC model, but the same definition of the strut diameter will be maintained. In Fig. 2a the 1D RUC model is shown and the direction of flow through the structure for transverse flow and parallel flow are both indicated. Transverse flow is regarded as flow perpendicular to the fibre axis and parallel flow is parallel to the fibre axis. The 2D (or two-strut) RUC model and its flow directions are shown in Fig. 2b, where in-plane flow is parallel to the plane formed by the two rectangular struts and through plane flow is perpendicular to this plane. Figure 2c shows the 3D (or three-strut) RUC model and consists of three rectangular struts that are mutually perpendicular. The struts represent the randomly distributed fibres in the case of fibre materials and the average strut geometry of foam matrices in the case of foam-like media. Inflow through this RUC model is indicated in Fig. 2c, from where the flow would consecutively be directed into the two transverse directions after which it will flow outwards as indicated.

In this study, a comparison between the 2D, 3D, two-strut and three-strut RUC models is conducted and an evaluation of which models would suit fibre-like media and which would suit foam-like media is also included with regard to permeability and specific surface area predictions. The 2D and 3D RUC models were specifically introduced in order to represent layered fibre arrangements and fibres distributed randomly in space, respectively, as previously mentioned, and the three-strut RUC model was introduced to represent foams. Fibres distributed randomly in space and high porosity foams would be expected to have a very similar structure and therefore large differences between the permeability and specific surface area predictions for high porosities are not expected. This will be verified later in this study. The two-strut RUC model was also applied to fibres by Van Heyningen (2014).

There are extensive studies on permeability predictions of the fibrous porous media types, but less studies on the specific surface area predictions. As previously mentioned, no models predicting the specific surface area of fibre media could be found in the literature and therefore such models will be introduced in this study for the sake of completeness using the RUC modelling approach. It is furthermore noticed that specific surface area predictions often depend on parameters such as the strut and pore diameters. Dietrich et al. (2009) presented an Ergun-type equation for foams in terms of the hydraulic diameter in order to provide a simple method for determining hydraulic diameters for foams from pressure drop measurements even with unknown geometric parameters such as the strut and pore diameters. In a similar manner, the specific surface area will be related to permeability values in this study in order to provide a method of determining the specific surface area of fibrous media from pressure drop measurements with unknown strut and pore diameter values. A comparison between two different approaches in obtaining the specific surface area of the RUC models will therefore be conducted where the one approach makes use of the pore-scale parameters, such as pore and strut diameters, and the other makes use of permeability predictions obtained from either the Darcy or the Forchheimer flow regimes. The former approach will be referred to as the geometric approach, whereas the latter will be referred to as the combined approach, similarly as was done by Woudberg et al. (2021) for compressed and uncompressed fibrous media including the Klinkenberg effect.

The combined approach involving the two-strut model for through plane flow and the three-strut model are the only two that have already been presented in the literature (Maré and Woudberg 2019; Woudberg et al. 2021). The permeability coefficients, obtained for both the Darcy and Forchheimer flow regimes, of each of the RUC models considered in this study will be provided. Most of the permeability coefficients obtained from flow in the Darcy regime for these models, with the exception of the two-strut RUC model for in-plane flow, are available elsewhere in the literature but the Forchheimer permeability coefficients of the 2D, 3D and two-strut RUC models (for both in-plane and through plane flow) will be newly proposed equations and adds novelty to this study. A weighted average method will be proposed for determining the 2D and 3D RUC models from the Forchheimer permeability coefficients predicted by the 1D RUC model. Comparison of the permeability predictions of all the proposed RUC models with one another, as well as with experimental data for the permeability, furthermore adds to the purpose of determining the most suitable and accurate RUC model predictions for the different media types. Since there is a lack of models and data for the specific surface area of fibre materials, this (i.e. proposing the most suitable model) will only be possible by using the 3D and three-strut RUC models, together with data for foam-like media, when predicting the specific surface area. Even though experimental data for the specific surface area for fibre materials were found in the literature, other corresponding parameters such as the permeability and pore or strut diameters were not provided, and therefore, the data could not be used for validation purposes of the models under consideration. A detailed comparative analysis of the 2D and 3D RUC modelling approaches to that of the two-strut and three-strut approaches provides further novelty to this study.

2 Permeability Coefficients of RUC Models

The permeability coefficients of the RUC models are given in this section, along with figures illustrating how the predictions of the different RUC models compare with one another, other models for fibrous porous media obtained from the literature and experimental and numerical data also from the literature.

2.1 2D and 3D RUC Models

The permeability coefficients of the Darcy flow regime of the 2D and 3D RUC models are determined, as previously mentioned, by applying weights to the Darcy permeability coefficient of the 1D RUC model for transverse and parallel flow. The Darcy permeability coefficients for the 2D in-plane, 2D through plane and 3D RUC models are given by Woudberg (2017). The weighting method that was used for the Darcy permeability coefficient was based on the “mixing rules” proposed by Mattern and Deen (2008), called the “unweighted resistivity” and is given by

$$\begin{aligned} \frac{1}{K} = \frac{\phi _{\parallel }}{K_{\parallel }} + \frac{\phi _{\perp }}{K_{\perp }} , \end{aligned}$$
(20)

where \(\phi _{\parallel }\) and \(\phi _{\perp }\) are the weights expressed as fractions and \(K_{\parallel }\) and \(K_{\perp }\) are the Darcy permeability coefficients obtained from the 1D RUC model for parallel and transverse flow, respectively. Woudberg (2017) distinguished between a fully staggered array and a regular array for transverse flow through the 1D RUC model where the difference was found in the coefficient of the \(K_{\perp }\)-expression. The general expression for \(K_{\perp }\) in terms of \(\epsilon\) and b is given by (Woudberg 2017)

$$\begin{aligned} K_{\perp } = b^{2} \frac{\pi (1 - \sqrt{1 - \epsilon })^{3}}{4 C (1 - \epsilon )^{3/2}} , \end{aligned}$$
(21)

where C equals 15 for a fully staggered array and 12 for a regular array. Similarly, the expressions for \(K_{\perp }\) for a fully staggered and regular array provided by the 2D RUC model for through plane flow are given by Woudberg (2017). A transversely isotropic 2D RUC model for through plane flow was also proposed by taking the average of the coefficients for one fully staggered array and one regular array yielding \(C = 13.5\). The latter value will be used in this study in the \(K_{\perp }\) equation for calculations of both the 2D and 3D RUC models. The expression for \(K_{\parallel }\) in terms of \(\epsilon\) and b is given by Woudberg (2017)

$$\begin{aligned} K_{\parallel } = b^{2} \frac{\pi \epsilon ^{3}}{192 (1 - \epsilon )^{2}} . \end{aligned}$$
(22)

For the 2D RUC model for through plane flow, there are two equal rods positioned perpendicular to one another (see Fig. 2b) and to the flow. Therefore, \(\phi _{\parallel } = 0/2\) and \(\phi _{\perp } = 2/2\), along with Eqs. (21) with \(C = 13.5\) and (22), can be substituted into Eq. (20) to obtain the expression for the 2D RUC model for through plane flow. Similarly applying Eq. (20) to the 2D RUC model for in-plane flow and the 3D RUC model, with weights respectively given by \(\phi _{\parallel } = 1/2\) and \(\phi _{\perp } = 1/2\), and \(\phi _{\parallel } = 1/3\) and \(\phi _{\perp } = 2/3\), the expressions for the permeability of these two models are obtained. The 2D and 3D Darcy permeability coefficients are given in Table 1.

Table 1 RUC model predictions for the Darcy and Forchheimer permeability coefficients in terms of the strut diameter and porosity
Full size table

Woudberg (2017) only provided Darcy permeability coefficients for the 2D and 3D RUC models and not Forchheimer permeability coefficients. In this study it is therefore proposed that the Forchheimer permeability coefficient of the 2D and 3D RUC models be determined in a similar way as the Darcy permeability coefficients, in that weights are applied using the following weighting rule:

$$\begin{aligned} \frac{1}{K_\textrm{F}} = \frac{\phi _{\parallel }}{K_{\textrm{F} \parallel }} + \frac{\phi _{\perp }}{K_{\textrm{F} \perp }} , \end{aligned}$$
(23)

where \(K_{\textrm{F} \parallel }\) and \(K_{\textrm{F} \perp }\) are the Forchheimer permeability coefficients obtained from the 1D RUC model for parallel and transverse flow, respectively. The Forchheimer permeability coefficient of the 1D RUC model for transverse flow is given by (Woudberg 20122012):

$$\begin{aligned} K_{\textrm{F}_{\perp }} = d_\textrm{s} \frac{2 \epsilon \left( 1 - \sqrt{1 - \epsilon }\right) ^{2}}{c_\textrm{d} (1 - \epsilon )} , \end{aligned}$$
(24)

where \(c_\textrm{d}\) is the interstitial form drag coefficient. For flow past a square rod, \(c_\textrm{d} = 2\), as determined by Roberson and Crowe (1985) and due to the RUC model geometry resembling square rods, this value for \(c_\textrm{d}\) is therefore assumed. The Forchheimer regime is where inertial drag effects dominate and specifically requires flow past an obstacle. The Forchheimer permeability coefficient obtained from the 1D RUC model for parallel flow will therefore be excluded from the mixing rule, due to there not being an obstruction in the flow in this case. Consequently, the \(K_{\textrm{F}_{\parallel }}\) term will be omitted from Eq. (23), leaving \(K_{\textrm{F}}\) only to dependent on the \(K_{\textrm{F}_{\perp }}\)-term. Equation (24), along with Eq. (23), was therefore used to determine the Forchheimer permeability coefficients for the 2D and 3D RUC models, with the weights defined similarly to the Darcy permeability coefficient case. These expressions are also given in Table 1.

The relations between the face (d), pore (\(d_\textrm{p}\)) and RUC strut dimensions (\(d_\textrm{s}\) and b) of the RUC models are provided in Table 2 so that the permeability coefficients can be determined in terms of either of these parameters.

Table 2 Relations between the dimensions of the RUC models
Full size table

The corresponding relations between the dimensions of the 2D and 3D RUC models provided in Table 2 (Woudberg 2017) are the same since both these RUC models are based on the 1D RUC model geometry. The relations were therefore attained from the 1D RUC model geometry as shown in Fig. 2a, where \(\epsilon = U_\textrm{f}/U_\textrm{o}\). The RUC strut edge width, \(d_\textrm{s}\), in terms of the pore diameter can also be determined from the expression \(d = d_\textrm{p} + d_\textrm{s}\) for all the RUC models as is evident from Fig. 2.

2.2 Two-Strut RUC Model

The pressure drop, and consequently the permeability coefficients, of the uncompressed two-strut RUC model for in-plane and through plane flow are determined in this section. The derivation as presented here is furthermore not found elsewhere in the literature. The permeability coefficients of both the two-strut and three-strut RUC models are obtained by determining the permeability directly from the geometry of the models as shown in Fig. 2b, c, or as previously explained, by applying the assumption of “double” piece-wise parallel plate flow through the duct sections of the models, so no weighting method is used in this case. This is done by first determining an analytical Ergun-type equation for the RUC model in question, as was done for the three-strut RUC model by Woudberg and Du Plessis (2016). For the Darcy flow section of the analytical Ergun-type equation, the following expression for the total pressure drop over the RUC is used (Woudberg et al. 2014):

$$\begin{aligned} \Delta p = \frac{S_{\parallel } \tau _{\textrm{w}_{\parallel }} + S_{\perp } \tau _{\textrm{w}_{\perp }}}{A_{p_{\parallel }}} , \end{aligned}$$
(25)

where \(S_{\parallel }\) and \(S_{\perp }\) are the total solid surfaces parallel and perpendicular to the stream-wise direction of the RUC model, respectively, \(\tau _{\textrm{w}_{\parallel }}\) is the magnitude of the stream-wise average wall shear stress, \(\tau _{\textrm{w}_{\perp }}\) is the magnitude of the transverse average wall shear stress and \(A_{p_{\parallel }}\) represents the cross-sectional flow area in the stream-wise direction. In Eq. (25), the wall shear stress for plane-Poiseuille flow is used due to the assumption of parallel plate geometry and \(\tau _{\textrm{w}_{\parallel }}\) and \(\tau _{\textrm{w}_{\perp }}\) are therefore given by the following expressions:

$$\begin{aligned} \tau _{\textrm{w}_{\parallel }} = \frac{6 \mu w_{\parallel }}{d_\textrm{p}} \quad \text {and} \quad \tau _{\textrm{w}_{\perp }} = \frac{6 \mu w_{\perp }}{d_\textrm{p}} , \end{aligned}$$
(26)

where \(w_{\parallel }\) and \(w_{\perp }\) are the average duct velocities in the stream-wise and transverse directions, respectively, and \(d_\textrm{p}\) is the distance between the parallel plates. Equations (26) are similar to those provided by Woudberg et al. (2014) and Woudberg et al. (2021). The latter authors, however, only applied it to compressed RUC models and therefore had a compression adjustable pore diameter to represent the distance between the parallel plates.

The Darcy flow section of the analytical Ergun-type equation for the two-strut RUC model for through plane flow can therefore be determined in the following manner and results in expressions obtained from Maré (2020), that are similar to expressions given by Van Heyningen (2014) and Woudberg et al. (2021), except this is for the uncompressed RUC model case. From Fig. 2b \(S_{\parallel }\), \(S_{\perp }\) and \(A_{p_{\parallel }}\) can be deduced in terms of the dimensions \(d_\textrm{s}\) and \(d_\textrm{p}\), resulting in

$$\begin{aligned} S_{\parallel } = 4 d_\textrm{s} d_\textrm{p};\quad S_{\perp } = 4 d_\textrm{s} d_\textrm{p} + 2 d_\textrm{s}^{2} \quad \text {and} \quad A_{p_{\parallel }} = d_\textrm{p}^{2} . \end{aligned}$$
(27)

The average duct velocities in the stream-wise and transverse directions are furthermore given by

$$\begin{aligned} w_{\parallel } = \frac{q d^{2}}{d_\textrm{p}^{2}} \quad \text {and} \quad w_{\perp } = \frac{q d}{d_\textrm{p}} , \end{aligned}$$
(28)

and the wall shear stresses are therefore

$$\begin{aligned} \tau _{\textrm{w}_{\parallel }} = \frac{6 \mu q d^{2}}{d_\textrm{p}^{3}} \quad \text {and} \quad \tau _{\textrm{w}_{\perp }} = \frac{6 \mu q d}{d_\textrm{p}^{2}} , \end{aligned}$$
(29)

obtained by substituting Eq. (28) into Eq. (26). Utilizing Eqs. (25), (27) and (29), the resulting pressure gradient is then given by

$$\begin{aligned} \frac{\Delta p}{L} = \frac{\Delta p}{d} = \frac{12 d_\textrm{s} (4 d - d_\textrm{s})}{d_\textrm{p}^{4}} \mu q . \end{aligned}$$
(30)

In order to determine the pressure gradient in terms of only the porosity and the fibre diameter, the relations between the dimensions of the two-strut RUC provided in Table 2 can be used. These relations were derived from the geometry of the RUC model as illustrated in Fig. 2b, where \(\psi\) denotes the geometric factor that is defined in terms of the volume partitioning of the fluid domain in the RUC models and can furthermore be expressed in terms of the porosity alone. Woudberg et al. (2021) gave a detailed explanation of how to calculate the geometric factor, which resulted in the following expression for the two-strut RUC model in terms of porosity:

$$\begin{aligned} \psi = \frac{1}{3} + \frac{2}{3} \sqrt{3 \epsilon + 1} \cos \left[ \frac{1}{3} \cos ^{-1}\left( \frac{9 \epsilon - 27 \epsilon ^{2} + 2}{2 (3 \epsilon + 1)^{3/2}}\right) \right] . \end{aligned}$$
(31)

Making use of the relationships in Table 2, Eq. (30) becomes

$$\begin{aligned} \frac{\Delta p}{L} = \frac{48 (\psi - \epsilon )^{3} (3 \psi + \epsilon )}{\pi \epsilon ^{4} b^{2}} \mu q . \end{aligned}$$
(32)

The Forchheimer term of the analytical Ergun-type equation is given by (Woudberg 20122012)

$$\begin{aligned} - \nabla \langle p \rangle _\textrm{f} = \frac{S_{\text {face}}}{2 \epsilon U_\textrm{o}} \, c_\textrm{d} \, \rho \, w_{\parallel }^{2} \, \underline{\hat{n}} , \end{aligned}$$
(33)

where \(S_{\text {face}}\) is the cross-sectional solid area that faces upstream and \(\underline{\hat{n}}\) denotes the macroscopic flow direction. The Forchheimer term of the analytical Ergun-type equation for the two-strut RUC model for through plane flow can also be calculated using Eq. (33). The total cell volume and the cross-sectional solid area that faces upstream can both be calculated using the geometry of Fig. 2b, resulting in

$$\begin{aligned} U_\textrm{o} = d^3 \quad \text {and} \quad S_{\text {face}} = 2 d_\textrm{p} d_\textrm{s} + d_\textrm{s}^{2} , \end{aligned}$$
(34)

with \(w_{\parallel }\) as given in Eq. (28). The expression for the Forchheimer term as a function of b can thus be determined from Table 2 and results in

$$\begin{aligned} - \nabla \langle p \rangle _\textrm{f} = \frac{2 \psi (\psi - \epsilon )^{2} (\psi + \epsilon )}{\sqrt{\pi } \epsilon ^{5} b} \rho q^{2} \, \underline{\hat{n}} . \end{aligned}$$
(35)

The analytical Ergun-type equation for the two-strut RUC model for through plane flow can finally be expressed as a superposition of Eqs. (32) and (35), i.e.

$$\begin{aligned} \frac{\Delta p}{L} = \frac{48 (\psi - \epsilon )^{3} (3 \psi + \epsilon )}{\pi \epsilon ^{4} b^{2}} \mu q + \frac{2 \psi (\psi - \epsilon )^{2} (\psi + \epsilon )}{\sqrt{\pi } \epsilon ^{5} b} \rho q^{2} , \end{aligned}$$
(36)

and from comparison with Eq. (1) the permeability coefficients, as given in Table 1, can be deduced.

An analytical Ergun-type equation for the two-strut RUC model for in-plane flow can be determined in a similar manner and provides novelty to this study. The following can be deduced for the two-strut RUC model for in-plane flow from Fig. 2b:

$$\begin{aligned} S_{\parallel } = 4 d_\textrm{s} d_\textrm{p} + 2 d_\textrm{s}^{2};\quad S_{\perp } = 4 d_\textrm{s} d_\textrm{p} \quad \text {and} \quad A_{p_{\parallel }} = d d_\textrm{p} . \end{aligned}$$
(37)

The average duct velocities in the stream-wise and transverse direction are given by

$$\begin{aligned} w_{\parallel } = \frac{q d}{d_\textrm{p}} \quad \text {and} \quad w_{\perp } = \frac{q d^{2}}{d_\textrm{p}^{2}} . \end{aligned}$$
(38)

Substituting Eq. (38) into Eq. (26) leads to the following expressions for the wall shear stresses:

$$\begin{aligned} \tau _{\textrm{w}_{\parallel }} = \frac{6 \mu q d}{d_\textrm{p}^{2}} \quad \text {and} \quad \tau _{\textrm{w}_{\perp }} = \frac{6 \mu q d^{2}}{d_\textrm{p}^{3}} . \end{aligned}$$
(39)

Utilizing Eqs. (25), (37) and (39), along with the relations between the dimensions of the two-strut RUC model given in Table 2, the pressure gradient for the Darcy term can be determined, resulting in

$$\begin{aligned} \frac{\Delta p}{L} = \frac{48 (\psi - \epsilon )^{3} (3 \psi + \epsilon )}{\pi \epsilon ^{3} \psi b^{2}} \mu q , \end{aligned}$$
(40)

where \(\psi\) is again given by Eq. (31). The Forchheimer flow term is once again determined from Eq. (33), where \(S_{\text {face}}\) is given by

$$\begin{aligned} S_{\text {face}} = d_\textrm{p} d_\textrm{s} , \end{aligned}$$
(41)

for the two-strut RUC model for in-plane flow and \(U_\textrm{o}\) remains the same as in Eq. (34), thus yielding

$$\begin{aligned} - \nabla \langle p \rangle _\textrm{f} = \frac{2 (\psi - \epsilon )^{2}}{\sqrt{\pi } \epsilon ^{2} \psi b} \rho q^{2} \, \underline{\hat{n}} . \end{aligned}$$
(42)

The analytical Ergun-type equation for the two-strut RUC model for in-plane flow is therefore given by

$$\begin{aligned} \frac{\Delta p}{L} = \frac{48 (\psi - \epsilon )^{3} (3 \psi + \epsilon )}{\pi \epsilon ^{3} \psi b^{2}} \mu q + \frac{2 (\psi - \epsilon )^{2}}{\sqrt{\pi } \epsilon ^{2} \psi b} \rho q^{2} , \end{aligned}$$
(43)

of which the permeability coefficients are given in Table 1.

2.3 Three-Strut RUC Model

Woudberg and Du Plessis (2016) provided the analytical Ergun-type equation of the three-strut RUC model as well as the permeability coefficients for the Darcy and Forchheimer flow regimes. These coefficients were used to determine the expressions for the coefficients in terms of the porosity and RUC strut edge width, along with the utilization of the relations presented in Table 2 and are given in Table 1. The geometric factor in these sets of equations representing the three-strut RUC permeability coefficients is given by Smit et al. (2005)

$$\begin{aligned} \psi = 2 + 2 \cos \left[ \frac{4 \pi }{3} + \frac{1}{3} \cos ^{-1}(2 \epsilon - 1)\right] . \end{aligned}$$
(44)

The relation between \(d_\textrm{s}\) and d for the three-strut RUC model is also found in the study of Woudberg and Du Plessis (2016).

2.4 Model Validation

The permeability coefficients of the 2D, 3D, two-strut and three-strut RUC models, for both the Darcy and Forchheimer regimes, are to be compared to one another, to other models obtained in the literature and to available experimental and numerical data from the literature that represent fibre type media. This will be done by plotting the dimensionless permeability predictions versus the porosity. The predictions of the permeability in terms of the fibre (or strut) diameter, as given in Table 1 will be used (rather than the pore or face diameters) since the customary procedure followed in the literature is to characterize fibres in terms of the fibre (or strut) diameter b. The average fibre diameters of fibres tend to be constant with increase in the number of fibres, whereas the definition of pore diameters of fibre type media in the literature are not consistent and are consequently and furthermore difficult to measure (Huang et al. 2015).

Similarly, the 3D and three-strut RUC models will be evaluated by comparison to foam models and data available in the literature. In this case, however, the predictions of the permeability in terms of the pore diameter are used, obtained by applying the relations provided in Table 2 to the equations in Table 1. This is because for foams the pore diameter is measured and reported more often in the literature rather than the strut diameter.

Fig. 3
figure 3

Dimensionless Darcy permeability coefficient versus porosity: comparison of 2D and two-strut in-plane RUC models as well as models and data from the literature

Full size image

In Fig. 3, the dimensionless Darcy permeability (in terms of the fibre diameter) versus the porosity of the 2D and two-strut RUC models for in-plane flow are compared to one another as well as to two other models from the literature, those of Tomadakis and Robertson (2005) and Van Doormal and Pharoah (2009) given by Eq. (2), with \(\epsilon _{p} = 0.11\) and \(\alpha = 0.521\), and Eq. (3), respectively. These equations were given in terms of the fibre radius, so \(b = 2 a\) was used to find the equations in terms of the fibre diameter. From Fig. 3, it can be seen that the trend of the model predictions are similar, except for the Van Doormal and Pharoah (2009) model which deviates slightly from the others at \(\epsilon > 0.9\), and that the 2D RUC model predictions are slightly higher than the two-strut RUC model predictions for the porosity values indicated. The 2D RUC model for in-plane flow furthermore corresponds better with the predictions of Tomadakis and Robertson (2005) than the two-strut RUC model. The two-strut RUC model, however, corresponds better with the predictions of the Van Doormal and Pharoah (2009) model for high porosities (i.e. above 0.83), whilst the Van Doormal and Pharoah (2009) model provides closer correspondence to the 2D RUC model for \(\epsilon < 0.83\). Fotovati et al. (2011) provided experimental data for the Darcy permeability for in-plane flow of some of the fibre type media they considered in their study. The data for higher porosity values, i.e. two out of the three data points provided, are shown in Fig. 3, and the two RUC models correspond equally well to these experimental data values. The numerical data obtained from Higdon and Ford (1996) are also included. Woudberg (2017) applied the unweighted resistivity mixing rule given by Eq. (20) and the weights used in the 3D RUC model to the numerical data for parallel and transverse flow provided by Higdon and Ford (1996). In this study, the mixing rule was similarly applied in the 2D case by using the weights ascribed to the 2D RUC model for in-plane flow. The resulting values are indicated in Fig. 3. High relative percentage differences are not uncommon where permeability data of porous media are compared to model predictions. Uncertainties in experimental data, especially of porosity measurements, furthermore have a significant effect on percentage difference results for higher porosity values due to the steep increase in permeability at high porosities. The average relative percentage difference in the model prediction of Tomadakis and Robertson (2005) versus the data in Fig. 3 is, for example, over \(3000 \%\). On average, the two-strut RUC model corresponds better with the models and data considered (with an average relative percentage difference of \(156 \%\) when compared to the data) even though the 2D RUC model (which has an average relative percentage difference of \(360 \%\) when compared to the data) corresponds closer to the model of Tomadakis and Robertson (2005).

Fig. 4
figure 4

Dimensionless Darcy permeability coefficient versus porosity: comparison of 2D and two-strut through plane models as well as models and data from the literature

Full size image

The Darcy permeability predictions, dimensionalized by dividing by \(b^{2}\), versus \(\epsilon\) for the 2D and two-strut RUC models for through plane flow are compared to one another in Fig. 4, along with experimental and numerical data obtained from the literature and other models for fibre type media with a 2D fibre arrangement for through plane flow. Models used for this comparison include 2D fibre through plane flow models obtained from Tomadakis and Robertson (2005), given by Eq. (2) with the values assigned for 2D through plane flow fibre arrangements, Van Doormal and Pharoah (2009) given by Eq. (4) and Tamayol and Bahrami (2011), given by Eq. (5). The experimental data set was again obtained from Fotovati et al. (2011), who also provided Darcy permeability values for through plane flow, from Gostick et al. (2006) and the numerical data from Higdon and Ford (1996). Gostick et al. (2006) measured the Darcy permeability of gas flow through common gas diffusion layer materials at different porosities. They tabulated the Darcy permeability values obtained for through plane flow. Fibre diameters for all the samples were furthermore provided and therefore the dimensionless Darcy permeability could be plotted in Fig. 4. The data obtained from Higdon and Ford (1996) was applied similarly as in the case of the 2D fibre arrangement for in-plane flow, but using the weights ascribed to the 2D RUC model for through plane flow instead. From Fig. 4, it can again be seen that the 2D and two-strut RUC models give similar trends and that both the model predictions correspond closely with the other models and data provided.

The two-strut RUC model corresponds closer to the model of Tamayol and Bahrami (2011) than the 2D RUC model and the 2D RUC model in turn corresponds closer to the model given by Tomadakis and Robertson (2005). The latter correspondence is quite remarkable. Taking all the models and data into consideration, the two-strut RUC model for through plane flow performed better on average than the 2D RUC model for through plane flow, where the former has an average relative percentage difference of \(166 \%\) when compared to the data considered and the latter an average relative percentage difference of \(204 \%\).

Fig. 5
figure 5

Dimensionless Darcy permeability coefficient versus porosity: comparison of 3D and three-strut RUC models as well as models and data from the literature

Full size image

In Fig. 5 a, comparison between the 3D and three-strut RUC dimensionless permeability models is shown, along with models obtained from the literature and experimental and numerical data for 3D fibre arrangements. The 3D models from the literature were obtained from Tomadakis and Robertson (2005) and Tamayol and Bahrami (2011), given by Eq. (2), with the corresponding values assigned for 3D fibre arrangements, and Eq. (6), respectively. The experimental data sets were obtained from Manzo et al. (2016) and Theron et al. (2017) and the numerical data set was once again obtained from Higdon and Ford (1996). Manzo et al. (2016) compared the properties of stainless steel fibres with those of glass fibres and provided the porosity and Darcy permeability data of these media. The permeability measurements described appeared to be for through plane flow of air. The data seem to be more applicable to a 3D fibre arrangement due to the thickness of the sheets being much larger than the fibre diameters of the media. Woudberg (2017) utilized data for the Darcy permeability obtained from cotton and polyester fibre materials, of which the experimental characterization is detailed in Theron et al. (2017). The data were compared to the 3D RUC model and is therefore similarly used in the current study for comparison purposes. Finally, numerical data obtained from Higdon and Ford (1996) were also included by using the weights ascribed to the 3D RUC model, and the resulting values are plotted in Fig. 5.

It is evident that the 3D and three-strut RUC models give similar predictions, as expected, and furthermore correspond closely with the model provided by Tomadakis and Robertson (2005). The model provided by Tamayol and Bahrami (2011) shows a different trend. Although the 3D and three-strut RUC models give similar predictions, the three-strut and 3D RUC models have average relative percentage differences of \(260 \%\) and \(274 \%\), respectively, and consequently, the three-strut RUC model corresponds closest on average to the models and data obtained from the literature.

Fig. 6
figure 6

Dimensionless Forchheimer permeability coefficient versus porosity: comparison of all the RUC models for fibrous media

Full size image

In Fig. 6, the dimensionless Forchheimer permeability provided by all the RUC model predictions versus porosity are shown. The RUC models for in-plane flow predict higher \(K_{\textrm{F}}/b\)-values than the RUC models for through plane flow and the RUC models corresponding to 3D fibrous media. There are larger discrepancies between the 2D and two-strut RUC models for in-plane flow than between those for through plane flow. The 3D and three-strut RUC models correspond closely to one another as once again expected. No other Forchheimer permeability coefficient models or experimental/numerical data for flow through fibrous media could be found in the literature for comparison. Tamayol et al. (2012) also mentioned the lack of studies done on higher Reynolds number flow through fibrous media.

Fig. 7
figure 7

Dimensionless Darcy permeability coefficient: comparison of 3D versus three-strut RUC models as well as one other model and experimental data from the literature

Full size image

In the case of the dimensionless Darcy permeability predictions of foam-like media, the equation obtained from the work of Dietrich et al. (2009) and given by Eq. (8), along with experimental data obtained from Kim et al. (2000), Topin et al. (2006), Dukhan (2006), Dietrich et al. (2009) and Mancin et al. (2012) are compared to the permeability predictions of the three-strut and 3D RUC models and presented in Fig. 7. It can be observed that the predictions for the Darcy permeability coefficients of the three-strut RUC model are significantly lower than that of the 3D RUC model and that the model predictions of the three-strut RUC model are closer to that of Dietrich et al. (2009). Kim et al. (2000) provided experimental data for the Darcy permeability coefficients for different porosity values. The pore diameter values were deduced from the PPI (pores per linear inch) number for the purposes of this study, as was done by Dukhan (2006) and Mancin et al. (2012) in their studies. Dukhan (2006) investigated different correlations for the pressure drop for flow through aluminium foam samples in which they considered both their own experimental data and predictions obtained elsewhere in the literature. Dietrich et al. (2009) also provided the required data but for alumina foams and Mancin et al. (2012) provided both the permeability coefficient measurements for copper foams which they obtained from their own experiments. The experimental data given by all these authors for the Darcy permeability are approximated more accurately by the three-strut RUC model than the 3D RUC model, where the three-strut RUC model has an average relative percentage difference of \(507 \%\) while that of the 3D RUC model is over \(2000 \%\) when compared to the experimental data.

Fig. 8
figure 8

Dimensionless Forchheimer permeability coefficient versus porosity: comparison of 3D versus three-strut RUC models as well as models and data from the literature

Full size image

In Fig. 8, the 3D RUC model, the three-strut RUC model, along with models obtained from Giani et al. (2006) and Dietrich et al. (2009) and experimental data from Topin et al. (2006), Dukhan (2006), Dietrich et al. (2009) and Mancin et al. (2012) are displayed for the dimensionless Forchheimer permeability coefficient. Topin et al. (2006) conducted an experimental analysis on metal foams and provided the air inertia coefficient (inverse of Forchheimer permeability coefficient) for allied nickel foams with different porosities, as well as the pore diameters of the foams. The 3D RUC model predictions are once again higher than that of the three-strut RUC model. It can further be observed from Fig. 8 that the three-strut RUC model provides more accurate correspondence with the other foam models and to the sets of experimental data indicated. In this case, the three-strut RUC model has an average relative percentage difference of \(194 \%\) , while that of the 3D RUC model is \(418 \%\).

When comparing Figs. 5 with 7 and 6 with  8, respectively, it is evident that there are larger discrepancies between the 3D and three-strut RUC model predictions when the permeability coefficients are dimensionalized using \(d_\textrm{p}\) than when using b. Fibre media are not usually measured or characterized by the pore diameter and due to this reason, the 3D RUC model shows larger discrepancies when the permeability coefficients are dimensionalized using the pore diameter.

From the evaluation of the permeability coefficients predicted by the RUC models, it can be deduced that in comparison with the other models obtained from the literature and the experimental and numerical data considered, the two-strut and three-strut RUC models give close, but slightly more accurate, predictions for the permeability of fibre type media than the 2D and 3D RUC models where the permeability in terms of the fibre (or strut) diameter is considered. The three-strut RUC model performed better than the 3D RUC model for foam-like media when compared to the literature models and experimental data where the permeability in terms of the pore diameter is considered. It is noted that the permeability predictions obtained from the three-strut RUC model give satisfactory predictions, whether dimensionalized using b or \(d_\textrm{p}\). The adaptability of the three-strut RUC model due to its relatively simpler mathematical expressions for the different fibrous media types adds favour to this model. The two-strut RUC model is therefore the preferred model to use for both in-plane and through plane flow through layered fibre-type media, and for fibres randomly distributed in space, the 3D and three-strut RUC models can be used with the three-strut model gaining slight preference. The three-strut RUC model is furthermore preferred for use for foam-like media.

In the following section, predicting equations for the specific surface area of fibres and foams will be given by using the respective RUC models.

3 Specific Surface Area Predictions of RUC Models

Two approaches will be used to determine the specific surface area predictions: a geometric approach and a combined geometric-kinetic approach.

3.1 Geometric Approach

The geometric approach for determining the specific surface area involves only using the dimensions of a model, which includes the porosity and face, pore or strut diameter. The specific surface area is the total surface area divided by the total volume and can therefore be expressed in RUC notation as by \(S_{v} = S_{f_{s}}/U_\textrm{o}\), where \(S_{f_{s}}\) denotes the total solid surface area within the RUC model in question. The differences between the 2D and two-strut RUC models, on the one hand, and the 3D and three-strut RUC models, on the other hand, encompassed the method of determining the permeability and the relations between \(d_\textrm{s}\) and b, d and \(d_\textrm{p}\), when calculating the permeability. The specific surface areas of the 2D and two-strut RUC models, obtained using a geometric approach, are therefore the same since their geometries are the same. The geometries of the 3D and three-strut RUC models are also the same, and consequently, the specific surface area equations are also the same. The specific surface area expressions based on the geometric approach in terms of \(d_\textrm{s}\) for the RUC models can be determined from their respective geometries as given in Fig. 2b, c. The geometric specific surface area for the 2D and two-strut RUC models are given by the following expression:

$$\begin{aligned} S_{v} = \frac{2}{\psi ^{3} d_\textrm{s}} (\psi - \epsilon )^{2} (\psi + 3 \epsilon ) , \end{aligned}$$
(45)

where \(\psi\) is given by Eq. (31) as a function of porosity and the specific surface area for the 3D and three-strut RUC models in terms of \(d_\textrm{s}\) are given by

$$\begin{aligned} S_{v} = \frac{3}{2 d_\textrm{s}} (3 - \psi ) (\psi - 1)^{2} , \end{aligned}$$
(46)

where \(\psi\) is given by Eq. (44). The derivation of Eqs. (45) and (46) are given by Woudberg et al. (2021) for the non-compressed model predictions, the only discrepancies being that both equations were given in terms of the face and pore diameters and not the RUC strut edge width. The specific surface area in terms of the face and pore diameters can be determined by making use of the equations given in Table 2 for the respective two-strut and three-strut RUC model geometries. Only the equations of the two-strut and three-strut RUC models are utilized because the specific surface area is based on the geometry of the models, and these are the equations derived using the geometry of the 2D (or two-strut) and 3D (or three-strut) RUC models. Furthermore, the specific surface area in terms of the fibre (or strut) diameter, b, can be determined by substituting \(d_\textrm{s} = \sqrt{\pi }/2 \, b\) into Eq. (45) for the 2D and two-strut RUC models or Eq. (46) for the 3D RUC model. For example, the equation for the specific surface area obtained using the geometric approach of the 2D (or two-strut) RUC model in terms of the strut diameter, b, is

$$\begin{aligned} S_{v} = \frac{4}{\sqrt{\pi } \, \psi ^{3} b} (\psi - \epsilon )^{2} (\psi + 3 \epsilon ) , \end{aligned}$$
(47)

and, by making use of the applicable relationship between linear dimensions provided in Table 2, i.e. the relationships provided for the two-strut RUC model, the equation for the specific surface area of the 2D (or two-strut) RUC model in terms of the pore diameter is given by

$$\begin{aligned} S_{v} = \frac{2 \epsilon }{\psi ^{3} d_\textrm{p}} (\psi - \epsilon ) (\psi + 3 \epsilon ) . \end{aligned}$$
(48)

Similarly, the specific surface area in terms of b, d and \(d_\textrm{p}\) can be determined for the other RUC models.

3.2 Combined Approach

In the combined approach for determining the specific surface area, an expression for the specific surface area is obtained in terms of the porosity and permeability coefficients instead of dimensions such as face, pore or strut diameters. This method of determining the specific surface area is therefore useful for when only the porosity and permeability data are available of the fibrous media. The specific surface area expressions obtained using the combined approach entails combining Eqs. (45) and (46) with the respective equations for the permeability predictions given in Table 1 to obtain predictions for the specific surface area in terms of either the Darcy permeability coefficient or the Forchheimer permeability coefficient. In order to illustrate the combined approach of determining the specific surface area, the 2D RUC model for in-plane flow will be considered. The permeability equations provided in Table 1 are given in terms of b, and therefore, the specific surface area equations for any of the RUC models in terms of b are required. The specific surface area equation in terms of b for the 2D RUC model is given by Eq. (47) and by rearranging this equation, b in terms of \(S_{v}\) can be obtained, yielding

$$\begin{aligned} b = \frac{4}{\sqrt{\pi } \, \psi ^{3} S_{v}} (\psi - \epsilon )^{2} (\psi + 3 \epsilon ) . \end{aligned}$$
(49)

Substituting Eq. (49) into the expression for the Darcy permeability of the 2D RUC model for in-plane flow as given in Table 1 then leads to

$$\begin{aligned} K&= \left[ \frac{4}{\sqrt{\pi } \psi ^{3} S_{v}} (\psi - \epsilon )^{2} (\psi + 3 \epsilon ) \right] ^{2} \, \cdot \, \frac{\pi }{4} \left[ \frac{1}{2} \left[ \frac{48 (1 - \epsilon )^{2}}{\epsilon ^{3}} \right] \right. \nonumber \\&\quad +\left. \frac{1}{2} \left[ \frac{13.5 (1 - \epsilon )^{3/2}}{\left( 1 - \sqrt{1 - \epsilon } \right) ^{3}} \right] \right] ^{-1} \, . \end{aligned}$$
(50)

Finally, Eq. (50) can be rearranged to give the specific surface area in terms of the Darcy permeability and the resulting expression is given in Table 3. Similarly, the specific surface area can be determined in terms of the Forchheimer permeability by substituting Eq. (49) into the expression for the Forchheimer permeability of the 2D RUC model for in-plane flow as given in Table 1.

Table 3 Equations for the RUC model predictions of the specific surface area based on the combined approach in terms of the permeability coefficients and porosity
Full size table

The resulting expressions for the specific surface area in terms of the permeability coefficients and the porosity for all the other RUC models are also given in Table 3.

3.3 Comparison with Experimental Data for Foams and Tetrakaidecahedron Model

Five sets of experimental data were acquired from the literature in order to evaluate the specific surface area predictions obtained using the geometric and combined approaches. The data needed encompasses porosity, specific surface area, pore or strut diameter and permeability coefficient values in order to compare both the geometric and combined approaches for obtaining the specific surface area of RUC models with experimental data. Experimental data was found only for foam-like media and none were found by the authors for fibre-type porous media. Consequently, only the 3D and three-strut RUC models could be evaluated in this section. The data sets were acquired from Kim et al. (2000), Topin et al. (2006), Dukhan (2006), Dietrich et al. (2009) and Mancin et al. (2012) and were previously utilized in the permeability section of this study for comparison. All these authors also provided specific surface area values. Kim et al. (2000) only presented Darcy permeability values and not Forchheimer permeability values, and therefore, only the specific surface area in terms of the Darcy permeability coefficient could be evaluated when the combined approaches for determining the specific surface area were considered in this case. Each of these data sets and the corresponding model predictions are consequently compared in parity diagrams displayed in Figs. 9, 10, 11, 12, 13 and 14, i.e. a figure for each model. As discussed in the introduction section of this study, the results obtained from the geometric tetrakaidecahedron model for the specific surface area given by Eq. (14) with a coefficient of 5.621 instead of 12.979 are shown as well, in Fig. 9, for comparison purposes. In Figs. 9, 10, 11, 12, 13 and 14 reference lines are added where the solid black line represents equality between the predicted and measured specific surface area values and where the dashed lines represent the average relative percentage difference of each of the respective models.

Fig. 9
figure 9

Parity diagram of specific surface area: tetrakaidecahedron model versus experimental data

Full size image

In order to present the predictions acquired from the geometric approach, Eq. (46) was utilized, but in terms of the pore diameter. The resulting specific surface area obtained using the geometric approach is therefore the same for both the 3D and three-strut RUC models since the geometry of the 3D and three-strut RUC models are the same and will furthermore be referred to as the three-strut RUC geometric approach in this section. The specific surface area predictions were plotted, using the respective experimentally measured porosity and pore diameter values provided for each of the data sets, against the specific surface area data values obtained from the same respective data sets. The results are displayed in Fig. 10. For the predictions of the specific surface area determined using the combined approach, the equations in Table 3 for the 3D and three-strut RUC model are utilized, where the specific surface area predictions acquired using Darcy and Forchheimer permeability coefficients are plotted in Figs. 11, 12, 13 and 14, respectively, against the specific surface area data provided.

Fig. 10
figure 10

Parity diagram of specific surface area: three-strut RUC model geometric approach versus experimental data

Full size image
Fig. 11
figure 11

Parity diagram of specific surface area: 3D RUC model K-combined approach versus experimental data

Full size image
Fig. 12
figure 12

Parity diagram of specific surface area: three-strut RUC model K-combined approach versus experimental data

Full size image
Fig. 13
figure 13

Parity diagram of specific surface area: 3D RUC model \(K_{\textrm{F}}\)-combined approach versus experimental data

Full size image
Fig. 14
figure 14

Parity diagram of specific surface area: three-strut RUC model \(K_{\textrm{F}}\)-combined approach versus experimental data

Full size image

The average relative percentage differences, as shown in Figs. 9, 10, 11, 12, 13 and 14, reveal that the predictions acquired using the three-strut RUC geometric approach corresponds closest to the experimental data. It furthermore reveals that the three-strut RUC model performs better on average (with an overall average percentage difference of \(32 \%\)) than the 3D RUC model (with an overall average percentage difference of \(33 \%\)) even though (i) the 3D RUC model provides the closest correspondence with the experimental data when the \(K_{\textrm{F}}\)-combined approach is considered and (ii) the difference of \(1 \%\) between the overall average percentage differences of the two models is small, as expected. The K-combined 3D RUC model approach provides less satisfactory correspondence, whilst all the other 3D and three-strut RUC model approaches correspond better to the experimental data than the tetrakaidecahedron geometric model, which is satisfactory.

The models evaluated in Figs. 9, 10, 11, 12, 13 and 14 show a general under prediction when compared to the experimental data, with the exception of Figs. 7 and 12 where the K-combined approaches of the 3D and three-strut RUC models are presented. The K-combined approach of the three-strut RUC model furthermore shows an even scatter of data. This, along with the average relative percentage difference of \(35 \%\) that corresponds to the performance of the tetrakaidecahedron model, gives preference to the model. Another observation is that the combined approach that makes use of the Forchheimer permeability coefficient tend to give closer correspondence with the experimental data than the combined approach that makes use of the Darcy permeability coefficient. The better performance of the former combined approach can be ascribed to the fact that the Darcy permeability coefficient of which the experimental data is used in the model prediction appears to a power of \(-\frac{1}{2}\) in the equation for \(S_{v}\). Any experimental error will thus also be raised to this power which results in a higher percentage difference than in the case of the Forchheimer permeability, which is to a power of \(-1\), due to the permeability measurements being less than 1. The percentage difference of the combined approaches’ predictions with the experimental data of the three-strut RUC model only differ slightly, however, and therefore both the permeability coefficients are still useful to obtain the specific surface area predictions. The percentage difference of the combined approach predictions of the three-strut RUC model furthermore also correspond closely with those of the geometric approach of the same model. In terms of model preference, the three-strut RUC model based on the combined approach is therefore an effective method for determining the specific surface area of foams using the permeability and porosity as input parameters.

4 Conclusion

Comparison of the Darcy permeability predictions of fibre type media revealed that the corresponding 2D and two-strut RUC models, on the one hand, and the 3D and three-strut RUC models, on the other hand, give similar predictions. For Darcy permeability flow through 2D in-plane fibre arrangements, the two-strut in-plane RUC model performed better on average (by over \(200 \%\)) than the 2D in-plane RUC model when compared to the models and experimental data provided. The two-strut RUC model for through plane flow also performed better than the 2D RUC model when compared to the corresponding fibre arrangement models and data and the three-strut RUC model and 3D RUC model gave similar predictions, where the three-strut RUC model gains slight preference, for the comparison involving the Darcy regime flow through fibre type media with random orientations. The Forchheimer coefficient predictions were also provided for fibre type media, but no other models or data were found in the literature for comparison purposes. The only concluding remark in this case is that the 2D and two-strut RUC models provided very similar predictions as well as the 3D and three-strut RUC models. The 3D RUC model does not provide satisfactory predictions for the permeability coefficients when the permeability is dimensionalized with the pore diameter. The average relative percentage difference between the Darcy permeability prediction and the experimental data amounts to over \(2000 \%\) for the 3D RUC model and \(418 \%\) when the Forchheimer permeability prediction is compared to the experimental data for foam-like media. The predictions of the three-strut RUC model, however, result in relative percentage differences of \(507 \%\) and \(194 \%\) when the Darcy and Forchheimer permeability predictions are, respectively, compared to experimental data. These differences should be evaluated in line with relative percentage differences obtained from model predictions from the literature as large as \(3000 \%\), as mentioned in this comparative study. The three-strut RUC model therefore performs better than the 3D RUC model when compared to corresponding models and data for foam-like media. It is noted that large discrepancies between the model predictions and experimental data are not uncommon due to the large scattering of experimental data and uncertainties in experimental measurements. The usefulness of the combined approach proposed in this study for predicting the specific surface area of fibrous porous media is that only measured permeability coefficients and porosity values are necessary to predict the specific surface area, i.e. mercury porosimetry (or other methods) need not be performed to determine the pore diameter or fibre (or strut) diameter. Or else the geometric approach can be used if only geometric parameters are available. The three-strut RUC model performed better on average when compared to the experimental data obtained from the literature, with an average relative percentage difference of \(32 \%\). Evaluation of the foam RUC models showed that the combined approach for obtaining the specific surface area making use of both the Darcy and Forchheimer permeability coefficients, respectively, give satisfactory results where all resulted in an average relative percentage difference of \(40 \%\) or less. Comparison with the Forchheimer permeability coefficient performed better, however, with average relative percentage differences of \(31 \%\) and \(32 \%\) for the 3D and three-strut RUC model, respectively. Based on the Darcy permeability comparisons, the model that would be recommended for use when 2D fibre type media for in-plane or through plane flow are considered is the two-strut RUC model rather than the 2D RUC model. The three-strut and 3D RUC models provided similar permeability predictions, as expected, although the three-strut model gains preference in terms of usefulness and accuracy. For specific surface area predictions of foam-like media, the three-strut RUC model, based on the geometric or combined approach, would be recommended, although the difference from the model predictions provided by the 3D model is only \(1\%\) on average. The equations presented in this study for the permeability and specific surface area are available for other authors to use in their experimental and/or numerical studies for further validation and analysis due to its user friendliness in terms of simplicity and it being functions of measurable macroscopic parameters. Another useful aspect of the RUC models presented is that they can provide predictive equations for the permeability coefficients as well as both approaches of determining the specific surface area. Such a model characteristic could not be found for other models from the literature.