Automated Classification of Well Test Responses in Naturally Fractured Reservoirs Using Unsupervised Machine Learning

Abstract

Understanding the impact of fractures on fluid flow is fundamental for developing geoenergy reservoirs. Pressure transient analysis could play a key role for fracture characterization purposes if better links can be established between the pressure derivative responses (p′) and the fracture properties. However, pressure transient analysis is particularly challenging in the presence of fractures because they can manifest themselves in many different p′ curves. In this work, we aim to provide a proof-of-concept machine learning approach that allows us to effectively handle the diversity in fracture-related p′ curves by automatically classifying them and identifying the characteristic fracture patterns. We created a synthetic dataset from numerical simulation that comprised 2560 p′ curves that represent a wide range of fracture network properties. We developed an unsupervised machine learning approach that can distinguish the temporal variations in the p′ curves by combining dynamic time warping with k-medoids clustering. Our results suggest that the approach is effective at recognizing similar shapes in the p′ curves if the second pressure derivatives are used as the classification variable. Our analysis indicated that 12 clusters were appropriate to describe the full collection of p′ curves in this particular dataset. The classification exercise also allowed us to identify the key geological features that influence the p′ curves in this particular dataset, namely (1) the distance from the wellbore to the closest fracture(s), (2) the local/global fracture connectivity, and (3) the local/global fracture intensity. With additional training data to account for a broader range of fracture network properties, the proposed classification method could be expanded to other naturally fractured reservoirs and eventually serve as an interpretation framework for understanding how complex fracture network properties impact pressure transient behaviour.

Article Highlights

• Detailed characterization of naturally fractured geoenergy reservoirs using pressure transient analysis.

• Proof-of-concept workflow that identifies the characteristic pressure derivative responses using machine learning.

• Identification of key geological controls on pressure derivative responses in naturally fractured geoenergy reservoirs.

1 Introduction

The characterization of fractures is fundamental for assessing geoenergy reservoirs (i.e., geothermal, CO₂ storage, or hydrocarbon reservoirs) as they can control fluid flow in geological formations. Pressure transient analysis (PTA), which is based on the study of the evolution of the fluid pressure in a well during injection or withdrawal periods, could provide key information for estimating properties of naturally fractured reservoirs (NFRs) if the links between the fractures and the pressure derivative responses (p′) are properly understood. These p′ curves (hereafter simply referred to as p′) represent a magnified picture of the variation of pressure with time, which in the context of NFRs are a function of fracture (e.g., aperture, length, intensity, and connectivity) and matrix properties.

Barenblatt et al. (1960) developed the standard analytical model for PTA in NFRs (later introduced to the western literature by Warren and Root 1963). The most prominent feature of this model is the concave-up inflection (the so-called “v-shape”) in p′, which has been largely regarded as the key diagnostic of NFRs. However, Kuchuk and Biryukov (2014) noted that this v-shape signature rarely appears in real well tests.

Different studies (e.g., Kuchuk and Biryukov 2013, 2014; Egya et al. 2019) have demonstrated that the assumptions behind the Warren and Root model (1963) and similar models (e.g., de Swaan 1976; Gringarten 1984; Streltsova 1983) are too restrictive for representing common features inherent to many real fracture systems. That is, NFRs that do not conform to the underlying assumptions of dual-porosity models (e.g., fractures are disconnected or only partially connected, fracture apertures vary, fracture densities are non-uniform across the volume of investigation, wells are connected to the matrix not the fractures) could result in p′ that are significantly different to the one suggested by Warren and Root (1963). In addition, the pressure transient behaviour obtained from dynamic tests reflects weighted averages of the reservoir properties within specific reservoir zones (Oliver 1990), which means that p′ may vary not only as a function of the global fracture properties but also the local fracture characteristics. Considering that numerous possible fracture topologies and internal characteristics exist in nature, it is obvious that p′ can vary widely from one case to another.

Two important challenges are encountered when performing PTA in NFRs. First, it can be difficult to associate p′ with the presence of fractures as the characteristic v-shape that has traditionally been used to infer fracture properties fails to represent many NFRs. It is not known what other p′ could provide a better diagnostic tool in these situations. Kuchuk and Biryukov (2013, 2014) used semianalytical solutions to investigate the pressure transient behaviour of continuously and discretely fractured reservoirs. Egya et al. (2019) used numerical simulation to investigate p′ for different NFRs with varying properties (e.g., fracture conductivity, fracture skin, fracture connectivity, matrix permeability). While these studies have substantially advanced our understanding of PTA in NFR, they are mostly based on a small number of fracture network geometries (e.g., fully connected or fully disconnected fracture networks, periodically spaced fractures, constant fracture apertures, etc.) and hence do not comprehensively classify the different forms p′ can take and link them back to the properties of the fractures. Second, the actual range of variability of p′ in NFRs is unknown but expected to be large. If an effective classification scheme could be developed, it would facilitate identifying general patterns in p′ that can be used to infer the characteristics of the fracture networks.

In this study we present a proof-of-concept workflow that aims to address these two challenges. The method presented in this paper allows us to handle large samples of p′ and classify them based the similarities of the shapes of p′, which is key because the shape of p′ is used is used as a visual indicator to find suitable models for well test interpretation. We show that the proposed method yields consistent results that link p′ to the underlying fracture networks characteristics, thus providing a more robust NFRs diagnosis tool and interpretation framework compared to conventional PTA for NFRs (e.g., using Warren and Root 1963). We note, however, that this proof-of-concept study is limited with respect to the range of fracture and fluid properties in our training dataset and hence not a universal classification. For specific reservoir studies, a bespoke training dataset that captures the range of fracture properties that might be present in the reservoir would need to be created.

To generate a sufficiently diverse sample of p′ from NFRs to test our method, we used numerical simulations in the framework of geological well testing (Corbett et al. 2012). We resorted to numerical simulations and not to real data because we needed to know the exact link between the input (fracture network) and the output (p′) to analyse the consistency of the results. Our dataset encompassed p′ from more than 2500 individual fracture network geometries. Each fracture scenario was generated using a discrete fracture network (DFN) generator that honours strict geological rules (e.g., relationship between fracture length and aperture, fracture spacing, etc.) and is subject to numerical model constraints (e.g., the gridding requires the fracture planes to exist in specific locations). We represented all fractures explicitly through an appropriately refined simulation grid and avoid common modelling simplifications such as dual-porosity or dual-permeability models, thus providing a more reliable representation of the impact of the fractures in the observed pressure transient behaviour.

We used machine learning to classify the dataset of p′. Machine learning techniques have proven effective to analyse and classify other complex geoscience and geoenergy engineering applications that encounter similarly large amounts of (non-linear) data and high dimensionality, for example in groundwater flow modelling (e.g., Sahoo et al. 2017), geophysics (e.g., Ehret 2010; Köhler et al. 2010; Raiche 1991), pore-scale modelling (e.g., Menke et al. 2021; Wang et al. 2021), reservoir geology (e.g., Demyanov et al. 2019; Su et al. 2018), subsurface modelling (e.g., Pyrcz et al. 2006; Scheidt et al. 2015), uncertainty quantification (e.g., Caers et al. 2010; Maldonado-Cruz and Pyrcz 2021), reservoir engineering (e.g., Brantson et al. 2018), or production optimization (e.g., Insuasty et al. 2015).

Specifically, we used clustering, an unsupervised machine learning method, to identify structures in unlabeled data (p′ ensemble) in such way that the objects within a cluster are more similar to each other than to objects in other clusters (Han et al. 2001). We use the k-medoids algorithm to identify the most centrally located p′ in each cluster and assign the rest of the p′ to their closest medoid. This approach allowed us to identify similar p′ patterns in the p′ ensemble. We combined the k-medoids algorithm with dynamic time warping (DTW) to account for the different durations over which individual p′ were sampled (the duration of p′ depends on the underlying fracture properties). DTW is a well-established algorithm that estimates the similarity between two time series (Sakoe and Chiba 1971).

Our approach is fundamentally different to previous applications of Artificial Intelligence in the field of PTA (e.g., Al-Kaabi and Lee 1990; Allain and Horne 1990; Deng et al. 2000; Ershaghi et al. 1993; Kumoluyi et al. 1995; Sinha and Panda 1996; Sung et al. 1995). Previous studies focused on the automatic identification of analytical models for PTA to assist the well test interpretation, assuming that appropriate analytical models to represent real reservoirs exist. As noted above, it is increasingly well understood that the influence of fractures on p′ cannot always be described using analytical solutions. Morton et al. (2013) applied Global Sensitivity Analysis to determine the main fracture properties that govern the evolution of the p′ as a function of time. Their findings were used as a starting point to compare the results of our study.

This paper is organised as follows. Considering that this study combines aspects of fractured reservoir modelling, PTA, and machine learning, we start with a brief review of each field to establish the key terminology and outline the main concepts used in our work. Next, we describe the methodology and experimental design, discuss the pertinent details of the DFN generator, and validate our simulation approach. Given that the k-medoids algorithm combined with DTW are central to our work, we also show a detailed validation of this algorithm. Finally, we present the proof-of-concept classification for the our p′ ensemble, analyse how the identified clusters represent the key behaviours observed in p′ that can be linked back to the characteristics of the underlying fracture network, and discuss the limitations of our approach.

2 Background

2.1 Model Concepts for Fractured Reservoirs

Fracture properties, including but not limited to the fracture aperture a, fracture length $L_{{\text{f}}}$, fracture intensity I, fracture connectivity C, and fracture orientation $\Theta$ influence fluid flow in NFRs.

The fracture aperture a controls the permeability of an individual fracture. Assuming laminar flow through a fracture of length L that is bounded by smooth parallel plates, the relationship between flow rate Q and pressure drop $\Delta p/L$ is proportional to the cube of the fracture aperture a (Snow 1968)

$$Q = \frac{{k ah_{{\text{f}}} }}{\mu }\frac{\Delta p}{L},$$

(1)

where $h_{{\text{f}}}$ is the fracture height, µ is the fluid viscosity, Q is the flow rate, and k is the fracture permeability, which can be approximated as

$$k = \frac{{a^{2} }}{12}.$$

(2)

Equation 1 is applicable for a wide range of fracture apertures (Denetto and Kamp 2016), with a lower limit of apertures of 2 µm (Whitherspoon et al. 1980). Most fractures that act as conduits for fluid flow have apertures above this threshold. In this study, we hence assume that the cubic law (Eq. 1) is appropriate to approximate the permeability of the fractures.

The distribution of fracture apertures across a formation can be modelled through one of the following approaches (unless geomechanical simulations are used): the Barton-Bandis model (Barton and Bandis 1980; Barton 1982), power-law scaling (Hooker et al. 2012, 2014), or (sub-)linear length-aperture scaling (Lawn and Wilshaw 1975; Olson 2003). In this work, we use the length-aperture relationship to model fracture apertures, which relates L and a as

$$a = \xi *L^{\beta } ,$$

(3)

where $\xi$ is a constant that depends on the geomechanical characteristics of the host rock and the exponent β controls the (non-)linear scaling (Scholz 2010, 2011; Olson 2003).

The fracture length L therefore influences the effective reservoir permeability $\overline{k}$ (Narr et al. 2006), not only because long fractures carry fluids across long distances, but also because of the relationship between the L and a (Eq. 3). The distribution of $L$ in a reservoir typically has an exponential form or follows a truncated power law (Gillespie et al. 1993; Marrett 1997), the latter takes the form

$$F\left( L \right) = \left( {\frac{L}{{L_{\min } }}} \right)^{\varrho } ,$$

(4)

where F is the inverse cumulative probability density function and $\varrho$ represents the slope of the distribution.

The fracture intensity I quantifies the degree of fracturing on a given area Λ according to

$$I = \frac{{\mathop \sum \nolimits_{i = 1}^{N} L }}{\Lambda },$$

(5)

where N is the total number of fractures that exist within Λ. The fracture spacing $\epsilon$ (i.e., the spatial distribution of the fractures across Λ) commonly follows a log-normal probability density function (Narr and Suppe 1991). That is, the fractures tend to cluster into closely-spaced groups separated by relatively unfractured rock (Narr et al. 2006). This geological observation is important at the scale of conventional well tests as the existence of clusters of fractures can affect the pressure response in a distinctive manner as compared to more scattered fractures.

The parameter I is related to the fracture connectivity C, which can be computed as

$$C = \frac{J}{\Lambda * N},$$

(6)

where J is the total number of fractures intersections. Especially in fractured reservoirs with low matrix permeability, I and C control the overall impact of the fractures on fluid flow (Bisdom 2016).

The fracture orientation $\Theta$ also controls fluid flow because different fracture sets may have different intrinsic fracture properties (e.g., a or L) and because $\Theta$ impacts in C.

The interplay between a, I, L, and $\Theta$ ultimately governs the nature of the fractured reservoirs and determines the appropriate model concept to represent the fracture system. Kuchuk and Biryukov (2015) proposed four categories for fractured reservoirs:

• Category I. Continuously fractured reservoirs;

• Category II. Discretely fractured reservoirs;

• Category III. Compartmentalized faulted reservoirs;

• Category IV. Unconventional fractured basement reservoirs.

This classification scheme is convenient as it is linked to the topology of the fracture system. Here, we consider categories I and II as we assume networks of naturally occurring fractures in a low-permeability matrix. We did not differentiate explicitly between these categories; instead, we created fracture network samples with I ranging from scattered (discretely fractured) to heavily fractured systems (continuously fractured).

Different model concepts exist to simulate fluid flow through fractures and fracture networks. Berre et al. (2018) summarised these model concepts as implicit fracture representation (single-continuum and multi-continuum models) and explicit fracture representation. The aforementioned Warren and Root (1963) model is an example of an implicit multi-continuum model where the fractures are upscaled to a secondary continuum that interacts with the primary continuum (the rock matrix) via transfer functions. As mentioned previously, we use an explicit representation of the fractures in order to avoid the simplifications normally required for implicit methods. We employ a commercial finite-difference simulator to model flow through the matrix and fractures by solving the pressure diffusion equation for slightly compressible single-phase flow

$$\frac{{\partial \left( {\varphi \rho } \right)}}{\partial p} = \nabla \cdot \left[ {\frac{{\rho {\varvec{k}}}}{\mu }\nabla p} \right] + q\rho ,$$

(7)

where φ is the porosity, q is a source/sink term (i.e., the flow rate at the well), p is the pressure, ρ is the fluid density, and k is the spatially varying permeability tensor. Depending on whether a grid cell represents a matrix block or a fracture, a fixed matrix permeability or a fracture permeability corresponding to the given fracture aperture (Eq. 2) is assigned to this grid block. The simulator that we use discretises Eq. 7 in space using a finite differences scheme with two-point flux approximation and upstream weighting and in time using a fully implicit scheme.

2.2 Clustering

Clustering identifies structures in unlabeled datasets by automatically organizing data into groups where the within-group similarity and the between-group dissimilarity are maximized (Liao 2005). We applied the k-medoids clustering algorithm. The k-medoids method is closely related to the well-known k-means method, with the difference that in k-medoids a member of the population—the most centrally located one, known as the medoid—is used to represent the cluster, as opposed to k-means where the centroid is obtained through averaging of the cluster members. This is a desirable feature for clustering p′ as it is impossible to ensure that an average p′ could be linked to geologically consistent fracture geometries.

K-medoids clustering can be described as follows (e.g., Park and Jun 2009). Let $R = \left\{ {R_{1 } , R_{2 } , \ldots ,R_{n } } \right\}$ denote a set of n objects, $R_{u } = \left\{ {r_{u1 } , r_{u2 } , \ldots ,r_{um } } \right\}$ be the uth ($1 \le u \le n$) data element with m attributes, and c be the number of clusters. The k-medoid algorithm minimizes the objective function O given by

$$O = \mathop \sum \limits_{z = 1}^{c} \mathop \sum \limits_{i = 1}^{{n_{z} }} d\left( {R_{uz} ,M_{z} { }} \right),$$

(8)

where $M_{z}$ is the medoid of cluster z, $n_{z}$ is the number of data elements in R assigned to cluster z, and d is a generic expression to measure the similarity between data elements. In this study, R represents the ensemble of p′ obtained from the simulation of drawdown tests. The parameter m represents the total number of pressure derivative points in the ith simulation run.

For the minimization of O, we applied the partitioning around medoids algorithm (PAM) (Kaufman and Rousseeuw 1990), which is considered a robust solution to the high computational cost of k-medoids clustering (Park and Jun 2009). The iterative PAM method is based on the following steps:

• 1. Initialization: The number of clusters $c\left( {2 \le c \le n} \right)$ and the tolerance ε for the minimization process are selected. The initial cluster medoids $M_{z}$ are assigned arbitrarily.

• 2. Cluster assignment: The data elements $R_{u}$ are assigned to their closest cluster medoid $M_{z}$ based on the selected distance measure d.

• 3. Medoids update: New medoids $M_{z}$ are calculated as the data elements that minimize the distance to other elements in their respective clusters.

• 4. Steps 2 and 3 are repeated until $O^{l} - O^{l + 1} \le \varepsilon$ or the maximum number of iterations $l_{\max }$ is reached; l is the iteration counter.

The initialization step includes two key challenges: (1) selecting the most appropriate number of clusters and (2) randomly initializing the clusters. A fundamental problem in cluster analysis is the appropriate determination of the number of clusters (Cao et al. 2010). We used the elbow method to estimate the threshold for which the decrease in the objective function with every iteration becomes negligibly small. The random initialization of the clusters can lead to local instead of global optima and can hence directly impact the quality of the clusters (Gupta et al. 1999). We overcame this issue by randomly initializing every clustering task ten times and compared the results. Park and Jun (2009) suggested that random initializations of the clusters lead to similar convergence rates compared to more systematic approaches where the initial cluster medoids are selected based on specific criteria (e.g., the outmost objects or the preliminary clustering based on subsets of the population). Recently, Schubert and Rousseeuw (2019) showed that the PAM algorithm can be accelerated, which is particularly beneficial for large datasets. Since our dataset is comparatively small, we use the conventional PAM algorithm and obtain results in less than 30 min using a standard desktop PC.

One challenge in the context of classifying p′ is that the k-medoids method is designed to be applied to static data. However, certain adaptations can improve its performance for time series clustering. Liao (2005) recommended to replace the distance/similarity measure for static data with an appropriate measure for time series. As noted above, DTW is a commonly used similarity measure for classifying time series (Ding et al. 2008; Ye and Keogh 2009). Sakoe and Chiba (1971, 1978) developed the concept of DTW for speech recognition applications. Berndt and Clifford (1994) applied DTW to time series classification domain. Today, DTW is regarded as the most robust distance measure for comparing time series signals (Rakthanmanon et al. 2012). DTW finds the optimal alignment (or coupling) between two sequences of numerical values and therefore captures similarities by aligning the coordinates inside both sequences (Petitjean et al. 2011). This concept is illustrated in Fig. 1. In simple terms, DTW is a distance measure that accounts for the relative shape of the time series.

Fig. 1

Illustration of time series alignment using DTW (modified after Dau et al. 2016). G and V are time series; the light grey lines represent the mapping of points in G onto V (left). Matrix representation of the mapping (alignment) of time series G onto V (right)

More formally, DTW aligns the time series $R_{x } = \left\{ {r_{x1 } , r_{x2 } , \ldots , r_{xi } , \ldots ,r_{xv } } \right\}$ and $R_{{y{ }}} = \left\{ {r_{{y1{ }}} ,{ }r_{{y2{ }}} ,{ } \ldots ,r_{{yj{ }}} , \ldots r_{{yg{ }}} { }} \right\}$ so that their difference is minimized. For this purpose, a matrix $A\left( {v{ } \times { }g} \right)$ is constructed, where the $\left( {i,j} \right)$ element contains the distance $d$($r_{{xi{ }}} ,r_{{yj{ }}}$)—usually the Euclidean distance—between points $r_{{xi{ }}}$ and $r_{yj}$. A warping path $S = \left\{ {s_{1} , s_{2} , \ldots s_{h} , \ldots s_{H} } \right\}$, where $\max \left( {v,g} \right) \le H \le v + g - 1$, is defined as a sub-set of elements of A that satisfies the following three constraints (Liao 2005). First, each element belongs to adjacent cells (continuity). Second, the points are monotonically spaced. Third, the warping path starts and finishes in diagonally opposite corners of A. That is, $s_{1} = \left( {1,1} \right)$ and $s_{H} = \left( {v,g} \right)$. The best possible alignment between pairs of time series is the warping path S that minimizes $d_{{{\text{DTW}}}}$, which is given by

$$d_{{{\text{DTW}}}} = \frac{{\mathop \sum \nolimits_{h = 1}^{H} s_{h} }}{H}.$$

(9)

The warping path in A can be constrained within a specified window $\left| {i - \left( {v/\left( {g/j} \right)} \right)} \right| < w$, where w is a positive integer that reflects the window width. The parameter w is key to avoid forced alignments where a single point in one time series maps onto a large subsection of another time series, which results in a singularity (Keogh and Pazzani 2001). The impact of w on the clustering of p′ will be explored later.

3 Methodology

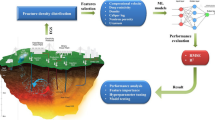
Figure 2 outlines the workflow utilized in this work. Step 1 is the generation of the DFN ensemble, which aims to cover a wide range of fracture network geometries. Step 2 is the numerical generation of the ensemble of over 2500 p′, which provides the data used to classify the pressure transient behaviour for the different NFRs. Step 3 is the configuration and application of the clustering method to classify the p′ obtained in Step 2.

3.1 DFN Models

The DFN models were created using a DFN generator designed specifically for this study. The DFN generator is written in MATLAB and available as open access (Freites et al. 2022). The DFN generator creates stochastic realisations of fracture distributions following a series of geological constraints derived from outcrop observations by Bisdom (2016). The reasons for developing this fit-for-purpose DFN generator rather than using options available in commercial or academic packages are twofold: First, our DFN generator offers more flexibility to represent the relationships of the fracture network parameters L, a, I, and $\epsilon$. Second, our DFN generator allows us to adapt the projection of the fractures in space to ensure compatibility with the structured grids used in the numerical simulations.

A fundamental assumption of our DFN generator is that the fractures are bed-bound, sub-vertical, and with limited extent in the vertical direction and therefore gravity effects are negligibly small. Hence, the resulting DFN can be modelled in 2D. We also assumed that the fractures are organized in two orthogonal fracture sets (x- and y-directions). The reason for such assumption is related to the simulation grid rather than to a particular geological reason. The explicit representation of non-orthogonal fractures would require complex unstructured grids and/or more complex numerical algorithms (e.g., embedded discrete fracture methods), which typically require longer simulation times. As we aimed to minimize the amount of numerical artefacts that could be introduced in the simulations and relied on a standard commercial simulator, we used a structured grid that provided simulation results in manageable CPU time, which is key considering the large number of cases that we had to run. More details about the simulation grid are presented in the following subsection.

The DFN generator creates stochastic realisations of fracture distributions. It requires four input parameters, the fracture intensities $I_{x }$ and $I_{y }$ and the minimum fracture lengths $L_{{x_{\min } }}$ and $L_{{y_{\min } }}$. As noted above, the constraints for these parameters come from the data analysed by Bisdom (2016) for outcrop analogues for fractured reservoirs. The fracture intensity I is used to constraint the amount of fracture planes that the DFN generator creates to complete each directional fracture set. $L_{\min }$ is used to generate the probability density function from Eq. 4 by sampling L for the individual fracture planes. Figure 3 presents an example of the resulting probability density function L for the case where $L_{\min }$ = 2 m and $\varrho = - 1.5$, which are similar values to those observed by Bisdom (2016) in a range of outcrop studies.

Fig. 2

Summary of the workflow used to generate the ensemble of p′ curves to classify the transient pressure behaviour and fracture network characteristics across a range of geologically consistent NFRs

We specified $\beta = 0.5$ (sub-linear fracture aperture-length relationship) and $\xi = 0.0001$ in Eq. 3 to calculate a. We model the spatial distribution of the fractures using a log-normal probability density function with a mean fracture distance of 125 m and standard deviation of 200 m (Fig. 3). These values were chosen because they yield fracture sets with distinguishable groupings along corridors at the scale of our study (1 km × 1 km), while also providing a large numbers of fractures that are spaced between 5 and 20 m. The resulting values for L and $\epsilon$ are also similar to those observed by Bisdom (2016).

The DFN generator executes the following steps to create a fracture set in the x- and y-directions (here the steps for the fracture set in the x-direction are explained, the procedure for the y-direction is analogous):

• 1. A random number is sampled from a uniform distribution within the coordinate limit of the y-axis. This number represents the reference for spacing the fractures in the y-direction.

• 2. The y-coordinate of a new fracture is defined by sampling a number (i.e., distance) from the appropriate probability density function (see Fig. 3) and positioning this coordinate relative to the reference point defined in Step 1. The x-coordinate of this fracture is defined randomly within the limits of the y-axis.

• 3. L for this new fracture is defined by sampling Eq. 4 and the corresponding value of a is calculated from Eq. 3.

• 4. A collision test is performed to detect whether the new fracture is superimposed on an existing fracture. If the test is positive, Steps 2 and 3 are repeated until the new fracture does not overlap with an existing fracture.

• 5. Steps 2–4 are repeated until the desired $I_{x }$ is reached.

Fig. 3

Probability density function used by the DFN Generator for sampling the fracture lengths L using $L_{\min }$ = 2 m and $\varrho = - 1.5$ (left) and probability density function for defining the spatial position of the fractures using an average distance from the reference point of 125 m and standard deviation of 200 m (right)

In order to sample a wide range of fracture network models, i.e., fracture networks ranging from slightly fractured (scattered fractures) to moderately fractured, we used a four-level full factorial design of experiments for the input parameters $I_{x, } I_{y , } I_{\min x, } I_{\min y}$. The chosen values for these parameters are listed in Table 1. We emphasise that these parameters do not encompass the full range of fracture network properties encountered in nature but still provide a dataset with sufficient variability in the resulting p′.

Table 1 Input parameters and values used to generate the fracture networks

The lower bound of I is close to the limit observed by Bisdom (2016) for fracture zones with limited fracture occurrence. The upper bound I is related to limitations of the grid structure in the numerical simulations. As will be discussed below, the minimum separation between two parallel fractures is set to 2 m. If I values larger than 0.25 are selected, the DFN generator has difficulties placing new fractures on the grid. Similarly, the lower bound for $L_{\min }$ is limited by the grid structure in the numerical simulations. The upper bound for $L_{\min }$ was constrained by the shape of the probability density function to favour the generation of a significant number of long fractures, which could potentially span the limits of the model.

The full factorial design of experiments yielded 256 combinations of input parameters. To minimize bias caused by the stochastic nature of the DFN generation process, we created ten equiprobably realisations for each of the 256 parameter combinations, resulting in R = 2560 DFN models. Illustrative examples of the resulting fracture architectures are shown in Fig. 4.

Fig. 4

Illustrative examples of the DFN models generated for different fracture network input parameters: $L_{\min x}$ = 2 m, $L_{\min y}$ = 2 m, $I_{x}$ = 0.0312 m⁻¹, and $I_{y}$ = 0.03125 m⁻¹ (left), $L_{\min x}$ = 2 m, $L_{\min y}$ = 2 m, $I_{x}$ = 0.0312 m⁻¹, and $I_{y}$ = 0.0625 m⁻¹ (centre) and $L_{\min x}$ = 2 m, $L_{\min y}$ = 2 m, $I_{x}$ = 0.156 m⁻¹ and $I_{y}$ = 0.125 m⁻¹ (right). The red lines represent the fracture set oriented parallel to the x-direction and the blue lines the fracture set oriented parallel to the y-direction

3.2 Numerical Simulations to Compute p′ Curves

We performed numerical simulations to generate a synthetic p′ for each of the 2560 DFN models. As noted above, the fracture geometry is 2D based on the assumption that the fractures are bed-bound, sub-vertical and their vertical extent is limited. The simulation model therefore employed a 2D grid as well. We also assumed that the fractures were placed symmetrically along the x-axis so we only modelled half of the x-axis domain. This grid is designed to represent the fractures explicitly without having an excessively large number of grid cells such that each simulation could be run in an acceptable time on a standard desktop PC (i.e., 2–4 h per run). For this purpose, coarse cells with dimensions of 2 m × 2 m were intertwined with finer cells with dimensions of 0.05 m × 0.05 m (Fig. 5). A coarse cell only represents a matrix block. A fine cell represents either a matrix block or a fracture, depending on whether or not a fracture plane intersects this cell. If a fracture plane intersects a fine cell, this cell inherits the properties of the fracture (φ, k, and fracture compressibility γ). If no fracture plane intersects this cell, the matrix properties are assigned to it. A typical fine grid cell has a width of 5 cm, which is larger than the actual fracture aperture. If a cell is intersected by a fracture, the cell’s permeability is rescaled to ensure that the total volumetric flow through this cell is computed correctly.

Fig. 5

Schematic representation of the simulation grid (not in scale). The shaded area corresponds to the region with local grid refinement containing the well

The chosen grid resolution implied that the minimum distance between two parallel fractures and $L_{\min }$ was 2 m, which translated to a maximum possible fracture intensity $I_{\max } = I_{x} + I_{y}$ of 0.5 m⁻¹. The well was located centrally in the y-axis, within a locally refined region of 10 m × 10 m designed to ensure that the early time pressure transient behaviour was captured adequately. Other input parameters used to set up the numerical simulation case are summarised in Table 2.

Table 2 Parameters used in the numerical simulation model

We compared our simulation model against well-known analytical solutions, namely the radial homogeneous models (Earlougher 1977) and the infinite wellbore-intersecting fractures models (Gringarten et al. 1974), following the methodology presented in Freites et al. (2019) and Egya et al. (2019) to ensure that simulation results are free from numerical artefacts arising from the fractures projection onto the simulation grid or the boundary effects due to the assumption of symmetry.

Since the fractures were assumed to extent vertically across a formation of limited height, the porosity of a grid block containing a fracture $\varphi_{{\text{f}}}^{*}$ can be calculated as

$$\varphi_{{\text{f}}}^{*} = \frac{a}{\ell },$$

(10)

and the corresponding fracture permeability $k_{{\text{f}}}^{*}$ as

$$k_{{\text{f}}}^{*} = \frac{k * a}{\ell },$$

(11)

where $\ell$ is the length (or width) of the grid block perpendicular to the direction of the fracture. This rescaling was needed to ensure that the volumetric properties and transmissibilities of the grid blocks containing a fracture were physically correct given that the grid block was still wider than the actual fracture aperture. The process of assigning each fracture from an ensemble member of the 2560 DFN models to the simulation grid was scripted in a commercial geomodelling software.

The following assumptions are common to all simulation cases: Fluid flow is governed by slightly compressible single-phase flow (Eq. 7) in a 2D domain, i.e. gravity forces are negligibly small. We only simulate the drawdown period of a well test (single-rate) and assume the absence of skin, wellbore storage, and superposition effects. We consider only the transient period of the pressure response. Given the parameters in Table 2, it is important to point out that all simulations consider a significant fracture-matrix permeability contrast with k_m = 1 mD and k ≥ 1.68 × 10⁶ mD. The lower bound k = 1.68 × 10⁶ mD represents the permeability of a fracture of $L_{\min }$ = 2 m. The value can be estimated by using $L_{\min }$ = 2 m in Eq. 4 and the resulting a from Eq. 3

We focus only on the transient period by stopping the simulations whenever a change in pressure was detected in the grid cells located at the model boundaries. These grid cells are located 500 m away from the wellbore (Fig. 5). The impact of this approach is that many of the p′ appear to show only partial signals; that is, p′ does not exhibit a recognizable period where individual p′ values are constant other than for the periods that correspond to the matrix permeability. In these situations, the combined permeability of the matrix plus fracture network could not be calculated. It is important to note, however, that a volume of investigation encompassing reservoir boundaries located 500 m from the wellbore is not very different to what we may expect in real well tests and hence the same issue of partial signals can be expected in real field data.

We modelled situations where the well was located in the matrix adjacent to fractures or where the well intersected fractures. As will be shown later, both cases yielded completely different p′. Pressure was recorded as a function of time for the grid block that contained the well. Since the wellbore storage and boundary effects were excluded and the matrix was defined homogeneous, the shape of transient response was a direct consequence of the fracture network properties.

The recorded wellbore pressures were resampled to equally spaced points in time and the first and second derivatives calculated. We defined p′, the first derivative of pressure p at a given time t, as

$$p^{\prime } = \frac{{\left( {\left( {\frac{{\left( {p_{b + 1} - p_{b} } \right)}}{{\ln \left( {{{t_{b + 1} } \mathord{\left/ {\vphantom {{t_{b + 1} } {t_{b} }}} \right. \kern-0pt} {t_{b} }}} \right)}}} \right) * \ln \left( {{{t_{b + 2} } \mathord{\left/ {\vphantom {{t_{b + 2} } {t_{b + 1} }}} \right. \kern-0pt} {t_{b + 1} }}} \right)} \right) + \left( {\left( {\frac{{\left( {p_{b + 2} - p_{b + 1} } \right)}}{{\ln \left( {{{t_{b + 2} } \mathord{\left/ {\vphantom {{t_{b + 2} } {t_{b + 1} }}} \right. \kern-0pt} {t_{b + 1} }}} \right)}}} \right) * \ln \left( {{{t_{b + 1} } \mathord{\left/ {\vphantom {{t_{b + 1} } {t_{b} }}} \right. \kern-0pt} {t_{b} }}} \right)} \right) }}{{ \ln \left( {{{t_{b + 2} } \mathord{\left/ {\vphantom {{t_{b + 2} } {t_{b + 1} }}} \right. \kern-0pt} {t_{b + 1} }}} \right) + \ln \left( {{{t_{b + 1} } \mathord{\left/ {\vphantom {{t_{b + 1} } {t_{b} }}} \right. \kern-0pt} {t_{b} }}} \right)}},$$

(12)

where t is time and b is a counter such that $1 \le b < m$ (Bourdet et al. 1989). The second derivative p″ was defined as

$$p^{\prime \prime } = \frac{{\ln \left( {{{p_{b + 1}^{\prime } } \mathord{\left/ {\vphantom {{p_{b + 1}^{\prime } } {p_{b}^{\prime } }}} \right. \kern-0pt} {p_{b}^{\prime } }}} \right)}}{{\ln \left( {{{t_{b + 1} } \mathord{\left/ {\vphantom {{t_{b + 1} } {t_{b} }}} \right. \kern-0pt} {t_{b} }}} \right)}}.$$

(13)

The resulting p′ and p″ curves were smoothed using moving averages to remove spurious oscillations that could obscure the subsequent analysis. Two examples of this smoothing are shown in Fig. 6, corresponding to a well located in the matrix and a well that intersects a fracture, respectively. Initially, the noise in the second derivative was large at early times (corresponding to seconds in real time) but the smoothing process produced adequate curves for interpretation.

Fig. 6

Examples illustrating the smoothing of the pressure derivative data for a well located in the matrix (left) and well that intersects a fracture (right)

The results in Fig. 6 are presented in terms of the dimensionless variables p_d and t_d, which were defined as

$$p_{{\text{d}}} = \frac{{2 \pi k_{{\text{m}}} h }}{ qB\mu }\left[ {p - p_{{{\text{wf}}}} \left( t \right)} \right]$$

(14)

and

$$t_{{\text{d}}} = \frac{{ k_{{\text{m}}} t }}{{ \mu \left( {\varphi_{{\text{m}}} \gamma_{{\text{m}}} + \varphi \gamma } \right) r_{{\text{w}}}^{2} }}.$$

(15)

where h is the reservoir thickness and $p_{{{\text{wf}}}}$ is the wellbore flowing pressure.

3.3 Validation of the Clustering Algorithm

We first validated the clustering algorithm described above by applying it to two synthetic datasets for which the classification was known. Validation dataset 1 considered R = 16 sets of p′ generated from drawdown tests using four different analytical models (Table 3). Each analytical solution yielded distinct shapes in the p′. For each case we used m = 50 equally spaced points in logarithmic scale. By using different combination of parameters in the analytical models, we introduced significant lateral displacements in the transition between flow regimes while keeping a reference vertical position around a pressure derivative of p′ = 10 (Fig. 7).

Table 3 Analytical models used to create the two validation datasets

Fig. 7

Validation dataset 1 showing the pressure derivatives based on four different analytical solutions (Table 3): the radial homogeneous model with closed boundary (top-left), the dual-porosity model (top-right), the well-intersecting vertical fracture with infinite conductivity model (bottom-left) and the radial composite model (bottom-right). U represents the distance to the closed boundary in the radial homogeneous case and the distance to the discontinuity in the radial composite model; ω is the storativity ratio, λ is the interporosity coefficient, $X_{{\text{f}}}$ is the fracture half-length, $M_{{\text{r}}}$ is the mobility ratio. Note that the mobility ratio $M_{{\text{r}}}$ in the radial composite model refers to contrasts in hydraulic diffusivity between reservoir zones rather than the differences in fluid mobility as in the conventional definition for multi-phase flow

The differences and similarities between the individual p′ are easy to recognise for the human eye: there are four different classes of behaviours, i.e. four different clusters with four members each. The k-medoids algorithm with DTW therefore needs to detect an optimum number of four clusters, each with four members, as well.

The validation dataset 2 was generated using the same analytical models as for the validation dataset 1. However, for validation dataset 2, we introduced a displacement of the curves in the vertical direction by varying the permeability (Fig. 8). DTW can effectively align time series differences in the horizontal direction, i.e., local acceleration or deceleration of the time series, but has problems with vertical translations (Keogh and Pazzani 2001). Validation dataset 2 therefore presented a more challenging case for our approach.

Fig. 8

Validation dataset 2 showing the pressure derivatives based on four different analytical solutions (Table 3). The variations in permeability were set to introduce vertical displacement in the resulting p′ curves

We initially ran the k-medoids algorithm for validation dataset 1 using $c = \left[ {2, 4, 6 ,8} \right]$ clusters. For each case, we generated 10 random initializations and stopped the iteration process at $l_{\max } = 5$ after which we observed no considerable improvement in the minimization of the objective function O (Fig. 9). Note that many cases did not reach the global minimum, which emphasizes the importance of working with multiple initializations. Using the elbow method, we estimated the appropriate number of clusters to describe the validation dataset 1 as c = 4. This value is obviously correct because we used four different analytical solutions to generate the input data.

Fig. 9

Minimization of O using multiple random initializations for the validation dataset 1 for $c = 2 \left[ {2,4,6,8} \right]$ and corresponding change in O (top four plots). For the elbow method, we plot the lowest value of O for each c

To further inspect the clustering results we made use of a confusion matrix (Fig. 10) and introduced the concept of the matching coefficient τ. The confusion matrix allowed us to easily identify whether a member R of the dataset was assigned correctly to each cluster. Elements in the principal diagonal of the confusion matrix represent samples correctly classified, while off-diagonal elements are misclassified. Figure 10 shows the row- and column-normalized summary of correctly and incorrectly classified observations. For validation dataset 1, the k-medoids algorithm correctly classified the four cases for each cluster. In contrast, for validation dataset 2, the confusion matrix shows that 9 of the 16 p′ were not classified correctly.

Fig. 10

Confusion matrix for validation dataset 1 (left) and validation dataset 2 (right). Blue colours indicate samples that have been correctly classified and orange colours indicate misclassified samples

The matching coefficient was defined as $\tau = \frac{{R_{c} { }}}{{n{ }}}$ where $R_{c}$ is the total number of elements in the dataset containing n entries that were correctly classified by the k-medoids algorithm. τ represents a quantitative measure of the quality of the clustering results. For validation dataset 1, we obtained τ = 1. We also note that the cluster medoids $M_{z}$ were correctly identified as the non-extreme members of each model (orange or yellow lines in Fig. 7).

In the case of the validation dataset 2, the clusters were not identified correctly for all input data. When set to the expected value c = 4, τ decreased to 0.4375. The k-medoids algorithm was particularly deficient in classifying the radial homogeneous and dual-porosity cases, assigning them mainly to the vertical fracture model. The reason for this poor performance, as noted above, are the inherent difficulties of the DTW to properly handle the vertical offset between time series. It will be later shown that the p′ derived from our NFRs dataset exhibit significant vertical displacement among the curves so we needed to ensure that the clustering method effectively handled this issue.

We explored two alternative options to try to improve the clustering. In the first option, we standardized the dataset to $\overline{R} = 0{ }$ and $\sigma_{R} = 1$ where $\overline{R}$ and $\sigma_{R}$ are the mean and standard deviations of each dataset member, respectively. In the second option, we took the second derivative p″ (i.e., the shape of p′) of the dataset members (Fig. 11). The first approach increased τ to 0.5625, which is only a marginally better. The second option, however, led to an increase of τ = 0.95.

Fig. 11

Second pressure derivatives p″ for validation dataset 2 (see Fig. 8 for the corresponding p′)

The second derivative p″ provides a convenient way to identify flow regimes in the reservoir. A period of constant p″ is related to particular flow regimes, with the value indicating its type. For example, a wellbore-intersecting vertical fracture with infinite conductivity manifests itself as consecutive periods of p″ = 0.5, variable p″, and p″ = 0 (Gringarten et al. 1974), denoting linear, transition, and radial flow regimes, respectively (Fig. 11).

In addition, using p″ has obvious advantages that are rooted in the physical processes governing fluid flow in fractured geological formations. First, p″ measures the rate of variation of the first derivative, which is a function of the fracture properties. Second, p″ effectively removes a major part of the vertical offset among the curves, allowing a direct comparison of the shapes of the p′. With this approach, both the vertical and the horizontal displacements of the time sequences are appropriately handled, by using p″ for vertical and DTW for the horizontal displacement between pairs of time sequences.

Figure 12 shows the confusion matrix for the clustering exercise using p″ instead of p′. One instance of the radial composite model (blue line in Figs. 8 and 11) was misclassified as being part of the vertical fracture model. While this classification error only occurs in dataset 2, the analysis shows that even an improved clustering approach may not be able to correctly identify all cases. These classification errors are due to the chosen distance metric and the clustering algorithm itself.

Fig. 12

Confusion matrix for the validation dataset 2 using p″

Nevertheless, the performance of the clustering process using p″ proved to be reliable enough to be deployed in the automated classification exercise for the entire p′ ensemble.

4 Results

Figure 13 shows the rate at which the objective function O (Eq. 8) changes as a function of c for the classification of the R = 2560 cases, using p″ as the classification variable. We tested classifications using $c = \left[ {2,{ }4,{ }6{ },8,10,12,16,20} \right]$ and $w = \left[ {5,{ }10,{ }20,{ }40,{ }100} \right]$. By including different w in the analysis, we were able to track the minimization of O while assessing the amount of warping required for this purpose. We performed this tracking to avoid extreme distortions in the alignment between the cluster medoids and the respective cluster members. Using the elbow method, we identified that no significant reduction in O was obtained for c > 12 independently of w.

Fig. 13

Elbow method for different window sizes w for the dataset comprising 2560 p′

In order to quantify the amount of warping considered for each combination of c and w, we defined the warping factor W as

$$W = \frac{{\left( {\mathop \sum \nolimits_{z = 1}^{c} \mathop \sum \nolimits_{e = 1}^{{n_{z} }} \frac{{L_{w} - \max \left( {L_{{M_{z} }} ,R_{uz} } \right)}}{{\max \left( {L_{{M_{z} }} ,L_{{R_{uz} }} } \right)}}} \right)}}{n},$$

(16)

where $L_{w}$, and $L_{{M_{z} }}$ refers to the length of w and $M_{z}$, respectively. $L_{{R_{uz} }}$ is the length of the elements of R assigned to cluster z. Note that W is bound by $0 \le W < 1$. W values close to one imply that a high amount of warping was required to align the pressure derivative curves. It is ideal to obtain the best possible alignment with the least amount of warping, i.e., W close to zero. Figure 14 shows O as a function of w for c = 12. Note that W decreases noticeably for w < 20. However, this decrease is at the expense of a substantial increase in O. We selected the number of clusters c = 12 for the pressure derivative curves as suggested for w = 20, which is an acceptable trade-off between accuracy and warping.

Fig. 14

Change in objective function O and warping factor W as a function of window size w for $c = 12$ clusters for the entire dataset of 2560 p′

Figures 15 and 16 show the results of the clustering exercise for p′ and p″, together with their respective cluster medoids. Since the medoid curves represent the most centrally located p′ shape in each cluster they are likely to concentrate most—or at least some—of the relevant features of the collection of p′ shapes assigned to each cluster. The use of the cluster medoids for assisting the interpretation of p′ is discussed later.

Fig. 15

Clustering of p′ for the entire dataset. The black line represent the medoid of each cluster, the grey lines the remaining curves in the cluster

Fig. 16

Clustering of p″ for the entire dataset. The black line represent the medoid of each cluster, the grey lines the remaining curves in the cluster

We evaluated the performance of the clustering algorithm by using the silhouette index Y, which is widely used for clustering validation. Y measures how close a point in one cluster is to other points in neighbour clusters (Kassambara 2020) and is calculated as

$$Y = \frac{B\left( u \right) - A\left( u \right)}{{\max \left( {B\left( u \right),A\left( u \right)} \right)}}\quad {\text{with}}\;\left( { - 1 \le \gamma \le 1} \right),$$

(17)

where $A\left( u \right)$ is the average distance from the uth p″ curve to the other p″ curves in the cluster and ${ }B\left( u \right)$ is the minimum average distance from the uth p″ to the other p″ in a different cluster, minimized over clusters. Note that α values close to one indicate that the observation (in this case the p″) is well clustered while Y values close to zero indicate that the observation lies between two clusters. A negative Y value indicates that the observation is probably in the wrong cluster. Figure 17 shows the silhouette plot for the clustering results depicted in Figs. 15 and 16 with c = 12. In general, the clustering yields acceptable values with an average silhouette index of $\overline{Y} \approx 0.3$; only 12% of the samples have been misclassified as evidenced by the negative Y values in Fig. 17.

Fig. 17

Silhouette plot for the clustering results of entire dataset of 2560 p′ (Figs. 15 and 16), indicating how close each p″ in the dataset is to the cluster to which it was assigned

5 Discussion

Figures 15 and 16 show the significant variability of the p′ shapes that one could expect to see in well tests in NFRs. The clustering provided an effective way to group the curves based on the similarity of their shapes. An important question is whether this p′ classification is physically consistent and can capture the similarities (or dissimilarities) of the underlying fracture network properties.

We hence created a visual representation of the classification results by applying non-metric multi-dimensional scaling (MDS). MDS is a dimensionality reduction technique and highlights the relative distances, measured using DTW, between the p″ cluster members. Figure 18 shows that the clusters of p″ are relatively well separated in 3D space. More distant cluster regions indicate more distinct differences in the p′ between clusters, which could facilitate the identification of characteristic patterns in the p′ and the subsequent association of these patterns with the properties of the fracture networks.

Fig. 18

3D representation of the relative distance between the p″ after dimensionality reduction using multi-dimensional scaling. Each colour represents a different cluster. The larger points represent the medoids of each cluster

The specific way in which the clusters were organized in 3D space also provided important information. p′ belonging to clusters 1–8 plotted narrowly along the origin of the x-axis, while clusters 10–12 plotted at a significant distance away from the origin of the x-axis, indicating that these p′ were considerably different in comparison. The reason for this difference becomes clearer in Fig. 19, which shows a box plot summarizing the median and the 25 and 75 percentiles of the average fracture length $\overline{L}$, the average fracture aperture $\overline{a}$, the total fracture intensity $I = I_{x} + I_{y} ,{ }$ the distance between the wellbore and the nearest fracture $d_{fw}$, and the fracture connectivity C for the entire ensemble of 2560 p′. We used the median of each parameter as reference in the following analysis. We reiterate that this analysis does not mean to imply that the results are universal but is intended to confirm that, for the given dataset, the results are consistent and interpretable.

Fig. 19

Box plots showing median, P25 and P75 for $\overline{L}$, $\overline{a}$, I, $d_{fw}$, and C. The red crosses represent outliers

Clusters 1–9 mainly contained cases where the wellbore was located in the matrix (89% of all p′ in the cluster), as opposed to clusters 10–12, which almost exclusively contained cases where the well intersected a fracture (99% of all p′ in this cluster). The strong dependency of p′ on the position of the wellbore with respect to the fracture network may indicate that $d_{fw}$ is a first-order control for the shape of p′. A similar observation was made by Morton et al. (2013) who established that the early time behaviour of p′ is dominated by whether the well intersects a fracture. While it seems intuitive that the p′ would be completely different depending on the position of the well relative to the fractures, the widely used Warren and Root (1963) model is unable to represent the behaviour observed in cases where the well intersects fractures.

Clusters 1 and 2 rank among the lowest in terms of I (0.12 m⁻¹) and  C (7.37 × 10⁻⁷ and 5.60 × 10⁻⁷ m⁻², respectively), but highest in terms of $d_{fw}$ (4.6 and 4.1 m, respectively). These factors combine for a very small deviation from the early time radial flow regime, which reflects the matrix properties for cases in which the fracture do not intersect the wellbore. However, it is noticeable that 20% of the members in cluster 1 show a similar shape in p′ when the fracture networks are well connected and fracture intensity is high. This observation suggests that intensively fractured networks may show derivatives similar to that of homogeneous single-porosity (matrix-only) reservoirs, with the difference that the permeability would correspond to the contribution of both the matrix and fracture systems. The relative closeness of cluster 12 to cluster 1 (Fig. 18) seems to support this observation, i.e., the shape of clusters 1 and 12 show a relatively low deviation from a radial flow regime where p″ = 0.

Clusters 3–9 showed a much more distinct influence of the fracture compared to clusters 1 and 2. This difference was driven either by a smaller $d_{fw}$, higher I and C, or a combination of both. Within the subgroup of clusters 3–9, there were evident similarities in p′ (especially between clusters 3–5 and clusters 6–9) that complicated linking particular clusters of p′ to their underlying fracture network characteristics. All the cases where the well was located in the matrix showed a radial flow regime with p″ = 0.5, followed by a downward trend with p″ < 0. The relative difference among the p′ curves falls within the magnitude of p″ over the period during which p″ < 0 and the transition to p″ ≥ 0.

Cluster 3 contained cases with slightly longer fractures ($\overline{L} = 15.4$ m) and networks of higher connectivity (C = 8.3 × 10⁻⁷ m⁻²) compared to cluster 4 ($\overline{L} = 11.8$ m and C = 7 × 10⁻⁷ m⁻²). However, the cases in cluster 4 seem to be more affected by the presence of fractures because many cases in cluster 4 deviate strongly from the initial radial flow regime and reach more negative values for p″ compared to the cases in cluster 3. We used the medoids of the respective clusters to further analyse them.

Figure 20 shows the local values for I as a function of the distance from the wellbore D for the medoids of clusters 3 and 4. Despite the fact that the overall fracture intensity was the same for both cases (I = 0.15 m⁻¹), the spatial distribution of the fractures differ. The fracture intensity I close to the wellbore was substantially larger for the medoid of cluster 4 while $d_{fw}$ was smaller (8.2 m vs. 4.1 m). In general, these factors (i.e., smaller $d_{fw}$ and larger local I) increased the influence of the fractures on the shape of p′, which caused some of the difference between the members of cluster 4 and cluster 3.

Fig. 20

Fracture intensity I as function of distance from wellbore D for the medoids of clusters 3 and 4

Clusters 6–9 mainly represented cases where the well is located in the matrix which was intensely fractured such that all fractures were well connected. In these scenarios, the pressure perturbation migrated quickly away from the well towards the model boundaries and hence masked the formation of flow regimes beyond the period of p″ < 0.

Clusters 10 and 11 contained cases with early time linear flow regime where p″ = 0.5. Such behaviour is typically attributed to well-intersecting vertical fractures with infinite conductivity (Gringarten et al. 1974). Note that we worked with fracture permeabilities that can be considered as infinitively conductive (k ≥ 1.65 × 10⁶ mD). Cluster 10 contained p′ that are mostly associated with scattered fractures with poor connectivity. In these cases, any fracture that intersected the well tended to be isolated from its neighbouring fractures. The p′ in cluster 11 showed a similar behaviour but fractures that intersect the well tended to be better connected to the fracture network.

Despite the fact that the vast majority of p′ in cluster 12 also resembled the classical shapes of a pressure transient with well-intersecting fractures, the early time linear flow regime was not observed. This absence was mainly because cluster 12 contained well connected fracture networks with high fracture intensity that masked the development of linear flow.

In summary, the clustering led to consistent separation of clusters with distinct p′, which encapsulated the characteristic properties of the fracture networks in the current dataset, namely $\overline{L}$, $\overline{a}$, I, $d_{fw}$ and C (Fig. 20). Within the constrains of the dataset, $d_{fw}$ appears to be a primary control for the shape of p′, separating the cases in two distinctive groups, clusters 1–9 and clusters 10–12. Within these sub-groups $\overline{L}$, $\overline{a}$, C, and the local and global values for I, are secondary controls for p′.

6 Limitations

We presented an analysis of how the clusters of p′ can be linked back to the fracture properties encapsulated in our fracture network ensemble. Despite the significant variability observed in p′ for this particular dataset, we were able to classify behaviours that allows us to identify general patterns in the pressure transient data which can assist well test interpretations.

However, we emphasise that our classification results are not universal. While it is likely that some of the observations could be applicable to other NFRs as our dataset contains a wide range of fracture networks that might replicate key flow behaviours found in nature, there are two reasons why the classification approach is still a proof-of-concept. First, the generation of the fracture networks is based on a series of assumptions (e.g., sub-vertical and bed-bound fractures, 2D orthogonal fracture sets, particular statistical distributions) that are not universally applicable to all NFRs. Second, the clustering method is not yet able to provide a classification of p′ that is both, uniquely interpretable and physically consistent; some degree of human judgement is required to interpret the classification results. For example, clusters 3–5 and clusters 6–9 were recognized as different responses but look similar on visual inspection. Hence, a well test interpreter may decide to merge clusters 3–5 and 6–9.

The use of the medoids as a reference p′ is also important. Type curves based on pressure derivatives have been widely used in well test interpretation (Bourdet et al. 1983). It would be ideal if a more universal classification could provide a similar type curve concept. The medoids in our dataset appear to capture the main trends in p′ that are representative of the other cluster members, but it is not yet clear if this observation will hold for a larger dataset with a wider range of fracture network properties. The similarity among the cluster members governs the representativeness of the medoid as reference curve for the cluster: the largest the dissimilarity among the p′ members of one particular cluster corresponds to the least representative medoids. Additional training data is needed for further fracture networks to confirm if trends in p′ are more universal. Alternatively, specific training data that capture uncertainties in fracture network properties in specific field cases need to be constructed to identify trends in p′ on a case-by-case basis.

Lastly, the use of p″ as classification variable may also pose a challenge because p″ amplifies the noise in the pressure signal for both, real field data and data from numerical simulations. An appropriate smoothing of p″ appears to alleviate this problem (Fig. 6) but it remains to be seen if this holds for a much larger dataset as well.

7 Conclusions

In this paper, we presented the results of an automated clustering method that allowed us to classify pressure derivative responses in NFRs. The p′ ensemble is based on a dataset containing over 2500 individual curves which were created using numerical simulations that employ geologically consistent discrete fracture networks.

We showed that the k-medoids algorithm combined with dynamic time warping as similarity measure and second pressure derivatives p″ as the clustering variable allowed us to classify the first pressure derivatives based on the similarities of their overall shape. Despite the variability of p′ in our dataset, only 12 clusters were needed to describe the behaviour of the full dataset in a physically and geologically consistent way. These clusters capture the main trends in p′, and the trends can be linked to the underlying characteristics of the fracture networks.

We identified that the distance from the well to the closest fracture was a first-order control on the shape of p′. That is, wells connected to the matrix showed a distinctly different early pressure transient behaviour compared to wells that were connected to an individual fracture or a network of fractures. The effect of the fracture length and apertures, the local and global fracture intensity and the fracture network connectivity are second-order controls.

Our classification results are not universally applicable to NFRs and more work is needed to account for a wider set of fracture network properties and/or specific field applications. However, some of the more general trends observed in the shape of p′ were still valuable to quantify pressure transient behaviours in naturally fractured reservoirs and establish links to the fracture network characteristics. Hence, the classification method proposed in this study could be replicated for different datasets, providing an interpretational framework that will help us to better quantify the presence and properties of fracture networks in subsurface reservoirs.