1 Introduction

Advanced horizontal drilling techniques and multistage hydraulic fracturing have revolutionized the extraction of hydrocarbons from unconventional reservoirs (Liu et al. 2019; Yasin et al. 2018b). These techniques have a significant potential for storing large volumes of carbon beneath complex subsurface geological conditions and enhancing geothermal systems (EGS) (Vo Thanh et al. 2022; Yasin et al. 2022a). Therefore, the subsurface fracture network should be identified, mapped, and characterized to optimize completion designs for enhancing hydrocarbon production, developing high permeability zones for EGS, and determining reservoirs' integrity for capturing and storing carbon. A natural fracture significantly impacts reservoir behavior, affecting fluid flow and conductivity. Identifying and characterizing these fractures will allow us to understand better the subsurface and design completion strategies that maximize production and minimize costs (Siler et al. 2019; Yasin et al. 2023a).

In recent years, the growing global energy demand has led to EGS becoming an attractive option for sustainable energy production and reducing carbon emissions (Okoroafor et al. 2022b). However, the successful management of EGS reservoirs depends heavily on reservoir simulation, which can be expensive due to factors like reservoir heterogeneity, matrix-fracture interactions, and complex physical processes (Ishitsuka and Lin 2023). The development of EGS requires improving the permeability of hot crystalline rocks. Still, significant technical and non-technical challenges must be overcome for EGS reservoirs to be economically viable. EGS requires an increase in the permeability of deep rocks as their natural permeability is usually insufficient (Jia et al. 2022). Technical barriers include the need for better stimulation technologies, while non-technical obstacles include land access, permitting, and financing issues.

Geothermal energy exploration and development demand a complete understanding of geothermal reservoirs, including lithology, porosity, permeability, reservoir temperature and pressure, stress, faults and fractures, and chemical composition. The availability of geochemical, geological, and geophysical information in oil-producing regions, along with an extensive understanding of geological models and geothermal resource assessment, are vital for evaluating and developing geothermal resources (Xiao et al. 2023; Guo et al. 2024). A recent study conducted in Nevada and Oregon (USA) showed potential geothermal reservoirs in structurally complex geological settings. Siler et al. (2019) reported that closely spaced and intersecting faults in such settings exhibit high-temperature anomalies. The study also suggests that structurally complex geological settings may be conducive to geothermal energy development. However, the complexity of the geological environment makes it challenging to identify, evaluate, and develop a fracture network. Further research in structurally complex geological settings could help unlock new renewable energy sources and contribute to a more sustainable future (Kölbel et al. 2020).

With technological advances and a better understanding of geothermal systems, detecting and extracting proper quantities of energy from geothermal systems is becoming more accessible. Energy from geothermal sources can become the world's largest energy source, displacing oil and natural gas combined in terms of energy supply potential (Okoroafor et al. 2022a). Over the past few decades, it has gradually developed into a clean, renewable form of thermal energy in urban and rural areas. Geothermal energy is widely accepted due to its reliability, low cost, ease of maintenance, and the fact that there are no ground-related restrictions regarding laws and policies. US Geological Survey report estimates that at least 70 percent of the world's geothermal resources remain unexplored (Siler et al. 2019). It is found throughout the world. Developing geothermal resources safely and responsibly can significantly benefit local communities, the economy, and the environment.

Because of recent scientific and technological breakthroughs, several authors have tried to investigate the true potential of geothermal fluid by applying the most advanced machine learning (ML) approaches, such as different inversion schemes used for seismic data (Qiang et al. 2020). Soft computing techniques including convolutional neural networks (CNN) offer solutions to seismic inversion for predicting the spatial variation of rock properties. Okoroafor et al. (2022b) used the CNN method to predict fracture development zones in the geothermal reservoir by mapping logging porosity and seismic multi-attributes. Dalgaard et al. (2019) used artificial neural networks–Hidden Markov models to classify lithofacies and estimate porosity in geothermal reservoirs. Recently, Yasin et al. (2023b) used a soft-porous petrophysics model combined with a CNN-LSTM-based deep neural network to extract porosity and fractures in geothermal reservoirs. They validated the model's fracture prediction results using formation micro-image (FMI) logging. The application of ML techniques to engineering problems has been successful due to their ability to predict outcomes and optimize processes. Nevertheless, one of the significant challenges of this application is the presence of human bias in the selection of ML algorithms and hyperparameters (James et al. 2022; Okoroafor et al. 2022b). It is important to note that this bias is highly dependent on the expertise and domain knowledge of the operator, which may result in suboptimal selections that do not accurately reflect the problem at hand. The impact of human bias can be reduced through physics-informed ML. These ML models, incorporating informed prior knowledge and constraints on the issue, can offer consistent prediction results in extrapolation tasks and remain robust to dataset limitations (Karniadakis et al. 2021). The physics-informed neural network can predict the fracture development zone, temperature, and pressure in various geothermal reservoirs in structurally complex geological settings (Ishitsuka and Lin 2023). The neural network trains the data with physics-informed knowledge to ensure that intelligent decision tools can be adopted for similar data characterization. Therefore, the physics-informed neural network has the potential to map natural fractures using well logs to optimize the fracture mapping for EGS at a low cost.

In addition to ML, thin section analysis FMI logs and scanning electron microscope (SEM) are useful for identifying natural fractures. Examining rock samples under a petrographic microscope allows one to gain insight into their microscopic structure (Ren et al. 2022; Healy et al. 2017). With specialized staining techniques, fractures become more visible, and it is possible to differentiate between primary structures, such as bedding planes, and secondary features, like fractures (Golsanami et al. 2019). These are valuable methods for understanding the characteristics and nature of rock fractures, but they are time-consuming, labor-intensive, and prone to biases.

The geometries and fracture networks of naturally fractured reservoirs play a significant role in the fluid flow of geothermal energy production. Identifying faults and fractures is, therefore, crucial to unlocking the full potential of a fault-bounded EGS (Okoroafor et al. 2022a; Zhou et al. 2021). A sonic and micro-resistivity imaging log has traditionally been used to describe natural fracture intensity (i.e., how many fractures are present per meter). However, these techniques have several significant disadvantages, including the risk of human bias during the interpretation of logs and the long interpretation time required. Although these deficiencies are well-known within the industry, no standard procedures have been developed to address them. Recent research has demonstrated that fracture zones have marked effects on the log reading (Aghli et al. 2019, 2016; Aguilera 2008; Tokhmchi et al. 2010; Tokhmechi et al. 2009). According to these studies, density, resistivity, sonic, and porosity logs, in particular, gamma-ray (uranium), and caliper logs, in general, are the best tools for mapping fractures or fracture zones (Martinez et al. 2002; Saboorian-Jooybari et al. 2015; Yasin et al. 2018a). A resistivity log can detect changes in electrical conductivity caused by fractures. Fractures are generally characterized by lower resistivity values than the surrounding rock, making identifying their location and orientation possible. Additionally, sonic and density logs may help identify fractures, as they detect changes in rock mechanical properties associated with fractures (Yasin et al. 2022b).

In this study, an analysis of fractures in geothermal carbonate reservoirs was performed using four supervised ML techniques: multilayer perceptron (MLP), random forest (RF), extreme gradient boosting (XGBoost), and support vector regression (SVR). The ML models have been trained and tested based on diverse well-logging data, including the natural fracture density from acoustic borehole image logs. It has been demonstrated that ML algorithms with optimized hyperparameters and data division can predict fractures with high accuracy from limited standard well logs through the application of ML algorithms. The application of ML algorithms in the exploration and exploitation of geothermal resources has been demonstrated to be successful in identifying fractures in heterogeneous reservoirs.

2 Contributions to the current literature

The characterization of fractures is an essential part of the geothermal reservoirs. They play an important role in increasing the efficiency of geothermal systems since they act as flow conduits and contribute significantly to reservoir permeability. Fractures are particularly important in EGS. Characterizing fractures involves determining their nature, network, density, and stress-related properties, which is relevant for drilling wells and modeling and predicting geothermal reservoir performance (Okoroafor et al. 2022b; Yasin et al. 2023a, b). Four main types of fractures are typically encountered in the reservoir rock: netted fractures, straight split fractures, oblique fractures, and horizontal fractures (Wang et al. 2023). A typical fracture density in the reservoir is 10 to 20 fractures per 10 m, with an average fracture width of 0.2 to 9 mm and an average fracture length of 0.5 to 48 cm.

It is laborious and time-consuming to manually pick the fractures using resistivity image logs spanning over 1000 m. There is no doubt that human input is required in various processes. However, the quality of such input may not always be perfect. Consequently, it is difficult to establish a ground truth for fracture density prediction, which is necessary to set a benchmark for an EGS. Moreover, this process is prone to human error, making it more challenging to achieve an accurate interpretation. As a result, manual fracture identification can take months to complete, and it is possible to consider the potential for human error in the interpretation process. Also, this process is often subject to bias due to the different levels of expertise present in the process of interpretation.

Figure 1 shows the resistivity-based image log analysis of the carbonate rock to pick faults and fractures for the EGS. The fault's strike is mainly NEE-SWW, close to the strike of NEE-SWW's major fault in the region. The occurrence of unconformity and major faulting in the formation has caused significant instability, evidenced by the substantial changes in the attitude of the strata near depths of 4300 m and 4600 m (shown with arrow). The FMI images of the faults at these depths further demonstrate the significant changes in the deposition of the strata above and below the faults. These significant disparities emphasize the need for technology that can accurately monitor and predict faults and fractures to eradicate the possibility of human bias and minimize the time and effort required for fracture analysis. Considering this critical need, Zhang et al. (2015) proposed a method for estimating fracture stiffness, in situ stresses, and elastic parameters of a hypothetical naturally fractured reservoir. The process is based on a hybrid artificial neural network (ANN) and genetic algorithm (GA) approach, commonly called displacement back analysis. ML techniques have gained popularity in geothermal exploration and production in recent years. A recent study by Okoroafor et al. (2022a) and Zhou et al. (2021) demonstrated using a deep neural network surrogate model to determine the fracture density and fractal dimension of a geothermal reservoir's discrete fracture network. Several researchers have highlighted the potential of ML techniques for improving geothermal exploration and production; however, they cannot identify fracture density in complex geothermal systems. Advanced algorithms and models can help us better understand geothermal reservoirs and improve the efficiency and sustainability of geothermal energy production. In this study, we applied advanced ML algorithms and chose the most appropriate one for accurate fracture density prediction using well logs.

Fig. 1
figure 1

An interpretation of fracture density in a test well (313). Columns 1, 2, 3, 4, 5, 6, 7, and 8 represent the depth, mixed logs (GR: gamma-ray; CAL: caliper), image log, classification of fractures based on image log, stereo-net plot, type of faults based on image log, induced and resistive fractures, and fracture aperture, and FMI log, respectively

Full size image

3 Geothermal settings and reservoir characteristics

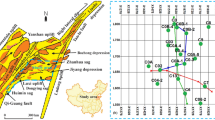
Geothermal energy is a promising renewable energy source that can reduce greenhouse gas emissions and dependence on fossil fuels. Northeast China has significant potential for geothermal projects. This region can greatly benefit from the use of geothermal energy. The study area's Depression is a typical geothermal field that undergoes heat conduction. The primary sources of heat are the mantle and crust (Zhou et al. 2023). Water supply comes from atmospheric precipitation (Fig. 2b). In the south Zhuangdong Depression, in the north Bozhong Depression, and to the east and west, the Chengbei low uplift and Bonan low uplift, respectively. The subsurface structure is controlled by NNE and NE near EW basement faults, with a structural pattern of 'one uplift', 'two depressions', and many 'buried hills' with high, middle, and low surrounding, EW zoning, and NS blocking (Fig. 2a).

Fig. 2
figure 2

a A description of the regional tectonic framework of the study area, b geothermal evolution model for the study area (modified after Liu et al. 2023)

Full size image

There are mainly high-resistivity fractures and drilling-induced fractures. Both high-conductivity and high-resistivity fractures belong to structural fractures, primarily formed by releasing regional palaeotectonic stress. The high-resistivity fracture is formed by filling with high-resistivity material or closed fracture (Fig. 1). Thin section and core analysis show that microfractures are relatively developed and corroborate the presence of natural fractures (Fig. 3). According to reservoir sample analysis, the porosity of the reservoir is 2.1% to 34%, and permeability is 0.01 to 800 mD. The Paleozoic strata is the main geothermal reservoir, which belongs to the porous geothermal reservoir of high-resistivity fractures.

Fig. 3
figure 3

Thin sections for identification of the fractures in wells a 302, b 306, c 307

Full size image

4 Materials and methods

The process of developing the ML model begins with collecting datasets. More than 6,000 data points were interpreted from FMI logging data in 7 wells (307, 306, 302, 313, 301, 39, 40). For the model, we used five wells (306, 302, 301, 39, 40) for training, one well (307) for validation, and one well (313) for testing. This data division allowed us to train our model and accurately assess its performance effectively. We chose this approach to ensure that our model was reliable and that the results of our tests were accurate. The model features were acquired using conventional well logs, including compressional velocity (DTP), gamma-ray (GR), shallow and deep resistivity (RS and RD), density, caliper, and neutron porosity (CNL) logs. We obtained the near-wellbore fracture density from a resistivity-based image log (FMI) for labeling and training purposes. The FMI log provides high-resolution images of the formation, which can be used to characterize fractures in the near-wellbore region.

The steps in developing ML models are data pre-processing, optimizing the model and hyperparameters, and testing the performance of the best model on a blind well.

4.1 An Overview of data pre-processing

Pre-processing is essential for obtaining accurate and reliable results from data analysis. Scanning of all the features present in the dataset is conducted as part of this process. For this purpose, the K-Nearest Neighbor (KNN) imputation was used to fill in all missing values in the dataset. It is useful when less than 20% of data is missing for a specific feature (Troyanskaya et al. 2001). This study employed the KNN imputation technique with 90% accuracy.

Additionally, control limit lines (CLLs) were used to identify outliers in the dataset. The CLL method utilized the mean of each batch of data (plus or minus) with standard deviations to establish the upper and lower control limit lines. This approach allowed the outliers for each feature to be identified and separated from the rest of the data points. The results were more accurate as the analysis did not consider the outliers. Statistical characteristics of features are often studied in data science to identify underlying patterns in the data. Nevertheless, specific ML techniques may be challenging when features present a nonstandard distribution. It is often necessary to transform the features to a normal distribution using the quantile transformation to address this issue. A normal distribution of features tends to improve the performance of ML techniques. ML algorithms are often based on the Gaussian assumption, which assumes normal distributed data. Therefore, we can improve the performance of these algorithms by transforming nonstandard distributions into normal distributions. Table 1 displays the statistical characteristics of input features. The high standard deviation of the GR and resistivity logs indicates a large variation in the data. The heterogeneous nature of the rocks and minerals in the formation or a change in lithology causes the variation.

Table 1 Basic statistics of the training wells
Full size table

Identifying highly correlated parameters in a dataset is an essential step in selecting and reducing features to improve the accuracy and efficiency of ML models. A highly correlated dataset contributes to multiple complexities during the training process by reducing the variability of the input dataset. When two or more features are highly correlated, their effects on the target variable may be redundant, resulting in redundant inferences during model training. In this case, the model may overfit, resulting in perfect results on the training dataset but poor results on the test dataset. The Pearson correlation coefficient and Spearman rank correlation coefficient are two methods for detecting positively correlated features. The Pearson correlation coefficient (r) is a statistical measure used to determine the strength and direction of the linear relationship between two variables. It has a range from −1 to + 1. When 'the r-value is 1, the two components being compared are perfectly linearly related. For this study, those features with a 90% or more correlation were considered “strong” correlations and removed from the dataset. Removing highly correlated features from the dataset helped improve the model's accuracy and avoid overfitting. The number of features has been reduced from 12 to 8 after feature reductions (Fig. 4). This reduction was made possible through collinearity detection and feature transformation techniques.

Fig. 4
figure 4

Heat map correlation matrix between final features

Full size image

4.2 Model selection and hyperparameter tuning

The dataset collected from the geothermal well logs consists of 13 training features and 6029 rows of records. The sampling interval was set at one record per 0.05 microsecond, significantly improving the ML algorithm's data analysis and prediction capabilities. With this level of precision in the data, the ML algorithm can better identify patterns and trends, leading to more accurate predictions. The target values for natural fractures obtained from the FMI log interpreted by individuals have the same number of rows. These values range from 0.0 to 2.2 natural fractures per meter. All features were carefully selected to ensure accuracy and effectiveness. In addition, min–max normalization was used to normalize all features. This normalization ensures that all features are represented on a common scale to prevent one particular feature from dominating the analysis due to its relative importance.

The process of partitioning data is essential to the development of ML models. This step separated the dataset into two groups: testing and training. Training groups develop training models while testing groups evaluate the performance of predictive models. The ratio of partitioning data into training and testing has not been established according to any specific principle. Earlier research has shown that the percentage of training data affects the accuracy of ML models (Vo Thanh et al. 2022). To improve the accuracy of ML models' outputs, the data proportions for the training model need to be considered in several ways. We partitioned the entire database into four segments (training and test datasets): 60–40%, 70–30%, 80–20%, and 90–10%, where the first partition represents the training group and the second part describes the testing group. Table 2 illustrates various regression algorithms, their corresponding hyperparameters, the models evaluated, and the parameters used to optimize their performance. The pre-processing of the data, selection of the ML model, and optimization of the hyperparameters were significantly faster than expected; the entire process took approximately an hour. This workflow is much more efficient than manual pre-processing, yielding excellent results. This workflow illustrates the power of automation and its ability to accelerate workflows.

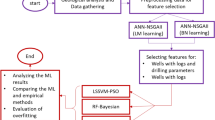
Table 2 Regression algorithms with associated optimized hyperparameters
Full size table

4.3 Workflow of developing machine learning models for fracture identification

Several steps were involved in the ML model for predicting fractures in carbonate geothermal reservoirs. The workflow is summarized into five steps, as shown in Fig. 5.

  1. 1.

    The conventional logging data along with FMI and thin sections were collected and pre-processed to develop ML models.

  2. 2.

    Cross-plot of logging curves were drawn for the fracture labels and non-fracture labels, the response characteristics of conventional logging of fractures were defined, and sensitivity curves were selected. Then one or more wells are randomly selected as blind wells, and the rest of the data is used for training, validation, and testing the model.

  3. 3.

    Due to the huge difference in the proportion of fractured and unfractured label data, it is easy to ignore the fractured label data with a small proportion when it is directly used for model training, resulting in a poor fracture identification effect. The data balancing method used in this study was under-sampling. After under-sampling, the unfractured label data that was originally too high is relatively balanced.

  4. 4.

    Supervised ML techniques for target data were proposed using the four scenarios of database segments. Then, the models with good recognition effects in both the training set and test set were selected as the optimal model for fracture recognition.

  5. 5.

    From four ML algorithms developed for predicting fractures in carbonate rocks, the best model was determined based on the performance of each model.

  6. 6.

    The final step was a blind well test to evaluate the validity of the best model. In detail, one or more wells not used for training are used as inputs, and the output of the model was compared with the FMI and thin sections description results. If the fourth and fifth steps are completed, it is considered that the established model has high accuracy and can be applied to fracture identification.

Fig. 5
figure 5

Workflow of fracture identification using ML models

Full size image

4.4 Evaluation metrics

The fracture prediction model performance was evaluated using R2, RMSE, and mean absolute error (MAE) metrics (Eqs. 1–3).

$${{\varvec{R}}}^{2}=1-\frac{\sum {\left(\widehat{{{\varvec{Y}}}_{{\varvec{i}}}}-{{\varvec{Y}}}_{{\varvec{i}}}\right)}^{2}}{\sum {\left(\overline{{\varvec{Y}} }-{{\varvec{Y}}}_{{\varvec{i}}}\right)}^{2}}$$
(1)
$${\varvec{RMSE}}=\sqrt{\frac{1}{{\varvec{N}}}\sum_{{\varvec{i}}=1}^{{\varvec{N}}}{\left({\widehat{{\varvec{Y}}}}_{{\varvec{i}}}-{{\varvec{Y}}}_{{\varvec{i}}}\right)}^{2}}$$
(2)
$${\varvec{MAE}}=\frac{1}{{\varvec{N}}}\sum_{{\varvec{i}}=1}^{{\varvec{N}}}\left|{\widehat{{\varvec{Y}}}}_{{\varvec{i}}}-{{\varvec{Y}}}_{{\varvec{i}}}\right|$$
(3)

where fracture prediction is estimated using \({\widehat{{\varvec{Y}}}}_{{\varvec{i}}}\), while \({{\varvec{Y}}}_{{\varvec{i}}}\) represents the measured fracture value, \(\overline{{\varvec{Y}} }\) is the average value of measured fracture, and N indicates the total number of samples.

5 Results and discussion

5.1 Sensitivity analysis of well logs for fractures

Sensitivity analysis of logging curves is fundamental to fracture identification and is crucial in ensuring the accuracy of fracture. By analyzing log response characteristics using well logs labeled by fracture descriptions from thin sections and FMI logging fracture interpretations, the fracture logging response characteristics of the reservoirs can be determined. Figure 6 shows the cross plots of the fracture and non-fracture development segment. The data distribution represents the fracture development section and the non-fractured section of the curve, respectively. The more obvious the differentiation between the fracture and non-fracture curves, the better the differentiation effect of the curve. There is a difference in the peak values of the curves between fractured and non-fractured samples.

Fig. 6
figure 6

Sensitivity analysis of well logs, a K3 vs CNL porosity cross plot, b AC vs 1/RS cross plot (Yasin et al. 2022b)

Full size image

It is important to note that there are specific physical property changes along the fracture development, such as low density, high neutron porosity, differentiation of shallow and deep resistivity, and variations in borehole diameter. These features are often used to identify and evaluate the development of fractures. However, each logging curve is a result of the combined effects of lithology, fractures, fluids, boreholes, and other factors, making the logging response characteristics very complex.

5.2 Performance of ML models on validation and test dataset

When selecting the most appropriate ML method, there is no one-size-fits-all solution. A careful consideration of the characteristics of the data is essential to choosing the most appropriate method for the particular scenario (Vo Thanh et al. 2022). Four scenarios were examined to determine the most suitable ML method for a given database segment. Table 3 summarizes the predictions made by four ML models. We observe that the training and testing phases of the developed ML models are accurate to 70 to 90% in all scenarios of data proportions. XGBoost and RF models were found to predict fractures based on 6029 data samples accurately.

Table 3 The performance of ML models for predicting fractures
Full size table

The overall performance of the ML model on each data division shows that the XGBoost method is more accurate with high fracture prediction accuracy than RF, MLP, and SVR. XGBoost achieves stable prediction results both in the training dataset and testing dataset. Also, XGBoost achieves the highest prediction accuracy for all data portions, ranging from 80 to 20%. According to the results, the XGBoost model reached the highest level of accuracy out of all four ML models, both on the training and testing data portions. The SVR model, on the other hand, has the lowest accuracy among the four models. As a result, XGBoost, RF, MLP, and SVR were ranked in order of overall performance. The models were further evaluated by dividing the data into 80%–20%. Table 3 compares the prediction performance achieved for different regression problems based on the percentage of data division. It is important to note that the optimal ratio of data division may vary depending on the specific regression problem. Therefore, it is recommended to carefully consider this factor when developing regression models and selecting the appropriate percentage of data division. The effectiveness of ML methods depends significantly on the division of the data during training and testing. Carefully selecting the data division can enhance prediction performance and lead to successful ML results.

A cross plot of testing performance based on data division 80–20% by four ML models for fracture prediction is shown in Fig. 7. Specifically, XGBoost and RF models have proven to be highly effective in fitting FMI log data to predictive results (Fig. 7a, b). In addition to their accuracy, both models are well known for their ability to handle large datasets. The MLP and SVR models show overfitting and fail to establish a good correlation between the FMI logs data and predicted fracture density (Fig. 7c, d).

Fig. 7
figure 7

Comparison of fracture density estimation from FMI logs and ML models for the validation well (307)

Full size image

Figure 8 compares fracture density prediction for four ML models in the blind test well. The XGBoost predicts relatively close results to the original fractures, indicating good prediction accuracy. In contrast, the MLP and SVR models have many predicting points spreading far from the original fractures, indicating a lower prediction accuracy (Fig. 8c, d). This finding emphasizes the importance of selecting the appropriate ML algorithms for a given problem to achieve accurate predictions. Thus, the results presented in a blind test well demonstrate that XGBoost is the most reliable model with optimized hyperparameters among all the tested models for fracture density prediction. XGBoost outperforms all other models in accuracy and robustness. The testing points of the XGBoost distribution in the blind well are consistent with the FMI data (Fig. 8a). The study's findings are expected to significantly contribute to the development of more accurate and reliable models for fracture density prediction.

Fig. 8
figure 8

Optimization of regressor models for geologically complex geothermal reservoirs with a test well (313)

Full size image

5.3 Relative importance of influence predictors

It is important to note that a variety of critical factors influence fractures. To understand how each input feature affects the fracture prediction for geothermal reservoirs, it is essential to analyze the crucial variables in the XGBoost model. Figure 9 demonstrates the results of ranking important features for fracture prediction in the present study. Figure 9 shows that DTP is an essential feature of fracture identification in a geological formation. A fracture in a rock formation, which consists of a break or crack, can significantly affect transmission speed. This is because fractures create spaces within a formation that are less dense than the surrounding rocks. A lower density may reduce the ability of the formation to transmit signals. Furthermore, open fractures allow fluid to flow more quickly through the formation. This phenomenon can further reduce the density of the formation, making it even more difficult for signals to penetrate. Thus, fractured zones will likely experience slower transmission speeds (Yasin et al. 2018a, 2022b). Therefore, sonic logs are the best fracture indicator.

Fig. 9
figure 9

Essential features ranked for the XGBoost model. Where DTP = compressional velocity, GR = gamma-ray, RS = shallow resistivity, RD = deep resistivity, DEN = density, CAL = caliper log, CNL = neutron porosity

Full size image

Identifying fractures and fluid content in a reservoir using deep and shallow resistivity is critical in the oil and gas industry. The deep resistivity (RD) values are typically lower in fracture zones containing fluid invasion, typically salt water. As a result, the fluid in fractures can significantly decrease RD. The lower the RD value, the greater the probability of fractures in the reservoir (Saboorian-Jooybari et al. 2015). According to previous research, it has been observed that density (DEN) tends to decrease notably at fracture zones (Yasin et al. 2022b). Kölbel et al. (2020) reported that it is caused by an increase in fluid volume in these areas, as the density of fluids is lower than that of rocks (Aghli et al. 2019). Therefore, a developed model incorporating appropriate input features can simplify utilizing ML models to map fracture networks in EGS. Streamlining this process will enable the researchers to map fracture networks more quickly and easily.

5.4 Error analysis and comparison of XGBoost model optimization

The XGBoost model is evaluated for its applicability and performance based on William's plot. These plots allow researchers to gain insight into the most significant variables in their data. The plot is drawn by considering the standardized residual (SR) and leverage values (Vo Thanh et al. 2022). The calculation of leverage parameters involves several statistical steps. These steps are described in detail in Hemmati-Sarapardeh et al. (Hemmati-Sarapardeh et al. 2016). Figure 10 shows William's plot of the XGBoost regression model used for data applicability and error analysis. It is evident from the figure that the majority of data points are bounded close to the zero line, indicating that the prediction of fracture density is statistically valid and the proposed models are reliable. The training and testing results analysis reveals that a significant portion of the data falls within the 3 ≤ SR ≤ 3 range. Distribution of this kind is desirable in many modeling and prediction tasks because it allows for greater accuracy and precision. However, few data points deviate from the zero line, which can be attributed to outliers in the dataset. The data analysis suggests that the XGBoost model has high reliability and statistical trueness and is suitable for predicting fracture density.

Fig. 10
figure 10

Applicability of data and error analysis of XGBoost model

Full size image

A comparative analysis was performed to assess the performance of the XGBoost model using several optimization algorithms such as Q-learning, grid search, Bayesian optimization, and ant colony optimization. Table 4 presents a comparison of the prediction accuracy and computational time for each algorithm. It is important to note that all the algorithms were executed on the same computer configuration.

Table 4 Accuracy and computational time comparison of optimization algorithms
Full size table

Figure 11 compares the fracture prediction performance of XGBoost models optimized with different algorithms. The XGBoost model using Q-learning achieves an R2 of 0.95 and an RMSE of 0.0018%.

Fig. 11
figure 11

Comparison of performance for the XGBoost models optimized by different algorithms

Full size image

5.5 Comparison of the performance of XGBoost with the previous study

The XGBoost model in this study has been found to have the highest accuracy compared to other popular ML models like RF, MLP, and SVR. However, it is essential to assess the stability and robustness of the XGBoost model to ensure its reliability. We compare the performance of the XGBoost model with previously developed ML models proposed by Fathi et al. (2022). The comparison confirms that the XGBoost model performs consistently and provides accurate predictions. Table 5 summarizes the statistical indicators for the XGBoost model with the proposed features and hyperparameters tuning based on an improved Q-learning algorithm.

Table 5 The comparison analysis demonstrates the robustness of the nominated ML model
Full size table

XGBoost is superior to the previous KNeighbors model in producing the highest R2 and lowest RMSE values throughout the training and testing phases. The performance metrics indicate that the XGBoost model makes accurate and consistent predictions.

5.6 XGBoost model verification

5.6.1 Fracture porosity and permeability

XGBoost's application perspective is verified by comparing its predictions to actual measurements of reservoir fracture porosity. The results can help determine the effectiveness of the XGBoost model in predicting porosity and identifying potential reservoirs. Figure 12 shows the regression analysis for XGBoost prediction and reservoir fracture porosity in a blind test well of carbonate rocks. The results shown in the figure are well-fitting, with R2 values of 0.72. On comparing, it can be observed that the prediction performance of XGBoost closely corresponds with that of reservoir fracture porosity. In addition, Table 6 compares the fracture density measured from FMI logs and the XGBoost model. The comparative analysis conducted in a blind test well indicated positive results regarding the efficacy of the developed XGBoost model. The results confirm that the model is suitable for exploring EGS. The model's success in the blind test well further solidifies its potential for future EGS exploration applications.

Fig. 12
figure 12

Correlation between fracture density from XGBoost models and reservoir fracture porosity in a blind test well

Full size image
Table 6 Comparison of the fracture density from FMI logs and XGBoost model in a blind test well
Full size table

Permeability is a crucial property of carbonate rocks, and its influence on fracture density distribution is essential. We conducted sensitivity analyses to determine the effect of permeability on fracture density distribution.

Figure 13 presents the results of a sensitivity analysis of permeability and fracture density distribution derived from the XGBoost model. The results show higher permeability values are associated with higher fracture density distribution values. The analysis suggests that the XGBoost model can be used to explore EGS accurately. The model can capture the relationships between permeability and fracture density distribution, providing a reliable and efficient tool for analyzing EGS.

Fig. 13
figure 13

Correlation between fracture density from XGBoost models and reservoir permeability in a blind test well

Full size image

5.6.2 Thin section analysis

Understanding the distribution, orientation, and connectivity of fractures in geothermal reservoirs through thin-section analysis is crucial for assessing reservoir permeability and fluid flow pathways and ultimately optimizing geothermal energy extraction strategies (Kölbel et al. 2020). Figure 14 corroborates the presence of natural and healed fractures, supporting the accuracy of identifying natural fractures from the XGBoost model. The agreement between the ML predictions and thin section analysis strengthens the reliability of the results and provides valuable insights for geothermal reservoir characterization. The research contributes to understanding fracture networks in geothermal systems and can aid in optimizing geothermal energy extraction strategies. Further studies could explore the integration of ML with other geophysical and geological data for a more comprehensive analysis of fracture systems in geothermal reservoirs.

Fig. 14
figure 14

Thin section interpretation for identification of fractures in wells a 306, b 301, c 307, d 302

Full size image

5.7 XGBoost model’s application in spatial fracture distribution

We employed the XGBoost model to determine fracture density spatial distribution (Fig. 15a, b). The fracture density from the XGBoost model in the study area is high along the highly fractured wells (302, 307, 313), evidenced by the thin sections of these wells (Fig. 14). Furthermore, promising areas for EGS based on high fracture density can be selected for hydraulic fracturing operations. Therefore, comprehending the characteristics and distribution of these fractures is imperative for optimizing hydraulic fracturing design. The red color in the seismic profile shows the areas of high fracture density where fluid flow and heat transfer are expected to be most efficient. These locations optimize geothermal wells and maximize energy extraction from the subsurface.

Fig. 15
figure 15

XGBoost model’s application for spatial fracture distribution in the study area

Full size image

6 Conclusions

  • ML workflows have remarkable potential for reducing the time and cost of fracture mapping in EGS while producing accurate, robust, reproducible, and assessable results. ML algorithms facilitate data analysis more quickly, accurately, and highly reliably. Furthermore, selecting ML models with optimizing hyperparameters and data division can eliminate human bias from the decision-making process, leading to more accurate and impartial results.

  • For predicting fractures in carbonate geothermal reservoirs, the XGBoost model was found to be the most reliable model. XGBoost performs better in both phases (training and testing) for a blind test well than other ML algorithms: RF, MLP, and SVR. XGBoost is faster and more accurate, achieving the highest correlation factor (R2 = 0.92 and RMSE = 0.02). Optimization of the XGboost model using Q-learning outperformed the grid search, Bayesian optimization, and ant colony optimization.

  • Fracture network mapping plays a vital role in understanding the behavior of EGS reservoirs and optimizing their performance. An effective fracture network mapping can be achieved with the appropriate input features, resulting in improved reservoir management and optimization.

  • The XGBoost model selected in this study provides a reliable and accurate method for predicting fractures in any geological formation for EGS. Analysis, evaluation, and validation demonstrate its utility and potential for widespread application.

  • An analysis of permeability and thin-section confirmed the presence of natural fractures that may affect the reservoir's potential as a source of high-temperature fluid.

7 Limitations

ML models exhibit strong stability and scalability, as they can handle both large-scale and small-sample data and are capable of efficiently processing data of varying sizes. However, ML models have certain limitations.

  • The feature representation process needs to be strengthened. Since the original feature vectors are high-dimensional, the enhanced feature vectors used in the XGBoost model can easily be overwhelmed.

  • As a supervised learning method, these models place high demands on the quality of the labels in the original data. Therefore, for the problem of intelligent identification of fractures in conventional well logs using core and FMI logs, it is crucial to select fracture label data located in the middle of a continuous fracture development segment and discard marginal label data to ensure label quality.

  • The issue of data imbalance in the original dataset should not be ignored. Choosing an appropriate data balancing method to improve the distribution proportion of different labels in the dataset is crucial for ensuring the training effectiveness of the fracture identification model.