1 Introduction

Proton exchange fuel cells (PEFCs) are energy conversion devices, which generates electricity from electrochemical reactions between hydrogen and oxygen, producing water and heat as by-products (O’hayre et al. 2016; Barbir 2006). PEFCs are expected to play a relevant role in the automotive industry due to zero greenhouse gas emissions, high efficiency, quick start-up, quiet operation and long lasting (Watabe and Leaver 2021; Muthukumar et al. 2021). However, there are still technological challenges that hinder widespread commercialization of PEFCs. Cost reduction, extended durability and enhanced power density are still needed in light-duty vehicles (Jiao et al. 2021; Cullen et al. 2021; Ajanovic and Haas 2021).

Efficient water management plays a critical role for the design of high-performance PEFCs, limiting oxygen transport at the cathode (García-Salaberri et al. 2015a, b). A high oxygen concentration in the cathode catalyst layer (CL) is crucial to reduce activation losses caused by the sluggish oxygen reduction reaction (ORR) and mass transport losses (Owejan et al. 2013, 2014; Neyerlin et al. 2006). This task must be accomplished by an optimized design of the flow field (FF) and the components of the membrane electrode assembly (MEA): gas diffusion layer (GDL), microporous layer (MPL), catalyst layer (CL) and proton exchange membrane (PEM) (Jiao and Li 2011; Secanell et al. 2010). The adverse effect of water flooding on oxygen transport can be alleviated by promoting water back diffusion to the anode with ultra-thin PEMs and super-hydrophobic cathode CLs, as well as a tailored design of the MPL, GDL and FF (Steinbach et al. 2018; Folgado et al. 2018; Xing et al. 2019). An adequate design of the multiscale pore structure of the MPL/GDL/FF assembly can significantly enhance water transport in vapor phase, facilitate water removal in liquid phase and improve oxygen transport toward active catalytic sites (Secanell et al. 2021).

A large body of numerical work has been devoted to analyze two-phase transport in the MEA. Modeling two-phase transport in PEFCs has been always a challenging task due to the large spectrum of spatial and temporal scales and variety of physical phenomena that take place (mainly, capillary transport of liquid water, water vapor diffusion, phase change, and sorption/desorption, electro-osmotic drag and diffusion of dissolved water in ionomer) (Weber et al. 2014; Jiao and Li 2011; García-Salaberri 2022). The most extended methods used to model water transport in GDLs have been macroscopic continuum modeling (García-Salaberri et al. 2017; Weber et al. 2014), morphological image analysis (Schulz et al. 2007), pore network modeling (PNM) (Gostick 2013; Carrere and Prat 2019) and direct numerical simulation (DNS), such as the lattice Boltzmann (LBM) (García-Salaberri et al. 2015; Jeon and Kim 2015; Sepe et al. 2020) and the volume of fluid (VOF) (Chen et al. 2020; Zhu et al. 2008) methods. In this work, PNM was selected to model water invasion in a macroporous GDL due to its reduced computational cost and ability to reproduce physical phenomena at a reasonable level of detail. DNS has a much higher computational cost, and sometimes, the required information at small spatial scales is not available at the same resolution. For example, the effective electrical and thermal conductivities of GDLs are affected by the internal anisotropy of carbon fibers, an aspect that should be considered when running DNS. However, the value and the anisotropy ratio of the conductivity of carbon fibers are unknown in many cases, so an isotropic value is assumed and compared against experimental values measured in the full layer (García-Salaberri et al. 2018). A similar situation applies when modeling capillary transport to include the effect of nanoscale roughness and locally variable contact angles of carbon and PTFE. In addition, the small characteristic time of capillary transport at the pore scale makes it necessary too short integration time steps. For this reason, DNS is not usually performed at real capillary numbers, but some orders of magnitude higher to reduce computational cost, assuming that physics are not significantly affected (Ferreira et al. 2017; Niblett et al. 2020). A review of previous work presented in the literature dealing with two-phase transport in GDLs is presented below.

From the numerical side, Rebai and Prat (2009) compared the predictions of pore network (PN) and continuum models to describe liquid capillary transport in thin GDLs. They concluded that continuum models are expected to offer poor predictions of water distribution in macroporous GDLs due to a lack of length scale separation between pore and layer scales. Gostick (2013) presented a PN model of a carbon-paper GDL (Toray TGP-H series) based on a Delaunay/Voronoi tessellation of the porous medium, which required a low number of input parameters to match morphological and effective transport properties. The saturation profile computed from a water injection simulation showed the characteristic concave shape arising from invasion percolation (IP), decreasing from around \(s\approx 0.9\) at the inlet to \(s\rightarrow 0\) at the outlet (breakthrough point). The high peak inlet saturation dramatically reduced the through-plane effective diffusivity in agreement with García-Salaberri et al. (2015a). Alink & Gerteisen (2014) proposed an iterative algorithm to integrate a liquid water percolation model into a 3D continuum PEFC model. The continuum model served to solve for thermodynamic processes relevant for water management, while the discrete model was used to calculate saturation distributions depending on the injection pressure and the condensation scenario. Good agreement was found with saturation distributions from synchrotron visualization regarding the effect of PTFE content, MPL addition, GDL perforation and ionomer desorption rate. Medici et al. (2016) presented a cross-sectional sandwich PEFC model, which coupled a continuum model and a PN model through an iterative solution scheme previously presented in Zenyuk et al. (2015). The continuum model was used to determine spatially resolved current, heat and mass fluxes for the PN model, which was then used to determine effective transport properties discretized along the GDL/electrode interface, thereby providing updated boundary conditions for the continuum model. They found that including stacked GDLs at the anode led to a highly porous interfacial region, which allowed more efficient water movement in the anode and higher temperatures at the cathode, thus reducing cathode flooding. Carrere and Prat (2019) developed a PN model of the cathode GDL. The model provided a significant advancement compared to previous works, being able to reproduce different water transport regimes observed in PEFCs over a wide range of temperatures from \(40\) to \(80\) °C and relative humidities from 0% to 100%. Four regimes were identified: (i) the dry regime, (ii) the dominant condensation regime, (iii) the dominant liquid injection regime, and (iv) the mixed regime where both capillary-controlled invasion in liquid phase and condensation are important.

From the experimental side, Santamaria et al. (2014) examined ex-situ dynamic liquid water transport and removal in GDLs. Among other results, they observed that the breakthrough pressure increased at higher PTFE loadings, larger thickness and smaller injection areas, leading to a greater resistance to droplet formation. Quesnel et al. (2015) investigated water percolation in GDLs with and without an MPL by injecting water at the top of a sample and allowing water droplets to detach freely from the bottom uninterruptedly. It was found that MPL-coated GDLs led to a reduction of invading water clusters during the dynamic cycle of droplet appearance, growth and detachment. Zenyuk et al. (2015) analyzed the effect of inhomogeneous compression caused by the rib/channel pattern on capillary transport of water in SGL carbon paper. Liquid water transported preferentially through the region under the channel due to the larger pore sizes present there (compared to the region under the rib), thus suggesting that the saturation distribution could be engineered using GDLs with modulated porosity. Nagai et al. (2019) studied the effect of MPL porosity at the cathode on water transport in the GDL at full humidification (\(\mathrm {RH}\approx 100\%\)) and \(40\) °C by means of 4D operando X-ray imaging. They observed that cathode MPLs with larger, microscopic pores featured better performance (\(1.3\;\mathrm {A\,cm^{-2}}\) vs. \(1.2\;\mathrm {A\,cm^{-2}}\) at \(0.4\;\mathrm V\)) due to formation of low-tortuosity water pathways from the bottom to the top of the GDL, which efficiently merged small liquid water clusters coming from the CL. Xu et al. (2021) examined water saturation in three different GDLs (Freudenberg, Toray and SGL) during dynamic current jump characterizations with subsecond operando X-ray tomographic microscopy (time step of \(0.1\;\mathrm s\)). They found that the current density at \(0.1\;\mathrm V\) increased in the following order: Freudenberg (\(1.6\;\mathrm {A\,cm^{-2}}\))>SGL (\(1.2\;\mathrm {A\,cm^{-2}}\))>Toray (\(1.0\;\mathrm {A\,cm^{-2}}\)). The significantly higher performance of the Freudenberg GDL was explained by its low thermal conductivity, which decreased water saturation at the GDL/CL interface under the channel: \(\mathrm{Freudenberg~(0.04)}<\mathrm {SGL ~(0.25)}\approx \mathrm {Toray~(0.33)}\). The water saturation level under the rib remained similar for all the GDL types examined: \(\mathrm{Freudenberg~(0.4)}\approx \mathrm{Toray~(0.36)} \approx \mathrm{SGL~(0.46)}\). Recently, Shojaei et al. (2022) analyzed water transport in GDLs with different PTFE loadings in ex-situ water drainage experiments using high-resolution 3D X-ray imaging. The contact angle distribution measured in GDLs showed a wide distribution with values above and below \(90\) °C, confirming the mix wettability of PTFE-treated GDLs.

The present model is built on the previous works of Garcia-Salaberri (2021) and Zapardiel and García-Salaberri (2022) using a control volume (CV) representation to describe macroporous thin transport layers in which discrete and continuum formulations are combined on a single computational mesh (hybrid model). The local effective transport properties, namely the local entry capillary pressure and the local anisotropic effective diffusivity, are determined in each CV according to a virtual PN representation of the porous medium. The aim of this work is two-fold: (i) to extend the validation of the hybrid model against numerical and experimental data in a wider range of scenarios, and (ii) to examine the combined effect of GDL thickness and open area fraction at the GDL/FF interface on capillary-dominated invasion of liquid water and channel–CL oxygen transport resistance. Water invasion is modeled using a standard IP algorithm without trapping (all-or-nothing water filling law) and oxygen diffusion using a continuum species conservation equation. No diffusion takes place in CVs filled by liquid water. The organization of the paper is as follows. In Sect. 2, the numerical model and the case studies are briefly presented. In Sect. 3, the results of the parametric analysis are discussed, including two subsections: (i) the interplay between GDL thickness, inlet invaded area fraction and inhomogeneous compression, and (ii) the coupled effect of GDL/FF open area fraction and GDL thickness. Finally, the conclusions are presented in Sect. 4.

2 Numerical Model

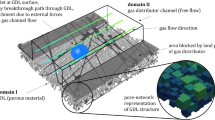
The numerical model, implemented in ANSYS Fluent, combines a discrete formulation to model water IP and a continuum formulation to model oxygen diffusion in a macroporous carbon-paper GDL with a pseudo 2D microstructure (similar to Toray TGP-H series) (Garcia-Salaberri 2021, 2022; Zapardiel and García-Salaberri 2022). As shown in Fig. 1, the GDL domain is represented as a structured tessellation of (parallelepiped) CVs according to the structured microstructure of the examined porous medium. A subdivision of the porous medium into CVs is used due to the impossibility to establish a well-defined representative elementary volume (REV) lower than the thickness in macroporous thin layers (\(\mathrm{pore~size}/\mathrm{thickness}\sim 10^{-1}-1\)) (García-Salaberri et al. 2018). Each CV is meshed with \(\beta\) computational cells (27 cells/CV, three in each spatial direction, were used here based on the grid independence study of Zapardiel and García-Salaberri (2022)). The CV tessellation embeds a virtual structured PN composed of one parallelepiped pore body with six connecting parallelepiped throats in each CV, so that one throat passes through every face between two neighboring CVs. The virtual PN is used to determine the local anisotropic effective diffusivity and the local entry capillary pressures (six, one per CV face) in each CV. Species transport through the heterogenous macroporous layer is simulated by solving the diffusion equation with the determined local effective diffusivities and considering a vanishing diffusivity in invaded CVs. Water IP is evolved by invading the CV with the minimum entry capillary pressure adjacent to the invasion front without trapping. The process is stopped when the invasion front reaches the GDL/channel interface, so that a connected water transport pathway is formed between the GDL inlet and the channel outlet. A residual lower than \(10^{-12}\) was set for the continuum oxygen diffusion equation. More details can be found in Garcia-Salaberri (2021); Zapardiel and García-Salaberri (2022).

Fig. 1
figure 1

Schematic of the control volume (CV) tessellation used to model transport in heterogeneous macroporous thin GDLs, colored as a function of the local pore size, \(r_{c,p}\). The close-up view shows the geometry of the virtual structured pore-throat geometry embedded in each CV, which is used to determine the local dry effective diffusivity tensor, \({\bar{{\bar{D}}}_{l}^{\mathrm{eff,dry}}}\), and the six local entry capillary pressures, \(p_{c,t,i}^{e}\). The main geometrical dimensions are indicated, including the characteristic throat radius, \(r_{c,t}\), used to calculate \(p_{c,t,i}^{e}\). See (Garcia-Salaberri 2021; Zapardiel and García-Salaberri 2022) for further details

Full size image

The present hybrid model is different from the full morphology models presented by Sabharwal et al. (2018) and Cetinbas et al. (2019). Here, microstructural information is incorporated through local effective transport properties and local entry capillary pressures determined from a virtual PN representation of a macroporous medium. Consequently, the computational time of the present model is significantly lower (around one minute per case on a conventional laptop). In fact, accounting for both nanometric and micrometric pores in the modeling approaches presented in Sabharwal et al. (2018); Cetinbas et al. (2019) will lead to an exceedingly high computational cost, especially when domains with large active areas are to be modeled. A hybrid formulation based on a CV representation, such as the one used here, provides a versatile framework to simultaneously describe transport in heterogeneous thin porous media without and with separation between pore and layer scales at moderate computational cost (e.g., GDL+MPL) (Garcia-Salaberri 2022). Transport in thin porous layers with a well-defined length scale separation can be modeled using a macroscopic description. In addition, it is worth noting that the formulation proposed in Cetinbas et al. (2019) to model liquid water transport can suffer from numerical instabilities when a phase change source term is included due to the singularity introduced by having a (numerically) zero capillary diffusivity and a non-zero source term. This issue can be avoided using a hybrid continuum/discrete formulation. Description of heterogeneous transport properties in macroporous thin layers could be generalized using a polyhedral Delaunay/Voronoi tessellation extracted from tomography images.

2.1 Local Effective Transport Properties

The sizes of parallelepiped pore bodies in three spatial dimensions (\(r_{p,x}\), \(r_{p,y}\) and \(r_{p,z}\)) were distributed according to the log-normal bimodal pore size distributions (PSD) determined by Zenyuk et al. (2016)

$$\begin{aligned} \mathrm{PSD}(r)=\sum _{k=1,2} f_{r,k}\left\{ \dfrac{1}{r \sigma _{k}\sqrt{2\pi }}\exp \left[ -\dfrac{\left( \mathrm{ln\,}r-\mathrm{ln\,}r_{0,k}\right) ^2}{2\sigma _{k}^2}\right] \right\} \end{aligned}$$
(1)

where \(f_{r,k}\) is the fraction of pores that compose distribution k, and \(r_{0,k}\) and \(\sigma _k\) are the characteristic radius and standard deviation of distribution k, respectively. Throat dimensions were calculated based on the mean size of neighboring pores to reproduce the high porosity of macroporous GDLs (\(\varepsilon ^{\mathrm{avg}}\sim 0.6-0.9\))

$$\begin{aligned}&r_{c,t}= \Gamma _{t}\dfrac{H_t+W_t}{2}\end{aligned}$$
(2a)
$$\begin{aligned}&r_{c,p}= \Gamma _{p}\dfrac{r_{p,x}+r_{p,y}+r_{p,z}}{3} \end{aligned}$$
(2b)

where \(H_t\) and \(W_t\) are the half-height and the half-width of throat t, and \(\Gamma _t=1.05\) and \(\Gamma _p=1.02\) are dimensionless parameters that account for subpore scale irregularities, which were adjusted to match experimental \(p_c\)-\(s^{\mathrm{avg}}\) curves (Garcia-Salaberri 2021; Zapardiel and García-Salaberri 2022). The size of parallelepiped CVs (\(L_{\mathrm{CV},x},L_{\mathrm{CV},y},L_{\mathrm{CV},z}\)) was kept constant throughout the GDL and calibrated during the generation of the virtual PN to ensure that: (i) the CV size was larger than any pore size in the porous medium (\(L_{CV,i}>L_{p,i}\)), and (ii) the average porosity and the anisotropic permeability and diffusivity were similar to previous data reported for Toray TGP-H series carbon paper (García-Salaberri et al. 2018; Zenyuk et al. 2016; Hwang and Weber 2012; Rashapov and Gostick 2016).

Local effective diffusivity in each CV was extracted from the embedded virtual PN, leading to an orthotropic effective diffusivity tensor (for the virtual structured PN used here) (Garcia-Salaberri 2021)

$$\begin{aligned} {\bar{{\bar{D}}}_{l}^{\mathrm{eff,wet}}}=D \begin{bmatrix} f_{l,x}g_{l} &{} 0 &{} 0\\ 0 &{} f_{l,y}g_{l} &{} 0\\ 0 &{} 0 &{} f_{l,z}g_{l} \end{bmatrix} \end{aligned}$$
(3)

where D is the bulk gas diffusivity. The local blockage of liquid water on gas diffusion was accounted for by setting a (numerically) zero isotropic relative effective diffusivity in water-filled CVs, \(g_{l}=10^{-16}\) (\(g_{l}=1\) in dry CVs). The binary approach used to describe water saturation was adopted due to the lack of length scale separation in thin GDLs (Rebai and Prat 2009; García-Salaberri et al. 2018). The local dry normalized effective diffusivity in i-direction, \(f_{l,i}\), is given by the harmonic mean of the normalized diffusive conductances of pore p, \(g_{p,i}=A_{p,i}/L_{p,i}\), and throats \(t_1\) and \(t_2\), \(g_{t,i}=A_{t,i}/L_{t,i}\), according to

$$\begin{aligned} f_{l,i}=\dfrac{D_{l,i}^\mathrm{eff}}{D}=\dfrac{\left( \dfrac{L_{t1,i}}{A_{t1,i}}+\dfrac{L_{p,i}}{A_{p,i}}+\dfrac{L_{t2,i}}{A_{t2,i}}\right) ^{-1}}{\dfrac{A_{CV,i}}{L_{CV,i}}} \end{aligned}$$
(4)

where \(A_{i}\) and \(L_i\) are the cross-sectional area and length of a pore/throat perpendicular to and along i-direction, respectively. Note that \(L_{CV,i}=L_{p,i}+2L_{t,i}\) since pores are centered in each CV and the lengths of the two throats in i-direction are the same. Expressions for absolute permeability can also be found in Garcia-Salaberri (2021). For effective transport properties that rely on the solid phase (e.g., electrical and thermal conductivity), special attention must also be paid to contact points between fibers (Zhang et al. 2021).

The entry capillary pressures of the throats were determined by Purcell’s equation (modified Washburn equation) to capture the converging–diverging geometry of the fibrous pore space (Gostick 2013; Tai et al. 2020)

$$\begin{aligned} p_{c,t,i}^{e}= -\dfrac{2\sigma }{r_{c,t}}\dfrac{ \cos \left( \theta -\alpha \right) }{1+\dfrac{d_f}{2r_{c,t}}(1-\cos \alpha )},\quad i=1,\ldots ,6 \end{aligned}$$
(5)

where \(\sigma\) is the surface tension, \(r_{c,t}\) is the characteristic half-spacing between fibers, \(d_f\approx 10\;\mu \mathrm m\) is the fiber diameter, \(\theta\) is the average contact angle and \(\alpha\) is the angle corresponding to the maximum meniscus curvature

$$\begin{aligned} \alpha = \theta -\pi + \mathrm{arcsin}\left( \dfrac{\sin \theta }{1+2r_{c,t}/d_f}\right) \end{aligned}$$
(6)

2.2 Capillary-Dominated Water Transport (Invasion Percolation) and Oxygen Diffusion

A standard IP algorithm was used to describe transport of liquid water under isothermal conditions. The evolution scheme considers quasi-steady-state transport due to the much lower characteristic capillary time, \(t_{c,c}\), compared to the characteristic viscous time, \(t_{c,v}\), found in GDLs during PEFC operation (i.e., extremely low capillary number, Ca) (Wilkinson and Willemsen 1983; Zapardiel and García-Salaberri 2022; Lenormand et al. 1988)

$$\begin{aligned} \left. \begin{aligned} t_{c,c}&\sim \dfrac{\rho v_{c}r_{c,p}^2}{\sigma } \\ t_{c,v}&\sim \dfrac{r_{c,p}^2}{\nu } \end{aligned} \right\} Ca\sim \dfrac{t_{c,c}}{t_{c,v}}\sim \dfrac{\mu v_c}{\sigma }\sim 10^{-8} \end{aligned}$$
(7)

where \(v_c\sim I M_w/(2F\rho _w)\) is the characteristic liquid-phase velocity (with I the generated current density), \(M_w\) and \(\rho _w\) are the molecular mass and the density of water, respectively, and F is Faraday’s constant. For \(I\sim 1.5\;\mathrm {A\,cm^{-2}}\), we yield \(v_c\sim 10^{-6}\;\mathrm {m\,s^{-1}}\).

The algorithm was initialized by setting a prescribed inlet invaded area fraction, \(A_{w}^{in}\), among the CVs facing the inlet face. At each quasi-steady-state time step (i.e., numerical iteration), water transport evolved by invading the CV adjacent to the invasion front where the neighboring throat with the minimum entry capillary pressure was located, \(p_{c,t}^{e,\mathrm {min}}\). The meniscus advancement within pores and throats arising from a balance between capillary and viscous forces was not explicitly modeled (Medici and Allen 2011; Médici and Allen 2016). The invasion process was finished at the breakthrough event when the invasion front reached the open area between the GDL and the channel. Invasion continued when an impermeable rib surface was reached. In addition, no description of the creeping regime during droplet growth and detachment was considered. Nevertheless, DNS of water invasion in GDLs and in operando X-ray tomography have shown that the GDL water distribution does not change significantly after breakthrough (Jeon 2019; Jeon and Kim 2015; Mularczyk et al. 2021). Hence, the present simulations are a good approximation to evaluate average saturation and oxygen transport resistance. By definition, the average saturation is given by the ratio of the sum of the local pore volume of all invaded CVs to the total pore volume, \(V_{\mathrm{gdl},p}\), i.e.,

$$\begin{aligned} s^{\mathrm{avg}} = \dfrac{\sum _{j=1}^{N}s_{l}^{j}V_{l,p}^{j}}{\sum _{j=1}^{N}V_{l,p}^{j}}=\dfrac{\sum _{j=1}^{N}s_{l}^{j}V_{l,p}^{j}}{V_{\mathrm{gdl},p}} \end{aligned}$$
(8)

where \(s_{l}^{j}\) and \(V_{l,p}^{j}\) are the local saturation (1/0 in wet/dry CVs) and local pore volume in CV j, respectively, and N is the total number of CVs in the GDL.

The contribution of convection to oxygen transport in PEFCs (in the absence of forced convection) can be typically neglected due to low Peclet number, \(Pe\sim v_c \delta _{\mathrm{gdl}}/D_{\mathrm{O_2,air}}^\mathrm{eff}\sim 10^{-5}\). Thus, the continuum oxygen conservation equation reduces to

$$\begin{aligned} -\nabla \cdot \left( \varvec{\overline{{\overline{D}}}_{l} ^\mathrm{eff,wet}}\nabla C\right) =0 \end{aligned}$$
(9)

where C is the oxygen molar concentration.

After the water breakthrough event, the through-plane effective diffusivity (y-direction) was determined by imposing Dirichlet boundary conditions, \(C^{in}=1\;\mathrm {mol\,m^{-3}}\) and \(C^{out}=0\;\mathrm {mol\,m^{-3}}\), and D = 1 m2 s−1. (Note that the normalized effective diffusivity is independent of the chosen bulk value.) Using the trapezoidal rule for volume averaging, we yield

$$\frac{{D_{{g,y}}^{{\rm eff,wet}} }}{D} = \frac{{\delta _{{\rm gdl}} }}{{V_{{\rm gdl}} }}\int_{{V_{{\rm gdl}} }} {j_{y} } \;dV = \delta _{{\rm gdl}} j_{y}^{{\rm avg}} \approx \frac{{\delta _{{\rm gdl}} }}{N}\sum\limits_{{i = 1}}^{{\beta N}} { - f_{{l,y}} g_{l} \left. {\frac{{\partial C}}{{\partial y}}} \right|_{i} }$$
(10)

where \(j_{y}^{\mathrm{avg}}\) is the volume-averaged through-plane diffusive flux and \(\delta _{\mathrm{gdl}}\) is the uncompressed GDL thickness. Using this value, the overall oxygen transport resistance from the channel to the CL, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\), including the diffusive resistance of the MPL, was calculated to compare numerical results against previous experimental data. The expression for \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\) is given by

$$\begin{aligned} R_{\mathrm{O_2}}^{\mathrm{chcl}}=R_{\mathrm{O_2,gdl}}+R_{\mathrm{O_2,mpl}};\quad R_\mathrm{O_2,gdl}= \dfrac{\delta _{\mathrm{gdl}}}{D_{\mathrm{O_2,gdl}}^{\mathrm{eff,wet}}}, R_{\mathrm{O_2,mpl}}= \dfrac{\delta _{\mathrm{mpl}}}{D_{\mathrm{O_2,mpl}}^\mathrm{eff, wet}} \end{aligned}$$
(11)

where \(D_{\mathrm{O_2,gdl}}^{\mathrm{eff,wet}}=(D_{g,y}^\mathrm{eff,wet}/{D})D_{\mathrm{O_2,air}}\) and \(D_{\mathrm{O_2,mpl}}^{\mathrm{eff, wet}}\) are the (through-plane) effective diffusivities of oxygen in the GDL and the MPL, respectively, and \(\delta _{\mathrm{mpl}}\) is the MPL thickness. \(\delta _{\mathrm{mpl}}=50\;\mu \mathrm m\) and \(D_\mathrm{O_2,mpl}^{\mathrm{eff, wet}}=0.1D_{\mathrm{O_2,air}}\) were assumed according to previous works (Chan et al. 2012; Andisheh-Tadbir et al. 2015; Lee et al. 2015; Fishman and Bazylak 2011). The bulk diffusivity of oxygen in air depends on the temperature, T, and the gas pressure, \(p_{\mathrm{gas}}\), according to

$$\begin{aligned} D_{\mathrm{O_2,air}}= 2.65\times 10^{-5} \left( \dfrac{T}{333}\right) ^{1.5}\left( \dfrac{10^{5}}{p_\mathrm{gas}}\right) \qquad [\mathrm{m^2\,s^{-1}}] \end{aligned}$$
(12)

where T and \(p_{\mathrm{gas}}\) are expressed in K and Pa, respectively.

2.3 Case studies

The modeled domain included the GDL volume comprised below one central channel and the half-width of the two neighboring ribs. Examples of carbon-paper GDLs (Toray TGP-H series) examined in the simulation campaign are shown in Fig. 2a–b. The parameters of the GDL model, together with the operating conditions and MPL data used for the calculation of the channel–CL oxygen transport resistance, are listed in Table 1. Three uncompressed and inhomogeneously compressed samples were examined, with uncompressed and compressed thicknesses equal to \(\delta _\mathrm{gdl}=135,270,405\;\mu \mathrm m\) and \(\delta _\mathrm{gdl}^{cr}=108,216,324\;\mu \mathrm m\), respectively (compression ratio, \(\mathrm{CR}=(\delta _{\mathrm{gdl}}-\delta _{\mathrm{gdl}}^{cr})/\delta _\mathrm{gdl}=20\%\)). In addition, two representative active areas were considered, \(L_x\times L_z=1.98\times 1.98\; \mathrm {mm^2}~\text {and}~1.98\times 0.99\; \mathrm {mm^2}\) (with x the rib–channel direction), together with three channel widths, \(w_\mathrm{ch}=0.5,1,1.5\;\mathrm {mm}\). The above geometrical dimensions are reduced to two dimensionless parameters: (i) the GDL/FF open area fraction, \(A^{\mathrm{out}}\), and (ii) the GDL slenderness ratio, \(\Pi _{\mathrm{gdl}}\), given by

$$\begin{aligned}&A^{\mathrm{out}}&=\dfrac{w_{\mathrm{ch}}}{L_x} \end{aligned}$$
(13)
$$\begin{aligned}&\Pi _{\mathrm{gdl}}&=\dfrac{\delta _{\mathrm{gdl}}}{L_x} \end{aligned}$$
(14)

For \(L_x\approx 2\;\mathrm {mm}\), the values of \(A^{\mathrm{out}}\) and \(\Pi _{\mathrm{gdl}}\) corresponding to the channel widths and GDL thicknesses examined are equal to \(A^{\mathrm{out}}=0.25,0.5,0.75\) and \(\Pi _{\mathrm{gdl}}=0.07,0.135,0.2\), respectively. The resulting average uncompressed/compressed porosity and pore radius were \(\varepsilon ^{\mathrm{avg}}\approx 0.74/0.6\) and \(r_{p}^{\mathrm{avg}}\approx 15/12\;\mu \mathrm m\), with through- and in-plane dry normalized effective diffusivities equal to \(f_{tp}\approx 0.3/0.2\) and \(f_{ip}\approx 0.4/0.3\), respectively (García-Salaberri et al. 2018). Besides, four inlet invaded area fractions were analyzed in the ranges \(A_{w}^{in}=0~\text {(dry)},0.2-0.25,0.35-0.6,0.7-0.9\). The invaded CVs at the inlet were arbitrarily selected, so that their entry capillary pressures at the bottom surface were lower than a calibrated threshold value. Although ignoring water phase change is a gross oversimplification, the modeled scenario approximates that found in operating PEFCs in the dominant liquid injection and mixed regimes identified by Carrere and Prat (2019) (see, e.g., in operando water distributions in Xu et al. (2021); Eller et al. (2016); Nagai et al. (2019)). In total, 72 cases (\(2\times 3\times 3\times 4\), domain size\(\times\)thickness\(\times\)channel width\(\times\)inlet invaded fraction) were simulated under both uncompressed and inhomogeneously compressed conditions, including ten sample realizations in each case. Therefore, the total number of simulations amounted up to 14,400, with an average computational time of 0.4 min per simulation. Calculations were run on 4 processors in a workstation equipped with Intel Xeon 6230 at 2.1 Ghz and 256 GB RAM.

Table 1 Ambient conditions, model parameters and average computed properties of uncompressed (unc) and inhomogeneously compressed (comp) carbon-paper GDLs, and MPL thickness and wet effective diffusivity (used for the calculation of the channel–CL oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\)). The variables examined in the parametric analysis are underlined
Full size table
Fig. 2
figure 2

3D pore size distributions of examined GDL domains with different uncompressed thicknesses (\(\delta _\mathrm{gdl}=135,~270~\text {and}~405\;\mu \mathrm m\)): (a) Uncompressed and (b) inhomogeneously compressed samples. The GDL/FF open area fraction corresponds to the baseline case (\(A^{\mathrm{out}}=0.5\), \(w_\mathrm{ch}= 1\;\mathrm {mm}\)) and the length in z-direction is \(L_z\approx 2\;\mathrm {mm}\). The compression ratio of the inhomogeneously compressed samples is \(\mathrm {\rm CR}\approx 20\%\). See Table 1 for further details

Full size image

3 Discussion of Results

The discussion of results is divided into two sections. In Sect. 3.1, the interplay between GDL thickness, inlet invaded area fraction and inhomogeneous assembly compression (\(\delta _{\mathrm{gdl}},A_w^{in},\mathrm{CR}\)) is analyzed in terms of three output variables: (i) average saturation, \(s^{\mathrm{avg}}\), (ii) through- and in-plane saturation distributions, \(s_y\) and \(s_x\), respectively, and (iii) channel–CL oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\). Then, Sect. 3.2 is devoted to the combined effect of the GDL/FF open area fraction and the GDL thickness (\(A^{\mathrm{out}},\delta _{\mathrm{gdl}}\)) on the same three output variables.

3.1 Interplay Between GDL Thickness, Inlet Invaded Area Fraction and Inhomogeneous Compression

Figure 3a–b shows the variation of average saturation, \(s^{\mathrm{avg}}\), with the inlet invaded area fraction, \(A_{w}^{in}\), for the three GDL thicknesses examined, \(\delta _\mathrm{gdl}\), under uncompressed and inhomogeneously compressed conditions. The outlet area fraction, \(A^{\mathrm{out}}\), is fixed to 0.5 (\(w_\mathrm{ch}=1\;\mathrm {mm}\)). The error bars indicate the range of variation of the computed results among the ten sample realizations and the two domain sizes examined (i.e., 20 simulations per case). For both uncompressed and compressed samples, there is a net increase of \(s^{\mathrm{avg}}\) with \(A_{w}^{in}\) due to the higher probability of invasion throughout the GDL as the number of injection sites into the GDL is increased. The average saturation roughly doubles its value (\(s^{\mathrm{avg}}\approx 0.1-0.2\)) in the range \(A_{w}^{in}\approx 0.2-0.9\). This result reproduces the scenario found in running PEFCs when the current density is increased and the liquid water flux from the CL to the GDL also increases. Interfacial accumulation of water can also arise due to the presence of interfacial gaps between the GDL and the MPL, as observed by Simon et al. (2017). Comparing Fig. 3a–b, the average saturation reached in the inhomogeneously compressed samples (\(s^\mathrm{avg}\approx 0.08\)) is nearly half the saturation in the uncompressed samples (\(s^{\mathrm{avg}}\approx 0.15\)) due to the smaller pore sizes present in the region under the rib. As a result, almost all liquid water is transported through the region under the channel where the capillary resistance is lower (Zenyuk et al. 2015). In contrast, the GDL thickness does not show any clear influence on \(s^{\mathrm{avg}}\), even though the number of invaded CVs increases in thicker samples. This is because the prescribed area fraction of invaded CVs at the inlet represents a larger portion in thin GDLs (see Appendix A). A rather constant average saturation with GDL thickness was also recently reported using DNS by Jeon (2020) and using PNM by Gholipour et al. (2021) for a fully saturated inlet. These results highlight the importance of interfacial regions in the design of MEAs with ultra-thin GDLs during water invasion. Further work should be conducted to analyze the effect of interfacial regions including phase change (Garcia-Salaberri 2022). The range of variation of \(s^{\mathrm{avg}}\) among different sample realizations is also rather independent of the GDL thickness (and the compression ratio), being around \(\Delta s^{\mathrm{avg}}\approx 0.1\) (comparable to \(s^{\mathrm{avg}}\)). The stochastic variations of the average saturation, \(s^{\mathrm{avg}}\sim 0.1-0.4\), are in the range reported for GDLs in previous ex-situ and in-situ works (see, e.g., Rosen et al. (2012); Xu et al. (2021); Satjaritanun et al. (2018); LaManna et al. (2014); Nagai et al. (2019); Mularczyk et al. (2021); Jeon (2020); Gholipour et al. (2021); Lee and Kim (2022) among others).

Fig. 3
figure 3

Variation of the average saturation, \(s^{\mathrm{avg}}\), as a function of the inlet invaded area fraction (colored bars), \(A_{w}^{in}\approx 0.25,0.6,0.9\), corresponding to three GDL thicknesses, \(\delta _{\mathrm{gdl}}=135,270,405\,\mu \mathrm m\): (a) uncompressed and (b) inhomogeneously compressed samples. The error bars show the range of variation of \(s^{\mathrm{avg}}\) among sample realizations. \(A^{\mathrm{out}}=0.5\) (\(w_{\mathrm{ch}}= 1\;\mathrm {mm}\))

Full size image

The saturation distributions in the through-plane and rib–channel directions, averaged over all sample realizations, are shown in Fig. 4a–b. Numerical predictions are compared with available numerical and experimental data (Zenyuk et al. 2015; García-Salaberri et al. 2015a; Lee and Kim 2022; Gostick 2013; Lamibrac et al. 2015). The interfacial region (corresponding to inlet invaded CVs) and the rib/channel regions are indicated by dashed lines. The normalized thickness of the interfacial region decreases from around 20% for \(\delta _{\mathrm{gdl}}=135\;\mu \mathrm m\) to 6-10% for \(\delta _\mathrm{gdl}=270-405\;\mu \mathrm m\). As shown in Fig. 4a, overall good agreement is found between the computed through-plane saturation distributions and the ex-situ experimental data of Lamibrac et al. (2015) for Toray TGP-H060 and SGL 24BA, as well as the numerical results of Gostick (2013) for Toray TGP-H series. Water IP in heterogeneous GDLs leads to a steep decrease of the saturation distribution from the peak value at the inlet (\(s_y\sim 0.2-0.9\)) down to \(s_y\sim 0.2-0.4\) in the region facing the inlet face (approx. 20% of GDL thickness) (Lamibrac et al. 2015; Gostick 2013; Lee and Kim 2022; Zenyuk et al. 2015). Saturation in the remaining bulk thickness (approx. 80% of GDL thickness) slightly increases in thicker GDLs due to the increase of the number of invaded CVs (pores) at breakthrough (i.e., gas–liquid interfacial area between CVs) (Gholipour et al. 2021). As shown in Appendix A, the increase in the gas–liquid interfacial area with the GDL thickness also leads to an increase in the breakthrough pressure because of the higher probability of accessing throats with a larger entry capillary pressure (Mortazavi and Tajiri 2014; Santamaria et al. 2014). The in-plane saturation distributions in Fig. 4c–d clearly show the impact of GDL inhomogeneous compression. The computed saturation distributions of uncompressed samples are similar to the ex-situ experimental data of Zenyuk et al. (2015) and García-Salaberri et al. (2015a) with setups including and not including a rib–channel pattern, respectively. Unlike predictions of macroscopic models (see, e.g., García-Salaberri et al. (2015b, 2017) and references therein), the effect of rib walls is outweighed by the effect of local capillary resistance, leading to a stochastic variation of water saturation in the material plane (\(s_x\sim 0.1-0.3\)). This result agrees with the predictions of many previous DNS and PN models (Gholipour et al. 2021; Liao et al. 2021; Qin et al. 2019; Jeon 2020, 2019; Ira et al. 2021; Lee and Kim 2022). Inhomogeneous compression leads to a preferential accumulation of water in the region under the channel due to the lower average entry capillary pressure present there (higher average pore size). Consequently, as commented before, the through-plane saturation profiles of the inhomogeneously compressed samples have about half the saturation of the uncompressed samples, a similar situation to that found in the recent DNS results of Lee and Kim (2022). A preferential accumulation of liquid water under the channel was also found in the ex-situ measurements of Zenyuk et al. (2015) for SGL 10 BA. Note that this result is independent of the carbon-paper fabric (SGL or Toray), since it arises from the relative variation of capillary resistance between the regions under the channel and under the rib. The coupled effect of inhomogeneous compression and GDL heterogeneity on capillary resistance, gas species diffusivity and thermal conductivity considering water phase change warrants closer attention (Garcia-Salaberri 2022).

Fig. 4
figure 4

Variation of local area-averaged saturation along the y-direction (through-plane direction), \(s_y\), and along the x-direction (rib–channel direction), \(s_x\), corresponding to three GDL thicknesses (colors), \(\delta _{\mathrm{gdl}}=135,270,405\;\mu \mathrm m\), and three inlet invaded area fractions (markers), \(A_{w}^{in}\approx 0.2-0.25~(\mathrm{L}),0.35-0.6~(\mathrm{M}),0.7-0.9~(\mathrm{H})\): (a, c) uncompressed and (b, d) inhomogeneously compressed samples. The dashed lines in the upper plots indicate the inlet interfacial regions, while those in the lower plots indicate the under-the-channel region. \(A^{\mathrm{out}}=0.5\) (\(w_\mathrm{ch}= 1\;\mathrm {mm}\)). The average through-plane saturation profiles were cubically interpolated using the computed discrete results. Previous numerical and experimental data are included for comparison: (a) saturation profiles at the breakthrough event between \(30-40\;\mathrm {\rm mbar}\) in Fig. 8 for Toray TGP-H060 and saturation profile at the breakthrough event at 19 mbar (2nd imbibition) in Fig.11 for SGL 24BA (Lamibrac et al. 2015), saturation profile in Fig. 11 for Toray carbon paper (Gostick 2013); (b) saturation profiles at the breakthrough event averaged between the regions under the channel and under the rib in Figs. 5c3–c4, 7d2–d5 and 8d2–d5, corresponding to \(\mathrm {\rm CR}=0\%,~20\%~\text {and}~40\%\), respectively, for a carbon-paper GDL (Lee and Kim 2022); (c) saturation profile close to the breakthrough event at \(2\;\mathrm {\rm kPa}\) in Fig. 5b for 10% PTFE-treated Toray TGP-H120 (García-Salaberri et al. 2015a), saturation profile close to \(1.8\;\mathrm {\rm kPa}\) (\(\mathrm {CR}=15\%\)) in Fig. 2a for SGL 10BA (Zenyuk et al. 2015); (d) saturation profile at \(2.45\;\mathrm {kPa}\) (\(\mathrm {\rm CR}=35\%\)) in Fig. 2b for SGL 10BA (Zenyuk et al. 2015)

Full size image

Figure 5a–b shows the variation of the channel–CL oxygen transport resistance under wet and dry conditions, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\) and \(R_{\mathrm{O_2}}^{\mathrm{chcl,dry}}\), with the GDL thickness and the inlet invaded area fraction, corresponding to uncompressed samples. The transport resistance of inhomogeneously compressed samples was not analyzed, since the preferential accumulation of water in the region under the channel is less representative of operating PEFCs, where condensation increases water saturation under the rib. The transport resistance of uniform samples provides an estimation that can be compared with previous in-situ measurements (Xu et al. 2021; Carrere and Prat 2019; Eller et al. 2016; Nagai et al. 2019; Garcia-Salaberri 2022). The proportionality constant between the dry transport resistance and the GDL thickness is lower than one (\(R_{\mathrm{O_2}}^\mathrm{chcl,dry}\propto 0.7\delta _{\mathrm{gdl}}\)) due to the decrease of the diffusive flux in the region far below the rib regardless of the GDL thickness. Thus, \(R_{\mathrm{O_2}}^{\mathrm{chcl,dry}}\) doubles from around \(0.4\;\mathrm {s\,cm^{-1}}\) to \(0.8\;\mathrm {s\,cm^{-1}}\) when the thickness is tripled (from \(\delta _{\mathrm{gdl}}=135\;\mu \mathrm m\) to \(\delta _\mathrm{gdl}=405\;\mu \mathrm m\)). The wet transport resistance increases approximately in the same proportion as the dry resistance, remaining the relative resistance rather constant around \(R_\mathrm{O_2}^{\mathrm{chcl}}/R_{\mathrm{O_2}}^{\mathrm{chcl,dry}}\approx 1.6\). Quantitatively, the wet resistance increases from \(R_{\mathrm{O_2}}^\mathrm{chcl}\approx 0.5-2\;\mathrm {s\,cm^{-1}}\) (\(\delta _{\mathrm{gdl}}=135\;\mu \mathrm m\)), passing through \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\approx 1-2.5\;\mathrm {s\,cm^{-1}}\) (\(\delta _{\mathrm{gdl}}=270\;\mu \mathrm m\)), up to \(R_\mathrm{O_2}^{\mathrm{chcl}}\approx 1.5-4\;\mathrm {s\,cm^{-1}}\) (\(\delta _\mathrm{gdl}=405\;\mu \mathrm m\)). Note that, for a given thickness, \(R_\mathrm{O_2}^{\mathrm{chcl}}\) increases non-linearly with increasing \(A_{w}^{in}\) due to the bottleneck effect that arise near the inlet region (Simon et al. 2017; Zapardiel and García-Salaberri 2022; García-Salaberri et al. 2015a). The computed wet resistances are in the range of those reported in previous experimental studies, varying between \(R_{\mathrm{O_2}}^\mathrm{chcl}=0.5-2.5\;\mathrm {s\,cm^{-1}}\) (see Fig. 3 (Owejan et al. 2013), Fig. 2 (Owejan et al. 2014), Fig. 8 (Wan et al. 2018), Fig. 6 (Simon et al. 2017), and Figs. 8 and 9 (Pang et al. 2019)). The stochastic fluctuations from sample to sample increase with the GDL thickness due to the larger amount of invaded percolation sites and the larger variability of finite-sized distribution of water in thick samples. As a result, peak oxygen transport resistances as high as \(R_\mathrm{O_2}^{\mathrm{chcl,max}}\approx 2-8\;\mathrm {s\,cm^{-1}}\) are reached for \(\delta _{\mathrm{gdl}}=405\;\mu \mathrm m\) (compared to \(R_{\mathrm{O_2}}^\mathrm{chcl,max}\approx 1-4\;\mathrm {s\,cm^{-1}}\) for \(\delta _{\mathrm{gdl}}=270\;\mu \mathrm m\) and \(R_{\mathrm{O_2}}^{\mathrm{chcl,max}}\approx 0.3-2.5\;\mathrm {s\,cm^{-1}}\) for \(\delta _{\mathrm{gdl}}=135\;\mu \mathrm m\)). This situation is illustrated in Fig. 6, which shows discrete saturation and continuum oxygen concentration distributions corresponding to uncompressed samples with a high oxygen transport resistance (\(A_{w}^{in}\approx 0.6\), \(A^{\mathrm{out}}=0.5\)). As can be seen, thin GDLs lead to less complex water distributions and facilitate oxygen transport.

Fig. 5
figure 5

(a) Variation of the wet oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\), with the inlet invaded area fraction (see color code in Fig. 3), \(A_{w}^{in}\approx 0.25,0.6,0.9\), and the GDL thickness, \(\delta _{\mathrm{gdl}}=135,270,405\,\mu \mathrm m\), corresponding to uncompressed samples. (b) Variation of the dry oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl,dry}}\)b. The inset in (a) shows the peak oxygen transport resistance, \(R_\mathrm{O_2}^{\mathrm{chcl,max}}\), computed among all realizations. \(A^\mathrm{out}=0.5\) (\(w_{\mathrm{ch}}= 1\;\mathrm {mm}\))

Full size image
Fig. 6
figure 6

Water saturation and oxygen concentration distributions for the three GDL thicknesses examined, \(\delta _\mathrm{gdl}=135,270,405\;\mu \mathrm m\) (\(\Pi _{\mathrm{gdl}}=0.07,0.135,0.2\)), corresponding to uncompressed samples. \(A_{w}^{in}\approx 0.6\), \(A^{\mathrm{out}}=0.5\) (\(w_{\mathrm{ch}}= 1\;\mathrm {mm}\)) and \(L_z\approx 1\;\mathrm {mm}\). The associated oxygen transport resistances are equal to: \(R_{\mathrm{O_2}}^{\mathrm{chcl,max}}\approx 0.7\;\mathrm {s\,cm^{-1}}\) (\(135\;\mu \mathrm m\)), \(R_{\mathrm{O_2}}^\mathrm{chcl,max}\approx 1.1\;\mathrm {s\,cm^{-1}}\) (\(270\;\mu \mathrm m\)), \(R_\mathrm{O_2}^{\mathrm{chcl,max}}\approx 2\;\mathrm {\rm s\,cm^{-1}}\) (\(405\;\mu \mathrm m\))

Full size image

3.2 Coupled Effect of GDL/FF Open Area Fraction and GDL Thickness

Figure 7a–d shows the variation of the average saturation for the three examined GDL/FF open area fractions, \(A^{\mathrm{out}}=0.25,0.5,0.75\), and three GDL thicknesses, \(\delta _\mathrm{gdl}=135,270,405\;\mu \mathrm m\), for \(A_{w}^{in}\approx 0.35-0.6\). The corresponding GDL slenderness ratios are equal to \(\Pi _\mathrm{gdl}=0.07,0.135,0.2\). As shown in Fig. 7a–b, the variation of \(s^\mathrm{avg}\) with \(A^{\mathrm{out}}\) is the opposite in uncompressed and inhomogeneously compressed samples. For uncompressed samples, \(s^{\mathrm{avg}}\) gradually decreases with increasing \(A^{\mathrm{out}}\) due to facilitated water transport from the GDL to the FF. Similar conclusions were drawn in the 2D numerical study of Gholipour et al. (2021), even though the reported local fluctuations in the rib–channel direction were larger due to the reduced dimensionality of their PN model (see Fig. 7c). IP in 3D smoothes out saturation fluctuations due to the increase of percolation sites for transport in a given position of space. On the contrary, for inhomogeneously compressed samples, \(s^{\mathrm{avg}}\) increases with \(A^{\mathrm{out}}\), since more water is accumulated in the uncompressed region under the channel where the capillary resistance is lower (see Fig. 7d). Quantitatively, \(s^\mathrm{avg}\) decreases from 0.2 (\(A^{\mathrm{out}}=0.25\)) to 0.15 (\(A^\mathrm{out}=0.25\)) without inhomogeneous compression, whereas \(s^{\mathrm{avg}}\) increases from 0.05 (\(A^{\mathrm{out}}=0.25\)) to 0.15 (\(A^\mathrm{out}=0.75\)) with inhomogeneous compression. The stochastic variations of water saturation between samples are reduced as capillary transport of water is facilitated (i.e., the GDL/FF open area fraction is increased/decreased for uncompressed/inhomogeneously compressed samples, respectively).

The above results show that capillary transport of water across GDLs can be facilitated using (i) high open area fractions (high \(A^\mathrm{out}\)) in combination with (ii) high slenderness ratios (high \(\Pi _{\mathrm{gdl}}\)) to provide uniform compression both under the channel and under the rib (see García-Salaberri et al. (2011)). Meeting the above two design criteria using a thin GDL can be achieved with a highly porous FF having an average pore size comparable to the GDL thickness (i.e., \(w_{\mathrm{ch}}\sim t_{\mathrm{gdl}}\sim 100\; {\mu \mathrm m}\gg w_{\mathrm{rib}}\sim {10}\; {\mu \mathrm m}\)). In addition, a porous FF can reduce cold rib surfaces where water condensation takes place via phase change-induced flow and increase gas-phase channel velocity (lower cross-sectional area) to facilitate water removal from the FF (Bednarek and Tsotridis 2020). Recent works with porous FFs have shown that mass transport losses can be significantly reduced, leading to high current densities around \(1.5\;\mathrm {A\,cm^{-2}}\) at lower voltages than usual (\(V_{\mathrm{cell}}\approx 0.45~\mathrm V\) vs. \(V_{\mathrm{cell}}\approx 0.55~\mathrm V\)) (Liu et al. 2020; Zhang et al. 2021). Such voltage decrease at maximum power density is typically found in high-temperature PEFCs operated above \(100\) °C (see, e.g., Chen et al. (2016); Krishnan et al. (2019); Peng et al. (2021)). In addition, previous work with corrugated FFs has shown a superior cell performance when the GDL/FF open area fraction is increased (Nikam and Reddy 2006; Merida et al. 2001).

Fig. 7
figure 7

(a, b) Variation of the average saturation, \(s^\mathrm{avg}\), as a function of the GDL/FF open area fraction (colored bars), \(A^{\mathrm{out}}=0.25,0.5,0.75\), corresponding to three GDL thicknesses, \(\delta _{\mathrm{gdl}}=135,270,405\;\mu \mathrm m\), for (a) uncompressed and (b) inhomogeneously compressed samples. (c, d) Variation of the local area-averaged saturation along the x-direction (rib–channel direction), \(s_x\), corresponding to the three GDL/FF open area fractions examined and \(\delta _{\mathrm{gdl}}=135\;\mu \mathrm m\) for (c) uncompressed and (d) inhomogeneously compressed samples. \(A_w^{in}\approx 0.35-0.6\)

Full size image

Figure 8a–b shows the results of the wet and dry channel–CL oxygen transport resistance of uncompressed samples for the same conditions examined in Fig. 7. An increase of the open area fraction from \(A^{\mathrm{out}}=0.25\) to \(A^{\mathrm{out}}=0.75\) reduces the wet transport resistance by a factor of two (\(R_{\mathrm{O_2}}^\mathrm{chcl}\approx 1\;\mathrm {s\,cm^{-1}}\) vs. \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\approx 0.5\;\mathrm {s\,cm^{-1}}\) for \(\delta _{\mathrm{gdl}}=135\; \mu \mathrm m\)) due to both the (slight) reduction of the average saturation and the better utilization of the region under the rib (i.e., reduction of the effective diffusion length across the GDL). Moreover, the stochastic variations of \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\) among sample realizations decrease at high open area fractions (see inset in Fig. 8a). Therefore, the use of thin GDLs with high open area fractions can ensure a more homogeneous oxygen flux throughout the cell active area (an aspect that can be important to reduce durability issues). Illustrative water and oxygen concentration distributions corresponding to the three open area fractions examined (\(A^{\mathrm{out}}=0.25,0.5,0.75\)) for \(\delta _\mathrm{gdl}=135\;\mu \mathrm m\) and \(A_{w}^{in}\approx 0.6\) are shown in Fig. 10 (Appendix A). As can be seen, oxygen transport is facilitated when the open area fraction is increased due to the reduction of the effective diffusion length from the channel to the CL, above and beyond the water distribution in the GDL. Manufacturing of porous FFs integrated with GDL/MPL layers using multiscale 3D printing can be a good practice to decrease mass transport losses, while leading to small electrical contact resistances.

Fig. 8
figure 8

(a) Variation of the wet oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\), as a function of the GDL/FF open area fraction (colored bars), \(A^{\mathrm{out}}=0.25,0.5,0.75\), corresponding to three GDL thickness, \(\delta _{\mathrm{gdl}}=135,270,405\,\mu \mathrm m\), for uncompressed samples. (b) Variation of the oxygen transport resistance, \(R_\mathrm{O_2}^{\mathrm{chcl,dry}}\), for the three examined open area fractions and thicknesses. The inset in (a) shows the peak oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl,max}}\), computed among all realizations. \(A_w^{in}\approx 0.6.\)

Full size image

4 Conclusions

The gas diffusion layer (GDL) thickness, \(\delta _{\mathrm{gdl}}\), and the open area fraction at the flow field interface, \(A^{\mathrm{out}}\), play a key role to decrease mass transport losses in proton exchange fuel cells (PEFCs). In this work, the combined effect of \(\delta _{\mathrm{gdl}}~(135\;{\mu \mathrm m},270\;{\mu \mathrm m},405\;{\mu \mathrm m})\) and \(A^{\mathrm{out}}~(0.25,0.5,0.75)\) on capillary-dominated transport of water and channel–catalyst layer (CL) oxygen transport resistance at various inlet invaded area fractions, \(A_{w}^{in}=0.2-0.25,0.35-0.6,0.7-0.9\), has been examined numerically under uncompressed and inhomogeneously compressed conditions (compression ratio, \(\mathrm{CR}\sim 20\%\)). A hybrid 3D model based on a control volume subdivision of the GDL has been used. The model combines a discrete formulation to model water invasion percolation (IP) and a continuum formulation to model oxygen diffusion owing to the lack of separation between pore and layer scales in macroporous thin GDLs. To asses stochastic variations, twenty simulations were carried out for each case examined (i.e., a combination of \(\delta _{\mathrm{gdl}}\), \(A^\mathrm{out}\) and \(A_{w}^{in}\)), corresponding to two different active areas (domain sizes) with ten sample realizations.

The numerical results of the parametric analysis were successfully compared qualitatively and quantitatively against previous numerical and experimental data of saturation distribution, s, oxygen transport resistance, \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\), and breakthrough pressure, \(p_{bt}\). It was found that anisotropic thin GDLs (\(\delta _{\mathrm{gdl}}\lesssim 100\;\mu \mathrm m\)) significantly reduce oxygen transport resistance mainly due to a decrease in the dry diffusion length across the GDL. The additional increase in the oxygen transport resistance caused by water blockage (relative resistance) is rather independent of the GDL thickness, being around \(R_{\mathrm{O_2}}^{\mathrm{chcl}}/R_{\mathrm{O_2}}^{\mathrm{chcl,dry}}\sim 1.6\). Thin GDLs also decrease the number of invaded pores at breakthrough, which reduces the stochastic formation of complex water distributions that can lead to a high local channel–CL oxygen transport resistance. Water capillary transport from the CL and oxygen transport from the channel in thin GDLs can be further enhanced using high open area fractions between the GDL and the flow field to increase oxygen accessibility under the rib. As a result, low channel–CL oxygen transport resistances in the order of \(R_{\mathrm{O_2}}^{\mathrm{chcl}}\sim 0.5\;\mathrm {s\,{cm}^{-1}}\) may be reached. Porous flow fields are a good option to meet all the above requirements, while facilitating water removal from the flow field thanks to increased gas-phase velocity in pores with a similar size to the GDL thickness (\(w_{\mathrm{ch}}\sim \delta _{\mathrm{gdl}}\sim 100\; \mu \mathrm m < 1\;\mathrm {mm}\)). Besides, porous flow fields can lead to a more uniform GDL compression, thus reducing spatial variations between channel and rib regions.

Several aspects warrant future work. The effect of phase change of water should be incorporated in the hybrid model using a quasi-steady-state formulation to better reproduce the scenario found in operating PEFCs. The microporous layer and the catalyst layer, where a representative elementary volume can be defined, should bemodeled by means of a macroscopic formulation. The multiscale, multiphase model should be then integrated into a multiphysics model of a PEFC to examine performance and durability. Special attention is to be devoted to the analysis of porous flow fields.