Abstract
This review provides an overview of concepts and approaches for the quantification of passive, non-reactive solute mixing in steady uniform porous media flows across scales. Mixing in porous media is the result of the interaction of spatial velocity fluctuations and diffusion or local-scale dispersion, which may lead to the homogenization of an initially segregated system. Velocity fluctuations are induced by spatial medium heterogeneities at the pore, Darcy or regional scales. Thus, mixing in porous media is a multiscale process, which depends on the medium structure and flow conditions. In the first part of the review, we discuss the interrelated processes of stirring, dispersion and mixing, and review approaches to quantify them that apply across scales. This implies concepts of hydrodynamic dispersion, approaches to quantify mixing state and mixing dynamics in terms of concentration statistics, and approaches to quantify the mechanisms of mixing. We review the characterization of stirring in terms of fluid deformation and folding and its relation with hydrodynamic dispersion. The integration of these dynamics to quantify the mechanisms of mixing is discussed in terms of lamellar mixing models. In the second part of this review, we discuss these concepts and approaches for the characterization of mixing in Poiseuille flow, and in porous media flows at the pore, Darcy and regional scales. Due to the fundamental nature of the mechanisms and processes of mixing, the concepts and approaches discussed in this review underpin the quantitative analysis of mixing phenomena in porous media flow systems in general.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mixing is the process that homogenizes initially segregated miscible constituents (Danckwerts 1952), increases the volume occupied by a solute, and decreases peak concentrations (Kitanidis 1994). Thus, mixing has different facets. The dilution that goes along with mixing is a key process for the attenuation of contaminant concentrations (Council et al. 2000). At the same time, the mixing of different waters can lead to the spoiling of freshwater such as in seawater intrusion in coastal aquifers (Bear et al. 1999). On the other hand, mixing facilitates chemical reactions and therefore is a key process in many natural and engineered systems (Valocchi et al. 2018; Rolle and Le Borgne 2019).
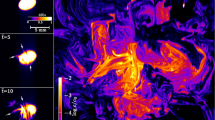
The process of mixing is fundamentally due to molecular diffusion. However, as diffusion is a relatively slow process, with diffusion coefficients of the order of or smaller than \(10^{-9}\) m\(^2\)/s (Grathwohl 2012), it is inefficient on large scales. Mixing is enhanced by stirring, the action that deforms material fluid elements and creates lamellar structures (Villermaux 2019) as illustrated in Fig. 1. In porous media, the medium itself stirs the fluid as it permeates through, driven by a pressure gradient (Bear 1972; Villermaux 2012). This action is due to spatial heterogeneity of the pore space at the pore scale (de Josselin de Jong 1958; Saffman 1959) and spatial variability of the hydraulic conductivity at the Darcy and regional scales (Gelhar 1993; Dagan 1989). At the pore-scale concentration gradients are destroyed by molecular diffusion, while at the Darcy-scale, at large temporal and spatial scales, the corresponding mechanisms are diffusion and mechanical dispersion (Bear 1972).
Fluid stretching due to stirring steepens concentration gradients and thus enhances diffusive mass transfer. The folding of material lines back on themselves brings initially segregated solutes so close together that they can eventually homogenize by diffusion. These mechanisms can be quantified by lamellar representations of mixing (Villermaux 2019). Also, the advective stirring action leads, through the creation of a lamellar structure, to the spreading of the solute distribution, which has been quantified by hydrodynamic dispersion and macrodispersion (Bear 1972; Gelhar and Axness 1983). While spreading is a precursor of mixing, it must be carefully distinguished from it (Kitanidis 1988). This is a central issue for mixing in porous media, for which diffusion or dispersion times over characteristic heterogeneity length scales may be orders of magnitude larger than characteristic advection times, and the solute distribution may be spread or stirred, but not mixed. The relative importance of advective and diffusive mass transfer over a characteristic length scale \(\ell _c\) is measured by the Péclet number \(Pe = \tau _D/\tau _v\), where \(\tau _D\) is the characteristic diffusion time and \(\tau _v\) the characteristic advection time over \(\ell _c\).
Mixing results from the interaction of large-scale (stirring) and small-scale (diffusion, local dispersion) processes, which themselves fluctuate due to the multiscale spatial heterogeneity inherent to porous media. The identification and quantification of the mixing dynamics that emerge from these interactions, and their relation to quantifiable medium and flow properties are key challenges across a wide range of porous media applications.
In this review, we focus on the mixing of passive solutes in the steady single-phase flow through heterogeneous porous media driven by a uniform pressure gradient. That is, we do not consider charge transport and the transport of stable isotopes, mixing of gases in porous media, or mixing in reactive, multiphase, variable density, non-Newtonian, or unstable flows, or mixing in temporally fluctuating porous media flows. Nevertheless, the processes and mechanisms under consideration here are relevant for and can be applied to underpin quantitative analysis of mixing phenomena in these porous media systems. We focus on passive mixing in steady porous media flows in order to discuss concepts and approaches to quantify the fundamentals of hydrodynamic mixing in porous media. New theoretical and experimental approaches for mixing in porous media have emerged in recent years in addition to classical methods based on the concept of hydrodynamic dispersion. The idea of this paper is to provide a comprehensive review of classical and recent approaches for mixing in porous media that can be applied across scales, and in the broader context of porous media systems.
The state of the art on reactive mixing in porous media is reflected in the recent reviews by Berkowitz et al. (2016), Valocchi et al. (2018) and Rolle and Le Borgne (2019). Berkowitz et al. (2016) provide a summary of reactive transport measurement and modeling approaches in geological media contrasting advection–dispersion–reaction equations and reactive continuous time random walk models. These authors emphasize the key role of mixing and spreading of reacting species. Valocchi et al. (2018) provide a comprehensive review on the quantification of mixing-limited reactions in porous media at the pore scale and the upscaling to the continuum scale. These authors focus on the pore-scale controls of reactive mixing and approaches to predict them across scales. Rolle and Le Borgne (2019) summarize advances for the characterization and modeling of mixing and reactive fronts in the subsurface with emphasis on displacement scenarios and continuously released plumes from the pore to the aquifer scale.
The focus here is on concepts and approaches to characterize and quantify mixing in porous media from the pore to the regional scales, and relate medium and flow properties to mixing behaviors. Due to the fundamental nature of the mechanisms and phenomena of mixing, methods and approaches to quantify them apply across scales. As pointed out above, the medium stirs the mixture and spreads the solute due to the complex pore-space geometry at the pore scale, and spatial variability of hydraulic conductivity at the Darcy or continuum scale. The microscopic mass transfer processes that attenuate concentration gradient are diffusion on the pore and diffusion and hydrodynamic dispersion at the Darcy scales. In the following, we provide a road map through this review.
Section 2 considers the basic concepts of mixing by diffusion and mixing by porous media with an emphasis on the distinction of stirring, mixing and spreading. Section 3 reports on approaches to quantify and characterize mixing that are valid at pore and continuum scales. Thus, it discusses in Sect. 3.1 concepts of hydrodynamic dispersion, as a straightforward generalization of diffusion to quantify the impact of small-scale fluctuations on solute mixing. Section 3.2 reviews the characterization and quantification of mixing and the evolution of mixing in terms of concentration statistics. This includes the dilution index as a measure of the mixing volume, and the concentration variance and probability distribution function (PDF) of concentration point values as measures for the homogeneity and concentration content of a mixture. It discusses the evolution equations for the concentration variance and PDF and their classical closures.
Section 3.3 focuses on the quantification of the stirring process and its action on the stretching and folding of the fluid support of a mixture. It discusses these processes for shear-dominated flows characterized by algebraic stretching, and chaotic flows, characterized by exponential stretching. Section 3.4 provides a summary of the lamellar mixing approach for porous media with focus on stretching-enhanced diffusion, which describes mixing at early times, and random aggregation, which describes the mixing process due to folding at late times. Section 3.5 describes methods for the reconstruction of a heterogeneous mixture based on the diffusive strip method, and the Lagrangian concentration approach.
Section 4 is dedicated to the discussion of mixing across scales. This includes mixing in Poiseuille flow in Section 4.1, at the pore scale in Section 4.2 and at the Darcy scale in Section 4.3. Each section reports on the characterization and quantification of the phenomena and mechanisms of mixing in the light of the concepts and approaches reviewed in Section 3. Section 5 gives a brief overview on mixing in more general porous media systems.
2 Concepts
In this section, we first discuss the fundamental process of mixing by diffusion. We introduce the Langevin equation that describes the diffusive motion of solute particles, and the diffusion equation that describes the evolution of the concentration of solute. The purely diffusive mixing process is then contrasted with the mixing process by porous media. We introduce the advection–diffusion equation and the equivalent Langevin equation to describe the evolution of a solute in a steady heterogeneous flow field. This description is used to discuss the basic concepts of mixing by porous media.
2.1 Mixing by Diffusion
Diffusion is the fundamental process that facilitates mixing. In the absence of external forcing, a substance dissolved in a fluid mixes into the host fluid due to diffusion, which is the result of thermal fluctuations exerted on the molecules of the substance by the fluid molecules. This process can be described by the kinematic equation
where \({{\mathbf {v}}}(t)\) is the particle velocity, which results from accelerations due to collisions of the solute particles with the fluid molecules, and damping by the Stokes drag due to the viscosity of the host fluid. The fluctuating particle velocity is modeled as a stochastic process (Gardiner 1986; Risken 1996). It is characterized by zero mean and a correlation function that decreases exponentially rapidly with time \(\langle v_i(t) v_j(t') \rangle = \delta _{ij} \sigma _v^2 \exp (-|t - t'|/\tau _c)\), where \(\tau _c\) is the correlation time and \(\sigma _v^2\) the velocity variance. The angular brackets denote the average over all realizations of \({{\mathbf {v}}}(t)\), which in the following is termed noise average.
Langevin equation In the limit of times \(t \gg \tau _c\), Equation (1) can be written as (Risken 1996)
where \({\varvec{\xi }}(t)\) is a vectorial Gaussian white noise with zero mean and variance \(\langle \xi _i(t) \xi _j(t') \rangle = \delta _{ij} \delta (t-t')\). The angular brackets denote the noise average. The dispersion coefficient D is defined by
The diffusion coefficient is related to the fluctuation mechanisms in terms of velocity variance and correlation time. The Einstein–Smoluchowski relation gives \(D = k_B T/ 6 \pi \eta _f r_0\) with \(k_B\) the Boltzmann constant, \(\eta _f\) the shear viscosity of the fluid, T absolute temperature and \(r_0\) the particle radius. We will find relations such as Eq. (3) also in the context of hydrodynamic dispersion.
Diffusion equation The Langevin equation (2) is equivalent to the diffusion equation (Risken 1996)
which describes the evolution of the spatial distribution \(c({{\mathbf {x}}},t)\) of solute molecules. The solutions of this equation for a point-like injection, \(c({{\mathbf {x}}}, t = 0) = \delta ({{\mathbf {x}}})\) into an infinite domain is given by the Gaussian
where d is the dimension of space.
Mixing Diffusion mixes a dissolved substance into the ambient fluid by increasing the volume that it occupies and thereby decreasing its maximum concentration with time as seen by setting \({{\mathbf {x}}}= {\mathbf {0}}\) in the Gaussian in Eq. (5). In order to illustrate the efficiency of mixing by diffusion, we consider the diffusion of chloride in water at rest. The diffusion coefficient for chloride anions in water is about \(D = 10^{-9}\) m\(^2\)/s. Chloride has been used as a passive tracer in a series of large-scale tracer experiments (Boggs et al. 1992; LeBlanc et al. 1991), and for the characterization of catchment travel times (Kirchner et al. 2000). The characteristic diffusion time over a length \(\ell\) is given by \(\tau _D = \ell ^2/D\). Thus it follows that the time for chloride to mix by diffusion into one liter of water, that is, \(\ell = 10^{-1}\) m, is of the order of 100 days. Likewise, the typical diffusion length during the time t is \(\lambda _D = \sqrt{D t}\). It increases with the square-root of time.
Diffusion in porous media is even slower due to the tortuous geometry of the pore space. At the continuum scale, the effective diffusion coefficient is given by Bear (1972); Ghanbarian et al. (2013); Tartakovsky and Dentz (2019)
where \(\phi\) is the porosity of the medium and \(\tau\) tortuosity. For granite, porosity is about \(2 \times 10^{-3}\) and tortuosity has been found to be between 5 and 15 (Vilks et al. 2003). With these corrections, the effective diffusion coefficient of chloride anions in water saturated granite is of the order of \(D^e = 10^{-13}\) m\(^2\)/s. Note that for the diffusion of chloride in cement materials, ionic forces need to be taken into account (Zhang and Gjørv 1996; Fenaux et al. 2019). For unconsolidated bead packs, the effective diffusion coefficient is \(D^e \sim 2/3 D\). For sandstones and carbonates, values for \(D^e\) are typically \(\sim D/2\) and \(\sim D/10\), respectively. That is, diffusion is not efficient for mixing at large scales.
2.2 Mixing by Porous Media
In a porous medium, the medium stirs the fluid through the spatially variable flow field, which eventually leads to large-scale solute mixing. This is illustrated in Fig. 1 for flow and solute transport at the Darcy scale. In this section, we introduce the governing equations for the detailed evolution of the distribution of a solute. We discuss the notions of stirring and mixing and introduce averaging as a systematic means of quantifying the impact of spatial heterogeneity on mixing.
Governing equations In order to discuss concepts and approaches to quantify mixing, we consider here and in Sect. 3 the generic scenario of advective-diffusive solute transport in a steady incompressible flow field \({{\mathbf {u}}}({{\mathbf {x}}})\). The evolution of the solute concentration \(c({{\mathbf {x}}},t)\) is described by the advection–diffusion equation
As discussed in Sect. 4, at the pore-scale \({{\mathbf {u}}}({{\mathbf {x}}})\) is given by the Stokes equation, at the Darcy scale by the Darcy equation. At the Darcy scale, the diffusion coefficient is replaced by the local dispersion tensor.
The advection–diffusion equation (7) is equivalent to the following Langevin equation for the particle position \({{\mathbf {x}}}(t|{{\mathbf {a}}})\)
where \({{\mathbf {x}}}(t = 0|{{\mathbf {a}}}) = {{\mathbf {a}}}\). We defined the particle velocity \({{\mathbf {v}}}(t|{{\mathbf {a}}}) = {{\mathbf {u}}}[{{\mathbf {x}}}(t|{{\mathbf {a}}})]\). Note that the particle velocity depends on diffusion through its argument \({{\mathbf {x}}}(t|{{\mathbf {a}}})\), which determines how the Eulerian flow field is sampled by the particle.
The concentration distribution \(c({{\mathbf {x}}},t)\) is given in term of the particle trajectories as
where \(c({{\mathbf {x}}},t = 0) = c_0({{\mathbf {x}}})\) is the initial solute distribution. Note that
is the transport Green function and satisfies Eq. (7) for the initial condition \(g({{\mathbf {x}}},t = 0|{{\mathbf {a}}}) = \delta ({{\mathbf {x}}}- {{\mathbf {a}}})\).
Stirring and mixing In the absence of diffusion, Eq. (8) provides a map between the initial positions \({{\mathbf {a}}}\) and the particle position \({{\mathbf {x}}}(t|{{\mathbf {a}}})\), which allows also to change between Eulerian and Lagrangian reference frames. The solute distribution for a constant initial concentration \(c_0\) within a domain \(\Omega _0\) of volume \(V_0\) is given by
where \({{\mathbf {x}}}(t|{{\mathbf {a}}})\) satisfies (8) for \(D = 0\). The function \(\rho ({{\mathbf {x}}},t)\) is equal to one within the map \({{\mathbf {x}}}(t|{{\mathbf {a}}})\) of the set of initial points \({{\mathbf {a}}}\), and zero elsewhere. The volume comprised by \(\rho ({{\mathbf {x}}},t)\) is always equal to \(V_0\) because we consider here incompressible, that is, volume conserving flows. The top panels of Fig. 1 show the purely advective evolution of a solute from an initial slab of concentration \(c_0\) perpendicular to the mean flow direction. The solute distribution deforms, it disperses by stirring, but does not mix. Nevertheless, the stretching and folding of the fluid support, that is, stirring, leads to the spreading of the solute and the creation of a lamellar structure. This action facilitates mixing by increasing concentration gradients through the stretching and compression of the fluid support, and by decreasing the distance between lamellae such that diffusion can act efficiently to homogenize the mixture as shown in the bottom panels of Fig. 1. This phenomenology would suggest that the interaction of advection and diffusion can be reduced to superposing a diffusive profile on a structure that is created by pure advection. This picture, however, disregards the fact that the way a particle samples the flow velocity depends also on diffusion. This is of particular importance for mixing in stratified flow fields.
Averaging In order to systematically quantify the impact of spatial flow variability on stirring, solute dispersion and mixing, one considers suitably defined averages. These are typically spatial averages over a sufficiently large support volume (Brenner and Edwards 1993; Whitaker 1999) or ensemble averages in the framework of stochastic models for the Eulerian or Lagrangian flow velocities \({{\mathbf {u}}}({{\mathbf {x}}})\) and \({{\mathbf {v}}}(t) = {{\mathbf {u}}}[{{\mathbf {x}}}(t)]\), respectively (Gelhar 1993; Dagan 1989). Under ergodic conditions, spatial and ensemble averages can be interchanged (Hristopulos 2020; Wang and Kitanids 1999; Wood et al. 2003). We term the average (spatial and ensemble) over the spatially varying flow field as disorder average and denote it by an overbar in order to distinguish it from the noise average, denoted by angular brackets. The noise average was introduced in Sect. 2.1 in order to quantify the impact of microscale velocity fluctuations on diffusive motion. The average Eulerian flow velocity is thus denoted by \({\overline{{{\mathbf {u}}}}} = \overline{{{\mathbf {u}}}({{\mathbf {x}}})}\). It is assumed to be constant and aligned with the 1-direction of the coordinate system in the following.
3 Approaches
In this section, we summarize approaches that account for the impact of spatial flow variability on mixing. They apply to mixing in steady confined flows in capillaries and channels and the pore and Darcy scales. We first discuss the classical concept of hydrodynamic dispersion, and the meaning of ensemble and effective dispersion. Then, we focus on concentration statistics, entropy, concentration variance, segregation intensity and concentration point statistics to quantify the mixing state and mixing evolution. Finally, we discuss the mechanisms of mixing in terms of the characterization of the stirring process and its integration in lamellar representations of mixing.
3.1 Hydrodynamic Dispersion
The classical approach for the quantification of the impact of velocity fluctuations on solute mixing has been to define dispersion coefficients, in analogy to diffusion. According to (3), diffusion coefficients can be defined by the ensemble average over all realizations of the stochastic particle velocity \(\varvec{{{\mathbf {v}}}}(t)\). As discussed at the end of the previous section, we can consider two averages, one over the disorder and the other over the noise. The meaning of the dispersion coefficients depends on the order in which these two averages are taken. First, we consider the ensemble dispersion coefficient, which is defined by simultaneously averaging over disorder and noise. It quantifies the advective spreading of a solute distribution. Second, we consider the effective dispersion coefficient, which is obtained by first performing the noise and then the disorder average. It characterizes the typical width of a solute plume originating from a point-like injection, that is, of the transport Green function.
3.1.1 Ensemble Dispersion
As a straightforward generalization of the diffusion concept discussed in Sect. 2.1, we consider a single averaging process that consists of taking simultaneously the disorder and noise averages. Thus, the particle velocity is decomposed into the mean \({\overline{{{\mathbf {v}}}}} \equiv \overline{\langle {{\mathbf {u}}}[{{\mathbf {x}}}(t)] \rangle }\) and zero mean fluctuations \({{\mathbf {v}}}'(t)\) about it. Thus, we may write the Langevin equation (8) as
Note that we assume that the particle velocity is stationary in the sense that its average is independent of time. Hydrodynamic dispersion coefficients can then be quantified by the Taylor-Green-Kubo relation
which was originally derived to quantify diffusion by turbulent motion (Taylor 1922), the friction constant of Brownian particles in a gas (Green 1951), and the conductivity and diffusivity of independently moving charged particles (Kubo 1957). The ensemble dispersion coefficient can be equivalently defined by the method of moments (Aris 1956) as
where the moments of the average solute concentration \({\overline{c}}({{\mathbf {x}}},t)\) are defined by
The second centered moments of the average solute distribution are defined by \(\kappa _{ij}^m(t) = {\overline{m}}_{ij}(t) - {\overline{m}}_i(t) {\overline{m}}_j(t)\), and are measures for the spatial extension of \({\overline{c}}({{\mathbf {x}}},t)\).
The \(D_{ij}^m(t)\) in general evolve in time, and under certain conditions (Isichenko 1992; Dentz et al. 2004) converge to constant asymptotic values
This relation gives an intuitive way for estimating the dependence of the dispersion coefficients on local-scale mass transfer mechanisms. This becomes clear if one writes
where \(\sigma _{ij}^2\) is the velocity variance and \(\tau _{c}\) the correlation time. We assume for simplicity that \(\tau _c\) is isotropic. Note that the correlation time in general depends on the diffusion coefficient D and is a function of the Péclet number. Recall that the particle velocity \({{\mathbf {v}}}(t)\) depends on diffusion, which determines, how it samples the Eulerian velocity. The off-diagonal elements of the dispersion tensor are typically zero for uniform flow under a constant pressure gradient. We denote the dispersion coefficient in direction of the pressure gradient by \(D_L^m(t)\) and transverse to it by \(D_T^m(t)\). In the limit \(D \rightarrow 0\), the correlation time \(\tau _c\) reduces to the purely advective correlation time. If the ensemble dispersion coefficients are finite in this limit, they measure purely advective solute spreading. In highly heterogeneous porous media, the longitudinal dispersion coefficients may evolve as a power-law with time, that is \(D_L^m(t) \sim t^{\alpha -1}\) with \(1 \le \alpha \le 2\). This behavior is termed superdiffusive, or non-Fickian in the literature (Bouchaud and Georges 1990; Berkowitz et al. 2006) as opposed to diffusive behaviors, which are characterized by a constant dispersion coefficient. Superdiffusive behaviors have been found at the pore and Darcy scales in porous and fractured media (Berkowitz et al. 2006; Bijeljic and Blunt 2006; Le Borgne et al. 2008; Kang et al. 2011). The case \(\alpha = 1\) indicates ballistic dispersion. Ballistic behavior is typically found for the early time dispersion because particles move at approximately constant velocities for times smaller than the correlation time \(\tau _c\). Ballistic dispersion also describes solute spreading under pure advection in stratified flow fields.
For times \(t \gg \tau _c\), the large-scale concentration distribution can be described by the advection–dispersion equation
where \({\varvec{1}}\) denotes the identity matrix. This equation for the average coarse-grained solute concentration can be derived in a more rigorous way using volume or stochastic averaging (Brenner and Edwards 1993; Whitaker 1999; Gelhar 1993).
As indicated above, the representation of solute transport by the advection–dispersion equation (18) does not mean, that the system is locally well-mixed. In fact, in the absence of diffusion, \({{\mathbf {D}}}^a\) quantifies the purely advective spread of the interface as illustrated in Fig. 1. In this case, the average concentration \({\overline{c}}({{\mathbf {x}}},t) = c_0 {\overline{\rho }}({{\mathbf {x}}},t)\), see Eq. (11), is a measure for the volume fraction of solute in an unmixed sampling volume. As there is no mixing, \({\mathbf {D}}^a\) measures the deformation of the interface rather than the mixing volume. This is true even in the presence of diffusion, as long as the sampling volume has not been homogenized by diffusion.
Also, the correlation time \(\tau _c\) may be much larger than observation times of practical interest. It has been shown that Eulerian flow fields in highly heterogeneous media are characterized by broad distribution of flow velocities, which induces a broad distribution of characteristic mass transfer times. The large-scale advection–dispersion equation (18) is only valid at asymptotically long times, while at relevant observation times memory effects become important. Modeling frameworks for non-Fickian pre-asymptotic solute dispersion are, for example, the continuous time random walk (Berkowitz et al. 2006), spatial Markov models and time-domain random walks (Sherman et al. 2021; Painter et al. 2008), multirate mass transfer approaches (Haggerty and Gorelick 1995; Carrera et al. 1998), and fractional advection–dispersion equations (Benson et al. 2013), which account for broad spectra of mass transfer time scales inherent to highly heterogeneous porous media (Berkowitz et al. 2006; Frippiat and Holeyman 2008; Neuman and Tartakovsky 2008).
3.1.2 Effective Dispersion
In order to separate solute spreading from mixing, one can decompose the particle velocity \({{\mathbf {v}}}(t)\) into its noise mean and fluctuations about it, \({{\mathbf {v}}}(t) = \langle {{\mathbf {v}}}(t) \rangle + \delta {{\mathbf {v}}}(t)\). Thus, the Langevin equation (8) can be written as
The noise mean of \(\delta {{\mathbf {v}}}(t)\) is zero by definition. Also, it is identically zero for \(D = 0\). Note that \(\delta {{\mathbf {v}}}(t)\) is different from \({{\mathbf {v}}}'(t)\) of the previous section because it is defined with respect to the noise average only. The difference between \(\delta {{\mathbf {v}}}(t)\) and \({{\mathbf {v}}}'(t)\) is given by
It quantifies the center of mass fluctuations of the solute plume with respect to the disorder averaged center of mass position. In analogy to (13), we define the effective dispersion coefficient as
Unlike \(D^m_{ij}(t)\), the effective dispersion coefficient \(D_{ij}^e(t)\) is identically zero for \(D = 0\) because \(\delta {{\mathbf {v}}}(t) \equiv 0\) in this limit. The effective dispersion coefficient can be equivalently written in terms of the moments of the transport Green function \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\) as (Kitanidis 1988; Dentz and Carrera 2007)
where the moments of \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\) are defined by
The concept of effective dispersion was proposed by Kitanidis (1988). It quantifies the typical dispersion of \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\), that is, of a solute plume that originates from a point injection (Kitanidis 1988; Bouchaud and Georges 1990). Thus, it accounts for the impact of velocity fluctuations on the scale of the transport Green function on effective particle motion. Similarly, effective dispersion coefficients can be defined by setting the sampling scale equal to the characteristic mixing length, which evolves according to flow deformation and diffusion (Dentz and de Barros 2015). Figure 2 illustrates the difference between ensemble and effective dispersion. Ensemble dispersion is a measure for the spreading of the plume, while effective dispersion measures the width of the mixing interface.
The difference between the ensemble and effective dispersion coefficients,
is a measure of the center of mass fluctuations around the disorder mean. It goes to zero if the noise mean velocity converges toward the disorder mean, that is, if the average particle velocity is self-averaging (Bouchaud and Georges 1990). In this case, both the ensemble and effective dispersion coefficients evolve toward the same asymptotic value \(D_{ij}^a\) defined by (16).
As pointed out above, the effective dispersion coefficients describe the evolution of the spatial variance of the transport Green function \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\). If the Lagrangian velocity fluctuations \(\delta {{\mathbf {v}}}(t)\) follow Gaussian statistics, the evolution equation for the transport Green function can be approximated by Dentz (2012)
Note that in this approximation, \(\langle {{\mathbf {v}}}(t|{{\mathbf {a}}}) \rangle\) depends on the injection point, while \({\mathbf {D}}^e(t)\) quantifies the average evolution of the spatial variance of \(g({{\mathbf {x}}},t)\). Note also, that the dispersion tensor depends on the initial time, which here is set equal to 0, because \(\delta {{\mathbf {v}}}(t)\) is approximated by a correlated Gaussian noise. In this representation, advective stirring is represented by \(\langle {{\mathbf {v}}}(t|\mathbf a) \rangle\) and solute mixing by the effective dispersion tensor \({\mathbf {D}}^e(t)\). The effective dispersion concept was used to quantify preasymptotic reactive mixing at the pore and Darcy scales (Cirpka 2002; Jose and Cirpka 2004; Perez et al. 2019; Puyguiraud et al. 2021), and in the context of the estimation of the concentration variance (Fiori and Dagan, 2000; Fiori 2001).
3.2 Concentration Statistics
A straightforward generalization of the diffusion concept in terms of ensemble dispersion coefficients does not provide an adequate measure for solute mixing. Diffusion coefficients are not a measure for mixing per se either. They rather parameterize the observables that characterize mixing, such as, the mixing volume, that is the volume occupied by a dissolved substance, or the decay of the maximum concentration, or the evolution of the distribution of concentration point values, and its variance. In this section, we discuss measures of mixing and their evolution in time, which gives insight into the mechanisms of mixing.
3.2.1 Mixing Volume
Kitanidis (1994) defines the mixing volume based on the concentration entropy
where \(c({{\mathbf {x}}},t)\) is normalized to 1. The mixing volume is measured by the dilution index
It is a measure for the actual mixing volume as illustrated below.
Dynamics The time evolution of the dilution index is obtained by using Eq. (7) as
This expression emphasizes that any increase of the actual mixing volume is determined by a diffusive mass transfer process, and the attenuation of concentration gradients. Trivially, for \(D = 0\) the volume occupied by a solute remains constant.
Examples For the Gaussian concentration distribution (5) the dilution index is given by
The diffusion length after a time t is \(\ell _D(t) = \sqrt{2 D t}\). Thus, \(E(t) \propto \ell _D(t)^3\), that is, the mixing volume is inversely proportional to the maximum concentration \(c_m(t) = c({{\mathbf {x}}}= {\mathbf {0}},t) = (4 \pi D t)^{-d/2}\). The mixing volume for diffusive mixing is fully characterized by the diffusion coefficient.
In the case of purely advective transport characterized by the concentration distribution (11), for example, the dilution index is simply \(E = V_0\). It is constant and equal to the initial volume. No mixing occurs while the solute disperses according to the hydrodynamic dispersion coefficients \(D_{ij}^m(t)\).
3.2.2 Concentration Variance
The concentration variance, defined by
is a measure for the heterogeneity of the mixture. It decreases under mixing. The spatially integrated concentration variance is in the following denoted by
For the case of pure diffusion, the mean concentration decays as \({\overline{c}} \sim t^{-d/2}\) and the concentration variance as \(\sigma _c^2 \sim t^{-d}\). In the case of purely advective transport, the mean concentration is given by \({\overline{c}} = c_0 \overline{\rho }({{\mathbf {x}}},t)\) and the concentration variance by Dagan (1982)
where \({\overline{\rho }}({{\mathbf {x}}},t)\) is the volume fraction of solute in the unmixed sampling volume.
The degree of heterogeneity of a dissolved substance can be quantified by the segregation intensity (Danckwerts 1952)
It is one for complete segregation and zero for a uniform concentration distribution. For purely diffusive transport, the segregation intensity decreases as \(I(t) \sim t^{-d/2}\). For the purely advective case, it is \(I(t) = 1\).
Dynamics In order to illustrate the interplay between advective spreading or stirring of the fluid and diffusion, we consider the time derivative of the concentration variance. Under the assumption that the average concentration \({\overline{c}}({{\mathbf {x}}},t)\) obeys the macroscale advection–dispersion equation (18), one obtains an advection–dispersion-reaction equation for \(\sigma _c^2({{\mathbf {x}}},t)\) (Kapoor and Kitanidis 1998)
where \(c'({{\mathbf {x}}},t) = c({{\mathbf {x}}},t) - {\overline{c}}({{\mathbf {x}}},t)\). This equation reveals two key features of mixing and dispersion expressed by the sink and source terms on the right side. The second term on the right side represents the generation of concentration variability due to the deformation of the initial solute distribution. In the absence of diffusion, that is for \(D = 0\), the variance evolves solely by continuous stirring due to the flow heterogeneity as expressed by \({{\mathbf {D}}}^a\), and it is given exactly by expression (32) as can be checked by inspection. Concentration variability in this case refers to the variability of the volume fractions occupied in the otherwise unmixed sampling volumes. The first term on the right side is called the scalar dissipation rate and is denoted by \(\chi ({{\mathbf {x}}},t)\) in the following. It quantifies the destruction of concentration variance due to the attenuation of concentration gradients by diffusive mass transfer, whose creation is quantified by the second term. Equation (34) is not closed because the scalar dissipation rate depends on the concentration fluctuation. Closure approximations for the scalar dissipation rate are called mixing models (Pope 2000). The classical closure sets
where \(\eta\) is an (empirical) constant rate. By definition, it can be related to the length scale s of the concentration variability through \(\eta \sim D / s^2\). Equation (35) is the interaction by exchange with the mean (IEM) closure (Villermaux and Devillon 1972). It has been used in the context of mixing in Darcy-scale heterogeneous porous media (Kapoor and Kitanidis 1998; Andričević 1998; De Dreuzy et al. 2012), where it was found that \(\eta\) varies in time. This is intuitive because the characteristic concentration gradient scale is time-dependent. For example for the Gaussian distribution (5), the characteristic gradient scale is \(s(t) = \sqrt{2 D t}\), that is, it increases diffusively. The gradient scale can be seen as the distance below which the concentration can be considered uniform. In this sense it denotes the physical coarse-graining scale of a heterogeneous mixture (Villermaux and Duplat 2006; Le Borgne et al. 2011). For hydrodynamic mixing, the evolution of the coarse-graining scale is due to the interaction of fluid deformation and diffusion.
3.2.3 Probability Density Function (PDF) of Concentration
The heterogeneity of the distribution of a solute can be measured by the probability density function (PDF) of concentration point values. The concentration PDF in a region \(\Omega\) of volume V can be defined by
where \(\delta (c)\) denotes the Dirac delta. This definition allows to describe the mixing state in different regions within the mixture and to quantify its spatial evolution. In order to determine the global concentration statistics within a mixture, the sampling volume can be defined by all points \(\{{\mathbf {r}}|c({{\mathbf {x}}}+ {\mathbf {r}},t) \ge c_{\mathrm{th}}\}\) for which the concentration is larger than a threshold value. The distribution of concentration point values plays a central role as a characteristic of mixing with implications for quantification of nonlinear reactions (Tartakovsky et al. 2002; Cirpka et al. 2008a), and in the context of probabilistic risk assessment (Tartakovsky 2013).
The PDF of concentration values is the result of the interaction of large-scale advective motion and small-scale diffusive mass transfer. Thus, the quantification of the concentration PDF in a heterogeneous medium is challenging. For pure diffusion and purely advective transport, there are analytical expressions for \(p(c,{{\mathbf {x}}},t)\). Also, the concentration PDF is often modeled by suitable parametric function, like the Beta model.
Diffusion only The global concentration PDF for the Gaussian distribution (5) is given by
where \({\mathbb {I}}(\cdot )\) is the indicator, which is 1 if its argument is true and 0 else. It is fully characterized by the maximum concentration \(c_m(t)\) and thus by the diffusion coefficient.
Advection only For illustration, we consider the opposite case of purely advective transport and deformation of an initial solute distribution as given by (5). The global concentration PDF is then given by Dagan (1982)
where \({\overline{\rho }}({{\mathbf {x}}},t)\) is the volume fraction of solute in the unmixed sampling volume at \({{\mathbf {x}}}\). The overbar denotes the spatial average defined by the right side of (36).
Beta model The Beta distribution has been used as a parametric model for concentration PDFs at the Darcy scale (Fiorotto and Caroni 2002; Bellin and Tonina 2007; Cirpka et al. 2008b). It is defined by
where \(B(\alpha ,\beta )\) is the Beta function. The distribution is fully defined in terms of the concentration mean and variance (Bellin and Tonina 2007), which in general may depend on position \({{\mathbf {x}}}\) and time t, that is,
The segregation intensity \(I({{\mathbf {x}}},t)\) is defined in Eq. (33).
Dynamics The evolution equation for the concentration PDF \(p(c,{{\mathbf {x}}},t)\) is given by Pope (2000)
The angular brackets \(\langle \cdot | c \rangle\) denote the average conditional on the concentration value c. Equation (41) represents a closure problem. Under the same assumptions as in the previous section, one may set
It can be shown that this closure approximation is exact if the concentration and its gradient are jointly Gaussian distributed (Pope 2000). Furthermore, the evolution equation (34) of the concentration variance, implies that
With these approximations, the evolution equation for the concentration PDF can be written as
This approach for the concentration PDF is equivalent to the IEM closure discussed in Sect. 3.2.2 and thus has the same shortcomings.
3.3 Stirring
The stirring process due to spatial flow variability can be described by purely advective transport as described by the kinematic equation
Stirring can be separated into two related main actions. The stretching of the material fluid elements (lamellae) that support the solute, and the folding of lamellar structures back on themselves, which facilitates, in the presence of diffusion the coalescence or aggregation of lamellae and thus the homogenization of a mixture. Figure 1 illustrates the purely advective evolution of a solute initially distributed perpendicular to the mean flow direction. One clearly sees the stretching of the line at early times, and the stretching and folding back on itself at later times.
3.3.1 Stretching
The deformation of a fluid element can be characterized by the deformation gradient tensor \({\mathbf {F}}(t|{{\mathbf {a}}})\), which describes how an infinitesimal fluid element \(\delta {{\mathbf {x}}}(t|{{\mathbf {a}}}) = {{\mathbf {x}}}(t|{{\mathbf {a}}}+\delta {{\mathbf {a}}}) - {{\mathbf {x}}}(t|{{\mathbf {a}}})\) deforms with time from its initial state \(\delta {{\mathbf {a}}}\),
The time derivative of \({\mathbf {F}}(t|{{\mathbf {a}}})\) is by definition given by
where the Lagrangian deformation rate tensor is defined by
In the following, we will consider for illustration the evolution of a solute line that originates from an initial distribution perpendicular to the mean flow direction, that is, the initial state of \(\delta {{\mathbf {x}}}(t|{{\mathbf {a}}})\) is \(\delta a_2 \hat{{\varvec{e}}}_2\) with \(\hat{{\varvec{e}}}_2\) a unit vector perpendicular to the mean flow direction. The initial length of the line is denoted by \(\ell _0\). Its length \(\ell (t)\) after time t is given by
where \(|\cdot |\) denotes the absolute value.
Shear flow–linear stretching We consider the stretching of a line that evolves in a random shear flow \({{\mathbf {u}}}({{\mathbf {x}}}) = [u(x_2), 0]^\top\). Shear flows are typical scenarios for laminar porous media flows as for example at the pore scale close to grain walls, which constitute a no-slip boundary, and on the Darcy scale for aquifers characterized by a stratified hydraulic conductivity distribution. For a random shear flow, the particle trajectories are simply given by \({{\mathbf {x}}}(t|a_2) = [u(a_2) t, a_2]^\top\). The deformation rate tensor and deformation gradient tensor are obtained from Eqs. (48) and (47) as
where \(\varsigma (x_2) = d u(x_2)/dx_2\) is the shear rate. Thus, we obtain for the evolution of a line segment \(\delta \ell (|a_2) = |\delta {{\mathbf {x}}}(t|x_2)|\) from (46)
The line length is obtained from (49) as
Asymptotically, it increases linearly with time.
Porous media–algebraic stretching Note that for the random shear flow of the previous paragraph, a strip experiences always the same deformation as quantified by the shear rate \(\varsigma (a_2)\). In general however, a strip, as it is transported along the (curved) streamline of a heterogeneous flow field, passes through regions of different deformations (de Barros et al. 2012), see also Fig. 1. In order to account for this variability, the strip elongations \(\delta \ell (t)\) have been modeled as stochastic processes. For example, Le Borgne et al. (2013) used an empirical geometric Brownian motion for the evolution of \(\delta \ell (t)\).
Based on Eq. (46) and a stochastic description of the medium heterogeneity, Dentz et al. (2016b) and Lester et al. (2018) showed for two and three spatial dimensions that the evolution of \(\delta \ell (t)\) can be described by coupled continuous time random walks. For two dimensions, it has been found that the length of a lamella increases in average as a power-law, that is \(\langle \delta \ell (t) \rangle \sim t^\beta\) with \(1/2 \le \beta \le 2\) (Le Borgne et al. 2013; Dentz et al. 2016b), where \(\beta\) depends on the medium heterogeneity. For weakly heterogeneous media \(\beta \approx 1/2\). It increases with increasing heterogeneity.
For steady flow in two spatial dimensions, stretching cannot be stronger than algebraic because chaotic advection is prohibited by the Poincaré–Bendixson theorem. Streamlines cannot diverge without bound. This limitation is due to the topological constraint that streamlines act as confining boundaries and so cannot cross, leading to fluid stretching that is at most algebraic in time (Arnold 1965; Dentz et al. 2016b) and zero transverse hydrodynamic dispersion (Lester et al. 2021).
Chaotic advection–exponential stretching In three-dimensional porous media flows, this constraint may be relaxed and different transport, mixing and dispersion dynamics can result. These dynamics are known as chaotic advection (Aref 1984), so called because the advection equation (45) for the position \({\mathbf {x}}(t)\) of a massless infinitesimal fluid tracer particle represents a continuous dynamical system, which can exhibit chaotic dynamics if the velocity field \({\mathbf {u}}({{\mathbf {x}}})\) contains at least three degrees of freedom, which is fulfilled for three-dimensional steady flow (or unsteady two-dimensional flows). Thus chaotic advection is inherent to all steady random three-dimensional flows, unless there exist specific constraints or symmetries that constrain the kinematics (Aref et al. 2017). Note that Eq. (45) is also an identity for fluid velocity and defines the coordinate transform between the Eulerian \({\mathbf {x}}\) and Lagrangian \({\mathbf {a}}\) frames. The chaotic dynamics that result from Eq. 45 then manifest as Lagrangian particle orbits that form a chaotic tangle, and fluid elements are stretched exponentially in time. Hence chaotic advection is characterized by persistent exponential growth of the strip length as \(\langle \delta \ell (t) \rangle \sim \exp (\lambda t)\), where \(\lambda\) denotes the infinite time Lyapunov exponent of the flow that characterizes the strength of chaotic mixing, and so \(\lambda =0\) for non-chaotic flows. Such exponential stretching leads to highly efficient stirring and qualitatively augmented mixing and dispersion that can only be properly understood in the Lagrangian frame. Thus, chaotic solute mixing and dispersion requires an understanding of the Lagrangian kinematics of these flows, along with the impacts of these kinematics upon additional transport mechanisms such as molecular diffusion and hydrodynamic dispersion.
Schematic of chaotic advection in a steady three-dimensional flow. Here, the thick colored streamlines twist around each other in a braiding motion as they propagate in the mean flow direction. The non-trivial nature of this braiding motion means that the length of the black rectangular material boundary grows exponentially with the number of braiding motions, leading to efficient stirring and accelerated mixing. Adapted from Thiffeault and Finn (2007)
Whether at the pore or Darcy scale, a signature of chaotic advection is the non-trivial braiding of streamlines (Thiffeault and Finn 2007), as shown in Fig. 3. Here, the colored streamlines interchange positions transverse to the mean flow direction to form a braiding pattern, leading to rapid growth of fluid elements (as indicated by the black rectangle) as they wrap around the braiding streamlines, leading to chaotic advection and augmented mixing ensue. The inherently random nature of most porous media flows means that such tracer or streamline braiding can occur at the pore, Darcy or regional scales. All that is required is that there are sufficient degrees of freedom (three) in the flow for tracer for streamline braiding to arise, and the random nature of most porous media ensures such non-trivial braiding is inevitable as any random sequence of braiding motions must contain non-trivial braids.
In fact, in recent years it has been shown theoretically (Lester et al. 2013a, 2016b), computationally (Lester et al. 2016a; Turuban et al. 2018, 2019) and experimentally (Kree and Villermaux 2017; Souzy et al. 2020; Heyman et al. 2020, 2021) that chaotic advection is ubiquitous to steady three-dimensional pore-scale flow. In all of these cases, stagnation points at the pore boundary generate persistent exponential fluid stretching, and non-trivial streamline braiding arises via the continual branching and merging of pores.
The same streamline braiding can also arise in steady three-dimensional Darcy-scale flow in heterogeneous porous media. In steady homogeneous Darcy flow there is no mechanism for the generation of chaotic advection. Bresciani et al. (2019) provide a systematic analysis of flow patterns near stagnation points in homogenous Darcy-scale flow, but the exponential stretching near these points is transient, and so the associated Lyapunov exponent is zero and the flow is non-chaotic. An exception arises for isotropic heterogeneous porous media as flow through this type of media is characterized as being helicity-free (as velocity is everywhere perpendicular to vorticity) (Sposito 2001; Moffatt and Tsinober 1992), limiting the admissible types of fluid motion. Lester et al. (2021) show that the helicity-free condition constrains the Lagrangian kinematics to have the same dynamics of a steady two-dimensional flow, prohibiting streamline braiding and chaotic advection, even if the medium is random and highly heterogeneous. This has important implications for understanding mixing and dispersion in locally isotropic Darcy flow (Lester et al. 2021). Conversely, the helicity-free constraint does not apply to anisotropic heterogeneous porous media and so it is anticipated that such media exhibits chaotic advection under steady three-dimensional flow (Chiogna et al. 2015). However, this is yet to be established and so there exist fundamental questions regarding the nature of solute mixing in Darcy-scale flows.
3.3.2 Folding
In order to describe the folding action of the flow, we consider a two-dimensional scenario of an advective-diffusive line as shown in Fig. 4. Specifically, we focus on the fractal dimension of the lamellar structure that is created by the flow, which can inform on the distance between lamellae. As the line is dispersed through stretching and folding, its length is given by Eq. (49), while the characteristic length scale of the horizontal extension of the line support is given by macrodispersion as
as discussed in Sect. 3.1.1. The fractal dimension \(d_f\) relates the length \(\ell (t)\) of the line support and its extension \(\sigma _L(t)\) through (Le Borgne et al. 2015)
The scalings \(\ell (t) \sim t^\beta\) and \(\sigma _L(t) \sim t^{\alpha /2}\) imply that the fractal dimension of the line support is \(d_f = 2 \beta / \alpha\). Specifically, for \(\alpha = \beta\), the fractal dimension is \(d_f = 2\). For stratified flows, \(\alpha = 2\) and \(\beta = 1\). In this case, \(d_f = 1\) equal to the dimension of the line.
The fractal dimension of the line support can be related to the distribution \(p_\omega (w)\) of distances \(\omega\) between segments. Specifically, for \(1< d_f < 2\), the work by Catrakis and Dimotakis (1996) implies that
within a certain range \(w_1 \ll w \ll w_2\). Note that these authors consider the fractal dimension of one-dimensional point sets, while here the fractal dimension refers to the line support. Thus, their fractal dimension is equal here to \(d_f -1\). For a Poisson point process, that is, the distribution of spacings between line segments is exponential, \(p_\omega (w) = \exp (-w/w_0)/w_0\), the fractal dimension is \(d_f = 1\). This is the fractal dimension that characterizes folding in stratified flows.
The total number \(n_\ell (t)\) of line segments can be estimated from that fact the \(\ell (t) = n_\ell (t) \sigma _L(t)\) and therefore
From this expression, we see that the number of line segments remains constant for stratified flow because \(\beta = 1\) and \(\alpha = 2\). Assuming the vertical extent of the line support remains constant equal to \(\ell _0\), the average distance between segments behaves as
Expressions (56) and (57) show the close relation between the concepts of folding, stretching (\(\ell (t)\)), and purely advective spreading (\(\sigma _L(t)\)) for the advective motion of a line through a heterogeneous flow field. Folding and thus spreading and stretching enhance mixing by bringing line segments close so that they can coalesce by diffusion.
For chaotic advection, the braiding motion leads to exponential stretching and folding. Thus, the number of line segments that fold back on themselves also increase exponentially with time, \(n_\ell (t) \sim \exp (\lambda t) \sigma _L(t)\). As a result, the average distance between segments decreases exponentially fast.
3.4 Lamellar Mixing
The mixing process may be divided into two main stages (Villermaux 2012). In an early time regime, stirring by advection creates a lamellar structure of the solute distribution. Mixing is dominated by the deformation of individual lamellae and diffusion across them. In the late time regime mixing is dominated by the diffusive aggregation of lamellae and the homogenization of the lamellar structure. In the following, we describe the lamellar mixing approach to quantify the two stages of mixing, which has been developed for mixing in randomly stirred free fluids, and in recent years extended to porous media at the pore and Darcy scales. Finally, we briefly discuss the construction of the mixture as a superposition of Green functions, that is, elementary solutions of the fundamental advection–diffusion equation. A detailed account on the lamellar representation of mixing can be found in the recent review by Villermaux (2019).
3.4.1 Stretching-Enhanced Diffusion
In order to illustrate the impact of stretching on diffusive mass transfer, we consider the coordinate systems attached to the (infinitesimal) fluid elements that support the mixing interface of a solute (lamellae), see Fig. 5 The fluid element is deformed by to the spatially varying flow field. Due to volume conservation, elongation of the fluid element, or deformation into a sheet, implies compression in the direction perpendicular to the stretching directions, because the volume \(\delta A(t) \delta s(t) =\) constant, where area and width of the fluid element are denoted by and \(\delta A(t)\) and \(\delta s(t)\). Note that in two dimensions \(\delta A(t) = \delta \ell (t)\) is equal to the length of the lamella. Deformation in the lamella system is measured by the stretching rate
Furthermore, the flow velocity in this coordinate system can be approximated by \({{\mathbf {u}}}({{\mathbf {x}}}) = \gamma (t) (x,y,-z)^\top\), where the superscript \(^\top\) denotes the transpose. The \(x-\)axis is aligned with the stretching direction. If one disregards mass transfer along the stretching directions, the advection dispersion equation (7) can be written in the coordinate system attached to the lamella as (Ranz 1979; Meunier and Villermaux 2003)
Concentration gradients in the stretching direction can be disregarded because they are much smaller than the ones perpendicular to the lamella. The lamella represents the building block of the mixture, or in other words, it can be seen as a representation of the transport Green function in the local coordinate system attached to a material fluid element (Tennekes and Lumley 1972). The diffusive strip method of Meunier and Villermaux (2010) for two-dimensional flows and the diffusive sheet method of Martínez-Ruiz et al. (2017) for three dimensions are based on this concept and represent the heterogeneous mixture as the superposition of the concentration distributions attached to individual lamellae or sheets that are dispersed and deformed by the fluctuating flow field.
Schematic of an isolated lamella that is stretched along its main axis, and, as a consequence, compressed perpendicular to it. The concentration profile in the coordinate system attached to the lamella c(z, t) is given by the Gaussian (62). The concentration gradient along the lamella is negligible compared to the gradient perpendicular to it (after Villermaux 2012)
By defining the rescaled space and time coordinates
the advection–diffusion equation (59) can be mapped onto the diffusion equation
This represents a significant simplification of the complex advection and diffusion problem, which allows one to derive analytical or semi-analytical solutions for the concentration statistics and mixing characteristics.
The solution of (61) for the initial condition \({\hat{c}}({\hat{z}},t = 0) =c_0 \exp (-{\hat{z}}^2/2)/\sqrt{2 \pi }\) is given by \({\hat{c}}({\hat{z}},\tau ) = c_0 \exp \left[ - {{\tilde{z}}^2}/{2 (1 + 2 \tau )}\right] /\sqrt{2 \pi (1 + 2 \tau )}\). The solution of (59) is obtained by substitution of \({\hat{z}}\) and \(\tau\) according to (60) as
where the maximum lamella concentration \(c_m(t)\) is given by
The strip width under the action of stretching and diffusion is quantified by the spatial variance
In a heterogeneous flow field \({{\mathbf {u}}}({{\mathbf {x}}})\), the lamellae experience different deformations and deformation histories, which are encoded in expression (60) for \(\tau (t)\). This variability gives rise to a distribution of maximum concentrations via (63).
As the solute profile across the lamella is Gaussian, the concentration PDF is obtained from expression (37) by setting \(d = 1\) as
As long as the lamellae do not overlap, the concentration content of the solute distribution can be determined by summation of the PDFs across the lamellae that constitute the fluid support of the mixture
where \(A(t) = \sum _i \delta A_i(t)\) is the total area covered by the deformed lamellae or sheets. This expression can also be written in terms of the distribution \(p_m(c_m,t)\) of maximum concentrations \(c_m(t)\) in the mixture as
As mentioned above, the distribution of maximum concentrations is linked to fluid deformation and the deformation history through \(\tau (t)\). Thus, in principle, the flow deformation can be mapped onto the PDF of concentration point values. This approach is valid as long as the lamellae that form the mixture do not aggregate by diffusion.
To illustrate this approach, we consider briefly the behavior for two stretching protocols relevant in the context of porous media.
Algebraic stretching In order to illustrate the impact of fluid deformation, we consider algebraic elongation \(\delta \ell (t) \sim t^\beta\), which is a characteristic of shear dominated flow, such as steady two-dimensional random flows. This elongation behavior implies that \(\delta s(t) \sim 1/t^\beta\) and \(\tau (t) \sim t^{2 \beta + 1}\). As a result, the maximum concentration decays as \(c_m(t) \sim t^{-\beta - 1/2}\) as opposed to the decay of \(c_m(t) \sim t^{-1/2}\) for diffusion across an undeformed lamella. The spatial variance of the strip evolves asymptotically as \(\kappa (t) \sim D t\), that is, diffusion wins over compression. Souzy et al. (2018) present an experimental investigation of the stretching and concentration PDF for a linear shear flow, for which \(\beta = 1\).
Exponential stretching Under exponential stretching, typical for chaotic advection and at stagnation points, the strip elongation is \(\delta \ell (t) = \ell _0 \exp (\lambda t)\), which implies that \(\delta s(t) = s_0 \exp (-\lambda t)\) and \(\tau (t) = (D/\lambda ) \exp (2 \lambda t)/2\). Thus, the maximum concentration decreases as \(c_m(t) \sim \exp (-\lambda t)\) while the width of the strip asymptotes toward the Batchelor scale \(s_B \equiv \kappa ^{1/2} = \sqrt{D/\lambda }\). Although most flows comprise of a mixture of algebraic (shear) and exponential (stretching) fluid deformation, for times \(t > 1/\lambda\) chaotic deformation dominates.
3.4.2 Random Aggregation
With increasing time, lamellae may overlap due to diffusive broadening of their width, and due to a decrease in the distance between them due to folding, see Fig. 4. The distance between lamellae decreases if the elongation of the lamellae increases faster than the dispersion of the global solute distribution as discussed in Sect. 3.3.2. When two lamellae overlap in the time interval \(\Delta t\), the resulting concentration \(c(t + \Delta t)\) is, due to the linearity of the advection–diffusion equation, the sum of the concentrations of the overlapping lamellae,
Note that this implies that the two overlapping lamellae occupy the same volume. If the addition is fully random in the sense that the concentrations of adjacent lamellae are statistically independent, this process can be seen as a continuous convolution process, in which new aggregates are created at each time step at a rate r. If one additionally accounts for the fact that the concentrations in the aggregate decay due to stretching enhanced diffusion at rate k, one can write for \(p(c,t+\Delta t)\) (Duplat and Villermaux 2008)
where the first terms accounts for the aggregating, the second term for the non-aggregating lamellae, and the third term for the decrease of the aggregate concentration. For \(k = 0\), Equation (69) is the Smoluchowski equation (Smoluchowski 1917) for kinetic aggregation. For finite \(k > 0\) it is the coalescence-dispersion equation of Curl (1963). Its asymptotic solution is the exponential
The coalescence and decay rates r and k in general are time dependent and depend on diffusion and the kinematics of stretching and folding.
If the aggregation process is incomplete in the sense that not all overlaps are possible, Duplat and Villermaux (2008) showed that the concentration PDF across lamella aggregates follows the Gamma distribution
where n(t) denotes the average number of lamellae in an aggregate and \(\langle c_m(t) \rangle\) is the average maximum concentration for a single lamella. This approach has been used to quantify the concentration PDF at the pore and Darcy scales (Villermaux 2012; Le Borgne et al. 2015; Kree and Villermaux 2017).
3.5 Construction of the Mixture
The mixture is fully characterized by its spatial concentration distribution \(c({{\mathbf {x}}},t)\), which can be constructed as the superposition of transport Green functions \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\). The Green function describes the evolution of the concentration distribution from an instantaneous point injection, that is, it satisfies Eq. (7) for the initial condition \(g({{\mathbf {x}}},t = 0|{{\mathbf {a}}}) = \delta ({{\mathbf {x}}}- {{\mathbf {a}}})\). Thus, \(c({{\mathbf {x}}},t)\) can be written as
where \(c_0({{\mathbf {x}}})\) is the initial solute distribution.
3.5.1 Diffusive Strip Method
The lamellar mixing approach of Sect. 3.4 approximates the transport Green function locally by the solution of an advection–diffusion equation on a material fluid element that is transported by pure advection. Eq. (59) describes advection and diffusion in a coordinate system that moves, rotates and deforms with the fluid element. Thus, the concentration distribution (62) on each lamella can be considered an approximation for the Green function in the local coordinate system, where mass transfer in the stretching direction is disregarded.
This is implemented in the diffusive strip method of Meunier and Villermaux (2010) for mixing in two-dimensional stirred fluids and the diffusive sheet method of Martínez-Ruiz et al. (2017) for mixing in three-dimensions. These authors consider mixtures that are initially distributed within a band or sheet. The concentration distribution is reconstructed as the superposition of lamellar profiles (62) that are centered on their advective positions \({{\mathbf {x}}}(t|{{\mathbf {a}}})\) with \({{\mathbf {a}}}\) the initial position of the lamella. Meunier and Villermaux (2010) represent the spatial solute distribution in two dimensions by
where the subscript i denotes the respective quantity on the ith fluid element. The unit vector perpendicular to the stretching directions is denoted by \(\hat{{\varvec{e}}}_i(t)\). The profile along the stretching directions is denoted by \(G_i({{\mathbf {x}}})\), which is modeled by the Gaussian shaped function
where \(\hat{{\varvec{n}}}_i(t)\) is the unit vector in the direction of stretching, and \(\Delta \ell\) the characteristic strip length. The position \({{\mathbf {x}}}(t|{{\mathbf {a}}}_i)\) of the ith lamella evolves kinematically according to the advection equation (11). The concentration distribution can be determined for any Péclet number once the purely advective fluid support of the mixture is determined. In this approach, the center of mass of the lamella is set equal to the kinematic position of the deformed fluid support. It does not account for the fact that the center of mass positions are in general also affected by diffusion and do not remain on the same streamline. This becomes obvious for non-ergodic flow fields as for example Poiseuille flow in a pipe or channel. In this case, the diffusive strip is not able to capture the transition toward the Taylor regime of advective-dispersive transport as discussed in Sect. 4.1.
3.5.2 Lagrangian Concentration Approach
As discussed in Sect. 3.1.2, effective dispersion quantifies the typical width of the transport Green function \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\). The evolution of the Green function can be approximated by Eq. (25) such that \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\) is given by the Gaussian (Fiori 2001; Dentz and Tartakovsky 2010; Perez et al. 2019; Puyguiraud et al. 2020)
where d is the spatial dimension. The center of mass position \({\mathbf {m}}(t|{{\mathbf {a}}})\) and the spatial variances \(\kappa ^e_{ii}(t)\) are defined by
where \(\langle v_j(t|{{\mathbf {a}}}) \rangle\) is the center of mass velocity for an instantaneous solute injection at \({{\mathbf {a}}}\). We assume that the off-diagonal elements \(D^e_{ij}(t)\) are zero. The evolution of \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\) is encoded in the center of mass velocity \(\langle {{\mathbf {v}}}(t|{{\mathbf {a}}}) \rangle\) and the effective dispersion tensor \({{\mathbf {D}}}^e(t)\), which evolves due to the interaction of spatial flow variability and diffusive mass transfer. This approach was termed Lagrangian concentration approach in Fiori (2001).
4 Mixing Across Scales
In the following, we discuss the quantification of mixing in Poiseuille flow and in spatially heterogeneous media at the pore and Darcy scales. We focus on the conceptual points of view and approaches laid out in the previous section.
4.1 Mixing in Poiseuille Flow
Laminar flow in a straight pipe or in a plane channel is given by Poiseuille flow. The velocity components perpendicular to the pressure gradient are zero, and the velocity component v(r) aligned with it is given by
with \(r_0\) the pipe radius and half diameter of the channel in three and two spatial dimensions. The maximum velocity is \(v_0 = |\nabla P| r_0^2/12\mu\) in two and \(v_0 = |\nabla P| r_0^2/8 \mu\) in three dimensions. The kinematic viscosity is denoted by \(\mu\). The mean velocity is \({\overline{v}} = v_0/2\) in three and \({\overline{v}} = 2v_0/3\) in two dimensions. The flow field is not ergodic because the flow velocity is constant along a streamline. Mixing occurs due to diffusion between streamlines and the generation of concentration gradients by shear deformation. Particles can sample the flow by transverse diffusion only. The characteristic time for complete mixing over the pipe or channel cross section is \(\tau _D = r_0^2/D\).
4.1.1 Hydrodynamic Dispersion
Taylor dispersion The Taylor dispersion coefficient describes the growth of the width of the distribution of a solute for times \(t \gg \tau _D\). Particle velocities separated by the time \(\tau _D\) can be considered independent. The velocity variance is proportional to \({\overline{v}}^2\). Thus, we obtain from expression (17) for the Taylor dispersion coefficient \(D^a \propto {\overline{v}}^2 r_0^2/D\). The exact expressions are given by
in two and three dimensions (Taylor 1953; Aris 1956). At times \(t \gg \tau _D\), solute transport is quasi one-dimensional and governed by the advection–dispersion equation (Taylor 1953)
At times \(t < \tau _D\) this is in general not valid and the Taylor dispersion coefficient overestimates the actual solute mixing.
Preasymptotic dispersion
Preasymptotic dispersion in pipes or channels has been studied by many authors over the last 70 years, see the recent paper by Taghizadeh et al. (2020) for an extensive literature review. Most authors have focused on the longitudinal ensemble dispersion coefficient (14) and on the characterization of the evolution of the average solute concentration \({\overline{c}}(x_1,t)\) for a uniform line or areal source perpendicular to the flow direction. The ensemble dispersion coefficient evolves ballistically, \(D^m_L(t) = \sigma _v^2 t^2\) for times \(t \ll \tau _D\), where \(\sigma _v^2\) is the velocity variance in the initial distribution. For time \(t > \tau _D\), it converges toward to the asymptotic Taylor dispersion coefficient given by Eq. (78). The effective dispersion coefficient for these initial conditions is constant, \(D_L^e(t) = D\), for times \(t \ll \tau _D\) and evolves toward the asymptotic \(D^a_L\) for times \(t > \tau _D\). Dentz and Carrera (2007) showed that the ensemble and effective dispersion coefficients are related by
Haber and Mauri (1988) provide closed form expressions for the temporal evolution of the ensemble dispersion coefficient in rectangular conduits. Taghizadeh et al. (2020) developed an evolution equation for the cross-sectional averaged solute concentration for arbitrary initial conditions.
4.1.2 Mixing Dynamics
The mixing dynamics in channel or pipe flow are fully determined by shear, which is characterized by the linear shear rate
The shear mixing behavior was studied by Bolster et al. (2011) in terms of the concentration variance and scalar dissipation rate for a uniform line source and point sources in two-dimensional planar flow. These authors find two regimes of mixing, which reflect the initial shear stretching and the eventual homogenization of the concentration distribution by vertical diffusion. Perez et al. (2019) used the stretched lamella approach summarized in Sect. 3.4 and the Lagrangian concentration approach of Sect. 3.5.2 in order to quantify the global mixing in channel flow. The stretched lamella provides a good description of stretching-enhanced mixing for time \(t \ll \tau _D\). For increasing times, it overestimates the true mixing because it is based on the assumption of independent lamellae and does not account for the homogenization of the solute distribution across the channel. The Lagrangian concentration approach, based on the effective dispersion coefficient (80) on the other hand, quantifies the mixing behavior at all times.
Note that here streamlines are not ergodic in the sense that solute particles cannot sample the flow variability by advection. In the absence of diffusion, a particle remains on the same streamline and thus at the same velocity. Thus, the diffusive strip method (see Sect. 3.5.1), is not able to capture the mixing behavior because it requires an ergodic line support, on which the solute diffuses.
Even though Poiseuille flow provides a relatively simple model system that allows one to (analytically) study shear stretching and mixing, we are not aware of studies involving the characterization of the concentration PDF or its evolution (Sect. 3.2), and the use of mechanistic approaches to construct the concentration PDF as outlined in Sections 3.4.
4.2 Mixing in Pore-Scale Flow
At the pore scale (order of micrometers), the medium stirs the fluid as it flows through the pore space driven by a pressure gradient and thereby spreads the solute. Flow at low Reynolds numbers, typical for many porous media applications, is described by the Stokes equation,
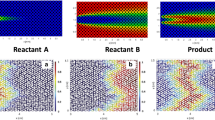
where \(p({{\mathbf {x}}})\) is fluid pressure. Solute transport is due to advection and molecular diffusion in the pore space, which are described by the advection–dispersion equation (7) and the Langevin equation (8). Figure 6 shows the distribution of pore-scale velocities and the stirring and spreading of a mixing interface in a two-dimensional porous medium. The characteristic advection time over the average pore length \(\ell _p\) is \(\tau _v = \ell _p/{\overline{u}}\) with \({\overline{u}}\) the average pore velocity. The characteristic diffusion time over \(\ell _p\) is \(\tau _D = \ell _p^2/D\). Thus, the Péclet number is defined here by \(Pe = {\overline{u}} \ell _p/D\).
4.2.1 Hydrodynamic Dispersion
Asymptotic dispersion The concept of hydrodynamic dispersion was classically used to quantify the impact of pore-scale velocity fluctuations on solute mixing. Unlike for channel flow, in a porous medium, the flow velocity changes along streamlines. Thus, the correlation time \(\tau _c\) of particle velocities may be estimated by the advection time \(\tau _v\). As the velocity variance is proportional to \({\overline{u}}^2\), expression (17) gives the estimate \(D^a \sim \ell _p {\overline{u}}\) for both longitudinal and transverse hydrodynamic dispersion coefficients. This implies that \(D^a/D \sim Pe\).
However, the dependence of longitudinal and transverse hydrodynamic dispersion on Pe is more intricate. Compilations of dispersion data from experiments and numerical simulations across different types of porous media and Péclet numbers indicate that the dispersion coefficients are nonlinear functions of Pe. In fact, at low \(Pe < 5\), they behave as \(D^a_{i} \sim 1\), while for increasing \(5< Pe < 300\) the behaviors \(D^a_L \sim Pe^{1.2}\) and \(D^a_T \sim Pe^{1.1}\) have been deduced (Bear 1972; Pfannkuch 1963; Sahimi 2011; Bijeljic and Blunt 2006, 2007; Delgado 2007). For \(Pe > 300\), both longitudinal and transverse dispersion coefficients have been observed to scale indeed as \(D^a/D \sim Pe\).
Nonlinear dependencies of the dispersion coefficients on Pe can be understood by the broad distributions of pore-scale flow velocities that vary between zero a the no-slip boundary with the solid matrix and maximum velocities in the pore centers. These behaviors can be quantified in terms of the distributions of travel times along pore channels, which depend on both advection and diffusion (de Josselin de Jong 1958; Saffman 1959). For flows dominated by the no-slip condition at grain boundaries similar to the Poiseuille profile (77), Saffman (1959) and Koch and Brady (1985) derived that
Using the travel time concept in a continuous time random walk (CTRW) approach Bijeljic and Blunt (2006) related the exponent of 1.2 for the Pe-dependence of \(D^a_L\) to the distribution of transition times determined from pore-network simulations. Also based on the travel time concept, Puyguiraud et al. (2021) derive a CTRW-based transport model that predicts the scaling
with \(0< \alpha < 1\). The exponent \(\alpha\) describes the behavior of the PDF of pore-scale velocities, \(p_v(v) \sim v^{\alpha -1}\) for \(v < {\overline{u}}\). Experimental and numerical works on different types of porous media, have found this type of behaviors for \(p_v(v)\) for a wide range of pore structures (Bijeljic et al. 2013; Siena et al. 2014; Gouze et al. 2021).
Approaches such as volume averaging (Brenner and Edwards 1993; Whitaker 1999) and homogenization theory (Hornung 1997) derive expressions for the hydrodynamic dispersion coefficients, whose evaluation for a specific medium structure requires the (numerical) solution of a closure problem. These approaches confirm the nonlinear dependence of the hydrodynamic dispersion coefficients on Pe.
Preasymptotic dispersion Similar to Taylor dispersion, asymptotic hydrodynamic pore-scale dispersion has been studied extensively over the past seven decades. Preasymptotic dispersion has received attention only over the last twenty years, and in this context, mainly the ensemble dispersion coefficients defined by Eq. (14), which quantify the spread of the average solute distribution. de Josselin de Jong (1958) and Saffman (1959), in their works on asymptotic hydrodynamic dispersion emphasize the importance of solute travel times over the characteristic pore lengths, which are determined by the pore-scale velocity and diffusion. This indicates that observed preasymptotic dispersion behaviors can be linked to the distribution of pore-scale flow velocities.
Bijeljic and Blunt (2006) use pore-network simulations in order to determine the time evolution of longitudinal ensemble dispersion. These authors find a superdiffusive increase of \(D^m_L(t) \sim t^{\alpha -1}\) for times \(t \ll \tau _D\) and convergence toward \(D_L^a\) for times \(t \gg \tau _D\). Bijeljic et al. (2011) and Gouze et al. (2021) show that these type of behaviors hold across different types of porous rocks and use a continuous time random walk approach to quantify them.
The experiments of Holzner et al. (2015) and Morales et al. (2017) in three-dimensional bead packs study the impact of velocity heterogeneity on the dispersion of tracer particles and develop continuous time random walk models to quantify observed preasymptotic dispersion behaviors. Puyguiraud et al. (2019) study anomalous dispersion for purely advective pore-scale transport in a digitized three-dimensional Berea sandstone sample and relate it to the point-distribution of pore velocities. Souzy et al. (2020) combine experiments and numerical simulations of advective particle transport in a three-dimensional bead pack to observe transient anomalous dispersion and link it to the pore-scale velocity distribution.
Dentz et al. (2018b) and Puyguiraud et al. (2021) develop upscaled models based on the continuous time random walk approach to quantify the impact of pore-scale velocity fluctuations and pore-scale mixing on pre-asymptotic solute dispersion in sand-like porous media and porous rocks.
Puyguiraud et al. (2020) study longitudinal effective dispersion in two-dimensional porous media composed of a distribution of cylindric obstacles and use them for the quantification of the global mixing dynamics in the Lagrangian concentration approach (Sect. 3.5.2).
4.2.2 Mixing Dynamics
The dynamics and mechanisms of mixing in pore-scale porous media driven by a constant pressure gradient have been studied mainly during the last decade. Lester et al. (2014) and Lester et al. (2014) show that chaotic advection is inherent in three-dimensional non-periodic porous networks and provide an analytical flow map to capture the stretching and folding behavior. Based on this chaotic advection model, Lester et al. (2016b) develop a continuous time random walk model for chaotic fluid stretching and combine it with a lamellar mixing approach (Sect. 3.5.1) in order to quantify and upscale chaotic mixing based on pore-scale flow and diffusion. These authors derive that the elongation of materials strips follows a lognormal distribution.
Kree and Villermaux (2017) study the mechanisms and quantification of mixing in a three-dimensional bead pack. Using an index-matching technique, these authors analyzed the mixing and dispersion processes of two dyes along the porous medium. This enables them to quantify the evolution of the maximum concentration in the mixture and distribution of concentration point values. The concentration PDFs at different downstream distances can be matched in their tails by a Gamma distribution. This is traced back to a random aggregation behavior (Sect. 3.4.2) and modeled based on exponential stretching, that is, chaotic advection.
Souzy et al. (2020) uses an index-matching technique to study stretching laws in a glass bead pack by numerical simulation of the advection of material lines in the velocity field obtained from particle tracing velocimetry. These authors clearly identify exponential line elongation and find a lognormal distribution of elongations, confirming the theoretical and numerical findings of Lester et al. (2016b). The experiments of Heyman et al. (2020) also use index-matching to scrutinize the mechanisms of exponential stretching and folding in three-dimensional glass bead packs and develop a predictive model for the rate of stretching and mixing using a lamellar mixing approach coupled with a geometric model for the number density of grain contacts in the medium. Heyman et al. (2021) have recently developed a new method to visualize chaotic advection in non-ideal porous media—including opaque gravels and porous rocks—and characterize the Lyapunov exponent and mixing rates.
These studies establish the ubiquity of chaotic advection at the pore-scale, and provide tools and techniques to understand and quantify solute mixing in a broad range of porous media. Pore-scale chaotic advection has been shown to accelerate pore-scale solute mixing (Lester et al. 2016a), as well as macroscopic transverse dispersion (Lester et al. 2018), while simultaneously retarding longitudinal dispersion (Lester et al. 2014).
Most quantitative studies on mixing in pore-scale flows have been conducted in idealized pore networks or experimentally and numerically in bead packs. We are not aware of mixing studies in more realistic porous media such as porous rocks that focus on the concentration statistics and their evolution, or in terms of fluid deformation and the mechanisms of mixing.
4.3 Mixing in Darcy-Scale Flow
The Darcy-scale flow and transport equations can be obtained from their pore-scale counterparts by averaging (Brenner and Edwards 1993; Whitaker 1999). The support scale of Darcy-scale continuum descriptions of flow and transport is termed the representative elementary volume (REV). It is typically of the order of centimeters (Bear 1972; Sahimi 1995). The standard continuum description for the REV-averaged fluid flow is the Darcy equation,
where \(K({{\mathbf {x}}})\) is the hydraulic conductivity, \(h({{\mathbf {x}}})\) is hydraulic head and \(\phi\) is porosity. We assume that porosity is constant. We furthermore assume \(\nabla \cdot \mathbf {{\mathbf {u}}}({{\mathbf {x}}}) = 0\), that is, we disregard the compressibility of the solid matrix and sinks and sources. While pore-scale velocity fluctuations are caused by the heterogeneous pore structure, on the Darcy scale they are due to spatial variability in the hydraulic conductivity \(K({{\mathbf {x}}})\). The characteristic heterogeneity length scale is the correlation length \(\ell _c\) of the log-hydraulic conductivity \(f({{\mathbf {x}}}) = \ln K({{\mathbf {x}}})\). Thus, the characteristic advection time is given here by \(\tau _v = \ell _c/{\overline{u}}\).
We consider time scales for which the REV can be considered well-mixed, that is, at each point in space, concentration can be characterized by a unique value. Under this condition, the impact of pore-scale velocity fluctuations on local-scale mixing can be quantified by hydrodynamic dispersion, and solute transport can be described by the advection–dispersion equation
The local dispersion tensor \({{\mathbf {D}}}({{\mathbf {x}}})\) accounts for the impact of pore-scale flow variability on solute mixing. It is defined by Bear (1972)
where \(D_0\) denotes the diffusion coefficient. The dispersivities \(\alpha _{I}\) and \(\alpha _{II}\) account for the impact of the medium geometry on dispersion, and may also depend on the pore-scale Péclet number as discussed in the previous section. The advection–dispersion equation (7) is equivalent to the Langevin equation (Kinzelbach and Ackerer 1986; Salamon et al. 2006)
where \({\mathbf {B}}({{\mathbf {x}}})^\top {\mathbf {B}}({{\mathbf {x}}}) = 2 {{\mathbf {D}}}({{\mathbf {x}}})\) and \({\varvec{\xi }}(t)\) is a Gaussian white noise defined in Section 2.1. Figure 7 illustrates the velocity distribution, and the spreading and mixing of a solute plume for a two-dimensional heterogeneous porous medium. The medium itself stirs the bulk fluid as it flows according to the Darcy equation through the medium characterized by spatial variability in hydraulic conductivity.
Most of the works discussed in the following do not account for spatial variability of local-scale dispersion, and set \({{\mathbf {u}}}({{\mathbf {x}}}) = {\overline{{{\mathbf {u}}}}}\) in expression (87). If \({\overline{{{\mathbf {u}}}}}\) is aligned with the one-direction of the coordinate system, this implies that \(D_L = D_0 + \alpha _I {\overline{u}}\), \(D_T = D_0 + \alpha _{II} {\overline{u}}\) and \(D_{ij} = 0\) for \(i \ne j\). The relevant dispersion time scale is \(\tau _D = \ell _c^2/D_T\).
4.3.1 Hydrodynamic Dispersion
The quantification of hydrodynamic dispersion in Darcy-scale porous media has a long history both for asymptotic and pre-asymptotic dispersion. Full accounts on methods and approaches can be found in the textbooks by Dagan (1989), Gelhar (1993), Dagan and Neuman (1997) and Rubin (2003).
Macrodispersion The macrodispersion concept was developed to explain a scale effect observed in experimental data of dispersion coefficients measured in heterogeneous porous media at different spatial scales. It is observed that the longitudinal dispersion coefficient increases with increasing heterogeneity scale (Lallemand-Barres and Peaudecerf 1978; Gelhar et al. 1992; Zech et al. 2015). The fundamental mechanisms leading to this scale effect are spatial velocity fluctuations. This scale effect can be understood from Eq. (17) that allows for an estimate of the asymptotic dispersion coefficients based on the velocity variance and correlation time. The velocity variance is proportional to \({\overline{u}}^2\), while the characteristic correlation time is \(\tau _v\). Thus, one obtains from Eq. (17) the estimate \(D^a \sim {\overline{u}}\ell _c\).
Gelhar and Axness (1983) derived for the longitudinal macrodispersion coefficient in two- and three-dimensional porous media with isotropic correlation structure,
where \(\sigma _f^2\) is the variance of \(f({{\mathbf {x}}}) = \ln K({{\mathbf {x}}})\) and \({\overline{u}} = K_G J\) with \(K_G\) the geometric mean conductivity and J the average head gradient. This result was obtained by using first-order perturbation theory in \(\sigma _f^2\) in the framework of a stochastic model for \(f({{\mathbf {x}}})\) that uses an exponential covariance function. Perturbation theory results are valid for low and moderate heterogeneity up to \(\sigma _f^2\) around one.
For transverse dispersion, first-order perturbation theory predicts that \(D^a_T\) is of the order of the local dispersion coefficient (Gelhar and Axness 1983) with
in two and three dimensions, respectively. Specifically, in the limit of purely advective transport, that is \(\alpha _I = \alpha _{II} = 0\), the stochastic perturbation approach predicts \(D^a_T = 0\). This turns out to be an exact result in two spatial dimensions which follows from a topological constraint due to the condition that \(\nabla \cdot {{\mathbf {u}}}({{\mathbf {x}}})\) is zero (Attinger et al. 2004). Experimental and numerical results indicate that there are macroscopic contributions (that is, contributions independent of local-scale dispersion) in three spatial dimensions (Tompson and Gelhar 1990; Janković et al. 2003, 2009; Hidalgo et al. 2009; Beaudoin and de Dreuzy 2013) due to higher order terms in the perturbation series in \(\sigma _f^2\).
For variances \(\sigma _f^2 > 1\), the estimates from first-order perturbation theory are only of limited validity. Fiori et al. (2003) obtain for \(\sigma _{f}^2 \gg 1\) in two and three dimensions the estimate \(D_L^a \propto {\overline{u}} \ell _c \exp (\sigma _f^2/2)\). Their analysis is based on the representation of the porous medium as random arrangements of inclusion whose conductivities are lognormally distributed. The numerical simulations of de Dreuzy et al. (2007) in two-dimensional multi-lognormal isotropic hydraulic conductivity fields find that \(D_L^a = {\overline{u}} \ell _c (0.7 \sigma _f^2 + 0.2 \sigma _f^4)\). A similar expression was obtained by Dentz and Tartakovsky (2008) using a self-consistent resummation scheme of the perturbation series for the dispersion coefficients. The numerical simulations of Beaudoin and de Dreuzy (2013) in three-dimensional heterogeneous porous media find that \(D_L^a \approx {\overline{u}} \ell _c \exp (\sigma _f^2/1.55)\), which confirms the estimate of (Fiori et al. 2003). For the transverse dispersion coefficient, these authors find that \(D_T^a \propto {\overline{u}} \ell _c \sigma _f^4\).
Preasymptotic Dispersion Matheron and de Marsily (1980) studied solute transport in a randomly stratified porous medium of infinite extent, that is \(K({{\mathbf {x}}}) = K(x_3)\) varies only perpendicular to the mean pressure gradient. In this case, the Darcy equation (85) gives \({{\mathbf {u}}}({{\mathbf {x}}}) = [u(x_3),0,0]^\top\). While transverse dispersion is equal to local-scale dispersion, longitudinal dispersion is super-diffusive, that is, \(D_L^m(t) \sim t^{1/2}\) increases as a power-law of time. Similar to flow in a pipe or a channel (Sect. 4.1), flow is not ergodic. The solute can only sample the flow field through transverse dispersion. In fact, if the medium is confined in the directions perpendicular to the mean pressure gradient, the longitudinal dispersion coefficient converges toward a constant asymptotic value of the same type as the Taylor dispersion coefficients, \(D^a_L \sim {\overline{u}}^2 a^2/D_T\), where a is the transverse extension of the medium. This stratified flow scenario has been intensively studied in the literature because it provides an exactly solvable model for anomalous, superdiffusive dispersion behavior.
The preasymptotic behavior of the longitudinal and transverse ensemble dispersion coefficients for purely advective solute transport in statistically isotropic heterogeneous porous media was quantified by Dagan (1984). This author uses first-order perturbation theory in \(\sigma _f^2\) to derive explicit analytical expressions for the second centered moments \(\kappa _L^m(t)\) and \(\kappa _T^m(t)\) in two- and three-dimensional media characterized by an exponential correlation structure, see also Dagan (1987). Dagan (1988) extended this study and derived explicit analytical expressions for statistically anisotropic heterogeneous porous media. As discussed in Sect. 3.1 and Sect. (3.3), in the absence of local-scale dispersion, the ensemble dispersion coefficients quantify the stirring action due to the heterogeneous medium instead of actual solute mixing. At early times \(t \ll \tau _v\), the dispersion coefficients behave ballistically \(D_L^m(t) \sim \sigma _f^2 {\overline{u}}^2 t\) and then evolve on the advection time scale \(\tau _v\) toward the asymptotic macrodispersion coefficient.
Dentz et al. (2000) and Dentz et al. (2003) studied the evolution of effective and ensemble dispersion in heterogeneous media analytically and numerically. Using first-order perturbation theory in \(\sigma _f^2\), Dentz et al. (2000) derive explicit analytical expressions for the longitudinal effective dispersion coefficients in two and three dimensions. They observe that the effective dispersion coefficient evolves on the dispersion time scale \(\tau _D\) toward the asymptotic macrodispersion coefficient. The numerical simulations of Beaudoin et al. (2010) and Beaudoin and de Dreuzy (2013) study longitudinal and transverse ensemble and effective dispersion coefficients in two- and three-dimensional heterogeneous porous media for logK-variances up to \(\sigma _f^2 = 9\). These authors find that the convergence to the asymptotic macrodispersion coefficients is slows down for increasing \(\sigma _f^2\). Also, the behaviors of pre-asymptotic dispersion predicted by perturbation theory diverge significantly from the numerical data.
In fact, for dispersion in highly heterogeneous formations, longitudinal ensemble dispersion coefficients have been observed to show power-law transients (Le Borgne et al. 2008) or power-law regimes (Comolli et al. 2019), \(D_L^m \sim t^{\alpha - 1}\). The pre-asymptotic evolution of longitudinal ensemble dispersion can be modeled by continuous time random walk approaches based on the Eulerian velocity distribution (Dentz et al. 2016a; Hakoun et al. 2019; Comolli et al. 2019).
4.3.2 Mixing Dynamics
Concentration variance Over the past four decades, mixing in Darcy-scale heterogeneous porous media has been quantified in terms of the concentration variance \(\sigma _c^2({{\mathbf {x}}},t)\) and its evolution, see, e.g., the textbooks by Dagan (1989) and Rubin (2003).
The quantification of \(\sigma _c^2({{\mathbf {x}}},t)\) in terms of the evolution equation (34) depends on the modeling of the rate \(\eta\) that relates the scalar dissipation rate \(\chi ({{\mathbf {x}}},t)\) to the concentration variance. Kapoor and Gelhar (1994) argue that the rate \(\eta\) should be constant based on the local analysis of the evolution of a solute blob due to the balance between compression induced by advection and local-scale dispersion. Kapoor and Kitanidis (1998) studied the evolution of concentration variance and the dilution index from direct numerical flow and transport simulations in two-dimensional heterogenous porous media. These authors find that \(\eta\), defined by the ratio of the spatially integrated scalar dissipation rate and concentration variance, increases in time and evolves on the dispersion time scale \(\tau _D\) toward a constant value that is about \(\eta = 1/3\tau _D\). De Dreuzy et al. (2012) propose to use the mixing length scale determined by Le Borgne et al. (2011) as the concentration gradient scale. Unlike other works, these authors consider weakly to strongly heterogeneous media. It should be noted, that for strongly heterogeneous media, the closure assumption involving the asymptotic macro-dispersion term in (34) may not apply because preasymptotic large-scale transport can in general not be described by an advection–dispersion equation.
Several authors quantified the concentration variance directly from its definition in terms of Lagrangian particle trajectories. Pannone and Kitanidis (1999) and Fiori and Dagan (2000) quantify the concentration variance along these lines for initial solute distributions that are small compared to the correlation length \(\ell _c\). Vanderborght (2001) derives equations for the mean and variance for a large initial plume. In his approach, the Green function \(g({{\mathbf {x}}},t|{{\mathbf {a}}})\) in a single realization is approximated by (75), that is, its spatial variance is given by the effective dispersion coefficients. This is similar to the Lagrangian concentration approach of Fiori (2001), see Sect. 3.5.2. de Barros et al. (2015) used this formulation in order to determine the dilution index for a solute blob in a heterogeneous porous medium. de Barros and Fiori (2021) employed the Lagrangian concentration approach to study the evolution of the maximum concentration and its controls in heterogeneous porous media.
Many studies are limited to media of moderate heterogeneity characterized by \(\sigma _f^2 < 2\). Le Borgne et al. (2010) investigated the evolution of the integrated scalar dissipation rate \(\Vert \chi ({{\mathbf {x}}},t)\Vert\) using direct numerical simulations of flow and transport in two-dimensional heterogenous media with \(\sigma _f^2\) between \(10^{-2}\) and 9. These authors find that \(\Vert \chi ({{\mathbf {x}}},t) \Vert \sim t^{-\alpha }\) with \(\alpha \ge 3/2\), that is, it decays faster than for a homogeneous medium. Caroni and Fiorotto (2005) determine the concentration variance for \(\sigma _f^2 > 1\) and find an increasing deviation from the first-order results for increasing \(\sigma _f^2\).
Andričević (1998) discusses the impact of local-scale dispersion and sampling volume on measured values of concentration mean and variance. Tonina and Bellin (2008) also investigate the impact of pore-scale dispersion, the logK variance, sampling and source volume on the concentration mean and variance. To this end, they generalize the first-order perturbation theory solutions of Fiori (2001). Both local-scale dispersion and an increase of the sampling volume decrease measured solute concentrations, while the latter must not be confused with the mixing process within the porous medium. Similar conclusion were drawn in the studies by Beckie (1996) and Rubin et al. (1999).
Concentration PDF The PDF of concentration point values in heterogenous porous media has been studied both numerically and in terms of parametric models such as the Beta model (37). At early times, the concentration PDF is bimodal with peaks at \(c = c_0\) and \(c = 0\). With increasing time, as the concentration distribution homogenizes, it becomes unimodal. PDF approaches at the Darcy scale have been used to quantify uncertainty due to the incomplete knowledge of system parameters (Tartakovsky 2013). Here we focus on efforts to determine concentration variability as the consequence of spatial heterogeneity and local-scale advective and dispersive mass transfer.
Fiorotto and Caroni (2002) and Caroni and Fiorotto (2005) employ the Beta PDF to model concentration PDF data from direct numerical simulations in two-dimensional heterogeneous porous media of different \(\sigma _f^2\). These authors use the concentration mean and variance in order to parameterize the Beta PDF model, and analyze the role of local-scale dispersion on the evolution of the concentration PDF. Bellin and Tonina (2007) provide a stochastic differential equation for the evolution of concentration point values which is such that the steady state concentration PDF is a Beta distribution. The Beta model is then used to interpret the data from numerical simulations and applied to the PDF of vertically averaged concentration available from the Cape Cod tracer test (LeBlanc et al. 1991). Meyer et al. (2010) propose a computational PDF model for the evolution of the joint PDF of concentration and Lagrangian velocity.
Schwede et al. (2008) investigate the impact of the sampling volume on the concentration PDF in cross-sectional layers of a steady state plume in a three-dimensional heterogeneous porous medium. These authors develop a mapping approach based on analytical expressions for the ensemble and effective dispersion coefficients and an assumed Gaussian distribution of lateral velocity fluctuations. These and the results of direct numerical simulations are interpreted with the Beta PDF model. The concentration PDF is shifted toward smaller values with increasing sampling volume. This artificial mixing due to a finite sampling volume must be clearly distinguished from hydrodynamic mixing in the porous medium. Dentz and Tartakovsky (2010) and Dentz (2012) use a mapping approach to derive analytical expressions for the concentration PDF for advective-diffusive transport in heterogeneous flow fields. Along the same lines, de Barros and Fiori (2014) study the concentration PDF based on the Lagrangian concentration approach of Fiori (2001).
Mixing mechanisms Spatial variability of the Darcy velocity leads to effective stirring of the bulk fluid, which manifests in the creation of lamellar structures as illustrated in Fig. 1. As outlined above, the spatially variable velocity field acts in two ways. First, through the deformation (stretching) of bulk material fluid elements, which enhances diffusion through the creation and sustaining of concentration gradients. Second, this stretching action creates lamellae, which fold back on themselves. This action enhances mixing through the coalescence of adjacent lamellae by transverse dispersion.
Werth et al. (2006) studied the impact of flow focusing in high conductivity inclusions on transverse mixing. As streamlines converge in such inclusions, the distance between streamlines decreases. For a bulk material fluid element, this implies stretching in the direction of flow and compression transverse to it during the time \(\ell _i/v_i\) where \(\ell _i\) is the length and \(v_i\) the velocity in the inclusion. For an isolated inclusion in two dimensions, the maximum velocity contrast between \(v_i\) and the velocity \(v_m\) in the matrix is two, \(v_i = 2 v_m\) (Wheatcraft and Winterberg 1985). This implies that the streamlines can be compressed at most by a factor of two. Werth et al. (2006) evaluated the impact of this effect on transverse mixing in an array of inclusion and in heterogeneous two dimensional conductivity fields through numerical simulations. Rolle et al. (2009) developed the concept of a flux-related dilution index in order to quantify transverse mixing due to flow focusing in quasi two-dimensional laboratory-scale experiments and find a significant increase of transverse mixing compared to homogeneous media. Ye et al. (2015b) report on a combined experimental, numerical and theoretical study of the impact of flow focusing in two- and three-dimensional porous media. These authors find that the enhancement of transverse mixing is less effective than in two-dimensional systems.
de Barros et al. (2012) studied the correlation between flow topology quantified by the Okubo-Weiss measure and solute mixing measured by the dilution index for two-dimensional heterogeneous porous media. The mixing enhancement is related to the deformation history of a solute plume as it sweeps the medium, which is quantified by an effective Lagrangian Okubo-Weiss function. The experiments of Hazas et al. (2022) show that the Okubo-Weiss function is strongly correlated to the evolution of mixing measured by the dilution index.
Villermaux (2012) proposed a lamellar mixing model for porous media that accounts for stretching enhanced diffusion and aggregation due to folding at large times sketched in Sect. 3.4. Based on this approach, Le Borgne et al. (2013) and Le Borgne et al. (2015) studied the mechanisms of stretching, folding and mixing in two-dimensional heterogeneous porous media using direct numerical simulation of the solute distribution evolving from a line source perpendicular to the mean flow direction. These authors develop analytical expressions for the concentration PDF, concentration mean and variance and the dilution index. They characterize fluid stretching by a multiplicative process for the elongation \(\delta \ell (t)\) of an infinitesimal line segment, which gives a lognormal PDF of elongations. The behavior of the mean elongation with time can be characterized by a power-law, \(\langle \delta \ell (t) \rangle \sim t^{\beta }\), where the exponent \(\beta\) is found to increase with the logK variance \(\sigma _f^2\), that is, with the heterogeneity of the medium. Furthermore, these authors develop an approach to account for partial and full coalescence of lamellae within the heterogeneous solute plume and its impact on the concentration PDF. Based on this approach, Le Borgne et al. (2017) derive a model for the evolution of concentration gradients in porous media and in general for heterogeneous flows. Dentz et al. (2018a) employ the stretched lamella approach to quantify the mixing of a solute blob in a two-dimensional heterogeneous porous medium and relate the mixing behavior to the hydraulic and medium properties using perturbation theory in \(\sigma _f^2\).
Cirpka et al. (2015) investigate solute mixing in three-dimensional heterogeneous media characterized by statistically stationary, and anisotropic non-stationary hydraulic conductivity fields. Transverse mixing is characterized for a steady solute injection using the flux-related dilution index. A significant increase of mixing is found in the non-stationary compared to the stationary medium. The non-stationary medium gives rise in average to helical flow, while the local Darcy flow is helicity-free. These features and the kinematics of this type of flows are studied by Chiogna et al. (2015) in terms of measures for fluid stretching and folding. Ye et al. (2015a) investigates the occurrence of helical flow and its impact on transverse mixing through laboratory scale experiments and direct numerical simulations.
Sposito (1994) and Sposito (2001) study the kinematics of three-dimensional Darcy flow through locally isotropic heterogeneous porous media. Flow in locally isotropic media is helicity-free, that is, the velocity vector is always perpendicular to vorticity. Sposito (2001) concludes that due to this constraint the streamlines are confined to two-dimensional Lamb surfaces, and as such, the kinematics of three-dimensional Darcy flow are essentially two-dimensional, and so precluding the occurrence of chaotic advection. Lester et al. (2019) showed that Lamb surfaces are not ubiquitous to three-dimensional Darcy flows with locally isotropic hydraulic conductivity. Their existence can only be rigorously shown for stratified media. Instead, these authors find that these flows admit a pair of families of two-dimensional streamsurfaces (Lester et al. 2021), where streamlines of the flow arise at the intersection of these streamfunctions. Hence the flow kinematics of locally isotropic Darcy flow are essentially two-dimensional (and so non-chaotic), but for different reasons than that suggested by Sposito (1994, 2001). Lester et al. (2021, 2022) show that this has implications for both solute mixing and dispersion despite the three-dimensional nature of the flow, as fluid stretching is algebraic and asymptotic transverse dispersion is conjectured to be zero in the purely advective limit. These kinematic constraints associated with helicity-free flows do not arise for anisotropic conductivity fields, and so these porous media have the potential to admit chaotic dynamics. Despite this potential, the existence of chaotic mixing in steady Darcy flow is an open question.
5 Mixing in Porous Media Systems
We have focused on the characterization and quantification of passive mixing in steady uniform flow through heterogeneous porous media from the pore to the regional scale. Nevertheless, the fundamental mechanisms of mixing as captured and quantified by the concepts and approaches detailed in Sect. 3–4 apply to a range of porous media systems, for which the processes and phenomena of mixing are a central concern. The scientific and technological applications of mixing in porous media are manifold and include the understanding of karst formation (Kuniansky et al. 2022), soil and aquifer remediation (Kitanidis and McCarty 2012), seawater intrusion (Werner et al. 2013), geological carbon dioxide storage (Niemi et al. 2017), underground hydrogen storage (Feldmann et al. 2016), radionuclide migration (Poinssot and Geckeis 2012), porous reactors and membranes (Seidel-Morgenstern 2010). These applications involve a range of porous media systems at multiple scales including reactive flows, unstable flow conditions, component transport in multiphase systems, variable density flow, unsaturated media, the hyporheic zone, fractured media and karst systems, under steady and temporally fluctuating flow conditions.
The mixing of initially segregated chemical species is essential for chemical reactions to occur. For fast chemical reactions, that is, if the reaction time is much smaller than the mixing time, the rate of reaction is limited by the rate of mixing. In this case, the reaction rate can be expressed in terms of the scalar dissipation rate (Kapoor et al. 1997; De Simoni et al. 2005), and the PDFs of conservative and reacting species (Cirpka et al. 2008; Bellin et al. 2011). Reactive mixing was also quantified in terms of lamellar approaches (de Anna et al. 2014; Le Borgne et al. 2014; Bandopadhyay et al. 2017; Guilbert et al. 2022) and in the light of concentration entropy (Chiogna et al. 2012). Other works employed the effective dispersion concept and the Lagrangian concentration approach to quantify reactive mixing in heterogeneous porous media at the Darcy and pore scales (Jose and Cirpka 2004; Perez et al. 2019; Puyguiraud et al. 2020). Comprehensive reviews on reactive transport and reactive mixing in porous media can be found in the recent articles by Berkowitz et al. (2016), Valocchi et al. (2018) and Rolle and Le Borgne (2019).
Mixing in unstable flows under convective instabilities (Schincariol 1998; Neufeld et al. 2010) and viscous fingering (Jha et al. 2011) has been analyzed in terms of the scalar dissipation rate and concentration variance (Jha et al. 2011; Amooie et al. 2017; Bonazzi et al. 2021), as well as lamellar approaches to quantify mixing and reactive mixing in the vicinity of stagnation points (Hidalgo et al. 2012; Hidalgo and Dentz 2018).
Amooie et al. (2017) studied the mixing and spreading processes of multiphase fluids in spatially variable porous media in terms of the spatial variance of component concentration, and the concentration variance and segregation intensity. Jiménez-Martínez et al. (2015, 2017) analyzed passive and reactive mixing in unsaturated media. These authors employed a lamellar mixing approach to relate flow features and observed mixing behaviors, while Raoof and Hassanizadeh (2013) and Karadimitriou et al. (2016) focused on saturation-dependent dispersion coefficients and non-Fickian transport features.
Solute mixing at the interface between freshwater and saltwater, that is under stable flow conditions, has been studied experimentally by Abarca and Clement (2009) based on the reactive mixing of two initially segregated constituents. Pool et al. (2015) studied the impact of tidal fluctuations and spatial heterogeneity on the mixing and spreading of the saltwater-freshwater interface. Sanford and Konikow (1989) and Rezaei et al. (2005) study the impact of mixing at the interface for mixing-induced dissolution-precipitation reactions. Pool and Dentz (2018) and Vriendt et al. (2020) analyzed the impact of flow deformation on mixing and reactive mixing, and its possible role in the formation of coastal karst. Landman et al. (2007) studied mixing using density-dependent dispersion coefficients. De Vriendt et al. (2022) used a lamellar mixing approach to quantify the variability of the interface width along the interface.
Hester et al. (2017) discuss the importance and possible mechanisms of mixing in the hyporheic zone and point toward the combination of spatial heterogeneity and temporal fluctuations. These authors provide an overview on the state of the art on transport and mixing in the hyporheic zone. Bandopadhyay et al. (2018) analyzed the mixing behavior in flow geometries typical for hillslopes and hyporheic zones using a lamellar mixing approach.
It has been found that polymer solution flow can lead to strong solute mixing (Groisman and Steinberg 2001) due to a phenomenon that is termed elastic turbulence (Groisman and Steinberg 2000). Dispersion and mixing in such flows are strongly dependent on the enhanced shear rate and flow deformation (Scholz et al. 2014; Aramideh et al. 2019). The recent paper by Browne et al. (2019) provides an overview on the flow and transport behavior of polymer solutions in porous media.
Finally, for transport in fractured media, strong mixing can be found at fracture intersection and within rough fractures (Johnson et al. 2006; Zou et al. 2017), which is a key driver for geochemical and biogeochemical reactions (Emmanuel and Berkowitz 2005; Martinez-Landa et al. 2012; Bochet et al. 2020; Lee and Kang 2020).
Note that this summary is only an incomplete account on mixing and transport in these porous media systems, which are beyond the scope of this article. Nevertheless, the concepts and approaches laid out in Sect. 2-4 can be used to underpin the qualitative and quantitative analysis of mixing in these systems.
6 Conclusions
Mixing in porous media is a multiscale process that depends on the medium structure and heterogeneity and small-scale mass transfer mechanisms. It is a result of the multiscale interaction of advection and diffusion and local-scale dispersion. The characterization and quantification of the mixing behaviors that emerge from these interactions are key challenges across a wide range of porous media systems.
The classical approach for the quantification of flow variability on mixing is through the concept of hydrodynamic dispersion. As a straightforward generalization of diffusion, it models small-scale velocity fluctuations as an uncorrelated (memory-less) process, and quantifies them through a dispersion coefficient. We discussed the shortcomings of this approach in the light of wide separation of mass transfer time scales, and the concept of stirring. Dispersion at preasymptotic times is rather a measure for the spread of a solute plume than mixing. In fact, in the absence of microscopic mass transfer mechanisms, a plume may be efficiently spread, but completely unmixed. Nevertheless, the stirring action that leads to efficient plume spreading is the precursor of mixing. Through the deformation of material fluid elements, it enhances diffusive mass transfer due to stretching, and the homogenization of the mixture through folding and diffusive merging of lamellar structures. The concept of effective dispersion aims at quantifying the evolution of the width of a mixing interface rather than its spread. Thus, it provides an operational concept for the representation of mixing in the Lagrangian concentration approach. This concept has mostly been used for heterogeneous porous media at the continuum scale, and only few works have studied effective dispersion at the pore-scale.
The mixing state and mixing dynamics can be characterized in terms of concentration statistics. The dilution index provides a measure for the volume occupied by a dissolved substance, which increases only by mixing. Its evolution equation identifies the creation of concentration gradients and diffusion as the drivers of mixing. Similarly, the concentration variance and concentration PDF provide measures of the mixing state, with implications for an operational characterization of mixing. The distribution of concentration point values can facilitate a stochastic approach for the mixing evolution, and plays a central role in probabilistic risk assessment. The evolution equation for the concentration PDF and variance are not closed and require closure approximations, so called mixing models, which are mostly heuristic or phenomenological, and lack a relation to the medium and flow properties.
The lamellar mixing representation provides an intuitive framework to quantify the fundamental mechanisms of mixing and folding using two different theoretical approaches adapted to the early and late time stages of mixing. At early times, the mixture is considered as consisting of independent stretched lamella, each with its own stretching history. The concentration PDF and mixing behavior can be obtained by mapping based on the (statistical) characterization of the stretching process. At large times, mixing is due to the interaction of lamella by diffusive merging, which is described as an aggregation process. These approaches have so far been applied to mixing in two-dimensional advective-diffusive Darcy-scale and three-dimensional pore-scale flow based on empirical stretching and merging relations. The relation of these processes on the medium and flow properties and their formulation for advective-dispersive mixing in three-dimensional porous media remain open questions.
The concepts and approaches discussed in this review have been used and can be applied at different spatial scales to characterize and quantify mixing. We reviewed dispersion and mixing dynamics in Poiseuille flow at the scale of a capillary or fracture, and at the pore and continuum scales in heterogeneous porous media. At the pore scale, most works focus on bead packs and granular media, while the impact of the complex structure of porous rocks on solute mixing remains an open question. At the Darcy scale, it has been common to disregard the velocity dependence of local-scale dispersion on solute mixing. We have seen, however, that mixing is driven by the concentration gradients on the one hand, and local-dispersive mass transfer on the other. That is, if large concentration gradients occur in stagnant regions of low velocities, mixing rates are also low, which can impact the assessment of large-scale mixing. The relation between medium structure and mixing behavior remains a challenge at the pore, continuum and regional scales. The ability to predict the mixing behavior based on structural or geostatistical medium characteristics is a key question in a wide range of porous medium applications.
In conclusion, the mechanism, concepts and approaches discussed in this review are fundamental enough so that they can be transferred to more complex porous media flow and transport systems. These concepts and approaches apply to the pore and continuum scale alike and in general to confined laminar flows. Open questions refer to the relation between structure and large-scale mixing and a unifying approach that comprises both solute mixing and (anomalous) dispersion.
References
Abarca, E., Clement, T.P.: A novel approach for characterizing the mixing zone of a saltwater wedge. Geophys. Res. Lett. 36, L06402 (2009)
Amooie, M.A., Soltanian, M.R., Moortgat, J.: Hydrothermodynamic mixing of fluids across phases in porous media. Geophys. Res. Lett. 44(8), 3624–3634 (2017). https://doi.org/10.1002/2016gl072491
Amooie, M.A., Soltanian, M.R., Xiong, F., Dai, Z., Moortgat, J.: Mixing and spreading of multiphase fluids in heterogeneous bimodal porous media. Geomech. Geophys. Geo-Energy Geo-Resour. 3(3), 225–244 (2017). https://doi.org/10.1007/s40948-017-0060-8
Andričević, R.: Effects of local dispersion and sampling volume on the evolution of concentration fluctuations in aquifers. Water Resour. Res. 34(5), 1115–1129 (1998)
Aramideh, S., Vlachos, P.P., Ardekani, A.M.: Nanoparticle dispersion in porous media in viscoelastic polymer solutions. J. Nonnewton. Fluid Mech. 268, 75–80 (2019)
Aref, H.: Stirring by chaotic advection. J. Fluid Mech. 143, 1–21 (1984)
Aref, H., Blake, J.R., Budišić, M., Cardoso, S.S.S., Cartwright, J.H.E., Clercx, H.J.H., El Omari, K., Feudel, U., Golestanian, R., Gouillart, E., van Heijst, G.F., Krasnopolskaya, T.S., Le Guer, Y., MacKay, R.S., Meleshko, V.V., Metcalfe, G., Mezić, I., de Moura, A.P.S., Piro, O., Speetjens, M.F.M., Sturman, R., Thiffeault, J.L., Tuval, I.: Frontiers of chaotic advection. Rev. Mod. Phys. 89, 025007 (2017). https://doi.org/10.1103/RevModPhys.89.025007
Aris, R.: On the dispersion of a solute in a fluid flowing through a tube. Proc R Soc London A 235, 67–77 (1956)
Arnold, V.I.: Sur la topologie des écoulments stationnaires des fluids parfaits. Comptes Rendus Acad Sci Paris 261, 312–314 (1965)
Attinger, S., Dentz, M., Kinzelbach, W.: Exact transverse macro dispersion coefficient for transport in heterogeneous media. Stoch. Environ. Res. Risk Assess. 18, 9–15 (2004)
Bandopadhyay, A., Le Borgne, T., Meheust, Y., Dentz, M.: Enhanced reaction kinetics and reactive mixing scale dynamics in mixing fronts under shear flow for arbitrary Damköhler numbers. Adv. Water Resour. 100, 78–95 (2017). https://doi.org/10.1016/j.advwatres.2016.12.008
Bandopadhyay, A., Davy, P., Le Borgne, T.: Shear flows accelerate mixing dynamics in hyporheic zones and hillslopes. Geophys. Res. Lett. 45(21), 11–659 (2018)
de Barros, F., Fiori, A., Boso, F., Bellin, A.: A theoretical framework for modeling dilution enhancement of non-reactive solutes in heterogeneous porous media. J. Contam. Hydrol. 175–176, 72–83 (2015). https://doi.org/10.1016/j.jconhyd.2015.01.004
de Barros, F.P.J., Fiori, A.: First-order based cumulative distribution function for solute concentration in heterogeneous aquifers: theoretical analysis and implications for human health risk assessment. Water Resour. Res. 50(5), 4018–4037 (2014). https://doi.org/10.1002/2013wr015024
de Barros, F.P.J., Fiori, A.: On the maximum concentration of contaminants in natural aquifers. Transp. Porous Media 140(1), 273–290 (2021). https://doi.org/10.1007/s11242-021-01620-3
de Barros, F.P.J., Dentz, M., Koch, J., Nowak, W.: Flow topology and scalar mixing in spatially heterogeneous flow fields. Geophys. Res. Lett. 39, L08404 (2012)
Bear, J.: Dynamics of Fluids in Porous Media. American Elsevier, New York (1972)
Bear, J., Cheng, A.H.D., Sorek, S., Ouazar, D., Herrera, I.: Seawater Intrusion in Coastal Aquifers: Concepts, Methods and Practices, vol. 14. Springer Science & Business Media, USA (1999)
Beaudoin, A., de Dreuzy, J.R.: Numerical assessment of 3-d macrodispersion in heterogeneous porous media. Water Resour. Res. 49(5), 2489–2496 (2013). https://doi.org/10.1002/wrcr.20206
Beaudoin, A., de Dreuzy, J.R., Erhel J.: Numerical monte carlo analysis of the influence of pore-scale dispersion on macrodispersion in 2-d heterogeneous porous media. Water Res. Res. 46(12), https://doi.org/10.1029/2010wr009576, (2010)
Beckie, R.: Measurement scale, network sampling scale, and groundwater model parameters. Water Resour. Res. 32(1), 65–76 (1996)
Bellin, A., Tonina, D.: Probability density function of non-reactive solute concentration in heterogeneous porous formations. J of Cont Hydrol 94, 109–125 (2007)
Bellin, A., Severino, G., Fiori, A.: On the local concentration probability density function of solutes reacting upon mixing. Water Res. Res. 47, W01514 (2011)
Benson, D.A., Meerschaert, M.M., Revielle, J.: Fractional calculus in hydrologic modeling: a numerical perspective. Adv. Water Resour. 51, 479–497 (2013). https://doi.org/10.1016/j.advwatres.2012.04.005
Berkowitz, B., Cortis, A., Dentz, M., Scher, H.: Modeling non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 44, RG2003 (2006)
Berkowitz, B., Dror, I., Hansen, S.K., Scher, H.: Measurements and models of reactive transport in geological media. Rev. Geophys. 54(4), 930–986 (2016). https://doi.org/10.1002/2016rg000524
Bijeljic, B., Blunt, M.J.: Pore-scale modeling and continuous time random walk analysis of dispersion in porous media. Water Resour. Res. 42, W01202 (2006)
Bijeljic, B., Blunt, M.J.: Pore-scale modeling of transverse dispersion in porous media. Water Res. Res. 43(12), https://doi.org/10.1029/2006wr005700, (2007)
Bijeljic, B., Mostaghimi, P., Blunt, M.J.: Signature of non-fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 107, 204502 (2011)
Bijeljic, B., Raeini, A., Mostaghimi, P., Blunt, M.J.: Predictions of non-fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys. Rev. E 87(1), (2013).https://doi.org/10.1103/physreve.87.013011,
Bochet, O., Bethencourt, L., Dufresne, A., Farasin, J., Pédrot, M., Labasque, T., Chatton, E., Lavenant, N., Petton, C., Abbott, B.W., Aquilina, L., Borgne, T.L.: Iron-oxidizer hotspots formed by intermittent oxic–anoxic fluid mixing in fractured rocks. Nat. Geosci. 13(2), 149–155 (2020). https://doi.org/10.1038/s41561-019-0509-1
Boggs, J.M., Young, S.C., Beard, L.M., Gelhar, L.W., Rehfeldt, K.R., Adams, E.E.: Field study of dispersion in a heterogeneous aquifer 1. overview and site description. Water Resour. Res. 28, 3281–3291 (1992)
Bolster, D., Valdés-Parada, F.J., LeBorgne, T., Dentz, M., Carrera, J.: Mixing in confined stratified aquifers. J. Contam. Hydrol. 120–121, 198–212 (2011). https://doi.org/10.1016/j.jconhyd.2010.02.003
Bonazzi, A., Morvillo, M., Im, J., Jha, B., de Barros, F.P.J.: Relative impacts of permeability heterogeneity and viscosity contrast on solute mixing. Phys. Rev. Fluids 6(6), (2021). https://doi.org/10.1103/physrevfluids.6.064501,
Bouchaud, J.P., Georges, A.: Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195(45), 127–293 (1990)
Brenner, H., Edwards, D.: Macrotransport Processes. Butterworth-Heinemann, MA, USA (1993)
Bresciani, E., Kang, P.K., Lee, S.: Theoretical analysis of groundwater flow patterns near stagnation points. Water Resour. Res. 55(2), 1624–1650 (2019). https://doi.org/10.1029/2018wr023508
Browne, C.A., Shih, A., Datta, S.S.: Pore-scale flow characterization of polymer solutions in microfluidic porous media. Small 16(9), 1903944 (2019). https://doi.org/10.1002/smll.201903944
Caroni, E., Fiorotto, V.: Analysis of concentration as sampled in natural aquifers. Transp. Porous Media 59(1), 19–45 (2005)
Carrera, J., Sánchez-Vila, X., Benet, I., Medina, A., Galarza, G., Guimerà, J.: On matrix diffusion: formulations, solution methods, and qualitative effects. Hydrogeol. J. 6, 178–190 (1998)
Catrakis, H.J., Dimotakis, P.E.: Scale distributions and fractal dimensions in turbulence. Phys. Rev. Lett. 77(18), 3795–3798 (1996). https://doi.org/10.1103/physrevlett.77.3795
Chiogna, G., Hochstetler, D.L., Bellin, A., Kitanidis, P.K., Rolle, M.: (2012) Mixing, entropy and reactive solute transport. Geophys. Res. Lett. 39(20)
Chiogna, G., Cirpka, O.A., Rolle, M., Bellin, A.: Helical flow in three-dimensional nonstationary anisotropic heterogeneous porous media. Water Resour. Res. 51(1), 261–280 (2015). https://doi.org/10.1002/2014wr015330
Cirpka, O.A.: Choice of dispersion coefficients in reactive transport calculations on smoothed fields. J. Contam. Hydrol. 58(3–4), 261–282 (2002). https://doi.org/10.1016/s0169-7722(02)00039-6
Cirpka, O.A., Schwede, R., Luo, J., Dentz, M.: Concentration statistics of reactive constituents in random heterogeneous media. J. Cont. Hydrol. 98, 61–74 (2008)
Cirpka, O.A., Schwede, R.L., Luo, J., M, D.: Concentration statistics for mixing-controlled reactive transport in random heterogeneous media. J. Cont. Hydrol. 98, 61–74 (2008)
Cirpka, O.A., Chiogna, G., Rolle, M., Bellin, A.: Transverse mixing in three-dimensional nonstationary anisotropic heterogeneous porous media. Water Resour. Res. 51(1), 241–260 (2015). https://doi.org/10.1002/2014WR015331
Comolli, A., Hakoun, V., Dentz, M.: Mechanisms, upscaling, and prediction of anomalous dispersion in heterogeneous porous media. Water Resour. Res. 55(10), 8197–8222 (2019). https://doi.org/10.1029/2019wr024919
Curl, R.L.: Dispersed phase mixing: I. theory and effects in simple reactors. AIChE J. 9(2), 175–181 (1963). https://doi.org/10.1002/aic.690090207
Dagan, G.: Stochastic modeling of groundwater flow by unconditional and conditional probabilities: 2. the solute transport. Water Resour. Res. 18(4), 835–848 (1982). https://doi.org/10.1029/wr018i004p00835
Dagan, G.: Solute transport in heterogenous porous formations. J. Fluid Mech. 145, 151–177 (1984)
Dagan, G.: Theory of solute transport by groundwater. Annu. Rev. Fluid Mech. 19(1), 183–213 (1987). https://doi.org/10.1146/annurev.fl.19.010187.001151
Dagan, G.: Time-dependent macrodispersion for solute transport in anisotropic heterogeneous aquifers. Water Resour. Res. 24(9), 1491–1500 (1988). https://doi.org/10.1029/wr024i009p01491
Dagan, G.: Flow and Transport in Porous Formations. Springer, New York (1989)
Dagan, G., Neuman, S.P. (eds.): : Subsurface Flow and Transport. Cambridge University Press (1997). https://doi.org/10.1017/cbo9780511600081
Danckwerts, P.: The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. A 3, 279–296 (1952)
de Anna, P., Dentz, M., Tartakovsky, A., Le Borgne, T.: The filamentary structure of mixing fronts and its control on reaction kinetics in porous media flows. Geophys. Res. Lett. 41, 4586–4593 (2014)
De Dreuzy, J.R., Carrera, J., Dentz, M., Le Borgne, T.: Time evolution of mixing in heterogeneous porous media. Water Resour. Res. 48, W06511 (2012)
De Simoni, M., Carrera, J., Sánchez-Vila, X., Guadagnini, A.: A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 41, 2005WR004056 (2005)
De Vriendt, K., Le Borgne, T., Pool, M., Dentz, M.: Subsurface mixing dynamics across the salt-freshwater interface. Geophys. Res. Lett. 49(7), e2021GL097094 (2022)
Delgado, J.: Longitudinal and transverse dispersion in porous media. Chem. Eng. Res. Des. 85(9), 1245–1252 (2007). https://doi.org/10.1205/cherd07017
Dentz, M.: Concentration statistics for transport in heterogeneous media due to stochastic fluctuations of the center of mass velocity. Adv. Water Resour. 36, 11–22 (2012). https://doi.org/10.1016/j.advwatres.2011.04.005
Dentz, M., de Barros, F.P.J.: Mixing-scale dependent dispersion for transport in heterogeneous flows. J. Fluid Mech. 777, 178–195 (2015). https://doi.org/10.1017/jfm.2015.351
Dentz, M., Carrera, J.: Mixing and spreading in stratified flow. Phys. Fluids 19, 017107 (2007)
Dentz, M., Tartakovsky, D.M.: Self-consistent four-point closure for transport in steady random flows. Phys. Rev. E 77(6), (2008). https://doi.org/10.1103/physreve.77.066307,
Dentz, M., Tartakovsky, D.M.: Probability density functions for passive scalars dispersed in random velocity fields. Geophys. Res. Lett. 37, L24406 (2010)
Dentz, M., Kinzelbach, H., Attinger, S., Kinzelbach, W.: Temporal behavior of a solute cloud in a heterogeneous porous medium, 1, point-like injection. Water Resour. Res. 36(12), 3591–3604 (2000)
Dentz, M., Kinzelbach, H., Attinger, S., Kinzelbach, W.: Numerical studies of the transport behavior of a passive solute in a two-dimensional incompressible random flow field. Phys Rev E 67,(2003). https://doi.org/10.1103/PhysRevE.67.046306
Dentz, M., Cortis, A., Scher, H., Berkowitz, B.: Time behavior of solute transport in heterogeneous media: transition from anomalous to normal transport. Adv. Water Resour. 27(2), 155–173 (2004)
Dentz, M., Kang, P.K., Comolli, A., Borgne, T.L., Lester, D.R.: Continuous time random walks for the evolution of Lagrangian velocities. Phys. Rev. Fluids 1(7), (2016a). https://doi.org/10.1103/physrevfluids.1.074004
Dentz, M., Lester, D.R., Borgne, T.L., de Barros, F.P.J.: Coupled continuous time random walks for fluid stretching in two-dimensional heterogeneous media. Phys. Rev. E (2016b)
Dentz, M., de Barros, F.P.J., Borgne, T.L., Lester, D.R.: Evolution of solute blobs in heterogeneous porous media. J. Fluid Mech. 853, 621–646 (2018). https://doi.org/10.1017/jfm.2018.588
Dentz, M., Icardi, M., Hidalgo, J.J.: Mechanisms of dispersion in a porous medium. J. Fluid Mech. 841, 851–882 (2018). https://doi.org/10.1017/jfm.2018.120
de Dreuzy, J.R., Beaudoin, A., Erhel, J.: Asymptotic dispersion in 2d heterogeneous porous media determined by parallel numerical simulations. Water Resour. Res. 43(10), (2007). https://doi.org/10.1029/2006wr005394,
Duplat, J., Villermaux, E.: Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86 (2008)
Emmanuel, S., Berkowitz, B.: Mixing-induced precipitation and porosity evolution in porous media. Adv. Water Resour. 28(4), 337–344 (2005). https://doi.org/10.1016/j.advwatres.2004.11.010
Feldmann, F., Hagemann, B., Ganzer, L., Panfilov, M.: Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages. Environ. Earth Sci. 75(16), 1–15 (2016)
Fenaux, M., Reyes, E., Gálvez, J., Moragues, A.: Modelling the transport of chloride and other ions in cement-based materials. Cement Concr. Compos. 97, 33–42 (2019)
Fiori, A.: The Lagrangian concentration approach for determining dilution in aquifer transport: theoretical analysis and comparison with field experiments. Water Resour. Res. 37(12), 3105–3114 (2001). https://doi.org/10.1029/2001wr000228
Fiori, A., Dagan, G.: Concentration fluctuations in aquifer transport: a rigorous first-order solution and applications. J. Cont. Hydrol. 45(1–2), 139–163 (2000)
Fiori, A., Janković, I., Dagan, G.: Flow and transport in highly heterogeneous formations: 2. semianalytical results for isotropic media. Water Resour. Res. (2003). https://doi.org/10.1029/2002wr001719
Fiorotto, V., Caroni, E.: Concentration statistics in heterogeneous aquifers for finite peclet values. Transp in Porous Media 48 (2002)
Frippiat, C.C., Holeyman, A.E.: A comparative review of upscaling methods for solute transport in heterogeneous porous media. J. Hydrol. 362(1–2), 150–176 (2008)
Gardiner, C.W.: Handbook of stochastic methods for physics, chemistry and the natural sciences. Appl. Opt. 25, 3145 (1986)
Gelhar, L.: Stochastic Subsurface Hydrology. Prentice Hall, Englewood Cliffs, NJ (1993)
Gelhar, L.W., Axness, C.L.: Three-dimensional stochastic analysis of macrodispersion in aquifers. Water Resour. Res. 19(1), 161–180 (1983)
Gelhar, L.W., Welty, C., Rehfeldt, K.R.: A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 28(7), 1955–1974 (1992)
Ghanbarian, B., Hunt, A.G., Ewing, R.P., Sahimi, M.: Tortuosity in porous media: a critical review. Soil Sci. Soc. Am. J. 77(5), 1461–1477 (2013)
Gouze, P., Puyguiraud, A., Roubinet, D., Dentz, M.: Pore-scale transport in rocks of different complexity modeled by random walk methods. Trans. Porous Media (2021). https://doi.org/10.1007/s11242-021-01675-2
Grathwohl, P.: Diffusion in Natural Porous Media: Contaminant Transport, Sorption/Desorption and Dissolution Kinetics, vol. 1. Springer Science & Business Media, London (2012)
Green, M.S.: Brownian motion in a gas of noninteracting molecules. J. Chem. Phys. 19(8), 1036–1046 (1951). https://doi.org/10.1063/1.1748449
Groisman, A., Steinberg, V.: Elastic turbulence in a polymer solution flow. Nature 405(6782), 53–55 (2000)
Groisman, A., Steinberg, V.: Efficient mixing at low reynolds numbers using polymer additives. Nature 410(6831), 905–908 (2001). https://doi.org/10.1038/35073524
Guilbert, E., Metzger, B., Villermaux, E.: Chemical production on a deforming substrate. J. Fluid Mech. 934, R1 (2022). https://doi.org/10.1017/jfm.2021.1122
Haber, S., Mauri, R.: Lagrangian approach to time-dependent laminar dispersion in rectangular conduits. part 1. two-dimensional flows. J. Fluid Mech. 190, 201–215 (1988). https://doi.org/10.1017/s0022112088001284
Haggerty, R., Gorelick, S.M.: Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 31(10), 2383–2400 (1995)
Hakoun, V., Comolli, A., Dentz, M.: Upscaling and prediction of lagrangian velocity dynamics in heterogeneous porous media. Water Resour Res (2019). https://doi.org/10.1029/2018WR023810
Hazas, M.B., Ziliotto, F., Rolle, M., Chiogna, G.: Linking mixing and flow topology in porous media: An experimental proof. Phys. Rev. E 105(3), (2022).https://doi.org/10.1103/physreve.105.035105,
Hester, E.T., Cardenas, M.B., Haggerty, R., Apte, S.V.: The importance and challenge of hyporheic mixing. Water Resour. Res. 53(5), 3565–3575 (2017). https://doi.org/10.1002/2016wr020005
Heyman, J., Lester, D.R., Turuban, R., Méheust, Y., Borgne, T.L.: Stretching and folding sustain microscale chemical gradients in porous media. Proc. Natl. Acad. Sci. 117(24), 13359–13365 (2020). https://doi.org/10.1073/pnas.2002858117
Heyman, J., Lester, D.R., Le Borgne, T.: Scalar signatures of chaotic mixing in porous media. Phys. Rev. Lett. 126, 034505 (2021). https://doi.org/10.1103/PhysRevLett.126.034505
Hidalgo, J.J., Dentz, M.: Mixing across fluid interfaces compressed by convective flow in porous media. J. Fluid Mech. 838, 105–128 (2018). https://doi.org/10.1017/jfm.2017.888
Hidalgo, J.J., Carrera, J., Dentz, M.: Steady state heat transport in 3d heterogeneous porous media. Adv. Water Resour. 32(8), 1206–1212 (2009). https://doi.org/10.1016/j.advwatres.2009.04.003
Hidalgo, J.J., Fe, J., Cueto-Felgueroso, L., Juanes, R.: Scaling of convective mixing in porous media. Phys. Rev. Lett. (2012). https://doi.org/10.1103/physrevlett.109.264503,
Holzner, M., Morales, V.L., Willmann, M., Dentz, M.: Intermittent lagrangian velocities and accelerations in three-dimensional porous medium flow. Phys. Rev. E (2015). https://doi.org/10.1103/physreve.92.013015,
Hornung, U.: Homogenization and Porous Media. Springer-Verlag, New York Inc (1997)
Hristopulos, D.T.: Random Fields for Spatial Data Modeling. Springer, Netherlands, (2020). https://doi.org/10.1007/978-94-024-1918-4
Isichenko, M.B.: Percolation, stochastic topography, and transport in random media. Rev. Mod. Phys. 64, 961–1043 (1992)
Janković, I., Fiori, A., Dagan, G.: Flow and transport in highly heterogeneous formations: 3. numerical simulations and comparison with theoretical results. Water Resour. Res. 39(9), (2003). https://doi.org/10.1029/2002wr001721,
Janković, I., Steward, D.R., Barnes, R.J., Dagan, G.: Is transverse macrodispersivity in three-dimensional groundwater transport equal to zero? a counterexample. Water Resour. Res. (2009). https://doi.org/10.1029/2009wr007741,
Jha, B., Cueto-Felgueroso, L., Juanes, R.: Fluid mixing from viscous fingering. Phys. Rev. Lett. 106(19), (2011). https://doi.org/10.1103/physrevlett.106.194502,
Jiménez-Martínez, J., de Anna, P., Tabuteau, H., Turuban, R., Borgne, T.L., Méheust, Y.: Pore-scale mechanisms for the enhancement of mixing in unsaturated porous media and implications for chemical reactions. Geophys. Res. Lett. 42(13), 5316–5324 (2015). https://doi.org/10.1002/2015gl064513
Jiménez-Martínez, J., Borgne, T.L., Tabuteau, H., Méheust, Y.: Impact of saturation on dispersion and mixing in porous media: Photobleaching pulse injection experiments and shear-enhanced mixing model. Water Resour. Res. 53(2), 1457–1472 (2017). https://doi.org/10.1002/2016wr019849
Johnson, J., Brown, S., Stockman, H.: Fluid flow and mixing in rough-walled fracture intersections. J . Geophys. Res.: Solid Earth 111(B12):n/a–n/a, (2006). https://doi.org/10.1029/2005jb004087,
de Josselin de Jong, G.: Longitudinal and transverse diffusion in granular deposits. Trans Amer Geophys Un 39, 67–74 (1958)
Jose, S.C., Cirpka, O.A.: Measurement of mixing-controlled reactive transport in homogeneous porous media and its prediction from conservative tracer test data. Environ. Sci. & Technol. 38(7), 2089–2096 (2004)
Kang, P.K., Dentz, M., Le Borgne, T., Juanes, R.: Spatial markov model of anomalous transport through random lattice networks. Phys. Rev. Lett. 107, 180602 (2011)
Kapoor, V., Gelhar, L.W.: Transport in three-dimensionally heterogeneous aquifers: 1. dynamics of concentration fluctuations. Water Resour. Res. 30, 1775–1788 (1994)
Kapoor, V., Kitanidis, P.K.: Concentration fluctuations and dilution in aquifers. Water Resour. Res. 34, 1181–1193 (1998)
Kapoor, V., Gelhar, L., Miralles-Wilhelm, F.: Bimolecular second-order reactions in spatially varying flows: Segregation induced scale-dependent transformation rates. Water Resour. Res. 33, 527–536 (1997)
Karadimitriou, N.K., Joekar-Niasar, V., Babaei, M., Shore, C.A.: Critical role of the immobile zone in non-fickian two-phase transport: a new paradigm. Environ. Sci. & Technol. 50(8), 4384–4392 (2016)
Kinzelbach, W., Ackerer, P.: Modélisation du transport de contaminant dans un champ d’écoulement non-permanent. Hydrolgéologie 2, 197–205 (1986)
Kirchner, J., Feng, X., Neal, C.: Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 403, 524–527 (2000)
Kitanidis, P.K.: Prediction by the method of moments of transport in heterogeneous formations. J. Hydrol. 102, 453–473 (1988)
Kitanidis, P.K.: The concept of the dilution index. Water Resour. Res. 30(7), 2011–2026 (1994)
Kitanidis, P.K., McCarty, P.L.: Delivery and Mixing in the Subsurface: Processes and Design Principles for in Situ remediation, vol. 4. Springer Science & Business Media, USA (2012)
Koch, D.L., Brady, J.F.: Dispersion in fixed beds. J. Fluid Mech. 154, 399 (1985)
Kree, M., Villermaux, E.: Scalar mixtures in porous media. Phys. Rev. Fluids , (2017). https://doi.org/10.1103/physrevfluids.2.104502,
Kubo, R.: Statistical-mechanical theory of irreversible processes. i. general theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12(6), 570–586 (1957). https://doi.org/10.1143/jpsj.12.570
Kuniansky, E.L., Taylor, C.J., Willams, J.H., Paillet, F.: Introduction to karst aquifers. The groundwater project, (2022).https://doi.org/10.21083/978-1-77470-040-2
Lallemand-Barres, P., Peaudecerf, P.: Recherche des relations entre la valeur de la dispersivité macroscopique d’un milieu aquifer, ses autres caracteristiques et les conditions de mesure. Bull BRGM, chap 3, 227–284 (1978)
Landman, A.J., Johannsen, K., Schotting, R.: Density-dependent dispersion in heterogeneous porous media part i: a numerical study. Adv. Water Resour. 30(12), 2467–2480 (2007)
Le Borgne, T., Dentz, M., Carrera, J.: A Lagrangian statistical model for transport in highly heterogeneous velocity fields. Phys. Rev. Lett. 101, 090601 (2008)
Le Borgne, T., Dentz, M., Bolster, D., Carrera, J., de Dreuzy, J.R., Davy, P.: Non-fickian mixing: temporal evolution of the scalar dissipation rate in heterogeneous porous media. Adv. Water Resour. 33, 1468–1475 (2010)
Le Borgne, T., Dentz, M., Davy, P., Bolster, D., Carrera, J., de Dreuzy, J.R., Bour, O.: Persistence of incomplete mixing: a key to anomalous transport. Phys. Rev. E 84, 015301(R) (2011)
Le Borgne, T., Dentz, M., Villermaux, E.: Stretching, coalescence and mixing in porous media. Phys. Rev. Lett. 110, 204501 (2013)
Le Borgne, T., Ginn, T., Dentz, M.: Impact of fluid deformation on mixing-induced chemical reactions in heterogeneous flows. Geophys. Res. Lett. 41, 7898–7906 (2014)
Le Borgne, T., Dentz, M., Villermaux, E.: The Lamellar Representation of Mixing in Porous Media. J. Fluid Mech. 770, 458–498 (2015)
Le Borgne, T., Huck, P.D., Dentz, M., Villermaux, E.: Scalar gradients in stirred mixtures and the deconstruction of random fields. J. Fluid Mech. 812, 578–610 (2017). https://doi.org/10.1017/jfm.2016.799
LeBlanc, D.R., Garabedian, S.P., Hess, K.M., Gelhar, L.W., Quadri, R.D., Stollenwerk, K.G., Wood, W.W.: Large-scale natural gradient tracer test in sand and gravel, cape cod, massachusetts: 1. experimental design and observed tracer movement. Water Resour. Res. 27(5), 895–910 (1991). https://doi.org/10.1029/91wr00241
Lee, S.H., Kang, P.K.: Three-dimensional vortex-induced reaction hot spots at flow intersections. Phys. Rev. Lett. 124(14), (2020). https://doi.org/10.1103/physrevlett.124.144501,
Lester, D., Trefry, M., Metcalfe, G.: Chaotic advection at the pore scale: Mechanisms, upscaling and implications for macroscopic transport. Adv. Water Resour. ,(2016). https://doi.org/10.1016/j.advwatres.2016.09.007
Lester, D.R., Metcalfe, G., Trefry, M.G.: Is chaotic advection inherent to porous media flow? Phys. Rev. Lett. 111, 174101 (2013). https://doi.org/10.1103/PhysRevLett.111.174101
Lester, D.R., Metcalfe, G., Trefry, M.G.: Anomalous transport and chaotic advection in homogeneous porous media. Phys. Rev. E 90, 063012 (2014)
Lester, D.R., Dentz, M., Borgne, T.L.: Chaotic mixing in three-dimensional porous media. J. Fluid Mech. 803, 144–174 (2016). https://doi.org/10.1017/jfm.2016.486
Lester, D.R., Dentz, M., Borgne, T.L., de Barros, F.P.J.: Fluid deformation in random steady three-dimensional flow. J. Fluid Mech. 855, 770–803 (2018). https://doi.org/10.1017/jfm.2018.654
Lester, D.R., Bandopadhyay, A., Dentz, M., Borgne, T.L.: Hydrodynamic dispersion and lamb surfaces in darcy flow. Transp. Porous Media 130(3), 903–922 (2019). https://doi.org/10.1007/s11242-019-01346-3
Lester, D.R., Dentz, M., Bandopadhyay, A., Borgne, T.L.: The Lagrangian kinematics of three-dimensional darcy flow. J. Fluid Mech. (2021). https://doi.org/10.1017/jfm.2021.362
Lester, D.R., Dentz, M., Bandopadhyay, A., Borgne, T.L.: Fluid deformation in isotropic Darcy flow. J. Fluid Mech. 945, A18 (2022)
Martinez-Landa, L., Carrera, J., Dentz, M., Fernàndez-Garcia, D., Nardí, A., Saaltink, M.W.: Mixing induced reactive transport in fractured crystalline rocks. Appl. Geochem. 27(2), 479–489 (2012). https://doi.org/10.1016/j.apgeochem.2011.09.016
Martínez-Ruiz, D., Meunier, P., Favier, B., Duchemin, L., Villermaux, E.: The diffusive sheet method for scalar mixing. J. Fluid Mech. 837, 230–257 (2017). https://doi.org/10.1017/jfm.2017.862
Matheron, M., de Marsily, G.: Is transport in porous media always diffusive? Water Resour. Res. 16, 901–917 (1980)
Meunier, P., Villermaux, E.: The diffusive strip method for scalar mixing in two dimensions. J. Fluid Mech. 662, 134–172 (2010)
Meunier, P., Villermaux, E.: How vortices mix. J. Fluid Mech. 476, 213–222 (2003). https://doi.org/10.1017/s0022112002003166
Meyer, D.W., Jenny, P., Tchelepi, H.: A joint velocity-concentration PDF method for tracer flow in heterogeneous porous media. Water Resour. Res. 46, W12522 (2010)
Moffatt, H.K., Tsinober, A.: Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24(1), 281–312 (1992). https://doi.org/10.1146/annurev.fl.24.010192.001433
Morales, V.L., Dentz, M., Willmann, M., Holzner, M.: Stochastic dynamics of intermittent pore-scale particle motion in three-dimensional porous media: Experiments and theory. Geophys. Res. Lett. 44(18), 9361–9371 (2017)
National Research Council.: Natural Attenuation for Groundwater Remediation. The National Academies Press, Washington, DC (2000). https://doi.org/10.17226/9792
Neufeld, J.A., Hesse, M.A., Riaz, A., Hallworth, M.A., Tchelepi, H.A., Huppert, H.E.: Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37(22), L22404 (2010). https://doi.org/10.1029/2010GL044728
Neuman, S.P., Tartakovsky, D.M.: Perspective on theories of anomalous transport in heterogeneous media. Adv. Water Resour. 32, 670–680 (2008). https://doi.org/10.1016/j.advwatres.2008.08.005
Niemi, A., Bear, J., Bensabat, J. (eds.): Geological Storage of CO2 in Deep Saline Formations. Springer, Netherlands (2017)
Painter, S.L., Cvetkovic, V., Pensado, O.: Time-domain random-walk algorithms for simulating radionuclide transport in fractured porous rock. Nucl. Technol. 163(1), 129–136 (2008)
Pannone, M., Kitanidis, P.K.: Large-time behavior of concentration variance and dilution in heterogeneous formations. Water Resour. Res. 35(3), 623–634 (1999). https://doi.org/10.1029/1998wr900063
Perez, L.J., Hidalgo, J.J., Dentz, M.: Upscaling of mixing-limited bimolecular chemical reactions in poiseuille flow. Water Resour. Res. 55(1), 249–269 (2019). https://doi.org/10.1029/2018wr022730
Pfannkuch, H.O.: Contribution a l’etude des desplacements de fluides miscibles dans un milieu poreux. Rev Inst Fr Petr 18, 215 (1963)
Poinssot, C., Geckeis, H. (eds.): Radionuclide Behaviour in the Natural Environment. Woodhead Publishing (2012)
Pool, M., Dentz, M.: Effects of heterogeneity, connectivity, and density variations on mixing and chemical reactions under temporally fluctuating flow conditions and the formation of reaction patterns. Water Resour. Res. 54(1), 186–204 (2018). https://doi.org/10.1002/2017wr021820
Pool, M., Post, V.E.A., Simmons, C.T.: Effects of tidal fluctuations and spatial heterogeneity on mixing and spreading in spatially heterogeneous coastal aquifers. Water Resour. Res. 51(3), 1570–1585 (2015). https://doi.org/10.1002/2014wr016068
Pope, S.B.: Turbulent Flows. Cambridge University Press (2000)
Puyguiraud, A., Gouze, P., Dentz, M.: Upscaling of anomalous pore-scale dispersion. Transp. Porous Media 128(2), 837–855 (2019). https://doi.org/10.1007/s11242-019-01273-3
Puyguiraud, A., Perez, L.J., Hidalgo, J.J., Dentz, M.: Effective dispersion coefficients for the upscaling of pore-scale mixing and reaction. Adv. Water Resour. 146, 103782 (2020). https://doi.org/10.1016/j.advwatres.2020.103782
Puyguiraud, A., Gouze, P., Dentz, M.: Pore-scale mixing and the evolution of hydrodynamic dispersion in porous media. Phys. Rev. Lett. 126(16), (2021). https://doi.org/10.1103/physrevlett.126.164501,
Ranz, W.E.: Application of a stretch model to mixing, diffusion and reaction in laminar and turbulent flows. AIChE J. 25(1), 41–47 (1979)
Raoof, A., Hassanizadeh, S.: Saturation-dependent solute dispersivity in porous media: pore-scale processes. Water Resour. Res. 49(4), 1943–1951 (2013)
Rezaei, M., Sanz, E., Raeisi, E., Ayora, C., Vázquez-Suñé, E., Carrera, J.: Reactive transport modeling of calcite dissolution in the fresh-salt water mixing zone. J. Hydrol. 311(1–4), 282–298 (2005)
Risken, H.: The Fokker-Planck Equation. Springer, Heidelberg New York (1996)
Rolle, M., Le Borgne, T.: Mixing and reactive fronts in the subsurface. Rev. Mineral. Geochem. 85(1), 111–142 (2019). https://doi.org/10.2138/rmg.2018.85.5
Rolle, M., Eberhardt, C., Chiogna, G., Cirpka, O., Grathwohl, P.: Enhancement of dilution and transverse reactive mixing in porous media: experiments and model-based interpretation. J. Contam Hydrol. 110, 130–142 (2009)
Rubin, Y.: Applied Stochastic Hydrogeology. Oxford University Press, New York (2003)
Rubin, Y., Sun, A., Maxwell, R., Bellin, A.: The concept of block-effective macrodispersivity and a unified approach for grid-scale-and plume-scale-dependent transport. J. Fluid Mech. 395, 161–180 (1999)
Saffman, P.G.: A theory of dispersion in a porous medium. J. Fluid Mech. 6(03), 321–349 (1959)
Sahimi, M.: Flow and Transport in Porous Media and Fractured Rock. VCH, Weinheim, Cambridge (1995)
Sahimi, M.: Flow and Transport in Fractured Media and Porous Rock. Viley VCH (2011)
Salamon, P., Fernàndez-Garcia, D., J, G.H.J.: A review and numerical assessment of the random walk particle tracking methods. J Cont Hydrol 87, 277–305 (2006)
Sanford, W.E., Konikow, L.F.: Simulation of calcite dissolution and porosity changes in saltwater mixing zones in coastal aquifers. Water Resour. Res. 25(4), 655–667 (1989)
Schincariol, R.A.: Dispersive mixing dynamics of dense miscible plumes: natural perturbation initiation by local-scale heterogeneities. J. Contam. Hydrol. 34(3), 247–271 (1998). https://doi.org/10.1016/s0169-7722(98)00081-3
Scholz, C., Wirner, F., Gomez-Solano, J.R., Bechinger, C.: Enhanced dispersion by elastic turbulence in porous media. EPL (Europhys. Lett.) 107(5), 54003 (2014)
Schwede, R.L., Cirpka, O.A., Nowak, W., Neuweiler, I.: Impact of sampling volume on the probability density function of steady state concentration. Water Resour. Res. (2008). https://doi.org/10.1029/2007wr006668,
Seidel-Morgenstern, A. (ed.): : Membrane Reactors. Wiley-VCH Verlag GmbH & Co. KGaA (2010). https://doi.org/10.1002/9783527629725
Sherman, T., Engdahl, N.B., Porta, G., Bolster, D.: A review of spatial markov models for predicting pre-asymptotic and anomalous transport in porous and fractured media. J. Contam. Hydrol. 236, 103734 (2021). https://doi.org/10.1016/j.jconhyd.2020.103734
Siena, M., Guadagnini, A., Riva, M., Bijeljic, B., Nunes, J.P.P., Blunt, M.J.: Statistical scaling of pore-scale Lagrangian velocities in natural porous media. Phys. Rev. E (2014). https://doi.org/10.1103/physreve.90.023013
Smoluchowski, M.: Versuch einer Mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z Physik Chem XCII:129–168 (1917)
Souzy, M., Zaier, I., Lhuissier, H., Borgne, T.L., Metzger, B.: Mixing lamellae in a shear flow. J. Fluid Mech. (2018). https://doi.org/10.1017/jfm.2017.916
Souzy, M., Lhuissier, H., Méheust, Y., Borgne, T.L., Metzger, B.: Velocity distributions, dispersion and stretching in three-dimensional porous media. J. Fluid Mech. (2020). https://doi.org/10.1017/jfm.2020.113
Sposito, G.: Steady groundwater flow as a dynamical system. Water Resour. Res. 30(8), 2395–2401 (1994). https://doi.org/10.1029/94WR01328
Sposito, G.: Topological groundwater hydrodynamics. Adv. Water Resour. 24(7), 793–801 (2001). https://doi.org/10.1016/S0309-1708(00)00077-4
Taghizadeh, E., Valdés-Parada, F.J., Wood, B.D.: Preasymptotic taylor dispersion: evolution from the initial condition. J. Fluid Mech. (2020). https://doi.org/10.1017/jfm.2020.56
Tartakovsky, D.M.: Assessment and management of risk in subsurface hydrology: a review and perspective. Adv. Water Resour. 51, 247–260 (2013). https://doi.org/10.1016/j.advwatres.2012.04.007
Tartakovsky, D.M., Dentz, M.: Diffusion in porous media: Phenomena and mechanisms. Transp. Porous Media 130(1), 105–127 (2019). https://doi.org/10.1007/s11242-019-01262-6
Tartakovsky, D.M., Lichtner, P.C., Pawar, R.J.: PDF methods for reactive transport in porous media. Acta Universitatis Carolinae Geologica 46, 113–116 (2002)
Taylor, G.I.: Diffusion by continuous movements. Proc. Lond. Math. Soc. s2–20(1), 196–212 (1922). https://doi.org/10.1112/plms/s2-20.1.196
Taylor, G.I.: Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203 (1953)
Tennekes, H., Lumley, J.L.: A First Course in Turbulence. The MIT Press (1972). https://doi.org/10.7551/mitpress/3014.001.0001
Thiffeault, J.L., Finn, M.: Topology, braids, and mixing in fluids. Philos. Transact. A Math. Phys. Eng. Sci. 364, 3251–66 (2007). https://doi.org/10.1098/rsta.2006.1899
Tompson, A., Gelhar, L.: Numerical simulation of solute transport in three-dimensional, randomly heterogeneous porous media. Water Resour. Res. 26(10), 2541–2562 (1990)
Tonina, D., Bellin, A.: Effects of pore-scale dispersion, degree of heterogeneity, sampling size, and source volume on the concentration moments of conservative solutes in heterogeneous formations. Adv. Water Resour. 31, 339–354 (2008)
Turuban, R., Lester, D.R., Le Borgne, T., Méheust, Y.: Space-group symmetries generate chaotic fluid advection in crystalline granular media. Phys. Rev. Lett. 120, 024501 (2018). https://doi.org/10.1103/PhysRevLett.120.024501
Turuban, R., Lester, D.R., Heyman, J., Borgne, T.L., Méheust, Y.: Chaotic mixing in crystalline granular media. J. Fluid Mech. 871, 562–594 (2019). https://doi.org/10.1017/jfm.2019.245
Valocchi, A.J., Bolster, D., Werth, C.J.: Mixing-limited reactions in porous media. Transp. Porous Media 130(1), 157–182 (2018). https://doi.org/10.1007/s11242-018-1204-1
Vanderborght, J.: Concentration variance and spatial covariance in second-order stationary heterogeneous conductivity fields. Water Resour. Res. 37(7), 1893–1912 (2001). https://doi.org/10.1029/2001wr900009
Vilks, P., Cramer, J., Jensen, M., Miller, N., Miller, H., Stanchell, F.: In situ diffusion experiment in granite: phase i. J. Contam. Hydrol. 61(1–4), 191–202 (2003)
Villermaux, E.: Mixing by porous media. C R Mécanique 340, 933–943 (2012)
Villermaux, E.: Mixing versus stirring. Annu. Rev. Fluid Mech. 51(1), 245–273 (2019). https://doi.org/10.1146/annurev-fluid-010518-040306
Villermaux, E., Duplat, J.: Coarse grained scale of turbulent mixtures. Phys. Rev. Lett. 97, 144506 (2006)
Villermaux, J., Devillon, J.C.: Représentation de la coalescence et de la redispersion des domaines de ségrégation dans un fluide par un modèle d’interaction phénom- enologique. In: Proc. 2nd International symposium chem. React. Engineering, New York, Elsevier (1972)
Vriendt, K.D., Pool, M., Dentz, M.: Heterogeneity-induced mixing and reaction hot spots facilitate karst propagation in coastal aquifers. Geophys. Res. Lett. 47(10), (2020). https://doi.org/10.1029/2020gl087529,
Wang, J., Kitanids, P.K.: Analysis of macrodispersion through volume averaging: comparison with stochastic theory. Stoch Environ Res and Risk Assess 13, 66–84 (1999)
Werner, A.D., Bakker, M., Post, V.E., Vandenbohede, A., Lu, C., Ataie-Ashtiani, B., Simmons, C.T., Barry, D.: Seawater intrusion processes, investigation and management: recent advances and future challenges. Adv. Water Resour. 51, 3–26 (2013). https://doi.org/10.1016/j.advwatres.2012.03.004
Werth, C.J., Cirpka, O.A., Grathwohl, P.: Enhanced mixing and reaction through flow focusing in heterogeneous porous media. Water Resour. Res. (2006). https://doi.org/10.1029/2005wr004511,
Wheatcraft, S.W., Winterberg, F.: Steady state flow passing through a cylinder a permeability different from the surrounding medium. Water Resour. Res. 21(12), 1923–1929 (1985). https://doi.org/10.1029/WR021i012p01923
Whitaker, S.: The Method of Volume Averaging. Kluwer Academic Publishers (1999)
Wood, B.D., Cherblanc, F., Quintard, M., Whitaker, S.: Volume averaging for determining the effective dispersion tensor: Closure using periodic unit cells and comparison with ensemble averaging. Water Resour. Res. 39(8), (2003). https://doi.org/10.1029/2002wr001723,
Ye, Y., Chiogna, G., Cirpka, O., Grathwohl, P., Rolle, M.: Experimental evidence of helical flow in porous media. Phys. Rev. Lett. 115(19), (2015a). https://doi.org/10.1103/physrevlett.115.194502,
Ye, Y., Chiogna, G., Cirpka, O.A., Grathwohl, P., Rolle, M.: Enhancement of plume dilution in two-dimensional and three-dimensional porous media by flow focusing in high-permeability inclusions. Water Resour. Res. 51(7), 5582–5602 (2015). https://doi.org/10.1002/2015wr016962
Zech, A., Attinger, S., Cvetkovic, V., Dagan, G., Dietrich, P., Fiori, A., Rubin, Y., Teutsch, G.: Is unique scaling of aquifer macrodispersivity supported by field data? Water Resour. Res. 51(9), 7662–7679 (2015). https://doi.org/10.1002/2015wr017220
Zhang, T., Gjørv, O.E.: Diffusion behavior of chloride ions in concrete. Cem. Concr. Res. 26(6), 907–917 (1996)
Zou, L., Jing, L., Cvetkovic, V.: Modeling of flow and mixing in 3d rough-walled rock fracture intersections. Adv. Water Resour. 107, 1–9 (2017). https://doi.org/10.1016/j.advwatres.2017.06.003
Acknowledgements
M.D. and J.J.H. acknowledge the support of the Spanish Research Agency (10.13039/501100011033), Spanish Ministry of Science through grants CEX2018-000794-S and HydroPore PID2019-106887GB-C31. J.J.H. acknowledges the sup- port of the Spanish Research Agency (10.13039/501100011033), the Spanish Ministry of Science and Innovation and the European Social Fund “Investing in your future” through the “Ramón y Cajal” fellowship (RYC-2017-22300).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dentz, M., Hidalgo, J.J. & Lester, D. Mixing in Porous Media: Concepts and Approaches Across Scales. Transp Porous Med 146, 5–53 (2023). https://doi.org/10.1007/s11242-022-01852-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-022-01852-x