1 Introduction

Microstructures or structural features at the cellular level such as cells, cellular spaces, gas cells, solid matrices and their organization contribute to the quality attributes of food products such as texture, sensory, rheological property and shelf-life (Houska et al. 2005; Drummond et al. 2009; Abera et al. 2014). On the other hand, microstructural elements strongly affect the transport properties of food especially porous food products as transport of bound and free water through the various microstructural features takes place at this scale (Aguilera et al. 2000; Aguilera 2005). In addition, food processing affects the stability of the microstructure, which in turn affect food quality (Cheng and Sun 2007; Feng and Sun 2014).

Mathematical modelling is a valuable tool to understand and optimize food processes (Zhang and Sun 2005). In particular, modelling at the microstructural level is a key to comprehend the microscale chemical and physical phenomena, which are lumped together in macroscale modelling (Sun and Hu 2003; Wang and Sun 2003; Ajani et al. 2019). Moreover, the multiscale modelling paradigm has been recently employed in food material modelling (Rahman et al. 2018a). For achieving reliable modelling results, accurate microstructural representations are needed, which in turn require adequate microstructural information.

Bread is one of the most common staple foods in the world, and steamed bread is a popular Chinese staple, which is mostly made from plain flour, water and yeast with or without stuffing (Kou et al. 2019). Steam bread is a typical porous food product. The transport properties of bread significantly affect their freshness, colour, crispiness, water diffusivity, microstructural stability, sensorial, textural, rheological properties and staling during steaming and storage (Altamirano-fortoul et al. 2012; Drummond and Sun 2012). The structure of steam bread consists of an assemblage of microstructures with a large number of pores or gas cells heterogeneously distributed across the interconnected solid matrices (Aguilera 2005); therefore, steam bread is complex with multiscale fractal-like hierarchical structures (Ajani et al. 2020; Heertje 2014).

Both descriptor-based and correlation function-based approaches are reliable for the characterization, classification, reconstruction and modelling of food microstructures (Derossi et al. 2014, 2016; Sundararaghavan and Zabaras 2005; Xu et al. 2014a). Microstructural reconstruction generally involves two main steps: the extraction of representative information from the microstructural image, which can be either a descriptor-based approach or a correlation function-based approach and the generation of the virtual microstructure, which includes Voronoi tessellation algorithm, ellipse tessellation algorithm, etc.

Among the two approaches for information extraction, the descriptor-based approach shows its strengths including adequate microstructural representation with well-defined physical meaning, and lower reconstruction cost (Thomas et al. 2008; Xu et al. 2014a) and thus, plays an important role in reliable mathematical modelling and is often used as representative element volume (REV) to model food transport phenomena during processing at the microscale (McDonald and Sun 2000; Rahman et al. 2018b). Geometry descriptors are computational methods used to analyse, quantify and represent an image in quantitative image analysis (Prakash et al. 2011; Xu et al. 2014a). These descriptors can be quantified by mean or higher-order moments such as variance, kurtosis depending on the availability of sufficient descriptor sets (Xu et al. 2014b).

For the generation of the virtual microstructure, some researchers used the Voronoi tessellation algorithm for developing microstructures of apples in different cultivars (Mebatsion et al. 2006a) and pome fruits (Abera et al. 2014), while others used ellipse tessellation algorithm for constructing the virtual microstructures of apples, onions, and conference pear tissues (Mebatsion et al. 2006b; Rahman et al. 2018b), showing better accuracy than the former. Both algorithms are descriptor based; however, in most cases, the use of the extracted geometrical descriptors in classifying and differentiating between the cells and intercellular spaces was not carried out, and the cells and intercellular spaces were randomly chosen in the developed microstructures, leading to low accuracies in modelling. Moreover, in some studies, only a single classifier was used in evaluating the sufficiency and sensitivity of the geometrical descriptors and detailed statistical evaluation of the prediction errors between the classes was not considered, resulting in a limited understanding of the discriminative power of the classifier. On the other hand, the application of both algorithms was mostly limited to the development of fruit microstructures, and no application has been found for foods such as bread. Although the microstructures of fruits are heterogeneous, which consist of cells, cell walls and intercellular spaces, their structural features and organization are different from those of bread. The bread microstructures primarily consist of pore or gas cell, laminae and networks of solid matrices which could be continuous or discontinuous, depending on the gas cell stability during processing (Sun and Wang 2006; Wang et al. 2011).

Due to the heterogeneous nature of food microstructures at the microscale, it is hard to differentiate their relevant features. Hitherto, only linear discriminant analysis (LDA) combined with relevant geometrical descriptors has been used as an automatic classifier for food microstructural features (Decost and Holm 2015; Pieczywek and Zdunek 2012; Rahman et al. 2018c), while the use of other relevant classifiers such as bagged trees ensembles (BTE) and Rusboosted trees ensembles (RTE), which could achieve better discrimination such as in the case of class imbalance (Tharwat et al. 2017), has not been investigated. Class imbalance exists when the samples in a class greatly outnumber those of the other classes in a dataset (Seiffert et al. 2010).

Although the connectivity of a 3D microstructure is greater than 2D counterpart, the latter is much easier to investigate, convenient to interpret, computationally economical, and has thus been mostly used for microscale and even multiscale modelling of food products with accurate predictions (Wang and Sun 2002a, b; Aregawi et al. 2014; Rahman et al. 2018b). Moreover, for practical industrial applications, morphological features in 3D images are often analysed using 2D projections and the developed 2D microstructures can be easily extended to 3D (Abera et al. 2014; Su and Yan 2020). Specifically, the fractal method is often used for bread analysis, assuming that the shapes are self-similar across different hierarchies and cross sections, thus making a 2D analysis sufficient (Liu and Scanlon 2003; Gonzales-Barron and Butler 2008; Zhang et al. 2013). In addition, the 2D microstructures developed in the current work could be used for microscale transport modelling and upscaled to 3D in the multiscale.

Presently, most microscale modelling of bakery products uses simplified homogenous or network models with no detailed geometrical features (Esveld et al. 2012). On the other hand, models with complex geometrical features often create singularity with results that are relatively hard to interpret (Rahman et al. 2018b), and there is thus a need to develop more accurate but simple REV for bread microstructures to modelling the microscale transport phenomena during processing. Therefore, in the current study, a descriptor-based approach for 2D reconstruction of steamed bread microstructures from microscopic images was developed. With the geometrical descriptors extracted from the microstructures, seven classifiers including LDA, BTE, Gaussian Naïve Bayes (GNB), fine tree (FT), quadrative support vector machine (QSVM), fine k-nearest neighbour (FKNN) and RTE were compared for automatic classification of the pores and solid matrices. Statistical information from SEM images together with Voronoi and ellipse tessellation algorithms was utilized for generating the virtual microstructures of the steamed bread, and the developed microstructural models were validated against the original SEM images by comparing various geometrical features including perimeter, area, orientation, centroid, convex area, circularity, and eccentricity.

2 Experimental Methods

SEM imaging was used for the development of 2D microstructural computational geometry in the current study. SEM images provide clear and detailed information on food microstructures even at microscale resolution with little or no chemical treatments (Pieczywek and Zdunek 2012; Rahman et al. 2018c). For the morphological observation by SEM, freshly prepared whole steamed bread samples were randomly purchased from a local bakery shop (Guangzhou, China), which were freeze-dried for about 24 h to remove the moisture, and the dried samples were stored in a desiccator. To reveal the microstructures, two samples were cut into cubes of about 1 × 1 × 1 cm from different cross sections and regions using a sharp cutter. The cut samples were firmly mounted on metal stubs using a double-sided tape, placed inside an automatic sputter coater and platinum-plated. The coated samples were then placed inside a high-resolution scanning electron microscope (Zeiss Merlin Field Emission SEM, Carl Zeiss NTS GmbH, Oberkochen, Germany). A total of 40 images were taken from different sections of the samples at an accelerating voltage of 5 kV and a magnification of 24. The 40 images with 400 × 400 pixels sizes (1 pixel = 4.686 μm) were identified by region of interest (ROI), and digitally analysed. The geometrical descriptors such as the area, circularity, eccentricity, orientation, and convex area, perimeter and centroid were then extracted from the 40 images.

3 Statistical Estimation and Theoretical Formulation

The geometric shape analysis can be done using the area-based or/and the boundary-based approach, and the choices are mostly based on the organization of the shapes (Thomas et al. 2008).

3.1 Geometrical Properties Estimation

Although geometrical property estimation approaches based on set theory are well adapted for estimating geometrical features, especially in the 3D (Schröder-Turk et al. 2013; McClure et al. 2018), Green’s theorem is suitable for less complex 2D microstructural reconstruction with reasonable accuracy and was thus employed in the current work. The geometrical descriptors, which are the characteristics of pores or gas cells, were estimated using ellipse fitting based on Green’s theorem (Mebatsion et al. 2006a; Mulchrone and Roy 2004). These geometric descriptors include surface area, circularity, eccentricity, convex area, perimeter, etc. Green’s theorem is one of the fundamental theorems of vector calculus, which defines the relationship between the macroscopic circulation of a curve and the sum of the microscopic circulation inside the curve (Chalifour et al. 2017). The theorem can also be used for calculating the amount of work done on a force field, the flux and flow on a vector field, the area of conics with line integral, etc. (Mebatsion et al. 2006a; Chalifour et al. 2017). Given a Cartesian plane with x and y representing the horizontal and vertical values of the coordinate pair, respectively, let C be a simple closed curve in the plane and F be the region bounded by C, and given two functions D(x, y) and E(x, y), having a boundary F, the differentiable functions can be expressed using Green’s theorem as

$$ \iint\limits_{{\text{C}}} {\left( {\frac{\partial D}{{\partial x}} - \frac{\partial E}{{\partial y}}} \right){\text{d}}x{\text{d}}y = \int\limits_{{\text{F}}} {\left( {D{\text{d}}x + E{\text{d}}y} \right)} } $$
(1)

The area A, also known as the zeroth moment of inertia, can be calculated as

$$ A = \iint\limits_{{\text{C}}} {{\text{d}}x{\text{d}}y} $$
(2)

The application of Green’s transformation to Eq. (2) in anticlockwise direction yields

$$ A = \frac{1}{2}\mathop \sum \limits_{k = 1}^{n} x_{k - 1} y_{k} - x_{k} y_{k - 1} $$
(3)

where the number of points on the pores is taken as n. The first moment \(\left( {\sigma_{x} } \right)\) with x-direction preference, otherwise known as the centroid of a region, is calculated as

$$ \sigma_{x} = \frac{1}{A}\iint\limits_{C} {xdxdy} $$
(4)

The application of Green’s transformation to Eq. (4) yields

$$ \sigma_{x} = \frac{1}{6A}\mathop \sum \limits_{k = 1}^{n} \left( {x_{k - 1} - x_{k} } \right)\left( {x_{k - 1} y_{k} - x_{k} y_{k - 1} } \right) $$
(5)

The first moment \(\left( {\sigma_{y} } \right)\) with y-direction preference is given as

$$ \sigma_{y} = \frac{1}{A}\iint\limits_{C} {y{\text{d}}x{\text{d}}y} $$
(6)

Similarly, the application of Green’s transformation to Eq. (6) yields

$$ \sigma_{y} = \frac{1}{6A}\mathop \sum \limits_{k = 1}^{n} (y_{k - 1} - y_{k} )\left( {x_{k - 1} y_{k} - x_{k} y_{k - 1} } \right) $$
(7)

3.2 Calculation of Eccentricity and Orientation

The eccentricity (aspect ratio) and orientation were also calculated from the images using ellipse fitting. Given a specific region on a boundary, having a number of points n, the second moment of the area can be calculated over \(x, y\), and \(xy\) plane, respectively, as follows

$$ \sigma_{xx} = \iint\limits_{R} {y^{2} }{\text{d}}x{\text{d}}y $$
(8)
$$ \sigma_{yy} = \iint\limits_{R} {x^{2} {\text{d}}x{\text{d}}y} $$
(9)
$$ \sigma_{xy} = \iint\limits_{R} {xy}{\text{d}}x{\text{d}}y $$
(10)

\(\sigma_{xx}\), \(\sigma_{yy}\), \(\sigma_{xy}\) are the second moments of area calculated over \(x\), \(y\), and \(xy\) plane, respectively. The application of Green’s transformation to Eqs. (8)–(10) yields

$$ \sigma_{xx} = \frac{1}{12A}\mathop \sum \limits_{k = 1}^{n} \left( {y_{k}^{2} + y_{k} y_{k + 1} + y_{k + 1}^{2} } \right)\left( {x_{k + 1} y_{k} - x_{k} y_{k + 1} } \right) $$
(11)
$$ \sigma_{yy} = \frac{1}{12A}\mathop \sum \limits_{k = 1}^{n} \left( {x_{k}^{2} + x_{k} x_{k + 1} + x_{k + 1}^{2} } \right)\left( {x_{k + 1} y_{k} - x_{k} y_{k + 1} } \right) $$
(12)
$$ \sigma_{xy} = \frac{1}{24A}\mathop \sum \limits_{k = 1}^{n} \left( {2x_{k} y_{k} + x_{k} y_{k + 1} + y_{k} x_{k + 1} + 2x_{k + 1} y_{k + 1} } \right)\left( {x_{k + 1} y_{k} - x_{k} y_{k + 1} } \right) $$
(13)

The orientation and eccentricity of the pores were calculated from the estimated central area moments in the 2D spatial domain as

$$ \alpha = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\mu_{11} }}{{\mu_{02} - \mu_{20} }}} \right) $$
(14)
$$ e = \frac{{l_{1} }}{{l_{2} }} $$
(15)

where \(\alpha \) is the orientation, \(e\) is the eccentricity, the central moments \({\mu }_{11}\), \({\mu }_{02}\), and \({\mu }_{20}\) were defined from their respective centroids and area moments of the pores, \({l}_{1}\) and \({l}_{2}\) are the major and minor length axes of the pores, respectively.

The summation of the distance among adjacent data set on the pore boundaries was used to calculate the perimeter. Circularity was calculated using the relationship below

$$ {\text{Circularity}} = \frac{{4\pi \;{\text{Pore}}\;{\text{area}}}}{{\left( {{\text{Convex}}\;{\text{perimeter}}} \right)^{2} }} $$
(16)

The circularity (Eq. 16) index ranges from 1 to 0 with 1 representing the perfectly circular shape and 0 representing irregularly shaped objects, which departs from circularity.

3.3 Identification of Key Descriptors for Classifying Pores and Solid Matrices

In previous works, most microstructural descriptors used for evaluating microstructural features are randomly chosen without providing any information on the significance of each descriptor to the microstructural features or properties of interest (Mebatsion et al. 2006a, b). Moreover, with the availability of a large number of microstructure descriptors, representing the microstructural features quantitatively using a descriptor set that is sufficient and yet small enough to be tractable is challenging (Xu et al. 2014a). Hence, machine learning (ML) approaches can be used to automatically evaluate the descriptors-features relationship and for fast selection of most relevant descriptors (Xu et al. 2014a, 2014b). Besides, the ML approach could be used to automatically classify the respective features in the reconstructed microstructures when imported as REV during microscale modelling especially in the case of large data set (Rahman et al. 2018c).

In the current study, the significance of each descriptor for classifying bread microstructural features (pores and solid matrices) was investigated. A dataset containing 6496 features (pores and solid matrices) of the bread was extracted from all the 40 images, and 80% of the dataset was used for training and 20% for testing. Specifically, 6037 pores and 459 solid matrices were identified from the images. The different types of pores that can be found in a porous food structure include open, closed, and blind pores (McDonald and Sun 2001a, b; Halder et al. 2011); hence, for steamed bread microstructures, all the pores were classified as a class, and the solid matrices as another. Seven classifiers were used for the automatic classification of the two classes, and the geometrical descriptors were used for training in MATLAB. Detailed mathematical formulations of the classifiers, which include LDA, RTE, GNB, FT, QSVM, FKNN, and BTE can be found in the literature (Hastie et al. 2008; Richards and Xiuping 2013). The classifiers used in this study were selected based on the class imbalance nature of the dataset (i.e. 6037 pores and 459 solid matrices), and their superior performance as demonstrated in similar works (Pérez-Ortiz et al. 2016; Rahman et al. 2018c; Seiffert, et al. 2010). The discriminative ability of the best classifier was further evaluated using confusion matrix since it shows the relationship between the classifier outputs and the true ones, which could not be revealed using Wilk’s (\(\lambda \)) (Novakovic et al. 2017; Pieczywek and Zdunek 2012; Rahman et al. 2018c). Furthermore, a “step forward” analysis was used to identify key descriptors for classifying the pores and solid matrices (Pieczywek and Zdunek 2012). The classification accuracy of each classifier was calculated using the equation below:

$$ {\text{Accuracy}} = \frac{{{\text{TN}} + {\text{TP}}}}{{{\text{TN}} + {\text{TP}} + {\text{FN}} + {\text{FP}}}} $$
(17)

where \({\text{TN}}\), \({\text{TP}}\), \({\text{FN}}\), and \({\text{FP}}\) are the true negatives, true positives, false negatives, and false positives, respectively.

3.4 Voronoi Tessellation (VT)

Given a set of sites, \(S= \{{s}_{i}, ..., {s}_{n}\}\) in the 2D Euclidean plane, Voronoi territory (\(V ({s}_{i})\)) of the sites can be given as the partitioning of the plane having all points close to \(S_{i}\) as to any other site, which can be mathematically defined as

$$ V\left( {s_{{\text{i}}} } \right) = \left\{ {\left| {s_{{\text{i}}} - x} \right| \le \left| {s_{{\text{j}}} - x} \right|,\forall j \ne i} \right\} $$
(18)

The divisions into spaces by Voronoi tessellation are based on the number of points available. Also, the same number of points (centroids) in space in the actual cellular images was used for the random generation of the Voronoi diagrams. The Voronoi tessellation was developed using a MATLAB function called Voronoi. The schematic diagram of the microstructural reconstruction methods including the Voronoi and ellipse tessellation is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of reconstruction methods

Full size image

3.5 Ellipse Tessellation (ET)

The ellipse-fitting algorithm (Mebatsion et al. 2006b) was used for ellipse tessellation as given below

$$ F\left( {\text{x,y}} \right) = ax^{2} + bxy + cy^{2} + dx + ey + f $$
(19)

where the ellipse coordinates and coefficients are denoted by (x, y), and a, b, c, d, e, f, respectively. The algebraic distance between the two-point function is expressed by F(x, y). Also, the constraint of the ellipse constraint is

$$ b^{2} - 4ac < 0 $$
(20)

Rewriting Eq. (19) yields

$$ F\left( {a;x} \right) = ax $$
(21)

where \(a = \left[ {a,b,c,d,e,f,} \right]^{T}\) and \(x = \left[ {x^{2} , xy, y^{2} , x,y,1} \right]^{T}\), respectively, with T representing the transposed vector.

Ellipse fitting of a general conic involves the minimization of algebraic distance over the set of data points in the least square sense. To fit the data point (x, y), the least square fitting can be used as follows (Rahman et al. 2018c)

$$ \min {\text{mize}}\mathop \sum \limits_{i = 1}^{N} F(x_{i} ,y_{i} )^{2} = \min {\text{imize}} \mathop \sum \limits_{i = 1}^{N} (a,x_{i} )^{2} $$
(22)

To ensure an ellipse-specificity of the solution, the vector \(a\) can be arbitrarily scaled, and the constraint equation given below is most appropriate

$$ 4ac - b^{2} = 1 $$
(23)

Equation (23) can be expressed in matrix form as

$$ a^{T} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 2 \\ 0 & { - 1} & 0 \\ 2 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right]a = 1 $$
(24)

The pores centroid and area were numerically estimated using Eq. (22). The ellipse algorithm used the centroid, length of the major and minor axis, and orientation for the microstructural reconstruction (“Appendix”). Unlike plant-based food microstructures developments with no overlapping of cell sites (Mebatsion et al. 2006b; Rahman et al. 2018a), the ellipses representing the pores were directly fitted with most overlapping, since most bread structures are predominantly open pores with few closed pores, which also allows for easy network flow during transport modelling (Wang et al. 2011; Esveld et al. 2012). In addition, an ellipse was developed from a centroid as long as the data points belong to it; otherwise, the data points were used for other pores. For steamed bread, the gluten–starch solid matrices are mostly connected with irregular shapes; hence, the residual points were used to develop them. The above algorithm was implemented using MATLAB codes and terminated after all the data points in the microscopic images were calculated.

3.6 Image Processing

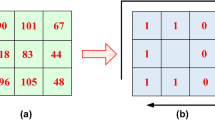
The post-processing of the images acquired from SEM was carried out in MATLAB (2019b, MathWorks, Natick, USA). The flowchart of the image processing is outlined in Fig. 1, including watershed segmentation, binarization, geometrical descriptor extraction, etc. The images were first segmented involving the discretization of the acquired images into different parts. The image intensities were used for marking discrete parts or regions from the background, and for more accurate pore boundary extraction, the watershed algorithm was used for segmentation (Brosnan and Sun 2002; Ng et al. 2006). Additionally, the points used for the watershed segmentation were obtained using the Pwdist function in MATLAB. From the grayscale images, the boundaries of the solid matrices and the pores were clearly distinct so that binarization based on a carefully selected threshold obtained by trial and error was sufficient enough to segment the pores from the solid matrices. However, the resulting image from the binarization process featured some noise, which was characterized by a typical salt and pepper noise. This noise was removed using the median filter. The extracted data were used for the reconstruction of the images with the ellipse and Voronoi algorithms. The reconstruction algorithms were selected due to their reputation for developing food microstructures with good accuracies (Abera et al. 2014; Rahman et al. 2018c). Moreover, the reconstructed microstructures were imported as a computational domain into COMSOL Multiphysics (v.5.5., COMSOL AB, Stockholm, Sweden) and meshed.

3.7 Statistical Validation and Analysis

The accuracy of the reconstructed microstructures was evaluated by comparison with the original microstructures using Kolmogorov–Smirnov (K–S) with a 5% level of significance, and all statistical analysis was carried out using MATLAB.

4 Result and Discussion

4.1 Steamed Bread Microstructural Features

To show the distributions of the bread microstructural features (pore and solid matrix) analysed in this study, two samples were randomly selected from the 40 images (Fig. 2). Boxplots were drawn to reveal the distributions of steamed bread microstructural features as shown in Fig. 3, and each plot consists of mean, minimum value, maximum value, upper and lower quartile and spacing between box lines. Generally, for the two samples presented, the solid matrices had higher mean values than the pores in terms of area, perimeter and convex area. For example, for sample 1, the mean areas of the pores and solid matrices were 1737 μm2 and 17,065 μm2, respectively, while for sample 2, those were 1031 μm2 and 1138 μm2, respectively, as shown in Fig. 3a and b. The marked difference between the mean areas of the solid matrices for both samples was due to their distribution as shown in Fig. 2. For sample 1, the mean circularities of the pores and solid matrices were 0.6587 and 0.2319, respectively, while for sample 2, those were 0.6233 and 0.5772, respectively, as shown in Fig. 3c and d. It can be inferred from the mean circularities and 2D pictorial images of the microstructures that the pores were more circular than solid matrices, as such, during reconstruction, only the pores were fitted while the residual data points were taken as solid matrices.

Fig. 2
figure 2

a Raw SEM image for sample 1, b denoised, segmented and binary image for sample 1 c Voronoi generated microstructure for sample 1, d ellipse generated microstructure for sample 1, e raw SEM image for sample 2, f denoised, segmented and binary image for sample 2, g Voronoi generated microstructure for sample 2, h ellipse generated microstructure for sample 2

Full size image
Fig. 3
figure 3

Area distribution of pores and solid matrix for a sample 1 and b sample 2, circularity distribution of pores and solid matrix for c sample 1 and d sample 2, orientation distribution of pores and solid matrix for e sample 1 and f sample 2, eccentricity distribution of pores and solid matrix for g sample 1 and h sample 2

Full size image

Orientation is also an important descriptor used to describe microstructural features (Pieczywek et al. 2011). For samples 1, the mean orientations of the pores and solid matrices were 43.4173 and 30.9401, respectively, while for sample 2, those were 44.9162 and 28.7213, respectively, as shown in Fig. 3e and f.

Therefore, descriptors such as areas, perimeter, convex area, circularity and orientation are important for classifying the pores and solid matrices, since there was consistent variation in the mean values between both classes, they could thus be used to automatically classify microstructural features, and to reconstruct steamed bread microstructures which serve as REV for microscale transport modelling. The mean eccentricities for both samples did not follow any trend; for example, the mean eccentricity of the pores was higher than that of the solid matrices for sample 1, and vice versa for sample 2 as shown in Fig. 3g and h, indicating that eccentricity might not be an important descriptor for classifying the pores and solid matrices.

4.2 Identification of Key Descriptors for Pores and Solid Matrix Classification

Although the descriptor’s mean value across bread microstructures provided some insights on potential descriptors for feature classification as discussed previously, it does not reveal their significance. The classification accuracies of the seven classifiers using all and individual geometrical descriptors are presented in Table 1. For all the descriptors, the most performed classifier was BTE with 98.40% accuracy, while the least performed was GNB with 92.10% accuracy. However, in some other studies involving the classification of fruit microstructures, LDA was adopted as the most suitable classifier (Pieczywek and Zdunek 2012; Rahman et al. 2018c). This might be attributed to the differences between bread and fruit microstructures, and specific ability of the respective classifiers in handling the microstructural features (Pérez-Ortiz et al. 2016). Furthermore, the average accuracy was 94.61% for all classifiers, and the geometrical features used were thus sufficient to classify the pores and solid matrices (Decost and Holm 2015). In addition, the accuracies of most classifiers with all descriptors used were higher than those obtained using individual descriptors as shown in Table 1, signifying that the use of more geometrical descriptors might increase the available information and classification accuracy.

Table 1 Results of binary classification between the pores and solid matrices using seven classifiers
Full size table

In terms of the individual descriptors, the area with an average accuracy of 91.53% for all classifiers had the most significant effect on the microstructural feature description. In addition, circularity performed quite well with most classifiers and had the highest accuracy (98.60%) among individual descriptors with the BTE classifier. However, the least accuracy of 7.90% was observed when circularity was used with the QSVM classifier (Table 1), which led to a reduction in its average classification accuracy (80.05%). Generally, this indicates that the type of classifier used affects the classification accuracy of a given descriptor (Seiffert et al. 2010). Particularly, QSVM is an extension of support vector machine that is specifically designed to separate data nonlinearly (Dagher 2008; Maheshwari et al. 2022). On the other hand, for a single descriptor, the solid matrix can be easily and effectively separated from the pore linearly, since the pore was more circular than the solid matrix (Sect. 4.1). However, QSVM separates the data of individual descriptors nonlinearly, which is hence the possible reason for the relatively lower performance observed with the QSVM classifier for most individual descriptors employed and especially for circularity. In addition, despite not following a specific trend, eccentricity with an average classification accuracy of 85.03% was quite significant. Moreover, other descriptors including centroid, orientation, perimeter and convex area with average classification accuracies of 88.04%, 88.39%, 88.89% and 85.69%, respectively, had a significant effect on classifying the pores and solid matrices (Table 1).

Since the classifiers using all descriptors had the highest average accuracy, a confusion matrix was used to have an in-depth understanding of their discriminative power as presented in Fig. 4. Figure 4a shows the description of the confusion matrix where negative (0) and positive (1) represent the pores and solid matrices, respectively. Although most of the classifiers provided high overall classification accuracy as shown in Table 1, their confusion matrices (Fig. 4b–h) show that most classifiers were biased as a large number of the solid matrices were misclassified due to class imbalance (Kumari and Kr. 2017; Pérez-Ortiz et al. 2016). For FT classifier, false negatives (FN) and false positives (FP) of 18.70% and 1.70% were obtained, respectively, as shown in Fig. 4b, implying that 18.70% of all the solid matrices were classified wrongly as pores, while only 1.70% of all the pores were classified wrongly as solid matrices. For LDA classifier, FN of 92.30% was realized as shown in Fig. 4c, meaning that 92.30% of all the solid matrices were wrongly classified, while all the pores were accurately classified. Although with a high accuracy of 93.50% (Table 1), LDA had the highest FN for the solid matrices likely due to its inability to handle the class imbalance between the pores and solid matrices in the bread microstructures (Pérez-Ortiz et al. 2016; Wang et al. 2011).

Fig. 4
figure 4

a Confusion matrix description, confusion matrix for b FT, c LDA, d GNB, e QSVM, f FKNN, g BTE, and h RTE

Full size image

For GNB classifier, FN and FP of 90.10% and 1.70% were obtained, respectively, as shown in Fig. 4d, implying that 90.10% of all the solid matrices were classified wrongly as pores, while only 1.70% of the pores were classified wrongly as solid matrices. On the other hand, for QSVM classifier, FN and FP of 67.00% and 0.10% were obtained, respectively, as shown in Fig. 4e, meaning that 67.00% of the solid matrices were classified wrongly as pores, while only 0.10% of the pores were classified wrongly as solid matrices. For FKNN classifier, FN and FP of 49.50% and 4.10% for solid matrices and pores were obtained, respectively, as shown in Fig. 4f, implying that 49.50% of all the solid matrices were classified wrongly as pores, while 4.10% of the pores were classified wrongly as solid matrices.

As the best performed classifier, BTE had FN and FP of 16.50% and 0.50% for solid matrices and pores, respectively, as shown in Fig. 4g, implying that 16.50% of all the solid matrices were classified wrongly as pores, while only 0.50% of the pores were classified wrongly as solid matrices. Besides having the highest accuracy (98.40%), BTE had the second least FN for solid matrices, and a very small FP (0.50%) for pores, hence, making it the most suitable classifier for bread microstructural feature classification. For the RTE classifier, FN and FP of 2.20% and 7.00% for solid matrices and pores were obtained, respectively, as shown in Fig. 4h, implying that 2.20% of all the solid matrices were classified wrongly as pores, while 7.00% of pores were classified wrongly as solid matrices. Moreover, RTE had the least FN (2.20%) for solid matrices, and its FP for pores was minimal. Therefore, the ensembles (BTE and RTE) were the best classifiers for classifying between both classes, primarily due to their adaptiveness in handling the problem of class imbalance associated with bread microstructural features (Galar et al. 2012; Kumari and Kr. 2017). Lastly, an increase in the dataset might increase the available information and classification accuracy.

Since the BTE was the most accurate classifier, a “step forward” analysis was used for identifying key descriptors (Pieczywek and Zdunek 2012). In the first step, convex area was excluded and its exclusion had no significant effects on the classifier’s accuracy (Table 2). In the next step, the removal of eccentricity led to an increase in the accuracy (Tables 2), implying that it was less significant to the classifier’s accuracy. In the third step, the removal of perimeter led to a decrease in accuracy, thus showing that perimeter was significant. Moreover, the highest accuracy of 98.80% was realized using five descriptors (circularity, area, centroid, orientation, and perimeter) as shown in Table 2. Furthermore, these five descriptors had higher classification accuracy than using all descriptors, implying that the addition of more descriptors might not necessarily increase the classification accuracy.

Table 2 Evaluation of key descriptors for feature classification using BTE
Full size table

4.3 Validation of Reconstructed Microstructures

Validation using actual microstructure provides a platform for accurate and real comparison with the developed microstructure and is much better than using a standardised microstructure (Rahman et al. 2018c). The randomly selected microstructures were used for validating the reconstructed counterpart. Figure 2 shows the images of the reconstructed microstructures and visual comparison showed that ellipse-fitted microstructures were more similar to the original images than Voronoi-fitted microstructures. This could be attributed to the use of more descriptors for the ellipse reconstruction than for Voronoi reconstruction (Rahman et al. 2018c). Specifically, the ellipse algorithm employed three descriptors (centroid, length of minor axis and major axis) (“Appendix”), while the Voronoi algorithm used only a single descriptor (centroid) for reconstruction. Moreover, in Voronoi-fitted microstructures, virtual equivalents of large pores bounded by small ones could not be generated (Pieczywek et al. 2011). In addition, a statistical comparison of the original and reconstructed microstructures was used to investigate the accuracy of the reconstructed microstructures. Figure 5a shows normal distributions of area for the SEM images, Voronoi and ellipse reconstructed microstructures for sample 1, and the distributions of ellipse reconstructed microstructure (p value = \(0.7948\)) were in better agreement with those of SEM images than Voronoi reconstructed microstructures (p value = 1.4554 × 10−5). Trends similar to those of area distributions for sample 1 were also observed for the normal distributions of the perimeter, eccentricity, and orientation of sample 1 as shown in Fig. 5b, c, e, respectively, and for all relevant normal distributions for sample 2. However, for both samples, the p value of circularity for the Voronoi reconstructed microstructure was higher than that of the ellipse reconstructed microstructure (Fig. 5d). Furthermore, to reveal the pores/solid matrices connectivity and distribution, meshed computational domains for both samples are shown in Fig. 6, and ellipse generated microstructures provided a better representation of steamed bread microstructures as compared with Voronoi generated microstructure. In addition, pores in ellipse generated microstructures were more open and well connected as depicted by the greyish mesh portions (Fig. 6b,d), compared with those in the Voronoi generated microstructures (Fig. 6a and c), thus, making the former similar to the pores in steamed bread, which are mostly open and interconnected as observed from micro-tomography experiment (Wang et al. 2011). In addition, the interconnected pores in the ellipse generated microstructures could also allow for accurate prediction of the transport properties during microscale and multiscale modelling. Finally, previous works on the development of fruit microstructures using both algorithms showed that the ellipse tessellation algorithm was superior to the Voronoi tessellation algorithm, which was in line with the current study (Mebatsion et al. 2006a, 2006b; Rahman et al. 2018c).

Fig. 5
figure 5

Comparison of normal distribution between microscopic images, Voronoi and ellipse generated microstructures for sample 1a area, b perimeter, c eccentricity, d circularity, e orientation

Full size image
Fig. 6
figure 6

Sample 1a Voronoi generated microstructural mesh, b ellipse generated microstructural mesh, sample 2c Voronoi generated microstructural mesh, d ellipse generated microstructural mesh

Full size image

5 Conclusions

A descriptor-based approach was used for the classification and reconstruction of steamed bread microstructures, and information obtained from the geometrical descriptors was sufficient for describing and reconstructing the pores and solid matrices. For the automatic classification using all descriptors, BTE with overall accuracy of 98.40% had the highest classification accuracy, while Gaussian Naïve Bayes was the least with 92.10% accuracy. In addition, the use of all geometrical descriptors provided better classifications as compared with using a single descriptor. On the other hand, from the step forward analysis, five descriptors namely circularity, area, centroid, orientation, and perimeter had higher overall accuracy than using all descriptors, implying that increase in descriptors might or might not increase the classification accuracy. Moreover, the ensembles (BTE and RTE) were better for classifying bread microstructures since they can handle the problem of class imbalance associated with its microstructural features. In addition, with the automatic classification, large number of images can be processed within a relatively short period of time. Furthermore, evaluating more descriptors beyond those used in the current work could increase information availability and classification accuracy of the microstructural features. Statistical validation of the two approaches with SEM images revealed that the ellipse reconstruction method was more accurate compared to the Voronoi reconstruction method. Also, pictorial evaluation of the reconstructed microstructures in the computational domain showed that the ellipse reconstruction method was more superior in representing the bread microstructural features, the ellipse generated steamed bread microstructures could thus be used as REV for microscale and multiscale numerical modelling of transport phenomena during the processing of steamed bread.