1 Introduction

Evaluation of geological formations as potential carbon capture and storage (CCS) reservoirs is of utmost importance for attempting to address the current global climate challenge. In order to offset the current global CO\(_{2}\) emissions estimated at 42.5 Gt per year (Friedlingstein et al. 2019) far greater effort is required in advancing CCS understanding and technology. The storage rate of all operational sites and those under construction was just 40 Mt per year at the close of 2019 (Page et al. 2019). CCS requires investing significant amounts of money in infrastructure with overall cost estimates exceeding 100 USD/t CO\(_{2}\) avoided in some cases (Metz et al. 2005; Rubin et al. 2015). Consequently, methods of assessing carbon security and capacity are required for industry and governments to make well-informed, environmentally worthwhile and financially viable decisions on CCS.

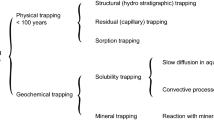
There are four key trapping processes which take place during CCS of varying security and on varying timescales. (i) Physical trapping occurs where an overlying low permeability layer, such as a shale, initially retains the buoyant injected fluid. This mechanism is vulnerable to breaching due to caprock failure or the presence of faults able to act as conduits (Song and Zhang 2013; Zhang and Song 2014; Abidoye et al. 2015). (ii) Capillary trapping results where the supercritical CO\(_2\) moves through the pore space and pockets of fluid may become trapped by formation water as ganglia (Blunt et al. 2013; Boot-Handford et al. 2014; Zhang and Song 2014). (iii) Solubility trapping occurs where the CO\(_2\) phase mixes and dissolves into the formation water forming a denser carbonic acid phase. This fluid phase is able to sink to the bottom of the formation (Ghesmat et al. 2011; Zhang and Song 2014; Unwin et al. 2016; Sun et al. 2020), trapping it. However, fluid pathways such as faults and degraded borehole walls can still act as conduits for leakage. (iv) Mineral trapping (MT) is the most secure method in which subsurface carbon may be stored, as a thermodynamically stable solid mineral phase. Introduction of the CO\(_{2}\) phase creates an acidic environment which causes hydrolysis of host silicate minerals and liberation of cations. These cations then react with carbonate ions in the fluid phase and form solid precipitates such as calcite, magnesite and ankerite (Ghesmat et al. 2011; Zhang and Song 2014; Zhang et al. 2015; Zhang and DePaolo 2017), storing carbon securely for geologically significant periods of time (Zhang and Song 2014). Mineral trapping becomes the most significant storage process with time (Zhang and DePaolo 2017) post-injection and so we focus on this process in this article.

It is the consensus that there are enough potential storage reservoirs globally to achieve the huge volumes of CO\(_{2}\) storage of over 1 Gt/year by 2040 to meet global targets (Page et al. 2019). For any of these reservoir candidates to be suitable for GCS, there are three key characteristics which are required; (i) significant porosity to accommodate CO\(_{2}\), (ii) suitably high permeability to allow injected fluid to move effectively through the reservoir and (iii) suitable mineralogy which can provide cations to form stable carbonate minerals.

Suitable mineralogy is a key component of making MT viable and is directly linked with the reaction parameters within a system. We aim to investigate how changes in these parameters impact the ability for carbon mineralisation to take place. We present a numerical model which achieves this by varying the Damköhler number which incorporates a reaction term. This is a popular approach used to study the impact of a range of reaction rates where a specific value is not certain (Ghesmat et al. 2011; Pec et al. 2015; Menke et al. 2017; Dashtian et al. 2019; Sun et al. 2020).

The geochemical system of a CCS reservoir has many layers of complexity (Xu et al. 2004; Hangx 2005; Audigane et al. 2007; Labus and Bujok 2011) which we have chosen to simplify in order to focus on the precipitation of one carbonate mineral alone, calcite. Calcite may be formed alongside kaolinite when anorthite reacts with carbonated fluid, offering one pathway through which to sequester carbon as a solid (Ghesmat et al. 2011).

Whilst many numerical modelling investigations have been made into the mineral dissolution process at the pore scale, far fewer have addressed precipitation. Valuable models have been built, describing the complex chemical and physical processes behind mineral dissolution (Molins et al. 2012, 2014; Nunes et al. 2016; Gray et al. 2016), and in particular the phenomenon of wormholing (Starchenko and Ladd 2018). In many cases, these studies are supported by experimental results or high resolution 3D imaging.

The work of Yoon et al. (2012) and Fazeli et al. (2020) show how further complex processes such as the accurate description of nucleation require consideration to describe mineral precipitation. Such factors introduce many unknowns and therefore, uncertainty (Noiriel and Soulaine 2021). These models are applied to simplified or 2D physical domains which fail to provide insight into the impact and distribution of mineral precipitation in true pore geometries in 3D. Therefore, in this article we demonstrate a simplified advection–diffusion–reaction direct numerical model for describing CaCO\(_{3}\) precipitation at the fluid–solid interface in a true 3D pore geometry.

Using the popular technique of X-ray micro-computed tomography (\(\upmu\)CT) for digital image analysis of geological material (Blunt et al. 2013; Mostaghimi et al. 2013; Jiang and Tsuji 2014; Bultreys et al. 2015, 2016; Singh et al. 2017; Hertel et al. 2018; Thomson et al. 2018, 2019, 2020; Payton et al. 2021; Shams et al. 2021), we are able to explore possible CCS reservoir rocks at appropriate resolutions for examining the intricacies of the pore space geometries. We present a method of using these high resolution images, reconstructed in 3D, as physical domains for numerical flow modelling to take place in.

In addition to investigating the influence of reaction parameters we aim to use this model to investigate if further geophysical properties contribute significantly to the effectiveness of artificially driven mineral precipitation in a subsurface reservoir. Tortuosity is one characteristic of interest due to its close relationship with porosity (Zhang and Knackstedt 1995; de Lima and Niwas 2000; Pape et al. 2000; Ghanbarian et al. 2013; Berg and Held 2016) and influence on permeability (de Lima and Niwas 2000; Gouze and Luquot 2011; Berg 2014; Cai et al. 2019). While the impact of precipitation on tortuosity has been investigated (Xie et al. 2015; Tsuji et al. 2019) understanding of the influence of tortuosity on precipitation is lacking.

In order to deduce the viability of MT in a given geological formation, it is necessary to investigate the carbonate precipitation process at the pore scale and over time periods which are relevant for the slow reaction rates involved in the system (Espinoza et al. 2011; Ghesmat et al. 2011). Experimental work on core flooding and associated chemical reactions is in practice limited to short time scales of days to months (Perrin et al. 2009; Labus and Bujok 2011; Edlmann et al. 2013; Phillips et al. 2013; Yoo et al. 2013; Wei et al. 2014; Zhao et al. 2015; Menke et al. 2016; Mouzakis et al. 2016), which is not consistent with MT taking place on the hundreds to thousands of years post-injection time scale. Artificial conditions are imposed to accelerate the process however, using reservoir conditions is desirable. We also see similarly short simulation times in numerical modelling studies with a focus on the many chemical reactions taking place (Kang et al. 2006, 2010; Jiang and Tsuji 2014) at the expense of a detailed representation of the pore geometry and flow conditions. Sigfusson et al. (2015) and Snæbjörnsdóttir et al. (2020) comment that MT becomes a more prominent carbon sequestering process with time, showing significantly more mineralisation from around 100 years after injection. This highlights the importance of geologically significant simulation durations.

In this article, we use finite element discretisation to solve the coupled advection–diffusion–reaction equations over a domain generated from a variety of sandstone samples. We examine the effect of pore geometry and chemical reactivity on carbon mineralisation post-injection. This is achieved under natural reservoir flow conditions over periods of time up to 2000 years, providing insight on the natural pore scale mineralisation process over time scales far greater than what is typically possible in an experimental laboratory set up.

2 Methods

We acquired X-ray CT images from a variety of sandstone reservoir units which include the Brae Formation sandstone (BFS), Wilmslow Sandstone Formation (WSF), Porcupine Basin (PB) Minard Formation sandstone and Fontainebleau Sandstone (FBS). With the exception of the FBS, images were acquired from 5 mm diameter core plugs extracted from core material and imaged using a Zeiss Xradia Versa 520 \(\upmu\)CT scanner at the London Natural History Museum Image Analysis Centre (Thomson et al. 2020; Payton et al. 2021). The FBS sample was imaged by Madonna et al. (2013) using synchrotron X-ray CT. Further details of the samples used in this study are given in Table 1.

Table 1 Details of samples used for simulation
Full size table

Thomson et al. (2020) and Payton et al. (2021) show that the Brae and Wilmslow sandstones may be of interest for subsurface carbon storage owing to their favourable geophysical properties such as significant connected porosity and permeability. The material from the Porcupine Basin, pertaining to the Minard Formation, has been explored previously as a hydrocarbon reservoir (Croker and Shannon 1987; MacDonald et al. 1987; Rensbergen et al. 2007) but was not deemed economically viable. We understand that there is still significant porosity and permeability in this unit (Croker and Shannon 1987; MacDonald et al. 1987; Rensbergen et al. 2007) and therefore it could have merit for consideration for GCS. The Fontainebleau Sandstone has a distinct and unusual pore structure, which is widely studied (Bourbie and Zinszner 1985; Lindquist et al. 2000; Youssef et al. 2007; Madonna et al. 2013; Revil et al. 2014; Thomson et al. 2018); therefore, we chose to include this sample due to the sharp nature of the pore geometry in our investigation of pore structure influence on precipitation.

2.1 X-ray Computed Tomography Meshing

The CT images obtained were digitally stitched together to produce a 3D volume of the cylindrical sample. One larger 1320 \(\upmu\)m\(^{3}\) subvolume was digitally extracted from the Brae sandstone sample on which simulations to investigate the influence of reaction parameters on precipitation were performed. For all four materials three smaller subvolumes of 500, 375 and 250 \(\upmu\)m\(^{3}\) were digitally extracted. Three sample volumes of each size were chosen randomly, totalling nine samples for each material. These smaller samples were used to investigate the influence of pore geometry on precipitation. All samples were then processed according to the following methodology.

2.1.1 Segmentation

Using ORS Dragonfly (Linux v4.1.0) segmentation of the pore space phase was carried out as depicted in Fig. 1a. Segmentation is the process by which different phases within a \(\upmu\)CT image are identified and labelled based upon differences in greyscale intensity which are proportional to the X-ray attenuation. Each material possesses a different linear attenuation coefficient, primarily based on density, which means that X-rays are attenuated variably by each phase. Brighter phases represent greater attenuation by typically denser phases whilst darker phases represent the opposite. In this case, the pore space is the darkest phase and solid materials are seen as brighter greys and white. To eliminate user bias in the segmentation process, we used the automatic phase segmentation algorithm designed by Otsu (1979). This performs a binary segmentation of the sample based on the range of greyscale intensities, distinguishing the pore space from the solid phases.

2.1.2 Extracting Connected Porosity

Next, we extracted only the connected porosity along the X axis using ORS Dragonfly, shown in green in Fig. 1b. We set markers on the minimum and maximum X axis images and executed the ‘keep intersected’ Boolean operation on the two markers and the segmented pore space phase. This isolates the pore space which connects the two markers, removing any which is disconnected, shown in purple in Fig. 1b. We used the ‘isolate (6 connected) nth first biggest’ tool on the connected porosity mask to remove any isolated islands of porosity which may have escaped the lower tolerance of the ‘keep intersected’ operation.

2.1.3 3D Surface Meshing

We then generated a 3D surface mesh using the contour mesh tool in ORS Dragonfly. The mesh underwent one iteration of Laplacian smoothing in order to reduce some of the sharp edges which can cause issues at the numerical modelling stage, shown in Fig. 1c. The voxel sampling frequency was chosen to try and find a suitable trade-off between accuracy of the mesh geometry and the computational cost of the simulation. Whilst a small amount of shrinkage occurs as a result of smoothing, this results in minimal uncertainty in the model output as just a small area of reactive surface is lost. Furthermore, the impact on tortuosity is minimal due to tortuosity being calculated using the centre of channels whereas smoothing targets the outer region of the channels.

2.1.4 Mesh Domain Labelling

We transferred the mesh in STL format to the software package Blender (Linux v2.81) in order to label the mesh domains shown in Fig. 1d. Any disconnected pore space created in the meshing process was removed using the inbuilt ‘separate’ function in the Blender Python console. Cells on the extreme planes of the X axis were allocated to separate submeshes or domains, shown as orange cells in Fig. 1d. This resulted in three submeshes representative of the inflow plane, outflow plane and the internal pore walls.

2.1.5 3D Volume Meshing

We exported these three submeshes to enGrid (Linux v1.2) in BEGC format in order to assign each submesh a unique callable identifier. Upon import, the order of the submeshes in the Blender object panel determined the numerical identifier assigned to each submesh from an index of 0. We employed the mesh generator NETGEN, hosted in enGrid, to build a tetrahedral volume mesh which respects the submesh labelling. The resulting volume mesh is shown in Fig. 1e.

2.1.6 Optimisation for Simulations

Next, we exported the labelled mesh using the ‘Gmsh (ASCII 2.0)’ option in MSH format. This file format is compatible with the dolfin library of FEniCS, the software used for numerical modelling. We used the dolfin-convert tool provided in FEniCS (Linux Ubuntu 2017.2.0) to obtain a labelled 3D volume mesh in XML format. Finally, to support reading of the mesh file in parallel by FEniCS the file was converted using a Python script to HDF5 format.

Fig. 1
figure 1

Step-by-step overview of the \(\upmu\)CT processing technique to arrive at a 3D volume mesh. (a) A 2D CT slice where the left half of the square shows the unsegmented raw image and the right half shows pore space segmented in green. (b) A 3D rendering of the connected (green) and disconnected (purple) porosity in the sample. (c) The result of using the Laplacian smoothing filter is shown where sharp angles which may cause issues during simulations are smoothed. (d) Boundary labelling in Blender of the inflow points shown in orange. (e) The final volume mesh in full on the left with a section shown on the right to reveal the internal volume mesh elements

Full size image

The resulting mesh file can be read in to FEniCS and used as the physical domain over which a set of governing PDEs may be solved to simulate fluid flow, described in Sect. 2.3. The labelling of the submeshes allows for boundary and initial conditions to be easily prescribed using the label number in a simple function as an argument. We refer the reader to the source code hosted in the Royal Holloway Figshare repository to see the implementation within our Python script.

2.2 Microstructure Characterisation

In order to characterise the extracted pore structures of the smaller volumes we imported the segmented images from ORS Dragonfly into the commercial digital rock physics package PerGeos (1.7.0). We used the ‘centroid path tortuosity’ tool to calculate a tortuosity value for each sampled subvolume. We also made measurements of pore volume by integrating over the domain and pore surface area using the open source tool FEMorph for FEniCS written by Schmidt (2018). Whilst voxelised images are known to result in over estimation of surface area due to the sawtooth pattern effect (Fei and Narsilio 2020), we suggest that our use of a smoothing algorithm minimises this effect in our measurements.

2.3 Numerical Methods

We built a numerical model, modified after Hier-Majumder (2020), using the Finite Elements method to describe the processes of advection and diffusion in a carbonic acid phase which is also reacting with a solid calcium-bearing anorthite phase to form a CaCO\(_{3}\) precipitate. We ran a series of simulations lasting for a duration of 300 seconds (short) and 2000 years (long) of simulated time. This allowed us to explore the effect of different reactivity regimes on both the physical flow characteristics at the pore scale and carbon production over geologically significant time periods. In both the short and long simulation cases, each simulation was split in to 100 timesteps; therefore, the simulated duration of each timestep is 20 years in the long simulations and 3 seconds in the short simulations. Each simulation took between 5 and 24 hours to run, depending on the complexity of the mesh geometry, on a workstation using 12 VCPUs. For further details on the simulation hardware please see the Supplementary Information.

The flow characteristics are described by the governing equations of the model, imposed on a 3D \(\upmu\)CT mesh, illustrated schematically in Fig. 2.

Fig. 2
figure 2

Schematic representation of the boundary conditions and initial conditions used in this study. The fluid inflow points are shown in green and the outflow points in red. The solid black line represents the pore space walls and the grey the volume of the pore space

Full size image

2.3.1 Model Assumptions

We assume that the initial critical step of CO\(_{2}\) dissolution into the formation water to form bicarbonate ions according to:

$$\begin{aligned} \hbox {sCO}_{2} + \mathrm{H}_{2}\mathrm{O}_{(l)} \rightleftharpoons \hbox {H}^{+}_{\mathrm{(aq)}} + \hbox {HCO}_{3} {}^{{-}} {}_{\mathrm{(aq)}} \end{aligned}$$
(1)

has already occurred at the start of our simulations. The chemical processes that we then model are as follows:

$$\begin{aligned} \hbox {CaAl}_{2}\hbox {Si}_{2}\hbox {O}_{8\mathrm{(s)}} + 8\hbox {H}^{+}_{\mathrm{(aq)}} \rightleftharpoons \hbox {Ca}^{2+}_{\mathrm{(aq)}} + 2\hbox {Al}^{3+}_{\mathrm{(aq)}} + 2\hbox {H}_{4}\hbox {SiO}_{4\mathrm{(aq)}} \end{aligned}$$
(2)
$$\begin{aligned} 2\hbox {Al}^{3+}_{\mathrm{(aq)}} + 2\hbox {H}_{4}\hbox {SiO}_{4\mathrm{(aq)}} + \hbox {H}_{2}\hbox {O}_{\mathrm{(l)}} \rightleftharpoons \hbox {Al}_{2}\hbox {Si}_{2}\hbox {O}5\hbox {(OH)}_{4\mathrm{(s)}} + 6\hbox {H}^{+}_{\mathrm{(aq)}} \end{aligned}$$
(3)
$$\begin{aligned} \hbox {Ca}^{2+}_{\mathrm{(aq)}} + \hbox {HCO}_{3} {}^{-} {}_{\mathrm{(aq)}} \rightleftharpoons \hbox {CaCO}_{3\mathrm{(s)}} + \hbox {H}^{+}_{\mathrm{(aq)}} \end{aligned}$$
(4)

We chose to simplify the geochemical system which may be expected to be present in a typical siliciclastic CO\(_{2}\) storage reservoir to only consider the most common set of aluminosilicate reactions (Ghesmat et al. 2011; Zhang and Song 2014), described by equations 2–4. Each of these reaction stages occur at different rates, which we account for in a single combined reaction term in our governing equations.

Our second key assumption is that the resulting precipitated CaCO\(_{3}\) has no significant impact on the pore structure in terms of porosity and pore geometry. Digital image analysis studies suggest that when cement volume fraction is less than 3-5% that no significant change to porosity or permeability are observed (Thomson et al. 2019, 2020). In the case of our model, we find that there is less than 0.02% by volume of CaCO\(_{3}\) precipitating in the most extreme simulated case, giving validity to this assumption.

Additionally, as is done by Sun et al. (2020), we ignore other possible reactions between the H\(_{2}\)CO\(_{3}\) rich fluid and CaCO\(_{3}\) and the slower reactions between the fluid and quartz (Espinoza et al. 2011). This allows us to assume that the pH level of the pore fluid is buffered and therefore, saturated with CaCO\(_{3}\). As determined by Sun et al. (2020) from Snæbjörnsdóttir et al. (2017) the fluid reaches CaCO\(_{3}\) saturation relatively rapidly given the large time scale of our simulations.

Finally, we make the assumption that the mass fraction of anorthite remains constant at the solid–fluid interface for the duration of our simulations. We assume that the amount of available An in the matrix far exceeds what may be consumed by the reaction process over the duration of the simulations. This would especially be the case in a volcanogenic sandstone, for example, where there is an abundance of reactive silicate minerals (Zhang et al. 2015; Zhang and DePaolo 2017).

2.3.2 Governing Equations and Boundary Conditions

A more detailed set of dimensional equations, the non-dimensionalisation scheme and further details of the numerical approach are provided in the Supplementary Material. For conciseness we show here the final dimensionless equations, of which the components are described in Table 2. All non-dimensional terms are indicated with an asterisk (*). In this case the fluid velocity, \(\varvec{u}^*\), is governed by Stokes flow,

$$\begin{aligned} {\nabla }^{*2} \varvec{u}^{*} - \varvec{\nabla }^{*} p^{*} = 0, \end{aligned}$$
(5)

where \(p^{*}\) is pressure and the fluid velocity is nondivergent,

$$\begin{aligned} \varvec{\nabla }^{*} \cdot \varvec{u}^{*}= 0. \end{aligned}$$
(6)

The rate of transport of dissolved carbonate in the pore fluid, \(C_{A}\), is controlled by advection, diffusion and reaction according to,

$$\begin{aligned} \frac{\partial C_{A}}{\partial t^*} + \varvec{u}^* \cdot \varvec{\nabla }^* \, C_{A} - \frac{1}{\mathcal {P}e} \, \cdot \nabla ^{*2} \, C_{A}= - \alpha _{A} \mathcal {D}a \, \Gamma^{*} \, C_{A} \, C_{B} , \end{aligned}$$
(7)

whilst the rate of consumption of anorthite, \(C_{B}\), and the rate of production of CaCO\(_{3}\), \(C_{C}\), are governed by reaction alone,

$$\begin{aligned} \frac{\partial C_{B}}{\partial t^*}= - \alpha _{B} \mathcal {D}a \Gamma^* \, C_{A} \, C_{B}, \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial C_{C}}{\partial t^*}= \alpha _{C} \mathcal {D}a \Gamma^* \, C_{A} \, C_{B} . \end{aligned}$$
(9)

In each case \(\Gamma^*\) is the rate of reaction which is weighted by the respective species, \(\alpha _{i}\). The dimensionless components are defined by,

$$\begin{aligned} \quad \mathcal {P}e = \frac{L\, u_{0}}{D}, \quad \mathcal {D}a = \frac{L\,\Gamma_{0}}{u_{0}}, \end{aligned}$$
(10)

where L is the length of the domain, \(u_{0}\) is fluid velocity, D is the diffusivity and \(\Gamma_{0}\) is the rate of chemical reaction.

Table 2 Non-dimensional numbers and dimensional constants used for the smaller volume pore structures investigating the influence of pore geometry on precipitation in this article
Full size table

The governing equations were solved within the constraints of the prescribed Dirichlet boundary conditions and initial conditions which are illustrated schematically in Fig. 2. The domain may be described by,

$$\begin{aligned} \varOmega \subset \mathbb {R}^{\mathrm {d}}, 1 \le \mathrm {d} \le 3, \end{aligned}$$
(11)

on which we imposed the following boundary conditions,

$$\begin{aligned} \varvec{u}^*= 0 \, \, \mathrm {on} \, \, \partial \varOmega _{w} \end{aligned}$$
(12)
$$\begin{aligned} \varvec{u}^*= \frac{Q}{A} \, \, \mathrm {on} \, \, \partial \varOmega _{i} \end{aligned}$$
(13)
$$\begin{aligned} C_{A}= 0.025 \, \, \mathrm {on} \, \, \partial \varOmega _{i}, \end{aligned}$$
(14)

where Q is the representative volumetric flow rate equal to \(1\times 10^{-15}\) m\(^{3}\) s\(^{-1}\) and A is the inlet boundary surface area. \(\varOmega _{w}\) and \(\varOmega _{i}\) are representative of the internal walls of the domain and the inflow along the X-min plane, respectively. In the cases of the smaller subvolume simulations, it was necessary to ensure that the volumetric flow rate of reactant over the inlet boundary was equal in all simulations and so the required inlet velocity was set accordingly in each case. In contrast, simulations run on the larger BFS2 mesh used the representative pore fluid velocity (Table 2) and so, \(\varvec{u}^* = 1\) on \(\varOmega _{i}\). The following initial conditions were prescribed,

$$\begin{aligned} C_{A}(x, y, z, 0) = 0, C_{B}(x, y, z, 0) = [\mathrm {An}], \varvec{u}^*(x, y, z, 0) = 0, \end{aligned}$$
(15)

where [An] is a constant representing the molar mass fraction of anorthite which is varied between simulation cases.

2.3.3 Outputs and Redimensionalisation

We calculated pore space volume, total mass fraction of CaCO\(_{3}\) precipitated, the spatial average precipitated CaCO\(_{3}\) and the precipitation rate of CaCO\(_{3}\) over the course of the simulation. In order for us to derive results from our model which are comparable to real world quantities we must dimensionalise these outputs. The calculation for the output and the subsequent dimensionalisations are as follows. Terms with an asterisk are considered nondimensional.

The time output is dimensionalised as follows:

$$\begin{aligned} T = t_{0} \,\, T^{*} \end{aligned}$$
(16)

to obtain a value in seconds where T is time and \(t_{0}\) is the characteristic time given by \(\frac{L}{\varvec{u}}\). Volume is calculated and then dimensionalised according to:

$$\begin{aligned} V^{*}= \int _{}{1 \,\, dv^*} \end{aligned}$$
(17)
$$\begin{aligned} V=V_{0} \,\, V^{*}, \end{aligned}$$
(18)

where V is volume and \(V_{0}\) is the characteristic volume in cubic microns. To dimensionalise precipitate masses we must calculate a mass of the total pore space as our results are given as mass fractions. We assume the pore space to be filled entirely with water with a density of 997 kg m\(^{-3}\) (\(\rho _{w}\)) and use the pore volume, V in m\(^{3}\) to calculate the pore space mass (\(M_{ps}\)) in micrograms accordingly,

$$\begin{aligned} M_{ps} = \rho _{w} \,\, V \times 10^{9}. \end{aligned}$$
(19)

We calculate total CaCO\(_{3}\) precipitated at the end of the simulation by integrating the mass fraction over the volume at the final time step according to:

$$\begin{aligned} CaCO_{3 \,\, tot}^{*}= \int _{}{C_{C} \,\, dv^*} \end{aligned}$$
(20)
$$\begin{aligned} CaCO_{3 \,\, tot}= CaCO_{3 \,\, tot}^{*} \,\, M_{ps}, \end{aligned}$$
(21)

where \(CaCO_{3 \,\, tot}^{*}\) is the total mass fraction of CaCO\(_{3}\) at the final time step, \(C_{C}\) is the mass fraction of CaCO\(_{3}\), \(CaCO_{3 \,\, tot}\) is the total CaCO\(_{3}\) precipitated in micrograms. We calculate the spatial average mass fraction of CaCO\(_{3}\) precipitated, \(CaCO_{3 \,\, avg}^{*}\) at each time step according to:

$$\begin{aligned} CaCO_{3 \,\, avg}^{*}= \frac{\int _{}{C_{C} \, \, dv^*}}{\int _{}{1 \, \, dv^*}} \end{aligned}$$
(22)
$$\begin{aligned} CaCO_{3 \,\, avg}= CaCO_{3 \,\, avg}^{*} \, \, M_{ps}. \end{aligned}$$
(23)

We calculated the CaCO\(_{3}\) precipitation rate, \(CaCO_{3 \,\, pptrate}^{*}\) and dimensionalise the result in micrograms per year according to:

$$\begin{aligned} CaCO_{3 \,\, pptrate}^{*}= \int _{}{CaCO_{3 \,\, frac} \,\, \mathcal {D}a \,\, C_{A} \,\, C_{B} \,\, C_{C} \,\, dv^*} \end{aligned}$$
(24)
$$\begin{aligned} CaCO_{3 \,\, pptrate}= \frac{CaCO_{3 \,\, pptrate}^{*} \,\, M_{ps}}{T}, \end{aligned}$$
(25)

where \(CaCO_{3 \,\, frac}\) is the molar mass fraction of CaCO\(_{3}\) in the reaction scheme, \(\mathcal {D}a\) is the Damköhler number and \(C_{A}\), \(C_{B}\) and \(C_{C}\) are the mass fractions of H\(_{2}\)CO\(_{3}\), An and CaCO\(_{3}\), respectively. A value for dimensional precipitation rate (\(CaCO_{3\,\, pptrate}\)) is obtained at each time step.

3 Results

3.1 Short Simulations—Flow Characterisation

The velocity map in Fig. 3 shows clear spatial variation throughout the pore network. Despite all of the pore structure being connected, there is a large disparity in fluid velocity between the central region and the distal more intricate parts of the pore space, varying by up to four orders of magnitude. The prescribed boundary condition for velocity on the inflow face is 1\(\times\)10\(^{-7}\) m s\(^{-1}\) showing that in some areas the fluid velocity reduces from the inflow condition by two orders of magnitude whilst in others it increases by two orders of magnitude only influenced by the pore geometry.

The central core of the structure shows a high fluid velocity pathway, isolating the extremities of the structure from flow. In the high velocity pathway, velocity peaks at bottlenecks where narrower throats connect larger pores. It is clear that the dominant flow path is from the central region at the inflow up towards the top region on the outflow face. Darker flow lines in the upper and lower central regions as well as in the more isolated regions of the pore structure towards the outflow indicate significantly lower fluid velocities. These areas are clearly separated from the bulk of the pore structure and receive far less fluid movement despite offering a fully connected pathway to the outflow points.

Fig. 3
figure 3

Velocity map through the entire BFS2 sample with flow from left to right. The pore structure is shown as opaque with flow velocity lines in full colour. Brighter colours represent greater fluid velocity and darker colours low fluid velocity on a logarithmic scale. A brighter high velocity path is clearly defined through the central region of the pore structure, moving upwards towards the outflow points. The lower right corner and upper areas show far lower fluid velocities, around two orders of magnitude lower than in the main channel, leaving them relatively isolated and deprived of flow. All velocity values are calculated where \(\mathcal {D}\)a = 1\(\times\)10\(^{-8}\) and \(\mathcal {P}\)e = 4.3\(\times\)10\(^{-2}\)

Full size image

The spatial variation in presence of precipitated CaCO\(_{3}\) over time, shown in Fig. 4, demonstrates a close relationship to the velocity map in Fig. 3. From 12 to 108 seconds, it is apparent that precipitation occurs predominantly around the inflow area with minor precipitation observed towards the centre of the pore structure, indicated by the paler colours in Fig. 4. The extremities of the structure to the lower right and upper left contain no precipitate at this point.

Upon reaching 297 seconds the majority of the pore structure possesses a significant precipitate mass fraction with the notable exception of the lower right and upper left regions. The central area of the structure is clearly shown to be the preferential pathway of fluid flow and consequently hosts the main reaction sites. At this point the spatial variation in precipitation bares a strong resemblance to the velocity map in Fig. 3. Despite the pore structure maintaining full connectivity there are some regions, also with the lowest fluid velocity, which are deprived of precipitation. As the central region is clearly favoured for precipitation this increases the chance of the pore structure’s extremities being sealed off by CaCO\(_{3}\) precipitation, reducing overall storage capacity.

Fig. 4
figure 4

Mass fraction maps of precipitated CaCO\(_{3}\) throughout the entire BFS2 sample at three different simulation times. A central area of greater precipitation is observed which reaches an outflow point by the final time step. A substantial portion of the pore structure is deprived of any precipitation at 108 seconds and even at 297 seconds. These low precipitation regions correlate very well with the observed low fluid velocity regions. At 108 seconds, we see some diffusive nature at the propagation front, however, generally the front is advection dominated, shown by the large CaCO\(_{3}\) mass fraction gradient at the front as reactant is pushed through. Time is given in seconds whereas CaCO\(_{3}\) mass fraction is nondimensional, calculated where \(\mathcal {D}\)a = 1\(\times\)10\(^{-8}\), \(\mathcal {P}\)e = 4.3\(\times\)10\(^{-2}\) and An = 10%

Full size image

An area of fluid flow deprived pore space in the upper central region shows that throat radius is an important limiting factor in fluid movement, highlighted in Fig. 5. At the early onset of fluid flow at 12 seconds, a high concentration of CaCO\(_{3}\) can be seen moving from right to left into the extremities of the pore space. However, at 12 seconds, there is no change in mass fraction of CaCO\(_{3}\) at the dead end of the pore structure. Two narrow throats can be seen with a very sharp gradient of CaCO\(_{3}\) across them at both 12 and 36 seconds, suggesting that the throat is inhibiting movement of the reactive fluid and subsequent precipitation. At 108 seconds, there is an increase in CaCO\(_{3}\) towards the dead end space, gradually increasing up until 297 seconds.

It is clear in Fig. 5 that the narrow pore throats in this particular part of the structure are causing a reduction in the extent of the fluid flow. The two pore throats measure 10 and 25 \(\upmu\)m in diameter. Similar throat diameters can be measured in other regions deprived of CaCO\(_{3}\) in the latter stages of the simulation, also corresponding with areas of low pore fluid velocity in Fig. 3. The combination of narrow throats, low velocity and high precipitation build up upstream of the throat is a favourable environment for sealing of the fluid pathway with CaCO\(_{3}\). This means that cumulatively significant volumes of the pore structure could become disconnected, ultimately reducing the overall capacity for mineralised carbon storage in a given material.

Fig. 5
figure 5

Mass fraction maps of precipitated CaCO\(_{3}\) throughout a BFS2 subsample at four different simulation times. The subsampled volume is shown in dark red as a portion of the whole sample seen in Fig. 4. We observe at 12 seconds a large mass fraction of CaCO\(_{3}\) building up behind two narrow pore throats, measuring 10 and 25 \(\upmu\)m in diameter. Between 12 and 36 seconds CaCO\(_{3}\) is able to form on the other side of the throats as the reaction front breaks through, allowing substantial precipitation by 297 seconds. This shows the effect of narrow pore throats on the reaction front, hindering the precipitation reaction. These narrow throats are likely to clog up with precipitate and cut off pore space from the connected network, reducing total precipitation and storage capacity. Time is given in seconds whereas CaCO\(_{3}\) mass fraction is nondimensional, calculated, where \(\mathcal {D}\)a = 1\(\times\)10\(^{-8}\), \(\mathcal {P}\)e = 4.3\(\times\)10\(^{-2}\) and An = 10%

Full size image

A greater \(\mathcal {D}\)a number results in substantial increases in CaCO\(_{3}\) precipitation by the end of the simulation period, shown in Fig. 6. The three scenarios illustrated in Fig. 6 show three values of \(\mathcal {D}\)a increasing by an order of magnitude from 1\(\times \, 10^{-9}\). There is a significant difference in the volume of the pore structure which is observed to host precipitated CaCO\(_{3}\) by the end of the simulation period. The spatial occurrence of greatest precipitation mirrors the position of the greatest flow velocity pathways in Fig. 3 regardless of the \(\mathcal{D}\)a number.

Fig. 6
figure 6

Mass fraction maps of precipitated CaCO\(_{3}\) throughout the entire BFS2 sample with three different Damköhler numbers each at 297 seconds. As the value of \(\mathcal {D}\)a increases more of the domain reaches a greater quantity of precipitate, including in the extremities of the pore structure. All values are nondimensional, calculated where \(\mathcal {P}\)e = 4.3\(\times\)10\(^{-2}\) and An = 10%

Full size image

A greater amount of anorthite results in a small increase in CaCO\(_{3}\) precipitation throughout the simulation, culminating in the final result at 297 seconds seen in Fig. 7. As the anorthite mass fraction increases from 5 to 15% the CaCO\(_{3}\) mass fraction, most notably at the reaction front, increases. This is most apparent in the main flow channel, highlighted in Fig. 3, with the extremities of the pore structure showing far less change in the lower right and upper left regions. This indicates that by increasing the amount of anorthite present a greater amount of precipitation is facilitated but with greatest effect on areas where precipitation was already readily occurring.

Fig. 7
figure 7

Mass fraction maps of precipitated CaCO\(_{3}\) throughout the entire BFS2 sample with three different anorthite mass fractions each at 297 seconds. We see when looking at the areas where the reaction front is present different intensities of CaCO\(_{3}\) precipitation in each case of anorthite fraction. At 5% anorthite, there is a weaker gradient across the reaction front where less precipitation is occurring. At 15% anorthite the gradient is much stronger with more precipitation occurring. A greater mass fraction of anorthite results in more reactant in the system and consequently a greater extent of precipitation of the reaction product. All values are nondimensional, calculated where \(\mathcal {D}\)a = 1\(\times\)10\(^{-8}\) and \(\mathcal {P}\)e = 4.3\(\times\)10\(^{-2}\)

Full size image

3.2 Long Simulations—2000 Years

3.2.1 Impact of Reaction Parameters on Precipitation

The total mass of CaCO\(_{3}\) precipitated after 2000 years in the pore structure increases significantly with an increasing Damköhler number, shown in Fig. 8. We show results from a range of Damköhler numbers both above and below the calculated value of 1\(\times\)10\(^{-8}\) to demonstrate the effect of uncertainty in the reaction rates of the system. For a constant value of anorthite fraction a uniform increase in total precipitate can be seen with increasing Damköhler number. An increase in \(\mathcal {D}\)a by one order of magnitude corresponds to an increase in precipitated mass by a very similar extent. In the case of an anorthite fraction of 5% with a range of the Damköhler number between 1\(\times \,10^{-10}\) to 1\(\times\, 10^{-6}\) the total range of precipitated CaCO\(_{3}\) mass is \(4.4\times 10^{-3}\) \(\upmu\)g. With the same range of Damköhler numbers but 25% anorthite fraction the range is \(2.2\times 10^{-2}\) \(\upmu\)g. This indicates that the Damköhler number’s affect on precipitation is not independent of the amount of anorthite available for the reaction to take place.

Fig. 8
figure 8

Total CaCO\(_{3}\) precipitated after 2000 years at anorthite mass fractions ranging 5–25% for a range of \(\mathcal {D}\)a numbers. All results are given using a \(\mathcal {P}\)e value of 4.3\(\times\)10\(^{-2}\). Increasing the \(\mathcal {D}\)a number by an order of magnitude results in an increase in precipitated CaCO\(_{3}\) by around an order of magnitude for each anorthite mass fraction. Within a series of results for a constant \(\mathcal {D}\)a the effect of increasing anorthite mass fraction is not as extreme. A shallow curve is observed from 5 - 25% anorthite which is steepest between 5 and 10% before rapidly starting to level off

Full size image

Similarly to the Damköhler number, an increase in the mass fraction of anorthite available in the system results in an increase in the total precipitated mass of CaCO\(_{3}\), shown by the dashed lines in Fig. 8. The total increase in precipitated mass from 5 to 25% anorthite content where \(\mathcal {D}\)a = 1\(\times\)10\(^{-6}\) is \(1.78\times 10^{-2}\) \(\upmu\)g with a range of 1.78\(\times\)10\(^{-6}\) \(\upmu\)g where \(\mathcal {D}\)a = 1\(\times\)10\(^{-10}\). This indicates that the affect on precipitation caused by the anorthite mass fraction is heavily reliant on the Damköhler number.

The overall increase in precipitated mass caused by increasing the anorthite fraction from 5 to 25% results in an increase of less than an order of magnitude. The greatest change in total precipitation resulting from a change in anorthite fraction occurs between 5 and 10%, shown by the steeper trend between these points in Fig. 8. The increase in precipitation resulting from further increase in the anorthite fraction is less, with a flattening off observed between 20 and 25%. This suggests that the rate of reaction, governed by the Damköhler number, is more influential than the mass fraction of anorthite in the system.

The precipitation rate of CaCO\(_{3}\) shows a rapid decline over the first 100 years before a flattening off trend is seen, shown by the trend lines in Fig. 9. Where \(\mathcal {D}\)a is equal to 1\(\times\)10\(^{-6}\) the precipitation rate shows a decline of 7.83\(\times\)10\(^{-11}\) \(\upmu\)g yr\(^{-1}\) over the first 100 years. In comparison, the precipitation rate drops by a further 1.36\(\times\)10\(^{-11}\) \(\upmu\)g yr\(^{-1}\) over the following 900 years. When \(\mathcal {D}\)a is equal to 1\(\times\)10\(^{-10}\), the rate declines by 7.83\(\times\)10\(^{-15}\) \(\upmu\)g yr\(^{-1}\), dropping by a further 1.36\(\times\)10\(^{-15}\) over the following 900 years.

Fig. 9
figure 9

CaCO\(_{3}\) precipitation rate over time for varying \(\mathcal {D}\)a numbers. For each result, the anorthite mass fraction is 10% and the value of \(\mathcal {P}\)e is 4.3\(\times\)10\(^{-2}\). Increasing the order of magnitude of the \(\mathcal {D}\)a number results in an increase of the precipitation rate by roughly an order of magnitude. In each case, a steep reduction in precipitation rate is observed over the first 100 years before a gentle negative gradient is seen. This is followed by a definite flattening off at around 1,000 years. The total reduction in precipitation rate over the 2000 year period is around 2 orders of magnitude

Full size image

An increase in the Damköhler number by one order of magnitude results in an increase in precipitation rate by around an order of magnitude also, shown in Fig. 9. This is similar to the relationship between the Damköhler number and total precipitation after 2000 years seen in Fig. 8. Again we show a range of Damköhler numbers around the calculated value to demonstrate the importance of constraining the reaction rates in obtaining accurate results. Importantly, we can see that even at the greatest value of \(\mathcal {D}\)a the rate does not decline below that of smaller Damköhler numbers. This means that an anorthite fraction of 10% is an effective amount to maintain the rate of precipitation over a 2000 year duration. A greater reaction rate or lower proportion of anorthite could result in full consumption of the reactant before the end of the simulation period, which we do not see in our cases.

The dominant influence of \(\mathcal {D}\)a over anorthite on precipitation is emphasised in Fig. 10. The average precipitated CaCO\(_{3}\) is shown for each Damköhler number over the range of 5 to 25% anorthite in the system. Over the entirety of the simulated 2000 year period, the different \(\mathcal {D}\)a cases do not overlap despite the range of anorthite mass fraction. This means that the presence of 25% anorthite in a system with a given value of \(\mathcal {D}\)a does not produce as much precipitation as 5% anorthite in a system with a \(\mathcal {D}\)a one order of magnitude greater. This highlights the greater significance of the reaction rate in the system than the amount of reactant.

Fig. 10
figure 10

Average precipitated CaCO\(_{3}\) throughout the domain over 2000 years for a range of Damköhler numbers with upper and lower limits defined by 25 and 5% anorthite mass fractions, respectively. For all results the \(\mathcal {P}\)e number is equal to 4.3\(\times\)10\(^{-2}\). An increase in both the anorthite mass fraction and value of \(\mathcal {D}\)a result in greater precipitate masses. None of the shaded areas overlap, indicating that increasing the anorthite mass fraction up to 25% does not produce as much precipitation as 5% anorthite in a system where the value of \(\mathcal {D}\)a is one order of magnitude higher; emphasising the stronger influence of \(\mathcal {D}\)a compared to anorthite mass fraction

Full size image

3.2.2 Impact of Pore Structure on Precipitation

The following measurements of CaCO\(_{3}\) precipitation per unit volume are only comparable between samples of the same sampled volume; 500, 375 or 250 \(\upmu\)m\(^{3}\) due to the difficulty in finding a representative elementary volume (REV). We found that whilst the Fontainebleau results agree relatively closely across sample volumes, which might indicate a very small REV, the other materials show far greater variability and therefore it is not possible to confirm a given volume as being representative. Due to the substantial computational cost of performing simulations on such complex meshes much larger than those included in this work, we were unable to find a REV for each sample and would therefore encourage further work to identify REVs to allow for precipitation measurements to be useful at different scales.

We observe a maximum in mass of CaCO\(_{3}\) precipitated per unit volume of 6.74 \(\times\) 10\(^{-13}\), 3.19 \(\times\) 10\(^{-13}\) and 8.57 \(\times\) 10\(^{-14}\) kg m\(^{-3}\) for sampled volumes of 500, 375 and 250 \(\upmu\)m\(^{3}\), respectively, controlled by pore surface area and tortuosity. We find that the surface area of a given pore structure shows a positive correlation with the mass of CaCO\(_{3}\) precipitated per unit volume. Figure 11a illustrates this relationship which persists throughout all four study materials. The gradient of the positive trends decreases as the sample volume increases, indicating that pore surface area is most influential on precipitation per unit volume when the sample volume is smaller. As the model assumes that the entirety of the pore surface is comprised of reactive anorthite, it stands to reason that a greater surface area in a given volume will allow for more reaction and consequent precipitation.

Fig. 11
figure 11

Pore surface area (a) and tortuosity of the pore structure (b) of each sample and the corresponding mass of CaCO\(_{3}\) precipitated per cubic meter after 2000 years. All simulations were run using an anorthite mass fraction of 25% and the \(\mathcal {D}\)a and \(\mathcal {P}\)e numbers calculated for the respective sample volume stated in Table 2

Full size image

In contrast, we observe a strong negative correlation between tortuosity of the pore structure and precipitation per unit volume in Fig. 11b. It is clear that this trend also persists throughout each material with the Fontainebleau samples producing a plateau in the trend as tortuosity exceeds a value of around 3. Between tortuosities of 3 and 2, a steady increase in precipitation per unit volume is observed. Below a tortuosity of 2 the gradient of the trend appears to become steeper still, indicating that a tortuosity of 2 may be a critical point. In the case of tortuosity we see that the trends appear similar when considering each sample volume size independently, suggesting that sample volume does not have a bearing on precipitation as with pore surface area.

4 Discussion

In this section, we analyse the results of two sets of simulations lasting for a duration of 300 seconds (short) and 2000 years (long) of simulated time. The short simulations allow investigation of flow characterisation and spatial distribution of precipitates. The long simulations are used to investigate carbon mineralisation over geologically significant periods of time. Due to the small physical size of the model domains, it is not possible to visually examine spatial distribution of the precipitate over such large time steps as the spatial contrast in CaCO\(_{3}\) reduces over time. This results in the need for two different time scale approaches.

4.1 Impact of Pore Geometry

Using the short period model output, it is apparent that the pore structure itself has a strong influence on the spatial distribution of reaction sites. Fig. 3 highlights a clear preferential flow pathway through the central region of the pore structure. This central region is likely the best connected area in the structure, offering the route of least resistance along the X axis between the inlet and outlet points. The propagating reaction front appears to be very sharp throughout this main flow path (Fig. 4), driven by advection.

In direct contrast, the regions of the pore structure which fork away from the preferential flow path, with a lower fluid velocity, show a relative lack of reaction occurring, apparent when comparing Figs. 3 and 4. This is despite the fact that the network is fully connected, showing that full connectivity does not guarantee all of the available pore space may be available for MT. Figure 5 highlights one such area and shows that narrow throats of <25 \(\upmu\)m inhibit fluid migration and consequent precipitation reactions. It is apparent that the fluid reaction front is far more disperse in Fig. 5 which indicates a diffusion dominated front, significantly different to that seen in the central channel (Fig. 4).

These observations suggest connected porosity and permeability are not the only control on the suitability of a pore geometry for MT. Fig. 3 clearly shows that branching can inhibit flow. We also demonstrate this to be the case by examining the tortuosity of the pore structures as a whole in Fig. 11. Here it is apparent that a lower tortuosity encourages a greater degree of precipitation. This might seem to be counterintuitive as greater tortuosity could be thought to result in more precipitation because reactive fluid would come into contact with more anorthite-bearing surface area when moving between two given points. This situation might be the case if a pore structure were uniformly of high tortuosity with no preferential pathways existing from inlet to outlet, which typically is the least tortuous path. However the preferred pathway results in significant precipitation reactions taking place in the dominant pathway with little reaction occurring elsewhere in the tortuous, branched regions. Consequently, the majority of the pore structure is deprived of precipitation. Reaction in these areas will follow eventually, facilitated by diffusion as opposed to advection, as shown by the diffuse reaction front in the branched areas in Figs. 4 and 5.

However, if the pore structure is dominantly comprised of many low tortuousity pathways then reactive fluid will move mostly via advection through a greater proportion of the pore structure. This allows for greater precipitation overall as the bulk of the pore space is easily accessible for reaction-enabling fluid. Therefore, despite the possibility of greater reactive surface contact in a more tortuous pore structure we find that the controlling condition is the preponderance of wide spread advection. This results in greater amounts of precipitation in those pore structures which show less overall tortuosity as fluids can more easily access more of the pore volume. This emphasises the idea that a non-branching pore network is a key factor to look for to enable a greater degree of carbonate precipitation. It has been suggested that a percolation threshold of ca. 10% total porosity exists in sedimentary materials, above which a network is near fully connected and most suitable for GCS (Thomson et al. 2020; Payton et al. 2021). However, pore structure tortuosity appears to be an additional important factor to consider alongside this.

The shape of the trend observed in Fig. 11 leads us to suggest that to achieve substantial CaCO\(_{3}\) precipitation that materials with an overall pore network tortuosity of greater than 3 should not be considered. Ideally, a tortuosity of less than 2 should be sought as the sharp increase in precipitation per unit volume observed below a tortuosity of 2 is substantial. Therefore, we suggest that if other factors such as porosity and permeability are similar between two materials that the one with a lower tortuosity be preferred where mineral precipitation is the goal.

It is also important to consider that the pore geometry itself will evolve over time during and after CO\(_{2}\) injection. We have seen how narrow throats, shown in Fig. 5, could be sites at which a backlog of reaction can take place. This has the possibility to produce enough precipitate under low velocity conditions to seal the throat and cut off the remaining pore space from the connected network. Such a process undoubtedly will result in changes to important factors such as tortuosity. As tortuous branches distal from the main flow pathways become blocked off the overall tortuosity may well decrease, having an impact on subsequent precipitation.

Solving of the moving boundary problem is not incorporated into the model presented here. As a consequence of the clear influence this could have on assessing materials for MT we encourage further development of methodologies, such as that presented here, to incorporate this challenging but influential process. Furthermore, the precipitate causing clogging is likely to be a combination of many minerals in addition to calcite, the only carbonate mineral considered in our model. Other precipitates might include ankerite, siderite and dawsonite (Xu et al. 2005; Naderi Beni et al. 2012; Zhao et al. 2015) which add a further layer of complexity as these solid phases will contribute additionally to pore clogging, reducing porosity and permeability (Gaus et al. 2005; Xu et al. 2005; Bacci et al. 2011; Naderi Beni et al. 2012; Jiang and Tsuji 2014), but also carbon stored.

4.2 Implications for MT

A key observation to make is that throughout all simulations performed at both time scales the influence of the Damköhler number, or reaction rate, is greater than that of the anorthite fraction. This is somewhat advantageous as manipulation of the Damköhler number in a storage reservoir may be more realistic than introducing more silicate minerals which contain crucial metals for MT such as calcium and magnesium. Figure 10 demonstrates that despite changing the anorthite fraction from 5 to 25% in all cases the Damköhler number results in a smaller increase in precipitation than keeping the anorthite fraction constant and increasing the Damköhler number by an order of magnitude.

If the aspiration is to promote MT within a CCS reservoir then there are a number of parameters which could be manipulated that would have the effect of increasing the Damköhler number. One consideration would be to try and decrease the fluid velocity so that a given package of reactive fluid can react entirely. However, this would have the effect of decreasing the injection rate and thereby reducing the volume of CO\(_{2}\) stored in a given period of time. In addition, if reactive fluid is in contact with a given surface for longer this could have particularly detrimental impacts on permeability around the injection zone (Bacci et al. 2011). Mineralisation at the injection point would lead to a proximal decrease in porosity and permeability, inhibiting injected CO\(_{2}\) from reaching deeper into the target formation.

Alternatively, making the environment more acidic would have the effect of increasing the availability of cations available to form carbonate precipitates thereby increasing rates of reaction. A lower pH would allow for more rapid dissolution of the host rock silicate minerals and increase the anorthite fraction which we have shown increases the amount of precipitation occurring. Unfortunately, this is counteracted by such a heavily acidic environment not being conducive for calcite precipitation but instead promoting dissolution.

The final factor to consider is the surface area available for reaction to take place. To increase this it would be desirable to have a high tortuosity in a highly porous network so that a given package of reactive fluid has to come into contact with a large area of pore wall as it moves through a given volume. However, we have found that unless the bulk of a given study volume is highly tortuous with no preferential flow pathways that in practise a lower tortuosity actually favours greater precipitation in a given volume. Furthermore, we found in our simulations that branching can lead to significant portions of the network being cut off due to the presence of low velocity, diffusive fronts allowing for cementation and throat choking. Therefore, we propose that materials with a lower overall tortuosity with minimal branching are desirable for promoting MT for long-term carbon storage security.

5 Conclusions

  • We have designed a numerical model with the capability of running on a 3D mesh generated from \(\upmu\)CT images of sandstone samples which could be considered as CCS reservoirs.

  • It is apparent that despite a fully connected pore structure there are still preferential flow pathways which develop. This results in heavily branched regions of the pore network becoming fluid-deprived and little precipitation is measured in these locations early on. The main flow pathway is dominated by advective transport whilst the reaction front in the branched areas is more diffusion dominated.

  • We suggest that in the heavily branched regions of connected pore structures, dominated by diffusive and low velocity reaction fronts, there is a significant chance of precipitation resulting in throat clogging. This will result in parts of the network becoming cut off and effectively reduce the amount of porosity available for storage. We observe this to occur in areas with throat radii <25 \(\upmu\)m.

  • It is apparent that an increase in the Damköhler number, or reaction rate, by an order of magnitude has a larger impact on precipitation than increasing the anorthite fraction by 20%. As a result, we suggest that it is of greatest benefit to investigate methods of raising the Damköhler number. This may be achieved by engineering reservoirs to increase reaction rate however, solutions to this raise additional problems which could inhibit carbonate precipitation.

  • We show that tortuosity exhibits a negative relationship with CaCO\(_{3}\) precipitated per unit volume. Consequently, we recommend considering tortuosity alongside porosity and permeability when assessing materials for MT.