Abstract
In this paper, a quantitative uncertainty estimation of the random distribution of the soil material properties to the probability density functions of the failure load and failure displacements of a shallow foundation is portrayed. A modified Cam Clay yield stress model is implemented alongside with a stochastic finite element model. The random distribution of the reload path inclination \(\kappa\), the critical state line inclination c of the soil and the permeability k of the water flow relation, has been tested with Monte Carlo simulations accelerated implementing the Latin hypercube sampling. It is proven that both failure load and failure displacements follow Gaussian normal distribution despite the excessive nonlinear behaviour of the soil. In addition, as the eccentricity increases the mean value of failure load decreases in small values of the eccentricity and then increases and the failure displacement always increases. The uncertainty of the output failure stress with the increase in the eccentricity of the load remains the same. The failure spline of clays can be defined within an acceptable accuracy with the aforementioned numerical scheme in all possible geometry and load conditions, considering the eccentricity of the load in combination with nonlinear constitutive relations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Availability of Data and Material
Upon communication with the corresponding author.
Code Availability
Open source code MSolve in programming Language C# . Information to the link http://mgroup.ntua.gr/.
Abbreviations
- \(N_f\) :
-
Friction variables
- \(N_q\) :
-
Friction variable indicating the influence of possible vertical load in the lateral of the foundation
- \(N_\mathrm{c}\) :
-
Friction variable indicating the influence of the cohesion of the soil
- \(N_{\gamma }\) :
-
Friction variable indicating the influence of the settlement dimensions alongside with the total weight of the soil
- \(S_f\) :
-
Shape variables
- \(S_q\) :
-
Shape variable indicating the influence of possible vertical load in the lateral of the foundation
- \(S_\mathrm{c}\) :
-
Shape variable indicating the influence of the cohesion of the soil
- \(S_{\gamma }\) :
-
Shape variable indicating the influence of the settlement dimensions alongside with the total weight of the soil
- \(\kappa\) :
-
Compressibility factor
- c :
-
Critical state line inclination
- k :
-
Permeability in units, \(\frac{\mathrm{m}^3 \mathrm{s}}{\mathrm{Mgr}}\)
- \(\phi _0\) :
-
Friction angle
- \({\mathbf {M}}\) :
-
Total mass matrix
- \({\mathbf {C}}\) :
-
Total damping matrix
- \({\mathbf {K}}\) :
-
Total stiffness matrix
- \(\mathbf {M_\mathrm{s}}\) :
-
Solid skeleton mass matrix
- \(\rho _\mathrm{d}\) :
-
Density of the soil
- \({\mathbf {B}}\) :
-
Deformation matrix
- \({\mathbf {E}}\) :
-
Elasticity matrix
- \(\mathbf {C_\mathrm{s}}\) :
-
Solid skeleton damping matrix
- \(\mathbf {K_\mathrm{s}}\) :
-
Solid skeleton stiffness matrix
- \({\mathbf {m}}\) :
-
Unity matrix
- \({\mathbf {b}}\) :
-
Loading vector
- \({\mathbf {k}}\) :
-
Matrix of permeability in units, \(\frac{\mathrm{m}^3 \mathrm{s}}{\mathrm{Mgr}}\)
- \(\mathbf {N^P}\) :
-
Shape functions for pore pressure
- \(\mathbf {N^u}\) :
-
Shape functions for displacements
- \({\mathbf {S}}\) :
-
Saturation matrix
- \(\mathbf {Q_\mathrm{c}}\) :
-
Coupling matrix
- \({\mathbf {H}}\) :
-
Permeability matrix
- \(\mathbf {f_S}\) :
-
Equivalent forces due to external loading
- Q :
-
Variable for combining the influence of bulk moduli of fluid and solid skeleton in porous problems
- \(\varvec{\sigma }\) :
-
Total stress tensor
- \({\mathbf {s}}\) :
-
Deviatoric component of the stress tensor
- \(p_\mathrm{h}\) :
-
Hydrostatic component of the stress tensor
- a :
-
Halfsize of the bond strength envelope
- \(\mathbf {s_L}\) :
-
Deviatoric component of the stress point of the centre of the plastic yield envelope
- \(p_L\) :
-
Hydrostatic component of the stress point of the centre of the plastic yield envelope
- \(\xi\) :
-
Similarity factor between the plastic yield envelope and bond strength envelope
- \(f_\mathrm{g}\) :
-
Generalized elliptic envelope
- \(f_\mathrm{p}\) :
-
Plastic yield envelope (PYE)
- F :
-
Bond strength envelope (BSE)
- \(\nu\) :
-
Specific volume of the soil
- q :
-
Von Mises stress
- e :
-
Deviatoric strain measure
- \(\varvec{\epsilon _{\mathrm{dev}}}\) :
-
Deviatoric component of the strain tensor
- f :
-
Random function
- \(f_i\) :
-
Value of the random function at nodal points
- \(N_i\) :
-
Shape functions
- \(N_0\) :
-
Total number of shape functions
- \(h_1\) :
-
Truncated normal PDF
- \(\phi (x)\) :
-
Standard normal PDF
- \({\varPhi }(x)\) :
-
Standard normal CDF
- \(\sigma _d\) :
-
Standard deviation of the random variable before truncation
- \(A, B, X_0\) :
-
Normalized coordinates of the subspace of the truncated PDF limits and x, respectively
- \(H_1({\mathbf {x}},\omega )\) :
-
Karhunen–Loeve random field
- \(N_s\) :
-
Number of subintervals in the Latin Hypercube Sampling
- \(\mu ({\mathbf {x}})\) :
-
Mean value of the random field
- \(X(x_1 , x_2 , \ldots x_n)\) :
-
Random vector created by the Latin Hypercube Sampling
- \(M_\mathrm{e}\), \(\lambda _i\), \(\phi _i\) :
-
Total number of eigenvalues \(\lambda _i\) and eigenfunctions \(\phi _i\), respectively
- b :
-
Correlation length
- \(\mathrm{COV}(\xi _i ,\xi _j)\) :
-
Covariance function
- \(\lambda ^*\) :
-
Load factor causing failure of the body at exactly the time which ends the rampload function
- \(a_\mathrm{w}\), \(b_\mathrm{w}\) :
-
Weight coefficients of the proposed algorithm for failure load calculation
- T :
-
Time which the rampload function ends
- \(T_p\) :
-
Symmetrization factor of the stochastic process
- \(\lambda _n\) :
-
Trial load factor of step n causing failure
- \(t_n\) :
-
Time of failure at the generalized load factor \(\lambda _n\)
- \(\lambda _{\text{max-no-failure}}\) :
-
Maximum trial load factor which causes safety
- \(\lambda _{1,\mathrm{fail}}\) :
-
Initial trial load factor causing failure
- \(\lambda _{1,\text{no-failure}}\) :
-
Initial trial load factor which causes safety
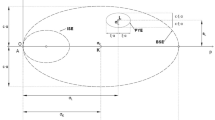
- \(q_1 - q_4\) :
-
Equivalent forces of the shallow foundation
- \((e_x=\frac{M_x}{N}, e_y=\frac{M_y}{N})\) :
-
Eccentricities of the footing settlement
- h :
-
Corresponding dimension of the footing settlement for each eccentricity
- \(l_x - l_y - l_z\) :
-
Dimensions of the total finite element mesh
- \(\sigma _v , \sigma _x , \sigma _y\) :
-
Geostatic stresses in vertical direction and directions x and y, respectively
- \(\lambda\) :
-
Inclination of isotropic compression line for the respective normally consolidated clay
- \(a_{\mathrm{initial}}\) :
-
Initial halfsize of the ellipse
- \(a_{\mathrm{residual}}\) :
-
Residual halfsize of the ellipse
- OCR:
-
Overconsolidation ratio
- G :
-
Shear modulus
- \(K_{\mathrm{bulk}}\) :
-
Bulk modulus
- \(\gamma\) :
-
Specific weight
- \(\nu _0\) :
-
Initial specific volume of the soil
- \(\mathbf {u_x}\) :
-
Displacement vector in direction x
- \(\kappa _{z=0}\) :
-
Compressibility factor at depth = 0
- \(\kappa _{z=\mathrm{max}}\) :
-
Compressibility factor at maximum depth
- \(R=\frac{\kappa _{z=\mathrm{max}}}{\kappa _{z=0}}\) :
-
Ratio of the compressibility factors measured at depth = 0 and at maximum depth
- \(\mu _R\) :
-
Mean value of ratio R
- \(\kappa _{z=\mathrm{max,mean}}\) :
-
Compressibility factor at maximum depth when the ratio R has its mean value
- \(\kappa _\mathrm{L}\) :
-
Linear distribution over depth for the compressibility factor
- \(\kappa _\mathrm{C}\) :
-
Constant distribution over depth for the compressibility factor
- \(\kappa _{\mu }\) :
-
Mean value of \(\kappa\)
- \(c_\mathrm{R}\) :
-
Random variable case for the critical state line inclination
- \(c_\mathrm{D}\) :
-
Deterministic case for the critical state line inclination
- \(k_\mathrm{R}\) :
-
Random variable case for the permeability
- \(k_\mathrm{D}\) :
-
Deterministic case for the permeability
- \(\mu _{\phi }\) :
-
Mean value of the friction angle
- \(\sigma _{\phi }\) :
-
Standard deviation of the friction angle
- \(\mu _{k}\) :
-
Mean value of the permeability
- \(P\mathrm{CoV}_{k}\) :
-
Coefficient of variation of the friction angle
- \(\kappa _{\mathrm{mean}}\) :
-
Mean value of the compressibility factor in the random field representation
- \(c_{\mathrm{mean}}\) :
-
Mean value of the critical state line inclination in the random field representation
- \(k_{\mathrm{mean}}\) :
-
Mean value of the permeability in the random field representation
- \(\sigma _{\kappa }\) :
-
Standard deviation of the compressibility factor in the random field representation
- \(\sigma _{\phi }\) :
-
Standard deviation of the critical state line inclination in the random field representation
- \(\sigma _{k}\) :
-
Standard deviation of the permeability in the random field representation
- \(\mu _{\nu }\) :
-
Mean values of the results
- \(\sigma _{\delta }\) :
-
Coefficient of variation of the results
- M :
-
Maximum values of the results
- \(\mu\) :
-
Minimum values of the results
- N :
-
Normal force
- \(u_{\mathrm{max}}\) :
-
Maximum displacement at failure
- \(u_{\mathrm{min}}\) :
-
Minimum displacement at failure
- \(\phi\) :
-
Rotation of the foundation at failure
- \(p_{\mathrm{vol}}\) :
-
Volumetric stress at failure
- \(q_{\mathrm{dev}}\) :
-
Von Mises stress at failure
- \(e_{\mathrm{vol}}\) :
-
Volumetric strain at failure
- \(e_{\mathrm{dev}}\) :
-
Deviatoric strain at failure
References
Ali, A., Lyamin, A., Huang, J., Li, J., Cassidy, M., Sloan, S.: Probabilistic stability assessment using adaptive limit analysis and random fields. Acta Geotechn. 12(4), 937–948 (2017). https://doi.org/10.1007/s11440-016-0505-1
Ang, A.S., Tang, W.: Probability Concepts in Engineering Planning and Design, vol. 1. Wiley (1975)
Assimaki, D., Pecker, A., Popescu, R., Prevost, J.: Effects of spatial variabilty of soil properties on surface ground motion. J. Earthq. Eng. 7, 1–44 (2003). https://doi.org/10.1080/13632460309350472
Baecher, G., Christian, J.: Reliability and Statistics in Geotechnical Engineering, pp. 177–203. Wiley (2003)
Barr, D.R., Sherrill, E.T.: Mean and variance of truncated normal distributions. Am. Stat. 53(4), 357–361 (1999). https://doi.org/10.1080/00031305.1999.10474490
Biot, M.A.: General theory of three dimensional consolidation. J. Appl. Phys. 12, 155–164 (1941). https://doi.org/10.1063/1.1712886
Borja, R.: Cam-clay plasticity, part 2: implicit integration of constitutive equation based on a nonlinear elastic stress predictor. Comput. Methods Appl. Mech. Eng. 88(2), 225–240 (1991). https://doi.org/10.1016/0045-7825(91)90256-6
Borja, R., Lee, S.: Cam-clay plasticity, part 1: implicit integration of elasto-plastic constitutive relations. Comput. Methods Appl. Mech. Eng. 78(1), 49–72 (1990). https://doi.org/10.1016/0045-7825(90)90152-c
Bouhari, A.: Adaptative monte carlo method, a variance reduction technique. Monte Carlo Methods Appl. 10(1), 1–24 (2004). https://doi.org/10.1515/156939604323091180
Brantson, E.T., Ju, B., Wu, D., Gyan, P.S.: Stochastic porous media modeling and high-resolution schemes for numerical simulation of subsurface immiscible fluid flow transport. Acta Geophys. 66(3), 243–266 (2018). https://doi.org/10.1007/s11600-018-0132-3
Chwała, M.: Undrained bearing capacity of spatially random soil for rectangular footings. Soils Found. 59, 1508–1521 (2019). https://doi.org/10.1016/j.sandf.2019.07.005
Chwała, M.: On determining the undrained bearing capacity coefficients of variation for foundations embedded on spatially variable soil. Studia Geotechnica et Mechanica 42(2), 125–136 (2020). https://doi.org/10.2478/sgem-2019-0037
Dimitrova, D., Kaishev, V., Tan, S.: Computing the kolmogorov-smirnov distribution when the underlying cdf is purely discrete, mixed or continuous. J. Stat. Softw. 95, 1–42 (2019)
Fenton, G., Griffiths, D.: Bearing capacity prediction of spatially random c-\(\phi\) soils. Can. Geotechn. J. 40(1), 54–65 (2003). https://doi.org/10.1016/j.probengmech.2005.06.003
Fu, D., Zhang, Y., Yan, Y.: Bearing capacity of a side-rounded suction caisson foundation under general loading in clay. Comput. Geotechn. 123, 103543 (2020). https://doi.org/10.1016/j.compgeo.2020.103543
Ghanem, R., Spanos, D.: Stochastic Finite Elements: A Spectral Approach, vol. 1, pp. 1–214. Springer (1991). https://doi.org/10.1007/978-1-4612-3094-6
Huysmans, M., Dassargues, A.: Stochastic analysis of the effect of spatial variability of diffusion parameters on radionuclide transport in a low permeability clay layer. Hydrogeol. J. 14(7), 1094–1106 (2006). https://doi.org/10.1007/s10040-006-0035-2
Kalos, A.: Investigation of the nonlinear time-dependent soil behavior. PhD Dissertation NTUA, vol. 1, pp. 193–236 (2014)
Karhunen, K.: Uber lineare methoden in der wahrscheinlichkeitsrechnung. Annales Academiae Scientarium Fenniciae Series A. 37, 1–79 (1947)
Kavvadas, M., Amorosi, A.: A constitutive model for structured soils. Geotechnique 50(3), 263–273 (2000). https://doi.org/10.1680/geot.2000.50.3.263
Kawa, M., Puła, W.: 3d bearing capacity probabilistic analyses of footings on spatially variable c-\(\phi\) soil. Acta Geotechn. 15, 1453–1466 (2020). https://doi.org/10.1007/s11440-019-00853-3
Kolmogorov, A.: Sulla determinazione empirica di una legge di distribuzione. G Ist Ital Attuari 4, 83–91 (1933)
Lewis, R.W., Schrefler, B.A.: The Finite Element Method in the Deformation and Consolidation of Porous Media, vol. 1, pp. 1–508. Wiley (1988). https://doi.org/10.1137/1031039
Li, C., Kiureghian, A.D.: Optimal discretization of random fields. J. Eng. Mech. 119(6), 1136–1154 (1993). https://doi.org/10.1061/(ASCE)0733-9399(1993)119:6(1136)
Li, D.Q., Qi, X.H., Cao, Z.J., Tang, X.S., Zhou, W., Phoon, K.K., Zhou, C.B.: Reliability analysis of strip footing considering spatially variable undrained shear strength that linearly increases with depth. Soils Found. 55(4), 866–880 (2015). https://doi.org/10.1016/j.sandf.2015.06.017
Li, S., Yu, J., Huang, M., Leung, G.: Upper bound analysis of rectangular surface footings on clay with linearly increasing strength. Comput. Geotechn. 129, 103896 (2021). https://doi.org/10.1016/j.compgeo.2020.103896
Li, Y., Fenton, G.A., Hicks, M.A., Xu, N.: Probabilistic bearing capacity prediction of square footings on 3d spatially varying cohesive soils. Geotechn. Geoeviron. Eng. 147(6), 04021035 (2021). https://doi.org/10.1061/(ASCE)GT.1943-5606.0002538
Liu, W., Belytschko, T., Mani, A.: Random fields finite element. Int. J. Numer. Methods Eng. 23, 1831–1845 (1986). https://doi.org/10.1002/nme.1620231004
Liu, W., Sun, Q., Miao, H., Li, J.: Nonlinear stochastic seismic analysis of buried pipeline systems. Soil Dyn. Earthq. Eng. 74, 69–78 (2015). https://doi.org/10.1016/j.soildyn.2015.03.017
Martin, C.: Exact bearing capacity calculations using the method of characteristics. In: Proceedings of the 11th International Conference IACMAG Graz, Austria (2005)
Matthies, H.G., Brenner, C.E., Butcher, G., Soares, C.G.: Uncertainties in probabilistic numerical analysis of structures and solids- stochastic finite elements. Struct. Saf. 19(3), 283–336 (1997). https://doi.org/10.1016/s0167-4730(97)00013-1
Meftah, F., Dal-Pont, S., Schrefler, B.A.: A three-dimensional staggered finite element approach for random parametric modeling of thermo-hygral coupled phenomena in porous media. Int. J. Numer. Anal. Methods Geomecha. 36, 574–596 (2012). https://doi.org/10.1002/nag.1017
Melenk, J.M., Babuska, I.: The partition of unity finite element method: basic theory and applications. Comput. Methods Appl. Mech. Eng. 139(1–4), 289–314 (1996). https://doi.org/10.1016/s0045-7825(96)01087-0
Michalowski, R.L.: An estimate of the influence of soil weight on bearing capacity using limit analysis. Soils Found. 37(4), 57–64 (1997). https://doi.org/10.3208/sandf.37.4_57
Michalowski, R.L.: Upper-bound load estimates on square and rectangular footings. Geotechnique 51(9), 787–798 (2001). https://doi.org/10.1680/geot.2001.51.9.787?journalCode=jgeot
Michalowski, R.L., Shi, L.: Bearing capacity of footings over two-layer foundation soils. J. Geotechn. Eng. (1995). https://doi.org/10.1061/(asce)0733-9410(1995)121:5(421)
Naderi, E., Asakereh, A., Dehghani, M.: Bearing capacity of strip footing on clay slope reinforced with stone columns. Arab. J. Sci. Eng. 43, 5559–5572 (2018). https://doi.org/10.1007/s13369-018-3231-1
Olsson, A., Sandberg, G., Dahlblom, O.: On latin hypercube sampling for structural reliability analysis. Struct. Saf. 25(1), 47–68 (2003). https://doi.org/10.1016/S0167-4730(02)00039-5
Papadopoulos, V., Giovanis, D.: Stochastic Finite Element Methods: An Introduction, vol. 1, pp. 30–35. Springer (2018). https://doi.org/10.1007/978-3-319-64528-5
Papadopoulou, K., Gazetas, G.: Shape effects on bearing capacity of footings on two-layered clay. Geotechn. Geol. Eng. 38, 1347–1370 (2020). https://doi.org/10.1007/s10706-019-01095-6
Papadrakakis, M., Papadopoulos, V.: Robust and efficient methods for the stochastic finite element analysis using monte carlo simulation. Comput. Methods Appl. Mech. Eng. 134, 325–340 (1996). https://doi.org/10.1016/0045-7825(95)00978-7
Peng, X., Zhang, L., Jeng, D., Chenc, L., Liao, C., Yang, H.: Effects of cross-correlated multiple spatially random soil properties on wave-induced oscillatory seabed response. Appl. Ocean Res. 62, 57–69 (2017). https://doi.org/10.1016/j.apor.2016.11.004
Popescu, R., Deodatis, G., Nobahar, A.: Effects of random heterogeneity of soil properties on bearing capacity. Probab. Eng. Mech. 20, 324–341 (2005). https://doi.org/10.1016/j.probengmech.2005.06.003
Pryse, S., Adhikari, S.: Stochastic finite element response analysis using random eigenfunction expansion. Comput. Struct. 192, 1–15 (2017). https://doi.org/10.1016/j.compstruc.2017.06.014
Rao, P., Liu, Y., Cui, J.: Bearing capacity of strip footings on two-layered clay under combined loading. Comput. Geotech. 69, 210–218 (2015). https://doi.org/10.1016/j.compgeo.2015.05.018
Robert, C.P.: Simulation of truncated normal variables. Stat. Comput. 5(2), 121–125 (1995). https://doi.org/10.1007/BF00143942
Savvides, A., Papadrakakis, M.: A computational study on the uncertainty quantification of failure of clays with a modified cam-clay yield criterion. SN Appl. Sci. 3, 659 (2021). https://doi.org/10.1007/s42452-021-04631-3
Sett, K., Jeremic, B.: Probabilistic elasto-plasticity: solution and verification in 1d. Acta Geotechn. 2(3), 211–220 (2007). https://doi.org/10.1007/s11440-007-0037-9
Simoes, J., Neves, L., Antao, A., Guerra, N.: Reliability assessment of shallow foundations on undrained soils considering soil spatial variability. Comput. Geotechn. 119, 103369 (2020). https://doi.org/10.1016/j.compgeo.2019.103369
Smirnov, N.: Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 19(2), 279–281 (1948). https://doi.org/10.1214/aoms/1177730256
Stavroulakis, G., Giovanis, D., Papadopoulos, V., Papadrakakis, M.: A gpu domain decomposition solution for spectral stochastic finite element method. Comput. Methods Appl. Mech. Eng. 327, 392–410 (2014). https://doi.org/10.1016/j.cma.2017.08.042
Stavroulakis, G., Giovanis, D., Papadopoulos, V., Papadrakakis, M.: A new perspective on the solution of uncertainty quantification and reliability analysis of large-scale problems. Comput. Methods Appl. Mech. Eng. 276, 627–658 (2014). https://doi.org/10.1016/j.cma.2014.03.009
Stickle, M.M., Yague, A., Pastor, M.: Free finite element approach for saturated porous media: consolidation. Math. Probl. Eng. (2016). https://doi.org/10.1155/2016/4256079
Sultana, P., Dey, A.K.: Estimation of ultimate bearing capacity of footings on soft clay from plate load test data considering variability. Indian Geotechn. J. 49, 170–183 (2019). https://doi.org/10.1007/s40098-018-0311-9
Szabo, B., Babuska, I.: Intoduction to finite element analysis: formulation, verification and validation. Wiley Ser. Comput. Mech. 1, 1–382 (2011). https://doi.org/10.1002/9781119993834
Terzaghi, K.V.: Theoretical Soil Mechanics. Wiley (1966)
Vrakas, A.: On the computational applicability of the modified cam-clay model on the ‘dry’ side. Comput. Geotechn. 94, 214–230 (2018). https://doi.org/10.1016/j.compgeo.2017.09.013
Wang, Y., Akeju, O.V.: Quantifying the cross-correlation between effective cohesion and friction angle of soil from limited site-specific data. Soils Found. 56(6), 1055–1070 (2021). https://doi.org/10.1016/j.sandf.2016.11.009
Yue, Q., Yao, J., Alfredo, H., Spanos, P.D.: Efficient random field modeling of soil deposits properties. Soil Dyn. Earthq. Eng. 108, 1–12 (2018). https://doi.org/10.1016/j.soildyn.2018.01.036
Zhang, P., Yin, Z.Y., Jin, Y.F., Chan, T.H.T., Gao, F.P.: Intelligent modelling of clay compressibility using hybrid meta-heuristic and machine learning algorithms. Geotechn. Geoeviron. Eng. 12(1), 441–452 (2021). https://doi.org/10.1016/j.gsf.2020.02.014
Zhou, H., Zheng, G., Yin, X., Jia, R., Yang, X.: The bearing capacity and failure mechanism of a vertically loaded strip footing placed on the top of slopes. Comput. Geotechn. 94, 12–21 (2018). https://doi.org/10.1016/j.compgeo.2017.08.009
Zienkiewicz, O.C., Chan, A.H.C., Pastor, M., Schrefler, B.A., Shiomi, T.: Computational Geomechanics with Special Reference to Earthquake Engineering, vol. 1, pp. 17–49. Wiley, Chichester (1999)
Acknowledgements
This work has been supported by the European Research Council Advanced Grant MASTER Mastering the computational challenges in numerical modelling and optimum design of CNT-reinforced composites (ERC-2011-ADG-20110209). The author also acknowledges support from the Bodossaki Foundation.
Author information
Authors and Affiliations
Ethics declarations
Conflict of interest
The authors state that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The following tables and figures are placed in this section
See Figs. Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22.
See Tables 5, 6, 7, 8, 9, 10 and 11.
PDFs of the maximum settlement stresses in kPa for non-porous medium
PDFs of the Normal force of the settlement in kN for non-porous medium
PDFs of the maximum displacement in m for non-porous medium
PDFs of the minimum displacement in m for non-porous medium
PDFs of the rotation of the settlement in rad for non-porous medium
PDFs of the maximum settlement stresses in kPa for porous analyses with deterministic shape functions for the stochastic material variables
PDFs of the Normal force of the settlement in kN for porous analyses with deterministic shape functions for the stochastic material variables
PDFs of the maximum displacement in m for porous analyses with deterministic shape functions for the stochastic material variables
PDFs of the minimum displacement in m for porous analyses with deterministic shape functions for the stochastic material variables
PDFs of the rotation of the settlement in rad for porous analyses with deterministic shape functions for the stochastic material variables
PDFs of the maximum settlement stresses in kPa for porous analyses with random field representation for the stochastic material variables
PDFs of the Normal force of the settlement in kN for porous analyses with random field representation for the stochastic material variables
PDFs of the maximum displacement in m for porous analyses with random field representation for the stochastic material variables
PDFs of the minimum displacement in m for porous analyses with random field representation for the stochastic material variables
PDFs of the rotation of the settlement in rad for porous analyses with random field representation for the stochastic material variables
Histograms of monitored output variables and the normal distribution fitting for 3 randomly selected analyses. a Porous analysis with constant distribution for \(\kappa\), random distribution for c and k with \(e=\,0\) and monitored output variable the Normal force. b Porous analysis of eccentricities \((e_x,e_y)=(\frac{h}{3},\frac{h}{6})\) with random field representations for all stochastic material variables and \(b=2\) m and monitored output variable the maximum failure displacement. c Porous analysis with linear distribution for \(\kappa\), random distribution for c and k with \((e_x,e_y)=(\frac{h}{3},\frac{h}{3})\) and monitored output variable the maximum settlement stress in kPa
Rights and permissions
About this article
Cite this article
Savvides, A.A. Stochastic Failure of a Double Eccentricity Footing Settlement on Cohesive Soils with a Modified Cam Clay Yield Surface. Transp Porous Med 141, 499–560 (2022). https://doi.org/10.1007/s11242-021-01731-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-021-01731-x