1 Introduction

The limit load to shallow foundations and the corresponding displacements and material states is one of the most investigated areas in the field of Geomechanics. Kötter and Prandtl [26, 45] were the first to investigate the problem providing analytical solutions to sliding line equations and bearing capacity in the context of the infinite halfspace soils. [35, 60] investigated the bearing capacity of soils taking into account the friction angle, the soil depth and soil density. Subsequently, a number of papers have been published which investigate the problem [18, 29, 38, 58, 66]taking into account the failure mechanism and applying Mohr–Coulomb material yield criterion alongside with linear elastic analysis. In most cases 1D or 2D physical problems have been examined taking into account homogeneous or layered soils: [40, 47]. All studies presented were applied to the foundation design regulations by introducing the variables N and S which are for material influence and shape influence, respectively. The material related variables N are three respecting for the 3 addends of the total bearing capacity. \(N_q\), \(N_c\), \(N_{\gamma }\) are defined for the influence of possible vertical load in the lateral of the foundation, the cohesion of the soil and the footing dimensions alongside with the total weight of the soil, respectively. In a similar manner the shape variables \(S_q\), \(S_c\), \(S_{\gamma }\) are determined.( [31, 36, 37])

The uncertainty quantification of the bearing capacity of saturated porous media in relation with the input variability such as the Young Modulus or the permeability is investigated with the implementation of the stochastic finite element method [17, 44]. In the aforementioned method, the input variability can be simulated by using two alternative methods [8, 12, 20, 23, 30, 32, 33, 41, 52]. The first method consists of the nodal points to be assumed as random variables and deterministic shape function are implemented for the interpretation of the material spatial distribution [5, 14, 28, 58]. An alternative approach is the implementation of random field series expansion such as the spectral representation or the Karhunen–Loeve expansion or the spatial average method for providing the material input variability [1, 4, 13, 41]. In both approaches, the sampling can be pseudorandom and non-biased or importance sampling methods can be implemented such as the Latin Hypercube Sampling (LHS) [3, 53]. Then, for both methods, the standard Monte Carlo simulation can be implemented. In some cases there are studies that implement realizations of non-Gaussian random fields to the input material variables [43].

In the related studies the problems and methodology proposed refer to 1D-2D elastic halfspace theory with material criterion the Mohr–Coulomb yield stress model. In the present work a numerical simulation approach with a modified Cam-Clay material yield model proposed by [24] is adopted, which is an accurate and reliable quantitatively material for clayey soil simulation ( [63]).This material model with the implementation of the finite element method can be used in general 3D loading and geometric circumstances. The excessive computational cost which is required by the Crude Monte Carlo simulation method, can be reduced by efficient computational methods as suggested in [55, 56]. For the calculation of failure load, a recurrence relation algorithm which provides accurate results with a relative small amount of trials and with one initial guess trial is implemented. The algorithm is theoretically set, proved and compared with the classic intersection method. The goal of the present paper, which is an extension of previous work by the authors [51], is to quantify the uncertainty of the failure load and displacement alongside with the uncertainty quantification of the failure mechanism in relation to the variability of the input parameters, i.e., the spatial distribution of the material variables and the soil depth. Soil depth is defined as the distance between the upper layer of the soil and the impermeable and rigid bedrock. As the soil depth increases the total stiffness of the soil mass is reduced, leading to smaller values for failure loads. Moreover, with the increase of the soil depth the Meyerhoff spline can be expanded to a more generalized failure mechanism in comparison with localized failure surfaces or punching shear failure( [15, 19, 61, 62]).

The input variability refers to three material variables, namely the compressibility factor \(\kappa\), the permeability k and the critical state line inclination c of the soil. The possible spatial distributions of the material variables with respect to the depth Z of the soil domain are the constant, the linear variation and the random field process calculated through the Karhunen–Loeve series expansion with an exponential autocorrelation function. In the constant and linear variation with respect to depth, the truncated normal random variable [7, 49] is assumed at the nodal points. It should be noted that LHS importance sampling method is adopted for the construction of the input random vectors. The geometrical dimensions of the 3D soil domain and correlation lengths are parametrically studied and compared with respect to the corresponding solid problem without considering the pore pressure.

2 Formulation of the dynamic soil–pore–fluid interaction and the numerical solution

The Biot system of equations governs the physical behavior of porous media static or dynamic loading. If the dynamic load is of low frequency or if static loading problems are analyzed the aforementioned system is reduced leading to a notable decrease of the computational effort. The u-p formulation of Biot system of equations consists of soil-fluid momentum balance with the Darcian flow, the stress–strain law and the boundary conditions. In the present article static forces are applied to the clay soil domain consequently the u-p formulation is adopted.

The finite element discretization of the u-p formulation takes the form:

$$\begin{aligned} {\mathbf {M}}\ddot{{\mathbf {x}}}+{\mathbf {C}}\dot{{\mathbf {x}}}+{\mathbf {K}}{\mathbf {x}}={\mathbf {F}}, \end{aligned}$$
(1)

where

$$\begin{aligned} {\mathbf {M}}= & {} \begin{bmatrix} \mathbf {M_1} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {0}} \end{bmatrix} {\mathbf {C}}=\begin{bmatrix} \mathbf {C_1} &{} {\mathbf {0}} \\ \mathbf {Q^T_c} &{} {\mathbf {S}} \end{bmatrix} {\mathbf {K}}=\begin{bmatrix} \mathbf {K_1} &{} \mathbf {-Q_c} \\ {\mathbf {0}} &{} {\mathbf {H}} \end{bmatrix} {\mathbf {F}}=\begin{bmatrix} \mathbf {F_1} \\ {\mathbf {0}} \end{bmatrix} {\mathbf {x}}=\begin{bmatrix} {\mathbf {u}} \\ {\mathbf {p}} \end{bmatrix} \end{aligned}$$
(2)
$$\begin{aligned} \mathbf {Q_c}= & {} \int _{V} {\mathbf {B}}^T {\mathbf {m}} \mathbf {N^p} dv \quad {\mathbf {H}}=\int _{V} (\bigtriangledown \mathbf {N^p})^T {\mathbf {k}} \bigtriangledown \mathbf {N^p} dv \quad \mathbf {S=\int _{V} N^p} \frac{1}{Q}\mathbf { N^p } dv \quad \end{aligned}$$
(3)
$$\begin{aligned} \mathbf {F_1}= & {} \int _{V} (\mathbf {N^p})^T \bigtriangledown ^T (\mathbf{k } \mathbf{b }) dv, \end{aligned}$$
(4)

where \({\mathbf {k}}\) is the matrix of permeability n units \([length]^3 [time]/[mass]\), \({\mathbf {b}}\) is the loading vector divided by the total mixture density and Q is a factor influenced by the bulk moduli of fluid and soil skeleton. \(\mathbf {N^p}\) are the shape functions of pore pressure in matrix representation. \(\mathbf {M_1 , C_1 , K_1}\) are the standard mass, damping and stiffness matrices of the solid skeleton. Furthermore, \(\mathbf {Q_c , H, S}\) are the coupling, permeability and saturation matrices, respectively. Finally, \(\mathbf {F_1}\) corresponds to the equivalent forces due to the external loading. Numerical schemes, such as the Newmark direct integration method, are implemented to obtain the solution to the problem.

3 The yield stress model

3.1 Definition of plastic and bond strength envelope

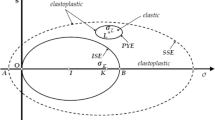
The material model,which here is presented in a brief description, is a modified Cam-Clay type model. All the stresses in the following equations of Sect. 3.1 are effective stresses in the solid skeleton. The implemented model is a two surface model, namely the plastic yield envelope (PYE) which defines the elastic region and the bond strength envelope (BSE) which defines the region in which PYE can be located as PYE is always inside BSE. [9, 10, 22, 24, 63]. BSE is directly influenced by the structure of the microtiles of the clay. If a stress point lies in BSE, the structure degradation rate of the clay is maximum. Both envelopes have ellipsoidal shape as depicted in Fig. 1. The mathematical representation of BSE is given by the following:

$$\begin{aligned} F(p_h,\mathbf{s },a)=\frac{1}{c^2} {\mathbf {s}}:{\mathbf {s}}+(p_h-a)^2-a^2=0, \end{aligned}$$
(5)

where \(p_h\) is the hydrostatic component of the stress tensor, s is the deviatoric component of the stress tensor, c is the critical state line inclination and a is the half-size of the large diameter of the ellipse

Furthermore, PYE is described by the function

$$\begin{aligned} f(p_h,\mathbf{s },p_L,\mathbf {s_L},a)=\frac{1}{c^2} (\mathbf {s-s_L}):(\mathbf {s-s_L})+(p_h-p_L)^2-(\xi a)^2=0, \end{aligned}$$
(6)

where \(p_L\) is the hydrostatic component of the centroid of PYE , \(\mathbf {s_L}\) is the deviatoric component of the centroid of PYE and \(\xi\) is the similarity factor

Fig. 1
figure 1

Graphical representation of the constitutive model

Full size image

Finally, inside PYE the isotropic poroelasticity theory applies, where the bulk and shear moduli have constant ratio, with the assumption of constant Poisson ratio. The bulk modulus is given by:

$$\begin{aligned} K_{bulk}=\frac{\nu p_h}{\kappa }, \end{aligned}$$
(7)

where \(\nu\) is the specific volume of the soil.

The constitutive model is valid for clays, for static and dynamic loads, regardless of the overconsolidation ratio. Clays of friction angle between 17\(^o\)-30\(^o\) can be simulated with substantial accuracy. This range of friction angles corresponds to the majority of the natural clayey soils. Furthermore, it is proved to be numerically stable because the majority of the equations of the criterion are in a closed form. Furthermore, when highly consolidated clays are investigated it can be easily transformed to take into account a possible cementation of the soil, i.e., to bear tensile stresses and the BSE to move to the left. It should also be noted that the stresses and the strains transformations are made in order to have energy conjugate amounts by applying the numerical transformations used in Von Mises yield criterion. To this context, the following variables are introduced \(q_s=\sqrt{\frac{3}{2}\mathbf {s:s}}=\sqrt{3J_2}\) and \(e=\sqrt{\frac{2}{3}\mathbf {\epsilon _{dev}:\epsilon _{dev}}}\). The variable \(q_s\) stands for the deviatoric stress measure also known as Von Mises stress, \(J_2\) is the second invariant of the deviatoric part of the stress vector and e stands for deviatoric strain measure.

4 Random fields, the truncated normal variables and the Latin hypercube sampling

4.1 The Karhunen–Loeve series and the truncated normal distribution

The input material variability can be simulated either assuming that the nodal points are random variables with deterministic shape functions, or by implementing the Karhunen–Loeve series expansion for the construction or a stochastic process [17, 23, 27, 39, 42, 46, 64, 65]. In the present study, both approaches are adopted in order to evaluate each approach influence. For the first technique, which is proposed in [64] the random function f is estimated with the usage of shape functions \(N_i\) by

$$\begin{aligned} f(x)=\sum _{i=1}^{N_0} N_i(x)f_i, \end{aligned}$$
(8)

where \(N_0\) is the total number of shape functions and the \(f_i\) are the values of f in the nodal points which can be random variables following a probability density function (PDF). In the present work, \(N_i\) are linear functions and the \(f_i\) follow the truncated normal distribution [2, 6, 7, 49] which has a pdf described by the equation \(g_1(x)=\frac{\phi (X_0)}{{\sigma _d} (\Phi (B)-\Phi (A))}\), where \(\phi (X_0)\) and \(\Phi (X_0)\) are the standard normal probability and cumulative distribution function for \(X_0\), respectively, and A, B, \(X_0\) are the normalized coordinates of the subspace limits and x, respectively. Also, \(\sigma _d\) and the mean value of the normalization refers to the pdf of the random variable before truncation.

For the Karhunen–Loeve implementation, let \(H_1(\mathbf{x } , \omega )\) be a random field of mean \(\mu ({\mathbf {x}})\) based on a known autocovariance function \(C_h(\mathbf {x_1},\mathbf {x_2})=\sigma (\mathbf {x_1}) \sigma (\mathbf {x_2}) \rho (\mathbf {x_1},\mathbf {x_2})\), where \(\rho (\mathbf {x_1},\mathbf {x_2})\) is the correlation function and \(\sigma (\mathbf {x_1})\) is the standard deviation of \(\mathbf {x_1}\). Therefore, any realization \(H_1\) of the field with M number of eigenfunctions \(\phi _i\) with corresponding eigenvalues \(\lambda _i\) can be expanded as:

$$\begin{aligned} H_1({\mathbf {x}},\omega )=\mu ({\mathbf {x}})+\sum _{i=1}^{M} \sqrt{\lambda _i} \phi _i({\mathbf {x}}-T) \xi _i(\omega ), \end{aligned}$$
(9)

where \(\xi _i\) is a set of random variables of zero mean and covariance function \(COV(\xi _i ,\xi _j)=\delta _{ij}\). Finally, for a Gaussian random field, as implemented in the present study, the \(\xi _i\) functions are a set of standard normal random variables. This type of expansion is the most common because it is strong and robust. In the present work the Karhunen–Loeve expansion is applied by adopting an exponential autocovariance function which has an analytical solution of the Fredholm eigenfunction problem [23, 46]

$$\begin{aligned} C_h(x_1,x_2)=\sigma _d^2 e^{-\frac{|x_1-x_2|}{b}}, \end{aligned}$$
(10)

where b is the correlation length. If the Fredholm equations cannot be solved analytically, and this occurs when the autocovariance function is more complicated, numerical methods can be applied such as the Galerkin method [20, 46]. In the present work, the input material variability is interpreted with both approaches discussed in this section. In the Karhunen–Loeve series expansion, the spatial variability is assumed only in vertical direction.

4.2 The Latin hypercube sampling

The selection of the samples of a random variable can be used by crude Monte Carlo simulation, using pseudorandom algorithms to take a large vector of random values, or variance reduction methods can be implemented such as the importance sampling [11] and the Latin Hypercube Sampling (LHS) [3, 53]. The implementation of LHS method saves a substantial computational effort in order to estimate mean value and coefficient of variation.

In the Latin Hypercube approach let X be a random vector (\(x_1\), \(x_2\),...\(x_n\)). The n dimensional LHS method is stated as follows: For each random variable \(x_i\), the interval [0,1] of the cumulative distribution function (CDF) into N equal subintervals is intersected. Then from each subinterval a random number is chosen and through the inverse CDF a sample of \(x_i\) is obtained. Once samples for all subintervals and all the random variables are acquired then the \(x_i\) vectors are randomly permuted and create the vector realization X. With this procedure, it is assured that to each possible row and each possible column in the nXn euclidean space exactly one sample is taken. The visualization of this feature is depicted in Fig. 2.

Fig. 2
figure 2

Visualization of the Latin Hypercube Sampling for dimension n=2. In each row and each column exactly one sample is obtained

Full size image

The advantage of this procedure is that a reduced amount of values in comparison with crude Monte Carlo approach are needed to integrate the PDF of the input and subsequently to estimate the variability of the output. Also, the subintervals in each dimension may not be equal thus taking into account possible asymmetries of the PDF of the input. Finally, this approach can be applied also to cross-correlated variables, i.e., when the correlation matrix is not diagonal thus it has a general use to the uncertainty quantification scientifical field. In the present work the variables are not cross-correlated and the LHS sampling is used to obtain the variables in the three dimensional space of the compressibility factor k, the critical state line inclination c and the permeability k. The above assumption is reasonable because from experimental data available in the literature the cross-correlation of \(\kappa\) and k can be set to zero due to the coefficient of variation of permeability can be found in some cases much higher than that of volume compressibility, while the correlation between \(\kappa\) and c can be neglected due to lack of experimental data that provide a correlation relation although indirect empirical expressions for the aforementioned variables have been conducted ( [21, 48]).

The material random variables expressed by the PDF \(g_1\) of Sect. 4.1 and the random fields realizations that occur from eq. (9) influence the finite element system of equations (1). The corresponding matrices \({\mathbf {C}}\), \({\mathbf {K}}\), and \({\mathbf {F}}\) are changing due to the randomness of the compressibility factor \(\kappa\), the critical state line inclination c and the permeability k. The selection of the samples follow the importance sampling method of Latin Hypercube Sampling Method.

5 An algorithm for the determination of failure load in ramp dynamic load function

In this section, an algorithm for the determination of failure load, when the dynamic loading function is the ramp loading function, is presented. Ramp loading time function is when the load-time relation is linear with zero initial load until time T. The aim of the algorithm is to find the failure load at the time of the end of the ramp loading. Assume the load function of the problem to be as depicted in Fig. 3.

Fig. 3
figure 3

Linearly increased-ramp dynamic load. Here \(\lambda\) stands for generalized dynamic load (i.e., Force, load factor, applied stress)

Full size image

The aim of this algorithm is to define the load factor \(\lambda ^*\) which causes failure of the continuum at exactly the time T. An initial guess of \(\lambda _1\) is taken leading to an initial time of failure \(t_1\) is obtained. Then, for each new trial \(\lambda _{n+1}\) if the load factor \(\lambda _n\) causes failure to the continuum is given by equation

$$\begin{aligned} \lambda _{n+1}=0,5 \left(\lambda _n \frac{t_n}{T} + \lambda _n\right) \end{aligned}$$
(11)

Otherwise, if the load factor \(\lambda _n\) is not causing failure, then the maximum no failure factor \(\lambda _{max-no-failure}\) is obtained from all previous trials implemented for the calculation of \(\lambda _{n+1}\), as follows:

$$\begin{aligned} \lambda _{n+1}=0,5 \left(\lambda _{max-no-failure} + \lambda _n\right) \end{aligned}$$
(12)

It should be noted that in practice this recurrence relation usually converges ”by the failure region” which means that only relation (11) is implemented. The difference between \(\lambda _{n+1}\) and \(\lambda _{n}\) is given by:

$$\begin{aligned} \lambda _{n+1}-\lambda _n=0,5 \left(\lambda _n \frac{t_n}{T} - \lambda _n\right) \end{aligned}$$
(13)

In eq. (13) it is obvious that as \(n \rightarrow \infty\), \(t_n \rightarrow T\) consequently, the left side of the equation tends to 0, thus the algorithm converges to the desired load factor \(\lambda ^*\).

Table 1 Comparison of the proposed algorithm with the bisection method for the calculation of the failure load \(\lambda ^*\) and failure displacement
Full size table

In comparison with the typical bisection method, where one should guess initial values of failure, safety values \(\lambda _{1,fail}\) and \(\lambda _{1,no-failure}\) and then calculate the new load factor by the bisection of maximum safety factor and minimum failure factor, this algorithm provides less or equal number of trials for the same initial failure guess and convergence tolerance, as can be seen in Table 1. Moreover, it needs only one initial guess, which in high uncertainty problems is very useful in general for avoiding divergence of the solution. Finally, as proven by the numerical tests presented in Table 1 and in Sect. 6, the difference in failure load and failure displacement between the two algorithms is less than 1%. The absolute percentage difference is computed considering as exact solution the bisection algorithm with initial value of safety stress 100 KPa. The performance in terms of the computational time for the 100 deterministic analyses of a Monte Carlo simulation is also depicted in Table 1. The proposed algorithm can save up to 35% of the time demanded for a Monte Carlo analysis to be performed indicating a notable advantage of the aforementioned recurrence relation.

6 Numerical tests in bearing capacity estimation of cohesive soils with random linear and nonlinear material properties

6.1 Description of the problem

The proposed numerical simulation model, which is defined by the set of equations (1) is implemented to porous problems. The geometry of the problem is portrayed in Fig. 5. A uniform vertical load q is applied to the whole soil domain and the ultimate value \(q_{fail}\) alongside with the ultimate displacement \(u_{fail}\) of point A in Fig. 5 are the monitored output variables. The values for the depth are chosen \(h=20\), 40, 50 m. The finite element mesh is with 8 node hexahedral finite elements with linear shape functions for u and p, which provides high numerical accuracy [34, 59]. The length in X and Y directions are \(l_x=l_y=4h\). The stresses due to geostatic loading are directly imported as initial conditions with the relations \(\sigma _v=\gamma z\), \(\sigma _x=\sigma _y=0,85 \sigma _v\) as portrayed in stress point L of Fig. 1. The duration of the simulation in all cases is 1 day in order to have quasi static conditions and in each load case a time step of dt=0.001 day is implemented. The other deterministic properties of the soil are given in Table 2.

Here, \(\nu _0\) stands for the initial specific volume of the soil and \(\lambda _c\) stand for the inclination of Isotropic Compression Line for the respective virgin normally consolidated clay and is considered proportional to \(\kappa\). The following equations apply to boundary surfaces: \({\mathbf {u}}_{x}(z=h)={\mathbf {u}}_{y}(z=h)={\mathbf {u}}_{z}(z=h)={\mathbf {0}}\), and the lateral boundary surfaces are free of constraints. The input material uncertainty consist of the material variables of the compressibility factor \(\kappa\), the critical state line inclination c and the permeability k.

Table 2 Deterministic parameters of the soil domain
Full size table
Fig. 4
figure 4

Graphical representation for the linear spatial distribution of the compressibility factor

Full size image
Fig. 5
figure 5

Geometry of the problem (h=20, 40, 50 m)

Full size image

For the compressibility factor \(\kappa\), the spatial distribution along the depth is considered as linear denoted as \(\kappa _{\mathcal {L}}\), or constant denoted as \(\kappa _{\mathcal {C}}\). For \(\kappa _{\mathcal {L}}\), \(\kappa _{depth=0}=0,008686\) and the ratio \(R=\frac{\kappa _{depth=max}}{\kappa _{depth=0}}\) follows the truncated normal distribution. The mean value of the ratio is \(\mu _{R}=0,469\) and the corresponding CoV\(=\frac{\sigma _{R}}{\mu _{R}}\) is 0,25 , as a consequence \(\kappa _{z=max,mean}=0,004074\) and the CoV increases with depth. These values are adopted in order for the mean stiffness of the soil to correspond to a shear velocity of 200 \(\frac{m}{s}\). In Fig. 4, the linear spatial distribution for \(\kappa\) is depicted where the realizations of the compressibility factor are depicted for the values of R: \(\mu _{R}\), \(\mu _{R}+\sigma _{R}\), \(\mu _{R}-\sigma _{R}\). At this point, it is emphasized that that bulk and shear moduli are assumed proportional, since Poisson ratio is assumed constant, consequently \(\kappa\) is directly associated with the shear velocity. In the case of \(\kappa _{\mathcal {C}}\), the mean value of \(\kappa\) is \(\kappa _{\mu }=0,004074\) and the CoV is 0,25.

For the critical state inclination c the spatial distribution with respect to depth is assumed constant. Two possible cases for the absolute value are considered: the random variable analysis and the deterministic value. In the random variable analysis denoted as \(c_{\mathcal {R}}\), the friction angle \(\phi\) follows the truncated normal distribution PDF \(g_1\) of Sect. 6. The mean value is \(\mu _{\phi }=23^o\) while the standard deviation is \(\sigma _{\phi }=2^o\) and this satisfies the condition that the friction angle \(\phi\) to be within an acceptable closed space for physical clays [24]. Subsequently, values of \(\phi\) are generated and c is computed from \(c=\sqrt{\frac{2}{3}} \frac{6sin(\phi )}{3-sin(\phi )}\). The deterministic value denoted as \(c_{\mathcal {D}}\) is c=0,7336 for friction angle \(\mu _{\phi }=23^o\).

Table 3 Non-porous (solid) analyses performed
Full size table
Table 4 Porous analyses performed
Full size table

Two types of analyses are examined. The porous analyses, where the pore pressure of the soil domain is taken into consideration and the solid analyses, where the water flow is neglected. The solid analyses simulated, indicated with (\({\mathbf {S}}\)) are depicted in Table 3, associating linear (L) or constant (C) distribution for \(\kappa\) and deterministic (D) or random variable (R) cases for c. The porous analyses simulated are portrayed in Table 4, combining linear (L), constant (C), and random field (RF) distribution for \(\kappa\), deterministic (D), random variable case (R) and random field (RF) distribution for c and random field distribution (RF) for k.

In the random field processes, the mean values are assumed: \(\kappa _{mean}=0.008686\), \(c_{mean}\)=0,7336 and \(k_{mean}=10^{-8} \frac{m^3 s}{Mgr}\) [50, 57, 67]. The standard deviations are adopted: \(\sigma _{\kappa }=0.25\kappa _{mean}\), \(\sigma _{\phi }=2^o\) and \(\sigma _k=0.25 k_{mean}\). The autocorrelation function depicted in 10 is implemented in all stochastic processes. The values of correlation length are b=75 (\(k_{\mathcal {RF}{\mathcal {75}}}\)) and b=100 (\(k_{\mathcal {RF}{\mathcal {100}}}\) ). The \(\kappa _{\mathcal {L}}\) and \(\kappa _{\mathcal {C}}\) spatial distributions for \(\kappa\) as well as the random variable distributions for all material variables correspond to a random variable case analysis. In addition, for c a constant deterministic analysis is adopted. The random field (RF) distributions refer to the Karhunen–Loeve series expansion and realizations of the spatial stochastic process are computed through equation \(H_1\) of Sect. 6 with the usage of the autocovariance function 10.

Fig. 6
figure 6

Convergence of the mean value and the standard deviation of a randomly selected Monte Carlo simulation for the output failure load. The reference value of the percentage difference is the statistical moment in the 100 samples

Full size image

The simulations are static, while the number of Fredholm eigenfunctions taken into account is eight. Failure is defined in the present work as when the first Gaussian Point is having softening behavior (i.e., plastic hardening modulus H0). Each Monte Carlo simulation was applied for 100 samples using the Latin Hypercube Sampling method, which were found sufficient in achieving convergence for the mean value and standard deviation of the monitored displacements as it is depicted in Fig. 6. Here, it should be noted that the cross-correlation in all material variables is set to zero and as a consequence the correlation matrix is diagonal.

6.2 Presentation of the results

6.2.1 Ultimate failure load and displacement

The results are depicted in Tables 5, 6, 7 and in Figs. 7, 8, 9, 10, 11, 12. In these tables the mean values \(q_{fail}\) and \(u_{fail}\) of point A in Fig. 5 are presented together with the standard deviation,the coefficient of variation (CoV), the maximum and minimum value of the Monte Carlo simulation.

Table 5 Monte Carlo results for the failure load (KPa) (left) and displacement (m) (right) for non-porous medium
Full size table
Fig. 7
figure 7

PDFs of failure load of solid analyses

Full size image
Fig. 8
figure 8

PDFs of failure displacements of solid analyses

Full size image

When the pore pressure is ignored, larger mean failure displacements and smaller CoV are obtained when \(\kappa _{\mathcal {L}}\) is assumed compared to \(\kappa _{\mathcal {C}}\), while larger mean failure load and corresponding variability are obtained when \(\kappa _{\mathcal {C}}\) is assumed as can be observed from Table 5 for all depths considered. In the numerical tests performed, the largest CoV of the output for \(q_{fail}\) is almost half the input variability while the corresponding CoV of the output for \(u_{fail}\) is practically the same as the input variability of 0,25 (see \({\mathbf {S}}\)-\(\kappa _{\mathcal {C}}\)-\(c_{\mathcal {R}}\) for \(h=20\) m). The mean value of \(u_{fail}\) in \({\mathbf {S}}\)-\(\kappa _{\mathcal {L}}\)-\(c_{\mathcal {D}}\) for \(h=50\) m is 48 % larger than the corresponding value for \(h=20\) m while the mean value for \(q_{fail}\) in \({\mathbf {S}}\)-\(\kappa _{\mathcal {C}}\)-\(c_{\mathcal {D}}\) for \(h=20\) m is 20 % larger than the corresponding value for \(h=50\) m. Consequently, the critical spatial distribution of \(\kappa\) for the CoV of the output of both \(q_{fail}\) and \(u_{fail}\) is the \(\kappa _{\mathcal {C}}\) case. The PDF’s of solid analyses are depicted in Figs. 7 and 8 . This behavior in failure displacements can be explained by the fact that in the \(\kappa _{\mathcal {L}}\) case the upper layers of the soil, which are the most compressible, have low CoV of \(\kappa\) leading to low CoV for both displacements and strains, while in constant distribution along the depth the soil domain tends to be more homogeneous and stiff thus more Gauss Points have larger stiffness leading to larger failure loads.

Table 6 Monte Carlo results for the failure load (KPa) (up) and failure displacement (m) (down) for porous analyses with linear and constant distribution for \(\kappa\)
Full size table
Fig. 9
figure 9

PDFs of failure load of porous analyses with linear and constant distribution for \(\kappa\)

Full size image
Fig. 10
figure 10

PDFs of failure displacements of porous analyses with linear and constant distribution for \(\kappa\)

Full size image

The CoV of the failure load in porous analyses is slightly influenced by the change in the considered depth, unlike the output variability of the failure displacements, as is portrayed in Table 6. The largest output CoV of \(q_{fail}\), which is found at \(\mathbf {P-}\) \(\kappa _{\mathcal {C}}\)-\(c_{\mathcal {R}}\)-\(k_{\mathcal {RF}{\mathcal {75}}}\) for \(h=20\) m, is 47 % lower than the input variability, while the corresponding maximum CoV of \(u_{fail}\) is 26 % greater than the input variability of 0,25 and is located at \(\mathbf {P-}\) \(\kappa _{\mathcal {C}}\)-\(c_{\mathcal {R}}\)-\(k_{\mathcal {RF}{\mathcal {100}}}\) for \(h=20\) m. Thus, when considering the pore pressure in the soil domain a reduction of variability of the failure load occurs and in failure displacements when there is constant spatial distribution for \(\kappa\) a significant variability increase take place as is portrayed in Figs. 9 and 10 . This is in accordance with the results obtained in [17]. This way of behaving is attributed to the fact that when constant spatial variability of a material variable is assumed all Gauss Points are provided with larger uncertainty leading to greater CoV for strains and displacements. In addition, taking into account that the bulk modulus in porous problems as seen from equation 7, are generally smaller than the respective solid problems, it is concluded that smaller mean values of failure load are expected and smaller variability due to tensile failure of the first Gauss Point as it will be proven numerically in Sect. 6.2.2. and since the tensile stress is set to 0 there are limited acceptable positions for BSE leading to the aforementioned results.

Table 7 Monte Carlo results for the failure load (KPa) (up) and failure displacement (m) (down) for porous analyses with random field representation for all stochastic material variables
Full size table
Fig. 11
figure 11

PDFs of failure load of porous analyses with random field representation for all stochastic material variables

Full size image
Fig. 12
figure 12

PDFs of failure displacements of porous analyses with random field representation for all stochastic material variables

Full size image

The porous analysis with random field representations for all material variables is subsequently performed as a more general case, since it takes into consideration the spatial randomness of the material properties of the soil. In the case of porous random field analyses, the largest CoV of the output for \(q_{fail}\) is 3,5 times the input uncertainty, while for \(u_{fail}\) the largest output variability is 2,2 times the CoV of the input. The mean values of failure load in porous random field analyses are significantly smaller than the corresponding porous random field analyses with deterministic shape functions for \(\kappa\) and c, while the mean values for failure displacement are notably greater when the linear distribution over depth is assumed for \(\kappa\) as is depicted in Table 7 in \(\mathbf {P-}\) \(\kappa _{\mathcal {RF}}\)-\(c_{\mathcal {RF}}\)-\(k_{\mathcal {RF}{\mathcal {100}}}\) of \(h=50\) m and \(\mathbf {P-}\) \(\kappa _{\mathcal {L}}\)-\(c_{\mathcal {D}}\)-\(k_{\mathcal {RF}{\mathcal {100}}}\) of the same depth. In porous random field analyses the increase of correlation length decreases the CoV of the output in both \(q_{fail}\) and \(u_{fail}\) in depth 20 and 40 meters and reverses in depth 50 m.The opposite occurrence is present for the mean failure load. These behavior can be explained by the fact that the types of failure of Gauss points, when the proposed material yield model is applied, are two: the failure from the “wet” side which in Fig. 1 is the stress points laying in the right side of the intersection between BSE and the critical state line and the “dry” side which is the stress points laying in the left side of the same intersection. Considering the large uncertainty of c and triaxial loading of the Gauss points the failure stress states may be significantly different leading to larger uncertainty of the output. Consequently, the critical spatial distribution for smaller mean failure load, which is the unfavorable situation in the present work, is the Karhunen–Loeve random field representation for all three input variables, which in most cases it also provides the greater output uncertainty.The PDFs of \(\mathbf {P-}\) \(\kappa _{\mathcal {RF}}\)-\(c_{\mathcal {RF}}\)-\(k_{\mathcal {RF}}\) analyses are portrayed in Figs. 11 and 12 .

The results acquired by the analyses examined depict the effect of the input uncertainty of each material variable in porous failure problems. The compressibility factor \(\kappa\), influences the mean value and the variability of both monitored variables. This influence in CoV of the output is more notable when the distribution of \(\kappa\) with respect to depth is constant. This holds in both porous and non-porous problems. This behavior can be interpreted by the fact that \(\kappa\) is directly related with the bulk modulus, consequently has a significant influence on the strains, the displacements and the stiffness of the soil domain leading to an influence in the ultimate load.

The permeability k influences to a lesser extent failure load and failure displacement. The spatial variability of k has a slight sensitivity of the CoV of the output in most Monte Carlo simulations for \(\kappa\) and c with the exception for porous analyses with stochastic processes for all material variables. For the same porous consolidation problem with the same load and deterministic parameters, the output displacement and stress field are not influenced by the permeability since the pore pressures are fully dissipated, leading to the behavior observed by the numerical results.

In conclusion, the variability of critical state line inclination c of the material model appears to have a significant effect on the output variability when the stochastic process calculated from the Karhunen–Loeve series expansion is adopted, while greater mean values are obtained when the \(c_R\) case is implemented. If a deterministic value for c is chosen the output variability is negligible leading to a conclusion that the influence of this material variable is the most important in comparison with \(\kappa\) and k. This is explained as c is directly associated with the failure state of the Gauss Point, leading to influence the limit state of the soil mass.

Fig. 13
figure 13

Histograms of output displacement in m or failure load in KPa and the normal distribution fitting for three randomly selected analyses. a Porous analyses with constant distribution for \(\kappa\), random distribution for c and Karhunen–Loeve Random Field for k with correlation \(b=75\) m depth \(h=20\) m and monitored output variable the failure load. b Same as a and monitored output variable the failure displacement. (c) Porous analysis of depth 20 m with random field representations for all stochastic material variables and \(b=75\) m and monitored output variable the failure load

Full size image

In order to prove that the output displacement and failure load follows the truncated normal or the lognormal distribution, the histograms of three randomly selected Monte Carlo simulations for an output monitored variable with the corresponding distribution fitting are presented in Fig. 13. As proven by the diagrams, the empirical PDF estimated by the histograms can be modeled by the truncated normal PDF \(g_1\) described in Sect. 6 or the lognormal PDF, respectively. The limit values indicated in Tables 5, 6, 7 are accurate values to set the truncation of the PDF. In addition, for proving numerically the Gaussian nature of the output random vectors, the Kolmogorov–Smirnov test is used [16, 25, 54]. In all output probability density functions, the null hypothesis \(H_0\), at the 5\(\%\) significance level is accepted, as is portrayed in Table 8, where for the Monte Carlo simulation analyses portrayed in Fig. 13 the aforementioned test is implemented. The maximum absolute deviation of the theoretical and empirical cumulative distribution function (CDF) of the Monte Carlo simulations depicted in Fig. 13 are presented and compared to the critical difference for accepting \(H_0\). In all analyses, the critical value is greater than the maximum absolute difference of the CDFs consequently, the output random vectors follow a Gaussian type distribution. This comes in agreement with the previous research literature [17].

Table 8 Kolmogorov–Smirnov test results for the Monte Carlo simulations of Fig. 13
Full size table

6.2.2 Ultimate stresses-strains and failure mechanism

The results are portrayed in Tables 9, 10, 11. In these tables the mean value, the CoV and the minimum values for the volumetric stresses denoted with \(p_h\), the deviatoric stresses denoted with \(q_s\), which is the Von Mises stress explained in Sect. 3.1. In addition, the mean value with the CoV of the volumetric strains denoted with \(\epsilon _{vol}\), deviatoric strains denoted with e are also depicted in Tables9, 10, 11. Moreover, the probability of first Gauss Point failure for all simulations is presented. Here, it should be noted that due to symmetry of the displacement field only the point with smaller coordinates is written. It is also pointed out that the volumetric strain at failure is tensile.

Table 9 Monte Carlo results for the stresses (KPa), the strains and the probability of the first Gauss point failure for non-porous medium
Full size table

In solid analyses, larger CoV of the output and smaller minimum value of failure stress is obtained when \(c_R\) case is adopted as it can be seen from Table 9. In most cases, the aforementioned distribution also provides greater mean values. The same spatial distribution assumption for critical state line inclination provides larger variability of the strains at failure, which on average are on the proximity of 3-4 ‰. In general, from the results of the Monte Carlo simulations it can be concluded that the percentage plastic deviatoric strains are larger leading to the conclusion that the distortional failure is critical. Finally, in most cases the Gauss Point (2,11 , 2,11 , 12,11) is the most probable failure point with the exception of the \(\kappa _c\) distribution at \(h=40\) m.

Table 10 Monte Carlo results for the stresses (KPa), the strains and the probability of the first Gauss point failure for porous analyses with linear and constant distribution for \(\kappa\)
Full size table

In porous analyses with deterministic shape functions for \(\kappa\) and c larger stress variability is obtained at \(h=20\) m with deterministic value for c and at greater depths with \(c_R\) case. The change of the correlation length influences notably the output variability at \(h=20\) m as is portrayed in Table 10. The maximum output variability in failure strains occurs at \(h=50\) m and correlation length for k \(b=75\) m. From the Monte Carlo simulations implemented, it can be seen that when the \(\kappa _c\)-\(c_R\) distributions are assumed the volumetric failure is critical, while when \(\kappa _c\)-\(c_R\) distributions are adopted the deviatoric failure occurs. In conclusion, the most probable failure point is the (2,11 , 2,11 , 12,11) for \(h=20\) m, the (2,11 , 2,11 , 32,11) for \(h=40\) m and the (2,11 , 2,11 , 2,11) for \(h=50\) m and linear distribution for \(\kappa\), while (2,11 , 2,11 , 42,11) is the unfavorable Gauss Point for \(h=50\) m and constant distribution along the depth for the compressibility factor.

Table 11 Monte Carlo results for the stresses (KPa), the strains and the probability of the first Gauss point failure for porous analyses with random field representation for all stochastic material variables
Full size table

In porous analyses with random field representation for \(\kappa\), c, k larger output CoV in stresses is obtained in general when \(b=75\) m except from the deviatoric stresses in \(h=40\) and 50 m as depicted in Table 11. The volumetric strains and the deviatoric strains have in all depths critical correlation length \(b_{critical,vol}\)=75 m and \(b_{critical,dev}\)=100 m, respectively. On average, considering the numerical results obtained by the aforementioned analyses, at \(h=20\) and 50 m the volumetric failure is critical, while at depth 40 m the distortional failure occurs. Finally, the most probable failure points in 20 m are the (2,11 , 2,11 , 2,11) for \(b=75\) m and (2,11 , 2,11 , 12,11) for \(b=100\) m, while in depth 50 m is the (2,11 , 2,11 , 32,11) for both correlation lengths. If the soil depth is 40 meters, there are many points with equally high probability of failure thus leading to a more uncertain position of the failure mechanism.

7 Conclusions

In this paper, the uncertainty quantification of the failure of clayey soils taking into account the pore pressure–soil interaction with the implementation of the stochastic finite element method is presented. The aim of this work is to introduce accurate quantitative results on the failure load of 3D clayey soil domain in relation with the input variability of soil material variables. The proposed numerical simulation model holds for every possible assumptions for the geometry, the loading properties and the material distribution of the soil domain. In this context, a detailed finite element simulation, alongside with a complicated material constitutive model is used. It is evident that similar computational study can be conducted for shallow foundations and it is a future research work that will be performed by the authors.

The numerical results obtained indicate that the output failure load and displacement follow a Gaussian random distribution despite the material nonlinearity, which in failure phenomena is excessive. The randomness of material poroelasticity plays an important role in the output CoV for failure load and failure displacement, especially when it has a Karhunen–Loeve random field representation along the depth of the soil domain. The same thing applies for the critical state line inclination variable c. When the random Karhunen–Loeve field is assumed for all stochastic material variables in discussion the CoV of the output exceeds the corresponding variability of the input in half of the Monte Carlo simulations. This variability increase varies from 30% to 3,5 times larger. The porous variable of permeability influences to a lesser extent the uncertainty of the output material variables. In porous media problems the failure load is smaller compared to the corresponding solid problems.

The random field representations for \(\kappa\), c and k provide the maximum variability for failure stresses and strains. In porous random field analyses in depths \(h=20\), 50 m the volumetric failure occurs, while when the soil domain is 40 m deep the distortional failure is critical. When deterministic shape functions for \(\kappa\) and c are implemented, the \(\kappa _c\)-\(c_R\) distributions provide with larger probability volumetric failure of Gauss Points, while \(\kappa _L\)-\(c_D\) distributions are adopted in order to obtain with larger probability deviatoric failure. Finally, in most cases (2,11 , 2,11 , 12,11) is the critical Gauss Point of failure thus it can be the starting point of the failure mechanism through the Meyerhoff spline.