On Optimal Designs Using Topology Optimization for Flow Through Porous Media Applications

Abstract

Topology optimization (TopOpt) is a mathematical-driven design procedure to realize optimal material architectures. This procedure is often used to automate the design of devices involving flow through porous media, such as micro-fluidic devices. TopOpt offers material layouts that control the flow of fluids through porous materials, providing desired functionalities. Many prior studies in this application area have used Darcy equations for primal analysis and the minimum power theorem (MPT) to drive the optimization problem. But both these choices (Darcy equations and MPT) are restrictive and not valid for general working conditions of modern devices. Being simple and linear, Darcy equations are often used to model flow of fluids through porous media. However, two inherent assumptions of the Darcy model are: the viscosity of a fluid is a constant, and inertial effects are negligible. There is irrefutable experimental evidence that viscosity of a fluid, especially organic liquids, depends on the pressure. Given the typical small pore-sizes, inertial effects are dominant in micro-fluidic devices. Next, MPT is not a general principle and is not valid for (nonlinear) models that relax the assumptions of the Darcy model. This paper aims to overcome the mentioned deficiencies by presenting a general strategy for using TopOpt. First, we will consider nonlinear models that take into account the pressure-dependent viscosity and inertial effects, and study the effect of these nonlinearities on the optimal material layouts under TopOpt. Second, we will explore the rate of mechanical dissipation, valid even for nonlinear models, as an alternative for the objective function. Third, we will present analytical solutions of optimal designs for canonical problems; these solutions not only possess research and pedagogical values, but also facilitate verification of computer implementations.

Graphical Abstract

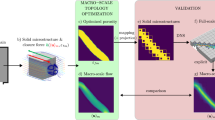
We have considered a pressure-driven problem with axisymmetry and got optimal material layouts using topology optimization by maximizing the total rate of dissipation. The left figure shows unphysical finger-like design patterns when the primal analysis does not enforce explicitly the underlying radial symmetry. The right figure shows that one can avoid such numerical pathologies if the primal analysis invokes axisymmetry conditions.

Appendix A. Mathematical Results

A function f(x) is said to be convex if

$$\begin{aligned} f(\lambda x_1 + (1 - \lambda ) x_2) \le \lambda f(x_1) + (1- \lambda ) f(x_2) \quad \forall \lambda \in [0,1] \end{aligned}$$

(A.1)

For twice-differentiable functions, a sufficient condition for convexity is (Boyd et al. 2004):

$$\begin{aligned} f^{''}(x)\ge 0 \end{aligned}$$

(A.2)

where a superscript prime denotes a derivative. Using this sufficient condition, it is easy to check the functions $x^3$ and 1/x are convex on the positive real line (i.e., $0< x < \infty$).

Lemma A.1

Given that $0 \le \gamma \le 1$ and $0 < r_i$, the quantities ${\widehat{\xi }}_{\mathrm {3D}}^{(1)}$ and ${\widehat{\xi }}_{\mathrm {3D}}^{(2)}$ defined in Eqs. (7.17) and (7.22), respectively, satisfy

$$\begin{aligned} 1 + \frac{1}{r_i} - \left( \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} + \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} \right) \ge 0 \end{aligned}$$

(A.3)

Proof

Noting that $f(x) = x^3$ is a convex function on the positive real axis and $\gamma \in [0,1]$, the definition of a convex function (A.1) implies the following:

$$\begin{aligned} ( \gamma (1) + (1 - \gamma ) r_i )^3 \; \le \; \gamma (1)^3 + (1 - \gamma ) r_i^3 \end{aligned}$$

(A.4)

This implies that

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} = \frac{1}{\root 3 \of {\gamma + (1 - \gamma )r_i^3}} \le \frac{1}{\gamma + (1 - \gamma )r_i} \end{aligned}$$

(A.5)

Using the fact that $f(x) = 1/x$ is a convex function on the positive real line, we establish the following inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} \le \frac{1}{\gamma + (1 - \gamma )r_i} \le \gamma + (1 - \gamma ) \frac{1}{r_i} \end{aligned}$$

(A.6)

By executing similar steps as above, we obtain the following inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} = \frac{1}{\root 3 \of {(1 - \gamma ) + \gamma r_i^3}} \le \frac{1}{(1 - \gamma ) + \gamma r_i} \le (1 - \gamma ) + \gamma \frac{1}{r_i} \end{aligned}$$

(A.7)

Adding the above two inequalities, we get the desired inequality:

$$\begin{aligned} \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(1)}} + \frac{1}{{\widehat{\xi }}_{\mathrm {3D}}^{(2)}} \le 1 + \frac{1}{r_i} \end{aligned}$$

(A.8)

$\square$