1 Introduction

Gas injection, a promising means of enhanced oil recovery (EOR), has a good displacement efficiency at the pore level. However, conformance problems exist, such as gravity segregation and fingering because of the low density and low viscosity of gas compared to in-situ fluids (Kim et al. 2005). As a result, the displacement front of gas injection is not stable, which contributes to a poor sweep efficiency. The sweep efficiency of gas injection in naturally fractured reservoirs is even poorer, because fractures act as highly permeable channels leading to early gas breakthrough.

Foam flooding, created by adding surfactant solution in gas injection, can be a good solution to conformance problems. Foam is an agglomeration of gas bubbles separated by surfactant-containing liquid films, called lamellae. It has applications in many fields, including acid diversion in stimulation (Thompson and Gdanski 1993), aquifer remediation (Hirasaki et al. 1997; Portois et al. 2018) and gas injection in EOR (Kovscek and Radke 1994; Rossen 1996). Foam application in EOR has been theoretically and experimentally studied for decades. During foam flooding, much gas is trapped in-situ in the pore space, greatly reducing gas relative permeability (Tang and Kovscek 2006; Balan et al. 2011). Because of the significant reduction of gas mobility (often by a factor of hundreds or more), foam can effectively maintain a stable displacement front and therefore increase the gas sweep and oil recovery.

In fractures, foam can also be generated, thus diverting gas into matrix and hence improving sweep (Kovscek et al. 1995). Fernø et al. (2016) conducted foam experiments in a fracture network. They found that foam was generated in situ in the fracture network during surfactant-alternating-gas (SAG) and co-injection of gas and surfactant solution over a range of gas fractional flow. They reported gas mobility-reduction factors varying from 200 to more than 1000, and foam significantly improved sweep and delayed gas breakthrough compared to gas injection.

The ability of foam to reduce the mobility of gas is strongly linked to the fraction of trapped gas, which is captured by capillary forces. Thus understanding the mechanism of gas trapping is crucial for an optimized design of field-scale foam application. Previous experimental studies (Radke and Gillis 1990; Friedmann et al. 1991) have been carried out to investigate gas trapping in cores, by fitting the profile of a gas tracer in the effluent using a 1D model for tracer transport. It has been concluded that between 80% and almost 100% is trapped. Tang and Kovscek (2006) also reported an experimental work of gas trapping in a sandstone core. They found that trapped-gas fraction ranged from 88 to 56% at gas superficial velocities between 0.4 and 30 m/day. Nguyen et al. (2009) used X-ray computed tomography to reconstruct the effluent tracer concentration. They found that the trapped-gas fraction decreases with an increasing gas rate, but weakly increases with a decreasing liquid rate. More recently, Kil et al. (2011) analyzed the CT images using a more-sophisticated mass-transfer model and estimated the trapped-gas fraction at 99%.

In recent years, the microfluidic device, a network of channels with widths of tens to hundreds of microns, became increasingly useful in the research field of foam EOR (Marchalot et al. 2008; Conn 2015). Its transparency allows direct observation of foam behavior at the pore scale. In microfluidic models, foam can be created by snap-off (Kovscek et al. 2007; Gauteplass et al. 2015). Snap-off takes place when water deposited by a liquid lens or lamella was displaced by gas from a narrow pore throat into a wide pore body. It can also result from fluctuations in capillary pressure on a scale larger than a single pore (Rossen 2008). In glass fracture models, besides snap-off, AlQuaimi and Rossen (2018a) also observed foam generation by lamella division at high gas fractional flow, when a lamella divided as it encountered a split in the flow path. Jones et al. (2018) studied gas trapping in a microfluidic model and reported a strong response of trapped-gas fraction to velocity variations. The fraction of trapped gas increased from 12 to 63% as superficial velocity dropped from 400 to 50 mm/s. They demonstrate that at lower velocities bubbles have a higher probability to coarsen to pore size, and in the process, more effectively block individual pores and increasing the trapped-gas fraction.

In this study, we use a 1-m-long, 15-cm-wide model representing a fracture, with one roughened and one smooth wall. The model is made of glass plates, which makes visualization and quantification of the flow processes possible. Foam flow and gas trapping through the model is directly monitored using a high-speed camera. In this paper, we describe our experimental setup, how foam evolves along the fracture and how we quantify gas trapping at given flow conditions. In addition, the effects of gas trapping on foam mobility are discussed. A fracture pore space possesses a very-different pore geometry compared to a grain framework. Therefore, we relate fracture pore-space geometry to the degree of gas trapping using the correlation of AlQuaimi and Rossen (2018b).

2 Experimental Apparatus and Materials

Figure 1 shows the experimental apparatus for foam tests. A dual-cylinder pulse-free pump (VINDUM Engineering, INC., Model VP1-12 K, range of 0–28 ml/min) injects the surfactant solution and a mass-flow controller (Bronkhorst Nederland B.V., F-230 M, range of 0.19–10 ml/min) regulates gas injection. Seven absolute-pressure transducers (DEMO MPXH6400A, 4 bar, accuracy at ± 10 mbar) measure the pressure at different locations along the model fracture and provide differential pressures from the injection point to the production point. A computer controls injection rates of the surfactant solution and gas and provides data-acquisition for the pressure transducers.

Fig. 1
figure 1

Experimental setup

Full size image

The fracture model has a dimension of 100 cm × 15 cm (length × width) and is made of two glass plates, including one smooth plate and one single-sided-roughened plate (Hijman Glas B.V., the Netherlands). The thickness of both plates is 20 mm.

To create a fracture model, the two plates are placed directly against each other and glued along four edges using Silicon rubber (ResinTechnology B.V., SR1-40B). Thereafter, the model is put into an aluminum clamping frame (Fig. 2). The space between the two plates represents fracture aperture. Over the length of the channel system, 11 holes have been drilled through the roughened plate for foam injection and production and connection to the pressure transducers. The model plate has been divided into six sections of 18 cm length, except for section 1 and section 6, which are 7 cm and 15 cm long, respectively. Two troughs with dimensions of 12 × 2 × 0.04 cm (length × width × depth) are engraved in the rough plate. The trough at the inlet of the fracture helps foam to flow evenly into the fracture plane along its width. The trough at the end of the fracture prevents foam from converging toward a point at the outlet.

Fig. 2
figure 2

Top view of the model fracture

Full size image

The glass plates are strongly water-wet. They are transparent and mounted stress-free to avoid optical effects. To create a direct image of foam inside the fracture, a light source below, combined with a high-speed camera (Photron Fastcam UX50, up to 160,000 fps) above, capture the foam process. A computer operates the camera and handles the image acquisition. A high-parallelism chip back-light device (VAL LED lighting, VL-CB-CL) is used as the light source. The setup is placed inside a tent to avoid external and internal reflections from the room, in order to improve the quality of the captured images.

In this study, the injected fluids used are demineralized water, surfactant solution with 1 wt% AOS C14-16 (Stepan® BIO-TERGE AS-40 KSB) in demineralized water (ELGA VEOLIA Labwater) and nitrogen (Linde Gas Benelux B.V., Purity ≥ 99.999%). Additional dyes have not been used. The surface tension of the surfactant solution to air at 20°C is 32.2 mN/m, measured using a KSV Sigma Tensiometer.

3 Methodologies

A glass plate with one roughened side represents the geometry of a geological fracture. The roughened surface can be characterized by a height profile with connected hills and valleys, creating a 2D network of pore bodies and throats against the flat plate. The roughened plate establishes a slit-like fracture channel between the two plates with variable aperture. The roughened plate of our model fracture shares the same pattern as sample 5 of AlQuaimi and Rossen (2018a). Figure 3a maps the topography of a 4 × 4 cm section of the roughened plate. The height data were profiled by using a white-light interferometer (Philips Innovation Services, Eindhoven, the Netherlands). Figure 3b shows the aperture distribution of the model fracture.

Fig. 3
figure 3

a Topography of the roughened plate. b Aperture distribution of the model fracture. Both (a) and (b) are constructed from height data of sample 5 of AlQuaimi and Rossen (2018a)

Full size image

Prior to conducting any foam experiment on the model fracture, the hydraulic aperture \({d}_{H}\) of the model is computed. We estimate \({d}_{H}\) by injecting demineralized water through the model at stepwise increasing rates. Once steady-state is reached at each rate, the pressure gradient is recorded. A regression of pressure gradient as a function of rate determines \({d}_{H}\) (Witherspoon et al. 1980):

$$ \left| {\nabla P_{w} } \right| = 12 q_{w} \frac{1}{{w d_{H}^{3} }} \mu_{w} $$
(1)

where \(\nabla {P}_{w}\) is the pressure gradient upon water injection. Here \({q}_{w}\) is volumetric water injection rate, \(w\) the width of the model fracture, and \({\mu }_{w}\) the viscosity of water. For our model \({d}_{H}\) is 80 \(\upmu \)m. The definition of hydraulic aperture approximates the model fracture as a smooth slit. It is then related to the permeability of the model fracture, \({k}_{f}\), by (Tsang 1992):

$$ k_{f} = \frac{{d_{H}^{2} }}{12} $$
(2)

For our model \({k}_{f}\) is 533 darcy.

In this study, a mixing tee (Upchurch Scientific IDEX Health & Science LLC, PEEK™, 10 \(\upmu \)m UHMWPE Frit) upstream the model fracture is used to pre-generate foam at a fixed foam quality (ratio of gas volumetric injection rate to total rate) \({f}_{g}\) of 0.9 and at varying total interstitial velocities \({v}_{t}\): 0.12, 0.23, 0.49, 0.89, 1.69, 3.14 and 6.79 mm/s. Foam then flows into the horizontally-placed model fracture. All experiments are performed at 20°C and ambient pressure. Before each new foam experiment, the model fracture is thoroughly cleaned and pre-saturated with surfactant solution for the next injection experiment.

The seven pressure transducers are used to record pressure data along the flow path. Equation 3 shows how the steady-state time-averaged pressure data are used to calculate the apparent viscosity of foam, \({\mu }_{app}\), to quantify the mobility of steady-state foam.

$$ \mu_{{{\text{app}}}} = \frac{1}{12}\frac{1}{{q_{t} }} \left| {\nabla P_{{{\text{foam}}}} } \right| w d_{H}^{3} $$
(3)

where \({q}_{t}={v}_{t} {d}_{H} w\) is the total volumetric flow rate, and \(\nabla {P}_{foam}\) is pressure gradient of steady-state foam flow.

To study gas trapping and bubble texture in the foam, multiple images are taken during steady-state foam flow. ImageJ software processes and analyses the images: thus the bubble density (number of bubbles per cm2 of image) and bubble-size distribution are calculated. The results are time- and location-averaged, meaning that images are taken at different times and also at different locations after each experiment reaches steady-state (Fig. 4).

Fig. 4
figure 4

Setup of the model fracture and the camera. Images are taken at places shown as squares shown in red in this figure

Full size image

In addition, we program a macro to study multiple time-lapse images during a 47-s foam flow. The macro indicates bubbles with a displacement smaller than the average bubble diameter as trapped gas. The area fraction of trapped gas \({S}_{g}^{^{\prime}}\) can then be estimated using image analysis:

$$ S_{g}^{^{\prime}} = \frac{{A_{{g, {\text{trap}}}} }}{{A_{{g, {\text{total}}}} }} $$
(4)

where \({A}_{g,\mathrm{trap}}\) is area of trapped gas, and \({A}_{g, \mathrm{total}}\) is the total area of gas. Equation 4 is a 2D estimation of trapped-gas fraction, because of the uneven aperture of the fracture surface. Because gas, trapped or flowing, tends to occupy locations of wider aperture, we believe it provides a useful measure of gas trapping and for relating it to pressure gradient and velocity.

4 Results and Discussion

4.1 Evolution of Foam Along Model Fracture

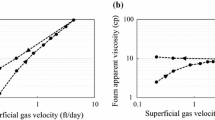
To investigate how foam evolves along the fracture, foam is first pre-generated through the mixing tee, and then flows into the fracture. Once steady-state is reached, the pressure data are recorded to compute apparent viscosity of foam (Eq. 3). Figure 5 shows the apparent viscosity of foam in the sections of the fracture (Fig. 2) at different total interstitial velocities.

Fig. 5
figure 5

Apparent viscosity of foam as a function of sections of the fracture at different total interstitial velocities

Full size image

As shown in Fig. 5, the apparent viscosity of foam monotonically decreases as velocity increases, reflecting the non-Newtonian nature of foam flow. For all velocities, apparent viscosity increases along the fracture, until it reaches its maximum magnitude in the last three sections: pre-generated foam is refined inside the fracture by in-situ foam generation. As foam propagates further along the fracture, it reaches a state with unchanging mobility.

Although the frit upstream of the model fracture is quite narrow (10 \(\upmu \)m), foam has coarsened by the time it enters the fracture. As a result, foam texture is refined as it flows through the fracture. In this study, using pre-generated foam, lamella division has been found to be the principal mechanism of foam generation inside the fracture. Illustrations of this process in the fracture are shown in the Appendix.

As a result of in-situ foam generation, as displayed in Fig. 6, bubble texture becomes finer along the fracture until it reaches a nearly constant state in the last three sections. It is also evident that the bubbles are not uniform. Figure 7 shows bubble density and bubble size at different sections for foam injected at \({v}_{t}\) = 0.89 mm/s. The statistics are provided in Table 1. The standard deviation of bubble size is large, indicating that foam bubbles in our model fracture are polydisperse (with an average polydispersivity index of 0.81). Despite the large standard deviation in bubble sizes, the uncertainty in the mean bubble size distribution is about one-tenth of the standard deviation in our study, based on the 95%-confidence interval (Wonnacott and Wonnacott 1972). Foam texture reaches a stable and constant state within our 1-m-long model fracture with bubble density increasing along the fracture up to its maximum average value (509 per cm2) in the last three sections, while average bubble area decreases to its minimum (0.139 mm2). The apparent viscosity is also the same in the last three sections at 60 cp for foam injected at \({v}_{t}\) = 0.89 mm/s (Fig. 5). We conclude that foam has achieved local equilibrium (LE) in our model fracture.

Fig. 6
figure 6

Evolution of foam texture at different sections along model fracture. Foam injected at \({v}_{t}\) = 0.89 mm/s. Gas is shown in black, liquid in white. Liquid occupies areas with tighter aperture in the model fracture. Image size: 1.57 × 1.26 cm

Full size image
Fig. 7
figure 7

Bubble density and bubble size of foam as a function of sections of model fracture. Foam injected at \({v}_{t}\) = 0.89 mm/s

Full size image
Table 1 Bubble properties in different sections along model fracture. Foam injected at \({v}_{t}\) = 0.89 mm/s
Full size table

At LE, the rate of bubble generation equals the rate of bubble destruction. We have not observed bubble destruction, either by capillary coalescence or diffusive coarsening, in our experiments. This is probably because capillary pressure is relatively low, and the critical time for foam coarsening by gas diffusion is longer than the residence time in the fracture (AlQuaimi and Rossen 2019). Since no bubble destruction is observed, the implication is that foam generation also stops in the last three sections.

4.2 Gas Trapping and Foam Mobility

In the rest of this paper, we examine the properties of foam in the last three sections, where foam is at LE. To study gas trapping, foam tests at different velocities have been conducted. Figure 8 shows that there is a strong link between bubble texture and total interstitial velocity. Bubble density increases and bubble size decreases (finer foam texture) as velocity increases. Bubble properties are displayed in Table 2. The large standard deviation of bubble size reflects the nonuniformity of foam bubbles, with an average polydispersivity index of 0.62.

Fig. 8
figure 8

Bubble density and bubble size of LE foam as a function of total interstitial velocities

Full size image
Table 2 Bubble properties of LE foam injected at different total interstitial velocities
Full size table

At higher velocities, there is greater foam generation by lamella division. Compared to \({v}_{t}\) = 0.12 mm/s, bubble density of LE foam injected at \({v}_{t}\) = 6.79 mm/s increases by a factor of 3 and bubble size decreases by a factor of more than 4. Foam is finer at greater injection velocity.

Figure 9 shows the fraction of trapped gas and corresponding pressure gradient of the LE foam injected at different velocities. Trapped-gas fraction decreases as velocity increases. This is consistent with the finding of Jones et al. (2018) in a microfluidic model. The inverse response of gas trapping with velocity reflects two factors. At low velocities, LE foam bubbles are coarser due to less in-situ division of bubbles (Fig. 10). Smaller bubbles are less likely to be trapped, because aperture does not vary as much across the bubble as it does for a larger bubble. In addition, pressure gradient increases at higher velocities. More gas bubbles become mobile because the increasing viscous forces dominate over capillary forces. Consequently, the amount of stagnant gas diminishes as velocity increases.

Fig. 9
figure 9

Fraction of trapped gas and corresponding pressure gradient of LE foam injected at different velocities

Full size image
Fig. 10
figure 10

Images of foam texture at different interstitial velocities in section 5: left, at velocity 0.12 mm/s; right, at velocity 6.79 mm/s. Flowing gas is portrayed in black, trapped gas in blue, liquid in white. Liquid occupies areas with tighter aperture in the model fracture. Image size: 1.57 × 1.26 cm

Full size image

Compared to previous studies in geological porous media and microfluidic models, the fraction of trapped gas found in our model fracture is very small. At \({v}_{t}\) = 0.12 mm/s, the fraction of trapped gas is 6.9% (Fig. 10, left). When injection velocity increases up to 6.79 mm/s, there is no gas trapping and all bubbles are able to flow (Fig. 10, right).

Figure 11 displays a strongly shear-thinning rheology in the model fracture. Apparent viscosity decreases by a factor of 17, from 258 cp at \({v}_{t}\) = 0.12 mm/s to 15 cp at \({v}_{t}\) = 6.79 mm/s, in spite of the refinement in foam texture (Fig. 9). Meanwhile, the fraction of flowing gas increases from 93.1% to 100%. At this high flowing-gas fraction, it is challenging to argue that gas trapping plays a key role in a 17-fold increase in foam mobility.

Fig. 11
figure 11

Apparent viscosity of LE foam as a function of total interstitial velocities. The shear-thinning rheology reflects a power-law exponent (Bird et al. 2002) of 0.32

Full size image

5 Discussion

Gas trapping results from the competition between viscous and capillary forces. In this study, trapped-gas fraction is much less than usually found in geological porous media and microfluidic models.

This reflects major difference in geometry between fractures and porous media. The trapping of non-wetting phase in porous media is conventionally correlated to the capillary number:

$$ N_{{{\text{ca}}}} = \frac{\nabla P K}{{\gamma \cos \theta }} $$
(5)

where \(K\) is the permeability of porous media, \(\gamma \) is the interfacial tension, and \(\theta \) is the contact angle.

The geometry of the fracture pore space affects the mechanism of gas trapping in ways different from other porous media. AlQuaimi and Rossen (2018b) formulated a new capillary number \({N}_{\mathrm{ca}}^{^{\prime}}\) (Eq. 6) by adding a term (in brackets) to account for the effects of fracture geometry on trapping of non-wetting phase.

$$ N_{{{\text{ca}}}}^{^{\prime}} = \left( {\frac{\nabla P K}{{\gamma \cos \theta }}} \right)\left[ {\left( \frac{12}{2} \right) \left( {\frac{{d_{t} }}{{d_{H} }}} \right)^{2} \left( {\frac{{L_{t} }}{{d_{t} }}} \right) \frac{1}{{1 - \left( {\frac{{d_{t} }}{{d_{b} }}} \right)}}} \right] $$
(6)

where \({d}_{t}\), \({d}_{b}\) and \({L}_{t}\) are pore-throat aperture, pore-body aperture and pore length, respectively, determined from the spatial distribution of aperture in the fracture.

Figure 12 displays trapped-gas fraction as a function of the new capillary number. Data apart from the blue diamonds are from the non-wetting phase desaturation experiments in model fractures with a variety of geometries of AlQuaimi and Rossen (2018b). The blue data are our experimental results for trapped-gas fraction. They correlate well with the predictions using the new capillary number. The agreement is good despite at least two differences between our results and the assumptions of AlQuaimi and Rossen (2018b). They assumed a non-wetting-phase droplet of about pore size trying to get through the pore throat; our bubbles are smaller. They also assumed isolated non-wetting droplets immersed in the wetting phase. In our case, the individual lamellae between bubbles are not as tightly curved as they pass through pore throats as in that case. Despite the fact that the bubble distribution of foam in our study is different from a single droplet immersed in water in the study of AlQuaimi and Rossen (2018b), we believe that geometric factors (pore-throat aperture, ratio of throat to body aperture, etc.) that differ from one fracture to another would have a similar effect on the mobilization of trains of bubbles as on a single droplet. Nonetheless, this agreement testifies that viscous force is more significant compared to capillary force at our experimental conditions, hence yielding a small fraction of trapped gas in the fracture. The agreement between our results and this correlation suggests that the correlation could apply to fractures with other aperture distributions.

Fig. 12
figure 12

Trapped-gas fraction as a function of new capillary number. Standard deviation of the blue data is smaller than the scale of the symbol

Full size image

6 Conclusions

In this experimental study, to investigate gas trapping and foam mobility at a microscopic scale, we report a series of foam experiments at a fixed foam quality of 0.9 and a varying total interstitial velocities in a glass model fracture. The following conclusions have been reached:

  • Pre-generated foam was further refined after being injected into the model fracture, mainly by lamella division.

  • Foam has reached local equilibrium, where the rate of bubble creation equals the rate of bubble destruction, within our 1-m-long model fracture. In the last three sections of the model, foam has the same texture and apparent viscosity.

  • Foam texture was finer with increasing total interstitial velocity, because more in-situ foam generation took place at greater pressure gradient.

  • The fraction of trapped gas decreased as velocity increased, which agrees with the findings of Jones et al. (2018) in a microfluidic model. However, the trapped-gas fractions found in our model fracture (less than 7%) are much lower than usually reported for either geological porous media or microfluidics. At such a low fraction of trapped gas, the effect of gas trapping on foam mobility is expected to be relatively insignificant.

  • The experimental results for trapped-gas fraction in our study correlate well with the capillary-number correlation of AlQuaimi and Rossen (2018b). Using this correlation, one could predict the extent of gas trapping in fractures of other geometries or at other velocities or pressure gradients.