1 Introduction

Enzymatically induced calcium carbonate precipitation (EICP) is an engineering technology that employs enzymatic activity for altering geochemistry, thus resulting in precipitation of calcium carbonate. This is mostly due to hydrolysis of urea and catalyzed by ureases, which are widespread enzymes in soil bacteria and plants (Kappaun et al. 2018). In this study, we focus on EICP via ureolysis by the enzyme urease extracted from ground seeds of the Jack Bean Canavalia ensiformis, which are known for their high urease content. Urease catalyzes the hydrolysis reaction of urea (\({({\text{NH}}_2)_2\text{CO}}\)), resulting at typical environmental conditions in the products bicarbonate \(({\hbox {HCO}_{3}^{-}})\) and ammonium \(({\hbox {NH}_{4}^{+}})\), i.e.,

$$\begin{aligned} (\hbox {NH}_2)_2\hbox {CO} + 3 \hbox {H}_2\hbox {O} \xrightarrow {urease} \hbox {NH}_{4}^{+} + \hbox {H}_2\hbox {NCOO}^{-} + 2 \hbox {H}_2\hbox {O} \longrightarrow 2 \hbox {NH}_{4}^{+} + \hbox {HCO}_{3}^{-} + \hbox {OH}^{-}. \end{aligned}$$
(1)

The products of ureolysis, \({\hbox {HCO}_{3}^{-}}\) and \({\hbox {NH}_{4}^{+}}\), dissociate depending on pH. In the presence of calcium ions (\({\hbox {Ca}^{2+}}\)), this results in calcium carbonate (\({\hbox {CaCO}_{3}}\)) precipitation:

$$\begin{aligned}&{\hbox {NH}_{3} + \hbox {H}^{+} \rightleftharpoons \hbox {NH}_{4}^{+}}, \end{aligned}$$
(2)
$$\begin{aligned}&\quad {\hbox {H}_2\hbox {CO}_{3} \rightleftharpoons \hbox {H}^{+} + \hbox {HCO}_{3}^{-} \rightleftharpoons 2\hbox {H}^{+} + \hbox {CO}_{3}^{2-}}, \end{aligned}$$
(3)
$$\begin{aligned}&\quad {\hbox {Ca}_{2}^{+} + \hbox {CO}_3^{2-} \rightleftharpoons \hbox {CaCO}_3 \downarrow }. \end{aligned}$$
(4)

This yields the overall reaction

$$\begin{aligned} {\hbox {CO}(\hbox {NH}_2)_2 + 2\hbox {H}_2\hbox {O} + \hbox {Ca}_2^{+} \rightleftharpoons 2\hbox {NH}_4^{+} + \hbox {CaCO}_3 \downarrow }. \end{aligned}$$
(5)

EICP offers an engineering option to precipitate calcium carbonate in situ, and by that to alter porous medium parameters such as porosity and permeability as well as the strength and stiffness of the porous medium. Hence, EICP can be used similarly to other methods of inducing mineral precipitation, such as, e.g., microbially induced calcium carbonate precipitation (MICP), to seal high-permeable leakage pathways. This has been demonstrated for MICP in various studies, (Cunningham et al. 2019; Phillips et al. 2016; Cuthbert et al. 2013; Phillips et al. 2013,[28]).

Applications for soil stabilization are described in (Whitaker et al. 2018; Mujah et al. 2017; van Paassen et al. 2010), for coprecipitation of heavy metals in (Lauchnor et al. 2013; Mitchell and Ferris 2005), or for building or monument restoration in (Minto et al. 2018). EICP itself has already been applied for dust control (Hamdan and Kavazanjian 2016),[41], soil strengthening (Neupane et al. 2013), or to modify permeability (Nemati and Voordouw 2003).

Successful sealing results from a complex interplay between the transport of chemicals and urease, determined by fluid dynamics, the ureolysis as well as the precipitation reaction leading to clogging and thus a change in the transport-determining porous medium properties. Numerical modeling can employ conceptual ideas for these individual processes and mechanisms, and account for complex interactions between different processes. As such it improves process-understanding, optimizes experimental and field setups, and predicts, e.g., the outcome of the application of EICP.

Field-scale applications require a Darcy-scale approach to be able to account for the large domain sizes. The Darcy-scale models of EICP or MICP, e.g., (Hommel et al. 2020; Minto et al. 2019; Cunningham et al. 2019; Nassar et al. 2018; van Wijngaarden et al. 2016; Hommel et al. 2018) currently rely on simple parametrizations of the effects of precipitation on porous-medium properties, such as permeability. Especially for the sealing applications of EICP or MICP, the correct prediction of permeability is of outstanding importance. To improve on the simplistic relations currently used to describe the change in porous-medium Darcy-scale properties due to EICP or MICP, the pore-scale needs to be considered, as here Darcy-scale properties can be observed and described as changes in geometry.

This is experimentally possible due to advances in imaging technologies and their use, e.g., (Blunt et al. 2013; Wildenschild et al. 2013). From a modeling perspective, there are different approaches to the challenge of describing calcite precipitation at the pore scale. One can introduce a calcite volume fraction and determine by a threshold value whether to allow fluid flow (Yoon et al. 2012). A different idea is to determine the evolving surface of precipitated calcite. Of various suitable methods (Molins et al. 2020), the most straightforward is to describe the surface as a free boundary problem. In such sharp-interface models (van Duijn and Pop 2004), the interface between pore space and precipitated calcium carbonate evolves in time and gets characterized by its movement in normal direction. This approach requires a constant remeshing of the pore space available for flow, or more sophisticated methods of tracking the boundary, e.g., (Ray et al. 2019; Molins et al. 2012).

As an alternative, a diffuse-interface approach can be used. Phase-field models employ an additional order parameter to indicate the current phase. This order parameter is smoothed out between different phases, leading to a small diffuse transition zone. Such models have been previously used to account for both dissolution and precipitation, e.g., (van Noorden and Eck 2011; Redeker et al. 2016; Bringedal et al. 2020; Rohde and von Wolff 2020), as well as MICP without and with electrodiffusion, (Zhang and Klapper 2010) and (Zhang and Klapper 2011), respectively. Phase-field models are widely used to model interface dynamics, for the related issue of dendritic growth see (Takaki 2014) for a review.

In this study, we develop a phase-field model for EICP based on (Bringedal et al. 2020; Rohde and von Wolff 2020). For the reactions, we adopt simplifying assumptions of a constant ureolysis rate, calculated for the experimental conditions of (Weinhardt et al. 2020) based on the ureolysis kinetics of (Hommel et al. 2020). The precipitation process is assumed to be an equilibrium reaction, therefore crystal growth will be limited by the diffusion of ions to the crystal interface from the aqueous bulk liquid, which is oversaturated due to ureolysis.

Experimental and modeling investigations complement each other. The very small dimensions of the experimental setup do not allow for reliable measurements of local concentrations. Only minuscule volumes would be available for analysis and the volume of the inlet and outlet structures as well as the tubing are much larger than the volume of the region of interest.

Using complementary modeling, detailed concentration distributions, crystal growth rates and growth directions within the region of interest can be predicted reliably. The distribution of crystal aggregates and their growth over time is a measure available in both the experiment and the numerical simulation, allowing for a validation of the developed model by comparison of the model predictions with the experimental data. Note, that the developed model does not have any additional calibration parameters; the model estimates the calcite oversaturation due to enzymatic ureolysis in the inlet region using the jack bean-meal (JBM) extract ureolysis kinetics of (Hommel et al. 2020).

In this study, we show that the developed model reproduces the following observations of pore-scale experiments:

  • Crystal aggregates grow faster on their upstream side than on their downstream side, leading to a shift of the center of mass in the upstream direction.

  • Crystal aggregates grow faster in places of high flow velocity.

The study shows that our approach of diffusion-limited crystal growth reproduces the patterns observed in the experiments such as preferential growth toward the higher concentration gradient on the upstream side or in advection-dominated flow in pore throats. Perspectively, within a multi-scale approach, pore-scale models might inform Darcy-scale models what relation to use for predicting the change in Darcy-scale hydraulic properties and how to parameterize those relations.

2 Micro-Fluidic Experiments

2.1 Experimental Setup and Procedure

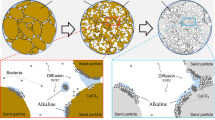
In this section, the micro-fluidic experiment is briefly described. More detailed information about the procedure and the setup can be found in the previous work of (Weinhardt et al. 2020). The micro-fluidic cells were produced by following the standard workflow of soft lithography (Karadimitriou et al. 2013; Xia and Whitesides 1998). The design of the micro-fluidic cell is shown in Fig. 1 and consists of an inlet channel, an outlet channel, and the actual domain of interest, which is a series of four identical circular pore bodies connected by rectangular pore throats. The details of the channels connected to the pressure sensors are not pictured here since the pressure measurements have been analyzed in detail in (Weinhardt et al. 2020) and are not in the focus of the present study here. There are two syringe pumps which induce the flow: Syringe 1 (\({{\mathrm{S}}_1}\)) is filled with an urea/calcium-chloride solution with equimolar concentrations of 1/3 \({\hbox {mol}}/{\hbox {L}}\). Syringe 2 (\({{\mathrm{S}}_2}\)) is filled with a solution extracted from a 5 \({\hbox {g}}/{\hbox {L}}\) JBM suspension by filtering through a 0.45 \(\mu\)m cellulose membrane. The reactive solutions mix in the T-junction, before entering the micro-fluidic cell via an inlet tube of the length 10 cm and an inner diameter of 0.5 mm.

The whole system was initially saturated with deionized water. The inlet tube, the inlet channel, the porous domain and the outlet channel were subsequently saturated with the reactant solutions. The pressure sensors end up in a dead end. Therefore, there is no flow in the channels connected to the pressure sensors. Once the micro-fluidic cell was saturated with the reactive solutions, a constant flow rate of 0.01 \({\mu }\)L/s was applied at both syringes for 5 h. The flow direction is indicated with blue arrows in Fig. 1. The transparent nature of polydimethylsiloxane (PDMS) allowed the direct visualization of the processes taking place in the pore space by using transmitted light microscopy. A description of the microscope used can be found in the work of (Karadimitriou et al. 2012). In Table 1, the concentrations of the reactive solutions, as well as the flow rates are summarized. The ambient temperature was \(23 ^\circ {\text {C}}\) throughout the experiment.

Fig. 1
figure 1

Schematic sketch of the micro-fluidic cell and its dimensions: It includes the inlet and outlet tubes (orange) connected to the inlet and outlet channels. The domain of interest consists of four pore bodies connected with pore throats. A part of it is shown enlarged in the bottom of the figure. The blue arrows indicate the flow direction of the reactive solutions, induced by the syringe pumps \({\mathrm{S}}_1\) and \({\text{S}}_{2}\), filled with urea calcium chloride solution and filtered JBM suspension respectively. Sketch based on (Weinhardt et al. 2020)

Full size image
Table 1 Concentrations and flow rate of the reactive solutions (based on (Weinhardt et al. 2020))
Full size table

2.2 Kinetics of Urea Hydrolysis

The hydrolysis of urea can be assumed to follow a first-order kinetic reaction with respect to the concentration of urea \(c_{\mathrm{urea}}\) (6) (Feder et al. 2020; Hommel et al. 2020). In this case, the reaction rate \(r_{\mathrm{u}}\) is a function of the molar concentration of urea \(c_{\mathrm{urea}}\) as well as the mass concentration of JBM extract, \(C_{\mathrm{JBM}}\).

$$\begin{aligned} r_{\mathrm{u}} = -\frac{d c_{\mathrm{urea}}}{dt} = k_{\mathrm{u}} c_{\mathrm{urea}} C_{\mathrm{JBM}} \end{aligned}$$
(6)

According to (Feder et al. 2020) and (Hommel et al. 2020), the temperature-dependent rate coefficient for enzymatic ureolysis, \(k_{\mathrm{u}}\), can be calculated using Arrhenius-type exponential relations. The expression (7) below is based on the experimental investigations of (Feder et al. 2020), with \(a_{\mathrm{u,0}}\) being the pre-exponential factor and \(a_{\mathrm{u,T}}\) being a lumped exponent describing the temperature dependence of the rate coefficient.

$$\begin{aligned} k_{\mathrm{u}} = a_{\mathrm{u,0}} e^{\left( \frac{a_{\mathrm{u,T}} }{ T}\right) } \end{aligned}$$
(7)

By integrating Equation (6) over time, the concentration of urea can explicitly be calculated at a certain time t, based on an initial concentration of urea, \(c_{\mathrm{urea, 0}}\):

$$c_{{{\text{urea}}}} (t) = c_{{{\text{urea}},0}} {\mkern 1mu} e^{{ - (k_{u} {\mkern 1mu} C_{{JBM{\kern 1pt} t)}} )}}$$
(8)

Consequentially, also the reaction rate can be determined explicitly at a certain time or, likewise, since the flow rate is constant, at a point along the flow path. The reaction takes place once the two solutions, as described in the previous section, mix. The mixing happens in the inlet tube, right after the T-junction (see Fig. 1). The residence time in the inlet tube, which is determined by the flow rate and the geometry of the inlet tube, is approximately 16 min. Since the residence time in the micro-fluidic cell is only a few seconds, we assume that the changes of the urea concentration are negligible. Therefore, the ureolysis reaction rate can be assumed to be constant throughout the micro-fluidic cell, while it is determined by the residence time in the inlet tube. Table 2 gives the relevant parameters to determine the ureolysis rate in the cell, assuming that there is no accumulation or inactivation of urease in the inlet tubing and the porous domain and the urease concentration is constant at the injected concentration of \(C_{\mathrm {JBM}}=2.5\,\, {\hbox {g}}/{\hbox {L}}\).

Table 2 Kinetic and other parameters to estimate the ureolysis rate based on Eq.  (6)
Full size table

2.3 Phase-Field Model

Multiphase problems can be modeled using a sharp- or a diffuse-interface approach. We consider here a diffuse-interface approach to allow for changes in topology, such as merging of crystal aggregates. Precisely, we rely on a phase-field model presented in (Rohde and von Wolff 2020). The model employs a phase-field parameter \(\phi\) for the volume fraction of fluid. That is, \(\phi = 1\) indicates the fluid phase and \(\phi = 0\) indicates the solid precipitate. The interface separating the fluid phase from the precipitated calcium carbonate is approximated by a thin diffuse transition region of width \(\varepsilon\). When the interface width \(\varepsilon\) approaches zero, the model converges to a classical sharp-interface model. Therefore, the interface width \(\varepsilon\) will be chosen small in comparison to the characteristic length scale of the micro-fluidic cell.

To present the model, we introduce as unknowns the phase-field parameter \(\phi\), the fluid velocity \({\mathbf {v}}\), the pressure p, and the inorganic carbon concentration c in the fluid. The model couples the equation for the transport, diffusion, and reaction of inorganic carbon

$$\begin{aligned} \partial _t (\phi c) + \nabla \cdot ((\phi {\mathbf {v}}+ J) c ) = \nabla \cdot (D \phi \nabla c) + \phi r_{\mathrm {u,cell}} - r_{\mathrm {precip}}(\phi ,c) \end{aligned}$$
(9)

with the Navier–Stokes equations in the fluid phase, given by

$$\begin{aligned} \nabla \cdot (\phi {\mathbf {v}})&= 0, \end{aligned}$$
(10)
$$\begin{aligned} \partial _t (\rho \phi {\mathbf {v}}) + \nabla \cdot (\rho (\phi {\mathbf {v}}+ J) \otimes {\mathbf {v}})&= -\phi \nabla p + \nabla \cdot (2 \gamma \nabla ^s {\mathbf {v}}) -\frac{12 \gamma }{h^2} {\mathbf {v}}- d(\phi ) {\mathbf {v}}. \end{aligned}$$
(11)

The phase-field parameter \(\phi\) is determined by the Cahn–Hilliard evolution

$$\begin{aligned} \partial _t \phi + \nabla \cdot J = - \frac{r_{\mathrm {precip}}(\phi ,c)}{c^*}, \qquad J = - M \nabla \mu , \qquad \mu = \frac{W'(\phi )}{\varepsilon } - \varepsilon \nabla ^2 \phi . \end{aligned}$$
(12)

Here, \(\rho\) is the fluid density, \(\gamma\) is the fluid viscosity, D is the diffusion coefficient of carbonate ions, and \(c^*\) is the molar density of the precipitated calcium carbonate. Values are taken from literature and listed in Table 1. From the Cahn–Hilliard evolution, we have a phase-field mobility M and a double-well potential W with minima at 0 and 1.

Equations (10), (11) are the Navier–Stokes equations, modified as follows. Firstly, they are formulated only for the fluid fraction \(\phi\). Secondly, the model is employed only in the two-dimensional geometry of the micro-fluidic cell. From the assumption of a parabolic flow profile across the height h of the cell, an additional drag term enters the Navier–Stokes equation, analogous to the derivation of a Hele–Shaw flow (Lamb 1932). Lastly, the model should ensure \({\mathbf {v}}\approx 0\) in the precipitated calcium carbonate, i.e., when \(\phi = 0\), and a no-slip condition between the solid and fluid phase. For this, the term \(d(\phi ) {\mathbf {v}}\) with

$$\begin{aligned} d(\phi ) = d_0 (1-\phi )^2 \end{aligned}$$

is introduced and the constant \(d_0\) is chosen sufficiently large. For more details, on the choice of \(d_0\), see Remark 2.3 in (Rohde and von Wolff 2020).

Equation (9) has two reaction terms on the right-hand side. The term \(r_{\mathrm {u,cell}}\) describes the hydrolysis of urea. As discussed in Sect. 2.2, this will depend on temperature, activity of urea, and mass concentration of enzyme. These values are assumed to be approximately constant in the micro-fluidic cell, as the time for fluid to pass through the cell is in the order of seconds. The value for \(r_\text {u,cell}\) is determined in Sect. 2.2 and is given in Table 2. In (Rohde and von Wolff 2020), no such bulk-reaction term is considered, but the extension of the analysis to the case with constant \(r_\text {u,cell}\) is straightforward. The second reaction term, \(r_{\mathrm {precip}}\), models the precipitation of calcium carbonate and is given by

$$\begin{aligned} r_{\mathrm {precip}}(\phi ,c) = k_{\mathrm {precip}} (c - c_{\mathrm {eq}} ) \max \big (\phi (1-\phi ) - 0.1 \;,\; 0\big ) . \end{aligned}$$
(13)

The reaction rate is proportional to the oversaturation \(c - c_{\mathrm {eq}}\) of inorganic carbon. The \(\phi\)-dependence of \(r_{\mathrm {precip}}\) ensures that precipitation only occurs at the interface to pre-existing crystals. As the precipitation process is fast in comparison to the hydrolysis of urea, it is assumed to be an equilibrium reaction. The choice for \(k_{\mathrm {precip}}\) is therefore not from literature, but instead big enough that equilibrium conditions can be observed at the interface at all times (Table 3).

Table 3 Parameters for the phase-field model
Full size table

2.4 Numerical Implementation

The Cahn–Hilliard evolution (12) does not ensure \(0\le \phi \le 1\), i.e., the fluid’s volume fraction \(\phi\) can exceed the physically relevant regime. To ensure that the phase-field model (10) - (12) does not degenerate because of \(\phi \le 0\), we modify our system exactly as in (Rohde and von Wolff 2020). A new small number \(\delta\) is introduced and quantities depending on \(\phi\) have to be modified by \(\delta\) to ensure positivity. The choice \(\delta = \text {5E-03}\) keeps the numerical system stable while barely perturbing the solution.

The equations are discretized by a finite element method, with Taylor–Hood elements for velocity \({\mathbf {v}}\) and pressure p, and second-order Lagrange elements for concentration c and phase-field parameter \(\phi\). All equations are discretized fully implicit in time, i.e., by implicit Euler method. We do not solve the system monolithically, but instead iterate between solving the Navier–Stokes equations (10), (11) and equations (9), (12) until convergence.

The implementation was done in Dune-PDELab (Bastian et al. 2010) using ALUGrid (Alkämper et al. 2016). This comes with the benefit of adaptive grid generation. The phase-field model requires small grid cells to resolve the diffuse interface, while grid cells at larger distance to the interfaces can be considerably larger. Fig. 2 shows a section of the grid containing one crystal aggregate. The grid is adapted after each timestep to account for the evolving interfaces.

Fig. 2
figure 2

Part of the grid used for the simulation in Sect. 3. The grid is refined at the interface between the fluid phase and the precipitated calcium carbonate

Full size image

One major challenge for the simulation is the relatively fast flow in the order of mm/s compared to the total runtime of the experiment of multiple hours. The flow regime introduces a severe restriction on the timestep dt. For the simulation of the full system, including the flow, small timesteps of size \(dt = 0.01 s\) are used, making the simulation computationally demanding. To tackle this problem, a special timestepping is introduced; small timesteps are needed to resolve the interplay between transport, diffusion, and reaction. After a few seconds in the simulation, transport, diffusion and reaction balance each other and all unknowns change on the timescale of minutes. This is facilitated by the laminar flow regime. At this stage, the only process leading to a change in unknowns is the growth of precipitated calcium carbonate. This growth happens rather slowly, i.e., on a larger timescale, and it is now possible to only update the phase field \(\phi\) using

$$\begin{aligned} \partial _t \phi = - \frac{r_{\mathrm {precip}}(\phi ,c)}{c^*} \end{aligned}$$
(14)

with a larger timestep \(dt = 10 s\), while keeping all other unknowns constant. After this big timestep, smaller timesteps with the full system are again performed until a quasi-static state is reached. A sketch of such a timestepping procedure is shown in Fig. 3

Fig. 3
figure 3

Sketch of the timestepping algorithm, with small and big timesteps

Full size image

2.5 Calculation of the Inflow Conditions

The simulation of the experiment is performed on the domain consisting of pore throats and pore bodies, without the inlet and outlet region of the micro-fluidic cell, see Fig. 1. At the inflow boundary of the simulation domain, both fluid velocity \({\mathbf {v}}_{\mathrm {in}}\) and inorganic carbon concentration \(c_{\mathrm {in}}\) have to be prescribed. The velocity is chosen as a parabolic flow profile with total flow rate of 0.02 \({\mu }\)L/s. In contrast, it is more difficult to determine the inorganic-carbon concentration \(c_{\mathrm {in}}\) at the inflow boundary.

The hydrolysis of urea begins as soon as the reactant solutions mix in the T-junction before the inlet tube. Due to the residence time in the tube of 16 min, see Table 2, the inorganic carbon produced in this time cannot be neglected. While integrating the reaction rate (6) over the residence time gives an upper bound for \(c_{\mathrm {in}}\), the actual value is much lower because of precipitation in the inflow tube and the inlet area of the micro-fluidic cell.

Therefore, to determine the concentration \(c_{\mathrm {in}}\), we have to take into consideration the distribution of precipitated carbonate in the inlet area of the micro-fluidic cell. We use the knowledge about the model reaching a quasi-static state as described in Sect. 2.4. In case the inlet area is long enough, this state will be reached before the inflow boundary of the main simulation. Figure 4 shows a picture of the inlet area taken at the end of the experiment. For the simulation, a section S of the inlet area is used as representative for the whole inlet area. This justifies using periodic boundaries at inflow and outflow boundary of S. Now, the flow profile around the precipitated carbonate can be calculated by solving for steady-state solutions of (10), (11) in S. Next, the inorganic-carbon concentration c in the inlet section is determined by

$$\begin{aligned} \nabla \cdot (\phi {\mathbf {v}}c ) = \nabla \cdot (D \phi \nabla c) + \phi r_{\mathrm {u,cell}} - r_{\mathrm {precip}}(\phi ,c). \end{aligned}$$
(15)

This equation is a steady state version of (9). The concentration \(c_\mathrm {in}\) is then calculated as the flux average

$$\begin{aligned} c_\mathrm {in} = \frac{\int _S c \phi {\mathbf {v}}\cdot {\mathbf {e}}_1 dx}{\int _S \phi {\mathbf {v}}\cdot {\mathbf {e}}_1 dx} \end{aligned}$$

where \({\mathbf {e}}_1\) is the unit vector pointing from inflow to outflow boundary of S. We obtain the slightly oversaturated inflow condition \(c_\mathrm {in} = 3.150E-04\,\, {\hbox {mol}}/{\hbox {l}}\).

Fig. 4
figure 4

Left: Calcite precipitation in the inlet area after the experimental run. A representative section S is highlighted by a white-colored boundary. Right: Simplified precipitate distribution in the section S used for simulation

Full size image

3 Results and Discussion

We compare results (Weinhardt et al. 2020) of the experiment described in Sect. 2.1 with the mathematical model of Sect. 2.3. The exact locations of the points of nucleation are different for each repetition of the experiment; they are obviously subject to effects which we have to denote for now as random since we attribute them to conditions that are not easy to analyze in the details, such as impurities of the PDMS surface as hypothesized in (Weinhardt et al. 2020). In any case, we cannot determine or predict the points of nucleation a-priori, thus we use here data from an experimental run 52 min after start to determine the initial nuclei for the simulation model.

The model leaves its range of validity in approaching conditions of clogging; it is therefore stopped shortly before clogging. We compare the results of the final state of the simulation with a corresponding state of the experimental run that shows similar clogging behavior. In the comparison, we characterize crystal aggregates by centroid and volume.

Fig. 5
figure 5

Top: Fluid volume fraction \(\phi\) in initial and final state of the simulation. Bottom: Corresponding states of the experimental run

Full size image

Figure 5 shows the initial and the final distribution of precipitated calcite in both experiment and simulation. All crystal aggregates show some growth, and we observe near-clogging at the end of the third pore body. For further investigation and more convenient referencing, we number the crystal aggregates from left to right, as shown in Fig. 6. The three crystal aggregates at the end of the third pore body are excluded from the comparison and thus numbering, since they merged during the experiment. Also, new nucleation points forming after the initial 52 min are not considered, as they would have to be placed into the running simulation. The black dot in the pore throat between the third and the fourth pore body is an impurity of the micro-fluidic cell and not a calcite crystal.

While the final state of the simulation and the corresponding state of the experimental run match fairly well, the elapsed time in experiment and model is different. The pictures of the experiment shown in Fig. 5 are at 52 min and 112 min after the start of the experiment. Compared to the elapsed 60 min, the simulation reaches its final state after 287 min. There are several reasons for this. Firstly, the model is two-dimensional and therefore cannot capture all effects of flow around the precipitates. In particular, it assumes that crystal aggregates span the whole height of the micro-fluidic cell, i.e., they form cylindrical shapes. Weinhardt et al. (2020) show that this is not true and this will be discussed further in Sect. 3.2. Secondly, the model neglects electrodiffusion, which has been shown to enhance the precipitation process in similar models, see (Zhang and Klapper 2011). Lastly, both the ureolysis rate \(r_\mathrm {u,cell}\) and the determination of the inorganic carbon concentration \(c_\mathrm {in}\) at the inflow boundary are subject to uncertainty. We find from multiple simulation runs that the crystal-growth rate is approximately reciprocal to \(r_\mathrm {u,cell}\).

3.1 Movement of Centroids

Fig. 6
figure 6

Growth of precipitates; top: Change of the position of the centroids as vector (20 times enlarged) for simulation (blue) and the experiment (red); bottom left: change of the position of centroids relative to the initial location for the crystal aggregates 2 and 4; bottom right: streamlines and inorganic carbon concentration c around the crystal aggregates 2 and 4, obtained from the simulation

Full size image

We determine the centroid of each crystal aggregate in the simulation by integrating over an area containing the crystal aggregate. For the experimental data, the same is done after image segmentation. In Fig. 6, the evolution of the centroids relative to the initial position is shown.

In both experiment and simulation, it can be observed that the values of the x-coordinate of the centroids decrease over time, i.e., the crystal aggregates grow in upstream direction. To comprehend this, we exemplary consider crystal aggregates with numbers 2 and 4. In Fig. 6, the inorganic carbon concentration around crystal aggregate 5 is shown. The oversaturated calcium carbonate gets transported to the upstream side of the aggregate and precipitates there due to the fast timescale of precipitation. When the fluid reaches the downstream side of the aggregate, little oversaturation of calcium carbonate is left and therefore nearly no precipitation is observed at this side.

We conclude from the simulation that the growth process is governed by the interplay of transport and diffusion close to the crystal aggregate. A lower flow rate and more diffusion lead to a less pronounced growth in the upstream direction. Indeed, this can be observed when comparing pore throats, which have a high flow rate, with pore bodies. Figure 6 shows that crystal aggregates located in pore throats grow more in the upstream direction than crystal aggregates located in pore bodies.

A second observation is that in both experiment and simulation the centroids mainly grow toward the center of the channel, as seen exemplary for crystal aggregate 4 in Fig. 6. The primary cause for this effect is that once the precipitate reaches a wall, it cannot grow further in this direction. Another cause is that the flow velocity close to the wall is small. Therefore, more calcium carbonate gets transported to the side of the crystal aggregate facing toward the center of the channel than to the most upstream point. Consequently, the centroid moves toward the center of the channel.

In contrast to the simulation, the centroid of crystal aggregate 1 moves toward the wall in the experiment, see Fig. 6. This is one of the major differences observed between model and experiment. One possible reason for this is a new nucleation point in front of crystal aggregate 1 that formed only during the experiment. This new nucleation point cannot be taken into account in the simulation, as it was not present in the model’s initial configuration. Another possible reason is challenges in image segmentation, due to the reflective surface of the crystal aggregate.

In conclusion, the model matches the observed data well, and thus can capture dominating mechanisms for determining crystal-growth directions in this micro-fluidic EICP setup. Growth of the crystal aggregates leads to a shift of centroids in the upstream direction, and this effect is more pronounced in pore throats, where the flow rate is higher.

3.2 Growth of Crystal Aggregates

While the previous section focused on the direction of growth of the precipitates, we compare now the volume change of the crystal aggregates. The mathematical model is two-dimensional and assumes that \(\phi\) is constant across the height of the micro-fluidic cell. Therefore, the volume of the precipitates can be computed by integrating over the calcite fraction \(1-\phi\) and subsequently multiplying by the height of the cell. The three-dimensional shape of the crystal aggregates is therefore obtained by extruding the two-dimensional data, which cannot analogously be applied for the experimental data. It has been shown by (Weinhardt et al. 2020), that the most suitable shape approximation for estimating the (3D) volume of the precipitates in micro-fluidic cells from (2D) optical microscopy data is the spheroidal shape. A representative radius is calculated from the projected area of the aggregates. Based on this radius, the volume can be derived for the assumption of a spheroidal shape. This approach is described in (Weinhardt et al. 2020) and is based on the idea given in (Kim et al. 2020). During the here investigated time frame of 60 min the radii of the crystal aggregates range from approximately 5 \(\mu\)m to 35 \(\mu\)m. Compared to the height of the channel of 85 \(\mu\)m, the radii of the crystal aggregates are smaller than half of the channel height. Therefore, the crystal aggregates are not expected to reach all the way from the bottom to the top of the micro-fluidic cell.

Fig. 7
figure 7

Growth of precipitates; (a) Total growth of volume over the velocity magnitude at the initial position of the crystal aggregates, obtained from stationary Stokes simulation without precipitates. (b) Total growth of the volume over the velocity integrated over the area around the crystal aggregates, as obtained from the numerical model (9)-(12)

Full size image

In Fig. 7(a), the growth of the precipitates is plotted over the velocity magnitude at the initial position of the precipitates. These velocity values are obtained from a stationary flow simulation without any precipitates present. More precisely, this means solving a stationary version of equations (10) and (11) with \(\phi =1\) and \(J=0\) everywhere. We will call velocities obtained from this simulation initial velocities.

As the growth of the precipitates is mainly driven by the transport of carbonate ions to the crystal aggregates, the initial velocity at the nucleation points gives a good estimate for the carbonate supply at specific locations in the domain. Exemplary, we compare crystal aggregates 4, 5 and 6, as labeled in Fig. 6. Crystal aggregate 6 is located at the outer part of a pore body. This leads to a relatively small initial velocity and a slow growth of volume. In contrast, crystal aggregate 5 lies in the center of the pore body and right after a pore throat. This implies a high initial velocity and, therefore, a large amount of carbonate ions passing by. Crystal aggregate 4 is in a pore-throat, where generally the velocities are high due to the reduced cross-sectional area. However, it sits right at the wall of the throat, where the velocity is reduced due to the shear forces caused by the wall friction.

From this analysis, we conclude that there is a tendency of the crystal aggregates to grow faster and bigger where the initial velocities are higher. This is directly linked to the supply of carbonate ions. The linear regressions, illustrated as dashed lines in Fig. 7(a), show a good agreement between simulation and the experiments. As already mentioned in Sect. 3.1, crystal aggregate 1 is again an obvious outlier and is therefore excluded for determining the linear regression of the experimental data. The coefficient of determination (R2) for the simulation data clearly indicates a linear trend, while the one for the experimental Dataset indicates a weaker, but still significant trend.

However, the initial velocity does not take into account that the fluid flow is influenced by the precipitates. Especially in pore-throats precipitates reduce the cross-sectional area and lead therefore to higher velocities. As our introduced mathematical model includes the influence of precipitates on the fluid flow, we expect a better correlation when evaluating the velocity for the full model. The result is shown in Fig. 7(b), where we use the velocity field obtained from the full numerical model for the initial calcite distribution. We cannot evaluate the velocity at the center of the crystal aggregates, as there is no fluid flow in the precipitates. Instead, we now integrate the magnitude of the velocity over a disk shaped area around the crystal aggregates. The center of the disk coincides with the center of the crystal aggregate, and the radius is 1.8 times the diameter of the crystal aggregate.

Compared to Fig. 7(a), the results in Fig. 7(b) show an more evident linear correlation between the velocity magnitude close to the precipitates and the volume growth of the precipitates. The coefficient of determination for the simulation increased from 0.72 to 0.75. We conclude that the velocity field plays a significant role for the growth of the precipitates and the influence of precipitates on the flow field should not be neglected.

4 Conclusions

We have developed a phase-field approach for modeling crystal growth in enzymatically induced calcite precipitation and compared it to micro-fluidic experiments. Without any additional calibration there is a good qualitative agreement between model and experiment. Quantitatively, there is a very good agreement for the movement of centroids, and a good agreement for the growth of crystal aggregates. Only the predicted time until near-clogging differs significantly.

This joint experimental and numerical study allows for new insights into the dominant processes and mechanisms involved in the growth of crystal aggregates. We have seen that growth is strongly dependent on the flow conditions, i.e., the flow field and corresponding concentrations of the inorganic carbon. The concentrations are subject to local changes due to reaction but also due to the complexity of the flow field which is influenced by the geometry of the flow cell and the pattern of precipitates. In particular, for a single crystal aggregate, the growth is determined by the interplay between transport around the aggregate and diffusion toward the surface.

It has been observed consistently in experiment and simulation that nuclei show a clear tendency toward growing upstream and toward the center of the channel. Additionally, the growth rate is correlated with the magnitude of flow velocity, leading to a faster growth in the center of the channel.

A better understanding of the pore-scale mechanisms involved in EICP-related growth of crystals will contribute to developing optimization strategies for an effective use of the EICP technology. Perspectively, the phase-field approach presented here can be further developed to describe also microbially induced precipitation (MICP), where the mechanisms of growth are even more complex due to the involvement of biofilm in the pore space.