A Reactive Transport Model for Biogrout Compared to Experimental Data

Abstract

Biogrout is a method for reinforcement of granular soil. In the Biogrout process, calcium carbonate is produced. This solid connects the grains, and therefore the strength of the soil is increased. The calcium carbonate is formed with the use of micro-organisms. Experiments and numerical simulations have been performed to demonstrate the process under various conditions. In this paper, it has been examined whether a reactive transport model can be used to describe a Biogrout experiment that was performed in a column with a length of 5 m. Four different models for the course of the reaction rate are considered. The concentration of micro-organisms and the reaction rate are fine-tuned in order to find a description of the experiment that is a best fit for the particular model. This is done by minimizing the error between the experimental and numerical results for the concentration of calcium carbonate and the by-product of the reaction.

1 Introduction

Biogrout is a method to reinforce granular soil. Some possible applications are: prevention of piping and liquefaction, stabilization of soil prior to tunneling and slope stabilization. In order to control the process, a reliable predictive model is needed.

The Biogrout process is based on microbially induced carbonate precipitation (MICP) (Bang et al. 2001; Cheng et al. 2014; DeJong et al. 2006) and is a bio-mediated soil improvement method (DeJong et al. 2010, 2013; Ivanov and Chu 2008). The proposed variant of Biogrout is urea-based. For a review on urea-based MICP, see Phillips et al. (2013).

Micro-organisms play an important role in the Biogrout process. They are present in the soil or injected into it. They are supplied with urea $({\hbox {CO}(\hbox {NH}_2)_2})$ and calcium chloride $({\hbox {CaCl}_2})$, and then, they catalyze the hydrolysis of urea. The hydrolysis reaction is given by

$$\begin{aligned} \hbox {CO}(\hbox {NH}_2)_2 + 2 \hbox {H}_\mathrm{2}\hbox {O} \xrightarrow {\hbox {bacteria}} 2 \hbox {NH}_4^+ + \hbox {CO}_3^{2-}. \end{aligned}$$

(1)

Via this reaction, carbonate $({\hbox {CO}_3^{2-}})$ and ammonium $({\hbox {NH}_4^+})$ are produced. In the presence of calcium $({\hbox {Ca}^{2+}})$, the carbonate precipitates as calcium carbonate $({\hbox {CaCO}_3})$:

$$\begin{aligned} \hbox {Ca}^{2+} + \hbox {CO}_3^{2-} \rightarrow \hbox {CaCO}_3\hbox {(s)}. \end{aligned}$$

(2)

In an aqueous solution, all ionic species form chemical equilibria, which highly depend on pH. In van Paassen (2009) and Whiffin et al. (2007), these reactions are discussed in more detail. The overall net reaction equation is given by

$$\begin{aligned} {\hbox {CO}({\hbox {NH}_2})}_2 + \hbox {Ca}^{2+} + 2 \hbox {H}_\mathrm{2}\hbox {O} \rightarrow 2 \hbox {NH}_4^+ + \hbox {CaCO}_3(\hbox {s}). \end{aligned}$$

(3)

Since hydrolysis is slow compared to precipitation, the hydrolysis rate determines the reaction rate of the overall reaction (3). In van Paassen (2009), reaction (3) has been modelled with and without including the equilibria. Both approaches led to the same results for urea, calcium, ammonium and calcium carbonate. Concentrations of all other species are less than 1 % of the main compounds and seem to be negligible. The final pH is hardly influenced by the combined reaction. Ammonium (${\hbox {NH}_4^+}$) is the by-product of this reaction and has to be removed.

The Biogrout process aims at producing calcium carbonate. This solid forms connections between the grains by which the strength of the soil increases. However, the formation of a solid in the pores decreases the porosity and also leads to a decrease in permeability. This influences the flow and transport. Furthermore, due to the reaction, the fluid concentrations change, which leads to a change in the fluid density. Combining these phenomena leads to a coupled reactive transport model. Some articles about modelling reactive flow and transport in porous media are Agosti et al. (2015), Chilakapati et al. (2000), Radu et al. (2013), Radu and Pop (2010), Radu and Pop (2011); Samper and Zhang 2006), van Noorden (2009), van Noorden et al. (2010), Yang et al. (2008), of which Agosti et al. (2015), Radu et al. (2013), van Noorden (2009) also consider a variable porosity. In van Noorden (2009), the level set function is used for the boundary of the crystals and a homogenization procedure is applied to obtain the upscaled equations. In Radu et al. (2013), the differential equation for the porosity is comparable to the one used in this article. In Radu and Pop (2010), Radu and Pop (2011), the Newton method is used to deal with the nonlinear equations and the convergence of this method is studied.

In this paper, it is examined whether the reactive transport model for Biogrout, proposed in van Wijngaarden et al. (2011), is able to describe a Biogrout experiment that was performed. This Biogrout experiment has been described in Whiffin et al. (2007) and van Paassen (2009). A 5-m-long PVC tube was placed vertically and filled with sand. Ten sample points were made in the column. The flow direction during the experiment was downward. First, micro-organisms were injected, followed by a pulse of a saline fluid to fixate the micro-organisms. Then, the column was filled with a urea and calcium chloride solution. After the injection of this solution, the flow was stopped, but the reaction could proceed. During the experiment, samples were taken from the sample points. At the end of the experiment, the calcium carbonate content in the tube was measured at several locations on samples of 1–4 g. The ammonium concentrations that were measured in the sample points and the final calcium carbonate content are used to fine-tune the concentration of fixated micro-organisms and the reaction rate.

In Sect. 2, this Biogrout experiment is described in more detail. The mathematical model is given in Sect. 3, including the initial conditions and boundary conditions that are used to simulate the experiment. In Sect. 4, it is discussed which numerical methods are used for these simulations. The results of both the experiment and the simulations are given in Sect. 5, and a discussion along with some conclusions can be found in Sect. 6.

2 Materials and Methods

In this section, the Biogrout experiment that was performed is described. More details are given in Whiffin et al. (2007) and van Paassen (2009).

2.1 Column Preparation

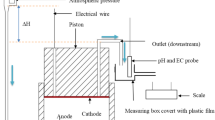
A 5-m-long PVC tube with an internal diameter of 66 mm was placed vertically and filled with a sand from a quarry in Itterbeck, Germany (Smals IKW, SZI 0032, also referred to as Itterbeck fine). This sand was uniform, fine to medium grained: $d_{10}=110\,\upmu \hbox {m}$ (10 % of the grains have a diameter of this size or lower); $d_{50}=165\,\upmu \hbox {m}; {d}_{90}=275\,\upmu \hbox {m}; {d}_{60}/d_{10}=1.64$; (BSI 1999). It is mainly siliceous (97 %). The packing of the sand was conducted under water to avoid the inclusion of air pockets. The mean particle size of the sand grains was 165 $\upmu$m, and the porosity was 0.378. Each end of the column was fitted with filter material. Ten pore fluid sampling ports were placed in the column, namely at 0.25 m from the top of the column, at 0.5 m, and thereafter at intervals of 0.5 till 4.5 m. The flow direction during the experiment was downward. A pump was installed at the bottom of the column to regulate the outflow rate. The top of the column was connected to the supply with the urea/calcium solution, and hence, no air could enter the column. During the experiment, samples were taken from the sampling ports.

2.2 Experiment

First, 6.34 l of a liquid containing micro-organisms were injected at a flow rate of 0.35 l/h. The micro-organism used was Sporosarcina pasteurii. It contains the enzyme urease which can hydrolyze urea. The production of ionic species from nonionic substrates generates an increase in overall conductivity of the solution. The urease activity of the micro-organisms is determined by measuring this increase in conductivity before injection. This activity was 0.23 mS/min. As determined in Whiffin (2004), this corresponds to $4.26\times 10^{-5}$ kmol-urea/m$^3$/s. In order to immobilize the micro-organisms in the column for use in subsequent cementation, the injection of micro-organisms was followed by 5.99 l of 0.050 kmol/m$^3$ calcium chloride solution, as proposed in Harkes et al. (2010). The flow rate was again 0.35 l/h. The next phase is the cementation phase, which also consists of two parts. First, 8.72 l of a 1.1 kmol/m$^3$ urea and calcium chloride solution was injected with a flow rate of 0.35 l/h. Subsequently, the flow is stopped and the column is left for 102 h to react. Finally, the column is flushed with tap water and dismantled, and the calcium carbonate content is determined at several locations. The injection scheme and the values of the various parameters (input for the simulations) are summarized in Tables 1 and 2.

Table 1 Injection scheme for the experiment

Table 2 Values of various parameters that are input for the simulations (part I)

3 Mathematical Model

In this section, the model equations and the initial and boundary conditions that are used to simulate the Biogrout experiment are given. They are discussed in more detail in van Wijngaarden et al. (2011) and van Wijngaarden (2013).

3.1 Model Equations

Important parameters in the Biogrout model are the concentrations of the species in chemical reaction (3). The advection–dispersion–reaction equation is used to model the concentration of the aqueous species:

$$\begin{aligned} \frac{\partial (\theta C^{i})}{\partial t}=\nabla \cdot (\theta \mathbf {D} \nabla C^{i}) - \nabla \cdot (\mathbf {q} C^{i}) + m_i \theta r_\mathrm{hp}. \end{aligned}$$

(4)

In this equation, $C^i$ (kmol/m$^3$) is the concentration of species $i, i \in \{\hbox {urea}, \mathrm {Ca^{2+}}, \mathrm {NH_4^+}\}$, $\theta$ (1) is the porosity, $\mathbf {D}$ (m$^2$/s) is the dispersion tensor, $\mathbf {q}$ (m/s) is the Darcy flow velocity, $r_\mathrm{hp}$ (kmol/m$^3$/s) is the rate of both the hydrolysis and the precipitation reaction which are equal during the major part of the reaction period (van Paassen 2009), and $m_i$ is a constant that follows from the stoichiometry of the reaction. As urea and calcium are consumed in the same ratio, their values of $m_i$ are equal and negative: $m_\mathrm{urea}=m_{\mathrm{Ca}^{2+}}=-1$. For the produced ammonium, the value is $m_{\mathrm{NH}_4^+}=2$. The coefficients of the dispersion tensor $\mathbf {D}$ are given by $D_{ij}=(\alpha _\mathrm{L}-\alpha _\mathrm{T})\frac{v_iv_j}{|\mathbf {v}|}+\delta _{ij}(\alpha _\mathrm{T}\sum _i \frac{v_i^2}{|\mathbf {v}|}$+$D_m)$, with $v_i=q_i/\theta$ (m/s) the pore water velocity and $D_m$ (m$^2$/s) the diffusion coefficient, see Zheng and Bennett (1995). The quantity $\alpha _\mathrm{L}$ (m) is the longitudinal dispersivity, and $\alpha _\mathrm{T}$ (m) is the transverse dispersivity. The term at the left-hand side of (4) is the accumulation term, and the first term at the right-hand side stands for dispersion and diffusion, the second term for advection, and the last term for the reaction. Urea and calcium are consumed in the same ratio. Choosing an equal dispersion tensor for urea and calcium gives two identical differential equations. Since the initial and boundary conditions are also identical, these concentrations are equal.

Calcium carbonate is a non-aqueous species, and it has been assumed that it is not transported. Hence, its partial differential equation does not contain an advection and dispersion/diffusion term. Its concentration $C^{{\mathrm{CaCO}_3}}$ (kg/m$^3$) is given in mass per total volume rather than per pore volume, as is done for the aqueous species. The molar mass of calcium carbonate $m_\mathrm{CaCO_3}$ (kg/kmol) is used to convert from kilomoles into kilograms. This gives the following differential equation for the calcium carbonate concentration:

$$\begin{aligned} \frac{\partial C^{\mathrm{CaCO}_3}}{\partial t}= m_{{\mathrm{CaCO}_3}} \theta r_\mathrm{hp}. \end{aligned}$$

(5)

The solid calcium carbonate is formed in the pores. This process decreases the porosity. The density of calcium carbonate, $\rho _{\mathrm{CaCO}_3}$ (kg/m$^3$), is used to calculate the volume that a certain amount of calcium carbonate occupies. Hence, the following differential equation for the porosity results:

$$\begin{aligned} \frac{\partial \theta }{\partial t}=-\frac{1}{\rho _{\mathrm{CaCO}_3}}\frac{\partial C^{\mathrm{CaCO}_3}}{\partial t}. \end{aligned}$$

(6)

Solving this differential equation gives the following relation between the calcium carbonate concentration and the porosity:

$$\begin{aligned} \theta (\mathbf {x},t)=\theta (\mathbf {x},0)-\frac{C^{\mathrm{CaCO}_3}(\mathbf {x},t)-C^{\mathrm{CaCO}_3}(\mathbf {x},0)}{\rho _{\mathrm{CaCO}_3}}. \end{aligned}$$

(7)

Substituting Eq. (5) into Eq. (6) gives the following differential equation for the porosity:

$$\begin{aligned} \frac{\partial \theta }{\partial t}=-\frac{m_{{\mathrm{CaCO}_3}}}{\rho _{\mathrm{CaCO}_3}} \theta r_\mathrm{hp}. \end{aligned}$$

(8)

This equation is similar to the differential equation for the porosity that is used in Radu et al. (2013), where a model for concrete carbonation is considered. Both differential equations for the porosity contain a precipitation reaction rate and a multiplication with the porosity $\theta$, indicating that the precipitation reaction does not take place in the solid, but in the pore space or on the boundary of the solid. There are also some differences, but they do not lead to any substantial deviations in the calculated results. The equation for the porosity in Radu et al. (2013) contains some extra terms to prevent the porosity from exceeding one or becoming negative. Besides this feature, dissolution is also taken into account and the value of the precipitation rate depends on the difference between the concentration of the chemicals in solution and its equilibrium. As discussed in Sect. 1, in (the urea-based) Biogrout the (net) dissolution is negligible. Since the reaction rate in this article is nonnegative, the porosity is non-increasing and due to its initial value between zero and one, the porosity will never exceed one in the current modelling. If the porosity becomes very small, the permeability will drastically decrease according to the Kozeny–Carman relation. In a pressure-driven case (with the pressure prescribed on boundaries rather than the flow), there will hardly be any flow to the clogged zone nor will there hardly be any supply of nutrients and the porosity will not decrease further. If the flow is prescribed on a boundary and the fluid is pressed through the clogged porous media, this will result in extremely high pressures. High pressures will lead to cracks and preferential flow through the cracks. One could use a poro-elastic model where one evaluates the local stresses to predict the initiation of cracks. The appearance of cracks could give a sudden increase in the porosity and permeability. This issue is not dealt with in the current modelling.

For the flow, the continuity equation that was derived in van Wijngaarden (2013) is used. This equation is an adaptation of the differential equation derived in van Wijngaarden et al. (2011).

$$\begin{aligned} \nabla \cdot \mathbf {q} = K \theta r_\mathrm{hp}. \end{aligned}$$

(9)

The constant K (m$^3$/kmol) deals with volume changes due to the reaction and has been defined as

$$\begin{aligned} K:=V_\mathrm{decrease\_of\_pore\_space}-V_\mathrm{decrease\_of\_liquid\_volume}. \end{aligned}$$

(10)

Next, the above formula will be explained. The constant K deals with two processes:

• 1. As a result of the production of the solid calcium carbonate in the pores, there is less space available for the fluid. This space reduction per kmol produced calcium carbonate equals the molar volume of calcium carbonate: $V_\mathrm{decrease\_of\_pore\_space}={m_{\mathrm{CaCO}_3}}/{\rho _{\mathrm{CaCO}_3}}$ m$^3$/kmol. Recall that $m_{\mathrm{CaCO}_3}$ is the molar mass of calcium carbonate and that $\rho _{\mathrm{CaCO}_3}$ is the density of calcium carbonate. Hence, the decrease in pore space per unit of time and volume is $V_\mathrm{decrease\_of\_pore\_space}\theta r_\mathrm{hp}={m_{\mathrm{CaCO}_3}}/{\rho _{\mathrm{CaCO}_3}} \theta r_\mathrm{hp}$.

• 2. The hydrolysis and precipitation reactions cause a decrease in liquid volume. This decrease is partly caused by the water uptake in reaction (3). Furthermore, urea and calcium do not occupy the same amount of volume as the produced ammonium. In van Wijngaarden et al. (2012), it has been derived that $V_\mathrm{decrease\_of\_liquid\_volume}=0.030$ m$^3$/kmol. Therefore, the decrease in liquid volume per unit of time and volume is $V_\mathrm{decrease\_of\_liquid\_volume}\theta r_\mathrm{hp}$.

Note that Eq. (9) is consistent with the Oberbeck-Boussinesq approximation as $r_\mathrm{hp}\rightarrow 0$, i.e., in the absence of the reaction.

Adding Eqs. (8) and (9) gives

$$\begin{aligned} \frac{\partial \theta }{\partial t} + \nabla \cdot \mathbf {q} = \left( K -\frac{m_{\mathrm {\mathrm{CaCO}_3}}}{\rho _{\mathrm{CaCO}_3}} \right) \theta r_\mathrm{hp}. \end{aligned}$$

(11)

Substitution of the definition of constant K (10) into Eq. (11) gives the following balance equation:

$$\begin{aligned} \frac{\partial \theta }{\partial t} + \nabla \cdot \mathbf {q} = - V_\mathrm{decrease\_of\_liquid\_volume} \theta r_\mathrm{hp}. \end{aligned}$$

(12)

The right-hand side of this equation is the decrease in liquid volume per unit of time and volume.

For a relation between the pressure and the flow, Darcy’s law is used, see Zheng and Bennett (1995):

$$\begin{aligned} \mathbf {q}=-\frac{k}{\mu } (\nabla p + \rho _l g \mathbf {e_z}). \end{aligned}$$

(13)

In Darcy’s law, p (Pa) is the pressure, k (m$^2$) is the intrinsic permeability, $\mu$ (Pa s) is the viscosity of the fluid, $\rho _l$ (kg/m$^3$) is the density of the fluid, g (m/s$^2$) is the gravitational constant, and $\mathbf {e_z}$ is a unit vector in vertical direction.

The Kozeny–Carman equation is used to determine the intrinsic permeability. This equation is an empirical relation between the intrinsic permeability and the porosity that is commonly used in ground water flow modelling (see Bear 1972):

$$\begin{aligned} k=\frac{(d_\mathrm{m})^2}{180}\frac{\theta ^3}{\left( 1-\theta \right) ^2}. \end{aligned}$$

(14)

In this relation, $d_\mathrm{m}$ (m) is the mean particle size of the sand. Since the permeability is an increasing function of the porosity (for $0<\theta <1$), a decrease in porosity will lead to a decrease in permeability.

The density of the fluid depends on the concentrations. The following relation, as derived in van Wijngaarden et al. (2011), is used:

$$\begin{aligned} \rho _l=1000+15.4996 C^\mathrm{urea}+86.7338 C^{\mathrm{Ca}^{2+}} + 15.8991 C^{\mathrm{NH}_4^+}. \end{aligned}$$

(15)

By substitution of Darcy’s law in Eq. (9), one gets the following differential equation for the pressure.

$$\begin{aligned} \nabla \cdot \left( -\frac{k}{\mu } (\nabla p + \rho _l g \mathbf {e_z})\right) = K \theta r_\mathrm{hp}. \end{aligned}$$

(16)

3.2 Reaction Rate

To complete the model, the rate $r_\mathrm{hp}$ of the biochemical reaction (3) is needed. In this section, it is explained how this reaction rate is composed.

3.2.1 Micro-organisms

First of all, before the reaction can take place, the micro-organisms should be present. It has been assumed that the rate is proportional to the number of micro-organisms per unit of volume. According to Harkes et al. (2010), the fixation procedure that was used in this experiment leads to a rather homogeneous distribution of micro-organisms. Hence, for the moment a homogeneous distribution of micro-organisms is used. The quantity $C^\mathrm{bac}$ (1) is defined as the normalized concentration of micro-organisms that is injected. It has $v_\mathrm{max}$ as its initial activity. The quantity $S^\mathrm{bac}$ (1) is defined as the ratio between the concentration of fixated bacteria and the (normalized) injected concentration of micro-organisms (the latter is, by definition, equal to one). This gives the following rate:

$$\begin{aligned} r_\mathrm{hp}=v_\mathrm{max}S^\mathrm{bac}. \end{aligned}$$

(17)

3.2.2 Presence of Urea

Secondly, before the reaction can take place, urea and calcium should be present. This relation is modelled with Monod kinetics (Monod 1949):

$$\begin{aligned} r_\mathrm{hp}=\frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}. \end{aligned}$$

(18)

In this equation, $K_{m,\mathrm{urea}}$ (kmol/m$^3$) is the half-saturation constant.

3.2.3 Time Effect

The rate may also depend on time. There are several processes that make it likely that the rate decreases. The micro-organisms need oxygen, which is only scarcely available in the soil. The micro-organisms are encapsulated by the calcium carbonate they produce, and hence they can be reached by the urea less easily. On the other hand, if the micro-organisms are not encapsulated, they can be flushed out of the sand. Four different models for the production rate of calcium carbonate (in kmol/m$^3$/s) are proposed. It was assumed that the decay starts at the beginning of the cementation phase.

• 1. The reaction rate is constant over time:

  $$\begin{aligned} r^\mathrm{cons}_\mathrm{hp}=\frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}. \end{aligned}$$

  (19)

  This is the simplest model. It neglects growth, death, and flush-out of micro-organisms, as well as other processes that may influence the rate.

• 2. The decay of the active population of micro-organisms is proportional to the active population (Samper and Zhang 2006), with decay constant b (s$^{-1}$):

  $$\begin{aligned} \frac{\partial S^\mathrm{bac,active}}{\partial t}=-bS^\mathrm{bac,active}, \text { for } t>t_\mathrm{cem}. \end{aligned}$$

  This results into an exponential decay, with the following solution for the active population:

  $$\begin{aligned} S^\mathrm{bac,active} =S^\mathrm{bac}e^{-b(t-t_\mathrm{cem})_+}, \end{aligned}$$

  with $S^\mathrm{bac}$ as the initial active population, present in the soil. The notation $(.)_+$ only uses the value of the quantity between brackets if it is positive and uses zero otherwise. This gives the following reaction rate:

  $$\begin{aligned} r^\mathrm{exp1}_\mathrm{hp}=\frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}e^{-b(t-t_\mathrm{cem})_+}. \end{aligned}$$

  (20)

  An exponential decay was also proposed in van Paassen (2009).

• 3. As a third model for the time effect, a simple engineering approach is proposed, which is a linearization of the exponential decay model, proposed above. It states that the rate is maximal at time $t=t_\mathrm{cem}$ and is zero from time $t=t_\mathrm{max}$. In between, the rate decreases linearly. That gives the following rate:

  $$\begin{aligned} r^\mathrm{lin}_\mathrm{hp}=\frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}\left( 1-\frac{(t-t_\mathrm{cem})_+}{t_\mathrm{max}}\right) _+. \end{aligned}$$

  (21)

• 4. The last model for the time effect is a variation on the exponential decay model proposed above, and it has two different decay constants. It has $b_1$ (s$^{-1}$) as the exponential decay constant during the flow part of the cementation phase and $b_2$ (s$^{-1}$) as the exponential decay constant during no flow:

  $$\begin{aligned} r^\mathrm{exp2}_\mathrm{hp}=\left\{ \begin{array}{l@{\quad }l} \frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}e^{-b_1(t-t_\mathrm{cem})} &{} \text {for } t_\mathrm{cem} \le t \le t_\mathrm{noflow}; \\ \frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}v_\mathrm{max}S^\mathrm{bac}&{} \\ \quad \times \, e^{-b_1(t_\mathrm{noflow}-t_\mathrm{cem})}e^{-b_2(t-t_\mathrm{noflow})} &{} \text {for }t > t_\mathrm{noflow}. \end{array} \right. \end{aligned}$$

  (22)

  Here, $t_\mathrm{noflow}$ (s) is the time in the cementation phase at which the flow is stopped. This model is continuous at $t=t_\mathrm{noflow}$ but provides another decay constant when the flow is switched off. This is feasible, since there is no flush-out of micro-organisms if there is no flow. Also other processes that influence the rate might depend on the flow.

All these rates will be used in order to find the best description of the experiment.

3.3 Parameter Values

Not all the values of the model parameters are given in Table 2. In Table 3, the values of the other model parameters that we need to have in order to do simulations are given.

Table 3 Values of various parameters that are input for the simulations (part II)

3.4 Initial and Boundary Equations

As the diameter of the column is quite small compared to the length, the variation in radial direction has been neglected and hence a 1D simulations is performed.

Initially, there is no urea, calcium, ammonium, or calcium carbonate present in the column. Hence, the initial concentrations are equal to zero. The initial porosity is equal to $\theta _0$.

For urea, calcium, and ammonium, a mass flux is prescribed at the inlet. Since ammonium is a reaction product, it is not being injected, so the inward mass flux equals zero. To prescribe the mass flux for urea and calcium, the inflow rate should be known. There is a pump at the bottom of the column that regulates the outflow, so the outflow rate is known. In the simulations, the inflow rate equals this outflow rate. In practice, there might be a small deviation, since at each sample time approximately 1 % of the pore volume is withdrawn and the reaction might also have an influence. In the determination of the inflow rate, this small change is neglected. At the outflow boundary, an advective flux is assumed for the concentrations of the aqueous species. Equations (9) and (16) describe the effect of the reaction on the flow. These equations imply that the flow is not necessarily uniform. Hence, on the outflow boundary, the pressure is prescribed rather than the outflow rate. This is also necessary to obtain a unique solution. The boundary conditions are summarized in Table 4.

Table 4 Boundary conditions for the simulations

4 Numerical Methods

In this section, the numerical methods that are used to solve the system of (partial) differential equations are given.

The differential equations for the pressure (16), the flow (13), and the concentrations (4) are solved using the standard Galerkin finite element method. These equations are multiplied by a test function $\eta$ and integrated over the domain $\varOmega$ to derive the weak formulation. For the time integration, an implicit scheme is used (Euler backward).

The Newton–Cotes quadrature rules (van Kan et al. 2005) are used for the development of the element matrices and vectors. Line elements are used in this 1D experiment in combination with linear basis functions.

Since the differential equation for calcium carbonate (5) is an ordinary differential equation in each grid point, the (implicit) backward Euler method is used to solve it.

The calculations are done with MATLAB. As a mesh size, $\Delta x=0.002$ m is used. This gives a mesh with 2500 elements. The time span is divided into several equal time steps, with length $\Delta t=36$ s. At each time step, first the density, porosity, and intrinsic permeability are updated, using Eqs. (7), (14), and (15). Then, the pressure and the flow are calculated, solving Eqs. (9) and (16). Subsequently, the concentrations are updated by solving Eqs. (4) and (5). Due to reaction term in the partial differential equation for urea, this equation is nonlinear. Newton’s method (Adams 2003; Radu and Pop 2010, 2011) is used to deal with that. As a stopping criterion

$$\begin{aligned} \frac{\Vert (\mathbf c ^{n+1,k+1}-\mathbf c ^{n+1,k})\Vert _2}{\Vert \mathbf c ^{n+1,k}\Vert _2}<10^{-10} \end{aligned}$$

is used, with vectors $\mathbf c ^{n+1,k+1}$ and $\mathbf c ^{n+1,k}$ the latest results of the iterative process. In our case, Newton’s method converges within a few iterations. The following list presents in pseudocode the order in which the equations are solved and the updates are done. The superscript n and $n+1$ denote the approximation at time $t^n$ and $t^{n+1}$.

• 1. $\rho _l^{n+1}{:}\,$ $\rho _l^{n+1}=\rho (C^{\mathrm {urea,n}},C^{\mathrm {Ca^{2+},n}},C^{\mathrm {NH_4^+,n}})$, from Eq. (15);

• 2. $\theta ^{n+1}{:}\,$ $\theta ^{n+1}=\theta (\theta _0,C^{\mathrm{CaCO_3},n})$, from Eq. (7);

• 3. $k^{n+1}{:}\,$ $k^{n+1}=k(\theta ^{n+1})$, from Eq. (14);

• 4. $p^{n+1}$:  $\nabla \cdot \left( \frac{k^{n+1}}{\mu }(\nabla p^{n+1} +\rho _l^{n+1} g \mathbf {e_z})\right) =K \theta ^{n+1} r_\mathrm{hp}^{n}$, from partial differential equation (16);

• 5. $\mathbf {q}^{n+1}$:  $\mathbf {q^{n+1}}=-\frac{k^{n+1}}{\mu } (\nabla p^{n+1} + \rho _l^{n+1} g \mathbf {e_z})$, from partial differential equation (9);

• 6. $C^{\mathrm{urea},n+1}$:  $\left( \theta ^{n+1}C^{\mathrm{urea},n+1}-\theta ^nC^{\mathrm{urea},n}\right) /\Delta t=\nabla \cdot (\theta ^{n+1} \mathbf {D^{n+1}} \nabla C^{\mathrm{urea},n+1}) - \nabla \cdot (\mathbf {q}^{n+1} C^{\mathrm{urea},n+1}) - \theta r_\mathrm{hp}^{n+1}$, from partial differential equation (4). Due to the reaction term, this partial differential equation is nonlinear in the urea concentration and Newton’s method is used;

• 7. $C^{\mathrm{NH}_4^+,n+1}$: $\left( \theta ^{n+1}C^{\mathrm{NH}_4^+,n+1}-\theta ^nC^{\mathrm{NH}_4^+,n+1}\right) /\Delta t$ $=\nabla \cdot (\theta ^{n+1} \mathbf {D^{n+1}} \nabla C^{\mathrm{NH}_4^+,n+1}) - \nabla \cdot (\mathbf {q}^{n+1} C^{\mathrm{NH}_4^+,n+1}) - \theta r_\mathrm{hp}^{n+1}$, from partial differential equation (4). The values for $r_\mathrm{hp}^{n+1}$ follow from the last Newton iteration in the previous step.

• 8. $C^{\mathrm{CaCO_3},n+1}$: $\left( C^{\mathrm {CaCO_3},n+1}-C^{\mathrm {CaCO_3},n}\right) /\Delta t= m_{\mathrm {\mathrm{CaCO}_3}} \theta ^{n+1} r_\mathrm{hp}^{n+1}$, from partial differential equation (5).

To solve the (coupled) model equations, a splitting is performed. This splitting introduces an error of $\mathcal {O}(\Delta t)$. Since the backward Euler time integration scheme also results in an $\mathcal {O}(\Delta t)$ error, the splitting does not worsen the order of convergence. The mass balance is regularly checked, and deviations are only in the order of a few tenths of a percent.

For each measurement of the ammonium concentration in the experiment, the value is compared with the outcome of the numerical simulation. The total error for ammonium is calculated by summing up the squares of the differences and taking the square root of this sum. Finally, the result is normalized by dividing it by the number of measurements $n_\mathrm{am}$ and the theoretical maximum of the ammonium concentration, which is 2.2 kmol/m$^3$ (if the small decrease in liquid volume due to the reaction is not taken into account):

$$\begin{aligned} E_\mathrm{am}=\frac{1}{2.2 n_\mathrm{am}}\sqrt{\sum _{i}\sum _j(y_{ij}-f(x_i,t_j))^2}, \end{aligned}$$

(23)

where $y_{ij}$ are the values of the ammonium measurements at location $x_i$ and time $t_j$ and $f(x_i,t_j)$ is the corresponding numerical value at the same time and location. In the same way, the error for calcium carbonate is defined (for which we only have experimental data at the end of the experiment):

$$\begin{aligned} E_\mathrm{cc}=\frac{1}{105.1 n_\mathrm{cc}}\sqrt{\sum _{i}(y_{i}-g(x_i))^2}, \end{aligned}$$

(24)

with $n_\mathrm{cc}$ the number of calcium carbonate measurements, $y_{i}$ the values of the calcium carbonate measurements at the end of the experiment at location $x_i$, and $g(x_i)$ the corresponding numerical value at the same time and location. The maximal calcium carbonate concentration measured was 105.1 kg/m$^3$.

The total error is calculated by summing both errors:

$$\begin{aligned} E_\mathrm{tot}=E_\mathrm{am}+E_\mathrm{cc}. \end{aligned}$$

(25)

The MATLAB built-in minimization algorithm fminsearch is used to find the unknowns [concentration of fixated micro-organisms and decay constant(s)] in the rate functions that minimize the total error (25). This is done for the four different rate functions that are considered.

With the error definition (23) and (24), steep fronts may lead to considerable errors, while the error in location of the front might be very small. Since the aim of the paper is to examine whether this reactive transport model can be used to model a Biogrout experiment, rather than finding the best solution, this simple error calculation is sufficient.

5 Results

In this section, the results of the experiment and the numerical results for the various models for the activity decrease are reported.

5.1 Experimental Results

The results of the experiment have been reported in detail in Whiffin et al. (2007) and van Paassen (2009). Here, only the evolution of the ammonium concentration in the various sampling ports is shown (Fig. 1) as well as the final calcium carbonate concentration (Fig. 3). As in Whiffin et al. (2007) and van Paassen (2009), the time is reset such that the cementation phase starts at time $t=0\,\hbox {h}$.

5.1.1 Ammonium

Figure 1 shows the ammonium concentration in time for various sample ports. The vertical line at time $t=24.9\,\hbox {h}$ divides the graph into the flow part (left) and the no-flow part (right) of the cementation phase.

Fig. 1

Course of the ammonium concentration (kmol/m$^3$) in the sample ports

There is no ammonium present in the column at the beginning of the cementation phase. Hence, the initial ammonium concentration equals zero. Initially, the reaction rate is quite high, causing a sharp increase in the ammonium concentration. Once the reactive front has passed a sample port, the ammonium concentration rapidly decreases. Since the supply is constant, it seems that the activity is decreasing.

Fig. 2

Ammonium concentration in the column at several times. Left During flow, right during no flow

Figure 2 shows the ammonium concentrations as a function of the position in the column. The left figure shows the ammonium profile at several times during the flow phase. Samples were only taken, when the concentration in the sample port was expected to be larger than zero, i.e., when the front is passing/has passed. This implies that a zero concentration is expected on the sample port locations where no data are shown. The ammonium penetrates further into the column as time proceeds. Furthermore, the concentration increases with the position in the column. This increase was expected, since ammonium is produced by the micro-organisms and a longer retention time results in a higher concentration. From the slope of the various graphs, it can be concluded that the production rate, which is a measure for the microbial activity, decreases in time. The right plot in Fig. 2 shows the ammonium profile at several times after $t=24.9\,\hbox {h}$, when the flow was stopped. Since there is still urea and calcium present in the column, the reaction continues. The ammonium concentration increases until it reaches a maximum at which all urea has been consumed. Based on the injected concentration of urea and the reaction stoichiometry, the theoretical maximum ammonium concentration is 2.274 kmol/m$^3$, taking the consumption of water in the hydrolysis reaction into account. However, the measured concentrations at the end of the cementation phase are significantly larger than this theoretical maximum, showing a structural difference of 8 % with an average of 2.459 kmol/m$^3$ and a standard deviation 10 % or 0.237 kmol/m$^3$. In the first sample port, the maximum is not reached within the time of the experiment.

5.1.2 Calcium Carbonate

The results for the final calcium carbonate concentration are shown in Fig. 3. Since the largest heterogeneity was expected in the first part of the column, additional samples were taken from this part. The first meter shows indeed a large spread in results. The results in the rest of the column only show a little deviation from the trend. In van Paassen (2009), several mechanisms which can explain the observed heterogeneities are suggested: Possibly, the micro-organisms were not distributed as homogeneously as expected. Perhaps, the initial column material contained some inhomogeneities. Furthermore, locally clogged areas (by micro-organisms or crystals) can cause preferential flow paths and stagnant zones.

Fig. 3

Concentration of calcium carbonate (kg/m$^3$) in the column at the end of the experiment

The calcium carbonate content is decreasing with the length of the column. This was expected, since the substrates are injected at $x=0$ m and the reaction time (the time needed for full conversion of the injected concentration) is comparable to the retention time. Consequently, the first part of the column has received more substrates resulting in a higher calcium carbonate concentration than in the last part. If the reaction rate would be very large, the substrates are converted before the end of the column is reached and in that case there would not be any calcium carbonate at the end of the column. Too high reaction rates could also cause clogging at the inlet. A high flow rate or a lower reaction rate would result in a more homogeneous distribution. However, high flow rates could possibly wash out micro-organisms, whereas low reaction rates will increase the reaction time.

5.1.3 Nitrogen Concentration

Considering that both the nitrogen (N) atoms in urea are converted to ammonium, at first sight, one could expect that the total nitrogen concentration in the cementation solution should not change, but since in the reaction also water is consumed, this concentration slightly increases. Since the injected concentration of urea equals 1.1 kmol/m$^3$, the total nitrogen concentration would increase from 2.2 to 2.274 kmol/m$^3$ when all urea is converted to ammonium. Assuming that the concentrations of urea and calcium are equal during the reaction in the sand column (which is justified since urea is injected at the same concentration as calcium and both react with the same rate), the total nitrogen concentration can be calculated by adding the calcium concentration, multiplied by two, to the ammonium concentration. Figure 4 shows the results of the calculations and the theoretical bandwidth. The figure shows that in many cases the deviation is considerable, potentially indicating significant measurement inaccuracies. The same discrepancy as mentioned earlier is observed, namely that at the final stage of the reaction the ammonium concentrations show structurally higher values than expected. Secondly, some outliers in the measurements were identified at which the total nitrogen concentration is significantly lower than expected. These outliers should not be taken into account when comparing the different model simulations with the experimental results.

Fig. 4

Concentration of nitrogen [$C^\mathrm{N}$ (kmol/m$^3$)] in the column [distance in (m)] at several times (green line) and the theoretical bandwidth for this concentration (two dotted horizontal lines)

5.2 Numerical Results

In this subsection, the numerical results are reported and compared with the experimental results.

5.2.1 Minimizing Errors

In Sect. 3.2, four different models were proposed for the reaction rate. In all cases, a value has to be assigned to one or more parameters. Table 5 shows which values minimize the error as defined in (23), (24), and (25) for these four cases.

Table 5 Values for which the error between the experimental and numerical results is minimal for the four models describing the course of the reaction rate

Biochemical rates (19) up to (22) are plotted as a function of time for the parameter values from Table 5. The graphs are shown in Fig. 5. The rates also depend on the urea concentration, which is a function of location and time. Since the focus here is on the course of the rates in time, the urea term ($\frac{C^\mathrm{urea}}{K_{m,\mathrm{urea}}+C^\mathrm{urea}}$) in all rate functions is replaced by 1.

Fig. 5

Activity of the micro-organisms in the column as a function of time for the four models that describe the course of the reaction rate. The urea term in the rate functions is neglected here

In the constant activity model, one parameter has to be estimated. Compared to the other models, it leads to the largest errors, both for the ammonium concentration and for the calcium carbonate concentration.

For both the exponential decrease model with one decay constant and the linear decrease model, two parameters need to be estimated. These two decay models perform similarly with respect to the error in the calcium carbonate content; however, the exponential decay model leads to a smaller error in ammonium concentration.

For the last proposed decay model, three parameters needed to be estimated. It is also an exponential decay model, but now with two decay constants, one for the period during flow and one for the period without flow. Although an extra parameter was involved, it led to an only slightly smaller error in calcium carbonate content, compared to the simpler exponential decay model.

It can be concluded that the models, which consider decay, should be preferred over the constant activity model. As it could be expected, involving more parameters led to smaller errors. The exponential decay model with one decay constant performed a little better than the linear decrease model, and therefore it should be preferred since it is based on physics rather than on linearization. In this experiment, it was not really worthwhile to introduce an extra decay constant for the period without flow. Other experiments are needed to conclude whether this is the case in general.

5.2.2 Ammonium Concentration

Figure 6 shows the experimental and numerical results for the ammonium concentration. After the first appearance, the ammonium concentration decreases during the flow part of the cementation phase, indicating a decreasing reaction rate. For both the exponential decay models, this decrease is captured quite well, where the first part of the column performs a little less well. There, the experiment shows a drastic decrease in activity. The constant activity model is not able to handle a decreasing activity as it is based on a constant activity. The small decrease in ammonium concentration is the result of the decreasing porosity. The latter causes a decrease in residence time which results in a lower amount of reaction product. The linear decrease model gives better results than the constant activity model, but performs worse than the two exponential decay models.

After 24.9 h, the flow was stopped and the substrates were left to react. The constant activity model gives the poorest results. It predicts that the maximum ammonium concentration is reached quite fast. In all sample ports, it is reached earlier than it really does in the experiment. The other three models perform better than the constant activity model, and they are comparable to each other. In some parts of the column, one model describes the experiment the best and in other parts another model. None of the models gives a good description of the final concentration at the sample port at $x=0.25$ m.

Fig. 6

Ammonium concentration (kmol/m$^3$) in the various sample ports as a function of time. Both the experimental and numerical values are shown. First row constant activity model, second row exponential activity decrease model, third row linear activity decrease model, and last row exponential activity decrease model with two decay constants

5.2.3 Calcium Carbonate Concentration

In this subsection, the experimental results are compared to the numerical results for the calcium carbonate concentration. Again, this comparison is made for the four different models for the activity decrease. The results are shown in Fig. 7. The numerical results are quite good for all models, and they hardly differ from each other. There is a large spreading in the experimental results for the calcium carbonate content in the first part of the column. Possible reasons for this scatter are discussed in Sect. 5.1.2.

Fig. 7

Calcium carbonate concentration in the column at the end of the experiment. Both the experimental values and the numerical values for the four models are shown

6 Conclusions and Discussion

In this paper, a reactive transport model which was developed to simulate the Biogrout process was compared to the results of a sand column experiment. This experiment is presented in Whiffin et al. (2007) and van Paassen (2009). The measured ammonium concentrations during the Biogrout experiment and the final calcium carbonate concentrations are shown in this paper as well.

From the ammonium measurements, it followed that the reaction rate is decreasing in time. For that reason, various models were proposed, in which the activity decreases in time. A model with a constant activity was also considered. These models were compared to a Biogrout experiment.

The amount of the final calcium carbonate content appeared to decrease with the distance to the injection, although the experimental results are quite scattered, especially close to the injection. Close to the inlet, the average amount of calcium carbonate is approximately 100 kg/m$^3$. This implies a porosity reduction from 0.378 to 0.341. According to the Kozeny–Carman relation (14), the permeability decreases with a factor 1.5. Close to the outlet, the calcium carbonate content is almost zero. On that location, the porosity and permeability were hardly influenced.

In a 1D experiment, the decreases in porosity and permeability are not very important, since there is only ‘one way’ to travel from the inlet to the outlet. In two or three dimensions, these reductions become more important, since the liquid will flow around a cemented zone, where the resistance is relatively high. Furthermore, the porosity reduction in general can be larger than in this experiment. Therefore, it is important that the porosity and permeability reduction are considered.

The mathematical model, proposed in this article, is quite detailed with respect to the flow equation in order to have conservation of mass. In van Wijngaarden (2013), it has been shown that small deviations in the flow equations have a minor effect on the final calcium carbonate content.

Analysis of the experimental data highlighted several inaccuracies in the measurements. First, the final ammonium concentrations obtained after completion of the reaction showed significantly higher values (8 %) than expected according to the theoretical stoichiometry. Second, assuming that the concentration of urea and calcium ions is equal throughout the experiment, the total nitrogen concentration was calculated from the ammonium concentrations and measured calcium concentrations. Analysis of this total nitrogen concentration identified several outliers with significantly lower values than expected. These outliers were not taken into account when comparing the various kinetic models. Finally, the volume of each liquid sample is approximately 5 ml. In the calculations for both the experiment and the simulations, this volume is neglected. However, especially in the no-flow part, this volume might influence the experimental results.

Considering the calcium carbonate concentration, all the models led to a similar description of the average final calcium carbonate concentration. This is partly because the experiment contains a no-flow part. In case of no flow, the value of the reaction rate does not influence the final distribution, as long as it is high enough to get full conversion in the course of the experiment. Changing the experimental conditions, such as the flow period and flow rate or initial activity and concentrations, would increase the differences between the various simulations. In the first part of the column, the calcium carbonate measurements showed large variations. Several mechanisms, explaining the observed heterogeneities, have been suggested in van Paassen (2009), including a heterogeneous distribution of bacteria, locally clogged areas (by bacteria or crystals) causing preferential flow paths and stagnant zones, and the kinetics of the precipitation reaction. The prediction of this local variability requires a far more advanced model, taking these processes into account. However, measurement of the parameters which are required to describe these processes at pore scale and the upscaling of these processes to continuum scale are hard to achieve and will introduce a significant amount of uncertainty. It is therefore questionable whether such a complex model will result in a better performance. In order to predict radial variations, a 1D simulation is not adequate. However, since this paper assumes a homogeneous distribution of micro-organisms, it is expected that a full 3D modelling approach for simulating this experiment will not lead to radial variation, except for a possible fingering effect as a result of buoyancy-driven flow. The latter could have occurred since a dense fluid is injected on top of a less dense fluid.

Ammonium, the by-product of the reaction, was measured at several times and locations during the experiment. Hence, these results are more appropriate to compare the various model scenarios. The constant reaction rate model does not perform very well since it is not able to model a decreasing reaction rate, which is observed in the experiment. The other models are able to capture a decreasing reaction rate, and they perform quite good. Only in the first meter of the column, they predict too high concentrations. The two exponential decay models can be preferred above the linear decay model since decay processes are often described using exponential models and since the two exponential models gave the smallest total error. It was excluded that the differences between the numerical and experimental results were caused by numerical errors by redoing a calculation for a finer mesh, combined with a smaller time step. The numerical results were overlapping, indicating that the numerical errors are very small.

According to the ammonium measurements, the microbial activity decreases drastically in the first meter of the column during flow. Trying to get a better fit for this part of the column during flow results in a rapidly declining reaction rate. Consequently, the simulated calcium carbonate concentrations are much lower than the experimental concentrations. It seems that in the first part of the column the reaction rate decreases during flow, but subsequently increases after the flow has been switched off. Since the time-dependent activity models that are used assume a continuous, monotonously decreasing rate, they are not able to handle this discontinuity in reaction rate.

Fig. 8

Activity of the micro-organisms in the first part of the column, calculated from the produced ammonium concentration

On the other hand, the measured ammonium concentrations in the first part of the column seem to be too low. If the concentrations of ammonium at $x=25$ cm and $x=50$ cm are used to calculate the final calcium carbonate concentration in the first 25 cm or 50 cm, values are found that are lower than the average measured calcium carbonate concentrations. These calculations are done as follows. The concentrations of (produced) ammonium at $x=25$ cm are used as a measure for the activity in the first 25 cm between that time and the next sample. This gives an upper bound since the activity decreases between the samples. This is shown in Fig. 8. From these activities, the amount of produced calcium carbonate during flow is calculated. This value is added to the amount of calcium carbonate that is produced during no flow. The latter is easily calculated by subtracting the ammonium concentration at the beginning of no flow from the final ammonium concentration and converting it into calcium carbonate. These calculations give an upper ound for the calcium carbonate content of 41 kg/m$^3$ for the first 25 cm and 58 kg/m$^3$ for the first 50 cm. From the measured calcium carbonate concentrations, a value of 86 kg/m$^3$ was expected in both cases. This value is much higher than the one calculated from the ammonium concentrations, which could indicate either an error or a large spread in radial direction in the ammonium measurements. The radial heterogeneity is confirmed by the variation in the final calcium carbonate concentration.

It can be concluded that, in order to properly simulate the Biogrout process, a time-dependent decay of the reaction rate should be included. The exponential decay models performed the best. From this experiment, it cannot yet be concluded whether an extra decay constant for the period without flow is really necessary. Although the models performed quite well, the concentration of micro-organisms and the decay rate were fine-tuned on the measurements to achieve a good fit. In order to improve the performance of these numerical simulations, more advanced models are required. These models should incorporate the placement of micro-organisms (including the way of cultivation of micro-organisms, sand type, pH, flow, concentrations) and other processes, such as process-induced preferential flow and the kinetics of the precipitation reaction (van Paassen 2009).