1 Introduction

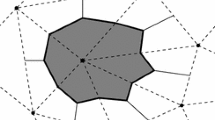
Finite volume and finite element discretizations have been extensively studied for the past few decades for different flow systems in heterogeneous and fractured porous media (Chen and Ewing 1997; Stefansson et al. 2018; Abushaikha 2018; Abushaikha et al. 2017; Ahmed et al. 2019; Xia and Zhang 2006; Khoei and Haghighat 2011). One important finite element method is the node control volume finite element (NCVFE) method which was developed by Baliga and Patankar (1980) to numerically solve fluid dynamics problems. They subdivided the domain using irregular triangular elements with control volumes surrounding nodes (vertices), Fig. 1. The pressure is solved on the nodes, while the velocity components are solved on the elements sequentially. The secondary control volume mesh is necessary to assure local conservation of mass, momentum, and energy since these entities are discontinuous at the element interfaces. Quadrilateral elements were first used by Schneider and Raw (1986), and Fung et al. (1991), Forsyth (1991), while Eymard and Sonier (1994) applied the method to subsurface reservoir engineering problems’. Paluszny et al. (2007) extended the method to domains composed of different types of elements (tetrahedron, hexahedron, prims and pyramids). After that, Geiger et al. (2004) implemented discrete fracture models representing subsurface geological fractures using line elements embedded in two-dimensional domains composed of triangle elements, while Monteagudo and Firoozabadi (2004) embedded triangles with tetrahedron elements to solve similar problems.

The usability of the NCVFE method to simulate multi-phase fluid flow in heterogeneous media and complex geological models has increased rapidly (Mello et al. 2009; Sadrnejad et al. 2012; Schmid et al. 2013) thanks to the mesh flexibility of the finite element method and the local conservation characteristics of the control volumes. However, since the geological data (material properties such as porosity and permeability) are assigned on the elements and the dynamic data (transport variables such as saturation) are computed on the control volumes, artificial fluid smearing is observed between regions of different material properties. The effect of this issue can be decreased by refining the mesh or through the use of adaptive spatial meshing techniques as proposed by Jackson et al. (2013). However, the method will always allow the transport variables to be contained in control volumes that represent elements with different material properties, as discussed later. Vermuelen (1973) imposed the properties on the control volumes which decreased the effect of the aforementioned issue; however, the shape of the control volume depends on the finite element mesh, thus the mesh flexibility is considerably decreased.

Nick and Matthai (2011) and Bazar-Afkan and Matthai (2011) proposed novel numerical approaches to solve the issue of artificial fluid smearing using triangular elements, and Abushaikha et al. (2015) changed the location of the degrees of freedom from the vertices to the interfaces to minimize the degree of smearing using tetrahedron elements. It is important to note that many papers have suggested new schemes that can eliminate the effect of artificial smearing (Abushaikha et al. 2017; Abushaikha 2018; Salinas et al. 2018; Abd et al. 2019; Abd and Abushaikha 2020; Abushaikha and Terekhov 2020; Li et al. 2020; Nardean et al. 2020) even when discrete fracture modeling is implemented (Zhang and Abushaikha 2019).

Fig. 1
figure 1

Triangle finite element mesh (dashed lines) with the corresponding node control volume mesh (solid lines) imposed on the vertices of elements. a The material properties (gray color) are defined on the elements, here representing a fracture (white is lower permeability matrix), b The pressure and transport variables are computed on the node control volumes (blue color). The control volume mesh spans both the fracture and matrix material properties promoting unphysical flow across the boundaries of elements

Full size image

In this paper, we quantify and numerically assess the artificial smearing produced by the NCVFE for multi-phase fluid flow in heterogeneous media. We use unstructured mesh with tetrahedron elements, while the total fluid mobility is calculated by using an arithmetic average of fluid saturations of the shared control volumes. This allows for the computation of the unphysical error of the artificial smearing for various tests using domains of hugely different material properties. To visualize the artificial smearing better, we plot the results on the actual control volumes contrary to most of the literature (Geiger et al. 2004; Monteagudo and Firoozabadi 2004; Mello et al. 2009; Sadrnejad et al. 2012; Schmid et al. 2013; Jackson et al. 2013; Vermuelen 1973; Nick and Matthai 2011; Bazar-Afkan and Matthai 2011; Edwards 2006) as they plot the solutions on the vertices of elements which tends to underestimate the extent of the problem. The paper is organized as follows. In Sect. 2, we introduce the governing equations followed by a brief description of the NCVFE method in Sect. 3. We then present some numerical tests in Sect. 4 and we end with some conclusions in Sect. 5.

2 Governing Equations

In the following, we present the equations of a two-phase immiscible fluid flow of water and oil in heterogeneous porous media. The flow is characterized by the continuity equation and Darcys law (Darcy 1856; Bear 1972), and a slightly compressible rock is considered. The mass balance for the fluid phase \(\alpha\) is,

$$\begin{aligned} \frac{\partial (\phi \rho _\alpha S_\alpha )}{\partial t}= -\nabla .[\rho _\alpha \nu _{\alpha }]+ \rho _\alpha q_{\alpha } \end{aligned}$$
(1)

S is the saturation of the phase, \(\phi\) is the porosity of the rock, \(\rho\) is the density of the phase, q is the volumetric source–sink rate of the phase, \(\nu\) is the Darcy velocity for phase, and t is time. We also assume capillarity and gravity forces are negligible. The Darcy phase velocity is,

$$\begin{aligned} \nu _\alpha = -\lambda _\alpha K\nabla P_\alpha \end{aligned}$$
(2)

where P is the phase pressure, K is the absolute rock permeability, and \(\lambda\) is the phase mobility,

$$\begin{aligned} \lambda _\alpha = \frac{k_{r\alpha }(S_\alpha )}{\mu _\alpha } \end{aligned}$$
(3)

where \(k_r\) is the relative permeability of phase and \(\mu\) is fluid viscosity of phase.

The relative permeability is saturation dependent, while the fluid viscosity is constant. We assume a closed system with known initial boundary conditions where source/sink terms are represented by wells. Moreover, a pressure equation is written based on the continuity equations for the phases (Eq. 1). The equations of each phase are combined to form a pressure equation where time derivatives of saturations are represented explicitly (Durlofsky 1993),

$$\begin{aligned} \phi C_r \frac{\partial P}{\partial t} - \nabla .\mathbf {K}\lambda _t\nabla P=q_t \end{aligned}$$
(4)

where \(C_r\) is rock compressibility, \(q_t\) is the total volumetric source-sink rate of both phases and \(\lambda _t\) is the total mobility given by:

$$\begin{aligned} \lambda _t=\frac{k_{ro}}{\mu _o} + \frac{k_{rw}}{\mu _w} \end{aligned}$$
(5)

Then, Darcy’s law, Eq. 2, is used to calculate the phase velocities using the solution of the pressure field, Eq. 4. Moreover, we use Eq. 1 to account for the advection and transport of fluid. The pressure and the advection equations are coupled nonlinearly using the total mobility, Eq. 5. The mobility depends on the saturation that changes over time and space.

3 Node Control Volume Finite Element (NCVFE) Method

In the NCVFE method, the domain is subdivided into finite elements and a secondary grid is imposed around the nodes (vertices) of the elements forming a control volume mesh, Figs. 1 and 2. The pressure is solved on the vertices of elements using the Galerkin finite element method and the transport variables (i.e., fluid saturation) are solved on the control volumes. The secondary grid is constructed to provide a continuous velocity field between the control volumes, since the velocity field is discontinuous between the elements’ interfaces (Fung et al. 1991; Geiger et al. 2004). This guarantees mass conservation of the system. Material properties, such as porosity and permeability are still defined on the elements. Some authors refer to this method as the control volume finite element (Baliga and Patankar 1980; Fung et al. 1991; Sadrnejad et al. 2012; Jackson et al. 2013). Here, we include the term “node” as qualifier for the sake of clarity, and to distinguish the method from newly development methods in the literature (Nick and Matthai 2011; Abushaikha et al. 2015).

Fig. 2
figure 2

a Tetrahedron mesh , b The corresponding node control volume mesh (red lines) imposed on the vertices of the tetrahedron finite elements

Full size image

In the NCFVE method, a multi-phase flow problem is solved in two steps. The first step is to calculate the pressure using finite element method; here we use the well-established Galerkin method (Huyakorn and Pinder 2014). Then, the advection of fluid between the node control volumes is calculated using the finite volume method. Next, we discuss these steps in detail.

3.1 Galerkin Finite Element Method

In the finite element method, an integral formulation for the governing flow equation is derived to solve for the pressure at each node in the mesh. Let us consider the differential operator

$$\begin{aligned} L[P]-F=0 \end{aligned}$$
(6)

where L[P] is the differential operator defining the pressure, and F is the external source–sink terms. An approximate solution of the pressure in each element is defined as

$$\begin{aligned} \widehat{P}^{(e)}= \sum _{i=1}^n N_i^{(e)}P_i \end{aligned}$$
(7)

where \(\widehat{P}^{(e)}\) is the approximate solution for pressure within element (e), n is the number of nodes within element (e), and \(P_i\) unknown values of pressure for each node within element (e), and \(N_i^{(e)}\) is the interpolation function for each node within element (e) and the sum of interpolation functions equals to one at every point within the element

$$\begin{aligned} \sum _{i=1}^n N_i^{(e)}(x,y,z)=1 \end{aligned}$$
(8)

In this paper, we use first-order Courant (Courant 1943) (linear) interpolation functions and the derivative of Eq. 7 equals

$$\begin{aligned} \nabla \widehat{P}^{(e)}=\sum _{i=1}^n P_i\nabla N_i^{(e)} \end{aligned}$$
(9)

When we substitute the pressure value in Eq. 6 with the approximate solution of pressure, Eq. 7, a residual R occurs at each node in the problem domain, and the pressure equation no longer equals zero

$$\begin{aligned} L(\widehat{P})-F=R\ne 0 \end{aligned}$$
(10)

Several methods are available to eliminate this error; here we use the method of weighted residuals (Geiger et al. 2004; Istok 2010). In this method, Eq. 10 is multiplied by a weighting function W and the weighted average of the residuals in the domain is forced to equal zero

$$\begin{aligned} \int _{\varOmega }W(L(\widehat{P} - F)d\varOmega =0 \end{aligned}$$
(11)

Replacing the differential operator in Eq. 11 with Eq. 4 leads to

$$\begin{aligned} \int _{\varOmega }W(\phi C_r \frac{\partial P}{\partial T} - \nabla .\mathbf {K}\lambda _t\nabla P-q_t)d\varOmega =0 \end{aligned}$$
(12)

In the Galerkin finite element method, the weighing function W is identical to the interpolation function N. Based on Eq. 12, the residual for node i in tetrahedron element (e) equals

$$\begin{aligned} R_i^{(e)}= & {} -(K\lambda _t)^{(e)} \int _{V^{(e)}}\nabla N_i^{(e)}\cdot \nabla \widehat{P^{(e)}}dV +(\phi C_r)^{(e)} \int _{V^{(e)}}N_i^{(e)}\left[ \frac{\partial \widehat{P^{(e)}}}{\partial t}\right] dV\nonumber \\&-\int _{V^{(e)}}N_i^{(e)}q_t^{(e)}dV \end{aligned}$$
(13)

where \(V^{(e)}\) is the volume of tetrahedron. The material properties (permeability and porosity) are assumed piece-wise constant within the element (Geiger et al. 2004; Nick and Matthai 2011), and the total fluid mobility is calculated by using an arithmetic average of fluid saturations of the shared control volumes (Baliga and Patankar 1980; Huber and Helmig 1999). For simplicity, we make Eq. 13 equal to

$$\begin{aligned} R_i^{(e)}= R_{M,i}^{(e)}+R_{C,i}^{(e)}+R_{F,i}^{(e)} \end{aligned}$$
(14)

where \(R_{M,i}^{(e)}\) is the conductance residual, \(R_{C,i}^{(e)}\) is the capacitance residual, and \(R_{F,i}^{(e)}\) is the force residual.

We integrate by parts the first term of Eq. 14 and replace the derivative of the approximate solution of pressure using Eq. 9

$$\begin{aligned} R_i^{(e)}=-(K\lambda _t)^{(e)} \int _{V^{(e)}}(\nabla N_i^{(e)}\sum _{i=1}^n P_i\nabla N_i^{(e)})dV +(K\lambda _t)^{(e)}\int _{S^{(e)}} N_i^{(e)}\frac{\partial \widehat{P}^{(e)}}{\partial x}dS \end{aligned}$$
(15)

Neglecting the second term in Eq. 15 since no-flow at boundaries and making the conductance matrix by rearranging the conductance residual equations of the nodes of element (e),

$$\begin{aligned} \begin{bmatrix} R_i^{(e)} \\ \vdots \\ R_n^{(e)} \end{bmatrix}_M = \begin{bmatrix} M^{(e)} \end{bmatrix} \begin{bmatrix} P_i \\ \vdots \\ P_n \end{bmatrix} \end{aligned}$$
(16)

where \([M^{(e) } ]\) is the conductance matrix, and for tetrahedron element equals,

Fig. 3
figure 3

Four tetrahedron elements (left), a node control volume (dashed lines) constructed on the shared node between the four tetrahedron elements (center), area normal vectors of one sector (grey areas) of a node control volume in a tetrahedron finite element (right)

Full size image
Fig. 4
figure 4

Node control volume sector around node I of a tetrahedron (top-left), vertices of sector (top-right), interface line vectors of faces for sector (bottom-left), and area normal vectors of sector (bottom-right)

Full size image
$$\begin{aligned}{}[M^{(e)}]_{4\times 4}=(K\lambda _t)^{(e)}V^{(e)} \begin{bmatrix} \frac{\partial N_i^{(e)}}{\partial x} &{} \frac{\partial N_i^{(e)}}{\partial y} &{} \frac{\partial N_i^{(e)}}{\partial z} \\ \frac{\partial N_j^{(e)}}{\partial x} &{} \frac{\partial N_j^{(e)}}{\partial y} &{} \frac{\partial N_j^{(e)}}{\partial z} \\ \frac{\partial N_k^{(e)}}{\partial x} &{} \frac{\partial N_k^{(e)}}{\partial y} &{} \frac{\partial N_j^{(e)}}{\partial z} \\ \frac{\partial N_l^{(e)}}{\partial x} &{} \frac{\partial N_l^{(e)}}{\partial y} &{} \frac{\partial N_l^{(e)}}{\partial z} \end{bmatrix} \begin{bmatrix} \frac{\partial N_i^{(e)}}{\partial x} &{} \frac{\partial N_j^{(e)}}{\partial x} &{} \frac{\partial N_k^{(e)}}{\partial x} &{} \frac{\partial N_l^{(e)}}{\partial x} \\ \frac{\partial N_i^{(e)}}{\partial y} &{} \frac{\partial N_j^{(e)}}{\partial y} &{} \frac{\partial N_k^{(e)}}{\partial y} &{} \frac{\partial N_l^{(e)}}{\partial y} \\ \frac{\partial N_i^{(e)}}{\partial z} &{} \frac{\partial N_j^{(e)}}{\partial z} &{} \frac{\partial N_k^{(e)}}{\partial z} &{} \frac{\partial N_l^{(e)}}{\partial z} \end{bmatrix} \end{aligned}$$
(17)

where \(\frac{\partial N_n^{(e)}}{\partial x}\),\(\frac{\partial N_n^{(e)}}{\partial y}\), and \(\frac{\partial N_n^{(e)}}{\partial z}\) are node n interpolation function derivatives in the X, Y and Z directions for element (e). They are given in "Appendix A".

For the second term in Eq. 14, we evaluate the time derivative of the approximate solution of pressure over the element volume. In this paper, we use the lumped formulation as it is considered more stable and produces fewer oscillations during multi-phase flow (Eymard and Sonier 1994; Bastian and Helmig 1999). The time derivative of the approximate solution of pressure is defined by,

$$\begin{aligned} \frac{\partial \widehat{P}^{(e)}}{\partial t}= \begin{bmatrix} N_i^{*(e)} \dots N_n^{*(e)} \end{bmatrix} \begin{bmatrix} \frac{\partial {P}_1}{\partial t}\\ \vdots \\ \frac{\partial {P}_n}{\partial t} \end{bmatrix} \end{aligned}$$
(18)

where \(N_i^{*(e)}\) are the lumped interpolation function for the time derivative of pressure at node i and its product equals,

$$\begin{aligned} N_i^* N_j^* = {\left\{ \begin{array}{ll} \frac{1}{n} &{} \text {if } i=j\\ 0 &{} \text {if }i \ne j \end{array}\right. } \end{aligned}$$
(19)

Substituting Eq. 18 in the second term of Eq. 14 gives the capacitance residual for node i in element (e),

$$\begin{aligned} R_{i,C}^{(e)}=\int _{V^{(e)}}N_i^{(e)}\begin{bmatrix}\phi C_r \begin{bmatrix} N_i^{*(e)} \dots N_n^{*(e)} \end{bmatrix}\begin{bmatrix} \frac{\partial {P}_1}{\partial t}\\ \vdots \\ \frac{\partial {P}_n}{\partial t} \end{bmatrix} \end{bmatrix}dV \end{aligned}$$
(20)

We make the capacitance matrix by rearranging the capacitance residual equations of the nodes of element (e),

$$\begin{aligned} \begin{bmatrix} R_i^{(e)} \\ \vdots \\ R_n^{(e)} \end{bmatrix}_C = \begin{bmatrix} C^{(e)} \end{bmatrix} \begin{bmatrix} P_i \\ \vdots \\ P_n \end{bmatrix} \end{aligned}$$
(21)

where \([C^e ]\) is the capacitance matrix of element (e) and applying Eq. 19 for Eq. 20 gives the lumped capacitance matrix for tetrahedron element,

$$\begin{aligned}{}[C^{(e)}]_{4\times 4}=\phi C_r \frac{V^{(e)}}{4} \begin{bmatrix} 1 &{} &{} 0\\ &{}\ddots &{} \\ 0 &{} &{}1 \end{bmatrix}_{4 \times 4} \end{aligned}$$
(22)

For the third term in Eq. 14, where the well is located in element (e), the flow rate is distributed on the elements nodes depending on the well location in the element,

$$\begin{aligned} \begin{bmatrix} R_i^{(e)} \\ \vdots \\ R_n^{(e)} \end{bmatrix}_F = \begin{bmatrix} F^{(e)} \end{bmatrix} =q_t^{(e)}V^{(e)} \begin{bmatrix} N_i^{(e)}(x_0,y_0,z_0) \\ \vdots \\ N_n^{(e)}(x_0,y_0,z_0) \end{bmatrix} \end{aligned}$$
(23)

where \((x_0,y_0,z_0)\) are the coordinates of the well location in element (e).

Discretizing the time derivative in Eq. 21 using backward Euler method and adding all the matrices in their corresponding global matrices, Eq. 12 becomes the final pressure equation,

$$\begin{aligned} ([C]^t+\triangle t[M]^t)[P]^{t+1}=[C]^t[P]^t+ \triangle t([F]^{t+1}) \end{aligned}$$
(24)

where t is the time index and we use implicit pressure and explicit saturation (IMPES) (Fanchi 2018). Eq. 24 is an \(Ax=B\) equation and is solved for the unknown, next time-step pressure \([P]^{t+1}\), using a linear solver. Next, we discuss the construction procedure of a node control volume mesh in a domain of tetrahedron elements.

3.2 Node Control Volume Mesh

A node control volume is a secondary grid constructed around the vertices of the finite element mesh. In this section, we discuss the procedure for constructing a node control volume mesh, and the computation of the area normal vectors for tetrahedral elements. Both the area normal vectors along with node control volume mesh are needed to assure that the fluxes on the interfaces of the control volumes are continuous and perpendicular to ensure local conservation of mass. This procedure is necessary since the velocity field is discontinuous between the elements interfaces.

A node control volume between tetrahedron elements is constructed around the shared node with hexahedron sectors. Each sector has eight vertices. The vertices are located at the shared node, the barycenter of the host element and the barycenter of the three interfaces and the three edges of the host element connected to the node; see Figs. 3 and 4. The area normal vector \(\mathbf {(AN)}\) of each control volume is calculated where each sector has three faces connected to the flow and each face has two interface line vectors, see Fig. 4. The cross-product of the interface line vectors gives the area normal vectors of each face,

$$\begin{aligned} \mathbf {AN_J} = {\left\{ \begin{array}{ll} \; \; \, (\mathbf {n}_{J1} \times \mathbf {n}_{J2} )&{} \text {if } T_l > 0\\ -(\mathbf {n}_{J1} \times \mathbf {n}_{J2}) &{} \text {if } T_l<0 \end{array}\right. } \end{aligned}$$
(25)
$$\begin{aligned} \mathbf {AN_K} = {\left\{ \begin{array}{ll} \; \; \, (\mathbf {n}_{K1} \times \mathbf {n}_{K2} )&{} \text {if } T_l > 0\\ -(\mathbf {n}_{K1} \times \mathbf {n}_{K2}) &{} \text {if } T_l<0 \end{array}\right. } \end{aligned}$$
(26)
$$\begin{aligned} \mathbf {AN_L} = {\left\{ \begin{array}{ll} \; \; \, (\mathbf {n}_{L1} \times \mathbf {n}_{L2} )&{} \text {if } T_l > 0\\ -(\mathbf {n}_{L1} \times \mathbf {n}_{L2}) &{} \text {if } T_l<0 \end{array}\right. } \end{aligned}$$
(27)

where \(\mathbf {AN}_J\) is the area normal vector of face J, \(T_I=(J-I)\cdot ((K-J)\times (L-J))\) and i, j, k, l are the coordinates of the vertices and all different. We use \(T_I\) as a reference to assure the flow is out of the control volume. \(\mathbf {n}_{J1}\) is the first interface line vector of face J. Please refer to "Appendix A" and Fig. 4 for the values of interface lines for the faces.

The equations are performed for each sector in the node control volume. The pore volume of a node control volume in a tetrahedron element mesh is calculated by,

$$\begin{aligned} V_{(n)}=\sum ^E_{e=1}\frac{V^{(e)}\phi ^{(e)}}{4} \end{aligned}$$
(28)

where \(V_{(n)}\) is the pore volume of the node control volume (n), and E is the number of elements sharing the control volumes.

3.3 Fluid Saturation Calculation in Node Control Volumes

After constructing the node control volume mesh and calculating the area normal vector for each sector in the node control volumes, we integrate the transport equation, Eq. 1, over the node control volume (n). After that, the divergence theorem is applied and the equation is discretized in time using the backward Euler approach (similar to Eq. 24). The next time-step phase saturation in control volume (n) is calculated by,

$$\begin{aligned} S_{w,(n)}^{t+1}=\frac{S_{w,(n)}^{t}CV^t+\triangle t\left[ -\sum _j^{SI} flux_{(n),j}+q_{(n),w}\right] }{CV^{t+1}} \end{aligned}$$
(29)

where SI is the number of faces in node control volume (n), and the \(flux_{(n),j)}\) is the flux of face j in node control volume (n) and calculated by,

$$\begin{aligned} flux_{(n),j}=(\lambda _w^{t^{(e}}K^{(e)}\nabla \phi ^{(e)})_{(n),j}\cdot \mathbf {AN}_{(n),j} \end{aligned}$$
(30)

where \(\lambda _w^t\) is calculated using the pervious time-step phase saturation of the upstream control volume, and \(\nabla P^{(e)}\) is calculated from Eq. 9. Equation 24 is calculated for every node control volume in the mesh, and in this paper we calculate the water saturation.

3.4 NCVFE Implementation Algorithm

Finally, we present algorithm 1 of the NCVFE implementation . The pressure is implicitly calculated and saturation calculations are explicit (IMPES). The number of nodes in the mesh represent the degrees of freedom of the system.

4 Numerical Tests

In this section, we perform a numerical study of the NCVFE method. We test its accuracy in modeling two-phase fluid flow in regions with large variations in their material properties, i.e. between matrix regions and sealing/conductive faults (Tests I and II).

A meshing software, GMSH, (Geuzaine and Remacle 2009) is used to create 3-D tetrahedron finite element meshes that are used in the upcoming test. Each test has a mesh of a different element size that is refined by manipulating the element length (h). A quadratic model is used to construct the oil and water relative permeability curves, and a unifrom porosity of 0.2 is used. The water and oil viscosities are 0.4 and 2.5 mPa.s respectively and the rock compressibility equals \(4.0 \times 10^{-10} Pa^{-1}\) . At intial conditions, we assume that the domain is fully saturated with oil.

The pore volume injected (PVI) is defined as

$$\begin{aligned} PVI=\frac{1}{V_P}\int _{o}^{t}q_tdv \end{aligned}$$
(31)

where \(V_P\) is the total pore volume of the system.

To visualize the tests results better, we plot the solutions on the control volumes.

figure a

4.1 Buckley–Leverett Validation

In this section, we compare the analytical solution of the Buckley–Leverett function with the saturation profiles produced by the NCVFE method at different mesh resolutions. The solution is one-dimensional with negligible gravity and capillarity effects. The tested domain is a rectangular tube dimensions of 1 m \(\times\) element length \(\times\) element length for the tetrahedron elements. The results are plotted in Fig. 5-a where both the analytical and the numerical profiles are shown. The analytical solutions produces a sharper front of water saturation which is expected, and a finer grid is needed (0.001 element length) to achieve a close match to the analytical solution. This shows that the NCVFE method is capable of mapping the water front movement for relatively fine grids. The upcoming tests will discuss in details the effect of the mesh resolution on the water saturation calculations.

Furthermore, we computed the error \(L_2 norm\) at the different mesh resolutions for tetrahedron elements to measure the rate of convergence using the following equation:

$$\begin{aligned} L_2^{S_w}=\sqrt{\sum _iV_i ({S_w}_i-{S_w}^{ex})^2} \end{aligned}$$
(32)

The sub-linear convergence rate is around 0.4 and can be noticed in Fig. 5b. The convergence rate is relatively low because of the sharp shock-front of the analytical solution and it is in line with other finite element descritization schemes (Geiger et al. 2004; Abushaikha et al. 2017). The overall results show that the NCVFE method is capable of modeling the nonlinear behavior of the two-phase flow and validated through Buckley–Leverett function.

Fig. 5
figure 5

Comparison of the analytical solution of the Buckley–Leverett problem at distance 0.5 m from the left-hand boundary to the numerical solution of the NCVFE method using three meshes for tetrahedron (left) Convergence of the \(L_2\) error of water saturation as a function of the mesh element length for the numerical solutions of the Buckley–Leverett problem using the 3-D tetrahedral elements

Full size image

4.2 Test I: Barriers Case

In our first test, we incorporate 20 barriers into a domain to test the sealing capability of the NCVFE method. The tested domain is a square of a side length of \(1\ m\) and a depth of \(0.05\ m\) where barriers aperture (width) is \(0.04\ m\). The injector is located at the left boundary of the domain, where water is injected at a constant rate. The resolution of the mesh is varied at the injector side as well. Figure 6 and Table 1 show the mesh properties along with error in the saturation calculation (we will discuss this error in details later).

Fig. 6
figure 6

a Domain of Test I; there are 20 barriers no-flow (zero permeability) regions in the domain with aperture size of 0.04 m, b Location of the injector and the producer, and the direction of the flow

Full size image
Table 1 The error of Test I resulting from estimating the water saturation in the barriers
Full size table

Figure 7 shows the water saturation employing the three different meshes from Table 1 at different injected pore volume. In the coarse mesh, as the water propagates inside the domain, it fully invades the barriers and does not honour the zero permeability property of the elements. The method allows the water to move in a control volume that contains elements with zero permeability; the correct solution should have no flow in such elements. The degree of nonphysical water invasion decreases as the mesh is refined. This is a classic case of the artificial fluid smearing produced by the NCVFE method between regions of different of material properties. To measure and quantify this behavior, we calculate the error in water saturation in the barriers using

$$\begin{aligned} e(S_w)=\frac{1}{V_Z}\int |S_w - S_w^{ref}| dv \end{aligned}$$
(33)

where \(V_Z\) is the total pore volume of the barriers, \(S_w^{ref}\) is the reference solution for water saturation in the zone which equals the initial water saturation.

Fig. 7
figure 7

Test I water saturation at injected pore volumes 0.1 (left), 0.25 (center), 1.0 (right) for: mesh of element size 0.05 m (top), mesh of element size 0.02 m (center), mesh of element size 0.01 m (bottom). See Table 1

Full size image

Figure 8 and Table 1 show this error. The error is large and decreases as the mesh is refined. We also calculate the convergence rate of the NCVFE method for this test (Janicke and Kost 1996),

$$\begin{aligned} e \sim N_{DF}^{(p/d)} \end{aligned}$$
(34)

where \(N_{DF}\) is the number of degrees of freedom, p is the order of convergence and d is the spatial dimension. For this case, p \(\equiv\) 1 (where \(d \ = \ 3\)) which is in agreement with the linear tetrahedron elements employed in the method (Janicke and Kost 1996).

Sealing faults or non-permeable layers are heavily present in subsurface reservoirs. They divide a field in to different reservoirs or compartments where the fluids are stored. Therefore modeling nonphysical communication between the reservoirs or permeability zones will produce inaccurate flow behaviors and predictions of recovery. High mesh resolutions are required to minimize this behavior, as we saw in this test.

To summarize , we used the NCVFE method to model water invasion into the non-permeable regions of a porous domain. This invasion caused the appearance of artificial smearing problems inside the region. This nonphysical flow is attributed to the procedure of constructing the control volume around the vertices of the elements. These elements with different material properties share interfaces which promotes nonphysical communication, however this behavior becomes less significant as the mesh of the domain is refined.

Fig. 8
figure 8

The error of Test I resulting from estimating the water saturation in the using NCVFE method at 0.5 and 1 pore volume injected as the element length varies

Full size image

4.3 Test II: Fractures Case

In this case, we model the fluid flow for a fractured network based on an outcrop sample taken from the Lias formation (limestone) from Bristol Channel, UK (Abushaikha 2013). We model the fractures explicitly using tetrahedron elements with different aperture sizes for the fractures ranging from 0.4 to 3 cm. The domain has dimensions of 68.4 \(\times\) 48.6 \(\times\) 1 cm and has 14 matrix blocks surrounded by conductive fractures; see Fig. 9. The injector is located at the right boundary where water is injected at a constant rate in a similar fashion to the schematic shown in Fig. 6b. The mesh properties are shown in Table 2.

Fig. 9
figure 9

a Outcrop sample from Lias formation (limestone) from Bristol Channel 2, b discrete fracture models of the outcrop case

Full size image
Fig. 10
figure 10

Test II water situations at injected pore volumes 0.075 (left), 0.15 (center), 0.45 (right) for: mesh of element size 100 mm (top), 10 mm (center), 5 mm (bottom). See Table 2

Full size image

To understand the implications of the flow attributed to the NCVFE method, we change the permeability of the matrix zones to negligible values. The results are considered as a reference solution that represents the water flow through the fractured zones without invading the matrices.The outcrop is shown in Fig. 9, where the permeability of the fractures is 10,000 mD.

Figure 10 shows the water saturation in three different meshes from Table 2 at different injected pore volumes. For the coarse mesh, the water heavily invades the matrix regions delaying the flow in the fractured network. As the mesh is refined, the water propagates faster inside the fracture regions with fewer invasion of the matrix. To analyze this behavior, we calculate the water cut at the right hand boundary as a function of pore volumes injected to measure the breakthrough time. The water cut is given by

$$\begin{aligned} WC=\frac{q_w}{q_t} \end{aligned}$$
(35)

where \(q_t=q_w+q_0\), \(q_w\) and \(q_o\) is the water and oil production flow rate, respectively.

Table 2 The error of Test II resulting from estimating the water saturation in the barriers
Full size table

Figure 11a shows the water breakthrough times at the right hand boundary for the meshes of Table 2 using Eq. 35. As observed in Fig. 10, the water reaches the right hand boundary faster when the mesh is refined. This behavior is in contradiction with common mesh convergence studies since the opposite is the norm (Fanchi 2018). To distinguish which type of dispersion is causing this behavior, physical or numerical, we mesh the fracture network without the matrix regions and estimate the water breakthrough times at the right hand boundary for the element lengths of Table 2 in Fig. 11b. We notice that as the fracture network is refined, the water breakthrough time is delayed; opposite to Fig. 11a. Therefore, the artificial smearing produced by NCVFE is causing this behavior where the physical dispersion is eclipsing the truncated numerical error of the mesh refinements promoting the delay of breakthrough times for the coarse meshes.

Fig. 11
figure 11

a The water cut at the right-hand boundary for Test II versus pore volumes injected for the meshes without the matrix regions. b The water cut at the right hand boundary for Test II versus pore volumes injected

Full size image
Fig. 12
figure 12

The error of Test II resulting from estimating the water saturation in the using NCVFE method at 0.1 and 0.45 pore volume injected as the element length varies

Full size image

To measure this artificial smearing in the matrix regions, we use Eq. 33 to define the error. Figure 12 and Table 2 show the error produced, and as the mesh is refined the error decreases. Similarly, using Eq. 34, a first-order convergence rate is noticed where \(d \ =\ 3\). It is worth mentioning that the first half of the convergence rate slope is also first order because the element length of the first two meshes is larger than the depth of the domain; effectively we have \(d \ = \ 2\).

In this test, a delay of flow in the fracture region and breakthrough time was noticed due to the numerical extension of the fracture width. This can be attributed to artificial smearing that causes inaccurate predictions of water saturation calculations. The role of fractures is very important in understanding the flow in reservoirs and optimizing recovery factors, and their properties (dimensions and aperture size) greatly influence the kinetics and the recovery of hydrocarbons. Therefore, high-resolution meshes are recommended for NCVFE when modeling highly conductive zones especially between regions with large variations in their material properties, as we saw in this test and the previous test. Simulations such as these could be used to determine empirical fracture- matrix transfer functions (Abushaikha 2008) that encapsulate the average recovery in geological realistic fracture networks to be used in full field case studies.

5 Summary and Conclusions

In this paper, we have investigated the accuracy of the NCVFE method to model two-phase fluid flow in heterogeneous and fractured porous media. In modeling sealing faults, the method performed poorly as the barriers were fully penetrated by the displacing water. The water did not respect the zero-permeabilities defined on the elements and flowed through them, because the NCVFE encompasses elements with both zero and finite permeabilities. In representing conductive faults (fractures), the NCVFE method did not perform any better. Very high mesh resolutions were needed to obtain a reasonable representation of the fluid flow inside the fracture region. The low resolution mesh suffered a large amount of unphysical flow to the matrix regions and a major delay in breakthrough time compared to the high-resolution meshes.

We conclude that NCVFE requires high mesh resolutions to model multi-phase flow in heterogeneous systems reasonably. The critical drawback of the NCVFE method is that the material properties are defined on the elements, while the fluid saturation is calculated on the vertices of elements. Essentially, the saturation is updated on a coarse mesh that is not aligned with the assignment of rock properties.