Numerical Modeling of Momentum Dispersion in Porous Media Based on the Pore Scale Prevalence Hypothesis

Abstract

A macroscopic model that accounts for the effect of momentum dispersion on flows in porous media is proposed. The model is based on the pore scale prevalence hypothesis (PSPH). The effects of macroscopic velocity gradient on momentum transport are approximated using a Laplacian term. A local Reynolds number Re_d, which characterizes the strength of momentum dispersion, is introduced to calculate the effective viscosity. The characteristic length used in defining Re_d is the pore size, while the characteristic velocity is the mixing velocity. A Taylor expansion is made for the effective viscosity with respect to Re_d. The two leading-order terms of the Taylor series are adopted in the present PSPH momentum-dispersion model. The model constants are determined from the direct numerical simulation results of a flow in the same porous medium bounded by two walls. The effective viscosity approaches the molecular viscosity when the porosity is increased to 1. It approaches infinity when the porosity approaches 0. The benchmark studies show that the effects of the macroscopic velocity gradient can be approximated by the Laplacian term. The proposed PSPH momentum-dispersion model is highly accurate in a wide range of Reynolds and Darcy numbers as well as porosities.

1 Introduction

A porous medium consists of a solid matrix with interconnected voids (Nield and Bejan 2017). Many industrial processes can be approximated as convection in porous media (Bruant et al. 2002; Taheri 2014; de Lemos 2012a; Kim et al. 2000). Turbulence is welcome in many processes (Bruant et al. 2002; Taheri 2014) since it might significantly enhance the heat and mass transfer. Turbulent convection in a porous medium can be calculated using direct numerical simulation (DNS), in which all geometrical details of the porous matrix are taken into account. However, DNS is often too computationally expensive and provides too much information to be practical in engineering applications. Therefore, convection in porous media is more often studied by solving macroscopic equations.

Macroscopic equations for simulating flow in a porous medium can be derived by time- and volume-averaging the Navier–Stokes equations (Pope 2000; de Lemos 2005). The effect of the porous matrix on the losses of mechanical energy is often approximated by the Darcy term when the flow velocity is low. The Forchheimer term is used to correct the Darcy equation when the velocity is high. In a recent study, Lasseux et al. (2019) proposed a more accurate and complicated model that involves two effective coefficients for accounting for the time-decaying influence of the flow initial condition. However, the Darcy–Forchheimer equation is still the most widely used model for solving engineering problems.

Another alternative to the Darcy equation is known as the Brinkman equation. A Laplacian term is introduced in the macroscopic momentum equation to model the effects of the velocity gradient, including the effects of momentum dispersion and molecular diffusion. In early papers, the effective viscosity $\tilde{\mu }$ in the Brinkman equation was assumed to have the same value as the molecular viscosity $\mu$, see Brinkman (1947). However, the experiments by Givler and Altobelli (1994) show that $\tilde{\mu }$ may be different from $\mu$, and the effects of this difference were investigated in Kuznetsov (1997). Later, Valdes-Parada et al. (2007) argued the effective viscosity is different from the fluid viscosity only for high porosity cases. By performing a series of numerical simulations, Vafai (2005) concluded that whether $\tilde{\mu }/\mu$ is larger or smaller than unity depends on the type of a porous medium. Ochoa-Tapia and Whitaker (1995) suggested that a value of $\tilde{\mu }/\mu$ can be approximated as $1/\phi$, where $\phi$ is the porosity of the porous medium. Thus, $\tilde{\mu }/\mu$ is larger than unity. Bear and Bachmat (1990) suggested $\tilde{\mu }/\mu$ to be equal to $1/\left( {\phi \tau^{ *} } \right)$, where $\tau^{ *}$ is the tortuosity of the porous medium and depends on the geometry of a porous matrix. Saez et al. (1991) also suggested that $\tilde{\mu }/\mu$ is close to the tortuosity which is thought to be less than unity. Based on the earlier work by Vafai and Tien (1981, 1982) and without strict validation, Hsu and Cheng (1990) proposed a momentum equation that models the momentum dispersion by the Brinkman term, in which $\tilde{\mu }/\mu$ is set to 1.

Some studies examined the validity of the Brinkman equation. Using the Green’s function approach, Durlofsky and Brady (1987) suggested that the Brinkman equation is valid for $\phi > 0.95$. Rubinstein (1986) showed that the Brinkman equation can be used when $\phi$ is as small as 0.8. Nield and Bejan (2017) argued that the Brinkman model is breaking down when a large value of $\tilde{\mu }/\mu$ is needed to match theory and experiment. Gerritsen et al. (2005) suggested that the Brinkman equation is not uniformly valid as the porosity tends to unity. Auriaut (2009) stated that the Brinkman equation appears to be valid for flows through fixed beds of particles or fibers at very low porosity. It cannot be physically justified for classical porous media with connected porous matrices. However, in another recent study Kuznetsov and Kuznetsov (2017) showed that the Brinkman model can fit experimental data when $\tilde{\mu }/\mu$ is as large as 8 and reported the confidence intervals for the effective viscosity. It is still not clear whether a Laplacian term, such as one used in the Brinkman model, can be used as a reasonable approximation of momentum dispersion, especially when the porosity is small.

Some other studies suggested that the Brinkman term does not need to be taken into account in many applications since its effect is significant only in a thin boundary layer, see Nield and Bejan (2017), Tam (1969), and Levy (1981). However, in a recent DNS study, Jin and Kuznetsov (2017) showed that the Brinkman term may have an important effect near a wall when the flow is turbulent.

Jin et al. (2015) and Uth et al. (2016) studied turbulent flows in porous media using DNS and proposed the pore scale prevalence hypothesis (PSPH). The PSPH states that the size of turbulent eddies is restricted by the pore size. Jin and Kuznetsov (2017) further indicated that both turbulent motions and momentum dispersion are characterized by the pore size. Chu et al. (2018) confirmed the PSPH if the porous matrix is not sparsely packed. However, the effect of the pore size on momentum dispersion is not explicitly accounted for in previous models (Brinkman 1947; Ochoa-Tapia and Whitaker 1995; Hsu and Cheng 1990).

The purpose of this paper is to develop a momentum-dispersion model based on the PSPH. Results of the PSPH momentum-dispersion model will be validated by the DNS results in which the detailed pore-scale geometry is accounted for. Through this study, we will also try to answer whether the effects of the velocity gradient on momentum transport can be reasonably well approximated by using the Laplacian term.

The structure of this paper is as follows. The governing equations and numerical methods in this study are introduced in Sect. 2. Equations for the model coefficients are discussed in Sect. 3. In Sect. 4, the developed macroscopic model is applied to simulating flows in two types of porous media to demonstrate its utility. Finally, the conclusions are given in Sect. 5.

2 Governing Equations and Numerical Methods

2.1 Governing Equations for Microscopic DNS

The governing equations for microscopic DNS of incompressible flows in porous media are the transient Navier–Stokes equations. They are

$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0,$$

(2.1)

$$\frac{{\partial u_{i} }}{\partial t} + \frac{{\partial u_{i} u_{j} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial p}{{\partial x_{i} }} + \nu \frac{{\partial^{2} u_{i} }}{{\partial x_{j}^{2} }} + g_{i} ,$$

(2.2)

The dimensions of the velocity $u_{i}$, distance $x_{i}$, time $t$, density $\rho$, pressure $p$, kinematic viscosity of the fluid $\nu$, and negative of the applied pressure gradient $g_{i}$ (assumed to be a constant value) in Eqs. (2.1) and (2.2) are [LT], [L], [T], [ML⁻³], [ML⁻¹T⁻²], [L²T⁻¹], and [LT⁻²], respectively, where L, T and M can be any units of length, time, and mass. These units are not specified so that the numerical results can be applied in any system of units.

The detailed geometry of the porous matrix is accounted for in microscopic DNS. The Navier–Stokes equations are solved directly without introducing any additional model. The purpose of performing microscopic DNS is to determine the model coefficients and to obtain the data for model validation.

2.2 Governing Equations for Macroscopic Simulation

Macroscopic equations for flows in porous media are derived by volume averaging the Navier–Stokes equations. The approach of derivation is similar to that used by de Lemos (2012a, b), who averaged the governing Eqs. (2.1)–(2.2) over volume and time. By contrast, only volume averaging was used in our derivation. The macroscopic equations are expressed as

$$\frac{{\partial \left( {\phi \left\langle {u_{i} } \right\rangle^{i} } \right)}}{{\partial x_{i} }} = 0,$$

(2.3)

$$\frac{{\partial \left( {\phi \left\langle {u_{i} } \right\rangle^{i} } \right)}}{\partial t} + \frac{{\partial \left( {\phi \left\langle {u_{i} } \right\rangle^{i} \left\langle {u_{j} } \right\rangle^{j} } \right)}}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{{\partial \left( {\phi \left\langle p \right\rangle^{i} } \right)}}{{\partial x_{i} }} + \phi g_{i} - \phi R_{i} + \nu \frac{{\partial^{2} \left( {\phi \left\langle {u_{i} } \right\rangle^{i} } \right)}}{{\partial x_{j}^{2} }} - \frac{{\partial \left( {\phi \left\langle {{}_{ }^{i} u_{i} {}_{ }^{i} u_{j} } \right\rangle^{i} } \right)}}{{\partial x_{j} }}.$$

(2.4)

The operator $\left\langle . \right\rangle^{i}$ denotes volume averaging over the fluid region of a representative elementary volume (REV). The porosity $\phi$ is defined as $\phi = \frac{{V_{f} }}{{V_{s} + V_{f} }}$, where $V_{s}$ and $V_{f}$ are the solid and fluid volumes in a REV, respectively. $R_{i}$ denotes the total drag caused by the effect of the porous matrix.

It should be noted that an undetermined tensor $\phi \left\langle {{}_{ }^{i} u_{i} {}_{ }^{i} u_{j} } \right\rangle^{i}$, which corresponds to momentum dispersion, appears in Eq. (2.4). The spatial deviation ${}_{ }^{i} \varphi$, where $\varphi$ could be any variable under consideration, is the difference between the real value and its intrinsic average, calculated as

$${}_{ }^{i} \varphi = \varphi - \left\langle {\varphi^{i} } \right\rangle$$

(2.5)

$\phi \left\langle {{}_{ }^{i} u_{i} {}_{ }^{i} u_{j} } \right\rangle^{i}$ needs to be closed before the macroscopic Eqs. (2.3)–(2.4) can be solved.

2.3 Total Drag

The total drag $R_{i}$ is usually approximated by the Forchheimer extension of the Darcy equation (Lage and Antohe 2000), calculated as

$$R_{i} = R_{Di} + R_{Fi} = \frac{\nu }{K}u_{Di} + \frac{{c_{F} }}{\sqrt K }\left| {{\mathbf{u}}_{D} } \right|u_{Di}$$

(2.6)

$u_{Di}$ denotes the seepage velocity $\phi \left\langle {u_{i}^{i} } \right\rangle$. ${\mathbf{u}}_{D}$ is the superficial velocity vector. $c_{F}$ is a dimensionless coefficient which accounts for the nonlinear increase of the form-drag with the velocity. Masuka and Takatsu (1996) and Wood et al. (2020) stated that the Darcy–Forchheimer law appears to be valid for both laminar and turbulent flows. The permeability $K$ is a measure of the ability of a porous medium to allow fluids to pass through it. For a homogeneous porous medium, $K$ is traditionally determined by the ratio of $\nu u_{D1}$ and $g_{1} - \frac{1}{\rho }\frac{{{{\Delta }}p}}{{{{\Delta }}x}}_{ }$ as the flow velocity is small (approaches 0), where ${{\Delta }}p$ is the increase of pressure over the length ${{\Delta }}x$.

Some studies show that $c_{F}$ is not a constant but is related to the superficial (filtration) flow velocity, see Lage et al. (1997). Here, we make a Taylor expansion for $R_{i}$ with respect to a local Reynolds number, ${\text{Re}}_{K}$, calculated as

$$R_{i} = \frac{\nu }{K}u_{Di} \left( {1 + c_{F1} {\text{Re}}_{K} + c_{F2} {\text{Re}}_{K}^{2} + \cdots + c_{Fn} {\text{Re}}_{K}^{n} + O\left( {{\text{Re}}_{K}^{n + 1} } \right)} \right)$$

(2.7)

$c_{F1}$, $c_{F2}$, …, $c_{Fn}$ are the coefficients of the Taylor series. ${\text{Re}}_{K}$ is the local Reynolds number based on the permeability, calculated as

$${\text{Re}}_{K}^{ } = \frac{{\sqrt K \left| {{\mathbf{u}}_{D} } \right|}}{\nu }$$

(2.8)

Comparing Eqs. (2.6) and (2.7), it is evident that $c_{F}$ is calculated as

$$c_{F} = c_{F1} + c_{F2} {\text{Re}}_{K}^{ } + \cdots + c_{Fn} {\text{Re}}_{K}^{n - 1} + O\left( {{\text{Re}}_{K}^{n} } \right)$$

(2.9)

In this study, $R_{i}$ is approximated with the three leading-order terms of Eq. (2.7), as

$$R_{i} \approx \frac{\nu }{K}u_{Di} \left( {1 + c_{F1} {\text{Re}}_{K} + c_{F2} {\text{Re}}_{K}^{2} } \right)$$

(2.10)

The dependence of $c_{F}$ on the velocity is taken into account in Eq. (2.9).

2.4 PSPH Model for Momentum Dispersion

The gradient of macroscopic velocity might affect the momentum dispersion $\phi \left\langle {{}_{ }^{i} u_{i} {}_{ }^{i} u_{j} } \right\rangle^{i}$, molecular diffusion $2\nu s_{Dij}$, and total drag $R_{i}$. A symmetric tensor $D_{ij} = 2\tilde{\nu }s_{Dij}$ is introduced to account for its effects, where $s_{Dij}$ is the strain rate of the superficial velocity ${\mathbf{u}}_{D}$, $\tilde{\nu}$ is an effective viscosity. The macroscopic Eq. (2.4) becomes

$$\frac{{\partial u_{Di} }}{\partial t} + \frac{{\partial \left( {u_{Di} u_{Di} /\phi } \right)}}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{{\partial \left( {\phi \left\langle p \right\rangle^{i} } \right)}}{{\partial x_{i} }} + \phi g_{i} - \phi R_{i} + \frac{{\partial D_{ij} }}{{\partial x_{j} }}$$

(2.11)

$\tilde{\nu }/\nu$ is often treated as a constant or a function of the porosity (Brinkman 1947; Ochoa-Tapia and Whitaker 1995). However, the DNS results by Jin and Kuznetsov (2017) showed that the magnitude of $\tilde{\nu }$ increases with an increase in the local Reynolds number, as the momentum dispersion becomes more important.

We propose a new Reynolds number that characterizes the strength of the local momentum dispersion. According to the PSPH, the characteristic length scale of the flow in a porous medium is the pore size $s$. In a review paper, Wood et al. (2020) suggested that the pore size can be characterized by the mean particle diameter for a generic porous matrix (GPM). In this study, we use $\sqrt K$ to characterize the pore size $s$, because $\sqrt K$ has a linear relationship with $s$ when the shape of the porous matrix is fixed. $\sqrt K$ is also used as the length scale because it is easy to determine $K$ for a porous matrix.

Jin and Kuznetsov (2017) suggested that the characteristic velocity for flows in porous media close to the wall is the product of $\sqrt K$ and the magnitude of the strain rate $\left| {s_{Dij} } \right|$, calculated as

$$\left| {s_{Dij} } \right| = \left( {2s_{Dij} s_{Dij} } \right)^{1/2}$$

(2.12)

This is similar to the mixing length model of Prandtl (1925) in which the fluid is assumed to mix within the mixing length due to turbulent fluctuations.

Using $\sqrt K$ and $\left| {s_{Dij} } \right|\sqrt K$ as the characteristic length and velocity, respectively, ${\text{Re}}_{d}$ is defined as

$${\text{Re}}_{d} = \frac{{K\left| {s_{Dij} } \right|}}{\nu }$$

(2.13)

For a one-dimensional wall bounded flow, ${\text{Re}}_{d}$ represents the ratio between the inertial force $u\left| {{\text{d}}u/{\text{d}}y} \right|$ and the resisting force according to the Darcy law, $\frac{\nu }{K}u$, where $u$ is the macroscopic streamwise velocity and $y$ is the distance from the wall.

The ratio $\tilde{\nu }/\nu$ approaches a constant value $c_{B1}$ when the Reynolds number ${\text{Re}}_{d}$ approaches 0. A Taylor expansion with respect to ${\text{Re}}_{d}$ can be made for $\tilde{\nu }/\nu$, as follows

$$\tilde{\nu }/\nu = c_{B1} + c_{B2} {\text{Re}}_{d} + \cdots + c_{Bn} {\text{Re}}_{d}^{n - 1} + O\left( {{\text{Re}}_{d}^{n} } \right)$$

(2.14)

where $c_{B1}$, $c_{B2}$, …, $c_{Bn}$ are the coefficients of the Taylor series. In this study, we take the two leading-order terms of Eq. (2.14), i.e.,

$$\tilde{\nu }/\nu \approx c_{B1} + c_{B2} {\text{Re}}_{d}$$

(2.15)

The effective viscosity $\tilde{\nu }$ in Eq. (2.11) can be determined using Eq. (2.15).

2.5 Numerical Methods

Two methods are used in the simulation. They are

• A finite volume method (FVM) which directly solves the Navier–Stokes equations.

• A Lattice–Boltzmann method (LBM) which determines the particle distribution; this method indirectly corresponds to solving the Navier–Stokes equations.

The FVM is used for solving the macroscopic Eqs. (2.3)–(2.4). The solver is developed based on the open source computational fluid dynamics (CFD) code OpenFoam 18.12. To compute the derivatives of the velocity, the variables at the interfaces of the grid cells are obtained with linear interpolation. This leads to a second-order central difference scheme for spatial discretization. The pressure at the new time level is determined by the Poisson equation. The velocity is corrected by the Pressure-Implicit scheme with Splitting of Operators (PISO) pressure–velocity coupling.

The LBM is used for solving the microscopic Eqs. (2.1)–(2.2) to determine the model coefficients and obtain the validation data. The basic equation of the present LBM is a discretized version of the Boltzmann equation (Aidun and Clausen 2009) with the collision operator being treated by the Bhatnagar–Gross–Krook (BGK) model (Bhatnagar et al. 1954), i.e.

$$f_{i} \left( {{\mathbf{x}} + {\varvec{\upxi}}_{\varvec{i}} {{\Delta }}t, t + {{\Delta }}t} \right) - f_{i} \left( {{\mathbf{x}}, t} \right) = - \frac{1}{{\hat{\tau }}}\left( {f_{i} \left( {{\mathbf{x}}, t} \right) - f_{i}^{\text{eq}} \left( {{\mathbf{x}}, t} \right)} \right)$$

(2.16)

where ${\varvec{\upxi}}_{\varvec{i}}$ is a discrete particle velocity, $f_{i} \left( {{\mathbf{x}}, t} \right)$ is the probability to find a particle with a velocity ${\varvec{\upxi}}_{\varvec{i}}$ at a position ${\mathbf{x}}$ at a time t, $f_{i}^{\text{eq}} \left( {{\mathbf{x}}, t} \right)$ is the equilibrium form of $f_{i} \left( {{\mathbf{x}}, t} \right)$, and $\hat{\tau }$ is the relaxation time, which is related to the viscosity of the fluid [see Chen and Doolen (1998)].

With the help of the Chapman–Enskog expansion (Chen and Doolen 1998), the compressible Navier–Stokes equations can be derived from the Lattice Boltzmann equation. Equation (2.16) is equivalent to the incompressible Navier–Stokes Eqs. (2.1)–(2.2) for small Mach numbers, i.e. for negligible compressibility of the fluid (Chen and Doolen 1998).

The bounce back model is used to account for the no-slip boundary condition at the solid walls. In this model the particles are bounced back to the flow domain without any loss of mechanical energy when the particles collide with a wall. This model ensures conservation of mass and momentum at the boundary. More details can be found in Mohamad (2011).

Both the FVM and LBM solvers have received intensive validations and verifications in our previous studies (Jin and Kuznetsov 2017; Jin et al. 2015; Uth et al. 2016). Therefore, these numerical methods are directly used in this study. The DNS solutions can be used to validate the model results. Typical DNS cases are calculated using different meshes to estimate the uncertainty of the DNS solutions due to mesh-dependence. It will be introduced below when the numerical results are discussed.

3 Model Coefficients

The model coefficients $K$, $c_{F1}$, $c_{F2}$, $c_{B1}$, and $c_{B2}$ are geometric parameters which are independent of the flow condition. They need to be determined before the macroscopic Eqs. (2.3)–(2.4) can be solved. Various empirical and half-empirical correlations exist for calculating these coefficients.

In the case of beds of particles or fibers, the permeability $K$ can be approximated by the Carman–Kozeny equation (Kozeny 1927; Carman 1956)

$$K = \frac{{D_{P2}^{2} \phi^{3} }}{{180\left( {1 - \phi } \right)^{2} }}$$

(3.1)

where $D_{P2}^{ }$ is an effective average particle or fiber diameter.

$c_{F}$ is often set to a constant in previous studies, so $c_{F}$ is identical to $c_{F1}$ and $c_{F2}$ is 0. Ward (1964) suggested that $c_{F}$ is a universal constant, with a value of approximately 0.55. In a later study, Beavers et al. (1973) showed that $c_{F}$ can be better expressed as

$$c_{F} = 0.55\left( {1 - 5.5\frac{d}{{D_{e} }}} \right)$$

(3.2)

where $d$ is the sphere diameter and $D_{e}$ is the size of the bed. Nield and Bejan (2017) suggested that $c_{F}$ depends on the nature of the porous medium, and can be as small as 0.1. Irmay (1958) suggested an alternate equation for calculating the total drag $R_{i}$, i.e.,

$$R_{i} = \frac{{\beta \left( {1 - \phi } \right)^{2} }}{{D_{P2}^{2} \phi^{3} }}u_{Di} + \frac{{\alpha \left( {1 - \phi } \right)}}{{D_{P2}^{ } \phi^{3} }}\left| {{\mathbf{u}}_{D} } \right|u_{Di}^{ } ,$$

(3.3)

which is known as Ergun’s equation. The model coefficients $\alpha$ and $\beta$ are set to 1.75 and 150, respectively. $K$ and $c_{F}$ in Eq. (3.3) are calculated as

$$K = \frac{{D_{P2}^{2} \phi^{3} }}{{\beta \left( {1 - \phi } \right)^{2} }},\quad c_{F} = \alpha \beta^{ - 1/2} \phi^{ - 3/2}$$

(3.4)

$c_{B2}$ has never been accounted for in the previous studies. Brinkman (1947) set $c_{B1}$ to 1. Thus, $D_{ij}$ in Eq. (2.11) is calculated as

$$D_{ij} = \nu \frac{{\partial u_{Di}^{ } }}{{\partial x_{j} }},$$

(3.5)

which neglects momentum dispersion. The same assumption is also used in the macroscopic equations proposed by Hsu and Cheng (1990).

The results of Ochoa-Tapia and Whitaker (1995) suggest that $c_{B1} = \frac{1}{\phi }$. $D_{ij}$ is then calculated as

$$D_{ij} = \frac{\nu }{\phi }\frac{{\partial u_{Di}^{ } }}{{\partial x_{j} }}$$

(3.6)

In practice, we find that the correlations above may produce considerable errors since these model coefficients are related to the geometry of the porous matrix. The concept of tortuosity was introduced in some studies to account for the variation of pore-scale geometries. However, it is hard to determine the tortuosity. Also, we have not found a clear relationship between the model coefficients and the tortuosity. Therefore, the concept of tortuosity is not used in this study.

With the fast development of high-performance computers, it is possible to determine the model coefficients directly from the CFD results. To determine the model coefficients, we use DNS to compute the flow in the porous medium that is bounded by two walls. Periodic boundary conditions are used in the streamwise and transverse directions. The number of REVs in the wall-normal direction should be large enough so that the flow near the central region is not affected by the walls.

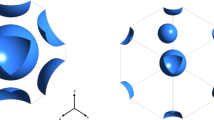
Two types of porous matrices are utilized in this study; they are composed of arrays of spheres or cubes. A schematic geometry of the porous matrix is shown in Fig. 1. The porous matrix is composed of 96 ($4 \times 8 \times 4$) REVs. The domain size is $4s \times 8s \times 4s$, where the pore size $s$ is defined as the distance between two adjacent solid elements. The viscosity $\nu$ is set to 0.002 L²T⁻¹. $g_{1}$ is varied to obtain different Reynolds numbers. The simulations are performed using the LBM. The grid points are uniformly distributed. $\left( {41s/d} \right)^{3}$ grid points are used in each REV for laminar flows. $d$ is the size of the porous element. $\left( {81s/d} \right)^{3}$ grid points are used in each REV for turbulent flows. Up to 161 million grid points are used in the study.

Fig. 1

Schematic geometry of the porous matrix

Since a wall only affects the flow in a few REVs next to it, the macroscopic equation in the central region of the channel can be simplified to

$$g_{1} - R_{1} = g_{1} - \frac{\nu }{K}u_{D1} \left( {1 + c_{F1} {\text{Re}}_{K} + c_{F2} {\text{Re}}_{K}^{2} } \right) = 0$$

(3.7)

In order to determine the value of K, we first specify $g_{1}$ and then calculate the seepage velocity $u_{D1}$. We then calculate the approximate value of K by fitting the DNS results with $g_{1} = \frac{\nu }{K}u_{D1}$ for $1 \le {\text{Re}}_{s} \le 20$, where ${\text{Re}}_{s}$ is the Reynolds number based on the pore size $s$. The corresponding values of ${\text{Re}}_{K}$ are in the range 0.04–0.8. Ward (1964) suggested that the transition from the Darcy regime to the Forchheimer regime occurs in the ${\text{Re}}_{K}$ range 1–10, so the flow is still in the Darcy regime. We did not determine $K$ for very small values of ${\text{Re}}_{s}$ because it leads to a considerable error for flows with large ${\text{Re}}_{K}$ values. We then set $c_{F2}$ in Eq. (3.7) to 0, and adjusted the values of $K$ and $c_{F1}$ by fitting the microscopic DNS results with Eq. (3.7) for ${\text{Re}}_{K} \le 3$. After $K$ and $c_{F1}$ are determined, the value of $c_{F2}$ is obtained by fitting the microscopic DNS results for ${\text{Re}}_{K} > 3$. The solution of Eq. (3.7) and the microscopic DNS results for the porous matrix composed of spheres are compared in Fig. 2. Typical turbulent cases are recalculated using a different resolution ($71^{3}$ grid points for each REV) to estimate the uncertainty due to the mesh resolution. It can be seen that our DNS solutions are generally mesh-independent. It is evident that $c_{F2}$ has significant effects at large ${\text{Re}}_{K}$ values.

Fig. 2

Applied pressure gradient $g_{1}$ versus Reynolds number ${\text{Re}}_{K}$. The porous matrix is made of arrays of spheres. $\phi = 0.48$ ($s/d = 1$), $K = 0.0026$, $c_{F1} = 0.049$, and $c_{F2} = 0.003$. The DNS solutions from a high-resolution mesh ($81^{3}$ grid points for each REV) and from a low-resolution mesh ($71^{3}$ grid points for each REV) are compared to indicate the numerical error

The values of $K$ for different geometries of porous elements are shown in Fig. 3. It can be seen that the geometry of the porous matrix has significant effects on the model coefficients. The correlations proposed in the previous studies produce considerable errors, particularly for large values of $\phi$. Therefore, instead of using the correlations in the references, the values of $K$ are determined by fitting with the DNS results obtained in this study.

Fig. 3

Permeability $K$ versus porosity $\phi$ for porous matrices composed of spheres and cubes. The $K$ values obtained from DNS results are compared with the results from the Carman–Kozeny (Eq. 3.1) and Ergun (Eq. 3.4) equations

The values of $c_{F} = c_{F1} + c_{F2} \text{Re}_{K}^{ }$ for the porous matrices composed of spheres and cubes are shown in Fig. 4. Values of $c_{F1}$ and $c_{F2}$ are also obtained directly by fitting the DNS results. It can be seen that the values of $c_{F}$ for a porous matrix composed of spheres are close to the lower limit of the values suggested by Nield and Bejan (2017). The values of $c_{F}$ for a porous matrix composed of cubes are even lower.

Fig. 4

The Forchheimer coefficient $c_{F}$ versus ${\text{Re}}_{K}$. The porous matrix is composed of spheres ($\phi = 0.48$) or cubes ($\phi = 0.42$). The values of $c_{F}$ in this study are calculated using $c_{F} = c_{F1} + c_{F2} {\text{Re}}_{K}^{ }$. $c_{F1}$ and $c_{F2}$ are determined from the DNS results. They are compared with the range 0.1–0.55 suggested by Nield and Bejan (2017) and the predictions of the Ergun equation (Eq. 3.4)

The macroscopic equation near the wall can be simplified as

$$\phi g_{1} - \phi R_{1} + \frac{\text{d}}{{{\text{d}}x_{1} }}\left( {\tilde{\nu }D_{12} } \right) = 0$$

(3.8)

The coefficients for calculating $R_{1}$ have already been determined above. $c_{B1}$ and $c_{B2}$ are determined by fitting the solution of Eq. (3.8) near the wall to the DNS results. The error of $R_{1}$ in the central region may affect the accuracy of $c_{B1}$ and $c_{B2}$. To avoid this uncertainty, the value of $c_{F2}$ is adjusted so that the calculated velocity at the center line $u_{cl}$ is identical to the DNS results.

We first set $c_{B2}$ to 0. $c_{B1}$ is adjusted until the solution of Eq. (3.8) averaged in the first REV close to wall is identical to the DNS results. The DNS results for ${\text{Re}}_{K} \le 1$ are used to determine $c_{B1}$. The values of $c_{B1}$ for different geometries of porous elements are shown in Fig. 5. It can be seen that $c_{B1}$ approaches 1 as $\phi$ increases asymptotically to 1, while it approaches infinity as $\phi$ decreases asymptotically to 0. This agrees with physical expectations. $c_{B1}$ does not change significantly when the geometry of the porous matrix is changed. It can be reasonably approximated as

$$c_{B1} = 49.63 \times \frac{{\left( {1 - \phi } \right)^{2} }}{{\phi^{0.5} }} + 1$$

(3.9)

Fig. 5

$c_{B1}$ versus porosity $\phi$ for different geometries of porous elements

$c_{B2}$ is determined by fitting the model results to the DNS results for ${\text{Re}}_{K} > 1$, see Fig. 6. $c_{B2}$ for porous matrices composed of cubes or spheres can be approximated by the following correlation

$$c_{B2} = 0.79 \times \frac{{\left( {1 - \phi } \right)^{2} }}{{\phi^{3} }}$$

(3.10)

$c_{B2}$ approaches 0 as $\phi$ increases asymptotically to 1, while it approaches infinity as $\phi$ decreases asymptotically to 0. Only two geometries of the porous elements are considered in this study. Our numerical results show that values of $c_{B1}$ and $c_{B2}$ are not affected significantly when the pore-scale geometry is changed.

Fig. 6

$c_{B2}$ versus porosity $\phi$ for different geometries of porous elements

4 Test Cases

The developed macroscopic equations are used to solve the flows in two types of porous media to demonstrate the utility of the developed macroscopic model. The first case deals with a flow in a channel occupied by a homogeneous and isotropic porous medium. The second case deals with a flow in a porous medium with two porosity scales.

4.1 Flow in a Channel Occupied by a Homogeneous and Isotropic Porous Medium

Microscopic DNS results for the flow rate in the same porous media have been used to determine the model coefficients. The purpose of this test case is to show that the PSPH momentum-dispersion model can be used for wide ranges of Darcy numbers (Da) and Reynolds numbers (${\text{Re}}_{cl}$). The Reynolds number ${\text{Re}}_{cl}$ is based on the half channel height $H$ and the centerline velocity in the channel $u_{cl}$, and is defined as

$${\text{Re}}_{cl} = \frac{{u_{cl} H}}{\nu }$$

(4.1)

The Darcy number is defined as

$${\text{Da}} = \frac{K}{{H^{2} }}$$

(4.2)

The instantaneous velocity magnitudes for representative Reynolds numbers are shown in Fig. 7. It may also be observed that the wall mainly affects the first REV next to it.

Fig. 7

Instantaneous velocity magnitude. In a, b the porous matrix is composed of spheres, $\phi = 0.48$. a${\text{Re}}_{cl}$ = 98, laminar; b${\text{Re}}_{cl}$ = 1730, turbulent. In c, d the porous matrix is composed of cubes, $\phi = 0.49$. c${\text{Re}}_{cl}$ = 127, laminar; d${\text{Re}}_{cl}$ = 2339, turbulent

We fix the Reynolds number ${\text{Re}}_{cl}$ (or $u_{cl}$) and reduce the pore size $s$, which results in three different scale ratios ($H/s$): 20, 30, and 40. The corresponding Darcy numbers are $8.5 \times 10^{ - 6}$, $3.8 \times 10^{ - 6}$, and $2.1 \times 10^{ - 6}$, respectively. Figure 8 shows that the distribution of $u_{D1}$ is steeper near the wall when ${\text{Da}}$ is smaller. The results of $u_{D1}$ from the PSPH model and DNS are averaged in each REV, so they can be compared quantitatively. The symbol $\left\langle \ldots \right\rangle^{\text{v}}$ in Fig. 8 denotes the whole REV-averaged velocity $\left\langle {u_{D1} } \right\rangle^{\text{v}}$ obtained from DNS and PSPH model results. It can be seen that the results from the PSPH model are in good agreement with the DNS results.

Fig. 8

$u_{D1} /u_{cl}$ and $\left\langle {u_{D1} } \right\rangle^{v} /u_{cl}$ versus the normalized distance from the wall $x_{2} /H$. The porous matrix is composed of cubes, $\phi = 0.49$, ${\text{Re}}_{cl} = 127$. Lines: $u_{D1} /u_{cl}$ obtained from continuous PSPH model results; hollow symbols: $\left\langle {u_{D1} } \right\rangle^{v} /u_{cl}$ from REV-averaged PSPH model results; solid symbols: $\left\langle {u_{D1} } \right\rangle^{v} /u_{cl}$ from REV-averaged DNS results

The numerical results in Fig. 8 are shown again in Fig. 9, but the distance from the wall $x_{2}$ is normalized with the pore size $s$ instead of $H$. The DNS results from two mesh resolutions are almost identical, indicating the mesh-independence of the DNS solution. The profiles of $u_{D1}$ collapse to a single curve, suggesting that the characteristic length of the flow is $s$; this is in accordance with the PSPH. Figure 9 also shows that the PSPH momentum-dispersion model is more accurate than the macroscopic model using Brinkman’s expression (Brinkman 1947) or Ochoa-Tapia and Whitaker’s expression (Ochoa-Tapia and Whitaker 1995).

Fig. 9

$u_{D1} /u_{cl}$ and $\left\langle {u_{D1} } \right\rangle^{v} /u_{cl}$ versus the normalized distance from the wall $x_{2} /s$. The porous matrix is composed of cubes, $\phi = 0.49$, ${\text{Re}}_{cl} = 127$

Different Reynolds numbers ${\text{Re}}_{cl}$ can be obtained by changing the applied pressure gradient $g_{1}$. Figure 10 shows the results for different values of ${\text{Re}}_{cl}$, which are in the turbulent regime. There are some perturbations of the velocity for the porous medium composed of spheres; this is also observed in Jin and Kuznetsov (2017). These perturbations are not found for the porous medium composed of cubes. The profiles of $u_{D1}$ for different values of ${\text{Re}}_{cl}$ collapse to a single curve when they are normalized with $u_{cl}$. The DNS results are mesh-independent, see Fig. 10b. The model results for both porous matrices are in good agreement with the DNS results.

Fig. 10

Streamwise velocity $\left\langle {u_{D1} } \right\rangle^{v}$ versus the normalized distance from the wall $x_{2} /s$ for different values of ${\text{Re}}_{cl}$. The porous matrix is composed of spheres (a) and cubes (b). Hollow symbols: PSPH model results; solid symbols: DNS results. Mesh 1: $101^{3}$ grid points for each REV; mesh 2: $76^{3}$ grid points for each REV

It can be also seen in Fig. 10 that, for the porous matrix under consideration, the wall only affects the flow in the first REV next to it. Therefore, in Fig. 11, we only compare the macroscopic and microscopic results for volume-averaged value of $u_{D1}$ in the first REV next to the wall. $c_{B2}$ has non-negligible effects when the flow is characterized by a large Reynolds number, particularly when the flow is turbulent, see Fig. 11b. The value of $u_{D1}$ next to the wall may be over-predicted by 10% if $c_{B2}$ is neglected.

Fig. 11

$\left\langle {u_{D1} } \right\rangle^{v}$ in the first REV next to the wall versus the applied pressure gradient $g_{1}$. The porous matrix is composed of cubes. a Whole range of values of the applied pressure gradient; b zoomed results in the turbulent regime

4.2 Flows in Porous Media with Two Porosities

To further investigate the generality of the proposed PSPH momentum-dispersion model, the flows in porous media with two porosities are simulated. The geometry of the porous matrix is shown in Fig. 12. A constant applied pressure gradient $g_{1}$ forces the fluid to flow with two characteristic velocities. The zone with a higher porosity has a higher velocity. Therefore, this type of flow has two characteristic Reynolds numbers based on the pore size $s$, calculated as

$${\text{Re}}_{1} = \frac{{u_{a} s}}{\nu };\quad {\text{Re}}_{2} = \frac{{u_{b} s}}{\nu }$$

(4.2)

where $u_{a}$ and $u_{b}$ are the macroscopic velocities in the two porous medium zones far away from the interface. The computational domain is composed of 128 ($4 \times 8 \times 4$) REVs. The two porous medium zones have the same pore size $s$ but different sizes of porous elements ($d_{1}$ and $d_{2}$), leading to two different porosities $\phi_{1}$ and $\phi_{2}$. Up to 661 million grid points are used for turbulent flows (each REV has $151^{3}$ points).

Fig. 12

Schematic geometry of a porous matrix with two porosities

Typical laminar and turbulent flows in this porous medium are shown in Fig. 13. The porosities of the two porous medium zones are $\phi_{1} = 0.42$ and $\phi_{2} = 0.49$, respectively. It can be seen that the effects of the interface are limited to the two REVs in the vicinity of the interface.

Fig. 13

Instantaneous velocity magnitude. The porous matrix is composed of cubes, $\phi_{1} = 0.42$, $\phi_{2} = 0.49$. a${\text{Re}}_{1} = 30$ and ${\text{Re}}_{2} = 60$ (laminar flow); b${\text{Re}}_{1} = 454$ and ${\text{Re}}_{2} = 860$ (turbulent flow)

Figure 14 shows the velocity profiles in the wall normal direction for $g_{1} = 0.07$ and $g_{1} = 1.1$. Both laminar and turbulent cases are calculated using a lower-resolution mesh (each REV has $91^{3}$ points). It can be seen that the results for the laminar flow are mesh-independent. The results for the turbulent flow are slightly mesh-dependent. The macroscopic model results are compared with the microscopic DNS results. It can be seen that the PSPH momentum-dispersion model is more accurate than the macroscopic model with Brinkman’s expression (Brinkman 1947) or Ochoa-Tapia and Whitaker’s expression (Ochoa-Tapia and Whitaker 1995). When the mesh resolution is improved, the DNS results become closer to the PSPH-model results.

Fig. 14

REV-averaged streamwise velocity $\left\langle {u_{D1} } \right\rangle^{v}$ versus the normalized distance from the wall $x_{2} /s$. The porous matrix is composed of cubes, $\phi_{1} = 0.42$, $\phi_{2} = 0.49$. a${\text{Re}}_{1} = 30$, ${\text{Re}}_{2} = 60$ (laminar flow); b${\text{Re}}_{1} = 454$, ${\text{Re}}_{2} = 860$ (turbulent flow). Mesh 1: $151^{3}$ grid points for each REV; mesh 2: $91^{3}$ grid points for each REV

The results for more values of $g_{1}$ and $\phi$ are shown in Fig. 15. This figure depicts the values of $u_{D1}^{\text{v}}$ in two REVs adjacent to the interface. It can be seen that the PSPH model can be used in a wide range of the flow conditions, including both laminar and turbulent flows. In general, the errors in velocity distributions predicted by the model for all conditions simulated here are small. The deviation of model predictions from DNS results may increase when the difference between the two porosities increases. The deviation may be related to the errors of both the momentum-dispersion model and Darcy–Forchheimer model.

Fig. 15

$\left\langle {u_{D1} } \right\rangle^{v}$ in the first REV next to the wall versus applied pressure gradient $g_{1}$. a Cubes, $\phi_{1} = 0.42$ and $\phi_{2} = 0.49$; b cubes, $\phi_{1} = 0.42$ and $\phi_{2} = 0.54$

5 Conclusions

A momentum-dispersion model for flows in porous media is proposed based on the PSPH, which states that the characteristic length scale for flows in porous media is the pore size. The effects of macroscopic velocity gradient are modeled by using a Laplacian term in the macroscopic momentum equation. The local Reynolds number ${\text{Re}}_{d} = \frac{{K\left| {s_{Dij} } \right|}}{\nu }$, which describes the strength of the local momentum dispersion, is introduced using the pore size (identified by $\sqrt K$) as the characteristic length and the mixing velocity, $\sqrt K \left| {s_{Dij} } \right|$, as the characteristic velocity. The effective viscosity is expanded as a Taylor series with respect to ${\text{Re}}_{d}$. The model coefficients are expected to be only related to the geometry of the REV. They can be determined from the DNS results for flows in a wall-bounded porous medium made of the REVs under consideration.

The proposed macroscopic equations are used to simulate the flows in two types of porous media: a porous medium bounded by two walls and a porous medium with two porosities. The model results are in good agreement with the DNS results in wide ranges of the Reynolds number, Darcy number, and porosity. The study shows that the effects of macroscopic velocity gradient on momentum transport in porous media can be reasonably well approximated using a Laplacian term.