1 Introduction

A hydrodynamic dispersion coefficient is the sum of a diffusion coefficient and a mechanical mixing coefficient. Slichter (1905) was the first to show interest in dispersion investigations and concluded that velocity variation is the principle cause of dispersion. The dispersion process shows a complex behaviour in porous media with uncertain flow field as it depends on the microscopic pattern of flow through porous media, and a correlation between Reynolds number and the dispersion is expected to exist.

In primary studies on dispersion (e.g. Day 1956; Scheidegger 1954), it was assumed that a perfect mixing in fluid flow through a system occurs with a constant rate, which is not always true in real natural or engineering porous media with heterogeneous microstructure. Velocity variations and pressure excitations caused by heterogeneity of porous media make the transport process within this kind of non-uniform structure anomalous and more complicated. Scheidegger (1961) proposed a general theory, which mathematically describes the dispersion mechanism of a viscous fluid moving through a porous media with random geometrical properties. Brenner (1980) used the approaches introduced by Aris (1956) to model the kinematics of flow in spatially periodic porous media based on Taylor (1953) on dispersion in cylindrical capillaries. Brenner (1990) also reviewed some subsequent developments on this Taylor–Aris model for macroscale transport processes, which is called the Taylor dispersion phenomena. This study illuminated elementary examples in macroscale modelling and physical interpretation of microscale convective–diffusive–reactive transport processes. Effects of some factors such as fluid viscosity, density, particle size distribution, shape of particles have also been investigated using packed column tests and experimental techniques of dispersion coefficients measurement (De Josselin de Jong 1958; Han et al. 1985; Delgado 2006; Çarpinlioğlu et al. 2009; Cheng 2011; Erdim et al. 2015; Allen et al. 2013; Majdalani et al. 2015; Vollmari et al. 2015; Hofmann et al. 2016; Norouzi et al. 2018).

Several theoretical and numerical techniques have been considered in order to incorporate the effects of these flow variations in the transport process modelling. For example: continuous time random walks (Montroll and Weiss 1965), integral transform methods (Cotta 1993), Taylor–Aris–Brenner moment methods (Shapiro and Brenner 1986, 1988), stochastic convective (Simmons 1982; Nezhad et al. 2011), central limit theorems (Evans and Kenney 1966) and homogenization methods (Sanchez-Palencia 1980). Most of these researches focus on understanding the dispersion process in heterogeneous porous media when the flow is within the Darcy regime (Nezhad and Javadi 2011; Nezhad et al. 2013; Dentz et al. 2004).

Fluid flow through porous media is governed by various forces that act on the fluid, including viscous forces, gravitational force, electromagnetic forces and forces due to pressure from surrounding fluid. Sum total of these forces is referred to as inertia force and according to the results of early researches on this field (i.e. Fand et al. 1987; Kececioglu and Jiang 1994; Bagcı et al. 2014), depending on the amount of contribution of inertial and viscous forces in deriving flow, four different flow regimes are generated which are distinguished by the type of relationship between fluid velocity and pressure drop though porous media. These three regimes which are defined are namely pre-Darcy, linear Darcy, nonlinear Forchheimer and turbulent flow regimes.

Inertial forces can influence the hydraulic conductivity and dispersion (Van der Merwe and Gauvin 1971). LeClair and Hamielec (1968) investigated the viscous flow at intermediate Reynolds numbers. This work employed the finite difference methods from Hamielec et al. (1967a, b) and used the results to develop the theoretical information of local velocity distributions about particles for the intermediate flow regime and discussed its application to the packed beds. Forchheimer (Forchheimer 1901 cited in Whitaker 1996) was the first to consider the nonlinear relationship between hydraulic gradient and flux at larger velocities, and Prausnitz and Wilhelm (1957) and Mickley et al. (1965) presented theoretical and experimental relationship between turbulence parameters and concentration fluctuations in packed beds. However, there are only few research investigating this correlation. Bijeljic and Blunt (2006) and Haserta et al. (2011) have investigated the contribution of inertial flow on longitudinal dispersion. It was indicated that in realistic heterogeneous porous media, the dispersion coefficient is unlikely to reach an asymptotic value and traditional advection–dispersion equation cannot model solute transport (Nezhad 2010).

Despite numerous experimental and theoretical studies on dispersion there is a lack of fundamental understanding of how complexity in flow field in high Reynolds number can influence on the dispersion and how these processes are influenced by heterogeneity of the porous media. Boundary of flow regimes would be varied among different experimental systems, because of the geometry-dependent manifestation of inertial effects, particularly from the transition to turbulence (Reddy et al. 1998). Importance of specifying a transition boundary between these regimes where fluid field gradually evolves from linear to nonlinear, and from laminar to turbulent flow are recognized when appropriate method should be used for transport modelling and calculation of dispersion coefficient.

In this paper, the effects of nonlinearity of fluid flow on dispersion are investigated using a set of tracer tests conducted on packed beds of spherical glass beads of different diameter size. The effects of fluid characteristics on the flow behaviour and transition boundary between flow regimes have not been investigated in this work and will be done in future work.

2 Experimental Setup

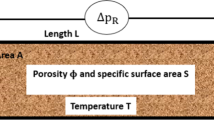
The experimental system used in this project was originally designed at the Aachen University of Technology in Germany, and Chandler (2012) developed it to analyse the vertical variation in diffusion coefficient within sediments. This system has been modified for use in this research. It consisted of an upstream and a downstream circular column, with a sample column in between having a diameter of 96 mm and a length of 200 mm. Figure 1 shows a schematic view of the modified system.

Fig. 1
figure 1

Schematic of experimental system setup

Full size image

Soda lime glass spheres with diameter of 1.85 mm and 3 mm were used to make the sample columns. Both samples were compacted to have the same porosity of 0.39. The spheres are non-reactive with Rhodamine WT which was used as dye for tracer experiments. The sample columns were placed on a stainless steel mesh with a pore size smaller than the particle diameters, in order to prevent spheres from clogging the outlets, avoiding any additional delay or fiction of the fluid flow. All the tests were done under the same temperature conditions and a temperature sensor and a Rapid 318 digital multimeter were attached to the downstream column wall to monitor the temperature in the system throughout experiments. The head difference was measured at two manometer tubes which were connected to upper and lower positions of the sample column. A WATSON MARLOW 505Di peristaltic pump was used to apply a steady flow to the system with constant operation temperature. The pump has the capacity to produce discharge rates of up to 18.95 m3/s, producing water flow from Darcy to non-Darcy regimes. Air bubbles were removed before doing any tests, to guarantee vacuum conditions. Only water was used as fluid in this study and effect of fluid characteristics on the flow behaviour are left to be investigated in future work.

A joint was inserted between the inflow pipes and was used to inject Rhodamine water tracing dye (Rhodamine WT) into the system with a syringe. Two Cyclops 7 Submersible Fluorometers were attached to both upstream (inlet) and downstream (outlet) columns to continuously record the cross-sectional temporal dye concentration distribution during the tests. The data measured by the fluorometers were recorded automatically and stored electronically in a Novus LogBox-AA. All sensors were calibrated prior to use and details of the calibration procedure are found in Liang (2017).

3 Results and Discussion

3.1 Flow Regime

In order to investigate the effects of nonlinearity of fluid flow on the transport behaviour in porous media, the experiments were conducted under both linear and nonlinear flow regimes. Nonlinear plots of the experimental data describing pressure drop versus Reynolds number which are presented in Fig. 2 prove the existence of nonlinear flow. Reynolds number as a factor to define the flow boundaries, it represents a ratio of inertial forces to viscous forces, indicates the change of flow regime when the inertial effect becomes important. Approaches for calculating the Reynolds number or for defining a criterion for specifying flow regimes in porous media are divergent and inconsistent, different authors had their own statements on distinguishing the critical zone of Darcy and non-Darcy flow, based on the comparison of experimental results and other literature (Zeng and Grigg 2006). In this work, Reynolds number were calculated as

$$ R_{\text{eL}} = \frac{\rho vL}{\mu } $$
(1)

where ρ is water density (kg/m3), v is Darcy velocity (m/s), μ is dynamic viscosity [kg/(m s)] and L is characteristic length (m). The L is defined as the inverse of specific interfacial area, the contact area of water and solid phase in unit volume (Petrasch et al. 2008).

Fig. 2
figure 2

Experimental pressure gradient versus Reynolds number for both \( 1.85 \times 10^{ - 3} \) m and \( 3 \times 10^{ - 3} \) m samples

Full size image

It is seen that under the same flow conditions a higher-pressure drop is observed for the sample with smaller particles. Although these two samples have the same porosity, the passages of flow in the \( 1.85 \times 10^{ - 3} \) m sample are narrower and much more circuitous. Therefore, the pressure gradient across the sample with the smaller particles is more sensitive to the change of the flow condition.

Identification of the boundaries between different flow regimes is a challenge. Some criteria have been proposed in the literature to specify such boundaries. Following the methodology proposed by Kececioglu and Jiang (1994), plotting the dimensionless pressure gradient versus Darcian Reynolds number and identifying the tracts where the slope of lines changes, it is possible to identify different flow regimes as it is shown in Fig. 3. A linear regression was used to find the trend lines for the dimensionless plots. The points are selected in order to have a high value of R2 (coefficient of determination) so that the regression line gives a good representation of the distribution of the points on the plot. It is shown that the Reynolds number (ReL) corresponding to the transition from linear to nonlinear flow is 2.48 for \( 1.85 \times 10^{ - 3} \) m sample and 3.24 for \( 3 \times 10^{ - 3} \) m sample.

Fig. 3
figure 3

Dimensionless pressure gradient and actual flow Reynolds number for \( 1.85 \times 10^{ - 3} \) m and \( 3 \times 10^{ - 3} \) m samples, distinction of different flow regime

Full size image

3.2 Determination of Intrinsic Permeability and Forchheimer Coefficient

Forchheimer equation with Ergun expression for Forchheimer coefficient is presented as

$$ - \frac{\Delta p}{L} = \frac{\mu }{k}v + \frac{{\rho C_{\text{E}} }}{\sqrt k }v^{2} $$
(2)

where CE is Ergun coefficient, which depends on the geometry of pore space distribution. Forchheimer coefficient β is defined as a function of the Ergun coefficient, where \( \beta = \frac{{C_{\text{E}} }}{\sqrt k } \).

Forchheimer and Ergun coefficients in the Forchheimer equation were calculated initially by implementing a nonlinear regression of the experimental data. The calculation was performed in two ways: (a) using whole sets of experimental data (labelled as B1, B2, B3 in Fig. 4); and (b) using only those within Reynolds number smaller than the value of the transaction from linear to nonlinear flow (labelled as B4, B5, B6, B7 in Fig. 4). The calculated coefficients were used to predict the pressure gradients. The experimental and predicted pressure gradient versus Reynolds number is presented in Fig. 4, which shows that the predictions reproduce the experimental data.

Fig. 4
figure 4

Pressure gradient versus Reynolds number for different Forchheimer coefficients for \( 1.85 \times 10^{ - 3} \) m sample

Full size image

In fact, both Ergun and Forchheimer coefficients are related to Darcy and non-Darcy terms in Forchheimer equation; they depend not only on the porous media properties but also on the fluid properties. This makes the accurate determination of the exact value, a complex and challenging process. For more reliable predictions, nonlinear regression was used only on experimental data within Reynolds number (using first 9 subsets of the experiments) to calculate intrinsic permeability. We used the concept of apparent permeability. Apparent permeability is the permeability calculated for porous media in high velocities, with nonlinear flow. It can be calculated using (Barree and Conway 2004)

$$ \frac{ - \Delta p}{L} = - \frac{\mu v}{{k_{\text{app}} }} $$
(3)

where kapp is apparent permeability. It is defined as

$$ \frac{1}{{k_{\text{app}} }} = \frac{1}{k} + \beta \frac{\rho v}{\mu } $$
(4)

Apparent permeability is equivalent to permeability in Darcy’s Law when the flow is within Darcy flow regime. It decreases with increasing discharge, as a result of apparent inertial effects. The intrinsic and apparent permeability values have been substituted in Eq. 4 to calculate Forchheimer coefficient for different of experiments, and it was concluded that the value of the Forchheimer coefficient varies if the nonlinearity effect is taken into account. As shown in Fig. 5, when the flow is at high velocity, Forchheimer coefficient tends to increase with Reynolds number linearly. If Forchheimer coefficient is proportional to Reynolds number, then this relation can be determined from the plots in Fig. 5, as stated in Eq. 5.

Fig. 5
figure 5

Linear relationship between Forchheimer coefficient and Reynolds number for \( 1.85 \times 10^{ - 3} \) m sample

Full size image
$$ \beta_{Re} = 575.52Re + 159.14 $$
(5)

Forchheimer equation (i.e. Eq. 2) can be written as

$$ - \frac{\Delta p}{L} = \frac{\mu v}{k}\left( {1 + \beta_{Re} \frac{k\rho v}{\mu }} \right) $$
(6)

where \( \beta_{Re} \) is the Forchheimer coefficient defined from Reynolds number.

The experimental data and \( \beta_{Re} \) were substituted back into Eq. 6 to calculate the predicted pressure gradient; results are plotted in Fig. 6 which shows a good fit. Then, the Ergun coefficient \( C_{\text{E}} \) from \( \beta_{Re} \) is calculated as

Fig. 6
figure 6

Pressure gradient versus Reynolds number for \( 1.85 \times 10^{ - 3} \) m sample

Full size image
$$ C_{{{\text{E}}12}} = \beta_{Re} \sqrt k = \sqrt k \left( {575.52Re + 159.14} \right) $$
(7)

3.3 Dispersion

Diffusion coefficients are calculated using a methodology presented in Chandler (2012). So we used

$$ D = \left( {\frac{\sqrt \pi }{{2C_{{{\text{o}} . {\text{s}}}} }} \frac{{{\text{d}}M_{w} }}{{{\text{d}}t^{1/2} }}} \right)^{2} $$
(8)

where \( C_{{{\text{o}} . {\text{s}}}} \) is the initial solute concentration within the porous medium, \( \frac{{{\text{d}}M_{w} }}{{{\text{d}}t^{1/2} }} \) is the initial slope taken from the temporal concentration profile, where Mw is the accumulated mass of the tracer, and t is the time.

In order to check the repeatability of the tracer tests, three tests for each Reynolds number were repeated. Figure 7 shows the downstream profiles for tracer tests under different Reynolds numbers. It is noticeable that, for slow flow the tests are non-repeatable and different concentration profiles are achieved. This is because of the unique path for dye movement in the porous media due to unique arrangement of the spheres in each sample. As it is complicated to determine the exact pore scale structure of the porous samples, tests associated to each flow rate were repeated for three times to obtain a reliable trend representing the dispersion profile.

Fig. 7
figure 7

Downstream profiles of the tracer tests with various Reynolds number in \( 1.85 \times 10^{ - 3} \) m sample

Full size image

Figures 8 and 9 show that the spreading of the dye increases with decreasing Reynolds number. The long tailing of curves in both figures are related to the time that particles spent for macroscopic spread in low-velocity regions, which is in agreement with findings of Bijeljic and Blunt (2006). For flow within the slow flow regime, the injected dye could not be well mixed before entering the sample. Some dye stuck to the surface of the particles in porous media and could not be easily removed with the very slow flow. It needed to be continually washed off with a long duration. Therefore, tests with slower flow show longer tails.

Fig. 8
figure 8

Downstream (B072 Cyclops at downstream) profiles for the tracer tests under various Reynolds number in the \( 1.85 \times 10^{ - 3} \) m sample

Full size image
Fig. 9
figure 9

Downstream (B072 Cyclops at downstream) profiles for tracer tests under various Reynolds number in the \( 3 \times 10^{ - 3} \) m sample

Full size image

3.4 Effect of Flow Regime and Particle Size on Dispersion Coefficient

As demonstrated by numerous studies, the dispersive regimes and the flow regimes in porous media can be identify, respectively, by Peclét number (\( Pe_{\text{p}} \)) and Particle Reynolds number (\( Re_{\text{p}} \)). As indicated in Wood (2007), the two numbers are related through the following expressions.

$$ Re_{\text{p}} = \frac{2}{3}\frac{{\rho_{\beta } \left\langle {v_{\beta } } \right\rangle^{\beta } d_{\text{p}} }}{{\mu_{\beta } }}\left( {\frac{{\varepsilon_{\beta } }}{{1 - \varepsilon_{\beta } }}} \right) $$
(9)
$$ Pe_{\text{p}} = \frac{2}{3}\frac{{\left\langle {v_{\beta } } \right\rangle^{\beta } d_{\text{p}} }}{{D_{A\beta } }}\left( {\frac{{\varepsilon_{\beta } }}{{1 - \varepsilon_{\beta } }}} \right) $$
(10)
$$ Pe_{\text{p}} = Re_{\text{p}} Sc $$
(11)

where, ρβ represents the fluid density (kg/m3), 〈vβ〉β represents the intrinsic averaged pore water velocity (m/s), dp represents the particle diameter (m), μβ represents the dynamic fluid viscosity (kg m−1 s−1), ɛβ represents the porosity, DAβ represents the molecular diffusion coefficient for the solute (3 m2/s), and Sc represents the Schmidt number.

The conventional dispersion regimes and the Peclét range value for water were defined as (Wood 2007):

  1. (1)

    Molecular diffusion regime (\( Pe_{\text{p}} < 0.2 \)): the molecular diffusion predominates over mechanical dispersion;

  2. (2)

    Transition regime (\( 0.2 < Pe_{\text{p}} < 5 \)): the molecular diffusion and mechanical dispersion have approximately the same order of magnitude;

  3. (3)

    Major mechanical dispersion regime (\( 5 < Pe_{\text{p}} < 4 \times 10^{3} \)): the interaction between mechanical dispersion and transverse molecular diffusion causes the spreading. The relationship between the effective dispersion coefficient (D) and Peclét number is expressed by the following power low equation

    $$ \frac{D}{{D_{AB} }} = \frac{{D_{{m,{\text{eff}}}} }}{{D_{AB} }} + \alpha_{1} Pe_{\text{p}}^{\delta } \quad 1.1 < \delta < 1.2 $$
    (12)
  4. (4)

    Pure mechanical dispersion regime (\( 4 \times 10^{3} < Pe_{\text{p}} < 200 \times 10^{3} \)): it is characterized by power low relation of this type:

    $$ \frac{D}{{D_{AB} }} = \alpha_{2} Pe_{\text{p}}^{\delta } \quad \delta = 1 $$
    (13)

Figure 10 shows the relation between the dispersion coefficient/molecular diffusion coefficient and Peclét number for experimental data related to the particle size of \( 1.85 \times 10^{ - 3} \) m and \( 3 \times 10^{ - 3} \) m. It is observed that the dispersion coefficient initially increases linearly with the increases of the Reynolds number up to the condition that the value of the Reynolds number reaches to one. Considering the range Peclét number mentioned in by Wood (2007), in both cases the experimental data fall under the major mechanical dispersion regime and the pure mechanical dispersion regime. Consequently, it is not possible to use the experimental data to identify Peclét number related to the molecular diffusion regime and transition regime. For these regimes we consider the literature values. As shown in Figs. 11 and 12 the increasing trends are similar for both particle sizes. Moreover, the smaller particles have a higher velocity that increases the fluctuation in flow field and consequently the dispersion.

Fig. 10
figure 10

Comparison of dispersion regime between particle \( 1.85 \times 10^{ - 3} \) and \( 3 \times 10^{ - 3} \) m

Full size image
Fig. 11
figure 11

Linear regression for the major mechanical dispersion regime (a) and the pure mechanical dispersion regime (b) for particle size of \( 1.85 \times 10^{ - 3} \) m

Full size image
Fig. 12
figure 12

Linear regression for the major mechanical dispersion regime (a) and the pure mechanical dispersion regime (b) for particle size of \( 3 \times 10^{ - 3} \) m

Full size image

For the major mechanical dispersion and pure mechanical dispersion regime Eqs. (12 and 13) are determined by a linear regression between \( \text{Log}\left( {\frac{D}{{D_{AB} }} - \frac{{D_{{m,{\text{eff}}}} }}{{D_{AB} }}} \right) \) and Log(Pep) in the first case and between \( \text{Log}\left( {\frac{D}{{D_{AB} }}} \right) \) and Log(Pep) in the second one. The results are shown in Fig. 12. For the major mechanical dispersion regime, the equation in logarithmic and non-logarithmic form results:

$$ \text{Log}\left( {\frac{D}{{D_{AB} }} - \frac{{D_{\text{eff}} }}{{D_{AB} }}} \right) = 1.2374\text{Log}\left( {Pe_{\text{p}} } \right) + 1.4805 $$
(14)
$$ \frac{D}{{D_{AB} }} = \frac{{D_{\text{eff}} }}{{D_{AB} }} + 30.2343Pe_{\text{p}}^{1.237} $$
(15)

The δ value is 1.237 and it is slightly higher than indicated in the literature studies, where which δ is between 1.1 and 1.2.

Peclèt number corresponding to the transition from major mechanical dispersion regime to pure mechanical dispersion regime is equal to 4.78 × 103. It is determined considering a range of data so that the regression model provides a good estimate of the experimental data. The value matches with the one indicated by Wood (2007) under which the major mechanical dispersion regime takes place for a Peclét number between 0.2 and 5 × 103.

Regarding the pure mechanical dispersion regime, as shown in Fig. 12b the R2 is very low. It means that the relation (12) does not estimate correctly the experimental data in the pure mechanical regime.

For the particle size of 0.003 m the equation of the major mechanical dispersion regime results:

$$ \text{Log}\left( {\frac{D}{{D_{AB} }} - \frac{{D_{\text{eff}} }}{{D_{AB} }}} \right) = 1.0281\,\text{Log}\left( {Pe_{\text{p}} } \right) + 1.753 $$
(16)
$$ \frac{D}{{D_{AB} }} = \frac{{D_{\text{eff}} }}{{D_{AB} }} + 56.6239Pe_{\text{p}}^{1.0281} $$
(17)

In this case the estimated value of δ is slightly lower than the one in the literature. The transition from the major mechanical dispersion regime and the pure mechanical dispersion regime occurs for a Peclét number of 5.28 × 103, a value slightly higher than the one found for the particle of \( 1.85 \times 10^{ - 3} \) m. Instead, for the pure mechanical dispersion regime the relation found in the form of Eq. 13 is:

$$ \text{Log}\left( {\frac{D}{{D_{AB} }}} \right) = 1.4119 \times \text{Log}\left( {Pe_{\text{p}} } \right) + 0.4235 $$
(18)
$$ \frac{D}{{D_{AB} }} = 2.6515Pe_{\text{p}}^{1.4119} $$
(19)

For this regime literature studies indicate a value of δ around 1. As shown before, the value found using experimental data is a little higher than 1 (Fig. 13).

Fig. 13
figure 13

Dispersion coefficient/diffusion coefficient versus Péclet number for all results

Full size image

As shown in Figs. 14 and 15, the increasing trends for different samples are similar. However, the sample with smaller diameter has larger dispersion/diffusion ratio and less travel time, which shows smaller particle size has more effects on shear dispersion. Longitudinal spreading is caused by the combined action of differential advection and transverse diffusion. When these two mechanisms act simultaneously, a shear-induced longitudinal dispersion process is generated. In shear flow, velocity varies in transverse direction. As the flow rate became larger and nonlinear, the difference of travel time between fine and coarse sample became smaller. The results show an agreement with Bedmar et al. (2008), which stated that due to the increase in pore-sized distribution and surface smoothness of particles the finer textured soils have higher dispersion coefficient value.

Fig. 14
figure 14

Travel time versus Reynolds number for all results

Full size image
Fig. 15
figure 15

Dispersion and flow regime for particle size of \( 1.85 \times 10^{ - 3} \) m and \( 3 \times 10^{ - 3} \) m

Full size image

To analyse the relation between the flow and dispersion regimes, the previous results on the flow regimes obtained by Darcian Reynolds number are combined with the ones related to the dispersion regimes calculated by Peclét number. It is done for the particles of \( 1.85 \times 10^{ - 3} \) m and \( 3 \times 10^{ - 3} \) m.

The comparison between the dispersion and flow regimes is made by referring to the Darcy velocity because it is common element between the different data set used for the analysis of the two regimes. The variables involved are related by Eqs. 9–11 and the following expression that binds Darcy velocity (v) and intrinsic velocity (〈vβ〉β):

$$ \left\langle {v_{\beta } } \right\rangle^{\beta } = \frac{v}{{\varepsilon_{\beta } }} $$
(20)

The results obtained are shown in Fig. 16 and in Tables 1 and 2.

Fig. 16
figure 16

Experimental results compared with dispersion regimes as a function of Péclet number

Full size image
Table 1 Dispersion and flow regime for particle size \( 1.85 \times 10^{ - 3} \) m
Full size table
Table 2 Dispersion and flow regime for particle size \( 3 \times 10^{ - 3} \) m
Full size table

As shown in Tables 1 and 2, in both cases the transition from linear to nonlinear flow occurs in the pure mechanical dispersion regime and the specific values of Darcian Reynolds number (Red), Peclèt number (Pep) and Particle Reynolds number (Rep) for the both particles size are shown below (Table 3).

Table 3 Values of Darcian Reynolds number (\( Re_{\text{d}} \)), Peclèt number (\( Pe_{\text{p}} \)) and particle Reynolds number (\( Re_{\text{p}} \)), corresponding to the transition from linear to nonlinear flow
Full size table

Ratio of dispersion to diffusion coefficient with respect to Péclet number is presented in Fig. 16 and are compared with some results from literature. It is proved that the tracer-determined hydrodynamic dispersion coefficient is a function of mechanical dispersion. The data show an increasing trend similar to other results from literature, but do not overlap with any other data. This is because of the dependency of dispersion coefficient to several physical properties of fluid and porous media including viscosity, density of fluid, particle size distribution and shape, fluid velocity, length of packed sample column, ratio of column diameter to particle diameter and ratio of column length to particle diameter (Delgado 2006). Any change in one of the variables would result in a different dispersion profile. For the profiles presented from literature, water was considered as the fluid of interest. The diffusion coefficient of the tracer used in this research (Rhodamine WT) is 2.9E−10 m2/s as determined by Gell et al. (2001) which is different form the tracers used in the tests from the literature. Since the diffusion coefficient of Rhodamine WT is slightly larger than the other tracers, different dispersion profiles and consequently different profiles for dispersion/diffusion ratio are achieved.

4 Conclusion

This study focused on the impact of porous media particle size on the flow regimes and dispersion process. Water flow and dye tests through man-made cylindrical samples containing spherical glass beads were conducted to study the contribution of the flow regimes on the dispersion. Different porous media and different flow conditions were examined in this paper in order to provide a knowledge base for understanding the relationship between flow behaviour and diffusion. This understanding is essential for studying the mixing processes in porous media with particle applications in hyporheic zone modelling. Results show that by reducing particle size the magnitude of the flow velocity in that nonlinear flow occurs is reduced up to 20%.

Observation within Darcian and non-Darcian regimes showed that, as the particle size increases, the diffusion effect reduces and dispersion coefficient decreases. The travel time required for dye to move through the smaller sized particles is also less than that of the larger one. This is because the finer textured sample has a more complex pore size distribution which causes a higher dispersion coefficient value. For the same Reynolds number, the dispersion coefficient of the fine particle is larger than the coarse particle. A small change in Reynolds number for smaller size particles results in a larger change of dispersion coefficient. This indicates that fine particles are more sensitive to flow regimes.