Fractional-Flow Theory for Non-Newtonian Surfactant-Alternating-Gas Foam Processes

Abstract

Foam can improve sweep efficiency in gas-injection-enhanced oil recovery. Surfactant-alternating-gas (SAG) is a favored method of foam injection. Laboratory data indicate that foam can be non-Newtonian at low water fractional flow f_w, and therefore during gas injection in a SAG process. We investigate the implications of this finding for mobility control and injectivity, by extending fractional-flow theory to gas injection in a non-Newtonian SAG process in radial flow. We make most of the standard assumptions of fractional-flow theory (incompressible phases, one-dimensional displacement through a homogeneous reservoir, instantaneous attainment of local equilibrium), excluding Newtonian mobilities. For this initial study, we ignore the effect of changing or non-uniform oil saturation on foam. Non-Newtonian behavior at low f_w implies that the limiting water saturation for foam stability varies as superficial velocity decreases with radial distance from the well. We discretize the domain radially and perform Buckley–Leverett analysis on each narrow increment in radius. Solution characteristics move outward with fixed f_w. We base the foam model parameters and non-Newtonian behavior on laboratory data in the absence of oil. We compare results to mobility and injectivity determined by conventional simulation, where grid resolution is usually limited. For shear-thinning foam, mobility control improves as the foam front propagates from the well, but injectivity declines somewhat with time. This change in mobility ratio is not that at steady state at fixed water fractional flow in the laboratory, however, because the shock front in a non-Newtonian SAG process does not propagate at fixed fractional flow (though individual characteristics do). Moreover, the shock front is not governed by the conventional condition of tangency to the fractional-flow curve, though it continually approaches this condition. Injectivity benefits from the increased mobility of shear-thinning foam near the well. The foam front, which maintains a constant dimensionless velocity for Newtonian foam, decelerates somewhat with time for shear-thinning foam. For shear-thickening foam, mobility control deteriorates as the foam front advances, though injectivity improves somewhat with time. Overall, however, injectivity suffers from reduced foam mobility at high superficial velocity near the well. The foam front accelerates somewhat with time. Conventional simulators cannot adequately represent these effects, or estimate injectivity accurately, in the absence of extraordinarily fine grid resolution near the injection well.

1 Introduction

1.1 Fractional-Flow Theory

Fractional-flow theory, or the method of characteristics, has proved useful for understanding a variety of processes for enhanced oil recovery (EOR) (de Nevers 1964; Claridge and Bondor 1974; Pope 1980; Lake 1989; Noh et al. 2004; Lake et al. 2014; Borazjani et al. 2016; Farajzadeh et al. 2019). Fractional-flow theory has been applied to foam EOR by Zhou and Rossen (1995), Rossen et al. (1999, 2011, 2017), Namdar Zanganeh et al. (2011), Boeije and Rossen (2018), Al Ayesh et al. (2017), and Salazar Castillo (2019a). Its predictions are not rigorous because of the number of simplifying assumptions made, but they provide valuable insights, even if the assumptions are not strictly satisfied. This theory applies to Newtonian displacements directly, and it has been extended to model a collection of non-Newtonian foam cases (Rossen et al. 2011). In this paper, we make the usual assumptions of fractional-flow theory (Rossen et al. 2011), namely:

• 1. One-dimensional (radial or linear) flow.

• 2. Two mobile and incompressible phases.

• 3. Instantaneous equilibrium adsorption of surfactant on the rock. In this study, for simplicity, we assume adsorption was satisfied during the injection of the preceding liquid slug.

• 4. No dispersive processes, including fingering, capillary diffusion or dispersion.

• 5. Instantaneous attainment of local steady-state mobilities, which depend on local saturations. In this study, mobilities depend on total superficial velocity as well.

• 6. No chemical or biological reactions.

In addition, in this study of non-Newtonian flow, we make an additional assumption:

• 7. Fixed total volumetric injection rate Q.

The isothermal flow of two immiscible and incompressible fluids through a permeable medium is governed by the following equation (Lake et al. 2014):

$$\frac{{\partial S_{\text{w}} }}{{\partial t_{\text{D}} }} + \frac{{\partial f_{\text{w}} }}{{\partial x_{\text{D}} }} = 0$$

(1)

where t_D and x_D denote dimensionless time and position, respectively, and S_w and f_w denote liquid saturation and liquid fractional flow, respectively. The dependence of t_D and x_D on the geometry of a cylindrical reservoir with wellbore radius r_w and open-outer-boundary radius r_e is described by the following equations:

$$x_{\text{D}} = \frac{{r^{2} - r_{\text{w}}^{2} }}{{r_{\text{e}}^{2} - r_{\text{w}}^{2} }}$$

(2)

$$t_{\text{D}} = \frac{Q t}{{\pi \left( {r_{\text{e}}^{2} - r_{\text{w}}^{2} } \right)h\varphi }} \cong \frac{Q t}{{\pi r_{\text{e}}^{2} h\varphi }}$$

(3)

where $\varphi$ and h denote porosity and the thickness of the reservoir, respectively.

The superficial velocity of an incompressible fluid injected at a fixed rate Q into a cylindrical reservoir decreases continuously from the wellbore radius to the outer radius. This implies that non-Newtonian fluids experience not only a different superficial velocity but different rheology, as a function of radial position. Mathematically, this means that f_w is a function of S_w and x_D. The fractional-flow analysis with this additional constraint results in characteristics that in general do not have a fixed dimensionless velocity (Rossen et al. 2011; Wu et al. 1993). Liquid fractional flow is fixed for each characteristic as it travels through the porous medium, although liquid saturation is not.

1.2 Foam in Porous Media

Foam increases sweep efficiency during gas injection in enhanced oil recovery applications (Holm 1968; Schramm 1994; Patzek 1996; Skauge et al. 2002; Blaker et al. 2002; Zhu et al. 2013; Lake et al. 2014). It is also used in aquifer remediation and in acid diversion in well-stimulation treatments (Thompson and Gdanski 1993; Behenna 1995; Hirasaki et al. 1997a, b; Talabani et al. 2001; Cheng et al. 2002; Maire et al. 2015; Portois et al. 2018). Foam flow in porous media exhibits two flow regimes: a low-quality (large f_w) regime and a high-quality (small f_w) regime (Osterloh and Jante 1992; Alvarez et al. 2001). The low-quality regime is characterized by a gas-mobility reduction and a pressure gradient independent of liquid superficial velocity, whereas the high-quality regime is characterized by a limiting capillary pressure P_c* and a pressure gradient independent of gas superficial velocity.

Foam can be non-Newtonian in both regimes. There are several reasons for this behavior. Foam flowing through smooth tubes shows shear-thinning behavior (Hirasaki and Lawson 1985). Flow in periodically constricted tubes is even more shear thinning (Xu and Rossen 2003). Gas trapping further reduces gas mobility (Falls et al. 1989), so if gas trapping declines as pressure gradient increases (Tang and Kovscek 2006); this provides a separate mechanism of shear-thinning behavior. Rheology in the low-quality regime is consistently found to be shear thinning with respect to total superficial velocity at fixed f_w, but foam can be either shear thickening or shear thinning in the high-quality regime. Rheology in the high-quality regime is controlled by the limiting capillary pressure P_c* (Khatib et al. 1988). Jimenez and Radke (1989) present a model that predicts that P_c* decreases with increasing gas velocity, which would imply that pressure gradient would decrease, rather than hold constant, as gas velocity increases with at liquid velocity.

Figure 1 shows two examples of the two flow regimes for two foams. On the top, the foam is shear thinning with respect to liquid superficial velocity, or with respect to total superficial velocity at fixed f_w. In the contour plot, increasing liquid superficial velocity from U_w1 = 0.1 to U_w2 = 0.5 m/s corresponds to an increase in pressure gradient from $\nabla P$₁≈ 800 psi/(2 ft) to $\nabla P$₂≈ 1200 psi/(2 ft). The power-law exponent corresponding to this behavior is n = [log$\nabla P$₂− log $\nabla P$₁]/[logU_w2− logU_w1] ≈ 0.30 (see Eq. 4, below). On the bottom of Fig. 1, foam is shear thickening with respect to liquid superficial velocity. In that case, as U_w increases from about 0.2 to 0.4 ft/d, ∇P increases from about 150 to about 450 psi/ft; n ≈ 1.7.

Fig. 1

Illustrations of the two steady-state foam regimes. On the top, pressure difference across a 2-ft sandpack as a function of superficial velocities of water (U_w) and gas (U_g). In this case, foam is shear thinning in the high-quality (upper left) regime (Osterloh and Jante 1992). On the bottom, pressure gradient as a function of superficial velocities in a coreflood study (Alvarez et al. 2001). This case is shear thickening in the high-quality regime

“Implicit Texture” models, here referred to as “IT’ models for simplicity, are regularly used in combination with fractional-flow theory to describe foam displacements (Rossen et al. 2011; Al Ayesh et al. 2017). Unlike “Population Balance” models (Patzek 1985; Falls et al. 1988; Fergui et al. 1998; Kovscek et al. 1994), they assume local equilibrium in the dynamics of bubble creation and destruction and represent the effects of foam on gas mobility through a mobility-reduction factor (Cheng et al. 2000). “Population Balance” models can also be constrained to conditions of local equilibrium between foam-generation and foam-destruction processes (Kam et al. 2007; Kovscek et al. 2010). In the present study, we use an IT model because it requires fewer parameters and avoids some of the numerical challenges that are present in “Population Balance” models (Ashoori et al. 2012).

Most IT models allow for non-Newtonian behavior in the low-quality regime (Computer Modeling Group 2015; Cheng et al. 2000) but not in the high-quality regime. The limiting capillary pressure, which controls behavior in the high-quality regime (Khatib et al. 1988), corresponds to a limiting water saturation S_w*. Since foam does not alter the liquid relative permeability function (Eftekhari and Farajzadeh 2017), a stronger foam corresponds to lower limiting liquid saturation, S_w* (Zhou and Rossen 1995). Thus, non-Newtonian behavior in the high-quality regime requires that S_w* be a function of water superficial velocity. If it depended on gas superficial velocity, the pressure-gradient contours in Fig. 1 would not be vertical. In this study, however, for simplicity, we assume that S_w* is a function of total superficial velocity.

1.3 Fractional-Flow Solution for Gas Injection in a Newtonian SAG

Surfactant-alternating-gas, or SAG, is the preferred method to inject foam into a reservoir for both operational and sweep-efficiency reasons (Blaker et al. 2002; Shan and Rossen 2004). This method of injection offers, among other advantages, better injectivity than direct foam injection and a low-mobility shock front that displaces the fluids ahead of it, while it propagates downstream. The shock is to a state at very low f_w and thus is governed by the high-quality regime (Fig. 2). Here, for simplicity, we focus on the injection of the first gas slug. The initial condition I is 100% saturation of surfactant solution, and the injection condition J is at residual water saturation, S_wr. The path connecting I and J along the fractional-flow curve f_w(S_w) does not have monotonically increasing slope df_w/dS_w; therefore, a portion of the trajectory is replaced by a discontinuity, or shock, from I to a point of tangency to the f_w(S_w) curve. Because of the abrupt foam collapse as a function of S_w near S_w* (Khatib et al. 1988), the f_w(S_w) curve is steep near S_w* (Rossen and Zhou 1995). This means the point of tangency is at low f_w, in the high-quality regime. An example is depicted in Fig. 2.

Fig. 2

On the left, a fractional-flow curve adapted from Boeije and Rossen (2017). Black diamonds are coreflood data used to construct the fractional-flow curve. Red dots denote the initial (I) and injection (J) conditions. On the right, an expanded view of the same curve near the point of tangency defining the shock

A spreading wave forms behind the shock. The spreading wave is made of characteristics that travel with fixed saturation and velocity (for a Newtonian process). Figure 3 shows the dimensionless time-distance diagram of one SAG process. The shock (solid line) mobility has a fixed value; behind it, the spreading wave contains many characteristics, with a continuous range of (fixed) mobilities. Figure 3 illustrates this for four characteristics (dotted lines).

Fig. 3

A dimensionless time-distance diagram for gas injection in a Newtonian SAG process (Boeije and Rossen 2017). The mobilities of the shock and of a few of the characteristics are included

The methodology described above has been shown to be more accurate than numerical simulation as long as the assumptions of fractional-flow theory apply (Rossen 2013). In particular, the abrupt transition imposed by the limiting capillary pressure is difficult to model correctly using finite-difference methods without using an extremely refined grid near the wellbore (Leeftink et al. 2015). Boeije and Rossen (2015) use the theory to derive an analytical formula to estimate the injectivity of the first gas slug in a SAG process. The formula predicts that, soon after injection begins, the pressure gradient across the foam bank is nearly constant as it advances.

2 Fractional-Flow Solution for Gas Injection in Non-Newtonian SAG Processes

There are a number of studies of non-Newtonian behavior in 1D linear flow, in which a single fractional-flow curve describes the process: e.g., Wu et al. (1992) and Yi (2004), and Subramanian et al. (1997, 1999) describe flow from one porous medium to another, described by a different fractional-flow function. Bedrikovetsky (1993) describes the solution for a 1D drainage of a dome-shaped reservoir with a gas cap. In this case, the fractional-flow function varies with vertical position. Jamshidnezhad et al. (2008) solve for steady-state gravity segregation in 2D radial flow for non-Newtonian fluids, where the fractional-flow function varies with radial distance from the well. Wu et al. (1991) solve for 1D linear displacement of a Newtonian fluid by a non-Newtonian fluid. El-Khatib (2006) studied numerically the immiscible displacement of non-Newtonian fluids in communicating stratified reservoirs.

A previous work on non-Newtonian foam displacements (Rossen et al., 2011) was limited to foam injection or gas injection in a SAG process behind the shock front and included only shear-thinning behavior. The SAG analysis showed the effect of changing gas saturation and non-Newtonian behavior in the near-well region after the shock passes out of this region. The results showed that shear-thinning behavior affects mobility near the well; this implies that the injectivity is better than that predicted by a Newtonian model. As in the Newtonian case, the finite-difference simulator requires an extremely refined grid (especially near the wellbore) to match the analytical solution.

In this study, we extend the previous work to include both shear-thinning and shear-thickening behavior, as observed in the laboratory (Fig. 1). Equally important, we provide a methodology to solve issues that arise, e.g., when new characteristics emerge from the shock or when a characteristic and the shock collide. Finally, we show the consequences of non-Newtonian behavior for overall injectivity and mobility control at the leading edge of the foam bank.

We consider a homogenous cylindrical reservoir that is initially fully saturated with surfactant solution. Starting at time zero, gas is injected at a fixed volumetric rate Q into the reservoir. In this situation, the gas-injection process is governed by the high-quality regime, where foam strength depends on the limiting water saturation, S_w*, named fmdry in the foam model described in “Appendix A.” Under these assumptions (including incompressible fluids), total superficial velocity u_t is a function of radial distance from the well.

In Fig. 1, total mobility of foam is a power-law function of water superficial velocity U_w, not total superficial velocity U_t. Here, for simplicity, we assume that it is a power-law function of U_t. In the high-quality regime, S_w≈ S_w*, i.e., fmdry in our model. For the purpose of deriving model parameters, consider injection of foam at fixed water fractional flow but decreasing superficial velocity as foam moves further from the well. From the power-law equation (Bird et al. 2007),

$$\nabla P = C U_{\text{t}}^{n}$$

(4)

Applying Darcy’s law to the water phase, with water saturation fixed at fmdry,

$$\nabla P = \frac{{k k_{\text{rw}} \left( {S_{w} = fmdry} \right) }}{{\mu_{\text{w}} }}f_{\text{w}} U_{\text{t}}$$

(5)

where n, C, $\nabla P$, $k$, $k_{\text{rw}} \left( {S_{\text{w}} } \right)$, and $\mu_{\text{w}}$ denote, respectively, the power-law exponent, a constant, pressure gradient, permeability, liquid relative permeability, and liquid viscosity. Combining these equations, one can show that the ratio $\left[ {k_{\text{rw}} \left( {S_{\text{w}} } \right)/U_{\text{t}}^{n - 1} } \right]$ is a constant, which considering cylindrical flow can be rewritten as $[k_{rw} \left( {S_{w} } \right)/ r^{1 - n} ]$. As next step, we apply this ratio to the outer radius r_e and at any other radius r. Finally, using a Corey model for k_rw (see “Appendix A”), we derive an expression for fmdry as a function of r:

$$fmdry\left( r \right) = S_{\text{wr}} + \left( {fmdry_{\text{e}} - S_{\text{wr}} } \right)\left( {\frac{r}{{r_{\text{e}} }}} \right)^{{\frac{n - 1}{{n_{\text{w}} }}}}$$

(6)

where fmdry(r) denotes the water saturation at which foam collapses at a given radial position, S_wr is the irreducible water saturation, r radius, and n_w the Corey–Brooke exponent for k_rw(S_w). The subscript e denotes a reference value, in our study taken at the outer radius r_e.

Equation (6) indicates that for a shear-thinning foam the fractional-flow curve shifts to the left (smaller S_w) as the radius increases, while for a shear-thickening foam it shifts to the right. Figures 4 and 5 illustrate this shifting for a shear-thinning foam with a power-law exponent of n = 0.33 and for a shear-thickening foam with an exponent n = 1.34, respectively. Figures 4 and 5 reflect non-Newtonian behavior only in the high-quality regime, not in the low-quality regime since it is the high-quality regime that dominates behavior during gas injection in a SAG process (Fig. 2).

Fig. 4

Fractional-flow curves for different radii for a shear-thinning foam with a power-law exponent of n = 0.33. The parameter fmdry varies from 0.356 at the wellbore radius (r_w = 0.1 m) (blue curve) to 0.312 at r = 1.0 m (red), 0.286 at r = 10 m (yellow), and 0.271 at the outer radius (r_e) = 100 m (purple)

Fig. 5

Fractional-flow curves for different radii for a shear-thickening foam (n = 1.34), where fmdry varies from 0.259 at r_w = 0.1 m (blue curve) to 0.262 at r = 1 m (red), 0.266 at r = 10 m (yellow), and 0.271 at the outer radius r_e = 100 m (purple)

We discretize the reservoir domain in increments along x_D. Within each increment, foam properties are assumed to be constant, i.e., Newtonian. Therefore, within each increment, the characteristics and the shock are straight lines. However, as each characteristic crosses to the next increment, its velocity changes. This continuous variation of velocity makes the characteristics curve on a large scale; Fig. 6 shows an example, using for illustration very large increments in x_D (∆x_D = 0.1); in our calculation, the increments are much smaller. The approximation to continuous variation in properties becomes exact in the limit as the increment in x_D approaches zero.

Fig. 6

On the left, an augmented view of characteristics on a diagram of dimensionless position (x_D) vs dimensionless time (t_D) for a shear-thinning foam. The characteristics are straight lines within each increment in x_D. On the right, larger scale of the same diagram showing how the characteristics curve

In a non-Newtonian scenario, a characteristic no longer carries its water-saturation value as it crosses between increments, but it does carry its water fractional-flow value instead (Wu et al. 1993; Rossen et al., 2011). The individual characteristics within the spreading wave do not collide with each other, because, at any value of x_D, velocity df_w/dS_w decreases monotonically with S_w. Thus, individual characteristics spread further apart as they move downstream. Interactions with the shock are possible, however. We use the approach of Lake et al. (2003) to resolve the complications raised by the collision between a characteristic and a shock or by an accelerating shock that sheds additional characteristics.

Figure 7 illustrates our solution approach for a shear-thinning foam. For illustration purposes, we use two very large increments in x_D. Within the first increment (Fig. 7a), starting at the wellbore, the fractional-flow curve is fixed and the Buckley–Leverett solution is the same as for a Newtonian SAG, i.e., a shock followed by a spreading wave. As the shock (point A) leaves the first increment and enters the second increment, conserving its value f_w (Fig. 7b), it slows down as it displaces initial condition I. As the characteristics behind the shock cross the boundary to the second increment, their velocities increase. An example is the characteristic B (denoted B’ in the second increment) directly behind the shock, which accelerates and intersects the shock. This collision imposes a new Buckley–Leverett problem with initial condition (f_w = 1) and injection condition B’. The solution is a new shock from f_w = 1 to B’; see Fig. 7c. This new shock does not necessarily satisfy the tangency condition, though, if it does not, other characteristics behind it approach as well; further collisions are possible. Whenever this occurs, we solve locally the arising Buckley–Leverett problem using the same methodology. Figure 8 illustrates the collision of a characteristic and the shock in a dimensionless time-distance diagram. In our discrete approximation to the continuous variation in properties, the shock velocity is recalculated as it enters each new increment. When a collision occurs within an increment, the characteristic that was the shock is eliminated, replaced by the characteristic that collides with (Ponners 2017; ter Haar 2018).

Fig. 7

Schematic of fractional-flow solution for a shear-thinning foam. The dashed lines represent the shock, and the dotted lines represent a characteristic. a Shock and a characteristic for the first increment in x_D, at the wellbore. b The shock and the characteristic in the second increment. Note that the shock velocity decreases while the velocity of the characteristic behind it increases with respect to the first increment. c The collision between the characteristic and the shock results in a new shock and the disappearance of the characteristic that had formerly been the shock

Fig. 8

Dimensionless time-distance diagram illustrating collision of characteristic and shock in a shear-thinning foam; cf. Figure 7

We construct the fractional-flow solution for a shear-thickening foam by considering, again, two large increments in x_D starting at the injection face. For a shear-thickening foam, the first increment corresponds to a weaker foam, represented by the red fractional-flow curve in Fig. 9. Within first increment, the solution is a shock from a point of tangency to point I at f_w = 1, followed by a spreading wave as in a Newtonian SAG; see Fig. 9a. As the shock enters the next increment in x_D (Fig. 9b), it imposes a new Buckley–Leverett problem with initial condition f_w = 1 and injection condition A’. The solution is a spreading wave from A’ to a new point of tangency and an accelerated shock. The state previously immediately upstream of the shock is now a characteristic within the spreading wave; see Fig. 9c. As the shock enters each new increment, additional characteristic(s) split off from it. Figure 10 summarizes the fractional-flow solution on a dimensionless time-distance diagram. Note that while collisions occur within increments for shear-thinning foam, additional characteristics are created at the boundaries between increments for shear-thickening foam (Ponners 2017; ter Haar 2018).

Fig. 9

Fractional-flow solution for a shear-thickening foam. The dashed line represents the shock, and the dotted line represents a new characteristic. a A shock forms in the first increment. b As the shock enters the next increment, it imposes a new fractional-flow problem in the second increment with initial condition, I, and with injection condition, A’. c Solution of the fractional-flow problem in the second increment including an accelerated shock and a new characteristic

Fig. 10

Dimensionless time-distance diagram corresponding to a shear-thickening foam

We carry out the calculations as follows. We discretize x_D into 1000 increments, spaced so that total superficial velocity decreases by 0.7% between consecutive increments of increasing radial position. Thus, increments are smaller near the wellbore, where total superficial velocity changes rapidly. For shear-thinning foam, we calculate velocities for 300 characteristics in the first increment. In each new increment in x_D moving outward, we calculate the intersection point between the shock and the characteristic immediately behind it. If the intersection is within the increment, we recalculate the new shock velocity and eliminate the characteristic from that point forward. We then check whether the next characteristic would then intersect the new shock trajectory within the increment; if so, we update shock velocity and eliminate the next characteristic, and so forth.

For shear-thickening foam, we calculate velocities for 300 characteristics starting in the outermost increment, corresponding to r_e. We carry out calculations moving inward; in essence working from Fig. 9a–c at each new increment moving inward. At each new increment, we calculate the shock velocity using the tangency condition. Any characteristics with larger velocities are eliminated. (Thus, in our calculations, characteristics are eliminated as we move inward, rather than created in moving outward.) In the example shown below, there are 169 characteristics left at r_w, so resolution is good throughout the domain of interest.

For both shear-thinning and shear-thickening cases, results were substantially unchanged whether we started with 200 or 300 characteristics, or whether they were initially spaced equally in S_w or in f_w. Also, for both rheologies, results were unchanged whether we started with 1000 or 1100 increments in x_D.

In the end, we have a table of dimensionless times at which each characteristic passes the outer boundary of each increment in x_D, along with the values of f_w and S_w for that characteristic. From S_w, the total mobility corresponding to that characteristic in that increment can be determined.

We compute the pressure difference between the wellbore and the outer radius by integrating ∇p(r) between r_w and r_e (Al Ayesh et al. 2017; Ponners 2017; ter Haar 2018). We define dimensionless pressure rise at the well P_D by dividing by the pressure difference needed to inject water into a fully liquid-saturated reservoir at the same volumetric injection rate Q. Assuming a water viscosity of 0.001 Pa s,

$$P_{\text{D}} = \frac{{\frac{Q}{2\pi kh}\mathop \smallint \nolimits_{{r_{\text{w}} }}^{{r_{\text{e}} }} \frac{1}{{r \lambda_{\text{rt}} \left( {s_{\text{w}} } \right)}}dr}}{{\frac{Q}{{2\pi kh\lambda_{\text{w}} }}ln\left( {\frac{{r_{\text{e}} }}{{r_{\text{w}} }}} \right)}} = \frac{{\mathop \smallint \nolimits_{{r_{\text{w}} }}^{{r_{\text{e}} }} \frac{1}{{r \lambda_{\text{rt}} \left( {s_{\text{w}} } \right)}}{\text{d}}r}}{{\frac{1}{1000} \times ln\left( {\frac{{r_{\text{e}} }}{{r_{\text{w}} }}} \right)}}$$

(7)

Computing P_D requires converting the table of dimensionless times when characteristics and shocks pass boundaries between increments into a table of positions of characteristics within the various increments at a fixed time. We use linear interpolation to calculate the dimensionless positions of the shock and characteristics within the increments. Within each increment, between each pair of characteristics, we take the average of the mobilities of the two characteristics to determine the difference in pressure between the two. Then, the total relative mobility (λ_rt) as a function of x_D at a fixed t_D can be used to numerically solve the integral in Eq. (7) by summing up the increments between characteristics. In our final results, we distinguish ∆P_f, the pressure difference across the foam bank, from ∆P_w, the pressure difference across the water-saturated region ahead of foam (region I in Figs. 8 and 10). For a Newtonian foam, the pressure difference across the foam bank ∆P_f approaches a constant value soon after injection begins (Boeije and Rossen 2018).

2.1 Application

We apply the methodology described above to a homogeneous cylindrical reservoir with wellbore and open-outer-boundary radii of 0.1 m and 100 m, respectively. The superficial velocity varies by a factor of 1000 from the outer radius to the wellbore radius. Experimental data on the non-Newtonian behavior of foam in the high-quality regime extend over ranges very much smaller than this (cf. Fig. 1); thus, our results illustrate the implications if these trends continue over a much-wider range of velocities.

The STARS foam model is able to reproduce an abrupt, though not complete, foam collapse at a water-saturation value fmdry (previously referred as S_w*) (Computer Modeling Group. 2015; Cheng et al. 2000). However, this version of the dry-out function can underestimate the injectivity observed in the field during gas injection in a SAG (Rossen et al. 2017). Therefore, in this study, we use the Namdar-Zanganeh modification of this model, which assumes complete foam collapse at residual water saturation S_wr (Namdar-Zanganeh et al. 2011; Rossen et al. 2016). See “Appendix A” for a description of the foam model used in this study.

With the exception of fmdry, all rheological and petrophysical properties are constant (Table 1). As the base case, we use the fmdry value determined by Kapetas et al. for Bentheimer sandstone (2017) and apply it to the outer radius (r_e = 100 m). At other radial positions, fmdry is given by Eq. (6). The experimental data of Kapetas reflect a very strong foam, with very low mobility.

Table 1 Summary of the input parameters used in this study (Kapetas et al. 2017)

We apply power-law exponents similar to those reported by Alvarez et al. (2001) (n = 1.34) and by Osterloh and Jante (1992) (n = 0.33) to the entire range of velocities. (Alvarez et al. present estimates for several sets of data; most are less shear thickening than that used for illustration in Fig. 1.) As noted, these trends were determined experimentally over a much-narrower range of velocities than assumed here. Our results illustrate the implications if those trends continue over the entire range of velocities around an injection well.

2.2 Results

2.2.1 Shear-thinning foam (n = 0.33)

For the shear-thinning case, we use the average power-law exponent, n = 0.33, from the data of Osterloh and Jante (1992). Figure 11 depicts the resulting dimensionless time-distance diagram using our methodology. The characteristics accelerate with increasing dimensionless distance, while the shock slows down.

Fig. 11

Dimensionless time-distance diagram for the shear-thinning foam with a power-law exponent n = 0.33. For illustration purposes, we plot only 50 characteristics

Figure 12 plots total relative mobility as a function of dimensionless position for t_D = 0.5. As expected, there is an abrupt transition in mobility at the shock. This drop in mobility offers good mobility control at the leading edge of the foam bank. Moving back toward the well, mobility increases, which helps gas injectivity. These advantages are also observed with a Newtonian foam.

Fig. 12

Total relative mobility (λ_rt) as a function of dimensionless position (x_D) at a fixed dimensionless time (t_D = 0.5) for a non-Newtonian foam with power-law exponent n equal to 0.33

Figure 13 plots water saturation behind the shock as a function of fmdry, as the shock advances from the wellbore to the outer radius. Also plotted is the water saturation satisfying the conventional tangency condition for the same values of fmdry. At the wellbore, the initial shock is determined by the tangency condition, but the two deviate as the shock advances. In addition, the mobility at the shock needs not match exactly the power-law function observed for fixed-quality (fixed f_w) injection in Fig. 1, used to construct our model parameters (Eq. 6). The mobility at fixed f_w in the high-quality regime depends primarily on fmdry, but the tangency condition in a SAG process is sensitive to other factors as well. Figure 14 shows total relative mobility at the shock as a function of dimensionless position. Also plotted is the mobility that would be computed from the tangency condition at each position. The mobility at the shock decreases as the shock advances, but not in exact agreement with the tangency condition.

Fig. 13

Water saturation behind the shock plotted as a function of fmdry, as both change with radial position, for shear-thinning foam with power-law exponent n equal to 0.33. The blue curve shows the water saturation behind the shock for the shear-thinning foam, and the green curve shows the saturation for the shock calculated with the tangency condition for a fractional-flow curve at the same dimensionless position

Fig. 14

Total relative mobility behind the shock (blue curve) as a function of dimensionless position for a shear-thinning foam with power-law exponent n equal to 0.33. The green curve shows total relative mobility for the corresponding positions calculated from the tangency condition

Figure 15 shows total dimensionless pressure rise at the well (P_D) during injection of the first pore volume of gas for this shear-thinning foam. The magnitude of pressure rise is very large, which reflects the extremely strong foam found by Kapetas et al. in their corefloods. We believe the trends here would also be reflected in weaker foams applied in the field. Total dimensionless pressure increases up to foam breakthrough, in contrast to a Newtonian SAG process. For comparison, Fig. 15 shows also P_D for two Newtonian foams, applying properties at the outer and wellbore radii, i.e., fmdry = 0.356 and 0.271, throughout the entire displacements. The injectivity of the shear-thinning foam lies between the injectivity corresponding to the two Newtonian limiting cases.

Fig. 15

Dimensionless pressure rise (P_D) as a function of dimensionless time (t_D) for a shear-thinning foam with power-law exponent n equal to 0.33

These results illustrate two general trends for gas injection in SAG with shear-thinning foam: mobility control at the foam front improves as foam advances from the well, but injectivity declines. The mobility at the shock is consistently less than that estimated from the tangency condition for the f_w(S_w) function starting at a radius, r = 0.13 m. Mobility at the shock decreases to about a factor of 0.04 of its original value, instead of (1000)^−0.67 ≈ 0.01 suggested by the power law.

2.2.2 Shear-Thickening Foam (n = 1.34)

Figure 16 presents the dimensionless time-distance diagram for a shear-thickening foam with a power-law exponent of 1.34, and this exponent is within the range of exponents reported by Alvarez et al. (2001) based on coreflood data. The characteristics slow down as they advance, and new characteristics appear at the shock, which accelerates. Figure 17 shows total relative mobility at the shock as it advances; in this case, it everywhere satisfies the tangency condition. The increase in mobility at the shock, however, is much less than suggested by the power-law exponent at fixed f_w. Mobility increases by about a factor of 3.3, instead of (1000)^0.34 ≈ 10.5 suggested by the power law. This discrepancy is explained by the fact that the shock satisfies the tangency condition at each increment and therefore no longer carries a unique f_w value.

Fig. 16

Dimensionless time-distance diagram for a shear-thickening foam with a power-law exponent (n) of 1.34. For illustration purposes, we plot only 50 characteristics

Fig. 17

Total relative mobility at shock as a function of dimensionless position for a shear-thickening foam with power-law exponent n = 1.34

Figure 18 plots dimensionless pressure rise at the well (P_D) as a function of dimensionless time. The maximum dimensionless pressure occurs near the start of gas injection, with value of P_D approximately equal to 55. As gas injection progresses, the dimensionless pressure drops to 40 before the shock breaks through. Thereafter, it decreases at an even faster rate. As the dimensionless pressure declines far from the injection well, the mobility control offered by the foam bank suffers. As in shear-thinning SAG, the shear-thickening case lies between the two limiting cases (based on mobilities at r_w and at r_e). However, in contrast with a shear-thinning foam, the strongest foam, with fmdry = 0.259, is located in the near-wellbore region.

Fig. 18

Total dimensionless pressure (P_D) as a function of dimensionless time (t_D) for the Newtonian foams that apply at the wellbore radius (on the left, fmdry = 0.259) and at the outer radius (on the right, fmdry = 0.271)

We also modeled a shear-thickening foam with n = 1.67, value reported by Alvarez et al. (2001). As seen in Fig. 5, for n = 1.34, fmdry approaches S_wr near the wellbore. For n = 1.67, and assuming a strong foam at r_e, fmdry approaches so close to S_wr near the wellbore that the adjustment of Namdar-Zanganeh, which requires foam collapse at S_wr, gives shear-thinning behavior very near the well. Therefore, we do not show that case. Details are in Ter Haar (2018).

2.2.3 Finite-Difference Simulation

In this section, we present the evolution of total dimensionless pressure for non-Newtonian SAG processes during gas injection, calculated using a finite-difference simulator. A description of the discretization scheme used in the simulator is included in Appendix B; see also Bos (2017). As in the fractional-flow calculations, the input parameters correspond to the petrophysical and foam parameters listed in Table 1.

Figure 19 shows total dimensionless pressure calculated using 100 and 500 grid blocks in radial geometry, linearly spaced in r, for shear-thickening foam with n = 1.34. With 500 grid blocks, the first block extends from the wellbore at 10 cm to 30 cm. The fluctuations in Fig. 19 reflect the movement of the shock through consecutive grid blocks (Rossen 2013). Qualitatively, the behavior resembles the fractional-flow results: injection pressure decreases from the beginning of gas injection and decreases even at a faster rate after foam breaks through. However, even with this extraordinary grid resolution, the injectivity calculated by the finite-difference simulator is in significant error.

Fig. 19

Effect of grid resolution on calculated injectivity using finite-difference simulation. In blue, the dimensionless pressure evolution calculated using 100 grid blocks, for a foam with power-law exponent n = 1.34. In green, using 500 grid blocks, for the same foam parameters; in red fractional-flow calculation

3 Conclusions

In this paper, we present a method of solution for initial gas injection in a non-Newtonian SAG process that includes the interactions between the shock and the characteristics. The methodology can be applied to both shear-thinning and shear-thickening behavior.

For a shear-thinning foam, we find that mobility control improves as the foam front propagates from the well, but injectivity declines somewhat with time. However, the injectivity is still more favorable than for a Newtonian foam with the same mobility at the outer radius. In a case of a foam with marginal mobility control, there could be problems with viscous fingering as foam initially advances from the near-well region. For a shear-thinning foam, the shock does not necessarily satisfy the conventional tangency condition that applies to Newtonian foam, though it does continually approach it. In addition, the mobility at the front needs not fit the power-law behavior seen at fixed gas fraction in the laboratory.

For a shear-thickening foam, mobility control deteriorates as the foam front advances, though injectivity improves somewhat with dimensionless time. However, injectivity is less favorable than for a Newtonian foam with the same mobility far from the well. In case of marginal mobility control, the foam could have problems with viscous fingering far from the injection well.

Overall, injectivity is a complex result of changing saturations and varying superficial velocities very near the well. Conventional simulators cannot adequately represent these effects, or estimate injectivity accurately, in the absence of exceptional grid resolution near the injection well.

Appendices

Appendix A: Corey–Brooks Relative Permeability Model and Foam Model

According to the Corey–Brooks relative permeability model, the water and gas relative permeabilities are defined as

$$k_{\text{rw}} = k_{\text{rw}}^{0} S^{{n_{\text{w}} }}$$

(A1)

$$k_{\text{rg}} = k_{\text{rg}}^{0} \left( {1 - S} \right)^{{n_{\text{g}} }}$$

(A2)

$${\text{S}} \equiv \frac{{S_{\text{w}} - S_{\text{wr}} }}{{1 - S_{\text{wr}} - S_{\text{gr}} }}$$

(A3)

where k_rw, k_rg, $k_{\text{rw}}^{0}$,$k_{\text{rg}}^{0}$, n_w, n_g, S, S_w, S_wr, and S_gr denote, respectively, liquid and gas relative permeabilities, the end-point water and gas relative permeabilities, the water and gas Corey–Brooks exponents, normalized water saturation, water saturation, and residual water and gas saturations.

In the presence of foam, the STARS model (Computer Modeling Group 2015; Cheng et al. 2000) incorporates a mobility-reduction factor, FM, in the gas phase as follows,

$$u_{\text{t}} f_{\text{g}} = - \frac{{k k_{\text{rg}}^{f} }}{{\mu_{\text{g}} }}\nabla p = - \frac{{k k_{\text{rg}} FM}}{{\mu_{\text{g}} }}\nabla P$$

(A4)

where u_t, f_g, k, k_rg, $k_{\text{rg}}^{f}$, μ_g, and $\nabla P$ denote, respectively, total superficial velocity, quality (gas fractional flow), permeability, gas relative permeability in the absence and the presence of foam, respectively, gas viscosity, and pressure gradient.

The mobility-reduction factor, FM, models the effects of surfactant concentration, water saturation, oil saturation, gas velocity, capillary number, and the critical capillary number on gas mobility. Here, we focus on the dependence on water saturation (and, by implication, on capillary pressure), which controls behavior in the high-quality regime and, for simplicity, exclude the effect of changing or non-uniform oil saturation. In that case

$$FM = \frac{1}{{1 + fmmob F_{2} }}$$

(A5)

where the parameter fmmob is the reference gas-mobility-reduction factor for wet foams. We further assume complete foam collapse at residual water saturation, S_wr, employing the version of F₂ proposed by Namdar-Zanganeh et al. (2011):

$$F_{2} = 0.5 + \frac{{{ \arctan }\left( {epdry\left( {S_{w} - fmdry} \right)} \right)}}{\pi } - \left[ {0.5 + \frac{{{ \arctan }\left( {epdry\left( {S_{wr} - fmdry} \right)} \right)}}{\pi }} \right]$$

(A6)

where fmdry denotes the limiting liquid saturation at which foam collapses and epdry is a parameter that controls the abruptness of this collapse.

Appendix B: Discretization Scheme in Finite-Difference Simulator/

Equation 1 is discretized as follows,

$$S_{\text{wi}} \left( {t + \Delta t} \right) = S_{\text{wi}} \left( t \right) + \Delta t\left( {\frac{{f_{\text{w}} \left( {S_{{{\text{wi}} - 1}} \left( t \right)} \right) - f_{\text{w}} \left( {S_{\text{wi}} \left( t \right)} \right)}}{\Delta x}} \right)$$

(B1)

where S_wi, S_wi−1, f_w, t, ∆t, and ∆x denote the saturation of the given grid block, the saturation of the grid-block upstream of this block, water fractional flow, time, time increment, and dimensionless grid-block length, respectively.

The pressure evolution is calculated using Darcy’s Law. In our discretization scheme, Darcy’s Law takes the form,

$$P_{i - 1} = P_{i} + \left( {\frac{Q}{4 \pi h K}} \right)\left( {\frac{1}{{\lambda_{\text{rt}} \left( {r_{i} ,S_{\text{w i}} } \right)}} + \frac{1}{{\lambda_{\text{rt}} \left( {r_{i - 1} ,S_{\text{w i}} } \right)}}} \right)ln\left( {\frac{{r_{i} }}{{r_{i - 1} }}} \right)$$

(B2)

where P_i−1, P_i, r_i, r_i−1, S_wi, λ_rt, Q, h, and k denote the pressures and radii at the inner and outer boundaries, respectively, of the grid block, the saturation in the grid block, total relative mobility, total volumetric injection rate, thickness of the reservoir, and permeability, respectively.

Appendix C: Description of Computer Programs for the Fractional-Flow Theory Solution and the Finite-Difference Numerical Solution

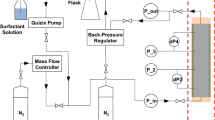
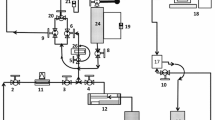
We coded in Matlab both the fractional-flow solution and the finite-difference simulator programs. We describe the structure of these programs in the flow diagrams presented in Fig. 20 and in Fig. 21.

Fig. 20

Flow diagram corresponding to the algorithm for the fractional-flow solution

Fig. 21

Flow diagram corresponding to the finite-difference simulator

We tested the convergence of both programs. For the fractional-flow theory solution program, we increased the number of characteristics from 200 to 300 and the number of rings (increments in x_D) from 1000 to 1100. The solutions converged at these resolutions. For the finite-difference simulator, we increased the number of grid blocks. We matched the fractional-flow solution for the Newtonian case using 2500 grid blocks and running the simulation up to a dimensionless time t_D = 0.01. Running a simulation with a longer t_D at this grid-block resolution was not possible because of RAM memory limitations.

The computation time for the fractional-flow solution was below 1 hour for the cases examined here using a personal computer with 16 GB of RAM and an Intel i7 processor. Whereas for the finite-difference simulator, the computation time increased exponentially as we increased the number of grid blocks Bos and Salazar Castillo (2019). In order to be able to run the program in a reasonable amount of time (below 2 h), we had to adjust the length of the simulation by reducing t_D.

The codes can be found in Bos and Salazar Castillo (2019) and in Salazar Castillo (2019b). More details and previous versions of the codes can also be found in Bos (2017), Ponners (2017) and ter Haar (2018).