1 Introduction

Poro-elasticity is the branch of mechanics that covers the reversible deformation of aggregates composed of a solid, assumed to behave linearly elastic, and a viscous and compressible fluid or several fluids, where we consider the term fluid to comprise liquids and gases. The composition of such mixtures is conventionally described by the volumetric fractions of the constituting phases, and in fact most of the time we use porosity as a quantification of the volume fraction not occupied by solid constituents. It is this notion of a pore space within a solid frame or skeleton that can be filled with an arbitrary fluid that leads to using the label “poro-elasticity”, apparently coined by Geertsma (1966). Much of the formal foundation as we use it today was, however, laid out earlier by Biot (1941) from a continuum perspective building partly upon the work of Terzaghi (1923, 1943) in the context of soil mechanics and Fillunger (1936) from the view point of fundamental concepts of Mixture Theory.

Today, users of the theoretical framework provided by linear poro-elasticity come from quite a number of scientific disciplines, e.g., civil engineering including soil mechanics (Verruijt 2010), theoretical mechanics (Cheng 2016), materials science (Silverstein et al. 2011), biomechanics (Mow et al. 1980), petroleum engineering (Detournay and Cheng 1993), hydrogeology (Verruijt 1969; Wang 2000), and rock mechanics (Guéguen et al. 2004). Not intending to belittle its complexity, it constitutes the most simple approach to the wide range of phenomena related to the coupled mechanical response of fluids and solids. The phenomena addressed by the theory have occupied men probably for long (foundations on quick sand, ground liquefaction in the wake of earthquakes, tidal well level fluctuations, etc.).

In the light of excellent texts by, e.g., Detournay and Cheng (1993), Rice and Cleary (1976), Lopatnikov and Cheng (2005) and Frenkel (1996), and the above-cited monographs, one may rightly wonder whether there is actually a need or motivation for another account of this subject. We find that Mixture Theory provides a framework for a rather rigorous development of the theory starting from the axioms of mechanics, the conservation laws for mass and momentum. Motivated by the studies of diffusion by Adolf Fick in the nineteenth century, Truesdell (1957) introduced the so-called continuum Mixture Theory, which in our days serves as the rational basis for the description of miscible and immiscible multiphase mixtures, cf. also the collections in Truesdell (1984). For the restricted case of immiscible and incompressible constituents, Bowen (1980) enhanced continuum Mixture Theory by the concept of volume fractions. In a further contribution, Bowen (1982) extended this framework for the more general case of compressible constituents. Bedford and Drumheller (1983) provided an overview of contributions to Mixture Theory up to 1983. Mixture Theory enhanced by the concept of volume fractions and especially applied to deformable porous media is also denoted as the Theory of Porous Media, cf. de Boer (2005) and Ehlers (2002). The latter author discusses finite element implementations of various models including finite deformations. An extensive review, including historical remarks about the conflict between Terzaghi and Fillunger, is given by de Boer (1996). Direct comparisons of Biot’s poro-elasticity and Mixture Theory can be found in Coussy et al. (1998) where it was shown that the basic constitutive equations for the total stress tensor and the pore pressure can be determined from a potential derived from the Clausius–Duhem inequality.

A particular value of the linear theory lies in the application to the propagation of elastic waves in porous media for material characterization or seismic exploration. Recent investigations include the role of micro- or mesoscale heterogeneities, like stratified media and/or those containing fractures or fracture networks, for wave-induced fluid flow and effective material properties, cf. Pride et al. (2004) or Quintal et al. (2011). Nevertheless, we do not present and discuss the governing set of poro-elastic equations describing acoustic waves because the dynamic extension of linear poro-elasticity is not influenced much by theoretical concepts of Mixture Theory. The contributions of Schanz and Diebels (2003) and Gurevich (2007) focused on comparing the properties of acoustic waves in poro-elastic media as obtained from poro-elasticity and Mixture Theory. Open question concerning acoustic waves in poro-elastic media is more related to physical and constitutive issues, like the role of dynamic permeability or tortuosity, cf. Smeulders (2005).

Here, we emphasize the “choices” made in the formulation of the theory and the relation to various previous approaches. Along the way, we clarify the basic step of formal linearization and present some unusual relations among the “multitude” of frequently used kinematic and dynamic variables and associated coefficients. The manuscript is organized as follows: After introducing the basic notions of Mixture Theory as applied to poro-elasticity, we discuss the partial balance equations for mass and momentum of both phases and introduce the related balance relations of the mixture. These balance relations are first treated in the most general global form and thus initially include nonlinearities, e.g., related to the material time derivatives. In a second step, the local balance relations are linearized. When introducing the constitutive relations linking the kinematic and dynamic variables, we put emphasis on clarifying the role of porosity as kinematic state variable.

2 Background/Foundation

2.1 The Subject of Poro-Elasticity

We consider it instructive to address the question how changes in state are imparted to the poro-elastic medium with a thought experiment involving an “ideal” membrane that (a) has no strength but transmits external loads to the medium without modifying them and (b) still ensures continuity of normal stresses at the medium’s surface. Furthermore, the membrane (c) imposes no kinematic restrictions to the deformation of the solid skeleton but (d) allows the medium to exchange fluid with its environment according to yet- to-be specified boundary conditions. When the material volume at consideration represents only a small part of a larger body, the neighboring volume elements play the role of the “ideal” membrane. In continuum mechanics, this latter view is often expressed by addressing the “material volume” as the “local” and the entire body as the “global” scale. In laboratory tests, any of the requests may be violated or only approximately achieved due to technical limitations. In numerical studies, boundary conditions can be prescribed in various ways; a prominent example is periodic boundary conditions that comply with (a)–(d).

In our thought experiment, we envision the membrane to transmit a hydrostatic pressure, commonly addressed as “confining pressure” by experimentalists, to a suspension, i.e., a specific case of a two-phase mixture in which the solid parts, the particles or grains, do not form a connected skeleton but float in the liquid. Obviously, for an ideal membrane, the fluid pressure will be identical with the external pressure and all solid grains experience a normal stress identical to the fluid pressure. Now, assume we allow for a leak in the membrane through which fluid escapes to a “reservoir” at lower pressure than the exerted confining pressure. Eventually, the solid grains will start touching each other during this consolidation at which point the leak is sealed. Now, some of the externally applied pressure is carried by the forming load-bearing frame or solid skeleton and some by the fluid. Consequently, mechanical equilibrium at the medium’s surface and interior involves fluid pressure and stresses of the solid grains, i.e., normal stresses applied at solid–fluid interfaces but also at solid–solid interfaces as well as shear stresses at solid–solid interfaces. All of our work restricts to media that reached this state of a load-bearing solid frame, whatever the actual genesis, e.g., fibrous growth or gravity-controlled sedimentation of particles.

From a thermodynamic perspective, poro-elasticity analyzes the relation of a material volume, characterized by certain rheologic properties, which mechanically interacts and may exchange matter with its environment, here specifically only one constituent, the fluid. Two limiting cases are distinguished regarding the fluid exchange with the environment, undrained conditions, i.e., no fluid exchange, or (perfectly) drained conditions, i.e., the fluid pressure remains constant during a change in mechanical state. We restrict to aggregates whose pore space is fully saturated by a single viscous fluid phase.

2.2 General Formulation for Binary Mixtures

We present (Biot’s) linear poro-elasticity from the perspective of continuum Mixture Theory that, albeit at the cost of theoretical formality, brings with it the benefit of clarifying the origin and role of various assumptions involved in poro-elasticity, some of which are, until today, controversially discussed, cf. Wilmański (2006). Trying to keep the mathematical and theoretical effort at a minimum, we concentrate on the basic aspects but refer the reader to standard textbooks of Mixture Theory for distinct contributions to the Theory of Porous Media, cf. Ehlers (2002); de Boer (2005) or extensions to tri- and multiphasic approaches including aspects of nonlinearities and further more sophisticated models, cf. Bowen (1976); Rajagopal and Tao (1996); Schneider and Hutter (2009); Coussy (1995).

Before introducing the basic modeling concepts of linear poro-elasticity, we compile the assumptions for the modeling framework:

  1. (a)

    linear constitutive relations, i.e.,

    • linear elastic (reversible) deformations of the solid skeleton and its components, considered to hold when restricting to small deformations, and

    • viscous fluid and linear equation of state for fluid pressure;

  2. (b)

    slow, quasi-static “diffusive” processes, inertia terms are neglected;

  3. (c)

    isotropy of the solid skeleton and the effective behavior of its constituents;

  4. (d)

    isothermal conditions, specifically all phases have identical thermal conditions;

  5. (e)

    macroscopic continuum theory, no inherent length or time scales;

  6. (f)

    pore space is fully saturated with a single fluid;

  7. (g)

    part of the pore space is connected such that the material body under investigation can exchange fluid with its environment.

In linear poro-elasticity, constitutive (material) relations between dynamic variables (e.g., stresses, pressures, drag forces) and kinematic quantities (e.g., strains, relative fluid velocity) are formulated in a phenomenological manner. Here, we refrain from a rigorous discussion of the thermodynamic consistency of the poro-elastic constitutive relations but take a “rheologic” approach to the basic phenomena, i.e., address the question how an ideal linear poro-elastic material behaves when its state changes.

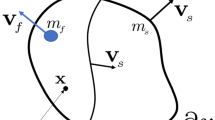
A continuum-based description of an elastic porous solid saturated with a compressible and viscous (pore) fluid requires to introduce various macroscopic field quantities characterizing the volumetric composition of this binary mixture. We rely on the concept of a material point denoted as \(\mathcal {P}\) (Fig. 1), i.e., the classical notion of continuum mechanics, that the length scales of problems at hand, the size of investigated bodies, sufficiently exceed the length scales involved with the geometrical characteristics of pores and solid constituents, and thus, locally the material has well-defined properties. At such a material point \(\mathcal {P}(\mathbf{x},\,t)\), the mixture is composed of the two constituents (here each constituent in particular represents a different phase) indicated by a subscript (for kinematic variables) or superscript (for all others) \(\alpha = \left\{ \mathfrak {f},\,\mathfrak {s}\right\} \) referring to either the fluid or the solid phase (Fig. 1). In the current or deformed configuration, a volume element of the mixture \(\mathrm{d}v\) is partly occupied by a fluid volume element \(\mathrm{d}v^\mathfrak {f}\) and a solid volume element \(\mathrm{d}v^\mathfrak {s}\) corresponding to volume fractions of \(n^\alpha (\mathbf{x},\,t) := \mathrm{d}v^\alpha / \mathrm{d}v\) for which it is obvious that \(0 \le n^\alpha \le 1\) and \(n^\mathfrak {s}+ n^\mathfrak {f}\equiv 1\). Depending on the specific deformation that a material volume is undergoing, the volume fractions \(n^\alpha (\mathbf{x},\,t)\) may evolve, i.e., in general the local amounts of the fluid or the solid phase at \(\mathcal {P}\) constitute field variables depending on spatial position (position vector \(\mathbf{x}\)).

In the context of (biphasic) poro-elasticity, it is common to replace the volume fractions by local porosity \(\phi (\mathbf{x},\,t)\), i.e., the percentage of the material volume occupied by the (pore) fluid, that is linked to the volume fractions according to \(\phi = n^\mathfrak {f}= 1 - n^\mathfrak {s}\). The relation between fluid volume and porosity is an expression of the saturation condition, i.e., the volume occupied by the fluid is identical with the pore volume at any point of time. In the following, we denote the initial (or reference or undeformed) configuration at \(t=t_0\) by a subscript “0”, specifically the initial porosity \(\phi (\mathbf{x},t_0) =: \phi _0(\mathbf{x})\) reads \(\phi _0 = \mathrm{d}v^\mathfrak {f}_0/\mathrm{d}v_0\).

The definition \(\phi = n^\mathfrak {f}= \mathrm{d}v^\mathfrak {f}/ \mathrm{d}v\) corresponds to the Eulerian spatial porosity, i.e., the porosity of the material volume currently occupying a specific point in space, of Coussy (2010, p. 52) who in addition introduced a Lagrangian porosity \(\tilde{\phi }:= \mathrm{d}v^\mathfrak {f}/\mathrm{d}v_0\), i.e., the porosity of the specific material volume that had the volume \(\mathrm{d}v_0\) in the reference configuration. The porosity in the Eulerian setting is related to the one in the Lagrangian setting via \(\tilde{\phi }\,\mathrm{d}v_0 = \phi \,\mathrm{d}v\). In linear poro-elasticity, the linearized Eulerian porosity coincides with the Lagrangian porosity, i.e., \(\text {lin}(\phi ) = \tilde{\phi }\). Only when poro-elasticity is extended and large (finite) deformations and nonlinear kinematic quantities have to be taken into account, the choice between Lagrangian and Eulerian porosities is not obvious but depends on the specific model. Differences in further kinematic quantities may arise when approaches rest on different perspectives, cf. Schreyer (2016, p. 816).

In addition to the volume element \(\mathrm{d}v\), we introduce a mass element \(\mathrm{d}m\) of the mixture as well as mass elements of the phases \(\mathrm{d}m^\alpha \). The density of the mixture follows in the standard way of continuum mechanics, i.e., \(\rho := \mathrm{d}m/\mathrm{d}v\). Two phase-specific densities are distinguished, partial densities \(\rho ^\alpha := \mathrm{d}m^\alpha / \mathrm{d}v\) and effective or true densities \(\rho ^{\alpha R}:= \mathrm{d}m^\alpha / \mathrm{d}v^\alpha \) that are linked via the volume fractions by \(\rho ^\alpha = n^\alpha \,\rho ^{\alpha R}\). Expressed by the partial densities, the density of the mixture reads \(\rho = \sum _\alpha \rho ^\alpha = \sum _\alpha n^\alpha \, \rho ^{\alpha R}\).

Fig. 1
figure 1

Material body \(\mathcal {B}\), material point \(\mathcal {P}\) of a biphasic mixture in current configuration t

Full size image

3 Kinematic State Variables and Mass Conservation

3.1 Choice of Kinematic Variables

Obvious kinematic state variables are the volumetric strains of the fluid and the solid as well as the shear strains of the solid. Here, we would like to emphasize the basic assumption made in the framework of (linear) poro-elasticity: Deformations of the solid are assumed to be small, i.e., strain measures do not exceed about 5 %. The appropriate kinematic quantities on which to base strain measures for the solid skeleton are the (Lagrangian) displacements given by \(\mathbf{u}_\mathfrak {s}= \mathbf{x}- \mathbf{X}_\mathfrak {s}\), where \(\mathbf{X}_\mathfrak {s}\) is the position vector of the solid phase at the initial state. In the small deformation framework, the strain tensor of the solid constituent \(\varvec{\varepsilon }_\mathfrak {s}= \varepsilon _{\mathfrak {s},ij}\,\mathbf{e}_i\otimes \mathbf{e}_j\) can be calculated from the displacement gradient

$$\begin{aligned} \varvec{\varepsilon }_\mathfrak {s}= \frac{1}{2}\,\left( \mathop {\mathrm {grad}}\nolimits \mathbf{u}_\mathfrak {s}+ \mathop {\mathrm {grad}}\nolimits ^T \mathbf{u}_\mathfrak {s}\right) \quad \text {with}\quad \varepsilon _{\mathfrak {s},ij} = \frac{1}{2}\left( \frac{\partial u_{\mathfrak {s},i}}{\partial x_j} + \frac{\partial u_{\mathfrak {s},j}}{\partial x_i}\right) \end{aligned}$$
(1)

where the upper index T is used for transposed tensors. The two kinematic state variables for the solid are gained from splitting the (partial) strain tensor into a scalar volumetric part \(e_\mathfrak {s}= \mathop {\mathrm {tr}}\nolimits (\varvec{\varepsilon }_\mathfrak {s}) = \mathop {\mathrm {div}}\nolimits \mathbf{u}_\mathfrak {s}\) and a second-order tensor, the deviatoric part or deviator \(\varvec{\gamma }_\mathfrak {s}\):

$$\begin{aligned} \varvec{\varepsilon }_\mathfrak {s}= \text {vol}(\varvec{\varepsilon }_\mathfrak {s}) + \text {dev}(\varvec{\varepsilon }_\mathfrak {s}) = \frac{1}{3}\,\text {tr}(\varvec{\varepsilon }_\mathfrak {s}) \mathbf{I}+ \text {dev}(\varvec{\varepsilon }_\mathfrak {s}) := \frac{1}{3}\,e_\mathfrak {s}\,\mathbf{I}+ \varvec{\gamma }_\mathfrak {s}. \end{aligned}$$
(2)

The volumetric strain of the fluid (at rest) calculates according to

$$\begin{aligned} e_\mathfrak {f}= \text {tr}(\varvec{\varepsilon }_\mathfrak {f}) = \mathop {\mathrm {div}}\nolimits (\mathbf{u}_\mathfrak {f}) . \end{aligned}$$
(3)
Fig. 2
figure 2

Individual motion of a fluid \({\chi }_\mathfrak {f}\) and a solid particle \({\chi }_\mathfrak {s}\). Only in the current configuration at time t, superposition in the Representative Volume Element (RVE) is observed

Full size image

The volumetric strains \(e_\mathfrak {s}\) and \(e_\mathfrak {f}\) can be geometrically interpreted on the basis of the previously introduced volume elements:

$$\begin{aligned} e_\mathfrak {s}= \frac{\mathrm{d}v- \mathrm{d}v_0}{\mathrm{d}v_0} \qquad \text {and} \qquad e_\mathfrak {f}= \frac{\mathrm{d}v^\mathfrak {f}- \mathrm{d}v^\mathfrak {f}_0}{\mathrm{d}v_0^\mathfrak {f}}. \end{aligned}$$
(4)

This comparison of differences in measures (here volumes) of the current and the initial configuration to the measure in the initial configuration follows classic definitions of strains in continuum mechanics (e.g., Haupt 2000; Hutter and Jöhnk 2003) and is consistent with the (linearized) map of volume elements. Volume elements of the skeleton are mapped with the Jacobian of the solid phase (\(\mathrm{d}v= J_\mathfrak {s}\,\mathrm{d}v_0\) with \(\det \mathbf{F}_\mathfrak {s}=:J_\mathfrak {s}\)), the Jacobian that links the previously introduced Eulerian and Lagrangian porosities, i.e., \(\tilde{\phi } = J_\mathfrak {s}\,\phi \), while the volume elements of the fluid phase are mapped with the Jacobian of the bulk fluid (\(\mathrm{d}v^\mathfrak {f}= J_\mathfrak {f}\,\mathrm{d}v^\mathfrak {f}_0\) with \(\det \mathbf{F}_\mathfrak {f}=:J_\mathfrak {f}\)). The two partial deformation gradients \(\mathbf{F}_\alpha \) are two-field tensors mapping line elements from the reference to the current configuration. The constituents have their own motion functions \(\varvec{\chi }_\alpha \) that only overlap in the current configuration (Fig. 2). The position vector \(\mathbf{x}\) in the current configuration refers to a RVE (with superimposed continua) while the constituents have individual position vectors \(\mathbf{X}_\alpha \) in the reference configuration. As an important consequence, only partial deformation gradients \(\mathbf{F}_\alpha \) (and the Jacobians \(J_\alpha \)) have a kinematic interpretation while a deformation gradient of the total mixture \(\mathbf{F}\) (and the associated Jacobian J) has no further physical significance. Making use of the linearized form of the Jacobian \(\mathop {\mathrm {lin}}\nolimits (J_\alpha ) = \mathop {\mathrm {div}}\nolimits (\mathbf{u}_\alpha ) + 1\) then immediately gives identity of (4) and (3) and the corresponding relation for the solid phase.

Equation (4) highlights the qualitative difference between the two volumetric strains. The strain of the solid skeleton \(e_\mathfrak {s}\) is identical to the total volumetric strain and constitutes the kinematic quantity which can be measured or controlled in a physical experiment but does not give information on the intrinsic strain of the solid material at any point in the skeleton. The volumetric strain of the fluid phase \(e_\mathfrak {f}\), in contrast, is a local measure of the state of the fluid phase, consistent with the definition of volume strains of real materials from de Boer (2005)

$$\begin{aligned} e_\alpha ^R = \frac{\mathrm{d}v^\alpha - \mathrm{d}v_0^\alpha }{\mathrm{d}v_0^\alpha } , \end{aligned}$$
(5)

cf. comments in Coussy (2010, Eq. 3.51). De Boer, in addition, introduced volumetric strains of the phases

$$\begin{aligned} \bar{e}_\alpha = \frac{\mathrm{d}v- \mathrm{d}v_0^\alpha }{\mathrm{d}v_0^\alpha } = \frac{\mathrm{d}v}{\mathrm{d}v_0^\alpha } - 1 \end{aligned}$$
(6)

that neither have simple geometric interpretations nor are consistent with the mapping rules of measurable kinematic quantities

The “increment of fluid content” introduced in Biot and Willis (1957, Eq. 26), i.e., the change in fluid volume in the material volume associated with a change in mechanical state and thus a measure of the fluid volume exchanged by the mixture volume with its environment, is calculated from the difference in the two volumetric strains as

$$\begin{aligned} \zeta = \phi _0\, \left( {e_\mathfrak {s}- e_\mathfrak {f}} \right) . \end{aligned}$$
(7)

The increment of fluid content is a convenient theoretical concept because it allows for a direct link to fluid flux or filter (or Darcy) velocity \(\mathbf{q}_\mathfrak {f}= \phi _0\,\mathbf{w}_\mathfrak {f}\) in the form \({\dot{\zeta }} = \phi _0\, \left( \dot{e}_\mathfrak {s}- \dot{e}_\mathfrak {f}\right) = \mathop {\mathrm {div}}\nolimits (\mathbf{q}_\mathfrak {f})\) that, in general, describes the motion of the fluid phase in a modified Eulerian framework where \(\mathbf{w}_\mathfrak {f}= \dot{\mathbf{u}}_\mathfrak {f}- \dot{\mathbf{u}}_\mathfrak {s}\) denotes the seepage velocity.

The geometrical interpretation of (7) has been presented in various previous studies (e.g., Detournay and Cheng 1993). A change in fluid volume present in the material volume due to a change in mechanical state has two contributions, owing to changes in fluid pressure (compressibility effect) and owing to changes in pore volume present in the (deforming) skeleton. Coussy (1995) introduced a more general, nonlinear relation

$$\begin{aligned} \zeta _\mathrm {{C}} = (e_\mathfrak {s}+ 1)\frac{ \rho ^{\mathfrak {f}R} }{\rho ^{\mathfrak {f}R}_0}\,\phi - \phi _0 \end{aligned}$$
(8)

that can be shown to be equivalent to (7) when linearized, and the introduced definitions \(\phi = \mathrm{d}v^\mathfrak {f}/ \mathrm{d}v\) and \(\phi _0 = \mathrm{d}v^\mathfrak {f}_0 / \mathrm{d}v_0\) are applied. Schreyer (2016) remarked recently that (8) is only equivalent to the increment of fluid content \(\zeta _\mathrm {{RC}}=(\phi - \phi _0)\,\rho ^{\mathfrak {f}R}/\rho ^{\mathfrak {f}R}_0\) defined in the work of Rice and Cleary (1976) and Wang (2000, p. 17, Eq. 1.5) when the solid skeleton is undeformable, i.e., \(e_\mathfrak {s}\equiv 0\).

3.2 Balance of Mass

In global form, i.e., for the total material body \({{\mathcal {B}}}\), the partial masses of the solid and the fluid phase are conserved according to

$$\begin{aligned} {{\mathcal {M}}}^\alpha = {{\mathcal {M}}}^\alpha _0 \qquad \text {or} \qquad [{{\mathcal {M}}}^\alpha ]'_\alpha = \left[ \int _{{\mathcal {B}}}\rho ^\alpha \,\mathrm{d}v\right] '_\alpha = 0 \end{aligned}$$
(9)

where the masses of the fluid \({{\mathcal {M}}}^\mathfrak {f}\) and the solid \({{\mathcal {M}}}^\mathfrak {s}\) combine to the total mass \({{\mathcal {M}}}={{\mathcal {M}}}^\mathfrak {s}+{{\mathcal {M}}}^\mathfrak {f}\) of the material body and \((\,\bullet \,)'_\alpha \) indicates the material or substantial derivative with regard to the velocity of the phase. Using standard arguments for continua, e.g., Haupt (2000), the localized form of the balance of masses of the constituents reads

$$\begin{aligned}&\partial _t(n^\alpha \,\rho ^{\alpha R}) + \mathop {\mathrm {div}}\nolimits (n^\alpha \,\rho ^{\alpha R}\,\mathbf{v}_\alpha ) = 0 \qquad \Leftrightarrow \nonumber \\&n^\alpha \,\partial _t (\rho ^{\alpha R}) + \rho ^{\alpha R}\,\partial _t (n^\alpha ) + n_\alpha \,\rho ^{\alpha R}\,\mathop {\mathrm {div}}\nolimits \mathbf{v}_\alpha + \mathbf{v}_\alpha \cdot \mathop {\mathrm {grad}}\nolimits (n^\alpha \,\rho ^{\alpha R}) = 0. \end{aligned}$$
(10)

Linearizing (10) around the reference state characterized by initial quantities \({{\mathcal {S}}}_0 = \left\{ \rho ^{\alpha R}_0, n^\alpha _0,e_{\alpha ,0} = 0 \right\} \), we obtain

$$\begin{aligned} n^\alpha _0\,\dot{\rho }^{\alpha R} + \rho ^{\alpha R}_0\,\dot{n}^\alpha + n^\alpha _0\,\rho ^{\alpha R}_0\,\dot{e}_\alpha = 0 \end{aligned}$$
(11)

or written out explicitly for the two phases

$$\begin{aligned} (1-\phi _0)\,\dot{\rho }^{\mathfrak {s}R} - \rho ^{\mathfrak {s}R}_0\,\dot{\phi } + (1-\phi _0)\,\rho ^{\mathfrak {s}R}_0\,\dot{e}_\mathfrak {s}&= 0 \quad \mathrm {and} \end{aligned}$$
(12)
$$\begin{aligned} \phi _0\,\dot{\rho }^{\mathfrak {f}R} + \rho ^{\mathfrak {f}R}_0\,\dot{\phi } + \phi _0\,\rho ^{\mathfrak {f}R}_0\,\dot{e}_\mathfrak {f}&= 0. \end{aligned}$$
(13)

In a linear kinematic description, the time derivatives are calculated from the partial time derivatives alone, e.g., \(\dot{\mathbf{u}}_\mathfrak {s}= \partial _t (\mathbf{u}_\mathfrak {s})\). The convective part of the more general material time derivative is of higher than linear order and assumed to be small for small strains and accordingly neglected. A formal derivation of the linearized mass balance for the single constituent is given in “Appendix A”.

Equations (12) and (13) express the dual role of porosity. On the one hand, the “constant parameter” initial porosity \(\phi _0 = n^\mathfrak {f}_0\) characterizes the mixture in the initial state and thus affects the linearized form of the balance of mass. On the other hand, porosity evolves. The appropriate evolution law has been a matter of discussion (e.g., Wilmański 1998, 2006), but the mass balances of the solid and fluid can obviously immediately be recast to

$$\begin{aligned} \dot{\phi } = (1-\phi _0)\,\frac{\dot{\rho }^{\mathfrak {s}R}}{\rho _{0}^{\mathfrak {s}R}} + (1-\phi _0)\,\dot{e}_\mathfrak {s}\end{aligned}$$
(14)

and

$$\begin{aligned} \dot{\phi } = - \phi _0\,\frac{\dot{\rho }^{\mathfrak {f}R}}{\rho _{0}^{\mathfrak {f}R}} - \phi _0\,\dot{e}_\mathfrak {f}, \end{aligned}$$
(15)

respectively. Furthermore, when the current configuration is summarized by \({{\mathcal {S}}}= \left\{ \rho ^{\alpha ,R}, n^\alpha ,\right. \left. e_{\alpha } \right\} \), integration of the linearized mass balance for the solid (13) gives

(16)

or after inserting \(n^\mathfrak {s}= 1 - \phi \)

$$\begin{aligned} \frac{\rho ^{\mathfrak {s}R}}{\rho ^{\mathfrak {s}R}_0} + \frac{1-\phi }{1-\phi _0} + e_\mathfrak {s}-2 = 0 \end{aligned}$$
(17)

which leads to an expression for the porosity

$$\begin{aligned} \phi = \phi (\rho ^{\mathfrak {s}R},\,e_\mathfrak {s}) = 2\,\phi _0 - 1 + (1-\phi _0)\,\left( \frac{\rho ^{\mathfrak {s}R}}{\rho ^{\mathfrak {s}R}_0} + e_\mathfrak {s}\right) . \end{aligned}$$
(18)

Analogously, integration of the linearized balance of mass of the fluid yields

$$\begin{aligned} \frac{\rho ^{\mathfrak {f}R}}{\rho ^{\mathfrak {f}R}_0} + \frac{\phi }{\phi _0} + e_\mathfrak {f}-2 = 0 \end{aligned}$$
(19)

giving a second expression for the porosity

$$\begin{aligned} \phi = \phi (\rho ^{\mathfrak {f}R},\,e_\mathfrak {f}) = 2\,\phi _0 - \phi _0 \left( \frac{\rho ^{\mathfrak {f}R}}{\rho ^{\mathfrak {f}R}_0} + e_\mathfrak {f}\right) . \end{aligned}$$
(20)

Equations (18) and (20) allow us to express one of the three field quantities \(\{n^\alpha ,\,\rho ^{\alpha R},\,e_\alpha \}\) by the two remaining ones, e.g., \(e_\alpha = e_\alpha (n^\alpha ,\,\rho ^{\alpha R})\). Thus, current porosity depends on effective density and volumetric deformation of the phases, yet to be further constrained by constitutive equations.

4 Dynamic State Variables and Conservation of Momentum

We first discuss the partial stress tensors \(\varvec{\sigma }^\alpha \) of the fluid and the solid constituent. In continuum Mixture Theory, the partial stress tensors are abstract quantities used for the formulation of the balance of momentum (and moment of momentum). They simply express the notion that each constituent contributes to the “load bearing”. We refer the interested reader to detailed discussions of the technical derivation of the balance relations in the framework of continuum Mixture Theory to Schneider and Hutter (2009), de Boer (1996), Ehlers (2002), or Coussy (2010).

From the conservation of partial moment of momentum, we simply obtain for poro-elastic media that the partial stress tensors are symmetric, i.e., \(\varvec{\sigma }^\alpha \equiv \varvec{\sigma }^{\alpha ,T}\), or in index notation for the components \(\sigma ^\alpha _{ij} \equiv \sigma ^\alpha _{ji}\) (e.g., Renner and Steeb 2015). The symmetry conditions also holds for the total stresses of the mixture, \(\varvec{\sigma }= \sum \varvec{\sigma }^\alpha \equiv \varvec{\sigma }^{T}\). Similar to the formal split performed for the strain tensor (2), we introduce a formal tensorial split of the partial (phase) stresses into a deviatoric and a volumetric part

$$\begin{aligned} \varvec{\sigma }^\alpha = \text {vol}(\varvec{\sigma }^\alpha ) + \text {dev}(\varvec{\sigma }^\alpha ) = \frac{1}{3}\,\text {tr}(\varvec{\sigma }^\alpha )\mathbf{I}+ \text {dev}(\varvec{\sigma }^\alpha ) := s^\alpha \,\mathbf{I}+ \varvec{\tau }^\alpha \end{aligned}$$
(21)

where \(s^\alpha \) is the partial mean stress. Analogously, the total stress of the mixture \(\varvec{\sigma }\) is split according to

$$\begin{aligned} \varvec{\sigma }= \sigma ^M \,\mathbf{I}+ \varvec{\tau }= (s^\mathfrak {s}+ s^\mathfrak {f})\,\mathbf{I}+\varvec{\tau }^\mathfrak {s}\end{aligned}$$
(22)

with the total mean stress \(\sigma ^M = s^\mathfrak {s}+ s^\mathfrak {f}\) and the fluid or pore pressure \(p := - s^\mathfrak {f}\).

The momentum \(\varvec{{{\mathcal {J}}}}^\alpha \) of a constituent is changed by the sum of the body forces \(\varvec{{{\mathcal {F}}}}^\alpha _{{{\mathcal {B}}}}\), contact forces \(\varvec{{{\mathcal {F}}}}^\alpha _{\partial {{\mathcal {B}}}}\), and interaction forces \(\hat{\varvec{{{\mathcal {P}}}}}^\alpha \), i.e.,

$$\begin{aligned} \left[ \varvec{{{\mathcal {J}}}}^\alpha \right] '_\alpha= & {} \varvec{{{\mathcal {F}}}}^\alpha _{{{\mathcal {B}}}} + \varvec{{{\mathcal {F}}}}^\alpha _{\partial {{\mathcal {B}}}} + \hat{\varvec{{{\mathcal {P}}}}}^\alpha , \end{aligned}$$
(23)
$$\begin{aligned} \left[ \int _{{\mathcal {B}}}\mathbf{v}_\alpha \,\rho ^{\alpha } \mathrm{d}v\right] '_\alpha= & {} \int _{{{\mathcal {B}}}} \rho ^\alpha \,\mathbf{b}\,\mathrm{d}v+ \int _{\partial {{\mathcal {B}}}} \mathbf{t}^\alpha \mathrm{d}a+ \int _{{{\mathcal {B}}}} \hat{\mathbf{p}}^\alpha \mathrm{d}v. \end{aligned}$$
(24)

Again, standard arguments from mechanics of continua yield the local form of the partial momentum balance

$$\begin{aligned} \rho \,\ddot{\mathbf{x}}_\alpha - \mathop {\mathrm {div}}\nolimits \varvec{\sigma }^\alpha = \rho ^\alpha \,\mathbf{b}+ \hat{\mathbf{p}}^\alpha . \end{aligned}$$
(25)

Similarly, the global conservation of momentum for the mixture

$$\begin{aligned} \left[ \varvec{{{\mathcal {J}}}} \right] '= & {} \varvec{{{\mathcal {F}}}}_{{{\mathcal {B}}}} + \varvec{{{\mathcal {F}}}}_{\partial {{\mathcal {B}}}}, \end{aligned}$$
(26)
$$\begin{aligned} \left[ \int _{{\mathcal {B}}}\mathbf{v}\,\rho \,\mathrm{d}v\right] '= & {} \int _{{{\mathcal {B}}}} \rho \,\mathbf{b}\,\mathrm{d}v+ \int _{\partial {{\mathcal {B}}}} \mathbf{t}\,\mathrm{d}a\end{aligned}$$
(27)

reads in local form

$$\begin{aligned} \rho \,\ddot{\mathbf{x}} - \mathop {\mathrm {div}}\nolimits \varvec{\sigma }= \rho \,\mathbf{b}. \end{aligned}$$
(28)

In the derived general partial and total balances of momentum (25) and (28), the first terms on the left side represent the inertia contributions. In the following, we restrict ourself to the discussion of linear poro-elasticity in the quasi-static regime and thus neglect these inertia terms that, however, are central in the treatment of elastic waves.

5 Constitutive Relations

Basically, the constitutive behavior of a poro-elastic medium has to be constrained for two situations, equilibrium and non-equilibrium. Equilibrium is reached when the fluid is at rest, i.e., when the pore pressure field \(p(\mathbf{x},\,t)\) is homogeneous and fluid flow driving pressure gradients are absent. In the non-equilibrium case, the porous medium is characterized by a fluid with a spatially inhomogeneous pore pressure distribution. Pressure gradients cause fluid flow in the pore space. Depending on the type of the porous medium and the boundary conditions under consideration, which can be drained or undrained for the pore fluid, the medium may be consolidated or pressure diffusion effects may be observed. In the non-equilibrium case, energy is dissipated owing to the viscous momentum interaction at the solid–fluid interface. In classical poro-elasticity, such (pore-scale) interface effects are, however, not explicitly taken into account. Implicitly, interface effects are captured in poro-elasticity through the solid–fluid momentum interaction term in (23) and (25).

In the sequel, we attribute the same sign to volume changes and the stresses causing them. Following the “engineering” sign convention, volume increase is considered positive, and thus, tensile stresses are positive, but fluid pressure is also positive.

5.1 Fluid Phase

The pressure of a compressible fluid is a thermodynamic state variable, i.e., it is determined by a constitutive equation (equation of state). In linear (isothermal) poro-elasticity, we assume that the pore fluid is a (linear) barotropic fluid, and thus, the pressure in the fluid is a function of the effective fluid density, i.e., \(p = p(\rho ^{\mathfrak {f}R})\propto \rho ^{\mathfrak {f}R}\). Introducing the bulk modulus of the fluid, \(K^\mathfrak {f}\), the linear relations connecting density at some elevated pressure with density at zero pressure (the reference state) read

$$\begin{aligned} p = K^\mathfrak {f}\, \left[ \frac{\rho ^{\mathfrak {f}R}}{\rho ^{\mathfrak {f}R}_0} - 1 \right] \quad \text {or} \quad \rho ^{\mathfrak {f}R} = \rho ^{\mathfrak {f}R}_0\, { \left[ \frac{p}{K^\mathfrak {f}} + 1 \right] . } \end{aligned}$$
(29)

Nearly, incompressible fluids, such as water and oil, are closely described by (29) in the vast majority of applications, while gases obey linear relations only for very restricted ranges in pressure.

5.2 Solid Phase

In the equilibrium case, the poro-elastic medium behaves like a biphasic elastic composite. For a fluid at rest, (viscous) shear stresses in the fluid do not occur and the solid–liquid interfaces are traction-free. Shear stiffness of the composite results only from the shear stiffness (modulus) G of the solid skeleton, determined by the (intrinsic) shear stiffness of the solid material \(G^\mathfrak {s}\) and the geometrical characteristics of the skeleton. The effective bulk stiffness of the composite is (potentially) affected by three different bulk moduli (or their inverses, compressibilities), the two describing the intrinsic behavior of the two phases, i.e., \(K^\mathfrak {f}\) for the compressible fluid phase introduced in (29) and \(K^\mathfrak {s}\) for the compressible solid material composing the skeleton, in turn described by the skeleton modulus K.

The moduli of the solid material composing the skeleton, e.g., anisotropic crystals and crystals with a range of compositions but also “empty” or fluid-filled isolated pores, generally require some upscaling from the properties of individual solid constituents to effective or average moduli, \(\bar{G}^\mathfrak {s}\) and \(\bar{K}^\mathfrak {s}\), that can typically be quantified in meaningful limits, the celebrated Voigt–Reuss or Hashin–Shtrikman bounds for general and isotropic material behavior, respectively (Nemat-Nasser and Hori 1993; Mavko et al. 2009). In the sequel, we will refrain from using this explicit notation for the material parameters, but \(G^\mathfrak {s}\) and \(K^\mathfrak {s}\) should be understood to represent effective parameters. The same bounding treatment can in principle be applied to the two-phase mixture to constrain the drained and the undrained modulus, but often the bounds are wide and thus of limited use owing to stark contrasts between the moduli of the solid and fluid phases. Without constraints on the structure of the skeleton (or the pore space), the bounds cannot be tightened.

A range of upscaling or homogenization methods yields the explicit results within the rigorous bounds (e.g., Klusemann and Svendsen 2010). The microstructural heterogeneities have to be significantly smaller than the material point under consideration (a requirement that also applies to the choice of sample size for experiments to yield meaningful material parameters). Methods frequently applied to derive effective properties of composite materials, such as the effective medium approximation (EMA) or the Mori–Tanaka methods (MTM), rely on the seminal work of Eshelby for ellipsoidal inclusions (Eshelby 1957, 1959). Every inclusion is considered to either be embedded in a matrix characterized by the sought effective elasticity coefficients (e.g., EMA) or to experience a mean strain (or stress) field (e.g., MTM). The various approaches also differ in the number of phases considered.

5.3 Mixture at Equilibrium

From the analyses of the balance of momentum, we found three stress quantities as obvious candidates for dynamic variables. Besides the deviatoric stress tensor \(\varvec{\tau }^\mathfrak {s}\) which only exists for the solid skeleton as the pore fluid at rest does not have any (elastic or viscous) shear resistance, these are the pore fluid pressure p and the total mean stress \(\sigma ^M\). From a thermodynamic perspective, the kinematic and dynamic variables constitute generalized displacements and forces, respectively. As a direct consequence of the evaluation of the second law of thermodynamics in form of the Clausius–Planck inequality, the generalized forces (sometimes also called response functions) result from partial differentiation of a thermodynamic potential, here a strain energy function W, with respect to the generalized displacements (sometimes also called process variables). The interested reader is referred to the technical derivations outlined, e.g., in Ehlers (2002).

Following the seminal work of Biot (1941), we use the set of kinematic variables \(\{\varvec{\gamma }_\mathfrak {s},\,e_\mathfrak {s},\,\zeta \}\) to formulate the most general strain energy function, which Biot (1941) called a potential energy density, of a linear poro-elastic material as

$$\begin{aligned} \begin{array}{rcl} W &{} = &{} \mathop {\mathrm {dev}}\nolimits (W) + \mathop {\mathrm {vol}}\nolimits (W) = W(\varvec{\gamma }_\mathfrak {s}) + W(e_\mathfrak {s}) + W(e_\mathfrak {s},\,\zeta ) + W(\zeta ),\\ &{} = &{} \displaystyle {a\,\left[ \varvec{\gamma }_\mathfrak {s}: \varvec{\gamma }_\mathfrak {s}\right] + b\,e_\mathfrak {s}^2 + c\,e_\mathfrak {s}\,\zeta + d\,\zeta ^2,}\\ \end{array} \end{aligned}$$
(30)

comprising a total of four linear independent coefficients \(\{a,\,b,\,c,\,d\}\) relating kinematic and dynamic variables, see also Wang (2000) and Cheng (2016, eq. 2.21). The decoupling of deviatoric (\(\varvec{\gamma }_\mathfrak {s}\)) and volumetric (\(e_\mathfrak {s}\), \(\zeta \)) contributions is a direct consequence of the additive decomposition of the strain tensor (2) and the assumption of linearity. Shear stresses and strains relate simply by \(\varvec{\tau }= \partial W/\partial \varvec{\gamma }_\mathfrak {s}\). The two remaining dynamic variables, fluid pressure and mean stress, allow for only two kinematic variables in a linear treatment. Using \(e_\mathfrak {f}\) instead of either \(e_\mathfrak {s}\) or \(\zeta \) does not change the form of the function but only the physical meaning of the involved coefficients. Thus, the linearity requirement for the strain energy function limits the number of constitutive parameters for isotropic poro-elastic media at equilibrium to four, of which three relate to volumetric relations.

The strain energy function (30) is a function of the kinematic variables. It acts as a potential for the dynamic variables and comprises a single term accounting for the stored elastic energy associated with deviatoric deformations and three terms related to volumetric deformations. One of the latter terms is a mixed term in the two volumetric kinematic variables reflecting the coupling between the (volumetric) deformations of the solid and the fluid phase: When the fluid-saturated pore space is deformed, we expect to observe a change in the fluid pressure and in the volumetric stresses of the solid phase.

Evaluating the partial derivatives of the strain energy function yields that shear stresses relate to shear strains by

$$\begin{aligned} \varvec{\tau }= \frac{\partial W}{\partial \varvec{\gamma }_\mathfrak {s}} = 2\,a\,\varvec{\gamma }_\mathfrak {s}. \end{aligned}$$
(31)

The remaining dynamic variables are obtained from the potential as

$$\begin{aligned} \sigma ^M = \frac{\partial W}{\partial e_\mathfrak {s}} = 2\,b\,e_\mathfrak {s}+ c\,\zeta \qquad \mathrm {and} \qquad p = \frac{\partial W}{\partial \zeta } = c\,\,e_\mathfrak {s}+ 2\,d\,\zeta . \end{aligned}$$
(32)

It is common practice to cast this result for the link between the two volumetric dynamic variables and the two volumetric kinematic variables in a matrix formulation:

$$\begin{aligned} \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] = \left[ \begin{array}{c@{\quad }c} 2\,b &{}\quad c\\ c &{}\quad 2\,d \end{array} \right] \; \left[ \begin{array}{c} e_\mathfrak {s} \\ \zeta \end{array} \right] \end{aligned}$$
(33)

or its inverse

$$\begin{aligned} \left[ \begin{array}{c} e_\mathfrak {s} \\ \zeta \end{array} \right] = \frac{1}{4\,b\,d-c^2} \left[ \begin{array}{c@{\quad }c} 2\,d &{}\quad -c\\ -c &{}\quad 2\,b \end{array} \right] \; \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] . \end{aligned}$$
(34)

These relations are particularly helpful for physical interpretation of the coefficients by consideration of thought or idealized experiments.

5.3.1 Physical Interpretation of the Coefficients in the Strain Energy Function

According to Hooke’s law for isotropic media, shear stresses relate to shear strains by

$$\begin{aligned} \varvec{\tau }= 2\,G\,\varvec{\gamma }_\mathfrak {s}\end{aligned}$$
(35)

and we thus identify the first coefficient in the strain energy function with the shear modulus of the skeleton, i.e., \(a=G\). Next, we investigate the relation between a change of total mean stress and the change in volumetric deformation for (a) undrained conditions and (b) drained conditions:

Undrained bulk modulus\(K_\mathrm {u}\): Undrained conditions, i.e., \(\zeta = \mathrm {const.}\) in (33), give

$$\begin{aligned} \left. \frac{\partial \sigma ^M}{\partial e_\mathfrak {s}}\right| _{{\zeta }} = 2\,b =: K_\mathrm {u} . \end{aligned}$$
(36)

Here and in the sequel, we use the conventional notation of thermodynamics to indicate the constraint under which a derivative is evaluated, a vertical bar with a subscript denoting the variable that is kept constant. Thus, for undrained conditions, the second coefficient of the strain energy function has a ready physical interpretation. It controls the relation between the change in mean stresses of the skeleton and a change in volumetric solid deformation and thus is conventionally identified as a “new” bulk modulus \(K_\mathrm {u}\), the undrained (or saturated) bulk modulus, sometimes also called Gassmann modulus honoring the work of Fritz Gassmann (Gassmann 1951).

Skempton parameterB: Evaluation of \(\zeta \) in (34) gives

$$\begin{aligned} 0 = -c \,\sigma ^M + 2\,b\,p \quad \Longleftrightarrow \quad \left. \frac{\partial p}{\partial \sigma ^M }\right| _{{\zeta =0}}=\frac{c}{2\,b}=: B \end{aligned}$$
(37)

demonstrating that, for undrained conditions, the variation in pore pressure per amount of applied total mean stress is fixed by the constitutive parameters. The constancy of the pressure–stress ratio motivates to introduce a related material property, called the Skempton coefficient (or parameter) B.

Drained bulk modulusK: Drained conditions, i.e., p in (34), lead to

$$\begin{aligned} \left. \frac{\partial e_\mathfrak {s}}{\partial \sigma ^M}\right| _{{p}} = \frac{2\,d}{4\,b\,d-c^2} =: \frac{1}{K} \end{aligned}$$
(38)

providing a relation between coefficients of the strain energy function and the skeleton’s bulk modulus K, which describes the stiffness of the “drained” or empty (or dry) skeleton. The terms “skeleton bulk modulus”, “drained bulk modulus”, and “dry bulk modulus” are thus synonymously used.

By now, we found three independent relations between the strain energy coefficients b, c, and d and three measurable material properties with simple physical interpretations \(\{ K,\,K_\mathrm {u},\,B\}\), and thus, the constitutive behavior of linear poro-elastic media is in principle fully described. Inverting (36), (37), and (38) gives \(b=K_\mathrm {u}/2\), \(c=B\,K_\mathrm {u}\), and \(d=B^2K_\mathrm {u}^2 /(2\,K_\mathrm {u}-2\,K)\). However, a number of further material parameters have been employed owing to their aptness in specific applications.

Unjacketed modulus\(K_\mathrm {uj}\): The condition that the sample is subjected to equal changes in external mean stress and pore fluid pressure, i.e., \(\sigma ^M=-p\), technically realized by performing a test on an unjacketed sample immersed in a fluid that—when its pressure is changed—exerts the loading on the outer surface and in the pore space (the inner surface), yields

$$\begin{aligned} \left. \frac{\partial \sigma ^M}{\partial e_\mathfrak {s}}\right| _{\sigma ^M=-p} = \frac{4\,b\,d-c^2}{2\,d+c} =: K_\mathrm {uj}. \end{aligned}$$
(39)

Biot–Willis coefficient\(\alpha \): According to an evaluation of the second line of (33) for drained conditions, i.e., \(p=\mathop {\mathrm {const}}\nolimits .\), the change in fluid increment per change in volumetric deformation of the solid skeleton is constant:

$$\begin{aligned} \left. \frac{\partial \zeta }{\partial e_\mathfrak {s}}\right| _{{p}} = -\frac{c}{2d} =: \alpha . \end{aligned}$$
(40)

This constant ratio is referred to as the Biot–Willis coefficient \(\alpha \), cf. Biot and Willis (1957).

Specific storage capacitys: Next, we consider the variation in fluid increment per change in pore pressure. This quantification of the yield and storage of fluid volume per change in fluid pressure is, for example, crucial for the assessment of (a) natural reservoirs hosting liquid resources that are produced through boreholes, i.e., owing to a local reduction in fluid pressure and (b) natural repositories for liquid wastes that are injected through boreholes. For a process during which the solid skeleton does not deform volumetrically, i.e., \(e_\mathfrak {s}= \mathrm {const.}\), the second line of (33) gives

$$\begin{aligned} \left. \frac{\partial \zeta }{\partial p}\right| _{{e_\mathfrak {s}}} = \frac{1}{2\,d} =: s_{e_\mathfrak {s}} =: \frac{1}{M}. \end{aligned}$$
(41)

The inverse of the specific storage capacity \(s_{e_\mathfrak {s}}\) is called storage modulus M, one of the parameters actually used by Biot (1941) in his treatment of the constitutive behavior of poro-elastic media. For a process during which the mean stress on the solid skeleton does not change, i.e., \(\sigma ^M = \mathrm {const.}\), the second line of (34) gives a second specific storage capacity:

$$\begin{aligned} \left. \frac{\partial \zeta }{\partial p}\right| _{{\sigma ^M }} = \frac{2b}{4\,b\,d-c^2} =: s_{\sigma ^M}. \end{aligned}$$
(42)

Concluding the physical interpretation of the coefficients of the strain energy function, we present the constitutive relations for the specific set \(\{G,\,K_\mathrm {u},\,\alpha ,\,M\}\) (skipping the details of the algebraic derivation)

$$\begin{aligned} \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] = \left[ \begin{array}{c@{\quad }c} K_\mathrm {u} &{}\quad -\alpha \,M\\ -\alpha \,M &{}\quad M \end{array} \right] \; \left[ \begin{array}{c} e_\mathfrak {s} \\ \zeta \end{array} \right] , \end{aligned}$$
(43)

with the inverse relation

$$\begin{aligned} \left[ \begin{array}{c} e_\mathfrak {s} \\ \zeta \end{array} \right] = \frac{1}{K_\mathrm {u} - \alpha ^2\,M} \left[ \begin{array}{c@{\qquad }c} 1 &{}\quad \alpha \\ \alpha &{}\quad K_\mathrm {u}/M \end{array} \right] \; \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] . \end{aligned}$$
(44)

Yet, the parameter set \(\{K_\mathrm {u},\,\alpha ,\,M\}\) of volumetric deformation-related parameters can be replaced by arbitrary combinations of three of the parameters introduced above. An extensive conversion table for poro-elastic constants can be found in the recently published monograph of Cheng (2016, Appendix B) but also in Kümpel (1991). For example, the drained and undrained moduli are related by

$$\begin{aligned} K=K_\mathrm {u}-\alpha ^2\,M, \end{aligned}$$
(45)

the unjacketed modulus holds the relation

$$\begin{aligned} K_\mathrm {uj}=\frac{K}{1-\alpha }, \end{aligned}$$
(46)

the two specific storage capacities obey

$$\begin{aligned} \frac{s_{e_\mathfrak {s}}}{s_{\sigma ^M}} = \frac{K}{K_\mathrm {u}}, \end{aligned}$$
(47)

and the Skempton coefficient reads

$$\begin{aligned} B = \frac{\alpha \,M}{K_\mathrm {u}}. \end{aligned}$$
(48)

5.3.2 Constitutive Relations for Alternative Choices of State Variables

It is straightforward to replace, for example, \(\zeta \) (or \(e_\mathfrak {s}\)) in (33) and (34) by the volumetric strain of the fluid \(e_\mathfrak {f}\) using (7). The constitutive relations for the pair (\(e_\mathfrak {s}\), \(e_\mathfrak {f}\)) were already given in Renner and Steeb (2015). In addition, it is straightforward to derive “mixed” relations for “state vectors” composed of dynamic and kinematic variables, e.g.,

$$\begin{aligned} \left[ \begin{array}{c} \sigma ^M \\ \zeta \end{array} \right] = \left[ \begin{array}{c@{\qquad }c} K_\mathrm {u} - \alpha ^2\,M &{}\quad -\alpha \\ \alpha &{}\quad 1/M \end{array} \right] \; \left[ \begin{array}{c} e_\mathfrak {s}\\ p \end{array} \right] , \end{aligned}$$
(49)

or again in inverted form

$$\begin{aligned} \left[ \begin{array}{c} e_\mathfrak {s}\\ p \end{array} \right] = \frac{M}{K_\mathrm {u}} \left[ \begin{array}{c@{\qquad }c} 1/M &{}\quad \alpha \\ -\alpha &{}\quad K_\mathrm {u} - \alpha ^2\,M \end{array} \right] \; \left[ \begin{array}{c} \sigma ^M \\ \zeta \end{array} \right] , \end{aligned}$$
(50)

or

$$\begin{aligned} \left[ \begin{array}{c} \zeta \\ p \end{array} \right] = \frac{1}{\alpha \,M} \left[ \begin{array}{c@{\qquad }c} -1 &{}\quad K_\mathrm {u}\\ M\,K_\mathrm {u} - \alpha ^2\,M^2 &{}\quad M \end{array} \right] \; \left[ \begin{array}{c} \sigma ^M \\ e_\mathfrak {s}\end{array} \right] . \end{aligned}$$
(51)

All these transformations of the relations from one set of variables to another correspond to matrix manipulations. Rather than aiming for comprehensiveness, we focus on formulations involving porosity as one of the two kinematic variables in the sequel because they have experienced less attention in the past than the sets investigated above.

Since we defined the type of pore fluid by (29), we can further elaborate on our results for the evolution of porosity \(\phi (\mathbf{x},\,t)\) from the balance of mass of the fluid. We replace the effective fluid density \(\rho ^{\mathfrak {f}R}\) in the balance of mass of the fluid (20) by the pore pressure using (29)

$$\begin{aligned} \phi = \phi _0 -\phi _0\left[ \frac{p}{K^\mathfrak {f}} + e_\mathfrak {f}\right] , \end{aligned}$$
(52)

and insert the definition of the increment of fluid content to arrive at

$$\begin{aligned} \phi = \phi _0 +\frac{\phi _0}{K^\mathfrak {f}} \left[ \alpha \,M - K^\mathfrak {f}\right] \,e_\mathfrak {s}+\frac{1}{K^\mathfrak {f}} \left[ K^\mathfrak {f}- \phi _0\,M\right] \,\zeta , \end{aligned}$$
(53)

or alternatively

$$\begin{aligned} \phi = \phi _0 +\frac{\phi _0}{K^\mathfrak {f}} \left[ M(\alpha - \phi _0)\right] \,e_\mathfrak {s}+\frac{\phi _0}{K^\mathfrak {f}} \left[ M\,\phi _0 - K^\mathfrak {f}\right] \,e_\mathfrak {f}. \end{aligned}$$
(54)

Thus, porosity (or its change \(\phi -\phi _0\)) linearly depends on pairs of the kinematic variables \(e_\mathfrak {s}\), \(e_\mathfrak {f}\), and \(\zeta \), i.e., the evolution of porosity depends on the volumetric deformations of the fluid and solid and/or the increment of fluid content. Thus, porosity is a “dependent” field variable governed by the previously chosen kinematic state variables. Porosity can, however, also be interpreted as a “fundamental” kinematic state variable, for example paired with \(e_\mathfrak {s}\). Replacing \(\zeta \) in (43) by the change in porosity \(\phi - \phi _0\) in (53) leads to

$$\begin{aligned} \left[ \begin{array}{c} e_\mathfrak {s} \\ \phi - \phi _0 \end{array} \right] = \frac{1}{K} \left[ \begin{array}{c@{\quad }c} 1 &{}\quad \alpha \\ \alpha -\phi _0 &{}\quad \alpha -\phi _0 \end{array} \right] \; \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] , \end{aligned}$$
(55)

after “some” algebraic manipulations. Analyzing (55) reveals that for unjacketed conditions, no change in porosity occurs, \(\phi - \phi _0=0\), despite the finite bulk volumetric strain of \(e_\mathfrak {s}=(1-\alpha )\sigma ^M/K\). Thus, all of the volumetric deformation has to come from volumetric deformation of the solid material composing the skeleton and the unjacketed modulus has to be identified with the “mean” bulk modulus of these solid constituents

$$\begin{aligned} K_\mathrm {uj}=K^\mathfrak {s}\quad \text {and thus}\quad \alpha =1-\frac{K}{K^\mathfrak {s}}\,. \end{aligned}$$
(56)

We see that the Biot–Willis coefficient reflects the ratio between the moduli of the specific configuration of a solid material and the material itself.

Ever since the work of Brown and Korringa (1975), who extended the considerations regarding homogeneity of the skeleton by Gassmann (1951), the constitutive relation for unjacketed conditions has been vividly discussed (e.g., Lehner 2011). Frequently, three moduli are introduced to express the balance of changes in bulk, pore, and skeleton volume, using various notations of which {\(K^\mathfrak {s}\), \(K^{\mathfrak {s}'}\), \(K^{\mathfrak {s}''}\)} is probably most common. As much as real rocks may warrant such an extended constitutive description owing to their microscopic inhomogeneity, a linear theory with two pairs of volumetric state variables does not allow for more than three independent volumetric coefficients but necessitates the equality of the three moduli \(K^\mathfrak {s}= K^{\mathfrak {s}'} = K^{\mathfrak {s}''}\). A treatment of material behavior beyond linear poro-elasticity requires introducing additional kinematic and dynamic state variables.

The inverse of (55) reads

$$\begin{aligned} \left[ \begin{array}{c} \sigma ^M \\ p \end{array} \right] = K^\mathfrak {s}\, \left[ \begin{array}{c@{\quad }c} 1 &{}\quad -\frac{\alpha }{\alpha -\phi _0}\\ -1 &{}\quad \frac{1}{\alpha -\phi _0} \end{array} \right] \; \left[ \begin{array}{c} e_\mathfrak {s} \\ \phi - \phi _0 \end{array} \right] , \end{aligned}$$
(57)

Recalling that the volumetric strain for the skeleton, \(e_\mathfrak {s}\), is identical to the bulk volumetric strain as used by Zimmerman et al. (1986), the result (57) is consistent with their constitutive description that is frequently used in rock mechanics. The chosen dynamic variables are the same as above, but Zimmerman et al. (1986) restricted to hydrostatic loading, and thus, the mean stress \(\sigma ^M\) reduces to “confining pressure”.

The specific forms of “stress–strain” relations (55) and (57), as well as the ones presented by Zimmerman et al. (1986), i.e., those that do not involve either \(e_\mathfrak {f}\) or \(\zeta \) or another fluid-related kinematic variable, depend only on two material parameters \(\{\alpha ,\,K^\mathfrak {s}\}\) or, using the definition of \(\alpha \) (56), the set \(\{K,\,K^\mathfrak {s}\}\). This reduction in number of required constitutive parameters is also evidenced by the interrelations between the four considered compressibilities presented in equations (12–14) of Zimmerman et al. (1986).

5.3.3 Concept of Effective Stress

Compressive normal stresses exerted on a poro-elastic medium and fluid pressure acting in its pore space oppose each other. The concept of effective stress, first introduced by Terzaghi for incompressible constituents (\(\rho ^{\alpha R} \equiv \rho ^{\alpha R}_0\)), formalizes the balance between the two dynamic variables. The constitutive relations of the type represented by (49) and (55) readily provide effective stress “laws” for the involved kinematic variables.

The first line of (49) actually entails an important aspect of linear poro-elasticity:

$$\begin{aligned} \sigma ^M + \alpha \,p = K\,e_\mathfrak {s}, \end{aligned}$$
(58)

i.e., only the weighted balance of mean stress and fluid pressure effectively loads the solid skeleton and causes its volumetric deformation. Any two mechanical states with the same (volumetric) effective stress \(\sigma _E^{M,\mathfrak {s}}:= \sigma ^M + \alpha \,p\) are characterized by the same volumetric deformation of the solid skeleton. The weighting factor, here the Biot–Willis coefficient \(0 \le \alpha \le 1\), is often referred to as the effective stress coefficient. Likewise, the second line of (44) and (48) gives an effective stress coefficient for the fluid increment of \(1/B\ge 1\) because \(0 \le B \le 1\). The effective stress coefficient for porosity changes is simply “1”, as readily seen from the second line of (55) (see also equation (35) of Zimmerman et al. 1986) and implicitly already used in the above discussion of unjacketed tests:

$$\begin{aligned} { \sigma ^M + p = K^\mathfrak {s}\,\frac{1-\alpha }{\alpha - \phi _0}\,(\phi -\phi _0) . } \end{aligned}$$
(59)

These examples demonstrate that the magnitude of effective stress is, in general, governed by material parameters.

5.4 Non-equilibrium Case

We now extend our treatment to situations where pore pressure gradients appear and therefore also fluid flow occurs. The derived partial balance of momentum (25) then necessitates considering the remaining dynamic variable \(\hat{\mathbf{p}}^\alpha \). Here, we shortly outline the derivation of the constitutive response without going into technical details but refer again to Ehlers (2002) for a comprehensive derivation.

First, the momentum interaction \(\hat{\mathbf{p}}^\mathfrak {f}= -\hat{\mathbf{p}}^\mathfrak {s}\) is split into an equilibrium and a non-equilibrium part

$$\begin{aligned} \hat{\mathbf{p}}^\mathfrak {f}= \hat{\mathbf{p}}^\mathfrak {f}_{eq} + \hat{\mathbf{p}}^\mathfrak {f}_{neq}, \end{aligned}$$
(60)

with

$$\begin{aligned} \hat{\mathbf{p}}^\mathfrak {f}_\mathrm {eq}= & {} p \, \mathop {\mathrm {grad}}\nolimits \phi , \end{aligned}$$
(61)
$$\begin{aligned} \hat{\mathbf{p}}^\mathfrak {f}_\mathrm {neq}= & {} - \frac{\phi ^2_0\,\gamma ^{\mathfrak {f}R}_0}{k^{\mathfrak {f}}}\,\mathbf{w}_\mathfrak {f}, \end{aligned}$$
(62)

where we introduced the effective weight of the fluid \(\gamma ^{\mathfrak {f}R}_0\) and the hydraulic conductivity (Darcy permeability) \(k^\mathfrak {f}\). In general, Eq. (61) takes into account the static contribution of porosity gradients to the equilibrium, cf. details in Ehlers (2002). The product \((p \, \mathop {\mathrm {grad}}\nolimits \phi )\) is, however, nonlinear and thus disappears in linear poro-elasticity. Equation (62) represents the viscous drag forces, i.e., viscous momentum exchange caused by fluid flow through the porous skeleton. These constitutive relations close the problem, by now allowing formulation of a set of coupled partial differential equations (PDEs).

6 Governing Set of PDEs of Linear Poro-Elasticity

The set of governing PDEs consists of the (quasi-static form) of the balance of momentum of the mixture (28) and the balance of momentum of the fluid (25) combined with the (linearized) form of the balance of mass in the form of (15). To derive the final set of equations, we start from the partial balance of momentum of the fluid. Insertion of the constitutive relation for the interaction term (61) into \(-\mathop {\mathrm {div}}\nolimits \varvec{\sigma }^\mathfrak {f}= \hat{\mathbf{p}}^\mathfrak {f}\) yields

$$\begin{aligned} \mathop {\mathrm {div}}\nolimits (\phi \,p\,\mathbf{I})= & {} p \, \mathop {\mathrm {grad}}\nolimits \phi - \frac{\phi ^2_0\,\gamma ^{\mathfrak {f}R}_0}{k^{\mathfrak {f}}}\,\mathbf{w}_\mathfrak {f}\,\Leftrightarrow \end{aligned}$$
(63)
$$\begin{aligned} \mathop {\mathrm {grad}}\nolimits p= & {} - \frac{\phi _0\,\gamma ^{\mathfrak {f}R}_0}{k^{\mathfrak {f}}}\,\mathbf{w}_\mathfrak {f}+ \rho ^{\alpha R}\, \mathbf{b}. \end{aligned}$$
(64)

Taking the divergence of (64) (body forces \(\mathbf{b}\) will cancel out) and replacing the seepage velocity \(\mathbf{w}_\mathfrak {f}\) by the rate of fluid increment \(\dot{\zeta }\) lead to

$$\begin{aligned} \dot{\zeta } = \frac{k^\mathfrak {f}}{\gamma ^{\mathfrak {f}R}_0}\,\mathop {\mathrm {div}}\nolimits \mathop {\mathrm {grad}}\nolimits p. \end{aligned}$$
(65)

Replacing the volumetric strain of the fluid in the linearized balance of mass for the fluid (15) by \(\dot{e}_\mathfrak {f}= \dot{e}_\mathfrak {s}- \dot{\zeta }/ \phi _0\) gives the following balance of four rate terms:

$$\begin{aligned} \frac{\dot{\rho }^{\mathfrak {f}R}}{\rho ^{\mathfrak {f}R}_0} + \frac{\dot{\phi }}{\phi _0} + \dot{e}_\mathfrak {s}- \frac{\dot{\zeta }}{\phi _0} = 0 . \end{aligned}$$
(66)

We specify the rate terms as functions of the two variables fluid pressure p and volumetric deformation of the solid \(e_\mathfrak {s}\). The first term corresponds to the rate formulation of the constitutive equation for the barotropic fluid (29):

$$\begin{aligned} \frac{\dot{\rho }^{\mathfrak {f}R}}{\rho ^{\mathfrak {f}R}_0} = \frac{\dot{p}}{K^\mathfrak {f}}. \end{aligned}$$
(67)

The second term represents a rate form of the porosity relation (53):

$$\begin{aligned} \frac{\dot{\phi }}{\phi _0} = \frac{\alpha \,M - K^\mathfrak {f}}{K^\mathfrak {f}}\,\dot{e}_\mathfrak {s}+ \frac{K - \phi _0\,M}{\phi _0\,K^\mathfrak {f}}\,\dot{\zeta }. \end{aligned}$$
(68)

The fourth can be evaluated with the help of (65). Insertion of these rate terms into (66) leads to the governing set of PDEs formulated in the solid displacements \(\mathbf{u}_\mathfrak {s}\) and the pore pressure p (and their spatial and temporal derivatives)

$$\begin{aligned} -\mathop {\mathrm {div}}\nolimits \, \varvec{\sigma }= & {} \rho \,\mathbf{b}, \end{aligned}$$
(69)
$$\begin{aligned} \frac{\dot{p}}{M}-\frac{k^\mathfrak {f}}{\gamma ^{\mathfrak {f}R}_0} \mathop {\mathrm {div}}\nolimits \,\mathop {\mathrm {grad}}\nolimits \, p= & {} - \alpha \,\dot{e}_\mathfrak {s}. \end{aligned}$$
(70)

Equation (69) contains the total stress \(\varvec{\sigma }\) for which the split into the partial stresses of the phases and their volumetric and deviatoric contributions were introduced in (21) and (22). According to the effective stress principle (compare the volumetric form in (58) and note that the deviatoric part of the total stress tensor is only a function of \(\varvec{\gamma }_\mathfrak {s}\) (35)), equation (69) is a vectorial PDE in the two variables \((p,\,\mathbf{u}_\mathfrak {s})\). The second scalar PDE (70) also depends on \((p,\,\mathbf{u}_\mathfrak {s})\); its coupling to (69) is given by the “source” term \(\alpha \,e_\mathfrak {s}\) which depends on the rate of volumetric solid deformation. The left side of (70) is a pressure diffusion equation.

The PDEs in the domain are supplemented by Dirichlet boundary conditions for the solid displacement, \(\bar{\mathbf{u}}_\mathfrak {s}\), the pressure, \(\bar{p}\), Neumann boundary conditions for the fluxes of the total stresses, \(\bar{\mathbf{t}}\), and the fluid, \(\bar{w}_\mathfrak {f}\),

$$\begin{aligned} \mathbf{u}_\mathfrak {s}= \bar{\mathbf{u}}_\mathfrak {s}\quad \text {on} \quad \varGamma _D^\mathfrak {s}&\qquad \text {and} \qquad&p = \bar{p} \quad \text {on} \quad \varGamma _D^\mathfrak {f}, \end{aligned}$$
(71)
$$\begin{aligned} \varvec{\sigma }\cdot \mathbf{n}= \bar{\mathbf{t}} \quad \text {on} \quad \varGamma _N^\mathfrak {s}&\qquad \text {and} \qquad&\mathbf{w}_\mathfrak {f}\cdot \mathbf{n}= \bar{w}_\mathfrak {f}\quad \text {on} \quad \varGamma _N^\mathfrak {f}. \end{aligned}$$
(72)

Special (even decoupled) forms of PDEs can be derived for specific boundary value problems. One example is the classical one-dimensional consolidation problem which leads to a “standard” diffusion equation extensively discussed (including an analytical solution) in the textbook of Verruijt (2010). The set of governing PDEs for linear poro-elasticity can be reduced to specific cases assuming a priori incompressible constituents expressed by constraints for the effective densities \(\rho ^{\mathfrak {s}R} = \rho ^{\mathfrak {s}R}_0\) and/or \(\rho ^{\mathfrak {f}R} = \rho ^{\mathfrak {f}R}_0\). When, for example, both constituents are assumed to be incompressible, (69) and (70) reduce to Terzaghi’s (1923, 1943) set of equations. For a detailed review of these reduced models, we refer to the discussion in Renner and Steeb (2015).

The set of PDEs (69) and (70) can be formulated in a weak form as the basis for subsequent finite element investigations. Primary variables in such a setting are, again, solid displacements and pore pressure. This displacement–pressure formulation allows for the formulation of physically sound boundary conditions which can be also controlled in related physical experiments. Mathematically, alternative sets of PDEs can be formulated, e.g., in the displacement and the increment of fluid content, but formulation of boundary conditions becomes cumbersome.

Analytical solutions of the set of PDEs are known for special cases. Here, we would like to mention the classical solutions of Cryer (1963) and Mandel (1953) or the one-dimensional consolidation problem (Verruijt 2010; Cheng 2016). General boundary value problems, however, require numerical solution techniques which are not topic of this discussion.

7 Summary and Outlook

Often, the term “poro-elasticity” is simply considered a set of constitutive equations containing a number of “familiar” parameters. Yet, the basic conservation laws for mass and momentum take on specific forms for poro-elastic media resulting in a set of coupled partial differential equations (PDEs) that govern their isothermal deformation. A variety of constitutive relations have been presented in the past, and it is all too easy to lose sight of the number of required independent state variables. Thermodynamic consistency demands an equal number of kinematic and dynamic state variables for a linear theory. Assuming perfect decoupling of shear and volumetric deformations, the number of volumetric strain-related dynamic variables is restricted to two, e.g., mean stress and fluid pressure. Also, the “zoo” of constitutive parameters may be rather confusing for the “newcomer”. Full description of an isotropic poro-elastic medium requires a maximum of three independent parameters for volumetric stress–strain relations (e.g., three bulk moduli) and one for shear-related deformations. All other parameters, handy in specific situations, follow from conversion relations. The number of volumetric strain-related parameters reduces to two (bulk modulus of the solid material and the skeleton it forms) when porosity is chosen as a kinematic state variable. In this respect, porosity is “peculiar”, but otherwise it is just one choice of state variable and its evolution law follows from mass balance constraining the relation to alternative kinematic state variables. One is mistaken to think that porosity is constant in linear poro-elasticity because only the “fixed” initial porosity \(\phi _0\) appears in the resulting set of PDEs. Porosity is a “hidden”-dependent field variable normally not used to formulate boundary value problems whose evolution, however, can always be calculated a posteriori. Porosity evolution is governed by the difference between mean stress and fluid pressure, i.e., an effective stress coefficient of 1 holds.

Even for the apparently “oversimplifying” case of linear poro-elasticity, analytical solution of the governing differential equations can be obtained only in few cases. Numerical solution techniques are required for most investigations. The finite element method is for sure a powerful and widely available solution tool, e.g., Zienkiewicz et al. (1999). Today, even some commercial finite element solvers allow a numerical treatment of poro-elastic boundary value problems.

Classical poro-elasticity disregards various phenomena observed during the deformation of porous media. For example, dilatancy effects, i.e., a volumetric strain occurring during pure deviatoric deformation commonly addressed as simple shear, are not taken into account. While widely accepted this process might not be fully inelastic and thus beyond the realm of an elastic theory for instance in (porous) granular media and in thus particularly in various types of soils. Especially, granular aggregates potentially require extended constitutive modeling that addresses various sources of nonlinear elastic behavior, resulting, for example, from contact problems on grain scale, cf. Brandt (1955), Digby (1981) or Walton (1987). Regarding extensions of poro-elasticity toward inelastic and nonlinear effects, we refer to the thermodynamical framework including the modification of the constitutive behavior of the solid constituent as presented, e.g., by Coussy (2010) and Ehlers (2002).

In a wide range of applications, inertia effects play a dominant role and have to be taken into account in poro-elasticity. Investigating ultrasound propagating through human cancellous bones (trabecular solid skeleton saturated with bone marrow) is an established noninvasive medical technique for the diagnosis of osteoporosis. The theory of sound wave propagation for (linear) poro-elastic media was already investigated more than 60 years ago by Biot (1956a, b); a fundamental result of Biot’s equations for acoustic waves is a second compressional wave (in our days often denoted as the Biot wave to honor his contribution). Further, in contrast to classical waves in elastic media, (both) compressional waves are highly dispersive with distinct frequency-dependent effects due to the momentum exchange between the solid and fluid.

Last and definitely not least, heterogeneities play an important role in various applications in geomechanics and/or geophysics and related fields. Heterogeneities can be observed nearly on every length scale of rocks and soils (from sub-pore (\(l < 10 \,\upmu \text {m}\) ) to the field or reservoir scale (\(l > 1 \,\text {km}\)). Heterogeneities are due to fractures or faults but also to sedimentary structures. Mechanical loading of such porous media causes wave-induced fluid flow sometimes also denoted as “squirt flow”, i.e., local morphology-dependent pressure diffusion that in principle can be captured even within linear poro-elasticity if heterogeneities are fully resolved, e.g., in a finite element model, cf. Vinci et al. (2014) or Quintal et al. (2011). The list of problems which have not been discussed here is “endless”, and we do not claim to give here a comprehensive overview of current problems related to poro-elasticity. Readers who are interested in state-of-the-art models and applications in the field of poro-elasticity can find numerous articles in this “topic-oriented” journal or in the multitude of journals in the various application fields.