1 Introduction

The Wooding problem [which was named as such by Pieters and Schuttelaars (2008)] may be described as one of the classical thermoconvective instability problems in fluid mechanics, one which is of Rayleigh–Bénard type, a thermoconvective instability. Wooding noted how the upward ground water movement which had been observed in Wairakei, New Zealand, when combined with surface cooling and evaporation, produces conditions whereby relatively dense fluid lies above relatively light fluid, and hence this provides the potential for thermoconvective instability to occur (Wooding 1960). The idealised problem shares some features with the Darcy–Bénard problem, but the two chief differences are the background vertical fluid motion and the fact that the porous region is of semi-infinite extent, rather than being of finite extent. The background fluid motion causes a thermal boundary layer to form naturally, and it is this which is potentially unstable. The semi-infinite nature of the domain means that convective motions may be found well outside of the thermal boundary layer.

Sutton (1970) considered the effect of a weak throughflow on the Darcy–Bénard problem in a finite box, and she provided numerical and series solutions for the variation of the critical Darcy–Rayleigh number with the aspect ratio of the box. In a significant paper, Homsy and Sherwood (1976) extended Sutton’s work numerically to a wide range of throughflow Péclet numbers and also provided the first energy stability analysis for this type of flow. They found that the linear and energy analyses gave the same critical value of \(\mathrm{Ra}\), the Darcy–Rayleigh number, only when there is no throughflow; otherwise, the value of \(\mathrm{Ra}_\mathrm{c}\) for the energy analysis is below that for a linear analysis, implying that subcritical convection arises due to the presence of throughflow. Pieters and Schuttelaars (2008) presented a very detailed account of nonlinear flow for Sutton’s configuration for a range of Péclet numbers. Using a projection method, detailed bifurcation diagrams are created to determine the possible range of flows. They also derive a weakly nonlinear theory, and their Fig. 2 suggests that the transition from supercritical onset to subcritical onset takes place when the Péclet number is roughly 4.1. An alternative weakly nonlinear theory may be found in Riahi (1989) where the heated surface is assumed to have an almost perfectly constant heat flux boundary condition. This mathematical device allowed the author to develop a three-dimensional analysis, and he was able to determine that both up-hexagons and square planforms are possible convection patterns.

Many other papers have appeared on this general topic, but these have provided information on how other effects affect the onset criteria, rather than being devoted to furthering the essential pure Wooding and Sutton problems beyond what has been presented above. Such papers include the following. Different boundary conditions were considered by Nield (1986). Shivakumara (1999) added the Brinkman and the advective inertia terms to Darcy’s law, while Khalili and Shivakumara (2003) also included the Forchheimer terms. Khalili and Shivakumara (1998), Yoon et al. (1998) and Deepika et al. (2017) considered internal heat generation within the layer, while Nield and Kuznetsov (2013, 2015) allowed layering. Shivakumara and Khalili (2001) considered double diffusion, i.e. two diffusing components, while Shivakumara and Sureshkumar (2007, 2008), Barletta and Storesletten (2016) and Rees (2018) analysed some non-Newtonian fluids. Hill (2007) has used an energy stability analysis to determine the effect of cubic Forchheimer terms on convection, while Hill et al. (2007) considered the effect of the water density maximum at \(4^\circ \)C. Rees (2009) considered a forced convection boundary layer flow in the presence of surface suction, and even in this case it is possible to obtain subcritical vortex convection given a sufficiently large upstream disturbance. Local thermal nonequilibrium effects were found by Patil and Rees (2013) to cause double minima in the neutral curve under some circumstances. Anisotropic effects were considered by Rees and Storesletten (2002). Solute immobilisation effects, such as one would find in mineral trapping for CO\(_2\) sequestration, have been considered by Maryshev and Lyubimova (2016). Ferroconvection was studied by Nanjundappa et al. (2015).

The present paper is concerned with the effects of inclination on the Wooding problem, and attention is confined to transverse rolls. This type of variation is not without its precedents, for Rees and Bassom (2000), Rees and Postelnicu (2001), Rees and Storesletten (2002) Rees and Barletta (2011) and Barletta and Storesletten (2011) all consider variants on the inclined Darcy–Bénard problem. Unlike the corresponding clear-fluid analogues, convection in the form of transverse rolls appears only within a certain range of inclinations about the horizontal. Indeed, Gill (1969), Lewis et al. (1995) and Straughan (1998), using different methods, have all shown that all disturbances decay when the layer is vertical. More specifically, it appears to be a general property of inclined porous layers that convection is extinguished once a critical inclination is reached [although this may not be true for hydrostatic pressure boundary conditions: see Barletta (2015)]. The overall aim for the present paper is to compare the stability properties of a semi-infinite system with those for finite-depth layers. Specifically we shall present the neutral curves, determine the variation of the critical values with inclination and find the isola point at which all convection ceases.

2 Governing Equations and Basic State

We are considering the stability of the convective flow which is induced by the presence of an inclined heated plate with uniform surface suction and which is embedded within a homogeneous isotropic porous medium. The full three-dimensional governing equations are given by the equation of continuity, Darcy’s law as modified by buoyancy forces subject to the Boussinesq approximation, and the equation of heat transport. When in dimensional form these respective equations are,

$$\begin{aligned}&\displaystyle {\displaystyle \frac{\partial {\overline{u}}}{\partial {\overline{x}}}} + {\displaystyle \frac{\partial {\overline{v}}}{\partial {\overline{y}}}} + {\displaystyle \frac{\partial {\overline{w}}}{\partial {\overline{z}}}} = 0, \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle {\overline{u}}= - {\displaystyle \frac{K}{\mu }} {\displaystyle \frac{\partial {\overline{p}}}{\partial {\overline{z}}}} + {\displaystyle \frac{\rho _\mathrm{f} \hat{g} \beta K}{\mu }}\left( T - T_\mathrm{c} \right) \sin \alpha . \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle {\overline{v}}= - {\displaystyle \frac{K}{\mu }} {\displaystyle \frac{\partial {\overline{p}}}{\partial {\overline{y}}}}, \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle {\overline{w}}= - {\displaystyle \frac{K}{\mu }} {\displaystyle \frac{\partial {\overline{p}}}{\partial {\overline{z}}}} + {\displaystyle \frac{\rho _\mathrm{f} \hat{g} \beta K}{\mu }}\left( T - T_\mathrm{c} \right) \cos \alpha , \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \sigma {\displaystyle \frac{\partial T}{\partial {\overline{t}}}} + {\overline{u}}{\displaystyle \frac{\partial T}{\partial {\overline{x}}}} + v{\displaystyle \frac{\partial T}{\partial {\overline{y}}}}+w{\displaystyle \frac{\partial T}{\partial {\overline{z}}}} = \kappa \left( {\displaystyle \frac{\partial ^2 T}{\partial {{\overline{x}}}^2}} + {\displaystyle \frac{\partial ^2 T}{\partial {{\overline{y}}}^2}} + {\displaystyle \frac{\partial ^2 T}{\partial {{\overline{z}}}^2}}\right) . \end{aligned}$$
(5)

Although all the terms introduced above take their common meanings for this type of context and are listed in the Nomenclature, we note specifically that the heated surface is aligned at an angle, \(\alpha \), to the horizontal, that the \({\overline{x}}\) and \({\overline{z}}\) axes are aligned parallel with and perpendicular to the heated surface, respectively, and that the \({\overline{y}}\) axis is horizontal. The value, \(\sigma \), is the ratio of the heat capacity of the saturated medium to that of the fluid:

$$\begin{aligned} \sigma = {\displaystyle \frac{(1 - \phi )(\rho c)_\mathrm{s} + \phi (\rho c)_\mathrm{f}}{(\rho c)_\mathrm{f}}}, \end{aligned}$$
(6)

where \(\phi \) is the porosity. The boundary conditions are that,

$$\begin{aligned} {\overline{z}}=0:\quad w=-W, \quad T=T_\mathrm{h}, \qquad {\overline{z}}\rightarrow \infty : \quad T\rightarrow T_\mathrm{c}. \end{aligned}$$
(7)

In the above, we need to have \(W>0\) so that the heated surface is a suction surface.

The nondimensionalisation of Eqs. (1) to (5) is achieved using the following substitutions,

$$\begin{aligned} (x,y,z)= & {} {\displaystyle \frac{({\overline{x}},{\overline{y}},{\overline{z}})}{L}}, \qquad (u,v,w) = {\displaystyle \frac{({\overline{u}},{\overline{v}},{\overline{w}})}{W}}, \end{aligned}$$
(8)
$$\begin{aligned} p= & {} {\displaystyle \frac{K}{\kappa \mu }}{\overline{p}}, \qquad \theta = {\displaystyle \frac{T - T_\mathrm{c}}{T_\mathrm{h} - T_\mathrm{c}}}, \qquad t = {\displaystyle \frac{\kappa }{L^2\sigma }} {\overline{t}}, \end{aligned}$$
(9)

where

$$\begin{aligned} L=\kappa /W \end{aligned}$$
(10)

is a lengthscale based upon the thermal diffusivity and the suction velocity; this value is also equivalent to the width of the resulting thermal boundary layer, and therefore it forms a natural lengthscale. Hence, we obtain the non-dimensional equations,

$$\begin{aligned}&\displaystyle {\displaystyle \frac{\partial u}{\partial x}} + {\displaystyle \frac{\partial v}{\partial y}} + {\displaystyle \frac{\partial w}{\partial z}} = 0, \end{aligned}$$
(11)
$$\begin{aligned}&\displaystyle ( u, v, w ) = -\Bigl ({\displaystyle \frac{\partial p}{\partial x}},{\displaystyle \frac{\partial p}{\partial y}},{\displaystyle \frac{\partial p}{\partial z}}\Bigr ) + \mathrm{Ra}\,\theta \Bigl (\sin \alpha , 0, \cos \alpha \Bigr ) , \end{aligned}$$
(12)
$$\begin{aligned}&\displaystyle {\displaystyle \frac{\partial \theta }{\partial t}} + u{\displaystyle \frac{\partial \theta }{\partial x}}+v{\displaystyle \frac{\partial \theta }{\partial y}}+w{\displaystyle \frac{\partial \theta }{\partial z}} ={\displaystyle \frac{\partial ^2 \theta }{\partial {x}^2}}+{\displaystyle \frac{\partial ^2 \theta }{\partial {y}^2}}+{\displaystyle \frac{\partial ^2 \theta }{\partial {z}^2}}. \end{aligned}$$
(13)

The quantity,

$$\begin{aligned} \mathrm{Ra}= {\displaystyle \frac{\rho _\mathrm{f} \hat{g} \beta ( T_\mathrm{h} - T_\mathrm{c} ) K L}{\mu \kappa }}, \end{aligned}$$
(14)

is the Darcy–Rayleigh number, where L is given by (10). The boundary conditions now become,

$$\begin{aligned} { z=0:\quad w=-1, \quad \theta =1, \quad \qquad {\overline{z}}\rightarrow \infty : \quad \theta \rightarrow 0. } \end{aligned}$$
(15)

The basic state which we will analyse for stability is obtained by first assuming that the flow is steady and dependent only upon z. Therefore, we obtain,

$$\begin{aligned} { u=\mathrm{Ra}\, \sin \alpha \, e^{-z}, \qquad v=0, \qquad w=-1, \qquad p=\mathrm{constant},\qquad \theta =e^{-z}. } \end{aligned}$$
(16)

This paper will be devoted to a two-dimensional linear stability analysis where disturbances take the form of transverse rolls, and this may be analysed by the introduction of a suitable streamfunction. Therefore, we set,

$$\begin{aligned} {u=-{\displaystyle \frac{\partial \psi }{\partial z}}, \qquad v=0, \qquad w={\displaystyle \frac{\partial \psi }{\partial x}}, } \end{aligned}$$
(17)

and so Eqs. (11) to (13) reduce to the forms,

$$\begin{aligned}&{\displaystyle \frac{\partial ^2 \psi }{\partial {x}^2}} +{\displaystyle \frac{\partial ^2 \psi }{\partial {z}^2}} = \mathrm{Ra}\, \Bigl [ {\displaystyle \frac{\partial \theta }{\partial x}}\cos \alpha - {\displaystyle \frac{\partial \theta }{\partial z}}\sin \alpha \Bigr ], \end{aligned}$$
(18)
$$\begin{aligned}&{\displaystyle \frac{\partial \theta }{\partial t}} = {\displaystyle \frac{\partial ^2 \theta }{\partial {x}^2}}+{\displaystyle \frac{\partial ^2 \theta }{\partial {z}^2}}\, + \, {\displaystyle \frac{\partial \psi }{\partial z}}{\displaystyle \frac{\partial \theta }{\partial x}}-{\displaystyle \frac{\partial \psi }{\partial x}}{\displaystyle \frac{\partial \theta }{\partial z}}. \end{aligned}$$
(19)

Within this formulation, the basic state is given by,

$$\begin{aligned} \psi =-x+\Bigl (e^{-z}-1\Bigr )\mathrm{Ra}\,\sin \alpha , \quad \theta =e^{-z}. \end{aligned}$$
(20)

We note that the constant term in the expression for \(\psi \) has been chosen to be such that \(\psi =0\) on \(z=0\), but it could take any constant value. We note also that the basic temperature field has an O(1) thickness which is independent of the angle of inclination of the heated surface. On the other hand, the magnitude of the induced flow field, which is parallel to the heated surface, depends strongly on \(\alpha \). Its strength is maximised when the surface is vertical, and no flow is induced (apart from the suction velocity) when it is horizontal.

3 Linear Stability Analysis

We now proceed to describe the linear stability of the basic state to two-dimensional disturbances. To that end we shall substitute,

$$\begin{aligned} \ \psi = -x + \Bigl (e^{-z}-1\Bigr )\mathrm{Ra}\,\sin \alpha +\Psi (x,z,t), \qquad \theta =e^{-z}+\Theta (x,z,t), \end{aligned}$$
(21)

into Eqs. (18) and (19). The disturbance quantities, \(\Psi \) and \(\Theta \), are assumed to have asymptotically small amplitudes, and therefore products of the disturbances are neglected. The resulting linearised stability equations are now,

$$\begin{aligned}&{\displaystyle \frac{\partial ^2 \Psi }{\partial {x}^2}} +{\displaystyle \frac{\partial ^2 \Psi }{\partial {z}^2}} = \mathrm{Ra}\, \Bigl [ {\displaystyle \frac{\partial \Theta }{\partial x}}\cos \alpha - {\displaystyle \frac{\partial \Theta }{\partial z}}\sin \alpha \Bigr ], \end{aligned}$$
(22)
$$\begin{aligned}&{\displaystyle \frac{\partial \Theta }{\partial t}} = {\displaystyle \frac{\partial ^2 \Theta }{\partial {x}^2}}+{\displaystyle \frac{\partial ^2 \Theta }{\partial {z}^2}} + {\displaystyle \frac{\partial \Theta }{\partial z}} + e^{-z}{\displaystyle \frac{\partial \Psi }{\partial x}} - (\mathrm{Ra}\,\sin \alpha )e^{-z}{\displaystyle \frac{\partial \Theta }{\partial x}}, \end{aligned}$$
(23)

where the boundary conditions are that both \(\Psi \) and \(\Theta \) are zero on the heated surface and tend to zero far from the surface. These equations may now be split into independent monochromatic modes in the x-direction by setting,

$$\begin{aligned} \Psi (x,z,t) = i\, f(z)e^{ikx+\lambda t} + \hbox {c.c.}, \qquad \Theta (x,z,t) = g(z)e^{ikx+\lambda t} + \hbox {c.c.}, \end{aligned}$$
(24)

where k is a wavenumber and \(\lambda =\lambda _r + i\lambda _i\) is the complex exponential growth rate for disturbances. The complex equations for f and g take the forms,

$$\begin{aligned}&f'' - k^2f = \mathrm{Ra}\Bigl [ (k \cos \alpha )g +(i\sin \alpha )g'\Bigr ], \end{aligned}$$
(25)
$$\begin{aligned}&g'' + g' - k^2g = k e^{-z} f + i k \mathrm{Ra}\sin \alpha \, e^{-z} g + \lambda g, \end{aligned}$$
(26)

and the boundary conditions are

$$\begin{aligned} z=0:\quad f=g=0, \qquad \quad z\rightarrow \infty : \quad f,g\rightarrow 0. \end{aligned}$$
(27)

4 Numerical Method

4.1 General Observations

Equations (25)–(27) may be regarded either as (i) an ordinary differential eigenvalue problem for the complex growth rate, \(\lambda \), as a function of \(\mathrm{Ra}\), k and \(\alpha \), or else (ii) as an ordinary differential eigenvalue problem for the Rayleigh number and \(\lambda _i\) as a function of k and \(\alpha \) by setting \(\lambda _r=0\) to marginally stabile conditions. The former point of view lends itself naturally to the solution procedure that was adopted by Rees and Bassom (2000) whereby all derivatives are approximated using second-order accurate finite differences, and the resulting ordinary differential eigenvalue problem is thereby reduced to that of a matrix eigenvalue problem. Then values of \(\lambda \) are computed on a fine grid of values of \(\mathrm{Ra}\) and k, and the neutral curves are obtained by contouring where \(\lambda _r=0\). This has the advantage that all neutral curves, including any isolated loops, are obtained. When taking the latter point of view, the equations may be solved by more conventional methods, such as a Runge–Kutta scheme and a shooting methodology in order to find \(\mathrm{Ra}\) in terms of the other parameters.

It was found that the general properties of these equations made it substantially more difficult to obtain accurate solutions than for the inclined Darcy–Bénard layer which was considered in Rees and Bassom (2000). There are a variety of reasons for this. Concentrating first on the matrix eigenvalue methodology, the fact that the domain is semi-infinite (as opposed to being of uniform thickness, as in Rees and Bassom 2000) means that a substantially larger number of grid points needs to be employed, and this leads to a very much slower computation. In addition, when k is large, then disturbances tend to occupy relatively narrow regions when compared with the basic state, and therefore the resolution of these regions becomes difficult. When k is small, then the decay rate for the streamfunction as z increases is rather small because the asymptotic profile for f may be shown to be proportional to \(e^{-kz}\). This combination of difficulties led us to take the more conventional Runge–Kutta/shooting-method route.

In a sense, the same difficulties exist when using the fourth-order Runge–Kutta method, except that solutions were obtained very much more quickly. The slowly decaying behaviour of f when k is small was modelled by replacing the \(f\rightarrow 0\) as \(z\rightarrow \infty \) boundary condition with the Robin condition,

$$\begin{aligned} f'+kf= 0 \quad \hbox {at} \quad z=z_\mathrm{max}. \end{aligned}$$
(28)

The presence of the \(g'\) term in Eq. (26) means that the e-folding distance for the temperature disturbances is of the order of unity, and therefore the value, \(z_\mathrm{max}=10\), for example, means that g has often decayed to below \(10^{-4}\) in magnitude. Therefore, the boundary condition in (28) accounts perfectly for the asymptotic exponential decay behaviour of f even when k is extremely small.

When k takes large values, the resolution of the narrow near-surface regions is not merely a matter of taking a sufficiently large number of intervals. However, the numerical problem now becomes stiff, and therefore our chosen method for overcoming this last difficulty was to adopt the variant known as multiple shooting. In the standard shooting method, Eqs. (25) and (26) form a \(4\mathrm{th}\)-order complex system, or equivalently, an \(8\mathrm{th}\)-order real system. The addition of two extra equations, \(\mathrm{Ra}'=0\) and \(\lambda _i'=0\), renders us with a \(10\mathrm{th}\)-order system overall. The adoption of the multiple-shooting technique was generally undertaken with five subregions being solved simultaneously, and with appropriate interface conditions being imposed—details are given below. This yields a system of \(42\mathrm{nd}\)-order with 37 unknown initial conditions, but despite its size it was found to yield accurate solutions quite quickly. Of course, even this complexity only delays to larger values of k the recurrence of the problem of stiffness, but we found that 5 subregions were sufficient for almost all our needs, and some computations with 10 subregions were undertaken to check that the methodology had been applied correctly.

4.2 Numerical Methodology

Our chosen basic method is the shooting method where the solver is the classical fourth-order Runge–Kutta method. Given the above discussion, no consistent value of \(z_\mathrm{max}\) was used, but this depended to some extent on which part of parameter space (\(\mathrm{Ra}\), k and \(\alpha \)) was being occupied, but at the earliest stages tests were conducted to assess how large the computational domain should be and how many grid points were to be employed. Generally \(z_\mathrm{max}\) was either 8 or 10, and further increases produced insignificant changes in the solution. With regard to the steplengths, our solutions are correct to five significant figures or better.

Neutral curves, which correspond to nonzero solutions to Eqs. (25) and (26), are found by setting \(\lambda _r=0\). These are found not always to be single-valued functions of the wavenumber, but can exhibit vertical tangents and therefore we have adopted a curve-following (or pseudo-arc-length) strategy to trace out the curves. At its most straightforward this means that we need to solve an 11th-order system of equations, as follows.

$$\begin{aligned} \hbox {Let~} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \\ v_7 \\ v_8 \\ v_9 \\ v_{10} \\ v_{11} \end{pmatrix}= & {} \begin{pmatrix} f_r \\ f_r' \\ f_i \\ f_i' \\ g_r \\ g_r' \\ g_i \\ g_i' \\ \mathrm{Ra}\\ \lambda _i \\ k \end{pmatrix} \qquad \Rightarrow \qquad \begin{pmatrix} v'_1 \\ v'_2 \\ v'_3 \\ v'_4 \\ v'_5 \\ v'_6 \\ v'_7 \\ v'_8 \\ v'_9 \\ v'_{10} \\ v'_{11} \end{pmatrix}\nonumber \\= & {} \begin{pmatrix} v_2 \\ k^2v_1+\mathrm{Ra}[(k \cos \alpha )v_3 - (\sin \alpha )v_8] \\ v_4 \\ k^2v_3 - v_4 + ke^{-z}v_1 - (k\mathrm{Ra}\sin \alpha )e^{-z} v_7 - v_{10}v_7 \\ v_6 \\ k^2v_5+\mathrm{Ra}[(k \cos \alpha )v_7 + (\sin \alpha )v_4] \\ v_8 \\ k^2v_7 - v_8 + ke^{-z}v_5 + (k\mathrm{Ra}\sin \alpha )e^{-z} v_3 + v_{10}v_3 \\ 0 \\ 0 \\ 0 \end{pmatrix} \end{aligned}$$
(29)

where \(\mathrm{Ra}\) and k will be replaced by \(v_9\) and \(v_{11}\), respectively, in the numerical codes but are retained here for clarity. The above equations were solved subject to the boundary conditions,

$$\begin{aligned} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \\ v_7 \\ v_8 \\ v_9 \\ v_{10} \\ v_{11} \end{pmatrix} = \begin{pmatrix} 0 \\ \blacksquare \\ 0 \\ 1 \\ 0 \\ \blacksquare \\ 0 \\ 0 \\ \blacksquare \\ \blacksquare \\ \blacksquare \end{pmatrix} ~~\hbox { at }z=0~~~~~~\hbox {and}~~~~~~ \begin{pmatrix} v_2+kv_1 \\ v_3 \\ v_6+kv_5 \\ v_7 \\ \mathcal{S} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \hbox {~~at }z=z_\mathrm{max}. \end{aligned}$$
(30)

The entries for \(z=0\) which are marked with a black square are those which are unknown and which need to be found by insisting that the given conditions at \(z=z_\mathrm{max}\) are satisfied. The values for \(v_4\) and \(v_8\) at \(z=0\) (i.e. \(g'(0)=1\)) are the normalisation conditions to ensure nonzero solutions, while those involving k at \(z=z_\mathrm{max}\) are equivalent to Eqs. (28). Finally, the quantity, \(\mathcal{S}\), is defined as,

$$\begin{aligned} { \mathcal{S}= (k-k_\mathrm{old})^2/\delta ^2_k+(\mathrm{Ra}-\mathrm{Ra}_\mathrm{old})^2/\delta _R^2-1. } \end{aligned}$$
(31)

In this expression \(k_\mathrm{old}\) and \(\mathrm{Ra}_\mathrm{old}\) are the values of k and \(\mathrm{Ra}\) at the previously computed point on the neutral curve, and the values \(\delta _k\) and \(\delta _R\) are the largest increments in k and \(\mathrm{Ra}\) allowed when moving along the neutral curve; typical values are \(\delta _k=0.001\) and \(\delta _R=0.5\). Satisfaction of this condition allows the code to compute the neutral curve past turning points.

The most important point on a neutral stability curve is its minimum. These points may be found by solving the system, Eqs. (25) and (26), together with that system which is formed by taking its k-derivative where \(\partial \mathrm{Ra}/\partial k=0\) is set. So if we set, \(F=\partial f/\partial k\) and \(G=\partial g/\partial k\), then this extra system is given by,

$$\begin{aligned} \begin{array}{rl} F'' - k^2F &{}= \mathrm{Ra}\Bigl [ (k \cos \alpha )G +(i\sin \alpha )G'\Bigr ] \\ &{}\quad +\,2kf +i\mathrm{Ra}\sin \alpha \, g',\\ \end{array} \end{aligned}$$
(32)
$$\begin{aligned} { \begin{array}{rl} G'' + G' - k^2G &{}= k e^{-z} F + i k \mathrm{Ra}\sin \alpha e^{-z} G + \lambda G \\ &{} \quad e^{-z} f + i \mathrm{Ra}\sin \alpha e^{-z} g + \Lambda g, \\ \end{array}} \end{aligned}$$
(33)

and the boundary conditions are

$$\begin{aligned} { z=0:\quad F=G=G'=0, \qquad \quad z=z_\mathrm{max}\quad F'+kF=-f,\,\,G=0.} \end{aligned}$$
(34)

In the above \(\Lambda =\partial \lambda /dk\). When minima are sought, Eqs. (32) and (33) are also converted into first-order form and solved simultaneously with Eq. (29). When using the standard shooting method, this extended system forms one of 20\(\mathrm{th}\)-order with eight unknown initial conditions. Solution of this system yields \(\mathrm{Ra}_\mathrm{c}\), \(k_\mathrm{c}\) and the values of \(\lambda \) and \(\partial \lambda /\partial k\) as functions of \(\alpha \).

The present stability problem admits both an isola point and a saddle point and these points require that both \(\partial \mathrm{Ra}/\partial k=0\) and \(\partial \mathrm{Ra}/\partial \alpha =0\) are satisfied simultaneously at isolated points in parameter space. The appropriate system which needs to be added to both Eqs. (25) and (26) and Eqs. (32) and (33) may be obtained by differentiating Eqs. (25) and (26) with respect to \(\alpha \) and by setting \(\partial \mathrm{Ra}/\partial \alpha =0\). If we set \(\mathcal{F}=\partial f/\partial \alpha \) and \(\mathcal{G}=\partial g/\partial \alpha \), then we have,

$$\begin{aligned} \begin{array}{rl} \mathcal{F}'' - k^2\mathcal{F}&{}= \mathrm{Ra}\Bigl [ ( k \cos \alpha )\mathcal{G}+(i\sin \alpha )\mathcal{G}'\Bigr ] \\ &{}\quad +\, \mathrm{Ra}\Bigl [ (-k \sin \alpha )g +(i\cos \alpha \, g'\Bigr ],\\ \end{array} \end{aligned}$$
(35)
$$\begin{aligned} { \begin{array}{rl} \mathcal{G}'' + \mathcal{G}' - k^2\mathcal{G}&{}= k e^{-z} \mathcal{F}+ i k \mathrm{Ra}\sin \alpha e^{-z} \mathcal{G}+ \lambda \mathcal{G}\\ &{} \quad +\, ik \mathrm{Ra}\cos \alpha e^{-z} g + \mathcal{L} g, \\ \end{array}} \end{aligned}$$
(36)

subject to the boundary conditions,

$$\begin{aligned} z=0:\quad \mathcal{F}=\mathcal{G}=\mathcal{G}'=0, \qquad \quad z=z_\mathrm{max}\quad \mathcal{F}'+k\mathcal{F}=0,\,\,\mathcal{G}=0, \end{aligned}$$
(37)

where \(\mathcal{L}=\partial \lambda /\partial \alpha \).

Finally, for large values of k and for large values of \(\mathrm{Ra}\) the equations become too stiff to be able to be solved in a sufficiently large computational domain that good accuracy is preserved, and therefore we resorted to using the method of multiple shooting using five subdomains, as mentioned above. As an example of this, we could define five equal domains lying between \(z=0\) and \(z=10\) and name them subdomains 1 through to 5, where \(0\le z\le 2\) in subdomain 1. The first eight variables shown in Eq. (29) have their counterparts in all the subdomains. For ease of bookkeeping, subdomain 1 contains variables 1 to 8, subdomain 2 contains variables 9 to 16 and so on. These 40 variables, together with the three corresponding to \(\mathrm{Ra}\), k and \(\lambda _i\), which are designated variables 41 to 43, are then solved in the region \(0\le z\le 2\) simultaneously, where appropriate adjustments are made to the exponential functions, \(e^{-z}\), in domains 2 to 5. The initial conditions given in Eq. (30) now apply in subdomain 1 and the final conditions given there apply in subdomain 5. Then it is necessary to apply continuity conditions between the subdomains; if we were to consider the interface between subdomains 1 and 2, then the continuity conditions would be,

$$\begin{aligned} v_i(2)=v_{i+8}(0),\quad \hbox {for }i=1,8. \end{aligned}$$
(38)

In this case, we would have 43 equations with 38 unknown initial conditions. A similar multiple-shooting idea was used for determining the minima (and, in some cases, maxima) in the neutral curves, but without the curve-tracking idea being implemented. In this case, we have 84 equations with 72 unknown initial conditions, and when we adopted 10 subdomains, we had 164 equations with 152 unknown initial conditions.

5 Results and Discussion

5.1 Neutral Curves

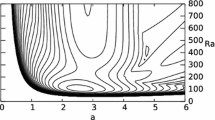
A selection of neutral curves is presented in Fig. 1 for a chosen set of values of the inclination, \(\alpha \). When \(\alpha =0\) we reproduce the Wooding problem which has been studied extensively by authors such as van Duijn et al. (2002) and Pieters and Schuttelaars (2008). When the heated surface is horizontal (\(\alpha =0\)) The minimum of the neutral curve corresponds to

$$\begin{aligned} { \mathrm{Ra}_\mathrm{c}=14.35219, \qquad \qquad k_\mathrm{c}=0.75887; } \end{aligned}$$
(39)

which upgrades slightly the data given in Rees (2009).

Fig. 1
figure 1

Neutral curves for different values of \(\alpha \). Black curves correspond to \(\alpha =0^\circ \), \(5^\circ \), \(10^\circ \), \(15^\circ \) and \(20^\circ \). Red curves correspond to \(\alpha =21^\circ \) to \(31^\circ \) in steps of \(1^\circ \). Continuous blue curves correspond to \(\alpha =29.2^\circ \) to \(29.8^\circ \) in steps of \(0.2^\circ \), while the dashed blue curve is \(\alpha =29.3^\circ \). The dashed green curve corresponds to \(31.5^\circ \). The black circles denote the isola and saddle points, while the black lines passing through them are the loci of extrema in the neural curves which are also labelled according to whether they form the main, left or right-hand branches

Full size image

As the inclination increases, the critical Rayleigh number increases because the vertical component of the buoyancy force diminishes. The critical wavenumber also increases and does so almost linearly at first. The narrow black line in Fig. 1 which emanates from the minimum when \(\alpha =0\) [see Eq. (39)] traces out the locus of minima (extrema, in general) of the neutral curves. Eventually this locus of minima arrives at an isola point at

$$\begin{aligned} { \mathrm{Ra}=89.2634, \qquad \qquad k=1.14247, \qquad \qquad \alpha =31.85473^\circ , } \end{aligned}$$
(40)

which marks the largest inclination at which one has incipient convective instability; it is the lower of the two black disks shown in Fig. 1. Such an isola point is a general feature of inclined thermoconvective stability problems in porous media, and Table 1 reproduces details of these points for different types of inclined layers.

Table 1 Locations of isola points for similar flows
Full size table

Here CT refers to constant temperature boundary conditions, CHF to constant heat flux and MIX to one of one type and one of the other. In addition, DB refers to a Darcy-Bénard-like heating from below, while IHG refers to internal heat generation within the layer. The very obvious closeness of the maximum inclinations shown in Table 1 appears to suggest that there might be a deep connection between these five convective instability problems. However, the study of an anisotropic version of the CT-DB problem by Rees and Postelnicu (2001) shows that \(\alpha _\mathrm{max}\) can achieve values as low as \(12^\circ \) and as high as \(47^\circ \) depending on the degree of anisotropy of the porous medium.

Table 1 also shows that there are some significant variations in the values of \(\mathrm{Ra}_\mathrm{c}\) and \(k_\mathrm{c}\) between the different problems represented. All three of those labelled, DB, are layers with unit thickness and heated from below, and therefore there isn’t a large variation in the respective values of \(\mathrm{Ra}_\mathrm{c}\) and \(k_\mathrm{c}\). The two labelled, IHG, correspond to situations where the temperature gradient is destabilising over only a lower fraction of the layer; thus \(Ra_\mathrm{c}\) must be larger and, given that cells will occupy mainly those regions where there is a negative temperature gradient, the wavenumbers will be substantially larger. For the present Wooding problem, the basic temperature field occupies a region which is larger than unity, and therefore both \(\mathrm{Ra}_\mathrm{c}\) and \(k_\mathrm{c}\) will be smaller than for the DB problems.

While a superficial glance at the general shapes of the neutral curves given here and those shown in Rees and Bassom (2000) might suggest that they are very similar, there are nevertheless some very important differences. One of these is that every neutral curve shown here (apart from when the heated surface is horizontal) corresponds to an onset mode which travels up the heated surface. This is due to the lack of symmetry in the basic state, a property which is shared with the configurations studied in Barletta and Storesletten (2011). The computed values of \(\lambda _i\) are always negative here, and therefore the speed of any convection pattern in the x-direction, which is given by \(-\lambda _i/k\) [see Eq. (24)], is always positive. On the other hand, the inclined Darcy–Bénard problem continues to exhibit stationary convection at each neutral curve minimum. Pairs of travelling modes do exist, but these bifurcate from the stationary branches at larger values of \(\mathrm{Ra}\), and therefore do not form the most unstable mode; a similar statement may be made for the CHF-DB problem studied by Rees and Barletta (2011).

The second difference is that the locus of extrema here consists of two disconnected branches, as opposed to the single branch shown in Rees and Bassom (2000). However, both configurations have a saddle point, the present one being located at

$$\begin{aligned} \mathrm{Ra}=281.9906, \qquad \qquad k=1.44005, \qquad \qquad \alpha =29.3386^\circ , \end{aligned}$$
(41)

and this is shown as the upper black disk in Fig. 1.

5.2 Variations with Inclination

Further detail which may be gleaned from Fig. 1 will be found more explicitly in Figs. 2, 3 and 4. Respectively, these Figures show the variation with inclination of the critical Darcy–Rayleigh number (\(\mathrm{Ra}_\mathrm{c}\)), wavenumber (\(k_\mathrm{c}\)), and what shall be called the relative cell velocity,

$$\begin{aligned} { \mathcal{U}=-\lambda _i/(k\mathrm{Ra}\sin \alpha ). } \end{aligned}$$
(42)

Figure 2 shows three branches and these correspond to extrema in the neutral curves in Fig. 1. The branches are labelled Main, Left and Right for ease of references. The Main branch shown in Fig. 2 is even about \(\alpha =0\) and therefore negative inclinations are not presented. For each value of \(\alpha \) on the main branch, linear instability corresponds to the region either above the main branch or, when \(\alpha \) is sufficiently large, to that region between the lower and upper sections of the main branch. The right and left branches form part of the solution structure for the linearised eigenvalue probem, but as they lie above the lower part of the main branch, they play no role for the physical problem in reality, for they correspond to large values of \(\mathrm{Ra}\). The turning point in the main branch corresponds to the isola point.

Fig. 2
figure 2

Variation with \(\alpha \) of the critical Darcy–Rayleigh number, \(\mathrm{Ra}_\mathrm{c}\), for all three branches which are shown in Fig. 1

Full size image

The variation of \(k_\mathrm{c}\) with \(\alpha \), as shown in Fig. 3, is very modest when \(\alpha \) increases from zero to the isola point (i.e. the turning point of the main branch shown here). To two decimal places this variation lies between 0.76 when the surface is horizontal and 1.14 when it is at an inclination of almost \(30^\circ \). In turn this means that the wavelength of the most unstable mode decreases by about from roughly 8.27 to 5.51; a wavelength decrease is a common qualitative feature of the effect of inclination on the onset of convection in porous media.

Fig. 3
figure 3

Variation with \(\alpha \) of the critical wavenumber, \(k_\mathrm{c}\), for all three branches which are shown in Fig. 1

Full size image
Fig. 4
figure 4

Variation with \(\alpha \) of the relative cell velocity, \(\mathcal{U}\), for all three branches which are shown in Fig. 1

Full size image

Figure 4 displays the variation with inclination of the relative speed of the cells, \(\mathcal{U}\), given in Eq. (42). The velocity of the cells up the layer has already been stated to be precisely, \(-\lambda _i/k\), but Eq. (16) shows that the maximum value of the basic velocity profile, which occurs when \(z=0\), takes the value, \(\mathrm{Ra}\sin \alpha \). Therefore, \(\mathcal{U}\) represents the velocity of the cells compared with the maximum for the basic state. It will generally be the case that the larger is \(\mathcal{U}\), the more the disturbance is confined to the near-surface region.

Although the speed of the disturbances along the layer is zero when the heated surface is horizontal, the numerical data suggest that there is a well-defined limit, as \(\alpha \rightarrow 0\), which is 0.2417. Thus, at very slight inclinations, the cells travel along the layer at roughly a quarter of the maximum velocity of the basic flow. As the inclination increases, both the wavenumber (see Fig. 3) and \(\mathcal{U}\) increase. Thus \(\mathcal{U}\) increases from 0.2417 to roughly 0.469 at the isola point. It is well-known that, for convective instability problems of boundary layer flows, the disturbance tends to be increasingly confined to the neighbourhood of the bounding surface when the wavenumber is large, and this may be traced mathematically to the e-folding distance of equations such as Eq. (25). Therefore, the disturbance tends to occupy regions where the background flow is faster, and hence the speed of the cells increases.

5.3 Disturbance Profiles

Finally, we display some disturbance profiles in Fig. 5. Four cases have been chosen, and these correspond to the respective minima in the neutral curves for \(\alpha =0^\circ \), \(20^\circ \), \(25^\circ \) and \(31.5^\circ \), the last one being very close to the isola point. Disturbance streamlines and isotherms have been created by taking the real parts of the functions given in Eq. (24). In each of the four diagrams composing Fig. 5 the height corresponds to \(z_\mathrm{max}=10\), while the horizontal width comprises precisely one period of the critical disturbance.

Fig. 5
figure 5

Streamlines (dashed) and isotherms (continuous) for the most unstable disturbances at the given angles of inclination. The height of each box is 10, but the width corresponds to one period of the disturbance in the x-direction

Full size image

As one would expect, the streamfunction and the isotherms are exactly out of phase when the inclination is zero, for then there is no basic flow in the horizontal direction. As the heated surface is inclined increasingly, the strength of the basic flow also increases and this, together with the z-variation of that basic flow, has the effect of deforming the convection cells. We also see that the isotherms are confined to a narrower region close to the heated surface than are the streamlines, as discussed earlier. Generally, it is the case that the isotherms are confined to a region which is, at most, given by what is displayed for \(\alpha =0^\circ \). When the wavenumber is large, it is possible for that region to be more restricted (such as for \(\alpha =31.5^\circ \) here) but it cannot be larger. The mathematical reason for the upper restriction on the width of the thermal disturbances is the presence of the \(g'\) term in Eq. (26), whose presence is a direct consequence of surface suction. On the other hand, for those cases where k is quite small (not depicted here for reasons of brevity), the streamfunction field expands substantially, and this is why we adopted the boundary conditions given in Eq. (28) which accounts for the correct exponential decay in the isothermal region well outside where thermal effects are significant.

6 Conclusions

In this paper, we have sought to provide a comprehensive account of the effect of inclination on the classical Wooding problem. While other authors have also considered the onset of convection in similarly inclined configurations, the chief difference here is that there is no second bounding surface, and thus the flow and instabilities take place in what is effectively a deep-pool situation. Practically, this means that very considerable care had to be taken to maintain accuracy, to avoid difficulties due to the governing equations being too stiff to use the usual shooting method, and to account for slowly decaying streamfunction disturbances. The combined modifications to our numerical method meant that overall numerical scheme was robust.

The inclined Wooding problem displays some characteristics which are common to very many other inclined convective instability problems, including a maximum inclination above which the system is linearly stable. But there are other characteristics which are not the same, such as whether the disturbances are stationary modes or travelling modes. It was also seen that the symmetry of the basic state allows one to predict which property is assumed by the system.

The authors are well aware that the Wooding problem is a classic example of one where the bifurcation to strongly convecting flow is subcritical at the critical wavenumber (see Rees 2009). By continuity, this will also be true for at least a range of inclinations near to the horizontal. It is intended that the present analysis will be extended in order to determine if this remains true for all inclinations for which instability is possible, or whether there is an inclination above which the onset of convection is supercritical. This could be undertaken using a weakly nonlinear theory, energy methods or by solving the full nonlinear equations directly. It is hoped to report on this aspect in due course.