Abstract
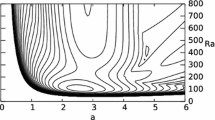
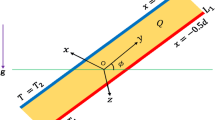
The linear stability for convection in an inclined porous layer is considered for the case where the plane bounding surfaces are subjected to constant heat flux boundary conditions. A combined analytical and numerical study is undertaken to uncover the detailed thermoconvective instability characteristics for this configuration. Neutral curves and decrement spectra are shown. It is found that there are three distinct regimes between which the critical wavenumber changes discontinuously. The first is the zero-wavenumber steady regime which is well known for horizontal layers. The disappearance of this regime is found using a small-wavenumber asymptotic analysis. The second consists of unsteady modes with a nonzero wavenumber, while the third consists of a steady mode. Linear stability corresponds to inclinations which are greater than 32.544793° from the horizontal.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bories S.A., Combarnous M.A.: Natural convection in a sloping porous layer. J. Fluid Mech. 57, 63–79 (1973)
Horton C.W., Rogers F.T.: Convection currents in a porous medium. J. Appl. Phys. 16, 367–370 (1945)
Kim M.C., Lee S.B., Kim S., Chung B.J.: Thermal instability of viscoelastic fluids in porous media. Int. J. Heat Mass Transf. 46, 5065–5072 (2003)
Kimura S., Vynnycky M., Alavyoon F.: Unicellular natural circulation in a shallow horizontal porous layer heated from below by a constant flux. J. Fluid Mech. 294, 231–257 (1995)
Lapwood E.R.: Convection of a fluid in a porous medium. Proc. Camb. Philos. Soc. 44, 508–521 (1948)
Mamou M., Mahidjiba A., Vasseur P., Robillard L.: Onset of convection in an anisotropic porous medium heated from below by a constant heat flux. Int. Commun. Heat Mass Transf. 25, 799–808 (1998)
Nield D.A.: Onset of thermohaline convection in a porous medium. Water Resour. Res. 11, 553–560 (1968)
Nield D.A., Bejan A.: Convection in Porous Media. 3rd edn. Springer-Verlag, New York (2006)
Rees D.A.S.: The stability of Darcy-Bénard convection. In: Vafai, K., Hadim, H.A. (eds) Handbook of Porous Media, Chapter 12, pp. 521–558. CRC Press, New York (2000)
Rees D.A.S., Bassom A.P.: Onset of Darcy-Bénard convection in an inclined layer heated from below. Acta Mech. 144, 103–118 (2000)
Rees, D.A.S., Mojtabi, A.: The effect of conducting boundaries on weakly nonlinear Darcy-Bénard convection. Transp. Porous Med. (2011) doi:10.1007/s11242-011-9722-0
Rees D.A.S., Postelnicu A.: The onset of convection in an inclined anisotropic porous layer. Int. J. Heat Mass Transf. 44, 4127–4138 (2001)
Rees D.A.S., Tyvand P.A.: Onset of convection in a porous layer with continuous periodic horizontal stratification. Part I. Two-dimensional convection. Transp. Porous Med. 77, 187–205 (2009)
Riahi N.: Nonlinear convection in a porous layer with finite conducting boundaries. J. Fluid Mech. 129, 153–171 (1983)
Sen M., Vasseur P., Robillard L.: Multiple steady states for unicellular natural convection in an inclined porous layer. Int. J. Heat Mass Transf. 30, 2097–2113 (1987)
Tyvand P.A.: Onset of Rayleigh-Bénard convection in porous bodies. In: Ingham, D.B., Pop, I. (eds) Transport Phenomena in Porous Media II, Chapter 4, pp. 82–112. Pergamon, New York (2002)
Vasseur P., Satish M.G., Robillard L.: Natural convection in a thin, inclined, porous layer exposed to a constant heat flux. Int. J. Heat Mass Transf. 30, 537–549 (1987)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rees, D.A.S., Barletta, A. Linear Instability of the Isoflux Darcy–Bénard Problem in an Inclined Porous Layer. Transp Porous Med 87, 665–678 (2011). https://doi.org/10.1007/s11242-010-9707-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-010-9707-4