Monte Carlo Assessment of the Impact of Oscillatory and Pulsating Boundary Conditions on the Flow Through Porous Media

Abstract

Stress and water injection induce deformations and changes in pore pressure in the soil. The interaction between the mechanical deformations and the flow of water induces a change in porosity and permeability, which results in nonlinearity. To investigate this interaction and the impact of mechanical vibrations and pressure pulses on the flow rate through the pores of a porous medium under a pressure gradient, a poroelastic model is proposed. In this paper, a Galerkin finite element method is applied for solving the quasi-static Biot’s consolidation problem for poroelasticity, considering nonlinear permeability. Space discretisation using Taylor–Hood elements is considered, and the implicit Euler scheme for time stepping is used. Furthermore, Monte Carlo simulations are performed to quantify the impact of variation in the parameters on the model output. Numerical results show that pressure pulses and soil vibrations in the direction of the flow increase the amount of water that can be injected into a deformable fluid-saturated porous medium.

1 Introduction

Worldwide, management of freshwater resources has become critical. Climate scenarios predict extreme periods of drought and rainfall. Traditionally, during periods of heavy rainfall, the approach is to transport water quickly to surface waters and the sea in order to prevent flooding. However, a new approach is emerging: storing water in wet periods for use in dry periods. In particular, the storing of water underground has large benefits. A prerequisite for effective storing of rainwater in periods of extreme precipitation is that the water can be stored quickly. A new method to quickly infiltrate high volumes of fresh water has been discovered recently. We refer to this method as fast, high-volume infiltration (FHVI).

Another field in which FHVI constitutes a significant breakthrough is in construction, where this method was originally discovered. Building sites have to be pumped dry to enable construction. In the past, extracted water was often released into surface water. However, since the potential impact on the ecology is negative, new regulations prescribe that water should be returned to the ground. Conventionally, infiltration has to be applied at a certain distance from the pit, thereby affecting groundwater levels in a relatively large area. FHVI can be much closer to the pit, as the infiltrated water is rapidly transported away from the infiltration points. This means that the effect on groundwater levels is much smaller. However, according to preliminary research and findings, this infiltration method does not obey the classical Dupuit’s law that is commonly used in hydrogeology, and it is currently impossible to predict its applicability.

In petroleum reservoirs, observations from the last 50 years suggest that seismic waves generated from earthquakes and passing trains may alter water and oil production. It has also been observed in some laboratory measurements and field applications that imposing harmonic signals into cores or reservoirs sometimes may induce higher fluid flow rates (Pan and Horne 2000). Further the fact that the pore pressure may undergo variations under the influence of seismic waves is well known to geotechnical engineers (Beresnev and Johnson 1994). In addition, laboratory experiments have shown that ultrasonic radiation can considerably increase the rate of flow of a liquid through a porous medium (Aarts and Ooms 1998). Furthermore, Davidson et al. (1999) performed experiments in a wide range of configurations, grain sizes, viscosities and flow factors, showing that high-amplitude pressure pulsing or mechanical excitation of a saturated porous medium under a pressure gradient increases the flow rate of the liquid along the direction of the flow gradient. Based on the experimental results, they concluded that flow rate enhancement occurred for all liquids, and for all the grain sizes that were tested.

Our aim is to investigate whether during FHVI, large injection rates induce an oscillatory or a pulsating force near the injection point and whether induced vibrations increase the amount of water that can be injected into the aquifer. In this publication, we tackle the second question by investigating the impact of soil vibrations and pressure pulses on the effective transmigration of water through the pores of the soil. For this purpose, a tube filled with a deformable fluid-saturated porous medium is simulated, into which water is injected. In the current paper, Biot’s consolidation model for poroelasticity (Biot 1941, 1955) is used to determine the local deformation of the porous medium as a result of the injection of water. Biot’s model is widely used in geomechanics, hydrogeology, petroleum engineering and biomechanics. Darcy’s law (Hubbert 1957) is used in Biot’s model to describe the fluid flow, while elasticity and poroelasticity of the porous medium determine the local deformations as a result of the vibrations. More precisely, we use in this paper a simplistic Hookean representation of the deformation of the soil.

The poroelasticity equations have been solved by Luo et al. (2015) using the finite volume method combined with a nonlinear multigrid method. In addition, stabilised finite difference methods using central differences on staggered grids are used by Gaspar et al. (2003, 2006) to solve Biot’s model. However, the numerical solution of the two-dimensional poroelasticity equations is usually approached using finite element methods (Bause et al. 2017; Lewis and Schrefler 1978; Phillips and Wheeler 2007). In this study, a finite element method based on Taylor–Hood elements, with linear and quadratic basis functions, has been developed for solving the system of incompressible poroelasticity equations. This method is commonly used for flow problems modelled by (Navier–)Stokes equations. Furthermore, the fully coupled scheme was employed which involves solving the coupled governing equations of flow and geomechanics simultaneously at every time step. Another approach that is widely used in coupling the flow and the mechanics in porous media is the fixed stress split method (Both et al. 2017; Kim et al. 2009; Mikelić and Wheeler 2013). In this manuscript, we consider a nonlinear relation between the permeability and the dilatation. Subsequently, to quantify the impact of variation of model parameters such as Young’s modulus, the oscillatory modes and the injection pressure pulses, we further present results from an uncertainty quantification. This uncertainty quantification is used to quantify the propagation of uncertainty in the input data. Such uncertainty quantifications have been applied in geomechanics (Luo 2017), where an uncertainty quantification is carried out by modelling the permeability as a stochastic field parameter.

The rest of this paper is organised as follows: Section 2 describes Biot’s consolidation model. In Sect. 3, we formulate the numerical method. Here we derive the weak form of the partial differential equations and describe the Galerkin finite element approximations. Section 4 presents some of our numerical experiments and results. Lastly, in Sect. 5 we give our conclusions and make some suggestions for further work.

2 Model Equations

Sand and gravel layers (aquifers) are not rigid, but constitute an elastic matrix, if the deformations are very small. To be able to determine the local displacement of the skeleton of the porous medium, as well as the fluid flow through the pores, after injection of water, the model provided by Biot’s theory of linear poroelasticity with single-phase flow is used (Biot 1941, 1955). In this model, flow in porous media is combined with mechanical deformations of the aquifer into which water is injected. Furthermore, Darcy’s Law (Hubbert 1957) and infinitesimal strain theory (Bower 2010) are used to describe the fluid flow and the local displacements, respectively. Note that this is an approximation if the displacements and the strains are large.

2.1 Biot’s Partial Differential Equations

The quasi-static Biot model for soil consolidation describes the time-dependent interaction between the displacement of the solid matrix and the pressure of the fluid. We assume the porous medium to be linearly elastic, homogeneous, isotropic and saturated by an incompressible Newtonian fluid. According to Biot’s theory, the consolidation process satisfies the following system of equations (Aguilar et al. 2008; Wang 2000):

$$\begin{aligned} \hbox {Mechanical balance:}\quad&\displaystyle {\nabla \cdot \varvec{\sigma }' - (\nabla p + \rho g \mathbf {e}_\mathrm{z}) = \mathbf {0}}; \end{aligned}$$

(1)

$$\begin{aligned} \hbox {Constitutive equation:}\quad&\displaystyle {\varvec{\sigma }' = \lambda tr(\varvec{\varepsilon }) \mathbf {I} + \mu (\nabla \mathbf {u} + \nabla \mathbf {u}^T)}; \end{aligned}$$

(2)

$$\begin{aligned} \hbox {Darcy's law:}\quad&\displaystyle {\mathbf {v} = -\frac{\kappa }{\eta } (\nabla p+\rho g \mathbf {e}_\mathrm{z})}; \end{aligned}$$

(3)

$$\begin{aligned} \hbox {Continuity equation:}\quad&\displaystyle {\frac{\partial }{\partial t} (\nabla \cdot \mathbf {u}) + \nabla \cdot \mathbf {v} = 0}, \end{aligned}$$

(4)

where $\varvec{\sigma }'$ is the effective stress tensor for the porous medium, p is the pore pressure, $\rho$ is the density of water, g is the gravitational acceleration, $\lambda$ and $\mu$ are the Lamé coefficients, $\mathbf {u}$ is the displacement vector of the porous medium, $\mathbf {v}$ is the percolation fluid velocity relative to the porous medium, $\kappa$ is the permeability of the porous medium and $\eta$ is the dynamic viscosity of the fluid.

2.2 Permeability and Porosity Relations

In the physical problem presented here, we will focus on the interaction between the mechanical deformations and the flow of water. Therefore, we consider the spatial dependency of the porosity and the permeability. We calculate the porosity using a procedure outlined by Tsai et al. (2006). Their derivation is based on the mass balance of solids in saturated porous media:

$$\begin{aligned} \frac{\partial [(1 - \theta ) \rho _\mathrm{s}]}{\partial t} + \nabla \cdot \left[ (1 - \theta ) \rho _\mathrm{s} \frac{\partial \mathbf {u}}{\partial t}\right] = 0, \end{aligned}$$

(5)

where $\theta$ is the porosity and $\rho _\mathrm{s}$ is the density of the solid skeleton. Assuming that $\rho _\mathrm{s}$ is constant and that $\mathbf {u}$ is sufficiently smooth to interchange the order of differentiation with respect to time and space, we get

$$\begin{aligned} \frac{\partial \theta }{\partial t} + \nabla \theta \cdot \frac{\partial \mathbf {u}}{\partial t} = (1 - \theta ) \frac{\partial }{\partial t} (\nabla \cdot \mathbf {u}). \end{aligned}$$

(6)

By Tsai et al. (2006), it is assumed that $|\frac{\partial \theta }{\partial t}| \gg |\nabla \theta \cdot \frac{\partial \mathbf {u}}{\partial t}|$; herewith, they arrive at

$$\begin{aligned} \frac{\partial \theta }{\partial t} = (1 - \theta ) \frac{\partial }{\partial t} (\nabla \cdot \mathbf {u}). \end{aligned}$$

(7)

From this equation, we get

$$\begin{aligned} \theta (\mathbf {x}, t) = 1 - \frac{1 - \theta _0}{\exp (\nabla \cdot \mathbf {u})}, \end{aligned}$$

(8)

with $\theta _0$ the initial porosity. Note that the above relation differs from the one of Tsai et al. (2006), where in Eq. (7) they used a linearisation. By not applying this linearisation, we think that our approach is slightly more accurate. The permeability $\kappa$ is determined using the Kozeny–Carman equation (Wang and Hsu 2009)

$$\begin{aligned} \kappa (\mathbf {x}, t) = \frac{d_\mathrm{s}^2}{180} \frac{\theta ^3}{(1 - \theta )^2}, \end{aligned}$$

(9)

where $d_\mathrm{s}$ is the mean grain size of the soil. As a result of the dependency of the permeability on the mechanical deformations, problem (1)–(4) becomes nonlinear.

2.3 The Set-up of the Model

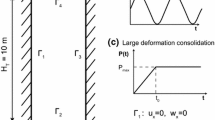
In this section, we will use Eqs. (1)–(4) to describe the flow pattern of water in a tube filled with a poroelastic material, after the injection of water into the left end of the tube. The situation is as shown in Fig. 1a. We assume that the gravity-induced contribution to the flow of water is much smaller than the other contributions, which yields that the flow is axisymmetric, hence $\frac{\partial }{\partial \hat{\theta }}(.) = 0$ in which $\hat{\theta }$ is the azimuthal coordinate. Therefore, it is sufficient to determine the solution for a fixed azimuth (for example, the grey region in Fig. 1a). The computational domain $\varOmega$ is thus a rectangular two-dimensional surface with cylindrical coordinates (x, r), as depicted in Fig. 1b.

Fig. 1

Sketch of the set-up for the tube problem: (left) physical problem and (right) numerical discretisation. Taking advantage of the symmetry of geometry and boundary conditions, only the grey region is discretised

In order to solve this problem, Biot’s consolidation model is applied on the computational domain $\varOmega$, with two spatial dimensions $\mathbf {x} = (x, r)$ and with t denoting time:

$$\begin{aligned} \begin{array}{rl} \displaystyle {-\mu \tilde{\Delta }\mathbf {u} - (\lambda +\mu ) \nabla (\nabla \cdot \mathbf {u}) + \nabla p = \mathbf {0}} &{}\displaystyle {\hbox {for}\ \ \mathbf {x} \in \varOmega ,\ t> 0;} \\ \displaystyle {\frac{\partial }{\partial t} (\nabla \cdot \mathbf {u}) - \nabla \cdot \left( \frac{\kappa }{\eta } \nabla p\right) = 0} &{}\displaystyle {\hbox {for}\ \ \mathbf {x} \in \varOmega ,\ t > 0,} \end{array} \end{aligned}$$

(10)

where $\tilde{\Delta }$ is the vector Laplacian. To complete the formulation of a well-posed problem, appropriate boundary and initial conditions are specified in Sects. 2.3.1 and 2.3.2.

2.3.1 Water Flow in a Vibrating Tube

To investigate the effect of vibrations on the water flow in the tube, we present two numerical experiments in this section. In these experiments, several ways of imposing vibrations are described, whereafter the effect on the volume flow rate at the right end of the tube is determined. In all problems, a tube of length L and initial radius R is considered. Furthermore, we assume that the casing of the tube is deformable, so that $R = R(x, t)$ holds. The poroelastic material in the tube is assumed to be isotropic and homogeneous.

Effect of an Oscillating Casing of the Tube on the Flow

In this problem, a tube is considered with a frictionless, impermeable casing on which transverse waves are imposed. Water is injected at a constant pressure into the soil through the left side surface ($x = 0$), while the right side surface ($x = L$) is kept at an ambient pressure at all times. Furthermore, filters are placed along the side surfaces to prevent that the grains exit the tube. More precisely, the boundary conditions for this problem are given as follows:

$$\begin{aligned} \frac{\kappa }{\eta }\nabla p \cdot \mathbf {n} = 0 \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _1 \cup \varGamma _3; \end{aligned}$$

(11a)

$$\begin{aligned} p = 0 \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _2; \end{aligned}$$

(11b)

$$\begin{aligned} p = p_\mathrm{pump} \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _4; \end{aligned}$$

(11c)

$$\begin{aligned} (\varvec{\sigma }' \mathbf {n}) \cdot \mathbf {t} = 0 \quad&\hbox {on}\quad \mathbf {x} \in \varGamma ; \end{aligned}$$

(11d)

$$\begin{aligned} \mathbf {u} \cdot \mathbf {n} = u_\mathrm{vib} \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _1; \end{aligned}$$

(11e)

$$\begin{aligned} \mathbf {u} \cdot \mathbf {n} = 0 \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _2 \cup \varGamma _3; \end{aligned}$$

(11f)

$$\begin{aligned} \mathbf {u} \cdot \mathbf {n} \le 0 \quad&\hbox {on}\quad \mathbf {x} \in \varGamma _4, \end{aligned}$$

(11g)

where $\varGamma = \varGamma _1 \cup \varGamma _2 \cup \varGamma _3 \cup \varGamma _4$, $\mathbf {t}$ is the unit tangent vector at the boundary, $\mathbf {n}$ is the outer normal vector, $u_\mathrm{vib}$ is a prescribed boundary displacement due to the vibrations and $p_\mathrm{pump}$ is a prescribed boundary pore pressure due to the injection of water. Figure 1b shows the definition of the boundary segments. Note that the boundary conditions on boundary segment $\varGamma _3$ are required by the definition of symmetry. The variational inequality in condition (11g) accounts for the fact that the grains cannot exit the tube through boundary segment $\varGamma _4$. More specifically, condition (11g) states: $\mathbf {u} \cdot \mathbf {n} \le 0 \ \hbox { and }\ (\varvec{\sigma }' \mathbf {n}) \cdot \mathbf {n} = 0\quad \hbox {or}\quad \mathbf {u} \cdot \mathbf {n} = 0$. This boundary condition could also be used on boundary segment $\varGamma _2$. However, in this case it is possible that $(\varvec{\sigma }' \mathbf {n}) \cdot \mathbf {n} = 0$ on both boundary segments $\varGamma _2$ and $\varGamma _4$. Then, there is no Dirichlet boundary condition for the horizontal displacement (in the x-direction). This leads to a degenerate elliptic operator for the displacement $\mathbf {u}$, which could make the problem ill-posed. Initially, the following condition is fulfilled:

$$\begin{aligned} \mathbf {u}(\mathbf {x}, 0) = 0 \quad \hbox {for} \quad \mathbf {x} \in \varOmega . \end{aligned}$$

(12)

As mentioned earlier, transverse waves are imposed for the boundary displacement $u_\mathrm{vib}$, represented by

$$\begin{aligned} u_\mathrm{vib}(x, t) = \gamma \sin \left( \frac{2 \pi }{\lambda _\mathrm{w}} (x - vt)\right) , \end{aligned}$$

(13)

with $\gamma$ the amplitude of the wave, $\lambda _\mathrm{w}$ the wavelength and v the phase velocity. Note that for $v < 0$ the wave is travelling to the left, while for $v > 0$ the wave is travelling to the right.

Effect of a Vibrating Imposed Load on the Flow

While in the previous section the vibrations were imposed as an oscillating casing of the tube, in this section the effect of an oscillating load applied on the casing is analysed. Accordingly, the boundary condition for the mechanical deformation on $\varGamma _1$ becomes

$$\begin{aligned} (\varvec{\sigma }' \mathbf {n}) \cdot \mathbf {n} = \sigma '_\mathrm{vib} \quad \hbox {on}\quad \mathbf {x} \in \varGamma _1, \end{aligned}$$

(14)

with $\sigma '_\mathrm{vib}$ is an oscillating vertical load. Similar to the previous section, transverse waves are used for the oscillating load

$$\begin{aligned} \sigma '_\mathrm{vib}(x, t) = \gamma _{\sigma } \sin \left( \frac{2 \pi }{\lambda _{\mathrm{w}, \sigma }} (x - v_{\sigma }t)\right) . \end{aligned}$$

(15)

On $t = 0$, the initial condition (12) is fulfilled.

2.3.2 Pulsed Injection

Instead of applying mechanical vibrations on the displacement, we can also investigate the effect of a pulsed injection of water into the left end of the tube. In this case, the prescribed boundary pore pressure $p_\mathrm{pump}$ caused by the injection of water will have a pulsating behaviour rather than being constant. Hence, for the boundary conditions for the mechanical deformation on $\varGamma _1$ and for the water pressure on $\varGamma _4$ holds

$$\begin{aligned} p = p_\mathrm{pump}(t) \quad \hbox {on}\quad \mathbf {x} \in \varGamma _4; \quad \quad \mathbf {u} \cdot \mathbf {n} = 0 \quad \hbox {on}\quad \mathbf {x} \in \varGamma _1, \end{aligned}$$

(16)

with $p_\mathrm{pump}(t)$ represented by the Heaviside step function

$$\begin{aligned} \mathscr {H}(t) = {\left\{ \begin{array}{ll} 0 &{}\quad t < 0 \\ 1/2 &{}\quad t = 0 \\ 1 &{}\quad t > 0 \end{array}\right. }. \end{aligned}$$

(17)

A rectangular pulse wave with period $T_\mathrm{p}$ and pulse time $\tau$ can now be defined as

$$\begin{aligned} p_\mathrm{pump}(t) = p_\mathrm{max}\sum _{k = 0}^{N_\mathrm{p}} (\mathscr {H}(t-kT_\mathrm{p}) - \mathscr {H}(t-kT_\mathrm{p}-\tau )), \end{aligned}$$

(18)

where $p_\mathrm{max}$ is the maximum injection pressure and $N_\mathrm{p}$ is the number of periods. Furthermore, the initial condition (12) is fulfilled.

3 Numerical Method

3.1 Weak Formulation

To present the variational formulation of these problems, we first introduce the appropriate function spaces. Let $L^2(\varOmega )$ be the Hilbert space of square integrable scalar-valued functions f on $\varOmega$ defined in cylinder coordinates (x, r) as $L^2(\varOmega ) = \{ f:\varOmega \rightarrow \mathbb {R} : \int _{\varOmega } |f|^2 r\ \mathrm{d} \varOmega < \infty \}$, with inner product $(f, g) = \int _\varOmega fgr\ \mathrm{d}\varOmega$. Let $H^1(\varOmega )$ denote the subspace of $L^2(\varOmega )$ of functions with first derivatives in $L^2(\varOmega )$. We further introduce the function space $\mathscr {Q} = \{q \in H^1(\varOmega ): {q = 0}\ \hbox { on }\ \varGamma _2\ \hbox { and }\ q = p_\mathrm{pump}\ \hbox { on }\ \varGamma _4 \}$ for all the problems that we consider. Subsequently, we use the function spaces $\mathscr {W} = \{ \mathbf {w} \in (H^1(\varOmega ))^2: \mathbf {w} \cdot \mathbf {n} = u_\mathrm{vib}\ \hbox { on }\ \varGamma _1\ \hbox { and }\ \mathbf {w} \cdot \mathbf {n} = 0\ \hbox { on }\ \varGamma _2 \}$ and $\mathscr {W}_0 = \{\mathbf {w} \in (H^1(\varOmega ))^2: \mathbf {w} \cdot \mathbf {n} = 0\ \hbox { on }\ \varGamma _1 \cup \varGamma _2 \}$ for the problems with boundary conditions as stated in Eqs. (11) and (16), respectively. For the problem with boundary conditions (14), we introduce $\mathscr {W} = \{\mathbf {w} \in (H^1(\varOmega ))^2: \mathbf {w} \cdot \mathbf {n} = 0\ \hbox { on }\ \varGamma _2 \}$. Furthermore, we consider the bilinear forms (Prokharau and Vermolen 2009)

$$\begin{aligned} a(\mathbf {u}, \mathbf {w})&= \lambda (\nabla \cdot \mathbf {u}, \nabla \cdot \mathbf {w}) + 2 \mu \sum _{i, j = 1}^2 (\varepsilon _{ij}(\mathbf {u}), \varepsilon _{ij}(\mathbf {w})); \end{aligned}$$

(19)

$$\begin{aligned} b(p, q)&= \sum _{i = 1}^2 \left( \frac{\kappa }{\eta } \frac{\partial p}{\partial x_i}, \frac{\partial q}{\partial x_i}\right) . \end{aligned}$$

(20)

The variational formulation in cylinder coordinates (x, r) for problem (10) with boundary and initial conditions (11)–(12) and also for problem (10) with initial and boundary conditions (12) and (16) consists of the following, using the notation $\dot{\mathbf {u}} = \frac{\partial \mathbf {u}}{\partial t}$: For each $t > 0$, find $(\mathbf {u}(t), p(t)) \in (\mathscr {W} \times \mathscr {Q})$ and $(\mathbf {u}(t), p(t)) \in (\mathscr {W}_0 \times \mathscr {Q})$ such that

$$\begin{aligned} a(\mathbf {u}(t), \mathbf {w}) - (p(t), \nabla \cdot \mathbf {w})&= h(\mathbf {w}) \quad \forall \quad \mathbf {w} \in \mathscr {W}_0; \end{aligned}$$

(21)

$$\begin{aligned} (\nabla \cdot \dot{\mathbf {u}}(t), q) + b(p(t), q)&= 0 \quad \forall \quad q \in \mathscr {Q}_0, \end{aligned}$$

(22)

with the initial condition $\mathbf {u}(0) = \mathbf {0},$ and where

$$\begin{aligned} h(\mathbf {w})&= -p_\mathrm{pump} \int _{\varGamma _4} \mathbf {w} \cdot \mathbf {n}\ r \ {rm d}\varGamma ; \end{aligned}$$

(23)

$$\begin{aligned} \mathscr {Q}_0&= \{q \in H^1(\varOmega ): q = 0\ \hbox { on }\ \varGamma _2 \cup \varGamma _4 \}. \end{aligned}$$

(24)

The variational formulation for problem (10) in cylinder coordinates (x, r) with initial and boundary conditions (12) and (14) consists of the following:

For each $t > 0$, find $(\mathbf {u}(t), p(t)) \in (\mathscr {W} \times \mathscr {Q})$ such that

$$\begin{aligned} a(\mathbf {u}(t), \mathbf {w}) - (p(t), \nabla \cdot \mathbf {w}) + c(p(t), \mathbf {w})&= h(\mathbf {w}) + g(\mathbf {w}) \quad \forall \quad \mathbf {w} \in \mathscr {W}; \end{aligned}$$

(25)

$$\begin{aligned} (\nabla \cdot \dot{\mathbf {u}}(t), q) + b(p(t), q)&= 0 \quad \forall \quad q \in \mathscr {Q}_0, \end{aligned}$$

(26)

with the initial condition $\mathbf {u}(0) = \mathbf {0},$ and where

$$\begin{aligned} c(p, \mathbf {w}) = \int _{\varGamma _1} p\ \mathbf {w} \cdot \mathbf {n}\ r \ \mathrm{d}\varGamma , \quad g(\mathbf {w}) = \int _{\varGamma _1} \sigma '_\mathrm{vib}\ \mathbf {w} \cdot \mathbf {n}\ r \ \mathrm{d}\varGamma . \end{aligned}$$

(27)

3.2 Finite Element Discretisation

Problems (21)–(24) and (25)–(27) are solved by applying the finite element method, with triangular Taylor–Hood elements (Braess 2001; Van Kan et al. 2008; Segal 2012). Let $\mathscr {P}_h^k \subset H^1(\varOmega )$ be a function space of piecewise polynomials on $\varOmega$ of degree k. Hence, we define finite element approximations for $\mathscr {W}$ and $\mathscr {Q}$ as $\mathscr {W}_h^k= \mathscr {W} \cap (\mathscr {P}_h^k \times \mathscr {P}_h^k)$ with basis $\{\pmb {\phi }_i = (\phi _i, \phi _i) \in (\mathscr {W}_h^k \times \mathscr {W}_h^k): i = 1, \ldots , n_\mathrm{u} \}$ and $\mathscr {Q}_h^{k'} = \mathscr {Q} \cap \mathscr {P}_h^{k'}$ with basis $\{\psi _j \in \mathscr {Q}_h^{k'}: j = 1, \ldots , n_\mathrm{p} \}$, respectively (Aguilar et al. 2008; Prokharau and Vermolen 2009). Subsequently, we approximate the functions $\mathbf {u}(t)$ and p(t) with functions $\mathbf {u}_h(t) \in \mathscr {W}_h^k$ and $p_h(t) \in \mathscr {Q}_h^{k'}$, defined as

$$\begin{aligned} \mathbf {u}_h(t) = \sum _{i = 1}^{n_\mathrm{u}} \mathbf {u}_i(t) \pmb {\phi }_i, \quad p_h(t) = \sum _{j = 1}^{n_\mathrm{p}} p_j(t) \psi _j, \end{aligned}$$

(28)

in which the Dirichlet boundary conditions are imposed. Then, the semi-discrete Galerkin approximation of problem (21)–(24) is defined as follows: for each $t > 0$, find functions $(\mathbf {u}_h(t), p_h(t)) \in (\mathscr {W}_h^k \times \mathscr {Q}_h^{k'})$ such that

$$\begin{aligned} a(\mathbf {u}_h(t), \mathbf {w}_h) - (p_h(t), \nabla \cdot \mathbf {w}_h)&= h(\mathbf {w}_h) \quad \forall \mathbf {w}_h \in \mathscr {W}_{0h}^k; \end{aligned}$$

(29)

$$\begin{aligned} (\nabla \cdot \dot{\mathbf {u}}_h(t), q_h) + b(p_h(t), q_h)&= 0 \quad \forall q_h \in \mathscr {Q}_{0h}^{k'}, \end{aligned}$$

(30)

and for $t = 0$:    $\mathbf {u}_h(0) = \mathbf {0}.$

Simultaneously, discretisation in time is applied using the backward Euler method. Let $\Delta t$ be the time step size and define a time grid $\{t_m = m \Delta t: m \in ~\mathbb {N}\}$, then the discrete Galerkin scheme of (29)–(30) is formulated as follows: For $m \ge 1$, find $(\mathbf {u}_h^m, p_h^m) \in (\mathscr {W}_h^k \times \mathscr {Q}_h^{k'})$ such that

$$\begin{aligned} a(\mathbf {u}_h^m, \mathbf {w}_h) - (p_h^m, \nabla \cdot \mathbf {w}_h)&= h(\mathbf {w}_h) \quad \forall \mathbf {w}_h \in \mathscr {W}_{0h}^k; \end{aligned}$$

(31)

$$\begin{aligned} (\nabla \cdot \mathbf {u}_h^m, q_h) + \Delta t\ b(p_h^m, q_h)&= (\nabla \cdot \mathbf {u}_h^{m-1}, q_h) \quad \forall q_h \in \mathscr {Q}_{0h}^{k'}, \end{aligned}$$

(32)

while for $m = 0$:    $\mathbf {u}_h^0 = \mathbf {0}.$

The discrete Galerkin scheme for problem (25)–(27) is derived similarly. These discrete Galerkin schemes are solved using triangular Taylor–Hood elements. The displacements are spatially approximated by quadratic basis functions, whereas continuous piecewise linear approximation is used for the pressure field. We remark that the Taylor–Hood elements are suitable as a stable approach for this problem. However, spurious oscillations are diminished but not completely removed for small time steps. To fully remove the non-physical oscillations, one may use the stabilisation techniques as considered by Aguilar et al. (2008). The numerical investigations are carried out using the matrix-based software package MATLAB (version R2011b). At each time step, we solve Eqs. (31)–(32) as a fully coupled system, where we use the permeability from the previous time step. After having obtained the numerical approximations for $\mathbf {u}$ and p, we update the porosity using Eq. (8). Subsequently, the Kozeny–Carman relation (9) is used to calculate the permeability. The new value for the permeability is then used for the next time step. An iterative method is not used in this approach because of efficiency and since no instability was observed in our results. In order to use Eq. (8), we determine the dilatation

$$\begin{aligned} \nabla \cdot \mathbf {u}_h^m = \frac{\partial u_{x,h}^m}{\partial x} + \frac{1}{r} \frac{\partial (r u_{r,h}^m)}{\partial r}, \end{aligned}$$

(33)

using the numerical solution $\mathbf {u}_h = (u_{x,h}, u_{r,h})$ at time $t_m$. The spatial derivatives in the dilatation

$$\begin{aligned} \omega _1^m = \frac{\partial u_{x,h}^m}{\partial x} \quad \hbox {and} \quad \omega _2^m = \frac{1}{r} \frac{\partial (r u_{r,h}^m)}{\partial r} \end{aligned}$$

(34)

are then computed by applying the finite element method. Firstly, we introduce the functions $d \in L^2(\varOmega )$ and we define the finite element approximation as $\mathscr {D}_h^k = L^2(\varOmega ) \cap \mathscr {P}_h^k$ with basis $\{\xi _i \in \mathscr {D}_h^k : i = 1, \ldots , n_u \}$. Secondly, we approximate the function $\omega _1^m$ with the function $\omega _{1,h}^m \in \mathscr {D}_h^k$, defined as

$$\begin{aligned} \omega _{1,h}^m = \sum _{i = 1}^{n_\mathrm{u}} \omega _{1,i}^m \xi _i. \end{aligned}$$

(35)

Hence, the discrete Galerkin scheme is given by

$$\begin{aligned} \hbox {For }m \ge 1,\hbox { find }\omega _{1,h}^m \in \mathscr {D}_h^k\hbox { such that: }\quad (\omega _{1,h}^m, d_h) = \left( \frac{\partial u_{x,h}^m}{\partial x}, d_h\right) \quad \forall \quad d_h \in \mathscr {D}_h^k. \end{aligned}$$

The discrete Galerkin scheme for the function $\omega _2^m$ is derived similarly. In these finite element schemes, the spatial derivatives are approximated by quadratic basis functions. For the integrals in the element matrices and the element vectors, exact integration is used. Regarding accuracy, our numerical experiments showed that this strategy produced sufficiently reliable results. We note that improvements of the accuracy can be obtained using gradient recovery techniques which yield superconverging behaviour (Zienkiewicz and Zhu 1992). The aim of this study is to investigate the impact of oscillatory and pulsating boundary conditions on the volume flow rate at the right end of the tube. We compute the volume flow rate at the right boundary segment, using the velocity field as described by Darcy’s law (3). To compute the velocity field for post-processing issues, the finite element method is applied analogously to the computation of the derivatives of the displacements, combined with piecewise linear approximation and exact integration.

4 Numerical Simulations

In this section, we discuss the solution results for the discrete Galerkin approximation of the quasi-two-dimensional problems that are presented in Sect. 2.3. The simulation domain is a rectangle with length $1.0\, \mathrm {m}$ and width $10\, \mathrm {cm}$ (see Fig. 1b). The domain is discretised using a 101 by 11 regular triangular grid, which provides sufficient resolution according to a mesh refinement study. The chosen values for the material properties of the porous medium are given in Table 1, where $\lambda$ and $\mu$ are related to the Young’s modulus E and the Poisson’s ratio $\nu$ by (Aguilar et al. 2008): $\lambda = \frac{\nu E}{(1+\nu )(1-2\nu )}$ and $\mu = \frac{E}{2(1+\nu )}$.

Table 1 An overview of the values of the material properties and the parameters of the model

The values in Table 1 are chosen based on discussions with experts from engineering and consultancy company Fugro GeoServices B.V. and on the literature (Van Wijngaarden 2015).

4.1 The Impact of an Oscillating Casing of the Tube on the Water Flow

In order to obtain some insight into the impact of an oscillating casing of the tube on the water flow, we present an overview of the simulation results in Figs. 2 and 3. In this simulation, water is injected into the soil at a constant pump pressure equal to $0.5\,\mathrm {bar}$. As a consistency check, we start with the simulation results for problem (31)–(32) without any vibrations, i.e. $u_\mathrm{vib} =~0$. The simulated pressure, fluid velocity, permeability and displacement profiles are provided in Fig. 2.

Fig. 2

Numerical solutions for the pressure, the fluid velocity, the permeability and the displacement, without vibrations, at time $t = 5$ using a constant time step size $\Delta t = 0.1$. The values of the remaining parameters are as depicted in Table 1. a Numerical solution for the pressure. b Numerical solution for the fluid velocity. c Numerical solution for the permeability. d Positions of the mesh points after subjecting them to the calculated displacement vector $\mathbf {u}$

As shown in Fig. 2, the simulated pressure is almost linear and the behaviour of the fluid velocity is completely horizontal. This means that the injected water flows in a horizontal direction through the tube from the left end of the tube to the right end. Mechanically, the deformations in the porous medium are negligible, other than a small shift of the grains to the right, as a result of the force exerted on the grains by the injected water. As a result of this small shift of the grains and the assumption that the grains cannot exit the tube, we expect a higher grain density near the right end. Consequently, the permeability will linearly decrease towards the right end of the tube, as depicted in Fig. 2c. In Fig. 3, the numerical solutions are shown for a test case of problem (31)–(32) with vibrations. In this test case, a transverse wave (13) travelling to the right is chosen as prescribed boundary displacement $u_\mathrm{vib}$, with $\gamma = 1\, \mathrm {cm}$, $\lambda _\mathrm{w} = 1\, \mathrm {m}$ and $v = 1\, \mathrm {m/s}$.

Fig. 3

Numerical solutions for the pressure, the fluid velocity, the permeability and the displacement, at time $t = 5$ using a constant time step size $\Delta t = 0.1$. For the vibrations a travelling wave to the right is chosen as prescribed boundary displacement $u_\mathrm{vib}$, with $\gamma = 1\, \mathrm {cm}$, $\lambda _\mathrm{w} = 1\, \mathrm {m}$ and $v = 1\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1. a Numerical solution for the pressure. b Numerical solution for the fluid velocity. c Numerical solution for the permeability. d Positions of the mesh points after subjecting them to the calculated displacement vector $\mathbf {u}$

In contrast to the pressure shown in Fig. 2a, the numerical solution for the pressure in the problem with vibrations is no longer linear, but shows an oscillatory behaviour, as depicted in Fig. 3a. The vibrations also provide an oscillatory profile in the permeability, as shown in Fig. 3c. In this figure, we can see that the permeability decreases when the grains are pressed together by the vibration, while it increases when the grains are pulled apart. The simulation results in Figs. 2 and 3 show an impact of the vibrations, imposed on the casing, on the water flow. However, by only looking at these results, the impact of vibrations on the amount of water that flows through the tube stays unmeasurable. For this reason, the impact of the vibrations and pulses on the water flow is defined in this publication as the impact on the volume flow rate Q at the right end of the tube. In Fig. 4, two graphs are presented that sketch the behaviour of the volume flow rate over time at the right end of the tube. In these simulations, the aforementioned test cases are used. For the test case without vibrations, the time average of the volume flow rate $\overline{Q}$ over the time interval (0, 5] is equal to $6.86\times 10^{-5}\, \mathrm {m}^3/\mathrm {s}$. For the test case with imposed vibrations, the time average of the volume flow rate $\overline{Q}$ over the time interval (0, 5] is equal to $9.69\times 10^{-4}\, \mathrm {m}^3/\mathrm {s}$. Thus, the percentage change $\overline{Q}_\%$ of the time average of the volume flow rate as result of the imposed vibration is $1311.7\%$. Based on these test cases, we can conclude that the volume flow rate at the right end of the tube increases as a result of the imposed vibrations on the casing, as depicted in Fig. 4. We finally note that the area enclosed by the Q-curve and the t-axis represents the total amount of water that flows out of the domain over a certain period.

Fig. 4

Volume flow rate at the right end of the tube over time, using a constant time step size $\Delta t = 0.1$. The blue line represents the volume flow rate for the test case without vibrations. The red line represents the volume flow rate for the test case with vibrations, in which for the vibrations a travelling wave to the right is chosen, with $\gamma = 1\, \mathrm {cm}$, $\lambda _\mathrm{w} = 1\, \mathrm {m}$ and $v = 1\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1

4.1.1 Monoparametric Variation

In this section, we will investigate the impact of the transverse waves (13) on the flow of water. Furthermore, the contributions of the variations in the values of the vibration characteristics to the volume flow rate are quantified by assigning a range of possible values to the parameters: $\gamma$, $\lambda _\mathrm{w}$ and v. Firstly, a monoparametric variation is applied whereby the values of the parameters are varied one by one, within ranges of possible values. In Fig. 5, the volume flow rate at the right end of the tube is depicted over time after applying a monoparametric variation in the values of the vibration characteristics $\gamma$, $\lambda _\mathrm{w}$ and v. For the variation, the following ranges of possible values are chosen: $\gamma \in [0, 1, 5, 10]\times 10^{-3}, \quad \lambda _\mathrm{w} \in [1/4, 1/2, 1], \quad v \in [-2.0, -1.0, -0.5, 0.5, 1.0, 2.0]$. In the generations of the simulation results presented in Fig. 5, the time step size $\Delta t$ is determined using the formula $\Delta t = \frac{1}{8 f}$, in which f is the frequency computed by: $f = \frac{|v|}{\lambda _\mathrm{w}}$. In case variation is applied to the values of $\lambda _\mathrm{w}$ or v, the maximum value of f is used to determine the time step size. Figure 5a indicates that an increase in the amplitude of the imposed wave, with fixed wavelength and phase velocity, results in an increase in the volume flow rate. However, an increase in the wavelength, with fixed amplitude and phase velocity, leads to a decrease in the volume flow rate, as shown in Fig. 5b. Figure 5c indicates that an increase in the phase velocity magnitude $|v|$, with fixed amplitude and wavelength, leads to a larger impact on the volume flow rate. Furthermore, assigning positive values to the phase velocity v (corresponding with transverse waves travelling to the right) results in positive volume flow rate profiles. Assigning negative values to the phase velocity v (corresponding with transverse waves travelling to the left) produces negative volume flow rates. As expected, the water flow, which is directed to the right, is stimulated by waves travelling in the same direction. However, waves travelling in the opposite direction counteract the flow, resulting in negative volume flow rates. In fact, the negative volume flow rates are a result of the force applied by the oppositely directed waves that is larger than the pump pressure. At a higher pump pressure, the effect of these waves on the volume flow rate is smaller, as illustrated in Fig. 6.

Fig. 5

Volume flow rate profiles at the right end of the tube over time, after applying a monoparametric variation in the values of the parameters $\gamma$, $\lambda _\mathrm{w}$ and v. For the vibrations, transverse waves (13) are used as prescribed boundary displacement $u_\mathrm{vib}$, with $\gamma \in [0, 1, 5, 10]\, \mathrm {mm}$, $\lambda _\mathrm{w} \in [0.25, 0.50, 1.00]\, \mathrm {m}$ and $v \in [-\,2.0, -\,1.0, -\,0.5, 0.5, 1.0, 2.0]\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1. a Volume flow rate over time, after applying variation in the values of $\gamma$. The other vibration characteristics are constant: $\lambda _\mathrm{w} = 1$ and $v = 1$. b Volume flow rate over time, after applying variation in the values of $\lambda _\mathrm{w}$. The other vibration characteristics are constant: $\gamma = 0.01$ and $v = 1$. c Volume flow rate over time, after applying variation in the values of v. The other vibration characteristics are constant: $\gamma = 0.01$ and $\lambda _\mathrm{w} = 1$

Fig. 6

Volume flow rate at the right end of the tube over time for different values of the pump pressure $p_\mathrm{pump}$, using a constant time step size $\Delta t = 0.1$. In all test cases, a travelling wave to the left is chosen as prescribed boundary displacement $u_\mathrm{vib}$, with $\gamma = 1\, \mathrm {cm}$, $\lambda _\mathrm{w} = 1\, \mathrm {m}$ and $v = -1\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1

4.1.2 Monte Carlo Method

In the previous section, the contributions of the variations in the values of the vibration characteristics to the volume flow rate were quantified by applying a monoparametric variation where the values of the parameters are varied one by one, within ranges of possible values. As we choose to fix a number of parameter values each time, we are not able to draw any conclusions from this monoparametric variation. In this section, Monte Carlo method is applied to the values of the vibration characteristics using samples of uniform distributions with chosen boundaries. In Fig. 7, the time average of the volume flow rate is depicted after applying Monte Carlo simulations to the values of the vibration characteristics $\gamma$, $\lambda _\mathrm{w}$ and v. For the simulations, 300 samples from the following uniform distributions are generated: $\gamma \sim \mathscr {U}(0.001, 0.01), \quad \lambda _\mathrm{w} \sim \mathscr {U}(1/4, 1), \quad v \sim \mathscr {U}(-2, 2)$. Figure 7a shows that an increase in the amplitude of the imposed wave leads to a larger impact on the time average of the volume flow rate $\overline{Q}$. However, an increase in the wavelength results in a smaller impact on $\overline{Q}$, as shown in Fig. 7b. In both figures, we observe a mirroring across a line near the horizontal axis. Values of $\overline{Q}$ above the mirror line correspond with positive values of the phase velocity, while values of $\overline{Q}$ bellow the mirror line correspond with negative values of v, as can be concluded from Fig. 7c. Furthermore, Fig. 7c shows that an increasing phase velocity magnitude $|v|$ leads to a larger impact on $\overline{Q}$. In addition, we observe in Fig. 7c that for $v<0$ some of the values of $\overline{Q}$ are positive, and these values correspond with small values of the amplitude. In this case, the pump pressure is larger than the force applied by the oppositely directed waves, which results in positive volume flow rates. Note that these results are consistent with the results from Sect. 4.1.1. From the formula for the frequency and Fig. 7, we can conclude that large amplitudes and high frequencies lead to high-volume flow rates for $v > 0$. In Table 2, the Pearson correlation coefficients are given together with the associated p-values. From this table, we can conclude that the vibration characteristics $\gamma$ and v have the most impact on the time average of the volume flow rate.

Fig. 7

Scatter plots of the time average of the volume flow rate over the time interval (0, 70.86], after applying Monte Carlo simulations to the values of $\gamma$, $\lambda _\mathrm{w}$ and v. For the vibrations, transverse waves (13) are used as prescribed boundary displacement $u_\mathrm{vib}$, with $\gamma \sim \mathscr {U}(1, 10)\, \mathrm {mm}$, $\lambda _\mathrm{w} \sim \mathscr {U}(1/4, 1)\, \mathrm {m}$ and $v \sim \mathscr {U}(-2, 2)\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1. a Time average of the volume flow rate as function of $\gamma$. b Time average of the volume flow rate as function of $\lambda _\mathrm{w}$. c Time average of the volume flow rate as function of v

To measure the real impact of the transverse waves (13) on the water flow, the percentage change $\overline{Q}_\%$ of the time average of the volume flow rates as result of the imposed vibrations is determined by the formula $\overline{Q}_\% = \frac{\overline{Q} - \overline{Q}_0}{\overline{Q}_0} \times 100$, where $\overline{Q}_0$ is the time average of the volume flow rate in the test case without vibrations. The percentage change $\overline{Q}_\%$ of the time average $\overline{Q}$ that is computed after applying the above-described Monte Carlo method (see Fig. 7), is depicted as function of $\gamma$ in Fig. 8.

Table 2 Pearson correlation coefficients together with the associated p values

Fig. 8

Scatter plot of the percentage change $\overline{Q}_\%$ over the time interval (0, 70.86] as function of $\gamma$, after applying Monte Carlo method to the values of $\gamma$, $\lambda _\mathrm{w}$ and v

Figure 8 shows that, for $v > 0$, the volume flow rate at the right end of the tube increases as a result of the imposed vibrations on the casing. For vibrations with a large amplitude and a high frequency, the time average of the volume flow rate can become as large as 42 times the time average of the volume flow rate in the test case without vibrations. The smallest percentage change in the volume flow rate as cause of the vibrations is equal to $6.0\%$. On the other hand, for $v < 0$, all vibrations lead to a negative percentage change $\overline{Q}_\%$, even the vibrations with small values of the amplitude $\gamma$. Given the probability space $(\varOmega _\mathrm{p}, \mathscr {F}, P)$, with sample space $\varOmega _\mathrm{p}$ (which is the set of all possible outcomes), the set of events $\mathscr {F}$ (where each event is a set with zero or more outcomes), and the probability P, with $P: \mathscr {F} \rightarrow [0, 1]$, we can compute the cumulative distribution function. In Fig. 9, the histogram and the cumulative distribution function of the percentage change $\overline{Q}_\%$ are presented. Since $51\%$ of the sampled values of v are negative, we see in Fig. 9 that $P(\overline{Q}_\% \le 0) \approx 0.51$. Furthermore, using the probability space we can compute the probabilities that the percentage change is greater than $100\%$: $P(\overline{Q}_\% \ge 100) \approx 0.43$ and $P(\overline{Q}_\% \ge 100 | v >0) \approx 0.89$.

Fig. 9

Histogram and the cumulative distribution function of the percentage change

4.2 The Impact of a Vibrating Load on the Water Flow

In this section, the impact of a vibrating load, which is applied on the casing of the tube, on the water flow is investigated. This numerical experiment makes it possible to analyse the contributions of the variations in the values of the porous medium properties to the volume flow rate. These contributions are quantified by assigning a range of possible values to the parameters: E, $\nu$, $\theta _0$ and $d_\mathrm{s}$. For this purpose, four types of soil are distinguished: clay, silt, sand and gravel. In the literature, there is a large consensus that the Kozeny–Carman equation (9) applies to sands but not to clays (Chapuis and Aubertin 2003). Therefore, this experiment is only applied to sand and gravel.

Fig. 10

Scatter plots of $\overline{Q}$ over the time interval (0, 25], after applying Monte Carlo simulations to the values of the material properties of sand using the ranges (36). For the vibrations transverse waves (15) are used as prescribed vertical load $\sigma '_\mathrm{vib}$, with $\gamma _{\sigma } = 10^4\, \mathrm {Pa}$, $\lambda _{w, \sigma } = 1/4\, \mathrm {m}$ and $v_{\sigma } = 1\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1

Fig. 11

Scatter plots of $\overline{Q}$ over the time interval (0, 25], after applying Monte Carlo simulations to the values of the material properties of gravel using the ranges (37). For the vibrations transverse waves (15) are used as prescribed vertical load $\sigma '_\mathrm{vib}$, with $\gamma _{\sigma } = 10^4\, \mathrm {Pa}$, $\lambda _{w, \sigma } = 1/4\, \mathrm {m}$ and $v_{\sigma } = 1\, \mathrm {m/s}$. The values of the remaining parameters are as depicted in Table 1

4.2.1 Monte Carlo Method for Sand and Gravel

Monte Carlo method is applied to the values of the material properties of sand and gravel, using samples of uniform distributions with boundaries found in the literature (“Geotechnical parameters” 2017; “Soil properties” 2017). As the values within these boundaries are all equally likely to occur, we have chosen to use uniform distributions instead of another frequently used distributions like the log-normal distribution. In Figs. 10 and 11, the time average of the volume flow rate at the right end of the tube is depicted after applying Monte Carlo simulations to the values of the material properties E, $\nu$, $\theta _0$ and $d_\mathrm{s}$. For sand, 300 samples from the following uniform distributions are generated:

$$\begin{aligned} \begin{array}{l} E \sim \mathscr {U}(30 \times 10^6, 50 \times 10^6), \quad \nu \sim \mathscr {U}(0.15, 0.40), \quad \theta _0 \sim \mathscr {U}(0.26, 0.46),\\ d_s \sim \mathscr {U}(0.05 \times 10^{-3}, 2.00 \times 10^{-3}), \end{array} \end{aligned}$$

(36)

while for gravel, 300 samples from these uniform distributions are generated:

$$\begin{aligned} \begin{array}{l} E \sim \mathscr {U}(80 \times 10^6, 160 \times 10^6), \quad \nu \sim \mathscr {U}(0.30, 0.40), \quad \theta _0 \sim \mathscr {U}(0.23, 0.38),\\ d_s \sim \mathscr {U}(2 \times 10^{-3}, 50 \times 10^{-3}). \end{array} \end{aligned}$$

(37)

Figures 10 and 11 show that water flows faster through porous media with large mean grain sizes or high initial porosities, after imposing a vibrating load on the casing. On the other hand, these figures show that the volume flow rate is invariant under variation in the values of Young’s modulus and Poisson’s ratio. This can also be concluded from the values of the Pearson correlation coefficients given in Table 3.

Table 3 Pearson correlation coefficients together with the associated p values

4.3 The Impact of a Pulsed Injection on the Water Flow

Based on over 160 laboratory tests, Dusseault (1999) demonstrated the beneficial effects of pressure pulsing on the water flow in porous media. To theoretically examine his findings, we investigated the impact of a pulsed injection of water, into the left end of the tube, on the water flow. The results of this research are presented in this section. In addition, the contributions of the variations in the values of the pulse wave characteristics to the volume flow rate are analysed. These contributions are examined by applying Monte Carlo method to the pulse wave period $T_\mathrm{p}$ and the relative pulse time $\tilde{\tau }$, defined as $\tilde{\tau } = \frac{\tau }{T_\mathrm{p}}$, with $\tau$ the pulse time (see Formula (18)). Subsequently, in order to be able to draw reliable conclusions about the impact of pressure pulsing on the volume flow rate, we compare the volume flow rate caused by the pulsed injection with the volume flow rate by a constant pump pressure $p_\mathrm{pump}$. In this comparison, the percentage change $\overline{Q}_\%$ of the time average of the volume flow rate $\overline{Q}$ is used, determined by $\overline{Q}_\% = \frac{\overline{Q} - \overline{Q}_C}{\overline{Q}_C} \times 100$, where $\overline{Q}_C$ is the time average of the volume flow rate caused by a constant pump pressure. In each simulation, the constant pump pressure is chosen equal to the total pump pressure over time by pulsed injection. Hence, for a particular relative pulse time $\tilde{\tau }$, the constant pump pressure is computed by $p_\mathrm{pump} = \tilde{\tau } p_\mathrm{max}$. In Fig. 12, the percentage change in the time average of the volume flow rate at the right end of the tube is depicted after applying Monte Carlo simulations to the values of the pulse wave characteristics $T_\mathrm{p}$ and $\tilde{\tau }$. For the simulation, 300 samples from the following uniform distributions are generated:

$$\begin{aligned} T_\mathrm{p} \sim \mathscr {U}(0.5, 4), \quad \tilde{\tau } \sim \mathscr {U}(0.1, 0.9). \end{aligned}$$

(38)

In the generations of the simulation results presented in Fig. 12, the time step size $\Delta t$ is determined by $\Delta t = \frac{T_\mathrm{p}}{20}$. As variation is applied to the values of $T_\mathrm{p}$, the minimum value of $\Delta t$ is used as time step size. Figure 12 shows that pressure pulsing with small relative pulse times $\tilde{\tau }$ leads to a major increase in the volume flow rate, while it increases slightly by increasing the pulse period $T_\mathrm{p}$. This can also be confirmed by the Pearson correlation coefficients and the p-values given in Table 4. In Fig. 13, the histogram and the cumulative distribution function of the percentage change $\overline{Q}_\%$ are depicted. Since $P(\overline{Q}_\% \le 0) = 0$, we can conclude from Figs. 12 and 13 that pulsed injection has a beneficial effect on the water flow in porous media.

Fig. 12

Scatter plots of the percentage change $\overline{Q}_\%$ of the time average of the volume flow rate over the time interval (0, 20], after applying Monte Carlo method to the values of $T_\mathrm{p}$ and $\tilde{\tau }$ using the distributions (38). For the pump pressure, pulse waves (18) are used with $p_\mathrm{max} = 0.5 \times 10^{5}\, \mathrm {Pa}$. The values of the remaining parameters are as depicted in Table 1. a $\overline{Q}_\%$ as function of $T_\mathrm{p}$. b $\overline{Q}_\%$ as function of $\tilde{\tau }$

Table 4 Pearson correlation coefficients together with the associated p values

Fig. 13

Histogram and the cumulative distribution function of the percentage change

5 Conclusions and Discussion

In this study, the poroelasticity system with nonlinear permeability is solved using the Galerkin finite element method based on Taylor–Hood elements, combined with a backward Euler time integration. The study contains simulations with oscillatory force boundary conditions as well as pressure pulses. Furthermore, to quantify the impact of variation of model parameters such as Young’s modulus, the oscillatory modes and the injection pressure pulses, a probabilistic approach is carried out.

To begin with, soil vibrations are applied on the casing of a tube as oscillatory displacement boundary condition. Numerical results showed that large amplitudes and high frequencies of the imposed mechanical vibrations lead to high-volume flow rates for positive values of the phase velocity, corresponding with transverse waves travelling to the right. Therefore, the volume flow rate at the right end of the tube increased as a result of the imposed mechanical vibrations. On the other hand, for negative values of the phase velocity, corresponding with waves travelling to the left, the vibrations lead to a decrease in the volume flow rate at the right end of the tube. As expected, the water flow, which is directed to the right, is stimulated by waves travelling in the same direction, while waves travelling in the opposite direction counteract the flow, resulting in negative volume flow rates in case the force applied by the oppositely directed waves is larger than the pump pressure.

Subsequently, applying an oscillating load on the casing of the tube showed that water flows faster through porous media with large grain sizes and/or high initial porosities. On the other hand, variation in the values of Young’s modulus and Poisson’s ratio indicated that these parameters do not have a large impact on the volume flow rate.

Numerical simulations of pressure pulsing pointed out that injection pulses with small relative pulse times lead to a major increase in the volume flow rate, while an increasing pulse period results in a slight increase in the flow rate. Most importantly, we can conclude that pulsed injection has a beneficial effect on the water flow in porous media.

In the current paper, we use a “brute-force” Monte Carlo simulation procedure. Doing simulations with thousands of samples can reduce the Monte Carlo error. However, as in our case each sample simulation takes about two hours, we instead adopted 300 samples. In recent studies (Cliffe et al. 2011), multilevel Monte Carlo methods (MLMC) have been applied to various systems, such as groundwater flow. These MLMC methods are characterised by the advantage that relatively few simulations are needed at high mesh resolutions, whereas one performs large numbers of simulations at lower resolutions. The MLMC methods are therefore thought to be a suitable candidate for future applications.

In conclusion, pressure pulses and soil vibrations in the direction of the flow increase the amount of water that can be injected into a tube filled with a deformable fluid-saturated porous medium. However, to elucidate the underlying mechanisms of FHVI, the injection of water into the aquifer should be simulated. In addition, further research should be carried out to examine the validity and applicability of the Kozeny–Carman equation especially for the problems in which vibrations can lead to very large gradients of the porosity and permeability in the soil. Furthermore, it is important to note that the model we are currently using is based on the assumption that the displacements and the strains are small. For this reason, we used Hooke’s law and the assumption that the strain tensor is only determined by the deformation gradient (and its transpose), while higher-order terms are neglected. However, as the mechanical vibrations can lead to large strains and displacements, it is probably more realistic to use a morphoelastic model or another plasticity model for soil. The treatment of large deformations would imply nonlinear terms. For the morphoelastic model, for example, an additional nonlinear time-dependent equation would have to be solved, which would increase the computational complexity. Since the purpose of this study is to investigate how vibrations can influence the fluid flow using uncertainty quantification, these nonlinear terms are neglected and the model is kept simple and cheap from a computational point of view.