Thin-Shell Model for Effective Thermal and Electrical Conductivity of Highly Porous Closed-Cell Metal Foams

Abstract

In this paper, a unit-cell model for determination of the effective thermal and electrical conductivity, respectively, of highly porous, closed-cell metal foams is presented. Hereby, (i) a large contrast between the transport properties of the conducting, solid material phase and the pore space is assumed, and (ii) thin, interconnected spherical shells of the solid material phase in a simple cubic arrangement are considered as a geometrical model. The unit-cell model prediction is compared to (i) literature data and (ii) well-established homogenization schemes from the effective medium theory.

1 Introduction

Metal foams are versatile engineering materials characterized by tunable stiffness and strength, superior damping performance, etc., hence their ever-increasing application in, e.g., automotive and transport industry. Furthermore, transport properties (thermal conductivity, electrical conductivity, etc.) may also be tuned via their porosity ${\phi }$, making metal foams a practical choice for application like heat exchangers (Odabaee et al. 2011) and/or electrodes. In this paper, we focus on the transport properties (thermal and electrical conductivity) of metal foams with closed-cell morphology. We further restrict our consideration to the case of a large contrast between conductivity of the solid material phase (volume fraction $f_{\hbox {s}}$) and the pore space (volume fraction ${\phi }$, hence $f_{\hbox {s}}=1-{\phi }$),¹ i.e., negligible conductivity in the pore space. The electrical and thermal conductivity of the solid material phase is denoted as ${\sigma }_{\hbox {s}}$ [S/m] and $k_{\hbox {s}}$ [W/(mK)], respectively; the constitutive equations for electrostatics and steady-state heat conduction have analogous form (see Table 1), with Ohm’s law reading

$$\begin{aligned} \mathbf{J}=-{\sigma }\nabla \varPhi , \end{aligned}$$

(1)

where $\mathbf{J}$ [A/m$^2$] denotes the electric current density and $\nabla \varPhi$ [V/m] the electrostatic potential gradient. Fourier’s law of heat conduction² has the form

$$\begin{aligned} \mathbf{J}=-k \nabla T. \end{aligned}$$

(2)

Here, $\mathbf{J}$ [W/m$^2$] denotes the heat flow vector and $\nabla T$ [K/m] is the temperature gradient. The so-called homogenization schemes relate the conductivity of the metal foam, e.g., the effective electrical conductivity ${\sigma }_{\hbox {eff}}$, to the conductivity and volume fraction of the solid material phase, taking into account morphology, i.e., ${\sigma }_{\hbox {eff}}={\sigma }_{\hbox {eff}}({\sigma }_{\hbox {s}},f_{\hbox {s}}=1-{\phi },\hbox {morphology})$. A review of homogenization schemes applicable to metal foams can be found in, e.g., Ranut (2015) for open-cell foam and Yang et al. (2013a), Cuevas et al. (2009) for closed-cell foams. As the underlying field equations for electrostatics and steady-state heat conduction are similar (see Table 1), the outcome of homogenization schemes derived for either one of the problems may be applied to the other one. This is the case for classical effective media and effective field, respectively, homogenization schemes [an excellent review of these methods can be found in Sevostianov and Kachanov (2013)]. These schemes include, with analytical expressions specialized for a matrix/spherical pore morphology and zero conductivity in the pore space:

Table 1 Similarities in field and constitutive equations

• Maxwell–Euken expression (Maxwell 1904), or Kanaun–Levin method (Kanaun and Levin 1994; Kanaun 2003; Markov 2001; Kanaun and Levin 2013), or Hashin–Shtrikman upper bound (Hashin and Shtrikman 1962):³

  $$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}=\displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= \displaystyle \frac{2f_{\hbox {s}}}{3-f_{\hbox {s}}}. \end{aligned}$$

  (3)

  Recently, Yang et al. (2013b) reanalyzed the Maxwell model, pointing out that the reduced effective conductivity with increasing porosity stems from (i) the reduced heat flow area and (ii) the elongated heat transfer distance. As regards the underlying modeling assumptions [i.e., the local temperature/potential distortion in the pore vicinity does not affect the temperature/potential field in the vicinity of neighboring pores (Yang et al. 2013b; Zaoui 1997, 2002)], this scheme may be employed for moderate porosity values with ${\phi }<{\sim }0.2$.

• The differential scheme (Bruggeman 1935; McLaughlin 1977; Norris 1985) represents an recurring application of the dilute distribution estimation (Eshelby 1957, 1961), with the latter representing the situation where the pores are (i) diluted in the matrix material and (ii) their interaction can be neglected. Starting with the homogeneous matrix material, the inclusion phase (spherical pores) is embedded in the matrix material in infinitesimal steps. Applying the dilute distribution estimation gives the matrix behavior for the subsequent step, finally leading to

  $$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}=\displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= f_{\hbox {s}}^{3/2}. \end{aligned}$$

  (4)

  As opposed to the Maxwell–Euken expression, the differential scheme has no restrictions as regards the value of the pore volume fraction; hence, it may be a suitable homogenization scheme for highly porous materials. Bauer (1993) and Yang et al. (2013c) obtained this result by solving the Laplace equation (combined field and constitutive equation, respectively, in Table 1) by perturbation of the (initially) uniform temperature gradient in the solid material due to the introduction of pores, giving $k_{\hbox {eff}}/k_{\hbox {s}}=f_{\hbox {s}}^{3{\beta }/2}$, with ${\beta }$ as a shape factor for consideration of non-spherical pore shape (regular polygons in the 2D case, polyhedrons in the 3D case), see numerical results and analysis in Zhang et al. (2009), Yang et al. (2013c).

  Pore shapes of type oblate and prolate spheroid, respectively, were investigated in Sevostianov et al. (2006), Sevostianov and Kachanov (2013), giving $k_{\hbox {eff}}/k_{\hbox {s}}=f_{\hbox {s}}^{\eta }$ for the differential scheme, where ${\eta }$ is a function of the aspect ratio of the spheroidal pores, see “Appendix”.

The listed effective media homogenization schemes are based on Eshelby’s problem of an ellipsoidal inclusion/inhomogeneity embedded in an infinitely extended, i.e., spatially dominant matrix phase. The physical interpretation of this configuration in the case of a highly porous material, in the present case of closed-cell foam, is vague.

Figure 1a, b depict data from the open literature for thermal and electrical conductivity, respectively, of closed-cell aluminum foam (Solorzano et al. 2008; Ye et al. 2015; Sevostianov et al. 2006). Figure 1c shows experimental data for the thermal conductivity of closed-cell graphitic foam (Klett et al. 2004). As regards morphology, the pores may be characterized as

• spherical bubbles for the graphitic foam investigated in Klett et al. (2004);

• having irregular shape for the aluminum foam studied in Solorzano et al. (2008);

• oblate spheroids for the aluminum foams investigated in Ye et al. (2015) and Sevostianov et al. (2006); hereby, an aspect ratio of 0.7 was quoted in Sevostianov et al. (2006).

A comparison with the homogenization schemes from the effective medium/field theory described above (see Eqs. 3 and 4, underlying spherical pore shape) shows that data approximately lie between the model response for the Maxwell–Euken expression and the differential scheme, respectively. Note: An extensive analysis of the influence of non-spherical pore shape within the scopes of the homogenization schemes from the effective medium/field theory can be found in Sevostianov et al. (2006), Sevostianov and Kachanov (2013), see Appendix.

Fig. 1

a Thermal conductivity of closed-cell aluminum foam [data taken from Solorzano et al. (2008), Ye et al. (2015), for modeling $k_{\hbox {s}}$ was set to 140 W/(mK)], b electrical conductivity of closed-cell aluminum foam (data taken from Sevostianov et al. (2006), for modeling ${\sigma }_{\hbox {s}}$ was set to 24 MS/m) and c thermal conductivity of closed-cell graphitic foam [data taken from Klett et al. (2004), for modeling $k_{\hbox {s}}$ was set to 900 W/(mK)]

Data and homogenization schemes were presented in a double-logarithmic diagram owing to the power-law dependence of the differential scheme (slope of 3/2 in Fig. 1). This is also the case for the Maxwell–Euken expression in the high porosity range with ${\sigma }_{\hbox {eff}}/{\sigma }_{\hbox {s}}= 2/3 f_{\hbox {s}}$ for $f_{\hbox {s}}\rightarrow 0$ ⁴ (slope of 1 in Fig. 1).

Motivated by the results depicted in Fig. 1, we will investigate a microstructural configuration, i.e., the arrangement of the conducting and the non-conducting material phase, respectively, differing from the configuration employed for the homogenization schemes from effective medium theory (matrix / spherical pore morphology).

2 Spherical Shell-Based Unit-Cell Model

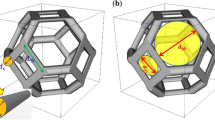
Employing a matrix/spherical pore morphology in the microstructural representation of closed-cell foams may not realistically depict the foaming process-dependent morphology. Hence, we propose a different configuration of the conducting and the non-conducting material phase, respectively: interconnecting spherical shells in a simple cubic arrangement, with two connected spherical half shells as a unit cell (see Fig. 2a). Thus, in this model two mechanisms contribute to the scaling of conductivity as a function of porosity:

• the decrease in shell thickness h reduces the heat flow area;

• the decrease in the overlap of the spherical shells (labeled $\bar{r}$ in Fig. 2a) elongates the heat transfer distance.

Fig. 2

Spherical shell-based unit-cell model for electrical conductivity [as regards modeling of thermal conductivity $\varPhi$ is replaced by T, ${\sigma }_{\hbox {s}}$ and ${\sigma }_{\hbox {eff}}$ are replaced by $k_{\hbox {s}}$ and $k_{\hbox {eff}}$]

The volume fraction of the solid material phase is related to the volume of the unit cell of $V=(2R)^3=8R^3$:

$$\begin{aligned} f_{\hbox {s}}=\displaystyle \frac{4\pi R^2 h}{(2R)^3}=\displaystyle \frac{\pi }{2}\displaystyle \frac{h}{R}, \end{aligned}$$

(5)

Hereby, the volume of the two thin half shells (with $h\ll R$) is determined from their surface $2\times 2 \pi R^2$. Hence, bear in mind that the resulting relation for the solid volume fraction of type $f_{\hbox {s}}\propto h/R$ is valid only in the high porosity regime.

Ohm’s (or Fourier’s) law (Eqs. 1 or 2) may be specialized for axisymmetric (with respect to the z-axis), circumferential transport as the electrical (or thermal) conductivity of the pore space is negligible, and hence, no current (or heat flux) occurs perpendicular to the shell:

$$\begin{aligned} |\mathbf{J}|=J=-{\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial s}, \end{aligned}$$

(6)

where s denotes the arc coordinate. Considering the steady state, the total current (or heat flowing) in circumferential direction is constant and given as

$$\begin{aligned} |\mathcal{J}|=|J(s)|~A(s)= {\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial s} 2r\pi h = \hbox {const}. \end{aligned}$$

(7)

In Eq. (7), r(s) denotes the radius of the considered ringlike cross section $A(s)=2r(s)\pi h$. Opposing the unit cell (Fig. 2a) to the sought-for effective material (Fig. 2b), the total current (or heat) passing through has to be equal:

$$\begin{aligned} |\mathcal{J}| ={\sigma }_{\hbox {eff}}\displaystyle \frac{\partial \varPhi }{\partial z} (2R)^2=\hbox {const}. ={\sigma }_{\hbox {eff}}\displaystyle \frac{{\Delta }\varPhi }{R} (2R)^2=\hbox {const}. \end{aligned}$$

(8)

In Fig. 2b, $2 {\Delta }\varPhi$ denotes the electrostatic potential (or temperature) difference between the upper and lower surface of the effective material. Considering the height of the unit cell of 2R, the potential (or temperature) gradient in the effective material is given as $\partial \varPhi / \partial z=2{\Delta }\varPhi /(2R)={\Delta }\varPhi /R$.

Now consider the same potential (or temperature) difference $2{\Delta }\varPhi$ between the upper and lower surface of the unit cell (Fig. 2a). Writing z as a function of arc length s

$$\begin{aligned} s={\beta }R; \quad \sin {\beta }=z/R; \quad \rightarrow \quad z=R\sin {\beta }=R\sin \displaystyle \frac{s}{R} \end{aligned}$$

(9)

allows rewriting the potential (or temperature) gradient in the thin shell with respect to the z-axis,

$$\begin{aligned} \displaystyle \frac{\partial \varPhi }{\partial s} = \displaystyle \frac{\partial \varPhi }{\partial z} \displaystyle \frac{\partial z}{\partial s} = \displaystyle \frac{\partial \varPhi }{\partial z} \cos \displaystyle \frac{s}{R}= \displaystyle \frac{\partial \varPhi }{\partial z} \cos {\beta }= \displaystyle \frac{\partial \varPhi }{\partial z} \displaystyle \frac{r}{R}. \end{aligned}$$

(10)

Inserting Eq. (10) into Eq. (7) and replacing $r^2$ by $R^2-z^2$ gives

$$\begin{aligned} |\mathcal{J}|={\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial z} 2\pi h \displaystyle \frac{r^2}{R}= {\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial z} 2\pi h \displaystyle \frac{R^2-z^2}{R}= {\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial z} 2\pi h R \left( 1-\displaystyle \frac{z^2}{R^2}\right) . \end{aligned}$$

(11)

Introducing the dimensionless coordinate $\xi =z/R$ and $\partial \varPhi /\partial z$ = $\partial \varPhi /\partial \xi \,\, \partial \xi /\partial z$ = $\partial \varPhi /\partial \xi \, 1/R$ gives

$$\begin{aligned} |\mathcal{J}|= {\sigma }_{\hbox {s}}\displaystyle \frac{\partial \varPhi }{\partial \xi } 2\pi h (1-\xi ^2), \end{aligned}$$

(12)

what allows determination of the potential (or temperature) difference along half of the height of the unit cell

$$\begin{aligned} \displaystyle \int _0^{\bar{\xi }} \displaystyle \frac{\partial \varPhi }{\partial \xi } d\xi = {\Delta }\varPhi = \displaystyle \frac{|\mathcal{J}|}{{\sigma }_{\hbox {s}}}\displaystyle \frac{1}{2\pi h} \displaystyle \int _0^{\bar{\xi }} \displaystyle \frac{1}{1-\xi ^2} d\xi = \displaystyle \frac{|\mathcal{J}|}{{\sigma }_{\hbox {s}}}\displaystyle \frac{1}{2\pi h} \hbox {artanh}\bar{\xi } \end{aligned}$$

(13)

with

$$\begin{aligned} \bar{\xi }=\displaystyle \frac{R\cos {\alpha }}{R}=\cos {\alpha }= \displaystyle \frac{R}{R+h/2} = \displaystyle \frac{1}{1+h/(2R)} \end{aligned}$$

(14)

referring to the cross section at the junction of the two half shells at $r=\bar{r}$, see Fig. 2a (labeled “constricting section of shell”). Note, as opposed to the potential (or temperature) distribution in the effective material, $\varPhi (z)$ is nonlinear, with $\varPhi (z)=|\mathcal{J}|/{\sigma }_{\hbox {s}}~1/(2\pi h)~\hbox {artanh}(z/R)$ (plus a constant, see Fig. 2).

Comparing Eq. (13) with Eq. (8) gives

$$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}= \displaystyle \frac{\pi h/(2R)}{\hbox {artanh}\displaystyle \frac{1}{1+h/(2R)}}. \end{aligned}$$

(15)

Finally, h/(2R) is replaced by the associated volume fraction $f_{\hbox {s}}$, with $h/(2R)=f_{\hbox {s}}/\pi$ (see Eq. 5), giving

$$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}= \displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= \displaystyle \frac{f_{\hbox {s}}}{\hbox {artanh}\displaystyle \frac{\pi }{\pi +f_{\hbox {s}}}}. \end{aligned}$$

(16)

Fig. 3

Comparison of experimental data with spherical shell-based unit-cell model: a thermal conductivity of closed-cell aluminum foam [data taken from Solorzano et al. (2008), Ye et al. (2015), for modeling $k_{\hbox {s}}$ was set to 140 W/(mK)], b electrical conductivity of closed-cell aluminum foam [data taken from Sevostianov et al. (2006), for modeling ${\sigma }_{\hbox {s}}$ was set to 24 MS/m], c thermal conductivity of closed-cell graphitic foam [data taken from Klett et al. (2004), for modeling $k_{\hbox {s}}$ was set to 900 W/(mK)]

3 Discussion

The nonlinear decrease in the effective thermal conductivity with increasing porosity [denominated “thermal stretching” in Yang et al. (2013b)] can be explained by the combination of two mechanisms: (i) the reduction in the average cross section of the conducting material and (ii) the increase in heat transfer distance (increase in the tortuosity of heat flow lines). In the presented unit-cell model, these mechanisms are triggered by:

• The shell thickness h is proportional to the volume fraction of the solid material phase (see Eq. 5). Accordingly, increasing porosity reduces the average cross section of the conducting material.

• The overlap of the spherical shells ($\bar{r}$ in Fig. 2a) decreases with increasing porosity and elongates the heat transfer distance (increasing tortuosity).

Note that the nonlinear response of the unit-cell model, i.e., ${\sigma }_{\hbox {eff}}/{\sigma }_{\hbox {s}}$, not proportional to $f_{\hbox {s}}$ stems from the latter, i.e., changing heat transfer distance due to shell overlap.

Figure 3 shows the model response according to Eq. (16) and a comparison with experimental data listed in the Introduction. The prediction of the spherical shell-based unit-cell model lies between the model response of the homogenization schemes from the effective medium/field theory introduced in Sect. 1, i.e., the Maxwell–Euken expression and the differential scheme, respectively. Note that for all three modeling approaches, a spherical pore morphology was underlain for derivation of the scaling relations depict in Fig. 3, as the focus of this paper is the assessment of an alternative geometrical configuration of conducting and non-conducting material phase, respectively: interconnected thin shells versus matrix/pore morphology in the classical homogenization schemes. Future work may be devoted to extension of the spherical shell-based unit-cell model toward more complex pore shapes, e.g., oblate or prolate spheroids, respectively, for a more realistic modeling of real-life materials. This extension is, however, beyond the scopes of this paper.

A thin spherical shell-based unit-cell model similar to the one shown in Fig. 2 has been employed in Pichler and Lackner (2012, 2013) for determination of the effective stiffness of closed-cell foams. From the modeling perspective, the latter is similar to the transport problems dealt within this paper—negligible stiffness and negligible conductivity, respectively, in the pore space. In the high porosity regime, unit-cell modeling leads to $E_{\hbox {eff}}/E_{\hbox {s}}\propto f_{\hbox {s}}^{3/2}$, representing experimental data well, with $E_{\hbox {eff}}$ and $E_{\hbox {s}}$ denoting Young’s modulus of foam and solid material phase, respectively. This lies between the model response of homogenization schemes from the effective medium theory: (i) $E_{\hbox {eff}}/E_{\hbox {s}}\propto f_{\hbox {s}}$ for the Mori–Tanaka scheme, the mechanical equivalent to the Maxwell–Euken expression (Mori and Tanaka 1973) and (ii) $E_{\hbox {eff}}/E_{\hbox {s}}\propto f_{\hbox {s}}^2$ for the differential scheme (McLaughlin 1977; Norris 1985). One may conclude that with a sound geometrical representation of the morphology of the highly porous materials cross-property (mechanical, thermal, electrical, etc.) application of homogenization procedures seems feasible.

Appendix: Consideration of Non-Spherical Pore Shape in Classical Homogenization Schemes According to Sevostianov et al. (2006), Sevostianov and Kachanov (2013)

For negligible conductivity in the pore space and isotropic orientation distribution of spheroidal pores, the shape factor ${\eta }$ can be determined as follows. With the aspect ratio ${\gamma }$ follows (Sevostianov et al. 2006; Sevostianov and Kachanov 2013)

$$\begin{aligned} G= & {} \displaystyle \frac{1}{{\gamma }\displaystyle \sqrt{1-{\gamma }^2}} \arctan \displaystyle \frac{\displaystyle \sqrt{1-{\gamma }^2}}{{\gamma }} \quad \hbox {for}\,\,\hbox {oblate}\,\,\hbox {shape}\,\,\,{\gamma }<1, \end{aligned}$$

(17)

$$\begin{aligned} G= & {} \displaystyle \frac{1}{2{\gamma }\displaystyle \sqrt{{\gamma }^2-1}} \ln \displaystyle \frac{{\gamma }+ \displaystyle \sqrt{{\gamma }^2-1}}{{\gamma }- \displaystyle \sqrt{{\gamma }^2-1}} \quad \hbox {for}\,\,\hbox {prolate}\,\,\hbox {shape}\,\,\,{\gamma }>1, \end{aligned}$$

(18)

further

$$\begin{aligned} F=\displaystyle \frac{{\gamma }^2 (1-G)}{2({\gamma }^2-1)}, \end{aligned}$$

(19)

and, finally,

$$\begin{aligned} {\eta }=A_1+A_2/3, \end{aligned}$$

(20)

with

$$\begin{aligned} A_1=\displaystyle \frac{1}{1-F} \quad \hbox {and} \quad A_2=\displaystyle \frac{1-3F}{2F(1-F)}. \end{aligned}$$

(21)

Figure 4 shows the shape factor ${\eta }$ as a function of aspect ratio ${\gamma }$; for oblate pore shape with ${\gamma }$ = 0.7, the shape factor is given as ${\eta }$ = 1.5180. Note that for non-spherical pore shape, the Kanaun–Levin method and the Mori–Tanaka scheme do not coincide, with

$$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}=\displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= \displaystyle \frac{1}{1+\displaystyle \frac{(1-f_{\hbox {s}}){\eta }}{1-2/3(1-f_{\hbox {s}}){\eta }}}= \displaystyle \frac{1-2/3{\eta }(1-f_{\hbox {s}})}{1+1/3{\eta }(1-f_{\hbox {s}})} \end{aligned}$$

(22)

and

$$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}=\displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= \displaystyle \frac{f_{\hbox {s}}}{f_{\hbox {s}}(1-{\eta })+{\eta }}, \end{aligned}$$

(23)

respectively. The prediction of the differential scheme is given as

$$\begin{aligned} \displaystyle \frac{{\sigma }_{\hbox {eff}}}{{\sigma }_{\hbox {s}}}=\displaystyle \frac{k_{\hbox {eff}}}{k_{\hbox {s}}}= f_{\hbox {s}}^{\eta }. \end{aligned}$$

(24)

Figure 5 shows the influence of consideration of prolate pore shape with ${\gamma }$ = 0.7 on the prediction of Mori–Tanaka scheme and differential scheme, respectively.

Fig. 4

Shape factor ${\eta }$ as a function of aspect ratio ${\gamma }$ according to Sevostianov et al. (2006), Sevostianov and Kachanov (2013)

Fig. 5

Influence of oblate pore shape with ${\gamma }$ = 0.7 on the prediction of Mori–Tanaka scheme and differential scheme, respectively (data taken from Sevostianov et al. (2006), for modeling ${\sigma }_{\hbox {s}}$ was set to 24 MS/m)