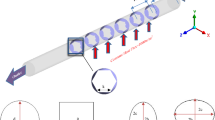
Abstract
The natural convection heat transfer of air in a porous media can be controlled by gradient magnetic field. Thermomagnetic convection of air in a porous cubic enclosure with an electric coil inclined around the \(Y\) axis was numerically investigated. The Biot–Savart law was used to calculate the magnetic field. The governing equations in primitive variables were discretized by the finite-volume method and solved by the SIMPLE algorithm. The flow and temperature fields for the air natural convection were presented and the mean Nusselt number on the hot wall was calculated and compared. The results show that both the magnetic force and coil inclination have significant effect on the flow field and heat transfer in a porous cubic enclosure, the natural convection heat transfer of air can be enhanced or controlled by applying gradient magnetic field.









Similar content being viewed by others
Abbreviations
- \({\varvec{b}}\) :
-
Magnetic flux density (T)
- \(b_{0}\) :
-
Reference magnetic flux density, \(b_0 =\frac{\mu _\mathrm{m} i}{L}\) (T)
- \({\varvec{B}}\) :
-
Dimensionless magnetic flux
- C :
-
\(C=1+\frac{1}{T_0 \beta }\)
- Da :
-
Darcy number, \(\frac{\kappa }{L^{2}}\)
- \(g\) :
-
Gravitational acceleration (m s\(^{-2}\))
- \(i\) :
-
Electric current in a coil (A)
- k :
-
Thermal conductivity (W m\(^{-1}\) K\(^{-1}\))
- \(L\) :
-
Length of a cubic enclosure (m)
- \(Nu_{m}\) :
-
Average Nusselt number
- Pr :
-
Prandtl number, \(Pr=\frac{\nu }{\alpha }\)
- \(p\) :
-
Pressure (Pa)
- \(P\) :
-
Dimensionless pressure
- \(r\) :
-
Radius of the coil (m)
- \({\varvec{r}}\) :
-
Position vector (m)
- \({\varvec{R}}\) :
-
Dimensionless position vector
- Ra :
-
Rayleigh number, \(Ra=\frac{g\beta (T_\mathrm{h} -T_\mathrm{c} )L^{3}}{\alpha \nu }\)
- \({\varvec{s}}\) :
-
Tangential element of a coil (m)
- \({\varvec{S}}\) :
-
Dimensionless tangential element of a coil
- \(T_{0}\) :
-
\(T_0 =\frac{T_\mathrm{h} +T_\mathrm{c} }{2}\) (K)
- \(T_\mathrm{c}\) :
-
Cold wall temperature (K)
- \(T\) :
-
Temperature (K)
- \(T_\mathrm{h}\) :
-
Hot wall temperature (K)
- \(u,v,w\) :
-
Velocity components (m s\(^{-1}\))
- \(U,V,W\) :
-
Dimensionless velocity components
- \(y_\mathrm{euler}\) :
-
Rotation angle around the \(Y\) axis (\(^{\circ }\))
- \(x,y,z\) :
-
Cartesian coordinates
- \(X,Y,Z\) :
-
Dimensionless Cartesian coordinates
- \(\alpha \) :
-
Thermal diffusivity (m s\(^{-1}\))
- \(\beta \) :
-
Thermal expansion coefficient (K\(^{-1}\))
- \(\gamma \) :
-
Dimensionless magnetic strength parameter, \(\gamma =\frac{\chi _0 b_0^2 }{\mu _\mathrm{m} gL}\)
- \(\theta \) :
-
Dimensionless temperature, \(\theta _f =\frac{T-T_0 }{T_\mathrm{h} -T_\mathrm{c}}\)
- \(\mu _{0}\) :
-
Magnetic permeability of vacuum (H m\(^{-1}\))
- \(\mu _\mathrm{m}\) :
-
Magnetic permeability (H m\(^{-1}\))
- \(\nu \) :
-
Kinematic viscosity (m\(^{2}\) s\(^{-1}\))
- \(\rho \) :
-
Density (kg m\(^{-3}\))
- \(\chi \) :
-
Magnetic susceptibility (m\(^{3}\) kg\(^{-1}\))
- \(\chi _{0}\) :
-
Reference mass magnetic susceptibility (m\(^{3}\) kg\(^{-1}\))
- \(\upkappa \) :
-
Permeability (m\(^{2}\))
- 0:
-
Reference value
- c:
-
Hot
- h:
-
Cold
References
Akamatsu, M., Higano, M., Takahashi, Y., et al.: Numerical computation on the control of aerial flow by the magnetizing force in gravitational and nongravitational fields. Numer. Heat Transf. A 43(1), 9–19 (2003)
Akamatsu, M., Higano, M., Takahashi, Y., et al.: Numerical prediction on heat transfer phenomenon in paramagnetic and diamagnetic fluids under a vertical magnetic field gradient. IEEE Trans. Appl. Supercond. 14(2), 1674–1681 (2004)
Bednarz, T., Tagawa, T., Kaneda, M., et al.: Magnetic and gravitational convection of air with a coil inclined around the X axis. Numer. Heat Transf. A 46(1), 99–113 (2004)
Bednarz, T., Tagawa, T., Kaneda, M., et al.: Convection of air in a cubic enclosure with an electric coil inclined in general orientations. Fluid Dyn. Res. 36(2), 91–106 (2005)
Bednarz, T., Fornalik, E., Ozoe, H., et al.: Influence of a horizontal magnetic field on the natural convection of paramagnetic fluid in a cube heated and cooled from two vertical side walls. Int. J. Therm. Sci. 47(6), 668–679 (2008)
Bednarz, T.P., Lei, C., Patterson, J.C., et al.: Effects of a transverse, horizontal magnetic field on natural convection of a paramagnetic fluid in a cube. Int. J. Therm. Sci. 48(1), 26–33 (2009)
Braithwaite, D., Beaugnon, E., Tournier, R.: Magnetically controlled convection in a paramagnetic fluid. Nature 354, 134–136 (1991)
Carruthers, J.R., Wolfe, R.: Magnetothermal convection in insulation paramagnetic fluids. J. Appl. Phys. 39(12), 5718–5722 (1968)
Filar, P., Fornalik, E., Kaneda, M.: Three-dimensional numerical computation for magnetic convection of air inside a cylinder heated and cooled isothermally from a side wall. Int. J. Heat Mass Transf. 48(9), 1858–1867 (2005)
Fornalik, E., Filar, P., Tagawa, T., et al.: Experimental study on the magnetic convection in a vertical cylinder. Exp. Therm. Fluid Sci. 29(8), 971–980 (2005)
Gray, D.D., Huang, J., Edwards, B.F.: Two dimensional magnetothermal plumes. Int. J. Eng. Sci. 39(16), 1837–1861 (2001)
Huang, J., Edwards, B.F., Gray, D.D.: Magnetic control of convection in nonconducting paramagnetic fluids. Phys. Rev. E 57(1), R29–E31 (1998a)
Huang, J., Gray, D.D., Edwards, B.F.: Thermoconvective instability of paramagnetic fluids in a nonuniform magnetic field. Phys. Rev. E 57(5), 5564–5571 (1998b)
Huang, J., Gray, D.D., Edwards, B.F.: Magnetic control of convection in nonconducting diamagnetic fluids. Phys. Rev. E 58(4), 5164–5167 (1998c)
Kaneda, M., Tagawa, T., Ozoe, H.: Convection induced by a cusp-shaped magnetic field for air in a cube heated from above and cooled from below. J. Heat Transf. 124(1), 17–25 (2002)
Lu, S.S., Lee, C.H.: Enhancement of heat transfer and flow rates of air flow in a pipe with an application of magnetic field. J. Enhanc. Heat Transf. 10(1), 45–60 (2003)
Qi, J.: Wakayama, N.I., Yabe, A.: Attenuation of natural convection by magnetic force in electro-nonconducting fluids media. J. Cryst. Growth 204(3), 408–412 (1999)
Qi, J., Wakayama, N.I., Yabe, A.: Magnetic control of thermal convection in electrically non-conducting or low conducting paramagnetic fluids. Int. J. Heat Mass Transf. 44(16), 3043–3052 (2001)
Shigemitsu, R., Tagawa, T., Ozoe, H.: Numerical computation for natural convection of air in a cubic enclosure under combination of magnetizing and gravitational forces. Numer. Heat Transf. A 43(5), 449–463 (2003)
Tagawa, T., Ozoe, H.: Convective and diffusive phenomena of air in a vertical cylinder under strong magnetic field. Numer. Heat Transf. B Fundam. 41(3), 1–14 (2002)
Vafai, K.: Handbook of porous media, 2nd edn. Taylor & Francis, New York (2005)
Wakayama, N.I.: Use of magnetic force to control convection. Proc. SPIE 3792, 48–55 (1999)
Wakayama, N.I., Yabe, A.: Magnetic control of thermal convection in electrically non-conducting or low conducting paramagnetic fluids. Int. J. Heat Mass Transf. 44(16), 3043–3052 (2001)
Wang, L.B., Wakayama, N.I.: Control of natural convection in non- and low-conducting diamagnetic fluids in a cubical enclosure using inhomogeneous magnetic fields with different directions. Chem. Eng. Sci. 57(11), 1867–1876 (2002)
Wang, Q., Zeng, M., Huang, Z., et al.: Numerical investigation of natural convection in an inclined enclosure filled with porous medium under magnetic field. Int. J. Heat Mass Transf. 50(17–18), 3684–3689 (2007)
Yang, L., Ren, J., Song, Y., et al.: Free convection of a gas induced by a magnetic quadruple field. J. Magn. Magn. Mater. 261(3), 377–384 (2003)
Yang, L., Ren, J., Song, Y., et al.: Convection heat transfer enhancement of air in a rectangular duct by application of a magnetic quadrupole field. Int. J. Eng. Sci. 42(5–6), 491–507 (2004)
Zeng, M., Wang, Q., Huang, Z., et al.: Numerical investigation of natural convection in an enclosure filled with porous medium under magnetic field. Numer. Heat Transf. A 52(10), 959–971 (2007)
Zeng, M., Wang, Q., Ozoe, H., et al.: Natural convection of diamagnetic fluid in an enclosure filled with porous medium under magnetic field. Prog. Comput. Fluid Dyn. 9(2), 77–85 (2009)
Acknowledgments
This work was financially supported by the Scientific Research Fund of Hunan Provincial Science and Technology Department (2013GK3063).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jiang, C., Feng, W., Zhong, H. et al. Magnetic and Gravitational Convection of Air in a Porous Cubic Enclosure with a Coil Inclined Around the Y Axis. Transp Porous Med 102, 167–183 (2014). https://doi.org/10.1007/s11242-014-0270-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-014-0270-2