1 Introduction

Shale (compacted clay or mudstone), the most common of all rocks, has long been known for its tendency to swell upon adsorption of water and lose its structural integrity due to swelling. Instability in slopes and embankments are commonly encountered (Brooker and Peck 1993). Water-sensitive shale formations cause costly and time-consuming problems in drilling and completion of wells in petroleum industry (O’Brien and Chenevert 1973; Cheatham and Nahm 1990; Ipek et al. 2006). In the USA, the estimated damage costs for buildings and infrastructure in swelling soils and rocks exceed \({\$}\)15 billion each year (Nelson and Miller 1992). The American Society of Civil Engineers estimates that each year expansive soils cause a greater financial loss to property owners than earthquakes, floods, hurricanes, and tornadoes combined.

Most of previous studies on swelling behavior of geomaterials focused on measurements of swelling pressure, swelling coefficients, and free swelling potential using conventional swell tests in which the test samples were exposed to fresh water. The conventional swell test on clay and shale is very time-consuming, and it could take several months or years to reach its ultimate swelling (Low 1980; Sherwood 1992; Bailey et al. 1998; Mitchell and Soga 2005). Thus, an accelerated swell test could be very helpful to overcome this problem in cost and time saving.

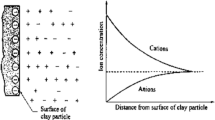
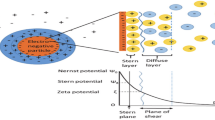
In clayey soil, direct observation of clay microfabric based on SEM and MIP measurements (Collins and McCown 1974; Delage and Lefebvre 1984; Griffiths and Joshi 1989) shows that clay sample is composed of two basic fabric elements: elementary particle clusters and particle assemblages. Elementary particle clusters are made up of clay particles in a dense and parallel (face-to-face contacts) configuration constituting aggregates of low internal porosity (inter-particle voids or microchannels). Water is adsorbed in this dense and parallel structure forming the so-called diffused double layer (DDL) system. Portion of the inter-particle water cannot flow freely in ambient condition. The amount of inter-particle water adsorbed to the clusters is controlled by the specific surface area (SSA) of the clay minerals and its physiochemical interaction between the adsorbed water and clay mineral surface area. Particle assemblages are formed by arrays of elementary particle clusters (edge-to-face contacts) forming the soil matrix or skeleton. The water occupying the pore spaces within the matrix (inter-matrix or macrovoids) is free water, which can move according to the applied or induced hydraulic gradient. Interaction between these two structures (micro- and macrovoids) governs the load transfer and fluid flow within the system. Changes in environmental load could induce not only pore fluid flow between the microvoids and macrovoids, but also stress transfer and redistribution between inter-particle aggregates and intra-matrix (Hueckel 1992).

Diffused double layer theory based on Gouy–Chapman model (Chapman 1913) has been used to describe the electrical potential and charge distribution for the case of adjacent interacting clay particles. The thickness of DDL is affected by pore fluid concentration, cation valence, pore fluid dielectric constant, and temperature (Mitchell and Soga 2005). The concept of osmotic pressure has been adopted to quantify the inter-particle repulsions due to the interacting double layers or the swelling of the double layers in clayey soils (Warkentin et al. 1957)) and compacted shales (Madsen and Muller-Vonmoos 1989). By this approach, the chemically induced or osmotic pressure required to prevent movement of water in clayey soil is assumed as a function of DDL thickness. As swelling is allowed to occur, the DDL thickness increases with the inward movement of the water molecules from the macrovoids to the microvoids. The pore fluid concentration inside the DDL decreases, and the osmotic pressure gradient between the micro- and macrovoids is reduced accordingly.

Multi-component mass transport under hydraulic, chemical, and electrical gradients in porous media is gaining increasing attention and interest in different fields of engineering. Acar and Alshawabkeh (1992, 1996a, b), Han et al. (2004), and Wu et al. (2007) applied an electrical potential through soils to extract contaminant ions from the soils. Cooper and Sanjit (1994) proposed the application of an electrical field to prevent the bit balling during the drilling process in shale formations. This study proposes the use of an electrical field to induce swelling in clay and shale samples.

There are quite a few mathematical models on multi-component mass (ion and fluid) transport process under hydraulic, chemical, and electrical gradients in macro (inter-matrix)-voids and micro (inter-particle)-channels in soil and shale (e.g., Acar and Alshawabkeh 1996b; Sherwood 1994; Mitchell and Soga 2005; Deriszadeh and Wong 2007).

The fluid flow through the macrovoids is dominantly controlled by the hydraulic and electrical gradients. In other words, the coupling effect of chemical gradient on the fluid flow is insignificant (Acar and Alshawabkeh 1996a, b). Therefore, the one-dimensional (1D) fluid flow equation could be written as follows:

$$\begin{aligned} q_\mathrm{w} =\frac{k_\mathrm{h} }{\gamma _\mathrm{w} }\frac{\partial u}{\partial x}+k_\mathrm{e} \frac{\partial E}{\partial x} \end{aligned}$$
(1)

where \(q_\mathrm{w}\) is the bulk fluid flow rate through macrovoids; \(u\) is the bulk fluid pressure; \(E\) is the electrical potential through the sample; \(k_\mathrm{h}\) and \(k_\mathrm{e}\) are the coefficients of hydraulic conductivity and electro-osmosis, respectively. The coefficient \(k_\mathrm{e}\) is a function of the permittivity and viscosity of the bulk fluid, the porosity of the sample, and the zeta potential (Acar and Alshawabkeh 1992). The value of \(k_\mathrm{e}\) is very small if the ionic concentrations are low.

Flux of each ionic species could be described as follows:

$$\begin{aligned} J_\mathrm{i} =-D_\mathrm{i} \frac{\partial c_\mathrm{i} }{\partial x}-c_\mathrm{i} q_\mathrm{w} -c_\mathrm{i} \frac{D_\mathrm{i} z_\mathrm{i} F}{RT}\left( {\frac{\partial E}{\partial x}}\right) \end{aligned}$$
(2)

where \(J_\mathrm{i}\) is the flow rate of each ionic species per unit area of the sample; \(D_\mathrm{i}\) is the coefficient of diffusion in the porous medium; \(F\) is the Faraday constant; \(R\) is the universal gas constant; \(T\) is the absolute temperature; and \(z\) is the valence of each ionic species. Recording the electrical current with time in the experiment could be useful to estimate the rate of ion production/consumption as well as the ionic flow through the sample. The electrical current is the net electrical charges passing through the sample. Therefore, the expected electrical current per unit area of the sample (i.e., current density) can be calculated as follows:

$$\begin{aligned} I=F \sum \limits _\mathrm{i} {z_\mathrm{i} J_\mathrm{i} } \end{aligned}$$
(3)

The application of an electrical potential gradient across a clay or shale sample saturated with NaCl solution is analogous to the electrolysis of brine, except that the sample contains potential swelling clay particles. In conventional swell tests, ions diffuse from the macrovoids out from the sample due to the chemical gradient, and the subsequent induced concentration gradient between the macrovoids and the microchannels is the main source of swelling process. However, the fluid flow from the macrovoids to the microchannels is a relatively quick process as illustrated by Sherwood (1994). Thus, the swelling process is dominated by the rates of ion and fluid flows through the macrovoids in the shale. For geomaterials with low coefficients of ion diffusion and hydraulic conductivity, the ion transport through the bulk fluid of the material is a time-consuming process (Mitchell and Soga 2005), and consequently, the fluid flow toward the inter-particle microchannels due to the chemically induced swelling would have a very low rate.

According to Eqs. (1) and (2), application of an electrical field could alter the behavior of the 1D swell test in two ways. Firstly, the fluid flow rate across the sample is enhanced by the electrical potential gradient, and its rate is no longer limited by the hydraulic flow. However, the drainage path is one way in this 1D experimental setup. Secondly, the applied electrical field might directly speed up the ion extraction from the bulk fluid by applying an additional driving force for the mass transport through the sample. While ions are extracted quickly, the concentration gradient between the macrovoids and the microchannels grows rapidly, and it subsequently results in the development of an osmotic pressure (Mitchell and Soga 2005). This osmotic pressure acts as a matric suction pressure and enhances the fluid flow from the macrovoids to the microchannels due to the osmotically induced hydraulic gradient. In addition, the dilution of ionic concentration in the macrovoids is further accelerated by the convective flow term, i.e., the second term of Eq. (2).

The presence of the electrical field not only provides an additional driving force for ionic flow (i.e., migration of ions), but also could be a source of ion production or consumption. In fact, passing an electrical current through the sample could result in chemical reactions. Depending on the required energy for probable reactions, either water or available ions might be reduced or oxidized in the vicinity of each electrical compartment or electrode. The probable reactions at the cathode are as follows:

$$\begin{aligned}&\displaystyle 2 \mathrm{{H}}_{2}\mathrm{{O}}+2{\mathrm{{\overline{e}}}}\rightarrow \mathrm{{H}}_{2} +2 \mathrm{{OH}}^{-} \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \mathrm{{Me}}^{n+}+n{\mathrm{{\overline{e}}}}\rightarrow \mathrm{{Me}} \end{aligned}$$
(5)

where Me refers to metals. Since the required energy for water reduction is less than common metal ions in clay or shale (e.g., \(\hbox {Na}^{+},\; \hbox {K}^{+},\; \hbox {Mg}^{2+},\; \hbox {Ca}^{2+}\), etc.), the reaction according to Eq. (4) will dominantly occur at the cathode (Oldham and Myland 1994).

In the vicinity of anode, both of water oxidization and negative ions oxidization might occur as follows:

$$\begin{aligned}&\displaystyle 2 \hbox {Cl}^{-}\rightarrow \hbox {Cl}_{2} +2{\mathrm{{\overline{e}}}} \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle 2 \hbox {H}_{2} \hbox {O}\rightarrow \hbox {O}_{2} +4 \hbox {H}^{+}+4 {\mathrm{{\overline{e}}}} \end{aligned}$$
(7)

In fact, the required energy for oxidization of some negative ions is less than that for water, and for some others it is more. For example, if chloride is present at the anode, it will practically be oxidized easier than water and the reaction shown in Eq. (6) occurs, i.e., generation of chlorine gas. However, the required energy for oxidization of sulfate is more than that for water, and consequently, water would be oxidized, i.e., production of oxygen gas as shown in Eq. (7).

It is worth to note that water reduction of Eq. (4) and oxidization of Eq. (7) would happen at the cathode and anode, respectively, during the early stages of the test regardless of the required energy. At later stages when the ions become available, cations such as \(\mathrm{{Na}}^+\) and \(\mathrm{{Ca}}^{2+}\) migrate toward the cathode and they would be reduced according to the secondary reaction of Eq. (5). Thus, the concentration of Na+ ions in the pore fluid decreases gradually with time. At the same time, chlorine gas might be produced according to Eq. (7). The acid generated at the anode advances through the sample toward the cathode under the electrical field. At the opposite side, the alkaline medium developed at the cathode advances toward the anode. Since the concentration of positive ions is higher in the bulk fluid in clay-based materials, water would be subjected to the drag force and flows from the anode to the cathode. This flow of water (i.e., the electro-osmosis flow) retards the flow of alkaline front. Therefore, the advance of alkaline front would be slower than the acid front. Consequently, the acid front dominates across the sample Acar and Alshawabkeh (1992). In addition, when \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) ions travel through the sample and meet, they could react and produce water molecules.

Since the rate of the mentioned electrochemical reactions depends on the electrical current, one could use the recorded electrical current during the experiment to estimate the rate of ion production/consumption in the vicinity of electrical compartments, and also to provide insight into the ionic flows.

The objective of this study presented in this paper is to experimentally demonstrate the use of electrical potential gradient in enhancing the swelling process in clay and shale specimens. The first part of the paper describes test materials used, experimental setup, and testing results. The second part deals with test observations and discussion followed by concluding remarks.

2 Test Materials

The materials used in this study include reconstituted clay samples and natural shale cores recovered from the field. Reconstituted clay samples were prepared from pure kaolinite and bentonite minerals with sodium chloride solution (Table 1). Each reconstituted clay sample was prepared by mechanically mixing mineral powder with sodium chloride solution of specific concentration. The amount of NaCl solution used in reconstitution was 5% by weight above the clay liquid limit. The clay liquid limit is defined as the moisture content (in percent) at which the clay passes from a liquid state to a plastic state, i.e., the liquid limit is equal to the mass of moisture divided by the mass of dry clay solid. The plastic limit is the moisture content at which the clay changes from a plastic state to a semi-solid state. The liquid and plastic limits of the test materials are shown in Table 1. The clay slurry was allowed to consolidate in a stainless steel oedometer of 76 mm in height and diameter under a total stress of 200 kPa for a week to achieve complete dissipation of excess pore pressure. After full consolidation, the sample was retrieved, sealed inside a plastic bag, and stored in a moisture room prior to swell tests.

Table 1 Physical dimensions and properties of reconstituted clay and shale samples
Full size table

Two natural clay shale cores were recovered from Westgate Formation, Cold Lake, Alberta, and Middle Shale Formation, Wabamun, Alberta, respectively. The Westgate Formation shale was taken at a depth of 295 m from an observation well in a heavy oil thermal recovery plant near Cold Lake, Alberta, Canada (Gautam and Wong 2006). The Middle Formation shale was taken at a depth of 9 m from a drilled hole at the Highvale Mine near Lake Wabamun, Alberta, Canada (Small and Morgenstern 1992).

Table 1 shows physical dimensions and properties of reconstituted clay samples and shale cores. The SSA was determined using methylene blue absorption method (Cocka and Birland 1993). Based on the SSA measurement, the reconstituted kaolinite clay sample has the least swelling potential, followed by the Westgate Formation shale, Middle Formation shale, and bentonite clay sample. The coefficients of the hydraulic conductivity of the reconstituted clay samples were estimated from 1D consolidation tests, whereas those of the shale samples were measured from constant flow rate tests with pore fluid. The kaolinite and bentonite clay samples display the two extremes in hydraulic conductivity, and the natural shale cores fall within the range (Table 1).

3 Experimental Setup

Figure 1 shows a schematic of the experimental setup, which consists of three compartments (cells) for sample holder, anode, and cathode. Acrylic glass (Plexiglass) materials were used as main materials because of their non-electrically conductivity and strength to withstand any external load applied to the test sample.

Fig. 1
figure 1

Schematic showing the experimental setup of the electrically induced swell tests

Full size image

The sample holder is a 30-cm-long hollow cylindrical section with its inner diameter slightly larger than the sample diameter (samples of 76 and 89 mm in diameters were used in this study). The wall thickness of the sample holder is 11 mm. The sample holder acts like the confining ring in a floating-type oedometer.

The upper (anode) cell is a 14-cm-long hollow cylinder section with two closed ends, and its outer diameter is equal to the test sample diameter. The two ends are made of 15-mm-thick circular discs. Two holes are provided at the top end to facilitate cable electrode connection and allow for produced gas escape and water filling. A seating recess is made at the center of the top disc for application of an external load to the test sample. The bottom end is equipped with holes and circular grooves facilitating water contact with the test sample (Fig. 2a). A circular titanium (Grade 1) mesh is attached to the bottom end, which acts as anode. The titanium material has a high resistance against chemical corrosion.

Fig. 2
figure 2

Details of a upper cell with titanium mesh as anode, and b lower cell with titanium mesh as cathode

Full size image

The lower (cathode) cell consists of a circular section reservoir and a side tube (Fig. 1). The top end of the reservoir acts as a support and cathode. It has features similar to the bottom end of the upper cell with titanium mesh, grooves, and holes (Fig. 2b). The side tube allows for cable electrical connection and water filling.

4 Testing Procedures

A latex sleeve was mounted on the test sample with the upper cell resting on the top of the sample. Chemically inert vacuum grease was applied on the outside surfaces of the sample and upper cell, which prevented any fluid flow through the space between the sample and latex sleeve and allowed for 1D flow and electrical current through the sample. Then, the test sample with the upper cell was inserted into the sample holder. Vacuum grease was applied to the inner wall surface of the sample holder to reduce any friction induced by swelling and developed between the test sample and holder. Since the fluid transport is one-dimensional in the experimental setup and its velocity is very small, the sample aspect ratio is not one of the experimental criteria. The sample holder was then secured to the lower cell using six tightened rods so that both ends of the test sample were in contact with the electrodes. The setup was mounted on a loading frame consisting of a lever system (Fig. 3). The load was applied to the top end of the upper cell. A linear variable displacement transducer of 0.001 mm accuracy was installed on the top end of the upper cell to monitor the swelling deformation of the test sample during the experiment. Electrodes were connected to an electrical power source (Power Design Model TW5005), which can supply a maximum 200 V electrical potential at a maximum current of 50 mA. Since the electrical resistance of the test sample increased with time, it was necessary to adjust the electrical potential applied across the sample during the experiment. When the measured electrical current recorded a significant drop, the electrical potential would be raised incrementally. The applied electrical voltage and induced current were recorded continually during the experiment to detect the depletion of NaCl within the sample.

Fig. 3
figure 3

Experimental setup for constrained swell test under external load

Full size image

Deionized distilled water was used in the experiment. A constant head of 10 cm was maintained in the upper cell or on the top end of the sample. The bottom end of the sample was in contact with water exposed to the atmosphere, which was maintained by filling water continually in the side tube of the lower cell.

At the end of the swell test, the sample holder with the swollen sample and the upper cell inside was removed from the setup. X-ray computed tomography scanning was conducted to investigate the swelling deformation profile along the sample length. The CT scanner used in this study is General Electric Model Hi Speed CT/i. The settings were as follows: 120 kV (KVP), 150 mA (X-ray tube current), 0.8 s full rotation scan, and 25 cm FOV (field of view). The resolution of each pixel is 0.25 mm by 0.25 mm by 3 mm. Three CT scans were made along the sample length, two near the ends of the sample, i.e., near the anode and cathode ends, and one at the middle.

5 Test Types

Two types of swell tests were conducted: (1) free swell and (2) constrained swell. In the free swell tests, samples were allowed to swell freely without any external load applied to the samples. For testing reconstituted clay samples, one swell test was conducted without application of the electrical potential (conventional swell test), and the test results were compared to those observed in another swell test with application of the electrical potential (electrically induced swell test). For testing natural shale cores, the swell test was modified and divided into two phases due to the limited number of cores. In the first phase, the swell test was carried out without the application of the electrical potential. When the swelling rate started to level off, the second phase commenced by applying the electrical potential across the sample. This modification in testing was aimed at illustrating the effect of the electrical potential on the swelling rate. In the constrained swell test, the sample was allowed to swell under an external load with or without application of the electrical potential.

6 Results and Discussion

Figure 4 compares the swelling deformation versus time in the conventional and electrically induced free swell tests on reconstituted kaolinite clay samples as listed in Table 1. In the conventional free swell test, the swelling follows a hyperbolic curve. It took about 165 h to achieve a swell strain of 0.5 %. In contrast, the sample only took less than 20 h to swell up to 1.2 % strain, and the swelling rate started to level off thereafter and maintained at a very small swelling rate. The applied electrical potential and recorded electrical current during the electrically induced swell experiment are plotted in Fig. 5. The applied voltage was increased in six stages to maintain a certain electrical current flowing through the sample. The electrical current is an indicator of the net charges flowing through the sample. At each incremental stage, the electrical current dropped quickly indicating the concentration of NaCl decreasing with time or the ions being removed from the sample. Drop in the electrical current flowing through the sample indicates decrease in ionic concentration within the sample. The electrical conductivity decreases with decreasing ionic concentration. At the later stages of the experiment (Fig. 5), the applied electrical potential was required to be raised to maintain a small electric current. At 164 h, the electrical potential was raised to 100 V and the recorded electrical current was about 6 mA and decreased to 2 mA in 24 h.

Fig. 4
figure 4

Swelling behavior of reconstituted kaolinite clay sample in conventional and electrically induced free swell tests

Full size image
Fig. 5
figure 5

Applied electrical potential and recorded electrical current across the sample in the electrically induced free swell test on reconstituted kaolinite clay sample

Full size image

The experimental data of the conventional and electrically induced free swell tests on reconstituted bentonite clay samples (Table 1) are shown in Figs. 6 and 7, respectively. From Fig. 6, the bentonite clay sample in the conventional free swell test exhibits a hyperbolic swelling curve similar to the kaolinite clay sample, except that it took about 2,000 h to swell to a strain of about 28 %. The swelling behavior of the bentonite clay sample during the first stage up to about 500 h in the electrically induced free swell test is very similar to that in the conventional free swell test. The application of 50-V electrical potential across the sample appears to have no effect on the swelling deformation and its rate. However, the recorded electrical current did drop from the initial value of about 42 mA to a very low value within a short time period of about 80 h. The ion depletion was quite fast through the sample length, and thus development of chemically induced (osmotic) pressure inside the sample, but the inflow of the water from the upper cell into and through the sample was very slow due to the low coefficients of hydraulic and electro-osmotic conductivities of \(10^{-12}\) m/s and \(3\times 10^{-10}\,\hbox {m}^{2}/\hbox {V}\,\hbox {s}\), respectively (Deriszadeh 2012). This behavior throws a clear contrast to the observations in the swell tests on the kaolinite clay samples shown in Figs. 4 and 5. The application of the electrical potential across the kaolinite clay sample has an instantaneous impact on the swelling even the electrical potential was at 4 V. This is attributed to the fact that the kaolinite clay sample has relatively high coefficients of hydraulic and electro-osmotic conductivities of \(10^{-9}\) m/s and \(10^{-9}\, \hbox {m}^{2}/\hbox {V}\,\mathrm{{s}}\), respectively (Deriszadeh 2012). However, from Fig. 6, the swelling rate of the bentonite clay sample started to increase once the applied voltage was increased from 50 to 75 V. The recorded electrical current was still low, confirming the almost complete depletion of mobile ions due to electrolysis. The swelling of the sample during this stage was dominated by the inflow due to the electrical potential gradient rather than the osmotically induced hydraulic gradient. The results of Fig. 6 show clearly the application that the electrical potential increases the swelling rate of the bentonite clay sample, and the rate is still significant compared to that observed in the conventional free swell test after 1800 h, showing no trend of leveling off.

Fig. 6
figure 6

Swelling behavior of reconstituted bentonite clay sample in conventional and electrically induced free swell tests

Full size image
Fig. 7
figure 7

Applied electrical potential and recorded electrical current across the sample in the electrically induced free swell test on reconstituted bentonite clay sample

Full size image

Addition of kaolinite to the bentonite sample has a significant effect on the swelling of the reconstituted clay mixture. Figures 8 and 9 compare the swelling behavior of reconstituted clay samples made of 50 % kaolinite and 50 % bentonite by weight saturated with 5 % NaCl solution (Table 1) under conventional and electrically induced free swell conditions. In the conventional swell test, the mixed sample expanded up to a 6.5 % strain over a period of about 410 h. The application of an electrical potential even at 8 V increased the swelling rate significantly. This is because the kaolinite content added increased the hydraulic conductivity of the sample (the coefficients of hydraulic conductivities of pure bentonite and mixed kaolinite–bentonite samples are \(10^{-12}\,\mathrm{{m}}/\mathrm{{s}}\) and \(8\times 10^{-11}\,\mathrm{{m}}/\mathrm{{s}}\), respectively), thereby increasing the fluid flow rate and supplying the fluid from the macrovoids to the microchannels for swelling (Deriszadeh 2012). The swell strain was about four times that in the conventional swell over the same period.

Fig. 8
figure 8

Swelling behavior of reconstituted kaolinite–bentonite clay sample in conventional and electrically induced free swell tests

Full size image
Fig. 9
figure 9

Applied electrical potential and recorded electrical current across the sample in the electrically induced free swell test on reconstituted kaolinite–bentonite clay sample

Full size image

Due to the limited availability of the shale samples, conventional and electrically induced free swell tests were conducted on a same shale sample. Figure 10 compares the swelling deformation of the Westgate Formation shale (Table 1) under conventional and electrically induced free swell conditions. Figure 11 shows the applied electrical potential and measured electrical current during the experiment. The shale sample was allowed to swell freely in water for about 470 h, and then an electrical potential was applied to the sample. During the first phase, the sample swelled up to 2.4 % strain and the swell rate started to level off. As the electrical potential was applied, the swell rate increased instantaneously and significantly. The electrical current dropped quickly at each voltage increment. Eventually, a swell strain of about 7 % was recorded after an electrical potential of 200 V was applied and maintained for a period of about 1,200 h. The test results clearly demonstrate that the application of the electrical potential did enhance the ion depletion and the fluid inflow, and thus the swelling.

Fig. 10
figure 10

Swelling behavior of Westgate Formation shale in conventional and electrically induced free swell tests

Full size image
Fig. 11
figure 11

Applied electrical potential and recorded electrical current across the sample in the free swell test on Westgate Formation shale

Full size image

The effect of application of an external load on the swelling behavior of the Westgate Formation shale under the conventional and electrically induced swell conditions was illustrated in Fig. 12. The external load applied in the experiment was 100 kPa. The swell strains without and with the application of electrical potential are 0.1 and 3.5 %, respectively, much less than those without the external load (Fig. 10). Figure 13 presents the applied electrical potential and recorded electrical current during the electrically induced swell test. The recorded electrical current decayed quickly in each increment.

Fig. 12
figure 12

Swelling behavior of Westgate Formation shale in conventional and electrically induced constrained swell tests

Full size image
Fig. 13
figure 13

Applied electrical potential and recorded electrical current across the sample in the constrained swell test on Westgate Formation shale

Full size image

The swelling behavior of Middle Formation shale (Table 1) under the conventional and electrically induced free swell conditions was displayed in Fig. 14. The applied electrical potential and measured electrical current across the sample during the experiment are shown in Fig. 15. The Middle Formation shale yields similar behavior to those observed in the swell test on the Westgate Formation shale, except that the swell strains of the Middle Formation shale are much higher. This observation is consistent with the measurement of the physical properties of the shale. Middle Formation shale contains more clay content, and its SSA is much higher. Its high liquid limit indicates that it contains of high clay content and swelling clay such as smectite.

Fig. 14
figure 14

Swelling behavior of Middle Formation shale in conventional and electrically induced free swell tests

Full size image
Fig. 15
figure 15

Applied electrical potential and recorded electrical current across the sample in the free swell test on Middle Formation shale

Full size image

The application of the electrical potential in the swell test increases the fluid flow rate through the sample. In the presence of the external electrical potential gradient, a net drag force is applied to the water molecules by positive ions. As a result, the fluid flows through the sample from the positive end (anode) toward the negative end (cathode). This direction is the flow direction of the positive sodium ions. Consequently, the swelling deformation of the sample under the applicant of the electrical potential gradient would not be symmetrical, i.e., swelling starts at the vicinity of the anode and extends toward the cathode. CT scanning was used to validate such non-symmetrical swelling. Three CT scans were made on the swollen samples, two near the ends and one at the middle. Each scan consisted of a square matrix of CT numbers. The circular portion containing the clay or shale material was cropped for analysis. Figure 16 plots the CT number profiles along the diametrical axis at three scanned positions for the bentonite sample swollen under the application of the electrical potential. The section near the anode has the least CT number profile, followed by those at the middle and near the cathode, respectively. The lower the CT number, the less dense the material, which confirms the non-symmetrical swelling along the sample length under the application of the electrical potential. The bulk density or swelling strain of the swollen sample could be estimated from the CT number based on the calibration of standard materials (Keller 1997), but was not conducted and included in this paper. Thus, the CT scanning results of the electrically induced swelling in Middle Formation shale sample are plotted in Fig. 17 based on the raw CT numbers, and qualitatively interpreted. The sample displays a non-symmetrical swelling, consistent with that observed in the bentonite clay sample. However, it is observed that the CT profiles in the shale sample are less uniform than the reconstituted clay sample. The irregularities are due to the existence of minute fissures in the natural shale resulted from the deposition process (Fig. 18). Figure 18 shows the CT images of swollen bentonite and Westgate shale samples. Discrete fissures are clearly present in the swollen shale sample. Fluid has a higher propensity to penetrate into those fissures than into the matrix.

Fig. 16
figure 16

CT profiles at sections along the sample length for reconstituted bentonite clay sample

Full size image
Fig. 17
figure 17

CT profiles at section along the sample length for Middle Formation shale samples

Full size image
Fig. 18
figure 18

CT images for a reconstituted bentonite clay and b Middle Formation shale samples

Full size image

It is also of importance to note that the swelling observed in the electrically induced swell test might be different from that in the conventional swell test because the effect of electrochemical reaction might have some impact on the DDL spacing. Generation of heat and gas along with consumption and production of ionic species must be taken into account in the swelling mechanism, which requires further research. In addition, other system variables such as temperature, pore pressure, electrolyte concentration cation valence, chemical reaction, and fluid dielectric constant have impact on the swelling behavior which are beyond the scope of this study.

7 Concluding Remarks

Experimental studies on the application of an electrical field through saturated reconstituted clay samples and natural shale cores demonstrate the feasibility of enhancing the swell test using an electrical potential gradient. The application of the electrical field could affect the behavior of the swell test in two ways. Firstly, it might directly enhance the ion extraction from the bulk fluid by applying an additional driving force for mass transport through the sample. Secondly, while ions are depleted quickly, the concentration gradient between the macrovoids and microvoids develops rapidly. Therefore, fluid flow toward the microchannels due to the chemically induced (osmotic) gradient would be accelerated if the electrical potential gradient enhance the fluid flow through the macrovoids or the hydraulic conductivity is high, and it subsequently results in a faster swell test. It would be of practical significance if the swelling potential developed in this electrically induced swell test was the same as that in the conventional swell test. In addition, control swell tests in which the clay samples are exposed to its pore fluid should be conducted to evaluate the effect of electrolyte concentration on swelling. A mathematical framework describing the proposed test would be useful and valuable in data interpretation and analysis.