Abstract
The IEEE Audio Video Bridging (AVB) technology is nowadays under consideration in several automation domains, such as, automotive, avionics, and industrial communications. AVB offers several benefits, such as open specifications, the existence of multiple providers of electronic components, and the real-time support, as AVB provides bounded latency to real-time traffic classes. In addition to the above mentioned properties, in the automotive domain, comparing with the existing in-vehicle networks, AVB offers significant advantages in terms of high bandwidth, significant reduction of cabling costs, thickness and weight, while meeting the challenging EMC/EMI requirements. Recently, an improvement of the AVB protocol, called the AVB ST, was proposed in the literature, which allows for supporting scheduled traffic, i.e., a class of time-sensitive traffic that requires time-driven transmission and low latency. In this paper, we present a schedulability analysis for the real-time traffic crossing through the AVB ST network. In addition, we formally prove that, if the bandwidth in the network is allocated according to the AVB standard, the schedulability test based on response time analysis will fail for most cases even if, in reality, these cases are schedulable. In order to provide guarantees based on analysis test a bandwidth over-reservation is required. In this paper, we propose a solution to obtain a minimized bandwidth over-reservation. To the best of our knowledge, this is the first attempt to formally spot the limitation and to propose a solution for overcoming it. The proposed analysis is applied to both the AVB standard and the AVB ST. The analysis results are compared with the results of several simulative assessments, obtained using OMNeT++, on both automotive and industrial case studies. The comparison between the results of the analysis and the simulation ones shows the effectiveness of the analysis proposed in this work.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Distributed real-time systems are nowadays found in many applications in, for example, automotive industry, industrial process control, smart buildings and energy distribution facilities. In these applications the amount of data to be exchanged within the distributed system is growing. Often, these data exchanges have constrains with respect to timing. Ethernet solutions are being considered as promising solutions to handle the mentioned applications due to their features of high bandwidth support and wide availability. In particular, the IEEE 802.1 Audio/Video Bridging (AVB) specifications are being followed by both automotive and industrial control domains.
The Ethernet AVB consists of a set of technical standards to allow real-time traffic transmission. For this purpose, the AVB standard divides the traffic into different classes according to their priorities (currently, two real-time classes are defined, i.e., the Stream Reservation (SR) Class A and B), and adds a credit-based shaper (CBS) to prevent traffic bursts. Bandwidth reservation is realized through the Stream Reservation Protocol (SRP), as defined in the AVB standards. The IEEE Time Sensitive Networking (TSN) group is working on several projects aiming to provide the specifications that will allow time-synchronized low latency streaming services through 802 networks. In this regard, Scheduled Traffic (ST) enhancements are addressed in the recently published IEEE 802.1Qbv standard (2015). The standard foresees a periodically time window, called Protected Window, that is reserved for the transmission of ST traffic. The Protected Window is scheduled according to a set of rules associated to the transmission queue and not to the single ST message.
A different approach to support ST traffic in AVB networks (called AVB ST) was presented in Alderisi et al. (2013), which suggests to handle the Scheduled Traffic in a separate highest-priority class to be added on top of the already defined SR classes, so as to guarantee preferential service to this time-sensitive traffic class, which requires both time-driven transmission and low latency. Also, a Time-Aware Shaper (TAS), which allows traffic transmission based on a time schedule, is adopted to provide temporal isolation between the ST traffic and the other traffic classes, thus avoiding any interference on the ST traffic from the other traffic. The AVB ST proposal brings the following benefits: (i) short and strict latencies for the ST traffic, (ii) time-driven transmission, with off-line scheduling possibility, for the ST traffic, hence meeting the needs of time-sensitive control traffic, (iii) temporal isolation with other traffic classes, and (iv) not significant effect on the other traffic classes. Our focus in this paper is on the AVB ST networks. Moreover, the AVB ST allows for scheduling one time window for each ST message, according to the specific ST message period and length, using offset scheduling techniques. This approach compared to the IEEE 802.1Qbv entails a finer-grained scheduling of ST messages, thus a more optimized bandwidth utilization. More details on the main differences between the IEEE 802.1Qbv standard and the AVB ST are presented in Sect. 3.3.
1.1 Contributions
In all real-time application domains, timeliness guarantees are required. In fact, it is essential to provide an analytical method to achieve the worst-case latency of the messages in the network. Several timing analysis approaches for messages in AVB networks were presented, e.g., Diemer et al. (2012) and Bordoloi et al. (2014), however, none of them can support response time computation of messages in the presence of ST messages. In this paper, we identify the elements which influence the delay of messages when ST messages cross through the network. Then, we present a response time analysis for the different classes of traffic in the AVB ST. We follow the same response time analysis method as presented in Bordoloi et al. (2014). However, our analysis has the following dissimilarities compared to the analyses presented in Diemer et al. (2012) and Bordoloi et al. (2014): (i) we consider the effect of ST messages on the analysis, and (ii) we discuss the effect of queuing jitter from higher priority messages by showing potential optimism when jitter is neglected in the analysis, using a counterexample.
Furthermore, we focus on bandwidth reservation for messages in AVB networks. We show that the previously presented analyses do not lead to a schedulable result in most of the cases because of the tight bandwidth allocation dictated by the AVB standard. This problem stems from: (i) not considering the blocking by lower priority messages in the bandwidth reservation, (ii) not considering the queuing jitter of a message crossing multiple switches for the bandwidth reservation, and (iii) the inevitable pessimism in the analyses. We formally demonstrate this limitation. A solution is to increase the dictated bandwidth for the traffic classes, known as bandwidth over-reservation. Here, we propose a solution to obtain a minimized bandwidth over-reservation. The solution is general and can be used for both AVB and AVB ST networks. To the best of our knowledge, we formally show the limitation and propose a solution for the first time.
Finally, we conduct experiments in two types of application domains, automotive and automation networks. The architecture and traffic of the networks are inspired by close-to-industry case studies. In particular, for the automotive case study we referred to an architecture designed by BMW group (Lim et al. 2011), while for the automation case study we adopted the maximum number of switches that the standard guarantees. Then, we compute the response time of messages using the timing analysis presented in this paper, considering the bandwidth over-reservation. Also, we simulate the networks using OMNeT++ to compare the message response times with the computed ones, in order to show the effectiveness of the presented response time analysis.
1.2 Organization
The rest of the paper is organized as follows. The next section discusses related works on Ethernet AVB. Then, Sect. 3 presents the Ethernet AVB and AVB ST. Section 4 provides the system model. Section 5 recalls the previous response time analysis, while Sect. 6 presents the response time analysis for the AVB ST networks. Section 7 discusses the limitation of the analysis when allocating the bandwidth based on the AVB standard, and presents a solution to overcome it. The experiments on automation and automotive case studies are conducted in Sect. 8. Finally, Sect. 9 concludes the paper.
2 Related work
In this section, we describe research and extensions relevant to Ethernet AVB. Moreover, we provide a brief overview of existing schedulability analysis approaches for AVB networks.
2.1 AVB related research
Recently, the real-time performance of IEEE AVB has been investigated extensively in multiple application domains, namely automotive, aeronautics, and industrial automation. For automotive networks, the work in Lo Bello (2011) and Tuohy et al. (2015) indicate AVB as one of the possible candidates for real-time communication domain. Moreover, the AVB suitability for supporting traffic flows of both Advanced Driver Assistance Systems (ADAS) and multimedia/infotainment systems was proven in Steinbach et al. (2012), Alderisi et al. (2012, 2012). In Lim and Volker (2011) the capability of AVB to be used as an in-car backbone network for inter domain communication is discussed. As far as the industrial automation communication is concerned, the Ethernet AVB ability to deal with real-time traffic requirements typically found in industrial automation is addressed in Imtiaz et al. (2011) and Jasperneite et al. (2009). In Jasperneite et al. (2009) the latency of forwarding the traffic is pointed out as one of the main challenges. In fact, due to the shaper in IEEE 802.1Q, a real-time message might be delayed in every bridge resulting in a poor performance. Therefore, further improvements are foreseen, including (i) shortening the non-real-time messages that interfere with real-time messages, (ii) allowing only real-time messages or (iii) providing mechanisms to avoid the mentioned interference. Focusing on the avionics application, AVB performance is discussed in Land and Elliott (2011) and Heidinger et al. (2012). In Heidinger et al. (2012) the reliability of AVB was evaluated and results showed that AVB solutions may be applicable to applications belonging to lower safety classes that have less demanding requirements on reliability. This is mainly due to the complexity of dynamic bandwidth reservation in AVB and failure probability of devices evaluated in Heidinger et al. (2012). In Schneele and Geyer (2012), the AVB is compared to the AFDX standard and the outcome is that further work is needed for making AVB suitable for the aeronautic industry requirements. In order to tackle the aforementioned improvements several kinds of traffic shapers were analyzed in Thangamuthu et al. (2015) and the Time-Aware Shaper (TAS) proved to be the one that can offer the lowest latency along with good jitter performance, albeit with an increased configuration cost for the switches. TAS prevents interference on the scheduled traffic, thus the traffic can be delivered faster. The only delay that the scheduled traffic suffers from is the forwarding latency crossing the switches.
Approaches to reduce latency for high priority traffic in the AVB networks, such as packet preemption and fragmentation, are discussed in Imtiaz et al. (2012). Moreover, TAS or time windows were proposed in Pannel (2012) and Cummings (2012) for isolating class A streams from the interference due to other traffic types. However, these approaches map all time-sensitive flows on the same class (class A) irrespective of their heterogeneous sizes and time constraints. Such a choice is not beneficial to low latency small-size traffic, which should not be handled in the same queue as large messages in AVB. For this reason, the work in Alderisi et al. (2013) proposed to add a separate class on top of the AVB Stream Reservation Classes A and B to introduce support for ST traffic, while maintaining the other traffic classes provided by the AVB standard. The work adopted TAS to enforce temporal isolation between ST and other classes of traffic. It also proved that ST traffic achieves both low and predictable latency, without significantly affecting the SR traffic. In this paper, we focus on the proposal in Alderisi et al. (2013), named AVB ST network, as it introduces relatively high performance in transmission of time-sensitive traffic. The details of the AVB ST are discussed in Sect. 3.2.
2.2 Timing analysis approaches for Ethernet AVB
A number of timing analysis techniques were proposed for the Ethernet AVB networks, such as Imtiaz et al. (2009), Lee et al. (2006) and De Azua and Boyer (2014), each one using different approaches. For instance, the analysis presented in De Azua and Boyer (2014) applies the Network Calculus framework (Leboudec and Thiran 2001), while the one presented in Imtiaz et al. (2009) adopts delay computation. However, these analysis techniques are restricted to the computation of worst-case response time per-class, without distinguishing the individual messages’ response times. It should be noted that in many industrial systems a large number of messages are transmitted. For instance, in a modern truck 6000 messages are exchanged across several networks (Keynote 2013). Therefore, the delays of each individual message should be bounded, but this is not possible using the mentioned analysis approaches. Another analysis framework for the Ethernet AVB is presented in Reimann et al. (2013) and is based on Modular Performance Analysis (MPA) (Wandeler et al. 2006). In the presented analysis the interference from higher priority messages is not formally considered, i.e., multiple activations of higher priority messages are not taken into account.
A formal timing analysis is given in Diemer et al. (2012), where the response time of each individual message is computed in an Ethernet AVB architecture consisting of multiple switches. The recent work presented in Bordoloi et al. (2014) showed that the analysis in Diemer et al. (2012) considers only one blocking factor that results from lower priority messages, which is not the case in the Ethernet AVB, due to the traffic shaper. Thus, a new response time analysis is developed in Bordoloi et al. (2014). However, the proposed analysis is still limited to the constrained deadline traffic model, and a single-switch architecture. In this paper, we extend the response time analysis presented in Bordoloi et al. (2014) in two directions: (i) computing the response time of messages in Ethernet AVB when ST traffic is transmitted through the network, and (ii) considering the effect of queuing jitter from higher priority messages in multi-hop architectures.
3 Ethernet AVB basics
In this section, we present the Ethernet AVB protocol. Further, we describe the AVB ST approach.
3.1 The Ethernet AVB
The IEEE AVB standard consists of a set of technical standards. For our purposes here we mention the IEEE 802.1AS (2011) and the IEEE 802.1Q (2014). The IEEE 802.1AS Time Synchronization protocol is a variation of the IEEE 1588 (2008) standard, which provides precise time synchronization of the network nodes to a reference time with an accuracy better than 1 \(\upmu \)s. The IEEE 802.1Q provides Stream Reservation Protocol (SRP) that allows for reservation of resources (i.e., buffers and queues) within the switches (called bridges in the AVB terminology) along the path between the talker (i.e., the stream source node) and the listener (i.e., the stream final destination node). Moreover, the IEEE 802.1Q provides Queuing and Forwarding mechanism for AV Bridges to split time-critical and non-time-critical traffic into different traffic classes and applies the CBS algorithm that prevents traffic bursts by exploiting traffic shaping at the output ports of bridges and end nodes. The AVB standard guarantees a fixed maximum latency for up to seven hops within the network for two different Stream Reservation (SR) classes, i.e., 2 ms for class A and 50 ms for Class B. According to the CBS algorithm, each SR traffic class has an associate credit parameter, whose value changes within two limits, called loCredit and hiCredit, respectively. Pending messages in the queues may be transmitted only when their associated credit is zero or higher. During the message transmission the credit decreases at the sendSlope rate defined for the class. The credit is replenished at the constant rate idleSlope defined for the class when (i) the messages of that class are waiting for the transmission or (ii) when no more messages of the class are waiting, but credit is negative. If the credit is greater than zero and no more messages of the corresponding traffic class are waiting, the credit is immediately reset to zero. Figure 1 illustrates the operation of the CBS algorithm for classes A and B. At the beginning \(m_2\) is being transmitted, hence its credit (class B) decreases. At time \(t_1\) message \(m_1\) is ready in the queue of class A, thus its credit starts to increase. When at time \(t_3\) the transmission of \(m_2\) finishes, the transmission of \(m_1\) is initiated, as the credit for class A is positive. Moreover, credit of class B starts to increase as there is \(m_3\) pending for transmission. At time \(t_4\) transmission of \(m_1\) finishes and finally \(m_3\) is started for transmission. At time \(t_5\) since there is no pending traffic for class A, the credit immediately becomes zero.
The AVB ST approach presented in Alderisi et al. (2013) is summarised in Sect. 3.2 that shows a promising solution towards the support of ST traffic over AVB networks. The analysis and results in this paper are based on the AVB ST design presented in Alderisi et al. (2013).
3.2 Ethernet AVB ST
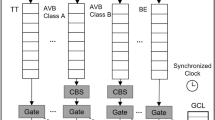
The AVB ST approach introduces a separate traffic class for scheduled traffic, called the Scheduled Traffic Class (ST Class), on top of the AVB SR Classes A and B. ST frames get the highest priority TAG according to the IEEE 802.1Q standard, as scheduled traffic includes time-sensitive high-priority flows (e.g., control traffic) that deserve the best service. For this reason, the ST class not only has a separate queue, but also does not undergo credit-based shaping, this way avoiding the latency increase that traffic shaping introduces. Conversely, SR class A and B take the second and the third highest priority, respectively, and undergo CBS shaper. Finally, best-effort traffic is handled by strict priority (as in the IEEE 802.1Q standard).
As ST flows are periodic, with fixed and a priori known period and frame size, they can be scheduled offline. Suitable scheduling techniques, e.g., offset scheduling (Palencia and González Harbour 1998), can be adopted at the network configuration time to ensure, by design, the absence of collisions between ST frames in the whole network (i.e., either in the end stations or in the bridges). The AVB ST approach requires that every node and every switch has to be aware of the right time for transmitting its ST traffic, therefore, synchronization is provided by the IEEE 802.1AS standard.
The AVB ST approach is based on two fundamental concepts, i.e., TAS and ST_Window. TAS is a mechanism that, in order to prevent any interference on ST frames from other traffic classes, inhibits the transmission of non-ST traffic that would delay the upcoming ST one. In other words, in AVB ST, the TAS temporally isolates the transmission of ST frames from non-ST frames, thus enabling time-sensitive frames to be transmitted from a bridge port without any interference from other traffic types. In the AVB ST approach the messages belonging to the SR Classes undergo both TAS and credit shaping, while best-effort messages go through TAS only, in compliance with the AVB standard. The traffic shaping in the AVB ST design presented in Alderisi et al. (2013) is shown in Fig. 2.
Traffic classes in AVB ST approach adopted from Lo Bello (2014)
According to the AVB ST design in Alderisi et al. (2013), the CBS and TAS operate as follows. When there is no ST transmission, the CBS operates as in Sect. 3.1.When there are ST messages to transmit, the TAS prevents the other classes far in advance to be certain that the ST transmission is fully protected. This protection window is the maximum transmission time of the registered SR classes in the worst-case, which is called a guard band. During the guard band and ST message transmission, the credit for SR classes that have pending messages increases at the rate of the relevant idleSlope. If there are no pending messages, the credit becomes immediately zero. Fig. 3 depicts an example of AVB ST transmission. An ST message (\(m_{\textit{ST}}\)) is scheduled for transmission at time \(t_3\). Although \(m_2\) from class A can be transmitted at time \(t_1\) as the credit is zero, the TAS prevents it as it would interfere with \(m_{\textit{ST}}\) transmission. Finally, \(m_2\) is sent after \(m_{\textit{ST}}\).
It should be noted that there is an intelligent way to assign a guard band. In fact, if the implementation determines which messages are waiting in the queue, for the guard band it is sufficient to use the maximum size of those messages instead of the maximum of all messages in that class.
The synchronization offered by the IEEE 802.1AS (2011) makes AVB bridges time-aware nodes (i.e., nodes provided with network timing information). Consequently, to implement TASs, only a suitable mechanism to allow/inhibit transmissions in a given time window and a way to configure the TAS based on the information provided by a Management Information Base (MIB) are needed.
The second fundamental concept for AVB ST is the ST_Window of each ST message. Such a window is defined as the time window, at the receiver side, within which the ST frame has to be received. In fact, as in the AVB ST approach ST frames are transmitted at known time instants and do not experience interference from the same class or from other traffic classes, the reception instant for any ST message can be calculated. The calculation has to consider the synchronization error between the nodes. The synchronization error is calculated using the drift of each node.
The results of comparative simulations of AVB ST and AVB in Alderisi et al. (2013) show a positive outcome for AVB ST, as ST traffic obtained low and predictable latency values, without significantly affecting SR traffic. The reason for this result is the combination of three features that are very beneficial for the ST class, namely, the offset-based scheduling, the temporal isolation provided by TAS and the absence of CBS shaping for the ST class.
3.3 Overview of the IEEE 802.1Qbv standard and differences with AVB ST
The standardization process of the IEEE TSN is in progress and several projects are ongoing. Recently, an amendment of the IEEE 802.1Q, called IEEE 802.1Qbv-2015 (2015), was released. The IEEE 802.1Qbv introduces the support for scheduled traffic. To achieve this goal, a transmission gate is associated with each queue and the state of the transmission gate determines whether or not queued frames can be selected for transmission. For a given queue the gate can be in one of two states, i.e., open or closed. According to the transmission selection algorithm, a frame waiting in a traffic class queue cannot be transmitted if the transmission gate relevant to the queue is in the closed state or if there is not enough time for transmitting the entire frame before the next gate-close event. The gate operations are contained in a list and are cyclically repeated with a period called OperCycleTime. Two consecutive gate operations (i.e., opening/closing of one or multiple gates) are spaced by an interval called TimeInterval. Such an interval is equal for all the operations contained in the list. The list of operations is configured to create the protected window (PW) for the queues in which the scheduled traffic is transmitted with no interference. This operational approach foresees a unique PW cyclically repeated for each scheduled traffic queue large enough to accommodate the transmission of all the ST messages within a cycle. This results in a non-optimized scheduling in the case of multiple ST messages with different lengths and periods leading to the consequent waste of bandwidth. In fact, the PW should be sized so as to accommodate the transmission of all the ST frames handled by a node within a cycle, regardless of whether some ST messages have a larger period and they are not transmitted in each cycle. Note that the IEEE 802.1Qbv standard does not exclude multiple PWs for one queue. However, scheduling multiple protected windows for each message may result in a very complex and difficult implementation. The main differences between the IEEE 802.1Qbv standard and AVB ST are summarized as follows.
-
According to the IEEE 802.1Qbv standard the idleSlope increases only if the gate is open, i.e., the idleSlope does not increase during the guard band and ST transmission. However, according to the design in Alderisi et al. (2013), the idleSlope for the SR classes increases even during the guard band and ST transmission (see Fig. 3).
-
The idleSlope increases in higher rate than when there is no ST transmission enabled. The duty cycle for the transmission gate is multiplied by the idleSlope according to Clause 8.6.8.2 in the IEEE 802.1Qbv standard (2015).
-
Unlike the IEEE 802.1Qbv standard the AVB ST provides scheduled windows, which consider the period and the length of each transmitted message. Therefore, ST Windows are scheduled only when there are ST messages to be transmitted and they are sized according to the frame length of the specific ST message, thus entailing a more efficient bandwidth utilization.
4 System model
In this section we describe the system model for the AVB network and the traffic, separately.
4.1 Network model
The AVB switches are considered to be full-duplex, i.e., the input and output of a switch port are isolated. Thus, the receiving message does not delay the transmission of a message. In this paper, we define a link as a connection between a node and a switch, as well as a connection between two switches. The link is denoted by l. Also, the switch has a fabric latency due to the hardware configuration for relaying messages, which is denoted by \(\epsilon \). This delay varies in different switches and usually is accounted for the time that the switch takes to process a received message and to insert it into the output port queue. The link delay due to wire and its physical characteristics is assumed to be very small and negligible.
Ethernet AVB uses a credit-based shaping algorithm to regulate the traffic transmission for two traffic classes, A and B, where class A has higher priority than class B. Assuming traffic class X, the replenishment rate (idleSlope) of the credit on link l is denoted by \(\alpha ^+_{X,l}\). Moreover, the credit is consumed when there is a transmission on a link, and the consumption rate (sendSlope) is specified by \(\alpha ^-_{X,l}\). The non-real-time traffic, known as best effort (BE) class, does not undergo the traffic shaper. Moreover, the total network bandwidth is denoted by R. It should also be noted that in the response time analysis the latency due to unprecise clock synchronization among the nodes is neglected.
4.2 Traffic model
For the traffic model, we use the real-time periodic model. A set of messages \(\Gamma \), composed by N messages, is characterized as follows:
In this model, \(C_i\) represents the transmission time of \(m_i\), that is obtained from the message size based on the total network bandwidth (R). In our model, a message is not larger than the maximum possible Ethernet size, hence message fragmentation is not required. Also, \(T_i\) and \(D_i\) denote the period and relative deadline of the message, respectively. In this paper, we consider the constrained deadline model, i.e., \(D_i \le T_i\). A message belongs to a traffic class based on its priority. Several messages in the set may share a priority level and be assigned to the same traffic class. In this case, the FIFO policy applies to them in the queues of the switch. Therefore, \(P_i\) represents the class of \(m_i\), e.g., \(P_i = \textit{class}\;A\). In the analysis, \(\textit{lp}(m_i)\), \(sp(m_i)\) and \(hp(m_i)\) are the sets of the messages with lower, the same and higher priority than that of \(m_i\), respectively. Moreover, \(F_i\) represents the message length, which can be derived as \(F_i = C_i \cdot R\). A message traversing several switches may get variation in delay, which is called queuing jitter and denoted by \(J_i\).
A message may traverse multiple switches to arrive to its destination node. A set of links that \(m_i\) passes through is defined by \(\mathcal {L}_i\), where the number of links in the set is defined by \(n_i = |\mathcal {L}_i|\). Each member of the set is a tuple \(l = \langle x, y \rangle \), that represents a link l between the nodes/switches x and y. Note that the sequence in the tuple shows the direction of the message transmission from x to y. In this analysis, we restricted the model to unicast streams, i.e., only one destination per message is assumed. The multicast and broadcast streams can be handled by transforming them into multiple unicast streams, however we leave that case as out of the scope of this paper for the sake of clarity. The response time of \(m_i\) is the temporal interval between the time at which the message is inserted in the queue of its source node (i.e., the time instant when it becomes ready for transmission), and the time at which the message is delivered to its destination node. The response time is specified by \(\textit{RT}_i\). Moreover, the response time of \(m_i\) when it is transmitted from a node/switch to another node/switch through link l in a multi-hop architecture is denoted by \(\textit{RT}^l_i\). Table 1 summarizes the notations that are used in this paper.
5 AVB response time analysis recap
In this section, we recall the response time analysis of messages in single-switch AVB networks (Bordoloi et al. 2014). Note that some optimization methods have been presented in Bordoloi et al. (2014), however we do not consider them when extending the analysis. The reason is that later in Sect. 7 we use the analysis to find the bandwidth over-reservation, which is not possible with the presented optimizations. New methods are required to achieve tighter analysis, which are left for future work. We present the response time analysis for each traffic class separately, considering that in plain AVB there are no ST messages transmitted in the network. Moreover, the presented analysis considers an architecture with a single switch. Therefore, the notation of link l is discarded from the equations.
5.1 Response time of messages belonging to class A
In Ethernet AVB, class A messages have the highest priority, hence there is no interference from higher priority messages for this class. On the other hand, there might be blocking by lower priority messages, e.g., a blocking by class B or BE traffic. As there are only two traffic classes, several messages may be assigned to the same class, therefore a message may be delayed by the messages with the same priority in the FIFO queue. Finally, as the message transmission is controlled by the traffic shaper, even if the message is ready for transmission it may be blocked due to a negative credit. To sum up, three different elements have to be considered in the worst-case response time of a message: (i) blocking by lower priority messages, (ii) interference from the same priority messages in the FIFO queue, and (iii) traffic shaping.
5.1.1 Blocking by lower priority messages
It has been shown in Bordoloi et al. (2014) that considering at most one lower priority message for the blocking is not enough. This is due to the traffic shaper behavior, as on every replenishment of the credit one message from the lower priority may be ready for transmission. We show the insufficiency of considering one lower priority message using an example illustrated in Fig. 4. In this example, \(m_1\) is the message under analysis, while LP and SP are lower and same priority messages, respectively. Initially, the credit increases as a lower priority message (\(\textit{LP}_1\)) is transmitted on the link. Afterwards, a message with the same priority, which is ahead of \(m_1\) in the FIFO queue, is transmitted. After the transmission of the same priority message, the credit becomes negative, therefore there is room for transmitting another lower priority message (\(\textit{LP}_2\)) with enough credit for transmission. Finally, \(m_1\) has a chance for transmission as the credit is positive. In this example, \(m_1\) experiences blocking by two lower priority messages, i.e., \(\textit{LP}_1\) and \(\textit{LP}_2\), due to traffic shaping.
However, it has been proved in Bordoloi et al. (2014) that considering an inflation factor for the same priority messages in the analysis makes it sufficient to take one lower priority message for the blocking term. This inflation factor is calculated by \(\left( 1 + \frac{\alpha ^-_A}{\alpha ^+_A}\right) \). We show the effect of the inflation factor using an example shown in Fig. 4. If we inflate the SP message by the mentioned inflated factor, it becomes the Inflated SP shown in Fig. 4. Thus, it covers \(\textit{LP}_1\), \(\textit{SP}\) and the replenishment of the credit to zero. Therefore, \(\textit{LP}_1\) does not need to be accounted for the analysis. The only lower priority message to consider is \(\textit{LP}_2\), which is transmitted before \(m_1\) in this example. In order to mathematically show the inflation factor, let us assume an interval of time in Fig. 4, in which the Inflated SP is transmitted. This interval is denoted by L in this example and it is the summation of \(\textit{LP}_1\), \(\textit{SP}\) and the replenishment duration denoted by H.
As the credit at the beginning and the end of the interval is zero, we can write:
Deriving H from above equation and inserting it in the calculation of L in Eq. (2), the interval length can be written as below:
Therefore, \(C_{\textit{SP}}\) can be inflated by the inflation factor, thus making the Inflated SP in Fig. 4, which does not include the transmission time of the lower priority message \(C_{\textit{LP}1}\). For more details the reader is referred to the formal proofs provided in Bordoloi et al. (2014).
5.1.2 Interference from the same priority messages
The interference from the same priority messages is the sum of the transmission times of all messages in the same traffic class. In a schedulable system where \(D_i \le T_i\), when a message is enqueued in a FIFO queue, at most one instance of the other messages can be ahead of the message in the queue (Davis et al. 2011). This means that if there are two instances of a message ahead of \(m_i\) in the FIFO queue, the system is not schedulable under the mentioned assumptions.
5.1.3 Traffic shaper effect
In the worst-case scenario the credit of the traffic shaper must be considered to be as the negative as possible when the message under analysis is ready for transmission (critical instant). In this case, the traffic shaper blocks the message until the credit increases to zero. Then, the worst-case response time is the time between the critical instant and the complete transmission of the message under analysis (WCRT in Fig. 5). In order to reduce the pessimism in the analysis, the traffic shaper effect is considered in the final phase, i.e., after the transmission of the message under analysis. Therefore, the negative credit replenishment time at the critical instant is removed, and the negative credit replenishment time after the transmission is added to the analysis (modified WCRT definition in Fig. 5). For more details the reader is referred to the proofs provided in Bordoloi et al. (2014).
According to the modified WCRT definition, the last interval of the transmission contains the blocking by a lower priority message, the message under analysis and the credit replenishment time. The replenishment time of the credit is computed as \(C_i\left( \frac{\alpha _A^-}{\alpha _A^+}\right) \). Therefore, the last interval is obtained as below:
Therefore, not only the same priority messages should be inflated by the inflation factor, but also the message under analysis should be inflated by the same inflation factor.
The response time of \(m_i\) in class A is computed using Eq. (6). The first term of the calculation is the blocking by lower priority messages, while the second term is the interference from the same priority messages when they are inflated. The transmission time of the message under analysis is added to the response time calculation, which is included in the second term of Eq. (6).
We can observe that, according to Eq. (6), the worst case response times of the messages in class A are equal. This scenario occurs due to the FIFO nature of the transmission queue. Basically, in the worst-case a message in a FIFO queue suffers from all other messages in the same queue. Therefore, the interference due to the same priority messages is the same for all messages in the queue. For class A, there is no interference from the higher priority messages and the blocking due to the lower priority messages is constant for all messages in class A. Thus, their worst-case response times are the same. Please note that this scenario occurs only for class A traffic.
5.2 Response time of messages belonging to class B
A message from class B is not only blocked by lower priority messages (i.e., by the BE traffic), but it can also suffer from the interference of the higher priority messages (i.e., by the traffic in class A). Therefore, besides the three elements mentioned in the class A analysis, the interference from higher priority messages should be also considered. Although we adopt the constrained deadline model, considering one instance of the message under analysis is not sufficient. Instead, the response time of several instances of the message during a busy period (Lehoczky 1990) must be calculated and the maximum among them is the worst-case response time. The busy period is the maximum time interval during which the resource is busy. Note that in Ethernet AVB the resource is busy either when there is an ongoing transmission on the link or when the queue is not empty, but the transmission is prevented due to a negative credit. The reason behind the need for considering multiple instances is the non-preemptive nature of the transmission, which is thoroughly discussed in the Controller Area Network (CAN) response time analysis (Davis et al. 2007). Under high network utilization, a message may delay subsequent transmission of the higher priority messages. Thus, the higher priority interference may be pushed through into the next period of the messages, causing larger response time in the next instance. Let us consider an example in Fig. 6, where we are interested in computing the response time for \(m_3\). In this example, \(m_1\) and \(m_2\) are higher priority messages than \(m_3\). Moreover, \(m_1\) has period of 4 time units, while the period of the other messages is 6 time units. The transmission time of \(m_1\) and \(m_3\) is 2 time units and for \(m_2\) is 1 time unit. The first instance of \(m_3\) is completely sent at time 5, hence its worst-case response time is 5 time units if we consider the first instance only. However, \(m_1\) is ready at time 4, but it cannot preempt \(m_3\) due to the non-preemptive nature of the transmission. Thus, its transmission starts at time 5 and its third transmission starts at time 8, thus pushing the transmission of \(m_3\). Then, transmission of the second instance of \(m_3\) starts at time 10 and completes at time 12, thus making the worst-case response time for the first instance equal to 6 time units instead of 5. Therefore, in the calculation of the worst-case response time, several instances should be examined.
Given the \(q^{th}\) instance of message \(m_i\) in the busy period, we compute the queuing delay \(w_i(q)\), which is the longest time from the start of the busy period until the beginning of the transmission of the \(q^{th}\) instance, as shown in Eq. (7). The equation is a recursive function that starts with an initial value for \(w_i(q)\) and terminates when the previous value of \(w_i(q)\) equals the new value derived by the equation.
The first term in Eq. (7) is the blocking by the lower priority messages. The second term is the transmission time of the message itself in the previous \(q-1\) instances. The third term is the interference from the same priority messages in the FIFO queue, excluding the message under analysis. The last term in the calculation is the interference from higher priority messages. Note that the inflation factor, as discussed before, is applied on the same priority messages including the message itself. Finally, the response time of \(m_i\), which is the maximum response time among the examined instances, is computed in Eq. (8). The first term of Eq. (8) is the queuing delay computed iteratively in Eq. (7), the second term is the number of periods for message \(m_i\) that has passed during the busy period, and the last term is the transmission time of the message itself.
The range of q for which the response time must be calculated is \([1, q_{\textit{max}}]\), where \(q_{\textit{max}}\) is the smallest positive integer q derived in Eq. (9). The left side of Eq. (9) is the length of the busy period. Therefore, by dividing the busy period length to the period of the message \(T_i\) (in the right side of Eq. 9), the maximum number of instances during the busy period is derived. The length of busy period is calculated by adding the blocking from lower priority messages, the interference from same and higher priority messages (i.e., the interference that makes the resource busy during the busy period).
6 Response time analysis for AVB ST networks
In this section, we present the response time analysis for class A and B messages for the case of AVB ST networks, in which the transmission of ST messages has to be taken into account. We also present the transmission delay of ST messages. To do so, we first present the analysis for different classes of messages in one link in the network. Then, we extend that to multi-hop networks.
6.1 Response time of messages in class A
In the approach presented in Alderisi et al. (2013) the messages in the queues associated to the SR classes undergo both TAS and CBS, while the BE messages go through TAS only. According to the TAS mechanism, any non-ST message that is queued and is ready for transmission has to wait not only for the duration of an ST message transmission, but also for an additional time, called a guard band. The guard band is enforced by TAS to avoid the transmission of non-ST traffic that would delay the next ST message. Therefore, when calculating the response time for messages in class A, not only the interference from ST messages should be taken into account, but also the guard band should be considered. For the response time analysis of messages in class A four elements are required. These elements include: (i) interference from higher priority messages (i.e., from ST messages and their guard band), (ii) blocking by lower priority messages, (iii) interference from the same priority messages in the FIFO queue, and (iv) traffic shaper effect.
6.1.1 Interference from higher priority messages
In the higher priority message interference for traffic class A, besides the ST messages, we have to consider the guard band of the ST messages. To do so, we define a virtual message per ST message, whose period and priority are the same as the ST message ones. Note that if ST messages are clustered for transmission, a virtual message for the whole cluster would be sufficient. However, this requires an offset-based scheduling algorithm for ST messages, that is out of the scope of this paper and is left for future work. The transmission time of the virtual message is the maximum transmission time of all messages in classes A, B and BE, whose transmission would not be finished before the starting of the ST message. This is due to the fact that TAS prevents any transmission that can interfere with ST transmission, which in the worst-case is the largest message taking the same route as the message under analysis. Fig. 7 shows a scenario in which a message from class A \(m_A\) could interfere with an \(\textit{ST}\) message \(m_{\textit{ST}}\) scheduled for transmission at time t, but it is prevented from being transmitted by the TAS. The virtual message in this case is depicted by \(C^*_{\textit{ST}}\).
Assuming \(m_k\) as an ST message with transmission time \(C_k\), the virtual message corresponding to \(m_k\) crossing link l is denoted by \(C^*_{k, l}\) and derived in Eq. (10). The equation gives the largest message among other traffic classes (A, B and BE), that traverse the same link as \(m_k\).
6.1.2 Blocking by lower priority messages
As it was discussed before, a high priority message may experience multiple instances of blocking by lower priority messages due to the traffic shaper. However, here we show that even when ST messages exist in the network, considering one blocking by the lower priority messages is sufficient if a proper inflation factor is applied to the same priority messages. To do so, we use the same methodology presented in Bordoloi et al. (2014).
A scheduling scenario for message \(m_1\) is depicted in Fig. 8 for link l. An interval of time is defined as the duration between the time at which the credit is zero and the time at which the credit is replenished to zero again, after the transmission of the ready messages (Fig. 8). In order to show that inflation of the same priority message covers the blocking time of class A messages by the lower priority message in presence of ST messages, we define an interval where LP, ST and SP messages are transmitted. In this example we consider that the ST message also includes the transmission time of its virtual message. The length of the interval L is calculated in the following equation, where H represents the time needed to replenish the negative credit to zero (see Fig. 8).
As the interval is defined between two zero credits, the total credit value remains zero. Thus, the credit value for the phase becomes:
Deriving H from the above equation, and inserting it to the interval length calculation (Eq. 11) we have the following:
Therefore, the length of the interval only depends on the transmission time of the same priority messages, even when ST messages exist in the network. The Inflated SP message is shown in Fig. 8. Note that there could be several same priority messages in one interval, where in that case \(C_{\textit{SP}}\) is the sum of them.
6.1.3 Interference from the same priority messages
In order to capture the worst-case scenario, we assume that all the same priority messages in the FIFO queue are ahead of the message under analysis. Moreover, as the model is constrained deadline, in a schedulable system, only one instance of the same priority messages can be ahead of the message under analysis in the FIFO queue.
6.1.4 Traffic shaper effect
Similar to the discussion for Fig. 5, the negative credit can be removed if the replenishment time after transmission of the message under analysis is taken into account.
The response time for messages in class A in link l is calculated in Eq. (14). The iteration starts from \(\textit{RT}^{l,(0)}_i = C_i\) and terminates when \(\textit{RT}^{l,(x)}_i = RT^{l,(x-1)}_i\), where x is the iteration number. The calculation does not need to examine several instances of the message in the busy period. The reason is that the ST messages are the only higher priority messages for class A, and they are strictly periodic. Also, TAS prevents any transmission that can interfere with the ST messages. Therefore, the ST messages cannot be pushed through into the next period of message \(m_i\). This means that the next instances of \(m_i\) cannot have larger response time than the first instance.
In Eq. (14), the first term represents the blocking by the lower priority messages, while the second term is the interference from the same priority messages, excluding the message itself. Also, the third term is the interference from the higher priority messages, which is only ST messages for class A. Therefore, the transmission time of virtual messages can be added to the ST transmission times, hence the guard band is also considered in the analysis. The fourth term is the transmission time of the message itself. As mentioned before, the inflation factor for the message under analysis is to cover the negative credit effect. When there is only one message in a class, i.e., \(sp(m_i) = \emptyset \), the credit of the class becomes negative only with that message. In a schedulable system with \(D_i \le T_i\), the credit should become zero at most by the next period of the message. Therefore, there is no negative credit for the message to be accounted for in the analysis. Consequently, the inflation factor of the message under analysis can be removed. Note that the message is delayed by the switch fabric latency (\(\varepsilon \)) accounted for the analysis.
6.2 Response time of messages in class B
Similarly to the analysis for class A traffic, blocking times due to lower priority messages and interference from the same and higher priority messages should be considered in the worst-case response time calculation for class B traffic. Following the same proof made in the previous analysis, considering one blocking by the lower priority messages is sufficient if the same priority messages are inflated by \((1 + \frac{\alpha ^-_B}{\alpha ^+_B})\). Moreover, the interference from higher priority messages does not only stem from ST messages, but also from messages in class A. In this analysis, we must consider multiple instances of the message under analysis. Therefore, the queuing delay \(w_i^l(q)\) in link l is calculated in Eq. (15). The first term in Eq. (15) is the blocking by lower priority messages, while the second term is the transmission of \(m_i\) in previous \(q-1\) instances. Again, the transmission time of \(m_i\) is inflated only when there is no same priority messages in the set. The third term is the interference from the same priority messages. Also, the fourth term is the interference from higher priority messages, consisting of classes A and ST messages. Finally, the last term is the interference of virtual messages to consider the guard band in the analysis. Note that the queuing jitter of traffic class A (not by ST) on link l is denoted by \(J_j^l\) and described in the next subsection (Sect. 6.5).
The maximum response time among \(q_{\textit{max}}\) instances of the message is the worst-case response time, as calculated in Eq. (16). Note that the switch fabric latency (\(\epsilon \)) is also included in the analysis. Moreover, the same scenario as in class A occurs for the transmission time of the message under analysis to account for the negative credit.
The response time must be examined for instances within a range \([1, q_{\textit{max}}]\), where \(q_{\textit{max}}\) is derived as the smallest positive integer value from Eq. (17). Similar to Eq. (9), the left side of Eq. (17) is the length of the busy period, hence dividing that by \(T_i\) gives the maximum number of instances that have passed during the busy period. To compute the busy period length the interference and blocking should be added to the transmission time of the message.
6.3 Transmission delay of messages in class ST
The ST messages are scheduled offline and TAS prevents any interference from lower priority messages. Therefore, the transmission delay of ST messages is equal to their transmission time and the switch fabric latency, which is shown in Eq. (18). Note that the switch fabric latency in the last link should be omitted as the last link is connected to the destination node, not a switch.
6.4 Multi-switch response time
In a multi-switch AVB architecture, messages are buffered in the queues of each switch through their route. Thus, the worst-case response time of a message traversing multiple switches is the sum of the per-hop response times, as shown in Eq. (19). Note that the wire latency is neglected in this calculation, whereas the switch fabric latency for each hop is already considered in each link. This means that as \(\epsilon \) was considered in each link, it is not needed in Eq. (19). Eq. (19) is used for classes A, B and ST.
6.5 Jitter of the higher priority interference
The response time analysis given in Bordoloi et al. (2014) is presented for a single-switch network without considering the traffic shaper of the nodes. Therefore, messages arrive to the switch at every period without variation in their delays. Thus, the queuing jitter due to crossing switches does not appear. The response time analysis presented in Diemer et al. (2012) covers multi-hop architecture, however the queuing jitter is not considered. Here we show using a counterexample that if we do not consider the queuing jitter of a message due to passing through switches, the analysis can give an optimistic result. In AVB ST the queuing jitter of class A can affect the response time of message in class B. However, the ST traffic is scheduled offline without interference from other traffic classes. Therefore, they do not have queuing jitter. In this section, we discuss the effect of queuing jitter from class A on the class B analysis.
Assume a network with 3 messages, from classes A, B and BE, for the same destination. The parameters of the messages are given in Table 2 (values refer to time units). The idleSlope (\(\alpha ^+_A\)) and sendSlope (\(\alpha ^-_A\)) for class A are 0.4 and 0.6, respectively, while the idleSlope (\(\alpha ^+_B\)) and sendSlope (\(\alpha ^-_B\)) for class B are both equal to 0.5. In this example we assumed \(\epsilon = 0\).
A possible scheduling trace with jitter is shown in Fig. 9. In this scenario, we assume that \(m_A\) is arrived with a jitter of 4 time units, and \(m_{BE}\) started its transmission slightly before that, as the credit for \(m_B\) was negative. According to the figure the response time of \(m_B\) is 10 time units. However, when the response time of \(m_B\) is calculated using the analysis presented in this paper, without considering jitter, the response time becomes 8 time units as shown in Eq. (21), that is less than 10 time units shown in the figure. This is in contrast with the scheduling scenario shown in Fig. 9. In Eq. (21), \(w_B\) and \(\textit{RT}_B\) are calculated using Eqs. (15) and (16), respectively. Note that the maximum number of instances calculated in Eq. (17) is 1 in this example, i.e., \(w_B\) and \(\textit{RT}_B\) are only calculated for \(q = 1\). Moreover, the inflation factor for the message under analysis \(m_B\) is not considered as there is no interference from the same priority as \(m_B\).
A scenario with jitter for the example depicted in Table 2
Now, when we consider the jitter of \(m_A\) in the calculation (according to Eq. 15) the response time of message \(m_B\) becomes 10 (see Eq. 21), that is just equal to the depicted one in the figure. Again, in this calculation \(q = 1\) from Eq. (17).
In this work, we apply jitter similarly to the other response time analysis for switched Ethernet networks, e.g., Martin and Minet (2006), by adding it to the calculation of busy period. In order to compute the queuing jitter of a message in class A, we need to find the difference between the worst-case and the best-case response times of the message from its source node to the link that we are calculating the response time of \(m_i\) in class B. This means that the response time for class A in all hops should be computed before the response time for class B. Equation (22) derives the queuing jitter of \(m_j\) from class A in link l.
Note that the switch fabric latency (\(\epsilon \)) is considered for both best- and worst-case response times, however it is subtracted in Eq. (22).
7 Bandwidth reservation for AVB networks
As mentioned before, two formal response time analysis techniques are presented in Diemer et al. (2012) and Bordoloi et al. (2014) to compute the delay of messages in AVB networks. The response time analysis techniques provide safe upper bounds on the worst-case response time of messages. In the presented analysis, besides the messages’ parameters, the idleSlope (reserved bandwidth) is taken into account. The standard defines how to set the idleSlope. Normally, the IEEE 802.1Q standard provides two modes of operation, which are (i) when the SRP is disabled or (ii) when the SRP is enabled. When the SRP is disabled, the idleSlope per class and per link is assigned by management through the adminIdleSlope parameter (see Clause 34.3 in IEEE 2014), which is equal to the operIdleSlope parameter. The operIdleSlope parameter is the actual bandwidth and its calculation is given in the standard (see Clause 34.4 in IEEE 2014). However, when the SRP is enabled, the SRP mechanism uses the Multiple Stream Registration Protocol (MSRP) to register the bandwidth through the operIdleSlope parameter per class and per link. According to the SRP, class A streams should transmit frames at a frequency multiple or equal to 8000 frames / s and class B streams at a frequency multiple or equal to 4000 frames / s. Also, in the case of lower message transmission frequencies, the same bandwidth for 8000 or 4000 frames / s has to be reserved. Such an over-reservation is very pessimistic when the frequency is lower than the one provided by the SR class. For this reason, in this paper, we assume that the SRP is disabled. Therefore, the bandwidth to be set in the operIdleSlope parameter is calculated as the product between the frame size (MaxFrameSize) and the frame transmission rate (maxFrameRate). This calculation, given in Clause 34.4 of the IEEE 802.1Q standard (2014), can be seen as the message utilization. Nevertheless, in most of the cases the response time analysis cannot converge to a schedulable result if the bandwidth is reserved according to the standard. This is because (i) lower priority blocking is not accounted for in the calculation of idleSlope, and (ii) the queuing jitter in multi-switch is not taken into account.
In the experiments that are performed in Diemer et al. (2012) bandwidth over-reservation is applied. The required idleSlope for the traffic shaper is multiplied by a value between 2 to 32, i.e., the reserved bandwidth for the messages is increased by 2–32 times. The over-reservation is considered for experimental purpose only, without giving a formal explanation about why and how to set it. Moreover, in the analysis presented in Bordoloi et al. (2014), the idleSlope is chosen randomly for the experiments. In this section, we show this limitation and for the sake of simplicity we show the limitation in the context of plain AVB (i.e., without ST traffic) and for the traffic class A. However, the limitation also applies to traffic class B and to AVB ST networks. Then, we propose a solution to find a minimum over-reservation (a new idleSlope) for classes A and B, such that the system becomes schedulable. We present the solution for the case of the AVB ST networks. However, the response time of AVB ST is the general form of AVB. This means that if in Eq. (15), which computes the queuing delay in AVB ST network, we set the number of ST messages to zero, we achieve Eq. (7) to calculate queuing delay in AVB networks.
7.1 Problem formulation
Here, we demonstrate the limitation in two different cases. First, we focus on the effect of lower priority blocking on the bandwidth reservation. Second, we show that even in a network without lower priority messages, the analysis may provide schedulable results only when the periods of all messages are equal. Otherwise, when the bandwidth is reserved according to the standard, the system is not schedulable in any setting.
7.1.1 Lower priority blocking
According to the system model, \(F_i\) is the length of \(m_i\). Moreover, according to the standard (see Clause 34.4 in IEEE 2014), the idleSlope for class A, (\(\alpha ^+_A\)), is defined based on the MaxFrameSize (denoted by F in this paper) and maxFrameRate parameters. The maxFrameRate parameter is the transmission rate of the frame and is calculated using the MaxIntervalFrames parameter, which is the maximum number of frames that the sender node may transmit in one “class measurement interval”. The class measurement interval is 125 \(\upmu \)s for class A and 250 \(\upmu \)s for class B (see Clause 34.4 of IEEE 2014). This calculation is given in Clause 34.4 of the standard (IEEE 2014), which is presented below for one message \(m_j\).
Therefore, the idleSlope for all messages in class X is calculated as in Eq. (25).
Since in this paper we characterized a message by its period T, then we rewrite the idleSlope based on the period of messages. Note that the period is the time interval between two consecutive transmissions of the message from the source node. Therefore, MaxIntervalFrames can be written based on T as below:
Therefore, the idleSlope for class A can be written as in Eq. (27) by inserting MaxIntervalFrames from Eqs. (26) to (25).
According to the standard, when the SRP is enabled the MaxIntervalFrames parameter is the maximum number of frames in one class measurement interval, which is a 16-bit unsigned integer value in the traffic specification (TSpec) field (see Clause 35.2.2.8.4 in IEEE 2014). Therefore, any period larger than a class measurement interval becomes equal to the class measurement interval, when computing the idleSlope. However, when the SRP is disabled, as we assumed in this paper, the TSpec for registering the bandwidth is not used. Thus, any value for the MaxIntervalFrames parameter can be foreseen to set the idleSlope.
The sendSlope is defined as \(\alpha ^-_A = R - \alpha ^+_A\), according to the standard (see sendSlope computation in Clause 8.6.8.2 in IEEE 2014). Therefore, the inflation factor discussed in the analysis can be rewritten as in Eq. (28).
We show the limitation by the following lemmas. It should be noted that Lemmas 1 and 2 are valid for the analysis presented in Bordoloi et al. (2014). However, due to the improvement in the inflation factor for the message under analysis in this paper, these effects disappear for the presented analysis in this paper. In contrast, Lemmas 3 and 4 are valid for both analyses.
Lemma 1
If there is only one message \(m_i\) from class A in the network, and there is no other traffic from other classes, the response time of \(m_i\) is equal to its period \(T_i\).
Proof
Considering the revised inflation factor in Eq. (28), the response time computation of class A in Eq. (6) can be reformulated in a new form, that is shown in Eq. (29).
Then, by replacing C with F (\(F_j = C_j \cdot R\)) in Eq. (29) the response time calculation can be written as in Eq. (30).
As there is no other messages than \(m_i\) in the network, the blocking term in the equation is zero, i.e., \(\max _{m_j \in lp(m_i)} \{\frac{F_j}{R}\} = 0\). Therefore, the response time of \(m_i\) is calculated as in Eq. (31).
From above, one can observe that the response time of \(m_i\) is equal to its period. \(\square \)
As one can see from the above lemma, the schedulability test is passed if we assume implicit deadline only, i.e., \(D_i = T_i\).
Lemma 2
If there is one message \(m_i\) from class A and one message \(m_j\) from class B in the network, the system is not schedulable according to the response time analysis in any settings.
Proof
Using Eq. (30) for the response time analysis and considering \(m_i\) and \(m_j\), the response time of \(m_i\) is computed as below.
As the response time analysis is given for a constrained deadline model, i.e., \( D_i \le T_i\), the above system is not schedulable. \(\square \)
We can conclude that, by setting the bandwidth according to the standard, the system cannot become schedulable using the analysis presented in Bordoloi et al. (2014), if there is at least one lower priority message in the network.
7.1.2 Same priority interference
The response time analysis is not only limited because of blocking by lower priority messages. Here, we investigate the schedulability of a system when there is no lower priority message in the network in two cases: (i) when the periods of messages are equal, and (ii) when at least the period of one message is larger than the others. The main intention is to show that the presented analysis can only provide schedulable results when the periods of all messages are equal.
Lemma 3
(equal periods) If there are N messages only from class A in the network, and their periods are equal, the response time of all of them is equal to their periods.
Proof
As there is no lower priority messages in the network, the blocking is zero. Also, the period of messages are equal, i.e., \(T = T_1 = T_2 = \cdots = T_N\). Note that the response time of all messages in class A are equal, as it is shown in Eq. (6). Therefore, here we only look at the response time of \(m_N\), i.e., the last message in the set. Using Eq. (30), the response time of \(m_N\) is calculated in Eq. (33).
One can observe that the response time of messages is equal to the messages’ period. Therefore, the system is always schedulable assuming implicit deadline for the traffic (\(D_i = T_i\)), for any setting of \(F_i\) and \(T_i\). \(\square \)
Lemma 4
(unequal periods) If there are N messages only from class A in the network, and their periods are equal except one message with larger period than the others, the system is not schedulable.
Proof
We assume N messages in the network, where \(T = T_1 = T_2 = \cdots = T_{N-1}\), and \(T_N > T\). As mentioned before, the period can be written as a number of class measurement intervals, i.e., \(T = y \cdot \textit{classMeasurementInterval}\), where \(y > 0\). For instance, if \(y = 1/2\) and assuming class B then \(T = 125\) \(\upmu \)s, which is 2 frames in one class measurement interval. Therefore, \(T_N = z \cdot \textit{classMeasurementInterval}\), where \(z>y\). For example, in class B if \(z = 1\) then \(T_N = 250\) \(\upmu \)s. From the above description for T and \(T_N\), we can derive the following:
Therefore, the relation between periods can be written as below, where \(z > y\) or \(z/y > 1\).
Redefining the variable as \(x = z/y\), we can rewrite the above equation as below, where \(x>1\).
Therefore, the response time for any message is calculated in Eq. (37).
Now if we show that the computed response time is larger than the message period, as the model is constrained deadline, the system is not schedulable. Let us assume that the system is not schedulable, i.e., \(\textit{RT}_i > T\), thus \(E > 1\) (Eq. 38).
By reorganizing the above inequality we can achieve Eq. (39). Further, we can take out \(x.F_N\) from the summation in the left side of the inequality, that becomes Eq. (40).
Finally, we reduce the above inequality to reach Eq. (41), as we can remove the summations from both sides.
One can observe that the final inequality shown in Eq. (41) is always true as we defined \(x > 1\). Therefore, Eq. (38) always holds. This means that the response time of the messages is always larger than the messages’ period, as we assumed in Eq. (38), hence the system is not schedulable. \(\square \)
To conclude, a system without any lower priority message is schedulable only if the periods of messages are equal (Lemmas 3, 4). In case of having even one lower priority message, the system is not schedulable in any setting (Lemmas 1, 2) using the presented analysis in Bordoloi et al. (2014).
7.2 Proposed solution
Through the previous section, we demonstrated that the system is not schedulable in most of the cases. Although, we show the limitation for class A traffic, the problem is inherited in other classes, as well as in AVB ST networks. In order to be able to use the response time analysis an over-reservation of the reserved bandwidth is essential. On the other hand, over-reservation may cause bandwidth waste due to reservation of the bandwidth being made unnecessarily high. Therefore, we propose a solution to find the minimum required over-reservation for classes A and B. We propose the solution in the context of the AVB ST networks, as a general form of the analysis for AVB. For the solution we define a new idleSlope for the traffic shaper of class X on link l of the network as \(\beta ^+_{X, l}\). Moreover, we define \(\beta ^+_{X,l,i}\) as the idleSlope for \(m_i\) of class X on link l. Intuitively, by increasing \(\beta ^+_{X, l}\) the response time becomes smaller, as the reserved bandwidth is larger. The intention of the solution is to find the minimum \(\beta ^+_{X,l,i}\) such that \(m_i\) meets its deadline. Then, \(\beta ^+_{X,l}\) is derived in Eq. (42) such that the whole set of messages in class X meet their deadlines, hence the system becomes schedulable.
In addition, according to the standard (IEEE 2014), a maximum reservable bandwidth is defined for each class of traffic, for which a reservation cannot be made larger. Therefore, the over-reservation is limited to the maximum reservable bandwidth. Assuming f as the maximum reservable portion of the bandwidth, the maximum idleSlope for traffic class X (\(\beta ^X_{max, l}\)) is calculated in Eq. (43).
Therefore, the calculated \(\beta ^+_{X, l}\) is valid if it is smaller or equal to \(\beta ^X_{max, l}\), otherwise the system cannot be schedulable with any over-reservation with the analysis presented in this paper. It should be noted that the over-reservation is derived based on the response time analysis presented in this paper. Therefore, the over-reservation is directly affected by the level of pessimism in the analysis. Moreover, when there is only one message in a class crossing a link, there is no need for over-reservation of bandwidth for that class in that link. The reason is that the idleSlope does not appear in the analysis when the same priority set is zero, i.e., \(sp(m_i) = \emptyset \). This can be seen in Eq. (14) for class A and in Eq. (16) for class B. Therefore, it is important to mention that the solution presented in this section applies only to the links crossed by traffic classes that have more than one message, i.e., \(sp(m_i) \ne 0\).
To make the system schedulable, the response time in its worst-case should be less or equal to the deadline of the message. However, as the response time is computed for one link, it should meet the deadline defined for that link, i.e., \(\textit{RT}_i^l \le D_i^l\). The sum of the deadlines for the links in the route of the message is \(D_i\), i.e., \(\sum _{l = 1\ldots n_i} D_i^l = D_i\). Defining the deadline of a message for each link can be done in several ways. The simple solution is to divide \(D_i\) equally among the number of links \(n_i\). However, a smarter solution is to divide the deadline proportional to the load on the links. Decomposition of the deadline has been studied in the real-time community, e.g., Chatterjee and Strosnider (1995) and Kao and Garcia-Molina (1993). In this paper, we do not focus on optimizing the results based on deadlines decomposition and we keep it as a future work. For the experiments in this paper, the end-to-end deadlines are divided proportionaly to the load on the links. The formulation is discussed in Sect. 8.
7.2.1 Solution for class B
Considering the revised inflation factor in Eq. (28), we can rewrite Eq. (15) for calculating \(w_i^l(q)\) in a new form, which is shown in Eq. (44). For simplicity of reading we name the blocking term and the same priority interference by \(B_i\) and \(A_i\), respectively (see Eq. 44).
Eq. (44) is a recursive function that starts with an initial value and continues until it stabilizes, i.e., the previous value and new output value of \(w_i^l(q)\) become equal. We can reformulate the equation to be as a function of time, where t evolves until \(w_i^l(t)\) becomes equal to t. This equation is presented in Eq. (45). Note that the equation is presented for a specific instant of q.
Equation (45) that is used to evaluate the response time of instant q is shown in Fig. 10, which is a step function. The first point that t meets \(w_i^l(t)\) is the queuing delay of \(m_i\), that is shown by \(Q_i\) in Fig. 10, i.e., \(Q_i = min(t>0):t = w_i^l(t)\). The intention is to find minimum \(\beta ^+_{B,l,i}\) from Eq. (45) such that the response time of \(m_i\) in instant q becomes equal to the deadline of \(m_i\). However, the operation is not trivial as there are floor operations in the equation. In order to simplify, we can approximate \(w_i^l(t)\) by removing the floor operations from Eq. (45). The approximation is shown in Eq. (46). Intuitively it can be seen that \(w_i^{l,apx}(t)\) is always larger or equal to \(w_i^l(t)\), which is still a safe upper bound. This function is depicted in Fig. 10, as a linear function of time. Similarly to the previous equation, we evolve time t until \(w_i^{l,apx}(t) = t\). This point is shown by \(Q_i^{apx}\) in the figure, and it is the queuing delay of \(m_i\).
With Eqs. (45) and (46) in mind, we continue to find \(\beta ^+_{B,l,i}\) by presenting in a lemma form.
Lemma 5
Assuming that the worst-case response time occurs in \(q'\)th instance, in order for \(m_i\) to meet its deadline using the approximation of queuing delay, \(\beta ^+_{B,l,i}\) should be set as follows:
Proof
The response time of \(m_i\) in link l is calculated using Eq. (16). As it is assumed in the lemma, the max operation occurs in \(q'\)th instance, so we can rewrite Eq. (16) by considering the revised inflation factor and \(w_i^{l, apx}(t)\) as a function of time, which is shown in Eq. (48).
In order for \(m_i\) to meet its deadline \(\textit{RT}_i^l \le D_i^l\). Let us for now assume that \(\textit{RT}_i^l = D_i^l\). Therefore, Eq. (48) becomes:
From the above equation we can derive \(w_i^{l, apx}(t)\), which is:
As it was mentioned before, in Eq. (46) we have to evolve t until \(w_i^{l, apx}(t) = t\), and this point is \(Q_i^{apx}\) (see Fig. 10). Thus, in a schedulable system \(w_i^{l, apx} = t = Q_i^{apx}\). We can rewrite Eq. (50) assuming that the deadline of \(m_i\) is met, as it is in the lemma, which is shown in Eq. (51).
On the other hand, we can write Eq. (46) as we are aiming \(m_i\) to meet its deadline, i.e., \(w_i^{l,apx} = t = Q_i^{apx}\). Therefore, Eq. (46) becomes:
Now we can insert \(Q_i^{apx}\) from Eqs. (51) to (52). By doing so, we achieve Eq (53).
We are interested to find \(\beta ^+_{B,l,i}\), thus we can extract it from Eq. (53), as it is a linear equation. The new idleSlope \(\beta ^+_{B,l,i}\) is calculated in Eq. (54), where for readability we name the numerator and denominator as N and M, respectively.
We assumed that \(\textit{RT}_i^l = D_i^l\) in the beginning of the proof. By relaxing the assumption and considering \(\textit{RT}_i^l \le D_i^l\), \(\beta ^+_{B,l,i}\) should be computed using Eq. (55), as by increasing the bandwidth the response time becomes shorter. Thus, we proved the lemma.
\(\square \)
In the above equations, to calculate \(\beta ^+_{B,l,i}\) we need \(q'\), which is unknown. We assumed \(q'\) is the instance within the range \([1, q_{\textit{max}}]\), where it causes the maximum response time in Eq. (16). However, to find the instance \(q'\), we need to examine all the instances within the range, for which the maximum \(q_{\textit{max}}\) is derived according to Eq. (17). Note that Eq. (17) is the function of \(\alpha ^+_{B, l}\), and with the new idleSlope it would be the function of \(\beta ^+_{B,l}\), which we are aiming to find. This means that while finding \(\beta ^+_{B,l,i}\), \(q_{\textit{max}}\) will change as well.
The algorithm to find \(\beta ^+_{B,l}\) is shown in Algorithm 1. It iterates for all messages in class B crossing through link l to calculate the over-reservation for each of them, then the maximum of the idleSlopes among the messages is the final idleSlope. Note that the algorithm finds \(\beta ^+_{B,l}\) for each link in a multi-switch AVB ST architecture, thus it should be executed for all links in the network.
The algorithm starts by finding \(\beta ^+_{B,l,i}\) using Eq. (47) for the first instance of the message, i.e., when \(q = 1\) (line 3). As it is mentioned before, if the over-reservation factor exceeds the maximum one, computed in Eq. (43), the system is not schedulable. Thus, the algorithm breaks after examining the maximum possible over-reservation in line (4), and returns the unschedulable flag (sched). Using the derived \(\beta ^+_{B,l,i}\), the maximum number of instances \(q_{\textit{max}}\) is calculated using Eq. (17) in line (7) of the algorithm. Note that we use the new idleSlope \(\beta ^+_{B,l,i}\) instead of \(\alpha ^+_{B,l}\). If the maximum number of instances is larger than 1, which \(\beta ^+_{B,l,i}\) is calculated based on that, the algorithm continues to find \(\beta ^+_{B,l,i}\) when \(q=2\) to \(q_{\textit{max}}\) in the loop starting from line (10). In each step, if the over-reservation is larger than the maximum possible over-reservation, the algorithm breaks and returns the unschedulable flag (line (12) and the following ones). However, if \(\beta ^+_{B,l,i}\) computed based on a q is larger than the previously calculated one, the maximum number of instances should be updated again (lines (15) and (16)). If the updated maximum number of instances \(\textit{newQ}\) is smaller than the current \(q_{\textit{max}}\), the algorithm does not need to continue calculating \(\beta ^+_{B,l,i}\), hence it breaks the loop and returns the new idleSlope \(\beta ^+_{B,l,i}\) for \(m_i\). If \(\textit{newQ}\) equals to the current \(q_{\textit{max}}\), the loop continues. However, if the \(\textit{newQ}\) becomes larger than qMax, then qMax is updated for the continuation of the loop. The loop will be eventually terminated as \(\beta ^+_{B,l,i}\) cannot exceed \(\beta ^+_{max, l}\) and will be broken in line (12). For each message in the loop of the algorithm, the maximum idleSlope is stored in \(\beta ^+_{B,l}\) in line (26). the complexity of the algorithm for link l in the network is \(O(N \times q_{\textit{max}} \times q_{\textit{max}})\). Note that the function findSlope is linear, and the function findQmax has an iteration with the maximum iteration number of \(q_{\textit{max}}\). Therefore, the algorithm has a polynomial time-complexity.

7.2.2 7Solution for class A
The response time for messages in class A is computed only for one instance, as shown in Eq. (14). We can write the response time equation as a function of time, similarly to the solution for class B. Moreover, we can write the approximation of the equation by removing the ceiling operation. Thus, the response time computation becomes as it is shown in Eq. (56), where we use the new idleSlope for \(m_i\) (\(\beta ^+_{A,l,i}\)), instead of \(\alpha ^+_{A,l}\). In Eq. (56) we evolve time t until \(\textit{RT}_i^l(t) = t\), which is the answer of the equation.
We are interested to find \(\beta ^+_{A,l,i}\), and we describe it in the following lemma. Then, the new idleSlope for all messages \(\beta ^+_{A,l}\) is calculated by Eq.(42).
Lemma 6
In order for \(m_i\) to meet its deadline using the approximation of the response time, the new idleSlope for \(m_i\) is set by:
Proof
In order for \(m_i\) to meet its deadline the response time should be less or equal to the link deadline, i.e., \(\textit{RT}_i^l \le D_i^l\). Let us assume for now that \(\textit{RT}_i^l = D_i^l\). This means the answer of Eq. (56) should be equal to the link deadline, which is \(\textit{RT}_i^l(t) = t = D_i^l\). By inserting \(D_i^l\) instead of both t and \(\textit{RT}_i^l(t)\) in Eq. (56) (as they are equal by evolving t to reach the answer), hence Eq. (56) becomes as a linear function shown in Eq. (58).
We also use the revised inflation factor for the same priority interference term in Eq. (58), which becomes as Eq. (59).
We can derive \(\beta ^+_{A,l,i}\) from Eq. (59), as it is a linear equation, that is shown in Eq. (60). Note that at the beginning of the proof we assumed \(\textit{RT}_i^l = D_i^l\), however in order to have \(\textit{RT}_i^l \le D_i^l\) the over-reservation should be equal or larger than the computed one in Eq. (60), which proves the lemma.
\(\square \)
7.3 Over-reservation in the AVB networks
Algorithm 1 can be also used to find the over-reservation of idleSlope in the AVB networks. The only change is to assume the set of ST messages is zero in all calculations, i.e., \(\{ST class\} = \emptyset \), as the presented analysis is the general form for AVB analysis.
7.4 Evaluation of bandwidth over-reservation
In this experiment we show the effect of accumulating delay over multiple hops on the bandwidth over-reservation. For this evaluation we consider a network with six switches, as illustrated in Fig. 11.
The total bandwidth capacity of the network is 100 Mbps, where 40 Mbps is set for each class of the SR traffic as the maximum reservable bandwidth. We assumed four messages, two from class A and two from class B. All messages have 500bytes payload with 2000 \(\upmu \)s period. The source of all four messages is N1, and we change their destination from N2 to N7, i.e., the number of hops that the messages are crossing is changing from one to six switches. We computed the idleSlope of class A and B based on the standard (i.e., \(\alpha ^+_A\) and \(\alpha ^+_B\)) in the destination link. For example, in case of crossing the switch 1, we computed the idleSlopes for link L2 which is the messages’ destination to node N2 (see Fig. 11). In addition, we calculated the new idleSlopes (i.e., \(\beta ^+_A\) and \(\beta ^+_B\)) based on the presented solution in this paper. The idleSlopes are illustrated in Fig. 12. As it can be seen in the Figure, the idleSlopes based on the standard are constant and equal (2.56 Mbps) by increasing the number of hops. This is because the standard for reserving bandwidth does not consider the queuing jitter from crossing previous switches. In contrast, the new idleSlopes increase with the number of hops. This means that the messages will get larger delay after crossing several switches, hence the reserved bandwidth should be higher to make the system schedulable. In this experiment higher bandwidth for class B is required, as it has higher priority interference, unlike class A.
In order to show the effect of the message parameters on the over-reservation, we run two experiments. In the first experiment, we fixed the value of payload for messages to 300 bytes and we changed the period of messages from 1600 to 3000 \(\upmu \)s. The new idleSlopes in every hop to the destination link for both classes A and B are presented in Fig. 13. In the second experiment, we fixed the value of periods to 2500 \(\upmu \)s and we increased the payload for all messages from 100 to 500 bytes. The idleSlopes for the second experiment are illustrated in Fig. 14. In general, increasing the period of messages or decreasing the payload of messages, the idleSlope decreases due to the decrease in the messages’ utilization. However, the trend in Figs. 13 and 14 shows that the messages in class B are affected more than messages in class A. This is indeed due to the interference from higher priority messages on class B.
8 Experiments
In this section, we conduct simulative assessments of two types of network architectures. The first one refers to an industrial network, the second to an automotive network. The messages parameters are taken from the automation and automotive application domains, respectively, and the total bandwidth is set to 100 Mbps. The industrial scenario is setup with flow periods in the order of few milliseconds that are typical of the microgrid automation applications (Rinaldi et al. 2015), while the topology is chosen to consider the maximum hops that the standard guarantees (i.e., 7 hops). Moreover, the traffic parameters in the automotive case study are inspired from the architecture designed by BMW group (Lim et al. 2011). The response time for the defined messages is computed using the analysis presented in this paper. Then, we simulate the examples using OMNeT++ and we measure the response time of the messages during run-time for 500 s. We compare the calculated and measured response times to assess the level of pessimism in the defined case studies. It should be noted that this is not the maximum pessimism as it is rather difficult to examine it.
In the experiments we need to split the deadline of the messages into the deadlines in each link. In this paper, we decompose the deadlines proportional to the load in each links. We use Eq. (61) to derive the deadline for \(m_i\) for link l.
The simulation model was implemented using the OMNeT++ framework, which is a discrete-event simulator. For the simulation of the physical layer of Ethernet the INET libraries were adopted, while the MAC layer (with the Forwarding and Queuing for Time-Sensitive Streams (FQTSS) defined in the standard (IEEE 2014), the TAS and the traffic generators were implemented from scratch. In the simulation model no clock synchronization protocol was implemented, as clocks are assumed to be synchronized in the system model. The Stream Reservation Protocol was disabled in order to assess the performance with the idleSlope values calculated offline. Statistics on the delays were taken at the application level and no processing time on the nodes was assumed (only the switch fabric latency of 5.2 \(\upmu \)s is considered). Two kind of nodes were implemented, the AVB ST host nodes and the AVB ST switches. The simulation model was validated assessing the behaviors of messages in several scenarios and comparing the timing parameters, calculated under predictable test scenarios, with those obtained in the simulation.
8.1 Industrial case study
In this case study, we assumed an architecture consisting of six switches connected in a line topology. The architecture is depicted in Fig. 15. In this example, there are eight nodes, seven of which are talkers and one is a listener. This results in a high load for the listener node.
We defined eight messages in different traffic classes. The parameters of the messages are shown in Table 3. The overhead of SR messages is assumed to be 42bytes, while for the ST messages is assumed to be 30Bytes due to removing 12Bytes of interpacket gap. Note that the listener for the messages is N8 in this example. In this experiment we do not have any BE traffic and the switch fabric latency \(\epsilon \) is assumed to be 5.2 \(\upmu \)s.
In the depicted architecture, we computed the idleSlope for classes A and B (\(\alpha ^+_A\) and \(\alpha ^+_B\)) based on the standard for each output link. Also, we calculated the over-reserved idleSlope (\(\beta ^+_A\) and \(\beta ^+_B\)) according to the presented solution in this paper. The results of idleSlopes are shown in Table 4, in Mbps. As it is mentioned in the system model, each link has two directions (full-duplex ports). Therefore, for each direction of a link, idleSlopes in class A and B are computed. In Table 4, for instance, L1<N1-SW1> shows link L1 with direction from N1 to SW1, hence it presents the idleSlope for output port of N1.
In Table 4, the zero values show that there is no traffic in that class that goes through that particular link and direction. For example, only a message belonging to class A crosses the link L1<N1-SW1>. Therefore, the idleSlope for class B is zero. Another observation is that the over-reservation for the links with higher load is larger. For instance, the idleSlope for class A on link L13<SW6-N8> is 8.26 Mbps since N8 is the listener for all defined messages. However, the over-reserved idleSlope is computed as 45.54 Mbps using the presented solution in this paper. This means that in order to have a schedulable system the idleSlope should be increased approximately 6 times for class A on link L13<SW6-N8>. This increase on the links with less load is lower. The reason is that by increasing the number of messages, the pessimism in the analysis becomes higher. Therefore, the bandwidth should be increased more to make the system schedulable. Furthermore, in some links no over-reservation is required. For instance, on link L1<N1-SW1> there is only one message crossing the link, hence, according to the analysis and solution, no over-reservation is required.
Using the over-reserved idleSlopes, we computed the response time of the messages. Moreover, we measured the response times in a simulation to be compared with the computed results. The simulation has been done with the original idleSlope (\(\alpha ^+\)) and the over-reserved idleSlope (\(\beta ^+\)) to show the effect of over-reservation in the simulation. We used offsets for ST messages. In the industrial case study there are two ST messages with 4 ms periods. The offsets are set to 0 s and 2 ms, respectively. Therefore, the interval between two consecutive ST messages is always 2 ms. The results are illustrated in Fig. 16. In the figure, the computed response times are indicated by RTA, while the simulation measurements are identified by Sim Max \(\alpha \) and Sim Max \(\beta \) for the maximum measured values for the original and over-reserved idleSlope, respectively. As it can be seen, all measured response times with the over-reserved idleSlope are always less than or equal to the computed ones. Moreover, the biggest difference between the maximum measured and calculated is for message 2, which shows around 86% pessimism. However, this level of pessimism is only for this example. Showing the level of pessimism for the analysis is rather difficult and it requires to provide a worst-case example ensuring that the simulation reaches the worst-case results. Note that the measured and computed response times for ST messages (messages 3 and 4) are equal as there is no interference or blocking on them. Also, their response times are much smaller than the other classes, thus showing the effectiveness of the AVB ST proposal. Another observation is that the measured response time for a message with the original idleSlope can be larger than the deadline of the message. In this case study, the measured response time of message 5 with the original idleSlope is 2033 \(\upmu \)s, which is larger than its deadline 1875 \(\upmu \)s, hence the system is not schedulable. We can conclude that there are case studies in which the system is not schedulable (with both response time analysis and simulation) if the idleSlope is assigned according to the standard. The over-reservation algorithm presented in this paper is very useful to achieve the minimum over-reservation and the system schedulability for such scenarios.
8.2 Automotive case study
In this case study we consider an example automotive network consisting of two switches in a double star topology, illustrated in Fig. 17. The network supports an ADAS system consisting of three cameras (CAM1–CAM3), which send video frames to a specialized processing unit, named the DACAM. The DACAM processes the video frames and produces both warnings, which are sent to a Control Unit (CU) and to a Head Unit, and aggregated flows, which are displayed by the Head Unit. The network also supports the bidirectional exchange of control messages between the CU, the DACAM, and the Head Unit. In addition to these safety-critical flows, the network also supports some multimedia/infotainment and telematics systems, which are real-time, but not safety-critical.
For this case study we define 30 messages whose properties are inspired by realistic automotive messages. Audio and video frames are assigned to class A and B. The various type of control messages are all set as ST class. The properties of the messages are presented in Table 5. The switch fabric latency is assumed equal to 5.2 \(\upmu \)s.
Similarly to the previous case study, we computed the idleSlope for classes A and B based on the standard, and according to the over-reservation approach in this paper. The results for each link are shown in Table 6.
Considering the over-reserved bandwidth for each link, we calculated the response time of messages according to the analysis presented in this paper. Also, we measured the response times during the simulation. The results are depicted in Fig. 18. Similarly to the previous experiment, RTA, Sim Max \(\alpha \) and Sim Max \(\beta \) indicate the computed, maximum measured response times of the messages with the original and over-reserved idleSlope, respectively. As it can be seen, the computed response times of messages belonging to classes A and B are always larger than the measured ones with the over-reserved idleSlope. Also, the measured and computed response times of ST messages are always equal, and small compared to the response times of the other classes of messages. The highest pessimism in this example is for message 4 with around 86%. In the figure, the measured response times for messages 1, 2 and 3 are not the same, while their parameters are the same. In the simulation, all messages arrive to the switch at the same time in an order that is maintained in the simulation. This is why the first message has shorter response time compared with the others. However, in the analysis we consider the worst-case for each individual message. This case study validates the practicality of the ST approach as the ST messages have very short latency compared to the SR classes. Moreover, the over-reservation algorithm helps reduce the messages’ response time, e.g., for message 27.
9 Conclusion and future work
In this work, we presented a response time analysis for multi-hop AVB ST networks, which can be applied to multi-hop AVB networks as well. The proposed analysis exploits a bandwidth over-reservation concept to overcome the limitations of state-of-the-art response time analysis approaches for AVB networks. We showed that the analysis based on the proposed bandwidth over-reservation method is effective by comparing the analysis results with the simulative ones obtained using OMNeT++. As we showed in the experiments, the presented analysis entails a level of pessimism. As decreasing the pessimism would lead to less bandwidth over-reservation and better resource utilization, future work will address a way to decrease such a pessimism, and the case for taking advantage from previous findings and approaches on stochastic analysis, such as the ones in Diaz et al. (2004) and Kaczynski et al. (2007), will be also considered. As future work we will address a response time analysis for the AVB ST combined with the frame preemption mechanism introduced by the IEEE 802.1Qbu standard.
References
Alderisi G, Caltabiano A, Vasta G, Iannizzotto G, Steinbach T, Lo Bello L (2012) Simulative assessments of IEEE 802.1 Ethernet AVB and time-triggered Ethernet for advanced driver assistance systems and in-car infotainment. In: Vehicular networking conference
Alderisi G, Iannizzotto G, Lo Bello L (2012) Towards 802.1 Ethernet AVB for advanced driver assistance systems: a preliminary assessment. In: IEEE 17th conference on emerging technologies factory automation
Alderisi G, Patti G, Lo Bello L (2013) Introducing support for scheduled traffic over IEEE audio video bridging networks. In: 18th IEEE conference on emerging technologies factory automation
Bordoloi UD, Aminifar A, Eles P, Peng Z (2014) Schedulability analysis of ethernet AVB switches. In: The 20th IEEE international conference on embedded and real-time computing systems and applications
Chatterjee S, Strosnider J (1995) Distributed pipeline scheduling: end-to-end analysis of heterogeneous, multi-resource real-time systems. In: Proceedings of the 15th international conference on distributed computing systems
Cummings R (2012) 802.1qbv scheduled traffic: Window options. In: 802.1 Interim meeting
Davis RI, Burns A, Bril RJ, Lukkien JJ (2007) Controller Area Network (CAN) schedulability analysis: refuted, revisited and revised. Real-Time Syst J 35:239–272
Davis R, Kollmann S, Pollex V, Slomka F (2011) Controller Area Network (CAN) schedulability analysis with FIFO queues. In: 23rd Euromicro conference on real-time systems
De Azua JAR, Boyer M (2014) Complete modelling of AVB in Network Calculus framework. In: 22nd international conference on real-time networks and systems
Diaz JL, Lopez JM, Garcia M, Campos AM, Kanghee K, Lo Bello L (2004) Pessimism in the stochastic analysis of real-time systems: Concept and applications. In: in Proceeding of 25th IEEE international real-time systems symposium
Diemer J, Thiele D, Ernst R (2012) Formal worst-case timing analysis of Ethernet topologies with strict-priority and AVB switching. In: 7th IEEE international symposium on industrial embedded systems
Heidinger I, Geyer F, Schneele S, Paulitsch M (2012) A performance study of audio video bridging in aeronautic Ethernet networks. In: 7th IEEE international symposium on industrial embedded systems
IEEE (2008) IEEE standard for a precision clock synchronization protocol for networked measurement and control systems. IEEE Std 1588-2008 (Revision of IEEE Std 1588-2002)
IEEE (2011) IEEE Std. 802.1AS-2011, IEEE standard for local and metropolitan area networks-timing and synchronization for time-sensitive applications in bridged local area networks (2011)
IEEE (2014) IEEE Std. 802.1Q, IEEE standard for local and metropolitan area networks, bridges and bridged networks
IEEE (2015) IEEE Std. 802.1Qbv, IEEE standard for local and metropolitan area networks, bridges and bridged networks, amendment 25: enhancement for scheduled traffic
Imtiaz J, Jasperneite J, Han L (2009) A performance study of Ethernet Audio Video Bridging (AVB) for industrial real-time communication. In: IEEE conference on emerging technologies factory automation
Imtiaz J, Jasperneite J, Schriegel S (2011) A proposal to integrate process data communication to IEEE 802.1 Audio Video Bridging (AVB). In: IEEE 16th conference on emerging technologies factory automation
Imtiaz J, Jasperneite J, Weber K (2012) Approaches to reduce the latency for high priority traffic in IEEE 802.1 AVB networks. In: 9th IEEE international workshop on factory communication systems
Jasperneite J, Schumacher M, Weber K (2009) A proposal for a generic real-time Ethernet system. IEEE Trans Ind Inform 5(2):75–85
Kaczynski GA, Lo Bello L, Nolte T (2007) Deriving exact stochastic response times of periodic tasks in hybrid priority-driven soft real-time systems. In: IEEE conference on emerging technologies and factory automation
Kao B, Garcia-Molina H (1993) Deadline assignment in a distributed soft real-time system. In: Proceedings the 13th international conference on distributed computing systems
Keynote Talk (2013) Experiences from EAST-ADL use. EAST-ADL Open Workshop, Gothenberg
Land I, Elliott J (2011) Architecting ARNIC 664 (AFDX) Solutions
Leboudec J, Thiran P (2001) Network calculus. Springer, Berlin
Lee KC, Lee S, Lee MH (2006) Worst case communication delay of real-time industrial switched Ethernet with multiple levels. IEEE Trans Ind Electron 53(5):1669–1676
Lehoczky J (1990) Fixed priority scheduling of periodic task sets with arbitrary deadlines. In: 11th real-time systems symposium (1990)
Lim HT, Zahrer P, Volker L (2011) Performance evaluation of the inter-domain communication in a switched Ethernet based in-car network. In: 36th IEEE conference on local computer networks
Lo Bello L (2011) The case for Ethernet in automotive communications. SIGBED Rev 8(4):7–15
Lo Bello L (2014) Novel trends in automotive networks: a perspective on Ethernet and the IEEE Audio Video Bridging. In: 19th IEEE international conference on emerging technologies and factory automation
Lim HT, Weckemann K, Herrscher D (2011) Performance study of an in-car switched Ethernet network without prioritization. In: Proceedings of the third international conference on communication technologies for vehicles
Martin S, Minet P (2006) Worst case end-to-end response times of flows scheduled with FP/FIFO. In: International conference on networking, international conference on systems and international conference on mobile communications and learning technologies
Palencia JC, González Harbour M (1998) Schedulability analysis for tasks with static and dynamic offsets. In: Proceedings of the IEEE real-time systems symposium
Pannel D (2012) Avb - generation 2 latency improvement options. In: 802.1 AVB group
Reimann F, Graf S, Streit F, Glas M, Teich J (2013) Timing analysis of Ethernet AVB-based automotive E/E architectures. In: 18th Conference on emerging technologies factory automation
Rinaldi S, Ferrari P, Ali NM, Gringoli F (2015) IEC 61850 for micro grid automation over heterogeneous network: Requirements and real case deployment. In: 13th IEEE international conference on industrial informatics
Schneele S, Geyer F (2012) Comparison of IEEE AVB and AFDX. In: IEEE/AIAA 31st digital avionics systems conference
Steinbach T, Lim HT, Korf F, Schmidt T, Herrscher D, Wolisz A (2012) Tomorrow’s in-car interconnect? a competitive evaluation of IEEE 802.1 AVB and time-triggered ethernet (as6802). In: Vehicular technology conference
Thangamuthu S, Concer N, Cuijpers P, Lukkien J (2015) Analysis of Ethernet-switch traffic shapers for in-vehicle networking applications. In: Design, automation and test in Europe conference and exhibition
Tuohy S, Glavin M, Hughes C, Jones E, Trivedi M, Kilmartin L (2015) Intra-vehicle networks: a review. IEEE Trans Intell Transp Syst 16(2):1–12
Wandeler E, Thiele L, Verhoef M, Lieverse P (2006) System architecture evaluation using modular performance analysis: a case study. Int J Softw Tools Technol Transf 8(6):649–667
Acknowledgements
This work is supported by the Swedish Foundation for Strategic Research via the PRESS, FiC and LUCIA projects.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ashjaei, M., Patti, G., Behnam, M. et al. Schedulability analysis of Ethernet Audio Video Bridging networks with scheduled traffic support. Real-Time Syst 53, 526–577 (2017). https://doi.org/10.1007/s11241-017-9268-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11241-017-9268-5