Games with possibly naive present-biased players

Abstract

We propose a solution concept for games that are played among players with present-biased preferences that are possibly naive about their own, or about their opponent’s future time inconsistency. Our perception-perfect outcome essentially requires each player to take an action consistent with the subgame perfect equilibrium, given her perceptions concerning future types, and under the assumption that other present and future players have the same perceptions. Applications include a common pool problem and Rubinstein bargaining. When players are naive about their own time inconsistency and sophisticated about their opponent’s, the common pool problem is exacerbated, and Rubinstein bargaining breaks down completely.

1 Introduction

Time-inconsistent present-biased preferences are among the most prominent and persistent behavioral biases in economics. For example, most people would prefer to do an unpleasant task on May 1 rather than on May 15 when faced with that choice on April 1. But on May 1, almost everyone will be inclined to postpone it to May 15. This type of time inconsistency (often also referred to as hyperbolic discounting or present-biasedness) has been put forward as an explanation of, for example, why economic agents would choose to use commitment devices to restrict their future selves.¹

O’Donoghue and Rabin (1999) provide a model for behavior with such present-biased preferences. In their model, an individual decision-maker either is time-consistent or has present-biased preferences. When present-biased, she can either be sophisticated about that, or she can be naive. A sophisticated individual knows that she will have present-based preferences in the future, and hence may today want to restrict the choices of her future self. If she is naive, then she believes that although she currently has present-biased preferences, her future self will behave in a time-consistent manner.

However, many situations of interest to economists concern the interaction between economic agents. Suppose for example that two individuals A and B bargain over the distribution of a future payoff. Again, player A’s behavior will depend on whether she is present-biased and, if so, whether she is naive or sophisticated about that. However, her behavior will also depend on whether she perceives player B to be time-consistent, and whether she believes player B is naive or sophisticated. It may even depend on her perceptions concerning player B’s perceptions about player A. Where the one-player model implies a game played between a current and future self, a two-player model effectively implies a game played between both A and B’s current and future selves.

In this paper, we study such games. We introduce a new solution concept for games played between possibly present-biased players. As a starting point, we take (O’Donoghue & Rabin, 1999) who consider a one-player game played by a current self against her future self. The authors introduce the concept of a perception-perfect strategy: a course of action that maximizes the current player’s utility given her perception about her future self’s type, and given the behavior that can rationally be expected of such a type. Here, ‘type’ refers to the extent to which her future self is present-biased.

We first extend their analysis to one-player games with a richer strategy space, both in the two-period case as well as in a set-up with more periods. We introduce a perception-perfect outcome,² an extension of O’Donoghue and Rabin (1999) perception perfect strategy that can also be extended to a multi-player set-up. We then analyze games with two players. We apply our solution concept to a common pool problem (the overconsumption that results when competitors seek to exploit an exhaustible resource), and to a model of Rubinstein bargaining (where two players take turns in either accepting their counterpart’s offer or making a counteroffer).

Players’ perceptions concerning types are going to play a crucial role. Also, behavior will depend not only on A’s perception of B, but also A’s perception of B’s perception of A, etcetera. To deal with this complication we impose, first, that players assume that their future selves have the same perceptions as their current self (intraplayer perception naivety). Second, we impose that players assume that other players have the same perceptions as they themselves have (interplayer perception naivety).

Our concept of a perception perfect outcome then entails the following. Consider player A. She has certain perceptions about her own future type, and about the future type of the other player. Given those, and under the assumption that all other present and future players have the same perceptions, we can derive the subgame perfect equilibrium that player A perceives to be played. We call this the ‘equilibrium as perceived by A’. Similarly, we can derive the equilibrium as perceived by B. The perception perfect outcome in period $t=1$ then consists of an action taken by A that is consistent with an equilibrium as perceived by A, and an action taken by B that is consistent with an equilibrium as perceived by B. In all later periods, the same is true, but given the actions that were played in the past.

From our two main applications, the common pool problem and Rubinstein bargaining, we derive the following insights. First, suppose that players are naive about their own future selves, but are sophisticated about the future self of others. This is consistent with psychological evidence, as e.g., Kahneman (2011) argues.³ In that case, we find that the common pool problem becomes much worse than in a standard world with rational actors. This can be seen as follows. Suppose A perceives B to have present-biased preferences in future. That implies that B will then claim a large share of the common pool. But that will give A an incentive to preempt B and to claim a large share today. The same holds for B. As a result, both players claim a large share of the pool today, completely exhausting it. We show that this effect is even stronger than in a case where both players know their future selves to also be present-biased.

In the case of Rubinstein bargaining, we show that the assumption that players are naive about themselves but sophisticated about others, implies a breakdown in bargaining. Suppose it is A’s turn to make an offer. She will base that offer on the assumption that B will have present-biased preferences in future. Yet B perceives herself to be time-consistent in future, and hence turns down A’s offer. This process will continue indefinitely.

The remainder of this paper is structured as follows. In Sect. 2, we discuss related literature. Section 3.1 looks at the case of one player. We first look at the case of a three-period model in which the player has to make two sequential decisions, and generalize the solution concept introduced by O’Donoghue and Rabin (1999). Section 4.1 further generalizes to a model with more than three periods, and Sect. 4.2 gives examples in the context of intertemporal consumption decisions. We then extend the analysis to a two-player game, and introduce the concept of a perception-perfect outcome. We do so for the three-period case in Sect. 5.1, and apply our solution concept to a common pool problem in Sect. 5.2. Section 6.1 looks at a multi-period model, and Sect. 6.2 applies our analysis to Rubinstein bargaining. Section 7 concludes.

2 Related literature

We are neither the first to develop approaches to solve games with possibly naive present-biased players, nor are we the first to solve Rubinstein bargaining with such players. Most notably, in an unpublished working paper, (Sarafidis, 2006) proposes “naive backward induction” with possibly naive present-biased players. Akin (2007) applies this to Rubinstein bargaining and allows naive players to learn.

In Sarafidis (2006), naive players assume that other players are also naive while sophisticated players are sophisticated not only about their own future time inconsistency, but also about the type of the other player. He then applies backward induction taking the perceptions of players into account, something he coins naive backward induction (NBI). Akin (2007) applies this concept to Rubinstein bargaining. In doing so, he imposes that players are always sophisticated about the type of the other player.

Instead, we assume interplayer perception naivety which implies that each player assumes others to have the same perceptions as she herself has. Thus, a player that is sophisticated about her opponent perceives her opponent to also be sophisticated about himself. A player that is naive about herself also perceives others to be naive about herself. This assumption helps in providing a consistent and flexible framework that can also be applied to simultaneous move games such as the common-pool problem. Indeed, we are the first to provide an analysis of such games with present-biased players. A second difference is that we also allow players to be naive about the type of their opponent. In Appendix A, we give an example of a simple game in which NBI and our perception perfect outcome yield different predictions.

Other related literatures include the following. In Akin (2009), a naive player plays against a sophisticated player but learns about her naivety in the course of play, Chade et al. (2008) analyze repeated games between sophisticated present-biased players. Akin (2012) studies the behavior of individuals with present-biased preferences who are either naive, partially naive or sophisticated, and are involved in costly, long-run projects. Gans and Landry (2019) focus on how initially naive present-biased players may update their beliefs concerning time inconsistency in a dynamic game. In Weinschenk (2021), present-biased players play a dynamic game in which they can collectively win a prize, and the probability of doing so is increasing in total effort exerted. In that context, present-biased preferences increase the incentive to exert effort to try to secure the prize quickly, hence helping to overcome the incentive to free ride. Naive players do better than sophisticated ones. Weinschenk (2021) implicitly assumes that players are equally naive (or sophisticated) concerning other’s present-bias as they are concerning their own. Turan (2019) studies a common-pool problem where one player perceives the other to have time-biased preferences with some probability, while the other player can manipulate those preferences through its actions. Compared to earlier work, our framework is more general.

Schweighofer-Kodritsch (2018) studies Rubinstein bargaining allowing for any time preference. However, he does assume both bargainers are sophisticated about their own time preference, and that of their counterpart. Consistent with our results in Sect. 6.2, he finds no delay for any form of present bias; a future bias for at least one of the bargainers is necessary for equilibrium delay. From our analysis, we have that naivety and present bias can also cause delay, or even a bargaining breakdown. Lu (2016) studies Rubinstein bargaining between two present-biased but sophisticated players that may have a different degree of present-biasedness.

3 The one-player case: three periods

3.1 Equilibrium concept

Consider an agent that has to make decisions at $t=1$ and $t=2.$ These determine the outcome in the final period 3. The agent may have present-biased preferences. Moreover, she may not be aware that her future self deciding at $t=2$ may also be present-biased. The problem of the current self then is what action to take now given her perceptions about her future self.

Throughout this paper, we consider the following preferences. Let $u_{t}$ be an agent’s instantaneous utility or felicity in period t. In a model with T periods, we let $U_{t}\left( u_{t},u_{t+1},\ldots ,u_{T} ;\beta ^{i}\right)$ represent her intertemporal preferences, where $\beta ^{i}$ is a parameter. We assume

$$\begin{aligned} U_{t}\left( u_{t},u_{t+1},\ldots ,u_{T};\beta ^{i}\right) \equiv u_{t} +\beta ^{i}\sum _{\tau =t+1}^{T}\delta ^{\tau }u_{\tau } \end{aligned}$$

(1)

with $0<\beta ^{i},\delta \le 1.$ With $\beta ^{i}=1,$ this collapses into the standard exponential discounting function with discount factor $\delta .$ With $\beta ^{i}<1,$ we have the canonical model of hyperbolic discounting introduced by Pollak and Phelps (1968). The agent then has present-biased preferences, where $\beta ^{i}$ represents her bias for the present.⁴ In other words, she is time-inconsistent.

In this context, consider a one-player game with three periods, $t=1,2,3,$ in which player A makes two sequential decisions at $t=1$ and $t=2$. At $t=1,$ she chooses action $a_{1}\in {\mathcal {A}}_{1},$ with ${\mathcal {A}}_{1}$ her set of feasible actions. At $t=2,$ she chooses action $a_{2}\in {\mathcal {A}}_{2} (a_{1}),$ with ${\mathcal {A}}_{2}(a_{1})$ her set of feasible actions at $t=2,$ which may depend on $a_{1}.$ Her felicity in period 1 depends on $a_1$; that in periods 2 and 3 will depend on both $a_1$ and $a_2$. Thus $u_{1}^{A}=u_{1}^{A}( a_{1}) ,$ while $u_{2} ^{A}=u_{2}^{A}\left( a_{1},a_{2}\right)$ and $u_{3}^{A}=u_{3}^{A} (a_{1},a_{2}).$

Her present bias at $t=1$ is denoted $\beta ^{A}.$ Following O’Donoghue and Rabin (1999), we allow for two possibilities: she either has present-biased preferences, so $\beta ^{A}=\beta ,$ where $\beta <1$ is exogenously given, or she is time-consistent and has $\beta ^{A}=1.$ For ease of discussion, we denote the true present-bias of the future self (i.e., that at $t=2$) as $\gamma ^{A},$ where we also assume $\gamma ^{A} \in \{\beta ,1\}$. Using (1) A’s lifetime utility at both dates is thus given by

$$\begin{aligned} U_{1}^{A}\left( a_{1},a_{2};\beta ^{A}\right)&=u_{1}^{A}(a_{1})+\beta ^{A}\delta u_{2}^{A}\left( a_{1},a_{2}\right) +\beta ^{A}\delta ^{2}u_{3} ^{A}\left( a_{1},a_{2}\right) \end{aligned}$$

(2)

$$\begin{aligned} U_{2}^{A}\left( a_{1},a_{2};\gamma ^{A}\right)&=u_{2}^{A}(a_{1} ,a_{2})+\gamma ^{A}\delta u_{3}^{A}\left( a_{1},a_{2}\right) . \end{aligned}$$

(3)

Following Strotz (1955) and Pollak (1968), we allow A either to be sophisticated (knowing her future preferences exactly), or to be naive (believing her future biases to be be identical to her current ones). We do not allow players to use probability distributions over their future present-biasedness, believing for example that they will be present-biased with a 50% probability. That would complicate the analysis even further.⁵

First, suppose that $\beta ^{A}=1.$ In that case, she must believe that $\gamma ^{A}=1$ as well. It makes no sense to believe one has present-biased preferences in future if that is not the case today. Second, suppose that $\beta ^{A}=\beta ,$ so she is present-biased. A naive player knows that she has a present-bias today, but does not realize she also has one in future: she assumes $\gamma ^{A}=1.$ Sophisticated players know they also have a present-bias in future and assume $\gamma ^{A}=\beta .$

Denote by $\mu ^{A}\left( \gamma \right)$ the player’s belief that she has $\gamma ^{A}=\gamma$ in future. Thus, a naive player has $\mu ^{A}(1)=1,$ a sophisticated player $\mu ^{A} (\beta )=1.$ In what follows, we use “perception” rather than “belief” to stress that beliefs are not rationally formed using Bayes’ rule. As noted, a time-consistent player will also have no present-bias in the future. Thus, $\beta ^{A}=1$ must imply $\mu ^{A}(1)=1.$

Our model is a generalization of O’Donoghue and Rabin (1999).⁶ They define a perception-perfect strategy as one in which a player always chooses the optimal action given current preferences and perceptions. Define $\mu ^{{\mathbf {A}}}$ as the vector of perceptions: $\mu ^{{\mathbf {A}}} \equiv \left( \mu ^{A}\left( \beta \right) ,\mu ^{A}(1)\right) .$ In our set-up, we then have:

Definition 1

In the three-period one-player game, a perception-perfect strategy at $t=1$ for a present-biased player, given her perceptions $\mu ^{{\mathbf {A}}},$ is a strategy profile $(a_{1}^{*},a_{2}^{*})$ such that

$$\begin{aligned} a_{2}^{*}(a_{1};\mu ^{{\mathbf {A}}})&\equiv \arg \max _{a_{2}\in {\mathcal {A}}_{2}(a_{1})}\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{A}\left( \gamma \right) U_{2}^{A}\left( a_{1},a_{2};\gamma \right) ,\forall a_{1}\in {\mathcal {A}}_{1};\end{aligned}$$

(4)

$$\begin{aligned} a_{1}^{*}(\beta ;\mu ^{{\mathbf {A}}})&=\arg \max _{a_{1}\in {\mathcal {A}}_{1} }U_{1}^{A}\left( a_{1},a_{2}^{*}\left( a_{1};\mu ^{{\mathbf {A}}}\right) ;\beta \right) \end{aligned}$$

(5)

Trivially, a perception-perfect strategy for a time-consistent player has

$$\begin{aligned} a_{2}^{*}\left( a_{1};\left( 0,1\right) \right)&=\arg \max _{a_{2} \in {\mathcal {A}}_{2}(a_{1})}U_{2}^{A}\left( a_{1},a_{2};1\right) \\ a_{1}^{*}\left( 1;\left( 0,1\right) \right)&=\arg \max _{a_{1} \in {\mathcal {A}}_{1}}U_{1}^{A}\left( a_{1},a_{2}^{*}\left( a_{1};\left( 0,1\right) \right) ;1\right) \end{aligned}$$

For the present-biased player, this can be understood as follows—First, given $a_{1},$ the current self assumes that the future self will take the action that maximizes the future self’s utility. In the current self’s perception, with probability $\mu ^{A}(\beta )$, the future self uses $U_{2}^{A}\left( a_{1},a_{2} ;\beta \right) ,$ while with probability $\mu ^{A}\left( 1\right) ,$ she uses $U_{2}^{A}\left( a_{1},a_{2};1\right) .$ The maximizer is given by (4) and denoted $a_{2}^{*}(a_{1};\mu ^{{\mathbf {A}}}).$ In period 1, given her perceptions, the current self’s lifetime utility if she takes action $a_{1}$ is given by $U_{1}^{A}\left( a_{1},a_{2}^{*}\left( a_{1};\mu ^{{\mathbf {A}}}\right) ;\beta \right) .$ The current self chooses $a_{1}$ to maximize this expression, hence (5). The perception-perfect strategy for the present-biased player follows directly from backward induction.

Definition 2

In the three-period one-player game, a perception-perfect outcome is a strategy profile $(a_{1}^{*},a_{2}^{*})$ such that $a_{1}^{*}$ is part of a perception-perfect strategy at $t=1$ while $a_{2}^{*}$ maximizes the future self’s utility at $t=2$, given $a_{1}^{*}$.

Note that there is a crucial difference between the two concepts; a perception-perfect strategy is a strategy profile that a player perceives to be played, while a perception-perfect outcome is the strategy profile that will be played. There may be a difference between the two if the player is present-biased and naive.

3.2 Application: intertemporal consumption, three periods

Consider a player that lives for 3 periods and has wealth 1 in period 1. Felicity in each period is given by $u_{t}^{A}\left( a_{t}\right) =\sqrt{a_{t}},$ with $a_{t}$ consumption in period t. For simplicity, we set $\delta =1$. A time-consistent player maximizes

$$\begin{aligned} U_{1}^{A}\left( a_{1},a_{2}\right) =\sqrt{a_{1}}+\sqrt{a_{2}}+\sqrt{1-a_{1}-a_{2}}. \end{aligned}$$

which implies $a_{1}^{*}=a_{2}^{*}=1/3.$ This simple decision problem satisfies our set-up. Two sequential decisions are made; $a_{1}$ and $a_{2},$ with ${\mathcal {A}}_{1}=\left[ 0,1\right]$ and ${\mathcal {A}} _{2}\left( a_{1}\right) =\left[ 0,1-a_{1}\right] .$ In period 3, she consumes whatever is left. Obviously, both the perception-perfect strategy and the perception-perfect outcome of a time-consistent player have $a_{1}^{*}=a_{2}^{*}=1/3$ as well.

We now solve for the perception-perfect strategy of the present-biased player. Using (4), at $t=2$, given first-period consumption $a_{1}$ and future present-biasedness $\gamma ,$ she chooses $a_{2}$ as to maximize

$$\begin{aligned} U_{2}^{A}\left( a_{1},a_{2};\gamma ^{A}\right) =\sqrt{a_{2}}+\gamma ^{A} \sqrt{1-a_{1}-a_{2}}. \end{aligned}$$

This yields

$$\begin{aligned} a_{2}^{*}\left( a_{1};\mu ^{{\mathbf {A}}}\right) =\frac{1-a_{1}}{1+\left[ \beta \mu ^{A}\left( \beta \right) +\mu ^{A}\left( 1\right) \right] ^{2} }=\frac{1-a_{1}}{1+{\tilde{\beta }}^{2}}, \end{aligned}$$

where, for ease of exposition, we write

$$\begin{aligned} {\tilde{\beta }}\equiv \beta \mu ^{A}\left( \beta \right) +\mu ^{A}\left( 1\right) . \end{aligned}$$

(6)

Perceived consumption in the last period is then given by

$$\begin{aligned} a_{3}^{*}\left( a_{1};\mu ^{{\mathbf {A}}}\right) =\frac{{\tilde{\beta }} ^{2}\left( 1-a_{1}\right) }{1+{\tilde{\beta }}^{2}}. \end{aligned}$$

Plugging this back into the lifetime utility of the current self yields

$$\begin{aligned} U_{1}^{A}\left( a_{1},a_{2}^{*}\left( a_{1};\mu ^{{\mathbf {A}}}\right) ;\beta \right)&=\sqrt{a_{1}}+\beta \sqrt{\frac{1-a_{1}}{1+{\tilde{\beta }} ^{2}}}+\beta \sqrt{\frac{{\tilde{\beta }}^{2}\left( 1-a_{1}\right) }{1+{\tilde{\beta }}^{2}}}\\&=\sqrt{a_{1}}+\beta \frac{1+{\tilde{\beta }}}{\sqrt{1+{\tilde{\beta }}^{2}}} \sqrt{1-a_{1}} \end{aligned}$$

The current self thus sets

$$\begin{aligned} a_{1}^{*}\left( \beta ;\mu ^{{\mathbf {A}}}\right) =\frac{1+{\tilde{\beta }}^{2} }{\beta ^{2}\left( 1+{\tilde{\beta }}\right) ^{2}+1+{\tilde{\beta }}^{2}}. \end{aligned}$$

A sophisticated present-biased player has $\mu ^{A}\left( \beta \right) =1$ and $\mu ^{A}\left( 1\right) =0,$ so ${\tilde{\beta }}=\beta$. She would thus choose

$$\begin{aligned} a_{1}^{*}\left( \beta ;\left( 1,0\right) \right) =\frac{1+\beta ^{2} }{\beta ^{2}\left( 1+\beta \right) ^{2}+1+\beta ^{2}}. \end{aligned}$$

and plan to have

$$\begin{aligned} a_{2}^{*}\left( a_{1};\left( 1,0\right) \right) =\frac{1-a_{1}^{*} }{1+\beta ^{2}}=\frac{\beta ^{2}\left( 1+\beta \right) ^{2}}{\left( 1+\beta ^{2}\right) \left( 2\beta ^{2}+2\beta ^{3}+\beta ^{4}+1\right) }. \end{aligned}$$

As the future self indeed has $\gamma ^{A}=\beta ,$ the profile $(a_{1}^{*}\left( \beta ;\left( 1,0\right) \right) ,a_{2}^{*}\left( a_{1};\left( 1,0\right) \right) )$ is the perception-perfect strategy as well as the perception-perfect outcome.

It is easy to see⁷ that $a_{1}^{*}\left( 1;\left( 1,0\right) \right) < a_{1}^{*}\left( \beta ;\left( 1,0\right) \right)$; a time-consistent player consumes less in the first period than a sophisticated present-biased player. As a present-biased player effectively has a higher short-run discount rate, she will choose to consume more today.

Now consider a naive present-biased player. She has $\mu ^{A}\left( \beta \right) =0$ and $\mu ^{A}\left( 1\right) =1,$ so ${\tilde{\beta }}=\beta$. Hence

$$\begin{aligned} a_{1}^{*}\left( \beta ;\left( 0,1\right) \right) =\frac{1}{1+2\beta ^{2}} \end{aligned}$$

and she plans to have

$$\begin{aligned} a_{2}^{*}\left( a_{1};\left( 0,1\right) \right) =\frac{1-a_{1}^{*} }{2}=\frac{\beta ^{2}}{1+2\beta ^{2}}. \end{aligned}$$

In period 2, however, she will find herself with $\gamma ^{A}=\beta$ rather than $\gamma ^{A}=1$ as she expected. Hence, true second-period consumption will be

$$\begin{aligned} a_{2}^{*}\left( a_{1},\beta \right) =\frac{1-a_{1}}{1+\beta ^{2}}=\frac{1}{1+2\beta ^{2}}. \end{aligned}$$

Thus, in this case, a perception-perfect strategy in period 1 is to choose $\left( a_{1}^{*},a_{2}^{*}\right) =\left( \frac{1}{1+2\beta ^{2} },\frac{\beta ^{2}}{1+2\beta ^{2}}\right) ,$ while the perception-perfect outcome turns out to be $\left( a_{1}^{*},a_{2}^{*}\right) =\left( \frac{1}{1+2\beta ^{2}},\frac{1}{1+2\beta ^{2}}\right) .$ It is interesting to note that $a_{1}^{*}\left( \beta ;\left( 0,1\right) \right) <a_{1}^{*}\left( \beta ;\left( 1,0\right) \right) .$ Hence, a naive player will choose a lower first-period consumption than a sophisticated one. This “sophistication effect” can be understood as follows. Different from naive players, sophisticated players are pessimistic about their future selves; they know them to be present-biased and squander most of their wealth quickly. As a consequence, sophisticated players restrict the tendency of the future self to over-consume by increasing immediate consumption, which restricts the availability of future resources. Rather than allowing future selves to squander the wealth, current selves prefer to do so themselves. Hence, first period consumption is higher.

4 The one-player case: more periods

4.1 Equilibrium concept

We now generalize the problem in Sect. 3.1 to one with $T+1>3$ periods, so T is the number of decisions to be made. This complicates matters. With $T=3$ for example, the decision made at $t=1$ will first of all be influenced by her perceptions concerning her type at $t=2.$ We denote these as $\mu _{12}^{{\mathbf {A}}}$: the first subscript reflects the current time period, the second the time period to which these perceptions apply. But the decision at $t=1$ will also be influenced by her perceptions concerning her type at $t=3,$ denoted $\mu _{13}^{\mathbf {A}}.$ Moreover, it will be influenced by her perception concerning the future self’s action at $t=2,$ which will in turn be affected by the perceptions of the self at $t=2$ concerning her future self. Or rather, the perceptions the current self has concerning these perceptions. Denote the latter as $\mu _{1}^{\mathbf {A}}\left( \mu _{23}^{\mathbf {A}}\right) ;$ these are the perceptions that, at $t=1,$ player A perceives her future self at $t=2$ to have concerning her type at $t=3.$ To simplify matters, we make the following assumptions⁸

Assumption 1

Perception consistency: Perceptions concerning the type of a future self are identical for all future selves: $\mu _{ij}^{\mathbf {A}}=\mu _{ik}^{\mathbf {A}}$ for all $i<T,$ $j,k\in \{i+1,\ldots ,T\}.$

Assumption 2

Intraplayer perception naivety: Perceptions of a future self are perceived to be identical to perceptions of the current self: $\mu _{i} ^{\mathbf {A}}(\mu _{jk}^{\mathbf {A}})=\mu _{ik}^{\mathbf {A}}$ for all $T\ge k>j>i.$

Note that there is a subtle difference between these two assumptions. Perception consistency implies that a player rules out that her type will change at some point in future. This seems a natural assumption to make; it is hard to justify a case in which, say, a player is naive concerning her future self in even periods but sophisticated concerning herself in odd periods.⁹ Intraplayer perception naivety implies that a player rules out that her future self will change her opinion about selves that are in the more distant future. Thus, we rule out that a player perceives today that her future self in two weeks is sophisticated, but maintains the possibility that one week from now she perceives that same future self to be naive.

This implies that we assume a naive player to never learn to become more sophisticated. This greatly simplifies the analysis and seems consistent with casual observation. Still, it is feasible to enrich our framework to allow for such learning, but we leave that for future research.

At time t,  define history ${\mathbf {H}}_{t}\equiv \left( a_{1},\ldots ,a_{t-1}\right) .$ Similar to (2) and (3), lifetime utility at time $t\le T$ can then be written

$$\begin{aligned} U_{1}^{A}\left( {\mathbf {a}};\beta ^{A}\right)&=u_{1}(a_{1})+\beta ^{A} \sum _{k=2}^{T}\delta ^{k-1}u_{k}^{A}({\mathbf {H}}_{k},a_{k})+\beta ^{A}\delta ^{T+1}u_{T+1}^{A}({\mathbf {H}}_{T+1}),\\ U_{t}^{A}\left( {\mathbf {a}};\gamma ^{A}\right)&=u_{t}\left( {\mathbf {H}}_{t},a_{t}\right) +\gamma ^{A}\sum _{k=t+1}^{T}\delta ^{k-t}u_{k} ^{A}({\mathbf {H}}_{k},a_{k})+\gamma ^{A}\delta ^{T+1}u_{T+1}^{A}({\mathbf {H}} _{T+1})\text { }\forall 1<t\le T, \end{aligned}$$

with ${\mathbf {a}}$ the vector of all decisions: ${\mathbf {a}}\equiv \left( a_{1},a_{2},\ldots ,a_{T}\right) ,$ and felicity in period $T+1$ also plays a role, just as we assumed in the case $T=2.$ Given the assumptions above, $\mu ^{{\mathbf {A}}}$ now reflects the perceptions at any time t concerning the type of the future self at any time $k>t.$ More precisely $\mu ^{{\mathbf {A}}}(\gamma )=\Pr \left( \gamma ^{A}=\gamma |\beta ^{A}=\beta \right)$ with $\gamma ^{A}$ the present-biasedness at any future period.¹⁰

Definition 3

In the $T+1$-period one-player game, a perception-perfect strategy at time $\tau$ for a present-biased player, given her perceptions $\mu ^{{\mathbf {A}}}$ and history ${\mathbf {H}}_{t}$ is a strategy profile $(a_{\tau }^{*},a_{\tau +1}^{*},\ldots a_{T}^{*})$ such that

$$\begin{aligned} a_{T}^{*}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}})&=\arg \max _{a_{T} \in {\mathcal {A}}_{T}\left( {\mathbf {H}}_{T}\right) }\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{A}\left( \gamma \right) U_{T}^{A}\left( {\mathbf {H}}_{T},a_{T};\gamma \right) ;\nonumber \\ a_{t}^{*}({\mathbf {H}}_{t};\mu ^{{\mathbf {A}}})&= \arg \max _{a_{t} \in {\mathcal {A}}_{t}\left( {\mathbf {H}}_{t}\right) }\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{A}\left( \gamma \right) U_{t}^{A}\left( {\mathbf {H}}_{t},a_{t},a_{t+1}^{*}\left( {\mathbf {H}}_{t+1};\mu ^{{\mathbf {A}}}\right) ,\right. \nonumber \\&\left. \ldots ,a_{T}^{*}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}} );\gamma \right) \forall \tau<t<T;\nonumber \\ a_{\tau }^{*}(\beta ;\mu ^{{\mathbf {A}}})&=\arg \max _{a_{\tau }\in {\mathcal {A}}_{\tau }\left( {\mathbf {H}}_{\tau }\right) }U_{\tau }^{A}\left( {\mathbf {H}}_{\tau },a_{\tau },a_{\tau +1}^{*}\left( {\mathbf {H}}_{\tau +1};\mu ^{A}\right) ,\ldots ,a_{T}^{*}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}} );\beta \right) . \end{aligned}$$

(7)

Trivially, a perception-perfect strategy for a time-consistent player has

$$\begin{aligned} a_{T}^{*}\left( {\mathbf {H}}_{T};\left( 0,1\right) \right)&=\arg \max _{a_{T}\in {\mathcal {A}}_{T}\left( {\mathbf {H}}_{T}\right) }U_{T}^{A}\left( {\mathbf {H}}_{T};1\right) \\ a_{t}^{*}\left( {\mathbf {H}}_{t};\left( 0,1\right) \right)&=\arg \max _{a_{t}\in {\mathcal {A}}_{t}\left( {\mathbf {H}}_{t}\right) }U_{t}^{A}\left( {\mathbf {H}}_{t},a_{t+1}^{*}\left( {\mathbf {H}}_{t+1};\left( 0,1\right) \right) ,\ldots ,a_{T}^{*}({\mathbf {H}}_{T};\left( 0,1\right) );1\right) \nonumber \\ \forall \tau \le t<T. \end{aligned}$$

For the present-biased player, this can be understood as follows. In the current self’s perception, the future self at $t=T$ has utility $U_{T}^{A}\left( {\mathbf {H}}_{t},a_{t};\beta \right)$ with probability $\mu ^{A}(\beta )$, and $U_{T}^{A}\left( {\mathbf {H}}_{t},a_{t};1\right)$ with probability $\mu ^{A}\left( 1\right)$. This yields (7). The maximizer is denoted $a_{T}^{*}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}).$ In the current self’s perception, the future self at $t=T-1$ has utility $U_{T-1}^{A}\left( {\mathbf {H}}_{T-1},a_{T-1},a_{T}^{*}\left( {\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}\right) ;\beta \right)$ with probability $\mu ^{A}(\beta )$, and $U_{T-1}^{A}\left( {\mathbf {H}}_{T-1},a_{T-1},a_{T}^{*}\left( {\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}\right) ;1\right)$ with probability $\mu ^{A}\left( 1\right)$.¹¹ This yields $a_{T-1}^{*}({\mathbf {H}}_{T-1};\mu ^{{\mathbf {A}}}).$ This process unravels until period 1, where the current self chooses the $a_{1}$ that maximizes her utility given her perceptions and given her true $\beta ^{A}$.

Definition 4

In the $T+1$-period one-player game, a perception-perfect outcome is a strategy profile $(a_{1}^{*},a_{2}^{*},\ldots ,a_{T}^{*})$ such that $a_{\tau }^{*}$ is part of a perception-perfect strategy at time $\tau$ for all $\tau =1,\ldots ,T.$

Note again the crucial difference between the two concepts: a perception-perfect strategy is a strategy profile that a player perceives to be played, while a perception-perfect outcome is the strategy profile that will be played.

It is relatively straightforward to extend the analysis to infinitely many periods. Solving such a model is similar to solving an infinite-horizon maximization problem with time-consistent preferences, but under the assumption that all future selves have the type the current self perceives them to have.

4.2 Application: intertemporal consumption, $T+1$ periods

Consider the same example as in Sect. 3.2, but now with $T+1$ periods;

$$\begin{aligned} U_{1}^{A}\left( {\mathbf {a}}\right) =\sqrt{a_{1}}+\sqrt{a_{2}}+\ldots \sqrt{a_{T}}+\sqrt{1-\sum _{t=1}^{T}a_{t}}. \end{aligned}$$

In this case, a time-consistent player would set $a_{1}^{*}=\cdots =a_{T}^{*}=\frac{1}{T+1}.$

Now solve for the perception-perfect strategy of a present-biased player. Define total past consumption at time $\tau$ as $h_{\tau } =\sum _{t=1}^{\tau -1}a_{t}.$ At $t=T,$ the player is perceived by the self at $t=1$ to maximize

$$\begin{aligned} U_{T}^{A}\left( {\mathbf {H}}_{T},a_{T};\gamma ^{A}\right) =\sqrt{a_{T}} +\gamma ^{A}\sqrt{1-h_{T}-a_{T}}. \end{aligned}$$

This yields

$$\begin{aligned} a_{T}^{*}\left( {\mathbf {H}}_{t};\mu ^{{\mathbf {A}}}\right) =\frac{1-h_{T} }{1+\left[ \beta \mu ^{A}\left( \beta \right) +\mu ^{A}\left( 1\right) \right] ^{2}}=\frac{1-h_{T}}{1+{\tilde{\beta }}^{2}}, \end{aligned}$$

where again ${\tilde{\beta }}$ is given by (6). Now move back to $T-1$:

$$\begin{aligned} U_{T-1}^{A}\left( {\mathbf {H}}_{T-1},a_{T-1},a_{T}^{*}\left( {\mathbf {H}} _{t};\mu ^{{\mathbf {A}}}\right) ;\gamma ^{A}\right)&=\sqrt{a_{T-1}} +\gamma ^{A}\sqrt{\frac{1-h_{T-1}-a_{T-1}}{1+{\tilde{\beta }}^{2}}}\\&+\gamma ^{A}\sqrt{1-h_{T-1}-a_{T-1}-\frac{1-h_{T-1}-a_{T-1}}{1+\tilde{\beta }^{2}}} \end{aligned}$$

Perception consistency implies that the self at $T-2$ is perceived to maximize

$$\begin{aligned} U_{T-1}^{A}=\sqrt{a_{T-1}}+{\tilde{\beta }}\sqrt{\frac{1-h_{T-1}-a_{T-1} }{1+{\tilde{\beta }}^{2}}}+{\tilde{\beta }}\sqrt{1-h_{T-1}-a_{T-1}-\frac{1-h_{T-1}-a_{T-1}}{1+{\tilde{\beta }}^{2}}} \end{aligned}$$

This yields

$$\begin{aligned} a_{T-1}^{*}=\frac{1+{\tilde{\beta }}^{2}}{{\tilde{\beta }}^{2}\left( 1+{\tilde{\beta }}\right) ^{2}+1+{\tilde{\beta }}^{2}}\left( 1-h_{t-1}\right) . \end{aligned}$$

Solving further is conceptually straightforward but analytically tedious.

5 The two-player case: three periods

5.1 Equilibrium concept

We now extend the analysis to multiple players. Now, the current decisions of a player not only depend on her perceptions concerning her own future type, but also on those concerning the other player’s future type, and possibly even about those concerning the other player’s perceptions, plus how those will affect future actions.

Consider two players, A and B. For ease of exposition, we refer to A as being female, and to B as being male. Player i’s present-bias is denoted $\beta ^{i}\in \left\{ 1,\beta \right\} .$ The true present-bias of player i’s future self is $\gamma ^{i}\in \left\{ 1,\beta \right\} .$ There are 3 periods, $t=1,2,3.$ In the first two periods both A and B make a simultaneous decision. In $t=1,$ player A chooses $a_{1}\in {\mathcal {A}}_{1},$ while B chooses $b_{1}\in {\mathcal {B}}_{1}$ . At $t=2,$ players learn the actions taken at $t=1,$ and player A chooses $a_{2}\in {\mathcal {A}} _{2}(a_{1},b_{1}),$ while B chooses $b_{2}\in {\mathcal {B}}_{2}(a_{1},b_{1}).$ We now have

$$\begin{aligned} U_{1}^{i}\left( a_{1},b_{1},a_{2},b_{2};\beta ^{i}\right)&=u_{1} ^{i}(a_{1},b_{1})+\beta ^{i}\delta u_{2}^{i}\left( a_{1},b_{1},a_{2} ,b_{2}\right) +\beta ^{i}\delta ^{2}u_{3}^{i}\left( a_{1},b_{1},a_{2} ,b_{2}\right) \\ U_{2}^{i}\left( a_{1},b_{1},a_{2},b_{2};\gamma ^{i}\right)&=u_{2} ^{i}\left( a_{1},b_{1},a_{2},b_{2}\right) +\gamma ^{i}\delta u_{3}^{i}\left( a_{1},b_{1},a_{2},b_{2}\right) , i\in \{A,B\}. \end{aligned}$$

In period 1, what A expects to happen in period 2 depends on her perceptions concerning her own, and those concerning B’s future type. For simplicity, players can observe each other’s current type, so both A and B observe $\beta ^{A}$ and $\beta ^{B}.$ This simplifies the exposition, but it is straightforward to also allow players to have perceptions concerning their competitor’s current type.

A straightforward extension of the one-player case is as follows. In the perception of player A, we have $\mu ^{AA}(\gamma )=\Pr ^{A}\left( \gamma ^{A}=\gamma |\beta ^{A}=\beta \right)$. The first superscript on $\mu$ denotes that perceptions are held by A,  the second that perceptions concern A. The superscript on $\Pr$ denotes that this is the probability perceived by player A. Similarly, $\mu ^{AB}(\gamma )=\Pr ^{A}\left( \gamma ^{B}=\gamma |\beta ^{B}=\beta \right)$. Naturally, $\mu ^{BA}(\gamma )=\Pr ^{B}\left( \gamma ^{A}=\gamma |\beta ^{A}=\beta \right)$ and $\mu ^{BB}(\gamma )=\Pr ^{B}\left( \gamma ^{B}=\gamma |\beta ^{B}=\beta \right) .$

It is also of concern what, for example, A perceives B to perceive about A, that is $\mu ^{{\mathbf {A}}}{{\mathbf {B}}}\left( \mu ^{{\mathbf {B}}}{{\mathbf {A}}}\right) .$ We also assume naivety in this respect, in the sense that this equals what A perceives about herself:

Assumption 3

Current interplayer perception naivety: Perceptions that the other player has are identical to one’s own perceptions: $\mu ^{{\mathbf {i}}}{{\mathbf {j}}}(\mu ^{{\mathbf {j}}}{{\mathbf {k}}} )=\mu ^{{\mathbf {i}}}{{\mathbf {k}}}$ for all $i,j,k\in \left\{ A,B\right\} .$

This is a natural extension of the intraplayer perception naivety we assumed in the one-player case. Rather than ruling out that a future self has perceptions different from the current self, we now assume that a player rules out that the other player has perceptions different from herself.

For ease of exposition, restrict attention to present-biased players. Suppose for example that A perceives both players to be time-consistent in future. If $(a_{1},b_{1})$ is played in period 1, she then expects a Nash equilibrium $(a_{2}^{A},b_{2}^{A})$ to be played in period 2 such that $a_{2}^{A}$ maximizes her future self’s utility given $b_{2}^{A}$ and given that she is time-consistent, and such that $b_{2}^{A}$ maximizes B’s utility, given $a_{2}^{A}$ and given that he is time-consistent. Thus,

$$\begin{aligned} a_{2}^{A}&=\arg \max _{a_{2}}U_{2}^{A}\left( a_{1},b_{1},a_{2},b_{2} ^{A};1\right) \\ b_{2}^{A}&=\arg \max _{b_{2}}U_{2}^{A}\left( a_{1},b_{1},a_{2}^{A} ,b_{2};1\right) \end{aligned}$$

where superscripts denote the perceptions of player A. More generally,

Definition 5

Consider the three-period two-player game played by present-biased players. In period 2, given $(a_{1},b_{1})$ an equilibrium as perceived by player $i\in \left\{ A,B\right\}$ is an outcome $\left( a_{2}^{i}(a_{1} ,b_{1};\mu ^{{{\mathbf {i}}}{{\mathbf {A}}}}),b_{2}^{i}(a_{1},b_{1};\mu ^{{{\mathbf {i}}}{{\mathbf {B}}}})\right)$ that forms a Nash equilibrium of the second-period game, given the perceptions of player i. Hence

$$\begin{aligned} a_{2}^{i}&=\arg \max _{a_{2}\in {\mathcal {A}}_{2}(a_{1},b_{1})}\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iA}\left( \gamma \right) U_{2}^{A}\left( a_{1},b_{1},a_{2},b_{2}^{A};\gamma \right) \\ b_{2}^{i}&=\arg \max _{b_{2}\in {\mathcal {B}}_{2}(a_{1},b_{1})}\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iB}\left( \gamma \right) U_{2}^{B}\left( a_{1},b_{1},a_{2}^{A},b_{2};\gamma \right) \end{aligned}$$

Moving back to period 1, given that player A has a perception of the play that will ensue in period 2 for any $\left( a_{1},b_{1}\right)$ in period 1, it is straightforward to write down the conditions for a subgame perfect Nash equilibrium as perceived by A. We refer to this simply as an equilibrium as perceived by A.

Definition 6

In period 1, an equilibrium as perceived by i is an outcome

$$\begin{aligned} \left( a_{1}^{i}\left( \beta ;\mu ^{{{\mathbf {i}}}{{\mathbf {A}}}}, \mu ^{{{\mathbf {i}}}{{\mathbf {B}}}}\right) ,b_{1} ^{i}\left( \beta ;\mu ^{{{\mathbf {i}}}{{\mathbf {A}}}},\mu ^{{{\mathbf {i}}}{{\mathbf {B}}}}\right) \right) \end{aligned}$$

that is part of a subgame perfect Nash equilibrium of the entire game, given the perceptions of player i. Thus,

$$\begin{aligned} a_{1}^{i}&=\arg \max _{a_{1}\in {\mathcal {A}}_{1}}U_{1}^{A}\left( a_{1} ,b_{1}^{i},a_{2}^{i}(a_{1},b_{1}^{i};\mu ^{{{\mathbf {i}}}{{\mathbf {A}}}}),b_{2}^{i}(a_{1} ,b_{1};\mu ^{{{\mathbf {i}}}{{\mathbf {B}}}});\beta \right) \nonumber \\ b_{1}^{i}&=\arg \max _{b_{1}\in {\mathcal {B}}_{1}}U_{1}^{B}\left( a_{1} ^{i},b_{1},a_{2}^{i}(a_{1},b_{1};\mu ^{{{\mathbf {i}}}{{\mathbf {A}}}}),b_{2}^{i}(a_{1} ,b_{1};\mu ^{{{\mathbf {i}}}{{\mathbf {B}}}});\beta \right) . \end{aligned}$$

(8)

Using these definitions, and considering play in period 1, we thus expect player A to take an action that she perceives to be part of a subgame perfect equilibrium for the entire game, while we expect player B to take an action that he perceives to be part of a subgame perfect equilibrium for the entire game.

Definition 7

A perception-perfect outcome is an outcome $(a_{1}^{*},b_{1}^{*},a_{2}^{*},b_{2}^{*})$ such that $a_{1}^{*}$ is part of an equilibrium as perceived by A;  $b_{1}^{*}$ is part of an equilibrium as perceived by B;  $a_{2}^{*}$ is an equilibrium as perceived by A given $(a_{1}^{*},b_{1}^{*})$; and $b_{2}^{*}$ is an equilibrium as perceived by B given $(a_{1}^{*} ,b_{1}^{*}).$

Note that $a_{1}^{*}$ and $b_{1}^{*}$ may not be part of the same equilibrium. Also, we assume that players do not learn about the perceptions or type of the other player. But we do allow them to base second-period play on actual play in period 1, rather than on what they expected play to be in period 1.

5.2 Application: the common pool problem

Consider the following common pool problem. Players A and B live for 3 periods with a joint wealth of 1. Felicity is given by $u_{t}^{i}\left( c\right) =c^{\rho },$ with $\rho <1$. For simplicity, $\delta = 1$. In each of 2 periods, each player takes an amount out of the common pool. What is left in the last period is equally shared.¹² We first derive the equilibrium for our four player types and then compare these.

5.2.1 Time-consistent players

Respective utility functions in period 1 are

$$\begin{aligned} U_{1}^{A}\left( a_{1},b_{1},a_{2},b_{2}\right)&=a_{1}^{\rho }+a_{2}^{\rho }+\left( \frac{1-a_{1}-a_{2}-b_{1}-b_{2}}{2}\right) ^{\rho }. \nonumber \\ U_{1}^{B}\left( a_{1},b_{1},a_{2},b_{2}\right)&=b_{1}^{\rho }+b_{2}^{\rho }+\left( \frac{1-a_{1}-a_{2}-b_{1}-b_{2}}{2}\right) ^{\rho } \end{aligned}$$

(9)

In period 1 player A correctly perceives the equilibrium in period 2 to satisfy

$$\begin{aligned} a_{2}^{A}&=\arg \max a_{2}^{\rho }+\left( \frac{W_{2}-a_{2}-b_{2}}{2} \right) ^{\rho } \end{aligned}$$

(10)

$$\begin{aligned} b_{2}^{A}&=\arg \max b_{2}^{\rho }+\left( \frac{W_{2}-a_{2}-b_{2}}{2} \right) ^{\rho }. \end{aligned}$$

(11)

with $W_{2}\equiv 1-a_{1}-b_{1}$ the amount of wealth left at the start of period 2. Taking the first-order condition

$$\begin{aligned} \rho a_{2}^{\rho -1}-\frac{1}{2}\rho \left( \frac{1-a_{1}-a_{2}-b_{1}-b_{2}}{ 2}\right) ^{\rho -1}=0, \end{aligned}$$

yields the reaction function

$$\begin{aligned} a_{2}=\Gamma _{tc}\left( W_{2}-b_{2}\right) \quad \quad \text {with} \quad \quad \Gamma _{tc}\equiv \frac{2^{\frac{1}{1-\rho }}}{2+2^{\frac{1}{1-\rho }}}. \end{aligned}$$

Imposing symmetry, this yields the Nash equilibrium

$$\begin{aligned} a_{2}^{*}=b_{2}^{*}=\theta _{tc}W_{2}\quad \quad \text {with} \quad \theta _{tc}\equiv \frac{\Gamma _{tc}}{1+\Gamma _{tc}}. \end{aligned}$$

(12)

Now move back to period 1. Plugging (12) back into (9),

$$\begin{aligned} U_{1}^{A}\left( a_{1},b_{1},a_{2},b_{2}\right) =a_{1}^{\rho }+\left( \theta _{tc}W_{2}\right) ^{\rho }+\left( \frac{1}{2}\left( 1-2\theta _{tc}\right) W_{2}\right) ^{\rho } \end{aligned}$$

Maximizing with respect to $a_{1}:$

$$\begin{aligned} \rho a_{1}^{\rho -1}-\rho \theta _{tc}\left( \theta _{tc}W_{2}\right) ^{\rho -1}-\frac{1}{2}\left( 1-2\theta _{tc}\right) \rho \left( \frac{1}{2}\left( 1-2\theta _{tc}\right) W_{2}\right) ^{\rho -1}=0 \end{aligned}$$

hence

$$\begin{aligned} a_{1}=\Omega _{tc}\left( 1-a_{1}-b_{1}\right) \quad \text {with} \quad \quad \Omega _{tc}\equiv \left[ \theta _{tc}^{\rho }+\left( \frac{1}{2}\left( 1-2\theta _{tc}\right) \right) ^{\rho }\right] ^{\frac{1}{\rho -1}}. \end{aligned}$$

This implies that first period consumption choices equal

$$\begin{aligned} a_{1}^{tc}=b_{1}^{tc}=\frac{\Omega _{tc}}{1+2\Omega _{tc}}, \end{aligned}$$

(13)

where superscripts tc denote equilibrium values for the time-consistent case.

5.2.2 Sophisticated present-biased players

In this case, at $t=1,$ the current self of player A perceives an equilibrium in period 2 to satisfy

$$\begin{aligned} a_{2}^{A}&=\arg \max a_{2}^{\rho }+\beta \left( \frac{1}{2}\left( W_{2}-a_{2}-b_{2}\right) \right) ^{\rho } \nonumber \\ b_{2}^{A}&=\arg \max b_{2}^{\rho }+\beta \left( \frac{1}{2}\left( W_{2}-a_{2}-b_{2}\right) \right) ^{\rho }. \end{aligned}$$

(14)

Taking the first-order condition of her own problem:

$$\begin{aligned} \rho a_{2}^{\rho -1}-\frac{1}{2}\beta \rho \left( \frac{1}{2}\left( W_{2}-a_{2}-b_{2}\right) \right) ^{\rho -1}=0, \end{aligned}$$

which implies the reaction function

$$\begin{aligned} a_{2}=\Gamma _{s}\cdot \left( W_{2}-b_{2}\right) \quad \quad \mathrm{with} \quad \quad \Gamma _{s} \equiv \frac{\left( \frac{1}{2}\beta \right) ^{\frac{1}{\rho -1}}}{2+\left( \frac{1 }{2}\beta \right) ^{\frac{1}{\rho -1}}}. \end{aligned}$$

(15)

Hence, along the same lines as above, this yields

$$\begin{aligned} a_{2}^{*}=b_{2}^{*}=\theta _{s}W_{2}\quad \quad \mathrm{with} \theta _{s} \equiv \frac{ \Gamma _{s}}{1+\Gamma _{s}}. \end{aligned}$$

Moving back to period 1, note the following. After period 1, $W_{2}$ is left. Player A perceives both players to consume $\theta _{s}W_{2}$ in period 2, hence in period 3, there is $\left( 1-2\theta _{s}\right) W_{2}$ left, which is equally shared among both players. Hence, using (9), the equilibrium in period 1 as perceived by A satisfies

$$\begin{aligned} a_{1}^{A}&=\arg \max _{a_{1}}a_{1}^{\rho }+\beta \left( \theta _{s}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-2\theta _{s}\right) W_{2}\right) ^{\rho }. \nonumber \\ b_{1}^{A}&=\arg \max _{b_{1}}b_{1}^{\rho }+\beta \left( \theta _{s}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-2\theta _{s}\right) W_{2}\right) ^{\rho }. \end{aligned}$$

(16)

The first-order condition for player A equals

$$\begin{aligned} \rho a_{1}^{\rho -1}-\beta \rho \theta _{s}\left( \theta _{s}W_{2}\right) ^{\rho -1}-\frac{1}{2}\beta \rho \left( 1-2\theta _{s}\right) \left( \frac{1 }{2}\left( 1-2\theta _{s}\right) W_{2}\right) ^{\rho -1}=0 \end{aligned}$$

or

$$\begin{aligned} a_{1}=\Omega _{s}\left( 1-a_{1}-b_{1}\right) \quad \quad \mathrm{with} \Omega _{s}\equiv \beta ^{\frac{1}{\rho -1}}\left[ \theta _{s}^{\rho }+\left( \frac{1}{2} \left( 1-2\theta _{s}\right) \right) ^{\rho }\right] ^{\frac{1}{\rho -1}}. \end{aligned}$$

Imposing symmetry:

$$\begin{aligned} a_{1}^{s}=b_{1}^{s}=\frac{\Omega _{s}}{1+2\Omega _{s}}, \end{aligned}$$

(17)

where superscript s denotes equilibrium values in the sophisticated case. As B faces the same problem and has the same perceptions, she has the same perceived equilibrium in periods 1 and 2 as A does. As players’ perceptions are correct, their perceived play in period 2 equals actual play.

5.2.3 Naive present-biased players

If players are naive concerning all future selves, then A perceives the equilibrium in period 2 to satisfy (10) and (11) so $a_{2}^{A}=b_{2}^{A}= \theta _{tc}W_{2}.$ The equilibrium perceived by A at $t=1$ thus satisfies

$$\begin{aligned} a_{1}^{A}&=\arg \max _{a_{1}}a_{1}^{\rho }+\beta \left( \theta _{tc}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-2\theta _{tc}\right) W_{2}\right) ^{\rho } \\ b_{1}^{A}&=\arg \max _{b_{1}}b_{1}^{\rho }+\beta \left( \theta _{tc}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-2\theta _{tc}\right) W_{2}\right) ^{\rho }. \end{aligned}$$

This problem is essentially the same as in (16)—but with $\theta _{tc}$ rather than $\theta _{s}.$ Maximizing thus yields

$$\begin{aligned} a_{1}=\Omega _{n}\left( 1-a_{1}-b_{1}\right) \quad \quad \mathrm{with}\quad \Omega _{n}=\beta ^{\frac{1}{\rho -1}}\left[ \theta _{tc}^{\rho }+\left( \frac{1}{2}\left( 1-2\theta _{tc}\right) \right) ^{\rho }\right] ^{\frac{1}{\rho -1}}. \end{aligned}$$

Imposing symmetry:

$$\begin{aligned} a_{1}^{n}=b_{1}^{n}=\frac{\Omega _{n}}{1+2\Omega _{n}}. \end{aligned}$$

(18)

As player B faces the same problem and the same perceptions, she has the same perceived equilibrium in periods 1 and 2 as player A does. However, perceptions turn out to be incorrect: the equilibrium in the second period has them both consuming $\theta _{s}W_{2}$ (as we saw in the previous analysis) rather than $\theta _{tc}W_{2}.$ Hence, actual consumption in period 2 will turn out to be

$$\begin{aligned} a_{2}^{n}=b_{2}^{n}=\theta _{s}\left( 1-\frac{2\Omega _{n}}{1+2\Omega _{n}} \right) . \end{aligned}$$

5.2.4 Naive about yourself, sophisticated about the other

The most interesting case has both players perceive themselves to be time-consistent, but their competitor to be present-biased in the future. In other words, each player is naive concerning herself, but sophisticated concerning the other. As noted in the introduction, Kahneman (2011) argues that this is the typical situation. In period 1, Player A then perceives a second-period equilibrium

$$\begin{aligned} a_{2}^{A}&=\arg \max a_{2}^{\rho }+\left( \frac{W_{2}-a_{2}-b_{2}}{2} \right) ^{\rho } \\ b_{2}^{A}&=\arg \max b_{2}^{\rho }+\beta \left( \frac{W_{2}-a_{2}-b_{2}}{2} \right) ^{\rho }. \end{aligned}$$

From the analysis above, reaction functions perceived by A are

$$\begin{aligned} a_{2}^{A}= & {} \Gamma _{tc}\left( W_{2}-b_{2}^{A}\right) \\ b_{2}^{A}= & {} \Gamma _{s}\left( W_{2}-a_{2}^{A}\right) , \end{aligned}$$

hence

$$\begin{aligned} a_{2}^{A}=\theta _{ns}W_{2}\quad \quad \mathrm{with} \quad \quad \theta _{ns}=\frac{\Gamma _{tc}\left( 1-\Gamma _{s}\right) }{1-\Gamma _{tc}\Gamma _{s}},\\ b_{2}^{A}=\theta _{sn}W_{2}\quad \quad \mathrm{with} \quad \quad \theta _{sn}=\frac{\Gamma _{s}\left( 1-\Gamma _{tc}\right) }{1-\Gamma _{tc}\Gamma _{s}}. \end{aligned}$$

Below, we show that $\theta _{ns}<\theta _{sn}$. Thus, A perceives to consume much less in period 2 than B. Note that reaction functions are strategic substitutes in the sense of Bulow et al. (1985) the higher the consumption of B, the lower the share that A will claim. Thus, as A perceives B to be very aggressive in period 2, she also perceives to make a much lower claim herself.

In period 1, A perceives the following game to be played:

$$\begin{aligned} a_{1}^{A}&=\arg \max _{a_{1}}a_{1}^{\rho }+\beta \left( \theta _{ns}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) W_{2}\right) ^{\rho } \\ b_{1}^{A}&=\arg \max _{b_{1}}b_{1}^{\rho }+\beta \left( \theta _{sn}W_{2}\right) ^{\rho }+\beta \left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) W_{2}\right) ^{\rho } \end{aligned}$$

Taking first-order conditions:

$$\begin{aligned} \rho a_{1}^{\rho -1}-\beta \theta _{ns}\rho \left( \theta _{ns}W_{2}\right) ^{\rho -1}- & {} \frac{1}{2}\beta \rho \left( 1-\theta _{ns}-\theta _{sn}\right) \left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) W_{2}\right) ^{\rho -1}=0 \\ \rho b_{1}^{\rho -1}-\beta \theta _{sn}\rho \left( \theta _{sn}W_{2}\right) ^{\rho -1}- & {} \frac{1}{2}\beta \rho \left( 1-\theta _{ns}-\theta _{sn}\right) \left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) W_{2}\right) ^{\rho -1}=0 \end{aligned}$$

so

$$\begin{aligned} a_{1}^{\rho -1}= & {} \beta \left( \theta _{ns}^{\rho }+\left( \frac{1}{2} \left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }\right) \left( 1-a_{1}-b_{1}\right) ^{\rho -1} \\ b_{1}^{\rho -1}= & {} \beta \left( \theta _{sn}^{\rho }+\left( \frac{1}{2} \left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }\right) \left( 1-a_{1}-b_{1}\right) ^{\rho -1} \end{aligned}$$

This implies

$$\begin{aligned} a_{1}=\Omega _{ns}\left( 1-a_{1}-b_{1}\right) \quad \quad \mathrm{with} \quad \quad \Omega _{ns}=\beta ^{\frac{1}{\rho -1}}\left[ \theta _{ns}^{\rho }+\left( \frac{1}{2 }\left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }\right] ^{\frac{1 }{\rho -1}}, \\ b_{1}=\Omega _{sn}\left( 1-a_{1}-b_{1}\right) \quad \quad \mathrm{with} \quad \quad \Omega _{sn}=\beta ^{\frac{1}{\rho -1}}\left[ \theta _{sn}^{\rho }+\left( \frac{1}{2 }\left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }\right] ^{\frac{1 }{\rho -1}}. \end{aligned}$$

This implies

$$\begin{aligned} a_{1}^{ns}= & {} \frac{\Omega _{ns}}{1+\Omega _{ns}+\Omega _{sn}} \\ b_{1}^{ns}= & {} \frac{\Omega _{sn}}{1+\Omega _{ns}+\Omega _{sn}} \end{aligned}$$

In period 1, A expects these shares to be played, but B expects the opposite shares. Both will thus consume $\Omega _{ns}/\left( 1+\Omega _{ns}+\Omega _{sn}\right) ,$ so after period 1, $W_{2}=1-2\Omega _{ns}/\left( 1+\Omega _{ns}+\Omega _{sn}\right)$ will be left. In period 2, both consume a share $\theta _{ns}$ of that wealth, and expect their opponent to consume $\theta _{sn}.$ We now have

Theorem 1

In the common pool problem, present-biased players always claim a larger first-period share than time-consistent players. Those naive about themselves but sophisticated about others claim the largest first-period share, while those that are completely naive claim the lowest: $a_{1}^{ns}>a_{1}^{s}>a_{1}^{n}>a_{1}^{tc}.$

Proof

In Appendix B. $\square$

This can be understood as follows. It is immediate that naifs consume more than time-consistent players. Sophisticated players consume more than naifs for two reasons. First, they know that their future selves will squander resources, which induces them to consume more today—an effect we also saw in Sect. 3.2. Second, they also know that their competitor will squander future resources, inducing them to consume even more today.

Now consider players that are naive about themselves, but sophisticated about their competitor. Each then perceives that in the future, her competitor will be very aggressive to the detriment of herself. The unfounded fear of getting an unequal share in the future gives both players an incentive to make a large claim today. This seriously exacerbates the common pool problem.

5.2.5 A numerical example

For $\beta =1/2$ and $\rho = 1/3$, Table 1 gives consumption levels and total utility for all scenarios.¹³ From the Table, time-consistent players indeed take much less from the common pool in period 1 than any present-biased player. The difference between sophisticated and naive is relatively small. First-period consumption is much higher if one is sophisticated about the other, but naive about oneself.

Interestingly, players end up better off when they are naive rather than sophisticated. That was not the case in the one-person games described earlier. There, sophisticated players realize they are time-inconsistent tomorrow and hence take measures today to minimize the impact of that. But now, sophisticated players are also sophisticated about their opponent’s future behavior, which induces them to behave more aggressively today, in an attempt to secure at least some of the resources. Sophistication thus triggers a prisoners’ dilemma in which both players claim more to avoid being short-changed tomorrow.

Table 1 Numerical example common pool problem; $\beta =1/2$, $\rho = 1/3$

Perception perfect outcomes with time-consistent players, sophisticated present-biased players, naive present-biased players, and present-biased players that are naive about their own present-biasedness but sophisticated about that of the other player (soph other). Columns give the consumption per player in the first ($a_1$), second ($a_2$) and third period ($a_3$) as well as total discounted lifetime utility in period 1.

5.2.6 Partial naivety

The analysis above can be easily extended to a case of partial naivety, in which players perceive their future self to have some present-bias ${\hat{\beta }} \in (\beta ,1)$, see fn. 5. In that case, the expression for $a_2^A$ in (14) has a $\beta$ rather than a ${\hat{\beta }}$, which in turn implies that the expression for $\Gamma _s$ in (15) becomes a ${\hat{\Gamma }}_s$ and has ${\hat{\beta }}$s rather than $\beta$s. Qualitatively, the equilibrium then converges from the sophisticated to the naive equilibrium as ${\hat{\beta }} \downarrow \beta$.

In the analysis where players are partially naive about themselves but sophisticated about the other, $\Gamma _{tc}$ is replaced by ${\hat{\Gamma }}_s$ and the remainder of the analysis goes through as above. Again, the equilibrium converges from the sophisticated equilibrium to the one derived above as ${\hat{\beta }} \downarrow \beta$.

6 Two-player case: more periods

6.1 Equilibrium concept

We now extend the two-player two-period model to a setting with $T+1$ periods, $T>2.$ This is conceptually straightforward, but notationally tedious. In $t=1$, A perceives that in period T a game is played between herself and B with both players having the type she perceives them to have. Moving back to $T-1$, she can then derive perceived equilibrium play in that period. Continuing in this manner yields a perceived equilibrium in period 1, and hence a course of action for A in period 1, with a similar analysis for B.

To analyze this problem, we again need to make simplifying assumptions concerning the perceptions of players. Not only do we need that A has to believe that she has the same perceptions as B concerning future types, we also need that higher-order perceptions are perceived to be equal. In other words, we also need that the perceptions that A has in period l concerning the perceptions of B in period m concerning the perceptions of A in period n,  equal the perceptions that A thinks she herself has in period l concerning herself in period n. Thus,

Assumption 4

Future interplayer perception naivety: Perceptions that the other player has concerning future perceptions, are assumed identical to one’s own: $\mu _{lm}^{{\mathbf {i}}}{{\mathbf {j}}}(\mu _{mn}^{{\mathbf {j}}}{{\mathbf {k}}})=\mu _{lm}^{{\mathbf {i}}}{{\mathbf {i}}}(\mu _{mn}^{{\mathbf {j}}}{{\mathbf {k}}})$ for all $i,j,k\in \left\{ A,B\right\} .$

Without this, we have to allow for the possibility that in some future period A maintains the possibility that B has different perceptions concerning future types than she herself has. This would require higher order beliefs for A concerning perceptions, which would highly complicate matters. Together with the previous assumptions, future interplayer perception naivety implies that all perceptions are always constant—and are always assumed to be constant.

History at time t is now defined as ${\mathbf {H}}_{t}\equiv \left( a_{1} ,b_{1};\ldots ;a_{t-1},b_{t-1}\right) .$ Lifetime utility at time $t\le T$ for player i can be written

$$\begin{aligned} U_{1}^{i}\left( {\mathbf {a}},{\mathbf {b}};\beta ^{i}\right)&=u_{1}^{i} (a_{1},b_{1})+\beta ^{i}\sum _{k=t+1}^{T}\delta ^{k-t}u_{k}^{i}({\mathbf {H}} _{k},a_{k},b_{k})+\beta ^{i}\delta ^{T+1}u_{T+1}^{i}({\mathbf {H}}_{T+1})\\ U_{t}^{i}\left( {\mathbf {a}},{\mathbf {b}};\gamma ^{i}\right)&=u_{t} ^{i}({\mathbf {H}}_{t},a_{t},b_{t})+\gamma ^{i}\sum _{k=t+1}^{T}\delta ^{k-t}u_{k} ^{i}({\mathbf {H}}_{k},a_{k},b_{k})+\gamma ^{A}\delta ^{T+1}u_{T+1} ^{A}({\mathbf {H}}_{T+1})\text { } \end{aligned}$$

$\forall 1<t\le T$ for $i\in \{A,B\},$ $\mathbf {a=}(a_{1},\ldots ,a_{T})$ and $\mathbf {b=} (b_{1},\ldots ,b_{T}).$

The analysis for $T=2$ naturally extends to more periods. Consider period T. In an equilibrium as perceived by i, actions taken then will be mutual best responses given the perceptions i has, and given the history of play. Again, we can write player i’s perceptions about j’s future type as $\mu ^{{\mathbf {i}}}{{\mathbf {j}}}$. Given perceived play in period T, i can then move to $T-1$ and derive a perceived equilibrium for that period. This process unravels until period 1.

Definition 8

In the $T+1$-period, 2-player game with present-biased players, an equilibrium at time $\tau$ as perceived by i, given her perceptions $\mu ^{{\mathbf {i}}}$ and history ${\mathbf {H}}_{t}$ is a sequence $(a_{\tau } ^{i},b_{\tau }^{i},a_{\tau +1}^{i},b_{\tau +1}^{i},\ldots ,a_{T}^{i},b_{T}^{i})$ such that

• 1. For period T

  $$\begin{aligned} a_{T}^{i}&=\arg \max _{a_{T}\in {\mathcal {A}}_{T}({\mathbf {H}}_{T})}\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iA}\left( \gamma \right) U_{T} ^{A}\left( {\mathbf {H}}_{T},a_{T},b_{T}^{A};\gamma \right) \\ b_{T}^{i}&=\arg \max _{b_{T}\in {\mathcal {B}}_{T}({\mathbf {H}}_{T})}\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iB}\left( \gamma \right) U_{T} ^{B}\left( {\mathbf {H}}_{T},a_{T}^{A},b_{T};\gamma \right) \end{aligned}$$

• 2. For periods t with $\tau<t<T$

  $$\begin{aligned} a_{t}^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right)&=\arg \max _{a_{t}\in {\mathcal {A}}_{t}\left( {\mathbf {H}}_{t}\right) }\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iA}\left( \gamma \right) U_{t}^{A}\left( {\mathbf {H}}_{t},a_{t},b_{t}^{i},a_{t+1}^{i}\left( {\mathbf {H}}_{t+1};\mu ^{{\mathbf {A}}}\right) ,\right. \\&\left. b_{t+1}^{i}\left( {\mathbf {H}} _{t+1};\mu ^{{\mathbf {A}}}\right) , \ldots ,a_{T}^{i}({\mathbf {H}}_{T};\mu ^{\mathbf { }^{A}}),b_{T}^{i}\left( {\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}\right) ;\gamma \right) \\ b_{t}^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right)&=\arg \max _{b_{t}\in {\mathcal {B}}_{t}\left( {\mathbf {H}}_{t}\right) }\sum _{\gamma \in \left\{ \beta ,1\right\} }\mu ^{iB}\left( \gamma \right) U_{t}^{B}\left( {\mathbf {H}}_{t}, a_{t}^{i},b_{t},a_{t+1}^{i}\left( {\mathbf {H}}_{t+1};\mu ^{{\mathbf {A}}}\right) , \right. \\&\left. b_{t+1}^{i}\left( {\mathbf {H}} _{t+1};\mu ^{{\mathbf {A}}}\right) , \ldots ,a_{T}^{i}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}),b_{T}^{i}\left( {\mathbf {H}}_{T}; \mu ^{{\mathbf {A}}}\right) ;\gamma \right) \end{aligned}$$

• 3. For $t=\tau$

  $$\begin{aligned} a_{\tau }^{i}&=\arg \max _{a_{\tau }\in {\mathcal {A}}_{\tau }\left( {\mathbf {H}}_{\tau }\right) } U_{\tau }^{A}\left( {\mathbf {H}}_{\tau }, a_{\tau },b_{\tau }^{i},a_{\tau +1} ^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right) ,b_{\tau +1} ^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right) , \right. \\&\left. \ldots ,a_{T} ^{i}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}),b_{T}^{i}\left( {\mathbf {H}} _{T};\mu ^{{\mathbf {A}}}\right) ;\beta \right) \\ b_{\tau }^{i}&=\arg \max _{b_{\tau }\in {\mathcal {B}}_{\tau }\left( {\mathbf {H}}_{\tau }\right) } U_{\tau }^{B}\left( {\mathbf {H}}_{\tau }, a_{\tau }^{i},b_{\tau },a_{\tau +1} ^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right) ,b_{\tau +1} ^{i}\left( {\mathbf {H}}_{\tau +1};\mu ^{{\mathbf {A}}}\right) , \right. \\&\left. \ldots ,a_{T} ^{i}({\mathbf {H}}_{T};\mu ^{{\mathbf {A}}}),b_{T}^{i}\left( {\mathbf {H}} _{T};\mu ^{{\mathbf {A}}}\right) ;\beta \right) \end{aligned}$$

Using these definitions, and considering play in period 1, we thus expect A to take an action that she perceives to be part of a subgame perfect equilibrium for the entire game, while we expect B to take an action that he perceives to be part of a subgame perfect equilibrium for the entire game.

Definition 9

A perception-perfect outcome is an outcome $\left( a_{1}^{*},b_{1}^{*},a_{2}^{*},b_{2}^{*},\ldots ,a_{T}^{*},b_{T}^{*}\right)$ such that $\forall \tau \in \{1,\ldots ,T\}$ $a_{\tau }^{*}$ is part of an equilibrium at time $\tau$ as perceived by A;  $b_{\tau }^{*}$ is part of an equilibrium at time $\tau$ as perceived by B.

Again players do not learn about the perceptions or type of the other player. But we do allow them to base second-period play on actual play in earlier periods, rather than on what they expected play to be.

6.2 Application: sequential bargaining

We apply our framework to a dynamic bargaining game as proposed by Stahl (1972) and Rubinstein (1982). Two players bargain over the division of a pie of size 1. There are T periods.¹⁴ In odd-numbered periods $(t=1,3,5,\ldots )$ A proposes a sharing rule $(x_{t},1-x_{t})$ that B can accept or reject. The first argument of the sharing rule always represents the share obtained by A, the second the share obtained by B. If B accepts, the game ends and the sharing rule is implemented. If B rejects, he makes a counteroffer in the next period that A can accept or reject. In the standard specification, both players have time-consistent preferences. If $(x,1-x)$ is accepted at time t,  payoffs are $(\delta _{A} ^{t}x,\delta _{B}^{t}\left( 1-x\right) ),$ with $\delta _{A}$ the discount factor of A and $\delta _{B}$ that of B.

6.2.1 Time-consistent players

To fix ideas, we first consider the solution to the standard model. Suppose T is even. We look for a subgame perfect equilibrium. In period T, A will accept any proposal. Player B will thus offer $\left( x_{T},1-x_{T}\right) =(0,1).$ Knowing this, in period $T-1$, player A claims the highest share that B would be willing to accept, and hence offers $(1-\delta _{B},\delta _{B}).$ With the same logic, in period $T-2,$ B makes sure A would be just willing to accept, offering $\left( \delta _{A}\left( 1-\delta _{B}\right) ,1-\delta _{A}\left( 1-\delta _{B}\right) \right) ,$ etc. The equilibrium has A making an offer in period 1 that is immediately accepted.

6.2.2 Present-biased players

Now consider present-biased players. Our solution concept requires that in each period each player chooses the action that is part of a subgame-perfect equilibrium, given her perceptions.

Suppose that both players use discount factor $\delta .$ Player A perceives her future self to have type $\gamma ^{AA}\in \left\{ \beta ,1\right\}$ and the future B to have type $\gamma ^{AB}\in \left\{ \beta ,1\right\} .$ She also perceives all present and future players to have the same perceptions. Hence, A perceives future selves to act as if A’s true discount factor is $\gamma ^{AA}\delta ,$ while B’s true discount factor is $\gamma ^{AB}\delta .$ In her perception, the game will thus unfold as follows. In period T,  player B will again offer (0, 1). Knowing this, in $T-1$, player A makes sure B is just willing to accept, offering $(1-\gamma ^{AB}\delta ,\gamma ^{AB}\delta ).$ In period $T-2$ the current A perceives B to offer her the lowest share she is willing to accept, which is $\left( \gamma ^{AA}\delta \left( 1-\gamma ^{AB}\delta _{B}\right) ,1-\gamma ^{AA} \delta \left( 1-\gamma ^{AB}\delta \right) \right) ,$ etcetera. The equilibrium as perceived by B can be derived in a similar manner.¹⁵

6.2.3 Infinite horizon

To derive qualitative predictions, we consider an infinite horizon. Suppose players are time-consistent and have discount factors $\delta _{A}$ and $\delta _{B}.$ In a period where it is player A’s turn to make an offer, we know that the unique equilibrium has a payoff to A that equals

$$\begin{aligned} \pi _{A}(\text {A moves first})=\frac{1-\delta _{B}}{1-\delta _{A}\delta _{B}}. \end{aligned}$$

If it is B’s turn to make an offer, we have

$$\begin{aligned} \pi _{A}(\text {B moves first)}=\frac{\delta _{A}\left( 1-\delta _{B}\right) }{1-\delta _{A}\delta _{B}}. \end{aligned}$$

Expressions for $\pi _{B}$ are similar. A straightforward proof can be found in Shaked and Sutton (1984) or Fudenberg and Tirole (1991) chapter 4.

Now consider the equilibrium as perceived by A in our model. With a finite horizon, that equilibrium is equivalent to one with time-consistent players where $\delta _{A}=\gamma ^{AA}\delta$ and $\delta _{B}=\gamma ^{AB}\delta .$ It is straightforward to see that that also applies to the infinite horizon case.¹⁶ Thus, for any future period where A moves first, $i\in \left\{ A,B\right\}$ perceives A’s continuation payoffs to be

$$\begin{aligned} \pi ^{i}_A(\text {A moves first})=\frac{1-\gamma ^{iA}\delta }{1-\gamma ^{iA}\gamma ^{iB}\delta ^2 }. \end{aligned}$$

and those of B:

$$\begin{aligned} \pi ^{i}_B(\text {A moves first})=\frac{\gamma ^{iA}\left( 1-\gamma ^{iB}\right) }{1-\gamma ^{iA}\gamma ^{iB}} \end{aligned}$$

More generally, for any future period where j moves first, i perceives the continuation payoffs of player k to be

$$\begin{aligned} \pi _{k}^{i}(j\text { moves first})=\left\{ \begin{array}{cc} \frac{1-\gamma ^{im}\delta }{1-\gamma ^{iA}\gamma ^{iB}\delta ^{2}} &{} j=k,m\not =j\\ \frac{\gamma ^{ik}\delta \left( 1-\gamma ^{ij}\delta \right) }{1-\gamma ^{iA}\gamma ^{iB}\delta ^{2}} &{} j\not =k \end{array} \right. \end{aligned}$$

for $i,j,k,m\in \left\{ A,B\right\} .$

Note that these expressions apply to any future period. By assumption, A can observe B’s current type $\beta ^B$. When making an offer in period 1, A will thus offer the lowest amount B is willing to accept, given that if he makes a counteroffer, his continuation payoff will be $\left( 1-\gamma ^{AA}\delta \right) /\left( 1-\gamma ^{AA}\gamma ^{AB} \delta ^{2}\right) .$ Thus, A offers

$$\begin{aligned} 1-x_{t}\left( \gamma ^{AA},\gamma ^{AB}\right) =\frac{\beta ^{B}\delta \left( 1-\gamma ^{AA}\delta \right) }{1-\gamma ^{AA}\gamma ^{AB}\delta ^{2}}. \end{aligned}$$

(19)

A similar analysis holds if it is player B’s turn to move.

In period 1, B perceives his continuation payoff to be

$$\begin{aligned} \pi _{B}^{B}(B\text { moves first})=\frac{1-\gamma ^{BA}\delta }{1-\gamma ^{BA}\gamma ^{BB}\delta ^{2}}. \end{aligned}$$

He will reject A’s offer (19) if he perceives it to give him a lower net present value than holding out and making a counteroffer in the next period, thus if

$$\begin{aligned} \frac{\beta ^{B}\delta \left( 1-\gamma ^{AA}\delta \right) }{1-\gamma ^{AA} \gamma ^{AB}\delta ^{2}}<\frac{\beta ^{B}\delta \left( 1-\gamma ^{BA} \delta \right) }{1-\gamma ^{BA}\gamma ^{BB}\delta ^{2}}. \end{aligned}$$

Hence

Theorem 2

In the perception-perfect outcome of the Rubinstein bargaining game, in period t,  player i will offer

$$\begin{aligned} \frac{\beta ^{j}\delta \left( 1-\gamma ^{ii}\delta \right) }{1-\gamma ^{iA} \gamma ^{iB}\delta ^{2}} \end{aligned}$$

to player j,  $i\in \left\{ A,B\right\} ,$ $j\not =i$ . Player j will accept if and only if

$$\begin{aligned} \frac{1-\gamma ^{ii}\delta }{1-\gamma ^{iA}\gamma ^{iB}\delta ^{2}}\ge \frac{1-\gamma ^{ji}\delta }{1-\gamma ^{jA}\gamma ^{jB}\delta ^{2}}. \end{aligned}$$

(20)

Note that this expression does not depend on $\beta .$ Thus, if we have present-biased preferences but no naivety, there is no delay in reaching an agreement. More generally, if A and B share the same perceptions (thus $\gamma ^{AA}=\gamma ^{BA}$ and $\gamma ^{BA}=\gamma ^{BB}$) both sides of (20) are equal and there is no delay. Any player offers what she perceives the other is willing to accept. If these perceptions are common, we get the same qualitative outcome as in the standard Rubinstein model, and the first offer is immediately accepted.

6.2.4 Bargaining breakdown

From (20), we immediately have

Corollary 3

In the Rubinstein bargaining model with present-biased players, an agreement is never reached when the following conditions hold:

$$\begin{aligned} \frac{1-\gamma ^{AA}\delta }{1-\gamma ^{AA}\gamma ^{AB}\delta ^{2}}&<\frac{1-\gamma ^{BA}\delta }{1-\gamma ^{BA}\gamma ^{BB}\delta ^{2}} \end{aligned}$$

(21)

$$\begin{aligned} \frac{1-\gamma ^{BB}\delta }{1-\gamma ^{BA}\gamma ^{BB}\delta ^{2}}&<\frac{1-\gamma ^{AB}\delta }{1-\gamma ^{AA}\gamma ^{AB}\delta ^{2}}. \end{aligned}$$

(22)

Suppose that both players are sophisticated about the other, but naive about themselves, so $\gamma ^{AB}=\gamma ^{BA}=\beta$ and $\gamma ^{AA}=\gamma ^{BB}=1.$ In that case, the denominators of both (21) and (22) are equal, and both conditions simplify to $1-\delta <1-\beta \delta$, which is always satisfied. Hence, bargaining breaks down and the two parties never reach an agreement.¹⁷

The intuition is as follows. If A makes an offer, she perceives the future B to be present-biased. Hence, her offer will be relatively low, as she perceives B to be impatient. However, B perceives his future self to be patient. Therefore, he will not accept A’s offer, as he perceives to be able to do better. The opposite is true when B makes an offer. Hence, players keep rejecting each others’ offers and an agreement is never reached.

For the sake of argument, now suppose that each player is sophisticated about herself, but naive about the other so $\gamma ^{AB}=\gamma ^{BA}=1$ and $\gamma ^{AA}=\gamma ^{BB}=\beta .$ Then, (21) and (22) simplify to $1-\beta \delta <1-\delta$, which is never satisfied. Players immediately reach an agreement. Player A now perceives a future B to be more patient that B himself perceives his future self to be. Hence, the offer of A is better than B was expecting, and he will gladly accept.

When players differ in their naivety, the outcome depends on who moves first. Suppose A is naive about both players, while B is sophisticated about both. Hence, $\gamma ^{AA}=\gamma ^{AB}=1$ and $\gamma ^{BA}=\gamma ^{BB}=\beta .$ Conditions (21) and (22) then simplify to

$$\begin{aligned} \frac{1-\delta }{1-\delta ^{2}}&<\frac{1-\beta \delta }{1-\beta \delta ^{2}}\\ \frac{1-\beta \delta }{1-\beta ^{2}\delta ^{2}}&<\frac{1-\delta }{1-\delta ^{2}} \end{aligned}$$

The first condition is always satisfied; the second never is. We thus have delay in bargaining: B rejects A’s offer, but A accepts the counteroffer. When B moves first, A accepts immediately, perceiving B’s offer as very generous.

6.2.5 Partial naivety

It is easy to apply the analysis above to the case of partial naivety, where players perceive their future self to have some present-bias ${\hat{\beta }} \in (\beta ,1)$. All the analyses above then simply go through with ${\hat{\beta }}$ rather than $\beta$. Hence, when players are sophisticated about others, then even the slightest naivety already leads to a complete bargaining breakdown.

7 Conclusion

In this paper, we proposed a solution concept, perception-perfect outcome, for games played between players with present-biased preferences that are possibly naive about their own future time inconsistency, and/or the time inconsistency of their competitor. A perception-perfect outcome essentially requires each player in each period to play an action that is consistent with subgame perfection, given the perception of that player concerning the time consistency of each player, and under the assumption that all other present and future players have the same perceptions.

We applied our solution concept to the common pool problem and to Rubinstein bargaining. In both cases, we showed that if we assume that players are sophisticated about their competitor’s future present-biasedness but naive about their own, the perfection-perfect equilibria of those games are disastrous. The common pool is exhausted much more quickly than with standard rational players, and even more quickly than present-biased players that are sophisticated, or naive about everyone. Bargaining in the Rubinstein model breaks down completely (as in Akin (2007)), as each offer is rejected.

Of course, our approach is just a first step in the analysis of such games. There is much room for further analysis. For example, our perception-perfect outcome requires that players are strategically naive, in the sense that they do not take into account the possibility that other players may have different perceptions. Second, naive players never learn about their own present-biasedness, and stubbornly persist in believing that in the future, they will be different. If players do learn in this respect, then our most extreme predictions may be softened. For example, bargaining may not break down completely, but only finish after many periods. Third, players do not learn from past behavior of other players. If offers in a bargaining game are rejected repeatedly, for example, one may expect players to take that into account and choose a somewhat different strategy when making further offers. Fourth, a highly sophisticated player may take advantage of her knowledge concerning the naivety of the other player to gain a strategic advantage.

Still, our framework is highly flexible and easily allows for extensions and modifications. For example, as we showed in the examples, it is easy to allow for cases in which players are partially naive and realize their future present-biased to some limited extent. Also, it is straightforward to extend our perception-perfect outcome to a case with more than two types, or with more than two players. Our framework may even be applied to other (mis)perceptions and behavioral biases to which players are possibly unaware.

Appendices

Appendix A: nbi and ppo

In this Appendix, we give a simple example where Naive Backward Induction, as introduced by Sarafidis (2006) and applied by Akin (2007), yields a different prediction than our perception perfect outcome.

Fig. 1

Illustrating the difference between nbi and ppo

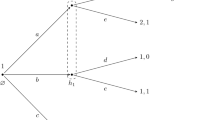
Consider the simple game in Fig. 1. At $t=1$, A decides whether to end the game by choosing R, or to delegate to B by choosing L. In the latter case, B can at $t=2$ secure some payoff at $t=3$ by choosing R, or delegate to his future self by choosing L. In the latter case, B can decide at $t=3$ to get 8 immediately (by choosing L) or to get 11 one period later (by choosing R). Assume that both players have present-biased preferences, with $\delta =1$ and $\beta =1/2.$

If we end up at the decision node at $t=3$, then B will choose L: as $\beta =1/2$ he prefers the lower payoff today. Now move back one period. If B is naive, he will perceive his future self to choose R at $t=3$. Choosing L at $t=2$ then gives a higher perceived payoff than choosing R. But if B is sophisticated, he knows he will choose L at $t=3$ and hence prefers R at $t=2$.

Suppose that player A is sophisticated about herself and sophisticated about B. Moreover, player B is naive about himself and sophisticated about A. With Naive Backward Induction (NBI), this implies that A knows B to be naive. Hence, she knows that if she delegates the decision to B, she will end up with a payoff of 2 in future. It is then clearly preferable for her to choose R, leaving her with a payoff of 10 now.

In our perception perfect outcome, a player A that is sophisticated about B also perceives B to be sophisticated about himself – as we impose interplayer perception naivety. Hence, if she delegates to B, she perceives to end up with a payoff of 24 which, although in future, is still preferable over the 10 she gets from playing R.

Hence, in this simple game, NBI would predict A to play R, while the perception perfect outcome would be for A to play L, and for B to respond by playing L and L.

Appendix B: Proofs of Sect. 5.2

Throughout, we make extensive use of the following straightforward result:

Lemma 1

The function $f(x)\equiv \frac{x}{a+bx}$ is strictly increasing in x for $a,b>0.$

As $\beta ,\rho \in \left( 0,1\right) ,$ we have that $\left( \frac{1}{2} \beta \right) ^{\frac{1}{\rho -1}}$ is decreasing in $\beta ,$ hence (from Lemma 1) $\Gamma _{s}$ is decreasing in $\beta .$ With $\Gamma _{s}\rightarrow \Gamma _{tc}$ as $\beta \rightarrow 1,$ this implies from Lemma 1 that $\Gamma _{s}>\Gamma _{tc},$ which in turn implies from Lemma 1 that $\theta _{s}>\theta _{tc}.$ Also note that, with $\rho \in \left( 0,1\right) ,$ we have $\left( \frac{1}{2} \right) ^{\frac{1}{\rho -1}}$ $>2,$ which implies $\Gamma _{tc}>1/2,$ hence $\theta _{tc}>1/3$. Hence, we have $\theta _s>\theta _{tc}>1/3$, a preliminary result we use below.

Define the function

$$\begin{aligned} \omega \left( \theta \right) \equiv \theta ^{\rho }+\left( \frac{1}{2}\left( 1-2\theta \right) \right) ^{\rho } \end{aligned}$$

As $\rho <1,$ we have

$$\begin{aligned} \frac{\partial \omega ( \theta ) }{\partial \theta }=\rho \left[ \theta ^{\rho -1}-\left( \frac{1}{2}-\theta \right) ^{\rho -1} \right] <0 \end{aligned}$$

(23)

for $\theta >1/4$.

We can write

$$\begin{aligned} \Omega _{n}= & {} \beta ^{\frac{1}{\rho -1}}\omega \left( \theta _{tc}\right) ^{ \frac{1}{\rho -1}}; \\ \Omega _{s}= & {} \beta ^{\frac{1}{\rho -1}}\omega \left( \theta _{s}\right) ^{ \frac{1}{\rho -1}}. \end{aligned}$$

From (23), $\omega$ is decreasing in $\theta$ for $\theta >1/4.$ With $1/4<\theta _{tc}<\theta _{s}$ and $\rho <1,$ this implies $\Omega _{n}<\Omega _{s},$ hence from Lemma 1, $a_{1}^{n}<a_{1}^{s}.$ Also note that $\Omega _{n}=\beta ^{\frac{1}{\rho -1} }\Omega _{tc},$ so $\Omega _{n}>\Omega _{tc},$ which implies $a_{1}^{n}>a_{1}^{tc}$. We have thus established $a_1^s> a_{1}^{n}>a_{1}^{tc}$.

It is more involved to show that also $a_1^{ns} > a_1^{s}$. To do so, we first establish a number of lemmas.

Lemma 2

We have the following:

• 1. $\theta _{ns}<\theta _{s}<\theta _{sn}.$

• 2. $\theta _{ns}+\theta _{sn}<2\theta _{s}.$

Proof

First note that $\Gamma _{tc}<\Gamma _{s}$ as $\Gamma _{s}$ is decreasing in $\beta$ and $\Gamma _{s}\rightarrow \Gamma _{tc}$ as $\beta \rightarrow 1.$ Consider

$$\begin{aligned} \frac{\theta _{ns}}{\theta _{s}}=\frac{\frac{\Gamma _{tc}\left( 1-\Gamma _{s}\right) }{1-\Gamma _{tc}\Gamma _{s}}}{\frac{\Gamma _{s}}{1+\Gamma _{s}}} = \frac{\Gamma _{tc}-\Gamma _{tc}\Gamma _{s}^{2}}{\Gamma _{s}-\Gamma _{tc}\Gamma _{s}^{2}} \end{aligned}$$

This is smaller than 1 as $\Gamma _{s}>\Gamma _{tc}.$ Next consider

$$\begin{aligned} \frac{\theta _{sn}}{\theta _{s}}=\frac{\frac{\Gamma _{s}\left( 1-\Gamma _{tc}\right) }{1-\Gamma _{tc}\Gamma _{s}}}{\frac{\Gamma _{s}}{1+\Gamma _{s}}} =\frac{\Gamma _{s}\left( 1-\Gamma _{tc}\right) \left( 1+\Gamma _{s}\right) }{ \Gamma _{s}-\Gamma _{tc}\Gamma _{s}^{2}} \end{aligned}$$

This is larger than 1 if the numerator is larger than the denominator, hence if $\Gamma _{s}\left( \Gamma _{s}-\Gamma _{tc}\right) >0,$ which is true as $\Gamma _{s}>\Gamma _{tc}.$ This establishes 1. Next consider

$$\begin{aligned} \frac{\theta _{ns}+\theta _{sn}}{2\theta _{s}}=\frac{\frac{\Gamma _{tc}\left( 1-\Gamma _{s}\right) +\Gamma _{s}\left( 1-\Gamma _{tc}\right) }{ 1-\Gamma _{tc}\Gamma _{s}}}{2\frac{\Gamma _{s}}{1+\Gamma _{s}}}=\frac{\Gamma _{tc}+\Gamma _{s}-2\Gamma _{s}\Gamma _{tc}}{1-\Gamma _{tc}\Gamma _{s}}\frac{ 1+\Gamma _{s}}{2\Gamma _{s}} \end{aligned}$$

This is smaller than 1 if $\left( \Gamma _{s}-\Gamma _{tc}\right) \left( 1-\Gamma _{s}\right) >0$ which is true, establishing 2. $\square$

Lemma 3

$\Omega _{ns} > \Omega _{sn}$ and $\Omega _{ns}>\Omega _{s}.$

Proof

For the first part, the fact that $\theta _{ns}<\theta _{sn}$ and $\rho >0$ imply that $\theta _{ns}^{\rho }+\left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }<\theta _{sn}^{\rho }+\left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }.$ With $\rho <1$, this immediately implies the result. For the second part, from their definitions, to have $\Omega _{ns}>\Omega _{s},$ we need

$$\begin{aligned} \theta _{ns}^{\rho }+\left( \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) \right) ^{\rho }<\theta _{s}^{\rho }+\left( \frac{1}{2}\left( 1-2\theta _{s}\right) \right) ^{\rho }. \end{aligned}$$

To prove that this is indeed the case, we proceed as follows. First, define $a\equiv \theta _{ns};$ $b\equiv \frac{1}{2}\left( 1-\theta _{ns}-\theta _{sn}\right) ;$ $c\equiv \theta _{s};$ $d\equiv \frac{1}{2}\left( 1-2\theta _{s}\right) .$ Consider the function $f(x)=x^{\rho }.$ Note that f is increasing and concave. We want to show

$$\begin{aligned} f(a)+f(b)<f(c)+f(d). \end{aligned}$$

From Lemma 2.1, $a<c.$ Also $b-d=\theta _{s}-\theta _{ns}>0$ so $b>d.$ Moreover $c+d=\frac{1}{2},$ while $a+b=\frac{1}{2}\left( 1+\theta _{ns}-\theta _{sn}\right) <\frac{1}{2}$ so $c+d>a+b.$ Define $\Delta \equiv \left( c+d\right) -\left( a+b\right) >0$ and consider $B\equiv b+\Delta .$ By construction, $a+B=c+d.$ However, with $a<c$ and $B>d,$ the fact that f(x) is increasing and concave then implies $f(a)+f(B)<f(c)+f(d).$ With $b<B,$ this immediately implies that indeed $f(a)+f(b)<f(c)+f(d),$ which establishes the result. $\square$

Using these lemmas, we now have

$$\begin{aligned} a_{1}^{ns}=\frac{\Omega _{ns}}{1+\Omega _{ns}+\Omega _{sn}}>\frac{\Omega _{ns} }{1+2\Omega _{ns}}>\frac{\Omega _{s}}{1+2\Omega _{s}}=a_{1}^{s}, \end{aligned}$$

where the first inequality follows from $\Omega _{sn}<\Omega _{ns}$ and Lemma 1, while the second follows from $\Omega _{ns}>\Omega _{s}$ and Lemma 1. We thus have $a_{1}^{ns}> a_{1}^{s}$ which, together with $a_1^s> a_{1}^{n}>a_{1}^{tc}$, establishes the theorem. $\square$