Relatively robust decisions

Abstract

It is natural for humans to judge the outcome of a decision under uncertainty as a percentage of an ex-post optimal performance. We propose a robust decision-making framework based on a relative performance index. It is shown that if the decision maker’s preferences satisfy quasisupermodularity, single-crossing, and a nondecreasing log-differences property, the worst-case relative performance index can be represented as the lower envelope of two extremal performance ratios. The latter is used to characterize the agent’s optimal robust decision, which has implications both computationally and for obtaining closed-form solutions. We illustrate our results in an application which compares the performance of relative robustness to solutions that optimize worst-case payoffs, maximum absolute regret, and expected payoffs under a Laplacian prior.

1 Introduction

Decisions under uncertainty aimed at providing absolute performance guarantees, so the standard logic goes, must be preoccupied with the most unfavorable states, however unlikely they might be. This focus on worst-case outcomes implies a “tunnel vision,” which not only leads to conservative strategies to mitigate negative contingencies, but also to a lack of scanning for positive opportunities—as favorable outcomes remain of (almost) no concern. The idea of relative robustness is to evaluate a decision based on how well it would perform as a fraction of the best payoff—viewed over all possible states. Its goal is to reach a relative performance guarantee which places the consequences of the optimal robust decision within the tightest possible percentage range of an ex-post optimal outcome, where the latter would have required perfect foresight and thus a complete absence of uncertainty.

The notion of measuring the success of an outcome against the possible rewards of an ex-post optimal action is what defines “regret,” and our approach is thus equivalent to using “relative regret” as a yardstick to evaluate all available actions. And while this criterion has been used sporadically in the past to determine robust actions by purely computational means, the contribution proposed here is to use simple structural properties, some of which have their roots in the field of lattice programming, to construct a general method for finding and analyzing “relatively robust decisions.” The following simple example illustrates our ideas. Consider an action space ${{\mathcal {X}}} = \{1,2,3\}$ which describes the available strategies and a state space ${{\mathcal {S}}}=\{s_1,{\hat{s}},s_2\}$ that contains all “states of nature.” The decision maker’s payoffs, denoted by u(x, s) for all (x, s) in ${{\mathcal {X}}}\times {{\mathcal {S}}}$, are given in Table 1 below, together with evaluations in terms of the performance ratio $\varphi (x,s) = u(x,s)/u^*(s)$ (where $u^*(s) = \max _{x\in {{\mathcal {X}}}} u(x,s)$), and the performance index $\rho (x)$ which is defined as the minimal performance ratio $\varphi (x,s)$ over all states $s\in {{\mathcal {S}}}$.

Table 1 Decision problem with relative robustness evaluation

We can see that maximizing the performance index $\rho (\cdot )$ leads to $x={\hat{x}}^*=2$ as the (unique) optimal robust action, which is not “ex-post optimal” contingent on any particular state.¹ In addition, we highlight that in this example (which satisfies certain properties) the overall performance index depends only on the performance ratios $\varphi (\cdot ,s_1)$ and $\varphi (\cdot ,s_2)$ in the “extremal states” $s_1$ and $s_2$, which here feature the lowest and the highest possible payoff, respectively. The optimal robust action occurs where—as the action increases (from $x=2$ to $x=3$)—the “boundary spread,” $\Delta (\cdot ) = \varphi (\cdot ,s_2) - \varphi (\cdot ,s_1)$, changes sign (from $\Delta (2)<0$ to $\Delta (3)>0$). Taking the optimal robust action ${\hat{x}}^*=2$, which achieves a performance index of $\rho ^* = 1/3$, guarantees that for any state s in ${\mathcal {S}}$ the payoff is never less than 1/3 of what could have been achieved under perfect foresight. As alluded to in the example, our main purpose here is to firmly establish relative robustness as a useful decision criterion under full ambiguity (i.e., in the absence of any distributional information). We further show that attractive representation results obtain under fairly general and natural assumptions, which are compatible with the theory of monotone comparative statics.

1.1 Literature

In the presence of complete ignorance about which state of nature might realize, based on a “principle of insufficient reason” by Bernoulli (1738), Laplace (1825) suggested to assign equal probabilities to all states. This does account for the various possibilities on average, but not for the potentially large payoff differences between different feasible decisions across contingencies, and it offers no performance guarantee. The suggestion of dealing with uncertain decision problems by assigning weights to decisions that might be suboptimal was introduced by Neyman and Pearson (1933) who also floated the idea of a distribution-free approach by minimizing the maximum loss (viewed as negative payoff). This minimax-loss idea was formalized by Wald (1939, 1945, 1950) who also related it to the theory of zero-sum games against nature (von Neumann and Morgenstern 1944; Milnor 1951). Instead of focusing attention directly on the objective function, Savage (1951, 1954) applied the minimax approach to the difference of the ex-post optimal payoff (under perfect state information) and the payoff achieved by a given decision in a given state, which he referred to as “regret.” Both of these minimax approaches provide absolute performance guarantees, which have been actively employed in applications (see, e.g., Snyder 2006; Lim et al. 2012). Decision making under uncertainty based on minimizing regret was introduced to the managerial sciences by Bell (1982) who at the time may have well been unaware of Savage’s earlier contribution. In economics, Wilson (1987, 1992) criticized the widespread strong assumptions in models of strategic interaction under asymmetric information, including the widespread premise of common knowledge about all agents’ beliefs. Minimax-regret has since been deployed in monopoly pricing (among others) by Bergemann and Schlag (2008, 2011) and Caldentey et al. (2017). Somewhat in contrast to the aforementioned approaches centered on minimizing absolute regret, Kahneman and Tversky (1984) noted that human decision makers tend to better respond to relative gains than absolute gains. The corresponding idea of using relative regret, or equivalently an achievement rate, goes back to the “competitive ratio” to evaluate the relative performance of algorithms (Sleator and Tarjan 1985; Ben-David and Borodin 1994). A relative achievement ratio has also been used in robust linear programming by Inuiguchi and Sakawa (1997), as well as Mausser and Laguna (1999). Kouvelis and Yu (1997) present a scenario-based approach using a relative-regret objective. More recently, relative performance objectives have been useful for fair allocations (Goel et al. 2009), dynamic trading (Park and Van Roy 2015), and inventory management (Levi et al. 2015). In the extant literature, the consideration of relative-regret objectives has been largely scenario-based and viewed almost entirely from a computational and algorithmic perspective.² Here we seek structural insights, based on the theory of monotone comparative statics (see, e.g., Topkis 1998), so as to obtain a parsimonious representation of the fairness objective as a function of a few “extremal” states. This ultimately yields a simple characterization of the set of “optimal robust actions” which maximize a relative performance index.

1.2 Outline

The paper proceeds as follows. Sec. 2 introduces the model primitives and the agent’s robust decision problem. Sec. 3 provides a simple representation of the performance index as lower envelope of extremal performance ratios. It also characterizes the agent’s optimal robust actions as a function of extremal performance ratios at the boundary. Sec. 4 illustrates our findings using a simple example, and Sec. 5 concludes.³

2 Robust decision model

An agent is faced with a decision of selecting a most preferred element (an “action”) from a given choice set. The agent’s preferences over his available actions are contingent on the (ex-ante unknown) realization of a state. We introduce a robust decision model which has three elements: first, a suitable state-dependent utility representation of the agent’s preferences; second, a set of “complete-information decision problems” that can be solved in the presence of complete state information; and finally, a “robust decision problem” that the agent can solve in the absence of any state information.

2.1 State-dependent utility

Let ${{\mathcal {S}}}\subset {{\mathbb {R}}}^m$ be a state space and let ${{\mathcal {X}}}\subset {{\mathbb {R}}}^n$ be a choice set, which are both nonempty and compact, where m, n are positive integers. Each state $s\in {{\mathcal {S}}}$ describes an ex-ante unknown contingency. Any choice $x\in {{\mathcal {X}}}$ specifies a decision option, one of which must be selected before the realization of the contingency s is observed. We assume that the agent’s state-dependent preferences $\preceq _s$ (which define a complete preordering of ${{\mathcal {X}}}$, for any $s\in {{\mathcal {S}}}$) are represented by a continuous state-dependent utility function $u:{{\mathcal {X}}}\times {{\mathcal {S}}}\rightarrow {{\mathbb {R}}}$.⁴ Thus, by the maximum theorem (Berge 1963, p. 116) the agent’s ex-post optimal utility,

$$\begin{aligned} u^*(s) = \max _{x\in {{\mathcal {X}}}} u(x,s), \ \ \ s\in {{\mathcal {S}}}, \end{aligned}$$

is a continuous function with values in the compact set $[{\underline{u}}^{\ast},{\bar{u}}^{\ast}]$, where ${\underline{u}}^{\ast}=\text{min}\,{u}^{\ast}({\mathcal{S}})$ and ${\bar{u}}^{\ast}=\text{max}\,{u}^{\ast}({\mathcal{S}})$ correspond to the agent’s “minimax utility” and “maximax utility,” respectively. To achieve sign-definiteness of the agent’s utility for the relevant decision options, we assume that there exists a “default decision” $x^0$ which produces a nonnegative utility for all possible states. That is,

$$\begin{aligned} \exists \,x^0\in {{\mathcal {X}}}: \ \ \ u(x^0,s) \ge 0, \ \ \ \forall \,s\in {{\mathcal {S}}}. \end{aligned}$$

(P0)

Let ${{\mathcal {X}}}_+$ be the set of decisions satisfying (P0), which we refer to as the set of individually rational choices,

$$\begin{aligned} {{\mathcal {X}}}_+ = \left\{ x\in {{\mathcal {X}}}: \min u(x,{{\mathcal {S}}})\ge 0\right\} . \end{aligned}$$

All elements of ${{\mathcal {X}}}_+$ attain a zero-utility threshold which can be viewed as the (normalized) utility of the agent’s “outside option.” Framed in this manner, property (P0) simply requires that the set ${{\mathcal {X}}}_+$ of individually rational choices is nonempty. It is always possible to make the agent’s utility function nonnegative by replacing u with $\hat{u}=u-{\underline{u}}\ge{0}$, where $\underline{u}=\text{min}\,u(\mathcal{X,S})$, so property (P0) can in fact be satisfied completely, that is, in such a way that ${{\mathcal {X}}}_+={{\mathcal {X}}}$; see also Remark 4 for a discussion of why this may not be always desirable. In addition,⁵ it is possible to normalize the worst-case utility of the default decision (which is achieved for some $s^0\in {{\mathcal {S}}}$) to zero, so

$$\begin{aligned} u(x^0,s^0) = \min _{s\in {{\mathcal {S}}}} u(x^0,s) = 0. \end{aligned}$$

(1)

The agent considers this utility function as his “money metric” which is determined up to a positive linear transformation.⁶

Remark 1

(Continuity) For any given $s\in {{\mathcal {S}}}$, the preference relation $\preceq _s$ is continuous if and only if the upper contour set $\{{\hat{x}}\in {{\mathcal {X}}}:x\preceq _s {\hat{x}}\}$ and the lower contour set $\{{\hat{x}}\in {{\mathcal {X}}}:{\hat{x}}\preceq _s x\}$ are closed, for all $x\in {{\mathcal {X}}}$. In that case, a continuous utility representation $u(\cdot ,s)$ for $\preceq _s$ (cf. footnote 4) exists (Debreu 1959, pp. 56–59). Here we require that u(x, s) be also continuous in s, so that for any sequence $(s_k)_{k=0}^\infty \subset {{\mathcal {S}}}$ with $\lim _{k\rightarrow \infty } s_k = s$ we have that $\exists \,N\ge 0$ such that $\forall \,k\ge N$: $x\prec _s {\hat{x}} \ \Rightarrow \ x\prec _{s_k}{\hat{x}}$, for all $x,{\hat{x}}\in {{\mathcal {X}}}$ and all $s\in {{\mathcal {S}}}$ (see, e.g., Kreps 1988, p. 27). It is important to note that the utility function u(x, s) is automatically continuous in x (resp., in s) if ${\mathcal {X}}$ (resp., ${\mathcal {S}}$) is finite. Thus, in virtually all practical settings (supported by a finite amount of data) the continuity requirement becomes vacuous when considering a finite choice set together with a finite state space.

2.2 Complete-information decision problem

The set of ex-post optimal actions ${\mathscr {X}}(s)$ in state s constitutes the solution to the agent’s complete-information decision problem:⁷

$$\begin{aligned} {\mathscr {X}}(s) = \arg \max _{x\in {{\mathcal {X}}}} u(x,s). \end{aligned}$$

(2)

Since $u(\cdot ,s)$ is by assumption continuous, the compact set $u({{\mathcal {X}}},s)$ takes on its maximum, so that the complete-information solution is nonempty; by the maximum theorem the set-valued solution ${\mathscr {X}}:{{\mathcal {S}}}\rightrightarrows {{\mathcal {X}}}$ is also compact-valued and upper-semicontinuous (Berge 1963, p. 116). Therefore the set of all ex-post optimal actions,

$$\begin{aligned} \hat{{\mathscr {X}}} = {\mathscr {X}}({{\mathcal {S}}}) = \bigcup _{s\in {{\mathcal {S}}}}\,{\mathscr {X}}(s), \end{aligned}$$

(3)

is compact.⁸ Any selector (or policy) $x:{{\mathcal {S}}}\rightarrow {\mathscr {X}}(s)$, describing which ex-post optimal action x(s) is implemented across the states s, is generically discontinuous if the solution set is not always a singleton.⁹ However, as noted before, the ex-post optimal payoff, $u^*(s) = u(x(s),s)$, is continuous for all $s\in {{\mathcal {S}}}$, also as a consequence of the maximum theorem.

2.3 Robust decision problem

By property (P0) there exists a feasible default decision $x^0$ which achieves a nonnegative utility across all possible states. Actions that would never achieve a higher payoff but sometimes a worse payoff are said to be dominated by the default action. Hence, the agent can restrict attention to (individually rational) decision options ${\hat{x}}$ (in ${{\mathcal {X}}}_+$) that are not dominated by the default action, and which must therefore lie in the set of (ex-ante) acceptable actions,

$$\begin{aligned} {{\mathcal {A}}}(x^0) = \hbox {cl}\left( {{\mathcal {X}}}_+\setminus \{x\in {{\mathcal {X}}} : \min _{s\in {{\mathcal {S}}}} \{ u(x,s) - u(x^0,s)\}<0, \ \max _{s\in {{\mathcal {S}}}} \{ u(x,s) - u(x^0,s)\}\le 0\}\right) . \end{aligned}$$

(4)

The (compact) set of acceptable actions (with respect to $x^0$) is obtained by removing from the initial choice set ${\mathcal {X}}$ all actions that are dominated by the default action $x^0$.

Remark 2

(Minimal Set of Acceptable Actions) Naturally, the set of acceptable actions ${{\mathcal {A}}}(x^0)$ depends on the default action $x^0$. By considering $\hat{u}=u-\underline{u}\ge{0}$ instead of the agent’s original utility function u any action in the choice set ${\mathcal {X}}$ could be considered an admissible default action (which satisfies (P0) for ${\hat{u}}$ instead of u). The minimal set of acceptable actions, denoted by $\hat{{\mathcal {A}}}$, can then be obtained as the (nonempty and compact) intersection,¹⁰

$$\begin{aligned} \hat{{\mathcal {A}}} = \bigcap _{x^0\in {{\mathcal {X}}}} {{\mathcal {A}}}(x^0). \end{aligned}$$

It is clear that pruning the choice set by eliminating dominated actions can have no impact on the rational choice of a most preferred decision; this “preprocessing” (once done) merely simplifies the search for such an action, and allows the agent to possibly ignore negative utility values (that are never relevant for acceptable actions). Henceforth, we can therefore restrict attention to the minimal set of acceptable actions $\hat{{\mathcal {A}}}$, which could always be replaced by a larger set of acceptable actions ${{\mathcal {A}}}(x^0)$ with respect to a specific default decision $x^0$. Note that whenever an ex-post optimal action ${\hat{x}}\in \hat{{\mathscr {X}}}$ is not in $\hat{{\mathcal {A}}}$, then that action must be dominated by another action in $\hat{{\mathscr {X}}}$. More precisely, an ex-post optimal action can be found unacceptable only relative to another action in $\hat{{\mathscr {X}}}$ which is ex-post optimal for more states.¹¹

Given any acceptable action ${\hat{x}}\in \hat{{\mathcal {A}}}$, the performance ratio,

$$\begin{aligned} \varphi ({\hat{x}},s) = \left\{ \begin{array}{ll} u({\hat{x}},s)/u^*(s), &{} \hbox {if } u^*(s)>0\\ 1, &{} \hbox {if } u^*(s) = 0 \end{array}\right\} \in [0,1], \ \ \ s\in {{\mathcal {S}}}, \end{aligned}$$

(5)

makes a relative comparison of the payoffs attained by taking the decision ${\hat{x}}$ for the state $s\in {{\mathcal {S}}}$ instead of an ex-post optimal (and therefore perfectly adapted) decision in $\hat{{\mathscr {X}}}(s)$. For example, a performance ratio of 80% means that at the current state s the action ${\hat{x}}$ attains 4/5 of the ex-post optimal payoff $u^*(s)$. As a consequence of the continuity of $\varphi$ in its second argument, the worst-case performance ratio over all states s in the compact state space ${\mathcal {S}}$ exists (by the extreme value theorem; see, e.g., Rudin 1976, Thm. 4.16). It is referred to as the performance index:

$$\begin{aligned} \rho ({\hat{x}}) = \min _{s\in {{\mathcal {S}}}} \varphi ({\hat{x}},s), \ \ \ {\hat{x}}\in \hat{{\mathcal {A}}}. \end{aligned}$$

(6)

A performance index of $\rho ({\hat{x}}) = 80\%$ means that by taking the ex-post optimal action ${\hat{x}}$ the agent never gets less than 4/5 of the ex-post optimal payoff, no matter what state realizes. The agent’s robust decision problem,

$$\begin{aligned} \hat{{\mathscr {X}}}^* = \arg \max _{{\hat{x}}\in \hat{{\mathcal {A}}}} \rho ({\hat{x}}), \end{aligned}$$

(*)

consists in selecting an optimal robust action ${\hat{x}}^*\in \hat{{\mathscr {X}}}^*$ that maximizes the performance index.¹² The robust decision problem (*) is well-defined, as long as the agent’s state-dependent preferences are represented by a continuous utility function (cf. Remark 1), which—in any nontrivial setup—can be chosen so that all acceptable actions produce nonnegative payoffs (meaning that (P0) is satisfied for all of them). We also recall at this point that the agent’s preferences are automatically continuous in situations where the choice set ${\mathcal {X}}$ and the state space ${\mathcal {S}}$ are finite.

Remark 3

(Minimax Relative Regret) Any solution to the robust decision problem (*) also minimizes the agent’s maximum relative regret, $r({\hat{x}}) = \max _{s\in {{\mathcal {S}}}} \left\{ (u^*(s)-u({\hat{x}},s))/u^*(s)\right\}$ over all ${\hat{x}}\in \hat{{\mathcal {A}}}$.

Remark 4

(Individual Rationality and Additional Actions) Why restrict attention to individually rational decisions in ${{\mathcal {X}}}_+\subset {{\mathcal {X}}}$, when—as pointed out in Sec. 2.1—it is possible to achieve ${{\mathcal {X}}}_+={{\mathcal {X}}}$ by considering the nonnegative utility $\hat{u}=u-\underline{u}$ instead of u ? There are two main reasons. First, by normalizing the worst-case utility of the default decision in Eq. (1) to zero (or some other value; cf. footnote 6), the agent sets a reference which is important for his evaluation of relative robustness in Eq. (6). Requiring individual rationality ensures that the performance ratio in Eq. (5) remains nonnegative. The second reason is more subtle and relates to the potential dependence of an optimal robust decision on the introduction of sub-par actions. To see this, assume that initially ${{\mathcal {X}}}_+={{\mathcal {X}}}$, so our agent does not have to worry about individual rationality and selects an optimal robust action by solving (*). Then a friend presents a new action (not yet in ${\mathcal {X}}$) to the agent, which is not dominated by any default decision, but which yields a negative utility in at least one state.¹³ The new action would then trigger a need to re-normalize the agent’s utility function (to retain nonnegativity of the performance ratio) and then re-solve his robust decision problem. However, if all choice-relevant actions must be individually rational, there can never be a need to recalibrate the agent’s utility after a choice-set augmentation, since adding “irrelevant” actions (with some low state-contingent payoffs) can then have no bearing on the agent’s optimal robust decision.

2.4 Example

Fig. 1

Solution of the robust decision problem (*) in Sec. 2.4

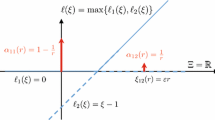
Consider an agent’s state-dependent preferences, represented by the continuous utility function $u(x,s) = 1 - (x-s)^2$, defined for all $(x,s)\in {{\mathcal {X}}}\times {{\mathcal {S}}}$, with ${{\mathcal {X}}} = [0,4]$ and ${{\mathcal {S}}}=[1,2]$. The complete-information decision problem (2) yields ${\mathscr {X}}(s) = \{x(s)\}$ with $x(s)\equiv s$, resulting in the optimal ex-post utility of ${{u}^{\ast}(s)} \equiv 1 \in [{\underline{u}^{\ast}}, {\bar{u}^{\ast}}]$ with ${\underline{u}^{\ast}}={\bar{u}^{\ast}}=1$. Consider now the default decision $x^0=1\in {{\mathcal {X}}}_+ = [1,2]$, which yields the utility

$$\begin{aligned} u(x^0,s) = 1 - (1-s)^2 \ge u(x^0,s^0) = 0, \ \ \ s\in {{\mathcal {S}}}, \end{aligned}$$

where $s^0\in \{2\} = \arg \min _{s\in {{\mathcal {S}}}} u(x^0,s)$, so that property (P0) is satisfied. By Eq. (3) the set of all ex-post optimal actions is $\hat{{\mathscr {X}}} = {{\mathcal {S}}}$, and by Eq. (4) the set of all ex-ante acceptable actions is

$$\begin{aligned} {{\mathcal {A}}}(x^0) = [1,2]\setminus \big \{x\in [0,4]: 1 - (x-s)^2 < 0, \ s\in [1,2]\big \} = [1,2], \end{aligned}$$

with a minimal set of acceptable actions (cf. Remark 2) of $\hat{{\mathcal {A}}} = \hat{{\mathscr {X}}} = [1,2]$. The agent can restrict attention to acceptable actions to evaluate the performance ratio in Eq. (5),

$$\begin{aligned} \varphi ({\hat{x}},s) = \frac{u({\hat{x}},s)}{u^*(s)} = 1 - ({\hat{x}}-s)^2 \in [0,1], \end{aligned}$$

for all $({\hat{x}},s)\in \hat{{\mathcal {A}}}\times {{\mathcal {S}}}$. By Eq. (6) the resulting performance index is

$$\begin{aligned} \rho ({\hat{x}}) = \min _{s\in [1,2]} \varphi ({\hat{x}},s) = \min \left\{ 1 - ({\hat{x}}-1)^2, 1 - ({\hat{x}}-2)^2\right\} , \ \ \ {\hat{x}}\in \hat{{\mathcal {A}}}. \end{aligned}$$

Finally, by solving the robust decision problem (*) the agent obtains a unique optimal robust action,

$$\begin{aligned} {\hat{x}}^*\in \hat{{\mathscr {X}}}^* = \left\{ 3/2\right\} = \arg \max _{{\hat{x}}\in \hat{{\mathcal {A}}}} \rho ({\hat{x}}), \end{aligned}$$

which yields an optimal robust performance index of $\rho ^* = \rho ({\hat{x}}^*) = 3/4$. Hence, when choosing ${\hat{x}}^* = 3/2$ the agent is guaranteed to achieve a utility payoff that is at least within $75\%$ of the ex-post optimal utility payoff (i.e., $u^*(s)\equiv 1$) that could have been achieved with complete information about the state realization. See Fig. 1 for an illustration.

3 Representation of relatively robust decisions

To solve the robust decision problem (*) it is necessary to maximize the performance index $\rho ({\hat{x}})$ over all elements ${\hat{x}}$ in the (minimal) set of acceptable actions $\hat{{\mathcal {A}}}$. For each acceptable action the performance index is obtained as the minimal performance ratio over the entire state space. Using principles from monotone comparative statics, we now show that it may be possible to represent the performance index as the minimum of just two “extremal” performance ratios, $\rho _1$ and $\rho _2$, which in turn may allow for a simple characterization of the agent’s optimal robust actions as those for which $\rho _1=\rho _2$.

3.1 Preliminary definitions

Given a positive integer n, consider a nonempty compact choice set ${{\mathcal {X}}}\subset {{\mathbb {R}}}^n$. For each pair of choices $x,{\hat{x}}\in {{\mathcal {X}}}$, with $x=(x_1,\ldots ,x_n)$ and ${\hat{x}} = ({\hat{x}}_1,\ldots ,{\hat{x}}_n)$, let the componentwise minimum,

$$\begin{aligned} x\wedge {\hat{x}} = (\min \{x_1,{\hat{x}}_1\},\ldots ,\min \{x_n,{\hat{x}}_n\}), \end{aligned}$$

denote the minimal compromise, and let the componentwise maximum,

$$\begin{aligned} x\vee {\hat{x}} = (\max \{x_1,{\hat{x}}_1\},\ldots ,\max \{x_n,{\hat{x}}_n\}), \end{aligned}$$

designate the maximal compromise (between x and ${\hat{x}}$). We assume that ${\mathcal {X}}$ is a lattice, so that (by definition) both compromises are again elements of the choice set, that is, $x\wedge {\hat{x}}\in {{\mathcal {X}}}$ and $x\vee {\hat{x}}\in {{\mathcal {X}}}$. For any two nonempty subsets ${\mathcal {B}}$ and $\hat{{\mathcal {B}}}$ of ${\mathcal {X}}$, we say that “$\hat{{\mathcal {B}}}$ is higher than ${\mathcal {B}}$” (in the strong set order), denoted by ${{\mathcal {B}}}\le \hat{{\mathcal {B}}}$, if and only if ¹⁴

$$\begin{aligned} (\beta ,{{\hat{\beta }}})\in {{\mathcal {B}}}\times \hat{{\mathcal {B}}} \ \ \ \Rightarrow \ \ \ (\beta \wedge {{\hat{\beta }}},\beta \vee {{\hat{\beta }}})\in {{\mathcal {B}}}\times \hat{{\mathcal {B}}}. \end{aligned}$$

Let ${\mathcal {Y}}$ be a nonempty subset of a Euclidean space (e.g., ${{\mathbb {R}}}^n$). A binary relation $\preceq$ is called a (complete) preordering of ${\mathcal {Y}}$ if for any $y,{\hat{y}}\in {{\mathcal {Y}}}$ either $y\preceq {\hat{y}}$ or ${\hat{y}}\preceq y$ (or both),¹⁵ and in addition the following two properties hold (for all $y,{\hat{y}},z\in {{\mathcal {Y}}}$):

$$\begin{aligned} y\preceq y \ \ \ \hbox {and} \ \ \ \big (y\preceq {\hat{y}}, \ {\hat{y}}\preceq z \ \Rightarrow \ y\preceq z\big ), \end{aligned}$$

with the former being referred to as “reflexivity” and the latter as “transitivity.” As in Sec. 2.1, let ${{\mathcal {S}}}\subset {{\mathbb {R}}}^m$ be a nonempty compact state space, for a given positive integer m. We assume that $\preceq$ denotes a preordering of the state space ${\mathcal {S}}$, and that for each $s\in {{\mathcal {S}}}$ the binary relation $\preceq _s$ denotes a preordering of the choice set ${\mathcal {X}}$, with a continuous utility representation $u:{{\mathcal {X}}}\times {{\mathcal {S}}}\rightarrow {{\mathbb {R}}}$. Throughout our developments, we say that the preordering $\preceq$ of the state space is consistent (with the agent’s utility representation u) or simply “u-consistent” if for all $s,{\hat{s}}:{{\mathcal {S}}}$:

$$\begin{aligned} \big ( u(x,s)\le u({x,\hat{s}}) \ \hbox {for all } x\in {{\mathcal {X}}}\big ) \ \ \ \Rightarrow \ \ \ s\preceq {\hat{s}}. \end{aligned}$$

Thus, a u-consistent preorder $\preceq$ of ${\mathcal {S}}$ must be such that a state ${\hat{s}}$ is (weakly) preferred over the state s if for all actions x in ${{\mathcal {X}}}$ the utility $u(x,\cdot )$ does not decrease when going from s to ${\hat{s}}$. The preceding consistency criterion (after switching the roles of $s,{\hat{s}}$) is equivalent to the requirement that for all $s,{\hat{s}}\in {{\mathcal {S}}}$:

$$\begin{aligned} s\prec {\hat{s}} \ \ \ \Rightarrow \ \ \ \big ( u(x,s)< u({x,\hat{s}}) \ \hbox {for some } x\in {{\mathcal {X}}}\big ). \end{aligned}$$

Therefore, if a state ${\hat{s}}$ is to be strictly preferred to the state s, then for at least one action $x\in {{\mathcal {X}}}$ the utility $u(x,\cdot )$ must strictly increase when going from s to ${\hat{s}}$.

3.2 Utility properties

To arrive at parsimonious representations of the performance index and the set of optimal robust actions, we now introduce three properties of the utility function u, under the standing assumption that u has been chosen so as to satisfy (P0) and that the preorder $\preceq$ on ${\mathcal {S}}$ is u-consistent. First, for each state $s\in {{\mathcal {S}}}$, assume that $u(\cdot ,s)$ is supermodular in the sense that

$$\begin{aligned} u(x,s) + u({\hat{x}},s) \le u(x\wedge {\hat{x}},s) + u(x\vee {\hat{x}},s), \ \ \ x,{\hat{x}}\in {{\mathcal {X}}}. \end{aligned}$$

(P1)

This property implies (in any given state s) that for all actions $x,{\hat{x}}$, if x is preferred to the minimal compromise $x\wedge {\hat{x}}$ (i.e., if $u(x\wedge {\hat{x}},s)\le u(x,s)$), then the maximal compromise $x\vee {\hat{x}}$ must be preferred to ${\hat{x}}$ (i.e., $u({\hat{x}},s)\le u(x\vee {\hat{x}},s)$). Second, we suppose that the agent’s utility exhibits (weakly) increasing differences in (x, s), so ¹⁶

$$\begin{aligned} x<{\hat{x}}, \ s\prec {\hat{s}}: \ \ \ u(x,s) - u({\hat{x}},s) \le u(x,{\hat{s}}) - u({\hat{x}},{\hat{s}}), \end{aligned}$$

(P2)

for all $x,{\hat{x}}\in {{\mathcal {X}}}$ and $s,{\hat{s}}\in {{\mathcal {S}}}$. This property implies that the preference between two choices $x,{\hat{x}}$ in state s cannot be (strictly) reversed in any state ${\hat{s}}$ that is preferred to s. Finally, we assume that for acceptable actions the agent’s utility also exhibits (weakly) $\log$-increasing differences:

$$\begin{aligned} x<{\hat{x}}, \ s\prec {\hat{s}}: \ \ \ u({\hat{x}},s)\,u(x,{\hat{s}}) \le u({\hat{x}},{\hat{s}})\,u(x,s), \end{aligned}$$

(P3)

for all $x,{\hat{x}}\in \hat{{\mathcal {A}}}$ and $s,{\hat{s}}\in {{\mathcal {S}}}$. As long as the values u(x, s) and $u(x,{\hat{s}})$ are positive, property (P3) requires that for any two acceptable actions $x,{\hat{x}}$ with $x<{\hat{x}}$ the ratio of the utility payoffs $u({\hat{x}},s)/u(x,s)$ cannot decrease when evaluated at a preferred state ${\hat{s}}$ (instead of at s).

Remark 5

(Behavioral Foundations) The supermodularity property (P1) is a cardinal property of the utility representation which is often associated with complementarity (Pareto 1909; Edgeworth 1897; Samuelson 1976).¹⁷ For example, if $x=(1,0)$ indicates the availability of a left shoe and ${\hat{x}}=(0,1)$ the presence of a right shoe, then the minimal compromise $x\wedge {\hat{x}}=(0,0)$ means that no shoes are available, whereas the maximal compromise $x\vee {\hat{x}}=(1,1)$ corresponds to a situation where a complete pair of shoes allows for a mutually beneficial use of both shoes together. In such a setting, property (P1) is naturally satisfied. While complementarities frequently arise in practice (see, e.g., Milgrom and Roberts 1990), supermodularity as a cardinal property is a rather weak requirement; indeed, Chambers and Echenique (2009) show that if an agent’s preferences are weakly monotonic on a finite lattice, then a supermodular utility representation always exists, which somewhat limits the restrictiveness of (P1). For the purposes of our results instead of (P1) the following ordinal property of quasisupermodularity, introduced by Milgrom and Shannon (1994), is (necessary and) sufficient,

$$\begin{aligned} \left\{ \begin{array}{lcr} x\wedge {\hat{x}} \preceq _s x &{} \Rightarrow &{} {\hat{x}}\preceq _s x\vee {\hat{x}}\\ x\wedge {\hat{x}} \prec _s x &{} \Rightarrow &{} {\hat{x}}\prec _s x\vee {\hat{x}} \end{array}\right\} , \end{aligned}$$

(P1’)

for all $x,{\hat{x}}\in \hat{{\mathcal {A}}}$ and $s,{\hat{s}}\in {{\mathcal {S}}}$. Similarly, instead of the cardinal increasing-differences property (P2) we merely require the ordinal single-crossing property

$$\begin{aligned} x<{\hat{x}}, \ s\prec {\hat{s}}: \ \ \ \left\{ \begin{array}{lcr} x\preceq _s {\hat{x}} &{} \Rightarrow &{} x\preceq _{{\hat{s}}} {\hat{x}}\\ x\prec _s {\hat{x}} &{} \Rightarrow &{} x\prec _{{\hat{s}}} {\hat{x}} \end{array}\right\} , \end{aligned}$$

(P2’)

for all $x,{\hat{x}}\in {{\mathcal {X}}}$ and all $s,{\hat{s}}\in {{\mathcal {S}}}$. Single-crossing requires that elevating a state to a higher state can only amplify an agent’s preferences (at least weakly). Provided positive u-values, the $\log$-increasing-differences property (P3) is in fact the same as (P2) applied to $\log u$ instead of u, which is an equivalent representation of the agent’s state-dependent preferences. Properties (P1’) and (P2’) are “ordinal,” in the sense that they are invariant with respect to which utility representation is used.¹⁸ Yet, in practical applications an absolute valuation (usually in monetary terms) is important, and the agent needs to be able to quantify his “ex-post preferences” (given state realizations) with a utility function u. This utility function u(x, s) is compatible with (P1’) if it is supermodular in x; it is compatible with (P2’) if it has increasing differences in (x, s). Finally, the cardinal property (P3) is equivalent to asking that $\log u(x,s)$ has increasing differences in (x, s). Since ${\hat{u}}(x,s) = \log u(x,s)$ can be thought of as an equivalent utility representation (cf. footnote 19), one finds that (P1’) holds if it is supermodular in x; (P2’) obtains if it has nondecreasing log-differences in (x, s) (analogous to condition (P3), only for ${\hat{u}}$); and finally, (P3) holds if it has increasing differences in (x, s). Thus, the set of practical requirements (in terms of standard verification techniques) remains essentially unaffected by changes in the utility representation.

For the remainder of this section, we assume that the agent’s preferences are represented by a continuous utility function as in Sec. 2 and that properties (P1)–(P3) are satisfied. Any additional assumption is stated explicitly.

3.3 Monotonicity

The cardinal properties (P1) and (P2), or (if $u>0$) alternatively (P1) and (P3), imply the ordinal properties (P1’) and (P2’), respectively.¹⁹ The latter yield that ex-post optimal actions are nondecreasing in the state realizations. The following result was obtained by Milgrom and Shannon (1994).

Lemma 1

By (P1’) and (P2’) the solution of the agent’s complete-information decision problem (2) is nondecreasing, in the sense that

$$\begin{aligned} s\prec {\hat{s}} \ \ \ \Rightarrow \ \ \ {\mathscr {X}}(s)\le {\mathscr {X}}({\hat{s}}), \end{aligned}$$

(7)

for all states $s,{\hat{s}}\in {{\mathcal {S}}}$.

By La. 1 the agent can choose a nondecreasing policy $x:{{\mathcal {S}}}\rightarrow {\mathscr {X}}(s)$ such that ${\hat{s}}\prec s$ implies $x(s)\le x({\hat{s}})$, for all $s,{\hat{s}}\in {{\mathcal {S}}}$. Thus, the agent can obtain ex-post optimal payoffs by implementing actions which are nondecreasing as the states increase.

3.4 Representation of performance index

A nondecreasing policy, together with the cardinal property (P3), guarantees that the performance ratio is single-peaked in the state realization.

Lemma 2

Let $x:{{\mathcal {S}}}\rightarrow \hat{{\mathcal {A}}}$ be a nondecreasing policy. For any given ${\hat{s}}\in {{\mathcal {S}}}$, the function $\varphi (x({\hat{s}}),\cdot ):{{\mathcal {S}}}\rightarrow {{\mathbb {R}}}$ is nondecreasing for $s\prec {\hat{s}}$ and nonincreasing for ${\hat{s}}\prec s$, for all $s\in {{\mathcal {S}}}$.

The quasiconcavity of $\varphi ({\hat{x}},\cdot )$ in La. 2 implies that the worst-case performance ratios must occur either at the lower boundary ${{\mathcal {S}}}_1$ or the upper boundary ${{\mathcal {S}}}_2$ of the state space, where

$$\begin{aligned} {{\mathcal {S}}}_1 = \left\{ s\in {{\mathcal {S}}}: s\preceq {\hat{s}}, \ \hbox {for all }{\hat{s}}\in {{\mathcal {S}}} \right\} \ \ \ \hbox {and} \ \ \ {{\mathcal {S}}}_2 = \left\{ {\hat{s}}\in {{\mathcal {S}}}: s\preceq {\hat{s}}, \ \hbox {for all }s\in {{\mathcal {S}}} \right\} . \end{aligned}$$

(8)

Consequently, the agent can restrict attention to the extremal performance ratios,

$$\begin{aligned} \rho _1({\hat{x}}) = \min _{s\in {{\mathcal {S}}}_1} \varphi ({\hat{x}},s) \ \ \ \hbox {and} \ \ \ \rho _2({\hat{x}}) = \min _{s\in {{\mathcal {S}}}_2} \varphi ({\hat{x}},s). \end{aligned}$$

(9)

This leads to a simple representation of the performance index.

Proposition 1

The agent’s performance index is the lower envelope of the extremal performance ratios, at the lower and upper boundaries of the state space. That is,

$$\begin{aligned} \rho ({\hat{x}}) = \min \{\rho _1({\hat{x}}),\rho _2({\hat{x}})\}, \end{aligned}$$

(10)

for all ${\hat{x}}\in \hat{{\mathcal {A}}}$.

The intuition for the preceding result is that the relative evaluation of two actions decreases towards the boundary of the state space, as a consequence of (P3). This means that $\rho _1$ and $\rho _2$ must produce the smallest performance ratios. No other performance ratio, evaluated for any “interior” state $s\in {{\mathcal {S}}}\setminus ({{\mathcal {S}}}_1\cup {{\mathcal {S}}}_2)$, can be worse than both of these extremal performance ratios.

3.5 Representation of optimal robust decisions

To characterize the agent’s optimal robust decisions, the easiest situation occurs when the agent’s preferences are “monotonic at the boundary,” in the sense that

$$\begin{aligned} (s_1,s_2)\in {{\mathcal {S}}}_1\times {{\mathcal {S}}}_2: \ \ \ x\le {\hat{x}} \ \ \ \Rightarrow \ \ \ {\hat{x}}\preceq _{s_1} x \preceq _{s_2} {\hat{x}}, \end{aligned}$$

(P4)

for all $x,{\hat{x}}\in \hat{{\mathcal {A}}}$. The following result provides a characterization of the set of optimal robust actions, as the roots of the boundary spread $\Delta = \rho _2 - \rho _1$ on a path-connected set of acceptable actions.²⁰

Proposition 2

If (P4) holds and $\hat{{\mathcal {A}}}$ is path-connected, then $\hat{{\mathscr {X}}}^*=\{{\hat{x}}\in \hat{{\mathcal {A}}}:\Delta ({\hat{x}})=0\}$ solves the robust decision problem (*).

In case (P4) is not satisfied, the boundary spread $\Delta$ is still nondecreasing on $\hat{{\mathcal {A}}}$ (as established in the proof of Prop. 2). However, the maximum of $\rho$ in Eq. (10) may be attained outside the contour set ${{\mathcal {D}}} = \{{\hat{x}}\in \hat{{\mathcal {A}}}:\Delta ({\hat{x}})=0\}$, and the agent’s performance index needs to be maximized using global optimization techniques.

Remark 6

(Path-Connectedness) If a randomization over different elements in $\hat{{\mathcal {A}}}$ is always feasible, then path-connectedness holds automatically. However, if the assumption of path-connectedness is not satisfied, as in Table 1, then the set of optimal robust actions is such that $\hat{{\mathscr {X}}}^*\subset {{\mathcal {D}}}_-\cup {{\mathcal {D}}}_+$, where ${{\mathcal {D}}}_- = \{{\hat{x}}\in \hat{{\mathcal {A}}}: \Delta ({\hat{x}})\le 0 \ {and} \ (x\in \hat{{\mathcal {A}}},\,x>{\hat{x}} \ \Rightarrow \ \Delta (x)>0)\}$ and ${{\mathcal {D}}}_+ = \{{\hat{x}}\in \hat{{\mathcal {A}}}: \Delta ({\hat{x}})\ge 0 \ {and} \ (x\in \hat{{\mathcal {A}}},\,x<{\hat{x}} \ \Rightarrow \ \Delta (x)<0)\}$, respectively. That is, for optimal robust actions, the boundary spread $\Delta$ is always about to change sign (from negative to positive in the direction of increasing actions, and from positive to negative in the direction of decreasing actions). Indeed, in Table 1, where $\hat{{\mathcal {A}}} = \{1,2,3\}$ (as pointed out in footnote 11), we have $\Delta (1)=-11/12$, $\Delta (2) = -3/12$, and $\Delta (3) = 11/12$. Thus, $\hat{{\mathscr {X}}}^* = \{{\hat{x}}^*\} = \{2\}\subset {{\mathcal {D}}}_-\cup {{\mathcal {D}}}_+$, where ${{\mathcal {D}}}_- = \{2\}$ and ${{\mathcal {D}}}_+ = \{3\}$. In general, with path-connectedness the boundaries of the upper and lower contour set of $\Delta$ (relative to the contour $\Delta =0$) coincide: ${{\mathcal {D}}}_- = {{\mathcal {D}}}_+ = {{\mathcal {D}}}$.

4 Application

Fig. 2

Complete preordering $\preceq$ on S; comparing ${\hat{s}}=({\hat{c}},{\hat{d}})$ with a given $s=(c,d)$

Consider an agent whose utility u(x, s) depends on the state of the world $s=(c,d)\in {{\mathcal {S}}}$ and the nonnegative amount x of a service consumed, at a fixed unit price $p>0$. The state space is of the form ${{\mathcal {S}}} = [c_0-\varepsilon ,c_0+\varepsilon ]\times [d_0-\delta ,d_0+\delta ] \subset {{\mathbb {R}}}_+^2$, where $s_0 = (c_0,d_0)\gg 0$ is a “nominal” state. The “perturbation” vector $(\varepsilon ,\delta )\in (0,c_0)\times (0,d_0)$ captures the dispersion in the agent’s information about the prevailing state of the world. The agent is unsure about his value for the service. For any x in the compact choice set ${{\mathcal {X}}} = [0,{\bar{x}}]\subset {{\mathbb {R}}}_+$ with ${\bar{x}} = (c_0+\varepsilon )/(d_0-\delta )$, the agent’s willingness-to-pay is $v(x,s) = c x - d x^2/2$, leaving him with a (net) utility objective of

$$\begin{aligned} u(x,s) = v(x,s) - px = (c-p)x - d x^2/2, \end{aligned}$$

for all $(x,s)\in {{\mathcal {X}}}\times {{\mathcal {S}}}$, to represent his state-dependent preferences $\preceq _s$ (as in footnote 4). Such quadratic utility functions have been used in numerous practical applications, including the Capital Asset Pricing Model (Sharpe 1964), the pricing of a service as an information good (Sundararajan 2004), or the use of electric vehicles (Avci et al. 2015). Relative to the default action of not consuming any service (i.e., $x^0=0$), the agent’s utility representation satisfies (P0). Assuming that the service price would never preclude the agent from consuming a positive amount, which means $p\in (0,c_0-\varepsilon )$, the agent’s ex-post optimal decision is the only element in the solution to his utility maximization problem (2),

$$\begin{aligned} {\mathscr {X}}(s) = \left\{ x(s)\right\} = \left\{ \frac{c-p}{d} \right\} , \ \ \ s\in {{\mathcal {S}}}. \end{aligned}$$

This leads to an optimal utility,

$$\begin{aligned} u^*(s) = u(x(s),s) = \frac{d}{2}\left( \frac{c-p}{d}\right) ^2 > 0, \ \ \ s\in {{\mathcal {S}}}. \end{aligned}$$

Given a binary relation $\preceq$, defined for any states $s=(c,d)$ and ${\hat{s}} = ({\hat{c}},{\hat{d}})$ in ${\mathcal {S}}$ by

$$\begin{aligned} s\preceq {\hat{s}} \ \ \ \Leftrightarrow \ \ \ \big ( c\le {\hat{c}} \ \ \ \hbox {or} \ \ \ {\hat{d}}\le d \big ), \end{aligned}$$

we obtain a complete preordering of the state space. The latter is equivalent to

$$\begin{aligned} s\prec {\hat{s}} \ \ \ \Leftrightarrow \ \ \ (c,-d)<({\hat{c}},-{\hat{d}}), \end{aligned}$$

and $s\sim {\hat{s}}$ if and only if the last inequality is not satisfied; see Fig. 2. With this, we are now ready to verify the three choice properties (P1)–(P3) introduced in Sec. 3.2. Note first that for any $x,{\hat{x}}\in {{\mathcal {X}}}$ with $x\le {\hat{x}}$ it is $x\wedge {\hat{x}} = x$ and $x\vee {\hat{x}} = {\hat{x}}$, so that (P1) (resp., (P1’)) is trivially satisfied by the reflexivity of the agent’s state-dependent preference relation $\preceq _s$. Since u(x, s) is twice continuously differentiable,²¹ with $u_{xc}=1>0$ and $u_{xd} = -x\le 0$, the agent’s utility function features increasing differences in $(x,(c,-d))$ (for $x>0$), so that

$$\begin{aligned} x<{\hat{x}}, \ s\prec {\hat{s}} \ \ \ \Rightarrow \ \ \ u({\hat{x}},s) - u(x,s) < u({\hat{x}},{\hat{s}}) - u(x,{\hat{s}}), \end{aligned}$$

for all $x,{\hat{x}}\in {{\mathcal {X}}}\setminus \{0\}$ and all $s,{\hat{s}}\in {{\mathcal {S}}}$, which implies that (P2) (resp., (P2’)) must hold. Finally, we note that

$$\begin{aligned} \partial ^2_{xd}\log u(x,s) = -\frac{c-p}{2}\left( \frac{x}{u(x,s)}\right) ^2< 0 < \frac{d}{2}\left( \frac{x}{u(x,s)}\right) ^2 = \partial ^2_{xc}\log u(x,s), \end{aligned}$$

which yields that $\log u(x,s)$ has increasing differences in $(x,(c,-d))$, so

$$\begin{aligned} x<{\hat{x}}, \ s\prec {\hat{s}} \ \ \ \Rightarrow \ \ \ u({\hat{x}},s)\,u(x,{\hat{s}}) < u({\hat{x}},{\hat{s}})\,u(x,s), \end{aligned}$$

for all $x,{\hat{x}}\in {{\mathcal {X}}}\setminus \{0\}$ and all $s,{\hat{s}}\in {{\mathcal {S}}}$, which in turn yields that (P3) is satisfied.

Fig. 3

State space ${\mathcal {S}}$ with extremal elements $s_1$ and $s_2$

Fig. 4

Performance comparison for solutions optimizing relative robustness (RR), minimax regret (MR), worst case (WC), and certainty equivalence (CE) [Sample Size: $N=4000$]

The lower and upper boundaries of the state space, ${{\mathcal {S}}}_1 = \{s_1\}$ and ${{\mathcal {S}}}_2 = \{s_2\}$, are both singletons with $s_1 = (c_0-\varepsilon ,d_0+\delta )$ and $s_2 = (c_0+\varepsilon ,d_0-\varepsilon )$; see Fig. 3. By La. 1 the set of ex-post optimal actions is an interval: $\hat{{\mathscr {X}}}=[x_1,x_2]$, where $x_1 = x(s_1)$ and $x_2 = x(s_2)$. This set is also equal to the minimal set of acceptable actions: $\hat{{\mathcal {A}}} = \hat{{\mathscr {X}}}$. To evaluate how any action ${\hat{x}}\in \hat{{\mathcal {A}}}$ is doing relative to any potential state realization $s\in {{\mathcal {S}}}$, we now consider the performance ratio in Eq. (5),

$$\begin{aligned} \varphi ({\hat{x}},s) = \left( 2 - \frac{{\hat{x}}}{x(s)} \right) \frac{{\hat{x}}}{x(s)}, \end{aligned}$$

which by La. 2 is quasiconcave in $s\in {{\mathcal {S}}}$, attaining its maximum of 1 at any state s where $x(s)={\hat{x}}$. By Prop. 1 the agent’s performance index can be written in the form

$$\begin{aligned} \rho ({\hat{x}}) = \min \left\{ \rho _1({\hat{x}}),\rho _2({\hat{x}})\right\} = \min \left\{ \left( 2 - \frac{{\hat{x}}}{x_1} \right) \frac{{\hat{x}}}{x_1},\left( 2 - \frac{{\hat{x}}}{x_2} \right) \frac{{\hat{x}}}{x_2} \right\} . \end{aligned}$$

It is straightforward to verify (e.g., by equivalently testing monotonicity of $\rho _1(\cdot )$ and $\rho _2(\cdot )$) that $u(\cdot ,s_1)$ is decreasing and $u(\cdot ,s_2)$ is increasing. This means that the agent’s preferences are monotonic at the boundary, so property (P4) has been established. Thus, by Prop. 2 the solution to the agent’s robust decision problem (*) is characterized by the condition

$$\begin{aligned} \Delta ({\hat{x}}^*) = 0, \end{aligned}$$

which in this context implies a unique optimal robust action:

$$\begin{aligned} {\hat{x}}^* = \frac{x_1 x_2}{(x_1+x_2)/2} = \frac{(c_0-p)^2 - \varepsilon ^2}{(c_0-p) d_0 + \varepsilon \delta }. \end{aligned}$$

The latter determines the optimal performance index,

$$\begin{aligned} \rho ^* = \rho ({\hat{x}}^*) = \left( \frac{\sqrt{x_1 x_2}}{(x_1+x_2)/2} \right) ^2 = \frac{4\,(x_1/x_2)}{(1+(x_1/x_2))^2} = \frac{\left( (c_0-p)^2 - \varepsilon ^2\right) \left( d_0^2 - \delta ^2\right) }{\left( (c_0-p)d_0 + \varepsilon \delta \right) ^2}. \end{aligned}$$

Remark 7

(Comparison with Other Criteria) Fig. 4 compares the optimal robust decision ${\hat{x}}^*$ in its relative performance (of $\rho ^* = 70.73\%$; measured in the sample at 71.43%) to other solutions of the agent’s decision problem under uncertainty, for the nominal state $(c_0,d_0) = (100,2)$, with dispersion vector $(\varepsilon ,\delta )=(20,0.75)$, price $p=4$, and $N=4000$ samples drawn uniformly from the state space ${\mathcal {S}}$.

(i) Worst-case optimization (WC). The minimax payoff approach amounts to solving

$$\begin{aligned} x^*_{\mathrm{WC}} \in \arg \max _{x\in {{\mathcal {X}}}} \min _{s\in {{\mathcal {S}}}} u(x,s), \end{aligned}$$

which leads to fairly low relative performance in optimistic states with $\rho _{\mathrm{WC}} = \rho (x^*_{\mathrm{WC}}) = 51.29\%$.

(ii) Certainty equivalence (CE). In the absence of uncertainty, the agent would take the nominal state $s_0=(c_0,d_0)$ to determine the ex-ante optimal decision, $x_{\mathrm{CE}}^* = (c_0-p)/d_0 \in {\mathscr {X}}(s_0)$, resulting in the performance index $\rho _{\mathrm{CE}} = \rho (x^*_{\mathrm{CE}}) = 48.15\%$. Given a Laplacian (uniform) prior on the state space ${\mathcal {S}}$, this action would maximize the agent’s expected utility. By contrast, the optimal robust decision is smaller:

$$\begin{aligned} {\hat{x}}^* = x_{\mathrm{CE}}^* - \left( \frac{\delta x_{\mathrm{CE}}^* + \varepsilon }{d_0^2 x_{\mathrm{CE}}^* + \varepsilon \delta }\right) \,\varepsilon < x_{\mathrm{CE}}^*. \end{aligned}$$

(iii) Minimax regret (MR). The maximal absolute regret is minimal for

$$\begin{aligned} x^*_{\mathrm{MR}} \in \arg \min _{x\in {{\mathcal {X}}}} {\bar{R}}(x), \end{aligned}$$

where the maximum regret is ${\bar{R}}(x) = \max _{s\in {{\mathcal {S}}}} \left\{ u^*(s) - u(x,s)\right\}$. This minimax-regret decision produces poor relative performance on both sides of the state spectrum, attaining a relative performance index $\rho _{\mathrm{MR}} = \rho (x^*_{\mathrm{MR}}) = 13.39\%$.

Table 2 provides numerical values for the optimal decisions and the attained objective values, for relative robustness and the three alternative robustness criteria. We note that the performance of our optimal robust decision (obtained by maximizing the relative performance index $\rho$) is least second-best across all four robustness criteria, which is an indication for the inherently very balanced nature of relative robustness as a decision criterion.

Table 2 Comparison of relative robustness (RR), worst-case/maximin (WC), certainty-equivalence (CE), and minimax regret (MR) as robustness criteria; cf. Remark 7

5 Conclusion

A “relatively robust” decision, concerned with maximizing the performance index, is taken ex ante—before any information about the prevailing state of nature has transpired. It provides a relative performance guarantee with respect to all possible states before any one of them has realized. The characteristics of a robust decision depend on the properties of the actions that are optimal ex post—under complete state information. Our analysis thus proceeded by first examining the structure of the agent’s complete-information decision problem and the corresponding performance ratio, so as to find a “minimal” representation of the performance index, which can then be used to characterize the agent’s optimal robust decisions.

Relatively robust decisions can be determined based on a utility representation of an agent’s state-dependent preferences over his actions in a compact domain ${{\mathcal {X}}}$ (on a compact state space ${\mathcal {S}}$), by solving the robust decision problem in Eq. (*). Nothing else is needed, except for sign-definiteness of the (individually rational) utility-payoffs relative to some default action, as formulated in property (P0) which comes without any loss of generality. Thus, while the preference properties that carry our results are not really necessary to uncover optimal robust decisions, they do lend a powerful helping hand—by providing substantial structural insight and computational simplification. In this vein, properties (P1)–(P3), which are naturally satisfied in many decision problems, imply a representation of the performance index as lower envelope of the performance ratios in two “extremal states,” at the upper and lower boundary of ${\mathcal {S}}$ (cf. Prop. 1). The additional property (P4) then allows for a simple characterization of optimal robust decisions as a function of the difference of these extremal performance ratios (cf. Prop. 2).

An optimal performance index provides a relative guarantee that solutions will always perform within a given percentage of the level to which perfect information or infinite flexibility would have led.²² The presented framework promises broad applicability to economic and managerial decision problems in situations where no probability distribution is available. It is also useful in settings that do not repeat (e.g., the introduction of an innovative new product), as well as in environments where performance guarantees are desirable or even required (e.g., when decisions are highly irreversible or their effects are delayed significantly as in social policy or climate-related emissions regulation).

Appendices

Appendix A: Proofs

Proof of Lemma 1

Fix $s,{\hat{s}}\in {{\mathcal {S}}}$, with $s\prec {\hat{s}}$. Let $x\in {\mathscr {X}}(s)$ and ${\hat{x}}\in {\mathscr {X}}({\hat{s}})$. Hence, by the optimality of a most preferred action in the agent’s decision problem (2) (cf. also footnote 7) it is

$$\begin{aligned} u(x\wedge {\hat{x}},s)\le u(x,s) \ \ \ \hbox {and} \ \ \ u(x\vee {\hat{x}},{\hat{s}})\le u({\hat{x}},{\hat{s}}). \end{aligned}$$

(11)

Applying the quasisupermodularity property (P1’) to the first inequality in Eq. (11) yields

$$\begin{aligned} u({\hat{x}},s)\le u(x\vee {\hat{x}},s), \end{aligned}$$

so that the single-crossing property (P2’) implies

$$\begin{aligned} u({\hat{x}},{\hat{s}})\le u(x\vee {\hat{x}},{\hat{s}}). \end{aligned}$$

Together with the second inequality in Eq. (11) this implies that $x\vee {\hat{x}}\in {\mathscr {X}}({\hat{s}})$.

Returning to the first inequality in Eq. (11) if $u(x\wedge {\hat{x}},s)<u(x,s)$, then by (P1’) it is $u({\hat{x}},s)<u(x\vee {\hat{x}},s)$. By (P2’) this further implies that $u({\hat{x}},{\hat{s}})<u(x\vee {\hat{x}},{\hat{s}})$, which in turn contradicts the second inequality in Eq. (11). Hence,

$$\begin{aligned} u(x\wedge {\hat{x}},s) = u(x,s), \end{aligned}$$

so $x\wedge {\hat{x}}\in {\mathscr {X}}(s)$. We have therefore shown that

$$\begin{aligned} (x,{\hat{x}})\in {\mathscr {X}}(s)\times {\mathscr {X}}({\hat{s}}) \ \ \ \Rightarrow \ \ \ (x\wedge {\hat{x}},x\vee {\hat{x}})\in {\mathscr {X}}(s)\times {\mathscr {X}}({\hat{s}}), \end{aligned}$$

that is ${\mathscr {X}}(s)\le {\mathscr {X}}({\hat{s}})$ in the strong set order (cf. Sec. 3.1), which concludes the proof. $\square$

Proof of Lemma 2

Let ${\hat{s}}\in {{\mathcal {S}}}$, and consider the behavior of $\varphi ({\hat{x}},\cdot )$ to the left of $s={\hat{s}}$. If ${\hat{s}}$ lies in the lower boundary of ${{\mathcal {S}}}$ (i.e., if ${\hat{s}}\in {{\mathcal {S}}}_1$), then there is nothing to show. Consider therefore the interesting case where ${\hat{s}}\in {{\mathcal {S}}}\setminus {{\mathcal {S}}}_1$. In this situation, select two states $s',s''\in {{\mathcal {S}}}$ with $s'\prec s''\preceq {\hat{s}}$, and accordingly set $x'=x(s')$, $x''=x(s'')$, as well as ${\hat{x}} = x({\hat{s}})$. By La. 1 it is $x'\le x''\le {\hat{x}}$. Thus, property (P3) of the agent’s state-dependent utility function yields:²³

$$\begin{aligned} \varphi ({\hat{x}},s'') = \frac{u({\hat{x}},s'')}{u(x'',s'')} \ge \frac{u({\hat{x}},s')}{u(x'',s')} \frac{u(x',s')}{u(x',s')} = \frac{u({\hat{x}},s')}{u(x',s')} \frac{u(x',s')}{u(x'',s')} \ge \frac{u({\hat{x}},s')}{u(x',s')} = \varphi ({\hat{x}},s'). \end{aligned}$$

Here we have used the fact that by the optimality of $x'$ (i.e., because $x'\in {\mathscr {X}}(s')$),

$$\begin{aligned} \frac{u(x',s')}{u(x'',s')}\ge 1. \end{aligned}$$

Thus, we have shown that

$$\begin{aligned} {\hat{s}}\in {{\mathcal {S}}}\setminus {{\mathcal {S}}}_1: \ \ \ s'\prec s''\preceq {\hat{s}} \ \ \ \Rightarrow \ \ \ \varphi ({\hat{x}},s')\le \varphi ({\hat{x}},s''), \end{aligned}$$

for all $s',s''\in {{\mathcal {S}}}$, which means that $\varphi ({\hat{x}},\cdot )$ is nondecreasing to the left of ${\hat{s}}$.

Consider now the case where ${\hat{s}}\in {{\mathcal {S}}}\setminus {{\mathcal {S}}}_2$, ignoring the trivial situation where ${\hat{s}}$ is in the upper boundary of the state space. For any two states $s',s''\in {{\mathcal {S}}}$ with ${\hat{s}}\preceq s'\prec s''$, property (P3) of the agent’s state-dependent utility implies that

$$\begin{aligned} \varphi ({\hat{x}},s') = \frac{u({\hat{x}},s')}{u(x',s')}\ge \frac{u({\hat{x}},s'')}{u(x',s'')} \frac{u(x'',s'')}{u(x'',s'')} = \frac{u({\hat{x}},s'')}{u(x'',s'')} \frac{u(x'',s'')}{u(x',s'')} \ge \frac{u({\hat{x}},s'')}{u(x'',s'')} = \varphi ({\hat{x}},s''), \end{aligned}$$

where we have used the fact that by the optimality of $x''$ (i.e., because $x''\in {\mathscr {X}}(s'')$):

$$\begin{aligned} \frac{u(x'',s'')}{u(x',s'')} \ge 1. \end{aligned}$$

It follows that

$$\begin{aligned} {\hat{s}}\in {{\mathcal {S}}}\setminus {{\mathcal {S}}}_2: \ \ \ {\hat{s}}\preceq s'\prec s'' \ \ \ \Rightarrow \ \ \ \varphi ({\hat{x}},s')\ge \varphi ({\hat{x}},s''), \end{aligned}$$

for all $s',s''\in {{\mathcal {S}}}$, which means that $\varphi ({\hat{x}},\cdot )$ is nonincreasing to the right of ${\hat{s}}$. $\square$

Proof of Proposition 1

Fix any state ${\hat{s}}\in {{\mathcal {S}}}$, and a monotonic policy $x:{{\mathcal {S}}}\rightarrow \hat{{\mathcal {A}}}$ which exists by La. 1. With this, we denote ${\hat{x}}=x({\hat{s}})$ a candidate decision for the agent’s robust decision problem (*). The corresponding performance index $\varphi ({\hat{x}},s)$ in Eq. (5) attains its maximum of 1 at the state $s={\hat{s}}$. By La. 2 we know that $\varphi ({\hat{x}},\cdot )$ is nondecreasing to the left of ${\hat{s}}$ and nonincreasing to the right of ${\hat{s}}$, so that the minimum of $\varphi ({\hat{x}},\cdot )$ must occur at the boundary of the state space, defined by ${{\mathcal {S}}}_1$ and ${{\mathcal {S}}}_2$ in Eq. (8). By Eq. (9) this implies that

$$\begin{aligned} \rho ({\hat{x}}) = \min _{s\in {{\mathcal {S}}}} \varphi ({\hat{x}},s) = \min _{s\in {{\mathcal {S}}}_1\cup {{\mathcal {S}}}_2} \varphi ({\hat{x}},s) = \min \{\rho _1({\hat{x}}),\rho _2({\hat{x}})\}, \end{aligned}$$

which completes our proof.$\square$

Proof of Proposition 2

The proof of this result has two parts (I and II). Part I establishes the monotonicity of the boundary spread (also referred to in the main text), and part II the representation of the solution to the agent’s robust decision problem (*).

Part I: Monotonicity of $\Delta$. The cardinal property (P3) ensures that the performance spread $\Delta = \rho _2 -\rho _1$ is nondecreasing:

$$\begin{aligned} x <{\hat{x}} \ \ \ \Rightarrow \ \ \ \Delta (x)\le \Delta ({\hat{x}}), \end{aligned}$$

(12)

for all $x,{\hat{x}}\in \hat{{\mathcal {A}}}$. To see this, let $(s_1,s_2)\in {{\mathcal {S}}}_1\times {{\mathcal {S}}}_2$ be a tuple of boundary states in accordance with Eq. (8), and let $(x_1,x_2)\in {\mathscr {X}}(s_1)\times {\mathscr {X}}(s_2)$ be a tuple of corresponding ex-post optimal actions. In addition, let $s,{\hat{s}}\in {{\mathcal {S}}}$ be two ordered states with $s\prec {\hat{s}}$, such that $x\in {\mathscr {X}}(s)$ and ${\hat{x}}\in {\mathscr {X}}({\hat{s}})$, with $x<{\hat{x}}$, are ex-post optimal actions with respect to those states. The difference of the performance ratios for those actions, at the lower boundary (i.e., for the state $s_1$), is

$$\begin{aligned} \rho _1({\hat{x}}) - \rho _1(x) = \frac{u({\hat{x}},s_1)}{u(x,s_1)} \frac{u(x,s_1)}{u(x_1,s_1)} - \frac{u(x,s_1)}{u(x_1,s_1)} \le \left( \frac{u({\hat{x}},s_2)}{u(x,s_2)} - 1\right) \frac{u(x,s_1)}{u(x_1,s_1)}, \end{aligned}$$

where the inequality is implied by property (P3). On the other hand, the difference of the performance ratios (for ${\hat{x}}$ and x) at the upper boundary of the state space is

$$\begin{aligned} \rho _2({\hat{x}}) - \rho _2(x) = \frac{u({\hat{x}},s_2)}{u(x,s_2)}\frac{u(x,s_2)}{u(x_2,s_2)} - \frac{u(x,s_2)}{u(x_2,s_2)} = \left( \frac{u({\hat{x}},s_2)}{u(x,s_2)} - 1\right) \frac{u(x,s_2)}{u(x_2,s_2)}. \end{aligned}$$

Subtracting the first of the two boundary differences from the second yields:

$$\begin{aligned} \Delta ({\hat{x}}) - \Delta (x) \ge \left( \frac{u({\hat{x}},s_2)}{u(x,s_2)} - 1\right) \left( \frac{u(x,s_2)}{u(x_2,s_2)} - \frac{u(x,s_1)}{u(x_1,s_1)}\right) = \left( \frac{u({\hat{x}},s_2)}{u(x,s_2)} - 1\right) \Delta (x). \end{aligned}$$

But this means that $\Delta (x)\ge 0 \ \ \Rightarrow \ \ \Delta ({\hat{x}})\ge \Delta (x)$, since

$$\begin{aligned} \frac{u({\hat{x}},s_2)}{u(x,s_2)} \ge \frac{u({\hat{x}},{\hat{s}})}{u(x,{\hat{s}})} \ge 1, \end{aligned}$$

by virtue of property (P3) and ex-post optimality of ${\hat{x}}$ (so $u({\hat{x}},{\hat{s}})\ge u(x,{\hat{s}})$). To prove the “second” implication (namely, $\Delta (x)\le 0 \ \ \Rightarrow \ \ \Delta ({\hat{x}})\ge \Delta (x)$), note that by property (P3) it is

$$\begin{aligned} \rho _2({\hat{x}})-\rho _2(x) = \left( \frac{u({\hat{x}},s_2)}{u(x,s_2)} - 1\right) \frac{u(x,s_2)}{u(x_2,s_2)} \ge \left( \frac{u({\hat{x}},s_1)}{u(x,s_1)} - 1 \right) \frac{u(x,s_2)}{u(x_2,s_2)}. \end{aligned}$$

From this, one can conclude in a similar manner as before that

$$\begin{aligned} \Delta ({\hat{x}}) - \Delta (x) \ge \left( \frac{u({\hat{x}},s_1)}{u(x,s_1)} - 1 \right) \Delta (x) \ge -\left( 1 - \frac{u({\hat{x}},s)}{u(x,s)}\right) \Delta (x), \end{aligned}$$

where the last inequality follows from (P3). Thus, if $\Delta (x)\le 0$, then by the ex-post optimality of $x\in {\mathscr {X}}(s)$ (so $u(x,s)\ge u({\hat{x}},s)$), we also have that $\Delta ({\hat{x}}) - \Delta (x) \ge 0$. This proves the implication $\Delta (x)\le 0 \ \ \Rightarrow \ \ \Delta ({\hat{x}})\ge \Delta (x)$. By combining both implications, one obtains $\Delta ({\hat{x}})\ge \Delta (x)$ irrespective of the sign of $\Delta (x)$, which establishes the claimed monotonicity of the boundary spread $\Delta$ in Eq. (12).

Part II: Representation of $\hat{{\mathscr {X}}}^*$. By Eq. (6), for any $x\in \hat{{\mathcal {A}}}$ the performance index is of the form

$$\begin{aligned} \rho (x) = \min \left\{ \rho _1(x),\rho _2(x)\right\} = \left\{ \begin{array}{ll} \rho _1(x), &{} \hbox {if } \Delta (x)\ge 0,\\ \rho _2(x), &{} \hbox {if } \Delta (x)\le 0. \end{array}\right. \end{aligned}$$

(13)

On the other hand, by the definition of the boundary performance ratios $\rho _1$ and $\rho _2$, we know that $\rho _1(x_1) = \rho _2(x_2) = 1$, which means that necessarily $\Delta (x_1)\le 0 \le \Delta (x_2)$. As a result,

$$\begin{aligned} \rho (x_1) = \rho _2(x_1)\le 1 \ \ \ \hbox {and} \ \ \ \rho (x_2) = \rho _1(x_2)\le 1. \end{aligned}$$

By the boundary monotonicity in (P4) we have that $u(\cdot ,s_1)$ is nonincreasing while $u(\cdot ,s_2)$ is nondecreasing. Thus, $\rho _2(\cdot ) = u(\cdot ,s_2)/u(x_2,s_2)$ is nondecreasing, while $\rho _1(\cdot )$ is nonincreasing. By the continuity of $\Delta$, the path-connectedness of $\hat{{\mathcal {A}}}$, and the intermediate value theorem (see, e.g., Rudin 1976, Thm. 4.22) the set ${{\mathcal {D}}} = \{{\hat{x}}\in \hat{{\mathcal {A}}} :\Delta ({\hat{x}}) = 0\}$ is nonempty and closed. Consider now any given continuous path $\xi (t)$ for $t\in [0,1]$, with $\xi (0) = x_1$ and $\xi (1)=x_2$, which is nondecreasing (i.e., for any $t',t''\in [0,1]$: $t'<t'' \ \ \Rightarrow \ \ \xi (t')\le \xi (t'')$. Then $\xi (t)$ must pass through ${\mathcal {D}}$, in the sense that there exist $t',t''\in [0,1]$, with $t'\le t''$, such that by virtue of Eq. (13) it is

$$\begin{aligned} \rho (\xi (t)) = {{\mathbf {1}}}_{\{t\in [0,t'']\}}\,\rho _2(\xi (t)) + {{\mathbf {1}}}_{\{t\in (t'',1]\}}\,\rho _1(\xi (t)) = {{\mathbf {1}}}_{\{t\in [0,t')\}}\,\rho _2(\xi (t)) + {{\mathbf {1}}}_{\{t\in [t',1]\}}\,\rho _1(\xi (t)), \end{aligned}$$

for all $t\in [0,1]$. In particular, $\rho (\xi (\cdot ))$ is nondecreasing on $[0,t']$, constant on $[t',t'']$, and nonincreasing on $[t'',1]$. As a result,

$$\begin{aligned} {{\mathcal {D}}} = \arg \max _{x\in \hat{{\mathcal {A}}}} \rho (x); \end{aligned}$$

that is, any maximizer of $\rho$ is characterized by the fact that the boundary spread $\Delta$ vanishes. The latter must occur by the continuity of $\Delta$ on the (by assumption path-connected) set $\hat{{\mathcal {A}}}$, concluding our proof. $\square$

Appendix B: Supplement

Alternative Robustness Criteria for the Example in Sec. 1. Table 3 provides an evaluation of (absolute) regret $R(x,s) = u^*(s) - u(x,s)$, maximum regret ${\bar{R}}(x) = \max R(x,{{\mathcal {S}}})$, and worst-case payoff $u_{\mathrm{WC}}(x) = \min u(x,{{\mathcal {S}}})$, for all $(x,s)\in {{\mathcal {X}}}\times {{\mathcal {S}}}$ with ${{\mathcal {X}}}=\{1,2,3\}$ and ${{\mathcal {S}}}= \{s_1,{\hat{s}},s_2\}$. The minimax regret is achieved for $x=3$, whereas worst-case optimality is obtained at $x=1$.

Table 3 Decision problem with (absolute) regret and worst-case payoff evaluation

Variation of the Application in Sec. 4. Quadratic utility functions are sometimes criticized for their lack of the fundamental “free disposal” property in choice theory, which presumes that an agent’s willingness-to-pay should not decrease when receiving too much of a product or service, as it may be always possible (so the theory goes) to discard or not use any excess. The example in Sec. 4 featured an agent with a willingness-to-pay that was decreasing past an ex-ante unknown consumption maximum, which led to a somewhat conservative choice behavior avoiding dissatisfaction from excess consumption, not only because of the price for these ex-post unwanted services but also because of the agent’s active dislike of excess consumption. To arrive at a more balanced assessment, allowing at least for indifference over quantities past the bliss point, we now consider an agent with an altogether nondecreasing willingness-to-pay, of the form

$$\begin{aligned} {\bar{v}}(x,s) = \left\{ \begin{array}{ll} v(x,s), &{} \hbox {if } x\in [0,c/d],\\ v^*(s), &{} \hbox {if } x\in [c/d,\infty ), \end{array}\right. \end{aligned}$$

where $v(x,s) = cx - dx^2/2$, with x in $[0,{\bar{x}}]\subset {{\mathbb {R}}}_+$ and $s = (c,d)\,\,{\text{in}}\,\, {{\mathcal {S}}} = [c_0-\varepsilon ,c_0+\varepsilon ]\times [d_0-\delta ,d_0+\delta ]\subset {{\mathbb {R}}}_+^2$, is as in Sec. 4, and all parameters are defined in the same manner as before (including the given preordering of ${\mathcal {S}}$). The agent’s maximum willingness-to-pay in any given state $s\in {{\mathcal {S}}}$ is $v^*(s) = v(c/d,s) = c^2/(2d)>0$. When faced with a per-unit service price $p\in (0,c_0-\varepsilon )$, the agent’s (net) utility is

$$\begin{aligned} {\bar{u}}(x,s) = {\bar{v}}(x,s) - px, \ \ \ (x,s)\in {{\mathcal {X}}}\times {{\mathcal {S}}}. \end{aligned}$$

Because a positive price decreases the agent’s marginal utility for extra service (thus precluding consumption up to the saturation point), the solution ${\mathscr {X}}(s) = \{x(s)\}$ to the agent’s complete-information decision problem (2) is the same as before, with

$$\begin{aligned} x(s) = \frac{c-p}{d}, \ \ \ s\in {{\mathcal {S}}}, \end{aligned}$$

leading also to the same ex-post optimal utility:

$$\begin{aligned} u^*(s) = {\bar{u}}(x(s),s) = \frac{d}{2}\left( \frac{c-p}{d} \right) ^2, \ \ \ s\in {{\mathcal {S}}}. \end{aligned}$$

The boundary performance ratios, for any candidate action ${\hat{x}}\in {{\mathcal {X}}}$, are

$$\begin{aligned} {{\bar{\varphi }}}_i({\hat{x}}) = \left\{ \begin{array}{ll} \varphi _i({\hat{x}}), &{} \hbox {if } {\hat{x}} \le c_i/d_i,\\ \varphi _i(c_i/d_i) - \left( {\hat{x}}-(c_i/d_i)\right) p/u^*(s_i), &{} \hbox {if } {\hat{x}} \ge c_i/d_i, \end{array}\right. \end{aligned}$$

for $i\in \{1,2\}$, where $(c_1,c_2) = (c_0-\varepsilon ,c_0+\varepsilon )$ and $(d_1,d_2) = (d_0+\delta ,d_0-\delta )$ (so $c_1<c_2$ and $d_1>d_2$). Clearly, since the agent’s willingness-to-pay weakly increased over the example in the main text (i.e., ${\bar{v}}\ge v$), including his marginal willingness to pay beyond the bliss point, one can conclude that—all else equal—the new optimal robust action ${\bar{x}}^*$ cannot be smaller than ${\hat{x}}^*$. Thus, at least for $p\rightarrow 0^+$ it is ${\bar{x}}^*\ge c_1/d_1$. On the other hand, overshooting the bliss point for all states can never be robustly optimal, so ${\bar{x}}^*\le c_2/d_2$. By Prop. 1 the performance index becomes

$$\begin{aligned}&{{\bar{\rho }}}({\hat{x}}) = \min \left\{ \left( 2 - \frac{c_1/d_1}{x_1} \right) \frac{c_1/d_1}{x_1} - \frac{2\left( {\hat{x}}-(c_1/d_1)\right) p}{d_1 x_1^2},\left( 2 - \frac{{\hat{x}}}{x_2} \right) \frac{{\hat{x}}}{x_2} \right\} ,\\&{\hat{x}}\in [(c_1/d_1),(c_2/d_2)]; \end{aligned}$$

for ${\hat{x}}\in [x_1,(c_1/d_1)]$ it is ${{\bar{\rho }}}({\hat{x}})=\rho ({\hat{x}})$, just as in the main text. This yields the optimal robust action

$$\begin{aligned}&{\bar{x}}^* = \left[ 1 - \frac{\sqrt{d_1^2x_1^2(x_1 - (c_1/d_1))^2 + 2d_1 p(x_2-(c_1/d_1)) x_1^2 + p^2 x_2^2} - p x_2}{d_1 x_1^2} \right] \,x_2,\\&p\in (0,{\bar{p}}], \end{aligned}$$

for small prices, which implies that $\lim _{p\rightarrow 0^+}{\bar{x}}^* = c_2/d_2$: at zero price, the agent finds it best to consume as much as might possibly be needed to achieve satiation. For larger prices, the bliss-point satiation becomes irrelevant, so

$$\begin{aligned} {\bar{x}}^* = {\hat{x}}^* = \frac{2\,x_1 x_2}{x_1+x_2}, \ \ \ p\in [{\bar{p}},c_1), \end{aligned}$$

where the threshold price ${\bar{p}}$, defined by $\left. {\hat{x}}^*\right| _{p={\bar{p}}} = c_1/d_1$, can easily be obtained in closed form. Fig. 5 compares the performance index of the (adjusted) relatively robust decision (${{\bar{\rho }}}^* = 87.99\%$, observed in the sample) to that of other solutions, again for the nominal state $(c_0,d_0) = (100,2)$, with dispersion vector $(\varepsilon ,\delta )=(20,0.75)$, price $p=4$, and $N=4000$ samples drawn uniformly from the state space ${\mathcal {S}}$: $\rho _{\mathrm{WC}}=50.95\%$, $\rho _{\mathrm{CE}} = 48.15\%$, $\rho _{\mathrm{MR}} = 82.70\%$.

Fig. 5

Performance comparison for solutions optimizing relative robustness (RR), minimax regret (MR), worst case (WC), and certainty equivalence (CE) [Sample Size: $N=4000$]