Risk aversion for losses and the Nash bargaining solution

Abstract

We call a decision maker risk averse for losses if that decision maker is risk averse with respect to lotteries having alternatives below a given reference alternative in their support. A two-person bargaining solution is called invariant under risk aversion for losses if the assigned outcome does not change after correcting for risk aversion for losses with this outcome as pair of reference levels, provided that the disagreement point only changes proportionally. We present an axiomatic characterization of the Nash bargaining solution based on this condition, and we also provide a decision-theoretic characterization of the concept of risk aversion for losses.

1 Introduction

In this paper, we propose a variation on the concepts of loss aversion and of risk aversion, called risk aversion for losses. A decision maker is risk averse for losses if this decision maker downgrades payoffs below a given reference level by a nondecreasing concave transformation.

We first formulate and apply this concept in the context of the two-person Nash bargaining model (Nash, 1950), as follows. Given a bargaining solution, assume that the bargainers regard the assigned payoffs as their reference levels. If they are risk averse for losses, then the problem (feasible set) is corrected by applying the associated concave transformations. We call a bargaining solution invariant under risk aversion for losses if after this correction the assigned outcome does not change, provided that the disagreement point only changes proportionally, i.e., the new, corrected, disagreement point is still on the straight line through the original disagreement point and the bargaining solution outcome. This last restriction is reasonable, and without it the axiom would be overly demanding. Invariance under risk aversion for losses is satisfied by many well-known bargaining solutions, including the Nash bargaining solution and the Kalai–Smorodinsky solution (Kalai & Smorodinsky, 1975).

We next concentrate on the Nash bargaining solution and provide an axiomatic characterization with invariance under risk aversion for losses as one of the axioms. The other axioms are Pareto optimality, symmetry, covariance, and expansion independence. This last condition requires the solution not to change if we add only payoff pairs exceeding the utopia payoff (i.e., maximally possible payoff) of one of the bargainers. We also show that the axioms are logically independent.

We finally present a decision-theoretic characterization of the new concept of risk aversion for losses, closely related to Yaari’s (1969) characterization of comparative risk aversion.

Our results are closely related to many other results in the literature, both on bargaining and on risk and loss aversion, but we postpone discussion of this literature until the relevant parts of the paper.

Section 2 introduces the Nash bargaining model, and Sect. 3 the concept of risk aversion for losses within this model. Sect. 4 presents the characterization of the Nash bargaining solution based on this concept. In Sect. 5, we provide the decision-theoretic characterization of risk aversion for losses.

2 Bargaining

A (two-person bargaining) problem is a convex and compact set $S \subseteq {\mathbb {R}}^2$ such that for the disagreement point $d(S)=(\min \{x_1 \mid x\in S\},\min \{x_2 \mid x\in S\})$, we have (i) $x > d(S)$ for some $x\in S$, and (ii) $y \in S$ whenever $y \in {\mathbb {R}}^2$ and $d(S) \le y \le x$ for some $x \in S$.¹² The set of all problems is denoted by ${\mathcal {B}}$.

The point $h(S) = (\max \{x_1 \in {\mathbb {R}}\mid x \in S\},\max \{x_2 \in {\mathbb {R}}\mid x \in S\})$ is the utopia point of $S\in {\mathcal {B}}$. The set $W(S) = \{x \in S \mid y \not > x \text{ for } \text{ all } y \in S\}$ is the weakly Pareto optimal subset of S and $P(S)= \{x \in S \mid y \ge x \text{ implies } y=x \text{ for } \text{ all } y \in S\}$ is the Pareto optimal subset of S. Problem S is symmetric if $S = \{(x_2,x_1) \in {\mathbb {R}}^2 \mid (x_1,x_2) \in S\}$. Note that this implies that $d_1(S)=d_2(S)$ and $h_1(S)=h_2(S)$.

A (bargaining) solution is a map $\varphi :{\mathcal {B}}\rightarrow {\mathbb {R}}^2$ such that $\varphi (S) \in S$ for all $S \in {\mathcal {B}}$. The following possible properties of $\varphi$ are standard.

Weak pareto optimality $\varphi (S)\in W(S)$ for all $S \in {\mathcal {B}}$.

Pareto optimality $\varphi (S)\in P(S)$ for all $S \in {\mathcal {B}}$.

Symmetry $\varphi _1(S)=\varphi _2(S)$ for all symmetric $S \in {\mathcal {B}}$.

Covariance $\varphi (aS+b)=a\varphi (S)+b$ for all $S\in {\mathcal {B}}$, $a \in {\mathbb {R}}^2$ with $a > 0$, and $b\in {\mathbb {R}}^2$, where $aS+b = \{ax+b \mid x\in S\}$.

The Nash solution N assigns to each problem S the point where the product $(x_1-d_1(S))(x_2-d_2(S))$ is maximized over S. Nash (1950) showed that N is the unique solution satisfying, besides Weak Pareto Optimality, Symmetry, and Covariance, the following property.³

Independence of irrelevant alternatives $\varphi (T)=\varphi (S)$ for all $S,T\in {\mathcal {B}}$ such that $d(S)=d(T)$, $S\subseteq T$, and $\varphi (T)\in S$.

Independence of irrelevant alternatives can be interpreted as follows. The solution $\varphi (T)$ of the bargaining problem T can be seen as the best compromise available in T: in this respect, it beats all other alternatives in T. But if this is the case, then it certainly beats all alternatives in a smaller set S, given that the disagreement point is still the same.⁴ On a similar ground, however, the condition can also be criticized: $\varphi (T)$ may be a good compromise in T but that does not necessarily imply that it is a good compromise in S, for instance, because the utopia point h(T), the pair of highest available payoffs in T, may be different from h(S), the utopia point of S. This led Kalai & Smorodinsky (1975) to propose the following alternative solution. The Kalai–Smorodinsky solution K assigns to each problem S the unique point of P(S) on the line segment connecting d(S) and h(S). This solution had been studied earlier in Raiffa (1953).

Kalai & Smorodinsky (1975) showed that K is the unique solution satisfying, besides Weak Pareto Optimality, Symmetry, and Covariance, the following property.⁵

Individual monotonicity $\varphi _i(T)\ge \varphi _i(S)$ for all $i \in \{1,2\}$ and $S,T\in {\mathcal {B}}$ such that $d(S)=d(T)$, $S\subseteq T$, and $h_j(S)=h_j(T)$ for $j \ne i$.

3 Loss aversion in bargaining

Loss aversion (Kahneman & Tversky, 1979) is the often observed phenomenon (e.g., Kahneman et al., 1990; Tversky & Kahneman, 1992) that people tend to downgrade utilities or payoffs that are below some reference level. If one expects to receive one Euro, then 99 cents is perceived as worse than the same 99 cents if one expects to receive less than 99 cents. This ‘expectation’ is usually called the ‘reference level’. In the context of game theory, including bargaining, loss aversion was first introduced by Shalev (2000, 2002), who assumed ‘linear loss aversion’: see below for a detailed discussion.

As usual, a decision maker with utility function v (say, on ${\mathbb {R}}$) is called more risk averse than a decision maker with utility function u if there is a nondecreasing concave function k such that $v = k \circ u$ (Arrow, 1971; Pratt, 1964; Yaari, 1969). The effect of increased risk aversion in bargaining has been studied extensively: the literature includes Kannai (1977), Kihlstrom et al. (1981), Peters & Tijs (1981), Roth & Rothblum (1982), de Koster et al. (1983), van Damme (1986), Safra et al. (1990), and more.

Here, we consider a property which is closely related to the concept of increased risk aversion, adapted to the bargaining context. Formally, let S be a bargaining problem. Bargainer i is risk averse for losses if for each $r_i \in [d_i(S),h_i(S)]$ there is a nondecreasing concave function $k_i[r_i] :[d_i(S),h_i(S)] \rightarrow {\mathbb {R}}$ such that $k_i[r_i](x_i) = x_i$ for all $x_i \in [r_i,h_i(S)]$. Here, $r_i$ is the reference level. Note that, if $r_i < h_i(S)$, this definition implies that $k_i[r_i](x_i) \le x_i$ for all $x_i \in [d_i(S),r_i]$. Thus, if bargainer i is risk averse for losses, then i’s payoffs below a reference level $r_i$ are downgraded in a way consistent with increased risk aversion. We call $k_i[r_i]$ bargainer i’s loss function at $r_i$.

The concept of linear loss aversion (Shalev, 2000, 2002; Köszegi & Rabin, 2006, 2007; see Peters (2012), for a preference foundation) is a special case of risk aversion for losses, obtained by taking $k_i[r_i](x_i) = x_i - \lambda _i(r_i-x_i)$ for every $x_i \in [d_i(S),h_i(S)]$ with $x_i \le r_i$, where $\lambda _i \in {\mathbb {R}}$ with $\lambda _i \ge 0$ is the ‘loss aversion coefficient’. Thus, linear loss aversion is stronger than risk aversion for losses. In turn, risk aversion for losses is a special case of (thus, stronger than) some of the loss aversion formulations in the literature: see Sect. 5, where we provide a preference foundation of risk aversion for losses in the spirit of Yaari (1969).

Shalev (2002) considered the following property based on the concept of linear loss aversion in the Nash bargaining model. Suppose a bargaining solution $\varphi$ is used, and consider a problem S. Suppose that the players are linearly loss averse with pair of loss aversion coefficients $\lambda =(\lambda _1,\lambda _2)$. If they regard the payoffs $r_i=\varphi _i(S)$, $i=1,2$, as their reference levels, then after correction for linear loss aversion the problem becomes $S(\lambda ,r) = \{ (x_1(\lambda _1,r_1),x_2(\lambda _2,r_2) )\mid (x_1,x_2) \in S\}$, with

$$\begin{aligned} x_i(\lambda _i,r_i) = \left\{ \begin{array}{ll} x_i &{} \hbox {if }x_i \ge r_i \\ x_i - \lambda _i(r_i-x_i) &{} \hbox {if }x_i < r_i \end{array} \right. \end{aligned}$$

for $i=1,2$. Shalev (2002) showed that the Nash bargaining solution is invariant under such a linear loss aversion correction, i.e., we have $N(S(\lambda ,N(S)) = N(S)$.

In the present paper, we consider risk aversion for losses instead of linear loss aversion. For a bargaining problem S, a pair of reference levels $r=(r_1,r_2) \in [d_1(S),h_1(S)]\times [d_2(S),h_2(S)]$, and a pair of loss functions $k[r]=(k_1[r_1],k_2[r_2])$, we denote by $S(k[r]) = \{(k_1[r_1](x_1),k_2[r_2](x_2)) \mid (x_1,x_2) \in S\}$ the problem corrected for risk aversion for losses. Now the condition $\varphi (S(k[\varphi (S)])) = \varphi (S)$ for a bargaining solution $\varphi$ is much more demanding than for linear loss aversion, and indeed the Nash bargaining solution does not satisfy it, as the following example shows.

Example 3.1

(See Fig. 1 for an illustration.) Let $S\in {\mathcal {B}}$ be the convex hull of the points (0, 0), (1, 0), (0, 1). Then $N(S)=(\frac{1}{2},\frac{1}{2})$. Let $k_2[\frac{1}{2}](x_2) = x_2$ for all $0 \le x_2 \le 1$, and let $k_1[\frac{1}{2}](x_1)=x_1$ for all $\frac{1}{4} \le x_1 \le 1$, and $k_1[\frac{1}{2}](x_1) = 5x_1-1$ for all $0 \le x_1 < \frac{1}{4}$. Then, S(k[N(S)]) is the convex hull of the points $(-1,0)$, (1, 0), $(\frac{1}{4},\frac{3}{4})$, and $(-1,1)$. Writing $T=S(k[N(S)])$, we have $N(T) = (\frac{1}{4},\frac{3}{4}) \ne (\frac{1}{2},\frac{1}{2}) = N(S)$. Note that there is no $\lambda _1$ such that $k_1[\frac{1}{2}](x_1) = x_1 - \lambda _1(\frac{1}{2}-x_1)$ for for all $0 \le x_1 < \frac{1}{2}$, hence bargainer 1 is not linearly loss averse. $\lhd$

Fig. 1

Example 3.1. Problem S is the triangle with vertices (0, 0), (1, 0), and (0, 1). The problem corrected for risk aversion for losses, T, is the shaded area

We will weaken the condition that the solution $\varphi$ does not change after correcting for risk aversion for losses, by imposing it only when the disagreement point changes proportionally, as follows. For $a,b \in {\mathbb {R}}^2$, let [a, b] denote the convex hull of a and b, i.e., the line segment with endpoints a and b.

Invariance under risk aversion for losses$\varphi (S(k[\varphi (S)])) = \varphi (S)$ for all $S \in {\mathcal {B}}$ such that $\varphi (S) < h(S)$, and loss function pairs $k[\varphi (S)]$ such that $d(S) \in [d(S(k[\varphi (S)])),$ $\varphi (S)]$.

It is not difficult to see that the Nash bargaining solution is invariant under risk aversion for losses. Geometrically, the Nash bargaining solution picks the point on the Pareto boundary of a bargaining problem S at which there is a supporting line with slope equal to minus the slope of the line through this point and the disagreement point d(S) (e.g., Lemma 2.2 in Peters, 1992). Clearly, if we correct S for risk aversion for losses, then the original supporting line of S at N(S) is still a supporting line at N(S) for the corrected problem, and if the disagreement point of the corrected problem is on the straight line through d(S) and N(S), then N(S) is still the Nash bargaining solution outcome of the corrected problem. For ease of reference, we formulate this observation as a lemma.

Lemma 3.2

The Nash bargaining solution is invariant under risk aversion for losses.

The above geometrical argument might suggest that invariance under risk aversion for losses is tailor-made for the Nash bargaining solution, but the following lemma shows that this is not quite true.

Lemma 3.3

The Kalai-Smorodinsky bargaining solution is invariant under risk aversion for losses.

Proof

Let $S\in {\mathcal {B}}$ and consider a pair of loss functions k[K(S)]. Write $\widetilde{S}=S(k[K(S)])$. It is easy to see that $h(\widetilde{S}) = h(S)$. If $d(S) \in [d(\widetilde{S}),K(S)]$, then K(S) is still on the line segment connecting $d(\widetilde{S})$ and $h(\widetilde{S})$. Hence, $K(\widetilde{S}) = K(S)$. $\square$

Thus, the Nash and Kalai–Smorodinsky bargaining solutions share the properties of Pareto optimality, symmetry, covariance, and invariance under risk aversion for losses. In the next section, we will add another property to single out the Nash bargaining solution.

4 A characterization of the Nash bargaining solution

We consider the following possible property of a solution $\varphi$.

Expansion independence $\varphi (T)=\varphi (S)$ for all $S,T\in {\mathcal {B}}$ such that $d(S)=d(T)$, $S \subseteq T$, and there is $i\in \{1,2\}$ for which $\varphi _i(S)< h_i(S) < x_i$ for all $x \in T\setminus S$.

Fig. 2

Expansion independence: $i=1$, and T is the union of S and $T \setminus S$

This property says the following (cf. Fig. 2). Suppose the solution of a problem S is a ‘true compromise’ on the part of bargainer i in the sense that i receives less than the maximally achievable payoff, i.e., the utopia payoff $h_i(S)$. If we now extend S to a problem T by adding only points that are better for bargainer i than this utopia payoff, then the solution should not change. Another way of stating this is that, if we cut off, from a problem T, payoffs exceeding a certain level for bargainer i, and the solution of the resulting problem S is below this level for bargainer i, then the solution of the original problem T should be equal to the solution of S. This property is a kind of dual of independence of irrelevant alternatives. It is a very weak version of the condition of ‘independence of irrelevant expansions’ used by Thomson (1981) in a characterization of the Nash bargaining solution. It also resembles the condition of ‘independence of irrelevant claims’ in Albizuri et al. (2020). Of course, it can be criticized on similar grounds as the independence of irrelevant alternatives condition.

Observe that, for the situation in the definition of expansion independence, any supporting line of S at $\varphi (S)$ is still a supporting line of T at $\varphi (S)$. Therefore, by the same geometric characterization of the Nash bargaining solution as used to prove Lemma 3.2, we obtain:

Lemma 4.1

The Nash bargaining solution is expansion independent.

The announced characterization of the Nash bargaining solution is as follows.

Theorem 4.2

The Nash bargaining solution is the unique solution satisfying Pareto optimality, symmetry, covariance, invariance under risk aversion for losses, and expansion independence.

Proof

The results of Nash (1950) and Lemmas 3.2 and 4.1 imply that N has the five properties stated in the theorem.⁶ Now, let $\varphi$ be a solution with these properties, and let $S \in {\mathcal {B}}$. We prove that $\varphi (S)=N(S)$.

By covariance, we may assume without loss of generality that $d(S)=(0,0)$ and $N(S)=(1,1)$. This also implies that the straight line through the points (2, 0) and (0, 2) is a supporting line of S at (1, 1).

Without loss of generality, let $h_2(S) \le h_1(S)$ (the other case is similar).

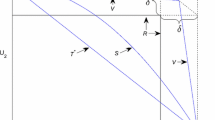
First suppose that $h_2(S) > 1$. Let $T \in {\mathcal {B}}$ be the convex hull of the points $(2-h_2(S),h_2(S))$, $(h_2(S),2-h_2(S))$, and $(2-h_2(S),2-h_2(S))$. (See Fig. 3). Then T is symmetric, with $d(T)=(2-h_2(S),2-h_2(S))$. By weak Pareto optimality and symmetry, $\varphi (T)=(1,1)$. Define the function $k_1 = k_1[1]$ on $[d_1(T),h_1(T)] = [d_1(T),h_2(S)]$ by $k_1(x_1)=x_1$ for all $x_1 \in [1,h_2(S)]$, and such that $\{(k_1(x_1),2-x_1) \mid x_1 \in [d_1(T),1]\} = \{x \in W(S) \mid x_1 \le 1\}$. Similarly, define the function $k_2 = k_2[1]$ on $[d_2(T),h_2(T)] = [d_2(T),h_2(S)]$ by $k_2(x_2)=x_2$ for all $x_2 \in [1,h_2(S)]$, $k_2(d_2(T))=0$, and such that $\{(2-x_2,k_2(x_2)) \mid d_2(T)< x_2 \le 1\} = \{x \in W(S) \mid d_2(T) < x_2 \le 1\}$. Then, $k_1$ and $k_2$ are nondecreasing concave functions, and $T(k_1,k_2) = \{x \in S \mid x_1 \le h_2(S)\}$. In particular, $d(T(k_1,k_2)) = (0,0) = d(S)$. By invariance under risk aversion for losses of $\varphi$, we have $\varphi (T(k_1,k_2)) = \varphi (T) = (1,1)$. Hence, $\varphi (\{x \in S \mid x_1 \le h_2(S)\}) = (1,1)$. Since $h_1(\{x \in S \mid x_1 \le h_2(S)\}) = h_2(S) > 1$, expansion independence now implies that $\varphi (S) = (1,1) = N(S)$.

Fig. 3

Proof of Theorem 4.2, case $1 < h_2(S) \le h_1(S)$. The thick triangle is the boundary of the set T, and the shaded set is the set T corrected for risk aversion for losses

Fig. 4

Proof of Theorem 4.2, case $1 = h_2(S) < h_1(S)$. The set $\widetilde{S}$ is the shaded set

Second, consider the case where $h_2(S)=1$ and $h_1(S)>1$. (See Fig. 4.) Since $(1,1)=N(S)$, this implies that we can take some $1 < \eta \le h_1(S)$ such that the set $\widetilde{S}$, obtained by taking the convex hull of S and $\{(0,\eta )\}$, is in ${\mathcal {B}}$. If $\varphi _1(S) > 1$, then by expansion independence, $\varphi (\widetilde{S}) = \varphi (S)$, but by the preceding part of the proof, $\varphi (\widetilde{S})=N(\widetilde{S})=(1,1)$, a contradiction. Hence, $\varphi _1(S) \le 1$, and therefore by Pareto optimality $\varphi (S) = (1,1) = N(S)$.

Finally, if $h(S)=(1,1)$ then S is convex hull of the points (0, 0), (1, 0), (0, 1), and (1, 1), and $\varphi (S)=(1,1)=N(S)$ by Pareto optimality.  $\square$

In the following example, we show that the conditions in Theorem 4.2 are logically independent. We also show that Pareto optimality cannot be replaced by weak Pareto optimality. Finally, we demonstrate that the comprehensiveness assumption on a bargaining problem, assumption (ii), cannot be relaxed without consequences.

Example 4.3

We show independence of five the conditions in Theorem 4.2 by exhibiting five examples.

• (i) The disagreement solution D, defined by $D(S)=d(S)$, satisfies all conditions except Pareto optimality.

• (ii) The dictator-1 solution $D^1$, which assigns to $S \in {\mathcal {B}}$ the Pareto optimal point of S with first coordinate $h_1(S)$, satisfies all conditions except symmetry.

• (iii) The lexicographic egalitarian solution, which assigns to $S\in {\mathcal {B}}$ the point of P(S) closest to the line through d(S) with slope equal to 1, satisfies all conditions except covariance.

• (iv) We construct a solution $\varphi$ satisfying all conditions except invariance under risk aversion for losses. We define $\varphi$ for bargaining problems S with $d(S)=(0,0)$ and $N(S)=(1,1)$—for arbitrary problems the solution is then extended by appealing to covariance. We distinguish two cases. If there are numbers $0 \le \alpha < 1$ and $1 < \beta \le \frac{3}{2}$ such that

  $$\begin{aligned}{}[(\alpha ,2-\alpha ),(1,1)] \cup [(1,1),(\beta ,3-2\beta )] \subseteq P(S), \end{aligned}$$

  then $\varphi (S) = D^1(S)$. See Fig. 5 for an example of such a problem. Hence, in this case the solution assigns the best Pareto optimal point for bargainer 1. In all other cases, $\varphi (S)=N(S)$. This solution satisfies Pareto optimality, symmetry, and covariance. It is not hard to check that it also satisfies expansion independence. Hence, Theorem 4.2 implies that it is not invariant under risk aversion for losses.

• (v) The Kalai–Smorodinsky solution K satisfies all conditions except expansion independence. In particular, K is invariant under risk aversion for losses by Lemma 3.3.

• (vi) We show that Pareto optimality cannot be replaced by weak Pareto optimality in Theorem 4.2. Define the solution $\psi$ as follows. If $S \in {\mathcal {B}}$ such that $N_2(S)=h_2(S)$ and $N_1(S)<h_1(S)$, then $\psi (S)=(d_1(S),h_2(S))$. In all other cases, $\psi (S)=N(S)$. Then, $\psi$ is weakly Pareto optimal but not Pareto optimal, and it also satisfies the four other conditions in Theorem 4.2.

• (vii) The comprehensiveness assumption (ii) on a bargaining problem is quite natural. Nevertheless, it is interesting to consider what happens if it is dropped.⁷ We show that in that case Theorem 4.2 no longer holds. Suppose we replace (ii) by (ii$'$): $d(S) \in S$. Let ${\mathcal {B}}'$ denote the set of all problems satisfying (i) and (ii$'$). Clearly, ${\mathcal {B}}\subsetneq {\mathcal {B}}'$; in particular, for an $S \in {\mathcal {B}}'$, it is possible that $(d_1(S),h_2(S)) \notin S$ or $(d_2(S),h_1(S)) \notin S$. Let ${\mathcal {B}}'_0$ be the subset of those problems S for which $|\{x \in S \mid d_1(S)< x_1 < h_1(S), x_2 = h_2(S)\}| = 1$ and $|\{x \in S \mid d_2(S)< x_2 < h_2(S), x_1 = h_1(S)\}| = 1$. An example of such a problem is the convex hull, say S, of the points (0, 0), (1, 3), and (3, 2). Then $K(S)=(\frac{7}{3},\frac{7}{3}) \ne (3,2) = N(S)$. Observe that for this problem S, a problem $T\in {\mathcal {B}}'$, $T\ne S$, as in the definition of expansion independence, does not exist. This leads us to define the bargaining solution $\varphi :{\mathcal {B}}' \rightarrow {\mathbb {R}}^2$ by $\varphi (S) = K(S)$ for all $S \in {\mathcal {B}}'_0$ and $\varphi (S)=N(S)$ for all $S \in {\mathcal {B}}' \setminus {\mathcal {B}}'_0$. Then, $\varphi$ satisfies all five conditions in Theorem 4.2 on ${\mathcal {B}}'$, but it is not the Nash bargaining solution. The characterization in the theorem can be restored to hold for ${\mathcal {B}}'$ if the expansion independence condition is strengthened by replacing ‘for all $x\in T \setminus S$’ by ‘for all $x \in P(T)\setminus S$’ in its formulation. We leave verification of these claims to the reader.

Fig. 5

A problem S as in Example 4.3 part (iv)

5 A preference foundation for risk aversion for losses

In the approach of Nash (1950), a bargaining problem arises as the set of expected utility payoff pairs from an underlying set of alternatives and associated lotteries. In this context, it is indeed meaningful to study the impact of risk aversion and loss aversion, as we did in the preceding sections. In this section, we provide a characterization of our concept of risk aversion for losses of a single decision maker. More precisely, we define the concept of risk aversion for losses in terms of preferences, and then show that this is equivalent to the same concept in terms of the specific payoff transformation as introduced earlier in the bargaining context.

Let A denote a nonempty set of alternatives, and let ${\mathcal {L}}$ denote the set of lotteries on A, i.e., the set of probability distributions on A with finite support. A preference $\succeq$ is a weak ordering (i.e., a complete, reflexive, and transitive binary relation) on ${\mathcal {L}}$. Instead of $(\ell ,\ell ') \in \ \succeq$ we write $\ell \succeq \ell '$, for $\ell ,\ell '\in {\mathcal {L}}$. By $\succ$ and $\sim$ we denote the strict and indifference parts of $\succeq$: for $\ell ,\ell '\in {\mathcal {L}}$, $\ell \succ \ell '$ if $\ell \succeq \ell '$ but not $\ell '\succeq \ell$, and $\ell \sim \ell '$ if both $\ell \succeq \ell '$ and $\ell '\succeq \ell$.

We assume that any preference $\succeq$ under consideration in this section can be represented by a von Neumann–Morgenstern⁸ utility function u, i.e., $\ell \succeq \ell ' \Leftrightarrow Eu(\ell ) \ge Eu(\ell ')$ for all $\ell ,\ell '\in {\mathcal {L}}$, where $Eu(\cdot )$ denotes expected utility: if lottery $\ell$ results with probability $p_j$ in alternative $a_j$ for $j=1,\ldots ,k$ for some $k \in {\mathbb {N}}$, then $Eu(\ell )=\sum _{j=1}^k u(a_j)$. Under this assumption, it is in particular sufficient to know the representing function u on the set of (riskless) alternatives A, i.e., to know $u : A \rightarrow {\mathbb {R}}$. See Herstein and Milnor (1953) for an axiomatic foundation of this assumption. Such a representation is unique up to positive linear transformations, i.e., v also represents $\succeq$ if and only if there are $\alpha ,\beta \in {\mathbb {R}}$ with $\alpha >0$ such that $v(a)=\alpha u(a) + \beta$ for all $a \in A$.

For a preference $\succeq$ and an alternative $a\in A$, we denote by ${\mathcal {L}}_\succ (a) = \{\ell \in {\mathcal {L}}\mid \ell \succ a\}$ the strict preference set of $\succeq$ with respect to a.⁹ For $r \in A$, define the set ${\mathcal {L}}_{\succeq ,r}$ by ${\mathcal {L}}_{\succeq ,r} = \{\ell \in {\mathcal {L}}\mid a \succeq r$ for all $a\in A$ in the support of $\ell$}. We call a (decision maker with) pair of preferences $(\succeq ,\succeq _r)$ risk averse for losses at r if ${\mathcal {L}}_{\succ _r}(a) \subseteq {\mathcal {L}}_\succ (a)$ and ${\mathcal {L}}_{\succ _r}(a) \cap {\mathcal {L}}_{\succeq ,r} = {\mathcal {L}}_\succ (a) \cap {\mathcal {L}}_{\succeq ,r}$ for all $a\in A$. In words: first, if such a decision maker strictly prefers a lottery $\ell$ over an alternative a at $\succeq _r$, then the decision maker also strictly prefers $\ell$ over a at $\succeq$; and, second, for any lottery $\ell$ of which the decision maker prefers every alternative in its support over r at $\succeq _r$, for any alternative a the decision maker strictly prefers $\ell$ over a at $\succeq _r$ if and only if the decision maker strictly prefers $\ell$ over a at $\succeq$. The first part of this definition is (a slight variation on) the usual definition of (a decision maker with preference) $\succeq _r$ being more risk averse than (a decision maker with preference) $\succeq$. The second part adds to this that lotteries involving no losses with respect to the reference alternative r are treated equally under $\succeq _r$ and $\succeq$.

The following result is a variation on classical results of Arrow (1971), Pratt (1964), and in particular (Yaari 1969)—see also Peters & Tijs (1981) and Wakker et al. (1985).

Theorem 5.1

Let $r \in A$, let $(\succeq ,\succeq _r)$ be a pair of preferences, and let $u : A \rightarrow {\mathbb {R}}$ represent $\succeq$. Assume that there exist ${\underline{a}},{\bar{a}} \in A$ such that $u(A) = [u({\underline{a}}),u({\bar{a}})]$. Then, the following two assertions are equivalent:

• (a) $(\succeq ,\succeq _r)$ is risk averse for losses at r.

• (b) There is a nondecreasing concave function $k : u(A) \rightarrow {\mathbb {R}}$ with $k(u(a)) = u(a)$ for all $a \in A$ with $a \succeq r$, such that $v : A \rightarrow {\mathbb {R}}$, defined by $v(a) = k(u(a))$ for all $a\in A$, represents $\succeq _r$.

Proof

The proof of the implication [(b) $\Rightarrow$ (a)] is straightforward and, therefore, omitted.

Now suppose (a) holds. Let $v : A \rightarrow {\mathbb {R}}$ represent $\succeq _r$ such that $v(r)=u(r)$ and $v({\bar{a}}) = u({\bar{a}})$ (this is possible since v is unique up to positive linear transformations). Consider $a,b \in A$. If $u(a)=u(b)$, then $b \succeq _r a$ since otherwise $a \in {\mathcal {L}}_{\succ _r}(b) \subseteq {\mathcal {L}}_\succ (b)$ and therefore $a \succ b$, so $u(a) > u(b)$, a contradiction. Similarly, $u(a)=u(b)$ implies $b \succeq _r a$, and hence $a \sim _r b$ and $v(a)=v(b)$. Hence the function $k : u(A) \rightarrow {\mathbb {R}}$ with $k(u(a)) = v(a)$ for all $a\in A$ is well-defined. Also, if $u(a) > u(b)$, then $v(a) \ge v(b)$ since otherwise $b \in {\mathcal {L}}_{\succ _r}(a) \subseteq {\mathcal {L}}_\succ (a)$, so that $u(b)>u(a)$, a contradiction. This implies that k is nondecreasing.

Let $x,y \in u(A) = [{u(\underline{a})},u({\overline{a})}]$, say $x = u(c)$ and $y= u(d)$ for some $c,d \in A$, and let $\lambda \in [0,1]$. Consider the lottery $\ell$ resulting with probability $\lambda$ in c and with probability $1-\lambda$ in d. Let $e \in A$ such that $u(e)=\lambda u(c) + (1-\lambda ) u(d) = Eu(\ell )$. Then, $\ell \notin {\mathcal {L}}_\succ (e)$, hence $\ell \notin {\mathcal {L}}_{\succ _r}(e)$, so that $\lambda k(x) + (1-\lambda )k(y) = \lambda k(u(c)) + (1-\lambda )k(u(d)) = Ev(\ell ) \le v(e) = k(u(e)) = k(\lambda u(c) + (1-\lambda ) u(d)) = k(\lambda x + (1-\lambda )y)$, proving concavity of k.

If $u(r)=u({\bar{a}})$ then the proof of (b) is complete. Now assume $u(r)<u({\bar{a}})$, and let $a\in A$ such that $u(r)<u(a)<u({\bar{a}})$, hence $u(a)=\lambda u(r) + (1-\lambda ) u({\bar{a}})$ for some $0<\lambda <1$. Let $\ell \in {\mathcal {L}}_{\succeq ,r}$ be the lottery resulting in r with probability $\lambda$ and in ${\bar{a}}$ with probability $1-\lambda$. Then, $u(a)=Eu(\ell )$, and $v(a)=k(u(a))=k(\lambda u(r) + (1-\lambda )u({\bar{a}})) \ge \lambda k(u(r)) + (1-\lambda ) k(u({\bar{a}})) = \lambda v(r) + (1-\lambda )v({\bar{a}})$, where the inequality follows from concavity of k. Suppose that this inequality is strict. Then let $\lambda ' < \lambda$ such that still $v(a) \ge \lambda ' v(r) + (1-\lambda ')v({\bar{a}})$, and let $\ell '$ denote the lottery resulting in r with probability $\lambda '$ and in ${\bar{a}}$ with probability $1-\lambda '$. Then $u(a) < \lambda ' u(r) + (1-\lambda ') u({\bar{a}}) = Eu(\ell ')$. Hence, $\ell ' \in {\mathcal {L}}_\succ (a)$, $\ell ' \notin {\mathcal {L}}_{\succ _r}(a)$, and $\ell ' \in {\mathcal {L}}_{\succeq ,r}$, in contradiction with ${\mathcal {L}}_{\succ _r}(a) \cap {\mathcal {L}}_{\succeq ,r} = {\mathcal {L}}_\succ (a) \cap {\mathcal {L}}_{\succeq ,r}$. Therefore, k is linear on $[u(r),u({\bar{a}})]$, and in particular $k(u(a)) = u(a)$ for all $a \in A$ with $a \succeq r$. This completes the proof of the implication [(a) $\Rightarrow$ (b)]. $\square$

A few further remarks on this result are in order. First, the theorem can be extended to cases where u(A) is a general subset of the real numbers, that is, not necessarily bounded, closed, or convex, by using, in particular, a result of Peters and Wakker (1987). For the purpose of the present paper, however, we do not need this. For a bargaining game S, we implicitly assume that the payoff pairs in S arise as expected utilities of lotteries on an underlying set of alternatives A, such that for each weakly Pareto optimal point of S there is an alternative in A resulting in that point. Note that, in Theorem 5.1, if $u(r) < u({\bar{a}})$, then the function k satisfies, additionally, that $k(u(a)) \le u(a)$ whenever $u(a) \le u(r)$—this follows since k is identity on $[u(r),u({\bar{a}})]$, and k is concave. In our bargaining application, the condition $u(r) < u({\bar{a}})$ is satisfied since in the definition of invariance under risk aversion for losses, it is required that the reference point is below the utopia point.

Also, similarly as in Peters (2012), Theorem 5.1 may be extended to characterize objects of the form $(\succeq ,\succeq _r)_{r\in A}$, in particular, to establish existence of a function k[r] for every $r \in A$, possibly with relations between these functions depending on the imposed axioms.

As mentioned earlier, linear loss aversion is a special case of our risk aversion for losses concept. On the other hand, the latter is a special case of some of the loss aversion concepts proposed in the literature. Bowman et al. (1999) and Blavatskyy (2011) propose quite general definitions of loss aversion, of which ours is a special case. Also, Köszegi & Rabin (2007) propose a rather general definition but focus on linear loss aversion. For still other formulations of loss aversion, see Neilson (2002), Köbberling & Wakker (2005), and Schmidt and Zank (2005).