Seeking consistency with paired comparisons: a systems approach

Abstract

It is well known that decision methods based on pairwise rankings can suffer from a wide range of difficulties. These problems are addressed here by treating the methods as systems, where each pair is looked upon as a subsystem with an assigned task. In this manner, the source of several difficulties (including Arrow’s Theorem) is equated with the standard concern that the “whole need not be the sum of its parts.” These problems arise because the objectives assigned to subsystems need not be compatible with that of the system. Knowing what causes the difficulties leads to resolutions.

1 Difficulties with paired comparisons

For reasons that include cost and convenience, paired comparisons are widely used to make decisions even though examples exist that cast doubt on the trustworthiness of certain approaches. As these techniques continue to be used, a useful goal (developed here) is to determine how they can be modified to yield more reliable outcomes.

The basic idea mimics the least-squares methodology by projecting information (e.g., data, results about pairs, etc.) into a space where consistent outcomes are assured. Unfortunately, an appropriate “consistency space” is not known even for the widely required condition of transitivity. This motivates finding a natural “transitivity consistency” space.

Even after identifying a desired space of outcomes, the appropriate projection need not be obvious. This tends to be true with nonlinear structures. The expectation is that

$$\begin{aligned} \text { Computed outcome } = \text { desired outcome } + \text { error, } \end{aligned}$$

(1)

where, if the summation is an orthogonal vector addition, standard projections apply. But if Eq. 1 fails (which, as shown below, is true with AHP, the Analytic Hierarchy Process), rather than helping, projections can aggravate the analysis by introducing new types of mistakes. To avoid these problems, the structure of the error term must be found.

Some techniques use modified forms of paired comparisons. An example is the Pugh matrix method (Pugh, 1991) where a particular alternative (often the status quo) serves as the base from which other alternatives are compared over several criteria. A standard approach is, for each criterion, to assign a $``-, 0, +"$ score to an alternative where

$$\begin{aligned} ``-" \text { means it is poorer, } ``0 "\text { if it is about the same, } ``+" \text { if it is better.} \end{aligned}$$

The final score is the number of $+$’s minus the number of −’s. Refined options include “double −’s and double $+$’s,” or perhaps 1, 2, 3, 4, 5, where 3 is equivalent to the base comparison. It is shown how to identify and overcome weaknesses of these approaches. .

A search to improve decision outcomes is desirable, but is it futile? The pessimism derives from Arrow’s Theorem (Arrow, 1963), which often is described as asserting that no decision approach is fair with three or more alternatives. Fortunately for this project, it is shown that this negative commentary is overstated.

Addressing these difficulties is part of a general project to understand systems whether from the social sciences, engineering, or biology. Toward this end, paired comparisons are treated as “subsystems;” i.e., the decision methods combine information from the subsystems to create an answer for the whole system. An advantage of first studying decision methods for this project is that their structures are specified, so they form a more tractable test bed to discover why system problems arise and how to correct them. Taking this point of view, Arrow’s Theorem’s negative conclusion becomes the standard “the whole can differ from the sum of its parts” concern (Sect. 2). The goal is to understand what causes conflicts between a system and its subsystems and how to avoid them.

A first step (Sect. 3) is to analyze the structure of the subsystems, which here is the space of paired comparisons. Guided by Eq. 1 and emphasizing summation methods, this space is orthogonally divided into two components—informally, call them the “desired” and “error” subspaces. Nothing goes wrong when any standard decision method uses information from the desired component. Consequently, all difficulties are caused by decision methods using information about pairs, or portion of pairs, from the error space. Accompanying the discussion are easily used computational tools.

An obvious message is to avoid subsystem outcomes (i.e., collections of paired outcomes) that rely upon the error space: this is how (in Sect. 4) the approaches described above are modified. A second class of decision methods (such as AHP) uses multiplicative procedures. In Sect. 5, results about these systems are derived by transferring material from Sect. 3. Most proofs are in Sect. 7.

2 Arrow's Theorem from a systems approach

A system starts with a stated objective. Arrow’s modest goal was to rank $n\ge 3$ specified alternatives. The content of the alternatives is immaterial; they could be design plans for a project, ways to invest money, or even names for a new puppy.

For notation, with alternatives $A_i$ and $A_j$, the symbol “$A_i\succ A_j$” denotes “$A_i$ is ranked above $A_j$,” while “$A_i \sim A_j$” has “$A_i$ and $A_j$ are ranked the same.” Arrow’s goal follows:

1. Objective: The ranking outcome for the $n \ge 3$ alternatives is complete¹ and transitive.²

The inputs can be essentially anything. For finance, they might be how various experts rank the alternatives, or how the alternatives fare on different markets. For an engineering or management plan, the alternatives could be ranked over different criteria such as, perhaps, taxes or availability of resources. For voting, they are the voters’ preference rankings. Namely, conditions are imposed on the structure, not the content, of the inputs.

2. Inputs: The outcome is determined by $a \ge 2$ complete, transitive rankings of the n alternatives. There are no restrictions on the rankings. A listing of the rankings from the a sources, called a profile, is denoted by ${\mathbf {p}}$.

A standard way to compute a system’s outcome is to use information coming from the separate subsystems (here, pairs).

3. Analysis. For each pair of alternatives, $\{A_i, A_j\}$, a method is designed to determine the pair’s outcome ranking of $A_i\succ A_j$, $A_i \sim A_j$, or $A_j\succ A_i$. The method developed for a specified pair uses only input information from a profile about how each of the a sources ranks that particular pair.

No restrictions are imposed on the design of these methods. As an extreme example, when locating a plant in Atlanta, Boston, or Chicago, should there be an innate preference for Chicago, then, when compared with either other city, the method would select Chicago if the rankings from the criteria of taxes and the availability of land are not both unfavorable for Chicago. A different method could rank Atlanta and Boston.

While these three conditions are all that are needed, they admit useless rules. One is where the methods assign fixed outcomes for the pairs; e.g., suppose for three alternatives that the $\{A_1, A_2\}$ outcome always is $A_1\sim A_2$, and the $\{A_2, A_3\}$ and $\{A_1, A_3\}$ outcomes always are $A_2\succ A_3$ and $A_1\succ A_3$. These constant methods satisfy the three conditions with a fixed $A_1\sim A_2 \succ A_3$ transitive ranking, but they are not of any real interest.

Another trivial choice is where each pair’s outcome always depends on a single source’s ranking, perhaps the foreman on a project, which may provide efficiency, or only tax information when selecting a city for a new plant, which could be disastrous. To understand systems, methods that rely upon inputs from more than one source must be explored.

The sole purpose of the following is to acknowledge that these uninteresting methods satisfy the first three conditions and then to exclude them.

4. Eliminating undesired rules:

• a. For each pair of alternatives, the method that is designed to rank the pair does not have a fixed outcome. That is, for at least two of the three possible rankings of the pair, each is the outcome for some profile.

• b. All outcomes for all of the pairs cannot always be determined by the ranking of the same single source.

As the role of #4 is to identify and dismiss methods that are of no interest, only condition #3 of the methodology applies. That is, the system’s outcome is determined by results coming from the individual subsystems. As asserted next, no such methodology exists.

Theorem 1

(Saari, 2018) For $n\ge 3$ alternatives and $a\ge 2$ sources of inputs, there do not exist ways to rank the individual pairs so that the above four conditions always hold.

The objective is modest. Yet this theorem asserts that no way can be found to always assemble information from the subsystems to achieve the objective of the full system. Thus, Theorem 1 manifests the system conundrum where “the whole can differ from its parts.” [A slightly stronger version of Theorem 1 is proved in Chap. 6 of (Saari, 2018).]

To establish that Arrow’s theorem is a special case of Theorem 1, note that conditions 1 and 2 are the same for both results. Arrow imposes a Pareto condition whereby if all sources rank a pair in the same strict (i.e., no ties) manner, then that unanimous choice is the pair’s ranking. The Pareto condition, then, is a very special case of 4a; it specifies a particular way to ensure that each pair has non-constant outcomes. There are, of course, many alternative choices. Arrow’s “no dictator” condition is a special case of 4b.

What remains is Arrow’s IIA (Independence of Irrelevant Alternatives); it asserts that if all sources rank a particular pair in the same way for any two profiles, the pair’s outcome remains unchanged. As shown below (Theorem 2), if a decision rule satisfies IIA, it can be expressed as a collection of independent paired comparisons; thus IIA satisfies #3.

To illustrate with the pair $\{A_1, A_2\}$ (underlined to assist comparisons), each source has the same $\{A_1, A_2\}$ ranking in the following two profiles

(2)

If the decision function F satisfies IIA for the $\{A_1, A_2\}$ pair, then both profiles must have the same $\{A_1, A_2\}$ ranking, perhaps

$$\begin{aligned} F({\mathbf {p}}_1) = {\underline{\mathbf {A}}}_1\succ A_4 \succ A_3 \succ A_5 \succ {\underline{\mathbf {A}}}_2, \quad F({\mathbf {p}}_2) = A_5\succ A_4\succ A_3 \succ {\underline{\mathbf {A}}}_1 \succ {\underline{\mathbf {A}}}_2. \end{aligned}$$

(3)

With this agreement, F defines a paired comparison rule for $\{A_1, A_2\}$ denoted by $g_{\{A_1, A_2\}}$. Namely, let $g_{\{A_1, A_2\}}({\mathbf {p}})$ be $F({\mathbf {p}})$’s ranking of the pair $\{A_1, A_2\}$. Thus, with Eq. 3,

$$\begin{aligned} g_{\{A_1, A_2\}}({\mathbf {p}}_1) = g_{\{A_1. A_2\}}({\mathbf {p}}_2) = A_1\succ A_2. \end{aligned}$$

(4)

Only profile information concerning $\{A_1, A_2\}$ rankings is used to define $g_{\{A_1, A_2\}}({\mathbf {p}})$, so it follows from Eq. 4 that this mapping can be re-expressed as

$$\begin{aligned} g_{\{A_1, A_2\}} \left( A_1\succ A_2, A_2\succ A_1, A_1\succ A_2 \right) = A_1\succ A_2, \end{aligned}$$

(5)

where whenever the first and third sources prefer $A_1\succ A_2$ and the second has $A_2\succ A_1$, the outcome must be $A_1\succ A_2.$ A general assertion follows.

Theorem 2

If a mapping F satisfies conditions 2, IIA, and ranks each pair, then, for each pair of alternatives, F defines a pairwise comparison rule where the outcome strictly depends on how each source ranks that pair. That is, IIA and #3 are equivalent.

The proof (Sect. 7) mimics the above discussion. Because Theorem 2 equates IIA and condition 3, Arrow’s theorem becomes a special case of Theorem 1.

An interesting consequence of Theorem 2 is how it identifies IIA’s main role to be a filter; it eliminates certain decision methods from consideration. (From a system perspective, it limits which systems are admissible.) In particular, if a decision rule fails to satisfy IIA, such as the plurality vote, this failure merely means that the rule cannot be described as a collection of independent paired comparison rules. By itself, this is not a negative feature. Instead, based on the following comments, it could be a positive one.

Because the IIA filter allows only paired comparison rules to be subject to the negative consequence of Arrow’s Theorem, rather than the traditional “with three or more alternatives, no rule is fair,” a more accurate representation of Arrow’s Theorem is that

“With three or more alternatives, no decision method based on a collection of independent paired comparison rules is fair.”

From a system’s perspective, Arrow’s theorem is a warning that there need not exist ways to determine the outcomes of independent subsystems (here, the pairs) that always are consistent with the objective of the whole. Beyond decision rules, expect similar negative assertions to arise should a system have a rich source of inputs along with a consistency condition on the “whole” that mandates how independent outcomes of the parts are related.

3 Connecting information

The source of “the parts do not agree with the whole” conclusion can be illustrated with Eq. 2 where the $A_1\succ A_2$ outcome is reasonable for ${\mathbf {p}}_1$, but questionable for ${\mathbf {p}}_2.$ Doubt about the ${\mathbf {p}}_2$ outcome has nothing to do with how each source ranks $\{A_1, A_2\}$ (it is the same in each profile), but how this pair is situated with respect to the other alternatives. Stated differently, the negative conclusion of Arrow’s result and Theorem 1 reflect the fact that each pair’s ranking is determined solely by the properties of the rule designed for that particular pair. As such, information coming from these subsystems need not adhere to the system’s requirements. In fact, condition 3 (or IIA) prohibits checking whether the subsystems’ (pairs’) outcomes agree with the system’s requirement (transitivity).

For an example, return to the above discussion of where to locate a plant. It could be that the status of taxes and the availability of land lead to the rankings Boston $\succ$ Chicago and Chicago $\succ$ Atlanta. The ranking of {Atlanta, Boston} is based on the ease of parking, where Atlanta $\succ$ Boston creates a cycle. The source of the problem is clear; each pairwise rule carefully makes a choice based on its specified responsibility. But there is nothing in these assignments to assure a transitive outcome.

The above holds even should the pairwise methods be designed to achieve excellence. Thus, a corollary of the above observation is the counterintuitive statement that

even imposing a high level of excellence in determining the outcome for each independent subsystem need not lead to an acceptable outcome for the full system.

Clearly, something other than achieving excellence in each subsystem’s outcome is involved. This underscores the need to discover whether the subsystems’ outcomes (here, pairs) can interact with one another in a manner that supports the system’s objective. The approach developed next assigns only those tasks to the subsystems where the outcomes will be consistent with the system’s objectives. (In general, this is difficult to do.)

3.1 The structure of pairs

Fundamentals that are known about the structure of the space of pairwise summation techniques (Saari, 2014) are expanded here. This structure holds independent of whether the ranking of pairs is determined by voting, decision rules, cost, size, or any other factor. After defining the space, a convenient way of computing is introduced.

Equation 1 objective is to describe the data (or preliminary paired comparison results) ${\mathbf {d}}$ as an orthogonal sum

$$\begin{aligned} {\mathbf {d}} = {\mathbf {d}}_{desired} + {\mathbf {d}}_{noise}. \end{aligned}$$

(6)

To achieve Eq. 6, the space of paired comparisons is orthogonally divided into a subspace where the pairs satisfy a strong form of transitivity (this assures satisfying the system’s objective of having transitive outcomes) and a subspace of cyclic behavior. It turns out that items from this second subspace create all of the ranking difficulties that can arise with paired comparison methods; they constitute the system’s error terms that force outcomes from the parts (the subsystems) to deviate from the full system’s transitivity requirement.

With $n\ge 3$ alternatives $\{A_1, A_2, \dots , A_n\}$, let $d_{i, j}$ be a numerical difference comparison between $A_i$ and $A_j$ where

$$\begin{aligned} d_{i, j} = -d_{j, i} \text { for all } i, j = 1, \dots , n, \text { so } d_{i,i}=0 \text { for all } i. \end{aligned}$$

(7)

The comparisons can be almost anything such as differences in costs of internet plans where $d_{i, j}$ is the monthly cost of plan $A_i$ minus that of plan $A_j$. Or, $d_{i, j}$ could the difference between the weights, or maybe the lengths, of objects $A_i$ and $A_j$; it could even be the clockwise angle between two vectors. In an election, a natural choice for $d_{i, j}$ is the difference between $A_i$’s and $A_j$’s tallies. Perhaps $d_{i, j}$ comes from a physics or chemistry experiment where it is the difference in temperatures of objects $A_i$ and $A_j$. Although the origin of the $d_{i, j}$ terms is immaterial as long as Eq. 7 is satisfied, it plays a role when evaluating conclusions; e.g., comparing costs of internet plans need not identify the optimal choice.

Thanks to Eq. 7, it suffices to know the ${n\atopwithdelims ()2} = \frac{n(n-1)}{2}$ independent $d_{i, j},$ $i<j$, values rather than all $n^2$ of them. Thus, the space of $d_{i, j}$ paired comparisons is identified with the $n\atopwithdelims ()2$-dimensional Euclidean space ${\mathbb {R}}^{n\atopwithdelims ()2}$. The $d_{i, j}$ values define the vector

$$\begin{aligned} {\mathbf {d}} = (d_{1, 2}, d_{1, 3}, \dots d_{1, n}; d_{2, 3}, \dots , d_{2, n}; d_{3, 4}, \dots ; d_{n-1, n}) \in {\mathbb {R}}^{n\atopwithdelims ()2}, \end{aligned}$$

(8)

where semicolons signal a change in the first listed alternative.

To motivate the next definition, recall how transitivity borrows the ordering properties of points on the line. For instance, should points satisfy $p_1>p_2$ and $p_2>p_3$, then $p_1>p_3$. Mimicking this relationship, transitivity requires that if $A_1\succ A_2$ and $A_2\succ A_3$, then $A_1\succ A_3$. In terms of $d_{i, j}$, if $d_{1, 2}>0$ and $d_{2, 3}>0$, then transitivity requires $d_{1, 3}>0$. A stronger concept of transitivity adopts the algebraic relationship of points on a line

$$\begin{aligned} (p_1-p_2) + (p_2-p_3) = (p_1-p_3). \end{aligned}$$

(9)

Definition 1

(Saari 2014) A vector ${\mathbf {d}}\in {\mathbb {R}}^{n\atopwithdelims ()2}$ is strongly transitive if each triplet of indices $\{i, j, k\}$ leads to the equality

$$\begin{aligned} d_{i, j} + d_{j, k} = d_{i, k}. \end{aligned}$$

(10)

.

The set of all strongly transitive vectors, denoted by ${\mathcal {ST}}^n,$ is the space of strongly transitive rankings.

The choices of comparing internet costs or weights of objects always are strongly transitive. But due to interaction effects, temperatures of pairs of objects in a chemistry experiment, or the angles between vectors in ${\mathbb {R}}^3$, need not satisfy this condition. For a voting example that fails the condition, suppose of 33 sources

$$ \begin{array} {lll} {\text { 6 prefer }}A_1\succ A_2\succ A_3, & 9 {\text { prefer }} A_1\succ A_3\succ A_2, &{} 1 {\text { prefers }} A_3\succ A_1\succ A_2, \\ 5 {\text { prefer }} A_3\succ A_2\succ A_1, &{} 2 {\text { prefer }} A_2\succ A_3\succ A_1, &{} 10 {\text { prefer }} A_2\succ A_1\succ A_3.\end{array} $$

(11)

The $\{A_1, A_2\}$ pairwise vote is $A_2\succ A_1$ with a 17:16 tally, the $\{A_2, A_3\}$ outcome of $A_2\succ A_3$ has tally 18:15, and the $\{A_1, A_3\}$ outcome of $A_1\succ A_3$ has tally 25:8. Trivially, the values

$$\begin{aligned} d_{1, 2} = 16-17=-1, \, d_{2, 3} = 18-15= 3, \, d_{1, 3} = 25-8=17 \end{aligned}$$

(12)

cannot satisfy the strong transitivity of Eq. 10 even though the outcome is transitive.

Any paired comparison decision tool that allows non-transitive outcomes has examples that violate strong transitivity. A simple illustration with eight sources has 4 preferring $A_1\succ A_2\succ A_3,$ 1 preferring $A_2\succ A_3\succ A_1,$ 2 preferring $A_3\succ A_2\succ A_1$, and 1 preferring $A_3\succ A_1\succ A_2$. The $A_1\succ A_2$ and $A_2\succ A_3$ outcomes both have a 5:3 tally. But the tied $A_1\sim A_3$ vote with tally 4:4 violates transitivity. Here $d_{1, 2} = 5-3=2, d_{2, 3} = 2,$ but $d_{1, 3} = 0,$ which, because $2+2 \ne 0$, fails the strong transitivity condition.

The structure of this space ${\mathcal {ST}}^n$ is captured by the following definition:

Definition 2

For each $i=1, \dots , n$, let vector ${{\mathbf {B}}}_{i} \in {{\mathbb {R}}}^{n\atopwithdelims ()2}$ be where $d_{i,j} = 1$ (so $d_{j, i} = -1$) for $j\ne i$, $j=1, \dots , n$, and $d_{k,j} = 0$ if $k, j\ne i.$

Thus, for alternative $A_j$, the ${\mathbf {B}}_j$ nonzero components occur only when $A_j$ is compared with any other alternative, and the $d_{j, i} =1$ value favors $A_j$. For $n=4$, ${\mathbf {B}}_1 = (1, 1, 1; 0, 0; 0), {\mathbf {B}}_2=(-1, 0, 0; 1, 1; 0), {\mathbf {B}}_3=(0, -1, 0; -1, 0; 1); {\mathbf {B}}_4=(0, 0, -1; 0, -1; -1).$ Notice that $\sum _{j=1}^4 {\mathbf {B}}_j={\mathbf {0}} = (0, 0, 0; 0, 0; 0) \in {\mathbb {R}}^{4\atopwithdelims ()2}.$ Each ${\mathbf {B}}_j$ is strongly transitive because $d_{j, k}=d_{j, s} =1,$ and $d_{k, s}=0$, so $d_{j,k}+d_{k, s} = d_{j, s}$ is satisfied.

Theorem 3

For $n\ge 3$, ${\mathcal {ST}}^n$ is a $(n-1)$-dimensional linear subspace of ${\mathbb {R}}^{n\atopwithdelims ()2}$ that is spanned by any $(n-1)$ of the $\{{\mathbf {B}}_i\}_{i=1}^n$ vectors.

According to Theorem 3, algebraic combinations of strongly transitive terms are strongly transitive. As properties of summing terms in ${\mathcal {ST}}^n$ resemble Eq. 9 addition, nothing goes wrong with ${\mathcal {ST}}^n$ terms. So, for decision methods based on algebraic combinations of $d_{i, j}$ values, nothing goes wrong with data ${\mathbf {d}} \in {\mathcal {ST}}^n$. Thus, ${\mathcal {ST}}^n$ is the sought after consistency space for transitivity. In turn, all terms causing system difficulties are orthogonal to this subspace.

3.2 Cyclic effects

Clearly, cycles of paired outcomes violate the system’s objective of transitivity. A longstanding mystery has been whether other effects exist. The answer, as developed next by determining the subspace orthogonal to ${\mathcal {ST}}^n$, is that cyclic terms are the sole cause of all pairwise ranking difficulties.

A typical example of a cycle is

$$\begin{aligned} A_1\succ A_4, \, A_4 \succ A_3, \, A_3\succ A_5, \; A_5\succ A_2, \, A_2\succ A_1, \end{aligned}$$

(13)

Using fixed $d_{i, j}$ differences, this cycle defines

$$\begin{aligned} d_{1, 4} = d_{4, 3} =d_{3, 5} =d_{5, 2} = d_{2, 1} = 1. \end{aligned}$$

(14)

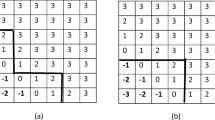
The Eq. 13 cycle subscripts can be identified with the list

$$\begin{aligned} \lambda ^* = (1, 4, 3, 5, 2), \end{aligned}$$

(15)

as specified on a loop or circle (Fig. 1a). Here, 1 is followed by 4, but, because of the loop structure, 1 follows 2 to reflect the concluding $A_2\succ A_1$ that completes the cycle. All cycles can be described with such lists.

Fig. 1

Division of a cycle

Definition 3

Let $\lambda = (i, j, k, \dots , s)$ be a list of at least three indices specified in a circular manner (so i is followed by j, and i follows s); each index appears only once. Define the cyclic vector ${{\mathbf {C}}}_{ \lambda } \in {{\mathbb {R}}}^{n\atopwithdelims ()2}$ as follows: If i and j are adjacent in the listing, where j immediately follows i, then $d_{i,j}=1$. If i and j are not adjacent, then $d_{i,j}=0.$ Vector ${{\mathbf {C}}}_{ \lambda }$ is the “cyclic direction defined by $\lambda$”.

With Eq. 15 and using $d_{i, j} = -d_{j, i}$ (so Eq. 14 becomes $d_{1, 4}=1, d_{3, 4}= -d_{4, 3} = -1, d_{3, 5}=1, d_{2, 5}= -d_{5, 2} = -1, d_{1, 2}= -d_{2, 1} = -1$), we have that

$$\begin{aligned} {{\mathbf {C}}}_{ \lambda ^*}= & {} (d_{1, 2}, d_{1, 3}, d_{1, 4}, d_{1, 5}; d_{2, 3}, d_{2, 4}, d_{2, 5}; d_{3, 4}, d_{3, 5}; d_{4, 5})\\= & {} (-1, 0, 1, 0; 0, 0, -1; -1, 1; 0). \end{aligned}$$

The analysis is significantly simplified by describing cycles in terms of triplets.

Proposition 1

Any ${{\mathbf {C}}}_{ \lambda }$ can be expressed as a sum of cyclic vectors defined by triplets.

To illustrate Prop. 1 with Fig. 1 and Eq. 15, first decompose the original $\lambda ^* = (1, 4, 3, 5, 2)$ (Fig. 1a) as a four cycle and a triplet by inserting an arrow (Fig. 1b) from node 3 to node 1; doing so defines the triplet (1, 4, 3). Next, an arrow from node 1 to node 3 defines the four-cycle (1, 3, 5, 2). This defines

$$\begin{aligned} {\mathbf {C}}_{1, 4, 3} + {\mathbf {C}}_{1, 3, 5, 2} = (0, \mathbf {-1}, 1, 0; 0, 0, 0; -1, 0; 0) + (-1, {\mathbf {1}}, 0, 0; 0, 0, -1; 0, 1; 0) = {\mathbf {C}}_{\lambda ^*}, \end{aligned}$$

where the arrows connecting 1 and 3 in opposite directions (the bold $d_{1, 3}$ variable) cancel in the sum. Next (Fig. 1c), divide (1, 3, 5, 2) into the triplets (1, 3, 5) and (1, 5, 2) to have

$$\begin{aligned} {\mathbf {C}}_{\lambda ^*} = {\mathbf {C}}_{1, 4, 3} + {\mathbf {C}}_{1, 3, 5} + {\mathbf {C}}_{1, 5, 2}. \end{aligned}$$

Of importance, this decomposition is not unique. While the above choice is centered about node 1, a decomposition centered about, say, node 4 would be

$$\begin{aligned} {\mathbf {C}}_{\lambda ^*} = {\mathbf {C}}_{4, 3, 5} + {\mathbf {C}}_{4, 5, 2} + {\mathbf {C}}_{4, 2, 1}. \end{aligned}$$

Theorem 4

For $n\ge 3$, let $\mathcal {CT}^n$ be the space of cyclic terms spanned by all cyclic vectors $\{{{\mathbf {C}}}_{ \lambda }\};$ $\mathcal {CT}^n$ is a linear subspace with dimension ${n\atopwithdelims ()2} - (n-1) = {{n-1}\atopwithdelims ()2}$ that is orthogonal to ${\mathcal {ST}}^n$. Thus, any ${\mathbf {d}}\in {\mathbb {R}}^{n\atopwithdelims ()2}$ can be uniquely expressed as an orthogonal sum

$$\begin{aligned} {\mathbf {d}} = {\mathbf {d}}_{ST} + {\mathbf {d}}_{CT} \end{aligned}$$

(16)

where ${\mathbf {d}}_{ST}\in \mathcal {ST}^n$ and ${\mathbf {d}}_{CT}\in \mathcal {CT}^n$.

The next assertion provides a convenient choice of bases for ${\mathcal {ST}}^n$ and $\mathcal {CT}^n$.

Corollary 1

For a vector ${\mathbf {d}}_{ST}\in {\mathcal {ST}}^n$, there are unique scalars $\beta _j$ so that ${\mathbf {d}}_{ST}$ can be uniquely expressed as

$$\begin{aligned} {\mathbf {d}}_{ST} = \sum _{j=1}^{n-1} \beta _{j}{\mathbf {B}}_{j} \end{aligned}$$

(17)

Each cyclic component of ${\mathbf {d}}_{CT}\in \mathcal {CT}^n$ that includes alternative $A_i$ can be uniquely represented, with scalars $\gamma _{j, k}$, by cyclic vectors with three indices as

$$\begin{aligned} {\mathbf {d}}_{CT} = \sum _{j, k \ne i, j < k} \gamma _{j, k} {\mathbf {C}}_{i, j, k}. \end{aligned}$$

(18)

There is no mystery about Eq. 18, it is just an analytic representation of Fig. 1c division of a cycle about node i. Comparing the $(n-1)$-dimension of ${\mathcal {ST}}^n$ with the ${n-1}\atopwithdelims ()2$ dimension of $\mathcal {CT}^n$ makes it clear that the space of problem-causing terms, $\mathcal {CT}^n$, quickly overwhelms ${\mathcal {ST}}^n$. As the $\mathcal {CT}^n$ dimension is $\frac{n-2}{2}$ times that of ${\mathcal {ST}}^n$, we must definitely anticipate cyclic error terms.

3.3 Computing

According to Theorem 4, paired comparison outcomes have an Eq. 1 orthogonal structure given by Eq. 16. This means that to eliminate system problems and the limitations of the decision methods discussed above, it suffices to project the paired conclusions defined by ${\mathbf {d}}$ into $\mathcal {ST}^n$. Doing so eliminates the troubling cyclic ${\mathbf {d}}_{CT}$ component, where it is arguable that the outcome should be a complete tie. A simple way to achieve this objective is, for each j, to compute the average $\{d_{j, i}\}$ value (where $d_{j, j}=0$).

Definition 4

For $n\ge 3$ and ${\mathbf {d}} \in {\mathbb {R}}^{n\atopwithdelims ()2}$, a Borda Rule assigns the number

$$\begin{aligned} b_j = \frac{1}{n} \sum _{i=1}^n d_{j, i}, \quad j=1, \dots , n. \end{aligned}$$

(19)

to each alternative. The BR ranking is determined by the $b_j$ values where larger is better.

To illustrate with Eq. 12 and its ${\mathbf {d}} = (d_{1, 2}, d_{1, 3}; d_{2, 3})= (-1, 17; 3),$ we have that $3b_1=d_{1, 2} + d_{1, 3} = -1+17=16, \, 3b_2= d_{2, 1} + d_{2, 3} = 1 + 3 = 4,$ and $3b_3= d_{3, 1} + d_{3, 2} = -17 -3 = -20$ leading to the BR ranking of $A_1\succ A_2\succ A_3.$

A way to interpret BR is that it does not treat the $d_{i, j}$ paired comparison outcomes as the final results of a decision analysis. Instead, BR treats them as the penultimate step. As the BR ranking is defined by scalar values (which are always transitive), BR avoids cycles. So the effect of the final BR step is to remove error-cyclic terms that violate the system’s objective of transitivity. Other BR properties are described next.

Theorem 5

If ${\mathbf {d}}\in \mathcal {CT}^n$, then all of its $b_j$ values equal zero. If ${\mathbf {d}}\in {\mathcal {ST}}^n$, then for each (i, j) pair,

$$\begin{aligned} d_{i, j} = (b_i-b_j). \end{aligned}$$

(20)

As ${\mathbf {d}} \in {\mathbb {R}}^{n\atopwithdelims ()2}$ is uniquely expressed as ${\mathbf {d}} = {\mathbf {d}}_{ST} + {\mathbf {d}}_{CT}$, where ${\mathbf {d}}_{ST} \in {\mathcal {ST}}^n, \, {\mathbf {d}}_{CT}\in \mathcal {CT}^n,$ the BR values and BR ranking of ${\mathbf {d}}$ are completely determined by the ${\mathbf {d}}_{ST}$ component. That is, the cyclic ${\mathbf {d}}_{CT}$ component does not influence, in any manner, the BR outcome.

According to Theorem 5, the projection of ${\mathbf {d}}$ to the transitive consistency space ${\mathcal {ST}}^n$ can be quickly determined from Eq. 20 and the Borda Rule (BR) outcome. This is because the linearity of addition requires

$$\begin{aligned} BR({\mathbf {d}}) = BR({\mathbf {d}}_{ST} + {\mathbf {d}}_{CT}) = BR({\mathbf {d}}_{ST}) + BR({\mathbf {d}}_{CT}) = BR({\mathbf {d}}_{ST}) \end{aligned}$$

and the $BR({\mathbf {d}}_{ST}) = BR({\mathbf {d}})$ values can be converted (by Eq. 20) to the ${\mathbf {d}}_{ST}$ values.

To illustrate with Eq. 12, rather than using linear algebra to project ${\mathbf {d}} = (-1, 17; 3)$ to ${\mathcal {ST}}^3$, with the above $b_1=\frac{16}{3}, b_2= \frac{4}{3}, b_3 = \frac{-20}{3}$ values, it is simpler to use Eq. 20 to obtain ${\mathbf {d}}_{ST} = (b_1-b_2, b_1-b_3; b_2-b_3) = (4, 12; 8).$ Indeed, $d_{1, 2} + d_{2, 3} = 4+8=d_{1, 3} = 12$, which verifies that ${\mathbf {d}}_{ST}$ is strongly transitive.

Because ${\mathbf {d}} = {\mathbf {d}}_{ST} + {\mathbf {d}}_{CT}$ and two of the vectors are known, it follows that

$$\begin{aligned} {\mathbf {d}}_{CT} = {\mathbf {d}} - {\mathbf {d}}_{ST}, \end{aligned}$$

(21)

which here is ${\mathbf {d}}_{CT} = (-1, 17; 3) - (4, 12; 8) = (-5, 5; -5) = -5(1, -1; 1) = -5{\mathbf {C}}_{1, 2, 3}.$ Again, it is arguable that the outcome for this cyclic ${\mathbf {C}}_{1, 2, 3}$ should be a complete tie.

It is interesting that, although ${\mathbf {d}} = (-1, 17; 3)$ is not strongly transitive (it includes cyclic terms), it defines the transitive rankings $A_2\succ A_1, A_2\succ A_3, A_1\succ A_3$ or $A_2\succ A_1\succ A_3.$ By beating all other alternatives, $A_2$ is called a Condorcet winner. The reason the Condorcet ($A_2$) and Borda ($A_1$) winners differ is strictly because the Condorcet winner is influenced by information that includes the cyclic error term ${\mathbf {d}}_{CT}$. Indeed, ${\mathbf {d}}_{CT}= 5(-1, 1; -1)$ is created by the profile ${\mathbf {p}}_{CT}$ where 5 sources have $A_2\succ A_1\succ A_3,$ five have $A_1\succ A_3\succ A_2$, and five have $A_3\succ A_2\succ A_1$, which creates the cycle $A_2\succ A_1, A_1\succ A_3, A_3\succ A_1$ (each with a 10:5 tally) where there is no optimal alternative.

In contrast, ${\mathbf {p}}_{ST}$ has the strongly transitive

$$ \begin{array} {lll} {\text { 6 prefer }}A_1\succ A_2\succ A_3, &{} 4 {\text { prefer }} A_1\succ A_3\succ A_2, \\ 1 {\text { prefer }} A_3\succ A_1\succ A_2, &{} 0 {\text { prefer }} A_3\succ A_2\succ A_1, \\ 2 {\text { prefer }} A_2\succ A_3\succ A_1, &{} 5 {\text { prefer }} A_2\succ A_1\succ A_3\end{array} $$

with the $A_1\succ A_2\succ A_3$ conclusion. Thus (as always true), the cyclic noise component, where no alternative is favored, is what causes the Condorcet and Borda winners to differ.

A way to think about this is that there are two sources of information; ${\mathbf {p}}_{ST}$ and ${\mathbf {p}}_{CT}$. The first group has a well defined ranking outcome. Because it is arguable that the second group does not favor any alternative, combining the two sources ${\mathbf {p}}_{ST} + {\mathbf {p}}_{CT}$ may seem to be innocuous. It is not; doing so changes the outcome.

A common difficulty in experiments is if some $d_{i, j}$ data values for certain pairs are close to each other. Such settings can raise doubt about the selection of an optimal choice. Suppose differences between temperatures in a chemistry experiment have $d_{1, 2} = -1, d_{2, 3} =3, d_{1, 3} = 9;$ although $A_2$ is warmer than $A_1$ or $A_3$, the small $d_{1, 2} = -1$ value can raise doubts about $A_2$. The Borda scores are $3b_1= -1+9 = 8, 3b_2 = 1+3=4, 3b_3=-3-9=-12,$ where $A_1$, not $A_2$, is the Borda winner. This difference arises because values supporting $A_2$, which are not as decisive as those supporting $A_1$, reflect cyclic noise in the data generated by a component in which “no alternative is better.” As shown next, this is a general phenomenon. (Equation 22 can be extended to all $n\ge 3$, but the expression is messy.)

Theorem 6

For $n=3$, if the Borda winner $A_1$ and the Condorcet winner $A_2$ disagree, then ${\mathbf {d}}$ is not strongly transitive (it includes cyclic components). The Borda ranking for ${\mathbf {d}}$ is $A_1\succ A_2\succ A_3$ (so the Condorcet winner is not bottom ranked), the Borda difference $b_1-b_2>0$ is smaller than $b_2-b_3>0$, and the cyclic term, is $c(1, -1; 1) = c{\mathbf {C}}_{1, 2, 3}$ where

$$\begin{aligned} (b_1-b_2)< -c < (b_2-b_3). \end{aligned}$$

(22)

For $n\ge 3,$ the Condorcet winner never is Borda bottom ranked; if there is a Condorcet loser (an alternative that loses all paired comparisons), the Condorcet winner is Borda ranked over the Condorcet loser.

The message: to have consistent, transitive outcomes, use the Borda Rule. But are there other approaches? The next theorem asserts that any such choice is equivalent to the Borda Rule. One possibility is the Borda Count, which is where a n-candidate ballot is tallied by assigning $n-j$ points to the $j^{th}$ positioned candidate. As another example, the Kruskal–Wallis procedure from non-parametric statistics is equivalent to the Borda Count (Haunsperger, 1989) and hence to the Borda Rule.³

Theorem 7

Any linear method of removing the error term of ${\mathbf {d}}$ to obtain ${\mathbf {d}}_{ST}$ is equivalent to the Borda rule. If each $d_{i, j}$ value is the difference of $A_i$’s and $A_j$’s majority vote tallies coming from $a\ge 2$ strictly transitive rankings of the $n\ge 3$ alternatives $\{A_1, \dots , A_n\}$, then $A_j$’s Borda Count tally, denoted by $\tau _j$, and Borda Rule value $b_j$ satisfy

$$\begin{aligned} 2\tau _j = (n-1)a + nb_j, \quad j=1, \dots , n. \end{aligned}$$

(23)

To illustrate Eq. 23 with Eq. 11, it follows from the above computations that $n=3$, $a=33$ (the number of sources), $3b_1=16, 3b_2= 4, 3b_3= -20$, while $\tau _1= 41, \tau _2= 35, \tau _3 = 23.$ Elementary computations prove that these values satisfy Eq. 23.

4 Modifying methods

Knowing what causes paired comparison problems identifies how to modify decision approaches to yield more acceptable conclusions. As developed in the previous section, the “transitive consistency space” is the strongly transitive ${\mathcal {ST}}^n$.

The projection of ${\mathbf {d}}$ to $\mathcal {ST}^n$ is done as follows:

• Find each pair’s pairwise $d_{i, j}$ value; e.g., for voting, compute each pair’s majority vote difference.

• Compute each alternative’s Borda tally (Eq. 19).

• Use these Borda tallies to compute the differences in tallies according to Eq. 20.

The success of this approach is captured by the following theorem, which asserts that by treating paired comparison outcomes as the penultimate step in a decision analysis, where the final ranking is determined by the above projection approach, the negativity of Arrow’s Theorem is avoided. That is, from a system perspective, the whole and the sum of parts agree. This holds for whatever methods are used to compute the paired outcomes.

Theorem 8

For $n\ge 3$ alternatives and $a\ge 2$ sources of inputs, the above projection approach defines pairwise rankings that always satisfies the four conditions of Sect. 2. The ranking coming from these tallies agrees with the BR ranking.

Stated differently, Arrow’s result is totally caused by the subsystem information where cyclic combinations compromise the system’s objective of transitivity. This makes sense; data with cyclic components must be expected to compromise the goal of transitivity. In contrast, the ${\mathcal {ST}}^n$ terms ensure agreement between the system and the subsystems.

4.1 Pugh matrix

According to the above, anticipate difficulties with any decision method based on paired comparisons where the pairs are separately analyzed. (This separation causes the system’s requirements to be ignored.) This message can be illustrated with the Pugh matrix (Pugh, 1991) approach, where the paired comparisons are made with respect to a base alternative. Even if the outcome for each pair is determined in a sound and excellent manner, the final conclusion could violate excellence.

As a five alternative example, suppose this approach judges the status quo $A_2$ as being better than $A_3, A_4, A_5$; only $A_1$ is better than $A_2.$ Presumably, this means that $A_1$ is the superior choice. But applying the Pugh approach to the same data where the supposedly superior $A_1$ now is the base of comparison, while $A_1$ remains better than $A_2$, the previously “inferior” $A_3, A_4, A_5$ could be judged as being better than the supposedly superior $A_1$!

A supporting example is

(24)

The paired outcomes involving the status quo $A_2$ are $A_1\succ A_2, A_2\succ A_3, A_2\succ A_4, A_2\succ A_5,$ so $A_2$ is beaten only by $A_1$. That $A_1$ is not the superior choice follows from the paired outcomes involving $A_1$, which are $A_1\succ A_2, A_3\succ A_1, A_4\succ A_1, A_5\succ A_1.$ So, $A_1$ is not the superior choice as it beats only $A_2.$ Finally $A_3\succ A_4, A_3\succ A_5, A_4\succ A_5.$

This difficulty arises because valued information is ignored; e.g., when $A_2$ is the basis of comparison, $A_1$ is not compared with any other alternative. Consequently, any assertion that $A_1$ is superior is dubious; it is based on a tacit, unsupported assumption that the system has transitive outcomes. This leads to a second problem; cyclic error terms introduce difficulties and the cycle here is $A_1\succ A_2, A_2\succ A_3, A_3\succ A_4, A_4\succ A_5, A_5\succ A_1.$ Which alternative should be chosen?

A resolution follows from Sect. 3 and Theorem 7: eliminate the problem-causing system error terms. For each criterion, rank all n alternatives where the base choice (e.g., the status quo) does not have a special status. According to Theorem 7, the Borda Count ranking of the alternatives captures what would happen should the paired comparisons be projected to ${\mathcal {ST}}^n$ to eliminate the system’s cyclic error terms. So, for each criterion’s ranking of the n choices, assign the scores of $(n-j)$ to the $j^{th}$ ranked alternative. Sum each alternative’s assigned values, and use them to rank the alternatives. Doing so for Eq. 24, where $A_2$ is the status quo, leads to the following:

(25)

The $A_3\succ A_2\succ A_4\succ A_1\succ A_5$ outcome indicates that only $A_3$ is better than the status quo $A_2$. This approach eliminates the above concern about missing information and the worry about how hidden cyclic components can distort answers.

As an answer is given, there is no reason to find ${\mathbf {d}}_{ST}$. But if there is a need, use Sect. 3 machinery to compute the $b_j$ values, which from Eq. 23 are $5b_j = 2\tau _j - 12$, or $5b_1= 2, 5b_2=2, 5b_3=6, 5b_4=0, 5b_5=-6.$ Indeed, if $A_j\succ A_k$ in this Eq. 25 outcome, we know (e.g., Theorem 5) that the outcome for that part of ${\mathbf {d}}_{ST}$ has $d_{j, k}>0$. And so, finally, the whole and parts agree.

4.2 Rank reversal

A stronger comment about agreement between the pairs and whole comes by explaining how dropping alternatives can cause a method to change, even reverse the ranking of the remaining alternatives. As shown next, again, this problem is caused by the cyclic terms.

Theorem 9

If ${\mathbf {d}}\in {\mathcal {ST}}^n$, and if ${\mathcal {P}}_k$ is a projection mapping that drops alternative $A_k$, then the ${\mathcal {P}}_k({\mathbf {d}})$ is strongly transitive and the ranking of the $(n-1)$ alternatives in ${\mathcal {P}}_k({\mathbf {d}})$ agrees with the ranking of the same alternatives in ${\mathbf {d}}.$ But if ${\mathbf {d}}\in \mathcal {CT}^n$ and $A_k$ is in a cycle of ${\mathbf {d}}$, then ${\mathcal {P}}_k({\mathbf {d}})$ is the sum of nonzero terms in $\mathcal {ST}^{n-1}$ and $\mathcal {CT}^{n-1}$.

To illustrate Theorem 9 with $n=4$, dropping $A_4$ corresponds to ignoring all $d_{j, 4}$ terms in ${\mathbf {d}}$. If ${\mathbf {d}}\in {\mathcal {ST}}^4$, then ${\mathbf {d}} = \sum _{j=1}^3 \beta _j {\mathbf {B}}_j$ (from Eq. 17). Dropping the $d_{j, 4}$ components from ${\mathbf {B}}_j\in {\mathcal {ST}}^4$ defines ${\mathbf {B}}_j\in {\mathcal {ST}}^3.$ Consequently, the ${\mathcal {P}}_4({\mathbf {d}})$ outcome remains the same $\sum _{j=1}^3 \beta _j {\mathbf {B}}_j$ but now in ${\mathcal {ST}}^3$.

To illustrate the last sentence of Theorem 9, consider ${\mathbf {C}}_{\{1, 2, 3\}} \in \mathcal {CT}^4$. All $d_{j, 4}$ terms in ${\mathbf {C}}_{\{1, 2, 3\}}$ are zero, so ${\mathcal {P}}_4( {\mathbf {C}}_{\{1, 2, 3\}}) = {\mathbf {C}}_{\{1, 2, 3\}} \in \mathcal {CT}^3;$ there is no change. But ${\mathbf {C}}_{\{1, 2, 3, 4\}} = (1, 0, -1; 1, 0; 1)$ involves $A_4$ and defines the cycle $A_1\succ A_2, A_2\succ A_3, A_3\succ A_4, A_4\succ A_1.$ Dropping $d_{j, 4}$ values from ${\mathbf {C}}_{\{1, 2, 3, 4\}}$ defines $(1, 0; 1)= [\frac{2}{3}{\mathbf {B}}_1 + \frac{1}{3}{\mathbf {B}}_2] + [\frac{2}{3}{\mathbf {C}}_{\{1.2, 3\}}]$, where the first bracketed component is a new ${\mathcal {ST}}^3$ term defining $A_1\succ A_2\succ A_3$, and the second ${\mathbf {C}}_{\{1.2, 3\}}\in \mathcal {CT}^3$ defines the $A_1\succ A_2, A_2\succ A_3, A_3\succ A_1$ cycle. This outcome is consistent with what happens by dropping $A_4$ from the ${\mathbf {C}}_{\{1, 2, 3, 4\}}$ rankings to define $A_1\succ A_2, A_2\succ A_3$.

To see how this behavior can cause changes in outcomes, the BR ranking of ${\mathbf {C}}_{\{1, 2, 3, 4\}}$ is a complete tie, while the BR ranking of ${\mathcal {P}}_4({\mathbf {C}}_{\{1, 2, 3, 4\}})$ is $A_1\succ A_2\succ A_3$, which manifests the strongly transitive term created from the cycle by dropping $A_4$. So, the BR ranking of ${\mathbf {d}} = 3{\mathbf {B}}_3 + 2{\mathbf {B}}_2 + {\mathbf {B}}_1 + 12 {\mathbf {C}}_{\{1, 2, 3, 4\}}$ is $A_3\succ A_2\succ A_1\succ A_4$, but because of the strong cyclic component, the BR ranking of ${\mathcal {P}}_4({\mathbf {d}})$ is $A_1\succ A_2\succ A_3.$

It follows from Theorem 9 that the only way to create a reversal example with a given method is to create a profile with appropriate cyclic terms. By dropping an alternative, the cyclic terms alter the strongly transitive portion of a profile, which, with a careful construction, allows almost any ranking to emerge. This means, for instance, that the Kruskal–Wallis approach from nonparametric statistics can suffer these problems.

The construction of examples follows the lead of the above example. To suggest what can be done, suppose the Kruskal–Wallis ranking for ${\mathbf {d}}$ is $A_3\succ A_2\succ A_1\succ A_4$ and we want to have an example where, by dropping $A_4$, the new ranking is $A_1\succ A_2\succ A_3.$ As above, just add to ${\mathbf {d}}$ a sufficiently large multiple of ${\mathbf {C}}_{\{1, 2, 3, 4\}}$. [To see how to design raw data values from ${\mathbf {d}}$, see (Bargagliotti and Saari 2010).]

A way to underscore the importance of Theorem 9 is to recognize that IIA in Arrow’s Theorem, or assumption 3 in Theorem 1, are projections of data to pairs. Slight extensions of Theorem 9 (e.g., consider all ${\mathcal {P}}_k$ projections, $k=1, \dots , n$) lead to Arrow-type conclusions based not on pairs, but on triplets, or on quadruples, or .... This means that subsystem-system difficulties are far more pervasive than suggested by Theorem 1 and Arrow’s result.

The continuing message is that the myriad of difficulties experienced in this wide general area, whether it be Arrow’s Theorem, problems in decision or statistical methods, are strictly caused by cyclic terms. To avoid problems, all analysis should strictly depend upon a profile’s strongly transitive portion; that is, remove this cyclic virus, retain only portions of the profile that are compatible with the objective of the system. From a systems perspective, expect independent subsystems to admit features that counter the systems’ objective,. They must be identified and removed.

5 Ratio scale methods

The ratio scaled comparison techniques constitute another important class of paired decision methods. Here, a comparison of $A_i$ and $A_j$ is represented by a value $a_{i, j}>0$, which is intended to be the multiple of how much $A_i$ is better than $A_j$. The defining comparisons for the n alternatives $\{A_1, A_2, \dots , A_n\}$ are the positive values

$$\begin{aligned} a_{i, j}>0 \text { where } a_{j, i} = \frac{1}{a_{i, j}} \text { for each } i, j, \text { so } a_{i, i}=1 \text { for each } i. \end{aligned}$$

(26)

According to Eq. 26 (and similar to Eq. 8), all information about the $n^2$ paired comparisons is contained in the $n\atopwithdelims ()2$-dimensional vector of positive entries

$$\begin{aligned} {\mathbf {a}} = (a_{1, 2}, a_{1, 3}, \dots , a_{1, n}; a_{2, 3}, \dots a_{2, n}; a_{3, 4}, \dots ; a_{n-1, n}) \in {\mathbb {R}}^{n\atopwithdelims ()2}_{+}. \end{aligned}$$

(27)

The system goal is to rank the n alternatives by using information from the subsystems—the $a_{i, j}$ paired comparisons. Because $a_{i, j}$ is a multiple of how much better $A_i$ is over $A_j$, this suggests there are scalar weights $w_j$ for $A_j$, $j=1, \dots , n$, that define the $a_{i, j}$ values. These desired $w_j$ weights exist if and only if they satisfy the consistency condition

$$\begin{aligned} a_{i, j} = \frac{w_i}{w_j} \text { for all pairs } (i, j). \end{aligned}$$

(28)

Of importance is the following known result (which is proved for completeness).

Theorem 10

Equation 28is true for all pairs if and only if

$$\begin{aligned} a_{i, j}a_{j, k} = a_{i, j} \text { for all triplets } (i, j, k). \end{aligned}$$

(29)

Proof

To prove the statement in one direction, if weights can be found where Eq. 28 always holds, then

$$\begin{aligned} a_{i, j}a_{j, k} = \left( \frac{w_i}{w_j}\right) \left( \frac{w_j}{w_k}\right) = \frac{w_i}{w_k} = a_{i, k}, \end{aligned}$$

which is the desired Eq. 29.

To prove the converse, because only $a_{i, j}$ values are known, candidate choices for the $w_j$ weights must be found. Choose an alternative as the basis of comparison, say $A_n$, and select a positive value for $w_n$. Define $w_j$, the candidate weight for $A_j$, to be

$$\begin{aligned} w_j= a_{j, n}w_n \text { or } a_{j, n} =\frac{w_j}{w_n}, \quad j=1, \dots , n. \end{aligned}$$

(30)

If Eq. 29 always holds, then $a_{i, j} = a_{i, n}a_{n, j} = a_{i, n} \frac{1}{a_{j, n}} = (\frac{w_i}{w_n})(\frac{w_n}{w_j}) = \frac{w_i}{w_j}$, which is Eq. 28. The selected $w_n>0$ value does not matter because for any scalar $\mu >0$, the $a_{i, j}$ values defined by $\{w_1, w_2, \dots , w_n\}$ are those given by $\{\mu w_1,\mu w_2, \dots , \mu w_n\}.$ $\square$

With this Eq. 29 structure, the ideal situation is if ${\mathbf {a}}$ belongs to the consistency space

$$\begin{aligned} \mathcal {CS}^n = \left\{ {\mathbf {a}} \in {\mathbb {R}}_+^{n\atopwithdelims ()2} \, | \, a_{i, j} a_{j, k} = a_{i, k} \, \text { for all triplets } (i, j, k)\right\} . \end{aligned}$$

(31)

Properties of $\mathcal {CS}^n$ follow from Eq. 29, which requires each $a_{j, k} = a_{j, 1}a_{1, k}$. This means that all $a_{j, k}$ values can be determined by Eq. 29 and the $(n-1)$ values of $a_{1, j}$ $j=2, \dots , n$. Thus, $\mathcal {CS}^n$ is a smooth $(n-1)$-dimensional manifold. If ${\mathbf {a}} \in \mathcal {CS}^n$, then Eq. 30 can be used to assign a weight $w_j$ to alternative $A_j, j=1, \dots , n$. $\square$

5.1 A difficulty

In general, ${\mathbf {a}} \not \in \mathcal {CS}^n$, which requires removing ${\mathbf {a}}$’s error component. As this error term had not been identified, methods were developed to adjust the $w_j$ and/or $\{a_{i, j}\}$ values. A natural choice is to project ${\mathbf {a}}$ to the space $\mathcal {CS}^n$; e.g., find the $\mathcal {CS}^n$ point closest to ${\mathbf {a}}$. But this approach carries the tacit assumption that ${\mathbf {a}}$ has an Eq. 1 form. Moreover, $\mathcal {CS}^n$ is a nonlinear submanifold of ${\mathbb {R}}^{n\atopwithdelims ()2}$. The nonlinearity follows immediately by finding all $a_{1, j}$ and $a_{j, 2}$ values so that $a_{1, j}a_{j, 2}=a_{1, 2}=1,$ which has the hyperbolic equation $xy=1$ form; e.g., see Fig. 2.

Fig. 2

The consistency space

The reality that projections can introduce new types of errors is illustrated in Fig. 2 where the dark hyperbola represents the space $\mathcal {CS}^n$. The nonlinearity of $\mathcal {CS}^n$ makes it reasonable to expect that a decomposition of ${\mathbf {a}}$ is given by the light curve passing through ${\mathbf {a}}$ and the $\mathcal {CS}^n$. That is, the curve constitutes error terms; where the curve passes through $\mathcal {CS}^n$ (point ${\mathbf {b}}$ in the figure) is the corrected form of ${\mathbf {a}}$. The dashed arrow, which represents a projection, defines ${\mathbf {c}} \in \mathcal {CS}^n$. If the above scenario is correct (as shown in Theorem 13, it is), then standard projection approaches must introduce new errors, which, in Fig. 2, is the ${\mathbf {c}}-{\mathbf {b}}$ difference.

Certain methods harness the power of the Perron-Frobenius result (from linear algebra) that a nonsingular $n\times n$ matrix with positive entries has only one eigenvector with positive entries. The AHP approach, promoted by Saaty (Saaty, 1977; Saaty & Alexander, 1989), uses the matrix $((a_{i, j}))$ and defines $w_j$ to be this eigenvector’s $j^{th}$ component. A linear algebra exercise shows that these weights satisfy Eq. 28 if and only if ${\mathbf {a}} \in \mathcal {CS}^n.$ Otherwise, adjustments are needed.

The geometric mean technique developed by Crawford and Williams (Crawford & Williams, 1985; Crawford, 1987), defines

$$\begin{aligned} w_j = (a_{j, 1} a_{j, 2} \dots a_{j, n})^{\frac{1}{n}}, \, j=1, \dots , n, \end{aligned}$$

(32)

so the $w_j$ weight assigned to $A_j$ is the product of all $a_{j, k}$ multiples raised to the $\frac{1}{n}$ power. While these weights do not satisfy Eq. 28 if ${\mathbf {a}}\not \in \mathcal {CS}^n$, by replacing each $a_{j,k}$ with $\frac{w_j}{w_k}$, the Eq. 29 consistency equation holds. This means that this technique does convert an ${\mathbf {a}}\not \in \mathcal {CS}^n$ into a $\mathcal {CS}^n$ point. But, is it the desired point? While numerical experiments suggest this geometric mean approach is better than several others [e.g., (Colany & Kress, 1993)], to the best of my knowledge, there has not been a theoretical justification. An argument is in Sect. 5.2.

5.2 A resolution

The error term of ${\mathbf {a}}\not \in \mathcal {CS}^n$ is what causes the system’s “parts and whole” problem. Resolving the difficulty is simple: transfer ${\mathbf {a}}$ to the space of paired comparisons that use summations (Sect. 3) where answers are now known.

To do so, identify each ${\mathbf {a}} \in {\mathbb {R}}_+^{n \atopwithdelims ()2}$ with a unique ${\mathbf {d}} \in {\mathbb {R}}^{n \atopwithdelims ()2}$ (Eq. 8) through the mapping $\ln : {\mathbb {R}}^{n\atopwithdelims ()2}_+ \rightarrow {\mathbb {R}}^{n\atopwithdelims ()2}$ defined as

$$\begin{aligned} {\mathbf {d}} = \ln ({\mathbf {a}}) = (\ln (a_{1, 2}), \dots , \ln (a_{1, n}); \dots ; \ln (a_{n-1, n})), \end{aligned}$$

(33)

The inverse of this diffeomorphism is the exponential mapping $e: {\mathbb {R}}^{n\atopwithdelims ()2} \rightarrow {\mathbb {R}}^{n\atopwithdelims ()2}_+$ where

$$\begin{aligned} e^{{\mathbf {d}}} = (e^{d_{1, 2}}, e^{d_{1, 3}}, \dots , e^{d_{1, n}}; e^{d_{2, 3}}, \dots ; e^{d_{n-1, n}}). \end{aligned}$$

(34)

Equation 26 defining condition of $a_{i, j} = \frac{1}{a_{j, i}}$ becomes, with the logarithm mapping, $\ln (a_{i, j}) = -\ln (a_{j, i});$ this is the required Eq. 7. Conversely, the $d_{i, j} =-d_{j, i}$ expression becomes $e^{d_{i, j}} =\frac{1}{e^{d_{j, i}}};$ this is the required Eq. 26 condition.

Thanks to these diffeomorphisms, finding ${\mathbf {a}}$’s error component reduces to finding the error component of $\ln ({\mathbf {a}})$ where Sect. 3 structure provides answers. The next statement is central to this discussion.

Theorem 11

For $n\ge 3$, the subspaces ${\mathcal {ST}}^n$ and $\mathcal {CS}^n$ are diffeomorphic; the Borda Rule (Eq. 19) and the geometric mean approach (Eq. 32) are equivalent.

The last sentence means that an error free approach to rank the alternatives in a ratio scale space is the geometric mean approach. The theorem also means that all of the above Sects. 3, 4 results have parallel conclusions for the multiplicative approach.

Proof

What mainly needs to be shown is that ${\mathcal {ST}}^n$ and $\mathcal {CS}^n$ are mapped onto each other with the indicated mappings. The $\mathcal {CS}^n$ space requires all triplets to satisfy Eq. 31. With the logarithm mapping, the condition $a_{i, j}a_{j, k}=a_{i, k}$ becomes $\ln (a_{i, j})+\ln (a_{j, k}) = \ln (a_{i, k})$, which is the strongly transitive condition (Def. 1). Thus, each ${\mathbf {a}}\in \mathcal {CS}^n$ is mapped to a unique ${\mathbf {d}} \in {\mathcal {ST}}^n$. Conversely, if ${\mathbf {d}}\in {\mathcal {ST}}^n,$ then for all triplets $d_{i, j}+d_{j, k} = d_{i, k}$, which under the exponential mapping becomes $e^{d_{i, j}+d_{j, k}} =e^{d_{i, k}}.$ Because $e^{d_{i, j}+d_{j, k}}= e^{d_{i, j}}e^{d_{j, k}}$, every ${\mathbf {d}}\in {\mathcal {ST}}^n$ is mapped to a unique ${\mathbf {a}} \in \mathcal {CS}^n$.

As for the geometric mean technique, $\ln (a_{j, 1} a_{j, 2} \dots a_{j, n})^{\frac{1}{n}} = \frac{1}{n}\sum _{i=1}^n\ln (a_{j, i}),$ which is the average $\{\ln (a_{j, k})\}$ value, or the Borda Rule value for alternative $A_j$. Conversely, $e^{\frac{1}{n} \sum _{k=1}^nd_{j, k}} = \left[ e^{d_{j, 1}} e^{d_{j, 2}} \dots e^{d_{j, n}} \right] ^{\frac{1}{n}}$, so the BR is mapped to the geometric mean rule. $\square$

The structures of $\mathcal {CS}^n$ and error terms follow by using the exponential mapping to transfer the ${\mathbf {B}}_j$ and ${\mathbf {C}}_{i, j, k}$ basis vectors of Corollary 1 to this ratio scale space. In doing so, component wise addition in the pairwise summation space transfers to coordinate wise multiplication in the ratio scale space; the vector ${\mathbf {0}} \in {\mathcal {ST}}^n$ is mapped to the vector ${\mathbf {e}} = (1, \dots , 1; 1, 1 \dots ; 1) \in \mathcal {CS}^n$ that has unity for each component. For notation, let ${\mathbf {a}}_{ST}$ and ${\mathbf {a}}_{CT}$ represent, respectively, the image of strongly transitive and cyclic terms; the first provide a basis for $\mathcal {CS}^n$ and the second for error terms.

Definition 5

For ${\mathbf {a}}, {\mathbf {b}} \in {\mathbb {R}}_+^{n\atopwithdelims ()2}$, define ${\mathbf {a}} \circ {\mathbf {b}}$ to be

$$\begin{aligned} {\mathbf {a}} \circ {\mathbf {b}} = (a_{1, 2}b_{1, 2}, a_{1, 3}b_{1, 3}, \dots , a_{1, n}b_{1, n}; \dots ; a_{n-1, n}b_{n-1, n}). \end{aligned}$$

(35)

Represent the product ${\mathbf {c}}_1\circ {\mathbf {c}}_2 \circ \dots \circ {\mathbf {c}}_k$ by $O_{j=1}^k {\mathbf {c}}_j$

For each $j=1, \dots , n-1$, let ${\mathbf {a}}_{ST}(\delta _j)$ be a vector such that each $a_{j, k}$ component equals ${\delta _j}$ and all other components equal unity. Similarly, if the error component involves $A_i$, let ${\mathbf {a}}_{CT}(\gamma _{j, k})$ be the vector where the $a_{i, j}$ and $a_{j, k}$ components equal ${\gamma _{j, k}}$, and the $a_{i, k}$ component equals $\frac{1}{{\gamma _{j, k}}}$; all others equal unity.

To illustrate with $n=4$, vector $2{\mathbf {B}}_2=(-2, 0, 0; 2, 2; 0)\in {\mathcal {ST}}^4$ is transferred to ${\mathbf {a}}_{ST}(\delta _2) = (\frac{1}{\delta _2}, 1, 1; {\delta _2}, {\delta _2}; 1) \in \mathcal {CS}^4$ where $\delta _2 = e^2$. The nonlinearity in the ranked comparison space is captured by the form of ${\mathbf {a}}_{ST}(\delta _2)$ where a term (here, $\delta _2$) is the value of some component in the vector but the denominator in another component. In a similar manner the $3{\mathbf {C}}_{1, 2, 3} = (3, -3, 0; 3, 0; 0)$ cyclic term involves $A_1$ so it is mapped to the ${\mathbf {a}}_{CT}(\gamma _{2, 3}) = ({\gamma _{2, 3}}, \frac{1}{ {\gamma _{2, 3}}}, 1; {\gamma _{2, 3}}, 1; 1)$ error term where $\gamma _{2, 3} = e^3.$ By letting the value of $\gamma _{2, 3}$ vary, it becomes clear that an error term has the nonlinear form suggested by Fig. 2.

Theorem 12

Vector ${\mathbf {a}}\in {\mathbb {R}}^{n\atopwithdelims ()2}_+$ can be uniquely expressed as ${\mathbf {a}} = {\mathbf {a}}_{ST} \circ {\mathbf {a}}_{CT}$ where ${\mathbf {a}}_{ST}\in \mathcal {CS}^n$ and all n of the geometric means of ${\mathbf {a}}_{CT}$ agree. If $A_i$ is involved in the error term, the vectors have the representation

$$\begin{aligned} {\mathbf {a}}_{ST} = O_{j=1}^{n-1} {\mathbf {a}}_{ST}(\delta _j), \quad {\mathbf {a}}_{CT} = O_{j, k \ne i, j <k} {\mathbf {a}}_{CT}(\gamma _{j, k}). \end{aligned}$$

As an $n=4$ example, which demonstrates the quick and simple computations, consider

$$\begin{aligned} {\mathbf {a}} = \left( \frac{5}{3}, \frac{15}{2}, \frac{5}{3}; \frac{3}{2}, 3; 6\right) . \end{aligned}$$

(36)

The geometric mean yields the weights $w_1= (\frac{5}{3}\times \frac{15}{2}\times \frac{5}{3})^{\frac{1}{4}} = [\frac{125}{6}]^\frac{1}{4},$ $w_2= (\frac{3}{5}\times \frac{3}{2}\times 3)^{\frac{1}{4}} = [\frac{27}{10}]^{\frac{1}{4}}, w_3= (\frac{2}{15}\times \frac{2}{3} \times 6)^{\frac{1}{4}} = [\frac{24}{45}]^{\frac{1}{4}}$, and $w_4 = (\frac{3}{5}\times \frac{1}{3} \times \frac{1}{6})^{\frac{1}{4}} = [\frac{1}{30}]^{\frac{1}{4}}$. A check on BR computations is whether $\sum b_j=0.$ This computational check translates for the geometric mean to determine whether $w_1w_2w_3w_4= [w_1w_2w_3w_4]^4=1.$ It does.

The BR weights define ${\mathbf {d}}_{ST}$ with $d_{i, j} = b_i-b_j$ (Eq. 20). As summations are converted to multiplications, the corresponding rule is Eq. 28, or $a_{i, j} = \frac{w_i}{w_j}$; e.g., in this example, $a_{1, 2} = \left[ \frac{\frac{125}{6}}{\frac{27}{10}}\right] ^{\frac{1}{4}} =\frac{5}{3}.$ A computation leads to ${\mathbf {a}}_{ST} = (\frac{5}{3}, \frac{5}{2}, 5; \frac{3}{2}, 3; 2) \in \mathcal {CS}^4,$ and that ${\mathbf {a}}_{ST} = {\mathbf {a}}_{ST}(\delta _1)\circ {\mathbf {a}}_{ST}(\delta _2)\circ {\mathbf {a}}_{ST}(\delta _3)$ where $\delta _1=5, \delta _2=3, \delta _3=2.$

According to Eq. 21, ${\mathbf {d}}'s$ cyclic component is ${\mathbf {d}}_{CT} = {\mathbf {d}}-{\mathbf {d}}_{ST}$. This becomes

$$\begin{aligned} {\mathbf {a}}_{CT} = {\mathbf {a}} \circ {\mathbf {a}}_{ST}^{-1}, \end{aligned}$$

(37)

for ranked comparisons where ${\mathbf {a}}_{ST}^{-1}$ inverts each ${\mathbf {a}}_{ST}$ component. (For any ${\mathbf {a}}\in {\mathbb {R}}^{n\atopwithdelims ()2}_+, {\mathbf {a}} \circ {\mathbf {a}}^{-1} = {\mathbf {e}}.$) The error term for the example is ${\mathbf {a}}_{CT} = (\frac{5}{3}, \frac{15}{2}, \frac{5}{3}; \frac{3}{2}, 3; 6)\circ (\frac{3}{5}, \frac{2}{5}, \frac{1}{5}; \frac{2}{3}, \frac{1}{3}; \frac{1}{2}) = (1, 3, \frac{1}{3}; 1, 1; 3)$, or ${\mathbf {a}}_{CT} = {\mathbf {a}}_{CT}(\gamma _{2, 3})$ for $\gamma _{2, 3} = 3.$

The structures of $\mathcal {CS}^n$ and the error terms follow from this mathematics. Illustrating with $n=3$, a parametric representation of $\mathcal {CS}^3$ is $(\frac{s}{t}, s; t)$ for $0<\delta _1=s, \delta _2=t < \infty .$ Similarly, weights $w_1, w_2,$ and $w_3=1$ define the point ${\mathbf {w}}^*=(\frac{w_1}{w_2}, w_1; w_2) \in \mathcal {CS}^3$. All possible terms with errors emanating from ${\mathbf {w}}^*$ define the nonlinear error curve

$$\begin{aligned} {\mathbf {u}} = \left( \frac{w_1u}{w_2}, \frac{w_1}{u}; w_2u\right) , \quad 0< u < \infty , \, u\ne 1. \end{aligned}$$

(38)

It follows from these nonlinearities that only rarely will the projection of an ${\mathbf {a}}\not \in \mathcal {CS}^n$ to $\mathcal {CS}^n$ to eliminate ${\mathbf {a}}$’s error provide a correct answer.

Theorem 13

If ${\mathbf {a}} \not \in \mathcal {CS}^n$, the closest point in $\mathcal {CS}^n$ to ${\mathbf {a}}$ does not, in general, eliminate ${\mathbf {a}}$’s error term. Indeed, for $n=3$ and $u\ne 1$, the nearest $\mathcal {CS}^3$ point to ${\mathbf {u}}$ (from Eq. 38) is the accurate ${\mathbf {w}}^*$ if and only if

$$\begin{aligned} w_1=w^2_2\ge 1 \text { and }u=\frac{(1+w_1)\pm \sqrt{(1+w_1)^2- 4}}{2}.\end{aligned}$$

(39)

With $w_3=1, w_2=2$, the projection approach works only in the special case where $w_1=4$, and even then only for the two points $u = \frac{5 \pm \sqrt{21}}{2}$ on the error curve.

5.3 Eigenvalue approaches

It is well known that ${\mathbf {a}}\in \mathcal {CS}^n$ if and only if the eigenvector with positive entries from the matrix $((a_{i, j}))$ has an eigenvalue equal to n. Otherwise the eigenvalue is larger. This larger value is a direct consequence of the ${\mathbf {a}}_{CT}$ portion of ${\mathbf {a}}$.

This is easy to prove with $n=3$ by using ${\mathbf {u}}$ (Eq. 38), which is a general $n=3$ form of a ratio scaled term with the corrected value of ${\mathbf {w}}^*$. The eigenvalue and eigenvector for the matrix defined by ${\mathbf {u}}$ are determined in Eq. 40.

$$\begin{aligned} ((a_{i, j}))({\mathbf {w}}^*) = \left( \begin{array} {lll} 1 &{} \frac{w_1u}{w_2} &{} \frac{w_1}{u} \\ \frac{w_2}{w_1u} &{} 1 &{} w_2 u\\ \frac{u}{w_1 } &{} \frac{1}{w_2u} &{} 1 \end{array}\right) \left( \begin{array}{c} w_1 \\ w_2 \\ 1 \end{array}\right) = \left( 1+u+\frac{1}{u}\right) \left( \begin{array}{c} w_1 \\ w_2 \\ 1 \end{array}\right) \end{aligned}$$

(40)

with eigenvalue (Eq. 40) $1+u+\frac{1}{u} \ge 3$: equality arises if and only if $u=1$, which is the error free term. The $n=3$ eigenvector does yield correct weights, but, in general, this is not true for $n\ge 4$. This is easily verified by using the general form of an ${\mathbf {a}}\not \in \mathcal {CS}^n$.

6 Concluding thoughts

Although decision methods based on paired comparisons constitute relatively simple systems, they indicate which features of more general systems must be examined. In all of the difficulties discussed here, the problems reflected a structural incongruity between the system and the subsystems. This comment makes it clear that, in general and in some manner, the information being used from each subsystem must be made consistent with the system’s requirements. For methods based on paired comparisons, this objective is achieved by identifying what causes the parts to deviate from the system’s requirement of transitivity. This issue is being explored.

7 Proofs

Theorem 2: For $n\ge 3$ alternatives, let F be a mapping as specified in Theorem 2. For any pair $\{A_i, A_j\}$, let $g_{(A_i, A_j)}$ be a mapping that ranks these two alternatives based strictly on how the $a\ge 2$ sources rank that particular pair. Namely, if ${\mathbf {p}}_{i, j}$ is a list of how each source ranks the pair, let ${\mathbf {p}}$ be a profile over the n alternatives and a sources where each source’s ranking of $\{A_i, A_j\}$ is as in ${\mathbf {p}}_{i, j}$. (As ${\mathbf {p}}_{i, j}$ ranks only one pair for each source, it is clear that these rankings can be embedded in a complete transitive profile for the a sources.)

Let $g_{(A_i, A_j)}({\mathbf {p}}_{i, j})$ be the $\{A_i, A_j\}$ ranking of $F({\mathbf {p}}).$ To establish that $g_{(A_i, A_j)}$ is well defined, let ${\mathbf {p}}*$ be another profile where each source’s $\{A_i, A_j\}$ ranking is as in ${\mathbf {p}}_{i, j}$. Because F satisfies IIA, the $\{A_i, A_j\}$ ranking in $F({\mathbf {p}})$ is the same as in $F({\mathbf {p}}^*).$ $\square$

Theorem 3: To show that ${\mathcal {ST}}^n$ is a linear $(n-1)$ dimensional subspace, notice from Eq. 10 that the component $d_{s, k}$ of a vector in ${\mathcal {ST}}^n$ can be expressed as $d_{s, k} = -d_{1, s} + d_{1, k}$. Thus, ${\mathcal {ST}}^n$ is uniquely and linearly determined by the $(n-1)$ values $\{d_{1, s}\}_{s=2}^n$. To show for a given j that ${\mathbf {B}}_j$ is strongly transitive, note that each $d_{j, k}=1$, while $d_{k, s}=0$ for $s, k \ne j.$ Thus, trivially, $d_{j, k} + d_{k, s} = d_{j, s}$. The reason $\sum _{j=1}^n {\mathbf {B}}_j={\mathbf {0}}$ is that each $d_{i, j}$, $i<j$, component appears in only two ${\mathbf {B}}_s$ terms. In ${\mathbf {B}}_i$ it has the value $d_{i, j} = 1,$ while in ${\mathbf {B}}_j$ it has $d_{j, i} = -d_{i, j} = 1;$ in the summation, the two terms cancel. To show that any $(n-1)$ of the terms are linearly independent, remove ${\mathbf {B}}_k$. For each $j\ne k$, ${\mathbf {B}}_j$ is the only vector with a nonzero $d_{j, k}$ component, so it cannot be expressed as a linear sum of the remaining vectors. $\square$

Proposition 1: Let ${\mathbf {C}}_{\lambda }$ be defined by $\lambda = (j, k, l, m, \dots , y, z)$ that has four or more entries. The first cycle defined by triplets is (j, k, l), where the remaining indices define the cycle $(j, l, m, \dots , y, z).$ In ${\mathbf {C}}_{(j, k, l)}$, $d_{j, l}=-1$ while $d_{j, l}=1$ in ${\mathbf {C}}_{j, l. m, \dots }$. In the sum ${\mathbf {C}}_{(j, k, l)} + {\mathbf {C}}_{(j, l. m, \dots )}$, the $d_{j, l}$ terms cancel leaving ${\mathbf {C}}_{\lambda }$. The next triplet is from the first three terms in $(j, l, m, \dots , y, z),$ or (j, l, m) leaving $(j, m, \dots , y, z)$. At each step, one new index is involved, so the process continues creating the triplets $(j, k, l), (j, l, m), \dots , (j, y, z).$ $\square$

Theorem 4: To prove that any cyclic vector is orthogonal to a ${\mathbf {d}}\in {\mathcal {ST}}^n$, consider an arbitrary cyclic vector defined by the triplet (i, j, k). The only nonzero components of ${\mathbf {C}}_{\{i, j, k\}}$ are $d^*_{i, j}=d^*_{j, k}=1,$ and $d^*_{i, k}=-1$. Therefore, the dot product with ${\mathbf {d}}$ equals $d_{i, j} + d_{j, k} - d_{i, k}$, which equals zero (Eq. 10). Thus, orthogonality is proved.

The dimension statement follows by listing the triplets ${\mathbf {C}}_{\{1, j, k\}}$ in the $(1, 2, 3), (1, 2, 4), \dots , (1, n-1, n)$ manner. This is illustrated for $n=5$ with the Eq. 41 array.

$$ {\mathcal {A}}= \left( \begin{array} {llllllllll} {\mathbf {C}}_{1, 2, 3} \\ {\mathbf {C}}_{1, 2, 4} \\ {\mathbf {C}}_{1, 2, 5} \\ {\mathbf {C}}_{1, 3, 4} \\ {\mathbf {C}}_{1, 3, 5} \\ {\mathbf {C}}_{1, 4, 5}\end{array} \right) = \left( \begin{array} {llllllllll} 1 &{} -1&{} 0 &{} 0;&{} 1&{} 0 &{} 0; &{} 0 &{} 0; &{} 0 \\ 1 &{}0&{} -1&{} 0;&{} 0 &{} 1&{} 0;&{} 0&{} 0; &{} 0 \\ 1 &{} 0 &{} 0 &{} -1;&{} 0&{} 0 &{} 1;&{} 0&{} 0;&{} 0 \\ 0 &{} 1 &{} -1 &{} 0; &{} 0 &{} 0 &{} 0;&{} 1 &{} 0;&{} 0\\ 0 &{} 1 &{} 0&{} -1;&{} 0 &{} 0&{} 0;&{} 0&{} 1;&{} 0 \\ 0&{} 0&{} 1&{} -1;&{} 0&{} 0&{} 0;&{} 0&{} 0;&{} 1\\ \end{array} \right). $$

(41)

The last ${{n-1}\atopwithdelims ()2}\times {{n-1}\atopwithdelims ()2}$ block always is an identity matrix. Thus, the matrix (${\mathcal {A}}$ for $n=5$) has maximal rank, which means that the dimension of $\mathcal {CS}^n$ is at least ${n-1}\atopwithdelims ()2$. But vectors in $\mathcal {CS}^n$ are orthogonal to the space ${\mathcal {ST}}^n$, so the dimension of $\mathcal {CS}^n$ is no more than ${n\atopwithdelims ()2} - (n-1) = {{n-1}\atopwithdelims ()2}$, which completes the proof. $\square$

This computation means that any cycle involving $A_1$ can be uniquely expressed in terms of ${\mathbf {C}}_{1, j, k}$ vectors. But cycles not involving $A_1$ cannot; this is a consequence of Theorem 9.

Corollary 1: The corollary follows from the facts that $\{{\mathbf {B}}_j\}_{j=1}^{n-1}$ is a basis for ${\mathcal {ST}}^n$ (Theorem 3) and $\{{\mathbf {C}}_{1, j, k}\}_{2\le j <k}$ is a basis for $\mathcal {CT}^n$ (from the proof of Theorem 4 and Eq. 41). $\square$

Theorem 5: In a cyclic vector’s defining list, index j is adjacent to two other indices, i that precedes j and k that follows j. The cyclic vector, then, has only two nonzero $d_{j, s}$ values of $d_{j, i} = -d_{i, j}=-1$ and $d_{j, k}=1.$ In the sum defining $b_j$ these terms cancel, which proves the assertion.

To prove Eq. 20, let ${\mathbf {d}}\in {\mathcal {ST}}^n$ and $i\ne j$. The $A_i$, $A_j$ Borda values are

$$\begin{aligned} b_i = \frac{1}{n}\sum _{k\ne i} d_{i, k}, \quad b_j = \frac{1}{n}\sum _{k\ne j}^n d_{j, k}. \end{aligned}$$

After removing the $d_{i, j}$ values from both sums the difference is

$$\begin{aligned} b_i-b_j = \frac{1}{n}\left( d_{i, j} + \sum _{k\ne i, j} d_{i, k} - \left[ d_{j, i} +\sum _{k\ne i, j} d_{j, k}\right] \right) = \frac{1}{n}\left( 2d_{i, j} + \sum _{k\ne i, j} [d_{i, k} - d_{j, k}]\right) . \end{aligned}$$

Each $[d_{i, k}-d_{j, k}] = [d_{i, k} + d_{k, j}] = d_{i, j}$, so the last sum equals $(n-2)d_{i, j}$, and Eq. 20 follows. The theorem’s last sentence follows from the orthogonal decomposition of ${\mathbb {R}}^{n\atopwithdelims ()2}.$ $\square$

Theorem 6: With the decomposition, ${\mathbf {d}}={\mathbf {d}}_{ST}+{\mathbf {d}}_{SC}$, where ${\mathbf {d}}_{SC}= c(1, -1; 1)$, $c\in (-\infty , \infty ).$ Using Eq. 20, the $d_{i, j}$ components of ${\mathbf {d}}_{ST}$ equal $(b_i-b_j)$, where $b_1>b_2>b_3$ has the $A_1\succ A_2\succ A_3$ Borda ranking. (By construction $b_1+b_2+b_3=0$.) Thus,

$$\begin{aligned} {\mathbf {d}} = ((b_1-b_2) +c, (b_1-b_3)-c; (b_2-b_3) + c). \end{aligned}$$

(42)

If $A_3$ could be the Condorcet winner, $A_3$ beats $A_1$ and $A_2$, or $d_{3, 1}>0, d_{3, 2}>0.$ Thus, ${\mathbf {d}}$’s $d_{1, 3}, d_{2, 3}<0$, which requires $c>0$ in $d_{1, 3}$ and $c<0$ for $d_{2, 3}$: As this is impossible, the Condorcet winner cannot be Borda bottom ranked.

If $A_2$ is the Condorcet winner, $A_2$ beats $A_1$, so $d_{2, 1} = -d_{1, 2} >0,$ or $0<(b_1-b_2) < -c.$ For $A_2$ to beat $A_3$, $d_{2, 3}$ must be positive, or $(b_2-b_3) > -c.$ This proves Eq. 22.

For $n\ge 3$, if $A_1$ is the Condorcet winner, then $A_1$ beats all other alternatives, so $d_{1, j}>0$ for $j=2, \dots n.$ This means that $b_1>0.$ Because $\sum _{j=1}^n b_j=0,$ there must be some j where $b_j<0$, which proves that the BR ranking never has the Condorcet winner bottom ranked. Similarly, if $A_2$ is the Condorcet loser, then $d_{2, j}<0$ for $j=1, 3, \dots , n.$ This forces $b_2<0$, so the Condorcet loser $A_2$ is BR ranked below Condorcet winner $A_1$. $\square$

Theorem 7: The first sentence follows from the fact that the image of any ${\mathbf {d}}$ is known, which means that, after expressing the linear process in matrix form, the associated matrix is known; it is a projection mapping that is equivalent to the Borda rule.

As known (e.g., (Saari 2018)), the Borda tally $\tau _j$ for $A_j$ is the sum of the tally $A_j$ receives in each $\{A_j, A_k\}$ paired comparison election. With a sources, a tied pairwise outcome is $\frac{a}{2}:\frac{a}{2}$. As $d_{j, k}$ is the difference between the $\{A_j, A_k\}$ tallies, $A_j$ receives $\frac{a + d_{j, k}}{2}$ votes. Summing over all $(n-1)$ pairs that include $A_j$ leads to $\tau _j =\frac{1}{2}[ a(n-1) + nb_j]$, or Eq. 23. $\square$

Theorem 8: That the ranking outcome is complete and transitive follows from the fact that it is determined by the $b_j$, $j=1, \dots , n$, scalars. That IIA is satisfied follows immediately from Eq. 20. $\square$

Theorem 9: The first part of the theorem follows from the following computational result.

Corollary 2

For $n\ge 3$, if ${\mathbf {d}} = \sum _{j=1}^n \beta _j {\mathbf {B}}_j^n$, then for each j, $b_j= \beta _j -\frac{1}{n}\beta$ where $\beta = \sum _{j=1}^n \beta _j.$

To prove the corollary, notice that ${\mathbf {d}} = \sum _{j=1}^n \beta _j {\mathbf {B}}_j^n$ becomes

$$\begin{aligned} {\mathbf {d}} = (\beta _1-\beta _2, \dots , \beta _1-\beta _n; \beta _2-\beta _3, \dots , \beta _2-\beta _n; \dots ; \beta _{n-1}-\beta _n). \end{aligned}$$

According to Eq. 19, for each j, $nb_j = \sum _{s=1}^n d_{j, s} = (n-1)\beta _j - \sum _{s\ne j} \beta _s$. By adding and subtracting $\beta _j$ to this expression, we have $nb_j = n\beta _j - \beta$, which is as specified in Corollary 2. Thus, the $\beta _j$ coefficients and BR values are closely related.

For the proof of the theorem, by dropping $A_k$ all $d_{i, j}$ terms with a subscript k are dropped. If ${\mathbf {d}}\in \mathcal {ST}^n$, the only difference between ${\mathbf {d}}$ and ${\mathcal {P}}_k({\mathbf {d}})$ are the missing $d_{i, j}$ terms with a subscript k. Thus, any triplet (i, j, s) without a k satisfies $d_{i, j} + d_{j, s}= d_{i, s}$ for both ${\mathbf {d}}$ and ${\mathcal {P}}_k({\mathbf {d}})$. As ${\mathbf {d}}$ is strongly transitive, so is ${\mathcal {P}}_k({\mathbf {d}})$.

Let ${\tilde{b}}_j$ be the BR weight for ${\mathcal {P}}_k({\mathbf {d}})$. Thus (Eq. 19) $(n-1) {\tilde{b}}_j = \sum _{s\ne k} d_{j, s}$. By adding and subtracting $\beta _j-\beta _k$ and using Corollary 2, we have $(n-1) {\tilde{b}}_j = nb_j - (\beta _j-\beta _k)= nb_j - (b_j+\frac{1}{n}\beta - \beta _k) = (n-1)b_j - (\frac{1}{n}\beta -\beta _k).$ That is, for each $j\ne k$, ${\tilde{b}}_j$ is found by subtracting the same amount $\frac{1}{n-1}(\frac{1}{n}\beta -\beta _k)$ from $b_j$. This subtraction can force the ${\tilde{b}}_j$ and $b_j$ values to differ, but subtracting the same value from each $b_j$ requires the ranking for each to remain the same.

The second part of Theorem 9 follows from the ${\mathbf {B}}^n_j$ basis vectors. A cyclic term defined by $\lambda = (\dots , i, j, k, l, \dots )$ is orthogonal to ${\mathbf {B}}^n_j$ because it contains only two d terms with subscript j; they are $d_{i, j} = -d_{j, k},$ where the difference in value ensures orthogonality. Now, if $A_k$ is dropped, then the $d_{j, k}$ term no longer exists, so the vector has a component in the strongly transitive ${\mathbf {B}}^n_j$ direction. Using the same argument shows the projection is not strongly transitive, so it also has a component in the cyclic directions.

Theorem 12: This is a direct consequence of Theorem 10 and the image of the basis vectors of Corollary 1.$\square$

Theorem 13: For the projection to eliminate the error in ${\mathbf {a}}$, ${\mathbf {a}}$ must be situated on a straight line passing through the correct value ${\mathbf {a}}' \in \mathcal {CS}^n$ and orthogonal to $\mathcal {CS}^n$ (i.e., a tangent space). The derivative of the error function proves it is not a straight line. This can be illustrated with $n=3$ by using ${\mathbf {u}}$ (Eq. 38) where $\frac{ d {\mathbf {u}}}{du} = (\frac{w_1}{w_2}, -u^{-2}w_1; w_2)$.

A parametric representation of $\mathcal {CS}^3$ is given by $(\frac{s}{t}, s; t)$ where the general weight for $A_1$ is $s>0$, for $A_2$ by $t>0$ and 1 for $A_3$ for the scaling. Thus the closest point to ${\mathbf {u}}$ on $\mathcal {CS}^3$, where $u\ne 1$, is given by the minimal value of $G(s, t) = (\frac{s}{t}-\frac{w_1u}{w_2})^2 + (s- \frac{w_1}{u})^2 + (t-w_2u)^2$. Setting the partials equal to zero yields $\frac{\partial G}{\partial s} = \frac{1}{t}(\frac{s}{t}-\frac{w_1u}{w_2}) + (s-\frac{w_1}{u}) = 0$ and $\frac{\partial G}{\partial t} = -\frac{s}{t^2}(\frac{s}{t}-\frac{w_1u}{w_2}) + (t-w_2u)=0.$ The closest point is the accurate ${\mathbf {w}}^*$, or $s=w_1, t=w_2$, iff $\frac{w_1}{w_2^2}(1-u) + w_1(1-\frac{1}{u}) = 0$ and $[-\frac{w_1^2}{w_2^3}+w_2](1-u) =0.$ Because $u\ne 1$, the second equation is satisfied iff $w_1=w_2^2,$ which verifies part of Eq. 39. By multiplying by u and collecting terms, the remaining equation becomes $u^2 -(1+ w_1)u+1=0$, with solution $u = \frac{(1+w_1) \pm \sqrt{(1+w_1)^2-4}}{2}.$ A real solution exists iff $w_1\ge 1$, which completes Eq. 39.