Abstract
Stephen Yablo has argued that ascriptions of belief and knowledge are sensitive to subject matter and that theorising in such terms may help resolve philosophical questions about the semantics of such ascriptions. Truthmaker semantics offers a way of theorising about subject matters. My main aim in this paper is to investigate what a semantics for knowledge or belief ascriptions might look like within truthmaker semantics. I then discuss what the resulting account might have to say about the problem of logical omniscience, the nature of concepts, and rational belief.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper has two main aims. The first is to investigate what a semantics for knowledge or belief ascriptions looks like within the setting of truthmaker semantics. The second is to evaluate how well that approach does as a solution to the various problems of logical omniscience, whereby agents are modelled as knowing too many logical consequences of what they know.
I will focus on belief, rather than knowledge, but much of what I say here applies equally to knowledge ascriptions. More importantly, I will situate the discussion within Finean truthmaker semantics (Fine, 2017a, b), as opposed to the Yabloesque approach (Yablo, 2014). The former takes primitive states, standing in a part-whole relation, as its conceptual starting point. The latter, by contrast, takes possible worlds as its primitive and constructs states from these. The former is more general, in that it can draw hyperintensional distinctions where the latter cannot (Fine, 2020; Yablo, 2018). It is also more foreign. We know far less about how to reason with and about states than we do with and about worlds. That is reason enough to explore.
The basic insight on how to model knowledge and belief in this setting, however, is from Yablo:
Knowledge-attributions care about subject matter, over and above truth conditions. They take note of how P is true or false in various worlds, not only which world is it is true or false in. (Yablo, 2014, p. 122)
You know you locked the front door. Do you thereby know that any apparent evidence to the contrary is misleading? It seems not. Reports of an open door might make you reconsider. So if we are not to concede too much everyday knowledge to the sceptic, we must accept that knowledge is not closed under simple known implications such as this. Yablo’s diagnosis highlights the change in subject matter, from how the door is to (something like) whether there is evidence from other sources concerning how the door is (Yablo, 2014, §7.4).
The paper proceeds as follows. Section 2 is a brief introduction to truthmaker semantics, à la Fine. Section 3 presents the basic semantics for belief ascriptions, which is then extended to a more general account in Sect. 4. Additional conditions—truth and positive introspection—are discussed in Sect. 5. We then turn, in Sect. 6, to how the resulting account handles the various problems of logical omniscience. Section 7 relates the account to some recent approaches to concept possession. Section 8 discusses an objection which affects similar responses to logical omniscience. Finally, Sect. 9 discusses the vexing issue of how an agent’s beliefs stand in light of her limited cognitive resources.
2 Truthmaker semantics
In this section, we sketch a very brief overview of truthmaker semantics and state some basic results. For further details, the reader is referred to Fine (2016, 2017a) and Fine (2019, forthcoming). Here we use the notation and presentation of Fine and Jago (forthcoming).
Truthmaker semantics is built around the notion of a state space: a set of states S with a part-whole structure \(\sqsubseteq \) on it. This is a complete partial order: it is reflexive and transitive and has unique least and greatest elements,  , such that
, such that  for every state \(s \in S\). Given this ordering, each subset T of U has a unique least upper bound \(\bigsqcup T \in S\) and a unique greatest lower bound
for every state \(s \in S\). Given this ordering, each subset T of U has a unique least upper bound \(\bigsqcup T \in S\) and a unique greatest lower bound  . (The least upper bound of a set T is the least state \(s \in S\) for which \(t \sqsubseteq s\) for each \(t \in T\). Similarly, the greatest lower bound of a set T is the greatest state \(s \in S\) for which \(s \sqsubseteq t\) for each \(t \in T\).) In particular,
. (The least upper bound of a set T is the least state \(s \in S\) for which \(t \sqsubseteq s\) for each \(t \in T\). Similarly, the greatest lower bound of a set T is the greatest state \(s \in S\) for which \(s \sqsubseteq t\) for each \(t \in T\).) In particular,  and
and  . For pairs of states, we write \(s \sqcup u\) for \(\bigsqcup \{s, u\}\), the fusion of s and u, and \(s \sqcap u\) for
. For pairs of states, we write \(s \sqcup u\) for \(\bigsqcup \{s, u\}\), the fusion of s and u, and \(s \sqcap u\) for  . \(\langle S, \sqcup \rangle \) and \(\langle S, \sqcap \rangle \) are complete semilattices, with identity elements
. \(\langle S, \sqcup \rangle \) and \(\langle S, \sqcap \rangle \) are complete semilattices, with identity elements  and
and  , respectively:
, respectively:  and
and  for each \(s \in S\). \(\sqcup \) and \(\sqcap \) are commutative, associative, and idempotent, and \(s \sqcup u = u\) iff \(s \sqcap u = s\) iff \(s \sqsubseteq u\). (In what follows, we mostly ignore \(\sqcap \).)
for each \(s \in S\). \(\sqcup \) and \(\sqcap \) are commutative, associative, and idempotent, and \(s \sqcup u = u\) iff \(s \sqcap u = s\) iff \(s \sqsubseteq u\). (In what follows, we mostly ignore \(\sqcap \).)
We shall work with a very simple propositional language:
(to be expanded with belief operators \(\textsf {B} _i\) in Sect. 3). We expand state spaces \(\langle S, \sqsubseteq \rangle \) to models by adding positive and negative valuation functions:
Definition 1
(Models) A model \({\mathcal {M}}\) is a quadruple \(\langle S, \sqsubseteq , V^+, V^- \rangle \), where \( \langle S, \sqsubseteq \rangle \) is a state space and \(V^+, V^-: {\mathcal {P}} \longrightarrow 2^S\) are functions from sentence letters to nonempty subsets of S.
We then define exact truthmaking ( ) and falsitymaking (
) and falsitymaking ( ) relations as follows:
) relations as follows:
Definition 2
(Exact truthmaking and falsitymaking) Given a model \({\mathcal {M}}\) (which we leave implicit), exact truthmaking  and exact falsitymaking
and exact falsitymaking  relations are defined by double recursion as follows:
relations are defined by double recursion as follows:

These are said to be exact relationships in that  says that s is wholly relevant to A’s truth (and
says that s is wholly relevant to A’s truth (and  says that s is wholly relevant to A’s falsity). This requirement leads to the unusual truthmaking clause for conjunction: a truthmaker for \(A \wedge B\) is the fusion of a truthmaker for A and a truthmaker for B. That state may itself not be wholly relevant to A’s (or B’s) truth and so, in general, truthmakers for conjunctions will not be truthmakers for their conjuncts. (Similar remarks apply to falsitymaking for disjunctions.)
says that s is wholly relevant to A’s falsity). This requirement leads to the unusual truthmaking clause for conjunction: a truthmaker for \(A \wedge B\) is the fusion of a truthmaker for A and a truthmaker for B. That state may itself not be wholly relevant to A’s (or B’s) truth and so, in general, truthmakers for conjunctions will not be truthmakers for their conjuncts. (Similar remarks apply to falsitymaking for disjunctions.)
That state will nevertheless be sufficient for (if not wholly relevant to) the truth of the conjuncts. This is the notion of inexact truthmaking, defined as follows.
Definition 3
(Inexact truthmaking and falsitymaking) In any model \({\mathcal {M}}\),  iff
iff  for some \(u \sqsubseteq s\), and
for some \(u \sqsubseteq s\), and  iff
iff  for some \(u \sqsubseteq s\).
for some \(u \sqsubseteq s\).
Inexact truthmaking, unlike its exact cousin, obeys the standard extensional clauses for conjunction and disjunction:

We define exact truthmaker and falsitymaker sets as follows:

and lift \(\sqcup \) to sets of states by setting:
We may then state the exact clauses in algebraic form:
We identify propositions with sets of states. More precisely, a unilateral proposition is a set of states \(P \subseteq S\), and a bilateral proposition is a pair \({\textbf {P}} = \langle P^+, P^- \rangle \) of sets of states. The idea here is that \(P^+\) contains \({\textbf {P}} \)’s truthmakers and \(P^-\) its falsitymakers. Given bilateral propositions \({\textbf {P}} = \langle P^+, P^- \rangle \) and \({\textbf {Q}} = \langle Q^+, Q^- \rangle \), we define bilateral Boolean operators as follows:
We may in addition require one or more closure conditions on propositions:
Definition 4
(Closure conditions)
- Closure (\(\sqcup \))::
-
A proposition P is closed when \(\bigsqcup Q \in P\) for any nonempty \(Q \subseteq P\)
- Convex closure (
 )::
):: -
A proposition P is convex when, for any \(t \in S\), if \(s, u \in P\) and \(s \sqsubseteq t \sqsubseteq u\), then \(t \in S\) too.
- Regular closure (\(*\))::
-
A proposition P is regular when it is both closed and convex.
We write \(P^\sqcup \),  , and \(P^*\) for the smallest closed, convex, and regular sets (respectively) that contain P.
, and \(P^*\) for the smallest closed, convex, and regular sets (respectively) that contain P.
Each proposition has a subject matter, which intuitively is what the proposition is about. For Yablo (2014, 2018), each instance of ‘there are n stars’ has the subject matter the number of stars, analogous to the question, ‘how many stars are there?’ Fine (2017b) has a slightly different notion of subject matter, on which each instance of ‘there are n stars’ has the subject matter whether there are n stars, which (for the same n) it shares with ‘there are not n stars’. Both agree that a proposition’s subject matter is not given merely by the objects it is about, for the headlines, ‘man bites dog’ and ‘dog bites man’ have quite different subject matter (Yablo, 2014, p. 24).
Following Fine (2017b), we define the subject matter \({\textbf {p}} \) of a unilateral proposition P to be \(\bigsqcup P\) and of a bilateral proposition \({\textbf {P}} = \langle P^+, P^- \rangle \) to be \({\textbf {p}} ^+ \sqcup {\textbf {p}} ^-\). (We could instead understand bilateral subject matter as the pair \(\langle {\textbf {p}} ^+, {\textbf {p}} ^- \rangle \). Fine (2017b, p. 697) calls these options ‘comprehensive’ and ‘differentiated’ subject maters, respectively. We adopt the former here because it captures the intuitive principle that negating a proposition does not affect its subject matter.)
Given a model \({\mathcal {M}}\) and sentence A, we shall for the most part be interested in the regular (unilateral and bilateral) propositions \(|A|^{+*}\) and \(\langle |A|^{+*}, |A|^{-*} \rangle \) associated with A. We use the notation \(\mathop {\textit{sm}^+}(A)\) and \(\mathop {\textit{sm}^\pm }(A)\) for their subject matters, respectively. These are determined purely by the subject matters of the letters appearing in A (and, for the unilateral case, by whether those letters occur positively or negatively, in the following sense).
Lemma 1
(Subject matter) Say that p occurs positively (or negatively) in A when p occurs within the scope of an even (odd) number of negations in A. Let \(\mathop {\textit{lett}}^+ (A)\) and \(\mathop {\textit{lett}}^- (A)\) be the sets of letters occurring positively and negatively in A, respectively, and set \(\mathop {\textit{lett}}(A) = \mathop {\textit{lett}}^+ (A) \cup \mathop {\textit{lett}}^- (A)\). Then, relative to any model \({\mathcal {M}}\):
-
(i)
\(\displaystyle \mathop {\textit{sm}^\pm }(A) = \bigsqcup _{p \in \mathop {\textit{lett}}(A)} \mathop {\textit{sm}^\pm }(p)\)
-
(ii)
\(\displaystyle \mathop {\textit{sm}^+}(A) = \! \bigsqcup _{p \in \mathop {\textit{lett}}^+(A)} \! \mathop {\textit{sm}^+}(p) \ \ \sqcup \! \bigsqcup _{p \in \mathop {\textit{lett}}^-(A)} \mathop {\textit{sm}^+}(\lnot p) \)
Proof
(i) is by induction on A. The base case is given by definition and, for the induction step, it suffices to note that, for \(\lnot \): \(\mathop {\textit{sm}^\pm }(\lnot A) = \mathop {\textit{sm}^\pm }(A)\) and \(\mathop {\textit{lett}}(\lnot A) = \mathop {\textit{lett}}(A)\), and for \(\wedge \) and \(\vee \): \(\mathop {\textit{sm}^\pm }(A \wedge B) = \mathop {\textit{sm}^\pm }(A \vee B) = \mathop {\textit{sm}^\pm }(A) \sqcup \mathop {\textit{sm}^\pm }(B)\) and \(\mathop {\textit{lett}}(A \wedge B) = \mathop {\textit{lett}}(A \vee B) = \mathop {\textit{lett}}(A) \cup \mathop {\textit{lett}}(B)\).
For (ii), let \(\mathop {\textit{lit}}(A)\) be the set of literals (letters or their negations) occurring in A and \(\mathop {\textit{dnf}\hspace{1.111pt}} (A)\) be any disjunctive normal form of A. DNFs have the property that \(p \in \mathop {\textit{lit}}(\mathop {\textit{dnf}\hspace{1.111pt}} (A))\) iff \(p \in \mathop {\textit{lett}}^+(A)\) and \(\lnot p \in \mathop {\textit{lit}}(\mathop {\textit{dnf}\hspace{1.111pt}} (A))\) iff \(p \in \mathop {\textit{lett}}^-(A)\). Moreover, given the equivalences in Fig. 1, \(\mathop {\textit{dnf}\hspace{1.111pt}} (A)\) is equivalent to A, hence \(|\mathop {\textit{dnf}\hspace{1.111pt}} (A)|^{+*} = |A|^{+*}\), and so \(\mathop {\textit{sm}^+}(A) = \mathop {\textit{sm}^+}(\mathop {\textit{dnf}\hspace{1.111pt}} (A))\). We also have
and so:
\(\square \)
We take sentences A, B to be equivalent, \(A \equiv _e B\) when they express the same unilateral proposition. Where we impose no closure conditions on propositions, equivalence amounts to A, B having the same truthmakers. But for technical reasons, it is preferable to insist that propositions be regular closed sets, so that \(A \equiv _e B\) when \(|A|^{+*} = |B|^{+*}\). This gives us the familiar equivalences shown in Fig. 1. (Of these, the majority hold on the basic semantics. Idempotence for \(\wedge \) requires closure. Distributivity for \(\vee \) requires both closure and convexity.)
We take (single-premise) entailment to be propositional inclusion: A exactly entails B when \(|B|^{+*} \subseteq |A|^{+*}\). As already noted, \(A \wedge B\) will not exactly entail A. Yet there is clearly an important relationship between \(A \wedge B\) and A. We say that the proposition expressed by A is a conjunctive part of that expressed by \(A \wedge B\):
Definition 5
(Conjunctive parthood) P is a conjunctive part of Q, \(P \le Q\), when:
- (Up):
-
Each \(s \in P\) is part of some \(u \in Q\) (i.e. \(s \sqsubseteq u\)); and
- (Down):
-
Each \(s \in Q\) has a part \(u \in P\) (i.e. \(u \sqsubseteq s\)).
When the first condition holds, we say that P subserves Q (\(P \sqsubseteq _{\forall \exists } Q\)) and when the second is met, we say that Q subsumes P (\(Q \sqsupseteq _{\forall \exists } P\)). We also say that Q contains P when \(P \le Q\).
Note that \(\le \) is a natural way to lift the parthood ordering \(\sqsubseteq \) from states to sets of states, since we have, in parallel to the usual order-lattice equivalence on states (\(s \sqsubseteq u \) iff \(s \sqcup u = u\)):
Lemma 2
(Fine, 2017a) \(P \le Q\) iff \(P \wedge Q = Q\)
3 Semantics for belief states
It is common in formal epistemology to take an agent’s total belief state to be a proposition (a set of worlds, situations, scenarios, states, or whatever) and to analyse belief in a particular proposition, P, in terms of P’s inclusion in (the consequences of) that total belief state. We may adopt that approach in the truthmaker setting, where we already have a notion of proposition. It remains to say only what the relevant sense of inclusion is. Spoiler: it is conjunctive parthood.
We will begin with a simplified semantics, in this section, before extending to the full analysis in Sect. 4. For the time being, we consider a single agent, for whom we introduce a belief operator \(\textsf {B} \) into the language, so that \(\textsf {B} A\) is a sentence whenever A is. An agent’s total belief state is modelled as a unilateral proposition: a set of states, \(D\). The agent believes that A when the proposition expressed by A is contained in (i.e. is a conjunctive part of) \(D\). (This, I take it, is how to understand Yablo’s idea that ‘[belief]-attributions care about subject matter’ (2014, p. 122) within Finean truthmaker semantics.) More precisely:
Definition 6
(Simple models and truth) A simple doxastic model is a quintuple \({\mathcal {M}} = \langle S, \sqsubseteq , D, V^+, V^- \rangle \), where \(\langle S, \sqsubseteq , V^+, V^- \rangle \) is as before and \(D \subseteq S\) is a regular unilateral proposition. For a \(\textsf {B} \)-free sentence A, \(\textsf {B} A\) is true in \({\mathcal {M}}\), \({\mathcal {M}} \models \textsf {B} A\), when \(|A|^{+*} \le D\). Entailment is preservation of truth-in-a-model and equivalence is two-way entailment.
This definition of truth is very limited, applying only to simple belief ascriptions, of the form \(\textsf {B} A\) where A itself is \(\textsf {B} \)-free. This is sufficient for a modest investigation into the entailment behaviour of belief ascriptions, which shall be the focus of this section. We shall give a more nuanced semantics in the next section.
As mentioned above, I take this approach to be the natural way of developing Yablo’s suggestion within Finean truthmaker semantics. As far as I know, Fine does not suggest a semantics of belief or knowledge along these lines. Hawke and Özgün (2023) develop a truthmaker semantics for knowledge ascriptions along quite different lines: see (Fine, 2023) for discussion. Elgin (2021) connects knowledge ascriptions to a notion of analytic consequence, which may in turn be understood in terms of truthmaker semantics (see Theorem 2 below), but does not offer a truthmaker semantics for knowledge ascriptions. So, as far as I am aware, this particular semantics for belief appears for the first time here. The closest existent approach I know of is Fine’s analysis of free-choice obligation (Fine, 2018), in which a deontic statement of obligation OA is true relative to a code of conduct \({\mathcal {C}}\) (a set of states) iff \(OA \le {\mathcal {C}}\). The parallel to the present approach is not exact, however.
Under what conditions does \(\textsf {B} A\) entail \(\textsf {B} C\), on this approach? The first source of closure conditions is the conditions on propositions themselves. If A and B express the same proposition, then \(\textsf {B} A\) will be equivalent to \(\textsf {B} C\). So (having assumed the regular semantics) pairs \(\textsf {B} A, \textsf {B} C\) will be equivalent for each pair A, C listed in Fig. 1: \(\textsf {B} (A \wedge C)\) is equivalent to \(\textsf {B} (C \wedge A)\), and so on.
The second source of closure conditions is the relation of conjunctive parthood that TMS claims to hold between a believed proposition P and the agent’s total belief state \(D\). So let us look at some of the properties of conjunctive parthood in more detail.
Lemma 3
(Fine, 2017a)
-
(i)
\(\le \) is reflexive and transitive
-
(ii)
If \(P \le Q\) and \(Q \le P\) then \(P = Q\)
-
(iii)
If \(P = P_1 \wedge P_2 \wedge \cdots \), then (i) \({\textbf {p}} = \bigsqcup _i {\textbf {p}} _i\) and (ii) P is the least proposition such that \(P_i \le P\) for each i
-
(iv)
If \(P \le R\) and \(Q \le R\) then \(P \wedge Q \le R\)
-
(v)
\(P \le Q\) iff \({\textbf {p}} \sqsubseteq {\textbf {q}} \) and \(Q \sqsupseteq _{\forall \exists } P\).
Part (v) will be especially useful in what follows, as it allows us to replace the (Down) condition on \(P \le Q\) with the simpler condition \({\textbf {p}} \sqsubseteq {\textbf {q}} \).
Given transitivity, if \(|C|^{+*} \le |A|^{+*}\), then \(\textsf {B} A\) will entail \(\textsf {B} C\). In particular, \(\textsf {B} (A \wedge C)\) entails both \(\textsf {B} A\) and \(\textsf {B} C\). And conversely, by (iv), \(\textsf {B} A\) and \(\textsf {B} C\) together entail \(\textsf {B} (A \wedge C)\). In fact, the agent’s total belief state \(D\) may be seen as the big conjunction of all the propositions \(P_i\) she believes: \(D= P_1 \wedge P_2 \wedge \cdots \). Its total subject matter is the fusion of the subject matters of each believed \(P_i\). Thus, fixing \(D\) fixes a subject matter \({\textbf {d}}= \bigsqcup D\) beyond which belief ascriptions may not transgress: \(\textsf {B} A\) only if the subject matter of the proposition expressed by A is part of \({\textbf {d}}\).
Let us now see how entailments between belief ascriptions, say from \(\textsf {B} A\) to \(\textsf {B} C\), relate both to the subject matter and the syntactic construction of A and C.
Lemma 4
\(\textsf {B} A\) entails \(\textsf {B} C\) only if \(\mathop {\textit{sm}^+}(C) \sqsubseteq \mathop {\textit{sm}^+}(A)\) in every simple doxastic model \({\mathcal {M}}\).
Proof
Consider a model \({\mathcal {M}} = \langle S, \sqsubseteq , D, V^+, V^- \rangle \) for which  . Given Definition 6, A and C must be \(\textsf {B} \)-free sentences and so \(|A|^{+*}\) and \(|C|^{+*}\) do not depend on the choice of D. Now let \({\mathcal {M}}_A\) be just like \({\mathcal {M}}\) but with \(|A|^{+*}\) in place of D. Then
. Given Definition 6, A and C must be \(\textsf {B} \)-free sentences and so \(|A|^{+*}\) and \(|C|^{+*}\) do not depend on the choice of D. Now let \({\mathcal {M}}_A\) be just like \({\mathcal {M}}\) but with \(|A|^{+*}\) in place of D. Then  in \({\mathcal {M}}_A\) and, given closure, \(\mathop {\textit{sm}^+}(C) \in |C|^{+*}\) but \(\mathop {\textit{sm}^+}(C) \notin |A|^{+*}\) (else \(\mathop {\textit{sm}^+}(C) \sqsubseteq \mathop {\textit{sm}^+}(A)\)) and so \(|C|^{+*} \nleq |A|^{+*}\). But then
in \({\mathcal {M}}_A\) and, given closure, \(\mathop {\textit{sm}^+}(C) \in |C|^{+*}\) but \(\mathop {\textit{sm}^+}(C) \notin |A|^{+*}\) (else \(\mathop {\textit{sm}^+}(C) \sqsubseteq \mathop {\textit{sm}^+}(A)\)) and so \(|C|^{+*} \nleq |A|^{+*}\). But then  and so \(\textsf {B} A\) does not entail \(\textsf {B} C\). \(\square \)
and so \(\textsf {B} A\) does not entail \(\textsf {B} C\). \(\square \)
Lemma 5
For \(\textsf {B} \)-free sentences A, C and simple doxastic models \({\mathcal {M}}\):
-
(i)
\(\mathop {\textit{sm}^\pm }(A) \sqsubseteq \mathop {\textit{sm}^\pm }(C)\) in each \({\mathcal {M}}\) iff \(\mathop {\textit{lett}}(A) \subseteq \mathop {\textit{lett}}(C)\)
-
(ii)
\(\mathop {\textit{sm}^+}(A) \sqsubseteq \mathop {\textit{sm}^+}(C)\) in each \({\mathcal {M}}\) iff \(\mathop {\textit{lett}}^+ (A) \subseteq \mathop {\textit{lett}}^+ (C)\) & \(\mathop {\textit{lett}}^- (A) \subseteq \mathop {\textit{lett}}^- (C)\)
Proof
For the left-to-right directions, we use a canonical model construction. Let L be the set of all literals and \(D \subseteq 2^L\) (i.e. a set of sets of literals). The D-canonical doxastic model is \({\mathcal {M}}^D = \langle 2^L, \sqsubseteq , D, V^+, V^- \rangle \), where \(\sqsubseteq \) is \(\subseteq \) restricted to \(2^L\), \(V^+ = \{\{p\}\}\), and \(V^- = \{\{\lnot p\}\}\). Given Lemma 1, in \({\mathcal {M}}^D\):
Now for (i), assume that \(\mathop {\textit{sm}^\pm }(A) \sqsubseteq \mathop {\textit{sm}^\pm }(C)\) in every simple doxastic model and that \(p \in \mathop {\textit{lett}}(A)\). Then \(\mathop {\textit{sm}^\pm }(A) \subseteq \mathop {\textit{sm}^\pm }(C)\) in \({\mathcal {M}}^D\), hence \(\{q, \lnot q \mid q \in \mathop {\textit{lett}}(A)\} \subseteq \{q, \lnot q \mid q \in \mathop {\textit{lett}}(C)\} \), and so \(p \in \mathop {\textit{lett}}(C)\). Similar reasoning for (ii) establishes that \(\mathop {\textit{lett}}^+ (A) \subseteq \mathop {\textit{lett}}^+ (C)\) and \(\mathop {\textit{lett}}^- (A) \subseteq \mathop {\textit{lett}}^- (C)\).
For (i) right-to-left: if \(\mathop {\textit{lett}}(A) \subseteq \mathop {\textit{lett}}(C)\) then, for an arbitrary simple doxastic model \({\mathcal {M}}\):
in \({\mathcal {M}}\) and so, by Lemma 1, \(\mathop {\textit{sm}^+}(A) \sqsubseteq \mathop {\textit{sm}^+}(C)\) in \({\mathcal {M}}\), and hence (since \({\mathcal {M}}\) was arbitrary) in every simple doxastic model. The reasoning for (ii) right-to-left is similar. \(\square \)
Theorem 1
\(\textsf {B} A\) entails \(\textsf {B} C\) only if \(\mathop {\textit{lett}}(C) \subseteq \mathop {\textit{lett}}(A)\).
Proof
Assume \(\textsf {B} A\) entails \(\textsf {B} C\) and \(p \in \mathop {\textit{lett}}(C)\). Then \(\mathop {\textit{sm}^+}(C) \sqsubseteq \mathop {\textit{sm}^+}(A)\) in every simple doxastic model (Lemma 4), hence \(\mathop {\textit{lett}}^+ (A) \subseteq \mathop {\textit{lett}}^+ (C)\) and \(\mathop {\textit{lett}}^- (A) \subseteq \mathop {\textit{lett}}^- (C)\) (Lemma 5). Moreover, either \(p \in \mathop {\textit{lett}}^+ (C)\), in which case \(p \in \mathop {\textit{lett}}^+ (A)\), or else \(p \in \mathop {\textit{lett}}^- (C)\), in which case \(p \in \mathop {\textit{lett}}^- (A)\). Either way, \(p \in \mathop {\textit{lett}}(A)\), and so \(\mathop {\textit{lett}}(C) \subseteq \mathop {\textit{lett}}(A)\). \(\square \)
This is the relevant logician’s variable sharing condition in overdrive! In particular, \(\textsf {B} p\) does not entail \(\textsf {B} (p \vee q)\). (This will be important in Sect. 6, when we consider the problems of logical omniscience.) In fact, the behaviour of disjunction within belief reports is fully accounted for by the equivalences listed in Fig. 1 (that is, \(\textsf {B} A\) and \(\textsf {B} C\) are equivalent when \(A \equiv _e C\)), plus the rule that, if \(\textsf {B} A\) entails \(\textsf {B} C\), then \(\textsf {B} (A \vee B)\) entails \(\textsf {B} (C \vee B)\). Conjunction within belief reports is characterised by a similar rule, plus conjunction elimination (from \(\textsf {B} (A \wedge C)\) to \(\textsf {B} A\)). These axioms and rules give us a deductive relation on sentences, the transitive closure of which is none other than Angell’s Analytic Containment (Angell, 1989):
Definition 7
(Analytic containment) \(\vdash _{\textbf {AC}} \) is the smallest relation between sentences which includes the axioms and is closed under the rules shown in Fig. 2. We read \(A \vdash _{\textbf {AC}} C\) as A analytically implies C and say that the associated proposition \(|A|^{+*}\) analytically contains \(|C|^{+*}\).
[The deductive equivalence of these rules to Angell’s formulation is shown in Fine (2016).]
Theorem 2
\(\textsf {B} A\) entails \(\textsf {B} C\) iff \(A \vdash _\textrm{AC} C\).
Proof
Fine (2016, Theorem 23) shows that \(A \vdash _\textrm{AC} C\) iff \(|C|^{+*} \le |A|^{+*}\) in every model \({\mathcal {M}}\), which is the case iff \(\textsf {B} A\) entails \(\textsf {B} C\). \(\square \)
These results bring out an idea discussed by Elgin (2021) and Yablo (2014), that subject matter is a limiting factor on knowledge or belief ascriptions. (They both focus on the case of knowledge.) Yablo’s idea (discussed in Sect. 1, now transposed to the case of belief) is that you may believe that you closed your front door, without thereby believing that any future evidence to the contrary is misleading. For your belief concerns the subject matter how the door is, which need not include the subject matter whether there is evidence from other sources concerning how the door is (Yablo, 2014, §7.4).
Elgin (2021) argues, on independent grounds, that knowledge is closed under known analytic implication. That is, knowing both that A and that A analytically implies C implies knowing that C. The connection to subject matter is given by the truthmaker semantics for analytic implication, on which analytic implication (\(A \vdash _\textrm{AC} C\)) amounts to conjunctive parthood (\(|C|^{+*} \le |A|^{+*}\)). Note that, on the present semantics, we have no way to express analytic implication, and hence no way to express belief or knowledge of an analytic implication, in the object language.
4 Embedded belief
The account presented in Sect. 3 does not allow us to embed belief reports. We cannot express, and so cannot analyse, an agent who believes she believes some proposition. The restriction is due to our semantics. Belief reports are analysed in terms of propositions (sets of states of affairs). So to analyse an agent who believes she believes some p, \(\textsf {B} \textsf {B} p\), we first need to say what proposition \(\textsf {B} p\) expresses. This is turn requires saying which states s make \(\textsf {B} p\) true. At present, we can say whether or not \(\textsf {B} p\) is true on a model, but not what makes it true or false. We have also focused on the beliefs of a single agent only, whereas much of the interest in epistemic logic arises in the multi-agent case. Let us now remedy these shortcomings.
We consider a finite number of agents i, adding a belief operator \(\textsf {B} _i\) to the propositional language for each, so that \(\textsf {B} _i A\) is a sentence whenever A is. Semantically, we introduce for each agent i a partial function \(\delta _i\) from states s to pairs of regular sets of states \(\langle D^+, D^- \rangle \), understood as the bilateral proposition giving agent i’s doxastic state according to s. \(D^+\) gives the agent’s positive doxastic state and \(D^-\) the agent’s negative doxastic state, relativised to a state of affairs s.
Definition 8
A model for n agents is a quintuple \({\mathcal {M}} = \langle S, \sqsubseteq , \{\delta _i \}_{i \le n}, V^+, V^- \rangle \), where \(\langle S, \sqsubseteq , V^+, V^- \rangle \) is as before and each \(\delta _i\) is a partial function \(S \rightharpoonup (2^S \times 2^S)\) from states to pairs of regular sets of states. Where \(\delta _i s = \langle D^+, D^- \rangle \), we write \(\delta _i^+s\) for \(D^+\) and \(\delta _i^-s\) for \(D^-\).
For agent i to believe A in virtue of s is then for A’s positive content to be part of \(\delta _i^+ s\):

or, spelling out the clause in full:

We may simplify (\(\textsf {B} \)-Up):
Lemma 6
(\(\textsf {B} \)-Up) is equivalent to (\(\textsf {B} \)-Up\('\)):  only if \(u \sqsubseteq \bigsqcup \delta _i^+s\).
only if \(u \sqsubseteq \bigsqcup \delta _i^+s\).
Proof
Given Lemma 3(v), (\(\textsf {B} \)-Up) simplifies to: \(u \in |A|^{+*}\) only if \(u \sqsubseteq \bigsqcup \delta _i^+s\). If  then \(u \in |A|^{+*}\) and so, given (\(\textsf {B} \)-Up), \(u \sqsubseteq \bigsqcup \delta _i^+s\). Thus (\(\textsf {B} \)-Up) implies (\(\textsf {B} \)-Up\('\)). Now assume (\(\textsf {B} \)-Up\('\)). Then \(u \in |A|^{+}\) implies \(u \sqsubseteq \bigsqcup \delta _i^+s\) and so \(\bigsqcup |A|^{+} \sqsubseteq \bigsqcup \delta _i^+s\). But \(\bigsqcup |A|^{+} = \bigsqcup |A|^{+*} = \mathop {\textit{sm}^+}(A)\) and so \(u \sqsubseteq \mathop {\textit{sm}^+}(A) \sqsubseteq \bigsqcup \delta _i^+s\) for any \(u \in |A|^{+*}\). Thus (\(\textsf {B} \)-Up\('\)) implies (\(\textsf {B} \)-Up). \(\square \)
then \(u \in |A|^{+*}\) and so, given (\(\textsf {B} \)-Up), \(u \sqsubseteq \bigsqcup \delta _i^+s\). Thus (\(\textsf {B} \)-Up) implies (\(\textsf {B} \)-Up\('\)). Now assume (\(\textsf {B} \)-Up\('\)). Then \(u \in |A|^{+}\) implies \(u \sqsubseteq \bigsqcup \delta _i^+s\) and so \(\bigsqcup |A|^{+} \sqsubseteq \bigsqcup \delta _i^+s\). But \(\bigsqcup |A|^{+} = \bigsqcup |A|^{+*} = \mathop {\textit{sm}^+}(A)\) and so \(u \sqsubseteq \mathop {\textit{sm}^+}(A) \sqsubseteq \bigsqcup \delta _i^+s\) for any \(u \in |A|^{+*}\). Thus (\(\textsf {B} \)-Up\('\)) implies (\(\textsf {B} \)-Up). \(\square \)
We also need to say when a state makes a belief ascription false. This is where the bilateral semantics earns its keep. The negative component of a total belief state, \(\delta _i^-s\), is intended to model what agent i fails to believe in virtue of state s. There may in general be many reasons for a failure of belief, from explicit evidence to the contrary to the agent’s lack of interest in the topic. We reflect this by allowing a state to be a falsitymaker for \(\textsf {B} _i A\) independently of whether it is a truthmaker for \(\textsf {B} _i A\). For agent i to fail to believe A in virtue of s, is for A’s positive content to be included in \(\delta _i^- s\):

As before, we understand exact entailment (\(A \models _e B\)) and exact equivalence (\(A \equiv _e B\)) in terms of the corresponding regular contents: \(|B|^{+*} \subseteq |A|^{+*}\) and \(|A|^{+*} = |B|^{+*}\), respectively. We shall henceforth call this the truthmaker semantics (TMS) account of belief ascription.
The falsitymaking clause uses (set-theoretic) inclusion, \(|A|^{+*} \subseteq \delta _s^-\), where the truthmaking clause uses parthood, \(|A|^{+*} \le \delta _i^+s\). Why is this? Suppose that, in virtue of some state s, I do not believe the object to be red. We might take s to be a state of visual evidence pertaining to the object’s colour. Then s must thereby count as evidence that the object is not scarlet. In forming my beliefs rationally based on that evidence, s makes it the case that I do not believe the object to be scarlet. The relationship between those contents, it is scarlet and it is red, is one of inclusion, not of parthood: any truthmaker for ‘it is scarlet’ is thereby a truthmaker for ‘it is red’, but some truthmakers for ‘it is red’ (such as the state that it is maroon) will not contain any truthmaker for ‘it is scarlet’.
More generally, we understand s to be a falsitymaker for \(\textsf {B} A\) in terms of \(|A|^{+*}\)’s inclusion in \(\delta _s^-\). Thus \(\delta _s^-\) may be seen as the disjunction of all not-believed content, just as \(\delta _s^+\) may be seen as the conjunction of all believed content. As a consequence, \(\lnot \textsf {B} _i A\) will be an exact consequence of \(\lnot \textsf {B} _i C\) whenever \(|A|^{+*} \subseteq |C|^{+*}\). In particular, \(\lnot \textsf {B} _i (A \vee C)\) will exactly entail \(\lnot \textsf {B} _i A\). (Indeed, if we think of the proposition it is red as the disjunction it is either scarlet or maroon or ..., then this entailment explains the previous example.)
By contrast, \(\lnot \textsf {B} _i A\) will not exactly entail \(\lnot \textsf {B} _i (A \wedge C)\). Because the object appears blue (s), I do not believe it to be red; and because the object appears cylindrical (u), I do not believe it to be rectangular. s alone explains my lack of belief that it is red, whereas s and u together explain my lack of belief that it is both red and rectangular. Of course, given that the object appears blue, I may infer and so come to disbelieve that it is not both red and rectangular. But then I lack that belief in virtue of s combined with my inference (t), not in virtue of s alone.
For positive belief reports \(\textsf {B} _i A\), we retain the if direction of Theorem 2:
Theorem 3
\(\textsf {B} _i A \models _e \textsf {B} C\) if \(A \vdash _\textrm{AC} C\).
Proof
Suppose \(A \vdash _\textrm{AC} C\). From Fine (2016, Theorem 23), \(|C|^{+*} \le |A|^{+*}\), so for any t: \(|C|^{+*} \le \delta ^+ t\) if \(|A|^{+*} \le \delta ^+ t\). Then we have \(|\textsf {B} _i C|^+ \subseteq |\textsf {B} _i A|^+\), hence \(|\textsf {B} _i C|^{+*} \subseteq |\textsf {B} _i A|^{+*}\) and so \(\textsf {B} _i A \models _e \textsf {B} C\). \(\square \)
In particular, \(\textsf {B} _i (A \wedge C)\) exactly entails \(\textsf {B} _i A\) but \(\textsf {B} _i A\) does not exactly entail \(\textsf {B} _i (A \vee C)\). Notice that we have:

Exact entailment does not contrapose. This not a specific feature of doxastic models, for even on the class of basic models \(\langle S, \sqsubseteq , V^+, V^- \rangle \), \(A \models _e C\) does not imply \(\lnot C \models _e \lnot A\).
We will look at more belief ascription entailments in Sect. 6, when we discuss logical omniscience.
5 Truth and introspection
Modal epistemic logics allow us to relate familiar axioms governing the belief operator to principles of the accessibility relation R on worlds. Of particular interest are the T and B axioms:

In the classical modal setting, these correspond to reflexivity and transitivity of the accessibility relation R, respectively. What is the picture on the TMS account?
It will be useful to introduce exact and inexact conditionals, at the level of models rather than states:
Definition 9
\(A \rightarrow C\) is true in a model \({\mathcal {M}}\) (\({\mathcal {M}} \models A \rightarrow C\)) just in case  whenever
whenever  in \({\mathcal {M}}\). Similarly, \(A \twoheadrightarrow C\) is true in \({\mathcal {M}}\) (\({\mathcal {M}} \models A \twoheadrightarrow C\)) just in case
in \({\mathcal {M}}\). Similarly, \(A \twoheadrightarrow C\) is true in \({\mathcal {M}}\) (\({\mathcal {M}} \models A \twoheadrightarrow C\)) just in case  whenever
whenever  in \({\mathcal {M}}\). \(A \rightarrow C\) or \(A \twoheadrightarrow C\) is valid on a class of models \({\mathcal {C}}\) when it is true in all models in \({\mathcal {C}}\).
in \({\mathcal {M}}\). \(A \rightarrow C\) or \(A \twoheadrightarrow C\) is valid on a class of models \({\mathcal {C}}\) when it is true in all models in \({\mathcal {C}}\).
The exact truth axiom, \(\textsf {B} _i A \twoheadrightarrow A\), is of little interest, for what makes it true that an agent has a given belief will not in general be what makes that belief true. The inexact version, (T) above, adequately captures the restriction to true belief. It says that states which contain a truthmaker for \(\textsf {B} _i A\) also contain a truthmaker for A. If we understand truth-at-a-state in terms of that state containing an appropriate truthmaker, then it implies that, at any state, the beliefs held there are true. The semantic condition required for (T) is just the projection function analogue of reflexivity:

Lemma 7
\(\textsf {B} _i A \rightarrow A\) is valid on the class of models which satisfy inclusion (for each agent i and state s).
Proof
Assume \({\mathcal {M}}\) satisfies (inclusion) and  . Then for some \(s^- \sqsubseteq s\),
. Then for some \(s^- \sqsubseteq s\),  and so \(|A|^{+*} \le \delta _i s^-\). By (inclusion), \(s^- \in \delta _i^+ s^-\) and so, by (\(\textsf {B} \)-Down), \(u \in |A|^{+*}\) for some \(u \sqsubseteq s^-\). Since \(u \in |A|^{+*}\), there is some \(u^- \sqsubseteq u\) for which
and so \(|A|^{+*} \le \delta _i s^-\). By (inclusion), \(s^- \in \delta _i^+ s^-\) and so, by (\(\textsf {B} \)-Down), \(u \in |A|^{+*}\) for some \(u \sqsubseteq s^-\). Since \(u \in |A|^{+*}\), there is some \(u^- \sqsubseteq u\) for which  . Then \(u^- \sqsubseteq u \sqsubseteq s^- \sqsubseteq s\) and so
. Then \(u^- \sqsubseteq u \sqsubseteq s^- \sqsubseteq s\) and so  . \(\square \)
. \(\square \)
Now we turn to positive introspection. The picture here is much more complex than in the classical setting, which considers just truth at accessible worlds. In the truthmaker setting, by contrast, we must consider the propositions P contained by a set of accessible states, \(P \le \delta _i s\). The condition required to guarantee (4) is the following, for any content P and state u:

Lemma 8
\(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i\textsf {B} _i A\) and \(\textsf {B} _i A \rightarrow \textsf {B} _i\textsf {B} _i A\) are both valid on the class of models which satisfy (\(\star \)).
Proof
We first show that \(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i\textsf {B} _i A\) is true on all such models. Assume \({\mathcal {M}}\) satisfies (\(\star \)) and  . Then \(|A|^{+*} \le \delta _i^+s\). Let \({\textbf {a}} = \bigsqcup |A|^{+*}\) and \({\textbf {ba}} = \bigsqcup |\textsf {B} _i A|^{+*}\). We show \(|\textsf {B} _i A|^{+*} \le \delta _i^+ s\):
. Then \(|A|^{+*} \le \delta _i^+s\). Let \({\textbf {a}} = \bigsqcup |A|^{+*}\) and \({\textbf {ba}} = \bigsqcup |\textsf {B} _i A|^{+*}\). We show \(|\textsf {B} _i A|^{+*} \le \delta _i^+ s\):
(Up): Consider any  . Then \(|A|^{+*} \le \bigsqcup \delta _i^+ t\) and, given (\(\star \)i), \(t \sqsubseteq {\textbf { a}} \). Since this holds for all \(t \in |\textsf {B} _i A|^+\), we have \(\bigsqcup |\textsf {B} _i A|^+ = \bigsqcup |\textsf {B} _i A|^{+*} = {\textbf {ba}} \sqsubseteq {\textbf { a}} \). Given \(|A|^{+*} \le \delta _i^+ s\), we also have \({\textbf {a}} \sqsubseteq \bigsqcup \delta _i^+ s\). Now consider any \(u \in |\textsf {B} _i A|^{+*}\). Then \(u \sqsubseteq {\textbf {ba}} \), hence \(u \sqsubseteq {\textbf {ba}} \sqsubseteq {\textbf {a}} \sqsubseteq \bigsqcup \delta _i s\) and so \(u \sqsubseteq \bigsqcup \delta _i^+ s\).
. Then \(|A|^{+*} \le \bigsqcup \delta _i^+ t\) and, given (\(\star \)i), \(t \sqsubseteq {\textbf { a}} \). Since this holds for all \(t \in |\textsf {B} _i A|^+\), we have \(\bigsqcup |\textsf {B} _i A|^+ = \bigsqcup |\textsf {B} _i A|^{+*} = {\textbf {ba}} \sqsubseteq {\textbf { a}} \). Given \(|A|^{+*} \le \delta _i^+ s\), we also have \({\textbf {a}} \sqsubseteq \bigsqcup \delta _i^+ s\). Now consider any \(u \in |\textsf {B} _i A|^{+*}\). Then \(u \sqsubseteq {\textbf {ba}} \), hence \(u \sqsubseteq {\textbf {ba}} \sqsubseteq {\textbf {a}} \sqsubseteq \bigsqcup \delta _i s\) and so \(u \sqsubseteq \bigsqcup \delta _i^+ s\).
(Down): Assume \(t \in \delta _i^+ s\). From (\(\star \)ii), \(|A|^{+*} \le \delta _i^+ u\) for some \(u \sqsubseteq t\). Then  and so \(u \in |\textsf {B} _i A|^{+*}\).
and so \(u \in |\textsf {B} _i A|^{+*}\).
It follows that \(|\textsf {B} _i A|^{+*} \le \delta _i^+ s\) and so  . Thus \(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i\textsf {B} _i A\) is valid in models satisfying (\(\star \)). For the inexact case, assume
. Thus \(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i\textsf {B} _i A\) is valid in models satisfying (\(\star \)). For the inexact case, assume  . Then
. Then  for some \(s^- \sqsubseteq s\). By the previous reasoning,
for some \(s^- \sqsubseteq s\). By the previous reasoning,  and so
and so  . So \(\textsf {B} _i A \rightarrow \textsf {B} _i\textsf {B} _i A\) too is valid in models satisfying (\(\star \)). \(\square \)
. So \(\textsf {B} _i A \rightarrow \textsf {B} _i\textsf {B} _i A\) too is valid in models satisfying (\(\star \)). \(\square \)
Condition (\(\star \)) does not look particularly intuitive, especially when compared to its classical analogue, transitivity of R. What does (\(\star \)) mean? Part (i) is a restriction on subject matter: if state s is to make it true that the agent believes that A, then s must be wholly relevant to A’s subject matter. (That is not to say that it makes A true: it need not.) Part (ii) says that for any containment relationship \(P \le Q\), each member t of Q has a part u for which \(P \le \delta _i^+ u\). (This is a slight generalisation, for (\(\star \)) applies only when \(Q = \delta _i^+ s\) for some s. But the point here is that (ii), unlike (i), is not primarily about state s.) There is a kind of transitivity here: if we can go from contents P to Q, and from Q to some \(\delta _i^+ u\) (with u as above), then we can go directly from P to \(\delta _i^+ u\).
6 Logical omniscience
A logic of belief tells us that, as a matter of logic, if certain things are believed then so must be some other things. If the relationship between those things is some strong notion of logical consequence, then we may have a problem: agents will be said to believe far more than any real agent could. Agents will be treated as believing all consequences of what they believe, including all logical validities. Someone with inconsistent beliefs—all of us—might even be treated as believing everything. This is the problem of logical omniscience. What does the TMS account have to say for itself in this regard and how does it compare to other responses in the literature?
On closer inspection, there is not just one problem of logical omniscience here. Fagin et al. (1995, pp. 335–336) and van Ditmarsch et al. (2008, p. 23) discuss the following closure conditions, all of which have been questioned:

Problems of logical omniscience are often addressed by weakening the logic underlying worlds [as, e.g., in Hintikka (1975), Levesque (1984), and Wansing (1990)]. If a paraconsistent logic is adopted, for example, then it is easy to model agents with inconsistent beliefs. And for any choice of sub-classical logic, it will be easy to model agents who do not believe all classical consequences of what they believe.
It is often undesirable to weaken the operative notion of logical consequence in this way, however (Fagin & Halpern, 1988; Jago, 2007). For although we want to accommodate an agent with inconsistent beliefs, we likely want our logic of belief ascription to remain consistent and to preserve some classical (or other strong) notion of consequence. One way to achieve this (within a worlds framework) is to distinguish between two classes of worlds. The normal (or possible) worlds behave classically, whereas the non-normal (or impossible) worlds need not. Belief is defined over all worlds, so that an agent’s beliefs need not be closed under classical consequence. But consequence for the logic is defined over the normal worlds only, so that classical consequence is preserved. This approach is not without problems (Berto & Jago, 2019; Jago, 2014a), but that is not our central concern here.
Let us see how the TMS account compares. As already noted, identity for TMS propositions obeys the commutativity, associativity, distributivity, idempotence, De Morgan, and double negation laws. We therefore have the corresponding exact equivalences for belief ascriptions: \(\textsf {B} _i A \equiv _e \textsf {B} _i C\) whenever \(|A|^{+*} = |C|^{+*}\) (i.e. those equivalences \(A \equiv _e C\) given in Fig. 1). We also have closure under conjunctive parthood: \(\textsf {B} _i A\) exactly entails \(\textsf {B} _i C\) whenever \(|C|^+ \le |A|^+\). In particular, \(\textsf {B} _i (A \wedge C)\) exactly entails \(\textsf {B} _i A\). And conversely, beliefs are closed under conjunction introduction:
Lemma 9
\(\textsf {B} _i A, \textsf {B} _i C\) together exactly entail \(\textsf {B} _i (A \wedge C)\).
Proof
Immediate from Lemma 3(iv) and the clause for \(\textsf {B} _i\). \(\square \)
A key feature of the TMS approach is that belief is not closed under disjunction introduction. \(\textsf {B} _i A\) does not exactly entail \(\textsf {B} _i (A \vee C)\) for arbitrary C, for \(|A \vee C|^+\) is not in general a conjunctive part of \(|A|^+\). The TMS approach validates only (C7) in our list of closure principles, where equivalence is understood classically. (It also validates the analogue of (C4) with equivalence understood as exact equivalence.)
Note that disjunction introduction is a valid exact entailment: A exactly entails \(A \vee C\) for arbitrary C. So belief is not closed under exact entailment (and so not under any of the stronger notions of entailment) on the TMS approach. Failures of omniscience are not achieved by weakening the operative notion of entailment, in other words. Indeed, TMS can recapture a wide variety of consequence relations, including classical entailment. We might take our operative notion of entailment to be the classical one, whilst still avoiding (C8), the entailment from \(\textsf {B} _i A\) to \(\textsf {B} _i (A \vee C)\). And, unlike on the non-normal worlds approach described above, TMS does this with a uniform treatment of the connectives, thus avoiding the compositionality objection.
The TMS approach thus takes beliefs to be closed under conjunction but not under disjunction. It is, in this respect, a dual approach to Lewis’s (1982) logic for equivocators, on which beliefs are closed under disjunction but not conjunction: \(\textsf {B} _iA\) and \(\textsf {B} _iC\) together do not imply \(\textsf {B} _i(A \wedge C)\). Lewis considers failures of omniscience which are due to a fragmented system of beliefs:
My system of beliefs was broken into (overlapping) fragments. Different fragments came into action in different situations, and the whole system of beliefs never manifested itself all at once. (Lewis, 1982, p. 436)
Fagin and Halpern (1988) give a formal model of belief along these lines, which they call a model of ‘local reasoning’. They think in terms of multiple ‘frames of mind’, each corresponding to one of Lewis’s belief fragments. On either approach, an agent believes whatever is believed in some fragment. This results in a degree of inconsistency tolerance. An agent may believe that A in one fragment and that \(\lnot A\) in another, and so believe both overall, without thereby believing arbitrary propositions. They need not believe the explicit contradiction, \(A \wedge \lnot A\), if they never ‘put two and two together’ and combine these fragments of belief.
On Lewis’s and Fagin and Halpern’s approach, each fragment of belief is treated in the classical way, as a set of possible worlds. Thus each fragment must be internally consistent, must contain every classical tautology, and must be closed under logical consequence. So even though the agent’s beliefs as a whole are not classically closed, it remains the case that they are closed under single-premise entailment. Thus, Lewis’s approach satisfies (C1), (C2), (C4), (C5), and (C8), plus (C7) left-to-right. As a response to the logical omniscience problem, Lewis’s approach leaves a lot to be desired. It nevertheless captures a degree of psychological realism. Agents often fail to combine individual beliefs they hold. Believing that A and separately that C does not automatically produce the combined belief that \(A \wedge C\).
We can easily incorporate Lewis’s insight into the TMS approach. We view a doxastic agent as a fragmented system, as with Lewis, but with each local fragment modelled as on the TMS account. Thus, a TMS model of local reasoning for a single agent with multiple frames of mind \(1, \ldots , n\) is a multi-agent model as given in Definition 8, with each doxastic function \(\delta _i\) now understood as giving the content of fragment i of the agent’s total belief state. We read \(\textsf {B} _i A\) as ‘the agent believes that A in fragment i’ and we introduce a new modality, \(\textsf {B} ^+\), to capture her beliefs overall, just as Lewis does:

To model multiple fragmented agents like this, we simply partition the fragments \(1, \ldots , n\) into equivalence classes \(E_1, \ldots , E_m\), each with its own belief modality \(\textsf {B} ^+_k\), with the slightly amended clause:

In what follows, I will ignore this complication with multiple fragments of belief and focus on agents with a single, unfragmented belief state.
Lewis’s approach is both a model of and a reasonable explanation for (C7)’s failure from right-to-left. The TMS account is a model of (C8)’s failure. Can it also supply a reasonable explanation? This will be the topic of the next section.
7 Concept possession
A plausible explanation of why (C8) fails is that it seems inadmissible to ascribe to an agent a belief that goes beyond her conceptual repertoire. Stalnaker (1984, p. 88) gives the example of William III, who in 1700 believed that war with France could be avoided. Yet it seems we cannot say that William thereby believed that nuclear war could be avoided, even though this is clearly implied by what he believed, for he had no grasp of the concept of nuclear war. Similarly, we should not say that he believed that either war or nuclear war could be avoided, even though that proposition is equivalent to what he did believe. Since a disjunction \(A \vee B\) may well involve concepts not present in A alone, we appear to have a plausible explanation for the failure of (C8).
Whether this explanation is acceptable depends on what it is to possess a concept (or, perhaps, on what concepts themselves are). On one approach, concepts are constituents of mental representations or thoughts. On the competing approach, concepts are better understood as abilities. In this section, I shall argue as follows. The former understanding does not provide a good explanation of (C8)’s failure. The latter might, but has a serious problem, which itself may be resolved by reformulating it in terms of truthmaker semantics.
The former cluster of approaches understand concepts as something like items of mental vocabulary or components of inner representations. This is an idea we find in defenders of the representational theory of mind, such as Carruthers (2006), Fodor (2003), and Millikan (2000). We may (for current purposes) also include here views on which concepts are abstract Fregean senses (Peacocke, 1992). What these approaches have in common is that one may possess the concept hesperus without possessing the concept phosphorus, or possess eye doctor without possessing ophthalmologist. One can then explain the cognitive significance of ‘Hesperus is Phosphorus’ or ‘ophthalmologists are eye doctors’ in those terms. On such views, it is natural to take belief ascriptions to be accurate when they correspond to the agent’s inner representations or Fregean thoughts. So possession of the relevant concepts (so understood) will be a necessary condition on belief ascription.
In the epistemic logic literature, logics of awareness draw on ideas along these lines. The approach, beginning with Fagin and Halpern (1988), is to combine a possible worlds approach with a syntactic filter, which specifies the primitive concepts of which the agent is aware. On Fagin and Halpern’s (1988) basic logic of awareness, valuations are restricted to the sentence letters in the agent’s awareness set. If a sentence A contains a letter p not in the awareness set, A will receive no truth-value at any epistemically accessible world. In particular, there may be accessible worlds relative to which A but not \(A \vee B\) is true and hence (C8) is invalidated. The syntactic awareness filter, central to these technical accounts, may be understood as corresponding to the concepts she possesses, in the representational or Fregean sense just given.
Even setting aside technical issues, this approach has philosophical problems. Consider Anna, describing in detail her poor eye health to Cath, an ophthalmologist. Anna does not possess (in the above sense) the concept ophthalmologist, instead thinking of Cath as the doctor at the hospital with expertise in eye problems. We might describe the situation as follows:

This ascription explains why Anna is talking to Cath, whilst conveying also that Anna does not conceptualise her (in the above sense) under ophthalmologist. The ascription is certainly coherent. So it is coherent to ascribe beliefs involving concepts which the agent does not herself use to represent the situation in question. But if so, concept possession (so understood) is not necessary for belief ascription and so we lose our explanation of why (C8) fails.
On the alternative understanding, concepts are understood as abilities of a certain kind (Dummett, 1993). To possess a concept is to able to draw certain distinctions in the world. For Yalcin (2018), ‘a concept determines a matrix of distinctions’ such that
To possess a concept is to have an ability to cut logical space in a certain way, to distinguish possibilities in terms of the sorts of things that answer to the concept. (Yalcin, 2018, p. 36)
In the example, Anna can distinguish ophthalmologists from non-ophthalmologists. What she lacks is competence with the word ‘ophthalmologist’ (and perhaps lacks corresponding inner representations). She stands in contrast in this respect to someone unable to distinguish doctors from non-doctors, to whom we should not attribute a belief like (1), even with the caveat. On this approach, the proper explanation of (C8)’s failure is that an agent may be competent with the concepts involved in A but not with those in B and hence not with all of those in \(A \vee B\).
There is an issue here, however. The ability to distinguish Fs is just the ability to distinguish \(F \wedge (F \vee G)\)s, since necessarily, these are the same individuals. But clearly, the ability to distinguish Fs does not imply the ability to distinguish \(F \vee G\)s. Someone who cannot distinguish Gs at all will be bad at distinguishing \(F \vee G\)s when the Gs are prevalent. But then we must allow in general that conceptual ability with a concept \(F \wedge G\) does not imply conceptual ability with G. So if competence with a concept is necessary for belief and hence for knowledge, this will imply that it is possible to know that something is an \(F \wedge G\) without knowing it to be a G. We surely want to avoid results like this.
My suggestion is that we understand conceptual competence, of the kind required to ascribe to an agent a belief with that conceptual content, in terms of her ability to identify states of the world which correspond exactly to that content. Competence with a concept F amounts to the ability to discern, for any suitable x, a state which exactly decides whether x is F. That state should be an exact truthmaker for \(Fx \vee \lnot Fx\). The requirement of exactness allows for the distinction between F and \(F \wedge (F \vee G)\), which the Lewis–Yablo–Yalcin possible worlds approach does not, and hence avoids the problem just discussed.
(It is an interesting question whether there is independent reason for thinking one can be competent with a conjunctive concept but not with its conjuncts. A referee suggests the following case: a creature unable to detect objects smaller than elephants might thereby count as competent with pink elephant but not with pink. Perhaps that is right for some notion of conceptual competence but, as just noted, this cannot be the operative notion if we wish to take conceptual competence as necessary for belief. One available response is as follows. The operative notion of conceptual competence should be understood relative to the agent’s relevant non-conceptual abilities. Thus, an agent’s competence with a visual concept like pink amounts to the ability to discern, amongst the kind of thing she can see clearly, states which exactly decide whether each such thing is pink. There is clearly much more to be said here, however.)
This approach is clearly close to Yalcin’s. There is a further similarity. For Yalcin, ‘a concept determines a matrix of distinctions’ (2018, p. 36), understood as a partition on possible worlds. Within the Lewis–Yablo tradition, partitions on worlds are also understood as explicating subject matters. So concepts, for Yalcin, are a certain kind of subject matter. On the TMS understanding, by contrast, subject matters are understood as ‘flattened’ propositions (\({\textbf {p}} = \bigsqcup P\) for a unilateral proposition P: see Sect. 2). Each subject matter is a state, not a partition on states (or worlds). We may also align concepts with subject matters, so understood. The concept F is the fusion, for every x, of all states which decide whether x is F. This is the subject matter of the proposition which says, of each individual, that it either is or isn’t an F. If we further identify universally quantified propositions with infinite conjunctions over all individuals (as van Fraassen (1969) does), then the concept F will be identified with the subject matter of \(\forall x (Fx \vee \lnot Fx)\). On this view, as on Yalcin’s account, concepts are not literally components of the propositions or beliefs which involve those concepts (except in the special case of the proposition that everything either has or lacks the concepts in question).
There is clearly much more to be said about Yalcin’s approach and its implementation within the TMS account. I should note that the basic TMS account is not committed to this understanding of concepts. Nevertheless, the overall approach seems to me a very promising way both of explaining the failure of (C8) within the TMS account of belief and of giving an account of concept possession which avoids the worry for Yalcin discussed above.
8 The rationality objection
I want now to address a worry for the TMS approach to belief. It is based on the following principle:

Any rational agent should believe all instances of \(A \vee \lnot A\) (or nearly all instances: we may ignore those cases in which LEM is thought to be questionable). All one need do, to believe any given instance \(A \vee \lnot A\), is to identify that the sentence has the syntactic form it does. I needn’t know what a babirusa is in the slightest to know that either babirusas are mammals or they aren’t. (And if I know it, I believe it.) A similar point can be made with a no-contradiction principle:

I needn’t know what a babirusa is to know that they aren’t both mammals and not mammals. On the TMS account, (nc) has the same effect on belief states as (lem) because \(\lnot (A \wedge \lnot A)\) is exactly equivalent to \(A \vee \lnot A\).
The objection is that accepting (lem) (or (nc)) will render any restriction based on concept possession, of the kinds discussed in Sect. 7, null and void. For in believing each instance of \(A \vee \lnot A\), the agent is thereby treated as possessing, or being competent with, each concept. If the only reason we cannot infer from \(\textsf {B} _i A\) to \(\textsf {B} _i (A \vee C)\) is because of some such restriction, then we may be forced to say the agent who believes both A and \(C \vee \lnot C\) must thereby believe that \(A \vee C\).
This objection affects the logic of awareness (Sect. 7) deeply. On Fagin and Halpern’s (1988) account, being aware of the concepts in a primitive sentence p amounts to believing \(p \vee \lnot p\). For complex sentences A, awareness of the concepts in A amounts to awareness of p for each subsentence p of A. So an agent aware of each A will believe any valid B and, more generally, will be fully logically omniscient in the logic of awareness (Fagin and Halpern, 1988, p. 47, Proposition 3.1).
Whether the worry also affects the TMS account depends on how we interpret (lem). Suppose we take it to mean the following:

This corresponds to the following semantic condition, which leads to troubling results.

Lemma 10
Let  . For any model M which satisfies (lem\('\)):
. For any model M which satisfies (lem\('\)):
-
(i)
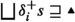 for any s
for any s -
(ii)
\(|A|^{+*} \le \delta _i^+s\) iff for any \(t \in \delta _i^+s\) there is some \(u \sqsubseteq t\) such that \(u \in |A|^{+*}\)
-
(iii)
 iff
iff  for all \(u \in \delta _i^+ s\)
for all \(u \in \delta _i^+ s\)
Proof
-
(i)
Consider any s for which \(\delta _i^+ s\) is defined and let u by any active state. Then \(u \in |A|^+\) for some A and so, by (lem\('\)), \(u \in (|A|^{+*} \cup |A|^{-*})^* \le \delta _i^+ s\). By (Up), \(u \sqsubseteq t\) for some \(t \in \delta _i^+ s\). So
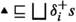 .
. -
(ii)
Consider any \(u \in |A|^{+*}\). By definition,
 for any
for any  and so
and so  . Since \(u \sqsubseteq \mathop {\textit{sm}^+}(A)\), it follows that
. Since \(u \sqsubseteq \mathop {\textit{sm}^+}(A)\), it follows that  . Then by part (i), \(u \sqsubseteq \bigsqcup \delta _i^+s\) if \(\delta _i^+s\) is defined. So (Up) is trivially satisfied and hence \(|A|^{+*} \le \delta _i^+s\) iff (Down).
. Then by part (i), \(u \sqsubseteq \bigsqcup \delta _i^+s\) if \(\delta _i^+s\) is defined. So (Up) is trivially satisfied and hence \(|A|^{+*} \le \delta _i^+s\) iff (Down). -
(iii)
Suppose
 and \(t \in \delta _i^+s\). Then \(|A|^{+*} \le \delta _i^+s\) and so there is some \(u \sqsubseteq t\) such that \(u \in |A|^{+*}\). Then there is a \(u^- \sqsubseteq u \sqsubseteq t\) such that
and \(t \in \delta _i^+s\). Then \(|A|^{+*} \le \delta _i^+s\) and so there is some \(u \sqsubseteq t\) such that \(u \in |A|^{+*}\). Then there is a \(u^- \sqsubseteq u \sqsubseteq t\) such that  and so
and so  . Now suppose
. Now suppose 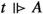 for all \(t \in \delta _i^+ s\) and consider any such t. Then there is some \(u \sqsubseteq t\) such that
for all \(t \in \delta _i^+ s\) and consider any such t. Then there is some \(u \sqsubseteq t\) such that  , hence \(u \in |A|^{+*}\). Since this holds for any such t, by (ii), \(|A|^{+*} \le \delta _i^+s\) and so
, hence \(u \in |A|^{+*}\). Since this holds for any such t, by (ii), \(|A|^{+*} \le \delta _i^+s\) and so  .
.
\(\square \)
Definition 10
(LP) \(\vdash _\text {FDE}\) is the smallest relation between sentences containing \(\vdash _\text {AC}\) and such that: \(A \vdash _\text {FDE} A \vee C\). \(\vdash _\text {LP}\) is the smallest relation between sentences (including \(\top \)) containing \(\vdash _\text {FDE}\) and such that: \(\top \vdash _\text {LP} A \vee \lnot A\). We write \(\vdash _\text {LP} A \vee \lnot A\) for \(\top \vdash _\text {LP} A \vee \lnot A\).
Theorem 4
Both \(\textsf {B} _iA \twoheadrightarrow \textsf {B} _iC\) and \(\textsf {B} _iA \rightarrow \textsf {B} _iC\) are valid on the class of models which satisfy (lem\('\)) whenever \(A \vdash _\text {LP} C\).
Proof
We show the result (for \(\twoheadrightarrow \)) holds for each axiom and rule of LP. Given Theorem 3, it holds for each axiom and rule of AC. From Lemma 10(iii),  iff
iff  for all \(u \in \delta _i^+ s\) only if
for all \(u \in \delta _i^+ s\) only if  for all \(u \in \delta _i^+ s\) iff
for all \(u \in \delta _i^+ s\) iff  . So \(\textsf {B} _i A \models _e \textsf {B} _i (A \vee C)\) and so \(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i (A \vee C)\). Thus the result holds for each axiom and rule of FDE. Finally, given (lem\('\)), \(\models _e \textsf {B} _i A \vee \textsf {B} _i \lnot A\) and so the result (for \(\twoheadrightarrow \)) holds for each axiom and rule of LP. Then by definition, it also holds for \(\rightarrow \). \(\square \)
. So \(\textsf {B} _i A \models _e \textsf {B} _i (A \vee C)\) and so \(\textsf {B} _i A \twoheadrightarrow \textsf {B} _i (A \vee C)\). Thus the result holds for each axiom and rule of FDE. Finally, given (lem\('\)), \(\models _e \textsf {B} _i A \vee \textsf {B} _i \lnot A\) and so the result (for \(\twoheadrightarrow \)) holds for each axiom and rule of LP. Then by definition, it also holds for \(\rightarrow \). \(\square \)
In this proof, we also established:
Corollary 1
(C8) is valid on models which satisfy (lem\('\)).
It is clear that the TMS account must deny (lem-e) if it is to be plausible. Fortunately, (lem-e) is stronger than we need to capture the thought behind (lem), which is simply that rational agents must believe \(A \vee \lnot A\). (lem-e), by contrast, says that every state makes it true that agents believe each instance of \(A \vee \lnot A\). This is not at all plausible, for what makes \(\textsf {B} _i(A \vee \lnot A)\) true and what makes \(\textsf {B} _i(C \vee \lnot C)\) true will often be distinct states. (lem) requires that such states exist, but not that one does the work of all. A state will treat the agent as being rational (with respect to believing instances of \(A \vee \lnot A\)) so long as it contains, for each instance \(\textsf {B} _i (A \vee \lnot A)\), a truthmaker for that instance. Those states need not all be identical. Thus the requirement on models is just that:

With this in place of (lem-e), the results above are blocked and, in particular, (C8) remains invalid.
It is worth delving a little deeper into how this approach accommodates the rationality requirement in (lem) whilst avoiding (C8). Say a state w is a world when  for each A and let W be the set of all worlds. Any such w will have a part u such that
for each A and let W be the set of all worlds. Any such w will have a part u such that  or
or  , so that \(u \in |A \vee \lnot A|^{+*}\). It follows that \(|A \vee \lnot A|^{+*} \le W\) for each A. But it will not be the case that W contains arbitrary disjunctions, say \(|A \vee C|^{+*} \le W\), for there are worlds (the consistent \(\lnot A \wedge \lnot C\)-worlds) with no part in \(|A \vee C|^{+*}\). Now if we set \(\delta _is = W\), then
, so that \(u \in |A \vee \lnot A|^{+*}\). It follows that \(|A \vee \lnot A|^{+*} \le W\) for each A. But it will not be the case that W contains arbitrary disjunctions, say \(|A \vee C|^{+*} \le W\), for there are worlds (the consistent \(\lnot A \wedge \lnot C\)-worlds) with no part in \(|A \vee C|^{+*}\). Now if we set \(\delta _is = W\), then  for each A. In particular, we might set
for each A. In particular, we might set  so that
so that  for each state s and each A. We thus obtain models satisfying (lem-i) but in which
for each state s and each A. We thus obtain models satisfying (lem-i) but in which  does not imply
does not imply  .
.
This demonstrates that the TMS account can treat agents as rational, in the sense of (lem) and the equivalent (nc), whilst avoiding (C8). So the rationality objection based on (lem), which affects awareness-style approaches, does not touch the TMS account.
9 Resources and the problem of rational belief
There is one further objection to the TMS account I wish to consider. It is often said that agents fail to believe some consequences of what they believe simply because they lack the resources to derive those consequences (Jago, 2009; Konolige, 1986). This applies to AI as well as human agents [see, e.g., (Alechina et al., 2006; Jago, 2006)]. The objection is that the TMS account fails to capture this.
Resources include time, memory, and the ability to focus on deductive reasoning. Even when we possess all the relevant concepts and combine all our beliefs pertaining to some deductive problem, complex solutions often elude us. Playing chess is a good example of this. Suppose you and I play a game of chess without time controls in which a draw counts as a win for black. This guarantees the game will have a winner. It is then a surprising mathematical fact that, at any stage of the game, one of us has a winning strategy: a function from the game’s previous moves to that player’s next move that is mathematically guaranteed to win, regardless of how the other player plays. That strategy follows deductively from the rules and the current game position, all of which I believe. Yet no one has ever calculated such a strategy (except in certain endgames, where the complexity reduces significantly). In general, it’s far too complicated. Even the most powerful computer doesn’t play chess purely by cranking out deductive consequences of possible moves. Heuristics, rather than pure deduction, are the backbone of chess strategy.
When I make a daft move, it’s not because I lack some chess-relevant concept, or because my chess-relevant beliefs fall into different fragments of my mind. It’s not that the better move wasn’t relevant to the question, ‘how should I move next?’, or somehow not part of the subject matter I’m considering. It’s just that there’s a limit to how much reasoning of the form, ‘if I move here, you’ll likely move here or here ...’ which I can perform before my mind gives up and starts thinking about pancakes.
Do considerations like these show that an accurate epistemic model should be built on some resource-sensitive logic? Such logics exist: linear logic (Girard, 1987) is a prominent example. Roughly speaking, \(A \vdash B\) can be derived in linear logic when A is exactly what is needed to prove B. Thus \(A, A \vdash B\) may not be derivable even if \(A \vdash B\) is, for the premise-list A, A represents a resource used twice. In this case, although A, A would be sufficient for B, it would be overkill in terms of resources. (There is thus a similarity with exact entailment here, in that \(A \wedge B\) is sufficient but not exactly relevant to A’s truth.)
It is not difficult to see that building an epistemic logic on top of linear logic is not the way to avoid the resourced-based problem of logical omniscience. Linear logic remains too strong in that it validates modus ponens, whereas agents’ beliefs are not in general closed under modus ponens. (Just consider the rules of chess written as implications.) Linear logic is also too weak, in that the doxastic agents we are considering (let us suppose) are happy to infer from \(A \vdash B\) to \(A, A \vdash B\) and vice versa. Indeed, it is not obvious what it could mean for an agent to believe that A twice over, but not believe it once over. The problem is that linear logic views formulas as resources, whereas in epistemic logic, (embedded) formulas represent believed propositions.
This is not merely a problem for linear logic or the TMS approach. It exists regardless of the logic we use to model doxastic agents. The problem at heart is the tug-of-war between the deductive principles we consider constitutive of rationality and the fact that agents do not believe all consequences (given these principles) of what they believe. Modus ponens is constitutive of rationality if any deductive principle is. Now suppose we say, here is a chap who believes that \(A \rightarrow B\) and believes that A, but he just doesn’t believe that B. He’s attentive to the question, he’s thought about it seriously for some time, but still, he doesn’t believe that B. What are we to make of this? We seem to be saying that the agent is irrational. (Perhaps there are genuine cases like this, although they are usually explained in other terms: perhaps the agent accepts some strange theory of the conditional or assigns some other meaning to ‘\(\rightarrow \)’. But in those cases, we should not say that she believes what we mean by \(A \rightarrow B\). Anyway, typical cases are not like this.)
This point is especially hard to avoid for those who accept the Dennettian view that the purpose of ascribing attitudes to an agent is to make rational sense, from our point of view, of her behaviour (Dennett, 1987). There may be behaviour indicative of rejecting an instance of modus ponens: say, the agent’s asserting both premises whilst explicitly denying the conclusion. This is evidence for the stronger ascription, that she believes the conclusion to be false. (And, as just noted, we might interpret such cases as her assigning an unusual meaning to the conditional.) The more typical case is where the agent seemingly fails to take any stance on the conclusion.
Elsewhere, I describe the problem of rational knowledge Jago (2014a, b); here I will call it the problem of rational belief ascription. We note that (i) rational agents seemingly believe the trivial consequences of what they believe, but (ii) they do not believe all logical consequences of what they believe. The problem is that (i) and (ii) are incompatible. Any logical consequence of a set of premises is derivable from those premises via a chain of trivial inferences and so, if one does not believe some logical consequence of what one believes, then one must fail to believe some trivial consequence of what one believes.
There is a structural similarity here with the sorites paradox, which is central to the problem of vagueness. The principle that rational agents believe the trivial consequences of what they believe plays the role that tolerance conditionals (for ‘heap’, say) play in the sorites. Clearly, not all such conditionals are true; but we cannot say or discover which is false. We must acknowledge the existence of borderline cases of ‘heap’ but we cannot say, of a particular case, that it is one such case. This is the phenomena of unassertibility at the borderline. Williamson (1992) puts the point by saying we can have inexact knowledge only and as a consequence we may not rationally assert precise claims in the vicinity of the borderline.
The situation is, I believe, similar in the case of belief ascriptions. We cannot rationally assert that this is the particular trivial inference which does not preserve the agent’s belief, even if that is in fact the case. My view is that such instances of belief failure are always indeterminate instances of belief failure Jago (2014a, b). There is never a case in which agent i determinately believes such-and-such, from which it trivially follows that A, such that it is determinate that i does not believe that A.
This analysis has a rather deflating consequence, however. There are no non-trivial logical principles of inference such that, if the determinately agent believes (or knows) the premises, then it logically follows that she determinately believes (or knows) the conclusion. That seems to imply that there can be no interesting logic of belief or knowledge. But that is too quick. A logic of belief is the attempt to use logical tools to draw interesting, non-trivial conclusions about what agents believe. Given the argument above, any such attempt must idealise away from the actual facts. Any interesting epistemic logic should be viewed as an idealisation away from an agent’s cognitive limitations.
This does not mean we should accept the picture of full omniscience which accompanies the original possible worlds account. We can idealise away from some aspects of an agent’s cognitive state without thereby ignoring all of them. The TMS approach incorporates and allows us to reason about several interesting features of belief. It tolerates incompatible sets of beliefs and even internally inconsistent beliefs. It captures the idea that a total belief state is restricted to a particular subject matter. And, given the arguments of Sects. 6 and 8, it does so better than awareness-based approaches. The TMS account [unlike the semantics given in Jago (2014a, b)] does not capture the way in which an agent’s resources cause her beliefs to ‘grey out’ at some indeterminate point. But likely, neither does any genuinely useful epistemic logic.
References
Alechina, N., Jago, M., & Logan, B. (2006). Modal logics for communicating rule-based agents. Proceedings of ECAI, 06, 322–326.
Angell, R. B. (1989). Deducibility, entailment and analytic containment. In J. Norman & R. Sylvan (Eds.), Directions in relevant logic (pp. 119–143). Kluwer.
Berto, F., & Jago, M. (2019). Impossible worlds. Oxford University Press.
Carruthers, P. (2006). The innate mind: Culture and cognition. Oxford University Press.
Dennett, D. C. (1987). The intentional stance. MIT Press.
Dummett, M. (1993). The seas of language. Oxford University Press.
Elgin, S. (2021). Knowledge is closed under analytic content. Synthese, 199, 5339–5353.
Fagin, R., & Halpern, J. (1988). Belief, awareness and limited reasoning. Artificial Intelligence, 34, 39–76.
Fagin, R., Halpern, J., Moses, Y., & Vardi, M. (1995). Reasoning about knowledge. MIT Press.
Fine, K. (2016). Angellic content. Journal of Philosophical Logic, 45(2), 199–226.
Fine, K. (2017a). A theory of truth-conditional content I: Conjunction, disjunction and negation. Journal of Philosophical Logic, 46(6), 625–674.
Fine, K. (2017b). A theory of truth-conditional content II: Subject-matter, common content, remainder and ground. Journal of Philosophical Logic, 46(6), 675–702.
Fine, K. (2018). Compliance and command II, imperatives and deontics. The Review of Symbolic Logic, 11(4), 634–664.
Fine, K. (2020). Yablo on subject-matter. Philosophical Studies, 177, 129–171.
Fine, K. (2023). An epistemized truthmaker semantics for epistemic logic: Response to Hawke’s and Özgün’s ‘Truthmaker semantics for epistemic logic’. In F. L. Faroldi & F. Van De Putte (Eds.), Kit fine on truthmakers, relevance, and non-classical logic (pp. 337–348). Springer.
Fine, K., & Jago, M. (2019). Logic for exact entailment. Review of Symbolic Logic, 12(3), 536–556.
Fine, K., & Jago, M. (forthcoming). An introduction to truthmaker semantics, Oxford University Press.
Fodor, J. (2003). Hume variations. Oxford University Press.
Girard, J.-Y. (1987). Linear logic. Theoretical Computer Science, 50(1), 1–101.
Hawke, P., & Özgün, A. (2023). Truthmaker semantics for epistemic logic. In F. L. Faroldi & F. Van De Putte (Eds.), Kit fine on truthmakers, relevance, and non-classical logic (pp. 295–335). Springer.
Hintikka, J. (1975). Impossible possible worlds vindicated. Journal of Philisophical Logic, 4, 475–484.
Jago, M. (2006). Logics for resource-bounded agents. PhD Thesis, University of Nottingham.
Jago, M. (2007). Hintikka and Cresswell on logical omniscience. Logic and Logical Philosophy, 15(4), 325–354.
Jago, M. (2009). Resources in epistemic logic. In J.-Y. Béziau & A. Costa-Leite (Eds.), Dimensions of logical concepts (Vol. 55, pp. 11–33). Coleção CLE.
Jago, M. (2014a). The impossible. Oxford University Press.
Jago, M. (2014b). The problem of rational knowledge. Erkenntnis, 79(6), 1151–1168.
Konolige, K. (1986). A deduction model of belief. Morgan Kaufman.
Levesque, H. J. (1984). A logic of implicit and explicit belief. In Proceedings of the fourth national conference on artificial intelligence (pp. 198–202).
Lewis, D. (1982). Logic for equivocators. Noûs, 16(3), 431–441.
Millikan, R. (2000). On clear and confused ideas. Cambridge University Press.
Peacocke, C. (1992). A study of concepts. MIT Press.
Stalnaker, R. (1984). Inquiry. MIT Press.
van Ditmarsch, H., Van Der Hoek, W., & Kooi, B. (2008). Dynamic epistemic logic (Vol. 337). Springer.
van Fraassen, B. (1969). Facts and tautological entailments. Journal of Philosophy, 66(15), 477–487.
Wansing, H. (1990). A general possible worlds framework for reasoning about knowledge and belief. Studia Logica, 49(4), 523–539.
Williamson, T. (1992). Inexact knowledge. Mind, 101(402), 217–242.
Yablo, S. (2014). Aboutness. Princeton University Press.
Yablo, S. (2018). Reply to fine on ‘aboutness’. Philosophical Studies, 175(6), 1495–1512.
Yalcin, S. (2018). Belief as question-sensitive. Philosophy and Phenomenological Research, 97(1), 23–47.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflict of interest involved in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jago, M. Belief in truthmaker semantics. Synthese 204, 123 (2024). https://doi.org/10.1007/s11229-024-04748-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-024-04748-z




 )::
)::

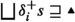 for any s
for any s iff
iff  for all
for all 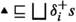 .
. for any
for any  and so
and so  . Since
. Since  . Then by part (i),
. Then by part (i),  and
and  and so
and so  . Now suppose
. Now suppose 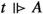 for all
for all  , hence
, hence  .
.