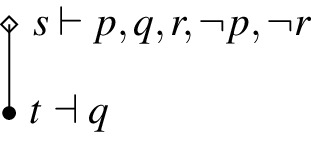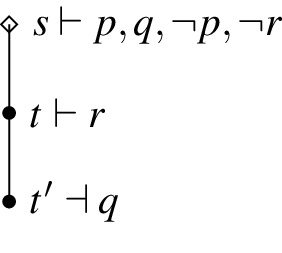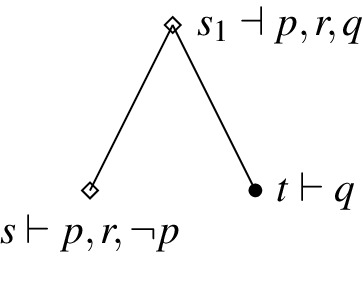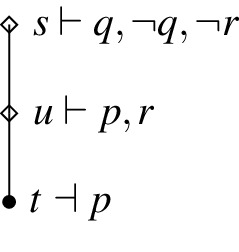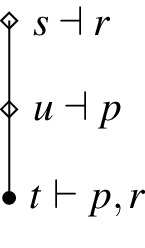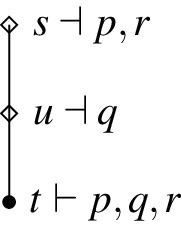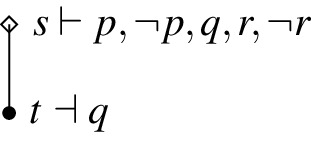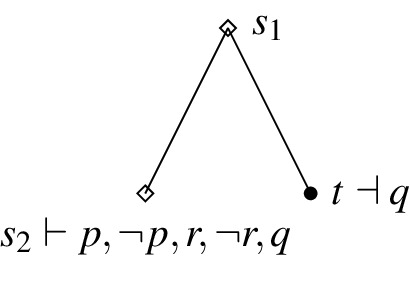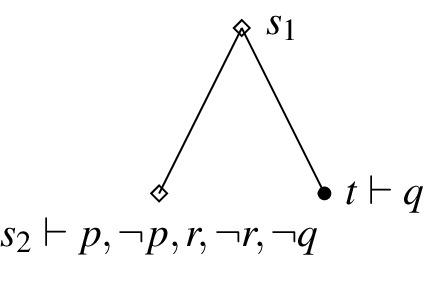Truthmaker Semantics for Epistemic Logic

Abstract

We explore some possibilities for developing epistemic logic using truthmaker semantics. We identify three possible targets of analysis for the epistemic logician. We then list some candidate epistemic principles and review the arguments that render some controversial. We then present the classic Hintikkan approach to epistemic logic and note—as per the ‘problem of logical omniscience’—that it validates all of the aforementioned principles, controversial or otherwise. We then lay out a truthmaker framework in the style of Kit Fine and present six different ways of extending this semantics with a conditional knowledge operator, drawing on notions of implication and content that are prominent in Fine’s work. We demonstrate that different logics are thereby generated, bearing on the aforementioned epistemic principles. Finally, we offer preliminary observations about the prospects for each logic.

Appendix

15.1.1 Auxiliary Lemmas

The following lemmas help us prove Propositions 2 and 3.

Lemma 1

Given a model $\langle S, P, \le , \texttt{v}\rangle$ and $s, t\in S$: if $s\not \in P$ then $s\sqcup t\not \in P$.

Proof

Let $s, t\in S$ such that $s\not \in P$ and suppose $s\sqcup t \in P$. This implies, since P is downward closed and $s\le s\sqcup t$, that $s\in P$, contradicting the assumption.

Lemma 2

Given a model $\texttt{M} = \langle S, P, \le , \texttt{v} \rangle$ and $\varphi \in \mathscr {L}_e$: $|\lnot \varphi |=\{ s\in S : s\dashv \varphi \}$.

Proof

Follows immediately by the exact verification and falsification clauses for $\lnot$ and the definition of $|\varphi |$.

Lemma 3

Given a model $\texttt{M} = \langle S, P, \le , \texttt{v} \rangle$ and $\varphi , \psi \in \mathscr {L}_e$, the following hold for all six interpretations of $K_\varphi \psi$:

• (1) if $|A \varphi |\not =\emptyset$ then $|A\varphi |=S$,

• (2) if $|\lnot A \varphi |\not =\emptyset$ then $|\lnot A \varphi |=S$,

• (3) if $|\varphi \Rightarrow \psi |\not =\emptyset$ then $|\varphi \Rightarrow \psi |=S$,

• (4) if $|\lnot (\varphi \Rightarrow \psi )|\not =\emptyset$ then $|\lnot (\varphi \Rightarrow \psi )|=S$,

• (5) if $|K_\varphi \psi |\not =\emptyset$ then $|K_\varphi \psi |=S$, and

• (6) if $|\lnot K_\varphi \psi |\not =\emptyset$ then $|\lnot K_\varphi \psi |=S$.

Proof

Easy consequence of the corresponding exact truthmaker semantics since none of the exact verification and falsification clauses for $A\varphi , \varphi \Rightarrow \psi$, and $K_\varphi \psi$ is state dependent.

Lemma 4

Given a model $\texttt{M} = \langle S, P, \le , \texttt{v} \rangle$ and $\varphi \in \mathscr {L}_e$: $|\varphi |$ and $|\lnot \varphi |$ are closed under non-empty fusions for all six interpretations of $K_\varphi \psi$.

Proof

The proof follows by induction on the structure of $\varphi$.

Case for $p\in \textsf{Prop}$: holds by the definition of a model (Definition 5).

Now suppose inductively that the statement holds for $\psi , \chi \in \mathscr {L}_e$.

Case for $\lnot \psi$: By the induction hypothesis (IH), we already have that $|\lnot \psi |$ is closed under fusion. Moreover, observe that $|\lnot \lnot \psi |=|\psi |$, by the exact verification and falsification clauses for $\lnot$. Therefore, again by IH, $|\lnot \lnot \psi |$ is a closed under fusion.

Case for $\psi \wedge \chi$: Let $\emptyset \not = T\subseteq |\psi \wedge \chi |$. This means, by the exact verification clause for $\wedge$, that for all $t\in T$, there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t$, $u\vdash \psi$, and $u^{\prime }\vdash \chi$. Denote $T_\psi =\{u\in S : u\vdash \psi \,\text {and there is}\, u^{\prime }\in S\,\text {such that}\,u\sqcup u^{\prime }\in T \,\text {and}\, u^{\prime }\vdash \chi \}$, and similarly, $T_\chi =\{u^{\prime }\in S : u^{\prime }\vdash \chi \,\text {and there is}\, u\in S\, \text {such that}\, u\sqcup u^{\prime }\in T\, \text {and}\, u\vdash \psi \}$. Since $T \not =\emptyset$, we have $T_\psi \not =\emptyset$ and $T_\chi \not =\emptyset$. Moreover, by IH, $\bigsqcup T_\psi \in |\psi |$ and $\bigsqcup T_\chi \in |\chi |$. Finally, since $T\subseteq |\psi \wedge \chi |$, we also have that $\bigsqcup T = \bigsqcup T_\psi \sqcup \bigsqcup T_\chi$. Therefore, by the exact verification clauses for $\wedge$, we obtain that $\bigsqcup T \in |\psi \wedge \chi |$. For $|\lnot (\psi \wedge \chi )|$: let $\emptyset \not = T\subseteq |\lnot (\psi \wedge \chi )|$. This means, by Lemma 2 and the exact falsification clause for $\wedge$, that for all $t\in T$, either $t\dashv \psi$ or $t\dashv \chi$, or there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t$, $u\dashv \psi$, and $u^{\prime }\dashv \chi$. Denote

$T_{\lnot \psi }=\{u\in S : u\dashv \psi \text{ and } \text{ either } u\in T{ orthereis}u^{\prime }\in S{ suchthat}u\sqcup u^{\prime }\in T{ and}u^{\prime }\dashv \chi \}$, and, similarly,

$T_{\lnot \chi }=\{u^{\prime }\in S : u^{\prime }\dashv \chi \, \text {and either}\, u^{\prime }\in T\,\text {or there is}\,u\in S\,\text {such that}\,u\sqcup u^{\prime }\in T\,\text {and}u\dashv \psi \}$. Since $T\not =\emptyset$, $T_{\lnot \psi }\cup T_{\lnot \chi }\not =\emptyset$. The rest follows similarly to the case for $|\psi \wedge \chi |$.

Case for $A \psi$, $\psi \Rightarrow \chi$, and $K_\psi \chi$: Follows from Lemma 3 and the fact that $\langle S, \le \rangle$ is a complete state space.    $\square$

In what follows, counter-models are given in figures immediately below the corresponding explanations. It is easy to see that the given counter-models are of type described in Definition 5. In figures of models, white diamonds represent impossible states and black dots represent possible states. Exact verification and falsification are given by labelling nodes together with symbols $\vdash$ and $\dashv$, respectively. We sometimes write “$\vdash \lnot p$” instead of “$\dashv p$” in order to keep figures clean.

15.1.2 Proof of Proposition 2

Let $\texttt{M} = \langle S, P, \le , \texttt{v} \rangle$ be a model and $s\in S$ be a state.

• (1) Recall the exact verification clause:

  • $s \vdash K_\varphi \psi$ iff for all $t\in P$ (if there is $t^{\prime }\in P$ such that $t^{\prime }\le t$ and $t^{\prime }\vdash \varphi$ then there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash \psi )$

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$:

  We prove only the former, the latter follows similarly: let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime } \vdash p\wedge q$. Thus, by the exact verification clause for $\wedge$, there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. Since $u\le t^{\prime }\le t$, we have $t\sqcup u=t\in P$ and $u\in P$ (since P is downward closed and $t\in P$). As $u\vdash p$ as well, we obtain that $s\vdash K_{p \wedge q} p$.

  Reflexivity: $K_p p$:

  Let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash p$. Since $t\sqcup t^{\prime } =t \in P$ as well, we obtain that $s\vdash K_pp$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_p q$ and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime } \vdash p$. Since $s\vdash K_p q$, the latter implies that there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash q$. Observe that $t^{\prime }\sqcup u\vdash p\wedge q$ (by the exact verification clause for $\wedge$) and $t\sqcup (t^{\prime }\sqcup u)=(t\sqcup t^{\prime })\sqcup u =t\sqcup u$ (since $\sqcup$ is associative and $t^{\prime }\le t$). Therefore, $t\sqcup (t^{\prime }\sqcup u)\in P$ and $t^{\prime }\sqcup u\in P$, thus, $s\vdash K_p(p\wedge q)$.

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime } \vdash p$. Then, by (a), there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash q$. Thus, by the exact verification clause for $\wedge$, we obtain $t^{\prime }\sqcup u\vdash p\wedge q$. Then, as $t^{\prime }\sqcup u\le t\sqcup u\in P$ and $t^{\prime }\sqcup u\in P$, by (b), we have that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ and $u^{\prime }\vdash r$. Now consider $t\sqcup u^{\prime }$. Since $t\sqcup u^{\prime }\le (t\sqcup u)\sqcup u^{\prime }\in P$, we have $t\sqcup u^{\prime }\in P$ (recall that P is downward closed). Since $u^{\prime }\vdash r$ as well, we conclude that $s\vdash K_p r$.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_p r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash p\wedge q$. Hence, by the exact verification clause for $\wedge$, there are $u, u^{\prime }\in S$ with $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. Then, since $u\le t^{\prime }\le t$, we have $u\in P$. Since $u\vdash p$, by (b), we obtain that there is $s^{\prime }\in P$ such that $s^{\prime }\sqcup t\in P$ and $s^{\prime }\vdash r$. Therefore, $s\vdash K_{p\wedge q} r$.

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity, note that $|p|=|\lnot \lnot p|$.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash p\wedge q$. This implies, by the exact verification clause for $\vee$, that $t^{\prime }\vdash p\vee q$. Since $t^{\prime }\sqcup t=t\in P$, we obtain that $s\vdash K_{p \wedge q} (p \vee q)$.

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash p$. This implies, by the exact verification clause for $\vee$, that $t^{\prime }\vdash p\vee \lnot p$. Since $t^{\prime }\sqcup t=t\in P$, we obtain that $s\vdash K_{p} (p \vee \lnot p)$.

  Apriority: $A p \Vdash K_\varphi p$

  Suppose $s\vdash Ap$. This means that for all $t\in P$ there is $t^{\prime }\in P$ such that $t^{\prime }\sqcup t\in P$ and $t^{\prime }\vdash p$. Therefore, $s\vdash K_\varphi p$.

  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime } \vdash p$. Then, by (a), there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash q$. Then, since $t\sqcup u\in P$, $u\le t\sqcup u$, and $u\vdash q$, by (b), we obtain that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ and $u^{\prime }\vdash r$. As $(t\sqcup u')\le (t\sqcup u)\sqcup u^{\prime }$ and P is downward closed, we have $t\sqcup u^{\prime } \in P$. Therefore, we have established that $s\vdash K_p r$.

  Monotonicity: $K_p r \Vdash K_{p\wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Suppose $s\vdash K_\varphi p$ and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash \varphi$. Then, by the assumption that $s\vdash K_\varphi p$, there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash p$. This means that $u\dashv \lnot p$, and that $u\dashv \lnot p\wedge q$. Therefore, $u\vdash \lnot (\lnot p\wedge q)$. As $t\sqcup u\in P$ as well, we conclude that $s\vdash K_\varphi \lnot (\lnot p \wedge q)$.

  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash K_\varphi q$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash \varphi$. Then, by (a), there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash p$. Since $t^{\prime }\le t\le t\sqcup u$, we obtain by (b) that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ and $u^{\prime }\vdash q$. Then, $u\sqcup u^{\prime }\vdash p\wedge q$. As $t\sqcup (u\sqcup u')=(t\sqcup u)\sqcup u^{\prime }\in P$ and $u\sqcup u^{\prime }\in P$ (since P is downward closed), we obtain that $s\vdash K_\varphi (p \wedge q)$.

  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash p \Rightarrow q$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash \varphi$. Then, by (a), there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash p$. Since $u\le t\sqcup u\in P$, we obtain by (b) that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ and $u^{\prime }\vdash q$. Since $u^{\prime }\le t\sqcup u^{\prime }\le (t\sqcup u)\sqcup u^{\prime }\in P$, we have $t\sqcup u^{\prime }\in P$ and $u^{\prime }\in P$. As $u^{\prime }\vdash q$ as well, we conclude that $s\vdash K_\varphi q$.

  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  Suppose (a) $s\vdash K_\varphi \lnot p$ and (b) $s\vdash K_\varphi (p \vee q)$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\vdash \varphi$. Then, by (b), there is $u\in P$ such that $t\sqcup u\in P$ and $u\vdash p\vee q$. Since $t^{\prime }\le t\sqcup u\in P$, we have by (a) that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ and $u^{\prime }\vdash \lnot p$. Therefore, there is no $s^{\prime }\le u$ such that $s^{\prime }\vdash p$: otherwise $(t\sqcup u)\sqcup u^{\prime }\not \in P$, by Lemma 1. Then, since $u\vdash p\vee q$, we have that $u\vdash q$. Since $t\sqcup u\in P$ as well, we conclude that $s\vdash K_\varphi q$.

• (2) Recall the exact verification clause:

  • $s \vdash K_\varphi \psi$ iff for all $t\in P$ (if there is $t^{\prime }\in P$ such that $t^{\prime }\le t$ and $t^{\prime }\dashv \psi$, then there is $u\in P$ such that $t\sqcup u\in P$ and $u\dashv \varphi )$

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$

  We prove only the former, the latter follows similarly: let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv p$. Thus, by the exact falsification clause for $\wedge$, we have $t^{\prime }\dashv p\wedge q$. Since $t\sqcup t^{\prime }=t\in P$ as well, we conclude that $s\vdash K_{p \wedge q} p$.

  Reflexivity: $K_p p$

  Let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv p$. Since $t\sqcup t^{\prime }=t\in P$ as well, we have that $s\vdash K_p p$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_p q$ and $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime } \dashv p\wedge q$. This means, by the exact falsification clause for $\wedge$, that either (1) $t^{\prime }\dashv p$ or (2) $t^{\prime }\dashv q$ or (3) there are $u, u^{\prime }\in S$ such that $t^{\prime }=u\sqcup u^{\prime }$, $u\dashv p$ and $u^{\prime }\dashv q$. If (1) is the case, since $t\sqcup t^{\prime }=t\in P$, we obtain that $s\vdash K_p (p\wedge q)$. If (2) is the case, then, by the assumption that $s\vdash K_p q$, there is $u^{\prime \prime }\in P$ such that $t\sqcup u^{\prime \prime }\in P$ and $u^{\prime \prime }\dashv p$. Therefore, $s\vdash K_p(p\wedge q)$. And, finally, assume that (3) is the case, that is, $t^{\prime }=u\sqcup u^{\prime }$ for some $u, u^{\prime }\in S$ such that $u\dashv p$ and $u^{\prime }\dashv q$. Then, as $u\le t^{\prime }\le t$, we have $t\sqcup u=t\in P$ and $u\in P$ (since P is downward closed). As $u\dashv p$, we have that $s\vdash K_p(p\wedge q)$.

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv r$. Then, by (b), there is $u\in P$ such that $t\sqcup u\in P$ such that $u\dashv p\wedge q$. This means that, either (1) $u\dashv p$, or (2) $u\dashv q$, or (3) there are $u^{\prime }, s^{\prime }\in S$ such that $u=u^{\prime }\sqcup s^{\prime }$, $u^{\prime }\dashv p$ and $s^{\prime }\dashv q$. If (1) is the case, we are done. If (2) is the case: since $u\le u\sqcup t$ we obtain by (a) that there is a $t^{\prime \prime }\in P$ such that $(u\sqcup t)\sqcup t^{\prime \prime }\in P$ and $t^{\prime \prime }\dashv p$. Since $t\sqcup t^{\prime \prime }\le (u\sqcup t)\sqcup t^{\prime \prime }\in P$, we have $t\sqcup t^{\prime \prime }\in P$. If (3) is the case: since $u^{\prime }\le u$, we have $u^{\prime }\le t\sqcup u^{\prime } \le t\sqcup u\in P$. We therefore have $t\sqcup u^{\prime }\in P$, $u^{\prime }\in P$, and $u^{\prime }\dashv p$. Hence, we can conclude that $s\vdash K_p r$.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_p r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv r$. Then, by (b), there is $u\in P$ such that $t\sqcup u\in P$ and $u\dashv p$. Then, by the exact falsification clause of $\wedge$, we have $u\dashv p\wedge q$. This implies that $s\vdash K_{p\wedge q} r$.

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity, note that $|\lnot p|=|\lnot \lnot \lnot p|$.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv p\vee q$. Thus, by the exact falsification clause for $\vee$, there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\dashv p$, and $u^{\prime }\dashv q$. This implies that $t^{\prime }\dashv p\wedge q$. Since $t\sqcup t^{\prime }=t\in P$, we have $s\vdash K_{p \wedge q} (p \vee q)$.

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Since no possible state exactly falsifies $p\vee \lnot p$, weak omniscience is vacuously valid.

  Apriority: $A p \Vdash K_\varphi p$

  Suppose $s\vdash Ap$. This means that for all $t\in P$ there is $t^{\prime }\in P$ such that $t^{\prime }\sqcup t\in P$ and $t^{\prime }\vdash p$. This implies that there is no $t\in P$ such that $t\dashv p$, thus, $s\vdash K_\varphi p$ is vacuously the case.

  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$, and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv r$. Then, by (b), there is $u\in P$ such that $t\sqcup u\in P$ such that $u\dashv q$. Then, as $u \le t\sqcup u\in P$, by (a), we have that there is $u^{\prime }\in P$ such that $(t\sqcup u)\sqcup u^{\prime }\in P$ such that $u^{\prime }\dashv p$. Since P is downward closed and $t\sqcup u^{\prime }\le (t\sqcup u)\sqcup u^{\prime }\in P$, we have $t\sqcup u^{\prime }\in P$. Therefore, $s\vdash K_pr$.

  Monotonicity: $K_p r \Vdash K_{p \wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Suppose $s\vdash K_\varphi p$ and let $t\in P$ such that there is $t^{\prime }\in P$ with $t^{\prime }\le t$ and $t^{\prime }\dashv \lnot (\lnot p \wedge q)$. The latter means, by the exact falsification of $\lnot$, that $t^{\prime }\vdash \lnot p \wedge q$. Thus, there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash \lnot p$, and $u^{\prime }\vdash q$. Since $u\le t^{\prime }\le t$ and P is downward closed, we have $u\in P$. Moreover, as $u\dashv p$, we obtain by the first assumption that there is $s^{\prime }\in P$ such that $t\sqcup s^{\prime }\in P$ and $s^{\prime }\dashv \varphi$. We then conclude that $s\vdash K_\varphi \lnot (\lnot p \wedge q)$.

  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash K_\varphi q$, and let $t\in P$ such that there is $t^{\prime }\in S$ with $t^{\prime }\le t$ and $t^{\prime }\dashv p \wedge q$. Therefore, either $t^{\prime }\dashv p$, or $t^{\prime }\dashv q$, or there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\dashv p$, and $u^{\prime }\dashv q$. If $t^{\prime }\dashv p$, then by (a) there is $s^{\prime }\in P$ such that $t\sqcup s^{\prime }\in P$ and $s^{\prime }\dashv \varphi$. If $t^{\prime }\dashv q$, then by (b) there is $s^{\prime }\in P$ such that $t\sqcup s^{\prime }\in P$ and $s^{\prime }\dashv \varphi$. If there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\dashv p$, and $u^{\prime }\dashv q$, we obtain the same results by (a) and (b) since $u, u^{\prime }\le t^{\prime }\le t$ and, thus, $u, u^{\prime }\in P$. Therefore, $s\vdash K_\varphi (p \wedge q)$.

  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  Counter-example: Since none of the possible states exactly falsifies or verifies p, we have $K_r p$ and $p \Rightarrow q$ exactly verified at every state. However, $t\in P$, $t\dashv q$ and $t\le t$ but there is no state $t^{\prime }\in P$ such that $t\sqcup t^{\prime }\in P$ and $t^{\prime }\dashv r$. Therefore, no state exactly verifies $K_rq$.

  

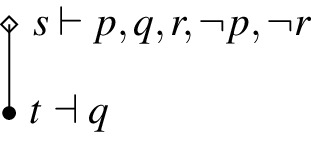
  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  Counter-example: Since none of the possible states exactly falsifies $\lnot p$ or $p\vee q$, we have $K_r \lnot p$ and $K_r (p \vee q)$ exactly verified at every state. Moreover, $t^{\prime }\in P$, $t^{\prime }\dashv q$ and $t^{\prime }\le t^{\prime }$ but there is no state $s^{\prime }\in P$ such that $s^{\prime }\sqcup t^{\prime }\in P$ and $s^{\prime }\dashv r$. Therefore, no state exactly verifies $K_rq$.

  

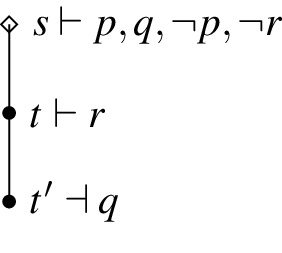
• (3) Recall the exact verification clause:

  • $s \vdash K_\varphi \psi$ iff for all $u\in S$ (if $u\vdash \varphi$ then there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash \psi$)

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$

  Let $u\in S$ such that $u\vdash p\wedge q$. This means that there are $t, t^{\prime }\in S$ with $t\sqcup t^{\prime }=u$, $t\vdash p$, and $t^{\prime }\vdash q$. Since $t, t^{\prime }\le u$, we conclude that $s\vdash K_{p \wedge q} p$ and $s\vdash K_{p \wedge q} q$.

  Reflexivity: $K_p p$

  Follows from the fact that for all $u\in S$, $u\le u$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_p q$ and let $u\in S$ such that $u\vdash p$. Then, by the assumption, there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash q$. Observe also that $u\sqcup u^{\prime }=u$. Then, by the exact verification clause of $\wedge$, we obtain that $u\vdash p\wedge q$. Since $u\le u$, we can conclude that $s\vdash K_p (p\wedge q)$.

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$, and let $u\in S$ such that $u\vdash p$. Then, by (a), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash q$. This implies, by the exact verification clause of $\wedge$, that $u\vdash p\wedge q$. Then, by (b), we conclude that there is $s^{\prime }\in S$ such that $s^{\prime }\le u$ and $s^{\prime }\vdash r$. Therefore, $s\vdash K_p r$.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $K_p r$, and let $u\in S$ such that $u\vdash p\wedge q$. This means that there are $t,t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\vdash p$, and $t^{\prime }\vdash q$. Then, by (b), there is $u^{\prime }\le t$ such that $u^{\prime }\vdash r$. As $u^{\prime }\le t\le u$, we conclude that $s\vdash K_{p\wedge q}r$.

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity, note that $|p|=|\lnot \lnot p|$.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Let $u\in S$ such that $u\vdash p\wedge q$. This implies, by the exact verification clause of $\vee$, that $u\vdash p\vee q$. Since $u\le u$, we obtain that $s\vdash K_{p \wedge q} (p \vee q)$.

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Let $u\in S$ such that $u\vdash p$. This means, by the exact verification clause of $\vee$, that $u\vdash p\vee \lnot p$. Since $u\le u$, we obtain that $s\vdash K_{p} (p \vee \lnot p)$.

  Apriority: $A p \Vdash K_\varphi p$

  Counter-example: Ap is exactly verified everywhere in the model since the only possible state is t and $t\vdash p$. However, although $s_2\vdash r$ there is no $u\le s_2$ such that $u\vdash p$. Therefore, no state exactly verifies $K_r p$.

  

  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$, and let $u\in S$ such that $u\vdash p$. Then, by (a), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash q$. This implies, by (b), that there is $t\in S$ such that $t\le u^{\prime }$ and $t\vdash r$. Since $t\le u^{\prime }\le u$, we conclude that $s\vdash K_p r$.

  Monotonicity: $K_p r \Vdash K_{p \wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Suppose $s\vdash K_\varphi p$ and let $u\in S$ such that $u\vdash \varphi$. Then, by the assumption, there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash p$. Then, following the exact verification and falsification clauses for $\lnot$ and $\wedge$, we obtain that $u^{\prime }\vdash \lnot (\lnot p \wedge q)$. Therefore, we obtain that $s\vdash K_\varphi \lnot (\lnot p \wedge q)$.

  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash K_\varphi q$, and let $u\in S$ such that $u\vdash \varphi$. Then, by (a), there is $t\in S$ such that $t \le u$ and $t\vdash p$. And, by (b), there is $t^{\prime }\in S$ such that $t^{\prime } \le u$ and $t^{\prime }\vdash q$. Therefore, $t\sqcup t^{\prime }\vdash p\wedge q$. Moreover, $t\sqcup t^{\prime }\le u$ since both $t \le u$ and $t^{\prime } \le u$. Therefore, $s\vdash K_\varphi (p \wedge q)$.

  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  Counter-example: There is no possible state that verifies p, thus, $p\Rightarrow q$ is vacuously exactly verified by every state. Moreover, s is the only state that exactly verifies r, $s\vdash p$ and $s\le s$. Therefore, $K_rp$ is also exactly verified by every state. However, there is no state u such that $u\le s$ and $u\vdash q$. Hence, $K_r q$ is not exactly verified.

  

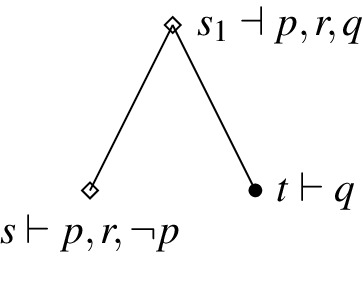
  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  Counter-example: u is the only state that exactly verifies r. We then have that $t\le u$ and $t\vdash \lnot p$, and $u\le u$ and $u\vdash p\vee q$ (since $u\vdash p$). Therefore, both $K_r \lnot p$ and $K_r (p \vee q)$ are exactly verified by every state in the model. However, there is no state $u^{\prime }$ such that $u^{\prime }\le u$ and $u^{\prime }\vdash q$. Therefore, $K_r q$ is not exactly verified in this model.

  

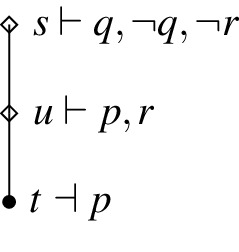
• (4) Recall the exact verification clause:

  • $s \vdash K_\varphi \psi$ iff for all $u\in S$ (if $u\dashv \psi$ then there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv \varphi$)

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$

  We prove only the former, the latter follows similarly: let $u\in S$ such that $u\dashv p$. This implies, by the exact falsification clause of $\wedge$, that $u\dashv p\wedge q$. Since $u\le u$, we conclude that $s\vdash K_{p \wedge q} p$.

  Reflexivity: $K_p p$

  Follows from the fact that for all $u\in S$, $u\le u$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_p q$ and let $u\in S$ such that $u\dashv p\wedge q$. Then, by the exact falsification clause of $\wedge$, we have that either (a) $u\dashv p$, or $u\dashv q$, or (c) there is $t, t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\dashv p$, and $t^{\prime }\dashv q$. If (a) is the case, we obtain the result since $u\le u$. If (b) is the case, then by the first assumption, there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv p$. If (c) is the case, we again obtain the result since $t\le u$.

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$, and let $u\in S$ such that $u\dashv r$. Then, by (b), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv p\wedge q$. This means that either (1) $u^{\prime }\dashv p$, or (2) $u^{\prime }\dashv q$, or (3) there are $t, t^{\prime }\in S$ such that $t\sqcup t^{\prime }=u^{\prime }$, $t\dashv p$ and $t^{\prime }\dashv q$. If (1) is the case, since $u^{\prime }\le u$, we have the desired result. If (2) is the case, by (a), there is $s^{\prime }\in S$ such that $s^{\prime }\le u^{\prime }$ and $s^{\prime }\dashv p$. As $s^{\prime }\le u^{\prime }\le u$ and $\le$ is transitive, we have that $s^{\prime }\le u^{\prime }$. If (3) is the case: since $t\le u^{\prime }\le u$, we have $t\le u$. Then, as $t\dashv p$, we obtain that the desired conclusion. Therefore, $s\vdash K_p r$.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $K_p r$, and let $u\in S$ such that $u\dashv r$. Then, by (b), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv p$. Then, by the exact falsification clause for $\wedge$, we have $u^{\prime }\dashv p\wedge q$. Therefore, $s\vdash K_{p\wedge q} r$.

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity, note that $|\lnot p|=|\lnot \lnot \lnot p|$.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Let $u\in S$ such that $u\dashv p\vee q$. This means that there are $t, t^{\prime }\in S$ such that $t\sqcup t^{\prime }=u$, $t\dashv p$, and $t^{\prime }\dashv q$. This implies that $t\dashv p\wedge q$. Since $t\le u$, we obtain that $s\vdash K_{p \wedge q} (p \vee q)$.

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Let $u\in S$ such that $u\dashv p\vee \lnot p$. This means that there are $t, t^{\prime }\in S$ such that $t\sqcup t^{\prime }=u$, $t\dashv p$, and $t^{\prime }\dashv \lnot p$. Since $t\le u$, we obtain that $s\vdash K_{p} (p \vee \lnot p)$.

  Apriority: $A p \Vdash K_\varphi p$

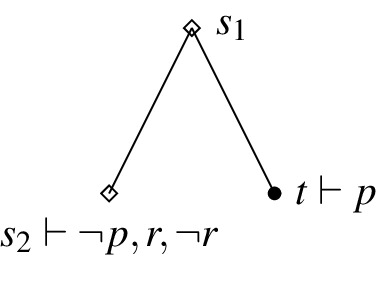
  Counter-example: Ap is exactly verified everywhere in the model since the only possible state is t and $t\vdash p$. However, although $u\dashv p$ there is no $u^{\prime }\le u$ such that $u^{\prime }\dashv r$. Therefore, no state exactly verifies $K_r p$.

  

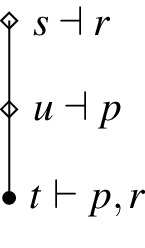
  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$, and let $u\in S$ such that $u\dashv r$. Then, by (b), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv q$. This implies, by (a), that there is $t\in S$ such that $t\le u^{\prime }$ and $t\dashv p$. Since $t\le u^{\prime }\le u$, we conclude that $s\vdash K_p r$.

  Monotonicity: $K_p r \Vdash K_{p \wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Suppose $s\vdash K_\varphi p$ and let $u\in S$ such that $u\dashv \lnot (\lnot p \wedge q)$. The latter means that $u\vdash \lnot p \wedge q$. Thus, there are $t, t^{\prime }\in S$ such that $t\sqcup t^{\prime }=u$, $t\vdash \lnot p$, and $t^{\prime }\vdash q$. Therefore, $t\dashv p$. Then, by the first assumption, there is $t^{\prime \prime }\le t$ such that $t^{\prime \prime }\dashv \varphi$. Since $t^{\prime \prime }\le t\le u$, we conclude that $s\vdash K_\varphi \lnot (\lnot p \wedge q)$.

  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash K_\varphi q$, and let $u\in S$ such that $u\dashv p \wedge q$. Therefore, either (1) $u\dashv p$, or (2) $u\dashv q$, or (3) there are $t, t^{\prime }\in S$ such that $t\sqcup t^{\prime }=u$, $t\dashv p$, and $t^{\prime }\dashv q$. If (1) is the case, then, by (a), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv \varphi$. If (2) is the case, then by (b), there is $u^{\prime }\in S$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv \varphi$. If (3) is the case, we obtain the same results by (a) and (b) since $t, t^{\prime }\le u$. Therefore, $s\vdash K_\varphi (p \wedge q)$.

  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  Counter-example: Since the only possible state is t and $t\vdash p$ and $t\vdash q$, we have that $p \Rightarrow q$ is exactly verified by every state in the model. The only state that exactly falsifies p is s, and we moreover have that $s\le s$ and $s\dashv r$. Therefore, $K_r p$ is also exactly verified by every state of the model. However, $u\dashv q$ but there is no $u^{\prime }$ such that $u^{\prime }\le u$ and $u^{\prime }\dashv r$. Therefore, $K_rq$ is not exactly verified.

  

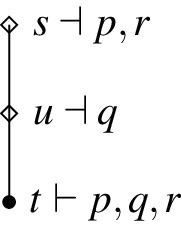
  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  Counter-example: The only state that exactly falsifies $\lnot p$ and $p\vee q$ is s. It moreover exactly falsifies r and $s\le s$. Therefore, both $K_r \lnot p$ and $K_r (p \vee q)$ are exactly verified by every state in the model. However, t is the only state that exactly falsifies q and there is no $u^{\prime }$ such that $u^{\prime }\le t$ with $u^{\prime }\dashv r$. Therefore, $K_r q$ is not exactly verified.

  

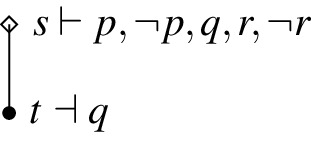
     $\square$

15.1.3 Proof of Proposition  3

Let $\texttt{M} = \langle S, P, \le , \texttt{v} \rangle$ be a model and $s\in S$ be a state.

• (5) Recall the exact verification clause:

  $$\begin{aligned} s \vdash K_\varphi \psi \,\text {iff}\,& (1) \, \text {for all}\, u\in S\, (\text {if}\, u\vdash \varphi \, \text {then there is}\, u^{\prime }\in S\nonumber \\ {} &\quad \quad \text {such that}\, u^{\prime }\le u\, \text {and} \,u^{\prime }\vdash \psi ), \,\text {and}\nonumber \\ & (2)\, \text {for all}\, u\in S\, (\text {if}\, u\dashv \psi \, \text {then}\, u\dashv \varphi ),\, \text {and}\nonumber \\ & (3)\, \text {for all}\, u\in S\, (\text {if}\, u\vdash \psi \, \text {then there is}\, u^{\prime }\in S\nonumber \\ {} &\quad \quad \text {such that}\, u\le u^{\prime }\, \text {and}\, u^{\prime }\vdash \varphi ).\nonumber \end{aligned}$$

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$

  We prove only the former, the latter follows similarly. Item (1) is proved for the third definition of knowledge. For (2), let $u\in S$ such that $u\dashv p$. This implies, by the falsification clause for $\wedge$, that $u\dashv p\wedge q$. For (3) let $u\in S$ such that $u\vdash p$. Since $q^+\not =\emptyset$, there is $u^{\prime }\in S$ such that $u^{\prime }\vdash q$. Therefore, $u\sqcup u^{\prime }\vdash p\wedge q$. Moreover, $u\sqcup u^{\prime }\ge u$. Hence, we have (3).

  Reflexivity: $K_p p$

  Item (1) is proven for the third definition of knowledge. Item (2) is vacuously true. Item (3) follows from the fact that $u\le u$ for all $u\in S$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_pq$ and show $s\vdash K_p(p\wedge q)$. Item (1) is proven for the third definition of knowledge. For (2): let $u\in S$ such that $u\dashv p\wedge q$. This implies that either (a) $u\dashv p$, or (b) $u\dashv q$, or (c) there are $t, t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\dashv p$, and $t^{\prime }\dashv q$. If (a) is the case, we are done. If (b) is the case, then $u\dashv p$ since $s\vdash K_pq$. If (c) is the case, then $t^{\prime }\dashv p$ again by $s\vdash K_pq$. Then, since $p^-$ is closed under fusion, $t\dashv p$, and $t\sqcup t^{\prime }=u$, we have that $u\in p^-$. I.e., $u\dashv p$. For (3): let $u\in S$ such that $u\vdash p\wedge q$. This means, by the exact verification clause of $\wedge$, that there are $t, t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\vdash p$, and $t^{\prime }\vdash q$. Since $s\vdash K_pq$, the fact that $t^{\prime }\vdash q$ implies that there is $u^{\prime }\in S$ such that $t^{\prime }\le u^{\prime }$ and $u^{\prime }\vdash p$. Since $p^+$ is closed under fusion, we have that $u^{\prime }\sqcup t\in p^+$, i.e., $u^{\prime }\sqcup t\vdash p$. Since $u=t^{\prime }\sqcup t$ and $t^{\prime }\le u^{\prime }$, we also have that $u\le u^{\prime }\sqcup t$. We therefore obtain the result.

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$:

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$. Item (1) is proven for the third definition of knowledge. For (2): let $u\in S$ such that $u\dashv r$. Then, by (b), we have that $u\dashv p\wedge q$. Then, either (a$^*$) $u\dashv p$, or (b$^*$) $u\dashv q$, or (c$^*$) there are $u_1, u_2$ such that $u=u_1\sqcup u_2$, $u_1\dashv p$, and $u_2\dashv q$. If (a$^*$) is the case, we are done. If (b$^*$) is the case, by (a), we have that $u\dashv p$. If (c$^*$) is the case, by (a), we have that $u_2\dashv p$. Then, since $p^-$ is closed under fusion, we obtain that $u=u_1\sqcup u_2\dashv p$. For (3): let $t\in S$ such that $t\vdash r$. Then, by (b), there is $t^{\prime }\ge t$ such that $t^{\prime }\vdash p\wedge q$. This means that there are $u, u^{\prime }\in S$ such that $t^{\prime }=u\sqcup u^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. Then, by (a), there is $s^{\prime }\in S$ such that $s^{\prime }\ge u^{\prime }$ and $s^{\prime }\vdash p$. Observe that, since $t^{\prime }=u\sqcup u^{\prime }$ and $s^{\prime }\ge u^{\prime }$, we have that $u\sqcup s^{\prime }\ge t^{\prime }\ge t$. And, since $p^+$ is closed under fusion, $u\sqcup s^{\prime }\vdash p$. Therefore, $s\vdash K_p r$.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $K_p r$. Item (1) is proven for the third definition of knowledge. To prove (2) let $u\in S$ such that $u\dashv r$. Then, by (b), $u\dashv p$. This immediately implies that $u\dashv p\wedge q$. To prove (3), suppose $t\in S$ such that $t\vdash r$. Then, by (b), there is $t^{\prime }\in S$ such that $t^{\prime }\ge t$ and $t^{\prime }\vdash p$. We know that $q^+\not =\emptyset$ so there is $s^{\prime }\in S$ such that $s^{\prime }\vdash q$. This means that $t^{\prime }\sqcup s^{\prime }\vdash p\wedge q$. Since $t^{\prime }\ge t$, we have $t^{\prime }\sqcup s^{\prime }\ge t$, therefore, we obtain (3).

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Item (1) is proved for the third definition of knowledge. To prove (2) let $u\in S$ such that $u\dashv p\vee q$. This implies, by the exact falsification clauses of $\vee$ and $\wedge$, that $u\dashv p\wedge q$. To prove (3), suppose $t\in S$ such that $t\vdash p\vee q$. Then, either (a) $t\vdash p$, or (b) $t\vdash q$, or (c) there are $u, u^{\prime }\in S$ such that $t=u\sqcup u^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. If (a) is the case: we know that $q^+\not =\emptyset$ so there is $s^{\prime }\in S$ such that $s^{\prime }\vdash q$. This implies that $t\sqcup s^{\prime }\vdash p\wedge q$. Since $t\sqcup s^{\prime }\ge t$, we obtain the desired result. If (b) is the case: we know that $p^+\not =\emptyset$ so there is $s^{\prime }\in S$ such that $s^{\prime }\vdash p$. This means that $t\sqcup s^{\prime }\vdash p\wedge q$. Since $t\sqcup s^{\prime }\ge t$, we obtain the desired result. If (c) is the case, we have that $t\vdash p\wedge q$. As $t\ge t$, we obtain (3).

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Counter-example: For $t\vdash \lnot p$, we have $t\vdash p\vee \lnot p$. However, there is no $t^{\prime }\in S$ such that $t^{\prime }\ge t$ and $t^{\prime }\vdash p$. This violates item (3) in the above exact verification clause. Therefore, no state in the model exactly verifies $K_{p} (p \vee \lnot p)$.

  

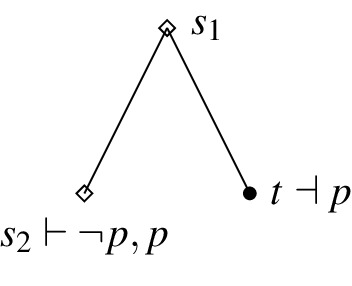
  Apriority: $A p \Vdash K_\varphi p$:

  See the counterexample in the proof of Proposition 2 for the third definition of knowledge. The same counterexample violates item (1).

  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$. Item (1) is proved for the third definition of knowledge. To prove (2) let $u\in S$ such that $u\dashv r$. Then, by (b), we have that $u\dashv q$. Then, similarly by (a), we have that $u\dashv p$. To prove (3), let $u\in S$ such that $u\vdash r$. Then, by (b), there is $u^{\prime }\in S$ such that $u\le u^{\prime }$ and $u^{\prime }\vdash q$. Then, similarly by (a), there is $u^{\prime \prime }\in S$ such that $u^{\prime }\le u^{\prime \prime }$ and $u^{\prime \prime }\vdash p$. Since $\le$ is transitive, we also have $u\le u^{\prime \prime }$. We therefore conclude $s\vdash K_p r$.

  Monotonicity: $K_p r \Vdash K_{p \wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Counter-example: $K_r p$ is exactly verified at every state of the model. However, for example, $t\vdash \lnot (\lnot p\wedge q)$ but there is no $u\ge t$ such that $u\vdash r$. This violates item (3) in the above exact verification clause. Thus, no state of the model exactly verifies $K_\varphi \lnot (\lnot p \wedge q)$.

  

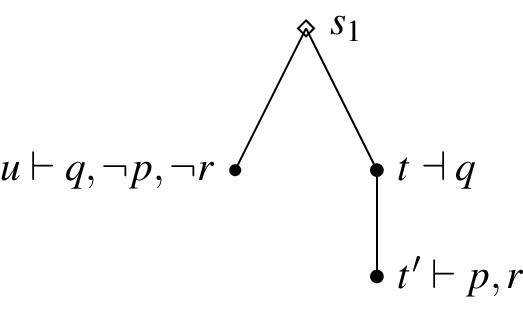
  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Suppose (a) $s\vdash K_\varphi p$ and (b) $s\vdash K_\varphi q$. Item (1) is proven for the third definition of knowledge. To prove item (2), let $t\in S$ such that $t\dashv p\wedge q$. Then, either (a$^*$) $t\dashv p$, or (b$^*$) $t\dashv q$, or (c$^*$) there are $u_1, u_2$ such that $t=u_1\sqcup u_2$, $u_1\dashv p$, and $u_2\dashv q$. If (a$^*$) is the case, by (a), we have $t\dashv \varphi$. If (b$^*$) is the case, by (b), we have that $t\dashv \varphi$. If (c$^*$) is the case, by (a) and (b), we have that $u_1\dashv \varphi$ and $u_2\dashv \varphi$. Then, by Lemma 4, we obtain that $t=u_1\sqcup u_2\dashv \varphi$. To prove (3) suppose $t\in S$ such that $t\vdash p\wedge q$. Then, there are $u, u^{\prime }\in S$ such that $t=u\sqcup u^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. Then, by (a) and (b), there are $s^{\prime }, t^{\prime }\in S$ such that $u\le s^{\prime }$ and $s^{\prime }\vdash \varphi$, and $u^{\prime }\le t^{\prime }$ such that $t^{\prime }\vdash \varphi$. Then, by Lemma 4, $s^{\prime }\sqcup t^{\prime }\vdash \varphi$. As $t=u\sqcup u^{\prime }$, $u\le s^{\prime }$, and $u^{\prime }\le t^{\prime }$, we also have $t\le s^{\prime }\sqcup t^{\prime }$, which proves item (3).

  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  See the counterexample in the proof of Proposition 2 for the third definition of knowledge. The same counterexample violates item (1).

  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  See the counterexample in the proof of Proposition 2 for the third definition of knowledge. The same counterexample violates item (1).

• (6) Recall the exact verification clause:

  $$\begin{aligned} s \vdash K_\varphi \psi \,\text {iff}\,& (1) \, \text {for all}\, t\in P\, (\text {if there is}\,t^{\prime }\in P\, \text {such that}\, t^{\prime }\le t \,\text {and}\, t^{\prime }\vdash \varphi \, \text {then} \nonumber \\ & \quad \quad \text {there is}\, u\in P\, \text {such that}\, t\sqcup u\in P\,\text {and}\, u\vdash \psi ), \,\text {and}\nonumber \\ & (2)\, \text {for all}\, u\in S\, (\text {if}\, u\vdash \psi \, \text {then there is}\, u^{\prime }\in S\nonumber \\ & \quad \quad \text {s.t.}\, u\le u^{\prime }\,\text {and}\, u^{\prime }\vdash \varphi \vee \lnot \varphi ),\, \text {and}\nonumber \\ & (3)\, \text {for all}\, u\in S\, (\text {if}\, u\dashv \psi \, \text {then there is}\, u^{\prime }\in S\nonumber \\ &\quad \quad \text {s.t.}\, u\le u^{\prime }\,\text {and}\,u^{\prime }\vdash \varphi \vee \lnot \varphi )\nonumber \end{aligned}$$

  Simplification: $K_{p \wedge q} p, K_{p \wedge q} q$

  Item (1) is proven for the first definition of knowledge. For (2) let $t\in S$ such that $t\vdash p$. Since $q^+\not =\emptyset$, there is $s^{\prime }\in S$ such that $s^{\prime }\vdash q$. Then, $t\sqcup s^{\prime }\vdash p\wedge q$. This implies that $t\sqcup s^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. As $t\sqcup s^{\prime }\ge t$, we obtain (2). Item (3) follows easily since $t\dashv p$ implies that $t\dashv p\wedge q$, i.e., $t\vdash \lnot (p\wedge q)$. Therefore, $t\vdash (p \wedge q)\vee \lnot (p\wedge q)$. The result then follows since $t\le t$.

  Reflexivity: $K_p p$

  Item (1) is proven for the first definition of knowledge. (2) and (3) follows from the facts that for all $t\in S$: $t\le t$, and if $t\vdash p$ or $t\vdash \lnot p$, we have $t\vdash p\vee \lnot p$.

  Cautious Aggloremation: $K_p q \Vdash K_p (p\wedge q)$

  Suppose that $s\vdash K_pq$. Item (1) is proven for the first definition of knowledge. To prove (2), let $u\in S$ such that $u\vdash p\wedge q$. This means that there are $t, t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\vdash p$ and $t^{\prime }\vdash q$. Therefore, $t\vdash p\vee \lnot p$. Moreover, $t^{\prime }\vdash q$ implies by the first assumption that there is $u^{\prime }\in S$ such that $t^{\prime }\le u^{\prime }$ and $u^{\prime }\vdash p\vee \lnot p$. As $u=t\sqcup t^{\prime }$ and $t^{\prime }\le u^{\prime }$, we have that $u\le t\sqcup u^{\prime }$. Moreover, by Lemma 4, we have that $t\sqcup u^{\prime }\vdash p\vee \lnot p$. Thus, we proved (2). To prove (3), let $u\in S$ such that $u\dashv p\wedge q$. We then have the following cases:

  If $u\dashv p$, we have that $u\vdash \lnot p$ and thus $u\vdash p\vee \lnot p$. Since $u\le u$, we obtain the result.

  If $u\dashv q$, then, by the first assumption, there is $u^{\prime }\in S$ such that $u\le u^{\prime }$ and $u^{\prime }\vdash p\vee \lnot p$.

  If there are $t, t^{\prime }\in S$ such that $u=t\sqcup t^{\prime }$, $t\dashv p$ and $t^{\prime } \dashv q$, we obtain that $t\vdash p\vee \lnot p$. Moreover, by $t^{\prime } \dashv q$ and the first assumption, there is $u^{\prime }\in S$ such that $t^{\prime }\le u^{\prime }$ and $u^{\prime }\vdash p\vee \lnot p$. As $u=t\sqcup t^{\prime }$ and $t^{\prime }\le u^{\prime }$, we have that $u\le t\sqcup u^{\prime }$. Moreover, by Lemma 4, we have that $t\sqcup u^{\prime }\vdash p\vee \lnot p$. Thus, we proved (3).

  Cautious Transitivity: $K_p q, K_{p\wedge q} r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_{p\wedge q} r$. Item (1) is proven for the first definition of knowledge. For (2): let $t\in S$ such that $t\vdash r$. Then, by (b), there is $t^{\prime }\in S$ such that $t^{\prime }\ge t$ and $t^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. We then have three cases:

  Case $t^{\prime }\vdash p\wedge q$: This means that there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash q$. The former implies that $u\vdash p\vee \lnot p$. Moreover, $u^{\prime }\vdash q$ implies by (a) there is $s^{\prime }\in S$ such that $s^{\prime }\ge u^{\prime }$ and $s^{\prime }\vdash p\vee \lnot p$. Since $s^{\prime }\ge u^{\prime }$, we obtain that $s^{\prime }\sqcup u\ge u\sqcup u^{\prime }=t^{\prime }\ge t$. Since $|p\vee \lnot p|$ is closed under fusion (by Lemma 4), we also have that $s^{\prime }\sqcup u\vdash p\vee \lnot p$.

  Case $t^{\prime }\vdash \lnot (p\wedge q)$: Then, we have three subcases.

  If $t^{\prime }\vdash \lnot p$, then $t^{\prime }\vdash p\vee \lnot p$. Since $t^{\prime }\ge t$, we obtain the desired result.

  If $t^{\prime }\vdash \lnot q$, then by (a), there is $s^{\prime }\ge t^{\prime }$ such that $s^{\prime }\vdash p\vee \lnot p$. Since $s^{\prime }\ge t^{\prime }\ge t$, we obtain the desired result.

  If there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash \lnot p$, and $u^{\prime }\vdash \lnot q$, it follows similar to the first case.

  Case $t^{\prime }\vdash (p\wedge q)\wedge \lnot (p\wedge q)$: Then, there are $u, u^{\prime }\in S$ such that $u\sqcup u^{\prime }=t^{\prime }$, $u\vdash (p\wedge q)$, and $u^{\prime }\vdash \lnot (p\wedge q)$. By a similar argument as in the first case, there is $s^{\prime }\in S$ such that $s^{\prime }\ge u$ and $s^{\prime }\vdash p\vee \lnot p$. Again, by a similar argument as in the second case, there is $s^{\prime \prime }\in S$ such that $s^{\prime \prime }\ge u^{\prime }$ and $s^{\prime \prime }\vdash p\vee \lnot p$. Since $s^{\prime }\ge u$ and $s^{\prime \prime }\ge u^{\prime }$, we have $s^{\prime \prime }\sqcup s^{\prime }\ge u\sqcup u^{\prime }=t^{\prime }\ge t$. Moreover, since $|p\vee \lnot p|$ is closed under fusion, we also have that $s^{\prime \prime }\sqcup s^{\prime }\vdash p\vee \lnot p$. Therefore, we have proven (2).

  Item (3) follows similarly.

  Cautious Monotonicity: $K_p q, K_p r \Vdash K_{p\wedge q} r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_p r$. Item (1) is proven for the first definition of knowledge. For (2): let $t\in S$ such that $t\vdash r$. Then, by (b), there is $t^{\prime }\ge t$ such that $t^{\prime } \vdash p\vee \lnot p$. We then have three cases:

  Case $t^{\prime }\vdash p$: Then, since $q^+\not =\emptyset$, there is $s^{\prime }\in S$ such that $s^{\prime }\vdash q$. Therefore, $t^{\prime }\sqcup s^{\prime }\vdash p\wedge q$. This implies that $t^{\prime }\sqcup s^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $t^{\prime }\sqcup s^{\prime }\ge t^{\prime }\ge t$, we obtain the desired result.

  Case $t^{\prime }\vdash \lnot p$: This implies that $t^{\prime }\dashv p\wedge q$, i.e., that $t^{\prime }\vdash \lnot ( p\wedge q)$. Therefore, $t^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $t^{\prime }\ge t$, we obtain the desired result.

  Case $t^{\prime }\vdash p\wedge \lnot p$: this means that there are $u, u^{\prime }\in S$ such that $t^{\prime }=u\sqcup u^{\prime }$, $u\vdash p$, and $u^{\prime }\vdash \lnot p$. Similar to the first case, there is $s^{\prime \prime }\in S$ such that $s^{\prime \prime }\ge u$ and $s^{\prime \prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Moreover, similar to the second case, $u^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $s^{\prime \prime }\ge u$, we have that $s^{\prime \prime }\sqcup u^{\prime }\ge u\sqcup u^{\prime }=t^{\prime }\ge t$. Moreover, since $|(p\wedge q)\vee \lnot (p\wedge q)|$ is closed under fusion (by Lemma 4), we have $s^{\prime \prime }\sqcup u^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. We can then conclude that (2) is the case. Item (3) follows in a similar way.

  Double Negation: $K_p (\lnot \lnot p)$

  Similar to the proof of Reflexivity.

  Weak Simplification: $K_{p \wedge q} (p \vee q)$

  Item (1) is proven for the first definition of knowledge. For (2), let $t\in S$ such that $t\vdash p\vee q$. We then have three cases:

  Case $t\vdash p$: Then, since $q^+\not =\emptyset$, there is $s^{\prime }\in S$ such that $s^{\prime }\vdash q$. Therefore, $t\sqcup s^{\prime }\vdash p\wedge q$. This implies that $t\sqcup s^{\prime }\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $t\sqcup s^{\prime }\ge t$, we obtain the desired result.

  Case $t\vdash q$: Similar to the above case, use $p^+\not =\emptyset$.

  Case $t\vdash p\wedge q$: this implies that $t\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $t\ge t$, we conclude that (2) is the case.

  For (3), let $t\in S$ such that $t\dashv p\vee q$. This means that there are $u, u^{\prime }\in S$ such that $t=u\sqcup u^{\prime }$, $u\dashv p$ and $u^{\prime }\dashv q$. Therefore $t\dashv p\wedge q$, i.e., $t\vdash \lnot ( p\wedge q)$. This implies that $t\vdash (p\wedge q)\vee \lnot (p\wedge q)$. Since $t\ge t$, we conclude that (3) is the case.

  Weak Omniscience: $K_{p} (p \vee \lnot p)$

  Item (1) is proven for the first definition of knowledge. For (2), let $t\in S$ such that $t\vdash p\vee \lnot p$. We then obtain (2) since $t\ge t$. For (3), let $t\in S$ such that $t\dashv p\vee \lnot p$. This implies that $t\vdash p\wedge \lnot p$. Then, by the exact verification clause for $\vee$, we obtain that $t\vdash p\vee \lnot p$. Since $t\ge t$, we have (3).

  Apriority: $A p \Vdash K_\varphi p$

  Counter-example: Ap is exactly verified everywhere in the model since the only possible state is t and $t\vdash p$. However, $t\vdash p$ but there is no u such that $u\ge t$ and $u\vdash r\vee \lnot r$. This violates item (2). Therefore, no state in the model exactly verifies $K_{r} p$.

  

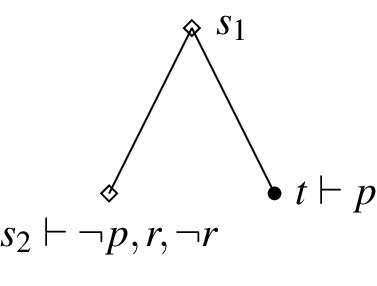
  Transitivity: $K_p q, K_q r \Vdash K_p r$

  Suppose (a) $s\vdash K_p q$ and (b) $s\vdash K_q r$. Item (1) is proved for the first definition of knowledge. To prove (2) let $u\in S$ such that $u\vdash r$. Then, by (b), we have that there is $u^{\prime }\in S$ such that $u\le u^{\prime }$ and $u^{\prime }\vdash q\vee \lnot q$. We then have three cases:

  If $u^{\prime }\vdash q$, then by (a), we obtain that there is $u^{\prime \prime }\in S$ such that $u^{\prime }\le u^{\prime \prime }$ and $u^{\prime \prime }\vdash p\vee \lnot p$. Since $u\le u^{\prime }\le u^{\prime \prime }$ and $\le$ is transitive, we obtain the result.

  If $u^{\prime }\vdash \lnot q$, then $u^{\prime }\dashv q$. Then, again by (a), we obtain that there is $u^{\prime \prime }\in S$ such that $u^{\prime }\le u^{\prime \prime }$ and $u^{\prime \prime }\vdash p\vee \lnot p$. Since $u\le u^{\prime }\le u^{\prime \prime }$ and $\le$ is transitive, we obtain the result.

  If there are $t, t^{\prime }\in S$ such that $u^{\prime }=t\sqcup t^{\prime }$, $t\vdash q$ and $t^{\prime } \vdash \lnot q$, we have by (a) that there are $u_1, u_2\in S$ such that $t\le u_1$ and $u_1\vdash p\vee \lnot p$ and $t^{\prime }\le u_2$ and $u_2\vdash p\vee \lnot p$. By Lemma 4, we have that $u_1\sqcup u_2\vdash p\vee \lnot p$. It is also easy to see that $u\le u^{\prime }=t\sqcup t^{\prime }\le u_1\sqcup u_2$, so we obtain the desired result. We can then conclude that (2) is the case. Item (3) follows in a similar way.

  Monotonicity: $K_p r \Vdash K_{p \wedge q} r$

  Same as the proof for Cautious Monotonicity.

  Negative Addition: $K_\varphi p \Vdash K_\varphi \lnot (\lnot p \wedge q)$

  Counter-example: It is easy to check that $K_rp$ is exactly verified at every state. However, $t\vdash \lnot (\lnot p\wedge q)$ but there is no u such that $u\ge t$ and $u\vdash r\vee \lnot r$. This violates item (2). Therefore, no state in the model exactly verifies $K_{r} \lnot (\lnot p\wedge q)$.

  

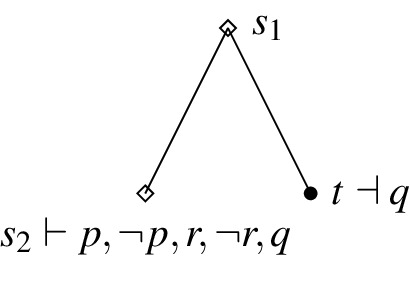
  Single-Premise Closure: $K_\varphi p, p \Rightarrow q \Vdash K_\varphi q$

  Counterexample: It is easy to check that $K_rp$ and $p\Rightarrow q$ are exactly verified at every state. However, $t\vdash q$ but there is no u such that $u\ge t$ and $u\vdash r\vee \lnot r$. This violates item (2). Therefore, no state in the model exactly verifies $K_{r} q$.

  

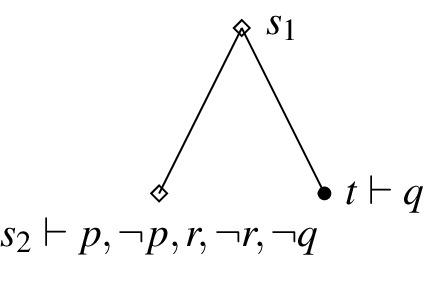
  Agglomeration: $K_\varphi p, K_\varphi q \Vdash K_\varphi (p \wedge q)$

  Follows similarly to the proof of Agglomeration for definition (5).

  Disjunctive Syllogism: $K_\varphi \lnot p, K_\varphi (p \vee q) \Vdash K_\varphi q$

  Suppose (a) $s\vdash K_\varphi \lnot p$ and (b) $s\vdash K_\varphi (p\vee q)$. Item (1) is proven for the first definition of knowledge. For (2): let $t\in S$ such that $t\vdash q$. This implies that $t\vdash p\vee q$. Then, by (b), we conclude that there is $t^{\prime }\ge t$ such that $t^{\prime }\vdash \varphi \vee \lnot \varphi$. For (3): let $t\in S$ such that $t\dashv q$. Since $p^-\not =\emptyset$, there is $s^{\prime }\in S$ such that $s^{\prime }\dashv p$. This means that $t\sqcup s^{\prime }\dashv p\vee q$. Then, by (b), there is $u^{\prime }\ge t\sqcup s^{\prime }$ such that $u^{\prime }\vdash \varphi \vee \lnot \varphi$. Since $t\le t\sqcup s^{\prime }\le u^{\prime }$, we conclude that (3) is the case.   $\square$