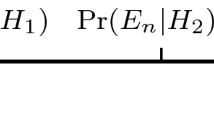Bayesian defeat of certainties

Abstract

When P(E) > 0, conditional probabilities P$(H|E)$ are given by the ratio formula. An agent engages in ratio conditionalization when she updates her credences using conditional probabilities dictated by the ratio formula. Ratio conditionalization cannot eradicate certainties, including certainties gained through prior exercises of ratio conditionalization. An agent who updates her credences only through ratio conditionalization risks permanent certainty in propositions against which she has overwhelming evidence. To avoid this undesirable consequence, I argue that we should supplement ratio conditionalization with Kolmogorov conditionalization, a strategy for updating credences based on propositions E such that P(E) = 0. Kolmogorov conditionalization can eradicate certainties, including certainties gained through prior exercises of conditionalization. Adducing general theorems and detailed examples, I show that Kolmogorov conditionalization helps us model epistemic defeat across a wide range of circumstances.

1 Beyond ratio conditionalization

Bayesian decision theory studies an idealized rational agent who assigns subjective probabilities, or credences, to propositions. The agent’s credences at each moment conform to the probability calculus axioms. The agent conditionalizes on E when she replaces her initial credences P_old(H) with new credences P_new(H) given by

$$ {P_{new}}(H) = {{{P_{old}}(H| E)}},$$

where P_old$(H|E)$ is the initial conditional probability of H given E. If P_old(E) > 0, then P_old$(H|E)$ is given by the familiar ratio formula:

$$ {P_{old}}(H|E) = \frac{{{P_{old}}(H\& E)}}{{{P_{old}}(E)}},$$

yielding the following formula for P_new:

$$ {P_{new}}(H) = \frac{{{P_{old}}(H\& E)}}{{{P_{old}}(E)}}.$$

(1)

When an agent updates her probabilities in accord with (1), I will say that she engages in ratio conditionalization.

Suppose that an agent is certain of H, in the sense that she sets P_old(H) = 1. If P_old(E) > 0, then the ratio formula and the probability calculus axioms entail that P_old$(H|E)$ = 1. It follows that ratio conditionalization cannot eliminate certainties. An agent who is certain of H and who updates her credences solely through ratio conditionalization will remain forever certain of H.

A striking illustration arises through the very exercise of ratio conditionalization. The ratio formula and the probability calculus axioms entail that P_old$(E|E)$ = 1, so an agent who conditionalizes on E must set P_new(E) = 1. She must also set P_new$(E|F)$ = 1 for any F such that P_new(F) > 0. Thus, subsequent exercises of ratio conditionalization cannot dislodge her newfound certainty in E, no matter what further evidence F she receives. This situation is widely regarded as disturbing (Jeffrey, 1983; Levi, 1980; Titelbaum, 2013; Williamson, 2000; Weisberg, 2009b). Surely an agent who conditionalizes on E can later receive strong evidence against E! For example, a scientist may conditionalize on the proposition that her experiment had a certain outcome and later learn that the experiment had a different outcome (e.g. her laboratory assistant initially misreported an experimental measurement). An agent who updates her credences only through ratio conditionalization risks permanent certainty in propositions against which she has overwhelming evidence.

Partly in response to such worries, Jeffrey (1983) develops an alternative framework that de-emphasizes conditionalization. Jeffrey contends that empirical propositions rarely if ever merit credence 1 and hence that one should rarely if ever update using ratio conditionalization. He proposes an update strategy, now usually called Jeffrey conditionalization, that does not mandate new certainties. Jeffrey conditionalization applies when an external influence causes an agent to reallocate credences across a partition containing countably many mutually exclusive, jointly exhaustive propositions E₁, E₂, …, E_i, …. Jeffrey proposes that, in response to the reallocated credences, the agent should form new credences given by:

$$ {P_{new}}(H) = \sum\limits_i {{P_{old}}(H|{E_i}){P_{new}}({E_i})} .$$

(2)

An agent who uses Jeffrey conditionalization rather than ratio conditionalization can update her credences without acquiring new certainties.

I think that Jeffrey conditionalization is a useful update strategy in some circumstances. However, I doubt that it can completely replace ordinary conditionalization. Ordinary conditionalization figures crucially within scientific applications of the Bayesian framework. Wholesale replacement of ordinary conditionalization by Jeffrey conditionalization would require sweeping changes to scientific practice, with major side effects both foreseen and unforeseen. It is far from clear that those changes would preserve the explanatory and pragmatic achievements of contemporary Bayesian practice (Rescorla, 2022).

In any event, I will follow a different path. The basic idea I will pursue is that an agent can eradicate certainties by conditionalizing on an E such that P_old(E) = 0. Although P_old$(H|E)$ = 1 whenever P_old(H) = 1 and P_old(E) > 0, there is no reason to expect that P_old$(H|E)$ = 1 when P_old(H) = 1 and P_old(E) = 0. On the contrary, one would expect that P_old$(H|E)$ < 1 for any H that entails ¬E. In principle, then, an agent who conditionalizes on probability zero propositions can lose certainties—including certainties gained through previous exercises of conditionalization.

Any account along these lines must look beyond the ratio formula to secure the needed conditional probabilities. Among the options found in the literature, I favor an approach that traces back to Kolmogorov (1933/1956) and that centers upon the notion of a regular conditional distribution (rcd). Rcds are central to probability theory. They also underlie countless scientific applications, especially within Bayesian statistics. Only recently have their virtues begun to receive sustained philosophical attention (Easwaran, 2008, 2011, 2019; Gyenis & Rédei, 2017; Huttegger, 2015; Huttegger & Nielsen, 2020; Meehan & Zhang, 2020, 2022; Nielsen, 2021; Rescorla, 2015b, 2018a, forthcoming). I will use them here to model certainty eradication across a range of situations.¹

Section 2 reviews basic aspects of rcds. Section 3 discusses how rcds support a kind of conditionalization, which I call Kolmogorov conditionalization. Sections 4 and 5 explore how Kolmogorov conditionalization can eradicate certainties. Section 6 articulates a rational norm, Rigidity, that constrains Kolmogorov conditionalization in many cases of epistemic defeat. Section 7 articulates a more general norm, Generalized Rigidity, that accommodates additional cases. The analysis from Sects. 6 and 7 indicates that rcds coupled with suitable rational norms can model numerous defeasible inferences. Section 8 highlights cases of epistemic defeat that my approach does not accommodate. Section 9 compares my approach with treatments due to Skyrms, Titelbaum, and Williamson.

2 Regular conditional distributions

Consider an idealized agent with prior credences modeled by a probability space (Ω, ${\mathscr{F}}$, P), where Ω is a set, ${\mathscr{F}}$ is a σ-field over Ω, and P is a probability measure on ${\mathscr{F}}$.² Elements of Ω are outcomes. Elements of ${\mathscr{F}}$, called events, serve as mathematical proxies for propositions. For each A ∈ ${\mathscr{F}}$, we construe P(A) as the credence that the agent attaches to A. In a measure-theoretic setting, the ratio formula becomes:

$$ P(H|E) = \frac{P(H \cap E)}{{P(E)}},$$

with intersection of events serving as a proxy for conjunction of propositions.

How should we define P$(H|E)$ when P(E) = 0? There is a pressing need for such conditional probabilities, quite independent of the considerations raised in Sect. 1. Scientific applications of Bayesian decision theory frequently require an agent to update her credences based upon learning that random variable X has value x. For example, an astronomer might learn that an asteroid has a certain velocity and, on that basis, update her credences regarding the time that the asteroid will reach Earth. Let

$$ X = x$$

be shorthand for the event {ω: X(ω) = x}. If X has uncountably many possible values, then orthodox probability theory requires that P(X = x) = 0 for all but countably many values x (Billingsley, 1995, p. 188). Thus, the ratio formula cannot supply all the conditional probabilities P$(H|x\,=\,x)$ that we need.

Kolmogorov (1933/1956) offers a theory of conditional probability that goes far beyond the ratio formula. His central insight is that, when P(E) = 0, we should consider E not on its own but rather as embedded in a larger collection of events (some of which may also have probability zero). Formally speaking, Kolmogorov’s theory centers on a subset ${\mathscr{G}}$⊆ ${\mathscr{F}}$, where ${\mathscr{G}}$ is itself a σ-field. His theory addresses scenarios where the agent gains new certainties over ${\mathscr{G}}$ and on that basis reallocates credences over the rest of ${\mathscr{F}}$. New certainties over ${\mathscr{G}}$ can be acquired through perception, testimony, introspection, or any other means. Some of the new certainties may only by implicit in the agent’s mental activity. Kolmogorov constructs a systematic framework that models credal updates in light of implicit new certainties over ${\mathscr{G}}$.³

To understand Kolmogorov’s approach, it helps to formalize the intuitive notion implicit new certainties over ${\mathscr{G}}$. For each ω ∈ Ω, define δ_ω: ${\mathscr{G}}$ → $\mathbb{R}$ by

$$ {\delta_{\omega} }(G) = \left\{ {\begin{array}{*{20}{c}} 1&{if}&{{\omega} \in G} \\ 0&{if}&{{\omega} \notin G} \end{array}} \right.\qquad for \, each\;G\in \mathscr{G}.$$

Call δ_ω a certainty profile over ${\mathscr{G}}$, and call ω an index of δ_ω. Each certainty profile δ_ω models a scenario where the agent becomes certain that the true outcome does or does not belong to any given G ∈ ${\mathscr{G}}$.⁴ To illustrate, suppose the agent becomes certain that random variable X has value x. Assuming that she represents x through any standard notational scheme for the real numbers, she should be willing to affirm or deny that X’s value lies between a and b, for each a, b ∈ $\mathbb{Q}$. Thus, she should be willing to assign probability 1 or 0 to each event

$${X^{ - 1}}\left( {a,b} \right) \qquad \qquad for \, any \, a,b \in \mathbb{Q}. $$

Let σ(X) be the σ-field generated by these events, i.e. σ(X) results from starting with the events X⁻¹(a, b) and closing under complementation and countable union. The agent’s new certainties over the events X⁻¹(a, b) determine a unique certainty profile over σ(X): namely, the certainty profile δ_ω, where ω is any outcome such X(ω) = x. This certainty profile is implicit in the agent’s newfound certainty that X has value x.

A certainty profile models a situation where the agent gains new certainties. In some cases, the agent’s certainty profile δ_ω tracks the truth:

$${\rm{For}}\;{\rm{each}}\;G \in {\mathscr{G}},{\delta _{\omega} }\left( G \right) = 1\;{\rm{iff}}\;{\rm{the}}\;{\rm{true}}\;{\rm{outcome}}\;{\rm{belongs}}\;{\rm{to}}\;G.$$

(3)

I will call (3) the factivity assumption. Kolmogorov’s framework accommodates scenarios where the factivity assumption prevails, and it also accommodates scenarios where the factivity assumption fails. In what follows, I will discuss scenarios of both kinds. As argued in (Rescorla, 2021), there is no principled reason to restrict attention to scenarios where the agent conditionalizes on truths. People make mistakes all the time. An agent’s certainties over ${\mathscr{G}}$ may be misplaced, i.e. they may violate the factivity assumption. Undoubtedly, though, it is a good thing when the factivity assumption prevails.

How should our agent reallocate credence over the rest of ${\mathscr{F}}$ in light of her newfound certainty profile δ_ω? To address this question, we will use a function C: ${\mathscr{F}}$ × Ω →  $\mathbb{R}$. Intuitively, C(·, ω) encodes probabilities over ${\mathscr{F}}$ conditional on the truth of all those G ∈ ${\mathscr{G}}$ such that δ_ω(G) = 1. I will notate C(A, ω) as C$(A|$ω). When convenient, I will notate C(·$|$ω) as C_ω. Our question now becomes what constraints we should place upon C. Since we are using probability measures to model credences, we demand that:

$$ {C_{\omega} }:{\mathscr{F}} \to \mathbb{R}\;{\rm{is}}\;{\rm{a}}\;{\rm{probability}}\;{\rm{measure},}\,{\rm{for}}\;{\rm{each}}\;{\omega} \in {\Omega}.$$

(4)

Kolmogorov additionally demands that, for each A ∈ ${\mathscr{F}}$, the one-place function C(A$|$·): Ω →  $\mathbb{R}$ is ${\mathscr{G}}$-measurable:

$$C{(A|\cdot)^{ - 1}}( - \infty ,a) \in {\mathscr{G},}\;{\rm{for}}\;{\rm{each}}\;a \in \;\mathbb{R}.$$

(5)

As explained in (Rescorla, forthcoming), ${\mathscr{G}}$-measurability formalizes the following intuitive thought: the agent’s newfound certainties over ${\mathscr{G}}$ dictate the new credences to be allocated over ${\mathscr{F}}$. Call any function C that satisfies clauses (4) and (5) an update rule for (Ω, ${\mathscr{F}}$) and ${\mathscr{G}}$.⁵

Kolmogorov supplements (4) and (5) with an additional constraint upon C. The constraint is now usually called the integral formula:

$$P(A \cap G) = \int_G {C{\rm{(}}} A{\rm{|}}{\omega} {\rm{)}}dP{\rm{(}}{\omega} {\rm{)},}\;{\rm{for}}\;{\rm{each}}\;A \in {\mathscr{F}}\;\, {\rm{and }}\,G \in {\mathscr{G}}.$$

(6)

The integral formula generalizes the law of total probability: for any partition E₁, E₂, …, E_i, … such that P(E_i) > 0 for all i,

$$ P(A) = \sum\limits_i {P(A|{E_i})P({E_i})} . $$

(7)

(7) follows from the ratio formula and the probability calculus axioms. Kolmogorov’s approach turns the entailment around, treating the law of total probability (generalized to the integral formula) not as a theorem but as a definitional constraint upon conditional probabilities.

A function C: ${\mathscr{F}}$ × Ω → $\mathbb{R}$ satisfying clauses (4)–(6) is called a regular conditional distribution (rcd) for P given ${\mathscr{G}}$. One can show that there exists an rcd for P given ${\mathscr{G}}$ in a wide variety of cases, including virtually all cases likely to arise in scientific applications.⁶ I will frequently notate an rcd for P given ${\mathscr{G}}$ as $P_{\mathscr{G}}$.

As a special case, suppose that ${\mathscr{G}}$ is generated by a countable partition E₁, …, E_i, …, where P(E_i) > 0 for each i. Then there exists a unique rcd for P given ${\mathscr{G}}$, defined by:

$${P_{\mathscr{G}}}(A|{\omega} ){ =_{df}}P(A|{E_i}) = \frac{{P(A \cap {E_i})}}{{P({E_i})}}\qquad {if}\,{\omega} \in {E_i} .$$

In this way, Kolmogorov’s theory subsumes the ratio formula. Kolmogorov’s theory also supplies conditional probabilities in numerous cases where the ratio formula goes silent.

Rcds are widely employed within probability theory (Billingsley, 1995; Kallenberg, 2002). Alternative theories of conditional probability are available (Dubins, 1975; Popper, 1959; Rényi, 1955), but they have exerted little impact upon mathematical or scientific practice. The main reason is that alternative theories typically impose few quantitative constraints beyond the ratio formula on the relation between conditional and unconditional probabilities, so they offer little useful guidance for computing conditional probabilities. In contrast, the integral formula tightly constrains conditional probabilities in relation to unconditional probabilities. Suppose that C and D are both rcds for P given ${\mathscr{G}}$. Then, for every A ∈ ${\mathscr{F}}$,

$$ C(A | {\omega} ) \, = D(A | {\omega} ) $$

except perhaps for those ω belonging to a set of P-measure 0. Alternative theories of conditional probability usually do not pin down conditional probabilities with nearly so much determinacy. For detailed comparison of rcds with alternative theories, see (Easwaran, 2019).⁷

3 Kolmogorov conditionalization

Rcds figure prominently in many scientific applications of Bayesian decision theory, including within statistics (Florens et al., 1990; Ghosal & van der Vaart, 2017; Schervish, 1995), economics (Feldman, 1987), and cognitive science (Bennett et al., 1996). Something like the following picture underlies these applications. At time t₀, the agent has unconditional credences encoded by a probability space (Ω, ${\mathscr{F}}$, P). She also has conditional credences encoded by C, an rcd for P given ${\mathscr{G}}$ ⊆ ${\mathscr{F}}$. At a later time t₁, an exogenous event causes the agent to acquire a new certainty profile δ_ω over ${\mathscr{G}}$. Based upon her new certainties over ${\mathscr{G}}$, she adopts new credences C_ω over ${\mathscr{F}}$. As I will put it, she uses rcd C to conditionalize on δ_ω. When an agent uses an rcd to conditionalize, I will say that she engages in Kolmogorov conditionalization.⁸

In general, a probability measure P determines conditional probabilities C(A$|$·) only up to measure 0. Thus, an agent’s unconditional credences do not typically determine unique conditional credences C. We must instead take C as an extra primitive element. This is an important difference between Kolmogorov conditionalization and ratio conditionalization, since the ratio formula uniquely determines conditional probabilities P$(H|E)$ when P(E) > 0. The extra primitive element seems a small price to pay for the benefits that it buys. Anyway, all theories of conditional probability agree that unconditional probabilities do not uniquely determine conditional probabilities once we move beyond the simple case where P(E) > 0.

Kolmogorov conditionalization is a very general update strategy, but it is not universally applicable. There are pathological cases where no rcd exists (Billingsley, 1995, p. 443). Even when an rcd exists, it may not support conditionalization. To see why, say that an update rule C for (Ω, ${\mathscr{F}}$) and ${\mathscr{G}}$ is proper at ω iff

$${\text{If}}\,{\omega} \in G, \, {\text{then}}\,C(G|\omega ) = 1\qquad \qquad for\;all\;G \in {\mathscr{G}} .$$

(8)

If C is improper at ω, then there exists G ∈ ${\mathscr{G}}$ such that

$$ C\left( {G|\omega } \right) < 1 \, \&\, {\omega} \in G,$$

which conflicts with the certainty profile’s assignment:

$$\delta_{\omega}(G)=1.$$

When such a conflict arises, the agent cannot use C to extend δ_ω to all of ${\mathscr{F}}$. Unfortunately, there are cases where every rcd for P given ${\mathscr{G}}$ is improper at some ω (Blackwell & Dubins, 1975). Fortunately, impropriety occurs rarely if ever in practice. In actual scientific applications, there usually exists an rcd that is proper everywhere.⁹ The probability spaces considered in this paper support rcds that are proper everywhere. For further discussion of impropriety, see (Easwaran, 2011; Meehan & Zhang, 2022; Rescorla, forthcoming).

Let X be a random variable, and let P_σ(X) be an rcd for P given σ(X). Then P_σ(X) dictates how to update credences in light of newfound certainty that X = x. Each possible value x corresponds to a distinct certainty profile that the agent might instantiate. When there are uncountably many possible values x, the model posits uncountably many possible mental states. Some readers may worry that any such model is inapplicable to ordinary humans, since it flouts the apparently finitary nature of human representational and discriminative capacities. The model may seem applicable only to an idealized superhuman with infinitary cognitive abilities that transcend our own.

In evaluating this objection, it is instructive to consider the Bayesian models offered within current cognitive science. Cognitive scientists offer Bayesian models of numerous core mental phenomena (Griffiths et al., 2008), including perception, motor control, decision-making, language acquisition, navigation, social cognition, and causal reasoning. The models have achieved notable explanatory and predictive success, especially as applied to perception (Rescorla, 2015a) and motor control (Rescorla, 2016). Typically, the models posit uncountably many possible mental states. For example, Bayesian perceptual models describe how the perceptual system estimates environmental conditions based on sensory stimulations (Knill & Richards, 1996). The models usually posit uncountably many possible sensory states (e.g. uncountably many possible retinal states) that serve as possible inputs to Bayesian inference. They also posit uncountably many outputs that might result from the Bayesian inference (e.g. uncountably many possible estimates of an object’s shape, size, or location). Nevertheless, the models generate powerful psychological explanations (Rescorla, 2018b, 2020). Thus, a Bayesian model may fruitfully apply to ordinary humans even though it posits uncountably many mental states.

I distinguish two possible reactions to such models. The first reaction accepts at face value the postulation of uncountably many mental states. On this reaction, we accept that an ordinary human can in principle instantiate uncountably many mental states. The second reaction regards the postulation of so many mental states as an infinitary idealization, akin to the postulation of an infinitely large biological population within population genetics. On this reaction, a Bayesian model that posits uncountably many mental states should eventually be replaced by a more psychologically realistic model.

Both reactions merit further exploration. The key point for present purposes is that, on either reaction, there is a legitimate role for Bayesian models that posit uncountably many mental states. The first reaction holds that such models may be literally true. The second reaction holds that they include infinitary idealizations to be banished from a literally true description. Either way, the mere fact that a Bayesian model posits uncountably many mental states does not bar it from making a useful theoretical contribution. The present paper is offered in that spirit.

4 Certainty eradication

Kolmogorov conditionalization offers a crucial advantage over ratio conditionalization: it can eradicate certainties. This is the flip-side of the fact that Kolmogorov conditionalization can raise probabilities from zero. Here is a simple example (not necessarily involving any kind of epistemic defeat). Suppose that P(X = x) = 0 and P(X ≠ x) = 1. If the agent becomes newly certain that X = x, then she can use an rcd P_σ(X) to conditionalize on a certainty profile δ_ω corresponding to her newfound certainty, i.e. a certainty profile indexed by an ω such that X(ω) = x. She can do so as long as her rcd P_σ(X) satisfies the condition:

$${P_{\sigma \left( X \right)}}(X = x|\omega ) = 1\;\&\; {P_{\sigma \left( X \right)}}(X \ne x|\omega ) = 0.$$

By using P_σ(X) to conditionalize, she demotes her former certainty in X ≠ x all the down to 0. In general, Kolmogorov conditionalization can raise probabilities from 0 to 1 or anywhere in between, and it can lower probabilities from 1 to 0 or anywhere in between.

Here is a slightly more elaborate example (still not necessarily involving epistemic defeat). Consider the following probability density function p(x, y) over $\mathbb{R}$²:

$$ p(x,y) = \left\{ {\begin{array}{*{20}{l}} 1&\qquad {if}&{0 \leqslant x \leqslant 1/2,0 \leqslant y \leqslant 1} \\ {3/2}&\qquad {if}&{1/2 < x \leqslant 1,0 \leqslant y \leqslant 1/2} \\ {1/2}&\qquad{if}&{1/2 < x \leqslant 1,1/2 < y \leqslant 1} \\ 0&{}&{otherwise} \end{array}} \right.$$

See Fig. 1. For any topological space T, let ${{\mathscr{B}}}$(T) consist of the Borel subsets of T. By integrating p(x, y), we define a probability measure P over ($\mathbb{R}$², ${{\mathscr{B}}}$($\mathbb{R}$²)):

Fig. 1

A simple probability density function over $\mathbb{R}$². All positive probability density is concentrated in the unit square

$P(H){ =_{df}}\iint\limits_H {p(x,y)dxdy}, \;for \, any \, Borel \, set\;H{ \subseteq{\mathbb{R}^2}}.$

Suppose an agent has credences given by P. For any x, we have

$$ P(X = x \cap Y \leqslant 1/2) = 0 $$

$$ P(X \ne x \cup Y > 1/2) = P({(X = x \cap Y \leqslant 1/2)^c}) = 1.$$

Let P_σ(X) be an rcd for P given σ(X). Using standard mathematical techniques (Billingsley, 1995, p. 432), one can show that P_σ(X) must satisfy (9) for almost all (x, y) such that x lies in the unit interval:

$$ {P_{\sigma (X)}}(X = x \cap Y \leqslant 1/2|x,y) = \frac{{\int_{\left[ 0, 1/2 \right]} {p(x,t)dt} }}{{\int_{\left[ {0,1} \right]} {p(x,t)dt} }}. $$

(9)

We may choose P_σ(X) so that it satisfies (9) for all (x, y) such that x lies in the unit interval. For all other (x, y) –- these lie within an event whose P-measure is 0 –- we may choose P_σ(X)(.$|$x, y) to be some fixed, arbitrary measure. Pick x₁ such that 0 ≤ x₁ ≤ ½. Then (9) yields

$${P_{\sigma (X)}}(X = {x_1} \cap Y \leqslant 1/2|{x_1},y) = \frac{{\int_{\left[ 0,1/2 \right]} {dt} }}{{\int_{\left[ {0,1} \right]} {dt} }} = 1/2, $$

(10)

for any y. See Fig. 2. An agent who becomes certain that X = x₁ and who updates her credences using P_σ(X) will raise her credence in X = x₁ ∩ Y ≤ ½ from 0 to ½. This is the intuitively correct reaction: the agent concentrates all credal mass on the vertical line X = x₁ from 0 to 1, where the prior probability density p(x, y) is constant. Since P_σ(X)(.$|$x₁, y) is a probability measure, (10) entails

$$ {P_{\sigma \left( X \right)}}(X \ne {x_1} \cup Y > 1/2| {x_1},y) \, = 1/2. $$

(11)

Thus, our agent demotes her former certainty in X ≠ x₁ ∪ Y > ½ from 1 to ½. In contrast, pick x₂ such that ½ < x₂ ≤ 1. Then (9) yields

$$ {P_{\sigma (X)}}(X = {x_2} \cap Y \leqslant 1/2|{x_2},y) = \frac{{\int_{\left[ 0,1/2 \right]}3/2dt} }{{\int_{\left[ 0,1/2 \right]}3/2dt} + \int_{\left( 1/2,1 \right]} 1/2dt} =\frac{{{\rm{ 3/4}}}}{{{\rm{ 3/4 + 1/4 }}}}= 3/4, $$

(12)

which entails

$${P_{\sigma \left( X \right)}}(X \ne {x_2} \cup Y > 1/2\left| {{x_2},y} \right.) = 1/4.$$

(13)

See Fig. 3. An agent who become certain that X = x₂ and who updates her credences using P_σ(X) will raise her credence in X = x₂ ∩ Y ≤ ½ from 0 to ¾, and she will lower her credence in X ≠ x₂ ∪ Y > ½ in from 1 to ¼. Again, this makes intuitive sense: the agent now concentrates all credal mass on the vertical line X = x₂ from 0 to 1, and p(x, y) is weighted three times higher along the bottom half of the line.

Fig. 2

Assuming 0 ≤ x₁ ≤ ½, probability density p(x, y) is constant along the vertical line X = x₁. If the agent conditionalizes based on newfound certainty that X = x₁, then she will allocate all her credence uniformly over this vertical line

Fig. 3

Assuming ½ < x₂ ≤ 1, probability density p(x, y) is higher along the bottom half of the vertical line X = x₂ than along the top half. If the agent conditionalizes based on newfound certainty that X = x₂, then she will allocate all her credence over this vertical line, with more credal mass assigned to the bottom half than the top half

The foregoing observations prompt us to reflect upon the meaning of “certainty” in Bayesian decision theory. “Certainty” may seem to connote immutable confidence that a proposition is true. Yet that is not what “certainty” means—not if we define “certainty” as “assignment of credence 1.” As noted in Sect. 2, the probability calculus axioms entail that P(X = x) = 0 for all but countably many values x of a random variable X. When you set P(X ≠ x) = 1 and P(X = x) = 0, it does not follow that you regard X = x as metaphysically impossible, or that have definitively ruled out X = x, or that no possible evidence could lead you to assign non-zero credence to X = x. All that follows is that you regard X = x as vanishingly unlikely. The probability calculus axioms entail that you must regard X = x as vanishingly unlikely for all but countably many values x. Even though your credence in X = x is currently 0, you are prepared to raise this credence in light of new evidence. If you do so, you must simultaneously downgrade your certainty in X ≠ x. You will typically downgrade many other certainties as well, as illustrated by (11) and (13). Kolmogorov conditionalization provides a principled basis for these credal transitions.

5 Certainty gained, then lost

Since Kolmogorov conditionalization can eradicate certainties, it is much more flexible than ratio conditionalization. In what follows, I leverage the increased flexibility to model defeasible inference across a range of cases. This section warms up by modeling an example where an agent conditionalizes on a proposition and then loses certainty in the proposition. Defects in the model will motivate refinements made in Sect. 6.

At time t₀, John awaits his medical test result for a rare disease. At time t₁, he receives his test result. Upon reading the report, he becomes certain that the test result was positive. He conditionalizes on the positive test result, substantially raising his credence that he has the disease. At time t₂, John re-reads the medical report and realizes that he misinterpreted it. In fact, the test result was negative. Intuitively, he should now conditionalize on the negative test result and downgrade his credence that he has the disease. But he cannot do so using ratio conditionalization because at t₁ he assigned zero credence to the negative test result. Call this example False Alarm.

Using rcds, we can elaborate False Alarm into a model that includes certainty eradication at t₂. Assume a suitable outcome space Ω, and let

Disease =:

the set of outcomes in which John has the rare disease.

No Disease =:

the set of outcomes in which John does not have the rare disease.

Positive =:

the set of outcomes in which the test has a positive result.

Negative =:

the set of outcomes in which the test has a negative result.

I assume that the test can only have a positive or negative result, so that Positive and Negative are complements. Let ${\mathscr{F}}$ be the σ-field generated by Disease and Positive. John’s credences at t₀ are given by (Ω, ${\mathscr{F}}$, P), where P is the unique probability measure over ${\mathscr{F}}$ such that:

$$\begin{array}{*{20}{l}} {P\left( {Disease} \right) = .025}&{P\left( {No\;Disease} \right) = .975}\\ {P\left( {Positive|Disease} \right) = .95}&{P\left( {Positive|No\;Disease} \right) = .05}\\ {P\left( {Negative|Disease} \right) = .05}&{P\left( {Negative|No\;Disease} \right) = .95} \end{array}$$

These credences reflect the base rate for the disease, the frequency of false positives, and the frequency of false negatives. By the law of total probability,

$$\begin{array}{lllll} P\left( {Positive} \right) = & P\left( {Positive|Disease} \right)P\left( {Disease} \right) + P\left( {Positive|No\;{\rm{ }}Disease} \right)P\left( {No\;{\rm{ }}Disease} \right)\\ & = .95 \times .025 + .05 \times .975 = .0725, \end{array}$$

so that P(Negative) = .9275. By Bayes’s theorem,

$$\begin{array}{lllll} P(Disease|Positive) = & \frac{{P(Disease)P(Positive|Disease)}}{{P(Positive)}} = \frac{{.025 \times .95}}{{.0725}} = 19/58\\ & \\ P(Disease|Negative) = & \frac{{P(Disease)P(Negative|Disease)}}{{P(Negative)}} = \frac{{.025 \times .05}}{{.9275}} = 1/742 \end{array}$$

At t₁, John conditionalizes on Positive, acquiring new credences

$$\begin{array}{l} {P_{{t_1}}}\left( {Positive} \right) = 1\\ {P_{{t_1}}}\left( {Negative} \right) = 0\\ {P_{{t_1}}}\left( {Disease} \right) = 19/58 \end{array}$$

So far, so standard.

Now comes the less standard part. To model John’s credal transition at t₂, let ${\mathscr{G}}$ be the sub-σ-field

$$\{ 0,Positive,Negative,{\Omega} \}.$$

John’s realization that the test was negative corresponds to a certainty profile δ_ν, where ν is any outcome belonging to Negative. We model John’s conditional credences at t₁ by stipulating

$$ \mu (Disease|{\omega} ) = \left\{ {\begin{array}{*{20}{c}} {19/58}&\quad {if}&{{\omega} \in Positive} \\ {1/742}& \quad {if}&{{\omega} \in Negative} \end{array}} \right.$$

$$ \mu (Positive|{\omega} ) = \left\{ {\begin{array}{*{20}{c}} 1&\quad {if} & {{\omega} \in Positive}\\ 0&\quad {if}& {{\omega} \in Negative} \end{array}} \right.$$

These stipulations extend to a unique function μ: ${\mathscr{F}}$ × Ω →$\mathbb{R}$ such that μ_ω is a probability measure for each ω ∈ Ω. It is easy to check that μ is an rcd for ${P_{t_1}}$ given ${\mathscr{G}}.$ Specifically, the integral formula is trivially satisfied. At t₂, John uses μ to conditionalize on δ_ν, where ν is any outcome belonging to Negative. Thus, he acquires new credences

$$\begin{array}{*{20}{l}} {{P_{{t_2}}}\left( {Positive} \right) = 0}\\ {{P_{{t_2}}}\left( {Negative} \right) = 1}\\ {{P_{{t_2}}}\left( {Disease} \right) = 1/742} \end{array}$$

He downgrades his certainty in Positive all the way down to 0 and downgrades his credence in Disease from 19/58 to 1/742.

Our model illustrates the increased flexibility afforded by Kolmogorov conditionalization. Over the course of John’s credal evolution, his credence in Positive goes from .0725 to 1 to 0, and his credence in Disease changes as dictated by his conditional credences. The postulated credal transitions look quite reasonable, given John’s initial credences.

Nevertheless, there is something disturbingly trivial about the model. I stipulated that μ(Disease$|$ω) = 1/742 if ω ∈ Negative, but I could have stipulated μ(Disease$|$ω) = .5, or .9999, or even 1. Each alternative stipulation would also yield an rcd for ${P_{{t_1}}}$ given ${\mathscr{G}}.$ Thus, John’s unconditional credences at t₁ leave his conditional credences at t₁ completely undetermined. Any alternative update rule μ* would satisfy the integral formula just as well as μ. Such extreme flexibility is undesirable. Ideally, a final theory of rational inference will pin down more determinately how credences evolve over time.

Our model of False Alarm shows that Kolmogorov conditionalization can, in principle, support acquisition and loss of certainties. But the model taken on its own is unsatisfying because it hinges upon arbitrary stipulation of an rcd μ. We must try to do better.

6 Rigidity

I now advance a rational norm, inspired by Jeffrey (1983), that tightly constrains credal evolution. I call the norm Rigidity. Section 6.1 introduces Rigidity. Section 6.2 discusses how Rigidity yields an improved treatment of False Alarm and similar examples.

6.1 Minimal change in conditional probabilities

Consider again the situation emphasized by Jeffrey: an external influence causes an agent to reallocate credences across a partition ${\mathscr{E}}$ = {E_i}, and on that basis the agent must assign credences to all remaining propositions. Why should we accept Jeffrey’s recommended credal update strategy (2)? Beginning with Jeffrey (1983), and continuing through the later literature (e.g. Earman, 1992, pp. 34–35; Joyce, 2009, pp. 35–35; Weisberg, 2009b), philosophers often motivate (2) by citing the invariance condition

$${P_{old}}\left( {H|{E_i}} \right) = {P_{new}}\left( {H|{E_i}} \right)\qquad for \; all \; H \; and \; all \; {E_i}\;such \; that\;{P_{new}}\left( {E_i} \right) > 0.$$

(14)

(2) follows from (14) together with the law of total probability (7).

The rationale underlying (14) is that, when all credal change stems from reallocation across a partition, probabilities conditional on partition propositions should remain fixed. Intuitively: reallocating probabilities across a partition tells you nothing new about how probability mass should be distributed inside any member of the partition. Credal reallocation over the partition provides no rational basis for changing your credences conditional on a given partition proposition. As Joyce (2009, p. 36) notes, this rationale reflects “a kind of minimal change ‘ethos’ which prohibits the posterior from introducing distinctions in probability among hypotheses that are not already inherent in the prior or explicitly mandated by new evidence.” (14) enforces the minimal change ethos by holding conditional probabilities as fixed as possible, given that probabilities assigned to partition propositions have changed.

The rationale for (14) has a causal dimension: we assume that an external event triggers the transition from P_old to P_new by instilling new credences across a partition ${\mathscr{E}}$. Different authors express this causal assumption in different ways. Earman (1992, p. 34) says that credal changes are “generated” by new credences across the partition. Joyce (2009, pp. 35–36) posits an event whose “only immediate effect” is to fix new credences for partition propositions. In (Rescorla, 2021), I said that the new credal assignment over the partition “mediates” the transition from P_old to P_new. The core idea behind these varying formulations is that an event alters the agent’s credences entirely by way of altering her credences over ${\mathscr{E}}$. Intuitively: we restrict attention to situations where all credal change stems from the new credal assignment over ${\mathscr{E}}$. Virtually all discussions of Jeffrey Conditionalization assume a restriction along these lines, although the restriction often figures only implicitly.

An important task for formal epistemology is to analyze more systematically the assumed restriction on causal structure. In (Rescorla, 2021), I offered one possible analysis. But I will not assume that analysis, or any other analysis. Even lacking a detailed analysis, the basic idea seems clear enough for present purposes.

It will prove helpful to articulate a more precise statement of the diachronic credal norm corresponding to (14). In (Rescorla, 2021), I formulated the norm as imposing the following requirement:

$$\begin{aligned} &{\rm{If}}\;{\rm{an}}\;{\rm{agent}}\;{\rm{begins}}\;{\rm{with}}\;{\rm{credences}}\;{P_{old}},{\rm{ and}}\;\mathscr{E} = \{ {E_i}\} \;{\rm{is}}\;{\rm{a}}\;{\rm{countable}}\;{\rm{set}}\;{\rm{of}}\\ &{\rm{mutually}}\;{\rm{exclusive, jointly}}\;{\rm{ exhaustive}}\;{\rm{propositions}}\;{\rm{such}}\;{\rm{that}}\;{P_{old}}\left( {{E_i}} \right) > 0\;{\rm{for}}\\ &{\rm{each }}\; i{\rm{,}}\;{\rm{and}}\;{\rm{she}}\;{\rm{subsequently}}\;{\rm{adopts}}\;{\rm{new}}\;{\rm{credences}}\;{P_{new}}\;{\rm{such}}\;{\rm{that}}\\ &\sum\limits_i {{P_{new}}} ({E_i}) = 1, {\rm{and}}\;{\rm{the}}\;{\rm{new}}\;{\rm{credal}}\;{\rm{assignment}}\;{\rm{ over}}\; {\mathscr{E}} {\rm{mediates}}\;{\rm{the}}\;{\rm{transition}}\\ &{\rm{from}}\;{P_{old}}\;{\rm{to}}\;{P_{new}},{\rm{ then}}\;{P_{old}}(.|{E_i}) = {P_{new}}({.| E_i})\;{\rm{for}}\;{\rm{all}}\;i\;{\rm{such}}\;{\rm{that}}\;{P_{new}}\left({{E_i}} \right) > 0, \end{aligned}$$

(15)

where the clause “the new credal assignment over ${\mathscr{E}}$ mediates the transition from P_old to P_new” reflects a causal assumption that credences change solely due to the new credal assignment over ${\mathscr{E}}$. For present purposes, one could equally well express the causal assumption through the language used by Earman (“generated”) or Joyce (“only immediate effect”).

The antecedent of (15) confines attention to situations where P_old(E_i) > 0 for each i, and the consequent addresses only those E_i such that P_new(E_i) > 0. These restrictions ensure that conditional probabilities, as specified by the ratio formula, are well-defined. However, I see no reason to impose the restrictions once we have in hand conditional probabilities beyond those given by the ratio formula. The intuitive rationale supplied by Joyce’s minimal change ethos applies just as well to cases where P_old(E_i) = 0 or P_new(E_i) = 0.

Indeed, the rationale applies just as well to numerous cases that do not feature a countable partition ${\mathscr{E}}$. Consider an agent with credences modeled by a probability space (Ω, ${\mathscr{F}}$, P), and let ${\mathscr{G}}$ ⊆ ${\mathscr{F}}$ be a sub-σ-field. ${\mathscr{G}}$ may or may not be generated by a countable partition. Suppose that the agent has conditional credences over ${\mathscr{F}}$ given ${\mathscr{G}}$, modeled by update rule C. Suppose that there occurs an exogenous shift in credal mass across ${\mathscr{G}}$, inducing further credal changes across ${\mathscr{F}}$. Following Meehan and Zhang (2020), I propose that the agent’s conditional credences C should remain fixed. More carefully, credal transitions should satisfy the following requirement:

RIGIDITY: If an agent begins with unconditional credences P_old over ${\mathscr{F}}$ and conditional credences C_old over ${\mathscr{F}}$ given ${\mathscr{G}}$, and she subsequently adopts new credences P_new over ${\mathscr{F}}$ and new conditional credences C_new over ${\mathscr{F}}$ given ${\mathscr{G}}$, and the new credal assignment over ${\mathscr{G}}$ mediates the transition from P_old and C_old to P_new and C_new, then C_old = C_new,

where the clause “the new credal assignment over ${\mathscr{G}}$ mediates the transition from P_old and C_old to P_new and C_new” reflects a causal assumption that the agent’s conditional and unconditional credences change solely due to the new credal assignment over ${\mathscr{G}}$. Again, we could equally well substitute other locutions that express the same causal assumption. Like (15), Rigidity is a minimal change principle. It leaves conditional probabilities as fixed as possible, given that credences over ${\mathscr{G}}$ have changed. Intuitively: credal reallocation across a sub-σ-field provides no rational basis for changes in credence conditional on the sub-σ-field.

It would be good to explore more fully the basis for Rigidity. In this paper, I focus on applying Rigidity. Actually, I will apply a fairly weak consequence of Rigidity:

WEAK RIGIDITY: If an agent begins with credences P_old over ${\mathscr{F}}$ and conditional credences C_old over ${\mathscr{F}}$ given ${\mathscr{G}}$, and she subsequently adopts new credences P_new over ${\mathscr{F}}$ and new conditional credences C_new over ${\mathscr{F}}$ given ${\mathscr{G}}$, and P_new$|$${\mathscr{G}}$ = δ_ω for some ω, and the new credal assignment over ${\mathscr{G}}$ mediates the transition from P_old and C_old to P_new and C_new, then C_old = C_new,

where P_new$|$${\mathscr{G}}$ is the restriction of P_new to ${\mathscr{G}}$. Weak Rigidity confines attention to cases where the new credal assignment over ${\mathscr{G}}$ is a certainty profile. For discussion of cases where the new credal assignment over ${\mathscr{G}}$ is not a certainty profile, see (Meehan & Zhang, 2020).

6.2 Credal evolution conforming to Rigidity

I propose the following picture of credal evolution. At t₀, an agent has unconditional credences modeled by a probability space (Ω, ${\mathscr{F}}$, P) and conditional credences modeled by C, an rcd for P given ${\mathscr{G}}$. At t₁, an exogenous change instills certainty profile δ_ω over ${\mathscr{G}}$. Assume that C is proper at ω. Then the agent can use C to conditionalize on δ_ω, adopting C_ω as her new credal allocation over ${\mathscr{F}}$. Her unconditional credences at t₁ are modeled by (Ω, ${\mathscr{F}}$, C_ω). Complying with Rigidity, she retains her conditional credences C. See Fig. 4.

Fig. 4

The agent gains new certainty profile δ_ω and responds by using C to conditionalize on δ_ω. Complying with Weak Rigidity, she retains her conditional credences C. In this diagram, and in subsequent such diagrams, unconditional credences lie above the dotted line and conditional credences lie below the dotted line

Theorem

Let (Ω, ${\mathscr{F}}$, P) be a probability space, let ${\mathscr{G}}$ ⊆ ${\mathscr{F}}$ be a sub-σ-field, and let C be an rcd for P given ${\mathscr{G}}$. Suppose that C is proper at ω. Then C is an rcd for C_ω given ${\mathscr{G}}$.

Proof

The only non-trivial clause is the integral formula, with C_ω serving as the unconditional probability measure: we must show that

$$ {C_{\omega} }(A \cap G) = \int_G {C(A|\nu )d{C_{\omega} }{(}\nu {)}}, $$

(16)

for every A ∈ ${\mathscr{F}}$ and G ∈ ${\mathscr{G}}$. Fix A ∈ ${\mathscr{F}}$ and G ∈ ${\mathscr{G}}$. Define

$$ H{ =_{df}}\{ v \in {\Omega} :C(A|{\omega} ) = C\left( {A|v} \right)\}.$$

C(A$|$·): Ω → $\mathbb{R}$ is ${\mathscr{G}}$-measurable, and H is the inverse image of {C(A, ω)} under C(A$|$·), so H ∈ ${\mathscr{G}}$. Since ω ∈ H, it follows from (8) that

$$ {C_{\omega} }\left( H \right) = 1\;\&\; {C_{\omega} }\left( {H^c} \right) = 0.$$

We now calculate:

$$ \begin{aligned} \int_G {C(A|\nu )d{C_{\omega} }{(}\nu {)}} { = } & \int_{G \cap H} {C(A|\nu )d{C_{\omega} }{(}\nu {)}}\,\, {+}\int_{G \cap {H^c}} {C(A|\nu )d{C_{\omega} }{(}\nu {)}} \\ { = } & \int_{G \cap H} {C(A|{\omega} )d{C_{\omega} }{(}\nu {)}} { + }0 = {C_{\omega} }(A)\int_{G \cap H} {d{C_{\omega} }{(}\nu {)}} = {C_{\omega} }(A){C_{\omega} }(G \cap H). \\ \end{aligned}$$

Either ω ∈ G or ω ∉ G. If ω ∈ G, then (8) entails

$$ {C_{{\omega}} }\left( G \right) = 1, $$

so that

$${C_{{\omega}}}(A){C_{\omega} }(G \cap H) = {C_{{\omega}} }(A) = {C_{\omega} }(A \cap G),$$

which confirms (16). If ω ∉ G, then (8) entails.

$${C_{\omega} }(G) = 0,$$

so that

$$ {C_{\omega} }(A){C_{\omega} }(G \cap H) = 0 = {C_{\omega} }(A \cap G), $$

which also confirms (16). We have therefore shown that C is an rcd for C_ω given ${\mathscr{G}}$. □

Consider again the agent depicted in Fig. 4: she begins with unconditional credences (Ω, ${\mathscr{F}}$, P) and conditional credences modeled by C, then transitions based on certainty profile δ_ω to new unconditional credences C_ω while holding fixed her conditional credences C. We have assumed that C is proper at ω. (Otherwise, the agent cannot use C to conditionalize on δ_ω in the first place.) Our theorem entails that C is also an rcd for the agent’s new unconditional credal allocation C_ω. The agent may therefore continue to use C to conditionalize. If a new exogenous change instills a new certainty profile δ_ν at t₂, then she can use C to conditionalize on the new certainty profile δ_ν, so long as C is proper at ν. See Fig. 5.

Fig. 5

The agent gains new certainty profile δ_ω and responds by using C to conditionalize on δ_ω. Then she gains new certainty profile δ_ν and responds by using C to conditionalize on δ_ν

Figure 5 is quite general. It applies to a wide range of situations in which an agent gains a certainty profile δ_ω over a sub-σ-field and then gains a different certainty profile δ_ν over the same sub-σ-field. I do not say Fig. 5 applies to all such situations. If an rcd does not exist, or if every rcd is improper at ω or ν, then Fig. 5 does not apply. However, such situations arise rarely if ever in scientific applications.

To illustrate the virtues of Fig. 5, let us revisit False Alarm. We saw in Sect. 5 that John can use μ at t₂ to conditionalize on his newfound certainty in Negative. The worry raised in Sect. 4.2 was that μ seemed arbitrary. Why should John update his credences using μ rather than another rcd μ*? Rigidity enables a principled answer. The key point here is that μ encodes conditional probabilities that John has at t₀. The conditional probabilities follow from our choice of P and from the ratio formula. When John conditionalizes on Positive at t₁, Rigidity mandates that he leave those conditional probabilities fixed. John’s fixed conditional probabilities, codified by μ, serve as a basis for conditionalization when at t₂ he becomes certain of Negative. Hence, Rigidity rationalizes the choice of μ rather than any alternative rcd μ*. Given John’s unconditional credences at t₀, μ is the unique rcd that conforms to Rigidity. See Fig. 6.

Fig. 6

Credal evolution in False Alarm. John’s initial unconditional credences P determine his conditional credences μ, via the ratio formula. John becomes certain of Positive and responds by forming new credences μ_ω, where ω is any arbitrary outcome belonging to Positive. Then he becomes certain of Negative and responds by forming new credences μ_ν, where ν is any arbitrary outcome belonging to Negative. Complying with Weak Rigidity, he retains his conditional credences μ throughout this process

Our revised analysis of False Alarm illustrates the benefits that Rigidity offers to Kolmogorov conditionalizers. By constraining conditional credence, Rigidity guides the course of iterated Bayesian inference. Here is another example along the same lines:

Mismeasurement

Jane is a scientist with credences P at time t₀. X is a random variable that reflects the outcome of an experiment. At t₁, Jane becomes certain that X = x₁ and updates her other credences on that basis. At t₂, she realizes that her certainty in X = x₁ was misplaced: she misread a measuring instrument, or the measuring instrument was poorly calibrated, or she was deceived by her assistant, etc. Jane becomes newly certain that X = x₂. How should she proceed?

Using Rigidity, we can elaborate Mismeasurement so as to include a principled credal update at t₂. Stipulate that Jane has conditional credences at t₀ given by P_σ(X), an rcd for P given σ(X). At t₁, she becomes certain that X = x₁ and on that basis acquires new credences P_σ(X)(.$|$ω₁), where ω₁ is any outcome such that X(ω₁) = x₁. Complying with Rigidity, she carries her conditional credences P_σ(X) forward from t₀ to t₁. At t₂, she becomes certain that X = x₂ and on that basis acquires new credences P_σ(X)(.$|$ω₂), where ω₂ is any outcome such that X(ω₂) = x₂. Given Rigidity, her conditional credences at t₀ uniquely determine how she should update her credences upon becoming certain at t₁ that X = x₁ and also how she should update her credences upon becoming certain at t₂ that X = x₂. See Fig. 7. Jane can implement Fig. 7 as long as P_σ(X) is proper at ω₁ and ω₂.

Fig. 7

Credal evolution in Mismeasurement

More specifically, suppose that at t₀ Jane has the probability density p(x, y) given by Fig. 1. This is not a useful density for real-world applications, but it suffices for heuristic purposes. At t₁, Jane becomes certain that X = x₁, where 0 ≤ x₁ ≤ ½. She forms new credences P_σ(X)(.$|$x₁, y), where y is any real number. In particular, she forms the credences given by (10) and (11). At t₂, she becomes certain that X = x₂, where ½ < x₂ ≤ 1. She forms new credences P_σ(X)(.$|$x₂, y), including the credences given by (12) and (13). Over the course of her credal evolution, her credence in X ≠ x₁ ∪ Y > ½ goes from 1 to ½ to ¾.

False Alarm and Mismeasurement illustrate how Rigidity can steer Kolmogorov conditionalizers through rational acquisition and loss of certainties. In each example, the agent’s initial doxastic state dictates how she should reallocate credence when she becomes certain of a conditioning proposition and also when she later becomes certain of a conflicting proposition.

Of course, we must assume initial conditional and unconditional credences to derive a determinate credal reallocation policy. But this is no problem for my approach, because all Bayesian theorizing assumes that the agent has certain initial credences. One must always assume some credal starting point. As noted in Sect. 2, the assumed credal starting point will usually include primitive conditional credences over and above the agent’s unconditional credences once we move beyond simple cases where the ratio formula prevails. The essence of the Bayesian framework is to place rational constraints on credal evolution given the agent’s initial conditional and unconditional credences. That is precisely what Rigidity accomplishes.

Figure 5 lends itself to iteration. Consider an agent who transitions from certainty profile ${\delta_{{\omega}_1}}$ to certainty profile ${\delta_{\omega_2}}$ to certainty profile ${\delta_{\omega_3}}$, and so on, all over a fixed sub-σ-field ${\mathscr{G}}$. So long as C is proper at each index ω₁, ω₂, ω₃, …, ω_n, … the agent can carry C forward at each stage, using it as her fixed update rule. At each stage, the agent downgrades certainties acquired at the previous stage. See Fig. 8.

Fig. 8

Sequential credal updates conforming to Weak Rigidity. At each time t_n after the starting point t₀, the agent gains new certainty profile ${\delta_{\omega_n}}$ and responds by using C to conditionalize on ${\delta_{\omega_n}}$, yielding new credences ${C_{\omega_n}}$. Complying with Weak Rigidity, she retains her conditional credences C

7 Generalized rigidity

Rigidity applies to situations where credences shift over a single fixed conditioning sub-σ-field ${\mathscr{G}}$. In many applications, though, there is not a single fixed conditioning sub-σ-field. Instead, the agent accumulates new evidence over a non-decreasing sequence of sub-σ-fields:

$$ {\mathscr{G}_1} \subseteq {\mathscr{G}_2} \subseteq {\mathscr{G}_3} \ldots \subseteq {\mathscr{G}_n} \subseteq \ldots$$

For example, an agent might progressively learn the values of random variables X₁, X₂, …, X_n, …, a situation we can model using the sub-σ-fields:

$$ \sigma \left( {X_1} \right) \subseteq \sigma \left( {{X_1},{X_2}} \right) \subseteq \sigma \left( {{X_1},{X_2},{X_3}} \right) \subseteq \ldots \subseteq \sigma \left( {{X_1},{X_2}, \ldots {X_n}} \right) \subseteq \ldots$$

I will now generalize Rigidity so as to accommodate sequential evidence accumulation.

7.1 Minimal change revisited

Consider an agent who begins with unconditional credences modeled by a probability space (Ω, ${\mathscr{F}}$, P). Fix ${\mathscr{G}}$₁ and ${\mathscr{G}}$₂ such that ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂ ⊆ ${\mathscr{F}}$. Suppose that the agent has conditional credences over ${\mathscr{F}}$ given ${\mathscr{G}}$₂, modeled by an update rule C: ${\mathscr{F}}$ × Ω →  $\mathbb{R}.$ Suppose that there is an exogenous shift in credences across ${\mathscr{G}}$₁, inducing additional credal changes over the rest of ${\mathscr{F}}$. I submit that this shift should leave fixed the agent’s credences conditional on ${\mathscr{G}}$₂. More precisely, I propose the following requirement on credal evolution:

GENERALIZED RIGIDITY: If an agent begins with credences P_old over ${\mathscr{F}}$ and conditional credences C_old over ${\mathscr{F}}$ given ${\mathscr{G}}$₂, and she subsequently adopts new credences P_new over ${\mathscr{F}}$ and new conditional credences C_new over ${\mathscr{F}}$ given ${\mathscr{G}}$₂, and ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂, and the new credal assignment over ${\mathscr{G}}$₁ mediates the transition from P_old and C_old to P_new and C_new, then C_old = C_new,

where the clause “the new credal assignment over ${\mathscr{G}}$₁ mediates the transition from P_old and C_old to P_new and C_new” registers that the agent’s credences change solely due to the new credal assignment over ${\mathscr{G}}$₁. Generalized Rigidity demands that, in such situations, credences conditional on ${\mathscr{G}}$₂ remain constant. Note that Generalized Rigidity entails Rigidity. Like Rigidity, Generalized Rigidity is a minimal change principle. Intuitively: credal reallocation across a sub-σ-field provides no basis for changing credences conditional on a larger sub-σ-field.

To illustrate, consider a partition ${\mathscr{E}}$ = {E_i} and a finer-grained partition ${\mathscr{D}}$ = {E_ij}, where

$${E_i} = \bigcup\limits_j {{E_{ij}}}. $$

Suppose that the agent at time t₁ gains new credences over ${\mathscr{E}}$ and that these new credences cause her to reallocate credences over all remaining propositions. Intuitively, the agent’s new credal allocation over ${\mathscr{E}}$ should not lead her to change her probabilities conditional on members of ${\mathscr{D}}$ . Reallocating credence over the E_i should not affect how credence is allocated within each E_i, so it should not change how credence is allocated within each E_ij. Indeed, one can easily show that Jeffrey conditionalization in response to new credences over ${\mathscr{E}}$ leaves fixed all conditional probabilities P$(H|E$_ij). Let ${\mathscr{G}}$₁ = σ(${\mathscr{E}}$), the σ-field generated by ${\mathscr{E}}$, and let ${\mathscr{G}}$₂ = σ(${\mathscr{D}}$), the σ-field generated by ${\mathscr{D}}$. Note that ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂. If the agent updates using Jeffrey Conditionalization, she will conform to Generalized Rigidity as applied to ${\mathscr{G}}$₁ and ${\mathscr{G}}$₂.

As with the original version of Rigidity, I focus exclusively on a weak consequence of Generalized Rigidity:

WEAK GENERALIZED RIGIDITY: If an agent begins with credences P_old over ${\mathscr{F}}$ and conditional credences C_old over ${\mathscr{F}}$ given ${\mathscr{G}}$₂, and she subsequently adopts new credences P_new over ${\mathscr{F}}$ and new conditional credences C_new over ${\mathscr{F}}$ given ${\mathscr{G}}$₂, and ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂, and P_new$|$${\mathscr{G}}$₁ = δ_ω for some ω, and the new credal assignment over ${\mathscr{G}}$₁ mediates the transition from P_old and C_old to P_new and C_new, then C_old = C_new.

Weak Generalized Rigidity entails Weak Rigidity. I will use Weak Generalized Rigidity to model cases of defeasible inference that cannot be modeled using Weak Rigidity.

7.2 Credal evolution conforming to generalized rigidity

I propose the following picture of credal evolution. At t₀, an agent has unconditional credences modeled by a probability space (Ω, ${\mathscr{F}}$, P). She also has conditional credences modeled by ${P_{\mathscr{G}_1}}$, a proper rcd for P given ${\mathscr{G}}$₁, and ${P_{\mathscr{G}_2}}$, a proper rcd for P given ${\mathscr{G}}$₂, where ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂. Moreover, for each ω ∈ Ω, ${P_{\mathscr{G}_2}}$ is an rcd for ${P_{\mathscr{G}_1}}(\,.\,\,|\omega )$ given ${\mathscr{G}}$₂. At t₁, an exogenous change instills certainty profile ${\delta_{\omega_1}}$ over ${\mathscr{G}}$₁. In response, the agent uses ${P_{\mathscr{G}_1}}$ to conditionalize on ${\delta_{\omega_1}}$, adopting ${P_{\mathscr{G}_1}}(\,.\,\,|{\omega_1})$ as her new credal allocation over ${\mathscr{F}}$. The agent retains the same fixed conditional credences ${P_{\mathscr{G}_1}}$ and ${P_{\mathscr{G}_2}}$, as mandated by Generalized Rigidity. At t₂, an exogenous change instills certainty profile ${\delta_{\omega_2}}$ over ${\mathscr{G}}$₂. In response, the agent uses ${P_{\mathscr{G}_2}}$ to conditionalize on ${\delta_{\omega_2}}$, adopting ${P_{\mathscr{G}_2}}(\,.\,\,|{\omega_2})$ as her new credal allocation over ${\mathscr{F}}$. Her credences conditional on ${\mathscr{G}}$₂ are still given by ${P_{\mathscr{G}_2}}$, as Generalized Rigidity mandates. See Fig. 9.

Fig. 9

Two credal updates conforming to Weak Generalized Rigidity. Note that the agent no longer has conditional credences ${P_{\mathscr{G}_1}}$ at t₂

Note that, at t₂, Generalized Rigidity does not require the agent’s credences conditional on ${\mathscr{G}}$₁ to be given by ${P_{\mathscr{G}_1}}$. This is as it should be. To see why, fix events E and F such that P(E ∩ F) > 0. If the agent ratio conditionalizes on E ∩ F, then she will not usually retain her initial conditional probabilities P$(H|E)$. She is now certain of E, so her new credence in H conditional on E is simply her new unconditional credence in H:

$$ {P_{new}}\left( {H|E} \right) \, = {P_{new}}\left( H \right) \, = P(H|E \cap F),$$

which may differ from P$(H|E)$. Intuitively: newfound certainty in F may alter credences conditional on E. Restating the point using the rcd formalism, let ${\mathscr{G}}$₁ be the σ-field generated by {E}, and let ${\mathscr{G}}$₂ be the σ-field generated by {E, F}. Assume that ${P_{\mathscr{G}_1}}$ is an rcd for P given ${\mathscr{G}}$₁ and that ${P_{\mathscr{G}_2}}$ is an rcd for P given ${\mathscr{G}}$₂, where these rcds are given by the ratio formula. If ${{\omega}_2} \in E \cap F$, then ${P_{\mathscr{G}_1}}$ may not be an rcd for ${P_{\mathscr{G}_2}}(\,.\,\,|{{\omega}_2})$ given ${\mathscr{G}}$₁. Intuitively: newfound certainties regarding ${\mathscr{G}}$₂ may alter probabilities conditional on ${\mathscr{G}}$₁.

We may extend Fig. 9 to scenarios where the agent sequentially accumulates evidence at times t₁, t₂, …, t_n, … regarding sub-σ-fields

$$ {\mathscr{G}_1} \subseteq {\mathscr{G}_2} \subseteq {\mathscr{G}_3} \ldots \subseteq {\mathscr{G}_n} \subseteq \ldots $$

Suppose that ${P_{\mathscr{G}_n}}$ is a proper rcd for P given ${\mathscr{G}}$_n. Suppose also that, for each ${\omega} \in {\Omega}$, ${P_{{\mathscr{G}_{n + 1}}}}$ is an rcd for ${P_{\mathscr{G}_n}}(\,.\,\,|\omega )$ given ${\mathscr{G}}$_n+1. At t_n, an exogenous change instills certainty profile ${\delta_{{\omega}_n}}$ over ${\mathscr{G}}$_n. In response, the agent uses ${P_{\mathscr{G}_n}}$ to conditionalize on ${\delta_{{\omega}_n}}$, adopting ${P_{\mathscr{G}_n}}(\,.\,\,|{{\omega}_n})$ as her new credal allocation over ${\mathscr{F}}$. Complying with Generalized Rigidity, she retains the conditional credences given by ${P_{\mathscr{G}_n}}$, ${P_{{\mathscr{G}_{n + 1}}}}$, ${P_{{\mathscr{G}_{n + 2}}}}$, …, ${P_{{\mathscr{G}_{n + m}}}}$, … She uses those conditional credences for credal updates at t_n+1, …, t_n+m, …. In this manner, the agent’s initial conditional credences dictate her credal evolution as she sequentially gains new evidence. See Fig. 10.

Fig. 10

Sequential credal updates conforming to Weak Generalized Rigidity. At each time t_n after the initial starting point t₀, the agent uses ${P_{\mathscr{G}_n}}$ to conditionalize on ${\delta_{{\omega}_n}}$, adopting new credences ${P_{\mathscr{G}_n}}(\,.\,\,|{{\omega}_n})$. Note that the agent no longer has conditional credences ${P_{{\mathscr{G}_{n - 1}}}}$ at time t_n

In presenting Figs. 9 and 10, I made two assumptions about the rcds ${P_{\mathscr{G}_n}}$. First, ${P_{\mathscr{G}_n}}$ is proper at ω_n. Second, ${P_{{\mathscr{G}_{n + 1}}}}$ is an rcd for ${P_{\mathscr{G}_n}}(\,.\,\,|{{\omega}_n})$ given ${\mathscr{G}}$_n+1. Only under those assumptions can a Kolmogorov conditionalizer use the rcds ${P_{\mathscr{G}_n}}$ to conditionalize at each time stage t_n.

Unfortunately, there is no global guarantee that the two assumptions are satisfiable. That ${P_{{\mathscr{G}_{n + 1}}}}$ is an rcd for P given ${\mathscr{G}}$_n+1 does not guarantee that it is an rcd for ${P_{\mathscr{G}_n}}(\,.\,\,|{{\omega}_n})$ given ${\mathscr{G}}$_n+1. Even if it is, it may not be everywhere proper. Thus, a Kolmogorov conditionalizer may not be able to comply with Fig. 10 even when rcds ${P_{\mathscr{G}_1}}$, ${P_{\mathscr{G}_2}}$,…, ${P_{\mathscr{G}_n}}$, … exist. Luckily, though, Sokal (1981) has proved that my assumptions are satisfiable in numerous cases, including all or virtually all cases likely to arise in scientific applications. Sokal shows that, under rather mild conditions, there exist ${P_{\mathscr{G}_1}}$, ${P_{\mathscr{G}_2}}$,…, ${P_{\mathscr{G}_n}}$, …. such that, for all n,

$$\begin{array}{l} {P_{{\mathscr{G}_n}}}\;{\rm{\;is}}\;{\rm{an}}\;{\rm{rcd}}\;{\rm{for}}\;P\;{\rm{given}}\;{\mathscr{G}_n}\\ {P_{{\mathscr{G}_n}}}\;{\rm{\;is}}\;{\rm{proper}}\;{\rm{at}}\;{\omega}, \;{\rm{for}}\;{\rm{all}}\;{\omega} \in {\Omega} \\ {P_{{\mathscr{G}_{n + 1}}}}{\rm{\;\;is}}\;{\rm{an}}\;{\rm{rcd}}\;{\rm{for}}\;{P_{{\mathscr{G}_n}}}(.|{\omega} )\;{\rm{given}}\;{\mathscr{G}_{n + 1}},\;{\rm{for}}\;{\rm{all}}\;{\omega} \in {\Omega} \end{array}$$

Sokal’s theorem ensures that, in numerous cases, a Kolmogorov conditionalizer can update her credences in accord with Fig. 10.¹⁰

More specifically, consider a standard setup from Bayesian statistics (Florens et al., 1990): we start with a parameter space (A, ${\mathscr{A}}$) and a sample space (S, ${\mathscr{S}}$) and form the product space (A, ${\mathscr{A}}$) ⊗ (S, ${\mathscr{S}}$) = _df (A × S, ${\mathscr{A}}$ ⊗ ${\mathscr{S}}$).¹¹ The parameter space (A, ${\mathscr{A}}$) models possible states of the worlds. The sample space (S, ${\mathscr{S}}$) models evidence the agent may receive. In many applications, (S, ${\mathscr{S}}$) has the form:

$$ ({T_1},{\mathscr{T}_1}) \otimes ({T_2},{\mathscr{T}_2}) \otimes ({T_3},{\mathscr{T}_3}) \, \ldots \otimes ({T_n},{\mathscr{T}_n}) \, \ldots $$

and models a stream of incoming evidence received at times t₁, t₂, …, t_n, …. Each outcome then has the form

$$ {\omega} = \left( {{\omega_0},{\omega_1},{\omega_2},{\omega_3}, \ldots ,{\omega_n}, \ldots } \right), $$

where ω₀ ∈ A and ω_n ∈ T_n for n > 0. Define random variable X_n: A × S → T_n by projection onto the nth coordinate:

$$ {X_n}(\omega ) = {\omega_n}.$$

To model sequential evidence accumulation regarding the sample spaces (T_n, ${\mathscr{T}}$_n), we use certainty profiles over the sub-σ-fields

$$ \sigma \left( {X_1} \right),\sigma \left( {{X_1},{X_2}} \right),\sigma \left( {{X_1},{X_2},{X_3}} \right), \, \ldots ,\sigma \left( {{X_1},{X_2}, \, \ldots ,{X_n}} \right), \, \ldots$$

In this setting, Sokal’s theorem applies whenever the probability space (A × S, ${\mathscr{A}}$ ⊗ ${\mathscr{S}}$, P) meets mild conditions–-conditions that are almost always met in the daily practice of Bayesian statistics.¹² Assuming the conditions met, there exist functions

$$ {P_{\sigma ({X_1})}},{P_{\sigma ({X_1},{X_2})}},{P_{\sigma ({X_1},{X_2},{X_3})}},\ldots,{P_{\sigma ({X_1},{X_2},\ldots,{X_n})}},...$$

such that, for all n,

$$\begin{array}{l} {P_{\sigma ({X_1},{X_2}, \ldots {X_n})}}\;{\rm{is}}\;{\rm{an}}\;{\rm{rcd}}\;{\rm{for}}\;P\;{\rm{given}}\;\sigma \left( {{X_1},{X_2},{\rm{ }} \ldots ,{X_n}} \right)\\ {P_{\sigma ({X_1},{X_2}, \ldots {X_n})}}\;{\rm{is}}\;{\rm{proper}}\;{\rm{at}}\;\omega, \;{\rm{for}}\;{\rm{all}}\; \omega \in \Omega \\ {P_{\sigma ({X_1},{X_2}, \ldots {X_{n + 1}})}}\;{\rm{is}}\;{\rm{an}}\;{\rm{rcd}}\;{\rm{for}}\;{P_{\sigma ({X_1},{X_2}, \ldots {X_n})}}(.|\omega )\;{\rm{given}}\;\sigma \left( {{X_1},{X_2},{\rm{ }} \ldots ,{X_{n+1}}} \right),\;{\rm{for}}\;{\rm{all}}\; \omega \in \Omega \end{array}$$

A Kolmogorov conditionalizer with these initial conditional and unconditional credences can update her credences in compliance with Generalized Rigidity.

Here is a simple example of Generalized Rigidity in action.

Rabies Infection

Pierre, who lives in nineteenth century Paris, is bit by a rabid dog on his 35th birthday. Knowing that rabies is 100% fatal, Pierre becomes certain that he will die before his 37th birthday. A week later, Pierre learns that Louis Pasteur has invented a vaccine for rabies and that the vaccine is highly effective if delivered soon enough after a bite by a rabid animal. Pierre contacts Pasteur and receives the vaccine. Pierre is not convinced that the vaccine will work, but he is no longer certain that he will die before his 37th birthday.

Using Generalized Rigidity, we can elaborate Rabies Infection into a model that includes principled acquisition and loss of certainties. Let Ω be a suitable outcome space, and let

Rabies =:

 the set of outcomes in which Pierre is infected with rabies on his 35th birthday.

Vaccine =:

the set of outcomes in which Pierre receives an effective rabies vaccine within a week after his 35th birthday

Dead =:

the set of outcomes in which Pierre dies before his 37th birthday

Let ${\mathscr{F}}$ be the σ-field generated by {Rabies, Vaccine, Dead}. Suppose Pierre has initial conditional and unconditional credences before his 35th birthday given by:

$$\begin{array}{l} P(Rabies) = 1/30,\!000,\!000\\ P\left( {Vaccine} \right){\rm{ }} = {\rm{ }}0\\ P(Dead|Rabies \cap Vaccine) = 1/2\\ P(Dead|Rabies \cap Vaccin{e^c}) = 1\\ P(Dead|Rabie{s^c}) = P(Dead|Rabie{s^c} \cap Vaccine) = 1/500 \end{array}$$

These credences reflect the following factors: the low rate of exposure to rabies in nineteenth century Paris; non-existence of an effective rabies vaccine, so far as Pierre initially knows; the chancy nature of a new vaccine for a fatal illness; the certain death that follows from a rabies infection absent an effective treatment; and the chance of death from other causes. Assume that P$(A|A)$ = 1 for all A. Through the law of total probability and the ratio formula, our assumptions determine a unique probability measure P over ${\mathscr{F}}$. For example, we compute:

$$ \begin{gathered} P\left( {Dead} \right) \, = P\left( {Dead|Rabies \cap Vaccine} \right)P\left( {Rabies \cap Vaccine} \right) \, \hfill \\ + P\left( {Dead|Rabies \cap Vaccin{e^c}} \right)P\left( {Rabies \cap Vaccin{e^c}} \right) \, \hfill \\ + P\left( {Dead|Rabie{s^c}} \right)P\left( {Rabie{s^c}} \right) \hfill \\ = \, 0 \, + 1/30,\!000,\!000 + 1/500 \times 29,\!999,\!999/30,\!000,\!000 \approx .00200003327 \hfill \\ \end{gathered}$$

and

$$ P\left( {Dead|Rabies} \right) = P(Dead|Rabies \cap Vaccin{e^c}) = 1. $$

Let ${\mathscr{G}}$₁ be the σ-field generated by {Rabies}, and let ${\mathscr{G}}$₂ be the σ-field generated by {Vaccine, Rabies}. Our stipulations determine a privileged rcd for P given ${\mathscr{G}}$₁, defined by

$$ {P_{{{\mathscr{G}}_1}}}(A|\omega ) = \left\{ {\begin{array}{*{20}{c}} {P(A|Rabies)}&\qquad{if}&{\omega \in Rabies} \\ {P(A|Rabie{s^c})}&\qquad{if}&{\omega \notin Rabies} \end{array}} \right.$$

and a privileged rcd for P given ${\mathscr{G}}$₂, defined by

$$ {P_{\mathscr{G}_2}}(A|\omega ) = \left\{ {\begin{array}{*{20}{c}} {P(A|Rabies \cap Vaccine){\kern 1pt} }&\qquad{if}&{\omega \in Rabies \cap Vaccine} \\ {P(A|Rabies \cap Vaccin{e^c})}&\qquad{if}&{\omega \in Rabies \cap Vaccin{e^c}} \\ {P(A|Rabie{s^c} \cap Vaccine)}&\qquad{if}&{\omega \in Rabie{s^c} \cap Vaccine} \\ {P(A|Rabie{s^c} \cap Vaccin{e^c})}&\qquad{if}&{\omega \in Rabie{s^c} \cap Vaccin{e^c}} \end{array}} \right. $$

It is not hard to check that, for every ω, ${P_{\mathscr{G}_2}}$ is an rcd for ${P_{\mathscr{G}_1}}(\,.\,\,|\omega )$ given ${\mathscr{G}}$₂. Let ω be the true outcome. When the rabid dog bites Pierre, he becomes certain of Rabies and responds by forming new credences ${P_{\mathscr{G}_1}}(\,.\,\,|\omega )$. In particular, he becomes certain of Dead. Complying with Generalized Rigidity, his credences conditional on ${\mathscr{G}}$₂ are still given by ${P_{\mathscr{G}_2}}$. When he receives the rabies vaccine, he becomes certain of Vaccine and responds by forming new credences ${P_{\mathscr{G}_2}}(\,.\,\,|\omega )$, so that his credence in Dead goes from 1 to ½. See Fig. 11.

Fig. 11

Credal evolution in Rabies Infection. ω is the true outcome

Rabies Infection illustrates the advantages that Weak Generalized Rigidity offers over Weak Rigidity. Pierre’s initial conditional credences carry forward in accord with Weak Generalized Rigidity. The conditional credences determine how he should conditionalize both when he learns that he is infected with rabies and when he later learns that he has received a rabies vaccine. In this manner, Weak Generalized Rigidity helps us model situations where the agent accumulates evidential certainties (modeled by certainties over ${\mathscr{G}}$₁ and then over ${\mathscr{G}}$₂). Weak Rigidity only helps us model situations where evidence gained at a later time eradicates evidential certainties gained at an earlier time (modeled by shifting certainties over ${\mathscr{G}}$₁).

Relatedly, Weak Generalized Rigidity is much more useful than Weak Rigidity when the factivity assumption (3) prevails. To apply Weak Rigidity in a non-trivial way, we must consider a scenario where a certainty profile δ_ν over ${\mathscr{G}}$ supplants a conflicting certainty profile δ_ω over ${\mathscr{G}}$. Conflicting certainty profiles cannot both satisfy the factivity assumption. At least one of them must be misplaced. In contrast, Generalized Rigidity helps us model cases where the agent conditionalizes on a certainty profile that satisfies the factivity assumption and subsequently conditionalizes on a distinct certainty profile that also satisfies the factivity assumption. Pierre correctly becomes certain that he is infected with rabies, then correctly becomes certain that he received an effective rabies vaccine. At neither time does he acquire misplaced certainties over a conditioning sub-σ-field. Nevertheless, evidence gained at the later time defeats evidence gained at the earlier time. He gains strong evidence that he will die before his 37th birthday (he was infected by rabies), then subsequently receives strong defeating evidence (he has received an effective rabies treatment). Thus, Generalized Rigidity helps us model cases of epistemic defeat where the defeated evidence is veridical and the defeating evidence is also veridical.¹³

Here is a more elaborate example along similar lines.

Ring Time

A timer will ring during an interval [x, x + y]. Frank chooses the start time x, and Mary independently chooses the interval length y. Sarah believes that, given x and y, the timer is equally likely to ring at any time z falling in the interval [x, x + y]. At t₀, Sarah is certain that Frank will choose a start time between 0 and 100, and she believes that he is equally likely to choose any start time within that interval. She is certain that Mary will choose interval length y₀. At time t₁, Sarah learns that Frank chose start time x₁ ∈ [0, 100]. This discovery, combined with her certainty that the interval length is y₀, leads Sarah to become certain that the timer will ring during the interval [x₁, x₁ + y₀]. At t₂, Sarah learns that Mary chose interval length y₂ > y₀. This discovery eradicates Sarah’s certainty that the timer will ring during the interval [x₁, x₁ + y₀].

Using Generalized Rigidity, we can fill in the story to rationalize Sarah’s certainty loss at t₂. We use a probability space ($\mathbb{R}$², ${\mathscr{B}}$($\mathbb{R}$²), π) to codify Sarah’s credences over possible start times x and interval lengths y. We use C: ${\mathscr{B}}$($\mathbb{R}$) ×  $\mathbb{R}$² →$\mathbb{R}$ to codify Sarah’s credences over ring times conditional on start time x and interval length y. Given how I described Sarah’s initial credences, we naturally choose π and C defined by

$$ \pi { =_{df}}{U_{[0,100]}} \otimes {\delta_{y_0}}$$

$$ C(.|x,\!y){ =_{df}}{U_{[x,x + y]}} $$

where ⊗ is the product measure (Billingsley, 1995, pp. 232–233) and ${U_{[a,b]}}$ is the uniform distribution over [a, b]. We define a probability measure P over the larger space ($\mathbb{R}$³, ${\mathscr{B}}$($\mathbb{R}$³)):

$$P(A) = \int {\left[ {\int {{I_A}(x,y,z){C_{x,y}}(dz)} } \right]} d\pi (x,y),\qquad {for} \; {any}\;A \in \mathscr{B}({\mathbb{R}^3})$$

(17)

where I_A is the indicator function for A:

$${I_A}(\omega ) = \left\{ {\begin{array}{*{20}{c}} 1&{if}&{\omega \in A} \\ 0&{if}&{\omega \notin A} \end{array}} \right.$$

P encodes Sarah’s credences over start times x, interval lengths y, and ring times z.¹⁴ It is easy to show that, for our choice of C and π, the measure P defined by (17) concentrates all probability mass over the event

$$ \{ \left( {x,{y_0},z} \right): \, 0 \leqslant x \leqslant 100 \, \&\; x \leqslant z \leqslant x + {y_0}\} .$$

See Fig. 12. Let X and Y be projection mappings onto the x and y coordinates, respectively. Then the following function ${P_{\sigma (X,Y)}}$ : ${\mathscr{B}}$($\mathbb{R}$³) ×  $\mathbb{R}$³ →  $\mathbb{R}$ is an rcd for P given σ(X, Y):

$$ {P_{\sigma (X,Y)}}(.|x,y,z) = {\delta_x} \otimes {\delta_y} \otimes {U_{[x,x + y]}}. $$

Note that ${P_{\sigma (X,Y)}}$ embeds the conditional credences C into corresponding conditional credences over the larger space ($\mathbb{R}$³, ${\mathscr{B}}$($\mathbb{R}$³)). One can also show that the following function P_σ(X): ${\mathscr{B}}$($\mathbb{R}$³) ×  $\mathbb{R}$³ →  $\mathbb{R}$ is an rcd for P given σ(X):

Fig. 12

Sarah’s credences at t₀. The whole probability space is three-dimensional, but Sarah’s initial credal mass lies entirely in the two-dimensional sub-space (pictured here) where Y = y₀. Sarah assigns credence 1 to the grey parallelogram

$${P_{\sigma (X)}}(.|x,y,z) = {\delta_x} \otimes {\delta_{y_0}} \otimes {U_{[x,x + {y_0}]}}.$$

Intuitively: newfound certainty that the start time is x, combined with prior certainty that Y = y₀, induces a uniform distribution over ring times falling in the interval [x, x + y₀]. In addition, one can show that ${P_{\sigma (X,Y)}}$ is an rcd for P_σ(X)(.$|$x, y, z) given σ(X, Y), for any x, y, z.¹⁵

At t₀, Sarah has unconditional credences codified by P along with conditional credences codified by P_σ(X) and ${P_{\sigma (X,Y)}}$. At t₁, she becomes certain that Frank chose start time X = x₁. We model her newfound certainty through a certainty profile ${\delta_{({x_1},y,z)}}$ over σ(X), where y and z are arbitrary. We may assume that Frank really did choose x₁, so that ${\delta_{({x_1},y,z)}}$ satisfies the factivity assumption. Sarah conditionalizes using P_σ(X), forming new credences:

$${P_{\sigma (X)}}(.|{x_1},y,z) = {\delta_{x_1}} \otimes {\delta_{y_0}} \otimes {U_{[{x_1},{x_1} + {y_0}]}}.$$

Thus, she is newly certain of the event

$$ \left\{ {x_1} \right\} \times \left\{ {y_0} \right\} \times \left[ {{x_1},{x_1} + {y_0}} \right]. $$

In other words: she is certain that John chose X = x₁, that Mary chose Y = y₀, and that the timer will ring in the interval [x₁, x₁ + y₀]. See Fig. 13. Complying with Generalized Rigidity, she retains P_σ(X) and ${P_{\sigma (X,Y)}}$ as conditional credences at t₁. At t₂, she becomes certain that Mary chose the interval length y₂ > y₀. We model Sarah’s newfound certainty through a certainty profile ${\delta_{({x_1},{y_2},z)}}$ over σ(X, Y). We may assume that Sarah is correct, so that ${\delta_{({x_1},{y_2},z)}}$ satisfies the factivity assumption. In response to her new certainty profile, she conditionalizes using ${P_{\sigma (X,Y)}}$. Her credences are now given by:

Fig. 13

Sarah’s credences at t₁. She assigns credence 1 to the event (pictured here by a black line segment) formed by intersecting the line X = x₁ with the grey parallelogram

$${P_{\sigma (X,Y)}}(.|{x_1},{y_2},z) = {\delta_{x_1}} \otimes {\delta_{y_2}} \otimes {U_{[{x_1},{x_1} + {y_2}]}}.$$

See Fig. 14. Thus, Sarah is newly certain of the event

$$ \left\{ {x_1} \right\} \times \left\{ {y_2} \right\} \times \left[ {{x_1},{x_1} + {y_2}} \right].$$

See Fig. 15. Her newfound certainty that Y = y₂ eradicates her certainty (gained at t₁) that the timer will ring in the interval [x₁, x₁ + y₀].

Fig. 14

Credal evolution in Ring Time

Fig. 15

Sarah’s credences at t₂. Her credal mass lies entirely in the two-dimensional sub-space (pictured here) where Y = y₂. She assigns credence 1 to the dotted black line segment reaching to (x₁, x₁ + y₂)

In both Rabies Infection and Ring Time, the agent’s credences evolve according to Fig. 9. Some certainties gained at t₁ are subsequently lost at t₂. The examples demonstrate that Kolmogorov conditionalization, aided by Weak Generalized Rigidity, can induce principled acquisition and loss of certainties even when the factivity assumption (3) prevails.

8 Scope and limits

I have illustrated Weak Rigidity and Weak Generalized Rigidity with four toy examples: False Alarm, Mismeasurement, Rabies Infection, and Ring Time. The toy examples only hint at the scope of Fig. 10. Sokal’s theorem guarantees the existence of suitable rcds across diverse circumstances, including the vast majority of cases likely to arise in scientific applications. Whenever suitable rcds exist, a Kolmogorov conditionalizer can sequentially update her credences while complying with Weak Generalized Rigidity. Quite often, the sequential credal updates will eradicate certainties gained through earlier credal updates.

Although Weak Generalized Rigidity is widely applicable, there are situations where it does not apply. Weak Generalized Rigidity imposes a substantive constraint only when the agent gains new certainties over a conditioning sub-σ-field ${\mathscr{G}}$. As Jeffrey emphasizes, though, an agent may gain new credences over ${\mathscr{G}}$ that are not certainties. Jeffrey focuses on situations where ${\mathscr{G}}$ is generated by a countable partition. The general case, where ${\mathscr{G}}$ is not necessarily generated by a countable partition, has received some attention (e.g. Diaconis & Zabell, 1982; Hild et al., 1999; Meehan & Zhang, 2020) but not as much as it deserves. I suspect that Generalized Rigidity can shed light upon the general case. In any event, there are plainly situations where Weak Generalized Rigidity offers little help.

Even if we restrict attention to credal changes sparked by new certainties, Weak Generalized Rigidity does not always offer useful guidance. Consider a variant of Mismeasurement: Jane learns at t₂ that her laboratory assistant (who reported the result of the experiment measuring X’s value) is a pathological liar. Clearly, Jane should downgrade her certainty in X = x₁. Assuming that X does in fact have value x₁, we cannot model this case using Weak Generalized Rigidity. Weak Generalized Rigidity imposes a substantive constraint on cases falling into two categories:

• (i) An agent acquires a certainty profile over a sub-σ-field ${\mathscr{G}}$, then subsequently acquires a different certainty profile over ${\mathscr{G}}$, and so on.

• (ii) An agent acquires a certainty profile over a sub-σ-field ${\mathscr{G}}$₁, then acquires a certainty profile over a sub-σ-field ${\mathscr{G}}$₂ such that ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂, and so on.

Our new variant of Mismeasurement does not fall under either (i) or (ii):

• (i) Distinct certainty profiles over ${\mathscr{G}}$ cannot both conform to the factivity assumption. So category (i) does not include cases where the agent gains true evidence at every stage.

• (ii) If certainty profiles over ${\mathscr{G}}$₁ and ${\mathscr{G}}$₂ both satisfy the factivity assumption, and ${\mathscr{G}}$₁ ⊆ ${\mathscr{G}}$₂, then certainties over ${\mathscr{G}}$₁ gained at t₁ persist when the agent gains new certainties over ${\mathscr{G}}$₂ at t₂.

Neither category (i) nor category (ii) includes cases where true evidence eradicates certainty in a true conditioning proposition. So my framework cannot model how Jane’s credences change in response to learning that her lab assistant is a pathological liar. More generally, my framework does not help us model an agent who conditionalizes on a true proposition E but later learns truths that defeat her warrant for E.¹⁶

In response, one option is to abandon the assumption that the sub-σ-fields are non-decreasing. Rather than consider a sequence of sub-σ-fields such that

$${\mathscr{G}_1} \subseteq {\mathscr{G}_2} \subseteq {\mathscr{G}_3} \ldots \subseteq {\mathscr{G}_n} \subseteq \ldots,$$

we can instead consider a sequence of sub-σ-fields

$${\mathscr{G}_{1}},{\mathscr{G}_{2}},{\mathscr{G}_{3}} \ldots ,{\mathscr{G}_{n}}, \, \ldots$$

that is not necessarily non-decreasing. An agent may conditionalize based on new certainties over ${\mathscr{G}}$₁, then conditionalize based on new certainties over ${\mathscr{G}}$₂, and so on. Kallenberg (2010) has investigated iterated Kolmogorov conditionalization in this alternative setting. The alternative setting does not assume that ${\mathscr{G}}$_n ⊆ ${\mathscr{G}}$_n+1, so Generalized Rigidity does not apply. In the alternative setting, the agent can gain certainties over ${\mathscr{G}}$_n and subsequently lose those certainties in response to new certainties over ${\mathscr{G}}$_n+1 even though all certainties conform to the factivity assumption. In future work, I will use the alternative setting to model cases where true evidence eradicates newfound certainty in a true conditioning proposition.

Clearly, Fig. 10 is not general enough to handle all cases of epistemic defeat. Still, it is general enough to handle many cases of epistemic defeat. In that respect, it marks significant progress over theories that rely solely on ratio conditionalization.

9 Comparisons

To clarify the scope and limits of my approach, I will now compare it with three treatments found in the literature. The treatments are due respectively to Skyrms (1983), Titelbaum (2013), and Williamson (2000).

9.1 Skyrms on memory

Skyrms (1983, p. 157) notes that, when we update credences through ratio conditionalization, “there is a certain peculiar sense in which we lose information every time we learn something. That is, we lose information concerning the initial relative probabilities of statements not entailing S” whenever we ratio conditionalize on S. He proposes that we “give a probability assignment a memory” (p. 157), so as to retain information that would otherwise be lost. He suggests two information retention strategies. The basic idea behind both strategies is to maintain a record of earlier probabilities P, so that conditional probabilities P$(H|F)$ can be computed using the ratio formula even after conditionalizing on a proposition E incompatible with F. The first strategy records unconditional probabilities from each time stage. The second strategy records initial unconditional probabilities along with total evidence to date.

By maintaining a record of previous unconditional probabilities and using that record to compute conditional probabilities, Skyrms’s treatment reflects roughly the same “minimal change ethos” as Rigidity and Generalized Rigidity. However, his proposed strategies retain more information than is needed to handle the defeasible inferences analyzed in this paper. If an agent conditionalizes on E and subsequently wishes to conditionalize on an incompatible F, then she does not need access to her initial unconditional probabilities. She only needs access to suitable probabilities conditional on F. By retaining earlier unconditional probability assignments, Skyrms’s two strategies retain extraneous information. In contrast, my approach retains only the needed conditional probabilities. In Mismeasurement, for example, Jane can conditionalize on X = x₁ at t₁ and then (in accord with Weak Rigidity) use the same conditional probabilities to conditionalize on X = x₂ at t₂. Jane’s unconditional probabilities from t₀ do not matter at t₂. All that matters are her t₁ conditional probabilities, as enshrined by P_σ(X).

More importantly, Skyrms’s two strategies do not handle examples featuring initial conditional probabilities beyond the ratio formula. We have seen that such examples arise routinely in scientific practice. We have also seen that the standard mathematical and scientific solution is to use rcds. My proposal builds upon the standard solution, carrying forward conditional probabilities as codified by rcds in accord with Weak Generalized Rigidity. In this way, my approach handles numerous cases that Skyrms’s does not, such as Rabies Infection, Ring Time, and versions of Mismeasurement where X has uncountably many possible values.¹⁷

Skyrms writes that, “[a]fter conditionalizing on S, one might wish to be able to decide that this was an error and ‘deconditionalize’” (1983, p. 157). He models deconditionalization using the second of his information retention strategies: the agent adds proposition S to her total evidence at one time stage and deletes S from her total evidence at a later time stage (p. 159); conditionalizing on total evidence at the later time stage yields the desired deconditionalization. Notably, though, Skyrms does not formally model the factors that impel the agent to delete S from her total evidence. For that reason, his proposal does not model everything we would like to model about deconditionalization.

The situation is roughly comparable if we employ the rcd formalism. Consider yet another variant of Mismeasurement, in which Jane decides at t₂ that it was a mistake to conditionalize on X = x₁ and retreats to her former uncertainty regard X’s value. By stipulation, Jane’s t₂ credences over σ(X) are given by P. In accord with Rigidity, she carries forward her conditional probabilities P_σ(X) from t₁ to t₂. Then it is straightforward to show that her t₂ credences over the entire space are given by P. Thus, Jane’s renewed uncertainty regarding X’s value carries her back to her t₀ credences, as one would intuitively expect. In this manner, the rcd formalism conjoined with Rigidity helps us model Jane’s evolution from uncertainty regarding X’s value to certainty and then back to uncertainty. But the result is arguably not too satisfying because it does not explicitly model why Jane decides that it was a mistake to conditionalize on X = x₁. A more satisfying treatment would explicitly model Jane’s t₂ evidence and how that evidence reinstates her t₀ credences over σ(X). I believe that, ultimately, deconditionalization requires us to grapple with the issues raised in Sect. 8.

9.2 Titelbaum on certainty loss

Titelbaum (2013) models certainty eradication within a broadly Bayesian framework. He advances a diachronic norm, Generalized Conditionalization, that generalizes ratio conditionalization but can also accommodate some cases where agents lose certainties. He admits, though, that his framework does not satisfactorily handle “cases in which an agent becomes certain of a claim in response to a piece of evidence, then withdraws that certainty upon encountering a defeater” (pp. 296–298).

Suppose that evidence e gained at t₁ leads an agent to become certain of hypothesis h and that further evidence d gained at t₂ eradicates her newfound certainty in h. Titelbaum’s framework allows this to happen, but only within a model that stipulates certainty in h at t₁. Such a model cannot capture why the agent’s doxastic state at t₀ mandates her certainty in h at t₁ in response to evidence e. As Titelbaum puts it, “nothing in the model is tracking e’s influence on h” (p. 297). In contrast, my framework can model how an agent’s initial credences (both conditional and unconditional) mandate new certainties at t₁ and loss of those certainties at t₂. False Alarm, Mismeasurement, Rabies Infection, and Ring Time all have that form. In each case, my model tracks e’s influence on h at t₁ (e.g. learning that he was bit by a rabid dog leads Pierre to become certain that he will soon die of rabies) and d’s influence on h at t₂ (e.g. learning that he received a rabies vaccine leads Pierre to lose that newfound certainty). So my framework supplies substantive rational constraints beyond those supplied by Titelbaum’s.

9.3 Williamson on evidence

Williamson (2000, pp. 205–206) suggests that you can gain evidence and assign it probability 1, then gain new evidence that has non-zero probability and on that basis rationally downgrade the probability of the old evidence. His main example runs as follows. You inspect a red ball and a black ball before placing them in an empty bag, which leads you to become certain that you placed a red ball and a black ball in the bag. You then execute 10,000 draws with replacement that all turn out red. According to Williamson, you should lose your certainty that you placed a black ball in the bag.

The proposition that you drew red 10,000 times has non-zero probability, so conditionalizing on that proposition cannot dislodge your certainty that you placed a black ball in the bag. Thus, as Williamson (pp. 219–220) emphasizes, his analysis mandates major revisions to Bayesian decision theory. He proposes an alternative framework that retains some Bayesian elements while rejecting the core Bayesian idea that agents should respond to new evidence by conditionalizing on it (p. 220). Williamson’s framework is designed to handle the bag example and other examples where evidence with non-zero probability supposedly dislodges certainties.

I see no reason to revise Bayesian decision theory along the lines suggested by Williamson. On the contrary, the standard Bayesian analysis of the bag example seems correct to me: if you really are certain that you placed a black ball in the bag, then drawing red 10,000 times cannot rationally dislodge that certainty. Of course, it is very unlikely that you would draw red 10,000 times if you placed a black ball in the bag. But unlikely events sometimes occur, and they are not in themselves a sound basis for certainty eradication. Perhaps you should not have initially become certain that you placed a black ball in the bag, yet given that you did become certain your certainty should persist despite the 10,000 red draws. Here it is crucial to distinguish between certainty that you placed a black ball in the bag and certainty that the bag currently contains a black ball. Even if you are certain of the first proposition, it does not follow that you are (or should be) certain of the second. After all, the black ball might have surreptitiously escaped through a small hole or some other chicanery. Drawing red 10,000 times may rationally lead you to downgrade your credence that the bag currently contains a black ball while remaining certain that you placed a black ball in the bag.

At any rate, my framework cannot model situations (if such there are) where evidence with non-zero probability rationally dislodges certainties. It can model numerous situations where evidence with probability zero rationally dislodges certainties. It models these situations without any revision to Bayesian decision theory. On my approach, certainties cannot be dislodged by mere unlikely evidence, but they can be dislodged by vanishingly unlikely evidence.

10 Conclusion

Philosophers should retire the canard that conditionalization always leaves certainties in place. This canard reflects an overly narrow focus on the ratio formula and distorts scientific practice. Kolmogorov conditionalization can eradicate certainties, including certainties gained through prior exercise of conditionalization. It generates reasonable credal updates across a range of cases, especially when supplemented with Weak Generalized Rigidity. Overall, then, Kolmogorov conditionalization offers significant advantages over ratio conditionalization, including an improved ability to model epistemic defeat.

I do not say that Kolmogorov conditionalization provides a universal basis for defeasible inference. No doubt there are situations where Jeffrey conditionalization or some other credal update strategy would be more appropriate. There are also situations where Kolmogorov conditionalization is inapplicable, such as when rcds do not exist or are improper. Still, Kolmogorov conditionalization is a valuable addition to the Bayesian toolbox. Further work will surely reveal additional philosophical applications beyond those discussed here. I submit that rcds have great potential to enrich formal epistemology, as they have already enriched other disciplines where Bayesian decision theory plays a prominent role. There awaits a vast terrain that philosophers have barely explored.