Abstract
We introduce an expected-value theory of linguistic modality that makes reference to expected utility and a likelihood-based confirmation measure for deontics and epistemics, respectively. The account is a probabilistic semantics for deontics and epistemics, yet it proposes that deontics and epistemics share a common core modal semantics, as in traditional possible-worlds analysis of modality. We argue that this account is not only theoretically advantageous, but also has far-reaching empirical consequences. In particular, we predict modal versions of reasoning fallacies from the heuristics and biases literature. Additionally, we derive the modal semantics in an entirely transparent manner, as it is based on the compositional semantics of Korean modal expressions that are morphosyntactically decomposed into a conditional and an evaluative predicate.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The account of modality due to Angelika Kratzer (1981, 1991, 2012) has been the foundation for many if not most great advances in our understanding of modality in natural language. Over the past decade, this classical account has met challenging objections stemming chiefly from the work of Lassiter (2011, 2017), who proposes an alternative view of epistemic modality grounded in probability measures, and of deontic modality grounded in expected utility. This new perspective on modality has triggered a rich interaction between linguistics and psychology, but not without a cost. Valuable explanatory insights exist in the classical account that find no counterpart in the new approach.
We present an expected value theory of epistemic and deontic modality that preserves one such explanatory insight from the classical theory: all modal expressions share a core modal semantics, and their precise modal flavor as epistemic or deontic modals is determined by context. At the same time, our theory shares central properties with Lassiter’s account of modality, which proposes that the probability calculus plays a key role in the interpretation of modals. This allows us to explore novel connections between epistemic and deontic semantics and the psychology of probabilistic reasoning, while providing a unified semantics for the two modalities that relies on context to disambiguate modal flavor. Additionally, we provide evidence from Korean modal expressions in support of the particular decomposition of modal semantics we propose. In a nutshell, the prototypical way of expressing modal constructions like English must in Korean employs a conditional evaluative. We submit that this evaluative corroborates the expected-value component of our proposal for a semantics for must. Finally, our proposal allows for tantalizing connections with a growing literature on Bayesian confirmation-theoretic behavior in human reasoning (Tentori et al., 2013; Crupi et al., 2018; Mangiarulo et al., 2021). For the remainder of this introduction, we summarize our proposal, our arguments for it, and its main applications.
Informally, a sentence ‘must \(\varphi \)’ will be true just in case assuming \(\varphi \) would lead to the only good enough expected value among all alternatives to \(\varphi \), where the calculation of expected value is a function of a contextually supplied body of information. For deontics, expected value will reduce to expected utility. But for epistemics, expected value will be what we call explanatory value—an aggregation of the individual probabilities of the propositions in the epistemic background, conditionalized on \(\varphi \). In this view, epistemic modals do not concern posterior probability of the prejacent, conditional on some epistemic facts. Instead, they assert that the prejacent is the only predictor of contextually relevant epistemic facts which has a good-enough explanatory power. For the simplest case when there is only one contextually relevant epistemic fact, the epistemic reading of ‘must \(\varphi \)’ against a salient epistemic fact e will reduce to the assertion that only \(Pr(e \mid \varphi )\) exceeds the good-enough threshold, whereas every relevant alternative \(\psi \) is such that \(Pr(e \mid \psi )\) does not meet this standard.
We submit that reconciling the two types of modals is not only theoretically preferable but also has interesting empirical consequences. Our unified theory preserves the decision-theoretic conception of deontic modality via expected utility, as proposed by Lassiter (2011, 2017), allowing us for example to provide an account of the miners puzzle (Kolodny & MacFarlane, 2010).
On the epistemic side, our proposal makes immediate sense of the longstanding intuition that epistemic must has a strong evidential flavor. When someone says “It must be raining outside”, the hearer typically concludes that that the speaker inferred this proposition from some weaker body of evidence, perhaps the fact that someone just entered the room with wet hair. On our view, “It must be raining outside” is true just in case the proposition that it is raining outside offers the only good-enough explanation for a contextually determined, salient body of evidence. Accordingly, we immediately account for the evidential flavor of epistemic must.
More tentatively, this view gives us an immediate account of modal variants of reasoning problems from the heuristics and biases literature. For example, in the conjunction fallacy (Tversky & Kahneman, 1983), participants read a description of an individual named Linda that asserts that in her youth she engaged in political activism. Then they are asked to choose which is most likely: (A) Linda is a bank teller, or (B) Linda is a bank teller who is active in the feminist movement. A staggering proportion of participants in the original experiments and countless replications since respond that option (B) is most probable. If participants mean that the probability of (B) conditional on the known facts about Linda is greater than that of (A) conditional on the same facts, they are violating the classical probability calculus. For (B) entails (A), and therefore cannot be more probable than (A) under the same conditionalization. Our theory of modality predicts that participants should be inclined to accept the modal sentence “Linda must be a bank teller who is active in the feminist movement” in the same context. The description of Linda constitutes the relevant epistemic background with respect to which the argument of must should maximize explanatory value. The sentence will be true only if the probability of the description of Linda conditional on option (B) is greater than the probability of the same description conditional on the alternative (A). Crucially, this assignment of probabilities is by no means incoherent with the probability calculus, and will indeed obtain under any realistic probability distribution. In effect, our theory brings into the realm of modality an account of the conjunction fallacy from psychology that builds on Bayesian confirmation theory (Crupi et al., 2008; Tentori et al., 2013). Conversely, our theory offers a philosophically-motivated explanation of why naive reasoners would opt for inductive reasoning despite fallacious consequences: the deontic counterpart—which uses the same formula to calculate relevant measures but only differs in the body of information attended to—manifests a rational strategy comparing the expected utilities of contextually salient alternatives. What in the deontic domain produces rational behavior by leveraging expected utility, generates a potential for fallacious reasoning in the epistemic domain, by resorting to explanatory value instead of maximizing posterior probabilities.
We derive the modal semantics in an entirely transparent manner. There is linguistic evidence that at least some languages combine conditionals and evaluative predicates to express modal meanings (Ammann & van der Auwera, 2002; Chung, 2019), the compositional semantics of which involves comparing expected utilities (deontic) or confirmation measures (epistemic). Korean is one such language:

Korean modal expressions are not black boxes in the sense that they are not monomorphemic as in many other languages (e.g., English must, should, \(\ldots \)). These conditional evaluatives (Kaufmann, 2017) can receive a compositional account thanks to their transparent morphosyntax. Under the assumption that conditionals roughly denote the degree of support for the consequent given the antecedent (Adams, 1965; Pearl, 2000, 2013), we simply compose our semantics of the evaluative predicate toy ‘eval’ with the conditional semantics to derive our theory of modality.
1.1 Extant theories of modality
We briefly introduce two competing theories of modality, one due to Kratzer (1981, 1991, 2012) and the other due to Lassiter (2011, 2017). Our purpose is not to offer a comprehensive review of the two theories, but rather to highlight the notable features of these accounts that ours builds on.
The classical theory due to Angelika Kratzer is a quantification-based approach. The truth conditions of ‘must \(\varphi \)’ are calculated in two steps: (i) universally quantify over the best worlds and (ii) assert that \(\varphi \) is true in every best world,Footnote 1 One of the important insights of the theory is that modal expressions, regardless of their flavor, share a common semantic core. The ambiguity in modal flavor is not due to lexical ambiguity but rather to context sensitivity. Kratzer parameterizes the modal semantics with respect to conversational backgrounds, functions from worlds to sets of propositions that are relevant to the interpretation. Each modal is interpreted with respect to a pair of conversational backgrounds. One identifies the set of relevant worlds, and the other is used to pick out the best worlds among the set of relevant worlds. The two conversational backgrounds, the modal base and the ordering source, jointly identify the domain of quantification of the modal. For epistemics, the modal base represents a set of relevant known facts and the ordering source captures what is stereotypically the case. Accordingly, ‘must \(\varphi \)’ is true just in case \(\varphi \) stereotypically follows from the relevant known facts. As for deontics, the modal base represents a set of relevant circumstances and the ordering source a set of ideals/goals. ‘Must \(\varphi \)’ is true just in case \(\varphi \) follows from what is ideally the case given the relevant circumstances.
This context-sensitive analysis of modals nicely captures the crosslinguistic generalization that the majority of modal expressions are ambiguous between an epistemic reading and a deontic reading. We find this context-sensitivity to be an essential feature of any theory of modality.
Lassiter’s theory significantly differs from Kratzer’s in that the entire theory operates on top of the probability calculus. Lassiter observes that a theory of modality based on a qualitative ordering has difficulties accounting for examples where a degree modifier applied to an epistemic adjective establishes an arithmetic relationship between degreesFootnote 2

Moreover, Yalcin (2010) has observed that extant theories of comparative modality based on qualitative orderings validate certain normatively invalid modal inferences, like the following:

Lassiter concludes that modal semantics has to encode more quantitative information and builds a theory of modality based on probability distributions. In short, all epistemic necessity modals require that the probability of the prejacent be greater than some threshold \(\theta \). Weak necessity modals such as should or ought differ from the strong necessity modal must in that \(\theta \) is sensitive to contextually salient alternatives. As for deontics, weak necessity modals are true just in case the expected utility of the prejacent is significantly greater than the contextually-determined threshold \(\theta \). The stronger must requires a very high \(\theta \) and also that each of the probable alternatives to the prejacent has an expected utility lower than indifference.
Lassiter’s theory has a number of advantages over the classical theory. In particular, the modal inferences it validates are in line with the probability calculus, and it does a better job of explaining the distribution of degree modifiers. However, the innovation comes at the cost of ignoring the cross-linguistic generalization that modals tend to share a common semantic core. In Kratzer’s theory, the relevant ordering ranks propositions and has a comparable role to epistemic/deontic measures in Lassiter’s theory. The way in which this ordering is calculated does not change depending on the modal flavor. By contrast, there is no single mechanism that derives expected utility and probability in Lassiter’s theory. In fact, expected utility is a function of probability, thus the former is a more complex notion than the latter.Footnote 3\(^{,}\)Footnote 4
1.2 The conjunction fallacy and Bayesian confirmation theory
In their seminal (1983) article, Tversky and Kahneman show that human reasoners will often assign subjective probabilities that violate the classical probability calculus in striking ways. The most famous example of this phenomenon is known as the conjunction fallacy, exemplified in (4).

Around 85% of participants judged that (4b) was more probable than (4a), and this response was largely independent of the level of education of participants, as well as their field of expertise. However, (4b) entails (4a), and so it must be that \(Pr((4b)) \le Pr((4a))\).
Why bring up the conjunction fallacy in an article about modality? The conjunction fallacy concerns people’s intuitions about comparative subjective probabilities, at least prima facie it does not seem to involve modality. Yet, there is important connective tissue between modality and comparative subjective probability that we argue makes these facts about reasoning relevant to theories of modality.
First, we observe that both Kratzer’s quantification-based theory and Lassiter’s probability-based theory relate comparative subjective probabilities to epistemic modality. Concretely, both theories offer accounts of the meanings of words like must that are closely related to their accounts of the meanings of words like probably. Lassiter’s probabilistic theory of modality wears this fact on its sleeve: the meaning of ‘must \(\varphi \)’ directly appeals to the subjective probability of \(\varphi \). In Kratzer’s account there is no reference to probability measures, but the theory provides an account of probability talk such as is involved in constructions like ‘\(\varphi \) is a better possibility than \(\psi \)’, and that account is largely shared between constructions like this and bona fide modal constructions such as ‘must \(\varphi \)’.
Given this theoretical convergence, it is important to ask whether our semantic theories of epistemic and probability operators can shed light on facts about reasoning with epistemic and probability operators.
The theory we present in the next section will do just that, while building on independent tools from formal epistemology. Crupi et al. (2008) provide an account of the conjunction fallacy in (4) in terms of Bayesian confirmation theory. The core idea is that participants in these experiments engage in a kind of hypothesis testing, where (4a) and (4b) are competing hypotheses, and the description of Linda that precedes them is evidence meant to adjudicate between them. Intuitively, (4b) “bank teller active in the feminist movement” is a better theory of the available evidence about Linda than (4a) “bank teller”.
There are multiple alternative Bayesian measures of confirmation in the literature (see for example Fitelson (1999)), and Crupi et al. (2008) show that all of them work as accounts of the conjunction fallacy. For example, the Difference (D) measure defined below quantifies the extent to which learning some evidence increases one’s belief in a particular hypothesis by subtracting the prior from the posterior.
Under any plausible probability measure, learning about Linda’s prior engagement with various activist movements will increase one’s belief in (4b). That is to say, the posterior probability of (4b) conditional on the description is greater than the prior probability of (4b). This is not so for the alternative hypothesis (4a). Sure enough, the posterior probability of (4a) conditional on the description will be higher than that of (4b) conditional on the same description. But crucially the posterior on (4b) increased more relative to its prior than the posterior of the alternative (4a) relative to its prior.
An even simpler measure of the explanatory power of a theory can be found in the likelihood of a hypothesis, that is the probability of the evidence conditional on the hypothesis. On this view, hypothesis testing is an intrinsically contrastive task: one should ask “which hypothesis has the greater likelihood for the available evidence?” (Edwards, 1992). As before, any plausible probability measure will ensure that the probability of the description of Linda conditional on (4b) is greater than the probability of the same description conditional on (4a). Likelihoodism, as this view is often dubbed, stands in opposition to a multitude of non-contrastive, properly Bayesian measures of hypothesis testing, such as the D measure reviewed above (Fitelson, 2007). But even in the Bayesian approach, likelihoods have a role. For example, the likelihood ratio measure L below is a respectable Bayesian alternative to the D measure, and it will be familiar to any reader acquainted with standard model-comparison techniques say in experimental psychology.
A rich literature exists in formal epistemology and philosophy of science on the virtues of the likelihoodist and Bayesian views, and within the latter on the complex trade-offs provided by the various alternative measures of Bayesian confirmation on the market. Our account of modality most straightforwardly produces a likelihoodist view of explanatory adequacy in the epistemic case, as we will show shortly. But we will also illustrate how a more properly Bayesian measure can be achieved.
Before we move on, three important disclaimers are warranted. First, we do not purport here to offer a comprehensive view of the phenomena associated with reasoning by representativeness, such as the conjunction fallacy. There is a rich and complex literature on such phenomena that goes beyond the scope of this work. For example, Stolarz-Fantino et al. (2003) report that the order in which hypotheses are assessed influences people’s judgments. Also, there is a closely-related phenomenon dubbed the disjunction fallacy, where people judge a disjunction less probable than its disjunct.Footnote 5 There are theories that address these issues, e.g., Busemeyer et al. ’s (2011) quantum probability theory assigns perceived probabilities to each potential answer to a question under discussion (QUD). Depending on the QUD, the quantum probability theory introduces interference effects which account for the conjunction fallacy, the disjunction fallacy, and the order effects.Footnote 6
Second, in focusing on the benefits of a confirmation-theoretic account of the conjunction fallacy and related phenomena, we do not mean to suggest that such an account explains the entirety of the phenomenon. For example, in the original conjunction-fallacy article, Tversky and Kahneman (1983) consider the possibility that the two options in the Linda problem in (4) are interpreted exclusively. Specifically, option (4a) “bank teller” could be interpreted by contrast with its alternative, and taken to mean “bank teller who is not active in the feminist movement”. Under such an interpretation, it is no longer a violation of the classical probability calculus to consider option (4a) more probable than option (4b), since one is no longer included in the other. Tversky and Kahneman (1983) control for this pragmatic enrichment in a follow-up experiment, blocking it altogether. They observe that conjunction errors are still prevalent, though their rate dropped from about 85% to about 65%. Later work by Dulany and Hilton (1991) applied a more sophisticated Gricean theory of pragmatics, considering what are now called primary implicatures or ignorance inferences, finding similar results: the conjunction error is mitigated by blocking pragmatic enrichments of the “bank teller” option, but by no means does it disappear. These classical results, replicated multiple times, point to the need for a multi-factor theory of the conjunction fallacy, at least incorporating pragmatic effects. What seems clear is that no single-factor theory of the conjunction fallacy on the market can explain the entirety of the phenomenon. With that said, the confirmation-theoretic view has produced powerful, insightful, and general models of the conjunction fallacy and of other phenomena in the representativeness literature and even deductive reasoning (Sablé-Meyer & Mascarenhas, 2022), demonstrating beyond any doubt its validity as a top contender for an explanation of the non-pragmatic dimension of conjunction errors.
Third and final, we will consider as case studies in this article modalized versions of the conjunction fallacy, where the two possible responses to the task to choose from are “Linda must be a bank teller” and “Linda must be a bank teller and be active in the feminist movement”. We will argue based on introspective judgments that such sentences produce conjunction errors much like in the original conjunction fallacy paradigm, and we will show how our account of must predicts and explains these putative fallacies. Crucially, we are not prepared to argue that the original conjunction fallacy paradigm ought to be explained in modal terms. That is, we do not propose in this article that silent modals occur in the logical forms of the options in (4), and that those silent modals explain the phenomenon, via our proposed semantics for must.Footnote 7
2 Proposal
We propose that necessity modals compare the probability-weighted measure of the prejacent to the probability-weighted measure of each of its alternatives. Specifically, ‘must \(\varphi \)’ is true if and only if the expected value of the prejacent is (significantly) greater than the contextually determined threshold, but the expected value of each alternative to \(\varphi \) does not exceed the threshold. Depending on the flavor of the modal, expected value either corresponds to expected utility or explanatory value. The flavor is determined by a single parameter R, which represents a set of ideals/rules for deontics and a set of relevant known facts in need of an explanation (i.e., pieces of evidence) for epistemics. Alternatives to the prejacent \(\varphi \) in our proposal are determined by the context in the shape of a question under discussion if available: for the deontic case, a set of possible courses of action under consideration and for the epistemic case, a set of candidate explanations for the salient body of information at hand.Footnote 8
To formalize our proposal, we first define \({\mathbb {E}}[\psi \mid \varphi ]\) as in (5).Footnote 9 It is the probability-weighted average of the value of \(\psi \) over \(\varphi \)-worlds normalized with respect to the probability of \(\varphi \). This is equivalent to the expected value of \(\psi \) conditioned on \(\varphi \). We parameterize the probability function \(Pr(\cdot )\) with respect to the world of evaluation—accordingly the expected value function \({\mathbb {E}}\) as well—to reflect that probability assignments are world dependent.

We will later elaborate on how this relates to expected utility or explanatory value. Also, we will show in Sect. 4 that the compositional semantics of Korean conditional evaluatives serves as natural language evidence that at least some modals employ the above expected-value calculation.
Our formal analysis of modal necessity is given in (6), which reads as follows: For deontics, the expected utility of \(\varphi \) is greater than \(\theta \) but no alternative to \(\varphi \) is such that its expected utility is greater than \(\theta \).Footnote 10 For epistemics, the explanatory value of \(\varphi \) is greater than \(\theta \) but no alternative to \(\varphi \) is such that its explanatory value is greater than \(\theta \). We use the notation \( Alt (\varphi )\) to indicate the set of alternatives to \(\varphi \), abstracting away from the details of how they are determined.

We find it useful and intuitive to read the formula as follows: In a deontic context, \(\varphi \) is the only good-enough choice among the available options. In an epistemic context, \(\varphi \) is the only good-enough explanation of the evidence among the available hypotheses.
We define \(\mu _{\textsc {eval}}\) as a measure function which takes a world argument and returns the degree to which the given world supports the contextually-supplied body of information R. Technically, this amounts to counting the number of relevant propositions \(r \in R\) that are true at w.

As in Kratzer’s standard theory, a single parameter determines the flavor of a modal. Conversational backgrounds determine the flavor in Kratzer’s theory, and R—a set of relevant propositions—in ours.
Let us first demonstrate how \({\mathbb {E}}_{w}[\mu _{\textsc {eval}} \mid \varphi ]\) yields the expected utility of \(\varphi \) in the deontic case. For deontics, the measure function employs a deontic \(R_{D}\), which characterizes the set of relevant rules or ideals. The measure function \(\mu _{\textsc {eval}}\) takes a world w and checks how many ideals/rules \(d \in R_{D}\) are realized/abided by at w (technically, true at w). The more ideals/rules are realized/abided by at w, the better the world w is. In this sense, the number of ideals/rules realized/abided by at a given world is the utility value of the world. Thus, we can interpret \(\mu _{\textsc {eval}}\) as a function which takes a world and returns the utility value of the world argument.

Replacing \(\psi \) with \(\mu _{\textsc {eval}}\) in (5) yields the following, which demonstrates that \({\mathbb {E}}[\mu _{\textsc {eval}} \mid \varphi ]\) corresponds to the expected utility of \(\varphi \):

The formula conditionalizes on \(\varphi \), and for each \(\varphi \)-world, it calculates the utility value of the world. It then calculates the probability-weighted average of the utility values of \(\varphi \)-worlds. This is by definition the expected utility of \(\varphi \).Footnote 11
Let us turn to the epistemic case. The epistemic interpretation of \(\mu _{\textsc {eval}}\) employs an epistemic \(R_{E}\), which characterizes the set of relevant known facts (i.e., pieces of evidence).

For the epistemic interpretation of \({\mathbb {E}}_w[\mu _{\textsc {eval}} \mid \varphi ]\), we find it more intuitive to reformulate the measure function \(\mu _{\textsc {eval}}\) as in (11). The two formulae are equivalent since each \(e \in R_{E}\) is a proposition (i.e., returns 1 if true and 0 otherwise). Using this formulation, (12) shows that \({\mathbb {E}}_w[\mu _{\textsc {eval}} \mid \varphi ]\) denotes the sum over the probabilities of each relevant known fact \(e_{i} \in R_{E}\) conditionalized on \(\varphi \). In other words, it is the sum over the likelihoods (i.e., inverse probabilities) of \(\varphi \) with respect to each relevant known fact \(e_{i} \in R_{E}\).Footnote 12


In the simplest case where there is only one piece of evidence, say e, the expected value of \(\varphi \) reduces to the likelihood of \(\varphi \) with respect to e at w. Since this is one way to cash out the degree to which evidence e supports and is explained by \(\varphi \), we call this measure the explanatory value of \(\varphi \).
This analysis of epistemic modality is sharply different from Lassiter’s. Lassiter argues that epistemic modals compare the (posterior) probability of the prejacent to a contextually determined threshold, whereas we propose that epistemic modals are concerned with the explanatory value of \(\varphi \) which is based on likelihoods.
Note that the proposed semantics indirectly compares the expected value of the prejacent to those of its alternatives: it conveys that the expected value of \(\varphi \) is greater than those of its alternatives by asserting that only the former is greater than \(\theta \). There is an alternative formulation (though not equivalent) that makes direct comparisons, and that under certain conditions produces the L confirmation measure mentioned in Sect. 1.2. The alternative formulation in (13) conveys that the expected value of \(\varphi \) is greater than the expected values of its alternatives by at least \(\theta \).

If we assume that (i) the only alternative to \(\varphi \) is its negation, (ii) there is a single piece of evidence,Footnote 13 and (iii) take the logarithm of each measured value, ‘must \(\varphi \)’ is true if and only if \(L(\varphi , e)\) is greater than the contextually supplied threshold \(\theta \), as shown belowFootnote 14:

Both our proposal in (6) and the alternative in (13) are enough to capture the evidential flavor of typical utterances involving epistemic must. Imagine someone conspicuously enters the room soaking wet. In so doing, they establish a set \(R_E\) of salient information in need of an explanation, say simply the singleton set containing a proposition to the effect that “This person is wet”. On our account, an onlooker might now utter “It must be raining”, only if rain is the only good-enough explanation for the salient body of evidence at hand, as is intuitively the case.
An interesting implication arises from our theory of modality: people’s conception of modality facilitates rational decision making with deontics, but the very same mechanism can be a source of irrationality when assessing comparative subjective probabilities with epistemics. Note that expected utility is a rational measure employed in decision theory. By contrast, explanatory value in terms of confirmation theory is a measure that will often diverge from that standard of probabilistic rationality offered by posterior probabilities, which form the basis of all other extant probabilistic accounts of must. Our theory, then, predicts an undersized role for rational posterior probabilities in epistemic utterances with must.
3 Case studies
We present three case studies that our theory accounts for and explains. We start with the miners puzzle on the deontic side (Kolodny & MacFarlane, 2010). For epistemics, we discuss two related but distinct examples from the heuristics and biases literature: the conjunction fallacy and base-rate neglect (Kahneman & Tversky, 1973; Tversky & Kahneman, 1983).
3.1 The miners puzzle (Kolodny & MacFarlane, 2010)
As Lassiter (2011) points out, an expected-utility theory of deontic modality naturally addresses the issue of interpreting modals under epistemic uncertainty. A representative case of the issue is known as the miners puzzle, given in (15) and summarized in Table 1 (Kolodny & MacFarlane, 2010). Given the situation described in Table 1, examples (15a)–(15c) are all intuitively true.

However, the classical theory of modality predicts that the three examples cannot all be true. Below is a proof sketch:Footnote 15

Kolodny and MacFarlane argue that the issue arises because Kratzer’s conversational backgrounds are not seriously information-dependent, that is, one’s preferences cannot change upon obtaining new information.
An expected-utility analysis of the miners puzzle naturally encodes this information dependence into the semantics, as conditionalizing on new information adjusts the probability weights used to calculate expected utilities (Lassiter, 2011). Our common-core semantics for modality in terms of expected value reduces to expected utility in the deontic case, as we explained above. This means that our approach should be able to resolve the miners puzzle without much difficulty. In what follows, we show that this is the case.
First, notice that the miners puzzle as phrased in the literature and in (15) above is a puzzle about ought, rather than must. We will address and assess our predictions for must-sentences in this scenario at the end of this section. For now, we give the simplest possible semantics for ought (and should, for that matter) that keeps with the spirit of our proposal for must in this article. Specifically, we propose that ‘ought \(\varphi \)’ is true just in case \(\varphi \) is the best good-enough option among the alternatives under consideration.


This is the semantics for ‘must \(\varphi \)’, minus the requirement that \(\varphi \) be the only good-enough alternative. This simple approach is motivated by observations very much in this direction in the literature on teleological modality (von Fintel & Iatridou, 2005), and on work specifically on weak necessity modals (Sloman, 1970; Jackson, 1985; Goble, 1996; Finlay, 2009).
Regarding ‘we ought to block neither shaft’, in this analysis the requirement is that the expected utility of blocking neither shaft (i.e., block-neither) is higher than the contextual threshold \(\theta \), and greater than the expected utility of blocking shaft A (i.e., block-A) and the expected utility of blocking shaft B (i.e., block-B). We posit the following \(R_{D}\), which was borrowed from Cariani et al. (2013):

We take it that the subjective probabilities of the miners being in shaft A, respectively shaft B, are both 0.5. Given these background assumptions, \(\mu _{\textsc {eval}}\) returns 9 as the utility for each block-neither-world. This is because the context guarantees that 9 miners will be saved if we block neither shaft. Consequently, the expected utility of block-neither is 9, as we show in (19).

On the other hand, \(\mu _{\textsc {eval}}\) returns 10 for each \({\textbf {block-A}} \wedge {\textbf {miners-in-A}}\)-world, and 0 for each \({\textbf {block-A}} \wedge {\textbf {miners-in-B}}\)-world. As we show in (20), the expected utility of block-A is 5 assuming that miners-in-A and miners-in-B are equally probable and the propositions representing our actions and the miners’ whereabouts are independent. Analogously, the expected utility of block-B is also 5.


We analyze (15a) as in (22). Informally, “blocking neither shaft is the best good-enough choice among the available options”. The sentence is accurately predicted to be true, under the reasonable assumptions we’ve been making about the probability distribution underlying this scenario.


We turn to the analysis of the deontic conditional in (15b). Following Lassiter (2011), we take it that the if-clause requires the expected utility calculation to additionally conditionalize on the antecedent proposition.Footnote 16
Conditionalizing on miners-in-A does not change the expected utility of block-neither since exactly one miner will drown irrespective of the location of the miners. However, this does raise the expected utility of block-A, as we show in (23). The expected utility of block-A, assuming miners-in-A, is 10, which is greater than 9, the expected utility of block-neither. Moreover, the conditionalization on miners-in-A reduces the expected utility of block-B to 0. The upshot is that the expected utility of block-A is greater than the expected utilities of block-neither and block-B.

We flesh out our analysis of (15b) in (24). Informally, “given that the miners are in shaft A, blocking shaft A is the best good-enough choice among the available options”.

What we presented in this section is more or less a reproduction of Lassiter’s analysis.Footnote 17
This is no surprise because both theories compare expected utilities of contextually salient alternatives. Things start becoming more interesting, in our view, once we consider the predictions for the strong necessity modal must. Sticking to the same scenario as described in (15), consider now the following sentences:

We submit first of all that (25b) and (25c) are just as felicitous, and crucially ring just as true, as their ought variants. Our judgments are less sharp for (25a), but we suspect that an alternative reading, with ‘neither’ scoping above the modal, is causing interference. Notice that we can rephrase (25a) to unambiguously zoom in on the intended reading:

We will address possibility modals as in (26c), in Sect. 6. For now, we take it that (26a) and (26b) are felicitous and true in the scenario at hand.
With our semantics for must, (26a) and (26b) will be true just in case block-neither is the only good-enough option, a stronger set of truth conditions than for the ought variant. These truth conditions will still obtain very easily: recall that the expected utility for block-neither is 9, while that of each of its alternatives block-A and block-B is 5. It will therefore be trivial to find a threshold \(\theta \) between 5 and 9 to ensure that the sentence is true.
The situation is more complex for the conditional sentences in (25b) and (25c). Take (25b), without loss of generality. We predict that this sentence will be true just in case block-A is the only good-enough option, once we assume that the miners are in shaft A. Now, as we showed above, the expected utility of block-A in this conditionalization is 10, while the expected utility of block-neither is 9 and that of block-B is 0. But if must requires that the prejacent be the only alternative above the threshold, then we will need for our threshold to be \(10 > \theta \ge 9\), while for the unconditional sentence in (26a) we had that \(9 > \theta \ge 5\). These two requirements are of course incompatible.
This intriguing tension, in that a shift of standards of evaluation \(\theta \) is required to judge all the sentences in (25) as true, will emerge not only in our analysis of a must variant of the miners puzzle, but indeed in any account of the original puzzle that requires that the utility of the prejacent at hand be the only one above the standard of evaluation \(\theta \). Such an account for example is sketched by Lassiter (2011): Suppose that there are good reasons to spend my vacation with my parents whom I have not met for a long time and, although incompatible with the first plan, visit my ailing grandparents. Lassiter notes that both of the following sentences are odd because there isn’t a unique best option with significant probability which is better than being indifferent:

We cannot fully resolve the issue in this article, but we have two remarks we think are promising. First, the idea of shifting thresholds so easily might actually not be much of a problem. It is plausible for thresholds of this sort to be highly sensitive to the set of alternatives under consideration and to the modal base in question. Regarding alternatives, it seems clear that deontic must sentences will be felicitous with prejacents that are quite “bad”, so long as the fully transparent alternative set is exhaustive with respect to all plausible possibilities and has the property that none of the alternatives is “good” in a positive or absolute sense. We conjecture further that thresholds might be able to shift seamlessly depending on different modal bases, that is in our terms different conditionalizations, as is the case in the threshold tension at hand with the miners puzzle. Additionally, an interesting fine-grained prediction emerges from this need for shifting thresholds, shared by any account of the relevant operators that requires that the prejacent be the only good-enough alternative. We predict that there should be some processing signature of the shift in \(\theta \) between judging the truth of the unconditional sentence and the truth of the conditional sentences.Footnote 18
3.2 The conjunction fallacy (Tversky & Kahneman, 1983)
Recall the most well-known variant of the conjunction fallacy, accepted by about 85% of experimental subjects (Tversky & Kahneman, 1983).

As we argued in the introduction, there is a convergence between both Kratzer and Lassiter’s theories of modality regarding the connection between epistemic modality and probability talk. This theoretical convergence at the very least primes the question whether we find with must the same reasoning behavior that we find with probable. Specifically for the conjunction fallacy, we propose that a large proportion of experimental subjects would commit a modal conjunction fallacy: when faced with the same setup as the classical task, people would generally find (29b) a more attractive response than (29a).Footnote 19

The original conjunction fallacy asked participants to pick the option that was most probable, but this task becomes somewhat odd when the options to choose from are modal statements as in (29).Footnote 20 The roots of the oddity are unclear. In theories where modal operators involve conditions on probabilities, such as ours, this task would require a judgment of the probability of a certain statement about probabilities, which is by no means incoherent, as consistent theories of higher-order probabilistic statements exist (Gaifman, 1988). But it is an unusual move, and one where there is no consensus on what the right theory is, so that it is best to avoid this and other complications arising from embeddings of probability and modality (Goldstein & Santorio, 2021).
We propose to evaluate our prediction in a betting paradigm. In one of their experiments, Tversky and Kahneman (1983) asked participants to bet on one of the statements about Linda. They observed some mitigation of conjunction errors, a drop from about 85% to about 65% error rates. While the reason for this mitigating effect of the betting paradigm is unclear, the result is still that sizable conjunction errors were observed. Applying this paradigm to our proposed modal conjunction fallacy, the task would be to decide on one of the two modal statements in (29) to bet on, thus avoiding the linguistic and conceptual awkwardness of explicitly attempting to assess the probability of a modal statement.
To the best of our knowledge, the heuristics and biases literature, or the modality literature for that matter, has not investigated this issue experimentally. Yet introspection tells us and a group of informants in our social circles that (29b) is in a clear sense more attractive than (29a). Introspection is an entirely valid means of establishing empirical facts under the appropriate circumstances, and we submit that those conditions obtain in the case at hand.
For concreteness, we provide reasonable probability assignments concerning the Linda scenario in (30) and (31). We restricted our attention to the two most relevant pieces of information about Linda, namely that she was deeply concerned with issues of discrimination and social justice (i.e., social-justice) and participated in anti-nuclear demonstrations (i.e., anti-nuclear-protests).




Given that the explanatory value of the hypothesis feminist-teller is (significantly) greater than the explanatory value of the hypothesis teller, one is led to conclude that the former hypothesis is the only good explanation of the evidence among the salient hypotheses.

If (29b) constitutes a modal conjunction fallacy as we strongly suspect, our theory explains it fully and immediately, while building on tools from formal epistemology that have been applied very successfully to the psychology of reasoning.
The conjunction fallacy plays only a supporting role in our thesis in this article. First, it demonstrates that confirmation-theoretic mechanisms such as our proposal for the semantics of necessity epistemics are part of higher cognition. If we see evidence of confirmation theory in deliberate reasoning, it should not strike us as too alien to find it in the meaning of some modal expressions in natural language. Second, our theory of necessity epistemics immediately predicts the existence of modal versions of the conjunction fallacy, demonstrating its generative power.Footnote 21\(^{,}\),Footnote 22
3.3 Lawyers and engineers (Kahneman & Tversky, 1973)
Kahneman and Tversky (1973) argue that human reasoners neglect prior probabilities when solving ostensibly probabilistic problems, relying instead on judgments of typicality. In the “lawyers and engineers” experiment, subjects were asked to provide the probability of Jack being an engineer based on the description in (35).

Kahneman and Tversky tested two conditions between participants: in one, Jack’s description was drawn randomly from a sample of 30 engineers and 70 lawyers, as in (35) above. In the other condition the prior probabilities were reversed, and the sample consisted instead of 30 lawyers and 70 engineers. They found that participants’ judgments were unaffected by these prior probabilities: participants in the 30–70 condition gave the same response to the question about the probability that Jack is an engineer as participants in the 70–30 condition. This suggests that indeed they were not resorting to the normative standard provided by Bayes’ theorem to decide on their response.Footnote 23
In our introspection, it seems possible to replicate the issue with modalized expressions. Given the same description of Jack, upon being asked to guess whether Jack is a lawyer or an engineer, it is reasonable to utter the following:

Our prediction is that naive human participants would prefer (36) to an alternative “Jack must be a lawyer”. This is just as surprising as the reported result in the original experiment: to assent to (36) in such an experiment is to display a semantics for must that is not as sensitive to prior and posterior probabilities as extant probabilistic semantics for must would predict.
We argue that the explanatory value of engineer with respect to the provided description is greater than the explanatory value of lawyer, and that the prior probabilities of the two hypotheses have little to no direct effect on such a calculation of explanatory adequacy.Footnote 24
To illustrate the mechanics of our account, we will consider in detail the two most relevant pieces of information about Jack, namely that he shows no interest in political and social issues and enjoys solving mathematical puzzles. Below is what we deem to be reasonable probability assignments regarding the two crucial pieces of evidence:Footnote 25\(^{,}\)Footnote 26


The probability of Jack showing no interest in political and social issues given that he is an engineer is 0.78, and the probability of him enjoying mathematical puzzles given the same hypothesis is 0.55. By contrast, the probabilities of Jack showing no interest in political and social issues and him enjoying mathematical puzzles given that he is a lawyer are 0.35 and 0.28, respectively.


Given the above probability assignments, ‘Jack must be an engineer’ is true if and only if ‘the hypothesis that Jack is an engineer is the only good-enough explanation of the given evidence among the candidate hypotheses’.

4 Natural language evidence: conditional evaluatives
In this section, we compositionally derive our proposed semantics from Korean conditional evaluatives (repeated below as (42)), which have a transparent morphosyntax.

We conjecture that the above conditional evaluative construction is the transparent version of the English necessity modal must. Despite the fact that modal necessity is expressed via an auxiliary in English but via a full-fledged conditional construction in Korean, we conjecture that their meanings more or less converge for the following reason: People’s understanding of obligation/permission/utility (deontic) or probability (epistemic) is rather consistent regardless of their mother tongue; otherwise we would expect abundant communication failures between native speakers of different languages in a modal talk.Footnote 27 And since modal expressions are precisely the means to convey such concepts, it is reasonable to assume that English and Korean modal expressions convey similar meanings.Footnote 28
For a compositional analysis, we will break down the conditional evaluative into three subcomponents: (i) the evaluative predicate, (ii), the conditional, and (iii) the exhaustifier. We first show that composing the first two subcomponents yields an expected utility measure for deontics and a likelihood-based confirmation measure for epistemics. The exhaustifier is responsible for comparing the relevant measures.
4.1 Deriving relevant measures from conditional semantics
We assume that the evaluative predicate toy ‘eval’ is a measure function with the semantics already presented in (7), repeated below as (43).Footnote 29

As for the semantics of conditionals, we assume that conditionals denote the degree of support for the consequent, given the antecedent. Technically, the value of ‘if \(\varphi \) then \(\gamma \)’ is the expected value of \(\gamma \) given \(\varphi \).Footnote 30\(^{,}\)Footnote 31

Note that when the value of the consequent is either 0 (false) or 1 (true), the expected value reduces to the probability of the consequent given the antecedent; the probability-weighted average of \(\gamma \) given \(\varphi \) is by definition the conditional probability of \(\gamma \) given \(\varphi \). This proves that conditional probability is a special case of expected value, and it follows that the posited semantics is in accordance with Adams (1965), Douven (2008), and Pearl ’s (2000, 2013) analyses of conditionals (see also (Lewis, 1976; Jackson, 1979; Gibbard, 1980; Jeffrey & Edgington, 1991; Kaufmann, 2005; Crupi & Iacona, 2022), for relevant work in linguistics and philosophy). However, we depart from previous work in that we do not restrict the type of the consequent of conditionals to propositions. This is particularly important for our analysis because the consequent of Korean conditional evaluatives is not a proposition but rather a measure function.
To derive the proposed measure, we simply have to replace the consequent \(\gamma \) of the conditional in (44) with the evaluative predicate toy ‘eval’. Note that this yields exactly what we proposed in (9) and (12). We take this as natural language evidence that such a measure is employed by at least some modals.

Note that the conditional denotes a degree rather than a proposition. Following Lassiter (2017), we suggest that a degree representation can be mapped to a bivalent one by invoking the thresholding operation.Footnote 32

Feeding the denotation of the conditional to \(\Theta \) yields the semantics in (47) informally read as follows: the conditional is true if and only if the measured value of \(\varphi \) is greater than the contextually determined threshold \(\theta \).

We are only half through composing the semantics of the conditional evaluative construction, as we have not considered the exhaustification component of -(e)ya ‘only if’ yet. In what follows, we claim that the exhaustification component indirectly compares the measured value of \(\varphi \) to the measured values of its contextually salient alternatives.
4.2 Exhaustification
We simply assume that the exhaustification component of -(e)ya ‘only if’ takes a proposition \(\varphi \) and negates each of its alternatives, along with conveying that \(\varphi \) is true.Footnote 33 This is exactly what we proposed for the analysis of modal necessity in (6).

Hence we have independent evidence from natural language that a decision theoretic notion of expected utility and Bayesian confirmation theoretic measures are relevant to the interpretation of linguistic modality.
5 Prior probabilities and the problem of success
One of the key features of our theory in its current form is that modal interpretation ignores the prior probabilities of the prejacent and its alternatives. While this insensitivity to priors matches intuitions at multiple empirical junctures, and allows our theory to address puzzles of failure of reasoning (i.e., why do people make fallacious inferences?), it naturally raises a question as to how the theory can explain the puzzle of success (i.e., how can people make classically sound inferences despite all?).
The puzzles of failure and success are the two sides of the human reasoning coin, and it is unusual for a theoretical approach to answer both questions in comparable terms. In particular, linguists and philosophers have traditionally focused on the puzzle of success, while psychologists mostly paid attention to the puzzle of failure. What we presented in earlier sections is a linguistic theory of the meaning of must that predicts what might look like failures of reasoning, based on a novel modal semantics. For the remainder of this section, we give tentative directions as to how the puzzle of success can be considered within the spirit of our theory.
Let us first note that the lack of an extensive explanation of the puzzle of success does not immediately provide sufficient grounds to reject our theory. Just as much as our theory suffers from the puzzle of success, alternative theories that build on priors have trouble handling the puzzle of failure and need to stipulate that people often ignore priors for extrinsic and often mysterious reasons. While reasoning experiments do not seem to favor a particular theory, we have good evidence that at least some modals are interpreted in the way we proposed: analyzing the Korean modal data in a what-you-see-is-what-you-get manner yields the expected value-based semantics.
However, priors clearly can factor into modal reasoning. Consider the example in (49). Upon hearing that John did not come to work, one could reasonably conjecture that he must have caught a cold. By contrast it is infelicitous to say that he must be dead, despite the fact that his being dead would fully predict and explain the relevant fact that he is absent.Footnote 34

Different measures of hypothesis testing make different predictions regarding this example, but let us focus on the ones relevant to our theory. In terms of likelihoods, the hypothesis that John is dead is the best explanation of his being absent since \(Pr({\textbf {absent}} \mid {\textbf {dead}}) = 1\). This hypothesis remains attractive even in view of the likelihood ratio measure, as \(Pr({\textbf {absent}} \mid {\textbf {dead}}) \gg Pr({\textbf {absent}} \mid \lnot {\textbf {dead}})\). Given its strong preference for the hypothesis that John is dead, our core theory as it stands incorrectly predicts that (49a) is false whereas (49b) is true. Note that the prediction remains unaltered even if one entertains a different alternative to dead such as ‘John caught a cold’, as \(Pr({\textbf {absent}} \mid {\textbf {dead}}) \gg Pr({\textbf {absent}} \mid {\textbf {cold}})\).


One could opt for other Bayesian measures of confirmation that are sensitive to priors such as the D measure introduced in Sect. 1.2. Recall that D is the difference between the posterior probability and the prior. While still making the right predictions for the conjunction fallacy, the D measure penalizes hypotheses with extremely low priors and posteriors. Let us illustrate with plausible probability assignments:


According to the above probability assignments, \(D({\textbf {cold}}, {\textbf {absent}})\) is significantly greater than \(D({\textbf {dead}}, {\textbf {absent}})\), primarily due to the fact that the prior and posterior of dead are extremely low. Consequently, the difference between the prior and the posterior is minute.
Despite the appeal, there is one serious drawback to employing such a measure: we would lose the established parallelism between deontic and epistemic modals. Recall that expected utilities and likelihoods are derived exactly in the same manner and this was part of the motivation for our analysis of epistemic modality. But we see no simple way of similarly deriving expected utilities and the D confirmation measure from one and the same core definition. Since this connection remains at the heart of our theory, we must seek alternative routes to account for the sensitivity to priors.
We suspect that the best way to capture the contrast in (49) is to require that the prior probability of the modal prejacent is reasonably high, although it need not be higher than the prior probabilities of its alternatives. This requirement would be entirely independent of the particular modal domain, in keeping with our goal to give a core semantics for must. That is, a sufficiently high prior probability would be a requirement for epistemic, deontic, and other modalities. Such a requirement can be viewed intuitively as a plausibility requirement: whether the statement ‘must \(\varphi \)’ is epistemic or deontic or teleological, the proposition \(\varphi \) had better be plausible or feasible.
In the epistemic domain, this requirement makes (49a) a reasonable thing to say because a cold is quite common a condition and accordingly has a relatively high prior. By contrast, (49b) is false or infelicitous because dead is extremely unlikely in a normal context. Accordingly, the sentence improves if John’s country of residence is in a war situation and his neighborhood is bombarded on a regular basis, or if John is very old.
This view makes the following prediction regarding the lawyers and engineers scenario: if the group of interviewees consists of 99 lawyers and 1 engineer, one would be reluctant to accept ‘Jack must be an engineer’ for the same reason that ‘John must be dead’ sounds odd in a normal context. In fact, there are reports in the psychology literature that priors are more diagnostic when they have extreme values (Wells & Harvey, 1977; Ofir, 1988; Koehler, 1996).
In the deontic and teleological domains, the requirement translates naturally as a requirement of plausibility/feasibility.Footnote 35 Thus, (54a) and (54b) would be infelicitous or plain false (more on which below), showing that the requirement extends to weak necessity modals. Similarly for (55).


What is the status of this plausibility requirement? We have somewhat conflicting judgments. The sentences with strong necessity modals strike us as plain false: in order to get to Bushwick, it is simply not the case that you have to take a helicopter, for there are multiple alternative ways of accomplishing your goal, irrespective of the impracticality of the helicopter alternative. This suggests that the requirement should be seen as an entailment affecting the truth conditions of the sentence. Accordingly, the negated sentences in (56) seem felicitous and true.

Yet, some not-at-issue projective content is happy with negation: “The king of France was not in attendance at the party last night” isn’t too hard to read as plain true. Additionally, it is hard to disentangle propositional negation, which is what we intend in the sentences in (56), from its meta-linguistic uses, at least when targeting presuppositions. We thus find the data from (56) at best suggestive of an at-issue, non-projecting content analysis of the plausibility requirement.
To our ears, the interrogative versions of these sentences can be addressed in dialog with negation, but the hey-wait-a-minute construction strikes us as entirely appropriate:

Similarly for the epistemic domain:

Let us take stock of this section. We argued that our proposal makes sense of seeming rationality violations with must: where it looks like humans are erroneously ignoring prior probabilities, we say that they are doing so rationally, because modal operators in the epistemic domain are not about maximizing posterior probability, but rather explanatory power. However, our proposal gets into trouble for predicting no effect of prior probabilities whatsoever across the board in the epistemic domain. This view is clearly too radical, and must be tempered somehow. One large domain of possibilities is to use Bayesian confirmation measures (i.e., not simply the likelihood of the prejacent), for in many of these measures the prior probabilities play a role, as we illustrated with the D measure, which subtracts the prior probability from the posterior. This avenue is extremely promising for the epistemic case, but it seems it would defeat one of the central goals of our work in this article, namely to give one and the same fundamental semantics for modals, irrespective of modal domain.Footnote 36 So, we proposed instead that prior probabilities play a role in the form of a plausibility requirement: the prejacent must have a prior probability above some contextual standard for plausibility. We showed how this proposal handles the problematic epistemic cases and makes reasonable predictions on the expected-utility side. We could not determine the exact nature of this requirement, in particular whether it is standard truth-conditional content or projective content. On the one hand, family-of-sentences tests suggest that this content does not project. On the other, some kinds of projective content, for example definite descriptions, are easy enough to “trap” inside truth conditions under negation and other operators, and we’ve shown that it is entirely appropriate to react to the modal sentences in question by targeting the plausibility requirement as one would target say a factive presupposition.
6 On the interpretation of possibility modals
Thus far, we developed a semantics for so-called necessity modals. A natural question to ask is how possibility modals such as might or may relate to necessity ones: as an anonymous reviewer points out, we want to systematically rule out statements such as “It must be raining, but of course it might not be”. The Kratzerian account and modal logic capture this by assuming that necessity and possibility modals are duals, e.g., ‘might \(\varphi \)’ is equivalent to ‘\(\lnot \)must \(\lnot \varphi \)’. Assuming duality in our theory yields the following semantics:

The formula reads as “might \(\varphi \) is true if and only if the explanatory value of \(\lnot \varphi \) is not sufficiently high, or there exists an alternative to \(\lnot \varphi \) such that its explanatory value is sufficiently high”. We find this a reasonable proposal for the meaning of might. Consider the first disjunct: if \(\lnot \varphi \) is not sufficiently explanatory then we do not have sufficient grounds to reject \(\varphi \), hence it is possible that \(\varphi \) is true. Regarding the second disjunct, we first observe that, while the literature has presented arguments in favor of the idea that must is sensitive to alternatives, we are unaware of such arguments in favor of alternative sensitivity of might. Adapting a scenario from Dretske (1972), imagine that Kim will only inherit the considerable fortune their parents left them if they get married. They can marry anyone they like, the condition is simply that Kim be married in order to inherit. Suppose Kim is planning on marrying Pat, and consider the must sentences in (60), where small caps indicate focus.

There is a clear contrast: sentence (60a) is either true or true enough, while sentence (60b) is plain false. Any reasonable alternative-sensitive approach to must accounts for this. On our proposal, (60a) with neutral focus plausibly contrasts the prejacent with its negation as an alternative, yielding truth, while focus in (60b) strongly suggests a question under discussion concerning other individuals Kim might marry, and is accordingly predicted to be plain false, since marrying Pat is by no means the only good-enough course of action given the stated goals, when the alternatives concern other individuals Kim might marry. Crucially, no such contrast is to be found with analogous might sentences:

To our ears, (61b) sounds a little odd, since one can’t quite make out what justifies the focus on Pat. But there is no truth-conditional contrast between the two sentences. We conclude from these facts that there is no evidence in favor of alternative sensitivity for might, at least not of the same kind as the alternative sensitivity of must. Vitally, this is not to say that the semantics and the truth conditions of might sentences have nothing in them that formally corresponds to an alternative set. It only means that the alternatives of might, if there are any, cannot be manipulated by context, or can be manipulated but never make a difference for truth conditions. With this in mind, we propose that the expression \( Alt (\varphi )\) that occurs in (59) is in fact non-manipulable, and is fixed as the polar alternative to \(\varphi \). The second disjunct of our entry in (59) then says that a sentence of the shape ‘might \(\varphi \)’, analyzed as ‘\(\lnot \) must \(\lnot \varphi \)’, will be true if the alternative to the prejacent \(\lnot \varphi \), namely \(\varphi \), has a sufficiently high explanatory value, which indeed is a good reason to accept ‘might \(\varphi \)’.
It is interesting to note that the alternative analysis we considered in Sect. 2, which directly makes reference to the L confirmation measure (cf. (14)) offers a perhaps even more intuitive interpretation of might:

The above formula states that ‘might \(\varphi \)’ is true if and only if the L confirmation measure of \(\varphi \) is greater than the contextually determined threshold \(- \theta \). Recall that positive values indicate positive confirmation, negative values signify negative confirmation, and deviation from 0 by \(\theta \) conveys significance. So intuitively, the formula conveys that ‘might \(\varphi \)’ is true if and only if \(\varphi \) is not significantly disconfirmed. Thus in our alternative analysis, must and might concern significant confirmation and lack of significant disconfirmation, respectively. This perspective has the cost of oversimplifying the semantics: since the set of relevant alternatives exclusively consists of the prejacent and its negation even in the must case, this view effectively renders the semantics insensitive to more interesting alternative sets. While there might be reasons to endorse this insensitivity to alternatives in the epistemic domain (e.g., Yalcin ’s (2005) argument concerning Kyburg ’s (1961) lottery scenario), it would be largely inadequate in the deontic domain. We leave further development for future work.
7 Further implication: the weakness of epistemic necessity
The theory of strong necessity modals we offered here generates a rather weak interpretation of must in the epistemic domain, in that a proposition \(\varphi \) needn’t have a high probability for ‘must \(\varphi \)’ to be true. Rather, what matters is the explanatory value of \(\varphi \) with respect to a salient body of evidence. How does our account deal with other arguments for a weak semantics for must?
In a now classic article on necessity modals, von Fintel and Gillies (2010) establish an important puzzle for strong semantics for must, which we’ve nodded to at multiple points in this article. They point out that there is a contrast between (63) and (64), and submit that this is because, in (63), Billy directly obtained the information that it is raining, while in (64) this information was indirectly acquired.


In this article, we proposed that epistemic ‘must \(\varphi \)’ asserts that \(\varphi \) is the only good-enough explanation for a contextually determined, salient body of evidence. In (64), the context makes it clear that the evidence to be explained is the fact that someone just came in with a wet umbrella. An event of rain would be an excellent explanation for that fact, and our account predicts this: presumably, conditional on rain, the probability of a wet umbrella for someone who was just outside is extremely high, and no alternative pops to one’s mind in this bare-bones context. The case of (63) is more interesting, for there the salient evidence to explain is rain itself. Formally, the probability of rain conditional on rain is, of course, as high as any probability can get. As discussed so far then, our account technically predicts that (63) should be a true and felicitous sentence. However, the analytical intuition behind our account, as we’ve explained in detail above, is that epistemic must is about explanatory power. And a proposition \(\varphi \) is no explanation or argument for \(\varphi \) itself, this is a clear instance of question begging.
We propose to rule out cases of checking probabilities of the shape \(Pr(\varphi \mid \varphi )\) for pragmatic reasons, essentially a probabilistic version of the pragmatic principles that generate infelicity for tautological sentences in a bivalent semantics. For notice that our predicted truth conditions for (63) are “the probability of rain conditional on rain is above the threshold \(\theta \), and none of the probabilities of alternatives to rain are above \(\theta \)”. The second clause of these truth conditions isn’t exactly trivial,Footnote 37 but the first clause requires that we consider a probability of the shape \(Pr(\varphi \mid \varphi )\), which we would expect to trigger infelicity. To be clear, our view here is not that “it must be raining”, in the context at hand, is a trivial, tautological sentence. Rather, the sentence is deviant because it crucially involves the at-issue assessment of a trivial probability of the shape \(Pr(\varphi \mid \varphi )\). Zooming out, this sensible constraint will rule out any must statement where the prejacent entails the evidence to be explained. This is as intended, and meant to block question-begging (non-)explanations.
Above and beyond this natural pragmatic requirement for non-trivial explanations, our proposal captures the idea that any epistemic must sentence with a known prejacent should be infelicitous (Giannakidou & Mari, 2016; Goodhue, 2017), for it considers alternatives to the prejacent as possible antecedents to conditionals, in a manner we elucidate presently.
Goodhue notes that from the perspective of a skeptical epistemologist, ‘it must be raining’ can be felicitous even when she observes the pouring rain, as in (65).

Goodhue proposes that this context dependency of the felicity condition can be accounted for if ‘must \(\varphi \)’ requires that \(\varphi \) is not known and Lewis ’s (1996) context dependent theory of knowledge is adopted:

In this view, the professional epistemologist does not deduce that it is raining from observing the pouring rain outside the window, because she considers far-fetched possibilities where it does not rain despite her observing the rain (e.g., she has a delusion). By contrast, not having been trained as a professional epistemologist, Billy ignores such distant possibilities and infers that ‘it is raining’ is known.
Assuming that conditional reasoning underlies modal interpretation (cf. Sect. 4 on deriving the semantics from Korean conditional evaluatives), our theory of modality independently motivates such a felicity condition: our analysis of ‘must \(\varphi \)’ involves reasoning with conditionals of the form ‘if \(\varphi \), then eval’ as well as ‘if \(\psi \), then eval’ for each alternative \(\psi \) to \(\varphi \). It is well-known that an indicative conditional is felicitous only if its antecedent is a possibility (Stalnaker, 1976). From our perspective, this implies that ‘must \(\varphi \)’ is felicitous only if \(\varphi \) and each alternative to \(\varphi \) are possibilities. Insofar as some alternative to \(\varphi \) contains a \(\lnot \varphi \)-world—which we believe to be a reasonable assumption—we cannot eliminate every \(\lnot \varphi \) possibility. As a consequence, epistemic necessity modals are felicitous only if the prejacent is not known.Footnote 38
8 Conclusion
This article presented a novel theory of modality in terms of comparisons between the expected values of the prejacent and its alternatives. We defined a general notion of “expected value” that allows for a single lexical entry to cash out expected value in terms of likelihoods as a proxy for explanatory value in the epistemic case, and in terms of expected utilities in the deontic case. The difference between the two cases, in our approach, lies purely in the properties of a contextually supplied set of propositions: facts in need of explanation in the epistemic case, ideals in the deontic case. Our proposal preserves the classical insight that very many languages of the world use a shared pool of modal constructions irrespective of modal domain, in that we give a single lexical entry for each modal operator that makes no distinction between the epistemic, deontic, or other modal domains. At the same time, our view incorporates the successes of more recent approaches to modality that avail themselves of the probability calculus and of decision-theoretic tools. We developed a detailed analysis of the strong necessity modal must in English and its Korean counterpart, a complex construction that we argue wears this kind of expected-value semantics on its sleeve. We also gave the beginnings of a semantics in the same spirit for weak necessity modals like ought or should, and we argued that an analysis of possibility modals in terms of duals of strong necessity in our system yields a reasonable interpretation for English might or can.
We considered three case studies in some detail, and evaluated the predictions of extant accounts of modality that are representative of the two main camps in the field: quantificational semantics based on ordinal relations between possible worlds, and probabilistic approaches. We summarize these predictions in Table 2.
This table is to be taken with a grain of salt. In particular, we are in no way claiming that other theories are constitutionally incapable of being modified in order to make the same predictions as our account. Regarding Kratzer’s influential account, a central source of inspiration for our own version of a single lexical entry for each modal force and sophisticated modal backgrounds interacting interestingly to create different modal flavors, conjunction elimination for must is valid, making an account of our proposed modal conjunction fallacy extremely hard, if it is to be proposed within the realm of modality itself. An articulated theory of modality and, say, representativeness à la Kahneman and Tversky (1973) is perhaps a reasonable way for this view to integrate our predictions, but such a combination is by no means a straightforward matter. Similar remarks apply to the quantificational approach in the case of our proposed modal lawyers and engineers puzzle, and the facts we summarize in the table for the miners puzzle are generally accepted in the field. On the probabilistic side, we find greater success with the miners puzzle, though more conservative predictions for the must case than our own, a matter that will likely require experimentation with naive participants to settle. For our novel epistemic puzzles on reasoning with must, extant probabilistic approaches, given their across-the-board adherence to Bayesian standards of rationality, make predictions entirely opposed to our theory’s and, we have argued, to introspective intuitions.
Our somewhat radical new approach leaves multiple questions unanswered for the time being, beyond just whether our preliminary proposals for weak necessity and possibility modals are on the right track. In particular, in our effort to understand naive reasoning with epistemic must (a woefully understudied topic in the psychology of human reasoning), we could only sketch an analysis of how it is possible in a system like ours to still approximate the usual standards of rationality in terms of Bayesian update by factoring in prior probabilities via a plausibility requirement. Our project in this first article was to demonstrate with a detailed proof of concept the feasibility of our research program for modality, to show in particular that facts well established in linguistics and philosophy about the weakness of necessity modals in the epistemic case and similarly pervasive facts about apparent failures of human reasoning could be combined with a rational semantics in terms of expected utility for the deontic domain, all within one single lexical entry.
Notes
Moreover, one cannot reduce the probability weights in an expected utility formula (e.g., (9) on page 10) to the probability of the corresponding proposition. For example, to calculate the expected utility of \(\varphi \), one needs to consider the probability of each world conditional on \(\varphi \), and use those conditional probabilities as the probability weights of each \(\varphi \)-world. In short, Lassiter’s epistemic and deontic measures make use of different kinds of probability, one being an unconditional probability and the other a conditional one.
There have also been attempts to make Kratzer’s theory more sensitive to decision-theoretic considerations, e.g., Cariani (2016a), Cariani (2016b), and Blumberg and Hawthorne (2023). Abstracting away from the differences between them, these approaches are sensitive to alternatives just like Lassiter’s theory, and rank these alternatives by their expected utilities. Yet, unlike Lassiter’s approach, these theories are inherently quantificational in the sense that deontic modals are quantifiers over the best-ranked alternative worlds.
While Tentori et al. ’s (2013) account of the conjunction fallacy does not extend to the disjunction fallacy, confirmation-theoretic approaches can in principle partially account for it. For example, likelihood-based measures including explanatory value allow for the confirmatory value of a disjunct to be higher than that of a disjunction containing it. Specifically for a likelihoodist view, there is nothing wrong with a probability assignment where \(Pr(e \mid h_1) > Pr(e \mid h_1 \vee h_2)\). Nonetheless, there are cases in which likelihood-based approaches, and therefore our own proposal, are not directly applicable: as reported by Morier and Borgida (1984), in the Linda scenario naive reasoners judge that feminist \(\vee \) teller is more probable than feminist \(\wedge \) teller. This is in line with posterior probabilities and against the predictions of a likelihoodist view.
While our view does not share many features with the quantum probability theory, it is in line with Busemeyer et al. ’s (2015) perspective that theories using inductive confirmation are not incompatible with the quantum probability theory. Rather, one can be used to constrain the other.
We are extremely grateful to an anonymous reviewer for making us see that this possible proposal was compatible and even suggested in an earlier draft of this article. See also Footnote 21 for additional comments about this intriguing theoretical possibility.
We will have little more to say about sources of alternatives in this article. In the absence of a rich-enough context to determine alternatives, we assume that the presence of focus in a constituent of the prejacent will trigger a QUD and set of alternatives as in the classical analysis of the semantics of focus, and that a simple set of polar alternatives based on the prejacent constitutes a default fallback mechanism. These considerations are in line with related instances of sensitivity to alternatives in the modal domain (Dretske, 1972; Heim, 1992; Villalta, 2008)
For convenience, we use Greek letters to represent both object- and meta-language formulae.
Cariani (2016a) convincingly shows that theories of expected value contrastivism, along with actualist theories such as Jackson (1985) and Jackson and Pargetter (1986), invalidate the plausible inference of Weakening: ought\((\varphi )\), ought\((\psi )\) \(\vDash \) ought\((\varphi \vee \psi )\). Our theory is in the same situation, for it contrasts the expected utilities of salient alternatives. We thank an anonymous reviewer for pointing this out.
An anonymous reviewer notes that this analysis crucially assumes that the cardinality of \(R_{E}\) is finite, and asks what would happen if the cardinality of \(R_{E}\) was infinite. We agree that things get tricky when there are infinite pieces of evidence. However, given that \(R_{E}\) represents a salient body of evidence to be explained—something one should be able to entertain in their mind at the time of utterance—we think that this is a reasonable assumption, although we acknowledge this is yet another departure from the standard semantics.
In fact, it is common practice in the confirmation-theoretic literature on the conjunction fallacy for example to conjoin several pieces of evidence into a single proposition. In our terms, this amounts to conjoining the relevant known facts \(e_i \in R_{E}\) and using the conjunction as evidence. It is an open question whether this is a necessary move, and there will be differences in empirical predictions depending on whether one considers the conjunction of \(R_E\) or the set with multiple pieces of evidence.
The purpose of using logarithms is to interpret positive values as confirmation, zero as irrelevance, and negative values as disconfirmation. Therefore, our alternative formulation of modality can be understood as directly encoding the L confirmation measure.
There is independent motivation for this assumption. In Sect. 4, we show that the expected utility of \(\varphi \) can be derived from the compositional semantics of ‘if \(\varphi \), then eval/suffice’, which we claim to be part of the underlying logical representation of modal necessity. Under this hypothesis, the analysis of ‘if miners-in-A, ought block-A’ involves interpreting ‘if miners-in-A, then if block-A, then eval/suffice’, which is equivalent to ‘if \({\textbf {miners-in-A}} \wedge {\textbf {block-A}}\), then eval/suffice’ if we take the Import–Export Principle (Gibbard, 1980; McGee, 1985) for granted. Given the assumptions to be presented in Sect. 4, the latter denotes the expected utility of \({\textbf {miners-in-A}} \wedge {\textbf {block-A}}\).
Precisely speaking, Lassiter ’s semantics for ought does not directly compare the expected utility of the prejacent to its alternatives, but rather to a contextually-determined threshold. There is also some difference between our analysis of deontic must and Lassiter ’s: while both theories submit that the expected utilities of the alternatives are somewhat low, the latter imposes a stronger requirement, namely that they are lower than the expected utility of indifference—the union of salient alternatives. Lassiter thus would make the wrong prediction that (25b) and (25c) are false, because although block-neither is not the best choice given that the miners are in shaft A (outranked by block-A), its expected utility is still much higher than that of indifference, i.e., \({\textbf {block-neither}} \cup {\textbf {block-A}} \cup {\textbf {block-B}}\).
Bouletics display a similar sort of threshold-shifting effect (Crni, 2011; Lassiter, 2011; Blumberg & Hawthorne, 2022) An anonymous reviewer brings up the following case: suppose you like pizza much more than any of the other options on the menu, and you like ramen only a little more than hotdogs. In this context, “I want pizza but if they don’t have pizza, then I want ramen” sounds true. If desire verbs were to be given scalar semantics as in Lassiter (2011), the felicity of the aforementioned example can only be explained in terms of threshold-shifting under conditionalization.
An anonymous reviewer points out that the must version in (29b) sounds odd to their ears, while a version with ought substituted for must is appreciably more felicitous. One very plausible source for this judgment is the strong semantics of must, an idea somewhat reminiscent of Lassiter ’s (2011) analysis of deontic must: the prejacent is the only good-enough explanation for the salient body of evidence. Indeed, Linda’s being “a bank teller who is active in the feminist movement” might well be good-enough explanation for the facts in the description, while by no means being the only good-enough explanation. The alternative set under consideration will matter greatly: any speaker who is restricting attention to the explicitly given alternatives (“bank teller” and “bank teller who is active in the feminist movement”) should be happy to consider the conjunctive alternative as the only good-enough explanation. But a speaker who also considers “active in the feminist movement” as an alternative, plausibly generated from the conjunctive alternative via deletion (Katzir, 2007), should in fact consider the must statement in (29b) as plain false. We suspect that the version with ought (or should) will be far more acceptable to these speakers because the semantics of ought as a weak necessity modal does not have the same exhaustification component as must in our approach, in ways we outline in Sect. 3.1.
We thank a reviewer for pressing us on this matter.
Thanks to comments by an anonymous reviewer, we realized that our theory of must suggests a more ambitious possible account of the original conjunction fallacy as discovered by Tversky and Kahneman (1983). Various scholars in philosophy of language and formal pragmatics have proposed assertion operators that would apply in a systematic manner to declaratives meant to impart information. The pragmatic version of this move sees it not as a covert operator in logical form, but as an inference, for example: if the speaker uttered assertion \(\varphi \), then the speaker believes \(\varphi \) (Stalnaker, 1978; Grice, 1975; Sauerland, 2004). Other, non-pragmatic approaches postulate explicit operators in logical form (Meyer, 2013). All such proposals we are familiar with postulate box-type modal operators, that is universal quantifiers over possible worlds or situations, analogous to strong necessity modals like must. If this class of proposals is on the right track, it is interesting to consider whether the semantics for must we give in this article might be a reasonable contender for such an assertion operator. In the event that it is, the original conjunction error could be explained as a result of such a silent assertion operator’s having the kind of semantics we propose here for the overt English modal must and its overt counterparts in other languages. Even more ambitiously, one would ask whether other instances of unexpected confirmation-theoretic inference-making behavior in the psychology of reasoning find their root in such a silent assertion operator. We cannot present a careful consideration of this theoretical possibility in this article, and must leave it for later research.
An anonymous reviewer points out that our theory will have trouble explaining the so-called A-B paradigm which contrasts with the Linda problem in that it does not introduce a context establishing a psychologically salient connection with one of the hypotheses. Given the following task, Tversky and Kahneman report that 58% of the participants considered the conjunction (\(h_{1} \wedge h_{2}\)) more probable than one of its conjuncts (\(h_{1}\)).

We acknowledge that our theory, which is more or less in line with Crupi et al. ’s (2008) analysis based on inductive confirmation, is not immediately applicable to the A-B paradigm due to the presupposition of the existence of relevant pieces of information/evidence. We have two remarks on the A-B paradigm. First, people make significantly more mistakes in the Linda case (85%) than in the aforementioned heart attack case (58%). This casts doubt on the view that a single factor is solely responsible for the conjunction fallacy in all its variants. Second, there is an alternative inductive confirmation-based explanation due to Tentori et al. (2013), which does not compare the degrees to which given evidence confirms two salient hypotheses, but rather, directly measures the degree to which one conjunct (\(h_{1}\)) inductively confirms the other (\(h_{2}\)). Tentori et al. experimentally verify that this measure is a good predictor of the A-B paradigm. But such innovation comes at a cost; it loses the original appeal of Crupi et al. ’s (2008) theory, namely that people compare the inductive confirmatory values of competing hypotheses.
The two between-subjects conditions are of the essence, as the mere fact that priors have little to no effect in one condition is not enough to argue that elements of Bayes’ theorem are being ignored. This is because an extreme likelihood term (probability of the description of Jack assuming he is an engineer) will have the effect of diluting the role of priors determining posteriors, following Bayes’ theorem. But such an extreme likelihood term should then be visible in the other condition, where priors were flipped: Bayes’ theorem would lead us to expect an even higher posterior probability for engineer, as long as responses were not at ceiling, which indeed they were not. Instead, Kahneman and Tversky (1973) found that participants in the two conditions gave indistinguishable responses, providing a compelling case that in the lawyers-and-engineers task as administered in this experiment, participants are indeed ignoring prior probabilities.
The illustration we give here uses our likelihoodist semantics for must which altogether ignores prior probabilities. Other, more sophisticated Bayesian measures of confirmation show non-zero degrees of sensitivity to prior probabilities, and might make for a more complete account.
The probabilities were taken from a norming study on the lawyers and engineers scenario (Guerrini et al., 2022)
Tversky and Kahneman (1983) and Tentori et al. (2013) reject likelihoods as the relevant measure due to the following Wimbledon scenario:

Tversky and Kahneman report that people judge (i-a) more likely than (i-b), but this cannot be explained in terms of likelihoods. They argue that “it makes no sense to assess the conditional probability that Borg will reach the finals given the outcome of the final match”. Tentori et al. make a similar point: “the inverse probability analysis must imply the utterly implausible judgmental strategy of focusing on the probability of Borg’s Wimbledon record, which is in fact an established datum from the past, as conditional on future events concerning the outcome of the final match”. We think that their dismissal was too hasty. As weird as it may seem, the relevant likelihood is mathematically well-defined. There is no problem treating the alleged future tense will as a modal, and in this case, the relevant likelihood measure merely conditions on a modal rather than a future event. Moreover, in economics, conditioning on future events is a widely used methodology. For instance, in a time series analysis, it is common to calculate \(Pr(X(1)> 10 \mid X(2) > 30)\) where X(t) denotes a stock price at time t and the current time is 0. We thank Janek Guerrini for discussion of this argument.
More bluntly put: Suppose that you—a native speaker of English—are advising an international student. When you give directions, do you expect the student to accidentally disobey the order because they have a different understanding of obligation as a non-native speaker of English?
We do not intend to claim that all modal expressions across languages convey exactly the same meaning. In fact, Deal (2011) argues that Nez Perce does not lexically distinguish modal necessity from modal possibility, and this is evidence that we cannot always find a one-to-one correspondence of modal expressions in any given pair of languages.
We gloss Korean toy as ‘eval’ to emphasize its bleached status. In other contexts, the morpheme seems to convey the meaning of ‘suffice’, as exemplified below:

We want to make it clear that we are not claiming that (44) is precisely what conditionals denote. It suffices for our purposes to adopt the simplest formulation among extant expected value-based theories of conditionals. We leave it open as to whether the skeleton of our theory can be made compatible with a more nuanced semantics such as Douven (2008) or Crupi and Iacona (2022).
An anonymous reviewer asks whether it is possible to give an expected value-based analysis of subjunctive conditionals while capturing the seemingly close connections between indicatives and subjuntives. Pearl (2000) develops a probabilistic analysis of subjunctive conditionals which builds on his theory of causation. In this view, subjunctive conditionals are interpreted with respect to a network of causally relevant variables. Abstracting away from the details, a counterfactual assumption \(\varphi \) severs the causal connection between the variable related to \(\varphi \) and its causes (i.e., intervenes on \(\varphi \)). Given this modified network, a subjunctive conditional ‘
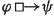 ’ denotes the expected value of \(\psi \) conditionalized on \(\varphi \) and its causally relevant, true propositions. Pearl notes that the crucial difference between subjunctives and indicatives is whether the interpretive process involves intervening on the antecedent or merely observing the truth of the antecedent. While Pearl ’s theory departs from Lewis ’s (1973) similarity-based semantics in that causation is taken as a primitive, there have been attempts in linguistics and philosophy to incorporate Pearl ’s insights: Kaufmann (2005) offers an analysis of subjunctives in terms of expected value and causal structure. Moreover, Schulz (2011), Kaufmann (2013), Ciardelli et al. (2018), and Santorio (2019) modifies premise semantics (Kratzer, 1979) in such a way that it is sensitive to a causal structure.
’ denotes the expected value of \(\psi \) conditionalized on \(\varphi \) and its causally relevant, true propositions. Pearl notes that the crucial difference between subjunctives and indicatives is whether the interpretive process involves intervening on the antecedent or merely observing the truth of the antecedent. While Pearl ’s theory departs from Lewis ’s (1973) similarity-based semantics in that causation is taken as a primitive, there have been attempts in linguistics and philosophy to incorporate Pearl ’s insights: Kaufmann (2005) offers an analysis of subjunctives in terms of expected value and causal structure. Moreover, Schulz (2011), Kaufmann (2013), Ciardelli et al. (2018), and Santorio (2019) modifies premise semantics (Kratzer, 1979) in such a way that it is sensitive to a causal structure.The thresholding operation is reminiscent of the pos morpheme of Kennedy and McNally (2005) and Kennedy (2007). We make a distinction between \(\Theta \) and pos only because \(\Theta \) is a function from degrees to truth values whereas pos is of a higher order type due to compositional issues. Apart from the type-related concern, no part of our analysis hinges on making such a distinction.
We remain agnostic on whether conveying that \(\varphi \) is true is a presupposition or an assertion, as there is no evidence that the exhaustification component of -(e)ya ‘only if’ behaves exactly like English only. Besides, we would like to focus on the formulation of modality, due to reasons of space.
We thank Benjamin Spector for pointing out to us this prediction of our theory.
We are not saying that this strategy is in principle incompatible with our goal of having a single lexical entry for each modal. We see no immediate reason to suspect so. But it is clear that the simple, intuitive lexical entry we propose in this article for must cannot be straightforwardly adapted to work with the D measure without bringing serious issues on the deontic (utility) front. But of course this is not to say that it is impossible to give such an entry, or that there aren’t other Bayesian confirmation measures that would solve the issues on the epistemic side without destroying our results on the deontic side.
In principle, it might be possible to weave a context where rain is the evidence to be explained, but there are two alternative explanations, rain versus \(\psi \), where the probability of rain conditional on \(\psi \) is also above the threshold \(\theta \). Since thresholds are hard or impossible to manipulate with any precision, at least with the tools of introspection, we cannot decide here whether this configuration can be induced while preserving coherence. See also the discussion at the end of Sect. 3.1 on how easily thresholds must be allowed to shift in order to account for the miners puzzle in exhaustive semantics for must like ours.
Deontic necessity modals do not require such a felicity condition, and correctly so. In fact, Chung (2019) proposes that Korean conditional evaluatives receiving a deontic interpretation requires analyzing the conditional as a counterfactual conditional. If this is on the right track, our analysis of deontic modality will compare causal expected utilities as opposed to evidential expected utilities (Gibbard & Harper, 1978). An exploration of this subtle but substantive distinction is beyond the scope of the present article.
References
Adams, E. (1965). The logic of conditionals. Inquiry, 8(1–4), 166–197. https://doi.org/10.1080/00201746508601430
Ammann, A., & van der Auwera, J. (2002). KoreanModality—Asymmetries between necessity and possibility. In Selected Papers from the 12th international conference on Korean linguistics (pp. 101–115).
Blumberg, K., & Hawthorne, J. (2022). Desire. Philosophers’ Imprint, 22(8), 1–17. https://doi.org/10.3998/phimp.2116
Blumberg, K., & Hawthorne, J. (2023). Inheritance: Professor Procrastinate and the logic of obligation. Philosophy and Phenomenological Research, 106(1), 84–106. https://doi.org/10.1111/phpr.12846
Busemeyer, J. R., Pothos, E. M., Franco, R., & Trueblood, J. S. (2011). A quantum theoretical explanation for probability judgment errors. Psychological Review, 118(2), 193–218. https://doi.org/10.1037/a0022542
Busemeyer, J. R., Wang, Z., Pothos, E. M., & Trueblood, J. S. (2015). The conjunction fallacy, confirmation, and quantum theory: Comment on Tentori, Crupi, and Russo (2013). Journal of Experimental Psychology: General, 144(1), 236–243. https://doi.org/10.1037/xge0000035
Cariani, F. (2016a). Consequence and contrast in deontic semantics. The Journal of Philosophy, 113(8), 396–416. https://doi.org/10.5840/jphil2016113826
Cariani, F. (2016b). Deontic modals and probability: one theory to rule them all? In N. Charlow & M. Chrisman (Eds.), Deontic modality (pp. 11–46). Oxford University Press.
Cariani, F., Kaufmann, M., & Kaufmann, S. (2013). Deliberative modality under epistemic uncertainty. Linguistics and Philosophy, 36(3), 225–259. https://doi.org/10.1007/s10988-013-9134-4
Chung, W. (2019). Decomposing deontic modality: Evidence from Korean. Journal of Semantics, 36(4), 665–700. https://doi.org/10.1093/jos/ffz016
Ciardelli, I., Zhang, L., & Champollion, L. (2018). Two switches in the theory of counterfactuals. Linguistics and Philosophy, 41(6), 577–621. https://doi.org/10.1007/s10988-018-9232-4
Crni, L. (2011). Getting even (Unpublished doctoral dissertation). Massachusetts Institute of Technology.
Crupi, V., Elia, F., Aprà, F., & Tentori, K. (2018). Double conjunction fallacies in physicians’ probability judgment. Medical Decision Making, 38(6), 756–760. https://doi.org/10.1177/0272989X18786358
Crupi, V., Fitelson, B., & Tentori, K. (2008). Probability, confirmation, and the conjunction fallacy. Thinking & Reasoning, 14(2), 182–199. https://doi.org/10.1080/13546780701643406
Crupi, V., & Iacona, A. (2022). The evidential conditional. Erkenntnis, 87(6), 2897–2921. https://doi.org/10.1007/s10670-020-00332-2
Deal, A. R. (2011). Modals without scales. Language, 559–585.
Douven, I. (2008). The evidential support theory of conditionals. Synthese, 164(1), 19–44. https://doi.org/10.1007/s11229-007-9214-5
Dretske, F. I. (1972). Contrastive statements. Philosophical Review, 81(4), 411–437. https://doi.org/10.2307/2183886
Dulany, D. E., & Hilton, D. J. (1991). Conversational implicature, conscious representation, and the conjunction fallacy. Social Cognition, 9(1), 85–110. https://doi.org/10.1521/soco.1991.9.1.85
Edwards, A. W. F. (1992). Likelihood. Johns Hopkins University Press.
Finlay, S. (2009). Oughts and Ends. Philosophical Studies, 143(3), 315–340. https://doi.org/10.1007/s11098-008-9202-8
Fitelson, B. (1999). The plurality of Bayesian measures of confirmation and the problem of measure sensitivity. Philosophy of Science, 66, 362–378. https://doi.org/10.1086/392738
Fitelson, B. (2007). Likelihoodism, Bayesianism, and relational confirmation. Synthese, 156(3), 473–489. https://doi.org/10.1007/s11229-006-9134-9
Gaifman, H. (1988). A theory of higher order probabilities. In B. Skyrms & W. L. Harper (Eds.), Causation, chance and credence. (Vol. 41). Springer.
Giannakidou, A., & Mari, A. (2016). Epistemic future and epistemic MUST: nonveridicality, evidence, and partial knowledge. In J. Błaszczak, A. Giannakidou, D. Klimek-Jankowska, & K. Migdalski (Eds.), Mood, aspect, modality revisited: New answers to old questions (pp. 75–117). University of Chicago Press.
Gibbard, A. (1980). Two recent theories of conditionals. Ifs (pp. 211–247). Springer.
Gibbard, A., & Harper, W. L. (1978). Counterfactuals and two kinds of expected utility. In W. L. Harper, R. Stalnaker, & G. Pearce (Eds.), Foundations and applications of decision theory (pp. 125–162). Springer.
Goble, L. (1996). Utilitarian deontic logic. Philosophical Studies, 82(3), 317–357. https://doi.org/10.1007/BF00355312
Goldstein, S., & Santorio, P. (2021). Probability of epistemic modalities. Philosophers’ Imprint, 21(33), 1–37.
Goodhue, D. (2017). Must \(\varphi \) is felicitous only if \(\varphi \) is not known. Semantics and Pragmatics, 10(14), 1–27. https://doi.org/10.3765/sp.10.14
Grice, P. (1975). Logic and conversation. In P. Cole & J. L. Morgan (Eds.), Syntax and semantics: Speech acts (Vol. 3, pp. 41–58). Academic Press.
Guerrini, J., Sablé-Meyer, M., & Mascarenhas, S. (2022). An explanation of representativeness: Contrastive confirmation-theoretical reasoning motivated by question-answer dynamics. In (Talk given at the 44th Annual Meeting of the Cognitive Science Society).
Heim, I. (1992). Presupposition projection and the semantics of attitude verbs. Journal of Semantics, 9(3), 183–221. https://doi.org/10.1093/jos/9.3.183
Jackson, F. (1979). On assertion and indicative conditionals. The Philosophical Review, 88(4), 565–589. https://doi.org/10.2307/2184845
Jackson, F. (1985). On the semantics and logic of obligation. Mind, 94(374), 177–195. https://doi.org/10.1093/mind/XCIV.374.177
Jackson, F., & Pargetter, R. (1986). Oughts, options, and actualism. The Philosophical Review, 95(2), 233–255. https://doi.org/10.2307/2185591
Jeffrey, R. C. (1965). The logic of decision. University of Chicago Press.
Jeffrey, R. C., & Edgington, D. (1991). Matter-of-fact conditionals. Proceedings of the Aristotelian Society, Supplementary Volumes, 65, 161–209.
Kahneman, D., & Tversky, A. (1973). On the psychology of prediction. Psychological Review, 80(4), 237–251. https://doi.org/10.1037/h0034747
Katzir, R. (2007). Structurally-defined alternatives. Linguistics and Philosophy, 30, 669–690. https://doi.org/10.1007/s10988-008-9029-y
Kaufmann, M. (2017). What ‘may’ and ‘must’ may be in Japanese. In K. Funakoshi, S. Kawahara, & C. Tancredi (Eds.), Japanese/Korean Linguistics 24.
Kaufmann, S. (2005). Conditional predictions. Linguistics and Philosophy, 28(2), 181–231. https://doi.org/10.1007/s10988-005-3731-9
Kaufmann, S. (2013). Causal premise semantics. Cognitive Science, 37(6), 1136–1170. https://doi.org/10.1111/cogs.12063
Kaufmann, S. (2017). The limit assumption. Semantics and Pragmatics, 10(18), 1–29. https://doi.org/10.3765/sp.10.18
Kennedy, C. (2007). Vagueness and grammar: The semantics of relative and absolute gradable adjectives. Linguistics and philosophy, 30(1), 1–45. https://doi.org/10.1007/s10988-006-9008-0
Kennedy, C., & McNally, L. (2005). Scale structure, degree modification, and the semantics of gradable predicates. Language, 345–381.
Klecha, P. (2014). Bridging the divide: Scalarity and modality (Unpublished doctoral dissertation). The University of Chicago.
Koehler, J. J. (1996). The base rate fallacy reconsidered: Descriptive, normative, and methodological challenges. Behavioral and Brain Sciences, 19(1), 1–17. https://doi.org/10.1017/S0140525X00041157
Kolodny, N., & MacFarlane, J. (2010). Ifs and oughts. The Journal of Philosophy, 107(3), 115–143.
Kratzer, A. (1979). Conditional necessity and possibility. In R. Bäuerle, U. Egli, & A. von Stechow (Eds.), Semantics from different points of view (pp. 117–147). Springer.
Kratzer, A. (1981). The notional category of modality. In H. J. Eikmeyer & H. Rieser (Eds.), Words, worlds, and contexts, new approaches to word semantics (pp. 38–74). Walter de Gruyter.
Kratzer, A. (1991). Modality. In A. von Stechow & D. Wunderlich (Eds.), Semantics: An international handbook of contemporary research (pp. 639–650). De Gruyter.
Kratzer, A. (2012). Modals and conditionals: New and revised perspectives (Vol. 36). Oxford University Press.
Kyburg, H. E. (1961). Probability and the logic of rational belief. Wesleyan University Press.
Lassiter, D. (2011). Measurement and modality: The scalar basis of modal semantics (Ph.D. thesis). New York University.
Lassiter, D. (2017). Graded modality: Qualitative and quantitative perspectives. Oxford University Press.
Lewis, D. (1973). Counterfactuals. Oxford University Press.
Lewis, D. (1976). Probabilities of conditionals and conditional probabilities. In W. L. Harper, R. Stalnaker, & G. Pearce (Eds.), Ifs (pp. 129–147). Springer.
Lewis, D. (1996). Elusive knowledge. Australasian Journal of Philosophy, 74(4), 549–567. https://doi.org/10.1080/00048409612347521
Mangiarulo, M., Pighin, S., Polonio, L., & Tentori, K. (2021). The effect of evidential impact on perceptual probabilistic judgments. Cognitive Science. https://doi.org/10.1111/cogs.12919
McGee, V. (1985). A counterexample to modus ponens. The Journal of Philosophy, 82(9), 462–471. https://doi.org/10.2307/2026276
Meyer, M.-C. (2013). Ignorance and grammar (Unpublished doctoral dissertation). Massachusetts Institute of Technology.
Morier, D. M., & Borgida, E. (1984). The conjunction fallacy: A task specific phenomenon? Personality and Social Psychology Bulletin, 10(2), 243–252. https://doi.org/10.1177/0146167284102
Ofir, C. (1988). Pseudodiagnosticity in judgment under uncertainty. Organizational Behavior and Human Decision Processes, 42(3), 343–363. https://doi.org/10.1016/0749-5978(88)90005-2
Pasternak, R. (2016). A conservative theory of gradable modality. Semantics and Linguistic Theory, 26, 371–390.
Pearl, J. (2000). Causality: Models, reasoning, and inference. Cambridge University Press.
Pearl, J. (2013). Structural counterfactuals: A brief introduction. Cognitive Science, 37(6), 977–985. https://doi.org/10.1111/cogs.12065
Sablé-Meyer, M., & Mascarenhas, S. (2022). Indirect illusory inferences from disjunction: A new bridge between deductive inference and representativeness. Review of Philosophy and Psychology, 13, 567–592. https://doi.org/10.1007/s13164-021-00543-8
Santorio, P. (2019). Interventions in premise semantics. Philosophers’ Imprint, 19(1), 1–27.
Sauerland, U. (2004). Scalar implicatures in complex sentences. Linguistics and Philosophy, 27, 367–391. https://doi.org/10.1023/B:LING.0000023378.71748.db
Schulz, K. (2011). If you’d wiggled A, then B would’ve changed. Synthese, 179(2), 239–251. https://doi.org/10.1007/s11229-010-9780-9
Sloman, A. (1970). Ought’ and ‘better. Mind, 79(315), 385–394. https://doi.org/10.1093/mind/lxxix.315.385
Stalnaker, R. C. (1976). Indicative conditionals. In W. L. Harper, R. Stalnaker, & G. Pearce (Eds.), Ifs (pp. 193–210). Springer.
Stalnaker, R. C. (1978). Assertion. In P. Cole (Ed.), Pragmatics (Vol. 9, pp. 315–332). Academic Press.
Stolarz-Fantino, S., Fantino, E., Zizzo, D. J., & Wen, J. (2003). The conjunction effect: New evidence for robustness. American Journal of Psychology, 116(1), 15–34. https://doi.org/10.2307/1423333
Tentori, K., Crupi, V., & Russo, S. (2013). On the determinants of the conjunction fallacy: Probability versus inductive confirmation. Journal of Experimental Psychology: General, 142(1), 235–255. https://doi.org/10.1037/a0028770
Tversky, A., & Kahneman, D. (1983). Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychological Review, 90(4), 293–315. https://doi.org/10.1037/0033-295X.90.4.293
Villalta, E. (2008). Mood and gradability: An investigation of the subjunctive mood in Spanish. Linguistics and Philosophy, 31, 467–522. https://doi.org/10.1007/s10988-008-9046-x
von Fintel, K., & Gillies, A. S. (2010). Must...stay...strong! Natural Language Semantics, 18(4), 351–383. https://doi.org/10.1007/s11050-010-9058-2
von Fintel, K., & Iatridou, S. (2005). What to do if you want to go to Harlem: Anankastic conditionals and related matters (Unpublished manuscript). MIT.
Wells, G. L., & Harvey, J. H. (1977). Do people use consensus information in making causal attributions? Journal of Personality and Social Psychology, 35(5), 279–293. https://doi.org/10.1037/0022-3514.35.5.279
Yalcin, S. (2005). A puzzle about epistemicmodals. MIT Working Papers in Linguistics, 51, 231–272.
Yalcin, S. (2010). Probability operators. Philosophy Compass, 5(11), 916–937. https://doi.org/10.1111/j.1747-9991.2010.00360.x
Acknowledgements
We thank Nadine Bade, Janek Guerrini, Benjamin Spector, the audiences of the LINGUAE and LANG-REASON seminars at Ecole Normale Supérieure, the audience of Sinn und Bedeutung 25, and three anonymous reviewers for invaluable comments.
Funding
This work was supported by Agence Nationale de la Recherche grants ANR-18-CE28-0008 (LANG-REASON; PI: Mascarenhas) and ANR-17-EURE-0017 (FrontCog; Department of Cognitive Studies, Ecole Normale Supérieure), and by the New Faculty Startup Fund from Seoul National University (Chung).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chung, W., Mascarenhas, S. Modality, expected utility, and hypothesis testing. Synthese 202, 11 (2023). https://doi.org/10.1007/s11229-023-04191-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04191-6







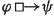 ’ denotes the expected value of
’ denotes the expected value of