Abstract
In this article, I try to shed new light on Frege’s envisaged definitional introduction of real and complex numbers in Die Grundlagen der Arithmetik (1884) and the status of cross-sortal identity claims with side glances at Grundgesetze der Arithmetik (vol. I 1893, vol. II 1903). As far as I can see, this topic has not yet been discussed in the context of Grundlagen. I show why Frege’s strategy in the case of the projected definitions of real and complex numbers in Grundlagen is modelled on his definitional introduction of cardinal numbers in two steps, tentatively via a contextual definition and finally and definitively via an explicit definition. I argue that the strategy leaves a few important questions open, in particular one relating to the status of the envisioned abstraction principles for the real and complex numbers and another concerning the proper handling of cross-sortal identity claims.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Setting the stage: from the methodology of Grundlagen to that of Grundgesetze
When Frege designed the architecture of his main work Grundgesetze der Arithmetik, he most likely knew that it was a key prerequisite for his envisaged definitions of numbers of all kinds as extensions of concepts or value-ranges of functions (cf. Frege, 1893, §9) to improve methodologically on Die Grundlagen der Arithmetik in some important respects. In saying this, I do not have any technical or terminological or similar improvements in mind. Among the methodological requirements that had to be met in Grundgesetze were these:
-
(i)
Frege had to abandon the dubious assumption that the reader of his work knows (precisely) what extensions of concepts are (cf. Frege, 1884, §68).
-
(ii)
It was mandatory to argue convincingly for the assumed purely logical nature of extensions of concepts.
-
(iii)
It was requisite to specify the range of the first-order variables.
Besides the need to meet these requirements and others, Frege had to fulfil the central task he had set himself, namely to derive in a gapless fashion the basic laws of arithmetic from logical axioms and definitions and in this way to establish and justify the assumed logical nature of these laws or, in the terminology of Grundlagen, their supposed analyticity. In Grundlagen, Frege had only roughly outlined some of those proofs. In Grundgesetze, he followed the outline more or less closely and apparently for his benefit. As to (i) and (ii), this meant specifically that extensions of concepts (or more generally: value-ranges of functions) had to be introduced as logical objects in a methodologically sound manner instead of taking their logical nature for granted as Frege had done in Grundlagen, §68. When he began writing Grundgesetze, he probably believed that logical abstraction in terms of an initial semantic stipulation (Frege, 1893, §3), in liaison with some additional stipulations (in §10–§12), satisfied this condition and thus could be regarded as a road to success in pursuit of his logicist project. I call a Fregean abstraction principle of the form “Q(α) = Q(β) = Req(α, β)” logical if its right-hand side is formulated in purely logical terms or in other words: if the equivalence relation can be defined in second-order logic. The metalinguistic stipulation in §3 reads as follows:
I use the words “the function Φ(ξ) has the same value-range as the function Ψ(ξ)” generally as coreferential [gleichbedeutend] with the words “the functions Φ(ξ) and Ψ(ξ) always have the same value for the same argument”.
Following Heck (2012), I call it henceforth the Initial Stipulation. The Initial Stipulation was later incorporated in the formal version of Basic Law V by converting the informal and stipulative nature of the former (cf. §3 and §10) into the formal and assertoric mode of the latter and by preserving coreferentiality. Note that identity of sense was not stipulated in §3 and, hence, could not have been transferred from the Initial Stipulation to Basic Law V. Basic Law V presents itself as a concept-script sentence (cf. Frege, 1893, §20) by means of which it is asserted that a truth-value name (expressing a thought) refers to the True (cf. Frege, 1893, §32).
Despite this initial achievement, Frege fell short of advancing a cogent argument for the logical nature of value-ranges. The reason is that he did not argue persuasively for the logical character of Basic Law V which governs value-ranges. Thus, it is not unfair to Frege if we note that by his own standards he failed to meet requirement (ii). Regarding requirement (iii), it could seem that he did not take this desideratum seriously enough. In my view, there is some evidence that Frege was vacillating between the assumption of an all-encompassing first-order domain and the limitation of the domain to those objects whose existence was required by the axioms of his logical system: the truth-values and value-ranges.Footnote 1 Yet his apparent insouciance or indecision concerning such an important issue in his logical foundation of arithmetic had, in my judgement, a number of unpalatable consequences. In short, although in the transition from the methodological framework of Grundlagen to that of Grundgesetze Frege made remarkable progress in various ways,Footnote 2 his starting position in his opus magnum was far from being ideal.
In Grundgesetze, Frege knew from the start that by choosing a second-order abstraction principle as the appropriate means of affording us the right cognitive access to logical objects in their own right via their identity conditions he had to face the re-emergence of a semantic problem that was worrying him in Grundlagen: the Julius Caesar problem. In Grundlagen, it gave rise to the indeterminacy of the reference of the (second-level) cardinality operator “the cardinal number that belongs to the concept φ”.Footnote 3 By contrast, in Grundgesetze it was no longer the cardinality operator (now treated as a function-name of first level) whose reference gave rise to concern. It was rather the semantics of the value-range operator “ φ(ε)” and of canonical value-range namesFootnote 4 that was preoccupying Frege at an even more basic level in his foundational project. The introduction of the metalinguistic analogue of “
φ(ε)” and of canonical value-range namesFootnote 4 that was preoccupying Frege at an even more basic level in his foundational project. The introduction of the metalinguistic analogue of “ φ(ε)”, namely “the value-range of the function φ”, in Grundgesetze I, §3 by means of the Initial Stipulation differed crucially from his standard elucidations of the other primitive function-names of his logical system which characteristically fix the values of the corresponding functions for all fitting arguments. Frege’s line of argument in Grundgesetze I, §10 makes it clear that the Initial Stipulation is afflicted by referential indeterminacy of value-range names, even if he had imposed strict constraints on the size of the first-order domain along the lines I mentioned above. And since Frege intended to define cardinal, real and complex numbers as special value-ranges (cf. Frege, 1893, §9, 1903, §162), the referential indeterminacy of “
φ(ε)”, namely “the value-range of the function φ”, in Grundgesetze I, §3 by means of the Initial Stipulation differed crucially from his standard elucidations of the other primitive function-names of his logical system which characteristically fix the values of the corresponding functions for all fitting arguments. Frege’s line of argument in Grundgesetze I, §10 makes it clear that the Initial Stipulation is afflicted by referential indeterminacy of value-range names, even if he had imposed strict constraints on the size of the first-order domain along the lines I mentioned above. And since Frege intended to define cardinal, real and complex numbers as special value-ranges (cf. Frege, 1893, §9, 1903, §162), the referential indeterminacy of “ φ(ε)” would have affected any term of the formal language that was supposed to refer to a cardinal, real or complex number. Yet by pursuing a piecemeal reference-fixing strategy regarding value-range names in Grundgesetze I, §3, §10–§12, Frege thought that he had succeeded in conferring determinate references on them. He was aware that this was a prerequisite for introducing Basic Law V and for answering the fundamental question of arithmetic: “how do we apprehend logical objects, in particular, the numbers?” (cf. Frege, 1903, p. 295).Footnote 5
φ(ε)” would have affected any term of the formal language that was supposed to refer to a cardinal, real or complex number. Yet by pursuing a piecemeal reference-fixing strategy regarding value-range names in Grundgesetze I, §3, §10–§12, Frege thought that he had succeeded in conferring determinate references on them. He was aware that this was a prerequisite for introducing Basic Law V and for answering the fundamental question of arithmetic: “how do we apprehend logical objects, in particular, the numbers?” (cf. Frege, 1903, p. 295).Footnote 5
2 Grundlagen, §104: real and complex numbers, cross-sortal identity claims and the problem of referential indeterminacy
In Grundlagen, §104, Frege maps out the following strategy for the envisaged introduction of fractions, irrational and complex numbers:
everything will in the end depend on the search for a judgeable content which can be transformed into an equation, whose sides are just the new numbers. In other words, we must fix the sense of a recognition-judgement for such numbers. In doing so, we must bear in mind the doubts that we discussed (in §§63–68) with respect to such a transformation. If we follow the same procedure as we did there, then the new numbers will be given to us as extensions of concepts.
Thus, the strategy for the definitional introduction of the real and complex numbers and the (likely) proof of an associated abstraction principle in each case was apparently designed to proceed along the lines of the definitional introduction of the cardinals and the projected proof of Hume’s Principle—NxF(x) = NxG(x) ↔ Eqx(F(x),G(x))Footnote 6—or its two directions, first the right-to-left direction and then the left-to-right direction. More concretely, in a first step one must contrive a suitable second-order equivalence relation for the case of the real numbers and—in the spirit of Frege, I assume—another for the complex numbers each of which can be defined in a purely logical vocabulary. In a second step, the reals are tentatively introduced by transforming Req(F, G) into an identity of reals Σ(F) = Σ(G) and by presenting this transformation as a contextual definition of the real number operator “Σ”. I refer to the envisioned abstraction principle for the reals “Σ(F) = Σ(G) ↔ Req(F, G)” as “APR”. Analogous remarks apply to the case of the complex numbers.Footnote 7 The projected abstraction principle for the complex numbers, say “Ω(F) = Ω(G) ↔ Ceq(F, G)”, may be referred to as “APC”. Following Frege’s suggestive remarks in §104, I presume that in analogy to Hume’s Principle the envisaged equivalence relations Req and Ceq are supposed to hold between first-level concepts and not more generally between monadic first-level functions as is the case with the relation of coextensiveness in Basic Law V.Footnote 8 If this is correct, “Σ(F)” and “Ω(F)” are to be regarded as combinations of a second-level abstraction operator and a first-level concept expression. As to the projected contextual definitions of “Σ” and “Ω”, Frege points out that one has to be aware of the logical doubts to which the transformation of an equivalence relation other than identity into an identity of new abstracta gives rise. In particular, from the paradigm case of cardinal numbers and equinumerosity one may expect that the criterion of identity embedded, for example, in APR does not place us in a position to determine the truth-value of any equation of the form “Σ(F) = t”. “t” is here any singular term that does not have the form of “Σ(G)”, for example, “Σ(F) = 2” or “Σ(F) = Nx(x = 0 ∨ x = 1)” or “Σ(F) = @φ(Ex(φ(x), x = 0 ∨ x = 1))” or “Σ(F) = {0,1}” or “Σ(F) = {\(\emptyset\),{\(\emptyset\)}” or “Σ(F) = Ω(G)” or even “Σ(F) = the Leaning Tower of Pisa” if in Grundlagen Frege takes the first-order domain to be homogeneous and all-encompassing, and as he most likely does. Likewise, we cannot determine the truth-value of any equation of the form “Ω(G) = t” by appeal to APC. Consequently, APR and APC qua contextual definitions do not uniquely fix the reference of “Σ” and that of “Ω”. This difficulty has to be resolved in order to keep the logicist programme for real and complex analysis alive. The proposed solution is that the real numbers are finally defined as equivalence classes of Req and the complex numbers as equivalence classes of Ceq.Footnote 9 And the foundational machinery for real and complex analysis can then go on as Frege may have imagined around 1884.Footnote 10
So, if Frege had carried out his plan to define, in a first step and after the fashion of the tentative contextual definition of the cardinality operator, fractions, irrational and complex numbers by using in each case what he considers to be an adequate second-order abstraction principle, he would have faced a whole family of Caesar or indeterminacy problems, each of which is supposed to be resolved by framing an appropriate explicit definition for the relevant numbers in terms of equivalence classes. Yet Frege provides no clue as to how far the analogy between the explicit definition of the cardinality operator EDC: NxF(x): = @φ(Eqx(φ(x),G(x))) in Grundlagen, §68 and the envisaged explicit definitions of the higher numbers was supposed to go. Did he think that he had to constrain the explicit definition of, say, “Σ” in such a way that APR could be proved from it within second-order logic? If so, did he believe that APR could play a pivotal role in the formal proofs of the fundamental theorems of real analysis similar to the role that Hume’s Principle (or each of its two directions) was designed to play in the envisaged concept-script proofs of the basic laws of cardinal arithmetic? Suppose that he did believe this. In this case, he would have had to impose exactly that constraint on the explicit definition of “Σ” which I just mentioned. For unless Frege considered APR, unlike Hume’s Principle, to be a primitive law of logic—which in my opinion was a genuine option neither in Grundlagen nor in Grundgesetze nor in his post-Paradox period—how else could he have secured the requisite analytic nature of APR, once its initial status as a definition of “Σ” was abandoned, due to the impact that the Caesar problem was supposed to have on the definitional introduction of the real numbers via logical abstraction?Footnote 11 Recall in this connection that in Grundlagen Frege is most likely operating with a first-order domain which is both homogeneous and all-inclusive. Still on the speculative side, we may further ask why he suggested that the real and complex numbers should be introduced at all along the lines of his definitional introduction of cardinal numbers. Thus, on what grounds did Frege suggest that regarding the “higher” numbers he should likewise start with a heuristic contextual definition of an abstraction operator instead of defining these numbers straightaway as equivalence classes? For clearly, before he presented CDC, he knew that it was bound to fail, due to the emergence of the Caesar problem. And with the wisdom of hindsight he further knew that this would also have applied, mutatis mutandis, to the contextual definitions of “Σ” and “Ω”. So, why does he propose to take once again a definitional detour? And which recipe, if any, for tackling the problem of cross-sortal identity claims of the kind, say, “Σ(F) = N(G)” or “Ω(F) = N(G)” or “Σ(F) = Ω(G)” might he have had in mind?
My answer to the penultimate question follows largely from my preceding account. In Grundlagen (see especially §62), Frege pointed out that it is a key requirement for the introduction of abstracta of any kind (not only for cardinal numbers) to state a specific and, in the ideal case, generally applicable criterion of identity for them. The fact that in his envisaged project of laying the logical foundations of real and complex analysis he intended to proceed along the lines of his definitional strategy for cardinal arithmetic in Grundlagen seems to confirm this, although in Grundlagen §62 there is still no evidence that he would take a similar path regarding the projected definitional introduction of the real and complex numbers. Note in this connection that in EDC the identity criterion of equinumerosity for cardinal numbers has not disappeared from the screen. Plainly, it is no longer directly displayed as in the tentative contextual definition of the cardinality operator in terms of Hume’s Principle. Yet it essentially underlies EDC from which follows that it is at the same time the identity criterion for equivalence classes of equinumerosity: @φ(Eqx(φ(x),F(x))) = @φ(Eqx(φ(x),G(x))) ↔ Eqx(F(x),G(x)). Analogous remarks apply to Frege’s envisaged explicit definitions of the real and complex numbers. Not only in Grundlagen but also in Grundgesetze laying down adequate identity conditions was considered a crucial step to success whenever the introduction of abstract or logical objects was on the agenda. Yet pursuing this methodological key idea also gave rise to a serious problem which Frege attempted to resolve in different ways in the two works.
In Grundlagen, §62, Frege remarks that it might not always be in our power to apply a certain criterion of identity, for example, the criterion of identity for cardinal numbers which is central in Grundlagen. Unfortunately, he does not spell out what he means exactly by this remark. I presume that in his view the identity criterion of equinumerosity usually fulfills its purpose when it is applied to equations of the form “NxF(x) = NxG(x)”. Yet Frege was possibly aware that in special cases the determination of the truth-value of an equation of the form “NxF(x) = NxG(x)” by appeal to the identity criterion of equinumerosity might be beyond the reach of our cognitive capacities. As a matter of fact, Hume’s Principle does not always place us in a position to establish the truth-value of such an equation. Take, for example, (q) “Nx(x = x) = NxFCN(x)”, where “NxFCN(x)” is to abbreviate the predicate “finite cardinal number”. As Boolos shows (1987, p. 16), (q) is an undecidable sentence in the formal system FA (Frege Arithmetic), which is standard second-order logic plus Hume’s Principle. (q) is true in some models of FA but false in others. Heck (1999, p. 262) mentions further examples of equations of the form “NxF(x) = NxG(x)” whose truth-value is undecidable (for us).
3 A glance at Grundgesetze
In Grundgesetze, Frege likewise begins his exposition by stating a criterion of identity for logical objects. Yet the similarity between the approaches in Grundlagen and Grundgesetze ends at this point. Having drawn the right conclusion from the methodological lacuna that he had left behind in Grundlagen,Footnote 12 he takes a different route. Independent of the fact that in Grundgesetze Frege regards contextual definitions as inadmissible on purely definition-theoretic grounds—contextual definitions are said to offend against the principle of the simplicity of the definiendum and possibly against the principle of completeness as well—he directly introduces what he considers fundamental and irreducible objects of logic, namely value-ranges of functions. He does so via the Initial Stipulation. He concedes though that value-ranges depend on something even more fundamental in logic, namely on functions (cf. Frege, 1967, p. 130 fn. 5, 210; Frege, 1969, p. 134, 199; Frege, 1976, p. 121): The function takes logical precedence of its value-range; function is the logically prior notion. In a second step, Frege completes the unfinished semantic business left by the Initial Stipulation, namely fixing the references of value-range names up to uniqueness. Having achieved this, he transforms the Initial Stipulation into Basic Law V (§20). Unlike the former, the latter asserts something. In a fourth step, Frege defines cardinal numbers as special value-ranges, as equivalence classes of equinumerosity. In a fifth step, he proves the right-to-left direction and the contraposition of the left-to-right direction of Hume’s Principle (Theorems 32 and 49; for the proofs of these theorems see Grundgesetze I, §54–§65 and §68–§69; cf. Heck, 2012, p. 173–178; May & Wehmeier, 2019; Schirn, 2016). In this way, he believes to have established the two directions as logical truths—or in accordance with his definition of “analytic” in Grundlagen, §3: as analytic truths—and to have set the right scene for performing further steps in his foundational project for cardinal arithmetic. In Grundgesetze II, Frege introduces moreover the real or “measurement” numbers. He does so without providing an associated abstraction principle which was specifically tailored for the real numbers, similar to the role which Hume’s Principle (or its two directions) plays (play) for the cardinal numbers. Furthermore, the formulation of such an abstraction principle was probably not intended at a later stage in the development of Frege’s theory of magnitude, say, in a projected third volume of Grundgesetze. Be that as it may, Frege only missed his chance to define the real numbers as Relations on Relations—as ratios of magnitudes of a domain that belongs to a positive class—by a hair. A Relation is the value-range of a binary first-level function whose value for every fitting pair of arguments is either the True or the False, in short, it is the extension of a first-level relation. Overshadowed by Russell’s Paradox, Frege’s theory of magnitude remained a fragment.Footnote 13
In sum, “always provide an effective criterion of identity for logical objects before they are allowed to do essential work in the foundation of arithmetic” is a methodological guideline that underlies the foundational strategies both in Grundlagen and Grundgesetze. Note, however, that in the two works this guideline is operative in different ways.
4 Local and global abstraction principles and cross-sortal identity
Bearing all this in mind, an answer to the second of the questions which I raised above, namely which method, if any, of dealing with the issue of cross-sortal identity claims, for example, of the kind “N(F) = Σ(G)” or “Σ(F) = Ω(G)”, Frege might have thought about in Grundlagen, could at best rest on speculation. Yet there are at least two things I am fairly sure of: First, unless Frege had explicitly introduced an axiom governing extensions of second-level concepts in general via an identity criterion for those extensions, he would not have got around the problem of adequately treating statements of the form, say, “N(F) = Σ(G)” or “Σ(F) = Ω(G)”. Second, an acceptable solution would have required more than a few minor tweaks. In particular, there is no evidence that Frege would have suggested settling the truth-value of an equation of the form, say, “N(F) = Σ(G)” or “Σ(F) = Ω(G)” either by appeal to the “sameness” (coextensiveness) or “difference” (non-coextensiveness) of the equivalence relation(s) associated with N, Σ and Ω or by appeal to the relevant equivalence classes or by pursuing a mixed or even an entirely different strategy. As I pointed out before, he intended to define numbers of all kinds as extensions of concepts (as equivalence classes of the relevant second-order equivalence relation), but in Grundlagen does not yet state a global abstraction principle, endowed with the status of a logical axiom, which invariably takes care of the identity conditions of logical objects of all those specific kinds that are deemed to be indispensable for laying the logical foundations of arithmetic in its entirety. In Grundgesetze, examples of such special logical objects are equivalence classes of equinumerosity; magnitudes (Relations); domains of magnitudes; classes of finite cardinal numbers (Grundgesetze II, §164); ordered pairs (Grundgesetze I, §144), for example, pairs whose first member is a positive whole number or 0 and whose second member is a class of whole positive numbers (Grundgesetze II, §164); classes of Relations (downward closure, limit), Relations belonging to a positival class; Relations belonging to a positive class; and Relations on Relations.Footnote 14
In Grundlagen, §73, Frege sketches what he regards as the quintessence of the proof of the right-to-left direction of Hume’s Principle. In this sketch, he seems to rely on an abstraction principle which states for second-level concepts and their extensions what Basic Law V states for first-level concepts and their extensions. In order to prove the right-to-left direction of Hume’s Principle, Frege must show, according to EDC, NxF(x): = @φ(Eqx(φ(x),G(x))), that Eqx(F(x),G(x)) → @φ(Eqx(φ(x),F(x))) = @φ(Eqx(φ(x),G(x))) holds. That is to say: he has to prove that “under this hypothesis” the following two sentences hold generally: (a) Eqx(H(x),F(x)) → Eqx(H(x),G(x)) and (b) Eqx(H(x),G(x)) → Eqx(H(x),F(x)). So, it seems that Frege is here converting the statement that the extension of a special second-level concept coincides with the extension of another second-level concept into the statement that these concepts are coextensive. We might thus presume that in introducing extensions of second-level concepts Frege tacitly relied on the third-order analogue of Basic Law V, if the latter is seen as restricted to first-level concepts and their extensions:
Yet if this applies, then it remains obscure why Frege does not explicitly invoke this abstraction principle to provide a proper grounding of the explicit definition of the cardinality operator (a) by way of solving the Caesar problem instead of merely shifting it from cardinal numbers to extensions of concepts (which in a sense amounts to postponing the problem into the unkownFootnote 15) and (b) by establishing the requisite logical nature of equivalence classes of equinumerosity instead of presupposing it without further ado. By Frege’s own standards, appealing to the fact that equinumerosity is definable in second-order logic does not yet justify bestowing the status of “full-blown” logical objects on those equivalence classes.
I characterized Basic Law V as a global abstraction principle. As such it contrasts with Hume’s Principle which, following Frege, I consider a local abstraction principle. He does not use these terms. As I said, the global character of Basic Law V rests on the supposed fact that it provides an identity criterion for logical objects in general, and I add: if (a) logical objects of each kind are given as value-ranges and if (b) we gauge the scope of the identity criterion from Frege’s perspective. Recall that Frege identifies not only the cardinals and (projectively) the reals with special extensions but also the truth-values. Thus, there are transsortal identifications of three kinds in Grundgesetze.
One further observation may be in order in this connection. Basic Law V is designed to govern value-ranges of monadic first-level functions, the “simple” value-ranges. As I mentioned above, Frege also introduces value-ranges of dyadic first-level functions at a later stage (in Grundgesetze I, §36). He does so after having defined the application operator “ξ ∩ ζ” (in §34). This function-name is omnipresent from there on out, not only in the definitions of Grundgesetze I and II (with only two exceptionsFootnote 16) but also in the proofs which Frege carries out. Note that the introduction of double value-ranges,Footnote 17 unlike the introduction of simple value-ranges in Grundgesetze I, §3, does not proceed via an informal stipulation which states an identity criterion for them in its own right. The reason is that Frege apparently saw no need to lay down an additional basic law for double-value-ranges. If he had done this, this law would most likely have been formulated as follows (converting here his special notation for the first-order universal quantifier into modern notation): ( (f(ε,α)) =
(f(ε,α)) =  (g(ε,α))) = (∀x∀y(f(x,y) = g(x,y))).Footnote 18 Heck (1997, p. 283f.; cf. also Heck, 2019, p. 503) adequately explains why Frege probably thought that he could do without such an additional axiom.Footnote 19 Note that the names for double value-ranges can be formed by means of the notation which is available for simple value-ranges.
(g(ε,α))) = (∀x∀y(f(x,y) = g(x,y))).Footnote 18 Heck (1997, p. 283f.; cf. also Heck, 2019, p. 503) adequately explains why Frege probably thought that he could do without such an additional axiom.Footnote 19 Note that the names for double value-ranges can be formed by means of the notation which is available for simple value-ranges.
5 Cross-sortal identity claims again: a final synopsis of Grundlagen and Grundgesetze
Speaking generally, the question of whether in a logical or mathematical theory T which includes the use of abstraction principles one has to cope with cross-sortal identity claims of the form “@1(P) = @2(Q)” depends, in my view, not least on the size of the first-order domain and the conceptual and referential resources of the language T* in which T is couched. If T contains just one second-order abstraction principle, equations of the form “@1(P) = @2(Q)” probably do not occur in T, unless T were expanded at some stage of its evolution by adding one or the other second-order abstraction principle to the originally available abstraction repertoire. Equations of the form “@(P) = t” may of course occur in T independently of the question of whether T initially contains only one second-order abstraction principle or has been expanded by another at a later stage. The letter “t” is supposed to represent here any well-formed singular term of T* which, regarding the last link of its formation pedigree, is not formed from a second-level abstraction operator by filling its argument-place with a monadic first-level function-name or first-level concept-expression, simple or complex. The term “t” may of course contain a second-level abstraction operator as a constituent. In the concept-script of Grundgesetze, the definite description “\ (—ε)” would be an example of such a term. It is obtained by first inserting “—ξ” into the argument-place of “
(—ε)” would be an example of such a term. It is obtained by first inserting “—ξ” into the argument-place of “ φ(ε)” and by subsequently inserting “
φ(ε)” and by subsequently inserting “ (—ε)” into the argument–place of the description operator “\ξ”.
(—ε)” into the argument–place of the description operator “\ξ”.
There is no question that the syntax of the concept-script of Grundgesetze licences the formation, for example, of equations of the form “ Φ(ε) = N
Φ(ε) = N Ψ(α)” (cross-sortal identity claims with the proviso that in Grundgesetze Frege does not state Hume’s Principle as a whole; see below). “N
Ψ(α)” (cross-sortal identity claims with the proviso that in Grundgesetze Frege does not state Hume’s Principle as a whole; see below). “N Ψ(α)” is obtained, in the final step of its constructional history, by filling the argument-place of the cardinality operator “Nξ” with a value-range name “
Ψ(α)” is obtained, in the final step of its constructional history, by filling the argument-place of the cardinality operator “Nξ” with a value-range name “ Ψ(α)” of arbitrary complexity. The cardinality operator is explicitly defined in Frege (1893, §40) and governed by the right-to-left direction and the contraposed left-to-right direction of Hume’s Principle as well as by Basic Law V. Cardinal numbers are just value-ranges. In Frege’s view, the truth-value of “
Ψ(α)” of arbitrary complexity. The cardinality operator is explicitly defined in Frege (1893, §40) and governed by the right-to-left direction and the contraposed left-to-right direction of Hume’s Principle as well as by Basic Law V. Cardinal numbers are just value-ranges. In Frege’s view, the truth-value of “ Φ(ε) = N
Φ(ε) = N Ψ(α)” can straightforwardly be settled by appeal to the definition of the cardinality operator and Basic Law V.Footnote 20 Just replace “N
Ψ(α)” can straightforwardly be settled by appeal to the definition of the cardinality operator and Basic Law V.Footnote 20 Just replace “N Ψ(α)” with a coreferential canonical value-range name which refers to the relevant equivalence class and use Basic Law V to determine the truth-value of the resulting canonical value-range equation.
Ψ(α)” with a coreferential canonical value-range name which refers to the relevant equivalence class and use Basic Law V to determine the truth-value of the resulting canonical value-range equation.
The logical system of Grundgesetze contains in fact only one fully-fledged abstraction principle, namely Basic Law V. The likely reason for this limitation is that Frege considered Basic Law V “omnipotent” in pursuit of his logicist project. Furthermore, nowhere does he combine the right-to-left direction and the contraposition of the left-to-right direction of Hume’s Principle to form an identity or a biconditional. And even if for some logical or specifically proof-theoretic or epistemological reason(s) Frege had united the two directions—in my judgement, such a reason emerges neither in the proof-analyses preceding the proof-constructions of Theorems 32 and 49 nor in the proof-constructions themselves—the unification would not have resulted exactly in Hume’s Principle as we usually understand it.Footnote 21 This is not to say that this departure from the norm is of any great importance in Grundgesetze.
We have seen that Fregean abstraction principles almost invariably give rise to an indeterminacy problem of some kind, at least in a Fregean setting, even if prior to stating the principles and putting them into use, the first-order domain had been narrowed down to just those objects that are required for laying the logical foundations of a branch of mathematics, that is, whose existence is required by the axioms of the system. In the context of Grundgesetze, this would mean that the domain has been brought down to the two primitive objects of logic, the True and the False, and value-ranges of (first-level) functions. (However, I argue elsewhere that on closer examination this is not the case; see Schirn, 2018 and the discussion in Wehmeier, 1999 who shares my view.) I have further observed that in Grundgesetze, §10 Frege diagnoses a pervasive referential indeterminacy of value-range names deriving from the Initial Stipulation. He thinks that he succeeds in removing the indeterminacy by making just the right additional stipulations. Thus, in Grundgesetze Frege proceeds in striking contrast to the strategy which he maps out in Grundlagen to resolve the indeterminacy of the cardinality operator. Both strategies are unsuccessful, but for fundamentally different reasons.
So much for Frege’s plan in Grundlagen to introduce the higher numbers, with side glances at Grundgesetze: (i) via tentative contextual definitions providing the requisite criteria of identity in terms of logical abstraction, and (ii) definitively via explicit definitions that replace the contextual definitions but still incorporate those criteria and at the same time extend their ranges of application. With the help of such explicit definitions and further definitions adjoined to second-order logic Frege planned to prove fundamental theorems about the higher numbers in a work that was probably thought to follow hard on the heels of Grundlagen.Footnote 22 Yet what matters when we assess his overall logicist project in Grundlagen is the fact that he did not disapprove of logical abstraction per se as a potential means to introduce cardinal, real and complex numbers as logical objects in their own right, that is, under waiver of using extensions as target objects of transsortal identifications. It was solely the referential indeterminacy of abstraction operators, if contextually defined, that eventually forced him to engage in a new definitional strategy which nonetheless derived much benefit from the old one. Clearly, if in Grundlagen or in its projected immediate successor a solution to the problem of referential indeterminacy for each number operator and the terms formed from them had been feasible, say, by making just the right kind of additional stipulation(s) in connection with the relevant contextual definition—perhaps, anachronistically speaking, modelled upon the pattern of the twin stipulations in Grundgesetze I, §10—then there would have been no intrinsic need from Frege’s viewpoint in Grundlagen (a) to set up an explicit definition of the term “the cardinal number which belongs to the concept F” in terms of a name which refers to an equivalence class and (b) to propose explicit definitions of the higher numbers in terms of extensions of concepts in order to successfully present the logicist programme in outline.Footnote 23 All numbers would then be treated as logical objects sui generis, unaffected by any ontological reduction.Footnote 24 To re-emphasize, we may find the potential no-class perspective only at a certain stage of the logicist development in Grundlagen, but not in Grundgesetze. In Grundgesetze, the idea that the prototype of a logical object, namely the value-range of a function, is indispensable for laying the logical foundations of all branches of arithmetic and must be governed by a primitive law of logic embodying an identity criterion which applies uniformly to logical objects was set in stone at the very outset of the project.
6 Conclusion
Let me summarize the main points I have made in this essay.
-
(1)
I first discussed Frege’s envisaged introduction of the “higher” numbers in Grundlagen. It was intended to be carried out in a book that was probably supposed to follow hard on the heels of Grundlagen. In Sect. 1, I argued that in the transition from Grundlagen to Grundgesetze Frege had to make methodological progress in at least three important respects: (a) Extensions of concepts, or more generally, value-ranges of functions had to be introduced in a methodologically sound manner by providing a general criterion of identity for them; (b) the assumed logical nature of value-ranges had to be justified; (c) the range of the first-order variables had to be specified. I further pointed out that despite Frege’s novel introduction of value-ranges of (first-level) functions in Grundgesetze his view of the nature of logic had not undergone massive changes in the transition from Grundlagen to Grundgesetze.
-
(2)
If Frege had carried out his plan in Grundlagen to define, in a first step and after the fashion of the tentative contextual definition of the cardinality operator, fractions, irrational and complex numbers via second-order abstraction principles, he would have faced a whole family of Caesar or indeterminacy problems, each of which was supposed to be resolved by framing an appropriate explicit definition for the relevant numbers in terms of equivalence classes. Yet the definitions would have posed a challenge for Frege: Cross-sortal identity claims of a certain kind—those in which “=” is flanked by terms formed from distinct abstraction operators—had to be dealt with primarily and in an appropriate manner. Giving the treatment of those equations priority follows immediately from the paramount importance that Frege attaches to logical abstraction principles in his foundational project.
-
(3)
“Always provide an effective criterion of identity for logical objects before they are allowed to do essential work in the foundation of arithmetic” is a methodological guideline that underlies the foundational strategies both in Grundlagen and Grundgesetze, but in the two works is operative in different ways.
-
(4)
There is no evidence that Frege would have suggested settling the truth-value of an equation of the form, say, “N(F) = Σ(G)” or “Σ(F) = Ω(G)” either by appeal to the “sameness” (coextensiveness) or “difference” (non-coextensiveness) of the equivalence relation(s) associated with N, Σ and Ω. And it is unclear whether he would have pursued a “mixed strategy”.
-
(5)
The question of whether in a logical or mathematical theory T which includes the use of abstraction principles one has to cope with cross-sortal identity claims of the form “@1(P) = @2(Q)” depends, in my view, not least on the size of the first-order domain and the conceptual and referential resources of the language T* in which T is couched.
-
(6)
In Grundgesetze, the truth-value of an equation of the form “
 Φ(ε) = N
Φ(ε) = N Ψ(α)” can straightforwardly be settled by appeal to Frege’s definition of the cardinality operator and Basic Law V. If “
Ψ(α)” can straightforwardly be settled by appeal to Frege’s definition of the cardinality operator and Basic Law V. If “ Φ(ε)” refers to an equivalence class of equinumerosity, the truth-value of “
Φ(ε)” refers to an equivalence class of equinumerosity, the truth-value of “ Φ(ε) = N
Φ(ε) = N Ψ(α)” could also be determined by appeal to Hume’s Principle: an embarassment of riches. However, Hume’s Principle is powerless to decide the truth-value of, for example, “
Ψ(α)” could also be determined by appeal to Hume’s Principle: an embarassment of riches. However, Hume’s Principle is powerless to decide the truth-value of, for example, “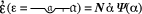 ”.Footnote 25
”.Footnote 25 -
(7)
Under certain circumstances, it would not have been necessary, from the point of view of Frege’s logicist project in Grundlagen, to define cardinal numbers as extensions of concepts.
-
(8)
In Grundgesetze, value-ranges of functions are considered indispensable for laying the logical foundations of arithmetic. By contrast, earlier in Grundlagen Frege, if we take him at his word, did not yet attach decisive importance to using extensions of concepts at all.
Notes
See the discussion in Schirn (2018, §2, pp. 228–234).
Cook and Ebert (2016) characterize the methodological change from Grundlagen to Grundgesetze as a move from “Frege’s simple recipe” to “Frege’s generalized recipe”. The latter is said to emerge from the former by virtue of two modifications. Both the simple and the generalized recipe are described and analyzed in detail by the authors. Leaving issues of methodology aside, I do not think that Frege’s view of the nature of logic has undergone dramatic changes in the transition from Grundlagen to Grundgesetze. I say this despite the novel introduction of value-ranges of functions in Grundgesetze which in the Foreword Frege highlights as an essential step forward without which one would never be able to get by.
Initially, Hume’s Principle does not even enable us to decide whether, say, the number of planets is equal to 0. The situation changes when Frege comes to define “0” in terms of the cardinality operator (Frege, 1884, §74), after having explicitly defined the latter (§68). Thus, there was no need to quote the bizarre example of Julius Caesar in order to show that the cardinality operator, if it is governed by Hume’s Principle, is affected by referential indeterminacy. The Caesar problem which Frege raises in Grundlagen, §56 in connection with his tentative inductive definition of the finite cardinal numbers is, unlike its successor in §66, only spurious; see the arguments in Schirn (2003).
Once the second-level function-name “
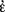 φ(ε)” is available in the formal language and we are entitled to apply the rule of insertion (cf. Frege, 1893, §30) as one of the two permissible modes of forming new names beginning with the formation of proper names from two primitive function-names, we may regard any term that results from the insertion of a monadic first-level function-name into the argument-place of “
φ(ε)” is available in the formal language and we are entitled to apply the rule of insertion (cf. Frege, 1893, §30) as one of the two permissible modes of forming new names beginning with the formation of proper names from two primitive function-names, we may regard any term that results from the insertion of a monadic first-level function-name into the argument-place of “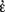 φ(ε)” as a canonical value-range name. Similarly, we may call equations in which the terms flanking “=” are both canonical value-range names canonical value-range equations. The other mode of formation is the extraction of function-names from more complex names by means of what I call gap formation (cf. Frege 1893, §26). Note that in Frege’s formal language monadic first-level function-names may also be formed, in the last step of their constructional history, by inserting a proper name into the argument-place of a dyadic first-level function-name (simple or complex).
φ(ε)” as a canonical value-range name. Similarly, we may call equations in which the terms flanking “=” are both canonical value-range names canonical value-range equations. The other mode of formation is the extraction of function-names from more complex names by means of what I call gap formation (cf. Frege 1893, §26). Note that in Frege’s formal language monadic first-level function-names may also be formed, in the last step of their constructional history, by inserting a proper name into the argument-place of a dyadic first-level function-name (simple or complex).On Grundgesetze, see the groundbreaking work in Ebert and Rossberg 2013, 2019 and Heck 2012. In the ideal case in which Frege succeeds in uniquely fixing the references of canonical value-range names, the Initial Stipulation may ensure the truth of Basic Law V only jointly with the twin stipulations, and, following his explicit strategy in Grundgesetze I, §10, in combination with the stipulations in §11–§12 as well, which in the relevant literature is almost entirely neglected. The stipulations in §11–§12 are standard elucidations of the last two primitive function-names of first level that Frege introduces in his system: the definite description operator (§11) and the name of the conditional function (§12). Thus, without the contribution that in his view these standard elucidations make to uniquely fixing the reference of the value-range operator—in addition to the reference-fixing contributions of the other stipulations concerning “
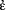 φ(ε)”—Frege could not have laid down Basic Law V. Note that by means of the elucidations of the definite description operator and the name of the conditional function Frege is able to kill two birds with one stone: “a determination of the value-ranges as well as of those functions” (Grundgesetze I, §10).
φ(ε)”—Frege could not have laid down Basic Law V. Note that by means of the elucidations of the definite description operator and the name of the conditional function Frege is able to kill two birds with one stone: “a determination of the value-ranges as well as of those functions” (Grundgesetze I, §10).In words: The number that belongs to the concept F is equal to the number that belongs to the concept G if and only if F and G are equinumerous. Frege defines the relation of equinumerosity in second-order logic in terms of one-to-one correlation (cf. Frege, 1884, §72). Note that the above formulation of Hume’s Principle is a schematic one; here its two sides are (closed) sentences, that is, “F” and “G” are schematic letters for monadic first-level predicates, not variables for first-level concepts. By contrast, in “∀F∀G(NxF(x) = NxG(x) ↔ Eqx(F(x),G(x)))” “F” and “G” are variables for first-level concepts; here we have the universal closure of the open sentence “NxF(x) = NxG(x) ↔ Eqx(F(x),G(x))”.
For more on infinitesimals and magnitudes in Frege, see Tappenden (2019).
The relation of coextensiveness on the right-hand side of Basic Law V holds generally between monadic first-level functions, including first-level concepts as special functions.
In their inspiring essay ‘Abstraction and Identity’, Cook and Ebert (2005) investigate what they call the C–R problem—which is a restricted version of Frege’s more general Julius Caesar problem. The C–R problem arises if we try to settle the truth-value of equations similar to those which I have just been discussing from a Fregean viewpoint in the context of Grundlagen. The authors refer to equations of the form “@1(P) = @2(Q)” as cross-sortal identity claims. The terms flanking “=” are supposed to have been introduced via two distinct abstraction principles. Cook and Ebert discuss two strategies that might enable us to resolve the C–R problem. The first strategy is designed to provide a means to determine the truth-value of “cross-abstraction identities in terms of whether or not the equivalence relations appearing on the right-hand side of the abstraction principles are identical, while the second strategy settles such identities by appeal to the relevant equivalence classes” (p. 121). For the sake of convenience, Cook and Ebert focus on mathematical structures which are simpler than the real and complex numbers structures. Regarding the second strategy, they offer three ways of carrying it out which, for reasons of space, I cannot consider here appropriately. In any event, Cook and Ebert argue, not least by endorsing a critical assessment of the equivalence-class-identification strategy for abstracts by Kit Fine (2002; see especially p. 47), that this strategy is doomed to failure since it leads to absurdities. Cook and Ebert conclude that the only promising option for solving the C–R problem is to develop formally the first strategy and to implement it accordingly. For an original discussion of the cross-sortal identity principle ECIA2 in Cook and Ebert (2005)—they label it Equivalence Class Identity Axiom 2, cf. p. 136: ECIA2: (X(X))(Y(X))@1(X) = @2(Y) (Z)(E@1(X,Z) E@2(Y,Z))—see Ebels-Duggan (2021). He renders ECIA2 slightly shorter as (X)(Y)(@1(X) = @2(Y) (Z)(E1(X, Z) E2(Y, Z))), in words: Abstracts of different kinds are identical if and only if the equivalence classes of their concepts are extensionally the same. Ebels-Duggan (2021) argues for a cross-sortal identity principle which embodies a structural criterion of cross-sortal identity: the structural similarity of abstracta. In his view, this new principle is at least as successful as ECIA2. For a fruitful discussion of Cook and Ebert (2005) see also Mancosu (2015, Sect. 7). I recommend the interested reader to study all these stimulating essays carefully.
Cf. the remarks in Schirn (2016, pp. 92–94).
The fact that the relation of equinumerosity between concepts F and G can be defined in second-order logic as the one-to-one correlation of the objects falling under F with those falling under G does not yet establish Hume’s Principle as an analytic truth. I take this to be Frege’s view in Grundlagen. Theoretically, there are just three cases in which he could or would regard Hume’s Principle as an analytic truth: (1) It is justifiably acknowledged as a primitive law of logic, that is, it is seen as meeting the basic contraints which Frege imposes on the acceptance of a sentence or judgeable content (thought) as a primitive logical law: truth, utmost generality, self-evidence (indubitability or incontestability), possession of significant cognitive value; (2) it has been assigned the status of a definition which accords with the principles of correct definitions. The latter must be recognized as analytic propositions as well, not only the primitive laws of logic and the definitions from which a truth is derived and in this way established as analytic; (3) Hume’s Principle has been proved purely logically from a primitive law of logic (or primitive laws of logic) and/or from a definition (or definitions). Provability or actual derivation from primitive laws of logic and definitions is Frege’s (incomplete) definition of “analytic” in Grundlagen, §3.
In Grundlagen, §68, Frege introduces extensions of concepts rather abruptly and spares himself the trouble of arguing for their assumed purely logical nature. Moreover, he refrains from stating explicitly a general criterion of identity, say, for extensions of second-level concepts on which he focuses in his enquiry. The criterion of equinumerosity governs only equivalence classes of equinumerosity. Note that in §68 Frege appeals to both extensions of first-level concepts (based on the equivalence relation of parallelism between straight lines) and extensions of second-level concepts (based on the relation of equinumerosity between first-level concepts). Yet it is almost only “second-order” equivalence classes which play a role in his logicist enterprise in Grundlagen. There is one exception, though. In Grundlagen, §83, Frege refers to the extension of a first-level concept which, in the light of the prior focus on equivalence classes of equinumerosity, emerges as a kind of lonely tree in the landscape of Fregean extensions. He must prove, he says, that the extension of the concept belonging to the natural number series ending with a, but not identical with a is the same as the extension of the concept belonging to the natural number series ending with d. No identity criterion for extensions of first-level concepts is provided. This issue is not even raised.
A few remarks on Frege’s attitude towards Cantor and Dedekind’s theories of real numbers may be in order. For reasons of space, I cannot comment on neo-logicist proposals to introduce the real numbers by means of abstraction principles, inspired by Frege and Dedekind’s approaches. In Grundgesetze II, Frege discusses at length the supposed definitional defects of Cantor’s theory of irrational numbers, but pays comparatively little attention to the underlying mathematical ideas of this theory. He comments much less on Dedekind’s theory of real numbers in Stetigkeit und irrationale Zahlen (Dedekind, 1872). The only thing which we learn in Grundgesetze II, §139 is that—endorsing mathematical platonism himself—Frege finds fault with Dedekind’s creation of irrational numbers by means of what I call “cut-generation”. Yet we learn virtually nothing about what Frege might have seen as one or the other affinity between Dedekind’s and his own mathematical approach to real analysis. In my view, amalgamating what might be considered the better half of Frege’s theory with what might be considered the better half of Dedekind’s would possibly have resulted in a mésalliance. In Grundgesetze, Frege does not comment on Dedekind’s creation of the natural numbers by means of what I call “structural abstraction” or “Dedekind-abstraction” in Was sind und was sollen die Zahlen? (Dedekind, 1888). Had Frege followed Dedekind in wedding abstraction to structure and had Dedekind reciprocated by abandoning his creative method of abstraction in favour of Frege’s (allegedly) non-creative abstractionism, they might have discovered more common ground in their foundational approaches. After all, Dedekind and Frege were united in the idea of providing a logical foundation of arithmetic. But they pursued the idea in significantly different ways; see in this connection Reck (2013a, 2013b, 2019), Shapiro (2000), and Schirn (forthcoming). I disregard here the inconsistency of Frege’s approach to real analysis. Boccuni and Panza (2022) rephrase Frege’s envisaged but inconsistent definition of real numbers in a consistent framework (dispensing with value-ranges) and investigate the question of whether the rephrased definition they offer supports a logicist view of real analysis. I recommend the study of this essay to all those who are interested in Frege’s logicist approach to real analysis.
Reading through Frege’s largely positive comments on the logical power of Basic Law V (in his pre-Paradox period), conceived of as the lynchpin of his logicist project, one could gain the impression that he saw the universe of value-ranges, developed by him into the finest branches of his system, as a kind of logical Cockaigne. Panza (2021) discusses the question of whether there are objects other than value-ranges in Frege’s logical universe.
I surmise that regarding a proper solution to the Caesar problem in Grundlagen, Frege knew his metes and bounds at that stage of his foundational project.
The exceptions are the definitions of 0 and 1 (cf. Grundgesetze I, §41 and §42).
In the proofs of Grundgesetze, reference to double value-ranges is slightly more frequent than reference to simple value-ranges. We probably cannot infer from this that for Frege’s logicist concerns double value-ranges play a more important role than simple value-ranges. However, in the definitions of Grundgesetze I and II the use of names of double value-ranges conspicuously prevails for reasons I shall not go into here. When in Grundgesetze II Frege comes to prove several theorems of his theory of magnitude, reference to value-ranges decreases almost continuously; it is strikingly less numerous than in his prior proofs of fundamental theorems of cardinal arithmetic. Leaving the part of a proof called “analysis” out of account and focusing on the part called “construction”, it is, as far as I see, only in §166, §172, §176, §228 and §230 where Frege refers to value-ranges outside of the context of a definition which he draws upon in the proof. Going through all the proofs in Grundgesetze I and II reveals why the distribution ratios of the reference to value-ranges are as they are. On the role of (simple and double) value-ranges in Frege’s formal system and, in particular, in his proofs of the basic laws of cardinal number see the enlightening analyses in Heck (2012). See also the careful discussion of the status of double value-ranges in Grundgesetze in Simons (2019).
As far as I can see, in the Grundgesetze-proofs Frege does not use equations in which “=” is flanked by names of double value-ranges. However, since such equations are well-formed, he could have used them if he had been convinced of their usefulness in carrying out certain proofs. (The equations might be called canonical value-range equations of type 2.) What Frege does use are equations of the form “(∫
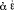 f(ε,α)) =
f(ε,α)) = 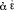 g(ε,α)”; see especially Grundgesetze I, §87. I use here the symbol “∫” for the designation of the converse of a relation instead of Frege’s special sign for that function-name which he defines in Grundgesetze I, §39. In Grundgesetze I, §87, Frege completes the proof of Theorem 71: The relation of a cardinal number to that immediately following it in the cardinal number series is single-valued. Theorem 89 says accordingly that the relation of a cardinal number to that immediately preceding it in the cardinal number series is single-valued. Frege proves Theorem 89 in §88–§95.
g(ε,α)”; see especially Grundgesetze I, §87. I use here the symbol “∫” for the designation of the converse of a relation instead of Frege’s special sign for that function-name which he defines in Grundgesetze I, §39. In Grundgesetze I, §87, Frege completes the proof of Theorem 71: The relation of a cardinal number to that immediately following it in the cardinal number series is single-valued. Theorem 89 says accordingly that the relation of a cardinal number to that immediately preceding it in the cardinal number series is single-valued. Frege proves Theorem 89 in §88–§95.Theorem 2 of Grundgesetze—f(a, b) = a ∩ (b ∩
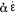 f(ε,α))—is the analogue of Theorem 1: f(a) = a ∩
f(ε,α))—is the analogue of Theorem 1: f(a) = a ∩ 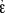 f(ε). Theorem 1 is Frege’s generalization of the comprehension principle of set theory. The theorem not only applies to first-level concepts and their extensions but more generally to monadic first-level functions and their value-ranges. Analogous remarks apply to Theorem 2.
f(ε). Theorem 1 is Frege’s generalization of the comprehension principle of set theory. The theorem not only applies to first-level concepts and their extensions but more generally to monadic first-level functions and their value-ranges. Analogous remarks apply to Theorem 2.According to Frege, this criterion emerges so to speak organically from the nature of the cardinal numbers, namely their counting function. For the sake of convenience, I use here “N” instead of Frege’s special concept-script sign or the designation of the first-level cardinality operator (see the definition in Grundgesetze I, §40). Unlike “
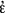 φ(ε)”, “Nξ” is not introduced as a primitive name via an informal stipulation in the form of an abstraction principle. As I said, “Nξ” is explicitly defined. The definition depends crucially on Basic Law V—and the previous definitions of the application operator (§34), the mapping-into by a relation (§38) and the converse of a relation (§39). These function-names are in turn defined by using either a name of a simple value-range (§34) or a name of a double value-range (§38 and §39) and, hence, their definitions likewise rest essentially on Basic Law V. (For a discussion of Grundgesetze I, §34–§40 see Panza 2021.) The term “N
φ(ε)”, “Nξ” is not introduced as a primitive name via an informal stipulation in the form of an abstraction principle. As I said, “Nξ” is explicitly defined. The definition depends crucially on Basic Law V—and the previous definitions of the application operator (§34), the mapping-into by a relation (§38) and the converse of a relation (§39). These function-names are in turn defined by using either a name of a simple value-range (§34) or a name of a double value-range (§38 and §39) and, hence, their definitions likewise rest essentially on Basic Law V. (For a discussion of Grundgesetze I, §34–§40 see Panza 2021.) The term “N Φ(ε)” combines two abstraction operators, although not in such a way that one fills the argument-place of the other. A direct combination of a second-level and a first-level abstraction operator is “
Φ(ε)” combines two abstraction operators, although not in such a way that one fills the argument-place of the other. A direct combination of a second-level and a first-level abstraction operator is “ (Nε)”. It is a well-formed value-range name. As to Frege’s use of equations of the form “N
(Nε)”. It is a well-formed value-range name. As to Frege’s use of equations of the form “N Φ(ε) = N
Φ(ε) = N Ψ(α)” in a proof, see, for example, Grundgesetze I, §87, §93. Equations of this form play an important role in Frege’s foundation of cardinal arithmetic while canonical value-range equations do not.
Ψ(α)” in a proof, see, for example, Grundgesetze I, §87, §93. Equations of this form play an important role in Frege’s foundation of cardinal arithmetic while canonical value-range equations do not.See in this connection May and Wehmeier (2019).
In the Preface to Grundgesetze (p. IX), Frege writes: “The reason why the implementation appears so late after the announcement is owing in part to internal changes within the concept-script which forced me to jettison a nearly completed handwritten work.”.
It is obvious that just as in the case of the cardinal numbers the Julius Caesar problem would only be pushed back to extensions of concepts instead of sorting it out. Towards the end of Grundlagen (§107), Frege observes that he attaches no decisive importance to drawing upon extensions of concepts at all. Taken at face value, this observation clashes with the foundational strategy carried out in Grundlagen. In any event, the observation remains rather vague since Frege leaves it unexplained. In my opinion, there are just two options regarding the idea of dispensing with extensions of concepts in pursuit of the logicist project which he might have had in mind: (a) identifying the cardinal numbers with objects other than extensions or, as I just mentioned, (b) resuming the tentative contextual definition of the cardinality operator and combining it with an additional stipulation without invoking extensions of concepts. In Schirn (2010, p. 49f). I argue that within the logical framework of Grundlagen option (a) would have had no chance of success. I further argue that from Frege’s perspective option (b) might have turned out to be promising. Regarding the potential additional stipulation in connection with the contextual definition of the cardinality operator, Frege would have had to make sure (i) that it does not rest on intuition or experience and (ii) that it is consistent with the definition. As to the dual stipulation in Grundgesetze, §10, with the help of which Frege intends to achieve (almost) referential uniqueness for value-range names, it does meet conditions (i) and (ii). It rests neither on intuition nor on experience. Furthermore, it is consistent with the Initial Stipulation, as Frege establishes by means of his permutation argument in §10.
For a new investigation of number-set identity in the light of the logicist reduction (identification) of numbers to (with) sets, see Ebels-Duggan (2022). The paper includes a critical discussion of Benacerraf’s multiple-reductions argument (in Benacerraf 1965) and Wright’s analysis of criteria of identity for cardinals and sets (in Wright 1983 and Hale and Wright 2001). See in this connection also Avron and Grabmayr (2022). The authors argue that there are metaphysically important reasons to prefer von Neuman ordinals over other set-theoretic reductions of arithmetic. Avron and Grabmayr’s presentation differs significantly from the philosophical assumptions made by Ebels-Duggan (2022). Those readers who are interested in reconsidering Benacerraf’s multiple-reductions argument from a new perspective may benefit from reading these essays in tandem.
The number 1 is obviously not given as a value-range by the numeral “1”. According to Frege’s initial argument in the second footnote to Grundgesetze I, §10, 1 could therefore be identified with its unit class. However, since Frege identifies cardinal numbers with equivalence classes of equinumerosity—for example, he defines 1 as the class of all classes equinumerous with
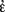 (ε = 0), that is, as
(ε = 0), that is, as 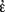 (ε ~
(ε ~ 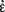 (ε = 0)), if, for the sake of simplicity, we use here “~” as the sign for the relation of equinumerosity between classes—he could not at the same time identify 1 with
(ε = 0)), if, for the sake of simplicity, we use here “~” as the sign for the relation of equinumerosity between classes—he could not at the same time identify 1 with 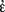 (ε = 1) (its unit class) without contradicting Basic Law V. For an extension of this argument see Schirn (2018, p. 259f., footnote 62).
(ε = 1) (its unit class) without contradicting Basic Law V. For an extension of this argument see Schirn (2018, p. 259f., footnote 62).
References
Avron, A., & Grabmayr, B. (2022). Breaking the tie: Benacerraf’s identification argument revisited. Philosophia Mathematica. https://doi.org/10.1093/philmat/nkac022
Benacerraf, P. (1965). What numbers could not be. The Philosophical Review, 74, 47–73.
Boccuni F., & Panza, M. (2022). Frege’s theory of real numbers: A consistent rendering. The Review of Symbolic Logic, 15, 624–667.
Boolos, G. (1987). The consistency of Frege’s foundations of arithmetic. In J. J. Thomson (Ed.), On being and saying. Essays for Richard Cartwright (pp. 3–20). The MIT Press.
Cook, R. T., & Ebert, P. A. (2005). Identity and abstraction. Dialectica, 59, 121–139.
Cook, R. T., & Ebert, P. A. (2016). Frege’s recipe. The Journal of Philosophy, 113, 309–345.
Dedekind, R. (1872). Stetigkeit und irrationale Zahlen. Friedr. Vieweg & Sohn.
Dedekind, R. (1888). Was sind und was sollen die Zahlen? Friedr. Vieweg & Sohn.
Ebels-Duggan, S. (2021). Identifying cardinal abstracts. Philosophical Studies, 178, 1603–1630.
Ebels-Duggan, S. (2022). On number-set identity: A study. Philosophia Mathematica, 30, 223–244.
Ebert P. A., & Rossberg M. (Trans. & Eds.). (2013). Basic laws of arithmetic. Derived using concept-script (Vols. I, II). Oxford University Press.
Ebert, P. A., & Rossberg, M. (Eds.). (2019). Essays on Frege’s basic laws of arithmetic. Oxford University Press.
Fine, K. (2002). The limits of abstraction. Oxford University Press.
Frege, G. (1884). Die Grundlagen der Arithmetik. Eine logisch mathematische Untersuchung über den Begriff der Zahl. W. Koebner.
Frege, G. (1893). Grundgesetze der Arithmetik. Begriffsschriftlich abgeleitet (vol. I). H. Pohle, Jena.
Frege, G. (1903). Grundgesetze der Arithmetik. Begriffsschriftlich abgeleitet (vol. II). H. Pohle, Jena.
Frege, G. (1967). Kleine Schriften. I. Angelelli, G. Olms, & Hildesheim (Ed.).
Frege, G. (1969). Nachgelassene Schriften. H. Hermes, F. Kambartel, F. Kaulbach, F. Meiner, & Hamburg (Eds.).
Frege, G. (1976). Wissenschaftlicher Briefwechsel. G. Gabriel, H. Hermes, F. Kambartel, C. Thiel, A. Veraart, F. Meiner, & Hamburg (Eds.).
Hale, B., & Wright, C. (2001). The Reason’s proper study. Oxford University Press.
Heck, R. K. (1997). The Julius Caesar objection. In R. K. Heck (Ed.), Language, thought and logic. Essays in honour of Michael Dummett (pp. 273–308). Clarendon Press.
Heck, R. G. (1999). Grundgesetze der Arithmetik I §10. Philosophia Mathematica, 7, 258–292.
Heck, R. K. (2012). Reading Frege’s Grundgesetze (pp. 497–537). Oxford University Press.
Heck, R. K. (2019). Formal arithmetic before Grundgesetze. In Ebert, & Rossberg (Eds.), Essays on Frege’s basic laws of arithmetic (pp. 497–537). Oxford University Press.
Mancosu, P. (2015). In good company. Hume’s principle and the assignment of numbers to infinite concepts. The Review of Symbolic Logic, 8, 370–410.
May, R., & Wehmeier, K. F. (2019). The proof of Hume’s principle. In Ebert, & Rossberg (Eds.), Essays on Frege’s basic laws of arithmetic (pp. 182–206). Oxford University Press.
Panza, M. (2021). ‘Anzahlen and Werthverläufe’. Are there objects other than value-ranges in Frege’s universe? An argument from Grundgesetze, §§34–40. In F. Boccuni & A. Sereni (Eds.), Origins and varieties of logicism. On the logico-philosophical foundations of mathematics. Routledge.
Reck, E. H. (2019). Frege’s relation to Dedekind. In Ebert, & Rossberg (Eds.), Essays on Frege’s basic laws of arithmetic (pp. 264–284). Oxford University Press.
Reck, E. H. (2013a). Frege or Dedekind? Towards a reevaluation of their legacies. In E. H. Reck (Ed.), The historical turn in analytic philosophy (pp. 139–170). Palgrave.
Reck, E. H. (2013b). Frege, Dedekind, and the origins of logicism. History and Philosophy of Logic, 34, 242–265.
Schirn, M. (2003). Fregean abstraction, referential indeterminacy and the logical foundations of arithmetic. Erkenntnis, 59, 203–232.
Schirn, M. (2010). On translating Frege’s Die Grundlagen der Arithmetik. History and Philosophy of Logic, 31, 47–72.
Schirn, M. (2016). On the nature, role and proof of Hume’s principle in Frege’s logicist project. In S. Costreie (Ed.), Early analytic philosophy. New perspectives on the tradition (pp. 49–96). Springer Nature.
Schirn, M. (2018). The semantics of value-range names and Frege’s proof of referentiality. The Review of Symbolic Logic, 11, 224–278.
Shapiro, S. (2000). Frege meets Dedekind. Notre Dame Journal of Formal Logic, 41, 335–364.
Simons, P. (2019). Double value-ranges. In Ebert, & Rossberg (Eds.), Essays on Frege’s basic laws of arithmetic (pp. 167–181). Oxford University Press.
Tappenden, J. (2019). Infinetesimals, magnitudes, and definitions in Frege. In Ebert, & Rossberg (Eds.), Essays on Frege’s basic laws of arithmetic (pp. 235–263). Oxford University Press.
Wehmeier, K. F. (1999). Consistent fragments of Grundgesetze and the existence of non-logical objects. Synthese, 121, 309–328.
Wright, C. (1983). Frege’s conception of numbers as objects. Aberdeen University Press.
Acknowledgements
My special thanks go to Daniel Mook for carefully reading the penultimate draft of this essay and providing some helpful suggestions. Many thanks are also due to the editor of Synthese, Otávio Bueno, for his effective help, advice and encouragement and his special interest in my work on Frege’s philosophy of mathematics. I also thank two anonymous referees for their apprecation of my paper and some useful suggestions. Last but not least, I thank Roopika Dhayanithy for her technical help in her capacity as JEO assistant for Synthese.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schirn, M. Frege on the introduction of real and complex numbers by abstraction and cross-sortal identity claims. Synthese 201, 193 (2023). https://doi.org/10.1007/s11229-023-04150-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04150-1



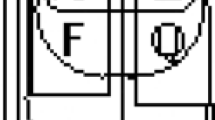

 Φ(ε) = N
Φ(ε) = N Ψ(α)” can straightforwardly be settled by appeal to Frege’s definition of the cardinality operator and Basic Law V. If “
Ψ(α)” can straightforwardly be settled by appeal to Frege’s definition of the cardinality operator and Basic Law V. If “ Φ(ε)” refers to an equivalence class of equinumerosity, the truth-value of “
Φ(ε)” refers to an equivalence class of equinumerosity, the truth-value of “ Φ(ε) = N
Φ(ε) = N Ψ(α)” could also be determined by appeal to Hume’s Principle: an embarassment of riches. However, Hume’s Principle is powerless to decide the truth-value of, for example, “
Ψ(α)” could also be determined by appeal to Hume’s Principle: an embarassment of riches. However, Hume’s Principle is powerless to decide the truth-value of, for example, “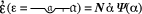 ”.
”.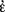 φ(ε)” is available in the formal language and we are entitled to apply the rule of insertion (cf. Frege,
φ(ε)” is available in the formal language and we are entitled to apply the rule of insertion (cf. Frege, 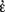 φ(ε)” as a canonical value-range name. Similarly, we may call equations in which the terms flanking “=” are both canonical value-range names canonical value-range equations. The other mode of formation is the extraction of function-names from more complex names by means of what I call gap formation (cf. Frege
φ(ε)” as a canonical value-range name. Similarly, we may call equations in which the terms flanking “=” are both canonical value-range names canonical value-range equations. The other mode of formation is the extraction of function-names from more complex names by means of what I call gap formation (cf. Frege 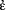 φ(ε)”—Frege could not have laid down Basic Law V. Note that by means of the elucidations of the definite description operator and the name of the conditional function Frege is able to kill two birds with one stone: “a determination of the value-ranges as well as of those functions” (Grundgesetze I, §10).
φ(ε)”—Frege could not have laid down Basic Law V. Note that by means of the elucidations of the definite description operator and the name of the conditional function Frege is able to kill two birds with one stone: “a determination of the value-ranges as well as of those functions” (Grundgesetze I, §10).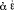 f(ε,α)) =
f(ε,α)) = 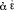 g(ε,α)”; see especially Grundgesetze I, §87. I use here the symbol “∫” for the designation of the converse of a relation instead of Frege’s special sign for that function-name which he defines in Grundgesetze I, §39. In Grundgesetze I, §87, Frege completes the proof of Theorem 71: The relation of a cardinal number to that immediately following it in the cardinal number series is single-valued. Theorem 89 says accordingly that the relation of a cardinal number to that immediately preceding it in the cardinal number series is single-valued. Frege proves Theorem 89 in §88–§95.
g(ε,α)”; see especially Grundgesetze I, §87. I use here the symbol “∫” for the designation of the converse of a relation instead of Frege’s special sign for that function-name which he defines in Grundgesetze I, §39. In Grundgesetze I, §87, Frege completes the proof of Theorem 71: The relation of a cardinal number to that immediately following it in the cardinal number series is single-valued. Theorem 89 says accordingly that the relation of a cardinal number to that immediately preceding it in the cardinal number series is single-valued. Frege proves Theorem 89 in §88–§95.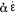 f(ε,α))—is the analogue of Theorem 1: f(a) = a ∩
f(ε,α))—is the analogue of Theorem 1: f(a) = a ∩ 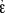 f(ε). Theorem 1 is Frege’s generalization of the comprehension principle of set theory. The theorem not only applies to first-level concepts and their extensions but more generally to monadic first-level functions and their value-ranges. Analogous remarks apply to Theorem 2.
f(ε). Theorem 1 is Frege’s generalization of the comprehension principle of set theory. The theorem not only applies to first-level concepts and their extensions but more generally to monadic first-level functions and their value-ranges. Analogous remarks apply to Theorem 2.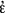 φ(ε)”, “Nξ” is not introduced as a primitive name via an informal stipulation in the form of an abstraction principle. As I said, “Nξ” is explicitly defined. The definition depends crucially on Basic Law V—and the previous definitions of the application operator (§34), the mapping-into by a relation (§38) and the converse of a relation (§39). These function-names are in turn defined by using either a name of a simple value-range (§34) or a name of a double value-range (§38 and §39) and, hence, their definitions likewise rest essentially on Basic Law V. (For a discussion of Grundgesetze I, §34–§40 see Panza
φ(ε)”, “Nξ” is not introduced as a primitive name via an informal stipulation in the form of an abstraction principle. As I said, “Nξ” is explicitly defined. The definition depends crucially on Basic Law V—and the previous definitions of the application operator (§34), the mapping-into by a relation (§38) and the converse of a relation (§39). These function-names are in turn defined by using either a name of a simple value-range (§34) or a name of a double value-range (§38 and §39) and, hence, their definitions likewise rest essentially on Basic Law V. (For a discussion of Grundgesetze I, §34–§40 see Panza  Φ(ε)” combines two abstraction operators, although not in such a way that one fills the argument-place of the other. A direct combination of a second-level and a first-level abstraction operator is “
Φ(ε)” combines two abstraction operators, although not in such a way that one fills the argument-place of the other. A direct combination of a second-level and a first-level abstraction operator is “ (Nε)”. It is a well-formed value-range name. As to Frege’s use of equations of the form “N
(Nε)”. It is a well-formed value-range name. As to Frege’s use of equations of the form “N Φ(ε) = N
Φ(ε) = N Ψ(α)” in a proof, see, for example, Grundgesetze I, §87, §93. Equations of this form play an important role in Frege’s foundation of cardinal arithmetic while canonical value-range equations do not.
Ψ(α)” in a proof, see, for example, Grundgesetze I, §87, §93. Equations of this form play an important role in Frege’s foundation of cardinal arithmetic while canonical value-range equations do not.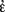 (ε = 0), that is, as
(ε = 0), that is, as 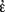 (ε ~
(ε ~ 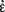 (ε = 0)), if, for the sake of simplicity, we use here “~” as the sign for the relation of equinumerosity between classes—he could not at the same time identify 1 with
(ε = 0)), if, for the sake of simplicity, we use here “~” as the sign for the relation of equinumerosity between classes—he could not at the same time identify 1 with 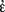 (ε = 1) (its unit class) without contradicting Basic Law V. For an extension of this argument see Schirn (
(ε = 1) (its unit class) without contradicting Basic Law V. For an extension of this argument see Schirn (