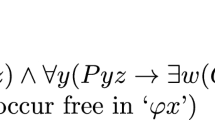Universalism and extensionalism revisited

Abstract

We present a new notion of mereological sum that is inequivalent to extant ones in the literature and does not fall prey to reasonable complaints that can be raised against some such notions. In light of this notion, we then revisit the relation between mereological universalism and extensionalism. In particular we argue that Varzi’s claim to the point that universalism entails extensionalism is justified only insofar as one sticks to Varzi’s notion of sum. In effect, we distinguish different versions of extensionalism and argue that universalism—when cashed out in terms of our new notion of sum—entails some versions but not others. Most significantly it does not entail extensionality of proper parthood. In the light of the above we set forth a new mereological system, Universalist Quasi-Supplemented Mereology, that can be considered a worthy alternative to different mereological systems in the literature.

1 Introduction

Mereological universalism (U) is the thesis that any plurality of entities has a fusion. It comes in different versions, depending on how the notion of fusion is characterized. Mereological extensionalism (E) is the thesis that composite entities having the same proper parts are identical. In this paper we address the relationship between U and E in light of a novel notion of sum that is not equivalent to extant ones in the literature. The attentive reader has probably noted that we just mentioned two notions, that of fusion, and that of sum. This is because, at this stage, we simply assume a distinction between a somewhat “intuitive notion” of fusion of a plurality of entities, and the various technical notions of sum that are introduced to capture it. Here is the plan. First, we introduce the debate on Universalism and Extensionalism (Sect. 2). We then put forward a notion of general sum that allows us to overcome a number of issues related to the problem of fusing pluralities of entities (Sect. 3). Finally, we show how this notion can be exploited to shed new light on the debate at hand (Sect. 4). The rest of this introduction is dedicated to setting the stage.

The debate on universalism and extensionalism focuses on two related questions:

• Q1: What notion of fusion is available to non-extensionalists;

• Q2: Whether, once a particular notion of fusion is adopted, U entails E.

In this respect, Varzi (2009) argues that, of the three notions of sum that are usually recognized in the literature, only one is sufficiently well-behaved so as to be used in the formulation of U. And, provided parthood obeys Transitivity and Supplementation, it turns out that U entails E.¹ Varzi’s argument has been challenged from two different perspectives. Cotnoir, in (2016), shows that, sticking to the notion of sum that Varzi uses, one can forgo the entailment from U to E, by changing the notion of proper parthood (specifically, by rejecting a basic principle like the antisymmetry of parthood). In addition, Cotnoir claims that this is in fact the only way to forgo such entailment. This is because, for the sake of argument, he grants Varzi that both Transitivity and Supplementation fix the meaning of the notion of parthood. As Varzi writes [p. 601]:

If one’s notion of parthood is so different from the standard notion as to violate either (1) [Transitivity] or (2) [Supplementation], then the meaning of (U) and (E) would change accordingly and the relationship between such theses might well be up for grabs.

By contrast, both Gilmore in (2009) and Loss in (forthcoming) suggest that replacing Supplementation with weaker principles is enough to undercut the entailment from U to E. As we will see shortly, what is crucial for our purposes is that since the foregoing accounts depend crucially on the endorsement of the very notion of sum that Varzi adopts, they are forced either (i) to abandon the idea that parthood is a partial ordering or (ii) to accept mereological models where sums present some peculiar features. Put differently, it seems to us that what Varzi has successfully shown is that, given a certain notion of sum, the only mereological systems where parthood is a partial ordering and sums do not present peculiar features are systems where U entails E. In the present paper we show that, by resorting to an alternative notion of sum, we can both preserve the standard account of parthood and avoid peculiar mereological models.² In doing so, we address the debate from a radically new perspective. In particular:

• (1) We put forward a new definition of sum that Varzi, Cotnoir and Loss do not consider, and argue it is immune from the complaints in Varzi (2009);

• (2) We distinguish different principles of extensionality, namely First Fusion Extensionality, Second Fusion Extensionality, and Proper Part Extensionality—the latter coinciding with E.³

• (3) We propose a new mereological system that does not include Supplementation but includes both Antisymmetry and U —thus being different from the extant ones in the literature;

• (4) Finally, drawing on (1)–(3), we provide two new answers to the questions Q1 and Q2 above. In particular we argue that there is a notion of sum available to anti-extensionalists, and that, given that notion, U entails only some principles of extensionality but not others.

In view of the above, we can indeed reassure Varzi that the relationship between U and E is not entirely up for grabs. In effect, that relationship is similar to the one he envisaged, and yet not identical to it. On top of that, we contend that the reassessment of the debate provided in this paper is not only important in and on itself. Indeed, we will also be able to amend problematic claims in Cotnoir (2016), and show that the notion of sum in Sect. 3 and the mereological system in Sect. 4 are worth discussing on independent grounds because of their philosophical significance. Let us first introduce the basic formal frameworks we will work with.

A two-sorted first-order logic is assumed, containing constants and variables for individual entities (lowercase letters) and plural entities, or pluralities (uppercase letters).⁴ The following notation is used throughout⁵

x : X:	primitive	(x is one of the X)
$a\le b$:	primitive	(a is a part of b)
$a\ll b$:	$a\le b\wedge a\ne b$	(a is a proper part of b)
$a\wr b$:	$a \nleq b \wedge b \nleq a$	(a is incomparable with b)
$X\le a$:	$\forall x(x:X\rightarrow x\le a)$	(all Xs are parts of a)
$X\ll a$:	$\forall x(x:X\rightarrow x\ll a)$	(all Xs are proper parts of a)
$a\circ b$:	$\exists x(x\le a\wedge x\le b)$	(a overlaps b)
$a\parallel b$:	$\lnot (a\circ b)$	(a is disjoint from b)
$a\circ X$:	$\exists x(x:X\wedge a\circ x)$	(a overlaps some of the Xs)
$a\parallel X$:	$\lnot (a\circ X)$	(a is separated from all the Xs)

There are three notions of sum that are routinely used in the mereological literature,⁶ and are exactly the ones Varzi considers in Varzi (2009):

Definition 1

Notions of sum and extensionality.

• 1. $Sum_{1}(a,X):=X\le a\wedge \forall x(x\le a\rightarrow x\circ X)$ a is a $Sum_{1}$ of the items in X if and only if all the items in X are parts of a and every part of a overlaps at least one item in X.⁷

• 2. $Sum_{2}(a,X):=\forall x(x\circ a\leftrightarrow x\circ X)$ a is a $Sum_{2}$ of the items in X if and only if a overlaps all and only the items that are overlapped by at least one item in X.⁸

• 3. $Sum_{3}(a,X):=X\le a\wedge \forall y(X\le y\rightarrow a\le y)$ a is a $Sum_{3}$ of the items in X if and only if all the items in X are parts of a and a is part of all the items all the items in X are parts of.⁹

Extensionality (E): $\exists x (x \ll a) \wedge \forall x (x \ll a \leftrightarrow x \ll s) \rightarrow a = s$.

E states that composite entities having the same proper parts are identical.¹⁰ Finally, we call Minimal Mereology, MM, the mereological system in which the notion of parthood is characterized merely as a partial ordering, i.e., as a reflexive, transitive and antisymmetric relation.

2 The debate

In Varzi (2009) Varzi shows that U entails E in Supplemented Mereology, SM, which is minimal mereology plus Supplementation.

Supplementation (SP): $x\ll s \rightarrow \exists y(y\le s \wedge y\parallel x)$.

Since U can be formulated differently using different notions of sum, one obtains various universalist axioms by plugging in such notions in the following schema¹¹

• Universalism$_i$ (U$_i$): $\exists x (x: X) \rightarrow \exists s (Sum_i (s, X))$.

What Varzi shows is then that U$_1$ entails E. Let us see how.

2.1 From universalism to extensionalism

In SM + U$_1$ (the system obtained by adding axiom U$_1$ to SM), we can prove the so called Proper Part Principle (PPP), to the point that any composite entity having as proper parts the proper parts of a has a as part. And PPP ensures extensionality.¹²

• Proper Part Principle (PPP): $\exists x (x \ll a) \wedge \forall x (x \ll a \rightarrow x \ll s) \rightarrow a \le s$.

Proposition 1

PPP is provable in SM + U$_1$

Proof

By contraposition. Suppose a is composite, and $a \nleq s$. Then $s\ll a+s$, which is guaranteed to exist given U$_1$. So, for some x, $x\le a+s$ and $x\parallel s$, by SP. Thus, $x\circ a$, since $x\parallel s$, so that a, being composite, has some proper part that is not a proper part of s, which proves the conclusion. $\square$

Proposition 1 establishes that, provided SM is assumed, anyone who accepts U$_1$—and thus $Sum_1$ as the basic notion of fusion— is forced to accept extensionality, and therefore the full Classical Extensional Mereology.

2.2 Problems with weaker decomposition principles

It is important to note that having $Sum_1$ as a basic notion of fusion provides justification for accepting a supplementation principle like SP. To be sure, consider the weaker decomposition principles discussed in the literature:

• Company (C):

•       $a \ll b \rightarrow \exists x(x\ll b\wedge a\ne x)$

• Strong Company (SC):

•       $a \ll b \rightarrow \exists x(x\ll b\wedge a\nleq x)$

• Quasi Supplementation (QS):

•       $a \ll b \rightarrow \exists x \exists y(x\le b\wedge y\le b\wedge x\parallel y)$

• Minimal Supplementation (MS):

•       $a \ll b \rightarrow \exists x (x \le b \wedge x \wr a \wedge \exists y \exists z (y \le a \wedge z \le x \wedge y \parallel z))$

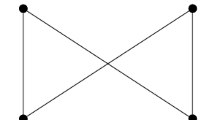
In plain English, C requires that any composite object has at least two proper parts; SC requires that any object having a part has another part that is not part of the first one; QS requires that any composite object has at least two disjoint proper parts; finally, MS requires that if something has a proper part it has another part that is incomparable with the first and such that some of their parts are separated. The last two principles are the ones that have been suggested in the literature as potential replacement for Supplementation in order to resist Varzi’s argument.¹³ At the present stage of the dialectic we need simply note that they are too weak to exclude the following models:

As we can see, Model 1a satisfies both C and QS, while Model 1b satisfies all the principles we have introduced. Still, in these models x, $s_1$ and $s_2$ are all $Sum_1$ of all the entities that are below x—where “below” tracks the order induced by the proper parthood relation. This is the peculiar feature that strikes us as problematic: two things that stand in the proper parthood relation count as sums of the same entities. Indeed, we find natural to say that, if x is a sum of some items neither a proper part of x nor a proper extension of x should count as a sum of the same items.

Summing up what we take to be the two most important consequences of the discussion so far, we have that:

• 1. If the notion of fusion is appropriately captured by $Sum_1$, then we are justified in accepting a system of Supplemented Mereology, given that decomposition principles weaker than SP do not rule out models in which $Sum_1$ behaves problematically.

• 2. If, in addition, we endorse Universalism—in its U$_1$ variant— then we are justified in accepting Classical Extensional Mereology, given that in Supplemented Mereology, U$_1$ entails E.

Hence, accepting Universalism forces us into the following dilemma¹⁴: either accept the full strength of Classical Extensional Mereology or reject the assumption that the notion of fusion is appropriately captured by $Sum_1$. However, as we will see shortly, this second horn seems to be precluded.

2.3 From fusion to $Sum_1$

As we mentioned, one can be tempted to get out of the dilemma by rejecting $Sum_1$ as an appropriate characterization of fusion. We want to argue that, at the end of the day, this is not a viable option, provided one only focus on the alternative notions of sum proposed in Sect. 1. To do this, let us first define a relation of equivalence between pluralities.

Definition 2

$X_1 \equiv X_2:= \forall x(x\parallel X_1 \leftrightarrow x\parallel X_2)$.

Two pluralities are equivalent just in case they are disjoint from the same entities. This notion of equivalence is introduced to capture the specific connection that exists between two pluralities that intuitively amount the “same portion of reality”—to use Lewis’s suggestive phrase—.¹⁵ like the plurality of all cats and the plurality of the cells of the cats. The basic idea is that these two pluralities are equivalent because what overlaps a cat also overlaps some of its cells and vice-versa. So that what is disjoint from all the cats is also disjoint from all of their cells and vice-versa. It is important to note that the two pluralities—given orthodox assumptions about plural logic, e.g. the standard Plural Comprehension Principle—are not identical, and yet are, in a crucial sense, identically related so to speak, to the same portion of reality.

Armed with this, we can now distinguish different kinds of extensionalism (here Fusion stands for the intuitive notion of fusion that needs to be rigorously framed via different kinds of $Sum_i$, such as the ones proposed in Sect. 1).

• First Fusion Extensionality (FE1):

•       $Fusion(s_1,X)\wedge Fusion(s_2,X)\rightarrow s_1 = s_2$.

• Pluralities have unique fusions. This principle gives us a first desideratum on the conditions a fusion has to satisfy, since it excludes that fusing the same portion of reality might produce different entities.

• Second Fusion Extensionality (FE2):

•       $Fusion(s,X_1)\wedge Fusion(s,X_2)\rightarrow X_1 \equiv X_2$.

• Pluralities with the same fusion are equivalent. This principle gives us a second desideratum on the conditions a fusion has to satisfy, since it excludes that fusing different portions of reality might produce the same entity.

• Proper Part Extensionality (E):

•       $\exists x (x \ll s_1) \wedge \forall x (x \ll s_1 \leftrightarrow x \ll s_2) \rightarrow s_1 = s_2$.

• This is the principle introduced before. It is not uncontroversial as a desideratum, but can be justified by FE1 if one requires that any entity is identical with the fusion of its proper parts.

We will now argue that both $Sum_2$ and $Sum_3$ are controversial as regimentations of the notion of fusion, due to the fact that they do not satisfy the first two desiderata. Indeed, the following propositions are now provable.

Proposition 2

In SM + U$_1$, $Sum_1$ satisfies FE1.

Hence, $Sum_1(s_1,X)\wedge Sum_1(s_2,X)\rightarrow s_1 = s_2$.

Proof

Let s be the $Sum_1$ of $s_1$ and $s_2$, which exists by U$_1$. Suppose $s_i\ne s$, where $i=1,2$. Since $s_i\le s$, by the definition of U$_1$, we have $s_i\ll s$. Thus, $x\le s$ and $x\parallel s_i$, for some x, by SP. Still $x\le s$ implies $x\circ s_i$, for all x, again by the definition of U$_1$. Therefore, $s_i= s$, where $i=1,2$, and so $s_1=s_2$. $\square$

Proposition 3

In SM + U$_1$, $Sum_1$ satisfies FE2.

Hence, $Sum_1(s,X_1)\wedge Sum_1(s,X_2)\rightarrow X_1 \equiv X_2$.

Proof

Suppose $X_1 \not \equiv X_2$. Then, by the definition of $\equiv$, there is some x such that either $x\circ X_1$ and $x\parallel X_2$ or $x\parallel X_1$ and $x\circ X_2$. Without loss of generality, suppose the first. Since $x\circ X_1$, x has a part that is part of one of the $X_1$, and so it has a part that is part of s, by the transitivity of $\le$ and $Sum_1(s,X_1)$. Since $x\parallel X_2$, all the parts of x are disjoint from $X_2$, and so no part of x is part of s, by the definition of $Sum_1$, contradicting $Sum_1(s,X_2)$. $\square$

Proposition 4

In SM + U$_2$, $Sum_2$ satisfies FE2.

Proof

Straightforward, by the definition of $Sum_2$. $\square$

Proposition 5

In SM + U$_2$, $Sum_2$ does not satisfy FE1.

Hence, it is possible that $Sum_2(s_1,X)\wedge Sum_2(s_2,X)\wedge s_1 \ne s_2$.

Proof

Consider the following model

This model is supplemented, since every entity having a proper part x has another proper part that is disjoint from x. Furthermore, every plurality has a $Sum_2$, since $s_1$ and $s_2$ are $Sum_2$ of any plurality. Finally, $s_1$ and $s_2$ are distinct $Sum_2$ of the same plurality, namely $X = \{a_1, a_2\}$. $\square$

Proposition 6

In SM + U$_3$, $Sum_3$ satisfies FE1.

Proof

Straightforward, by the definition of $Sum_3$. $\square$

Proposition 7

In SM + U$_3$, $Sum_3$ does not satisfy FE2.

Hence, it is possible that $Sum_3(s,X_1)\wedge Sum_3(s,X_2)\wedge X_1 \not \equiv X_2$.

Proof

Consider the following model

This model is supplemented, since every entity having a proper part x has another proper part that is disjoint from x. Furthermore, every plurality has a $Sum_3$, since s is a $Sum_3$ of any plurality. Finally, s counts as a $Sum_3$ of at least two inequivalent pluralities, namely $X_1 = \{a_1, a_2\}$ and $X_2 = \{a_2, a_3\}$. $\square$

The foregoing propositions show that $Sum_2$ and $Sum_3$ have serious drawbacks. As to $Sum_2$, Model 1a shows that it is possible for a $Sum_2$ to not contain as parts some of the summands. Furthermore, it shows that it is possible for a $Sum_2$ to have none of the summands as parts, since $s_1$ counts as a $Sum_2$ of $s_2$, which seems problematic,¹⁶ Similarly, Model 2b shows that a $Sum_3$ can have parts that are disjoint from its summands, since s counts as a $Sum_3$ of $a_1, a_2$, and yet x has a part, $a_3$, disjoint from both, which seems again problematic,¹⁷

Where are we? We have seen that, among the three usual definitions of sums, only $Sum_1$ seems to be acceptable when we work in a framework like SM + U$_i$.¹⁸ Unfortunately, $Sum_1$ is the worst posssible notion for non-extensionalists, since it entails the full extensionalist package—by Proposition 1-2-3. What can anti-extensionalists do?

Let us take a new look at the lay of the land. The argument for extensionalism rests on three tenets:

• (i) The acceptance of SM;

• (ii) The acceptance of U$_1$;

• (iii) A crucial argument to the point that $Sum_1$ is the only well-behaved notion, so that it is the only notion to be used in the formulation of U.

Hence, provided we buy into the partial ordering axioms for parthood, it seems we do end up with full-blooded Classical Extensional Mereology. Is that the last word?

Not necessarily. Or at least this is what we think. We already argued that, in mereologies that are weaker than SM, $Sum_1$ suffers from drawbacks akin to the ones $Sum_2$ and $Sum_3$ face—this was the gist of our argument from Models 1a and 1b in Sect. 2.1 to the point that it is problematic that two entities related by proper parthood count as sum of the same entities. We think we should consider such drawbacks seriously—at least as seriously as we considered the drawbacks of $Sum_2$ and $Sum_3$. By parity of reasoning, provided SP is not assumed, it seems that $Sum_1$ is unsatisfactory as well. But if we drop $Sum_1$, we are not really doing the anti-extensionalist any favor. In effect, we simply deprived everyone of any usueful notion of Sum, together with the possibility of formulating a thesis like U. And so we are left in the dark. But there’s a glimmer of light in the corner, a glimmer we did not see because we were just staring into the darkness. If we go look in that corner we’ll find a new notion of Sum which, maybe, can be of help.¹⁹

3 A novel notion of Sum

The new notion of Sum that was waiting for us in the corner is the following—we will call it General Sum:

Definition 3

General Sum. $Sum(a,X):=X\le a\wedge \forall x(x\parallel X\rightarrow x\parallel a)\wedge \forall y(X\le y\rightarrow a\le y)$

In plain English, a is the.²⁰Sum of the items in X if and only if (i) all the Xs are parts of a, (ii) a is separated from any thing which is separated from all the Xs, and (iii) a is part of any thing which has all the Xs as parts. Thus, our notion of Sum is simply the conjunction of three different requirements that one can impose on a notion of sum. The first requirement has it that the sum is inclusive enough to have all the things it is a sum of as parts. The second one requires that such a sum is not too inclusive, that is, does not admit as parts things that do not even overlap any of the things it is a sum of. According to the third and final requirement a sum is included in everything that includes the things it is the sum of. We do not want to defend our notion of Sum here.²¹ We just want to address the consequences of adopting such a notion for the debate on Universalism and Extensionalism. Before we do that we need to argue in favor of two related, yet separate claims. First, Sum is stronger than any $Sum_i$, if no strong decomposition principle is assumed. Second, Sum is immune to the complaints raised by both Varzi and us in Sect. 2.

To see that Sum is in general stronger than any $Sum_i$ we argue as follows.

Proposition 8

If Sum(a, X), then $Sum_i(a,X)$, for $i=1,2,3$.

First, note that $\forall x(x\parallel X\rightarrow x\parallel a)$ entails $\forall x(x\circ a\rightarrow x\circ X)$, by contraposition, and so $\forall x(x\le a\rightarrow x\circ X)$, given that every part of a overlaps a. Furthermore, note that $X\le a$ entails $\forall x(x\circ X\rightarrow x\circ a)$, given that every entity that overlaps one of the X also overlaps anything having the X as parts. So, suppose that Sum(a, X). Since $X\le a$ and $\forall x(x\parallel X\rightarrow x\parallel a)$, being a Sum entails both being a $Sum_1$ and being a $Sum_2$. Since $X\le a$ and $\forall y(X\le y\rightarrow a\le y)$, being a Sum also entails being a $Sum_3$.

Proposition 9

It is possible for something to be a $Sum_i$, for $i=1,2,3$, without being a Sum.

Consider again Models 2a and 2b:

It is not difficult to see that in these models $s_1$ is a $Sum_1$ and a $Sum_2$ of $a_1$ and $a_2$ respectively, while s is a $Sum_3$ of $a_1$ and $a_2$. By contrast, neither $s_1$ nor s is a Sum of those pluralities. This establishes that Sum is indeed stronger than any $Sum_i$.

We can conclude that Sum is not subject to the aforementioned, reasonable complaints by Varzi and us. Let us unpack this last statement. In Model 1a, $s_1$ and x are both $Sum_1$ of $a_1$ and $a_2$, and yet at most one should be, given that they are proper-parthood related. In Model 2a, $s_1$ is a $Sum_2$ of $s_2$, and yet it should not be, given that $s_2$ is not part of $s_1$. In Model 2b, s is a $Sum_3$ of $a_1$ and $a_2$, and again it should not be, given that s has also $a_3$ as part. Sum is not subject to any of these complaints. In effect, neither $s_1$ nor s qualify as a Sum of the relevant entities. If so, we contend, we should consider what work Sum can do—if any—for anti-extensionalists. It is to this that we now turn to.

4 Quasi supplemented universalist mereology

Now that we have a robust, complaint-free notion of sum we are finally able to re-evaluate the relationship between U and E. Let us first highlight how having a new notion of sum allows us to break the chain of arguments leading from U to E. We saw that the notion of $Sum_1$ supports the choice of SP as an acceptable decomposition principle. This is because weaker principles admit of models that we would like to exclude, in that $Sum_1$ is not well-behaved in those models. However, since we are no longer forced to stick to $Sum_1$, we are now free to select a decomposition principle which is weaker than SP and still powerful enough to prevent undesired consequences. In fact, it is not difficult to check that, in Models 1a and 1b, no entity above x counts as a Sum of any plurality of entities below x. Let us spend a few more words on the general dialectic here. The argument in Sect. 2.1 was that decomposition principles as strong as SP are required to rule out Models 1a and 1b because in these models $Sum_1$ is not well-behaved. Our claim is that Sum on the other hand is well behaved in those models. So there is no reason to rule them out.²² And this opens the possibility to accept weaker decomposition principles. Note that, from a more general perspective, this is also in line with different developments in the mereological literature that questioned Supplementation on independent grounds.²³

This already marks a significant difference with some other proposals in the literature. As we are going to see, Gilmore suggested in (2009) to replace Supplementation with Quasi Supplementation, and we will adopt the same strategy. Yet, the difference in the resulting systems is important, since we crucially rely on a stronger notion of sum. It is precisely this fact that allows us to avoid the problematic consequences of Models 1a and 1b that Quasi Supplementation is not strong enough to rule out. By contrast, Gilmore still uses $Sum_1$, which entails that (i) he cannot use the argument we put forward, and (ii) he is committed to the problematic consequences derived from accepting those models. A similar argument—mutatis mutandis—applies for Loss’s system in (forthcoming). This, we contend, is reason enough to explore thoroughly the alternative mereological system we are about to set forth. Indeed, we can go a step further and prove that these systems are also different with respect to the extensionality principles they entail, a fact that is plainly most relevant in the context at hand.

In the light of the above, let us consider the mereological system that consists of the following axioms²⁴:

• Transitivity: $x \le y \wedge y \le z \rightarrow x \le z$

• Anti-Symmetry: $x \le y \wedge y \le x \rightarrow x = y$

• Quasi-Supplementation: $x \ll y \rightarrow \exists z \exists w (z \le y \wedge w \le y \wedge z \parallel w)$

Importantly, all the models we used so far are models of such mereological system. Let us now add U, using Sum:

• Universalism $\exists x (x: X) \rightarrow \exists s (Sum (s, X))$

This system, call it Quasi Supplemented Universalist Mereology (QSUM), has never been considered in the debate.

4.1 Comparison with existing systems

There are, in fact, significant differences distinguishing it from explored systems. First, Cotnoir insists that we should drop Antisymmetry. By contrast we retain it. Second, both Varzi and Cotnoir retain Supplementation, whereas we focus on the weaker Quasi Supplementation. Third, Loss suggests to replace Supplementation with Minimal Supplementation whereas we suggested to replace it with Quasi Supplementation instead. Finally, Cotnoir, Varzi, Gilmore and Loss all use $Sum_1$ in their formulation of U, whereas we use Sum instead.

Both the systems proposed by Gilmore and the system proposed by Loss are similar to the one we put forward, in that they maintain antisymmetry. Still, we claim that QSUM should be preferred to them. The main reason is that QSUM allows us to prove that our notion of sum satisfies the basic desiderata on the notion of fusion introduced above, thus avoiding the complaints we raised against $Sum_1$—more on this shortly.

On Gilmore’s system Let Quasi-Supplemented Mereology, QSM, be the system obtained by adding Quasi-Supplementation to minimal mereology. In (Forthcoming) Gilmore introduces a system which is equivalent to QSM + U$_{1}$ and shows that E is not derivable in it. Still, QSM + U$_{1}$ falls short of satisfying our desiderata, since it does not exclude models where the same entities give rise to different sums, i.e., it does not satisfy FE1. Let us show this.

Proposition 10

In QSM + U$_{1}$, $Sum_{1}$ does not satisfy FE1.

Proof

Consider this model

Model 3a is quasi-supplemented: every composite entity has disjoint proper parts. It also satisfies U$_{1}$, for every plurality has a $Sum_{1}$. In fact, $s_{2}$ is a $Sum_{1}$ of any plurality. However, both $s_{1}$ and $s_{2}$ are $Sum_{1}$ of $\{a_{1},a_{2}\}$. Hence, the model does not satisfy FE1. $\square$

On Loss’ system Let Minimally Supplemented Mereology, MSM), be the system obtained by adding Minimal Supplementation to minimal mereology. Then, Loss endorses a system which is equivalent to MSM + U$_{1}$. The following is provable:

Proposition 11

In MSM + U$_{1}$, $Sum_{1}$ does not satisfy FE1.

Proof

Consider this model.

Model 3b is minimally supplemented. It also satisfies U$_{1}$, for every plurality has a $Sum_1$. In fact, a is a $Sum_1$ of every plurality. However both $b_1$ and a are $Sum_1$ of $\{c_1, c_2\}$. Hence the model does not satisfy FE1. $\square$

In what follows we show that, by contrast, FE1 is derivable in QSUM. Note that this is exactly the reason why Sum does not fall prey to the arguments against $Sum_1$. It is not possible for a given plurality to have distinct Sum-s, let alone distinct Sum-s that are related by proper parthood—as it happens with $Sum_1$.²⁵

4.2 Strength of QSUM

We are going to show that FE1 is derivable in QSUM. More generally, the key point is that QSUM is both universalist, having U among its axioms, and strong enough to derive both FE1 and FE2.

As we pointed out in Sect. 2.2, we want to distinguish three different versions of extensionalism, namely:

• FE1: Things that are Sum of the same plurality are identical;

• FE2: Pluralities that have the same Sum are equivalent;

• E: Composite things that have exactly the same proper parts are identical.

To shed light on the entailments from U to any of these variants, let’s have a look at the following model, where r is Romeo, j is Juliet, L is the relation of loving, [L(r, j)] is the state of affairs that Romeo loves Juliet, [L(j, r)] is the state of affairs that Juliet loves Romeo, and $+$ is the operation of binary sum²⁶:

This model of QSUM is interesting not only for clarifying the connection of U and E, but also for advancing at least one application of the present system, thus showing its significance to the current debate on the metaphysical structure of the world—in this case for capturing the relations involved in a world of states of affairs without introducing non-mereological notions.

This should not be underestimated. It will open the possibility of endorsing mereological monism—roughly the thesis that there is but one notion of composition, namely mereological composition—and still accept the existence of states of affairs—that were supposed to provide alleged counterexamples to such a metaphysical thesis.²⁷

Upon inspection, it is plain that E fails, as there are distinct things in the model with the same proper parts, namely [L(r, j)] and [L(j, r)]. By contrast, QSUM has FE1 and FE2 as theorems, since they both follow from the definition of Sum and Antisymmetry alone. It is instructive to see that this is in fact the case. We restrict ourselves here to FE1 and leave the proof of FE2 to the reader.

Proposition 12

FE1 is provable in QSUM

Proof

Assume the antecedent of FE1, that is $Sum (s_1, X)$ and $Sum (s_2, X)$. Then, $X \le s_1$, and $X \le s_2$, by the definition of Sum. Thus, $s_1\le s_2$ and $s_2 \le s_1$, again by the definition of Sum, and so $s_1 = s_2$, by Antisymmetry. $\square$

In light of this, we can now provide new, detailed answers to the questions Q1 and Q2 about the relationship between U and E in the present context.

• Answer to Q1. If non-extensionalists rest content with the failure of E, then the notion of Sum will suit their purposes;

• Answer to Q2. If Sum is used in the formulation of U, then U still entails FE1, and FE2, but does not entail E.

One might be skeptical about one detail of our answer to Q2. There, we seem to suggest that it is really U that does the heavy lifting in deriving E. But the proof of Proposition 12 clearly shows this is not the case. Sum and Antisymmetry alone are more than capable of doing the job. This is correct, but clearly does not detract from our argument. On top of this, U can be used crucially to derive another extensionalist principle, Universal Unique Fusion:

• Universal Unique Fusion (UUF): $\exists x: X \rightarrow \exists ! s (Sum (s, X))$

Note that UUF is strikingly similar to Tarski’s axiom of Unrestricted Unique Fusion in his axiomatization of Classical Mereology.²⁸ It is easy to see that:

Proposition 13

UUF is provable in QSUM

Proof

By U any non empty plurality has a Sum. By FE1 such a Sum is unique. $\square$

It is now clear that this time it is indeed U that does the heavy lifting. However, having changed the notion of sum in U is still crucial. Indeed, Tarski’s axiom, being formulated in terms of $Sum_1$, is strong enough, given Transitivity, to derive all the principles characterizing Classical Extensional Mereology, whereas our axiom is consistent with rejecting E.

Let us now highlight a crucial consequence of the previous discussion. We have focused on different mereological systems that accept at least MM, that is, systems that endorse the partial ordering axioms for parthood, namely CEM, defended in Varzi (2009), QSM + U$_1$, defended in Gilmore (2009), MSM + U$_1$, defended in Loss (Forthcoming), and the one we just suggested as a worthy alternative, that is, QSUM. We can now classify these three mereological systems with respect to the extensionality principles we distinguished. The result is summed up in Table 1 below:

Table 1 Mereological sytems and extensionality principles

Before concluding the section, we want to use what has been established so far to respond to a problematic claim by Cotnoir in (2016). Cotnoir writes:

[H]ere is a quite general result: if parthood is a partial order, then any model in which a F”-type fusion [our $Sum_3$] is unrestricted simply cannot have a counterexample to extensionality. Why? Because in the presence of the partial order axioms, particularly antisymmetry,²⁹ F”-type fusions guarantees the existence of a least upper bound. These must be unique (Cotnoir, 2016, p. 123).

So far so good. But immediately before he wrote:

[E]xtensionality states that composed objects with the same proper parts are identical (Cotnoir, 2016, p. 122).

We can now see that, given that definition of extensionality, the conclusion drawn by Cotnoir does not follow, since there are systems of mereology that feature U among their axioms, that is the universalist thesis in terms of Sum, but not E among their theorems. This notwithstanding, we still have that U entails both FE1 and FE2. Thus, it seems that the two passages above do not sharply distinguish between E and FE1. By making such distinction, we are in a position to claim that there is a sense in which any system obtained by adding U to Minimal Mereology is extensional, in that it at least provides extensionality of fusions.

5 Conclusion

Let us take stock. We have introduced a novel notion of sum and used it to provide a better understanding of the relation between U and E. First, we have noted that the argument from U to E is strongly supported in a framework where $Sum_1$ is the only acceptable notion of sum among the available ones. In fact, accepting $Sum_1$ justifies the assumption of SP as an appropriate decomposition principle. And, working in a system of supplemented mereology, like SM, allows us to prove that U entails E. Second, we have introduced different extensionality theses and highlighted that the main drawbacks concerning alternative conceptions of fusion do not stem from violations of E, but rather, from violations of FE1 and FE2. Third, we have casted doubts on the acceptability of $Sum_1$ in a framework where SP is not assumed, since in such a framework we are not able to exclude some models that admit of sums that strike us as problematic, especially in light of some basic desiderata on the notion of fusion. Finally, we have advanced a new notion of sum not suffering from the problems afflicting $Sum_1$ and proved that this notion enables us to accept decomposition principles that are weaker than SP. Having done that, we think we have brought the debate on the connection between U and E back to its pure form: either to accept SP, thus buying the full package of Classical Extensional Mereology, or to reject SP in favor of principles like QSP, thus allowing for mereologies where it is possible for diverse entities to be composed of the same elements. The main result in this respect is that system QSUM, obtained by enriching minimal mereology—the mereological system comprising only the partial ordering axioms for parthood—via QSP and universalism of Sum, is powerful enough to discard all the problematic models we encountered, while preserving at the same time FE1 and FE2, thus granting us the largest amount of extensionality consistent with the rejection of E. More than that, QSUM enables us to describe interesting and independently motivated structures in mereological terms, like the structure of states of affairs or of similar structured wholes, thus opening a fascinating and virtually unexplored line of research.