1 Introduction

Classical mereology holds that any collection of things composes exactly one thing. It is a controversial theory but I will say nothing here in its defense. Instead, I want to discuss the following conditional: suppose classical mereology is correct, does that mean every object has a unique location? (Of course, the question tacitly assumes that we also have a stock of plausible principles linking parthood to location.) The question has been asked before by Claudio Calosi (2014) who argues extensively for an affirmative answer: given plausible background assumptions classical mereology is incompatible with multilocated objects; and, he adds, even if we drop some of these background assumptions, the combination ‘is highly problematic at best’ (2014, 132). Calosi thinks that the extensional character of classical mereology is to blame, a non-extensional mereology would fare better with multilocation.

If Calosi is right, this has far-reaching consequences because various theories entail multilocation. For example, many forms of endurantism are committed to multilocation (Beebee and Rush 2003; Gilmore 2006; Hansson Wahlberg 2009; Hawthorne 2008; McDaniel 2003), and some perdurantists also think multilocation is at least sometimes possible (Hudson 2001). Other examples include certain theories of universals (Paul 2006) and of musical works (Tillman 2011). If extensional mereologies such as classical mereology are a hostile environment for multilocated entities, then these theories should be combined with a non-extensional mereology when theorising about the part–whole structure of those multilocated entities.

But extensional mereologies are a lot more tolerant than Calosi suggests. In particular, if we assume classical mereology and all the background principles that Calosi takes on board, there is still room for multilocation. Moreover, nothing about this combination is problematic—unless, of course, one already finds one part of the combination problematic. So the question of mereological extensionality has no bearing on the way in which a multilocationist should respond to certain multilocation scenarios.

Indeed, Calosi’s argument is but one of many arguments about the (in)compatibility of multilocation with various mereological principles such as Transitivity, Weak Supplementation, Asymmetry of Proper Parthood, and the Irreflexivity of Proper Parthood. (See, for example, Barker and Dowe 2003; Beebee and Rush 2003; Daniels 2014; Donnelly 2010; Eagle 2016; Effingham and Robson 2007; Effingham 2010; Gilmore 2009; Kearns 2011; Kleinschmidt 2011; McDaniel 2003). All these principles are theorems of classical mereology. By showing that classical mereology is compatible with multilocation even when substantial assumptions are made about the interplay between parthood and location, the paper indirectly addresses these arguments too.

Here’s the plan. The next section introduces the formal bells and whistles needed to properly address the question at hand. Section 3 discusses Calosi’s arguments in depth and shows where they go wrong. In Sect. 4 I present countermodels to the two central claims of Calosi. Finally, in Sect. 5 I argue that extensional and non-extensional mereologists will respond in much the same way to various multilocation scenarios.

2 Formal Theories About Parthood and Location

Mereology studies the part–whole relation. Classical mereology is a particular theory about this relation and may be axiomatised in a language of first-order logic with identity using as a sole two-place primitive ‘P’ for parthood. In terms of parthood we define,

figure a

I will often use ‘\(+\)’ for the operation of mereological fusing. So, for example, ‘\(x+y+z\)’ is shorthand for ‘the fusion of the entities that are identical to x, y, or z’; and by ‘disjoint’ we mean ‘not overlapping’.

Here is one way to axiomatise classical mereology,

figure b

The first four axioms suffice for an extensional mereology; adding the last axiom schema turns this into classical mereology. As a reminder, extensional mereology is so-called because whenever objects are mereologically indiscernible in some sense (for example, they have the same overlappers) the theory identifies these objects, making them indiscernible in every sense. (See Varzi 2019 for more about mereology.)

The study of location has not resulted in a ‘classical’ theory of location; instead we have a plethora of principles. (From now on I use variables \(r_{1}, r_{2}, \ldots , r_{n}\) for regions while leaving the variables x, y, z, v, u, w for entities located at those regions. I follow Calosi in using a two-sorted language and such that both objects and regions are subject to the principles of classical mereology but there are no cross-categorical fusions consisting of an object and a region. Here the choice for a two-sorted language is philosophically moot; we could have used a language with a single domain and specific predicates for objects and regions instead. See Gilmore and Leonard (2020) for more discussion.) There are two main candidates for the role of the locational primitive: exact location and weak location. Here it is best to take exact location as primitive because the standard definition of exact location in terms of weak location entails that no entities are located at disjoint regions (Parsons 2007, p. 205) thus ending our investigation prematurely. Moreover, Calosi uses ‘exact location’ as his primitive; a fair evaluation of his arguments should follow suit.

Exact location is informally understood as the relation between an object and a region when the object has the exact same shape and size, and stands in all the same spatial relations to other entities, as the region. It is symbolised as ‘\(Lxr_{1}\)’ and, together with mereological notions, is used to define,

figure c

(Overfilling is sometimes called ‘pervading’, but I follow Calosi’s terminology.) The following principle states that no object is multilocated:

figure d

Any theory that does not have Functionality as a theorem would thus allow for multilocated objects. Let’s distinguish two versions of multilocation,

figure e

Strong Multilocation obviously entails Weak Multilocation. A weakly multilocated object that is not strongly multilocated is, for example, multilocated at two regions such that one is a proper part of the other. (Some instances of Weak Multilocation may be hard to detect. For example, if regions of space have a non-extensional mereological structure then an object might be multilocated at two regions that completely coincide and are yet—somehow—numerically distinct. But, to repeat, we will assume that regions of space obey the principles of classical mereology.) Our aim should be ambitious: classical mereology should have room for Strong Multilocation in order to be truly multilocation-friendly.

Calosi uses the following principles to establish the interplay between location and parthood. (We direct the reader to Casati and Varzi 1999; Parsons 2007; Gilmore 2018 for more elaborate discussions about these and other principles.)

figure f

(A small note about Totality. Officially Calosi assumes that everything that is weakly located has an exact location—which follows from the definition of Weak Location—and that every material object is weakly located somewhere (Calosi 2014, p. 126, fn. 13). Totality simply follows from this by basic logic.) In the context of multilocation Calosi rightly takes Region Dissection to be the most controversial principle (2014, 130). Together with the definition of proper parthood Region Dissection rules out that an object is multilocated at regions that stand in a proper parthood relation. So it is a weak anti-multilocation principle.

Call the first four principles taken together ‘The Core’. Calosi argues that (i) The Core together with Region Dissection and classical mereology blocks multilocation (i.e., entails Functionality) and (ii) The Core together with classical mereology entails Region Dissection. From (i) and (ii) we could conclude that The Core together with classical mereology entails Functionality. In the next section we consider his arguments for (i) and (ii).

3 Calosi’s Main Argument

Calosi’s argument for the claim that, assuming classical mereology, The Core plus Region Dissection blocks multilocation goes through a few steps. First, it helps to see that The Core entails what Calosi (2014, p. 127) calls ‘2.6’. I think it deserves a better name so I suggest to call it ‘Meeting’ since it makes mereological overlap materially equivalent with meeting somewhere in space, i.e. having overlapping locations.

figure g

(Proof. Left-to-right: suppose x and y overlap, then they share a part z. By Totality, z has a location, \(r_{1}\). Since z is part of x and of y, we get by two applications of Expansivity that \(r_{1}\) is both part of a region where x is located and part of a region where y is located. So there are regions of x and y that both have \(r_{1}\) as a part, i.e., they overlap. Right-to-left: Let x and y be located at overlapping regions \(r_{1}\) and \(r_{2}\). Let \(r_{3}\) be the region that, by the definition of overlap, is part of both \(r_{1}\) and \(r_{2}\). Both x and y overfill that region and thus have parts \(z_{1}\) and \(z_{2}\) exactly located there, by Arbitrary Partition. By No Colocation, \(z_{1} = z_{2}\); hence x and y overlap. (Proof is adapted from (Calosi 2014, pp. 127–28)).)

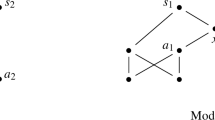
Calosi’s argument for the claim that multilocation is impossible given The Core, Region Dissection, and classical mereology can now be reconstructed thus. (To follow the argument it may help to look at Fig. 1.) Suppose x and y are disjoint objects and that x is multilocated at disjoint regions \(r_{1}\) and \(r_{3}\) while y is located at \(r_{2}\), a region disjoint from the two locations of x. Consider the fusion of x and y, i.e. \(w_{1}\). This object seems to be located at the region that is the fusion of the regions \(r_{1}\), \(r_{2}\), and \(r_{3}\). Call that region \(r_{4}\). Now, in that case, \(w_{1}\) overfills the region composed of \(r_{1}\) and \(r_{2}\); so, by Arbitrary Partition, \(w_{1}\) has some part \(w_{2}\) exactly located at the region composed of \(r_{1}\) and \(r_{2}\). But this latter region is a proper part of \(r_{4}\) so, by Region Dissection, \(w_{2}\) is a proper part of \(w_{1}\) hence \(w_{1} \ne w_{2}\). However, it seems that \(w_{1} = w_{2}\) because they overlap all and only the same things. And if that is the case, we end up in a contradiction.

Fig. 1
figure 1

If \(w_{1}\) is multilocated at both \(r_{4}\) and \(r_{1}+r_{2}\) (or both at \(r_{4}\) and \(r_{2}+r_{3}\)) then Region Dissection fails

Full size image

Calosi argues that \(w_{1} = w_{2}\) via extensionality and two reductiones ad absurdum. In both of these he assumes that some object overlaps only one of the w’s and derives a contradiction. So \(w_{1}\) and \(w_{2}\) overlap the same objects, and by extensionality (of overlap) it then follows that \(w_{1} = w_{2}\). The problem is that neither of the two contradictions actually arise. In each case Calosi (2014, p. 128) appeals to Meeting but that principle does not guarantee what needs to be guaranteed.

For example, to establish that \(w_{2}\) overlaps only objects that \(w_{1}\) overlaps, Calosi supposes for contradiction that \(w_{2}\) overlaps more things than \(w_{1}\): ‘Then there exists something, call it \(z_{1}\), that overlaps \(w_{2}\) but does not overlap x or y. \(z_{1}\) has an exact location, call it \(r_{5}\). Since \(z_{1}\) overlaps \(w_{2}\), it follows from the left-to-right direction of Meeting that \(r_{5}\) overlaps \(r_{1}+r_{2}\)’ (!) (Calosi 2014, p. 128—notation slightly altered). Since \(r_{5}\) overlaps \(r_{1}+r_{2}\), it must overlap either \(r_{1}\) or \(r_{2}\), in which case by the right-to-left of Meeting, \(w_{2}\) overlaps either x or y—contradicting our assumption.

The problem lies at the point where I have added an exclamation mark. The left-to-right direction of Meeting does not guarantee that \(r_{5}\) overlaps \(r_{1}+r_{2}\). It only guarantees that \(r_{5}\) overlaps with some region where \(w_{2}\) is located. And the second reductio ad absurdum fails for basically the same reason. So at two points Calosi either assumes a principle stronger than Meeting or assumes that \(w_{2}\) has only one location (and, in that case, also that x has only two locations and y only one).

Let us consider both options starting with the first. A principle stronger than Meeting that would do the job is the following:

figure h

If we replace the problematic uses of Meeting with Meeting Everywhere, Calosi’s argument does go through. But notice that the left-to-right direction of Meeting Everywhere blocks strong multilocation in any mereological system that validates the definition of overlap given above. Since everything overlaps itself, Meeting Everywhere implies that no object is multilocated at disjoint regions. This would be bad news for the multilocationist. The good news is, however, that the left-to-right direction of Meeting Everywhere does not follow from The Core together with Arbitrary Parition and classical mereology. To derive Meeting Everywhere one needs a stronger expansivity principle. For example, one could use the one from Casati & Varzi (1999) (sometimes called ‘weak expansivity’ (Gilmore 2018) but in the current context it is stronger than the expansivity principle above),

figure i

From Strong Expansivity and Totality we can derive the left-to-right of Meeting Everywhere. (Proof. Suppose x and y overlap and thus have a part z in common. By Totality, x, y, and z each have at least one location, \(r_{1}\), \(r_{2}\), and \(r_{3}\) respectively. Since z is part of x and these two objects are located at \(r_{3}\) and \(r_{1}\) respectively, \(r_{3}\) is part of \(r_{1}\) by Strong Expansivity. Similar reasoning will show that \(r_{3}\) is part of \(r_{2}\). So \(r_{1}\) and \(r_{2}\) overlap. Since the locations of x and y were arbitrary, we may apply universal generalisation: any locations of x and y will overlap if x and y overlap. The proof of the right-to-left direction of Meeting Everywhere is basically the same as that for Meeting.) Crucially, but unsurprisingly, Strong Expansivity entails that multilocated objects are located at regions that are part of each other. Hence, unless we deny Antisymmetry, Functionality follows directly from Strong Expansivity. And strong multilocation is impossible irrespective of whether we accept Antisymmetry. Hence, any multilocationist has good reasons to reject Strong Expansivity, whether or not they accept classical, or some other extensional, mereology. (Quite surprisingly, Strong Expansivity is a rather common assumption in discussions about the interrelation between mereology and location. No one seems to have noticed how problematic the principle is for multilocation.)

A second way to validate Calosi’s argument is by assuming that only x is multilocated, and at only two regions. (In private correspondence, Calosi told me he thinks this is what he implicitly assumed.) The conclusions drawn from Meeting then hold because there are no other regions where the relevant objects could meet. But a multilocationist may hold that more than one object is multilocated. Indeed, if one thinks a composite object can be multilocated, it makes good sense to take the parts of a multilocated composite object to be multilocated too. Still, Calosi’s argument shows that if an object is multilocated, at least one other object is multilocated, too.

Fig. 2
figure 2

When y and \(w_{1}\) are also multilocated, all is well

Full size image

A counterexample tailored to Calosi’s argument is given in Fig. 2. Here we give y an additional location which suffices to satisfy all the principles officially taken on board without running into a contradiction. (y has two locations, \(r_{2}\) and \(r_{4}\), and \(w_{1}\) is multilocated at both \(r_{5}\) and \(r_{6}\).)

3.1 Region Dissection

It is also worth discussing Calosi’s argument for the claim that Region Dissection follows from The Core and classical mereology. If sound, rather minimal principles suffice for a strong harmony between the mereological structure of space and the mereological structure of the occupant of that space. Occupiers whose regions stand in proper parthood relations would then stand in proper parthood relations themselves, simply in virtue of The Core.

Calosi’s (2014, pp. 131–132) argument that Region Dissection follows from The Core appeals to Meeting twice but, again, in both cases the argument either uses Meeting Everywhere instead or it needs to assume that other objects are not multilocated. We have already seen that Meeting Everywhere is too strong to use in an argument against multilocation. Hence, this argument that Region Dissection follows from The Core does not go through.

Still, there is an interesting relation between multilocation, Region Dissection, and some other principles from The Core worth pointing out. If we assume that no object is multilocated—i.e., we assume Functionality—then Region Dissection follows from Arbitrary Partition and No Colocation. (Proof. Suppose that x and y are located at \(r_{1}\) and \(r_{2}\) respectively and that \(r_{1}\) is a proper part of \(r_{2}\); and suppose for contradiction that x is not a proper part of y. So either \(x=y\) or x is not part of y. If we assume \(x=y\), then x is multilocated at \(r_{1}\) and \(r_{2}\)—contradicting Functionality. If x is not part of y, we reason as follows. Since y overfills \(r_{1}\) it must, by Arbitrary Partition, have a part z exactly located at \(r_{1}\). By No Colocation, \(z=x\); hence, x is part of y—contradiction.) So once multilocation is ruled out, Region Dissection is right around the corner. Of course, those who dislike both multilocation and Region Dissection can deny either Arbitrary Partition or No Colocation; and either move is available to extensionalists and non-extensionalists alike.

4 A Countermodel

Calosi’s argument for the claim that The Core together with Region Dissection blocks multilocation is thus invalid, as is his argument that The Core entails Region Dissection. But one might wonder whether there is another argument for either claim. In this section I show that there can be no such argument by presenting two countermodels: one in which The Core and Region Dissection hold, but everything is multilocated; and one in which The Core holds and Region Dissection fails.

Fig. 3
figure 3

GEM with multilocation. Dotted arrows signify the exact location relation

Full size image

Figure 3 deliberately omits the locations of the ys. Depending on where we take them to be, we have a counterexample to the claim that (i) The Core plus Region Dissection blocks multilocation, or to the claim that (ii) Region Dissection is entailed by The Core. In either case every object in the model is multilocated, so Functionality is false while all the principles of The Core are satisfied, as is easily checked. To get a countermodel for (i) we take, say, \(y_{1}\) to be located both at \(r_{1}+r_{2}\) and at \(r_{5}+r_{6}\) but at no other regions (and we assign \(y_{2}\) and \(y_{3}\) similar locations completely ‘on the left’ and completely ‘on the right’). In that case Region Dissection holds, as do all the principles of The Core, but Functionality is false.

In order to get a countermodel for (ii) we should give some more space to the y’s and hold that, for example, \(y_{1}\) is multilocated at \(r_{1}+r_{2}\), \(r_{1}+r_{6}\), \(r_{2}+r_{5}\), and \(r_{5}+r_{6}\). To see that Region Dissection now fails, note that by Expansivity, and since \(y_{1}\) is part of x and located at \(r_{2}+r_{5}\), x should have a location that has \(r_{2}+r_{5}\) as a part. This should be \(r_{4}+r_{8}\) but in that case since \(r_{4}\) is a proper part of \(r_{4}+r_{8}\) and x is not a proper part of itself, Region Dissection is not satisfied. (Note that some regions that classical mereology gives to us are not drawn, adding these would only clutter the image without changing the result.)

As it might be difficult to imagine all the additional dotted arrows in this second scenario, and since drawing them in a seven-element model clutters the whole imagine beyond all recognition, Fig. 4 presents a modest three-element model compatible with classical mereology in which The Core holds while Region Dissection fails: \(w_{1}\) is multilocated at \(r_{5}\), \(r_{6}\), and \(r_{7}\); and the last of these three regions has the other two as proper parts, but \(w_{1}\) is not a proper part of itself. It is easy to check that all principles of the Core are satisfied in Fig. 4. (When checking Arbitrary Partition, keep in mind that everything is a part of itself; since \(w_{1}\) has a part, itself, located at \(r_{5}\), it is perfectly acceptable that \(w_{1}\) overfills \(r_{5}\) by being located at \(r_{7}\). Relatedly, this illustrates that Arbitrary Partition does not rule out extended simples as long as an extended simple is multilocated at all proper subregions of its ‘largest’ exact location.)

Fig. 4
figure 4

The Core does not entail Region Dissection

Full size image

So, The Core together with Region Dissection is compatible with multilocated objects and classical mereology. And The Core together with classical mereology does not entail Region Dissection.

5 Multilocation and Mereological Indistinguishability

Multilocation is thus compatible with classical mereology. But would a non-extensional mereology not be a more suitable home for multilocated entities? Here I argue that extensionality is irrelevant to multilocation because both the extensional and the non-extensional mereologist will say the same things about multilocated objects—except, of course, that the extensional mereologist will identify certain objects that the non-extensionalist will distinguish. This latter fact sometimes makes the response of the extensional mereologist more straightforward than the response of the non-extensionalist (as will become clear). The point of this section is thus to point out, more generally, that multilocation does not provide a reason to accept a non-extensional mereology. (In private correspondence Calosi told me he no longer endorses the weaker arguments we are about to discuss.) It is worth discussing some multilocation scenarios to get a feel for the type of response a multilocationist can give—irrespective of whether they accept extensionality.

Since we now consider non-extensional mereologies and since these are often combined with colocation, we drop No Colocation from our set of assumptions. There are different ways to be a non-extensionalist but for our discussion the specific flavour of non-extensionality is irrelevant. I argue that any non-extensionalist who accepts multilocation will say the same thing as the extensionalist when confronted with certain puzzles. I argue for this claim indirectly by considering the puzzles Calosi puts forward as showing that ‘the conjunction of extensionalism and multilocation is highly problematic at best’ (2014, p. 132). In each case I solve the puzzle for the extensionalist and show that the non-extensionalist gives the same response.

The first puzzle Calosi discusses concerns the situation depicted in Fig. 1. It is a dilemma: either there is an object exactly located at region \(r_{1}+r_{2}\) or there is not. (We ignore this second option.) If there is an object located at \(r_{1}+r_{2}\) we ‘end up with a straightforward contradiction, for extensionality dictates that the object located at \(r_{1}+r_{2}\) must be identical to \(w_{1}\), whereas considerations about location strongly suggest that it is distinct from them’ (p.132). Calosi is right about the first half: whatever object is located at \(r_{1}+r_{2}\), it seems to have exactly the same parts as \(w_{1}\) and is thus, by extensionality, identical with it. He is, however, wrong about the second part: as soon as we allow for multilocation the fact that an object is located at a proper subregion of another object provides no evidence for thinking that the objects are distinct. It only provides such evidence if we assume Region Dissection but that principle is highly controversial in the context of multilocation and it does not follow from more innocuous principles. So an extensionalist can point to an object that occupies \(r_{1}+r_{2}\) without contradicting themselves.

A non-extensional multilocationist could also hold that the object located at \(r_{1}+r_{2}\) is \(w_{1}\). But since they allow for distinct objects with the same parts we should consider what happens if instead \(r_{1}+r_{2}\) is occupied by an object v distinct from \(w_{1}\). Then by Expansivity and since v has a part, x, which is located at \(r_{3}\), there should be a region where v is located and which has \(r_{3}\) as a part. One way to make this so is by insisting that v is also multilocated: both at \(r_{1}+r_{2}\) and at \(r_{4}\). So now \(w_{1}\) and v are multilocated and colocated. To avoid contradiction, Region Dissection must still be denied; hence the non-extensionalist and the extensionalist are on a par here. In general, both the extensionalist and the non-extensionalist have good reason to deny Region Dissection if they accept multilocation. The reason is simply that Region Dissection directly blocks some forms of multilocation.

Calosi discusses another argument for holding that, in Fig. 1, \(w_{1}\)—the fusion of x and y—is distinct from the object located at \(r_{1}+r_{2}\). These regions have different geometric properties and since an object’s exact location should match the geometry of the object, the objects located at these regions cannot be the same (2014, p. 133). The supposition is that a multilocated object cannot have, at one and the same time, different geometric properties. But the multilocationist will definitely hold that a multilocated object can be, at one and the same time, for example both straight and bent. If Socrates is multilocated then it seems he could be both standing and sitting—albeit at different regions. So this argument also fails to establish that \(w_{1}\) is distinct from the object located at \(r_{1}+r_{2}\). Hence, a multilocationist should hold that \(w_{1}\) is multilocated at \(r_{1}+r_{2}\) and at \(r_{4}\). Note, moreover, that the reasoning from geometric properties is independent from considerations of extensionality. So again the non-extensionalist can, and probably will, say the same thing.

A second puzzle Calosi discusses goes as follows. Consider a collection of multilocated particles, located exactly on the moon and exactly on earth. On the moon these particles compose a rock while on earth they compose a human. Calosi initially claims that the human ‘is not even weakly located on the moon’ whereas the rock ‘surely is weakly located at the moon’ (2014, p. 133). He takes this to be a problem.

First, I do not see why an extensional multilocationist should hold that the human is not even weakly located on the moon. Since by extensionality the rock and the human are one and the same object, the human is exactly located where the rock is. Hence, if the rock is exactly located on the moon, then so is the human. (Calosi also later explains that the human is, despite appearances, weakly located on the moon, but for different reasons as we will see shortly.) Of course, it sounds strange that the human is on the moon but this is simply part and parcel of the multilocationist way of looking at things, irrespective of mereology.

One might think it should nonetheless be harder to put someone on the moon. And since the non-extensionalist has no obvious reasons for identifying the rock with the human, their position seems to allow for multilocated parts without multilocated wholes. Moreover, even though non-extensionalists could copy the extensionalist’s claim (although without the extensionalist’s reasoning) this risks undermining their case for non-extensional mereology. The reasons for distinguishing, say, a statue from its matter seem applicable to the rock and the human too. For example, the rock may be destroyed without the human being destroyed. So a non-extensionalist has various reasons to distinguish the rock from the human although they have the same multilocated parts.

Still, saying that the rock and the human are numerically distinct does not mean that the human is not weakly located at the moon. Because, as Calosi (2014, p. 133) explains, being partially located at a region implies being weakly located there. (This is the reason Calosi gives for saying that the human is weakly located at the moon after all.) So since the human is partially located at the moon—for it has a part located at the moon—it is weakly located there. But from this and the definition of weak location it follows that the human is exactly located at a region overlapping the region on the moon where it is weakly located. (Similar reasoning will bring the rock down to earth.) Hence even if the non-extensionalist holds that the rock and the human are numerically distinct, they will also have to say that both are multilocated on earth and on the moon. So in both cases the human is located on the moon but in the non-extensionalist’s solution the human is numerically distinct from, but colocated with, a moon rock.

6 Conclusion

Some philosophers think certain entities can be multilocated. And some philosophers think composition is unique and unrestricted. Those who find themselves in both camps need not worry: their position is perfectly consistent even when we create a tight link between parthood and location.