Tough enough? Robust satisficing as a decision norm for long-term policy analysis

Abstract

This paper aims to open a dialogue between philosophers working in decision theory and operations researchers and engineers working on decision-making under deep uncertainty. Specifically, we assess the recommendation to follow a norm of robust satisficing when making decisions under deep uncertainty in the context of decision analyses that rely on the tools of Robust Decision-Making developed by Robert Lempert and colleagues at RAND. We discuss two challenges for robust satisficing: whether the norm might derive its plausibility from an implicit appeal to probabilistic representations of uncertainty of the kind that deep uncertainty is supposed to preclude; and whether there is adequate justification for adopting a satisficing norm, as opposed to an optimizing norm that is sensitive to considerations of robustness. We discuss decision-theoretic and voting-theoretic motivations for robust satisficing, and use these motivations to select among candidate formulations of the robust satisficing norm.

Introduction

We as a species confront a range of profound challenges to our long-term survival and flourishing, including nuclear weapons, climate change, and risks from biotechnology and artificial intelligence (Bostrom & Cirkovic, 2008; Ord, 2020). Policy decisions made in answer to these threats will impact the development of human civilization hundreds or thousands of years into the future. In the extreme, they will determine whether humanity has any future at all.

Unfortunately, severe cluelessness clouds our efforts to forecast the impact of policy decisions over long-run timescales. The term ‘deep uncertainty’ has been adopted in operations research and engineering to denote decision problems in which our evidence is profoundly impoverished in the way typical of problems in long-term policy analysis (Marchau, Walker, Bloemen, & Popper, 2019). The third edition of the Encyclopedia of Operations Research and Management Science defines ‘deep uncertainty’ disjunctively as arising in situations “in which one is able to enumerate multiple plausible alternatives without being able to rank the alternatives in terms of perceived likelihood” or—worse still—where “what is known is only that we do not know.” (Walker, Lempert, & Kwakkel, 2013: p. 397)¹ A multi-disciplinary professional organization dedicated to research on decision-making under deep uncertainty (DMDU) was established in December 2015.

Given the paucity of evidence that could constrain probability assignments under deep uncertainty, analysts associated with the study of DMDU argue that orthodox approaches to decision analysis based on expected value maximization are unhelpful. Thus, Ben-Haim (2006: p. 11) suggests that “[d]espite the power of classical decision theories, in many areas such as engineering, economics, management, medicine and public policy, a need has arisen for a different format for decisions based on severely uncertain evidence.” The DMDU community has developed a range of tools for decision support designed to address this need, including Robust Decision Making (RDM) (Lempert, Popper, & Bankes, 2003), Dynamic Adaptive Policy Pathways (Haasnoot, Kwakkel, Walker, & ter Maat, 2013), and Info-Gap Decision Theory (Ben-Haim, 2006).

These tools are not faithfully characterized as decision theories, at least not in the sense in which philosophers would most naturally understand that term. They primarily comprise procedures for framing and exploring decision problems. Sometimes their proponents seem reluctant to suggest normative criteria for solving decision problems once suitably framed. Thus, Lempert, Groves, Popper, & Bankes (2006: p. 523) write: “RDM does not determine the best strategy. Rather, it uses information in computer simulations to reduce complicated, multidimensional deeply uncertain problems to a small number of key trade-offs for decision-makers to ponder.”

This is the aspect of DMDU research highlighted in a recent paper by Helgeson (2020), one of the few papers by philosophers to examine research in this area in depth. Whereas decision theory, as practiced by philosophers, characteristically aims to instruct decision-makers in how to solve a decision problem that is appropriately framed, Helgeson argues that DMDU research focuses principally on how to frame the decision problem in the first place, and so provides “a counterbalancing influence to decision theory’s comparative focus on the choice task.” (p. 267).

DMDU researchers nonetheless also provide suggestions for normative criteria appropriate to the solution of the choice task faced in conditions of deep uncertainty. In particular, they tend to advocate normative criteria that emphasize achieving robustly satisfactory performance: to a first approximation, this means selecting options that “perform reasonably well compared to the alternatives across a wide range of plausible scenarios” (Lempert, Popper, & Bankes, 2003: p. xiv). Thus, Lempert (2002: p. 7309) states that DMDU decision support tools “facilitate the assessment of alternative strategies with criteria such as robustness and satisficing rather than optimality. The former are particularly appropriate for situations of deep uncertainty.”² In the same vein, Schwartz, Ben-Haim, & Dasco, (2011: p. 213) argue that “[t]here is a quite reasonable alternative to utility maximization. It is maximizing the robustness to uncertainty of a satisfactory outcome, or robust satisficing. Robust satisficing is particularly apt when probabilities are not known, or are known imprecisely.” In a sense, it is unsurprising that conceptual innovations in decision framing should be accompanied by the proposal of novel decision criteria, as any reasonable decision support tool must make some assumptions about what constitutes a good decision in order to determine what information should be emphasized in framing the problem at hand. Insisting on a clean separation between tools for decision framing and normative decision criteria would be misguided.

Our interest in this paper is in robust satisficing as a norm for decision-making under deep uncertainty. There has been remarkably little philosophical discussion of this norm, given its apparent popularity among those at the coalface working on DMDU. We hope to change that. In order to simplify the discussion, we focus specifically on robust satisficing in relation to the decision support tools characteristic of RDM and set aside other approaches.

In Sect. 2, we say more about how deep uncertainty has been conceptualized, present the decision support tools used in RDM to facilitate decision framing, and analyse a number of key claims about robustness and satisficing made by researchers involved in the development of RDM. In Sect. 3, we raise a pair of important methodological issues concerning how to evaluate the recommendation to assess policies using criteria framed in terms of robustness and satisficing. Sections 4 and 5 then proceed to evaluate that recommendation. Section 4 seeks to articulate the case for robustness as a desideratum, but also raises an important concern: namely, that a measure of robustness seems to represent a probability measure of the kind that is supposed to be unavailable under deep uncertainty. We suggest that this concern may be answerable. Section 5 considers why we should favour robust satisficing over a rival norm of robust optimizing. As we see it, there is no strict logical interrelationship between robustness and satisficing. We argue that the voting theoretic literature may help to justify a satisficing approach by allowing us to model robust satisficing as having virtues analogous to those claimed on behalf of the approval voting (Brams & Fishburn, 1983).

Introducing deep uncertainty, RDM, and robust satisficing

The three key goals of this section are to further characterize the notion of deep uncertainty, outline the procedures and decision support tools used to facilitate decision-making under deep uncertainty in the context of RDM, and highlight and interpret key claims about robustness and satisficing as decision criteria made by researchers associated with its development. Along with the methodological remarks in Sect. 3, this will set the stage for the subsequent critical discussion of robust satisficing in Sects. 4 and 5.

Deep uncertainty

Many decision theorists have felt that it is important to rank decision problems according to depth of uncertainty. The best-known taxonomy is due to Luce and Raiffa (1957: p. 13), according to whom decision-making under certainty is said to occur when “each action is known to lead invariably to a specific outcome,” whereas decision-making under risk occurs when “each action leads to one of a set of possible specific outcomes, each outcome occurring with a known probability,” and decision-making under uncertainty refers to the case where outcome probabilities are “completely unknown, or not even meaningful.”³,⁴

Theories of deep uncertainty aim to unpack the many gradations of uncertainty beneath Luce and Raiffa’s category of decision-making under risk.⁵ Although there is no agreed-upon taxonomy for deep uncertainty in the DMDU literature, one influential proposal is due to W.E. Walker and colleagues (Walker, Harremöes, Rotmans, van Der Sluijs, van Asselt, Janssen, & von Krauss, 2003), and parallels Luce and Raiffa in its account of the different levels of uncertainty. Walker et al. suggest that deep uncertainty should be seen as a matter of degrees of deviation, along one or more dimensions, from the limit case of certainty.

One dimension of uncertainty captures its location within our model of a decision situation. Some uncertainty centres around model context: which parts of the world should be included or excluded from the model? Another location is the structure and technical implementation of the model: which equations are used and how are they computed? This constitutes model uncertainty. Parameter uncertainty corresponds to the case where the location of uncertainty pertains instead to the parameters of the model. Uncertainty may also target the non-constant inputs, or data used to inform the model. An important insight is that uncertainty along these various locations need not be correlated. For example, we may be quite certain that the right model context has been found and the right inputs and parameters have been entered, but retain considerable model uncertainty about how the system is to be modelled.

For our purposes, the more important dimension of uncertainty is what Walker et al. call the level of uncertainty. Beneath full certainty lies what they call statistical uncertainty, where our uncertainty “can be described adequately in statistical terms.” (8) This plausibly corresponds to what Luce and Raiffa call ‘risk’. Below this, we have what Walker et al. call scenario uncertainty, in which “there is a range of possible outcomes, but the mechanisms leading to these outcomes are not well understood and it is, therefore, not possible to formulate the probability of any one particular outcome occurring.” (Ibid.) This corresponds to what Luce and Raiffa call ‘uncertainty.’ Walker et al. recognize yet deeper levels of uncertainty. Beneath scenario uncertainty they locate recognized ignorance, in which we know “neither the functional relationships nor the statistical properties and the scientific basis for developing scenarios is weak.” (Ibid.) Still further down is the case of total uncertainty, which “implies a deep level of uncertainty, to the extent that we do not even know that we do not know.” (9).

As we see it, there remain a number of non-trivial questions about how to relate Walker et al.’s hierarchy to relevant concepts used in contemporary decision theory to describe the doxastic states of highly uncertain agents.⁶ For example, it is not immediately clear where in Walker et al.’s hierarchy we might include cases of agents facing situations of ambiguity (Ellsberg, 1961) in which the decision-maker’s doxastic state cannot be represented by a unique probability distribution warranted by her evidence. One proposal would be to interpret ambiguity as a matter of the level of uncertainty, picking out the disjunction of all levels deeper than statistical uncertainty. Many philosophers will want to allow for the possibility that some types of ambiguity can be well captured by imprecise probabilities (Bradley, 2014). To accommodate this thought, we might enrich Walker et al.’s taxonomy with a new level of uncertainty, imprecise statistical uncertainty, located between statistical and scenario uncertainty, and occurring when imprecise but not precise probabilities can be constructed. On this reading, ambiguity refers to the disjunction of imprecise statistical uncertainty together with all deeper levels of uncertainty.

We may also wonder how the taxonomy captures what philosophers and economists call unawareness: that is, cases in which the agent fails to consider or conceive of some possible state, act, or outcome relevant to the decision problem (Bradley, 2017: pp. 252–61; Grant & Quiggin, 2013; Karni & Vierø, 2013; Steele & Stefansson, 2021). Unawareness may play several different roles in contemporary approaches to decision-making under deep uncertainty. It clearly informs the general procedures used for decision support, such as the use of computer-based exploratory modelling to capture a wide range of possibilities and the technique of encouraging participants to formulate new strategies on which to iterate the analysis, which we describe below. These processes help to diminish our unawareness. Lempert Popper, & Bankes (2003: p. 66) emphasize that “no one can determine a priori all the factors that may ultimately prove relevant to the decision. Thus, users will frequently gather new information that helps define new futures relevant to the choice among strategies … or that represents new, potentially promising strategies." Another possibility is that unawareness is taken to motivate the application of novel decision rules, like robust satisficing, to decision problems, once suitably framed, given that some degree of unawareness will inevitably remain.⁷ However, on our reading of the DMDU literature, we do not find clear evidence of this.⁸

Some might think of unawareness as the marker of truly deep uncertainty, and it seems plausible that unawareness characterizes the deep levels of uncertainty below scenario uncertainty in the Walker et al. taxonomy, especially the basement level of total uncertainty.⁹ At the same time, this framework urges a holistic view on which many factors beyond unawareness may modulate an agent’s level of uncertainty.

RDM

Having discussed the notion of deep uncertainty, our next goal is to introduce the method of Robust Decision-Making (RDM) under deep uncertainty.

The procedures and decision support tools used in RDM build on the techniques of scenario-based planning (Schwartz, 1996) and assumption-based planning (Dewar, Builder, Hix, & Levin, 1993). Scenario-based planning encourages decision-makers to construct detailed plans in response to concrete, narrative projections of possible futures. Assumption-based planning emphasizes the identification of load-bearing assumptions, whose falsification would cause the organization’s plan to fail.

Developed at RAND around the turn of the millennium, RDM uses computer-based exploratory modelling (Bankes, 1993) to augment these techniques. Computational simulations are run many times, in order to build up a large database of possible futures and evaluate candidate strategies across the ensemble. This contrasts with the small handful of user-generated futures considered in traditional scenario planning, with Schwartz (1996: p. 29) recommending use of just two or three scenarios for the sake of tractability. Once an ensemble of futures has been generated, RDM uses scenario discovery algorithms to identify the key factors that determine whether a given strategy is able to satisfactorily meet the organization’s goals. Data visualization techniques are used to represent the performance of alternative strategies across the ensemble of possible futures and identify key trade-offs.

By way of illustration, Robalino and Lempert (2000) apply RDM in exploring the conditions under which government subsidies for energy-efficient technologies can be an effective complement to carbon taxes as a tool for greenhouse gas abatement.

The first step of their analysis is to construct a system model. To that end, they develop an agent-based model in which energy consumption decisions made by a heterogenous population of agents generate macroeconomic and policy impacts, which in turn affect the behaviour of agents at later times.

Their second step is to settle on a set of policy alternatives to compare. Robalino and Lempert compare three strategies: a tax-only approach, a subsidy-only approach, and a combined policy using both taxes and technology subsidies.

Because model parameters are uncertain, the next step is to use data and theory to constrain model parameters within a plausible range. Sometimes this can be done with a point estimate: for example, the pre-industrial atmospheric concentration of carbon is estimated at 280 parts per million. Other parameters can be estimated only more imprecisely. For example, the elasticity of economic growth with respect to the cost of energy is constrained to the range [0, 0.1] (Dean & Hoeller, 1992). The resulting uncertainty space of allowable combinations of parameter values is intractably large. As a result, a genetic search algorithm was used to identify a landscape of plausible futures: a set of 1611 combinations of parameter values intended to serve as a good proxy for the larger uncertainty space.

To improve the tractability of the analysis and the interpretability of results, a dimensionality-reduction approach was used to identify the five most decision-relevant model parameters. Allowing these parameters to vary across the landscape of plausible futures and fixing the rest at their mean values generates an ensemble of scenarios in which the performance of policy alternatives can be compared. In each scenario, alternatives were assessed by their regret: the difference in performance between the given alternative and the best-performing alternative.¹⁰

The purpose of RDM is to identify robust alternatives, which in this case means seeking alternatives with low regret across the ensemble of scenarios. This analysis leads to policy-relevant conclusions. For example, Robalino and Lempert find that a combined policy can be more effective than a tax-only policy if agents have heterogenous preferences and there are either significant opportunities for energy technologies to deliver increasing returns to scale or for agents to learn about candidate technologies by adopting them.

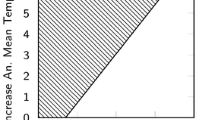
Although RDM models are not intended to deliver precise probabilistic forecasts, they can help us get a grip on the ways in which assignments of probabilities may inform policy choices. Thus, Robalino and Lempert also map the conditions under which different strategies are favoured given different probability assignments to the possibility of high damages from climate change and to the possibility that the economy violates classical assumptions about learning and returns to scale. They find that the combined strategy is preferable when both probabilities are moderate or large (Fig. 1).

Fig. 1

Performance of combined and tax-only strategies against climate damages and economic classicality—reproduced from Robalino and Lempert (2000: p. 15)

Because RDM analysis uses a subset of the full uncertainty space, the last step is to search through the full space for possible counterexamples to these strategy recommendations. If necessary, these counterexamples can be used to develop new alternatives or to constrain the landscape of plausible futures in a way more likely to discriminate between candidate alternatives, and then the analysis can be repeated.

Robust satisficing

The previous section gives a sense of the procedures and tools used in decision framing that characterize the RDM approach. Our aim in this sub-section is to highlight and offer some preliminary interpretation of the recommendation to engage in robust satisficing when solving decision problems of the kind to which RDM is applied.

Researchers associated with the development of RDM typically emphasize the extreme fallibility of prediction in the face of deep uncertainty and recommend identifying strategies that perform reasonably well across the entire ensemble of possible futures, as opposed to trying to fix a unique probability distribution over scenarios relative to which the expected utility of options can be assessed. It is granted that expected utility maximization is appropriate when uncertainties are shallow. Lempert, Groves, Popper, & Bankes (2006: p. 514) emphasize that “[w]hen risks are well defined, quantitative analysis should clearly aim to identify optimal strategies … based on Bayesian decision analysis … When uncertainties are deep, however, robustness may be preferable to optimality as a criterion for evaluating decisions.” They define a robust strategy as one that “performs relatively well—compared to alternatives—across a wide range of plausible futures.” (Ibid.)

In line with the example discussed in Sect. 2.2, it is common for RDM theorists to use a regret measure to assess the performance of different strategies within a scenario. Regret may be measured in either absolute terms or relative terms: i.e., as the difference between the performance of the optimal policy and the assessed policy, or as this difference considered as a fraction of the maximum performance achievable. Using either measure, a robust strategy is defined by Lempert, Popper, & Bankes (2003: p. 56) as “one with small regret over a wide range of plausible futures, F, using different value measures, M.”¹¹ No details are given about how to determine what counts as ‘small regret,’ so far as we are aware. Decision-makers who rely on RDM tools are presumably asked to define their own preferred satisficing threshold. In Sect. 5.3, we will provide reasons against interpreting satisficing in terms of a regret measure.

The standard approach when using RDM is to consider how well a given policy performs across the range of possible futures: i.e., its ability to produce satisfactory outcomes given different possible states of the world. So understood, robust satisficing could be considered as a competitor to standard non-probabilistic norms for decision-making under uncertainty like Maximin, Minimax Regret, or Hurwicz (Luce & Raiffa, 1957: pp. 278–86).

The assessment of a candidate policy against the norm of robust satisficing need not entirely forego probabilities, however. As we saw, Robalino and Lempert are willing to use probabilistic analysis to shed light on the ways in which economic non-classicality and damages from climate change bear on the optimality of taxes and subsidies. Lempert, Popper, & Bankes (2003: 48) note that the notion of robust satisficing “can be generalized by considering the ensemble of plausible probability distributions that can be explored using the same techniques described here for ensembles of scenarios.” In other words, we may choose to assess the robustness of a given policy by considering the extent to which its expected performance is acceptable across the range of probability distributions taken to be consistent with our evidence. So understood, robust satisficing may be considered as a competitor to norms for decision-making with imprecise probabilities, like Liberal or MaxMinEU (discussed in Sect. 4.3).

Notably, the norm of robust satisficing is presented by Lempert and Collins (2007) and Lempert (2019) as inspired by Starr’s domain criterion for decision-making under uncertainty, which canonically makes use of sets of probability assignments (Schneller & Sphicas, 1983; Starr, 1966). Roughly speaking, the domain criterion asks agents who are completely ignorant about which world-state is likely to be actual to consider the set of all possible probability assignments to the states, giving equal weight to each possible probability assignment and choosing the act which is optimal on the largest number of probability assignments.¹²

Apart from the more explicit focus on deciding by reference to sets of probability values, we find the inspiration drawn from the domain criterion to be striking, in that it serves to highlight two concerns about robust satisficing that we will explore in greater depth in this paper.

The first concerns the relationship between robustness and satisficing. The domain criterion is recommended by Starr in part on the basis of considerations of robustness. Starr (1966: p. 75) argues that his criterion is superior to the Laplace criterion¹³ because, he claims, a decision rule that relies on a unique probability assignment to the possible states is too sensitive to the particular probability vector that we choose. Nonetheless, the domain criterion compares strategies in terms of the number of probability assignments on which they maximize expected utility and is therefore naturally thought of as a norm of robust optimizing.¹⁴ In expositions of RDM, robustness and optimizing are frequently contrasted, and a desire for robustness is linked to satisficing choice. Starr’s domain criterion serves to highlight that there is no strictly logical connection here. What, then, explains the emphasis on satisficing choice that informs the design and application of RDM? We take up this issue in Sect. 5.

Secondly, we re-iterate that in Starr’s exposition, the domain criterion explicitly relies on higher-order probabilities. We are “to measure the probability that a randomly drawn [first-order probability assignment] will yield a maximum expected value for each particular strategy.” (Starr, 1966: p. 73) This is done using a uniform second-order probability measure over first-order probability functions, a strategy Starr takes to represent a more plausible interpretation of the Principle of Insufficient Reason¹⁵ than the Laplace criterion. Notably, in what may be considered the locus classicus for discussions of robustness as a decision criterion in the field of operations research, Rosenhead, Elton, & Gupta (1972) also emphasize the close kinship of their favoured principle to the Laplace criterion. In planning problems in which an initial decision $d_{i}$ must be chosen from a set $D$ and serves to restrict the set $S$ of alternative plans capable of being realized in the long run to a subset $S_{i}$, they define the robustness of $d_{i}$ in terms of $\left| {\tilde{S}_{i} } \right|{/}\left| {\tilde{S}} \right|$, where $\left| X \right|$ denotes the cardinality of set $X$ and $\tilde{S} \subseteq S$ is the set of long-run outcomes considered “acceptable according to some combination of satisficing criteria.” (419) They explicitly note that using their robustness criterion is equivalent to using the Laplace criterion if the agent’s utility function is defined to be 1 for any $s \in$ $\tilde{S}$ and 0 otherwise.

Given its pedigree, it would seem natural to expect that the robustness criterion appealed to in RDM must also involve reliance on a uniform first-order or second-order probability measure, if only implicitly. However, this seems at odds with the skepticism toward unique probability assignments that is otherwise characteristic of the DMDU community (see, e.g., Lempert, Popper, & Bankes, 2003: pp. 47–8). We consider this issue in greater depth in Sects. 4.3–4.4.

As one final point, we note that many formulations of the robust satisficing norm emphasize robustness not only with respect to different possible states of the world or different probability assignments, but also with respect to alternative valuations of outcomes. Thus, Lempert, Popper, & Bankes (2003: p. 56) state that a robust strategy must perform reasonably well as assessed “using different value measures”. For the sake of simplicity our discussion throughout this paper will ignore the issue of robustness with respect to different value systems and focus exclusively on robustness with respect to empirical uncertainty.

Methodological issues

Before we proceed to the critical evaluation of robust satisficing as normative principle for decision-making, we pause briefly to reflect on two methodological issues.

Normative guidance

As noted, RDM researchers have on occasion expressed reluctance to offer determinate normative guidance. Lempert (2019: p. 34) describes RDM as merely “a decision support methodology designed to facilitate problem framing.” This may raise the concern that we are reading too much into certain remarks. A closely related concern is that RDM research may consider and compare the results of alternative choice rules in a given problem (e.g., Cervigni, Liden, Neumann, & Strzepek, 2015), which may suggest that our focus on robust satisficing is overly narrow.¹⁶

Our approach here will simply be to take seriously the claim that “robustness and satisficing” are “particularly appropriate” as criteria for assessing different strategies in situations of deep uncertainty, as asserted by Lempert (2002: p. 7309). As we see it, this is a distinctive and interesting normative claim characteristic of research in the DMDU community. Granting that the decision support tools associated with RDM are compatible with and may be used in conjunction with the application of alternative choice rules, the recommendation to focus on robustness and satisficing is nonetheless suitably distinctive and interesting that we think it repays philosophical scrutiny.

A priori and a posteriori

The second issue relates to the distinction between a criterion of rightness and a decision procedure, familiar to moral philosophers from debates on utilitarianism (see, inter alia, Bales, 1971, Hare, 1981, Railton, 1984). As moral philosophers understand the term, a criterion of rightness specifies the general conditions under which a given act is right or wrong. It is natural to view normative standards of this kind as necessary and a priori. Adoption of a given criterion of rightness need not commit us to thinking that people in general should deliberate by considering whether the conditions specified by the criterion are satisfied. Deliberating in this way need not be a reliable means of choosing those acts that satisfy the criterion. Whether a given decision procedure is in fact a reliable decision-making tool for a given agent in a given context depends on factors that are contingent and a posteriori.

Orthodox normative decision theory is arguably in the business of specifying a priori criteria of rational choice. By contrast, research on fast and frugal heuristics (Gigerenzer, Todd, and the ABC Research Group, 1999) is explicitly concerned with what decision procedures work best in practice when deployed by boundedly rational agents, emphasizing the extent to which practical success is contingent on local features of the environment in which a heuristic is applied and experimentally testing the ‘ecological rationality’ of different algorithms.

How should we understand the recommendation to engage in robust satisficing when making decisions under deep uncertainty? It may seem natural to think that this must be a decision heuristic whose recommendation is contingent and a posteriori. This interpretation may be bolstered by the assertion by Lempert, Groves, Popper, & Bankes (2006: p. 518) that, “[u]ltimately, the claim that RDM will help decision-makers make better decisions in some important situations than traditional approaches must be empirically tested.”

If RDM or robust satisficing are treated as contingently reliable heuristics, then they should be supported by a posteriori evidence of successful decision-making. However, an obvious problem arises. These are recently developed tools for making policy decisions whose impacts will play out over long-run timescales. We are not yet in a position to observe these long-run impacts.¹⁷ Hence, if RDM and robust satisficing are treated as contingently reliable heuristics, we would seem to have little evidence to justify their use in long-term policy analysis.

It could be protested that there is ample empirical evidence of the failure of traditional decision-making methods under conditions of deep uncertainty (Goodwin & Wright, 2010). However, this evidence would not discriminate finely enough to favour RDM or robust satisficing over other extant or yet-to-be-developed methods. Alternatively, it may be replied that although we lack suitable track-record evidence pertaining to RDM specifically, our empirical evidence indicates that it is the kind of approach that should produce desirable long-run results given known facts about human psychology, the kind of decision problems that we face, and the interaction thereof.¹⁸ But, as we see it, our evidence concerning the success or lack thereof of different kinds of decision procedures over long-run timescales is severely impoverished in general. If it were not, we would not be so deeply uncertain; we would know (roughly) what works.¹⁹

Insofar as robust satisficing is appealing as a decision norm, we think there is a strong case to be made that its appeal has to reflect certain a priori intuitions about normative criteria for choice under deep uncertainty, and we focus principally on the nature and credibility of the intuitive considerations that may be taken to support robust satisficing as a decision norm, starting with the intuitive case for emphasizing robustness in the context of decision-making under deep uncertainty. However, we remain open to the possibility that there could be some indirect means of empirically supporting robust satisficing as a contingently reliable decision procedure.

Robustness

In this section, we explore what we take to be the core consideration put forward in the RDM literature for preferring decision norms that exhibit robustness, in the sense(s) outlined in Sect. 2. This takes the form of an intuitive objection to the application of subjective expected utility theory to problems involving deep uncertainty. This objection receives varied expression in the RDM literature. We show that it generalizes to other decision norms besides subjective expected utility maximization, but also serves as a flashpoint for the worry, mentioned in Sect. 2.3., that robust satisficing invokes a form of second-order probability theory.

Robustness and subjective expected utility theory

Consider the approach suggested by Broome (2012) for policy-making in the face of global climate change. Broome concedes that our evidence about climate impacts does not uniquely constrain the probabilities to be assigned to all relevant contingencies. His recommendation is that we should nonetheless assign these contingencies precise probabilities on the basis of a subjective best-guess estimate and maximize expected value relative to that assignment. Broome writes: “Stick with expected value theory, since it is very well founded, and do your best with probabilities and values.” (129).

The core worry that we perceive as animating the emphasis on robustness in the RDM literature is that a policy that is optimal relative to a subjective best-guess probability assignment may in principle be suboptimal, or even catastrophic in expectation, relative to the other probability assignments that were not excluded by our evidence. Intuitively, when this is the case, it is unwise to optimize relative to one’s subjective best-guess probability estimate (compare Sprenger, 2012), and decision-making may be improved by incorporating alternative, less committal ways of representing uncertainty.

This view is often adopted in discussions of climate change. For example, the most recent report of the Intergovernmental Panel on Climate Change (IPCC) communicates uncertainty using five qualitative levels of confidence, ranging from `very low’ to `very high’, together with a ten-point likelihood scale, with each term calibrated to correspond to an interval of precise probabilities (IPCC, 2010, 2014). This reflects the IPCC’s view that, given the depth of climate uncertainties, decision-makers may benefit from considering a range of plausible futures or likelihoods rather than optimizing policies to match a deeply uncertain best-guess probability assignment (Bradley, Helgeson, & Hill, 2017; Helgeson, Bradley, & Hill, 2018).

Robustness and imprecise probabilities

On its face, the intuitive objection raised against subjective expected utility maximization in 4.1 is also an objection to many standard norms for decision-making that reject precise probabilism and assume instead that the decision-maker’s doxastic state is modelled by a (non-singleton) set of probability functions, $R$, often called a representor (following van Fraassen, 1990). The representor is sometimes imagined metaphorically as a ‘credal committee’ (e.g., in Joyce, 2010): an assembly of agents each of whom has a definite degree of confidence for each proposition, corresponding to each probability function in $R$.

Consider the Liberal norm, which states that an act is rationally permissible just in case it maximizes expected utility relative to some $\Pr \left( { \cdot } \right) \in R$. Echoing the points noted in Sect. 4.1, it feels natural to object to the Liberal rule on the basis that it may be unwise to choose an act that is optimal relative to some arbitrary probability distribution over the possible states, without regard for whether the act may be evaluated very differently across the other probability assignments consistent with one’s evidence. For example, in an imprecise probabilistic recasting of the study by Robalino and Lempert, the Liberal norm would likely say that any of the candidate policies—taxation, subsidies, or a mixture of the two—is permissible, because for each policy there is some probability function consistent with the evidence that recommends this policy. The same concern extends to the Maximal rule, which states that an act is rationally permissible just in case there is no other act with greater expected utility relative to every $\Pr \left( { \cdot } \right) \in R$, since any act that is permissible according to Liberal is permissible according to Maximal. These decision rules seem to give individual probability functions too much power by allowing them to veto any recommendation against choice of a given policy that would otherwise be made by one’s ‘credal committee’.

A similar concern extends to other decision rules commonly discussed in the literature on imprecise credences, such as MaxMinEU and HurwiczEU. MaxMinEU ranks acts in terms of their minimum expected utility relative to the probability functions in $R$. HurwiczEU is a generalisation of MaxMinEU that ranks the available acts in terms of a convex combination of their minimum and maximum expected utilities relative to the probability functions in $R$. Intuitively, both rules give extremal probability functions too much power in settling the recommendation of one’s ‘credal committee’. Intuitively, we would like to object that policies should also be evaluated by their performance on more moderate probabilistic hypotheses, which give middling credence to market failures and other forms of non-classicality.

The charge made in the previous paragraph was that HurwiczEU ignores moderate probability functions, letting decision-making be driven only by the pair of most pessimistic and optimistic probability functions, respectively. One would like to put the point as follows: HurwiczEU does not change its recommendations about what should be done if all of the non-extremal probability functions are removed from the agent’s representor. But this way of putting the point is too hasty, since it is often held, following Levi (1980), that representors should be convex. Hence it does no good to object that HurwiczEU would not change its recommendations if these moderate mixtures were removed, because if convexity is a rational requirement, then it would be irrational for a decision-maker to remove them. But we can put the point in another way. Suppose that o and o′ are tax policies which perform comparably well in the classical limit and comparably poorly as market failures accumulate. But suppose that o, unlike o′, performs well under moderately nonclassical conditions. Intuitively, we would like to say that o is preferable to o′, because o is more robust to economic uncertainty. But HurwiczEU ranks o and o′ comparably, and if o′ outperforms o even slightly under extremal conditions, HurwiczEU may recommend o′ over o. This suggests that HurwiczEU, as well as the MaxMinEU rule that it generalizes, may place insufficient emphasis on robustness to deep uncertainty.

Robustness and higher-order probabilities

In formulating this line of objection as it applied to subjective expected utility maximization or the Liberal rule for imprecise credences, we emphasized that a policy that is optimal relative to some particular admissible probability assignment may in principle be suboptimal or even catastrophic in expectation relative to other probability assignments that are not excluded by our evidence. Intuitively, the objection is not simply that there is some other admissible probability function relative to which the policy fails to maximize expected utility. Thus, the intuitions to which we have appealed are plausibly not of the kind that would lead us to accept the so-called Conservative rule, according to which an act is rationally permissible just in case it maximizes expected utility relative to every $\Pr \left( { \cdot } \right) \in R$. Intuitively, the Conservative rule evokes the same concern about giving veto power to individual members of the agent’s ‘credal committee’ as the Liberal rule, albeit in the opposite direction. In our case study based on Robalino and Lempert (2000), the Conservative rule would presumably imply that no government policy is permissible because for each policy, some member of the representor recommends against that policy.

Plausibly, the intuitive objection that we have sought to articulate in Sects. 4.1–4.2 gains purchase only insofar as it makes sense to say things such as that there are more admissible probability functions on which the policy fails to maximize expected utility than on which it succeeds. The objection to rules such as Liberal, Maximal, MaximinEU and HurwiczEU is that they heed the advice of two or fewer probability functions, even when many more elements of the agent’s `credal committee’ disagree. However, one might worry that this talk of more and fewer admissible probability functions cannot be made precise without helping ourselves to a second-order probability measure on the set of admissible probability assignments, by which to quantify the size of a collection of first-order probability distributions.

For reasons we’ve already noted, this would, in a sense, be unsurprising. The robust satisficing norm is characterized in the RDM literature as a descendant of Starr’s domain criterion, which explicitly relies on a uniform second-order probability function. In a different sense, however, reliance on a (unique) second-order probability function would be very surprising for anyone driven by the sort of concerns that motivate RDM and the DMDU community as a whole. Prominent among them is the thought that it is inappropriate to require decision-makers facing severely uncertain long-term policy problems to express their uncertainty in the form of a unique probability distribution. Lempert (2002: p. 7310) notes that the decision support tools associated with RDM are designed “to help users form and then examine hypotheses about the best actions to take in those situations poorly described by well-known probability distributions and models.”

These remarks are to do with first-order probabilities. Nonetheless, it seems implausible to require precise second-order probabilities while conceding that our evidence is so incomplete and/or ambiguous that no precise probability assignment over the relevant first-order hypotheses is warranted by our evidence. In fact, there is a strong case to be made that this is simply incoherent.

We have in mind here the familiar objection, pressed by Savage (1972: p. 58), that probabilistic uncertainty with respect to the correct probability function over first-order hypotheses requires assigning a unique probability to each first-order hypothesis, corresponding to the (second-order) expectation of the first-order probability. Thus, suppose that the second-order probability represents the agent’s subjective probability with respect to the uniquely rational credence assignment warranted by her evidence. It seems very plausible that any rational agent’s subjective probabilities should defer to the uniquely rational credence function, so understood, in the sense that if $\Pr \left( { \cdot } \right)$ is the subjective probability function for an agent with total evidence $E$ and ${\text{Ev}}_{E} \left( {{ } \cdot { }} \right)$ is the uniquely correct credence function warranted by $E$, then we require that $\Pr {(}H{|} {\text{Ev}}_{E} \left( {{ }H} \right) = x) = x$ for any hypothesis $H$.²⁰ It then follows by the Law of Total Probability that $\Pr \left( H \right) = {\mathbb{E}}\left[ {{\text{Ev}}_{E} \left( H \right)} \right]$, where the expectation is defined relative to ${\text{Pr}}\left( { \cdot } \right)$. Thus, the agent, if she is rational, has some precise degree of confidence in $H$ after all.²¹

A solution?

In light of the foregoing, we think proponents of robust satisficing have some explaining to do about the relationship between their position and second-order probability theory. If the exposition and defence of robust satisficing relies on second-order probabilism, then we may find ourselves committed to a unique first-order probability assignment after all.

This problem may be answerable. In particular, there is the following rejoinder to the objection that a decision criterion formulated in terms of a robustness measure, μ, on $R$ presupposes second-order probabilities: namely, that μ cannot be a probability measure because $R$ is not a sample space. Roughly speaking, a sample space is a set of different ways things could be, exactly one of which is realized. However, $R$ need not be viewed as a set of probability functions exactly one of which is true or correct.

It could be suggested that there is always some credence function that is uniquely warranted by our evidence, whereas you and I lack the cognitive wherewithal to fix our credences with the required degree of precision. However, this sort of view is atypical in the recent philosophical literature on imprecise credences. Proponents of imprecise probabilism like Joyce (2005, 2010) instead take the view that even an ideally rational agent will, in some cases, refrain from assigning precise probabilities. Joyce (2010: p. 283) insists that “since the data we receive is often incomplete, imprecise, or equivocal, the epistemically right response is often to have opinions that are similarly incomplete, imprecise or equivocal.” Thus, it is not the case that some element of $R$ represents the epistemically right response. That role is to be played by the mushy credal state represented by $R$ itself.

If we take a view of this kind, then $R$ cannot be interpreted as a sample space, since its elements are not different candidates for the uniquely correct probability function. As a result, a measure on $R$ is not a probability measure. In this way, one might argue, a demand for robustness does not presuppose second-order probabilities.

We are not sure how persuasive this rejoinder will be found to be. Some may worry that, for all we have said, the intuitive appeal of relying on a measure on $R$ derives from implicitly treating $R$ as a sample space and the measure as a probability measure. We also note the following. It is relatively common in the RDM literature—indeed, throughout the DMDU literature—to describe cases in which decision-makers’ uncertainty about the future is not appropriately represented by a unique probability distribution as cases in which probabilities are unknown. Lempert, Popper, & Bankes (2003) write that since “traditional decision theory addresses the multiplicity of plausible futures by assigning a likelihood to each and averaging the consequences” (26), traditional decision theory is unhelpful for long-term policy analysis because there is “simply no way of knowing the likelihood of the key events that may shape the long-term future.” (27) Similarly, Marchau, Walker, Bloemen, & Popper (2019: p. 7) describe scenario-based planning as appropriate for cases in which “the likelihood of the future worlds is unknown”. These remarks are naturally taken to imply that there is some uniquely correct probability function among the set of probability functions that we take our evidence as failing to rule out. It is just that we don’t know what it is. In that case, we cannot argue, in the way we have done here, that the set cannot be construed as a sample space.

Here is a second point, in a similar vein. Readers may have noted that our discussion throughout this section has focused on robustness considered with respect to an ensemble of probability distributions, as opposed to the more common emphasis in RDM analyses on robustness with respect to the range of plausible future outcomes. Understood in the latter way, robust satisficing is to be considered akin to non-probabilistic norms for decision-making under uncertainty, like Maximin, Minimax Regret, or Hurwicz, and not to decision norms for imprecise probabilities like MaxMinEU or HurwiczEU.

As noted in our discussion of Rosenhead, Elton, & Gupta (1972) on robustness as a decision criterion, robust satisficing, so understood, also seems to require a measure over the set of states that behaves like a (uniform) probability distribution. Furthermore, in this context, there is no plausibility to the idea that the set which forms part of the measure space cannot be interpreted as a sample space. Clearly, exactly one of these states is the true state of the world. The objection that we are here just smuggling in probabilities via the back door strikes us as harder to evade.

Satisficing

Our discussion in Sect. 4 concerned the desirability of choosing options that are robustly supported, in the sense of being approved by a larger proportion of the probability functions in $R$. In this section, we explore the relationship between robustness and satisficing.

A confusion of tongues

The term ‘satisficing’ is used in different ways in different literatures. In this section, we examine the relationship between robust satisficing and three existing conceptions of satisficing choice in order to help shed light on the content of the robust satisficing norm, as well as its motivations.²²

Herbert Simon and those influenced by him often use the term ‘satisficing’ to pick out a particular dynamic decision heuristic (Selten, 1998; Simon, 1955). Heuristic satisficers set an aspiration level in one or more goods, to be used as a benchmark for satisfactory performance. Heuristic satisficers then search through options one at a time, checking whether each option meets their aspirations. When heuristic satisficers find an option which meets all of their aspirations, they halt their search and choose that option.

Recommendations to adopt a satisficing norm are sometimes likened in the RDM literature to Simon’s notion of satisficing choice (Lempert, Popper, & Bankes, 2003: p. 54, Lempert, Groves, Popper, & Bankes, 2006: p. 516). We find it plausible that the procedures for decision framing associated with RDM can be motivated by considerations like those that motivate heuristic satisficing. Consider the accuracy–effort trade-off: in many situations, the accuracy of judgments and the quality of decisions trades off against the effort of making them (Johnson & Payne, 1985). Thus, in our case study in Sect. 2.2, Robalino and Lempert found the full uncertainty space to be intractably large and used a smaller landscape of plausible futures as a less-effortful proxy.²³ RDM is also similar to heuristic satisficing in that it adopts a procedural conception of decision-making (Simon, 1976), emphasizing the importance of theorizing about the processes through which decision problems are framed and constructed (Helgeson, 2020).

Nonetheless, we find it implausible that robust satisficing as a decision norm for solving suitably-framed decision problems can be recommended on the very same grounds that support a satisficing approach in Simon’s work on bounded rationality. That is because robust satisficing is not a search heuristic. It is a norm that allows us to choose among options that are open to view all at once. This is not to deny that there is a search component in RDM. For example, RDM is often applied in contexts that do not have a fixed menu of candidate strategies. Lempert, Popper, & Bankes (2003: p. 66) note that “human participants in the analysis are encouraged to hypothesize about strategic options that might prove more robust than the current alternatives … These new candidates can be added to the scenario generator and their implications dispassionately explored by the computer.” Nonetheless, the robust satisficing decision rule recommended by Lempert and colleagues functions, so far as we can tell, as a criterion for the synchronous comparison of different candidate strategies. Asked to assess candidate policies side-by-side in an imprecise probabilistic setting, we are to prefer that which performs satisfactorily across a wider range of admissible probability distributions on possible futures. This recommendation is to be contrasted with Starr’s recommendation to prefer the act that performs optimally across a wider range of admissible probability distributions.

So far, we have discussed Simon’s conception of satisficing choice. A second tradition uses the term satisficing to paint a general contrast between maximizing and non-maximizing rules or procedures. In this vein, Gerd Gigerenzer writes: “Relying on heuristics in place of optimizing is called satisficing” (Gigerenzer, 2010, p. 529).

Robust satisficing differs importantly from traditional maximizing rules. Robust satisficing does not require agents to maximize expected utility, and does not extend familiar maximizing tools from neoclassical economics. Nor does robust satisficing rely on the insistence that maximizing a quantity within a problem framing will also maximize that quantity in the world. In fact, it is precisely because problem framings under deep uncertainty may not fully capture the underlying reality that it can make good normative sense to maximize quantities such as satisfactoriness, even if what we ultimately care about is welfare or utility.

Nonetheless, robust satisficing may be thought to have a maximizing component, since we try to maximize the robustness to uncertainty of achieving a satisfactory outcome. Formal specifications of the robust satisficing rule will thus involve maximizing a value function, and we set out one such specification in Sect. 5.2. But what we have here is a shallow sense of maximization that may also be shared by paradigmatic cases of heuristic cognition. For example, consider the heuristic of tallying or equal-weighted linear choice (Dawes & Corrigan, 1974). In binary choice, tallying instructs agents to add up the number of decision cues on which each option outperforms the other, then choose the option with the highest tally, or either option in the case of a tie. More formally, for option i, let t_ij = 1 if option i performs best on cue j; − 1 if option i performs worst; and 0 otherwise. Then tallying is equivalent to maximizing the value function V(o_i) = Σ_j t_ij. But this fact is not standardly taken to show that tallying involves any unacceptable type of maximization. Likewise, it may not be appropriate to regard robust satisficing as a maximizing rule even if the rule involves maximizing some value function.²⁴

A third tradition that will be most familiar to moral philosophers follows Slote (1984) in taking satisficing to describe a criterion of rightness on which it can be right to do less than the best. Slote argues that agents are sometimes rationally or morally permitted to choose a satisfactory outcome even when they know of a better outcome that is costlessly available to choose. For example, on this interpretation it may be rationally permissible to sell your house for a large amount of money, even if you could fetch a higher price with no additional effort and would prefer to do so, because the large amount is already good enough.

In Slote’s conception, satisficing is a norm for decision-making in static contexts, where the available options are open to view all at once. As a result, robust satisficing may be more in line with Slote’s conception of satisficing choice than with Simon’s conception, since robust satisficing also represents a criterion for the synchronous comparison of different candidate strategies. This could lead readers to worry that robust satisficing has similarly contentious implications: in particular, that it may permit the choice of dominated options when there are many (equally robustly) satisfactory strategies available. However, this would be to overstate the similarity with Slote. Whereas Slote maintains that meeting a satisficing threshold is a sufficient condition for rationally permissible choice, we could hold that robust satisficing is only a necessary criterion on rational choice in the contexts we are considering, allowing the choice between multiple robustly satisfactory options to be made on other grounds, such as by ruling out dominated options.

Having explored the relationship of robust satisficing to existing conceptions of satisficing, we next explore an analogy between robust satisficing and voting theory which could be used to justify the turn to robust satisficing.

Voting theory

In the literature on decision-making and imprecise probabilities, comparisons with social choice are abundant. For example, Weatherson (1998: p. 6) writes: “we can regard each of the [probability functions in the representor] as a voter which voices an opinion about which choice is best”. Viewed in this perspective, it is natural to consider voting rules as ways of aggregating preferences across members of the ‘credal committee’. The major impediment to doing so presumably comes in the form of doubts about the use of a measure that would allow us to compare the size of different subsections of the ‘electorate’, which we addressed in the previous section.

We can then think of the domain criterion as an example of plurality voting, the most commonly used voting method in democracies today. Each voter casts a ballot for her most preferred option, and the option with the most votes is the winner. We shall interpret the domain rule as stating that when the agent’s beliefs are modelled by a representor R and μ represents an indifferent weighing function over R, then any option o is valued at μ(M_o), the measure of the set M_o ⊂ R on which o maximizes expected utility, and choice of o is permissible just in case its value is maximal. Under the domain criterion, each admissible probability assignment may then be conceived as a voter who casts a ballot for her most preferred option, understood as that option that maximizes expected utility relative to the probability function whose vote is to be cast. So understood, the domain criterion requires choice of the option(s) with the greatest share of first-place votes.

An alternative to plurality voting is approval voting (Brams & Fishburn, 1983). Ballots no longer necessarily indicate each voter’s most preferred option, but rather all options that she finds acceptable, allowing each voter to vote for multiple candidates. Every ballot on which an option appears gives that option one vote. The election goes to the candidate(s) with the most votes. We can think of the norm of robust satisficing suggested in the RDM literature as an example of approval voting. In the imprecise probabilistic context, we interpret this decision rule as valuing options at μ(S_o), the measure of the set S_o ⊂ R on which o has satisfactory expected utility, with choice of a given option permitted just in case its value is maximal. In this case, each admissible probability assignment may be conceived as a voter who casts a ballot for every option that she finds satisfactory given the probability assignment whose vote is to be cast, with the winner as the option(s) with the most approval votes.

Earlier, we asked why the RDM literature links satisficing and robustness, as opposed to directing us to pick the option that is robustly optimal à la the domain rule. One way in which this question may be understood, we now suggest, is in terms of a choice between plurality voting and approval voting as a means of aggregating evaluations across the agent’s ‘credal committee’. The literature on voting methods contains a number of arguments for the relative superiority of approval voting (Brams, 2008; Brams & Fishburn, 1983). While some of these arguments fail to carry over to the current setting,²⁵ others can be transposed, given suitable tweaks. We discuss one such argument below.

Benefits of approval voting

Ideally, a voting rule should avoid problematic forms of vote-splitting. Suppose that a diverse electorate is asked to choose between taxation and a combined tax/subsidy hybrid policy for climate abatement. 60% of the electorate favours the hybrid, and only 40% of the electorate favours the tax. Under plurality voting, the hybrid will be chosen. But now suppose that voters are asked to choose between a tax-only policy and a pair of hybrids, one of which includes a more generous subsidy than the other. 40% of voters continue to favour the tax, but the remaining 60% of voters split evenly between the two hybrid options. Now, the tax-only approach wins under plurality voting.

That seems like the wrong result. The tax-only approach has been chosen only because votes against the tax policy were split between a pair of competing policies. Fortunately, approval voting allows us to avoid this result. It does not require voters to choose between the two hybrid options. Most voters who approve of one mixed policy would presumably approve of the other, and vote-splitting would thus be avoided. This provides a strong reason to prefer approval voting to plurality voting.

Cashing out the thought that approval voting is less vulnerable than plurality voting to perverse forms of vote-splitting places important constraints on how approval voting and vote-splitting are understood. On the one hand, approval voting must not be understood so broadly that it may in principle coincide with plurality voting. This would happen, for example, if voters are such that they always approve of only their most preferred candidate. On the other hand, immunity to vote-splitting must not be understood so broadly that it is satisfied even by approval voting in which each voter only ever approves of their more preferred candidates.²⁶

One natural type of immunity to vote-splitting is captured by Sen’s α. Where S is the set of electoral candidates, P is a set of preference orderings, and f (P, S) is a voting function that returns a subset of S as the winner(s) given P, f satisfies α just in case whenever x $\in$ f (P, S) and x $\in$ S′ $\subset$ S, it is the case that x $\in$ f (P, S′). In other words, a winning option would not have lost had we eliminated a different option from the ballot. Equivalently, no losing option would have won had some new alternative been added to the ballot. Thus, when f satisfies α, electoral outcomes are immune to the spoiler effect, whereby the entry of a new candidate into a political contest alters the electoral outcome in a way that favours an existing candidate rather than the entrant. As the example from the start of this section illustrates, plurality voting violates this condition.

Approval voting satisfies α so long as what counts as an approvable choice does not vary with the menu of options: for example, if any voter votes for any policy option just in case it yields (expected) GDP per capita above some fixed absolute threshold. Within the context of choice under deep uncertainty, the same can be said of a robust satisficing rule that scores options in terms of the value of μ(S_o) provided that Pr $\in$ S_o just in case o’s expected value along some dimension (or composite of dimensions) relative to Pr exceeds some fixed absolute threshold. Call this fixed threshold robust satisficing.

In our view, vote-splitting is no less of a concern in the context of decision-making under deep uncertainty, with voters conceived as members of the decision-maker’s ‘credal committee’. If anything, it is a greater concern. ‘Voters’ and ‘candidates’ in this context cannot make strategic choices to mitigate spoiler effects. Furthermore, the individuation of options is to a large extent arbitrary. A given policy can be subdivided indefinitely into its possible implementations, replacing one candidate with a multitude of clones. Insensitivity to spoiler effects in this context can be conceived as another kind of robustness: namely, as robustness with respect to arbitrary choices about how to individuate the decision-maker’s options. We take this to provide a strong reason to favour fixed threshold robust satisficing over the domain rule.

As we have already noted, the RDM literature does not typically define satisficing in terms of satisfaction of an absolute threshold. Instead, satisficing is typically understood in terms of a regret measure. As a result, what counts as a satisfactory choice can in principle vary with the menu of options, and the addition or subtraction of candidates from the menu of options can, respectively, change losers to winners or winners to losers. We think this provides a reason to reject the standard conception of the satisficing threshold appealed to in the RDM literature.

Of course, it may be objected that it is undesirable in some other respect to insist that decision-makers should decide in light of a fixed absolute threshold. Lempert, Popper, & Bankes (2003: p. 56) suggest that a regret measure is to be recommended because this “supports the desire of today’s decision-makers to choose strategies that, in retrospect, will not appear foolish compared to available alternatives.” For our part, we think insensitivity to spoiler effects should weigh much more heavily.

In addition, we think that there are good independent reasons to operate with an absolute satisficing criterion when considering issues in long-term policy analysis related to global catastrophic risks like those enumerated in the introduction, where the avoidance of catastrophe is paramount. A catastrophe, in the sense at issue here, is arguably not merely some outcome that is sufficiently worse than the best that might have been achieved. Thus, we would not hesitate to describe the unanticipated occurrence of a runaway greenhouse effect that renders our planet inhospitable to life as catastrophic just in case we simultaneously discovered that this outcome was by now unavoidable. It seems more plausible to understand a catastrophe, in the sense at issue here, as an event that is bad relative to some threshold that does not depend on what actions are available.

Directions for future research

We emphasize that the previous sub-section offers just a taste of what we think voting theory can offer the study of robust decision-making in the face of deep uncertainty. There is more that could be said in comparing plurality voting and approval voting in this context. For example, another advantage claimed for approval voting over plurality voting by Brams and Fishburn (1983) is its greater propensity to elect Condorcet winners: i.e., options that are preferred by a majority to every other option in any pairwise comparison. In addition, there is no reason ultimately to restrict our analysis to just these voting methods. This, we think, is ultimately the strongest obstacle to justifying an approach that marries a concern for robustness with an emphasis on satisficing, when it comes to long-term policy decisions involving imprecise probabilities. Even if approval voting in this context is preferable to plurality voting, it may well not be preferable to other voting methods that, like plurality voting, do not rely on any satisficing threshold to define when a candidate receives a vote.

Conclusion

Our aim in this paper has been to open a dialogue between philosophers and the DMDU community about robust satisficing as a decision norm, specifically when applied as part of RDM decision analysis. We think philosophers can learn interesting lessons by considering the approaches suggested by the DMDU community for solving the choice task, and not merely its contributions to the art of decision framing. We also think philosophers have something to offer in return, and we hope this paper helps to make our case.

As befits an attempt to open a dialogue, we do not draw any hard and fast conclusions. We’ve noted objections that may be raised against robust satisficing as a decision criterion and suggested how these objections could be met, albeit in ways that require revising aspects of the standard presentation in the RDM literature. Our primary conclusion is that the robust satisficing norm repays further clarification and assessment.²⁷