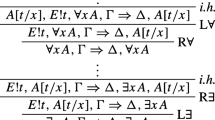Single-domain free logic and the problem of compositionality

Abstract

In this paper, I will defend a new compositional semantics for single-domain free logic. This semantics makes use of a distinction between the semantic value of a singular term and its semantic referent. The semantic value of a singular term is conceived of as a set that either contains the semantic referent or no element at all. The semantic referent is the object that the term designates. Before I will introduce this new semantics for single-domain predicate and an S5-type modal logic in detail, I will present five related problems of compositionality of the standard semantics for these logical systems. After that I will show in detail how my new proposed alternative semantics can be used to solve nearly all of the outlined five problems.

1 Introduction: empty singular terms, standard single-domain free logic and compositionality

Single-domain free logic makes room for the possibility of meaningful singular terms that lack a semantic referent. If one aims to capture all ordinary uses of singular terms in natural language by means of a formal semantic framework, it is also required to capture uses of singular terms that lack a semantic referent. Singular terms can lack a semantic referent for different reasons and be nevertheless meaningful.

Definite descriptions can lack a referent because they are incomplete, or they express a descriptive condition that is not actually or impossibly satisfied. For example, a definite description like “the possible sister of Dolf Rami” is incomplete¹ and it also seems to be impossible to add information that makes this description complete. Hence, it seems to be a good candidate for a definite description that lacks a referent. Furthermore, there are definite descriptions like “the actual winner of the Stanley Cup in 2005” that lack a semantic referent because the description is not satisfied by a single object. In 2005, there was a lockout and the whole season was suspended, hence, no team was able to win the Stanley Cup in 2005. As a last example, let me mention the description “the largest natural number”: this description lacks a semantic referent for metaphysical or conceptual reasons. It is part of the nature of natural numbers that there are infinitely many and, hence, a largest number is impossible. Certainly, these are only convincing examples of singular terms that lack a semantic referent for those who assume that definite descriptions are singular terms and not quantifier expressions. Interestingly, this view is a minority-view in Philosophy, but the majority-view in linguistics. I think, the linguists are right. However, for the skeptics there are also other kinds of examples.

The clearest cases, I think, are deictic expressions that are used with a pointing gesture that fails to identity a single object. For example, if one uses a demonstrative like “that” with an imprecise and blurred pointing gesture, it makes sense to assume that such a use of “that” has no semantic referent, although the user has a certain object in mind. Furthermore, if someone uses a complex demonstrative like “This dog” to point to a spatiotemporal region that contains no individual object at all and if there is no meaningful deferred interpretation of this pointing gesture, then it also makes sense to assume that the expression “this dog” lacks a semantic referent in such a context.

Furthermore, there also seem to be proper names that lack a semantic referent. It is generally agreed that proper names can be introduced into use either by using a definite description or a demonstrative/deictic expression to initially fix the referent of a name or establish a chain of uses of the very same name. For the outlined reasons, it can be possible that such a name-introducing deictic expression or definite description can lack a semantic referent. Nevertheless, it can be possible in such cases that the use of such a name gets established, although it lacks a referent unnoticed by the users, at least for a certain time. Consequently, we have a meaningful proper name that lacks a semantic referent. Names of phantom-islands are a very good real-life example of such kind of names. In such cases, apparently a name for an island is established, but later it turns out that the island in fact did not exist and that the assumption that it exists was based on some error or misconception.²

This shows, I think, that a proper formal semantic treatment of singular terms, has to be able to account for meaningful singular terms that lack a referent of the outlined kinds. To some extent this requirement seems to be independent from the fact whether one assumes non-existent objects or not. All the mentioned examples are compatible with the assumption of non-existent objects, but these examples to do not seem to provide good examples of expressions that refer to non-existent objects. In this paper, I will focus, for the sake of simplicity, only on the formal treatment of proper names that lack a semantic referent. However, my considerations can very easily be extended to the other mentioned examples.

Standard single-domain free logic promises, at first sight, to provide a plausible framework for the described purpose. However, this framework is subject to several problems that concern the compositional status of this semantics: (a) a general problem of compositionality and four related special problems that concern (b) the abstraction of correct Russellian propositions, (c) the correct semantic interpretation of names and predicates, (d) the interpretation of the compositional contribution of the existence predicate, (e) different plausible options concerning the compositional interpretation of identity sentences. In this essay, I will, at first, lay out the standard semantic framework of single-domain free logic. Secondly, I will introduce in detail the mentioned five problems. Thirdly, I will propose a modification of the standard semantic framework of a single-domain free logic, that makes use of a distinction between the semantic value of a singular term and its semantic referent. The semantic value of a name is conceived of as a set that either contains a single or no element. The semantic referent is the single element of this set if it has any. Against the background of this modification, I will develop a new and modified version of a single-domain free logic for first-order predicate logic and first-order modal logic, that allows us to solve most of the five mentioned problems.

2 Setting the stage: The standard semantic framework of a single-domain free logic

There are at least two general standard semantic frameworks a free logic can make use of: a single-domain or a dual-domain framework. The first framework makes use of a single domain that is both conceived of as the domain of reference and of quantification. However, in opposition to the semantic framework of classical logic, it allows that some singular terms lack a semantic referent. And according to one version of this kind of framework, universally free (inclusive) logic, it is also possible that the domain of reference and quantification is empty.³

The second mentioned framework distinguishes two different sorts of domains, an inner, possibly empty, domain and an outer domain that has to contain, according to the standard interpretation, at least one object and all objects of the inner domain.⁴ There are now at least three different options how this formal distinction between inner and outer domain is filled with flesh. Option 1: The inner domain is interpreted as the domain of quantification, the outer as the domain of reference. Quantifiers are typically existentially loaded.⁵Option 2: This option makes the reverse identification. Quantifiers are not existentially loaded. On this basis, we have a choice: either to identify the inner domain with the extension of the existence predicate or to conceive of the extension of the existence predicate as a proper subset of the inner domain. Option 3: There are two quantifiers, an outer and an inner quantifier. The outer domain is additionally also the domain of reference. Only the inner quantifier is existentially loaded.⁶ This option is a variation of a classical logic framework that makes use of quantifiers that are not existentially loaded. The main difference between such a framework and Option 3 is that, on this basis, we can define a second derived set of quantifiers by means of a quantifier domain restriction with the existence predicate. According to Option 3, we have two sets of primitive quantifiers. That is the only significant difference, hence, it is questionable whether Option 3 should be conceived of as a genuine version of free logic. It depends on further possible assumptions: (a) whether we additionally allow that both domains can be empty, or (b) whether we allow that singular terms may lack a semantic referent.

The main motivation for a single-domain framework is to allow for the possibility of meaningful singular terms that lack a semantic referent. This kind of framework provides a very modest modification of the classical semantic framework to allow for this possibility. There are also other options to account for the possibility of meaningful singular terms that lack a semantic referent. For example, we could also account for this possibility on the basis of a dual domain framework. That is, nothing speaks against the option that we allow both (a) singular terms that refer to non-existent objects and (b) singular terms that lack a semantic referent. Typically, it is assumed that we should choose between these two options. However, in this paper, I will exclusively draw my attention to the single-domain framework and some of its weaknesses and leave the other mentioned and not yet in detail investigated options to future research.

Let me at first outline those details of this framework that are relevant for the problems that I will discuss. On the basis of a single-domain free logic, we have several choices, how we semantically interpret sentences that contain at least one singular term that lacks a semantic referent. The most important question is, which truth-values we should assign to such sentences. There seem to be three prima facie options: (a) we assign, without exception, to each of these sentences the value FALSE, (b) we assign, without exception, to each of these sentence either no truth-value at all or the truth-value NEITHER TRUE NOR FALSE, (c) we allow that these sentence can have different truth-values; they can be true, false or neither true nor false.⁷

Typically, single-domain free logic is regarded as an alternative to classical first-order predicate logic. Against this background, it is a purely extensional language. That is, only the (actual) extensions of constituent expressions are relevant for the determination of the truth-value of a sentence and, hence, the substitution of co-extensional constituent expressions cannot change the truth-value of the evaluated sentence. But this is not the only way how one could develop a single-domain free logic. One could also make use of the key aspects of this framework on the basis of modal logical framework or any other non-extensional semantic framework.

Against the background of a purely extensional framework, it seems to be questionable whether we could assign the truth-value TRUE to an atomic sentence that contains at least one singular term that lacks a referent in a meaningful way, like, for example, the sentence “Fa” or “a = a”. If the referent of a singular term is identical with its extension and if only the extensions are relevant for the truth-value of a sentence, there seems to be no meaningful way to assign to such sentence the truth-value TRUE if we make use of the standard-truth-conditions of these sentences that require some sort of relation between the extension of the term and the extension of the predicate that such a sentence contains. If there is one extension missing, then such a relation cannot obtain, which is required for the truth of an atomic sentence like “Fa”, for example. That is, in the case of a sentence like “Fa”, this sentence can only be true if the extension of “a” is an element of the extension of “F”. Typically, a free logic is called positive, if it allows to assign to at least one kind of atomic sentence the truth-value TRUE. I think, there is no meaningful possibility of a positive free logic that is based on a purely extensional version of a single-domain semantic framework. However, non-extensional versions of positive free logic seem to be possible and defensible frameworks. Relative to such frameworks, the truth-value depends on some other semantic value than the extension of the expressions it is built from.

The remaining options seem, therefore, to be (a) a negative free logic that assigns to every atomic sentence that contains at least one singular term that lacks a referent the truth-value FALSE, (b) a neutral free logic that assigns to every atomic sentence that contains at least one singular term that lacks a referent the truth-value NEITHER-TRUE-NOR-FALSE, (c) a hybrid non-positive free logic that assigns either of the mentioned two truth-values to atomic sentences that contain at least one singular term that lacks a referent, but no other value.⁸

An additional important issue is which truth-values we assign to non-atomic sentences if they contain at least one singular term that lacks a semantic referent. To an important extent this issue depends on the framework we choose concerning atomic sentences of this kind, but it also depends on the interpretations of quantifiers and connectives. We will investigate these additional issues latter in this paper. The problems that I aim to discuss mainly concern atomic sentences, but the solution to these problems that I will propose will also have consequences for the semantics of quantifiers and connectives.

There are three different important kinds of atomic sentences that a free predicate logic may contain. Firstly, ordinary atomic sentences that contain non-logical predicates. Secondly, atomic sentences that contain the identity predicate. Thirdly, atomic sentences that contain the existence predicate. According to free logic, both the identity predicate and the existence predicate are logical predicates because they play a distinctively logical role. The first one accounts mainly for the validity of arguments of the following and related forms:

Fa

a = b

——–

Fb

The second one accounts for the validity of arguments of the following and related forms in free logic:⁹

∀xFx	Fa
E!a	E!a
——–	——–
Fa	∃xFx

The fact that we cannot only distinguish atomic sentences that contain logical predicates from those that contain non-logical predicates, but that we have to assign to each kind of atomic sentence that contains a logical predicate with a distinctive logical role independent truth-conditions allows the meaningful possibility of a hybrid non-positive free logic. That is, because we have to provide three different sets of independent truth- and falsity-conditions for all three mentioned kinds of atomic sentences, we are, hence, free to specify these conditions in very different ways if we can provide good reasons for these alterations.

The single-domain semantic framework that I make use of in the following consists of a single and possibly empty domain of discourse D. For the sake of simplicity, I will only use a single set of singular terms, namely individual constants. (That is, I will not make use of definite descriptions or other kinds of singular terms in this paper.)

Additionally, I make use of four different functions to specify the truth-conditions of the formulas in my framework: (1) a partial denotation function Den () that is relativized to the domain D and that can but need not to assign to every individual constant a single element of D, (2) a total assignment function δ() that is relativized to the domain D and that assigns to every individual variable a single element of D, (3) a total interpretation function I() that is relativized to the domain D and that assigns to every monadic predicate a subset of D and to every n > 1-adic predicate a set of n-tuples of elements of D, (4) a total valuation function V() that is relativized to all the other mentioned three functions and that assigns to each formula a truth-value.

Concerning atomic sentences that contain non-logical predicates we have the choice between at least two different options to assign truth-conditions to these sentences. These two kinds of options are the following paradigmatic truth-conditions for these sentences provided by standard negative¹⁰ and standard neutral free logic:¹¹

Negative free logic concerning non-logical atomic sentences:

V(Pt1…tn) = T	iff	Den(t1), …,Den(tn) are all defined12 and < Den(t1),…,Den(tn) > ∈ I(P);
V(Pt1…tn) = F		otherwise.

Neutral free logic concerning non-logical atomic sentences:

V(Pt1…tn) = T	iff	Den(t1), …,Den(tn) are all defined and < Den(t1),…,Den(tn) > ∈ I(P);
V(Pt1…tn) = F	iff	Den(t1), …,Den(tn) are all defined and < Den(t1),…,Den(tn) > ∉ I(P);
V(Pt1…tn) = N	iff	It is not the case that Den(t1), …,Den(tn) are all defined.

It seems to be difficult to think of any meaningful alternative to these two options if only extensional predicates are considered as constituents of atomic sentences. The choice between these two options depends on whether we believe in a specific linguistic conception of semantic presuppositions or not. According to this conception, every ordinary non-logical atomic sentence has the semantic presupposition that every singular term that such a sentence contains denotes something. If this presupposition is satisfied, then the sentence may have a classical truth-value. If it is not satisfied, the sentence is neither true nor false. If one believes in such a conception, it is natural to prefer the rendering of neutral free logic of atomic sentences over the rendering of negative free logic. The main motivation behind the treatment of non-logical atomic sentences according to negative free logic seems to be purely theoretical rather than linguistic. It aims to avoid the rejection of the law of excluded middle (and bivalence in general) and, hence, keeps the logic as simple and as classical as possible. Hence, it very much depends for which purpose we make use of our semantic framework. If we aim to use it as a formal semantics for natural languages, the choice might be different as if we would use it as the semantics of some sort of polished scientific or ideal language. We will come back to this issue later. In any case, there does not seem to be a plausible synthetic view that assigns to some non-logical atomic sentences the truth-conditions of negative free logic and to some those of neutral free logic if we, as we do, only consider purely extensional predicates as constituents of our atomic sentence. However, such hybrid views seem to be more plausible if we would additionally consider intensional or hyper-intensional predicates like “x is a possible thing” or “x is feared by y”.

Concerning atomic sentences that contain the identity predicate the two most plausible options are again captured by negative and neutral free logic.

Negative free logic concerning identity sentences:

V(s = t) = T	iff	Den (s) and Den(t) are both defined and Den(s) = Den(t);
V(s = t) = F		otherwise.

Neutral free logic concerning identity sentences:

V(s = t) = T	iff	Den(s) and Den(t) are both defined and Den(s) = Den(t);
V(s = t) = F	iff	Den(s) and Den(t) are both defined and Den(s) ≠ Den(t);
V(s = t) = N	iff	It is not the case that Den(s) and Den(t) are both defined.

The possible reasons for a choice between these two options are similar to the case of non-logical atomic sentences. However, there are additional complications that concern specific linguistic intuitions concerning identity that cannot be captured by both accounts. Firstly, at least some people tend to hold the intuition that trivial (reflexive) identity sentences like “a = a” are true irrespective of whether “a” designates something or not. As we will see, there are also some more theoretical reasons that may motivate such a view. My favourite examples for proper names that lack a semantic referent are names for phantom islands. “Sandy Island” is an example of this sort and there are people, like the inventor of free logic, Lambert, who accept the following claim as true:¹³

(1) Sandy Island = Sandy Island.

Lambert, however, does not hold that (1) is true just on the basis of our intuitive understanding of such sentences, he has philosophical and logical reasons for this acceptance:¹⁴ According to him, the law of identity “∀x(x = x)” is a logical law. He claims that if one holds that this generalisation is a law of logic, one must also accept that the instances of these law are logically true. (1) is an instance of this law; hence, (1) is, according to this reasoning, not only true, but logically true. However, this argumentation rests on a problematic implicit assumption. It is only valid if we assume a substitutional interpretation of quantification that makes use of substitution instances that contain constants that lack a semantic referent. However, it seems against the original idea of how quantifiers and variables work if one makes use of constants that lack a referent as substitutes for variables for the interpretation of quantifications. According to the original Tarskian semantics of quantifiers and variables, variables directly range over objects and, hence, substitution instances of a generalisation are completely irrelevant for the truth of a generalisation. On this basis, the truth of a generalisation is traced back to the truth of an open sentence relative to a variable-assignment that such a generalisation contains as syntactic constituent. Alternatively, there is the Mates-style semantics that, in opposition to Tarski, avoids the use of unbound-variables that are interpreted relative to assignments and interprets the semantics of bound variables by means of specific marked individual constants whose interpretation is permuted to mimic the semantic role of unbound variables relative to a Tarskian semantics.¹⁵ A third substitutional alternative to the mentioned two standard systems defines the truth of generalisations on the basis of all instances of a specific restricted set of constants that all in all denote every object in the domain of quantification. These three systems are extensionally and logically equivalent, but they are not equivalent to the semantics proposed by Lambert. If one thinks that a Tarskian semantics (or any of its variations mentioned) captures the true nature of generalisations, then Lambert’s proof is invalid. The burden of proof in this dispute seems to be on the side of Lambert.¹⁶

Secondly, certain people tend to hold the intuition that non-reflexive non-trivial identity sentences of the form “a = b” are simply false, if at least one of the two terms lacks a referent or if both of them lack a referent:

(2) Sandy Island = Sherlock Holmes.

(3) Tony Blair = Sandy Island.

Hence, identity sentences do not seem to be paradigmatic candidates to motivate a conception of semantic presuppositions for atomic sentences. In these cases, it is not so clear whether semantic presuppositions play any role concerning the assignment of truth-values to identity sentences.

Thirdly, there also seem to be cases of identity sentences of the form “a = b” that appear to contain two different empty names and that, however, appear to be intuitively true.¹⁷ The following sentence seems to be an example of this sort:

(4) Zeus = Jupiter

It seems to be true the neither “Zeus” nor “Jupiter” refer to objects that exist in the actual world, but these names have been introduced by Greek and Roman people into use on the basis of the false assumption that they refer to real objects. Hence, these names seem to be good candidates for names that lack a semantic referent. Furthermore, it also seems to be true that a sentence like (4) at least has a true reading. Therefore, we have prima facie good reasons to assume that (4) is an example of the described kind. In fact, it is not clear whether we should consider cases like (4) as clear cases for the literal truth of identity sentences of the logical form “a = b” that contain two empty names. However, one might also hold that (4) is only true because “Zeus” and “Jupiter” refer to the same non-actual mythological object. For example, someone might argue that these names were initially empty names but became names of mythological objects as soon as it was generally realized that the Greek and Roman gods do not exist. This shows in any case that there are no clear consistent data with respect to identity sentences that contain apparently empty proper names.

However, if one thinks that at least some of the outlined cases should be considered as data, different kinds of free logics seem to be required to capture these data. A negative free logic can only capture the second kind of cases. The first and third kinds of cases could only be captured on the basis of some kind of positive free logic. However, as I have already said, a purely-extensional single-domain positive free logic seems to be questionable from a compositional semantic standpoint. But that means: if we take the first kind of data seriously, identity sentences are either non-extensional or the extensional semantics with respect to names and identity sentences is more complicated than it is ordinarily assumed. We will come back to these issues later.

In the case of atomic sentences that contain the existence predicate, we seem to have at first sight the same two options as in the other two cases. However, in fact there seems to be a clear tendency for only one of the two options, at least from a purely linguistic point of view:

Negative free logic concerning singular existential sentences:¹⁸

V(E!t) = T	iff	Den(t) is defined.
V(E!t) = F	iff	Den(t) is undefined.

Neutral free logic concerning singular existential sentences:

V(E!t) = T	iff	Den(t) is defined.
V(E!t) = N	iff	Den(t) is undefined.

There is an important obvious asymmetry between the truth-conditions of existential sentences and the truth-conditions of all other introduced so far atomic sentences. There does not seem to be the possibility to assign to a sentence of the logical form “E!t” either the truth-value FALSE or the truth-value NEITHER-TRUE-NOR-FALSE. The main reason for this concerns one of the main attractive features of a single-domain semantic framework: it allows one to draw a tight connection between the fact that a singular term refers to something and the fact that a specific thing that is named by such a term exists. If we aim to make this connection, then we only have two options with respect to a reference-failure of a singular term: either we conceive of it as a sufficient condition for the non-existence of an object or we don’t. The first route is taken by standard negative free logic, the second route by standard neutral free logic. This specific status of singular existential sentences relative to a single-domain semantic framework distinguishes them from other atomic sentences. However, the question in the case of these sentences is whether we have the meaningful choice between the two mentioned semantic options at all. One thing is clear: in contrast to the neutral semantics with respect to non-logical atomic sentences, we cannot provide a motivation for the neutral semantics by making use of a conception of semantic presuppositions if we draw a close semantic connection between existence and successful reference. On this basis, singular existential sentences themselves express the very condition whose satisfaction is presupposed on the basis of a semantic conception of presupposition. Hence, it does not make sense to claim that these sentences have such a kind of semantic presupposition with respect to their constituent singular terms. The neutral semantics for existential sentences, hence, requires an alternative and independent motivation. Is there any kind of alternative motivation? There does not seem to be any linguistic motivation for such a view. The linguistic evidence is clearly on the side of the negative semantics. It is, for example, very plausible to assume that names for phantom islands are names that lack a semantic referent. Furthermore, if people know that “Sandy Island” is a name for a phantom island, they tend to evaluate the following sentence clearly as false:

(5) Sandy Island exists.

Hence, all the linguistic evidence seems to be on the side of the negative semantics for singular existential sentences. That is, if the proposed link between reference and existence makes sense at all, it clearly favors the negative semantics from a linguistic point of view.¹⁹

However, there could be purely theoretical reasons in favor of neutral semantics. There seem to be at least two general principles mentioned and discussed in the literature that may provide such a theoretical motivation: firstly, there is the principle of defectiveness²⁰ that says that every purely extensional sentence that contains a singular term that lacks a semantic referent is semantically defective and, hence, we cannot assign a classical truth-value to such a sentence.²¹ I agree with Evans and Sainsbury that there are good reasons to claim that this principle is too strong and not properly motivated.²² Maybe it is true that if a purely extensional atomic sentence has at least one constituent expression that lacks a semantic value, we can reasonably say that this sentence is semantically defective, and, hence, we should not assign a classical truth-value to this sentence. But the situation changes if we focus on connective and quantified sentences.

If we assign a non-classical truth-value to a semantically defective sentence, this value can function as an input for a truth-function that a specific connective expresses. Against this background, it seems to be in principle possible and meaningful to assign to a connective sentence that contains a constituent sentence with at least one non-classical truth a classical truth-value. Non-classical truth-values are proper semantic inputs for truth-functions. Evans provides external negation as a counterexample to the proposed restriction. Internal negation maps a non-classical truth-value of a sentence to the very same truth-value. External negation maps a non-classical truth-value to the truth-value TRUE. However, external negation is not only a meaningful theoretical possibility relative to a logical framework with at least three truth-values, there is also linguistic evidence that such kind of negation is also operative in natural languages. Consider the following two example sentences:

(6) It is not the case that Sandy Island is a planet.

(7) It is not the case that Sandy Island exists.

Whatever truth-value we may assign to the embedded sentences in (6) and (7), it seems intuitively so that both (6) and (7) are true and, hence, have a classical truth-value. The best explanation for these data seems to be to assume that (6) and (7) contain some kind of external negation.

I would like to add the case of disjunction as an additional counterexample. A classical disjunction is true if at least one of the disjuncts is true. It seems very plausible to generalize this principle with respect to non-classical logics with at least one non-classical truth-value. That is, the truth of exactly one of the disjuncts is (in general) sufficient for the truth of a disjunction. This meaningful theoretical possibility also seems to be confirmed by linguistic data. Intuitively, the following two sentences seem to have classical truth-values, although they contain constituent sentences without classical truth-values:

(8) Sandy island does not exist or Sandy island is an island.

(9) Sandy island is a planet or Jupiter is a planet.

Therefore, I conclude that the mentioned principle of defectiveness is too strong. It also seems to be possible to doubt its correctness with respect to quantified sentences. If one provides a Fregean analysis of quantifiers that treats them as properties of functions from objects to truth-values that are expressed by open sentences, then a quantification can have the classical value FALSE, although the corresponding function from objects to truth-values does not deliver any classical truth-value as output for any object. Consider, for example a function from objects to truth-values that is expressed by “x = a” if “a” lacks a semantic referent. This function does not map any object to the value TRUE. Nevertheless, it seems true that this function has the property of being satisfied by no object. If this property is responsible for the truth of “¬∃x(x = a)”, then it seems plausible to assume that “∃x(x = a)” is false.²³

Probably, the best we could do is to restrict the principle of defectiveness to extensional atomic sentences. In their case, one might argue that there is no meaningful possibility to assign to an atomic sentence a classical truth-value if at least one of the constituent expressions lacks a semantic value. However, the question is why we should restrict this claim to classical truth-values. Can’t we say, in more general terms, that if a sentence has (semantic) constituent expressions that lack a semantic value, it is impossible to compute a semantic value of the whole sentence in a compositional way? This question leads us to a second alternative principle that need not necessarily be restricted to atomic sentences.

Secondly, there is the no-input-no-output principle or principle of compositionality that says that the compositional calculation of the truth-values of sentences requires as inputs semantic values of the constituent expressions.²⁴ If one of the constituent expressions lacks a semantic value, a proper computation of the truth-values of a sentence is not possible and, hence, such a sentence will be treated as NEITHER-TRUE-NOR-FALSE. That is, we either assign no truth-value to such a sentence or the value N. We have already seen that under some circumstances this principle is compatible with cases of sentences that contain singular terms that lack a semantic referent. For example, in the case of connective sentences, if we treat the evaluation as neither true nor false as the assignment of non-classical truth-value to a sentence, then connective sentences that contain such constituent sentences do not violate this principle, even though they may contain proper names without a semantic value. Furthermore, we have seen there is an alternative Frege-inspired Tarskian semantics of quantified sentences that also allows the satisfaction of this principle, although such sentences may contain singular terms that lack a semantic referent. However, the crucial question now is, should we accept this principle also with respect to atomic sentences and could we, hence, find a way to adapt the semantics of atomic sentences for this purpose or could we justify a violation of this principle in these cases and justify the outlined negative semantics in such cases. That is one of the main questions that we will address in the next critical section. Now we have everything on the table to be able to address certain problems with the two kinds of standard semantics of a purely extensional single-domain free-logic semantic framework concerning three basic kinds of atomic sentences.

3 Five problems of the standard framework of a single-domain free logic

In this section, I will introduce five different problems that concern both distinguished versions of the standard single-domain semantic framework, namely negative and neutral semantics for atomic sentences. All of these problems seem to have a common source or at least seem to draw the attention to a fundamental background assumption of the standard single-domain semantic framework that is in tension with the compositionality principle and intimately related principles; the assumption that the semantic referent of a proper name is identical with the semantic value, that is, the truth-conditional compositional contribution of a proper name to the truth-conditions of sentences that contains this name. Based on the problems that will be outlined in this section, I will propose a rejection of this assumption and will argue for the distinction between the semantic referent and semantic value of a proper name.

3.1 The problem of compositionality

The first problem that I want to introduce is the objection from compositional semantics. The above mentioned no-input-no-output principle formulates a general constraint for compositional truth-conditional semantics. According to this conception of truth-conditional semantics, every meaningful expression that is a constituent of a sentence contributes a semantic value that is required as input for the computation of the truth-value of this sentence. A non-compositional evaluation of truth-values assigns to sentences a truth-value completely or partially independent of the semantic values of its constituent expressions. For example, the assignment of truth-values relative to modal sentences in non-normal modal logic is partially non-compositional. On the basis of negative and neutral semantics, atomic sentences that contain individual constants that lack a semantic referent also receive truth-values in a non-compositional way. However, this kind of evaluation is not completely arbitrary if there is some systematic semantic motivation for such a kind of non-compositional evaluation. Neutral free semantics paired with a semantic conception of presuppositions seems to offer such a kind of motivation. Atomic sentences with at least one individual constant that lacks a semantic referent are semantically defective, because a necessary precondition for truth-evaluability is violated. However, no justification is given why we can nevertheless assign a non-classical truth-value to such a sentence and why this kind of value can function as an input of truth-functions. This transition from a defect to a third semantic option is not properly motivated by a neutral free semantics combined with a semantic conception of presuppositions. Neutral free logic, on the one hand, excludes certain sentences from a compositional semantic treatment for good reasons, while on the other hand, it uses a semantic value of such sentences as input of the truth-functions denoted by connective expressions. Hence, the only properly motivated version of a neutral free logic has to take the principle of defectiveness on board. But we have already seen that this principle is questionable because of linguistic data that seem to falsify it.

Negative free semantics on the other hand does not have any a kind of systematic semantic motivation for the violation of the general principle of compositional semantics and, hence, the assignment of a classical value to atomic sentences that contain an individual constant that lacks a referent seems to be ad hoc and, therefore, not plausibly motivated.

A non-compositional assignment of truth-values to certain atomic sentences is in general problematic because atomic sentences in predicate logic are not literally atomic, they have a clear compositional structure. Hence, it seems to be a general requirement to provide a compositional assignment of truth-values in all possible cases. The burden of proof seems to be on the side of the defender of a negative or neutral free semantics, why the rejection of a compositional conception of semantics seems to be adequate in some exceptional cases, but in other cases not. It seems to be difficult for both views to offer the required motivations.

3.2 The problem of propositional abstraction

The second problem is the related problem of propositional abstraction. Propositions are still a hot-debated and controversial kind of being. For a larger number of people who believe in propositions and that propositions play a genuine semantic role, the conception of Russellian propositions is quite attractive. Russellian propositions are structured propositions that either have the semantic values or intuitive meanings of constituent expressions of a sentence that can be used to express these propositions as constituents. We must distinguish two fundamentally different versions of the Russellian view on propositions.²⁵

According to the semantic version of this view, Russellian propositions mainly play the role of semantic contents and are conceived of as structured abstractions from the semantic values of the constituent expressions of a sentence. That is, the logical forms of sentences can be represented as semantic trees that contain the semantic values of the constituent expressions at the branches of such a tree. Semantic Russellian propositions share the constituents with these semantic trees, but there is a different and distinctive sort of relation that ties these constituents to a whole, such that propositions essentially have specific (essential and language-independent) truth- and falsity-conditions. Propositions conceived as abstractions from semantic tress seem to be useful if one aims to have specific semantic objects as the possible contents of speech acts and propositional attitudes.

According to the metaphysical version of this view, propositions are abstractions from states of affairs, but not from sentences. The constituents of these states of affairs are objects, properties and relations. Metaphysical Russellian propositions share these constituents with states of affairs. However, the structure and, hence, the unifying relation of propositions is different from the unifying relation of states of affairs such that it is possible that the very same proposition can be either true or false. The constituents of propositions need not be identical with the semantic values of the constituents of sentences that can be used to describe specific states of affairs. However, according to this picture, there is at least a correspondence relation between the semantic values of the constituents of a sentence and the constituents of propositions and states of affairs that are expressed and described by this sentence. As a variation of this view, one could additionally assume that the constituents of propositions contain the intuitive meanings of the corresponding semantic values of the corresponding linguistic expressions and these are metaphysically prior to the semantic values of linguistic expressions and in general language-independent.

There is a familiar problem with false positive singular existential claims and true negative singular existential claims that is particularly pressing if one makes use either of a single-domain negative free or neutral free logic. On this basis, a sentence like “Sandy Island exists” has the logical form “E!a” and its contradictory negation “Sandy Islands does not exist” has the logical form “¬E!a”. These two logical forms have corresponding semantic trees, which contain at their branches the semantic values of the constituent expressions of the logical form. According to this standard picture, the semantic value of a proper name is an object, the semantic value of a predicate a set of objects to which a predicate applies. In our specific case, the semantic value of “E!” is the set of existing objects, but the name “a” has no semantic value, because this individual constant lacks a semantic referent. As a consequence, the semantic trees of “E!a” and “¬E!a” are incomplete, because “a” has no semantic value. Hence, there is no meaningful way to compute the semantic value of the whole sentence on the basis of the semantic values of its constituent expressions. On this basis, it seems to be impossible to abstract a semantic Russellian propositions from such an incomplete tree. A semantic Russellian proposition is a structure that metaphysically depends on the existence of its constituents. Hence, there is no semantic Russellian proposition that is expressed by “E!a” or “¬E!a” in the given case.

There also is a related problem for a metaphysical version of Russellian propositions. One would expect that a true sentence with the logical form “¬E!a” expresses a negative atomic state of affairs. e.g., a state of affairs of the general form that a certain object lacks a certain property, in our case, the property of existence. However, if negative and neutral single-domain free logic provide the correct answer concerning the analysis of the logical forms “E!a” or “¬E!a”, then there is no object that could be a constituent of a corresponding negative atomic state of affairs. But if there is no state of affairs that corresponds to such logical forms, then there also cannot be a proposition that we could abstract from such a state of affairs. Hence, we again face a problem if we abstract a proposition from the given analysis of the logical form of false positive and true negative singular existential sentences.

There are different options to respond to this problem. I will only briefly discuss the three most popular responses to our problem, and I will show why they cannot satisfy the so far outlined conditions of adequacy for a plausible solution.

Firstly, there is the quite popular option to claim that singular existential claims like “Sandy island exists” or “Sandy island does not exist” do not have the logical forms “E!a” and “¬E!a” that are proposed by a (single-domain) free semantic framework. There are linguistic reasons that speak against this option. If one is really interested in capturing the semantics of our ordinary language existence predicates, there are good linguistic reasons to stick with the proposed logical form.²⁶ If one takes into account the compositional semantic role of the verb “to exist” relative to all of its uses and relative to all its modified forms (e.g. as the adjective “existent”), then the best and most simple explanation of the use of this expression holds that it is a first-order predicate.²⁷ Furthermore, I also think there are good reasons to assume that the best semantic representation of proper names interprets them as some sort of individual constant (or variable). In any case, for our specific purposes this reaction to the problem is no option at all, because we aim to assess the prospects of single-domain free logic as a semantic framework for our ordinary existential discourse. Hence, we are bound to accept the mentioned thesis concerning the logical form of positive and negative singular existential sentences and try to find a solution to our problem on the basis of this presupposition.²⁸

Secondly, we could claim that the logical form of negative existential sentences essentially contains an external negation and, hence, even if sentences of the logical form “E!a” lack a classical truth-value, the negation of this form “¬E!a” receives the classical truth-value TRUE.²⁹ Several reasons seem to speak against such a kind of solution. On the one hand, there is linguistic evidence that speaks against this solution: (1) intuitively, we accept the sentence “Sandy Island exists” clearly as false and not as a sentence that is in some sense semantically defective. (2) Intuitively, there is no difference in truth-value between the following three sentences: “Sandy Island does not exist”, “Sandy Island is non-existent” or “Sandy Island lacks the property of existence”. However, only the first of these three sentences could literally have the logical form “¬E!a”, where “¬” is considered as an expression of external negation. This shows at least that the proposed solution is linguistically inadequate. Furthermore, there are also theoretical reasons that raise doubts whether such a solution is the best solution to our problem. This solution treats “E!a” as semantically defective, if “a” lacks a semantic referent. On this basis the sentence does not get a classical truth-value. As a further step this solution assigns a non-classical value to this sentence and this non-classical value can function as the input of the negation-truth-function. But if a sentence like “E!a” lacks semantic values that are necessary to compute a truth-value for this sentence, then it seems to be ad hoc and purely stipulative to assign to this sentence any sort of truth-value that may function as the input of any truth-functions designated by connective expressions. At least this position has the burden of proof to explain in a meaningful way why some sentences get their truth-values on the basis of a compositional evaluation that is grounded in the values of the constituent expressions, while other sentences get their truth-values in a completely non-compositional way.

Thirdly, we could conceptually stretch the notion of propositions and allow for the existence of so-called gappy-propositions.³⁰ These gappy-propositions receive their truth-values in a similar way as sentences/logical formulas that contain singular terms that lack a referent. That is, either on the basis of negative or neutral free semantics. What exactly are gappy propositions? According to this view, propositions are (in general) structures that have gaps that can optionally be filled with objects, properties and relations. On this basis, an atomic sentence of the logical form “Fa” could express three different sorts of gappy propositions: (1) a completely unfilled structure if “F” and “a” lack semantic values, (2) a partially unfilled structure if “F” lacks a semantic value, and (3) a partially unfilled structure if “a” lacks a semantic value.

There are several reasons to doubt that such a liberal conception of propositions provides the best way to solve our problem. (1) One might doubt that such structures could exist independently from their constituents. States of affairs are structures that can share their constituents with Russellian propositions. However, states of affairs can only exist if their constituents exist. If propositions are (according to metaphysical version of Russellian propositions) abstractions from states of affairs, it might be doubted whether such abstractions are legitimate that abstract away from the constituents of states of affairs. Intuitively, the only difference between a state of affairs and its corresponding Russellian proposition is the structure or the way that the constituents are related, but not the constituents themselves. Furthermore, intuitively, there is a state of affairs that Sandy Island does not exist. States of affairs are metaphysically grounded in their constituents. Hence, this state of affairs must have certain constituents. If it is possible to abstract a proposition from such a state of affairs, this proposition must also have constituents. Therefore, on the basis of the metaphysical version of Russellian propositions, the postulation of gappy propositions seems to be questionable.

Does this conception fare better on the basis of the semantic version of Russellian propositions? One might have similar metaphysical worries. An incomplete semantic tree is no proper semantic tree at all. We cannot compute the value of the top-node of a semantic tree, if any sub-node lacks a semantic value. Hence, incomplete semantic trees do not exist, because they do not fulfill their proposed function. Semantic Russellian propositions correspond to the semantic trees with respect to the logical form of a sentence. On this basis, there cannot be any meaningful gappy semantic Russellian propositions.

There are also additional semantic worries. Russellian propositions typically are filled structures. The computation of a semantic value of a filled Russellian proposition proceeds in a compositional fashion on the basis of constituent values as input for such a kind of evaluation. Hence, we have a similar compositional problem for gappy propositions that we have in the case of the logical forms of atomic sentences that lack a semantic referent. In the case of a partially or fully unfilled proposition the evaluation of the truth-value cannot proceed in a compositional way. Nevertheless, defenders of gappy propositions aim to assign either classical or non-classical truth-values to gappy propositions. Hence, they have to assign truth-values to these sentences in a non-compositional way. Such a non-compositional truth-value-assignment seems to be completely ad hoc and a defender of this view has the burden of proof to explain why some truth-values are assigned in a compositional way and others are not. Furthermore, they also have to explain why non-compositional assignments are not completely arbitrary.

If we accept gappy propositions, we are not only forced to accept gappy propositions that are unfilled with respect to any individual object position, but with respect to any possible position in a propositional structure. However, it is completely unclear whether such an extreme extension of the notion of a proposition really makes sense. There seem to be many more possible unfilled propositions than meaningful sentences that may express these kinds of propositions. Hence, the conception of a gappy proposition seems to extend the notion of a proposition in a more than acceptable way. If one aims to avoid such a full-fledged theory of gappy propositions, one has to provide a criterion to distinguish between acceptable and unacceptable gappy propositions. However, it seems to be difficult to find an independent criterion that is grounded in the nature of gappy propositions to fill this task. Again, the burden of proof is on the side of the defender of gappy propositions. In the light of all these outlined problems, I conclude that a solution to our problem based on gappy propositions is at least not the most desired of all possible solutions.

This short overview shows that an alternative solution to our problem would be desired that makes of some version of a purely extensional single-domain free logic that satisfies the outlined principle of compositionality in a plausible way.

3.3 The problem of semantic asymmetry

Our third problem concerns an overlooked and unfounded semantic asymmetry between the semantics of proper names and the semantics of predicates relative to standard Tarskian and Neo-Fregean semantics for atomic (and more complex) sentences that contain names and predicates.

Tarskian semantics for atomic sentences is a set-theoretic alternative to Fregean semantics, which mainly uses function-theoretic notions. According to the original version of a Fregean semantics proposed by Frege himself, the distinction between objects and functions is a fundamental metaphysical distinction: objects are complete entities; functions incomplete entities, in need of completion by objects. In Frege, this distinction is mirrored on the level of logical syntax by a distinction between proper names and concept-words. Proper names designate objects, concepts-words designate concepts, which are interpreted as functions that have objects as their arguments and truth-values as their values. Complete expressions designate complete objects, incomplete expressions incomplete objects. Frege’s main motivations for this kind of distinction seem to be syntactic and semantic. On the syntactic level, he can, on this basis, provide a nice criterion for well-formed formulas: a formula is well-formed if it contains at least one incomplete expression that is supplemented by the right number and kind of complete expressions. On the semantic level, Frege can provide, on this basis, a notion of compositionality purely based on the notion of functional application. The truth-value of a simple atomic sentence that contains a proper name for an individual and a concept-word is calculated on the basis of Fregean semantics by inserting the semantic value of the name as argument into the function, which figures as the semantic value of the concept-word. This brief outline shows that Frege himself had very good theoretical reasons to draw a sharp distinction between the semantic treatment of proper names and concept words. The semantic asymmetry between names and concept words seems to be well justified. A specific assimilation of the semantics of names and concept-words from one or the other end would not be an impossible task but it would spoil all the advantages of Frege’s system: (a) a nice and simple story about the well-formedness of formulas and (b) a simple, beautiful and clear notion of compositionality.³¹

More recent versions of Fregean semantics, do not anymore accept Frege’s metaphysical thesis that functions are incomplete objects and his semantic thesis that only (in)complete expressions can name (in)complete objects. According to Neo-Fregeans, functions are nothing but specific sets of ordered pairs; and Neo-Fregean first-order concepts are sets of ordered pairs that contain as first element an object and as second element a truth-value. But sets are complete objects for Frege. Hence, some restrictions concerning the function-argument structure of the semantic values of sentences, in particular with respect to atomic sentences, are lost on the basis of the more moderate Neo-Fregean picture: it is not anymore in principle forbidden that proper names have functions as semantic values and it is also not anymore mandatory that predicate expressions only designate so-called incomplete objects. However, in so far as a Neo-Fregean semantics still proposes functional application as the best way to account for compositionality, there also must be a difference in semantic type between argument-expressions and function-expressions. Hence, some sort of semantic asymmetry remains in place because of the formal requirements of compositionality conceived as functional application.³² Nevertheless, we are now free to lift the semantic values of proper names in general to (a) a higher-order combined type (b) or set-theoretically more complex entity in a similar way as this is already done in any version of Fregean semantics with respect to predicates. That is, if there are good semantic or compositional reasons to lift the semantic values of proper names from type e to type < e,t > or from individuals to sets of individuals, we then also have to lift or adapt the semantic values of the predicates that can form well-formed sentences together with these proper names. If Neo-Fregeans generally assign to singular terms functions from objects into truth-values, e.g. a function that only assigns a single object to the True and all other objects to the False as semantic values, they then have to adapt the semantic values of predicates to this lifting and interpret them as functions from functions of objects into truth-values into truth-values. Alternatively, if Neo-Fregeans generally assign to singular terms not individual objects but sets of these objects as semantics values, they then also have to conceive of the semantic values of predicates as functions from these sets into truth values. In a Tarskian semantic framework, a similar lifting of the semantic values of singular terms does not necessarily require any changes concerning the semantic values of predicates. Such changes would only require adaptions concerning the relations between the new values of singular terms and predicates that account for the truth-conditions of an atomic sentence.

Relative to a Tarskian semantic framework, atomic sentences share two features with their standard Neo-Fregean counterparts: firstly, proper names also designate individual objects. Secondly, atomic sentences also designate truth-values. However, there are two notable differences between the two systems: Firstly, in a Tarskian framework, predicates designate sets, and not functions from objects into truth-values. Secondly, compositionality is not a simple matter of functional application, but provided by a recursive definition of the truth-conditions for different kinds of sentences. The second difference is the crucial difference between the two approaches. The first is only notional. From a purely formal semantic point of view, specific sets of objects and specific corresponding functions from objects into truth-values can be seen as alternative but logically equivalent formal semantic representations of the extensions of predicates relative to a classical bivalent semantics.³³

Whether we are Tarskians or Neo-Fregeans there seem to be two different intuitive semantic relations, which play an essential role concerning the contribution of a proper name and a predicate to the truth-conditions of sentences that contain these kinds of expressions. In the case of names, this is the relation of (semantic) reference, in the case of predicates the relation of (semantic) application. As names may refer or not refer to things, predicates may apply or not apply to things. These relations intuitively play the following role concerning the determination of the truth-value of an atomic sentence:³⁴

(AT) “Fa” is true iff “a” refers to o and “F” applies to o.

(AF) “Fa” is false iff “a” refers to o and “F” does not apply to o.35

These two relations provide the desired connections between expressions and the world relative to a truth-conditional semantics and every version of truth-conditional semantics implicitly or explicitly relies on this kind of relations. But not every semantics uses these relations explicitly. In a Tarskian or Neo-Fregean semantics other more abstract semantic notions are used instead of the notion of semantic application but mainly for compositional or technical reasons. In a Fregean framework, the most important semantic relation with respect to predicates is the relation of designation, which can be seen as an abstracted or formally lifted counterpart of the more intuitive relation of application. This can be shown on the basis of the following valid and desired bridging principle:

(FA) “F” designates f iff for every object x: (f(x) = the True iff “F” applies to x).

In a Tarskian semantic framework, another kind of abstraction or mechanism of lifting is used and the most important semantic relation concerning predicates is a relation of designation between predicates and sets. In this case, it is even more clear that the following abstraction principle is implicitly used to determine the nature of the used set-theoretic extensions:

(TA) “F” designates {x | Fx} iff for every object x: (x ∈{x | Fx}36 iff “F” applies to x).

Equipped with a quite common deflationary understanding of the relation of semantic application, (FA) and (TA) can be transformed into semantic principles that do not seems to rely anymore on a more basic semantic relation:

(PA) For every object x: “F” applies to x iff Fx.

However, such a common deflationary understanding of semantic application conceals the fact that the intuitive semantic appeal of a principle like the following:

(TA*) “F” designates {x | Fx} iff for every object x: (x ∈{x | Fx} iff Fx),

rests on the intuitive implicit acceptance of (TA) and the instances of (PA).

On the basis of the intuitively acceptable principles (AT) and (AF), it seems to be clear that Fregean and Tarskian semantics perform a one-sided abstraction from (AT) and (AF) on the side of predicates. According to (AT) and (AF), names and predicates are semantically related to the same kinds of objects. The main semantic difference between them is that they are related in different ways to the same kinds of objects. Hence, the difference according to (AT) and (AF) stems from two different kinds of relations, but not two different kinds of relata. In Tarskian semantics, the situation is different: on both sides we have different semantic relations and different relata. Names still designate objects, but predicates designate sets of objects. Sets of objects are by no means the intuitive designations of predicates anymore. Tarskians seem to have good reasons for this asymmetric modification. Firstly, there are technical reasons. If predicates like names have individual designations, we can use one and the same interpretation function to assign semantic values to the basic expressions of the used formal language. But, secondly, there also seem to be more systematic reasons for this one-sided abstraction or lifting, namely the following two reasons: firstly, not only one or some objects are relevant for the overall determination of the truth-values of all sentences that contain a specific predicate, but all objects or the totality of all of these objects is required for this purpose. Hence, it seems more reasonable to make use of the sum or totality of these objects for this purpose. However, the sum of all objects to which a predicate applies also does not provide a proper semantic value for all possible uses of all meaningful predicates that can contribute to a meaningful sentence. There are also meaningful predicates that either actually or necessarily do not apply to any object. However, there isn’t an empty sum, which consists of no objects whatsoever. Hence, we need something different as a compositional value for all uses of all meaningful predicates. Sets are a very good candidate for this purpose because sets can also be empty. Functions from objects to truth-values are an equally good alternative candidate because such functions can map every object to the truth-value F. Both kinds of entities can be used to formally interpret the semantics of predicates that do not apply to any object. Therefore, the set of all objects to which a predicate applies or a related function of objects into truth-values is a very good candidate for playing the role of the semantic value with respect to every meaningful predicate.

But now here comes the twist: If the possibility of meaningful predicates that do not apply to any object provides a good motivation for preferring the set of all objects to which a predicate applies or a related function of objects into truth-values over the sum or totality of these objects, then the possibility of meaningful names without a semantic referent should equally well provide a good reason for preferring sets of the referents of proper names (or an equivalent function of objects into truth-values) as semantic values for proper names over the referent of a name itself. Even against the background of the familiar abstraction in case of the semantic values of predicates, it still remains the case that predicates have the primary function to apply to objects. That is, this function remains the basic semantic property of predicates, even if the semantic values of predicates are sets of objects or functions from objects into truth-values. Hence, it would also remain the primary semantic (or pragmatic) function of proper names to refer to things even if we would assume that the semantic value of a name is a set that contains its referent. Therefore, the defender of standard single-domain free logic based on a Tarskian or Neo-Fregean semantics seems to owe us a good reason for the apparently unfounded asymmetric semantic treatment of proper names that lack a semantic referent and predicates that don’t apply to any object. In other formal semantic frameworks, it is also quite usual to use similar formal abstractions to formally model the semantics of singular terms and to provide a uniform compositional semantics. Montague-semantics is a very good example of this sort.³⁷

3.4 The problem of the compositional status of the existence predicate

Our fourth problem concerns the specific status of the semantic value of the existence predicate relative to our favored negative semantics of singular existential sentences. As we have seen already, there is plenty of linguistic evidence to favour the proposed negative semantics for singular existential sentences over alternative analyses. However, there is also a problem concerning the compositional contribution of the existence predicate to the truth-conditions of a sentence of the form “E!a” on the basis of the following typically proposed truth- and falsity-conditions³⁸:

V(E!t) = T	iff	Den(t) is defined.
V(E!t) = F	iff	Den(t) is undefined.

These conditions provide the correct and desired distribution of the truth-values for singular existential sentences, but they do not provide meaningful compositional truth-conditions. The used necessary and sufficient condition for the truth of “E!a” is a condition that in fact only concerns the referential status of the individual constant “a”. This condition specifies the contribution of a proper name that refers to something in a sentence that contains this name, but it is in no distinctive way related to the semantic value of “E!”. That is, the individual contribution of the semantic value of “E!” to the truth-conditions of sentences of the form “E!a” remains a riddle on the basis of the given truth-conditions. The condition that is provided by the falsity-conditions of “E!a” is a condition that every non-referring proper name seems to contribute to the truth- or falsity-conditions of any sentence that contains such a name. It is again in no distinctive way related to a possible or meaningful semantic value of the existence predicate. Hence, we also need to improve the given formulation of our semantics for existential sentences if we aim to provide an adequate compositional semantics for these sentences, as we aim to give.

3.5 The problem of the semantic status of identity sentences

The fifth and last problem concerns the semantic status of identity sentences. As we have already mentioned, some people accept that a sentence of the logical from “a = a” is true independently of whether “a” has a semantic referent or not. Furthermore, people tend to hold that sentences of the form “a = b” are false, even in the following two cases: (a) if only one of these two singular terms refers to something, and (b) if none of these two singular terms refers to something. But if we only consider the purely extensional contribution of the contained referring expressions and the identity relation for the determination of a truth-value, it is completely unclear how we can provide a semantic foundation for these intuitive evaluations. Against the background of the outlined semantic framework of a single-domain free logic, the three examples of truth-value assignments given seem to be ad hoc, semantically unfounded and in no proper way licensed by a meaningful principle of compositionality. Hence, we either have to reject such evaluations of identity sentences or provide a more plausible semantic foundation for them.

4 A modification of the original framework that solves nearly all of our five problems

We now have introduced five different but related problems of the standard single-domain semantic framework, which are mainly concerned with a proper compositional semantic implementation of non-referring names into a single-domain free semantic framework.

Four of the mentioned problems only make deficits of the standard semantic single-domain framework obvious, but one of these problems also seems to provide the clue for a solution to most, or probably all of these problems. It is the third problem that proposes a more analogous semantic treatment of predicates and proper names that leads to the following new assumptions: (a) a distinction between the semantic value of a proper name and its semantic referent on the basis of a corresponding and familiar distinction between the semantic value of predicates and their semantic applicants, (b) an identification of the semantic value of a proper name with a set that contains the semantic referent of this name if the name has any,³⁹ or the empty set if the name does not refer,⁴⁰ which is based on the analogous identification of the semantic values of predicates with the set of objects to which the predicate applies.⁴¹

One might object that if we accept that semantic reference and semantic application are two different kinds of semantic relation, this difference can be used as a justification to assign completely different semantic values to names and predicates than a Tarskian semantics does.⁴²Prima facie such “relational” semantic differences seem to provide a good reason for a different formal semantic treatment of names and predicates. However, the mentioned differences do not seem to be sufficient to justify a Tarskian semantic treatment of singular terms. Some supplementary facts are required to justify the specific Tarskian treatment. For example, the Fregean thesis that logically proper names must have a semantic referent, while logically proper predicates may not apply to an object, would provide such an additional reason. However, there seem to be certain reasons that can be used to motivate single domain free logic that seem to falsify the Fregean thesis, namely the acceptance of meaningful singular terms that lack a semantic referent. Additionally, if the fact that predicates may not have any semantic applicants leads to the acceptance of sets as semantic values instead of the semantic applicants of these predicates, the fact that names may not have semantic referents should equally be seen as a reason against the identification of the semantic values and the semantic referents of names. Hence, in the light of the possibility of meaningful singular terms that lack a semantic referent and the fact that they might be used in a meaningful way as constituents of sentences with an inferential potential, only the mentioned difference between the semantic relations of reference and application does not provide a sufficient or good reason for a Tarskian semantic treatment of names and predicates.

A second possible objection against our proposal is the following: According to our new semantics of singular terms, there mainly seem to be two semantic differences between predicates and names: firstly, names can at most have one semantic referent as element of their extension, while predicates also can have more applicants in their extension. Secondly, names always have the very same extension/semantic value relative to every possible world, while predicates can have different extensions relative to different possible worlds. However, on this basis there does not seem to be a significant semantic difference between the name “Frege” and the predicate “x = Frege”. The identity predicate “=” is a logical predicate and “Frege” a rigid designator, hence, this predicate seems to have relative to every possible world the same singleton as its extension. But intuitively, there is a significant semantic difference between the name “Frege” and the predicate “x = Frege”.⁴³ It is true that “Frege” and “x = Frege” share some important semantic features relative to our framework, but there are also important differences. Although some names and predicates may have the same semantic values, (a) on the level of logical form and (b) on the level of truth-conditions of sentences, names and predicates play a different role and are represented in different ways. The different semantic contributions to the truth-conditions of sentences are captured by our recursive definitions of the truth-conditions of atomic sentences.⁴⁴ I think this shows that the mentioned semantic similarities between our two examples do not lead to a complete semantic identification.

A third possible objection that one could make is whether there aren’t any alternative ways to solve our problem that makes use of an alternative semantic framework and different semantic representations of predicates and names.⁴⁵ The main idea behind my solution is not to propose a semantic assimilation of proper names and predicates relative to all possible formal semantic frameworks. My concern is more modest. I only want to argue that if relative to a Tarskian (or Neo-Fregean) semantic framework the semantic values of predicates are lifted in a certain way for certain semantic or syntactic reasons, then the semantic values of proper names should be lifted in a similar way for similar reasons. In other kinds of frameworks such adjustments could be made in different ways. My main point is just that there are no good reasons to identity the semantic values of proper names with their referents and that there are certain problems with the semantic representations of proper names that may speak against such an assimilation. For example, if one aims to implement my proposed distinction between the semantic value and referent of a name relative to the Tarskian framework into a Fregean kind of semantics, one could still hold that predicates designate functions. However, it would be necessary to slightly modify these functions. Instead of functions from objects to truth-values, these functions would become functions from specific sets into truth-values. Against this background, Frege’s main idea behind the role of concepts would remain intact, namely that they are functions from the semantic values of singular terms into the semantic values of sentences. The semantic values of proper names and predicates would be different, but the system would function in a semantically equivalent way as our modified Tarskian semantics. Similar modifications could also be made on the basis of a Montegovian semantics, where the distinction between the semantic value and the referent of a name is already drawn, but for different reasons and not in a fashion that can be easily extended to empty names.

In Justice (2007), a formal semantics is proposed that to a large part resembles our new semantics for single-domain free logic. The similarities are the following: firstly, Justice also distinguishes between the semantic referent of singular terms and their denotation (semantic value.) Secondly, he also holds the view that individual objects are the semantic referents of singular terms and singletons that contain these referents are the semantic values of these terms. Thirdly, he also assumes that singular terms can lack a semantic referent and, in this case, would have an empty set as their extension. However, there are also significant differences between Justice’s and the present account. Firstly, although our semantics seems to be extensionally equivalent with respect to first order predicate logic, they rest on different meta-semantic assumptions. Justice uses a Fregean metasemantics, which assumes that the extensions of all singular terms are determined by certain Fregean descriptive conditions. I make use of a Kripkean metasemantics that holds that the referent of a name is determined by a chain of uses of a proper name. Secondly, while I make use of the tools of a Tarskian single domain free logic, Justice makes use of a modified version of Montague semantics. Thirdly, and most importantly, Justice’s main motivation for his semantics is the desire for a uniform treatment of singular terms that overcomes certain problems of a Montegovian unification of the semantics of singular terms and noun phrases. But Justice (2007) does not focus on the problems the present paper is concerned with and he, hence, does not use problems of compositionality that concern the introduction of empty singular terms into a formal semantic framework as a motivation for his approach. Furthermore, Justice does not discuss any of the delicate issues concerning a compositional semantics of existential sentences, which is a central concern of the present paper.

I will now implement the suggested changes into the standard Tarskian single-domain framework and show how we can solve nearly all of the outlined problems on this basis.

4.1 A compositional free semantics for non-logical atomic sentences

As we have already seen, the single-domain framework consists of a single domain of reference and quantification D and the following already introduced semantic functions: Den(), δ(), I() and V(). The proposed changes lead to modifications mainly with respect to Den(), δ() and V(), but there are also some slight modifications necessary concerning D.

The first required main modification concerns Den(). Instead of elements of D, the denotation function now assigns either a singleton containing an element of D or the empty set to our individual constants.

Against this background, we also have to adjust the role of the denotation function in atomic sentences. Firstly, we have to adapt the semantics of atomic sentences with non-logical predicates. For this purpose, we make use of the following quantified truth-conditions for the negative and the neutral semantics:

Modified negative free logic concerning non-logical atomic sentences⁴⁶:

V(Pt1…tn) = T	iff	∃x1 …. ∃xn(x1 ∈ Den(t1) &… & xn ∈ Den(tn) & < x1,…,xn > ∈ I(P));
V(Pt1…tn) = F		otherwise.

Modified neutral free logic concerning non-logical atomic sentences:

V(Pt1…tn) = T	iff	∃x1 …. ∃xn (x1 ∈ Den(t1) &… & xn ∈ Den(tn) & < x1,…,xn > ∈ I(P));
V(Pt1…tn) = F	iff	∃x1 …. ∃xn (x1 ∈ Den(t1) &… & xn ∈ Den(tn) & < x1,…,xn > ∉ I(P));
V(Pt1…tn) = N	iff	It is not the case that (∃x1… ∃xn (x1 ∈ Den(t1) &… & xn ∈ Den(tn))).

I have some sympathy for the idea of semantic presuppositions and would, hence, personally favour neutral semantics with respect to atomic sentences with non-logical predicates over a negative semantics. But our adapted semantics can be formulated in an equally plausible way for both kinds of semantics.

Against this background, we can now provide a solution to the compositionality problem with respect to atomic sentences with non-logical predicates. Our new truth- and falsity-conditions for this kind of sentences now assign to each semantically significant expression different semantic values that function as inputs for the determination of the truth-values of the respective sentences.⁴⁷

That is, it assigns to proper names sets that contain no or at most one element of D and to predicates sets or n-tuples of objects that are elements of D.

4.2 A compositional free semantics for existential sentences

We have already noticed that concerning singular existential sentences, a negative semantics seems to be the only plausible option if one aims to use our framework as formal semantic framework for natural languages and our ordinary existential discourse. Based on our proposed semantic modifications, there are different possibilities to solve the problem with respect to the compositional contribution of the existence predicate to the truth-conditions of singular existential sentences.

Insofar as according to our new semantics, proper names have two different semantic aspects that could function as the objects of application of predicates, namely their semantic values and their semantic referents, we now also have the choice in our formal syntax and semantics to distinguish two different kinds of predicates; namely those that can (only) apply to the semantic referents of singular terms, with which they are combined, and those that can (only) apply to the semantic values of singular terms, with which they are combined. It is necessary to mark this difference also syntactically such that our logical representations remain unambiguous. I will use ordinary predicates symbols like “F” for predicates of semantic referents and mark those predicates like “F*” with a star that are predicates of semantic values.⁴⁸ The interpretation function interprets predicates with such a star, like “F*”, in a different way than ordinary predicates: it assigns to monadic predicates sets that contain (arbitrary) subsets of D. It assigns to n-adic predicates, where n > 1, sets that contain n-tuples of subsets of D. On this basis, we can assign to atomic sentences that contain stared predicates the following truth-conditions:

V(P*t1…tn) = T	iff	<Den(t1) &… & Den(tn) > ∈ I(P*));
V(P*t1…tn) = F		otherwise.

On this basis, we now seem to have the choice to introduce two different existence-predicates, one of both varieties.

The first option conceives of the existence predicate as a predicate that expresses a property that applies to the semantic value, but not to the semantic referent of a proper name according to our newly drawn distinction. On this basis, the existence predicate “detects” whether a certain proper name has an empty or non-empty extension (semantic value). This conception has some similarities with Frege’s famous second-order interpretation of the notion of existence,⁴⁹ but there is one important difference between the two views. In our case, the property of existence is exclusively a property of the extension of singular terms. In Frege’s case, it is exclusively a property of the extension or semantic values of predicates. Hence, this property of existence is neither a classical first-order nor a classical second-order property. It is a restricted second-order property.

There are different ways to formulate the truth-conditions of atomic sentences that contain such an existence predicate. The first alternative makes use of a restricted second-order domain D! that can be defined as follows:⁵⁰

D!51 = the set of all subsets of D that contain exactly one element.

The second way makes use of a particular quantifier in the meta-language that “detects” whether the semantic value of a singular term is an empty or non-empty set. This new idea of interpreting the property of existence leads to the following adapted truth- and falsity-conditions of singular existential sentences:

Negative free logic concerning singular existential sentences

V(E!*t) = T	iff Den(t) ∈ D!	[or: ∃x(x ∈ Den(t)).]52
V(E!*t) = F	iif Den(t) ∉ D!	[or: ¬∃x(x ∈ Den(t)).]

On this basis, we can now clearly distinguish the semantic contribution of the singular term “t” and that of the predicate “E!*” in a sentence of the logical form “E!*t”. The singular term contributes the semantic value of “t”, which is either a singleton or the empty set and it is denoted by “Den(t)”. The predicate “E!*” semantically designates the extension D! (or contributes the property expressed by “∃x(x ∈…)” to the truth-conditions of “E!*t”, where the instances for the dots are syntactically restricted to extensions of singular terms).

On this basis we can solve our fourth compositionality problem. However, this solution also has its costs if the compositional contribution of “E!*” is as we have claimed. As a consequence of this interpretation, every atomic sentence of the form “Fa” that explicitly contains only non-logical predicates also expresses the property of existence because the identified property is also part of the truth-conditions of these sentences. In this sense, “Fa” is not only logically but semantically equivalent to “Fa & E!*a” (relative to a bivalent version of free logic).⁵³ That might appear to be a strange consequence at first sight, but closer inspection shows that this is not at all an unwelcome consequence. It seems to be quite plausible to assume that every purely extensional predicate is existence-entailing. Such predicates actually only apply to actually existing things. Hence, this consequence seems acceptable.

However, if one thinks that the property that our first option identifies with the property of existence, is in fact not a contribution of “a exists” to the truth-conditions of a sentence of the form “a exists”, but a contribution that is provided and enforced by the correct compositional combination of the semantic values of the constituent expressions, there is also an alternative possible interpretation of the compositional contribution of “E!” based on our modified framework, which leads to the following alternative truth- and falsity-conditions:

Negative free logic concerning singular existential sentences

V(E!t) = T	iff	∃x(x ∈ Den(t) & x ∈ D).
V(E!t) = F	iff	¬∃x(x ∈ Den(t) & x ∈ D).

This second option conceives of the existence predicate as a first-order predicate that can directly apply to the semantic referent of a proper name. According to the given truth- and falsity-conditions, the semantic contribution of “E!” to the truth-conditions of “E!t” is the first-order extension of “E!”, which is by stipulation identical with the domain D. Such a kind of stipulation is allowed because of the status of “E!” as a logical predicate that has truth- and falsity-conditions that are independent of the values that the interpretation function assigns. This stipulation also seems to provide a plausible and welcome interpretation of the semantics of “E!”.

According to this analysis, sentences of the logical form “E!t” have a similar semantic structure as ordinary monadic predicates of the form “Fa”. Their only difference concerns the fact that “E!” is not an ordinary, but a logical predicate. (However, this semantic symmetry is only given on the basis of a negative semantics for all atomic sentences. If we assume a neutral semantics for atomic sentences with ordinary predicates, then the semantic differences between ordinary atomic sentences and singular existential sentences are more substantial.) In any case, both options seem to provide a plausible answer to our fourth outlined problem.

4.3 A compositional free semantics for identity sentences

Let us now focus on different possibilities to solve our fifth special and the first general compositionality problem with respect to identity sentences. The simplest possible adaption of the truth- and falsity-conditions of identity sentences against the background of our proposed semantic modification is provided by the following adapted negative semantics for identity sentences:

Modified negative free logic concerning identity sentences

V(a = b) = T	iff	∃x∃y(x ∈ Den(a) & y ∈ Den(b)) & x = y).
V(a = b) = F	iff	¬∃x∃y(x ∈ Den(a) & y ∈ Den(b)) & x = y).

We have already mentioned the intuitive tendency of some philosophers to assign to identity sentences classical truth-values even in cases where these sentences contain at least one non-referring singular term. Hence, if one aims to provide a formal semantics for ordinary identity sentences, negative semantics seems to be the better choice as a neutral semantics. However, the given negative semantics does not provide all the mentioned desired results concerning the intuitive evaluation of truth-values of identity sentences which contain at least one non-referring name. Based on the given semantics, the following examples of sentences with (a) two non-referring names and (b) one non-referring name come out as false, which is the intuitively desired result:

(2) Sandy Island = Sherlock Holmes.

(3) Tony Blair = Sandy Island.

However, some people also have the intuition that the following apparently trivial identity sentences should come out as true, even if “Sandy Island” lacks a semantic referent:

(1) Sandy Island = Sandy Island. 54

Based on our distinction between the semantic referent and the semantic value of a name, we at least have the semantic resources to change the semantics in such a way that we can add cases like (1) to the class of true identities. This leads to the following modified positive semantics, which provides a non-extensional semantics for identity sentences because the exact logical form of an identity sentence plays an essential role concerning the determination of the truth-value of this sentence:

Extended positive free semantics concerning identity sentences

V(a = b) = T	iff	∃x∃y(x ∈ Den(a) & x ∈ Den(b) & x = y) ∨ Den(a) = Den(b) & ⌈a⌉ = ⌈b⌉.***55
V(a = b) = F	iff	¬(∃x∃y(x ∈ Den(a) & x ∈ Den(b) & x = y) ∨ Den(a) = Den(b) & ⌈a⌉ = ⌈b⌉).

At first sight, such a kind of disjunctive semantics for identity sentences might seem ad hoc. However, there seems to be a way to justify this kind of semantics. It distinguishes two different cases of identity. The first disjunct captures the standard case of metaphysical identity. That is, every object is metaphysically necessarily identical to itself. The second case concerns a semantic or metalinguistic case of identity that aims to capture an identity with respect to the same representational device. That is, according to this interpretation of a sentence of the form “a = a” it is true if I literally use the very same semantic device for the same object with the same semantic value twice in such a sentence. In the light of the intuitive evaluation of a sentence like (1) as true, we might interpret our intuitive notion of identity as a hybrid notion that aims to capture both kinds of cases, which concern different representational levels. However, for those who believe that the identity sign only expresses the notion of the first distinguished and purely metaphysical kind, the modified negative semantics would be the better option. But, I think, we should think of the option that our intuitive notion of identity in fact aims to capture both distinguished cases of identity as worth considering.

4.4 The abstraction of compositional semantic Russellian propositions

We have shown how the standard semantic framework of a single-domain free logic can be transformed in a meaningful way on the basis of a concessive solution to our third outlined problem, the problem of semantic asymmetry. Against the background of our new outlined semantics for atomic sentences, we can also now offer a partial solution to the problem of linguistic abstraction concerning semantic Russellian propositions. In so far as our semantics now conforms to the general principle of compositionality and provides for each meaningful constituent expression of an atomic sentence a semantic value that delivers an adequate input for the computation of the truth-value of the whole sentence, we can now also abstract away from the semantic values of our atomic sentences purely extensional semantic Russellian propositions that have the semantic values of our atomic sentences as their constituents. Furthermore, we can also transfer the truth-conditional composition of our atomic sentences to the abstracted semantic Russellian propositions. These semantic Russellian propositions are relatively coarse-grained, because on their basis properties are identified with the extensions of predicates. However, there are ways to improve on this issue. One could, for example, implement our framework into an S5-type modal logic and load the intensions of predicates instead of the extensions into our semantic Russellian propositions. On this basis, we get semantic Russellian propositions that are about genuine objects and necessarily equivalent with standard metaphysical Russellian propositions. Additionally, we also get plausible candidates of compositional semantic Russellian propositions about things that only appear(ed) to exist.

However, we cannot solve the problem of abstraction with respect to a metaphysical Russellian conception of proposition just on the basis of our modified semantic framework. For this purpose, we would have to be able to provide a new conception of states of affairs which can be described by sentences that contain empty names. Our framework does not provide the resources for such a conception and it would also be inappropriate to expect such a conception from our formal semantic framework. The only kind of Russellian conception of propositions we could provide on this basis is a semantic one. And it is in fact an important improvement if we can at least fix the problem with respect to semantic Russellian propositions.⁵⁶

4.5 Summary of our first results

Let us now sum up our first results: firstly, our solution to the mentioned problems started with a concessive solution to the problem of semantic asymmetry. We distinguished between the semantic referent and the semantic value of a proper name, and we identified the semantic value of a proper name with a set that contains the semantic referent of this name or the empty set if this name lacks one. Secondly, on the basis of this modification, we provided a new modified version of a single-domain free semantics for all kinds of atomic sentences. All our modified semantic proposals for different atomic sentences provide a well-motivated answer to the main problem of compositionality. On the basis of our account, empty proper names contribute empty sets as semantic values to the semantic trees that represent the logical forms of atomic sentences that contain such names. Thirdly, we also could offer two different viable solutions to the problem of the compositional status of the existence predicate. Fourthly, we could show how two alternative compositional semantics for identity sentences can be offered. The second of these accounts also had the resources to account for a variety of different truth-value intuitions concerning identity sentence with at least one empty name. Finally, we pointed out that our framework allows us to solve the problem of propositional abstraction with respect to the semantic conception of Russellian propositions, but that one should not expect on this basis new options to solve this problem with respect to a metaphysical conception of Russellian propositions. So far, so good!

As a next step I would like to extend our modified framework to quantified sentences and in a last step I will try to implement it into an S5-type modal logic.⁵⁷

5 The extension of the new framework to quantified sentences

There seems to be a quite easy and straightforward extension of our framework to quantified sentences that only requires certain small adaptions concerning the semantics of individual variables that are similar to our proposed changes with respect to individual constants. In the same way as we distinguished between the semantic referent and the semantic value of an individual constant, we now also have to distinguish between, on the one hand, the objects of D over which a bound variable ranges or the objects of D to which a free unbound variable refers, and on the other hand, the semantic values of bound and free unbound variables, which are now conceived as singletons that contain objects of D. There is an important semantic difference with respect to our new framework between individual constants and individual variables. The denotation-function assigns singletons containing objects of D or the empty set to individual constants. However, the denotation- or assignment-function only assigns singletons containing objects of D to our bound or unbound variables. Hence, there cannot be meaningful bound or unbound uses of individual variables, where these expressions range over or refer to nothing.

To provide an overall and uniform semantics for bound or unbound uses of variables and individual constants, we will make use of two functions that assign semantic values to individual variables. The primary function is the assignment function δ() that assigns to every individual variable of our language a singleton that contains an object that is element of the domain of discourse D. Additionally, we also now have the following multi-functional denotation-function, which unifies the semantics of individual variables and constants:

Denotation-function-restrictions:

If the argument α of Den() is an individual variable, then Den(α) = δ(α).

If the argument α of Den() is an individual constant, then Den(α) = a singleton containing an element of D or the empty set.

Based on these two modifications, we now only have to add the following slightly modified standard Tarskian truth- and falsity-conditions for quantified sentences to our formal framework to get the full expressive resources of a first-order predicate logic:

Modified negative free semantics concerning quantified sentences

Vδ(∀xA) = T iff for every object d ∈ D it is such that Vδ*(A) = T, where δ* is the same as δ except that it assigns {d} to x;

Vδ(∀xA) = F otherwise.

Vδ(∃xA) = T iff for at least one object d ∈ D it is such that Vδ*(A) = T, where δ* is the same as δ except that it assigns {d} to x;

Vδ(∃xA) = F otherwise.

Against this background, D remains as in a standard single-domain predicate logic both our domain of quantification and reference. In the same sense as individual constants may still refer to objects in the domain D and predicates may apply to objects in the domain D, quantifiers still quantify over objects in the domain D, although these objects are not the semantic values of the variables that we use for quantificational purposes anymore. The semantic values of variables are now singletons that contain an element of D.

For the sake of simplicity, in this paper, I will only introduce the negative free semantics for quantifications. However, based on our proposed neutral free semantic of atomic sentences with ordinary predicates, it is relatively easy to add alternatively a neutral free semantics for quantified sentences to our framework.⁵⁸ There are two things that I want to briefly add here concerning quantified sentences in our neutral semantic framework: firstly, if we provide a Tarskian semantics for quantified sentences based on our new general framework and a neutral free semantics for these sentences, this kind of semantics becomes fully compositional and, hence, it does not violate the no-input-no-output-principle. Therefore, it is not required to make use of a Fregean semantics for quantified sentences in combination with a neutral free logic instead of a Tarskian semantics to satisfy the no-input-no-output-principle, as it was formerly proposed in Lehmann (1994). Secondly, there seems to be a significant reason that speaks against the use of a neutral semantics for quantifiers if one aims to provide a proper semantics for existential sentences relative to purely (or basically) extensional single-domain free semantic framework. We have already seen that there are good linguistic reasons to favour a negative free semantics concerning existential sentences over a neutral free semantics. However, on this basis we get into trouble if we aim to account for the plausible equivalence between the extension of “E!x”, the extension of “∃y(y = x)” and the domain D. If we now assume a neutral free Tarskian semantics for quantifications based on our semantic framework, an implausible asymmetry between the following principle and intuitively true instances of this principle arise:

(ESP) ∀x(E!x ↔ ∃y(y = x))

(ESS) (E!a ↔ ∃x(x = a))

On this basis, we can still account for the truth of (ESP) and this principle can also be conceived of as a logical truth. However, certain instances of (ESS) come out as false if “a” does not refer. This is the case because “E!a” comes out as false on the basis of our favoured negative free semantics for existential sentences, but “∃x(x = a)” would come out as neither true nor false if we make use of a neutral free Tarskian semantics for quantifications.

We get a similar but reverse problem if we make use of Lehmann’s neutral free logic that makes use of a Fregean semantics for quantified sentences.⁵⁹ According to this semantics, “∃x(x = a)” comes out as false, if “a” has no semantic referent. However, “E!a” comes out as neither true nor false, because Lehmann commits himself to the no-input-no-output principle and in consequence applies it, based on his standard singular-domain framework, to singular existential sentences. Hence, according to Lehmann, certain instances of (ESS) also come out as false, although for different reasons. This shows that the two proposed neutral frameworks have unwelcome consequences for our purposes. Therefore, if one aims to provide an intuitively plausible semantics for singular existential sentences based on a single-domain free semantic framework and, hence, also aims to verify (ESP) and all instances of (ESS), there only seem to be two viable options. Both of these options require a commitment to our new semantic framework, which allows one to combine a negative free semantics of existential sentences with a commitment to the no-input-no-output principle. More specifically, the two options are the following: our new semantic framework may either be combined with the new negative free semantics or with a new and alternative Fregean semantics for quantifications. In fact, these two options lead to equivalent results. But there are, I think, two reasons in favour of the first option. Firstly, a Tarskian treatment of quantifiers fits much easier and nicer into our new framework. That is, some adaptations would be necessary to combine a Fregean semantics for quantifiers with our modified framework; and, furthermore, a Tarskian semantics seems to be the much more natural semantics for a predicative logic that contains variables with a genuine semantic contribution. Secondly, this framework makes use of the more intuitive and modest conception of the semantic values of predicates, because it maps them to sets of objects to which these predicates apply. The necessary adaption of a Fregean semantics for quantification would assign functions from singletons that contain elements of D to truth-values as semantic values to predicates. That is, if our focus is especially on a proper semantics for existential claims, then our outlined modified semantics for quantified sentences seems to be the most natural addition to our new framework.

6 The extension of the new framework to an S5-type modal logic

As a last step of the development of our new single-domain free semantic framework, I will extend our framework to an S5-type modal logic with domain-specific quantifiers (and optional additional total quantifiers). I have chosen an S5-type modal logic for two reasons. Firstly, from a purely semantic point of view, it is the simplest version of a normal modal logic because it can be introduced without the use of an accessibility relation. Secondly, in the light of the fact that some of our problems concerned the notions of existence and identity relative to a free semantic framework an S5-type modal logic seems to be the appropriate framework to address interesting additional questions concerning the modal status of both notions.

The standard semantics for an S5-type first-order modal logic makes use of a semantic Kripkean structure to interpret the sentences of the relevant formal language. For our purposes, I will make use of a slightly more complex structure⁶⁰ of the following kind: S = < W, D*, D(), Den(), I() > . This structure contains a non-empty sets of possible worlds W. A set of all actual and merely possible objects D*. A function D() from worlds to world-relative domains of quantification and reference that are subsets of D*.

With respect to Den(), we have two options: firstly, we can interpret Den() as an absolute and total function that assigns a singleton that contains an element of D* or the empty set to each individual constant of our language. On this basis, proper names come out as obstinately rigid⁶¹ expressions in three different senses: (1) proper names in an obstinately rigid way designate their semantic values; that is, with respect to all possible worlds. (2) Referring names refer in an obstinately rigid way to their referents. (3) Non-referring names lack in an obstinately rigid way a semantic referent. Secondly, we can interpret Den() as a world-relative and total function that assigns relative to every possible world w a singleton that contains an element of D(w) or the empty set to each individual constant of our language. There are at least two possible additional and relatively strong restrictions that one could add on this basis to turn proper names into rigid singular terms: (a) one adds the restriction: For every individual constant α and every possible world w and w*: Den(α, w) = Den(α, w*). On this basis, we reach the very same result as on the basis of the first mentioned un-relativized option. (b) Alternatively, if one is skeptical about whether we can name objects that do not actually exist, we could also add the following even more restrictive clause: for every individual constant α and every possible world w: Den(α, w) = Den(α, @). This restriction must be understood in such a way that every proper name has the same semantic value as with respect to the actual world with respect to every possible world. However, this does not mean that every object that exists with respect to the actual world and is named with respect to that world must exist in every possible world. It only means that names refer to the same object in the actual domain of quantification and reference, D(@), with respect to every possible world. This notion of actually restricted rigidity has some similarities with obstinate rigidity, but there are also significant differences. I will not go into the details here.⁶² I just wanted to point this option out. In the following, I will, for the sake of simplicity, work with the above introduced total denotation function and a notion of obstinate rigidity.

I() is our interpretation function that is now relativized to possible worlds.

Additionally, we now also make use of a modified world-relative valuation function V().

6.1 A compositional modal free semantics for non-logical atomic sentences

With these additions and modifications at hand, one can now provide the following world-relative truth- and falsity-conditions for non-logical atomic sentences with respect to a negative or neutral semantic framework:

Negative free modal logic concerning non-logical atomic sentences:

V(Pt1…tn, w) = T	iff	∃x1 …. ∃xn(x1 ∈ Den(t1) &… & (xn ∈ Den(tn) & < x1,…,xn > ∈ I(P, w));
V(Pt1…tn,w) = F		otherwise.

Neutral free modal logic concerning non-logical atomic sentences:

V(Pt1…tn, w) = T	iff	∃x1 …. ∃xn (x1 ∈ Den(t1) &… & (xn ∈ Den(tn) & < x1,…,xn > ∈ I(P, w));
V(Pt1…tn,w) = F	iff	∃x1 …. ∃xn (x1 ∈ Den(t1) &… & (xn ∈ Den(tn) & < x1,…,xn > ∉ I(P, w)));
V(Pt1…tn,w) = N	iff	It is not the case that (∃x1… ∃xn (x1 ∈ Den(t1) &… & xn ∈ Den(tn)))

These extensions and modifications are pretty straightforward; they provide a compositional semantics for an S5-type modal logic with empty names and do not require much explanation. One thing, however, that has to be noticed with respect to our meta-language: The particular quantifiers we use to specify the truth- and falsity-conditions of non-logical atomic sentences range over the total domain D*.

6.2 A compositional modal free semantics for existential sentences

More tricky and interesting is the question, how our two proposed treatments of existential sentences can be implemented into an S5-type modal logic. We proposed the following two different compositional semantics for the existence with respect to our first-order predicate logic: (a) a semantics that interpreted “E!*” as a property of the semantic value of singular terms and variables; (b) a semantics that interpreted “E!” as a predicate that has by stipulation the same extension as the domain D.

Is it possible to implement both interpretations into an S5-type modal predicate logic? With respect to our second proposal such an implementation seems to be relatively easy and straightforward. We just have to identify the world-relative extensions of the existence predicate with the world-relative domains of quantification that are the values of D() with respect to different possible worlds. This slight change leads to the following modal truth- and falsity-conditions for singular existential sentences:

Modified modal negative free logic concerning singular existential sentences I

V(E!t, w) = T	iff	∃x(x ∈ Den(t) & x ∈ D(w)).
V(E!t, w) = F	iff	¬∃x(x ∈ Den(t) & x ∈ D(w)).

Against this background, we can have contingently or necessarily true existential sentences that contain names that refer, and necessarily false existential sentences that contain names that lack a semantic referent. According to one possible compositional interpretation of this semantics, the semantic value of the existence predicate is the intension, which maps possible worlds to world-relative domains of quantifications.

Is it possible to implement our other semantic interpretation of existential sentences into our new modal framework as well? At first sight, it seems to be a difficult issue if we focus only on the second version of this alternative analysis because according to it, the truth-conditions for “E!*t” are provided by “∃x(x ∈ Den(t))”. But if one transfers these truth-conditions to our new modal framework, it is necessary to relativize these truth-conditions to possible worlds in some way. However, one can neither meaningfully relativize “Den(t)” on the basis of our treatment of proper names as obstinately rigid designators, nor could the particular quantifier that ranges over D* be relativized to world in a direct way. The only meaningful possibility to provide the desired relativisation seems to be given by an additional world-relative restriction of the used particular quantifier. The most straightforward way to provide such a relativisation is provided by the restrictor “x ∈ D(w)”. However, this kind of addition exactly leads to the very same truth-conditions, we assigned to the modal version of our second modified interpretation existential sentences above. The two semantics seem to collapse into one.

However, the situation changes if we make use of our first higher-order formulation of the semantics of atomic existential sentences. On this basis, it is much clearer what we have to do to relativize the truth-conditions of atomic existential sentences to possible worlds. For this purpose, we have to relativize the higher-order domain D! to possible worlds. We can treat D!(w) as a function from possible worlds into specific subsets of the world relative domains. That is, we have to define D!(w) as follows:

D!(w) = the set of all subsets of D(w) that contain exactly one element.63

Against this background, we can now provide the following truth- and falsity-conditions:

Modified modal negative free logic concerning singular existential sentences II

V(E!*t, w) = T	iff Den(t) ∈ D!(w)
V(E!*t, w) = F	iff Den(t) ∉ D!(w)

In the light of this analysis, it becomes now also clear, why there are two different ways to interpret the truth-conditions of singular existential sentences according to the first proposed analysis. The above outlined analysis allows two different ways to decompose the truth-conditions for existential sentences into constituent contributions. According to the first way, the compositional contribution of the existence predicate is expressed by the following complex condition “∃x(x ∈… & x ∈ D(w))”; i.e., the world-relative extension that is characterized by this condition is the semantic value of “E!*”. This decomposition is licensed by the outlined second modalized account; and the property expressed by “E!*” is a property of the semantic values of proper names, not of their referents. According to the second way, this contribution of “E!” to the truth-conditions is provided by the condition “x ∈ D(w)”; and the property expressed by this condition is a property of the semantic referent of individual constants and variables and, hence, the composition that is licensed by our first modalized analysis.

This shows that both distinguished accounts that we have developed for our first-order predicate logic can now be also transferred to our new modal framework.

6.3 A compositional modal free semantics for identity sentences

In this paper, we have already proposed two different and independent analyses of identity sentences for our new first-order free semantic framework. These proposals can very easily be implemented into our new modal framework, namely in the following way:

Negative free logic concerning identity sentences

V(a = b, w) = T	iff	∃x∃y(x ∈ Den(a) & x ∈ Den(b)) & x = y).
V(a = b, w) = F	iff	¬∃x∃y(x ∈ Den(a) & x ∈ Den(b)) & x = y).

Extended positive free semantics concerning identity sentences

V(a = b, w) = T	iff	∃x∃y(x ∈ Den(a) & x ∈ Den(b))& x = y) ∨ Den(a) = Den(b) & ⌈a⌉ = ⌈b⌉ .
V(a = b, w) = F	iff	¬(∃x∃y(x ∈ Den(a) & x ∈ Den(b))& x = y) ∨ Den(a) = Den(b) & ⌈a⌉ = ⌈b⌉).

This implementation is easy and unproblematic because identity is a logical relation with a fixed semantic contribution with respect to all possible worlds. The only thing we in fact have to change explicitly with respect to our initial proposal concerns the valuation function used. We now have to relativize this function to possible worlds. Apart from that, no other changes neither seem to be possible nor required. On this basis, we get two slightly different semantics for identity sentences. The second semantics validates the following schemata concerning identity, if these are interpreted on the basis of a standard semantics of the S5-necessity operator that is implemented into our modified modal framework:

(I1) □(a = a)64

(I2) ((a = a) → □(a = a))

(I3) ((a = b) → □(a = b))

According to our first semantics, the first schema (I1) is invalid because it also has false instances if “a” is a term that lacks a semantic referent. But the other two schemata are also true with respect to our first semantics.⁶⁵ Hence, we not only seem to get a proper compositional semantics for identity sentences within a modal semantic framework on the basis of our new modified treatment of free logic, we can also capture important intuitive and widely accepted properties concerning the notion of identity relative to this framework.

6.4 A compositional modal free semantics for quantified sentences

The last thing I would like to demonstrate in this paper is how our proposed new negative semantics for quantified sentences can also be quite easily transferred to our new S5-type modal framework. In the case of a modal predicate logic, we always have the choice between at least two different interpretations of the universal and the particular quantifier: we can either interpret them relative to variable and world-relative domains D(w) or relative to our constant and total domain D*.⁶⁶ The first choice leads to the following semantics for quantified sentences:

Modified modal negative free semantics concerning quantified sentences with variable domains

Vδ(∀xA, w) = T	iff for every object d ∈ D(w) it is such that Vδ*(< A, w > , T) where δ* that is the same as δ except that it assigns {d} to x;
Vδ(∀xA, w) = F	otherwise.

Vδ(∃xA, w) = T	iff for some object d ∈ D(w) it is such that Vδ*(< A, w > , T) where δ* that is the same as δ except that it assigns {d} to x;
Vδ(∃xA, w) = F	otherwise.

We can modify these truth- and falsity-conditions very easily in such a way that we get the alternative constant domain quantifiers. For this purpose, we only have to substitute “D*” for “D(w)” in the given truth- and falsity-conditions.

The differences between variable and constant domain quantifiers are well known and they become mainly apparent if quantifiers interact with modal operators. This is not the place to discuss these differences in detail. I only wanted to show how the distinction between these two different interpretations of modal quantified sentences can also be made on the basis of our new framework.

However, there is one thing I would like to elaborate on in a bit more detail that also concerns this distinction and the interaction of quantifiers with the identity and the existence predicate. The following principles are valid relative to certain of our given interpretations and the usual standard semantics for (a) modal operators and (b) logical connectives:

(M1) □∀x(E!x ↔ ∃y(y = x))67

(M2) □∀xE!x

(M3) □∀x∃y(y = x)

(M4) □∀x□∃y(y = x)

The first principle (M1) only holds relative to a variable domain interpretation of the quantifiers. Hence, and only here, we get the desired link between the existence predicate and quantifications.⁶⁸ However, there is also a way to get a similar valid principle on the basis of a constant domain framework.⁶⁹ For this purpose, we only have to slightly adjust the semantics of existential sentences. That is, we have to substitute the restrictive condition “x ∈ D(w)” with the, to some extend redundant, but compositionally relevant—at least relative to our second semantic interpretation of “E!”—restriction “x ∈ D*”. Such a change has some counter-intuitive consequences. All true singular existential sentences would come out as necessarily true and all false ones as necessarily false.⁷⁰ Hence, we would undermine some of the initial semantic motivations for a single-domain logical framework, if we extend it in such a way to a modal logic. Hence, I will not propose this option, I only wanted to mention it as a possible alternative to validate (M1).

The principle (M2) also comes out as logically valid on the basis of a variable domain interpretation of our quantifiers.⁷¹,⁷² At first sight, this might seem to be a counter-intuitive result because, intuitively, there are instances of (M2) that are false. But in fact, this apparently counter-intuitive result makes an important insight of free logic apparent, which can be formulated as follows: the truth of a universal quantification is not determined by the logical product of all its true instances, but by the objects that are assigned as values to the variables used. Hence, possibly false instances do not cause a real problem. So, if one thinks that the truth of the instances of a universal quantification should determine the truth-value of the quantification itself, then it would be more adequate to opt for a specific substitutional interpretation of (M2); namely such an interpretation that has among the class of possible substitutions for the open sentence “E!x” also non-referring terms.⁷³ On the basis of such an alternative interpretation, (M2) would come out as false. (M2) also comes out as false on the basis of a constant domain interpretation of the quantifiers.⁷⁴ However, one could restore the truth of (M2) on this basis if one again adjusts the semantics of “E!” as it was already outlined with respect to (M1). But such a change has similar counter-intuitive semantic consequences, as we have already mentioned with respect to a similar interpretation of (M1).

The truth of (M3) very much depends on specific details that concern the semantic interpretation of the quantifiers and whether the domains of the quantifiers can be empty or not.⁷⁵ If a universally free logic not only allows that world-relative domains can be empty, but also that the total domain can be empty, then (M3) is false with respect to both interpretations of the quantifiers. However, (M3) comes out as true if we hold that D* cannot be empty and we make use of a constant domain interpretation of our quantifiers.⁷⁶ This kind of interpretation of D* seems to be more plausible one, at least from a metaphysical point of view, because D* contains, apart from the real objects, also merely possible objects, and it seems to be a very strong view to assume that there could be nothing whatsoever. That is, it would be metaphysically possible to assume no objects at all; hence even merely possible objects would be excluded from D*. (M3) only comes out as true relative to a variable domain interpretation of the quantifiers if we exclude the possibility of empty world-relative domains. However, then our free logic is non-inclusive with respect to both possible domains and, hence, only a very weak form of free logic. With respect to (M4) everything is nearly the same as in the case of (M3) with one important difference: even if we exclude the possibility of empty domains whatsoever, (M4) still comes out as false on the basis of a variable domain interpretation of the quantifiers.

These brief comparisons with respect to the interaction of our existence and identity predicate with quantifiers on the basis of the two possible standard semantics of quantifiers in a modal logic conclude my presentation of our new semantic framework in application to free constant or variable domain modal predicate logics of the S5-type.

7 Summary

In this paper, I tried to show that standard (Tarskian) semantics for single-domain free logic faces problems that concern its compositional status. It turned out that this kind of semantics violates compositionality in many different respects. As a reaction to these problems, I introduced a new alternative semantics for single-domain free logic, which distinguishes not only with respect to predicates between the semantic values and the sematic applicants of such terms, but that also distinguishes between the semantic values and the semantic referents of singular terms. According to this new semantics, a singular term that has a semantic referent has the singleton that contains this referent as its semantic value; a singular term that lacks a semantic referent has the empty set as semantic value. I showed in detail how this semantics can be formulated for a first-order single-domain free logic and an S5-type modal free logic with constant or variable domain quantifiers and how we can, on this basis, solve nearly all of the outlined problems of compositionality that standard (Tarskian) semantics for single-domain free logic faces.