Abstract
Despite the ubiquity of uncertainty, scientific attention has focused primarily on probabilistic approaches, which predominantly rely on the assumption that uncertainty can be measured and expressed numerically. At the same time, the increasing amount of research from a range of areas including psychology, economics, and sociology testify that in the real world, people’s understanding of risky and uncertain situations cannot be satisfactorily explained in probabilistic and decision-theoretical terms. In this article, we offer a theoretical overview of an alternative approach to uncertainty developed in the framework of the ecological rationality research program. We first trace the origins of the ecological approach to uncertainty in Simon’s bounded rationality and Brunswik’s lens model framework and then proceed by outlining a theoretical view of uncertainty that ensues from the ecological rationality approach. We argue that the ecological concept of uncertainty relies on a systemic view of uncertainty that features it as a property of the organism–environment system. We also show how simple heuristics can deal with unmeasurable uncertainty and in what cases ignoring probabilities emerges as a proper response to uncertainty.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction: the challenge of uncertainty in decision-making research
“All things that are still to come lie in uncertainty; live straightaway” (Seneca 49/1990, p. 313). Even though the Roman philosopher Seneca wrote these words almost two millennia ago, they still ring true to the modern ear. Each of us today can recognize what it is like to face the unknown future and the uncertainties that lurk in even the most familiar settings: family, relationships, work, and health. In addition, as a society, we are facing uncertainty on a far more global scale. Among the risks and future challenges that humanity as a whole has to confront, the alarming rate of human-caused global warming and its consequences occupy the frontline. Intensifying patterns of automation and digitalization, compounded with challenges posed by social inequality, large-scale migration, ageing populations, and rising nationalist and populist politics also contribute to a soaring sense of uncertainty (see World Economic Forum 2018). At the end of the twentieth century, this general increase in the complexity of social issues led Beck (1992) to coin the term “risk society” to describe how new forms of social and economic organization produce new risks and how contemporary social life has become increasingly preoccupied with the future and its inherent unpredictability.Footnote 1
The issue of uncertainty not only looms large in our personal and social lives but also lies at the center of many disciplines and branches of scientific discourse. In recent decades there has been a remarkable interdisciplinary rise in interest in uncertainty and its kindred topics of risk, complexity, and unpredictability. Experimental psychologists study the way people perceive risk and make decisions when the outcomes of their actions are unknown (e.g., Gigerenzer 2008; Hastie and Dawes 2010; Hertwig and Erev 2009; Kahneman et al. 1982; Slovic 2000). Economists and decision theorists are interested in understanding rational behavior under conditions of risk, uncertainty, and ambiguity (e.g., Ellsberg 1961; Knight 1921/2002; Luce and Raiffa 1957). Statisticians and mathematicians propose models to quantify uncertainty (e.g., Lindley 2014). Physicists and philosophers face the question of how to understand the nondeterministic universe (e.g., Hacking 1990), while their colleagues in the philosophy of science and epistemology are concerned with the rules of inductive inference and reasoning under uncertainty (e.g., Hacking 2001; Skyrms 1966/2000). In cognitive science, theories of concept learning and causal reasoning—and in neuroscience, theories of predictive processing—portray human minds as probabilistic machines that follow rules of Bayesian inference, thereby reducing the uncertainty of the environment to build a coherent way of perceiving the world and acting in it (e.g., Clark 2015; Hohwy 2013; Tenenbaum et al. 2011). Finally, psychopathologists study uncertainty in terms of its effects on mental health and regard it as a major factor for anxiety disorders (e.g., Dugas et al. 1998; Grupe and Nitschke 2013).
Although a variety of scientific disciplines address the notion of uncertainty, there is no consensual definition of the phenomenon. The most prominent conceptual framework for understanding uncertainty relies on statistical reasoning and the calculus of probabilities. The idea that degrees of uncertainty can be measured and quantified as ranging from complete ignorance to total certainty is closely related to the emergence of the modern notion of probability in mathematics and philosophy in the seventeenth century (Arnauld and Nicole 1662/1850; Pascal 1654/1998, 1670/2000). This quantitative component of probability theory, which models degrees of confidence after the rules of chance, allowed for classifying uncertainty on a numerical scale from 0 (impossible) to 1 (completely certain) depending on the amount and nature of available information or supporting evidence (see Bernoulli 1713/2006; Gigerenzer et al. 1989; Hacking 1975/2006). Classical probability theory is also responsible for another influential classification: the distinction between aleatory and epistemic uncertainty (or objective and subjective uncertainty) that stems from the duality inherent to the modern concept of probability, which encompasses both epistemic probability (subjective degrees of belief) and aleatory probability (stable frequencies displayed by chance devices; Hacking 1975/2006). In a similar vein, epistemic uncertainty refers to incomplete knowledge or information, whereas aleatory (also sometimes called ontic) uncertainty stems from the statistical properties of the environment that exist independent of a person’s knowledge.Footnote 2
Along with its importance for classifying uncertainty according to its degrees and sources, the probabilistic approach to uncertainty also has a strong normative component. Initially, the laws of probability were conceived of as laws of thought itself. Classical probability theory was viewed as a “reasonable calculus” for “reasonable men” (Daston 1988/1995, p. 56). Similarly, in modern axiomatic decision theory, the expected utility model and the calculus of probabilities are used to provide rules for consistent decision making under risk and uncertainty (Savage 1954/1972; von Neumann and Morgenstern 1944/2007). Lindley (2014) went so far as to claim that probabilistic thinking is the only reasonable way to handle uncertainty, stating, “if you have a situation in which uncertainty plays a role, then probability is the tool you have to use” (p. 376).
Despite the profound impact of probability theory on the conceptual shaping and classification of uncertainty, the relation between uncertainty and quantitative probability is not unambiguous and there are strong voices challenging a purely probabilistic treatment of uncertainty. One significant contribution to the question of whether a probabilistic framework is suitable for accounting for uncertainty belongs to economic theory. In his book Risk, Uncertainty, and Profit, economist Frank Knight (1921/2002) suggested the famous distinction between measurable risk and unmeasurable uncertainty that has had a significant impact on decision research in economics and psychology ever since. He argued that in situations of risk, probabilistic information is either available a priori or can be gathered statistically, but in situations of uncertainty people have no choice but to rely on subjective estimates. These estimates are formed under conditions of unmeasurable uncertainty around unique events and situations for which no probabilistic information yet exists, such as starting an unprecedented business venture, developing a new technological idea, or—to take a contemporary example—planning for possible future consequences of global warming.
Another economist, John Maynard Keynes (1936/1973, 1937), also insisted that fundamental uncertainty cannot be measured. He specifically defined uncertainty as the unpredictability characteristic of the remote future and long-term expectations. Like Knight, he mentioned games of chance and insurance cases as examples in which probability calculations are admissible or even necessary. For other situations—such as the prospect of a war, the long-term prices of assets and commodities, or the future of inventions and major technological changes—Keynes (1937) claimed that “there is no scientific basis on which to form any calculable probability whatever. We simply do not know” (p. 214). Unlike Knight, however, who supported an objective interpretation of probability, Keynes’s (1921/1973) views on the unmeasurable nature of uncertainty were rooted in his logical—or, relational—interpretation of probability.
A third interpretation of probability, the subjectivist view, played a key role in Savage’s (1954/1972) formulation of the subjective expected utility theory and is responsible for what has become the most impactful conception of uncertainty in decision-making research. The clearest example of this conception can be found in Luce and Raiffa’s (1957) book Games and Decisions, in which they distinguished between certainty, risk, and uncertainty. The authors proposed that in situations involving certainty, decision makers know that their actions invariably lead to specific outcomes. In decision making under risk, “each action leads to one of a set of possible specific outcomes, each outcome occurring with a known probability. The probabilities are assumed to be known to the decision maker” (Luce and Raiffa 1957, p. 13). In contrast, the realm of decision making under uncertainty encompasses situations in which “either action or both has as its consequence a set of possible specific outcomes, but where the probabilities of these outcomes are completely unknown or are not even meaningful” (Luce and Raiffa 1957, p. 13). Generally, the main application of expected utility theory is in decision making under risk (i.e., decisions involving outcomes with known probabilities); in the subjective expected utility approach, it became similarly applicable to decisions under uncertainty (i.e., decisions involving outcomes with unknown probabilities, often referred to as ambiguity in economics; see Ellsberg 1961; Trautmann and van de Kuilen 2015). Assuming a subjective interpretation of probability, situations of uncertainty and ambiguity can be reduced to risk by assigning probabilities to possible outcomes based on the individual’s subjective degrees of belief. This point is important: In the framework of Bayesian decision theory (and contrary to Knight’s and Keynes’s notions of uncertainty), uncertainty is probabilistically unmeasurable only in the sense that it cannot be assigned objectively known probabilities. Yet, as long as one can form subjective distributions of probability that are consistent and add up to one, uncertainty can be treated in a way similar to risk. According to Ellsberg’s (1961) critical portrayal of this subjectivist spirit, “for a ‘rational’ man—all uncertainty can be reduced to risks” (p. 645).
The limitations of this framework did not escape the attention of decision theorists. For instance, Ellsberg (1961) showed that people violate Savage’s axioms when presented with gambles that involve risk (i.e., outcomes’ probabilities are known) and ambiguity (i.e., outcomes’ probabilities are unknown). Savage himself was well aware that he presented “a certain abstract theory of the behavior of a highly idealized person faced with uncertainty” (Savage 1954/1972, p. 5). Moreover, he proposed applying this approach only to what he called small worlds: decision situations in which all possible actions and their consequences can be enumerated and ordered according to subjective preferences, as is the case in highly simplified environments such as monetary gambles. In Savage’s (1954/1972) words, you can thus have enough information about your decision situation and “look before you leap” (p. 16). In large worlds, however, you must “cross the bridge when you come to it” (p. 16) and make a decision without being able to fully anticipate the future and all decision variables. Binmore (2009) in particular stressed not only the importance of these limitations but also that Savage was fully aware of them. Binmore argued that Bayesian decision theory only applies to decisions in small worlds of relative ignorance. Bradley and Drechsler (2014) also pointed out the limitations in Savage’s small world representation of decision problems and specified that in real-world decision making people are confronted with situations that include unforeseeable contingencies as well as limited knowledge of the available options, their consequences, and the respective values of those consequences.Footnote 3 Contemporary statistical decision theory has faced up to the limitations of the standard normative approaches in general and to the challenge of unmeasurable uncertainty in particular (see Wheeler 2018); some researchers, for instance, have advanced models of imprecise probabilities that attempt to capture the uncertainty associated with people’s rational beliefs (e.g., Augustin et al. 2014; Walley 1991). Yet, the implications of these theoretical developments for practical decision making remain unclear. For instance, there is no well-grounded theory for assessing how good imprecise probabilities are given the actual state of the world (e.g., in terms of strictly proper scoring rules; see Seidenfeld et al. 2012).
Another set of constraints of normative approaches to rational decision making was underlined in Simon’s (1955) article “A behavioral model of rational choice” and his other works (e.g., Simon 1983), in which he confronted normative concepts of rationality prominent in statistical decision theory as well as the rules and choice criteria they impose on human decision making. Simon intended to free uncertainty from a decision-theoretical framework and integrated it in his notion of bounded rationality (Simon 1972; see more on this in section 2). The increase in attention to the descriptive aspect of rationality that followed from Simon’s insights fueled behavioral research on decision making and cast doubts on the applicability of probability theory to people’s behavior in the real world. First, experiments on “man as intuitive statistician” showed that, even though the normative statistical model “provides a good first approximation for a psychological theory of inference”, there are also systematic discrepancies between normative and intuitive reasoning under uncertainty (Peterson and Beach 1967, p. 42). These differences led to adjustments in the portrayal of the “statistical man”, prompting descriptions of humans as “quasi-Bayesians” or conservative intuitive statisticians (Edwards 1968).Footnote 4
Further findings from studies on psychological processes underlying statistical inference grew considerably more dramatic as they challenged the view that people behave as any kind of Bayesians at all (Kahneman and Tversky 1972, p. 450). The most prominent results belong to the heuristics-and-biases research program, which has shown systematic deviations in human judgment and decision making from the assumed norms of rationality in general and from the rules of probabilistic reasoning in particular (Gilovich et al. 2002; Kahneman 2011; Kahneman et al. 1982; Tversky and Kahneman 1974). As one interpretation of Simon’s bounded rationality (for other interpretations see Gigerenzer and Selten 2002), Kahneman’s and Tversky’s approach sought to show how human reasoning and decision making diverge from the norms of probability theory, statistics, and axioms of expected utility theory. In this spirit, Kahneman (2003) described his view of bounded rationality in terms of systematic deviations between optimality and people’s actual cognitive behavior: “Our research attempted to obtain a map of bounded rationality, by exploring the systematic biases that separate the beliefs that people have and the choices they make from the optimal beliefs and choices assumed in rational-agent models” (p. 1449).Footnote 5 Thus, in their very influential research program Kahneman and Tversky did not contest the normative assumptions of probability and decision theory as the embodiment of rationality, but rather sought to show that real people do not behave according to these norms.
This brings us to the core of what rationality is and the criteria according to which people’s judgements and decisions can be characterized as rational or not. In general, rationality designates a connection between one’s actions, beliefs, or decisions and their underlying reasons. In Nozick’s (1993) words, “rationality is taking account of (and acting upon) reasons” (p. 120). This connection is supposed to be meaningful and justifiable, for instance because a belief is based on available evidence (theoretical or epistemic aspect) or because a decision leads to successful outcomes (practical aspect). There are different views and classifications of rationality in philosophy, for example, those that distinguish between value rationality and instrumental rationality (Weber 1968), rationality and reasonableness (Rawls 1993), theoretical and practical rationality (e.g., Mele and Rawling 2004), or procedural and substantive rationality (e.g., Hooker and Streumer 2004). Nozick (1993) argued that instrumental or “means–ends” rationality is a default notion that lies within the intersection of all theories of rationality (p. 133). This is definitely the case for the type of rationality that the interdisciplinary field of judgment and decision making is interested in: Here, rational decisions are those which rely on good reasons that justify the means by efficiently achieving the decision maker’s aims. What exactly constitutes “good reasons” depends on what rules or principles are taken as benchmarks of rational behavior. Such criteria or benchmarks of rationality can be generally divided in two categories (following Hammond 2000): coherence-based and correspondence-based criteria. In coherence-based views, to be rational is to reason in accordance with the rules of logic and probability theory (e.g., modus ponens, Bayes rule, transitivity) in a consistent way. In rational choice theory, axioms of expected utility theory (e.g., strategy of maximizing expected value) are taken as benchmarks of rational decision making. This approach is sometimes described as the standard picture of rationality (Stein 1996) and it remains the most commonly used normative approach to rationality in decision sciences. As we outlined earlier, the heuristics-and-biases research program has consistently relied on these normative principles and argued from a descriptive perspective that people typically diverge from such norms in their behavior. A different view of rationality founds its criteria not in internal coherence, but in external correspondence (e.g., accuracy and adaptivity of judgments and decisions in relation to the environment). Here rationality is still assessed against a certain benchmark, but this benchmark is no longer a set of rules and axioms; instead it is a measure of success in achieving one’s goals in the world—a consequentialist interpretation of rationality in cognition (Schurz and Hertwig 2019).
In this article, we are concerned with a view of bounded rationality that is decidedly different from the one espoused by the heuristics-and-biases program. In Simon’s bounded rationality and its direct descendant, ecological rationality, rationality is understood in terms of cognitive success in the world (correspondence) rather than in terms of conformity to content-free norms of coherence (e.g., transitivity; see also Arkes et al. 2016). Ecological rationality roots rationality in the ecological structures of the world, the internal structures of the human mind, and their interactions. It thus supplements the instrumental notion of rationality with an ecological dimension (Gigerenzer and Sturm 2012, p. 245). On this view, the essence of rational behavior consists in how an organism can adapt in order to achieve its goals under the constraints and affordances posed by both the environment and its own cognitive limitations. Contrary to representations of uncertainty that rely on probabilistic concepts, the notion of ecological rationality questions the applicability of the normative probabilistic model to decision making in the fundamentally uncertain world—what Savage called a “large world” and what Knight and Keynes referred to as situations of unmeasurable uncertainty. In this regard, one uncompromising position has been that “the laws of logic and probability are neither necessary nor sufficient for rational behavior in the real world” (Gigerenzer 2008, p. 7).
The ecological rationality research program not only relies on a normative view of rationality that differs from the standard view in psychology and economics but also implies a different conceptual approach to uncertainty. This approach stems from a tradition in cognitive science that assumes an ecological perspective and takes into account an organism’s cognitive capabilities as well its physical and social surroundings. It is our aim in this paper to further elaborate this conceptual view of uncertainty and its implications. We argue that an ecological interpretation of uncertainty relies on a systemic view of uncertainty that features uncertainty as a property of the organism–environment system. Another contribution ecological rationality makes to understanding uncertainty touches upon uncertainty’s unmeasurable nature and concerns the role of simple decision strategies and predictions in large worlds. One hypothesis of the ecological rationality program is that simple cognitive strategies called heuristics can be better suited than complex statistical models to conditions of low predictability and severe limits in knowledge. As human minds have been dealing with uncertainty since long before probability and decision theory established new rules of rational behavior, it is not implausible to start with the assumption that successful cognitive approaches to uncertainty in real-world environments rely on strategies that are not rooted in probabilities and utilities.
In order to understand how ecological rationality’s view on uncertainty has emerged, we first examine the program’s two theoretical sources: Simon’s bounded rationality and Brunswik’s lens model. While Simon’s approach established a new framework for understanding human rational behavior, Brunswik’s lens model made it possible to integrate environmental and subjective sources of uncertainty, which led to ecological rationality’s systemic view of uncertainty. We then turn to the following issues: the ecological adaptation of the lens model and the ensuing view of uncertainty as a property of the organism–environment system, and unmeasurable uncertainty and the adaptive use of heuristics in decision making.
2 Uncertainty in Simon’s bounded rationality
In developing his approach to bounded rationality, Simon aimed first and foremost to formulate a psychologically realistic theory of rational choice capable of explaining how people make decisions and how they can achieve their goals under internal and external constraints. Simon’s main objection to the existing models of choice (e.g., the family of expected utility approaches) was that their norms and postulates do not rely on realistic descriptive accounts in real-world environments. Instead, they assume unlimited cognitive resources and omniscience on the part of the decision maker (Simon 1983). In “A behavioral model of rational choice”, Simon (1955) spelled out the unrealistic assumptions of perfection that the classical approach to rationality, as embodied by expected utility theory, made about the agent:
If we examine closely the “classical” concepts of rationality outlined above, we see immediately what severe demands they make upon the choosing organism. The organism must be able to attach definite pay-offs (or at least a definite range of pay-offs) to each possible outcome. This, of course, involves also the ability to specify the exact nature of outcomes—there is no room in the scheme for “unanticipated consequences”. The pay-offs must be completely ordered—it must always be possible to specify, in a consistent way, that one outcome is better than, as good as, or worse than any other. And, if the certainty or probabilistic rules are employed, either the outcomes of particular alternatives must be known with certainty, or at least it must be possible to attach definite probabilities to outcomes (pp. 103–104).
In actual human choice such demanding requirements can rarely be met. Outside Savage’s small worlds real people cannot live up to the ideal of making decisions by specifying all possible outcomes, assigning them probabilities and values, and then maximizing the expected payoffs. It would be a misrepresentation, however, to assume that people cannot fulfill this decision-making ideal due to cognitive destitution or a mere lack of skill; Simon (1972) assigned a much larger role to the irreducible uncertainty that has a crucial impact on people’s reasoning and decision-making processes.
In order to show the impact of uncertainty, Simon (1972) distinguished three ways in which uncertainty imposes limits on the exercise of perfect optimizing calculations. The first way concerns incomplete information about the set of alternatives available to the decision maker. Due to time constraints and the limited scope of an individual’s experience, a decision maker can only take a fraction of alternatives into account. The second is related to “uncertainty about consequences that would follow from each alternative”, including the category of “unanticipated consequences” (Simon 1972, p. 169). Drawing on research on decision making by chess players, Simon pointed out that evaluating all possible consequences of all possible alternative strategies would be computationally intractable for them. In practice, instead of considering such an unrealistic outcome space (i.e., the set of all possible outcomes) chess players usually focus only on a limited set of possible moves and choose the most satisfying among them. The third way uncertainty limits optimized calculations is particularly interesting as it concerns the complexity in the environment that prevents a decision maker from deducing the best course of action. Here, as Simon stressed, there is no risk or uncertainty of the sort featured in economics and statistical decision theory. Rather, uncertainty concerns environmental constraints as well as computational constraints, which both prevent the subject from determining the structure of the environment (Simon 1972, p. 170). In contrast to the decision-theoretical identification of uncertainty with the situations of known outcomes and unknown probabilities, Simon’s notion of uncertainty includes the unknown outcome space, the limited knowledge of alternatives, and the environmental complexity.
In view of this irreducible uncertainty inherent to the real world, the very meaning of rationality had to be redefined. Whereas classical and modern decision-theoretical views of rational inference presuppose adherence to the rules of logic and probability theory, Simon stressed that the essence of rational behavior consists in how an organism can adapt to achieve its goals under the constraints of its environment and its own cognitive limitations. These two dimensions of rational behavior—cognitive and environmental—gave rise to the famous scissors metaphor that encapsulates bounded rationality’s theoretical core: “Human rational behavior […] is shaped by a scissors whose two blades are the structure of task environments and the computational capabilities of the actor” (Simon 1990, p. 7). A new interpretation of rationality goes hand in hand with new tools for rational behavior. Simon (1982) argued that successful tools of bounded rationality should differ considerably from the tools identified by the existing normative approaches. In his view, when faced with a choice situation where the computational costs of finding an optimal solution are too high or where such a solution is intractable or unknown, the decision maker may look for a satisfactory, rather than an optimal, alternative (p. 295).
While Simon believed that the relation between mind and environment is akin to that of the blades of a pair of scissors, matching and complementing each other, Austrian psychologist Egon Brunswik offered another contribution to the ecological perspective in human cognition. In his early works (Brunswik 1934; Tolman and Brunswik 1935/2001) and in subsequent contributions to psychology during his time in the United States, Brunswik emphasized the importance of the environment’s inherent uncertainty and the inferential nature of human cognition. His lens model depicts how this inference allows an organism to come to terms with the surrounding world (Brunswik 1952, 1957/2001). We will now address the conception of uncertainty that ensues from the lens model framework and its adaption to rational inference and decision making.
3 Uncertainty in Brunswik’s lens model framework
Brunswik proposed a probabilistic approach to the human mind and cognition called “probabilistic functionalism”, according to which organisms operate in environments full of uncertainties under internal epistemic constraints (Brunswik 1952, p. 22). The lens model was initially designed by Brunswik to illustrate general inferential patterns in visual perception. It has subsequently been adapted to model judgment and rational inference in fields as diverse as clinical judgment (Hammond 1955), juror decisions (Hastie 1993), faculty ratings of graduate students (Dawes 1971), and mate choice (Miller and Todd 1998).Footnote 6
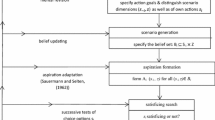
The adapted lens model captures the inferential nature of human judgment and reasoning by depicting the process of inference as mediated by the cues— pieces of information present in the environment (see Fig. 1). Using an analogy of an optical lens, which focuses light waves to produce an image of a distal object, Brunswik organized the process of cognition around two focal variables: the to-be-inferred distal criterion situated in the environment and the observed response on the part of an organism. The lens is in the middle of the diagram, mediating the two parts of the cognitive process through a conglomerate of proximal cues. The lens model shows how proximal cues diverge from a distal criterion and then converge at the point of an organism’s response (Dhami et al. 2004, p. 960).
The first part of the lens model—the environment—explores relations between available/proximal cues and distal objects/criteria. The second part—the organism—focuses on how the organism makes use of the cues to achieve its goals (e.g., judgments, decisions). In the lens model, the process of cognition is inferential, not direct, because it is mediated by ambiguous cues. This ambiguity implies that there is no one-to-one relation between causes and effects, or distal criterion and proximal cues, and that one must constantly guess what is or will be happening in the world. In Brunswik’s (1955b/2001) words, “the crucial point is that while God may not gamble, animals and humans do, and that they cannot help but to gamble in an ecology that is of essence only partly accessible to their foresight” (p. 157). In other words, the lens model indicates that the mind does not simply reflect the world, but rather guesses about or infers it (Todd and Gigerenzer 2001, p. 704). This applies not merely to perception, but to all the ways in which we reason and act in the world. For example, an employer must integrate different observable qualities of a potential employee in order to estimate how well they would perform. No single quality (e.g., education or previous job experience) is directly indicative of future success. There is, however, a partial—uncertain—relation between those qualities and future performance. Brunswik (1952) described these partial cue–criterion relationships in terms of their ecological validity: how well a cue represents or predicts a criterion. The ecological validity of cue–criterion relationships corresponds to the degree of uncertainty in the environment. Brunswik describes this partial relation as essentially probabilistic. On the one hand, this description indicates the uncertain character of inference in human cognition and rejects logical certainty as an ideal. On the other hand, it implies that ecological validity can be expressed as an objective measure of a criterion’s predictability.
The organism side of the lens model features cue utilization, or cue–response relationships. This describes the way the organism makes use of the available information in order to arrive at a judgment or decision. The validity of cue–response relationships is affected not only by external factors, but also by internal factors such as cognitive capacities, search strategies, and strategies used to make choices and inferences. Crucially, an overall achievement (the functional validity of judgment) depends on the match between the response and the environment (see also Karelaia and Hogarth 2008, p. 404). Functional validity corresponds to the degree to which a person’s judgment takes into account different cues and their ecological validities and thereby reflects or matches its environmental counterpart. Cognitively efficient achievement can also rely solely on the most valid cue (see Gigerenzer and Kurz 2001).
Understanding uncertainty in judgment and decision making therefore implies accounting for both how people make inferences and the characteristics of their environments. Thus, defining uncertainty in the lens model framework must capture not only the cue–criterion relationship, or the external part of the lens model, but also the internal cue–response relationship. Selecting and using cues is essentially an achievement of the organism. The choice (conscious or otherwise) of what cues to attend to, as well as inference itself, necessarily depend on the subject. As Brunswik (1952) pointed out, uncertainty is attributable to both the environment and the organism: “Imperfections of achievement may in part be ascribable to the ‘lens’ itself, that is to the organism as an imperfect machine. More essentially, however, they arise by virtue of the intrinsic undependability of the intra-environmental object-cue and means-end relationships that must be utilized by the organism” (p. 23). In other words, there are certain internal limits to human performance in any given task, while at the same time, human performance can be only as good as the environment allows it to be. As his quote illustrates, Brunswik indeed considered external or environmental sources of uncertainty to play a bigger role than internal sources, but nevertheless underlined the role of the organism’s imperfections or limitations as well (cf. Juslin and Olsson 1997, p. 345). Here it is important to stress that the lens model does not simply distinguish between the two parts of inference in cognition, but rather integrates them. Ecological rationality—a direct descendant of both Brunswik’s psychology of organism–environment relationships and Simon’s bounded rationality—goes one step further, striving to accommodate the twofold nature of uncertainty in decision making and investigating the adaptive nature of human behavior in the face of uncertainty by inquiring into the strategies people use to tame the inherent unpredictability of their environments.
4 Uncertainty as a property of the organism–environment system
The ecological adaptation of the lens model further develops Brunswik’s approach by emphasizing the inseparability of the two parts of the model (criterion and judgment). It defines the environment as inextricably linked to the organism and presents the information search and judgment process as dependent on the structure of the concrete environment. The ecological approach also focuses on the adaptive strategies that people apply to decision problems.
We have already shown that Brunswik and Simon had different views on how organisms relate to their environments. Brunswik (1957/2001) saw the environment as the objective surroundings of the organism rather than as the “psychological environment or life space” (p. 300). Even so he emphasized the importance of considering both systems as “partners” or as a married couple (p. 300). In this metaphor, an organism and its environment are two systems, each with its own properties, which should come to terms with one another. According to Brunswik, it is the task of psychology to study this “coming-to-terms” interaction, limited to neither the purely cognitive nor the merely ecological aspects. Simon, on the other hand, defined environment as closely related to the kind of agents that operate in it. For Simon (1956), the term “environment” does not describe “some physically objective world in its totality, but only those aspects of the totality that have relevance as the ‘life space’ of the organism considered” (p. 130). This interpretation takes on some important aspects of the concept of Umwelt proposed by German biologist Jakob von Uexküll (1934/1992). Umwelt describes the world as experienced from the perspective of a living organism, in terms of both perception and action. Whereas all organisms known to humankind share the same physical world, Earth, their phenomenal worlds may differ quite substantially from one another, so that the Umwelt of a butterfly would not be the same as that of a mantis shrimp.
The theory of ecological rationality clearly relies on Simon’s definition of the environment, but it also draws on Brunswik’s two-sided lens model as a framework for integrating two sources of uncertainty. Rather than taking Brunswik’s view of organism and environment as two independent but related systems, this perspective regards organism and environment as part of one shared system. The environment is not divorced from the agent; instead, it represents the “subjective ecology of the organism that emerges through the interaction of its mind, body, and sensory organs with its physical environment” (Todd and Gigerenzer 2012, p. 18). Viewing the organism and the environment as interdependent components of one system changes the conception of uncertainty. As we pointed out in the introduction, the duality inherent to the concept of probability (Hacking 1975/2006) resulted in the distinction between epistemic and aleatory uncertainty; the ecological approach, however, replaces this dualistic view with a synthesis of both types of uncertainty. Uncertainty is thus no longer to be blamed solely on the actor or the surrounding world but instead emerges as a property of the mind–environment system (Todd and Gigerenzer 2012, p. 18). This suggests, as we propose, a systemic view in which uncertainty comprises both environmental unpredictability and uncertainties that stem from the mind’s boundaries, such as limits in available knowledge and cognitive capabilities (for more on the systemic view of uncertainty see Kozyreva et al. 2019).
One implication of this systemic view is the importance of studying how organisms’ evolved cognitive capacities (e.g., recognition memory, perspective taking, motion traction) and strategies adapt to ecological structures. Ecological, or environmental, structures are statistical and other descriptive properties that reflect patterns of information distribution in an ecology. Although the study of environmental structures is an ongoing process, numerous properties have already been identified, including degree of uncertainty or predictability (how well available cues predict the criterion), sample size, number and dispersion of alternatives, variance (distribution of outcomes and probabilities), functional relations between cues and the criterion (e.g., linear or nonlinear), distribution of weights (e.g., compensatory or noncompensatory), cue redundancy (level of intercue correlations), and dominance (see Hertwig et al. 2019; Hogarth and Karelaia 2006, 2007; Katsikopoulos and Martignon 2006; Katsikopoulos et al. 2010; Martignon and Hoffrage 2002; Şimşek 2013; Todd and Gigerenzer 2012).
To illustrate the interdependence between the two parts of the organism–environment system let us consider how some of these environmental structures are influenced by both objective and subjective factors. For instance, the number of alternatives available to the decision maker, as shown in Simon’s approach, is highly dependent on the scope of the subject’s experience and on the way information is presented in the world. While some choice environments may present the decision maker with a limited number of easily assessable options (e.g., local restaurants on Google Maps), most environments that people face on a daily basis require that they discover available alternatives through experience. Navigating in an unfamiliar city, learning a new skill, or adapting to a new job requires experiential learning. Moreover, the more complex and dynamic the environment, the higher the number of new options that can be detected. Yet because of cognitive and motivational constraints, only a fraction of potential alternatives can be taken into account.
The same applies to knowledge of outcomes and probabilities: It depends on the inherent characteristics of informational environments and on the way that information is presented to or learned by the subject. In descriptive tasks, choice environments may be fully transparent for the decision maker; in experience-based tasks, one has to learn underlying payoff distributions via sampling (Hertwig 2012; Hertwig et al. 2004). Unanticipated consequences are by definition completely out of the set of the decision maker’s experience-based expectations. For example, in environments with skewed distributions in which rare events loom (e.g., an earthquake or nuclear accident), unexpected (low probability) outcomes might never be encountered empirically and therefore receive less weight in decision making than they objectively deserve (see Wulff et al. 2018). Unexpected and rare events themselves are relative notions, which are both object- and subject-dependent. Their rarity is an objective function of their relative occurrence in large samples of historic data; at the same time, this rarity is also a function of their occurrence in one’s experience and the state of one’s knowledge. For instance, what can be seen as a rare, extreme, and unpredictable event by the victims of a terror attack or financial crisis can be fully foreseeable for those who either plan or consciously contribute to such events (see Taleb 2007).
These decision variables depend upon both environmental structures and evolved cognitive capacities such as memory or sampling strategies. Generally, humans are frugal samplers, who even under no time pressure choose to consult a surprisingly small number of cues. Reliance on small samples is a robust finding in the decisions from experience paradigm (Wulff et al. 2018). Among other factors, memory limits play an important role in determining sample size: Short-term memory capacity can limit cognitively available samples and partially accounts for low detection and underweighting of rare events (Hertwig et al. 2004). Another rationale behind frugal sampling is related to the amplification effect, which states that small samples tend to amplify relevant properties of the choice options (e.g., variance in payoffs), thus rendering the differences in options clearer and choice easier (Hertwig and Pleskac 2010). Finally, frugal sampling might also be associated with people’s adaptation to their own cognitive limitations on information integration, which typically declines when more cues are taken into account (Hogarth and Karelaia 2007).
Because of its decisive role for determining what information is considered by the decision maker, sample size itself becomes an important environmental structure. It is crucial not only for appreciating rare events and available choice options, but also for estimating ecological validities of cue–criterion relationships (Katsikopoulos et al. 2010). Degree of uncertainty and sample size are therefore two closely related environmental properties. In stable, predictable environments, even small samples would yield reliable estimates, but in unpredictable ecologies such as financial and political forecasting, large samples of data are required for complex methods to provide above-chance results. Notably, however, this last point only holds for stationary environments. In dynamic environments, even large samples might not guarantee a model’s predictive accuracy (DeMiguel et al. 2007). As we will show in the next section, more information is not always better for high uncertainty and small samples.
Further, cognitive and other subjective characteristics of the organism affect both cue differentiation and inferential strategies. For instance, the continuous, sequential character of human conscious experience has an impact on information search, restricting the sample of cues that are available at any given point in time. In temporally unfolding real-world experience, not all cues can be made available simultaneously. Choosing a mate, for example, involves assessing cues such as physical attractiveness, intelligence, and psychological compatibility, which all require different time intervals. Moreover, the coevolution of circumstances in social settings means that certain relevant cues emerge only later in the process to inform decision making (e.g., feelings of love, respect, and trust). In such conditions, as Miller and Todd (1998) argued, judgment is better represented as a sequential achievement of aspiration levels rather than as a linear cue integration process (p. 195).
Similarly, the first-person perspective inherent to human experience helps form one’s expectations. Even if a distal criterion is a future state of the world (e.g., the price of oil in 2027 or the state of one’s marriage in 20 years), practical judgments and decisions have to be made in the present, first-person state of knowledge. According to Keynes (Keynes 1921/1973, 1937), in situations where available cues provide no relevant information for the future state of affairs, it might be not possible to formulate any probability relation whatsoever. Thus, when conceived through its interaction with the organism, the environment becomes dependent not only on its intrinsic structural characteristics but also on the cognitive capacities of the organism, such as its attention span, memory, sampling strategies, emotional preferences, cognitive biases, and general structures of phenomenal experience, including its first-personal nature.
To summarize: Our argument is that the ecological approach to uncertainty makes it possible to specify the nature of aleatory and epistemic uncertainties in human judgment and decision making and to show their interdependence. First, we can define both types of uncertainty in the framework and thereby maintain their distinction conceptually. On this view, ontic or aleatory uncertainty corresponds to the ecological validity of the cue–criterion correlation and epistemic uncertainty concerns limitations in cue differentiation and utilization. Uncertainty, therefore, can emerge in the ecological validity of cue–criterion relationships as well as people’s representations and estimates of those relationships. Such estimates depend not merely on environmental structures but also on the mental structures and scope of an organism’s experience. Second, in ecological rationality, the two types of uncertainty—epistemic and aleatory—are seen as interdependent. The complexity and unpredictability of environments have a direct impact on an individual’s capacity to know them, while a person’s cognition and overall experience shape their world and determine not only how they approach complex situations but also what they become uncertain about.
The distinction between epistemic and aleatory sources of uncertainty is only one dimension of uncertainty. Another dimension is the classification of uncertainty according to degrees (both numerical and qualitative) or levels of uncertainty on the spectrum from certainty to complete ignorance (e.g., Riesch 2013; Walker et al. 2003). Throughout this article, we have encountered conceptions of uncertainty that defy calculation-friendly approaches to the unknown from Knight, Keynes, and Simon. In the next section, we consider some surprising findings of research on simple heuristics that show how simplicity and ecological rationality can be seen as a proper response to the fundamental uncertainty characteristic of large-world environments.
5 Simple heuristics in large worlds
It follows from our definition of uncertainty as a property of the organism–environment system that the degree of uncertainty in judgment and decision making depends on both the type of information distribution in the environment and the scope of a decision maker’s cognitive capabilities, knowledge, and experience. For instance, the lowest degree of uncertainty indicates that the environmental structures are familiar and predictable, so a person can form reliable estimates and sound inferences. Such are the decision conditions in the small world of risk, when no unexpected consequences can disrupt the decision process. In the large world of uncertainty, however, important information remains unknown and must be inferred from small samples. Small samples in complex environments yield high degrees of uncertainty, as do large but no longer representative samples in dynamic environments.
The indicated variability of uncertainty in the organism–environment system raises the possibility that domain-specific cognitive strategies can be better suited for such conditions than the domain-general methods that are typically assumed to guide rational decision making. The idea of domain specificity, which has attracted considerable attention in cognitive science in recent decades, implies that different cognitive abilities are specialized to handle specific types of information and that “the structure of knowledge is different in important ways across distinct content areas” (Hirschfeld and Gelman 1994, p. xiii). This approach was developed in opposition to a long predominant view that people’s reasoning abilities are general forms suitable for any type of content. In the area of decision making, this view suggests that there is no single universal rational strategy (e.g., choosing an option with the highest expected value or utility) that people can apply to all tasks. Rather, strategy selection and its success (as well as its rationality) depend on the structure of concrete cognitive domains or ecologies. Importantly, this view does not diminish the role of domain-general intelligence, but underlines that intelligence can be interpreted differently across different tasks.
The argument of the ecological rationality program is that simple cognitive strategies called heuristics can be better suited for conditions of low predictability than complex statistical models. As Todd and Gigerenzer (2012) conjectured: “The greater the uncertainty, the greater can be the advantage of simple heuristics over optimization methods” (p. 16). At first, this argument can appear counterintuitive. After all, one might be inclined to think that more complex decision situations and higher uncertainty require more cognitive effort, including time, information, and computation. This intuition—also conceptualized in terms of the effort–accuracy tradeoff (Payne et al. 1993)—is deeply embedded in the long tradition of science and philosophy, where the quest for knowledge and the accumulation of evidence are held in the highest esteem. However, one of the findings of research on simple heuristics is that more information and more cognitive effort do not necessarily lead to better knowledge or sharper inferences.Footnote 7 What is more important is the adaptability of a decision strategy or prediction model to the uncertain environment at hand. Relatedly, cognitive limitations are not necessarily a liability, but rather can be regarded as enabling important adaptive functions (Hertwig and Todd 2003).
The principle that more information is not always better—known in the ecological rationality approach as the “less-is-more” effect—implies that in situations of high unpredictability, ignoring some information and simplifying the decision-making process may in fact lead to better decisions and predictions (Gigerenzer and Gaissmaier 2011, p. 471).Footnote 8 This point is not trivial. Even though under conditions of unmeasurable uncertainty every strategy inevitably relies on simplification, strategies still can be distinguished based on their level of complexity and success. Methods that are demanding in terms of information and computation, such as expected utility maximization and statistical linear models, require many variables to be taken into account. Their success depends on the availability of information and the agent’s computational capacities. In contrast, heuristic strategies are economically efficient: They rely on simple rules that are adapted to different types of environmental structures.
The term heuristic is derived from the Greek verb heuriskein, meaning to find or to discover. Heuristics as a general art of discovery referred to different rules and methods in scientific practice (Groner et al. 1983). Following the cognitive revolution in psychology and studies of artificial intelligence, “heuristics” came to mean simple methods in problem solving (as opposed to more complex analytic or optimizing approaches; Newell and Simon 1972; Polya 1945). In terms of decision making, heuristics are cognitive strategies that reduce the complexity of a decision task or problem by ignoring part of the available information or searching only a subset of all possible solutions (Hertwig and Pachur 2015). The simplification process defines what type of heuristic is used. There are different paths to simplification that are adapted to specific kinds of information distribution in the environment. For example, equal-weighting heuristics (equiprobable, tallying, 1/N) simplify decision making by ignoring the probabilities of outcomes (or the ecological validities of cues) and weighting them equally. Lexicographic heuristics follow a simple form of weighting by ordering cues but ignoring dependency between different cues. A subgroup of lexicographic heuristics known as one-reason decision making (e.g., take-the-best and hiatus heuristics) focuses on one good reason and ignores the rest (Gigerenzer and Goldstein 1999). Another group of heuristics, which includes recognition and fluency heuristics (Schooler and Hertwig 2005), relies on the evolved capacities for recognition and fast retrieval of information and is beneficial under conditions of partial ignorance (Goldstein and Gigerenzer 2002; Hertwig et al. 2008).
The use of heuristic rules in judgment and decision making is well documented and many researchers point out that humans—as well as other species—rely extensively on simplification strategies. Here we are not concerned with reviewing different heuristics,Footnote 9 but rather with how heuristics perform compared to more complex and computationally demanding strategies in the large worlds of uncertainty. In particular, we are interested in the group of equal-weighting heuristics that ignore probabilistic information for better results under conditions of unmeasurable uncertainty.
5.1 Ignoring probabilities when uncertainty looms
Equal weighting relies on a simple method: It ignores the probabilities of possible outcomes or ecological validities of uncertain cues and instead assigns equal decision weights to all outcomes or cues. Unit weighting takes into account both positive and negative values of cues, which are standardized and weighted as + 1 or − 1. Its close relative, the tallying heuristic, counts only the number of positive cues and sums them up, ignoring their weights and choosing the object or outcome with the highest number of cues (Gigerenzer and Goldstein 1996). Note that an outcome space does not need to be exhaustive. For instance, when choosing between possible alternatives—such as in a job search—based on several cues (e.g., location, prestige, salary), tallying ignores the ecological validities of the cues and favors the option that is supported by the majority of available cues. Similarly, in monetary gambles, when choosing between several uncertain options, the equiprobable heuristic treats all outcomes as if they were equally likely. A modification of the equal-weighting heuristic for resource allocation tasks, the 1/N heuristic, distributes resources equally between the available number of options (DeMiguel et al. 2007; Hertwig et al. 2002).
First findings showing the advantages of equal-weighting strategies appeared in research on linear models for judgments. Such mathematical models, stemming from a formalization of Brunswik’s lens model, measure both the ecological properties of available information and the organism’s response in terms of the linear additive integration of cues and their values (Hammond 2001; Hammond et al. 1964). The main example of an optimization strategy, the multiple regression equation, relies on a linear combination of the predictor variables, where each variable is weighted proportionally to its validity. The advantages of these mathematical models over human (including expert) judgments, which were demonstrated across different tasks—most consequentially in medical judgment starting with Meehl (1954)—arguably stem from their superior capacities for the unbiased integration of information as compared to imperfect human integration mechanisms (Dawes 1979).
One of the most surprising and interesting findings in this paradigm concerns the performance of simplified—or improper, in Dawes’s (1979) terms—linear models for judgment that employ the equal or unit-weighting strategy described above. For instance, Dawes and Corrigan’s (1974) study demonstrated the accuracy of equal-weighting strategies across several data sets, including predicting psychiatric diagnoses in hospital patients and the academic performance of graduate students. They showed that such simplified models not only significantly outperformed human predictions but also approximated the performance of the multiple regression model that was taken as an optimal benchmark. Equal-weighting models proved to be especially practical when making out-of-population predictions to unknown samples. Einhorn and Hogarth (1975) further developed a theoretical justification for the accuracy of equal weighting relative to the multiple regression model. Bishop (2000) pointedly argued that the success of such “epistemically irresponsible strategies” should warrant reconsideration of what is viewed as reliable epistemic practices and consequently change the conception of epistemically responsible reasoning.
Simulated competitions between different strategies, conducted by Thorngate (1980) and Payne et al. (1988) highlighted the question of the conditions under which ignoring probabilities in terms of, for instance, equal weighting emerges as an efficient strategy. In Thorngate’s simulation, both the equiprobable heuristic, which ignores probabilities, and the probable strategy, which makes only limited use of probability information, performed close to the optimal benchmark, even with large numbers of outcomes and alternatives. Payne et al. (1988) introduced more variability in the environmental conditions as well as time constraints; here the equal-weighting strategy proved to be advantageous under conditions of low probabilities dispersion and when dominance was possible. Moreover, heuristics were more accurate under severe time pressure than a complex weighted-additive strategy.
Hogarth and Karelaia (2007) compared linear and heuristic models of judgment across several environments, specifically examining the environmental conditions under which different prediction models show advantages over others. The results showed that an equal-weighting strategy predicts best in equal-weighting and compensatory environments when intercue redundancy is low. At the same time, they found that under conditions of ignorance, when the decision maker does not know the structure of the environment and therefore cannot order the cues according to their validity, equal weighting is the best heuristic.Footnote 10 An important normative implication of this study is the recommendation for the explicit use of the equal-weighting strategy in the absence of knowledge about the environmental structures (Hogarth and Karelaia 2007, p. 752). This last point is particularly important as it shows that equal weighting might be the best cognitive strategy to use in large worlds of uncertainty and ignorance (but see Katsikopoulos et al. 2010).
One might notice at this point that under conditions of complete ignorance, an equal-weighting heuristic strategy and the probabilistic principle of indifference are undistinguishable. They both recommend assigning equal weights to the possible outcomes. The principle of indifference can itself be seen as a simple rule for assigning epistemic probabilities when no statistical information is available. However, as soon as sampling from experience begins, heuristic and probabilistic strategies differ profoundly. In order to probe these differences and to test the performance of simple and complex inferential strategies in uncertain environments, Hertwig et al. (2019b) extended competition between different strategies from the small world of risk to the large world of uncertainty. Uncertainty was introduced via experiential learning: Not all probabilities and outcomes were described, so strategies had to learn by sampling. Another important difference from previous studies consisted in an attempt to test not merely heuristic performance relative to the benchmark of optimizing expected value calculation, but also how the experience-based version of this model would fare compared to simple strategies (i.e., when the expected value strategy was also required to sequentially learn information in the given environment). According to the results of this simulation, across 20 environments characterized by uncertainty, the equiprobable strategy, which ignores probabilities and therefore demands less cognitive effort, performed similarly to the experience-based expected value model. Averaged across 5, 20, and 50 samples, the expected value strategy scored 97.2% and the equiprobable strategy 93.8%, amounting to an average difference of just 3.4%. Moreover, under conditions of data sparsity (small samples), the equiprobable heuristic achieved the same level of accuracy as did the normative expected value strategy. The performance of the equiprobable strategy was particularly successful in the environments characterized by low variance in probability distribution, which confirms the ecological rationality hypothesis.
The key point to be made here is not that heuristics are inherently better than complex mathematical models, but rather that they might be advantageous under certain environmental conditions and cognitive constraints. This applies to real-world conditions as well as to simulated environments. The efficiency of equal-weighting strategies for practical decisions can be demonstrated by resource allocation in financial decision making. One equal-weighting heuristic—1/N— follows a simple rule of dividing resources equally between each of N alternatives. This naïve diversification strategy proved to be superior to 14 other optimizing strategies, including the Nobel prize-winning mean–variance portfolio, which seeks to optimize profits and minimize risks (DeMiguel et al. 2007). Advantages of the simple equal-weighting portfolio as compared to other investment methods in out-of-sample predictions are particularly pronounced when the number of assets is high and the learning sample size is small. For optimizing methods to outperform heuristics in these conditions, they would need at least 250 years of data collection for a portfolio with 25 assets and 500 years for a portfolio with 50 assets. In the nonstationary world of the stock market such learning samples are not, and in all likelihood will never be, available. Moreover, simple heuristics such as equal weighting work well not only for “games against nature”, but also prove to be robust solutions for complex social and strategic environments (see Spiliopoulos and Hertwig 2019).
The superior performance of equal-weighting strategies in uncertain environments—when the decision maker does not know the underlying statistical structures and relies on small samples—emerges as a robust finding across different studies. However, since Arnaud and Nicole’s Port-Royal Logic (1662/1850) and Pascal’s wager (1670/2000), weighting an event’s value by its likelihood of occurrence was a near-undisputed benchmark of rational behavior. The authors of Port-Royal Logic argued specifically against ignoring likelihoods when judging uncertain events: “In order to judge of what we ought to do in order to obtain a good and to avoid an evil, it is necessary to consider not only the good and evil in themselves, but also the probability of their happening and not happening” (Arnauld and Nicole 1662/1850, p. 360).
With this in mind, it may seem surprising that ignoring probabilities appears to be a proper response to uncertainty. However, we believe that this apparent controversy is consistent with our interpretation of uncertainty as a property of the organism–environment system and the challenges afforded by the concept of unmeasurable uncertainty. In the view we present here, uncertainty reflects not only the underlying ecology, but also an individual’s knowledge and experience. In small worlds, when probabilities of outcomes are either clearly stated (objective probabilities) or can be reliably estimated (subjective probabilities), it is indeed a viable strategy to take them into account. In large worlds of unmeasurable uncertainty, however, probabilistic information can be missing or inaccurate. In practical contexts, people often have no choice but to rely on small samples and learn through (time- and effort-consuming) experience how information is distributed in the environment. In the face of uncertainty that cannot be simply assigned probabilistic measures, ignoring probabilities indeed appears to be, counterintuitively, a good and sometimes even the best way “to obtain a good and to avoid an evil” (Arnauld and Nicole 1662/1850, p. 360).
5.2 Types of uncertainty and strategy selection
The human mind has a variety of tools to deal with its own limitations (and possibly even to exploit them; Hertwig and Todd 2003) and with the uncertainty of its surroundings. Some are the result of evolutionary processes or represent achievements of steady scientific progress in refining rules of logic and reasoning. Others are learned through individual and social experience and cemented in everyday habits and practices. Here we have demonstrated that simple heuristic rules offer fast and effective ways to grapple with uncertainty that can, under specific conditions, surpass the performance of more sophisticated methods, such as those based on probability and statistical decision theory. It is important to note that simple heuristics are not the opposite of complex approaches. In some cases, they represent precisely simplified versions of more demanding methods. For instance, as we have seen, equal weighting was first discovered as a simplified version of a linear model. But the mere discovery of this heuristic entails neither an explanation of its behavioral origin nor an account of psychological processes involved in its use. Equal diversification of resources (under the assumption that they are not extremely scarce) is a strategy that can be found in both humans and animals (e.g., in the case of parental investment; see Davis and Todd 1999; Hertwig et al. 2002). In a similar vein, using heuristics does not mean dispensing with probability and statistics. In fact, lexicographic heuristics (e.g., take-the-best) rely on limited use of probabilistic information to order cues based on their ecological validity, and they perform particularly well when the agent’s knowledge about their environment is limited or even very limited (Gigerenzer and Brighton 2009; Katsikopoulos et al. 2010).
Despite the fact that both simple and complex strategies can be seen as belonging to the mind’s toolbox, they have some important differences when it comes to tradeoffs between accuracy and cognitive effort. Contrary to a popular view that heuristics lose in accuracy what they might gain in simplicity and ease (the assumed accuracy–effort trade-off; Payne et al. 1993), ecological rationality shows that simplicity does not need to come at the cost of accuracy. In other words, a distinctive advantage of heuristics is that even modest amounts of cognitive effort can result in high accuracy. However, heuristics are efficient only when they successfully exploit statistical and other structural properties of the environment. “The rationality of heuristics is not logical, but ecological” (Gigerenzer 2008, p. 23). It is not based on a conformance to predefined rules but rather results from the fit between strategy and environment.
Ecological specificity of heuristics permits predictions not only about when their use should be successful, but also when they are likely to fail. For instance, Pachur and Hertwig (2006) showed that the recognition heuristic does not yield accurate inferences in environments hostile to its use, such as when the mediator value (frequency of mentions of a certain variable, e.g., different infectious diseases) and the criterion value (e.g., the infections’ incidence rates) are uncorrelated. In their case study, the recognition of different infectious diseases was not a good predictor of how prevalent these diseases were in the population, and hence the ecological validity of recognition in that task environment was low (e.g., infections such as cholera, leprosy, and malaria are commonly recognized by students in Germany despite being virtually extinct there). This, in turn, was also reflected in participants’ frequent choice to overrule recognition information. In a similar vein, while assuming equal distribution of payoffs or other decision variables might be the best strategy under conditions of ignorance and in equal-weighting environments (e.g., with low distribution of probabilities), the same type of strategy will be inefficient in environments where existing cues carry very different weights or where probability distributions are highly skewed (Hertwig et al. 2019b; Hogarth and Karelaia 2007).
The principle of ecological rationality applies to the use of more complex integrative methods as well. We believe that both complex and simple approaches are tools that the human mind applies to different tasks. Adaptively and ecologically rational decision making necessarily implies specificity. The point of heuristics is that in some environments and under certain cognitive constraints it is ecologically rational to prefer simple, frugal strategies (e.g., equal weighting or one-reason decision making) to more computationally demanding approaches. In the words of Hogarth and Karelaia (2006), there are different “regions of rationality” where success is directly dependent on applying appropriate decision rules. In some regions, especially environments with a high control over different variables, reliance on computationally demanding algorithms is justified and important (e.g., planning production in an oil refinery; Hogarth and Karelaia 2006). In other regions, however—in particular the wild regions of uncertainty (e.g., long-term investment, mate choice)—the most efficient tool might be found in the mind’s adaptive toolbox of heuristics.
Distinguishing degrees and sources of uncertainty in decision situations has a decisive impact on strategy selection. Strategy selection refers to the process of choosing a cognitive or behavioral strategy to suit a given situation (e.g., which heuristic to use). While the human mind has an extensive toolbox from which to pick a rule for the problem it faces, this very task can pose additional demands on the decision maker.Footnote 11 Strategy selection is a general problem in human cognition and it does not go away when people choose to rely on simple instead of complex approaches (for an account of meta-inductive strategy selection strategies see Schurz and Thorn 2016). Moreover, the very principles of ecological rationality and domain specificity make the strategy selection problem even more salient. Heuristics make certain assumptions about the structures of environments, and the decision maker must check whether those assumptions are correct in a given situation. Some heuristics demand a fine-grain knowledge of the task environment (e.g., take-the-best and other lexicographic heuristics). But some heuristics can be used specifically when the structure of the environment is mostly opaque. The degree of uncertainty plays a decisive role here: The less one knows about the environment, the greater the advantage of equal-weighting strategies or one-reason decision-making strategies. In the previous section, we reviewed several studies showing that the equiprobable heuristic might be a strategy of choice for conditions of severe uncertainty, when structures of the environment cannot be inferred from the available information and an informed strategy selection becomes impossible (Hertwig et al. 2019b).
Finally, it is worth remembering that ecological rationality is a direct descendent of Simon’s bounded rationality and therefore carries a cautious gene that should warn us of its own limits. These limits concern the degree of uncertainty in the organism–environment system. We have shown that simple heuristic inferences can be beneficial when leaving the small world of risk and entering the large world of uncertainty. When probabilities and even outcomes are to a large degree unknown, or when the environment provides a high level of complexity, decision makers might be better off relying on simple methods than trying to control the uncontrollable. More generally, Gigerenzer and Sturm (2012) argued that norms of good reasoning can be identified by studying the niches in which people should rely on heuristics in order to make better inferences (see also Schurz and Hertwig 2019 on the notion of cognitive success). Consequently, so they suggested, ecological rationality permits rationality to be, at least to some extent, naturalized.
Let us now turn to a degree of uncertainty that is so severe that there is virtually no information to make inferences. One particularly catchy expression—the “unknown unknown”—is often employed to designate this highest level of uncertainty that evades any kind of forecasting. Famously coined by the United States Secretary of Defense Donald Rumsfeld, the unknown unknown describes the category of potential events—“the ones we don’t know we don’t know” (Rumsfeld 2002)—that are completely unforeseeable from the perspective of human knowledge at a given point. While “known unknowns” indicate gaps in our knowledge of which we are aware, “unknown unknowns” extend to uncertainty beyond the actual state of knowledge itself. Recognizing this utter uncertainty as an important dimension of decision making in such situations can be useful by itself. And even if in that case we must resort to the Socratic heuristic of self-aware ignorance and admit that no method for prediction would perform better than any other, there are important practical implications of acknowledging such limitations. “The more unpredictable a situation is, the more information needs to be ignored to predict the future” (Gigerenzer and Gaissmaier 2011, p. 471). In utter uncertainty, however, we cannot predict the future at all and must recognize, 80 years after Keynes and more than 2400 years after Socrates, that we know that we simply do not know.
6 Conclusion
Unmeasurable uncertainty, which exceeds standard normative approaches to rationality provided by the statistical decision theory, presents a number of challenges for research on decision making. We have shown that the ecological rationality research program not only offers a new approach to bounded rationality but also a new conceptual approach to uncertainty. This approach stems from a tradition in cognitive science that emphasizes the importance of considering both external environments and internal cognitive characteristics for understanding intelligent behavior and cognition. In particular, we have identified Simon’s bounded rationality and Brunswik’s lens model framework as two important sources of the ecological perspective in judgment and decision-making research. In his theory of bounded rationality, Simon defined rationality in terms of adaptation between the mind and the environment. He also extended the scope of uncertainty to include the unknown outcome space, limited knowledge of the alternatives, and environmental complexity. Another ecologically oriented psychological approach—Brunswik’s lens model—and its adaptations to model judgment and decision making offered a new interpretation of the distinction between epistemic and environmental uncertainty. In this view, uncertainty concerns the ecological validity of cue–criterion relationships as well as people’s estimates of such relationships. We then argued that ecological rationality develops Brunswik’s and Simon’s frameworks even further and features uncertainty as a property of the organism–environment system, thereby underscoring the interdependence of environmental and epistemic sources of uncertainty. We also showed that the challenge of unmeasurable uncertainty in decision making can be successfully addressed by simple and domain-specific heuristic strategies. An ecological approach to rationality offers a fresh conceptual interpretation of uncertainty that comes with a new set of adaptive, efficient tools for navigating uncertainty in the real world.
Notes
Confirming this general tendency, use of the words “risk” and “uncertainty” in print increased since the second half of the twentieth century, with “risk” soaring from the 1970s onwards (this can be seen on Google Books Ngram Viewer). See also Li et al. (2018).
This distinction has become deeply ingrained in treatments of uncertainty across domains, including psychological approaches to decision making (Budescu and Wallsten 1987; Fox and Ülkümen 2011; Kahneman and Tversky 1982; Tannert et al. 2007; Thunnissen 2003; Ülkümen et al. 2016; Walker et al. 2003).
In sociology, a somewhat similar development occurred in discussions on the “risk society”. For instance, Beck (1992) pointed out that risk determinations are based not merely on mathematical calculations of probabilities but also on social interests and values. He underlined that beyond a limited area of domesticated and quantifiable risks there remains a whole dimension of incalculable threats and their impact on people’s lives that defies scientific rationality. This dimension is particularly saturated by the possibility of global catastrophes through ecological, financial, and military risks to which our globalized society is increasingly exposed (Beck 2002). In this regard, Beck (1992) called upon social rationality to be taken as a part of discussion on risk in the modern world (pp. 29–30).
The phrase “intuitive statistician” was originally coined by Brunswik (1955a, p. 212, 1956, p. 80) to describe the workings of the perceptual system in uncertain environments (see also Gigerenzer and Murray 1987, pp. 74–81). The metaphor was extended to other areas of cognition, such as judgment and rational inference. See also the research program on “the naïve intuitive statistician” (Fiedler and Juslin 2006; Juslin et al. 2007).
Kahneman’s theoretical justification for why human judgments and decisions are prone to biases and cognitive illusions relies on the dual-processing account of cognition, which distinguishes between two systems that make up the human mind: System 1, which is automatic and intuitive, and System 2, which is effortful and reflective (Kahneman 2011; for a review see Evans and Stanovich 2013).
One way to explain this effect is through the bias–variance framework (developed in machine learning; Geman et al. 1992). Heuristics can succeed because they smartly trade off two errors that each prediction model cannot help making: the bias component (measuring how well, on average, the model can agree with the ground truth), and the variance component (measuring the variation around this average). The fact that heuristics tend to have higher bias but lower variance than more complex models with more parameters also explains why heuristics perform better than complex models when making predictions from small environmental samples (Gigerenzer and Brighton 2009). The variance component presents a substantial source of error when information about the environment is sparse, thus exposing more complex models to the risk of overfitting by virtue of the flexibility granted by their parameters. Heuristics, however, are less flexible and thus less likely to overfit, which gives them the chance to outperform more complex models when knowledge about the environment is incomplete and uncertainty is high.
Note that in this study (as in all others), the linear model that integrates all cue values in an optimizing way was taken as a benchmark.
For an account of how strategy selection can be simplified through the interplay among strategies, cognitive capacities, and the environment see Marewski and Schooler (2011).
References
Arkes, H. R., Gigerenzer, G., & Hertwig, R. (2016). How bad is incoherence? Decision, 3(1), 20–39. https://doi.org/10.1037/dec0000043.
Arnauld, A., & Nicole, P. (1662/1850). Logic, or, the art of thinking: Being the Port-Royal Logic (T. S. Baynes, Trans.). Edinburgh: Sutherland & Knox.
Augustin, T., Coolen, F. P., de Cooman, G., & Troffaes, M. C. (Eds.). (2014). Introduction to imprecise probabilities. Chichester: Wiley.
Beck, U. (1992). Risk society: Towards a new modernity. London: SAGE Publications.
Beck, U. (2002). The terrorist threat: World risk society revisited. Theory, Culture & Society, 19(4), 39–55. https://doi.org/10.1177/0263276402019004003.
Bernoulli, J. (1713/2006). The art of conjecturing, together with letter to a friend on sets in court tennis (E. D. Sylla, Trans.). Baltimore: John Hopkins University Press.
Binmore, K. (2009). Rational decisions. Princeton: Princeton University Press.
Bishop, M. A. (2000). In praise of epistemic irresponsibility: How lazy and ignorant can you be? Synthese, 122(1–2), 179–208. https://doi.org/10.1023/A:1005228312224.
Bradley, R., & Drechsler, M. (2014). Types of uncertainty. Erkenntnis, 79(6), 1225–1248. https://doi.org/10.1007/s10670-013-9518-4.
Brunswik, E. (1934). Wahrnehmung und Gegenstandswelt: Grundlegung einer Psychologie vom Gegenstand her. Leipzig: Deuticke.
Brunswik, E. (1952). The conceptual framework of psychology. Chicago: University of Chicago Press.
Brunswik, E. (1955a). Representative design and probabilistic theory in a functional psychology. Psychological Review, 62(3), 193–217. https://doi.org/10.1037/h0047470.
Brunswik, E. (1955b/2001). In defense of probabilistic functionalism: A reply. In K. R. Hammond & T. R. Stewart (Eds.), The essential Brunswik: Beginnings, explications, applications (pp. 156–162). New York: Oxford University Press.
Brunswik, E. (1956). Perception and the representative design of psychological experiments. Berkeley: University of California Press.
Brunswik, E. (1957/2001). Scope and aspects of the cognitive problem. In K. R. Hammond & T. R. Stewart (Eds.), The essential Brunswik: Beginnings, explications, applications (pp. 300–312). New York: Oxford University Press.
Budescu, D. V., & Wallsten, T. S. (1987). Subjective estimation of precise and vague uncertainties. In G. Wright & P. Ayton (Eds.), Judgmental forecasting (pp. 63–82). New York: Wiley.
Clark, A. (2015). Surfing uncertainty: Prediction, action, and the embodied mind. New York: Oxford University Press.
Daston, L. (1988/1995). Classical probability in the Enlightenment. Princeton: Princeton University Press.
Davis, J. N., & Todd, P. M. (1999). Parental investment by decision rules. In G. Gigerenzer, P. M. Todd, & The ABC Research Group (Eds.), Simple heuristics that make us smart (pp. 309–324). New York: Oxford University Press.
Dawes, R. M. (1971). A case study of graduate admissions: Application of three principles of human decision making. American Psychologist, 26(2), 180–188. https://doi.org/10.1037/h0030868.
Dawes, R. M. (1979). The robust beauty of improper linear models in decision making. American Psychologist, 34(7), 571–582. https://doi.org/10.1037/0003-066X.34.7.571.
Dawes, R. M., & Corrigan, B. (1974). Linear models in decision making. Psychological Bulletin, 81(2), 95–106. https://doi.org/10.1037/h0037613.
DeMiguel, V., Garlappi, L., & Uppal, R. (2007). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? The Review of Financial Studies, 22(5), 1915–1953. https://doi.org/10.1093/rfs/hhm075.
Dhami, M. K., Hertwig, R., & Hoffrage, U. (2004). The role of representative design in an ecological approach to cognition. Psychological Bulletin, 130(6), 959–988. https://doi.org/10.1037/0033-2909.130.6.959.
Dugas, M., Gagnon, F., Ladouceur, R., & Freeston, M. H. (1998). Generalized anxiety disorder: A preliminary test of a conceptual model. Behaviour Research and Therapy, 36(2), 215–226. https://doi.org/10.1016/S0005-7967(97)00070-3.
Edwards, W. (1968). Conservatism in human information processing. In B. Kleinmuntz (Ed.), Formal representation of human judgment (pp. 17–52). New York: Wiley.
Einhorn, H. J., & Hogarth, R. M. (1975). Unit weighting schemes for decision making. Organizational Behavior and Human Performance, 13(2), 171–192. https://doi.org/10.1016/0030-5073(75)90044-6.
Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. The Quarterly Journal of Economics, 75(4), 643–669. https://doi.org/10.2307/1884324.
Evans, J. S. B., & Stanovich, K. E. (2013). Dual-process theories of higher cognition: Advancing the debate. Perspectives on Psychological Science, 8(3), 223–241. https://doi.org/10.1177/1745691612460685.
Fiedler, K., & Juslin, P. (2006). Information sampling and adaptive cognition. New York: Cambridge University Press.
Fox, C. R., & Ülkümen, G. (2011). Distinguishing two dimensions of uncertainty. In W. Brun, G. Keren, G. Kirkebøen, & H. Montgomery (Eds.), Perspectives on thinking, judging, and decision making: A tribute to Karl Halvor Teigen (pp. 1–14). Oslo: Universitetsforlaget.
Geman, S., Bienenstock, E., & Doursat, R. (1992). Neural networks and the bias/variance dilemma. Neural Computation, 4(1), 1–58. https://doi.org/10.1162/neco.1992.4.1.1.
Gigerenzer, G. (2008). Rationality for mortals: How people cope with uncertainty. New York: Oxford University Press.
Gigerenzer, G., & Brighton, H. (2009). Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science, 1(1), 107–143. https://doi.org/10.1111/j.1756-8765.2008.01006.x.
Gigerenzer, G., & Gaissmaier, W. (2011). Heuristic decision making. Annual Review of Psychology, 62, 451–482. https://doi.org/10.1146/annurev-psych-120709-145346.
Gigerenzer, G., & Goldstein, D. G. (1996). Reasoning the fast and frugal way: Models of bounded rationality. Psychological Review, 103(4), 650–669. https://doi.org/10.1037/0033-295X.103.4.650.
Gigerenzer, G., & Goldstein, D. G. (1999). Betting on one good reason: The take the best heuristic. In G. Gigerenzer, P. M. Todd, & The ABC Research Group (Eds.), Simple heuristics that make us smart (pp. 75–95). New York: Oxford University Press.
Gigerenzer, G., Hertwig, R., & Pachur, T. (Eds.). (2011). Heuristics: The foundations of adaptive behavior. New York: Oxford University Press.
Gigerenzer, G., & Kurz, E. M. (2001). Vicarious functioning reconsidered: A fast and frugal lens model. In K. R. Hammond & T. R. Stewart (Eds.), The essential Brunswik: Beginnings, explications, applications (pp. 342–347). New York: Oxford University Press.
Gigerenzer, G., & Murray, D. J. (1987). Cognition as intuitive statistics. London: Psychology Press.
Gigerenzer, G., & Selten, R. (2002). Rethinking rationality. In G. Gigerenzer & R. Selten (Eds.), Bounded rationality: The adaptive toolbox (pp. 1–12). Cambridge: MIT Press.
Gigerenzer, G., & Sturm, T. (2012). How (far) can rationality be naturalized? Synthese, 187(1), 243–268. https://doi.org/10.1007/s11229-011-0030-6.
Gigerenzer, G., Switjtink, Z., Porter, T., Daston, L., Beatty, J., & Krüger, L. (1989). The empire of chance: How probability changed science and everyday life. Cambridge: Cambridge University Press.
Gigerenzer, G., Todd, P. M., & The ABC Research Group. (1999). Simple heuristics that make us smart. New York: Oxford University Press.
Gilovich, T., Griffin, D., & Kahneman, D. (Eds.). (2002). Heuristics and biases: The psychology of intuitive judgment. Cambridge: Cambridge University Press.
Goldstein, D. G., & Gigerenzer, G. (2002). Models of ecological rationality: The recognition heuristic. Psychological Review, 109(1), 75–90. https://doi.org/10.1037/0033-295X.109.1.75.
Groner, M., Groner, R., & Bischof, W. F. (1983). Approaches to heuristics: A historical review. In R. Groner, M. Groner, & W. F. Bischof (Eds.), Methods of heuristics (pp. 1–18). New York: Routledge.
Grünwald, P., & Halpern, J. Y. (2004). When ignorance is bliss. In J. Y. Halpern (Ed.), Proceedings of the 20th conference on uncertainty in artificial intelligence (UAI’04) (pp. 226–234). AUAI Press, Arlington, Virginia.
Grupe, D. W., & Nitschke, J. B. (2013). Uncertainty and anticipation in anxiety: An integrated neurobiological and psychological perspective. Nature Reviews Neuroscience, 14(7), 488–501. https://doi.org/10.1038/nrn3524.
Hacking, I. (1975/2006). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge: Cambridge University Press.
Hacking, I. (1990). The taming of chance. Cambridge: Cambridge University Press.
Hacking, I. (2001). An introduction to probability and inductive logic. Cambridge: Cambridge University Press.
Hammond, K. R. (1955). Probabilistic functioning and the clinical method. Psychological Review, 62(4), 255–262. https://doi.org/10.1037/h0046845.
Hammond, K. R. (2000). Coherence and correspondence theories in judgment and decision making. In T. Connolly, H. A. Arkes, & K. R. Hammond (Eds.), Judgment and decision making: An interdisciplinary reader (pp. 53–65). Cambridge: Cambridge University Press.
Hammond, K. R. (2001). Expansion of Egon Brunswik’s psychology, 1955–1995. In K. R. Hammond & T. R. Stewart (Eds.), The essential Brunswik: Beginnings, explications, applications (pp. 464–478). New York: Oxford University Press.
Hammond, K. R., Hursch, C. J., & Todd, F. J. (1964). Analyzing the components of clinical inference. Psychological Review, 71(6), 438–456. https://doi.org/10.1037/h0040736.
Hastie, R. (1993). Algebraic models of juror decision processes. In R. Hastie (Ed.), Inside the juror: The psychology of juror decision making (pp. 84–115). Cambridge: Cambridge University Press.
Hastie, R., & Dawes, R. M. (2010). Rational choice in an uncertain world: The psychology of judgment and decision making. Los Angeles: SAGE Publications.
Hertwig, R. (2012). The psychology and rationality of decisions from experience. Synthese, 187(1), 269–292. https://doi.org/10.1007/s11229-011-0024-4.
Hertwig, R., Barron, G., Weber, E. U., & Erev, I. (2004). Decisions from experience and the effect of rare events in risky choice. Psychological Science, 15(8), 534–539. https://doi.org/10.1111/j.0956-7976.2004.00715.x.
Hertwig, R., Davis, J. N., & Sulloway, F. J. (2002). Parental investment: How an equity motive can produce inequality. Psychological Bulletin, 128(5), 728–745.
Hertwig, R., & Erev, I. (2009). The description–experience gap in risky choice. Trends in Cognitive Sciences, 13(12), 517–523. https://doi.org/10.1016/j.tics.2009.09.004.
Hertwig, R., Herzog, S. M., Schooler, L. J., & Reimer, T. (2008). Fluency heuristic: A model of how the mind exploits a by-product of information retrieval. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(5), 1191–1206. https://doi.org/10.1037/a0013025.
Hertwig, R., & Pachur, T. (2015). Heuristics, history of. In N. J. Smelser & P. B. Bates (Eds.), International encyclopedia of the social & behavioral sciences (pp. 829–835). Amsterdam: Elsevier.
Hertwig, R., & Pleskac, T. J. (2010). Decisions from experience: Why small samples? Cognition, 115(2), 225–237. https://doi.org/10.1016/j.cognition.2009.12.009.
Hertwig, R., Pleskac, T. J., Pachur, T., & The Center for Adaptive Rationality. (2019a). Taming uncertainty. Cambridge: MIT Press.
Hertwig, R., Hoffrage, U., & the ABC Research Group. (2013). Simple heuristics in a social world. Oxford: Oxford University Press.
Hertwig, R., & Todd, P. M. (2003). More is not always better: The benefits of cognitive limits. In D. Hardman & L. Macchi (Eds.), Thinking: Psychological perspectives on reasoning, judgment and decision making (pp. 213–231). Chichester: Wiley.
Hertwig, R., Woike, J. K., Pachur, T., & Brandstätter, R. (2019b). The robust beauty of heuristics in choice under uncertainty. In R. Hertwig, T. J. Pleskac, T. Pachur, & The Center for Adaptive Rationality (Eds.), Taming uncertainty. Cambridge: MIT Press.
Hirschfeld, L. A., & Gelman, S. A. (Eds.). (1994). Mapping the mind: Domain specificity in cognition and culture. Cambridge: Cambridge University Press.
Hogarth, R. M., & Karelaia, N. (2006). Regions of rationality: Maps for bounded agents. Decision Analysis, 3(3), 124–144. https://doi.org/10.1287/deca.1060.0063.
Hogarth, R. M., & Karelaia, N. (2007). Heuristic and linear models of judgment: Matching rules and environments. Psychological Review, 114(3), 733–758. https://doi.org/10.1037/0033-295X.114.3.733.
Hohwy, J. (2013). The predictive mind. Oxford: Oxford University Press.
Hooker, B., & Streumer, B. (2004). Procedural and substantive practical rationality. In A. R. Mele & P. Rawling (Eds.), The Oxford handbook of rationality (pp. 57–74). New York: Oxford University Press. https://doi.org/10.1093/0195145399.003.0004.
Juslin, P., & Olsson, H. (1997). Thurstonian and Brunswikian origins of uncertainty in judgment: A sampling model of confidence in sensory discrimination. Psychological Review, 104(2), 344–366. https://doi.org/10.1037/0033-295X.104.2.344.
Juslin, P., Winman, A., & Hansson, P. (2007). The naïve intuitive statistician: A naïve sampling model of intuitive confidence intervals. Psychological Review, 114(3), 678–703. https://doi.org/10.1037/0033-295X.114.3.678.
Kahneman, D. (2003). Maps of bounded rationality: Psychology for behavioral economics. American Economic Review, 93(5), 1449–1475. https://doi.org/10.1257/000282803322655392.
Kahneman, D. (2011). Thinking, fast and slow. London: Penguin Books.
Kahneman, D., Slovic, P., & Tversky, A. (Eds.). (1982). Judgment under uncertainty: heuristics and biases. Cambridge: Cambridge University Press.
Kahneman, D., & Tversky, A. (1972). Subjective probability: A judgment of representativeness. Cognitive Psychology, 3(3), 430–454. https://doi.org/10.1016/0010-0285(72)90016-3.
Kahneman, D., & Tversky, A. (1982). Variants of uncertainty. Cognition, 11(2), 143–157. https://doi.org/10.1016/0010-0277(82)90023-3.
Karelaia, N., & Hogarth, R. M. (2008). Determinants of linear judgment: A meta-analysis of lens model studies. Psychological Bulletin, 134(3), 404–426. https://doi.org/10.1037/0033-2909.134.3.404.
Katsikopoulos, K. V., & Martignon, L. (2006). Naïve heuristics for paired comparisons: Some results on their relative accuracy. Journal of Mathematical Psychology, 50(5), 488–494. https://doi.org/10.1016/j.jmp.2006.06.001.
Katsikopoulos, K. V., Schooler, L. J., & Hertwig, R. (2010). The robust beauty of ordinary information. Psychological Review, 117(4), 1259–1266. https://doi.org/10.1037/a0020418.
Keynes, J. M. (1921/1973). A treatise on probability. The collected writings of John Maynard Keynes (Vol. VIII). London: Macmillan.
Keynes, J. M. (1936/1973). The general theory of employment, interest, and money. The Collected writings of John Maynard Keynes (Vol. VII). London: Macmillan.
Keynes, J. M. (1937). The general theory of employment. The Quarterly Journal of Economics, 51(2), 209–223.
Knight, F. H. (1921/2002). Risk, uncertainty and profit. Washington, D.C.: Beard Books.
Kozyreva, A., Pleskac, T., Pachur, T., & Hertwig, R. (2019). Interpreting uncertainty: A brief history of not knowing. In R. Hertwig, T. J. Pleskac, T. Pachur, & The Center for Adaptive Rationality (Eds.), Taming uncertainty. Cambridge: MIT Press.
Li, Y., Hills, T., & Hertwig, R. (2018). A cultural history of risk. PsyArXiv https://doi.org/10.31234/osf.io/8vqhm.
Lindley, D. (2014). Understanding uncertainty. Hoboken: Wiley.
Luce, R. D., & Raiffa, H. (1957). Games and decisions: Introduction and critical survey. New York: Dover Publications.
Marewski, J. N., & Schooler, L. J. (2011). Cognitive niches: An ecological model of strategy selection. Psychological Review, 118(3), 393–437. https://doi.org/10.1037/a0024143.
Martignon, L., & Hoffrage, U. (2002). Fast, frugal, and fit: Simple heuristics for paired comparison. Theory and Decision, 52(1), 29–71. https://doi.org/10.1023/A:1015516217425.
Meehl, P. E. (1954). Clinical versus statistical prediction: A theoretical analysis and a review of the evidence. Minneapolis: University of Minnesota Press.
Mele, A. R., & Rawling, P. (2004). Introduction: Aspects of rationality. In A. R. Mele & P. Rawling (Eds.), The Oxford handbook of rationality (pp. 3–13). New York: Oxford University Press. https://doi.org/10.1093/0195145399.003.0001.
Miller, G. F., & Todd, P. M. (1998). Mate choice turns cognitive. Trends in Cognitive Sciences, 2(5), 190–198. https://doi.org/10.1016/S1364-6613(98)01169-3.
Newell, A., & Simon, H. A. (1972). Human problem solving. Englewood Cliffs: Prentice-Hall.
Nozick, R. (1993). The nature of rationality. Princeton: Princeton University Press.
Pachur, T., & Hertwig, R. (2006). On the psychology of the recognition heuristic: Retrieval primacy as a key determinant of its use. Journal of Experimental Psychology: Learning, Memory, and Cognition, 32(5), 983–1002. https://doi.org/10.1037/0278-7393.32.5.983.
Pascal, B. (1654/1998). Correspondance avec Fermat sur la règle des partis [Correspondence with Fermat on the problem of points]. In M. L. Guern (Ed.), Œuvres complètes [Complete works] (Vol. 1). Paris: Gallimard.
Pascal, B. (1670/2000). Pensées [Thoughts]. In M. L. Guern (Ed.), Œuvres complètes [Complete works] (Vol. 2). Paris: Gallimard.
Payne, J. W., Bettman, J. R., & Johnson, E. J. (1988). Adaptive strategy selection in decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14(3), 534–552. https://doi.org/10.1037/0278-7393.14.3.534.
Payne, J. W., Bettman, J. R., & Johnson, E. J. (1993). The adaptive decision maker. Cambridge: Cambridge University Press.
Peterson, C. R., & Beach, L. R. (1967). Man as an intuitive statistician. Psychological Bulletin, 68(1), 29–46. https://doi.org/10.1037/h0024722.
Polya, G. (1945). How to solve it: A new aspect of mathematics method. Princeton: Princeton University Press.
Rawls, J. (1993). Political liberalism. New York: Columbia University Press.
Riesch, H. (2013). Levels of uncertainty. In S. Roeser, R. Hillerbrand, P. Sandin, & M. Peterson (Eds.), Essentials of risk theory (pp. 29–56). Dordrecht: Springer. https://doi.org/10.1007/978-94-007-5455-3_2.
Rumsfeld, D. (2002). Transcript: Department of Defense news briefing, February 12, 2002. [Transcript]. http://archive.defense.gov/Transcripts/Transcript.aspx?TranscriptID=2636. Accessed 20 June 2018.
Savage, L. J. (1954/1972). The foundations of statistics. New York: Dover Publications.
Schooler, L. J., & Hertwig, R. (2005). How forgetting aids heuristic inference. Psychological Review, 112(3), 610–628. https://doi.org/10.1037/0033-295X.112.3.610.
Schurz, G., & Hertwig, R. (2019). Cognitive success: A consequentialist account of rationality in cognition. Topics in Cognitive Science, 11(1), 7–36. https://doi.org/10.1111/tops.12410.
Schurz, G., & Thorn, P. D. (2016). The revenge of ecological rationality: Strategy-selection by meta-induction within changing environments. Minds and Machines, 26(1–2), 31–59. https://doi.org/10.1007/s11023-015-9369-7.
Seidenfeld, T., Schervish, M. J., & Kadane, J. B. (2012). Forecasting with imprecise probabilities. International Journal of Approximate Reasoning, 53, 1248–1261.
Seneca, L. A. (49/1990). Moral essays (Vol. 2) (J. W. Basore, Trans.). Cambridge: Harvard University Press.
Simon, H. A. (1955). A behavioral model of rational choice. The Quarterly Journal of Economics, 69(1), 99–118. https://doi.org/10.2307/1884852.
Simon, H. A. (1956). Rational choice and the structure of the environment. Psychological Review, 63(2), 129–138. https://doi.org/10.1037/h0042769.
Simon, H. A. (1972). Theories of bounded rationality. Decision and Organization, 1(1), 161–176.
Simon, H. A. (1982). Models of bounded rationality: Empirically grounded economic reason (Vol. 3). Cambridge: MIT Press.
Simon, H. A. (1983). Reason in human affairs. Princeton: Princeton University Press.
Simon, H. A. (1990). Invariants of human behavior. Annual Review of Psychology, 41(1), 1–20. https://doi.org/10.1146/annurev.ps.41.020190.000245.
Şimşek, Ö (2013). Linear decision rule as aspiration for simple decision heuristics. In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, & K. Q. Weinberger (Eds.), Advances in neural information processing systems 26 (NIPS 2013), (pp. 2904–2912).
Skyrms, B. (1966/2000). Choice and chance: An introduction to inductive logic, 4th ed. Belmont: Wadsworth.
Slovic, P. (Ed.). (2000). The perception of risk. London: Earthscan Publications.
Spiliopoulos, L., & Hertwig, R. (2019). Strategic uncertainty and incomplete information: The homo heuristicus does not fold. In R. Hertwig, T. J. Pleskac, T. Pachur, & The Center for Adaptive Rationality (Eds.), Taming uncertainty. Cambridge: MIT Press.
Stein, E. (1996). Without good reason: The rationality debate in philosophy and cognitive science. New York: Clarendon Press.
Taleb, N. N. (2007). The Black Swan: The impact of the highly improbable. London: Penguin Books.
Tannert, C., Elvers, H.-D., & Jandrig, B. (2007). The ethics of uncertainty. EMBO Reports, 8(10), 892–896. https://doi.org/10.1038/sj.embor.7401072.
Tenenbaum, J. B., Kemp, C., Griffiths, T. L., & Goodman, N. D. (2011). How to grow a mind: Statistics, structure, and abstraction. Science, 331(6022), 1279–1285. https://doi.org/10.1126/science.1192788.
Thorngate, W. (1980). Efficient decision heuristics. Behavioral Science, 25(3), 219–225. https://doi.org/10.1002/bs.3830250306.
Thunnissen, D. P. (2003). Uncertainty classification for the design and development of complex systems. Paper presented at the 3rd annual predictive methods conference. Newport Beach, CA, June 2003.
Todd, P. M., & Gigerenzer, G. (2001). Shepard’s mirrors or Simon’s scissors? Behavioral and Brain Sciences, 24(4), 704–705. https://doi.org/10.1017/S0140525X01650088.
Todd, P. M., & Gigerenzer, G. (Eds.). (2012). Ecological rationality: Intelligence in the world. New York: Oxford University Press.
Tolman, E. & Brunswik, E. (1935/2001). The organism and the causal texture of the environment. In K. R. Hammond, & T. R. Stewart (Eds.), The essential Brunswik: Beginnings, explications, applications (pp. 17–34). New York: Oxford University Press.
Trautmann, S. T., & van de Kuilen, G. (2015). Ambiguity attitudes. In G. Keren & G. Wu (Eds.), The Wiley Blackwell handbook of judgment and decision making, II (pp. 89–116). https://doi.org/10.1002/9781118468333.ch3.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131. https://doi.org/10.1126/science.185.4157.1124.
Ülkümen, G., Fox, C. R., & Malle, B. F. (2016). Two dimensions of subjective uncertainty: Clues from natural language. Journal of Experimental Psychology: General, 145(10), 1280–1297. https://doi.org/10.1037/xge0000202.
von Neumann, J., & Morgenstern, O. (1944/2007). Theory of games and economic behavior. Princeton: Princeton University Press.
von Uexküll, J. (1934/1992). A stroll through the worlds of animals and men: A picture book of invisible worlds. Semiotica, 89(4), 319–391. https://doi.org/10.1515/semi.1992.89.4.319.
Walker, W. E., Harremoës, P., Rotmans, J., van der Sluijs, J. P., van Asselt, M. B. A., Janssen, P., et al. (2003). Defining uncertainty: A conceptual basis for uncertainty management in model-based decision support. Integrated Assessment, 4(1), 5–17. https://doi.org/10.1076/iaij.4.1.5.16466.
Walley, P. (1991). Statistical reasoning with imprecise probabilities. London: Chapman and Hall.
Weber, M. (1968). Economy and society: An outline of interpretive sociology. In G. Roth & C. Wittick (Eds.). New York: Bedminster Press.
Wheeler, G. (2018). Bounded rationality. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (Winter 2018 ed.). Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/win2018/entries/bounded-rationality.
Wheeler, G. (2019). Less is more for Bayesians, too. In R. Viale (Ed.), Routledge handbook on bounded rationality. London: Routledge.
World Economic Forum. (2018) The global risks report. http://www3.weforum.org/docs/WEF_GRR18_Report.pdf.
Wulff, D. U., Mergenthaler-Canseco, M., & Hertwig, R. (2018). A meta-analytic review of two modes of learning and the description–experience gap. Psychological Bulletin, 144(2), 140–176. https://doi.org/10.1037/bul0000115.
Acknowledgements
Open access funding provided by the Max Planck Society. The authors are grateful to Gerd Gigerenzer, Gregory Wheeler, Thorsten Pachur, Tim Pleskac, and the anonymous reviewers for various comments and suggestions. We also thank Deb Ain for editing the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kozyreva, A., Hertwig, R. The interpretation of uncertainty in ecological rationality. Synthese 198, 1517–1547 (2021). https://doi.org/10.1007/s11229-019-02140-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02140-w