Introduction

Intermolecular (or non-covalent) interactions are ubiquitous in real-life chemical systems. For example, these interactions are responsible for non-ideality of gases, they govern the three-dimensional structures of essential biomacromolecules, such as proteins, they determine the packing of the molecules in molecular crystals [1–5]. However, the accurate description of the subtle energetics of those interactions is a task that requires specialized instruments [1–4, 6, 7]. A rather popular model system for the study of weak non-covalent interactions are complexes of noble gas atoms with aromatic systems due to the absence of the possibility to form covalent bonds with the substrate [8–11].

Fig. 1
figure 1

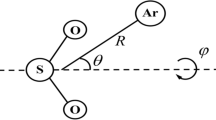
Structures of the protonated imidazole (\(\mathrm{ImH^+}\)) and its clusters (\(\mathrm{Im}_n\mathrm{H^+}, n=2,3\)) [12]

Full size image

In this work, we investigate how argon attaches to protonated imidazole (\({\mathrm{ImH}^+}\)) and its clusters (\({\mathrm{Im}_n\mathrm{H}^+}, n=2,3\)). The structures of these species are given in Fig. 1. Imidazole (Im) itself is an aromatic five-membered aromatic heterocycle with two nitrogen atoms. This molecule is a basic building block of many biologically important molecules, e.g., histamine and histidine. The imidazole units in the complexes we consider (\({\mathrm{Im_{2}H}^+}\) and \({\mathrm{Im_{3}H}^+}\)) are held together by \(\mathrm {N-H\ldots N}\) hydrogen bonds, which makes them the shortest imidazole wires: chains of imidazoles connected via N\(\cdots\)H−N hydrogen bonds. These wires have gained recent attention in theoretical and experimental studies in both gaseous and condensed phases due to their ability to conduct protons via the Grotthuss mechanism (i.e., proton migration via the hydrogen bond) [12–19].

The identification of the argon docking positions in the \({\mathrm{Im}_n\mathrm{H}^+}\) (n=1,2,3) complexes is made by comparing the IR vibrational predissociation spectra of these species obtained using argon tagging in Ref. [12] with the spectra described in the present work using helium as a tag. Helium is a less polarizable and less perturbing tag than argon. Therefore, the comparison of the spectra taken with the help of different noble gas atoms facilitates the isolation of the spectral features arising from the presence of argon. The theoretical calculations explain the observed spectral features. The docking preference of argon in the \({\mathrm{ImH}^+}\) – \({\mathrm{Im_2H}^+}\) – \({\mathrm{Im_3H}^+}\) sequence is rationalized by analyzing the intermolecular forces performed using the symmetry-adapted perturbation theory (SAPT) approach [3, 4].

Computational methods

General considerations

The quantum chemical calculations were performed using Orca 4 [20], Turbomole [21], Psi4 [22], and Gaussian [23] program suites. In order to reduce computational time, all the computations, except for those done in Gaussian, have applied the resolution of identity (RI) technique [24–30]. The def2-TZVPP, def2-TZVP, def2-SVPD, def2-SV(P), and aug-cc-pVTZ basis sets with a corresponding auxiliary basis were used [31–34]. The DFT calculations were using the B3LYP [35–37] exchange-correlation functional with D3 dispersion correction with Becke–Johnson (BJ) damping [6]. The intermolecular interactions of the \(\mathrm{Im}_{n}\mathrm{H}^+\) (n=1,2,3) complexes with argon were analyzed at the SAPT2+\(\delta\)MP2/aug-cc-pVTZ//B3LYP-D3/def2-TZVPP level of theory [3, 4, 38, 39]. Here and further, the notation X//Y will indicate that the energy of the molecule was obtained with method X at the geometry optimized with method Y.

Computations for ImH+ . . . X (X = He, Ar)

In the case of \(\mathrm{ImH^+}\) and the \(\mathrm{ImH^+ \ldots X}\) (X = He, Ar) complexes we have performed geometry optimizations at the B3LYP-D3/def2-SVPD, B3LYP-D3/def2-TZVPP, and MP2(full)/def2-SVPD levels of theory followed by harmonic frequency calculations. Geometries optimized at the B3LYP-D3/def2-TZVPP level were used for single point energy calculations at the DLPNO-CCSD(T) [40, 41], CCSD(T) with the def2-SVPD and def2-TZVPP basis sets, SAPT2+\(\delta\)MP2/aug-cc-pVTZ and SAPT2+3\(\delta\)MP2/aug-cc-pVTZ levels of theory [3, 4].

For calculations in the rigid monomer approximation, we have optimized the structure of the ImH\(^+\) species using the BP86/def2-TZVPP approach. Three unique grids \(24 \times 24 \times 20\) Bohr surrounding ImH\(^+\) with an increment of 1 Bohr (\(\approx 0.53\) Å) for possible He positions were computed at the B3LYP-D3/def2-TZVPP, MP2/def-SVPD, and DLPNO-CCSD(T)/def2-SVPD levels of theory. Additional single point energy computations of the ImH\(^+\) frame and inert gas atom were done to estimate the dissociation energies \(D_\mathrm {e}\) of this complex. The three-dimensional (3D) Schrödinger equation for the motion of the helium atom around the \(\mathrm{ImH^+}\) frame in the rigid monomer approximation was solved via an extended in-house Python script employing the discrete variable representation (DVR) method [42].

Computations for Im2H+ and Im2H+ . . . Ar

All the calculations for \(\mathrm{Im_2H^+}\) and \(\mathrm{Im_2H^+ \ldots Ar}\) were done at the B3LYP-D3/def2-TZVPP level. Geometry optimizations of Im\(_2\)H\(^+\) and four possible isomers of Im\(_2\)H\(^+ \ldots\)Ar (see Results section) were followed by harmonic frequency calculations and one-dimensional proton transfer scans along the proton transfer coordinate Q defined as

$$\begin{aligned} Q = \frac{r\mathrm {(N-H)}-r\mathrm {(N\ldots H)}}{2} \ , \end{aligned}$$
(1)

where \(r\mathrm {(N-H)}\) and \(r\mathrm {(N\ldots H)}\) are the two distances between hydrogen and the two nitrogens in the \(\mathrm{N-H \ldots H}\) part of \(\mathrm{Im_2H^+}\) (see Fig. 1).

The four possible isomers of \(\mathrm{Im_2H^+ \ldots}\) Ar were reoptimized at the B3LYP-D3/def2-SV(P) level of theory and used as starting points for NVE ab initio molecular dynamics (AIMD) simulations with Orca. Initial conditions were sampled from the Maxwell-Boltzmann distribution for \(T = 350\) K to induce the zero-point like motions in the vibrational modes with frequencies below 240 cm \(^{-1}\). For each of the isomers, a set of ten trajectories were produced. The simulation length was 6 ps with 1 fs time step, and the first 1 ps of each trajectory was ignored as an equilibration phase. The power spectra [43] for N–H stretching vibrations were computed using our in-house Python scripts employing frequency-shift correction, allowing large time steps without a loss of the accuracy for the high-frequency motions [44]. Argon distributions from AIMD trajectories were computed using the TRAVIS software [45].

Computations for Im3H+ and Im3H+ . . . Ar

The geometries of the four possible isomers of \(\mathrm{Im_3H^+\ldots Ar}\) were built by hand. They and the untagged \(\mathrm{Im_{3}H^+}\) were optimized at the B3LYP-D3/def2-TZVP level, followed by harmonic frequency calculations. The obtained optimized structures were also confirmed as the equilibrium structures at the B3LYP-D3/def2-TZVPP level of theory. The interaction energies of the \(\mathrm{Im_{3}H^+}\) complex with argon were computed at the SAPT2+ \(\delta\) P2/aug-cc-pVTZ//B3LYP-D3/def2-TZVPP level of theory.

Experimental methods

Experiments were carried out in an in-house tandem mass spectrometer at the EPFL (Lausanne) equipped with a cryogenic octupole ion trap described elsewhere [46]. We have produced protonated gas-phase ions by electrospraying imidazole (99% purity, Sigma Aldrich) dissolved in a mixture of water and methanol. The ions were focused in an electrodynamic ion funnel. The electrosprayed ions were accumulated in a hexapole ion trap and released in short ion packets that are mass-selected in a quadrupole mass filter and guided to a cryogenic octupole ion trap, maintained at 3.5 K. Multiple collisions with helium buffer gas in the octupole ion trap have led to trapping, cooling, and formation of weakly bound complexes with helium atoms. Then IR laser radiation excited the trapped ions in order to perform predissociation spectroscopy. If the helium-tagged ions absorb infrared light, the energy is redistributed in the cluster, leading to the removal of the tag, which is recorded as a depletion of ion yield in the mass spectra.

The vibrational spectra were taken in the range of 900–3500 cm\(^{-1}\); however, the laser power below 1200 cm\(^{-1}\) was insufficient to get a reasonable signal-to-noise ratio. Thus, we were not able to record proton transfer lines around 1100 cm\(^{-1}\) for \(\mathrm {Im_2H^+}\).

Results

General considerations

To explore the possible isomerism of the tag (He, Ar) attachment to the \(\mathrm {Im}_n\mathrm{H}^+\) ion, one has to consider the high IR frequency range corresponding to the stretching vibrations of N–H bonds (\(\ge\) 3000 cm\(^{-1}\)). These polarized bonds can serve as the attachment positions for inert gas atoms to the ions. Such attachment leads to shifts in the N–H stretching frequency. By comparing frequencies for different isomers with the ones predicted by computational chemistry, it is possible to conclude the structural motifs of the weak bonds in the van der Waals bonded complexes [47–50].

In order to do so, we use the following three sets of IR spectroscopic data (Table 1): the uncharged imidazole species (Im and Im\(_2\)) from Ref. [51] in helium droplets, and two sets of the ionic vibrational spectra for \(\mathrm{Im}_n\mathrm{H\ldots X}^+\) (n=1,2,3), measured with X=Ar reported in Ref. [12] and with X = He as described in the current work.

Table 1 Available experimental vibrational spectroscopy data on stretching vibrations (\(\nu\)) in imidazole and its protonated monomer, dimer, and trimer. All values are given in cm\(^{-1}\)
Full size table

Im2H+ . . . X (X=He,Ar)

According to previous investigations [53–55], the ion \(\mathrm{ImH^+}\) offers two attachment positions for the weakly bound tag X (Table 2), namely the hydrogen connected to nitrogen, denoted as \(\mathrm{ImH^+ \ldots X}(\sigma )\), and on top of the \(\pi\)-aromatic system of imidazole, which will be denoted as \(\mathrm{ImH^+ \ldots X}(\pi )\). In the case of the \(\mathrm {ImH^+ \ldots Ar}\) complex, all the applied quantum-chemical methods indicate a prevalence of the ImH\(^+ \ldots\)Ar(\(\sigma\)) isomer over ImH\(^+ \ldots\)Ar(\(\pi\)). Due to the large mass of argon, we can assume the harmonic approximation to be valid for estimating the difference between the zero-point vibrational energies (ZPVE) of these structures. At the B3LYP-D3/def2-TZVPP level of theory, the ZPVE of the ImH\(^+ \ldots\)Ar(\(\pi\)) isomer is higher than the ZPVE of ImH\(^+ \ldots\)Ar(\(\sigma\)) by 10 cm\(^{-1}\). Therefore, the inclusion of the ZPVE correction does not change the conclusions drawn from the single-point energy calculations.

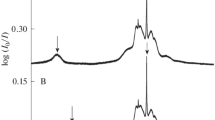
Table 2 Dissociation energies De of the tag X=He/Ar from the ImH+ moiety computed as the difference between optimized geometries De = E(ImH+)+E(X)−E(ImH+ . . . X) at the same level of theory. Structures were optimized at the B3LYP-D3/def2-TZVPP level, while single point energies were computed at the CCSD(T)/def2-TZVPP (CCSD(T)) and SAPT2+3δMP2/aug-cc-pVTZ (SAPT) levels of theory. The basis set superposition error (BSSE) in the CCSD(T) results was corrected using the counterpoise correction [59]. The mean values of these corrections were 32 cm−1 for the ImH+ . . .He clusters and 171 cm−1 for the ImH+ . . .Ar clusters
Full size table

The bonding motif in the \(\mathrm {ImH^+ \ldots Ar}\) complex is confirmed by comparison with IR spectra from Ref. [12]. In the experiment there is an observed splitting between N–H stretching vibrations of 45 cm\(^{-1}\) (see Table 1). The ImH\(^+ \ldots\)Ar(\(\sigma\)) isomer shows a similarly large splitting, while the splitting between N–H stretching frequencies does not exceed 7 cm\(^{-1}\) for the ImH\(^+ \ldots\)Ar(\(\pi\)) (see Fig. 2). The resulting frequencies themselves are also in favor of ImH\(^+ \ldots\)Ar(\(\sigma\)) for all three computational methods. This fully agrees with the conclusions about the ImH\(^+ \ldots\)Ar structure made in Ref. [12].

Fig. 2
figure 2

Experimental vibrational spectra of ImH\(^+\ldots\)Ar (Ref. [12]) and ImH\(^+\ldots\)He (this work) for N–H stretching vibration and their theoretical analogs computed at the B3LYP-D3/def2-TZVPP level of theory in the scaled harmonic oscillator (sHO) approximation. The scaling factor used was 0.9657 [56]. The gray area in the ImH\(^+\ldots\)He signal denotes the ± RMSD (root-mean-square deviation) of the background noise level measurements

Full size image

The analogous comparison of the computed frequencies for ImH\(^+ \ldots\)He and ImH\(^+\) shows no dependence of the N–H stretching frequencies on the helium atom position or even of the helium's presence. All three species (ImH\(^+\), ImH\(^+ \ldots\)He(\(\sigma\)), and ImH\(^+ \ldots\)He(\(\pi\))) agree equally well with our experimental data (Table 1). Such similarity in vibrational frequencies is due to the smaller polarizability of the helium tag compared to argon. This is confirmed by comparing the experimental data from ImH\(^+ \ldots\)Ar and ImH\(^+ \ldots\)He (Table 1). An attachment of Ar to the N–H bond mainly increases the reduced mass of the N–H vibration, thus lowering its frequency. Therefore the larger frequency in ImH\(^+ \ldots\)Ar (3469 cm\(^{-1}\)) corresponds to the free N–H stretching, and the smaller one (3424 cm\(^{-1}\)) comes from N–H\(\ldots\)Ar. The frequencies of N–H stretching in ImH\(^+ \ldots\)He (3468 cm\(^{-1}\)) and of the analogous vibrations in ImH\(^+ \ldots\)Ar (3469 cm\(^{-1}\)) are equal within the step size in our spectra. Thus, they correspond to the N–H vibration in ImH\(^+\) free of the tag.

Helium is a less perturbative tag than argon, and the potential of its interaction with the monomer has only shallow minima. Calculations (Table 2) suggest that the energy difference between the two forms ImH\(^+ \ldots\)He(\(\sigma\)) and ImH\(^+ \ldots\)He(\(\pi )\) is small, therefore the helium atom in the ImH\(^+ \ldots\)He cluster’s ground vibrational state may be delocalized over the ImH\(^+\) unit [8, 57]. In this case, ImH\(^+ \ldots\)He cannot be described as a single isomeric structure with a certain attachment point. To investigate this possibility, we performed calculations describing helium’s delocalization over ImH\(^+\) at a rigid monomer approximation. ImH\(^+\) was frozen at the geometry optimized at the BP86/def2-TZVPP level of theory, and the potential energy surface (PES) for movement of He around this monomer was computed at the DLPNO-CCSD(T)/def2-SVPD level of theory. A 3D Schrödinger equation describing the He motion was solved on the grid using the discrete variable representation (DVR) method [42]. The wavefunctions corresponding to the four lowest vibrational levels at PES from DLPNO-CCSD(T)/def2-SVPD are shown in Fig. 3.

Fig. 3
figure 3

Wavefunctions of the lowest vibrational states of He motion around \(\mathrm {ImH^+}\) in the rigid monomer approximation obtained for the PES from DLPNO-CCSD(T)/def2-SVPD calculation. The density of the dots corresponds to the density of the wavefunction describing helium’s position, and the color of the dots represents the wavefunction’s sign (positive is green, negative is magenta). Values E are the energies of each of the eigenstates, numbers #n (\(n=0\)-3) indicate the energy ordering of these states. The arrows indicate the pairs of tunneling levels, \(\Delta E\) are the energy differences of these levels and \(\tau =h/\Delta E\) is the corresponding tunneling timescale

Full size image

The result shows that, in the lowest vibrational states, the helium tag in the ImH\(^+ \ldots\)He particle is localized in the ImH\(^+ \ldots\)He(\(\pi )\) conformation. This supports localization preferences predicted by CCSD(T)/def2-TZVPP and SAPT2+3\(\delta\)MP2/aug-cc-pVTZ calculations (see Table 2). However, since the two vibrational levels differ only by one wavenumber, coupling with ImH\(^+\) degrees of freedom will probably delocalize helium over the molecule.

Im2H+ . . . X (X=He,Ar)

Fig. 4
figure 4

1D PES for proton transfer in Im\(_2\)H\(^+\) and Im\(_2\)H\(^+\ldots\)Ar at B3LYP-D3/def2-TZVPP with scaled harmonic frequencies of the N–H stretching vibration computed in the local minima. The given values correspond to the vibrations with the highest intensity in the dipole approximation. The proton transfer coordinate Q is given by Eq. (1)

Full size image

Based on the results for ImH\(^+ \ldots\)He, we can assume that the helium tag has a negligible influence on the N–H stretching frequencies, and it is impossible to assign a certain isomer of the \(\mathrm {Im_2H^+\ldots He}\) particle. However, we can expect to determine the docking position of Ar in \(\mathrm {Im_2H^+ \ldots Ar}\). In the case of the imidazole dimer, the variety of attachment positions for the Ar tag is increased: \(\mathrm {Ar(\sigma ) \ldots ImH^+ \cdots Im}\), \(\mathrm {Ar(\sigma ) \ldots Im \cdots ImH^+}\), \(\mathrm {Ar(\pi ) \ldots ImH^+ \cdots Im}\), and \(\mathrm {Ar(\pi ) \ldots Im \cdots ImH^+}\) structures are possible (see Fig. 4). However, proton transfer will interconvert two of these isomers into each other. This can be represented by the reaction \(\mathrm {Ar \ldots ImH^+\cdots Im \leftrightarrow Ar \ldots Im \cdots ImH^+}\). Thus similar to ImH\(^+ \ldots\)Ar, only two isomeric forms \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) and \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) are possible for \(\mathrm {Im_2H^+\ldots Ar}\). For these two isomers, we have computed a relaxed PES for proton transfer at the B3LYP-D3/def2-TZVPP level of theory. For the geometries at the local minima, additional optimizations were performed followed by harmonic frequency calculations. The results are available in Fig. 4. The \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) conformer has a symmetric PES similar to the \(\mathrm {Im_2H^+}\) ion, because argon does not influence the energies of the system in this configuration. On the contrary, \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) has a non-symmetric PES, where the minimum \(\mathrm {Ar(\sigma ) \ldots ImH^+ \cdots Im}\) is favored over \(\mathrm {Ar(\sigma )\ldots Im\cdots ImH^+}\) by approx. 120 cm\(^{-1}\).

Fig. 5
figure 5

Experimental vibrational spectra of Im\(_2\)H\(^+\ldots\)Ar (Ref. [12]) and Im\(_2\)H\(^+\ldots\)He (this work) for N–H stretching vibration and their theoretical analogs computed at the B3LYP-D3/def2-TZVPP level of theory in the scaled harmonic oscillator (sHO) approximation as well as scaled power spectrum from AIMD at the B3LYP-D3/def2-SV(P) level. Harmonic spectra for the argon isomers are given for the most stable conformers. The scaling factor for harmonic frequencies was 0.9657 [56], the maximum of AIMD peak was scaled to be at the frequency of 3492 cm\(^{-1}\). The gray area in the Im\(_2\)H\(^+\ldots\)He signal denotes the ± RMSD of the background noise level measurements

Full size image

A comparison of theoretical frequencies with the experimental data is given in Fig. 5, where the harmonic vibrational frequencies were scaled by 0.9657 [56] and the AIMD power spectrum averaged over all trajectories was scaled with its peak matching the 3492 cm\(^{-1}\) frequency. Theoretical calculations for \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) predict two peaks 50 cm\(^{-1}\) apart, while for the \(\mathrm {Im_2H^+\ldots Ar(\pi )}\), they predict two peaks separated by about 10 cm\(^{-1}\). These peaks have the same positions as for the pure \(\mathrm {Im_2H^+}\) cluster. Therefore, the results of the harmonic calculations favor the \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) to be the species observed.

The shape of the peak was reproduced by AIMD. The trajectories show prevalence of the \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) structure to \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) as 2-to-1. If we consider only the trajectories initiating from the \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) conformer, the ratio becomes 1-to-1. The argon distribution indicates strong conversion from \(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) to \(\mathrm {Im_2H^+\ldots Ar(\pi )}\). The trajectories that start from the \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) conformer show an even larger ratio of 3-to-1 for the initial conformer to stay. This preference of \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) in the simulations can be visualized through the distribution of the argon atom around the \(\mathrm {Im_2H^+}\) core given in Fig. 6. No matter which structure was the initial one (\(\mathrm {Im_2H^+\ldots Ar(\sigma )}\) or \(\mathrm {Im_2H^+\ldots Ar(\pi )}\)), both resulting distributions show significant probability of argon to be present near the center of the \(\mathrm {Im_2H^+}\) fragment. Thus, we can state that the AIMD simulations support the hypothesis of \(\mathrm {Im_2H^+\ldots Ar}\) existing primarily in the form of \(\mathrm {Im_2H^+\ldots Ar(\pi )}\). This form is observed to show only a minor influence on the proton transfer motion (see Fig. 4).

Fig. 6
figure 6

Argon atom distribution around the \(\mathrm {Im_2H^+}\) core as observed in AIMD simulations at the B3LYP-D3/def2-SV(P) level. Labels indicate the initial structure of the trajectory

Full size image

Additional support for this hypothesis on the \(\mathrm {Im_2H^+\ldots Ar}\) structure can be obtained from comparison with other experimental frequencies. In the spectra of \(\mathrm {Im_2H^+\ldots He}\), the N–H stretching frequency is 3495 cm\(^{-1}\), reproducing the frequency observed in \(\mathrm {Im_2H^+\ldots Ar}\) within 5 cm\(^{-1}\). Using the analogy with ImH\(^{+}\), we can conclude that there is no perturbation in frequency by the argon attachment to the hydrogen in the N–H bond; therefore, argon is most likely not attached to this bond, but is present somewhere else. The final argument can be obtained from the quasi-equilibrium chemical reaction describing proton transfer: \(\mathrm {ImH^+ \ldots Im \leftrightarrow Im \ldots ImH^+}\). Two forms of imidazole (Im and ImH\(^+\)) coexist and interconvert into each other, therefore the N–H stretching frequency should be an average of the corresponding values in Im (3518 cm\(^{-1}\)) and ImH\(^+\) (3468 cm\(^{-1}\)) [58]: \(0.5 \times (3518 + 3468) = 3493\) cm\(^{-1}\). This value is strikingly close to the one observed in the experiment (Table 1), and this is possible only if the symmetric proton transfer is allowed, which happens only in the \(\mathrm {Im_2H^+\ldots Ar(\pi )}\) form. Taking all these arguments together, we can conclude that the argon tag in the \(\mathrm {Im_2H^+\ldots Ar}\) ion exists predominantly in the form of \(\mathrm {Im_2H^+\ldots Ar(\pi )}\).

Im3H+ . . . X (X=He,Ar)

Previous studies determined that the protonated imidazole trimer exists in the form of an imidazole chain [12, 13]. Both IR spectra of \(\mathrm {Im_3H^+\ldots He}\) and \(\mathrm {Im_3H^+\ldots Ar}\) have only one N–H stretching frequency, 3505 and 3503 cm\(^{-1}\), respectively. \(\mathrm {Im_3H}^+\), in contrast to \(\mathrm {Im_2H}^+\), has no proton transfer. Such an intramolecular reaction would require a chemical equilibrium of the form

$$\mathrm { ImH^+\cdots Im\cdots Im \leftrightarrow Im\cdots ImH^+ \cdots Im \leftrightarrow Im\cdots Im \cdots ImH^+ } \ ,$$

i.e., the transfer can happen between equivalent structures, where the proton is located on the outer imidazoles in the chain. However, previous calculations performed have shown that the symmetric configuration \(\mathrm {Im\cdots ImH^+ \cdots Im}\) is the lowest energy structure with an energy preference of around 3000 cm\(^{-1}\) [13]. Therefore, this ion is \(\mathrm {ImH^+}\) solvated by two imidazoles. By comparing N–H stretching frequencies for pure imidazole (3518 cm\(^{-1}\)) with the ones obtained for \(\mathrm {Im_3H^+\ldots He}\) and \(\mathrm {Im_3H^+\ldots Ar}\), we can see that the frequencies differ only by 13 and 15 cm\(^{-1}\), respectively.

Fig. 7
figure 7

Total interaction energies of argon with \(\mathrm{Im_3H^+}\) for different isomers of \(\mathrm{Im_3H^+ \ldots Ar}\) at the SAPT2+\(\delta\)MP2/aug-cc-pVTZ//B3LYP-D3/def2-TZVP level of theory. All values are in cm\(^{-1}\)

Full size image

We have manually constructed four isomers of the \(\mathrm {Im_3H^+\ldots Ar}\) to cover the possible docking variety of the argon atom: #1 and #2, where argon is docked to the \(\pi\)-system on either of the two sides of the central \(\mathrm {ImH^+}\) fragment; #3, where argon is docked at the Im fragment’s \(\pi\)-system; and #4, where argon is attached to the N–H of the Im, imitating the \(\mathrm {Im\ldots Ar(\sigma )}\) fragment. Since both N–H bonds of the central \(\mathrm {ImH^+}\) fragment are blocked by the hydrogen-bonded Im fragments, no other \(\mathrm {Ar(\sigma )}\) isomers are possible. All these structures were fully optimized at the B3LYP-D3/def2-TZVP level of theory, and at these geometries, the SAPT2+\(\delta\)MP2/aug-cc-pVTZ dissociation energies of the argon from the \(\mathrm {Im_3H^+}\) moiety were computed. The results are given in Fig. 7, where we see that the \(\mathrm {Im_3H^+\ldots Ar(\pi )}\) structures (#1, #2, and #3) are far more preferable in energy than the \(\mathrm {Im_3H^+\ldots Ar(\sigma )}\) structure (#4). Extrapolation of the discussion for \(\mathrm {ImH^+\ldots Ar}\) and \(\mathrm {Im_2H^+\ldots Ar}\), together with a single observable N–H stretching band and the SAPT results, leads to the conclusion that the argon atom attaches to the \(\pi\)-system of the central imidazole but not to the proton of the outer N–H bonds.

This conclusion showcases the tendency of argon attachment in the row \(\mathrm {Im}_n\mathrm{H}^+\) (n=1,2,3). Although the bonding motif is different for \(\mathrm {ImH}^+\) with respect to \(\mathrm {Im}_n\mathrm{H}^+\) (n=2,3), argon, in general, tends to stick as close to the excessive charge of the ion as possible. When we try to solidify this result by comparison of theory and experiment, we will find that the spectra predicted for the lowest isomers are too similar to each other (see Fig. 8). The significant shift observed in the ImH\(^+ \ldots\)Ar (see Fig. 2) is not present for Im\(_3\)H\(^+\ldots\)Ar because the highest isomer has argon attached in-between the N–H and C–H bonds; therefore, its influence on the N–H stretching frequencies is less prominent.

Fig. 8
figure 8

Experimental vibrational spectra of Im\(_3\)H\(^+\ldots\)Ar (Ref. [12]) and Im\(_3\)H\(^+\ldots\)He (this work) for N–H stretching vibration and their theoretical analogs computed at the B3LYP-D3/def2-TZVP level of theory in the scaled harmonic oscillator (sHO) approximation. Numbering of the \(\mathrm {Im_3H\ldots Ar}^+\) conformers corresponds to the energy ordering in Fig. 7. The scaling factor used was 0.9671 [56]. The gray area in the Im\(_3\)H\(^+\ldots\)He signal denotes the ±RMSD of the background noise level measurements. The Im\(_3\)H\(^+\ldots\)Ar isomers are numbered according to Fig. 7

Full size image

Bonding motif of argon and ImnH+ (n=1,2,3) complexes

Fig. 9
figure 9

SAPT2+\(\delta\)MP2/aug-cc-pVTZ//B3LYP-D3/def2-TZVPP analysis of the interaction energies between the argon atom with the \(\mathrm{Im}_n\mathrm{H^+}\) (n=1,2,3) frame

Full size image

The observed docking preference of the argon atom for an increasing imidazole chain is puzzling:

  • in the case of the monomer (\(\mathrm{ImH^+}\)), argon attaches to the hydrogen involved in the N–H bond leading to the \(\mathrm{ImH^+\ldots Ar(\sigma )}\) structure;

  • in the case of the dimer (\(\mathrm{Im_2H^+}\)) and trimer (\(\mathrm{Im_3H^+}\)), argon prefers to be placed in the middle of the complex leaving the N–H bonds free, and thus leading to an \(\mathrm{ImH^+\ldots Ar(\pi )}\) structure to be observed.

We have performed SAPT2+\(\delta\)MP2/aug-cc-pVTZ single point energy calculations based on the B3LYP-D3/def2-TZVPP optimized molecular structures to rationalize this behavior of the complexes. The results are given in Fig. 9. SAPT disentangles the interaction energy in four terms [4]:

  • exchange (\(E_\mathrm {exch}\)), which is the repulsion of electronic densities of two fragments,

  • electrostatic interactions (\(E_\mathrm {el}\)), which is the interaction energy between static charges of two fragments,

  • induction (\(E_\mathrm {ind}\)), which appears due to polarization in one of the fragments by the static charges in another one,

  • dispersion (\(E_\mathrm {disp}\)), which appears due to the cross-polarization of the two fragments.

The \(\mathrm{Im}_n\mathrm{H^+\ldots Ar}(\pi )\) (n=1,2,3) complexes are all mainly stabilized by dispersion interactions for the following reason: when argon is located above the imidazole ring plane, it is in contact with as many atoms as possible. By increasing the size of the complex, more atoms come into contact with argon, increasing the magnitude of the dispersion interaction of this atom with the \(\mathrm{Im}_n\mathrm{H^+}\) frame, and thus compensating the decrease in the induction energy, which arises from delocalization of the charge between imidazole fragments.

The \(\mathrm{Im}_n\mathrm{H^+\ldots Ar}(\sigma )\) structures show a more complicated trend of energies. In the smallest cluster, \(\mathrm{ImH^+\ldots Ar(\sigma )}\), the main stabilization comes from induction, because argon is in direct contact with the proton, which is the source of the excessive charge. However, the larger the complex becomes, the larger is the delocalization of the charge. Such an effect leads to a decrease in the induction component of the interaction energy. To some extent, the loss of induction is being compensated by the increase of dispersion due to the increased size of the \(\mathrm{Im}_n\mathrm{H^+}\) core. However, this increase is smaller compared to that in the \(\mathrm{Im}_n\mathrm{H^+\ldots Ar}(\pi )\) structures, which leads to the change of the preferred position of the argon with respect to the \(\mathrm{Im}_n\mathrm{H^+}\) frame.

Conclusions

We characterized the protonated imidazole monomer, dimer, and trimer (\(\mathrm{Im}_n\mathrm{H^+}\), n=1,2,3) complexed with argon. This analysis is based on thorough examination of the vibrational spectra from the literature and our vibrational predissociation spectroscopy data for the \(\mathrm{Im}_n\mathrm{H^+}\) species combined with theoretical computations. Based on the experimental vibrational frequencies for N–H stretching vibrations and their computed analogs, we found the binding motifs of the argon tag to \(\mathrm{Im}_n\mathrm{H^+}\) (n=1,2,3) ions. Argon docking preference changes with an increase in the size of the \(\mathrm{Im}_n\mathrm{H^+}\) fragment: in the monomer, it attaches to the hydrogen connected to the nitrogen, while in the larger clusters, argon relocates to the top of the imidazole \(\pi\)-system. This change of the binding motif is dictated by the interplay between induction and dispersion interactions at different docking positions. This study contributes to a general understanding of how the different non-covalent interactions influence supramolecular structures in the presence of the ions, which may be relevant for the design of the molecular mechanics force fields.