Introduction

Traditionally, substituent effects are discussed by means of the relation between some actual data [P(X)] for a given series of substituted systems, generally represented as X–R–Y, and the characteristic of substituents, most often the Hammett substituent constants σ(X) [1, 2] or alike. The introduction of these constants was followed by an avalanche of papers on the subject, which later, in recent decades, was summarized in numerous review articles [3,4,5,6,7,8,9]. In 2007, a novel approach to describing the substituent effect appeared—the charge of the substituent active region, cSAR(X) [10, 11]. It is defined as the sum of the atomic charges on the substituted carbon atom (ipso atom) and the charges on all atoms of the substituent (X) (Eq. (1)).

$$ \mathrm{cSAR}\left(\mathrm{X}\right)=\mathrm{q}\left({\mathrm{C}}_{ipso}\right)+\mathrm{q}\left(\mathrm{X}\right) $$
(1)

It has been shown that cSAR(X) values are usually well correlated with traditional substituent constants [12,13,14,15,16].

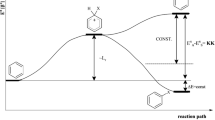
There is also another method for describing the substituent effect, called the stabilization energy of the substituent effect (SESE), proposed by Pross et al. [17]. It is the energy of intramolecular interaction (resonance) between two functional groups, X and Y, attached to the transmitting moiety R. It is calculated as energetic effect of the homodesmotic reaction presented in Eq. (2).

$$ \mathrm{X}-\mathrm{R}-\mathrm{Y}+\mathrm{R}<=>\mathrm{X}-\mathrm{R}+\mathrm{Y}-\mathrm{R} $$
(2)
$$ \mathrm{SESE}=E\left(\mathrm{X}-\mathrm{R}\right)+E\left(\mathrm{Y}-\mathrm{R}\right)-E\left(\mathrm{X}-\mathrm{R}-\mathrm{Y}\right)-E\left(\mathrm{R}\right) $$
(3)

This approach to substituent classification has been successfully used to evaluate the strength of resonance between NO2 and O− groups in variously substituted nitronaphtholates [18], as well as in studies of substituent effects in doubly substituted benzene derivatives [19,20,21].

However, the above-mentioned studies concern double-substituted systems. In the case of mono-substituted systems, the use of the cSAR concept allowed to additionally demonstrate that the properties of a substituent depend on the molecule to which it is attached. The values obtained for the nitro and amino groups, i.e., the most interesting and important substituents in organic and bioorganic chemistry and related fields [22], are presented in Table 1. They confirm the reverse substituent effect [24], describing changes in the electronic properties of a substituent due to the position and type of molecule to which it is attached.

Table 1 Values of cSAR (X), X = NO2 and NH2, determined by the Hirshfeld method, for mono-substituted benzene, cyclohexa-1,3-diene (CHD), and bicyclo[2.2.2]octane (BCO) [23]
Full size table

Another approach to describing substituent properties in mono-substituted systems may arise from the energetic characteristics of the substituent, as presented by Eq. (4)

$$ E{\left(\mathrm{X}\right)}_{\mathrm{R}}=E\left(\mathrm{R}-\mathrm{X}\right)-E\left(\mathrm{R}\right) $$
(4)

where E(R-X) and E(R) are the electronic energies of the substituted and unsubstituted R systems, respectively. Then, assuming benzene as the reference system, we can write Eq. (5)

$$ {E}_{\mathrm{rel}}\left(\mathrm{X}\right)=E{\left(\mathrm{X}\right)}_{\mathrm{R}}-E{\left(\mathrm{X}\right)}_{\mathrm{benz}} $$
(5)

It should be emphasized that this approach, Erel(X), allows the comparison of energy changes of different substituents. Similarly, as in the case of SESE, the values of Erel(X) can be interpreted as the energetic effect of the reaction shown in Scheme 1 for R = naphthalene.

Scheme 1
scheme 1

Homodesmotic reaction for the calculation of Erel(X) in mono-substituted naphthalene

Full size image

This work aims to investigate this approach and to show how it is related to other—geometric and electronic—characteristics of the substituent. To study these relationships in detail, we selected benzene and five polycyclic aromatic hydrocarbons, shown in Fig. 1. These systems were substituted with NH2 and NO2 groups at selected positions and divided into two categories based on their proximity: (i) interacting with two adjacent CH groups in the same ring, like to mono-substituted benzene derivatives (“benzene-like”), marked in green in Fig. 1, and (ii) interacting with one adjacent CH group and the other CH group of another ring, marked in red in Fig. 1.

Fig. 1
figure 1

Benzene (benz) and five polycyclic aromatic hydrocarbons—naphthalene (naph), anthracene (anth), phenantrene (phen), tetracene (tetr), and pentacene (pent). Derivatives of these, substituted with NH2 and NO2 groups at positions marked in red and green, are the target of this study. Colors denote positions with benzene-like proximity, green, and different proximity, red

Full size image

Substituent effects in polycyclic aromatic hydrocarbons were studied computationally in terms of the influence of strongly electron-withdrawing CH2+ group on aromaticity, geometry, and atomic charge distribution in the rings. [25] The results for substituted naphthalene, anthracene, phenanthrene, and pyrene showed that the CH2+ group withdraws π-electrons more strongly at position 2 than at position 1, which was confirmed by charge distribution and geometry changes. The aromatic character of the substituted rings was much lower than that of unsubstituted ones; besides, it was more lowered in the 2-substituted systems. It was shown that the influence on both aromaticity and charge distribution in the ring is stronger for shorter Cipso–CH2+ bonds.

Methodology

Calculations were performed at B3LYP/6-311++G(d,p) [26, 27] level of theory in Gaussian 16 suite of programs [28]. For all optimized structures, no imaginary vibrational frequencies were found. Energetic characteristics of the substituents (Eq. 5) were compared with their electronic (cSAR) and geometric characteristics (Fig. 2), as well as the deformation of the ring induced by them, expressed by changes in α angle relative to the unsubstituted ring, denoted as ∆α.

Fig. 2
figure 2

Geometric characteristics of the substituent, ∆α is the difference in α between substituted and unsubstituted system; Y = H, O

Full size image

The cSAR descriptor values were calculated according to Eq. (1). Atomic charges were obtained using the Hirshfeld method [29]. Geometry-based Harmonic Oscillator Model of Aromaticity (HOMA) index [30] was used as the aromaticity descriptor (Eq. (6)).

$$ \mathrm{HOMA}=1-\frac{1}{n}\sum \limits_i^n{\alpha}_j{\left({d}_{\mathrm{opt},\mathrm{j}}-{d}_{\mathrm{j},\mathrm{i}}\right)}^2 $$
(6)

where n is the number of bonds, αj is the normalization parameter for bond type j, αCC = 257.7, and dopt,j and dj,i are the reference and actual bond lengths, respectively. The value of reference CC bond length used in this paper, dopt = 1.3947 Å, was obtained from benzene geometry optimized at B3LYP/6-311++G(d,p) level of theory. For this fully aromatic molecule, i.e., all bonds are equal to dopt, HOMA=1, while for non-aromatic system HOMA=0.

Based on the computationally obtained wave functions, a topological analysis of electron density distributions was performed according to the quantum theory of atoms in molecules (QTAIM) [31] in the AIM2000 program [32].

Results and discussion

Dependence of E rel(X) on proximity effects

As shown in Fig. 3a, Erel(X) values are highly dependent on the proximity of the substituent, with similar trends applied to both NO2 and NH2 groups. The range of variability of Erel(X) in systems with benzene-like proximity (Fig. 1), is equal to 0.82 and 0.96 kcal/mol, for X = NH2 and NO2, respectively. The variability of this group is a consequence of varying characteristics of the substituted moiety. Within these characteristics, two main factors can be distinguished: (i) position of the substitution and (ii) kind of the substituted system, in particular ability of its electron (mostly π) structure to cooperate with the substituent. Therefore, values of Erel(X) are a measure of the reverse substituent effect [24], as it describes changes of substituent characteristics due to the changes in the system to which it is attached.

Fig. 3
figure 3

Values (in kcal mol−1) of a Erel(X) for all studied systems and b EHB for systems with different proximity than in benzene

Full size image

Values of Erel(X) greater than zero are observed for systems with different proximity than in benzene (Fig. 1). These values are a measure of intramolecular interactions of the substituent with neighboring CH groups, via the H-bonding. By subtracting Erel(X) of the non-benzene-like interacting system from Erel(X) of the corresponding benzene-like system, one can estimate the energetic effect of these interactions, denoted as EHB in Fig. 3b. The designation of these interactions as the H-bonds is supported by the results of the QTAIM analysis. In cases where Erel(X) > 0, stable bond critical points were found between the O atom of the NO2 group and the hydrogen of the CH group of the adjacent ring. In the case of 9-aminoanthracene, two stable critical points were found between the hydrogens of the NH2 and CH groups of adjoining rings. These NH∙∙∙HC interactions can be assigned to dihydrogen bonding [33]; their strength (EHB) is 2.8 kcal/mol. In 4-aminophenanthrene, the amino group interacts with the CH group by its lone pair, resulting in the strongest H-bond (EHB = 5.2 kcal/mol).

Energetic, electronic, and geometric characteristics in systems with “benzene-like” proximity

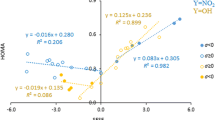
Comparison of energetic characteristics of the substituent, Erel(X), with electronic characteristics, cSAR(X), for benzene-like interacting systems presented in Fig. 4, shows that they are well correlated for linear acenes (benz, naph2, anth2, tetr2, pent2); however, kinked acenes (phen2 and phen3) are slightly deviating from these linear relations.

Fig. 4
figure 4

Dependencies of cSAR(X) for (a) X=NH2 and (b) X=NO2. Red points depict kinked phen2 and phen3 systems. Unfilled red points were not considered in linear regressions

Full size image

Overall trends show that the energy of the electron-donating NH2 group is smaller when its cSAR(X) value is more positive; i.e., group possesses less negative charge, while the opposite is true for the electron-withdrawing NO2 group. Moreover, these values are correlated with the number of coupled rings. The stabilization, and increased charge transfer to the substituent with an increase in the number of coupled rings, from benzene to pentacene, can be explained by the increasing number of ways for the substituent to withdraw, or donate, electrons to the π-electron system, when it consists of more rings. In terms of molecular orbital theory, extending the π-conjugated system leads to a monotonic decrease of the HOMO-LUMO gap, from 5.42 eV in aniline to 2.15 eV in 2-aminopentacene, and from 5.04 eV in nitrobenzene to 2.06 eV in 2-nitropentacene (Table S3). Additionally, the values of the pEDA parameter [34], obtained from the natural atomic orbital (NAO) occupancies of the 2pz orbitals, show that there are long-range π-electron-withdrawing (for NO2) and electron-donating (for NH2) interactions of substituents with distant rings (Fig. 5). Qualitatively, for larger systems, more resonance structures with a formal charge on the substituent and the C atoms of the ring corresponding to the charge transfer can be drawn. In phenanthrene, these long-range interactions with the distant rings, transmitted by the conjugated π system, are blocked by the middle, kinked ring, which is less aromatic, as shown by the low HOMA value of this ring (0.564; Table S2).

Fig. 5
figure 5

Values of pEDA of the NO2 and NH2 groups in 2-substituted linear acenes, referenced to the amino and nitrobenzene

Full size image

Interesting is the difference in Erel(X) between the two benzene-like phenanthrene derivatives substituted by NO2, phen3 and phen2 (0.33 kcal mol−1). This difference results from the different extent of long-range resonance interactions. To explain this, it is worth discussing the geometry of the middle phenanthrene ring. Firstly, it contains a short bond [1.357 Å; B3LYP/6-311++G(d,p) result for unsubstituted phenanthrene] between C9 and C10 atoms (Fig. 1), with highly localized π-electrons. Secondly, the bond connecting the two terminal rings is, on the contrary, a relatively long (1.457 Å) bond, with little π character. In phen3, the nitro group in the 3-position has a strong para electron-withdrawing effect on the carbon atom adjacent to the C9-C10 bond, which can be represented by a resonance structure (Fig. 6). This provides a favorable path for resonance with the distant third ring. On the other hand, it is not possible to draw the same resonance structure for phen2; in this case, the delocalization path passes through the above-mentioned long bond with little π character. This delocalization path is less favorable, and hence, the stabilization of the substituent by resonance is smaller, as shown by higher Erel(X) value. Better delocalization path for phen3 is confirmed by C9-C10 and adjacent bond lengths; the C9-C10 bond is 0.0019 Å longer for phen3 than for phen2, whereas the adjacent bond closer to the substituent is 0.0027 Å shorter (Fig. 6). The electron density at the critical point of the C9-C10 bond is smaller (by 1∙10−3 a.u.), while in the second case, it is higher (by 1.6∙10−3 a.u.) in phen3 than in phen2, which further supports this interpretation.

Fig. 6
figure 6

Resonance structures of 3-nitrophenanthrene (phen3) and 2-nitrophenanthrene (phen2), with indicated bond lengths (in Å); for comparison, the bond lengths in unsubstituted phenanthrene (phen) are also presented

Full size image

In the case of the electron-donating NH2 group, the differences in Erel(X) between phen2 and phen3 are slight. This can be explained by the lack of tendency of the highly localized, π-electron-rich, C9-C10 bond to delocalize negative charge; indeed, the difference in C9-C10 bond lengths between 2- and 3-aminophenanthrene is much lower (0.001 Å) than between their nitro equivalents.

Geometric characteristics of the substituent and the deformation of the substituted aromatic ring are other ways of describing the properties of a substituent in a given system. As shown in Fig. 7, Erel(X) is dependent on CN bond length, dCN, with good determination coefficients, although only for linear acenes, similar to Erel vs cSAR(X) relations. Moreover, this bond shortens as the number of rings increases, which is consistent with the already mentioned increase in resonance between the substituent and the rings. The relationships between Erel(X) and ∆α are also characterized by good determination coefficients for linear acene derivatives. Interestingly, the substitution with the electron-donating NH2 group reduces the α angle concerning the unsubstituted system (∆α < 0), whereas for the electron-withdrawing NO2 group, α increases (∆α > 0). This is in line with the Bent–Walsh rule [35, 36], which describes the rehybridization of atomic orbitals and the resulting geometry changes, due to substitution by groups of different electronegativity. Highly electronegative NO2 group [37, 38] is bonded to the Cipso atom by a hybrid orbital of increased p character compared to that in the unsubstituted system. Simultaneously, the p character of the hybrids bonding Cipso and Cortho atoms is reduced, and, as a consequence, the α angle increases. The amino group, which is electron-donating and less electronegative, has an opposite and weaker effect on the α angle than the NO2 group; the mean absolute value of the angle deformation is less by 0.9°. Therefore, Erel(X) values for NH2 and NO2 are related to ∆α with different signs (Fig. 7c, d). The same is true for the dependence of Erel(X) on the angle YNY. Angle ∠HNH of the NH2 group increases as the Erel(X) value decreases, contrary to ∠ONO of the NO2; moreover, the latter contains both linear and kinked acenes in one well-correlated relation (Fig. 7e, f).

Fig. 7
figure 7

(a–f) Relationships between Erel(X) and geometric parameters introduced in Fig. 2. X=NH2 marked in blue, X=NO2 marked in green. Red points depict kinked phen2 and phen3 systems. Unfilled red points were not included in linear regressions

Full size image

Thus, in systems of similar proximity, the energetic and geometric characteristics of the substituents are highly interdependent. The trends of these changes for substituted linear acenes can be explained again by the rehybridization of the orbitals and mutual relations between dCN and α angle on the Cipso atom, according to the Bent–Walsh rule. In this case, changes in electronegativity of the group are due to the varying strength of resonance with the π-electron system and the resulting changes in electronic properties of the substituent, as shown above by Erel(X) vs cSAR(X) relations (Fig. 4). The increase of positive charge on the substituent from benz to pent2, as for NH2, increases the electronegativity of this group. Thus, as the p character of the C–N hybrid increases, the α angle at the Cipso atom increases. In the case of the NO2 group, the increase in the negative charge on the substituent in benz–pent2 series lowers the p character of the hybrid, which is associated with the sharpening of the α angle. This interpretation of changes in hybridization at Cipso is also confirmed by an analysis of s and p orbital contributions in natural hybrid orbitals (NHOs) constituting the Cipso–Corto and Cipso–N natural bonding orbitals (NBOs) (Table 2) [39]. For the NH2 group, p contribution in the Cipso–N hybrid is higher by 0.07 in 2-aminopentacene than in benzene. In the case of the NO2 group, the p character is lower by 0.03. Hybridization of N orbitals in N–H and N–O bonds changes with the opposite sign; for NH2, it is lower by 0.09, while for NO2, it is higher by 0.03.

Table 2 Values of n in spn natural hybrid orbitals (NHOs) at the Cipso and the N atom of the substituent. Two extreme cases are considered—X-benzene (benz) and 2-X-pentacene (pent2); ∆ is the difference in p character, and ∆cSAR(X) is the difference in cSAR(X) between these two cases
Full size table

Electronic properties of the substituents

Electronic properties of the substituent, cSAR(X), are highly dependent on the bond length between Cipso and the N atom of the substituent, dCN, as shown for benzene-like and other systems in Fig. 8. However, another important factor which is the conformation of the substituent is clearly visible. In the case of the NH2 group, 4-aminophenanthrene (phen4) deviates from other systems. This is due to overcrowding and hence deformation of the rings, caused by the interaction of the NH2 group with the CH at the 5-position of phenanthrene. Specifically, in this case, the phenanthrene rings lose their coplanarity, and the two terminal rings containing NH2 and the mentioned CH group are twisted by about 20. As for NO2 group, deviating systems contain a rotated NO2 group. In the case of phen1 and phen9 systems, this rotation is by 37 and 34°, while for highly deviating anth9 and phen4, 59 and 55°, respectively. All these deviating systems are marked in red in Fig. 8. In summary, shortening the CN bond strengthens the electron-withdrawing/donating character of the substituent, while the rotation of the substituent weakens it due to the disruption of the resonance effect. It was previously shown by Dobrowolski et al. for the NO2 group in benzene. [40]

Fig. 8
figure 8

Dependence of cSAR(NH2) (a) and cSAR(NO2) (b) on the CN bond length, dCN, for the studied systems; unfilled red points were not included in the linear regressions

Full size image

E rel(X) and aromaticity of the rings

Values of HOMA index for the rings of unsubstituted systems and its changes as a result of substitution, estimated by ΔHOMA [ΔHOMA = HOMA(R-X)–HOMA(R)] are presented in Table S2 (Supporting Information). Deformation of the bond lengths of the substituted aromatic ring, expressed by ∆HOMA values, is an order of magnitude greater for systems forming intramolecular hydrogen bonds. For benzene-like linear acenes, although substituent effects on HOMA are small (the largest change is 0.020), the determination coefficients of the relationships between Erel(X) and ∆HOMA are acceptable (R2 ≥ 0.72, as shown in Fig. 9). The slopes of these equations have different signs, indicating that the NO2 group increases the aromaticity of the substituted ring when it conjugates with more rings, contrary to the NH2 group. Moreover, taking into account the slope values, the effect of the nitro group on the aromaticity of the substituted ring is about three times as large as that of the amino group. Interestingly, in the case of benzene derivatives, the opposite effect of these groups has been found [41]. The increase in HOMA of the substituted ring in the case of X=NO2, compared to the unsubstituted system, may result from the withdrawal of electrons from further rings into the NO2-containing ring. This is evidenced by the pEDA values of the rings (Fig. S5b). The addition of aromatic rings in acene leads to an increase in overall occupancy of carbon 2pz natural atomic orbitals (NAOs) in the substituted ring. In the case of X = NH2, the picture is not as clear (Fig. S5a), but the changes in the differences in pEDA for individual rings are slight and rather opposite to those observed for X = NO2. This may explain the smaller and opposite impact of introducing new rings in the amino-substituted acenes on HOMA aromaticity.

Fig. 9
figure 9

Dependence of Erel on HOMA changes for the substituted ring in linear acenes (benzene-like substituted). NH2 marked in blue NO2 marked in green

Full size image

Conclusions

To examine the possibility of describing the substituent effect using an energetic descriptor, mono-substituted polycyclic aromatic hydrocarbons were investigated. For this purpose, the amino and nitro groups were chosen as the substituents and the mono-substituted benzene derivatives as the reference systems. Substituent energy, E(X), can be calculated as the difference between the energies of the substituted and unsubstituted systems. However, changes in the energy of the substituents, estimated concerning the benzene analog, Erel(X), allow the energy of the different substituents to be compared. Also, the use of Erel(X) allows characterizing the proximity effects. For linear “benzene-like” substituted acenes, i.e., systems with similar proximity effects (as in benzene), the values of Erel(X) and cSAR(X) (X = NH2 and NO2) are very well correlated. Moreover, in these systems, the energetic and geometric characteristics of the substituents are highly interdependent, and the changes of the latter are consistent with the Bent–Walsh rule. It should also be noted that, based on the relationships between Erel(X) and ∆HOMA, the effect of the nitro group on the aromaticity of the substituted ring is about three times greater than that of the amino group.