Introduction

Metal complexes containing N-donor ligands in their coordination spheres have been of interest for many years. Investigations of the syntheses, crystal, molecular, and electronic structures of these metal complexes additionally with ambidentate ligands are of great interest in connection with the accumulation of metal complexes containing ambidentate ligands and with regulation of reactivities of active sites in metal complexes. Complexes of divalent metal(II) with thiocyanate ligands are interesting because of their architectures organized by non-covalent contacts as hydrogen bonds or π–π stacking interaction [1]. Cobalt(II) complexes with N-donor ligands are investigated due to their structural properties (ability to occur as cis and trans isomers), formation of coordination polymers in which pseudohalide ligands are bridging as linear anions, examination of solvatochromic behavior of metal complexes [2–6]. Their interesting structural properties and potential application are attractive in studies of magnetism or magnetic exchange ions [7–10].

In chemistry of cobalt(II) complexes, considerable attention was paid to application possibilities of the compounds, basic research directed to, for example, their electronic structures were less popular.

Herein, we present synthesis, crystal, molecular, and electronic structures, and the spectroscopic characterization of four isothiocyanate and two chloride cobalt(II) complexes with N(O)-donor ligands. The electronic structures of the complexes have been determined with the density functional theory (DFT) method, and employed for discussion of the bonding properties. Currently, DFT is commonly used to examine the electronic structure of transition metal complexes. It meets the requirements of being accurate, easy to use and fast enough to allow studies of relatively large molecules of transition metal complexes. Based on UV–VIS–NIR spectra of the complexes, the ligand field, repulsion Racah, and nepheloauxetic parameters were determined. Magnetic properties of the complexes were studied and weak anti- and ferromagnetic interactions mediated by hydrogen bonds were observed, as well as Co(II) ion anisotropy and the considerable spin–orbit coupling.

Experimental

All reagents used for the synthesis of the complexes are commercially available and were used without further purification.

Synthesis of [Co(SCN)2(L)4] (L = β-pic) and [Co(SCN)2(L)2] (L = pyCH2OH, py(CH2)3OH, tzpyrim)

These complexes were synthesized in a reaction between CoCl2·6H2O (0.24 g; 1 × 10−4 mol), NH4SCN (0.15 g; 2 × 10−4 mol) and stoichiometric volumes of β-picoline (β-pic), 2-hydroxymethylpyridine (pyCH2OH), 2-hydroxypropylpyridine (py(CH2)3OH), 1,2,4-triazolo[1,5-α]pyrimidine (tzpyrim), and urotropine (without SNC−) in methanol solution (50 cm−3). The mixtures of the compounds were magnetically stirred for 1 h and filtered. The crystals suitable for X-ray crystal analysis were obtained by slow evaporation of the reaction mixture.

[Co(SCN)2(β-pic)4] (1): Yield 84%. IR (KBr): 3134 νArH; 3000 νCH; 2094 ν(CN from SCN); 1582 νCN, νC=C; 1475 δ(C–CH in the plane); 1434 νPh; 1089 δ(C–CH in the plane); 1024 δ(C–H out of the plane); 809 ν(SC from SCN), 742 δ(C–C out of the plane); 693 δ(C–C in the plane); 491 δ(NCS), 419 ν(Co–Npic). UV–Vis (methanol; log ε): 1207.0 (1.04), 859.5 (1.03), 617.0 (0.96), 519.2 (1.23), 478.1 (sh), 290.8 (2.34), 269.4 (2.51), 262.8 (2.63), 257.4 (2.56), 212.0 (4.97).

[Co(SCN)2(pyCH2OH)2] (2): Yield 61%. IR (KBr): 3271 νOH; 2937 νCH; 2089, 2067 ν(CN from SCN); 1606 νCN, νC=C; 1489, 1274 δ(C–CH in the plane); 1449 νPh; 1032 δ(C–CH in the plane); 966 δ(C–H out of the plane); 818 ν(SC from SCN), 765 δ(C–C out of the plane); 727 δ(C–C in the plane); 470 δ(NCS), 426 ν(Co–Npy). UV–Vis (methanol; log ε): 1135.0 (0.79), 639.4 (1.02), 527.4 (1.29), 469.0 (sh), 290.6 (1.67), 268.4 (2.32), 262.0 (3.12), 211.6 (4.86).

[Co(SCN)2(py(CH2)3OH)2] (3): Yield 62%. IR (KBr): 3385 νOH; 3275 νArH; 2992, 2960, 2918, 2902 νCH; 2099 ν(CN from SCN); 1603 νCN; 1565 νC=C; 1482 δ(C–CH in the plane); 1409 νPh; 1182, 1144 νOH; 1036 δ(C–CH in the plane); 927 δ(C–H out of the plane); 822 ν(SC from SCN), 775 δ(C–C in the plane); 556 δ(NCS). UV–Vis (methanol; log ε): 1069.4 (0.92), 642.8 (1.01), 520.4 (1.31), 472.6 (sh), 411.4 (1.09), 290.8 (2.98), 268.2 (3.77), 261.8 (4.04), 211.8 (4.97).

[Co(SCN)2(CH3OH)2(tzpyrim)2] (4): Yield 77%. IR (KBr): 3108 νArH; 2082 ν(CN from SCN); 1622 νCN, νC=C; 1521, 1184 δ(C–CH in the plane); 1417 νPh; 1025 δ(C–CH in the plane); 957 δ(C–H out of the plane); 807 ν(SC from SCN), 778 δ(C–C in the plane); 493 δ(NCS), 421 ν(Co–Npic). UV–Vis (methanol; log ε): 1090.0 (1.09), 738.0 (1.11), 528.3 (1.29), 446.3 (1.17), 275.6 (3.05), 212.1 (4.89).

Synthesis of [CoCl2(urotrop)2] and [Co(DMIM)3]Cl2·H2O where urotrop = hexamethylenetetramine and DMIM = 2,2′-bis(4,5-dimethylimidazolyl)

[CoCl2(urotrop)2] (5): Yield 58%. IR (KBr): 3023 νCH; 1464; 1382, 1239, 1059, 1008, 925; 817; 690; 505 ν(C–N). UV–Vis (methanol; log ε): 1479.0 (1.00), 677.8 (1.08), 608.0 (0.97), 539.0 (1.17), 370.2 (1.67), 269.4 (2.85), 211.2 (4.89).

[Co(DMIM)3]Cl2·H2O (6): Yield 58%. IR (KBr): 3023, 2923 νCH; 1632 νCN; 1597 νC=C; 1502, 1174 δ(C–CH in the plane); 1410 νIm; 1051 δ(C–CH in the plane); 977 δ(C–H out of the plane); 768 δ(C–C in the plane). UV–Vis (methanol; log ε): 1479.0 (1.01), 677.8 (1.08), 608.0 (0.97), 539.0 (1.17), 370.2 (1.67), 269.4 (2.85), 211.2 (4.89).

Physical measurements

Infrared spectra were recorded on a Nicolet Magna 560 spectrophotometer in the spectral range of 4,000–400 cm−1 with the sample in the form of KBr pellet. Electronic spectra were measured on a Lab Alliance UV–VIS 8500 spectrophotometer in the range of 1,100–180 nm and the NIR region (1,100–2,100 nm) on a Jasco UV–VIS–NIR spectrophotometer in methanol solution.

Magnetic measurements were carried out on polycrystalline samples of ~80 mg using a Lake Shore 7225 AC susceptometer/DC magnetometer. Static susceptibility χDC at the external magnetic field of 1 kOe and dynamic susceptibility χAC (χAC = χ′ − iχ″) at the oscillating field of 2 Oe with frequency of 120 Hz were measured in the temperature range of 4.2–200 K in the zero-field-cooled mode. Susceptibility data were corrected for the temperature independent contribution χ0. Magnetization curves at T = 4.3 K were measured in the range of 0–56 kOe for increasing and decreasing field. For (4), the run at 18.8 K and low-temperature run at 2.3 K, performed with the auxiliary helium gas pump, were additionally carried out. For (5), ZFC–FC magnetization runs were performed in the field of 0.2 and 0.5 kOe. Landé factor (denoted as g χ) has been determined from Curie constant C obtained from the Curie–Weiss law fit to the temperature dependence of magnetic susceptibility χDC(T) and χAC(T), respectively. Estimation of Landé factor from the magnetization isotherm σ(H) at 4.3 K using the Brillouin fitting procedure was possible only for the initial range of the primary magnetization curve, and denoted as g primary.

DFT calculations

The calculations were carried out using Gaussian09 [11] program. The DFT/B3LYP [12, 13] method was used for geometry optimization and electronic structure determination. The calculations were performed using polarization functions for all atoms: 6-311g**—nickel, 6-31g(2d,p)—sulfur, 6-31g**—carbon, nitrogen and 6-31g(d,p)—hydrogen. The contribution of a group to a molecular orbital was calculated using Mulliken population analysis. GaussSum 2.2 [14] was used to calculate group contributions to the molecular orbitals and to prepare the density of states (DOS) and overlap population density of states (OPDOS) spectra. The DOS and OPDOS spectra were created by convoluting the molecular orbital information with Gaussian curves of unit height and FWHM of 0.3 eV.

Crystal structures determination and refinement

Crystals of [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), [CoCl2(urotrop)2] (5), and [Co(DMIM)3]Cl2·H2O (6) were mounted in turn on an Xcalibur, Atlas, Gemini ultra Oxford Diffraction automatic diffractometer equipped with a CCD detector, and used for data collection. X-ray intensity data were collected with graphite monochromated Mo Kα radiation (λ = 0.71073 Å) at ambient temperature, with ω scan mode. Ewald sphere reflections were collected up to 2θ = 50.10. The unit cell parameters were determined from least-squares refinement of the setting angles of 6597, 9675, 5445, 5729, 5588, and 1828 strongest reflections for complexes (1), (2), (3), (4), (5), and (6), respectively. Details concerning crystal data and refinement are gathered in Table 1. During the data reduction, the decay correction coefficient was taken into account. Lorentz, polarization, and numerical absorption corrections were applied. The structures were solved by direct method. All the non-hydrogen atoms were refined anisotropically using full-matrix, least-squares technique on F 2. All the hydrogen atoms were found from difference Fourier synthesis after four cycles of anisotropic refinement, and refined as “riding” on the adjacent atom with individual isotropic temperature factor equal to 1.2 times the value of equivalent temperature factor of the parent atom, with geometry idealization after each cycle. Olex2 [15] with SHELXS97, SHELXL97 [16] programs were used for all the calculations. Atomic scattering factors were those implemented in the computer programs.

Table 1 Crystal data and structure refinement details of [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), [CoCl2(urotrop)2] (5), and [Co(DMIM)3]Cl2·H2O (6) complexes
Full size table

Result and discussion

The reactions of CoCl2·6H2O with β-picoline, 2-hydroxymethylpyridine, 2-(hydroxypro-pyl)pyridine, 1,2,4-triazolo[1,5-α]pyrimidine, and ammonium thiocyanate have been carried out. Mixing the starting cobalt(II) salt with the ligands in methanol leads to hexacoordinate thiocyanate complexes of Co(II) with good yields. Additionally, the reactions between urotropine and 2,2′-bis(4,5-dimethylimidazolyl) with CoCl2·6H2O have been carried out, and finally complexes with coordination number 4—[CoCl2(urotrop)2] (5) and 6—[Co(DMIM)3]Cl2·H2O (6) have been obtained.

Crystal structure

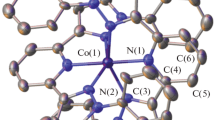
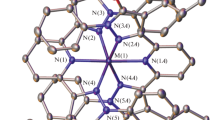
The complexes (1), (2), and (4) crystallize in orthorhombic space groups Pbcn and Pbca, respectively. The complexes (3) and (5) crystallize in monoclinic space groups P21/c and P21 and the complex (6) in hexagonal P64 space group. In Fig. 1, the molecular structures of the complexes are shown. The selected bond lengths and angles are listed in Table 2. In the complexes (1)–(4), cobalt(II) central ions have octahedral environment with thiocyanate ligands bonded to metal center through nitrogen atom and they are located in the twofold axis. Coordination environment of the metal atom consists of two thiocyanato ligands and four β-picoline ligands in complex (1), two 2-(hydroxymethyl/hydroxypropyl)pyridine in (2, 3) molecules and two 1,2,4-triazolo[1,5-α]pyrimidine and two methanol molecules in (4). In the case of complexes (1) and (4), the coordination polyhedron is an almost perfect octahedron with angular deviations smaller than 3°. The C–N and C–S bond length values fall in the 1.147(3)–1.153(2) Å and 1.622(2) Å, 1.635(18) Å ranges for the complexes, similar to those observed for thiocyanate complexes. The Co–N(heterocyclic ligand), Co–Cl and Co–O distances are normal and comparable with distances in other cobalt(II) complexes containing heterocyclic ligands. Co–N–C angles range from 159.17(16)° for complex (1) to 179.02(16)° for complex (2). In these complexes, the values of Co–N–C angles are in good agreement with those found for 3d metal complexes with a terminally bonded NCS ligand. The tetrahedral geometry of complex (5) is distorted which is visible in the angles between urotropine molecules (115.18(9)°) and chloride ligands (125.52(4)°). The cationic complex (6) has a distorted octahedral symmetry. The conformations of the complexes are stabilized by hydrogen bonds collected in Table 3. In Fig. 2, one-dimensional network formed by hydrogen bonds in the complex (4) is shown. The network is assembled into a two-dimensional plane by C–H···S bonds and into 3D packing structure.

Fig. 1
figure 1

ORTEP drawing of [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(CH3OH)2(tzpyrim)2] (2), [Co(SCN)2(pyCH2OH)2] (3), [Co(SCN)2(py(CH2)3OH)2] (4), [Co(SCN)2(urotrop)2] (5), and ½[Co(DMIM)3]Cl2 (6) with 50% probability displacement ellipsoids. Hydrogen atoms in complexes (1) and (6) are omitted for clarity

Full size image
Table 2 Selected bond lengths (Å) and angles (°) for [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), [CoCl2(urotrop)2] (5), and [Co(DMIM)3]Cl2·H2O (6) complexes
Full size table
Table 3 Hydrogen bonds for [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), [CoCl2(urotrop)2] (5), and [Co(DMIM)3]Cl2·H2O (6) complexes (Å and °)
Full size table
Fig. 2
figure 2

The crystals packing of complex 4 viewing down the a-axis with hydrogen bonds indicated by dotted lines

Full size image

Infrared spectra

Infrared spectra of the complexes present characteristic bands due to ligands vibrations. In the spectra of complexes (2) and (3), except for the bands characteristic to stretching modes of aryl C–H, bands with maxima at 3,271 and 3,385 cm−1, characteristic to OH groups, are visible. The alkyl C–H stretching modes give bands at 2937 cm−1 and 2992, 2960, 2918, 2902 cm−1 in the case of complexes (2) and (3), respectively. The νC=N band of pyridine ring appears at about 1,600 cm−1. The νCN, νCS, and δNCS frequencies of isothiocyanato ligands exhibit maxima at 2094 cm−1 (1), 2089 (2), 2099 (3), 2082, 2067 cm−1 (4), 809, 818, 822, 807 cm−1, and 491, 470, 556, 493 cm−1, respectively, and it is in good agreement with the end-on NCS coordination. In complex (2), two NCS ligands are in cis position and in the IR spectrum, two νCN stretches are recorded. The IR spectra of complexes (5) and (6) display sets of bands connected with N-donor ligands vibrations. The IR spectra of complexes (3) and (5) are presented in Fig. 3.

Fig. 3
figure 3

Experimental IR spectra of [Co(SCN)2(pyCH2OH)2] (3) and [Co(SCN)2(urotrop)2] (5) complexes with calculated frequencies

Full size image

Electronic structure

To form an insight into the electronic structures and bonding properties of the studied complexes, calculations using the DFT method were carried out. Before the calculations, their geometries were optimized in singlet states using the DFT method with the B3LYP functional. In general, the predicted bond lengths and angles are in good agreement with the values based on the X-ray crystal structure data, and the general trends observed in the experimental data are well reproduced in the calculations as one can see in the IR experimental and calculated spectra of (3) and (5) presented in Fig. 3. The interaction between ligands and central ions manifests itself in charges on the complex metal ions. The metal ions in all studied complexes are formally in +2 oxidation states, but the calculated natural charges are lower than +2, and they are in the range of 1.53–1.37 for complexes (1) to (5), respectively. The natural charges indicate that the donations from ligands to central ions have the advantage over the back donations from metal to ligands. The atomic charge calculations may describe the relocation of electron density of the compounds. The plots of the electrostatic potential for the complexes (1) and (5) are shown in Fig. 4. The isoelectronic contours are plotted at 0.05 a.u. (31 kcal/mol). The color code of these maps is in the range of 0.05 a.u. (deepest red) to −0.005 a.u. (deepest blue), where blue indicates the strongest attraction and red indicates the strongest repulsion. Regions of negative potential are usually associated with the lone pair of electronegative atoms. The negative potential in the complexes wrap thiocyanate ligands and oxygen atoms in the compounds with 2-(hydroxymethyl)–2-(hydroxypropyl)pyridine ligands and donor nitrogen atoms of urotropine not coordinated to the central ion. As one can see in Fig. 4, negative potentials on sulfur atoms in the complexes are smaller than the ones on nitrogen atoms (not to mention oxygen donor atoms). The natural charges obtained from NBO analysis are close to each other: N(NCS) −0.8, N(py) −0.6 and S(NCS) about −0.25. That is why, and additionally because of steric hindrance exerted by pyridine rings in compounds (1) and (2), the studied complexes do not form polymeric systems with NCS− connector.

Fig. 4
figure 4

Electrostatic potential (ESP) surfaces of [Co(SCN)2(β-pic)4] (1) and [Co(SCN)2(urotrop)2] (5) complexes. ESP surface is shown both in space (with positive and negative regions shown in blue and red, respectively) and mapped on electron densities (in the range of 0.05 a.u.—deepest red to −0.005 a.u.—deepest blue) of the molecule (ESP color scale is such that δ+ → δ− in the direction red → blue)

Full size image

The HOMO orbitals of the complexes are localized on thiocyanate or chloride ligands with notable contribution of d Co orbitals. The d orbitals of the central ions play a significant role in the lower HOMO–4/6 MOs in the complexes. The LUMO orbitals of hexacoordinate complexes (1)–(4) are localized on the pyridine derivative ligands, and in the case of complex (4), d Co orbitals (80–87%) participate in the β spin LUMO–LUMO + 3 orbitals. In virtual molecular orbitals, d orbitals of the central ions in the complexes (1)–(4) are visible in (β spin) LUMO + 2 to LUMO + 5 energy range. Because in the frontier region, neighboring orbitals may be a quasi-degeneracy of the energetic levels, considering that only the HOMO and LUMO may not yield a realistic description of the frontier orbitals. For this reason, the DOS in terms of Mulliken population analysis was calculated using the GaussSum program. The results provide a pictorial representation of MOs compositions. The DOS diagrams for complexes (1), (3), (4), and (5) are shown in Fig. 5, and they may enable us to ascertain the orbital composition characteristics with respect to the particular fragments. As one may see from the DOS diagrams, pyridine type ligands play a significant role in the virtual frontier and in the lower occupied molecular orbitals. Chloride ion contributes in wider range HOMO orbitals than pseudohalide NCS− ligands. Furthermore, the complexes with isothiocyanate ligands have smaller HOMO–LUMO gap than those with chloride ligands (1: 3.16 eV; 2: 2.78 eV; 3: 3.33 eV; 4: 2.29 eV; 5: 4.45 eV; 6: 3.95 eV). The HOMO term is shifted to higher energy by pseudohalide ligands which have an impact on the contribution of d orbitals of central ions in the HOMO orbitals. On the other hand, the OPDOS in terms of Mulliken population analysis provide a pictorial representation of MOs compositions and their contributions to chemical bonding. The OPDOS diagrams are shown in Fig. 6, and they may enable us to ascertain the bonding, nonbonding, and antibonding characteristics with respect to the particular fragments. A positive value in OPDOS plots means a bonding interaction, while a negative value represents antibonding interaction, and a near zero value indicates a nonbonding interaction. Additionally, a comparison of the interaction between ligands and central ions allows a comparison of donor–acceptor ability of ligands.

Fig. 5
figure 5

The partial density of states (DOS) diagrams for [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), and [Co(SCN)2(urotrop)2] (5) complexes

Full size image
Fig. 6
figure 6

The overlap partial density of states (OPDOS) diagrams for [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4) complexes

Full size image

As one can see from the OPDOS plots, the interaction between pyridine derivatives ligands and cobalt(II) ions in the complexes (1)–(4) is very small in frontier HOMO molecular orbitals which indicate a nonbonding character of these interactions and weak σ donor properties of the ligands toward Co(II) in the presence of isothiocyanate ligands (in the lower HOMO orbitals, the interaction of N-donor ligands with cobalt central ions have strongly bonding character). In the frontier virtual molecular orbitals, the pyridine type ligands present an antibonding interaction with Co(II) central ions and the values of the interaction indicate the ligands as rather strong π-acceptors. Additionally, the 1,2,4-triazolo[1,5-α]pyrimidine is the weakest ligand and the β-picoline and 2-hydroxymethylpyridine are comparable in terms of donor–acceptor properties.

Electronic spectra

The electronic spectra of the octahedral complexes exhibit absorption assigned to 4T1g(F) → 4T2g(F) (ν 1), 4T1g → 4A2g (ν 2), and 4T1g(F) → 4T1g(P) (ν 3) transitions in the NIR–VIS region (ν 1: 8811–11,635 cm−1; ν 2: 13,550–16,447 cm−1; ν 3: 18,553–19,260 cm−1). The ν 3/ν 1 ratios amounting to 1.7–2.1 for complexes (1)–(4), (6) are in the range expected for octahedral complexes of Co(II) [17]. In the case of complex (5), the experimental bands are attributed to 4A2(F) → 4T2(F), 4A2(F) → 4T1(F), and 4A2(F) → 4T1(P) transitions, respectively, due to its tetrahedral symmetry. The values of the ligand field parameter 10Dq, calculated on the basis of the positions of electronic bands for the complexes are equal to 10Dq = 8018 cm−1 (1), 4180 cm−1 (2), 5295 cm−1 (3), 4991 cm−1 (4), 2851 cm−1 (5), and 4612 cm−1 for (6). The lowest value of 10Dq for complex (5) is in agreement with its tetrahedral geometry. Racah parameter B is equal to 727, 368, 387, 372, 540, and 576 cm−1 for complexes (1), (2), (3), (4), (5), and (6), respectively. The Racah parameter B for a metal ion varies as a function of the ligand bound to the ion. The value of this parameter will be always lower for a complexed ion than that for a free ion. The decrease in the value of B is related to the extent of metal–ligand bond covalency. The metal–ligand bond becomes partially covalent when the d-orbitals overlap with the ligand orbitals. As a result, the interelectronic repulsion within the d-orbitals decreases and B value is lowered. The ratio B/B o = β gives a measure of covalency in the metal–ligand bond. The nepheloauxetic parameters calculated for the complexes are β = 0.75, 0.55, 0.57 for complexes (1), (5), and (6), respectively, and about 0.38 for (2), (3), and (4).

Based on the ligand field Dq and Racah B parameters, the strengths of ligand fields caused by the N-donors may be estimated. The 4T1 levels derived from 4F and 4P terms interact with each other (in octahedral ligand field) due to the same symmetry. The 4T1 ground level of Co(II) is splitting in octahedral field because of spin–orbit coupling and Zeeman effects. Generally, the interactions may be expressed by orbital reduction factor α which is defined by two parameters: α = κA. The κ parameter is referred to the orbital reduction factor and its origin lies in the covalency of the metal–ligand bonds. It takes values in the range 0 ≤ κ ≤ 1, and the greater the covalency is, the lower its value. The A parameter may be determined from the electronic spectra of Co(II) complexes and its value varies between 3/2 for weak field and 1 for strong ligand field. The A value is computed as:

$$ \begin{aligned} & A = \frac{{{\raise0.5ex\hbox{$\scriptstyle 3$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}} - c^{2} }}{{1 + c^{2} }} \\ & c = 0.75 + 1.875\frac{B}{Dq} - 1.25\left[ {1 + 1.8\frac{B}{Dq} + 2.25\left( \frac{B}{Dq} \right)^{2} } \right]^{1/2} \\ \end{aligned} $$

c is the coefficient of the function of the excited state [4T1(P)] in the ground state [4T1(F)] [18]. The calculated values of A parameter for the complexes are: 1.41 for (1) and (2), 1.38 for complexes (3) and (4). In the case of (6), the value is 1.51 which is expected for almost perfect octahedral complex. As one can see from the data, the ligand fields resulting from β-picoline and the N,O-donors as 2-(hydroxymethyl)pyridine, 2-(hydroxypropyl)pyridine ligands are comparable on the strengths. In complex (4), the value of LF strength is not comparable with that of other complexes due to its symmetry (D2h) and molecular structure built of two 1,2,4-triazolo[1,5-α]pyrimidine, two methanol molecules and two isothiocyanate ligands. Additionally, the electronic spectra of these complexes were calculated in the Gaussian program with PCM model. As the d → d transitions are forbidden, their oscillator strengths are very small (close to 0.0) and the experimental spectra in the energy region of 1,300–400 nm are wider that the calculated transitions adequate to theses ones. In Fig. 7, the NIR and visible part of experimental electronic spectrum of complex (3) with calculated transitions are depicted.

Fig. 7
figure 7

VIS–NIR spectrum of [Co(SCN)2(py(CH2)3OH)2] (3) complex with the calculated transitions

Full size image

Magnetic properties

Results of magnetic measurements are presented in Figs. 8, 9, 10, 11, 12, 13, 14 and in Table 4. Real component of AC susceptibility, χ′, (or χ′ reciprocal, as for (3)) is given for all complexes; the imaginary component is shown only for (5), as for the rest of compounds χ″ was less significant. Static susceptibility χDC was in agreement with χ′ and is depicted only for the samples (4) and (5). In the insets on the left, the temperature dependence of the χ′·T product is shown for (1), (2), (3), (5), and (6). For (4), the inset with χ′ and χ″ is included, while the χ′·T result, showing maximum of 15 emuK/mol at T = 4.2 K, is partly shown in the comparative Fig. 14. In the subsequent insets, σ(H) magnetization curves at constant temperature are presented for (1), (2), (3), (4), and (6). For (5), in the case of which weak ferromagnetic behavior was observed, the result of the ZFC–FC σ(T) magnetization run in the field of 0.5 kOe is shown in the inset.

Fig. 8
figure 8

Real part of AC susceptibility χ′ versus temperature T for (1). Left inset product χ′·T versus temperature T. Right inset magnetization σ versus H/T at 4.3 K. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 9
figure 9

Dynamic susceptibility χAC versus temperature T for (2). Left inset product χ′·T versus temperature T. Right inset magnetization σ versus H/T. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 10
figure 10

Reciprocal of real part of AC susceptibility 1/χ′ versus temperature T for (3). Left inset product χ′·T versus temperature T. Right inset magnetization σ versus H/T. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 11
figure 11

Static (χDC) and real part of AC (χ′) susceptibility versus temperature T for (4). Left inset magnetization σ versus H/T at 2.3 K, 4.3 K and 18.8 K. Right inset real (χ′) and imaginary (χ″) parts of AC susceptibility versus temperature T. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 12
figure 12

Static (χDC), real (χ′) and imaginary (χ″) parts of AC susceptibility versus temperature T for (5). Left inset: product χ′·T versus temperature T. Right inset: magnetization σ versus temperature T measured in the ZFC and FC modes at 0.5 kOe. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 13
figure 13

Real part of AC susceptibility χ′ versus temperature T. Left inset product χ′·T versus temperature T for (6). Right inset magnetization σ versus H/T at 4.3 K. The solid (red) line is for an estimation of Landé factor

Full size image
Fig. 14
figure 14

Product χ′·T versus temperature T depicted for all complexes under study

Full size image
Table 4 Magnetic data of [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), [Co(SCN)2(py(CH2)3OH)2] (3), [Co(SCN)2(CH3OH)2(tzpyrim)2] (4), [CoCl2(urotrop)2] (5), and [Co(DMIM)3]Cl2·H2O (6) complexes
Full size table

Based on the initial inspection of the results, it may be stated that all the complexes (1)–(6) are paramagnets just as in the case of thiocyanate Ni(II) and Mn(II) complexes [19, 20], although the samples (4) and (5) show transition to the collective magnetic state at low temperatures. Critical temperature determined from the minimum of the dχ′/dT derivatives is 4.5 K for (4) and 10 K for (5). Curie–Weiss law has been fitted to all susceptibility data available. Magnetic parameters Θ and Landé factor g (obtained from Curie constant \( C = \frac{{Ng^{2} \mu_{\text{B}}^{2} S(S + 1)}}{{3k_{\text{B}} }} \)) were determined independently from χDC and χAC. The high spin state S = 3/2 of the Co(II) d7 ion was approved. Averaged values of Θ and g χ are summarized in Table 4.

As it follows from the insets in Figs. 8, 9, 10, and 13, the magnetization process for (1), (2), (3), and (6) is slower than expected for a paramagnet and the σ(H) values in H > 10 kOe are lower than those resulting from the Brillouin function. Attempts to explain the reduced σ(H) values with some low spin metal content were unsuccessful. Very weak negative coupling Θ (e.g., ≈−0.1 K for (6)) cannot be the reason of such behavior, as well. Most probably, the slow σ(H) increase at high field is caused by the considerable anisotropy of the cobalt ion. It is known that the radial distribution function of d electrons for the Co(II) center deviates from the spherical one. Estimation of Landé factor from the magnetization isotherm σ(H) at 4.3 K using the Brillouin fitting procedure was possible only for the value compatible to the beginning of the primary magnetization curve, and this value, g primary, is quoted in Table 4. As it may be seen, g primary fits well to the average of g DC and g AC (g χ). Table 4 contains also the values of Curie constant C, effective magnetic moment μeff, and saturation moment σsat per formula unit, as estimated from the σ versus 1/H polynomial fit.

The temperature evolution of the χ·T product (= μ 2eff /8) reflects the sign of the magnetic coupling and the ability of the system to become magnetically ordered. For a paramagnet with Curie–Weiss temperature Θ equal to zero, effective magnetic moment μeff and the χ·T value do not depend on temperature. We measured small field AC susceptibility in order to examine the unperturbed magnetic state of the complexes. As it follows from the inset of Fig. 13, the [Co(DMIM)3]Cl2·H2O (6) sample may be regarded as a classic paramagnet. χ′·T versus T dependences for complexes (1), (2), and (3) show a very weak decrease upon cooling, compatible with small Θ, followed by a very low χ′·T maximum at T = 8.8 K (Figs. 8, 9, 10; Table 4). Such maximum suggests a tendency for interaction between the adjacent cobalt complexes, realized via hydrogen bonds. However, the short range of that weak coupling prevents the phase transition to a magnetically ordered state. As it is evident from the inset of Fig. 12, the χ′·T maximum for sample (5) is significantly stronger and it occurs also at T = 8.8 K. A maximum is also revealed in the χ′ and χ″ temperature dependences (Fig. 12), pointing to the phase transition to ferromagnetic state at T C = 10 K, yet probably only in the limited range of the crystal network. The ferromagnetic state is further evidenced with the different temperature dependences of magnetization measured consecutively in the ZFC and FC modes, as presented in the second inset of Fig. 12. Origin of the weak ferromagnetic interaction in (5), as compared to the antiferromagnetic one in the remaining complexes, should be the symmetry of t 2g and e g orbitals, which in the tetrahedral field is converse in comparison to that of the octahedral one. The only complex which may be said to be magnetically long range ordered at low temperature is [Co(SCN)2(CH3OH)2(tzpyrim)2] (4). The negative Θ and the shape of the magnetization curve at 2.3 K (see Fig. 11 left inset) point to the uncompensated antiparallel orientation of magnetic moments below Néel temperature T N = 4.5 K. The inflection for H ≈ 20 kOe in the σ(H) curve at 2.3 K and the shape of χ′ peak (insets of Fig. 11) point to the layered character of magnetic ordering, in compliance with a two-dimensional network of the C–H···S linkages revealed by crystallographic data. Thus, the magnetic collective state of the [Co(SCN)2(CH3OH)2(tzpyrim)2] (4) complex is not alike that of the [CoCl2(urotrop)2] (5) and this disparity may have an origin in the octahedral and tetrahedral symmetries of the given complexes.

It may be concluded that in the family of complexes under study, generally, the paramagnetic behavior dominates, as it was observed for the thiocyanate Ni(II) and Mn(II) complexes [19, 20]. However, by means of the AC susceptometry, the traces of nascent interactions are revealed for [Co(SCN)2(β-pic)4] (1), [Co(SCN)2(pyCH2OH)2] (2), and [Co(SCN)2(py(CH2)3OH)2] (3), better seen in [CoCl2(urotrop)2] (5). The [Co(SCN)2(CH3OH)2(tzpyrim)2] (4) complex shows the transition at T N = 4.5 K to the state with the canted antiparallel orientation of magnetic moments. Magnetic data for (4) conform to the layered network of the C–H···S linkages present in the crystal structure of this complex. No trace of magnetic coupling has been detected for [Co(DMIM)3]Cl2·H2O (6). Anisotropy of the Co(II) ion influences the magnetization process of the samples. The small orbital contribution to Landé factor has been observed for complexes (1), (2), (3), and the larger one for (5).

Conclusions

In the simple one-pot syntheses, isothiocyanate and chloride complexes of cobalt(II) with N- and N(O)-donors were obtained. The complexes were characterized by IR spectroscopy and their crystal structures were determined by X-ray diffraction. Electronic structures of the complexes were calculated using DFT method, and apart from the descriptions of frontier molecular orbitals and the relocation of electron density of the compounds, bonding properties in the complexes were determined. For the complexes, the crystal field (10Dq) and nepheloauxetic parameters were determined. The UV–VIS spectra were calculated by the time-dependent DFT method with accordance of electronic structure. Magnetic properties of the complexes were studied. Only [Co(DMIM)3]Cl2·H2O (6) may be regarded as a classic paramagnet. The AC magnetic susceptibility measurements revealed a weak magnetic coupling for [Co(SCN)2(CH3OH)2(tzpyrim)2] (4) leading to a transition to the canted antiferromagnetic state at Néel temperature T N = 4.5 K as well as some indications for a much weaker coupling in the remaining thiocyanate complexes (1), (2), and (3). A phase transition to ferromagnetic state at T C = 10 K, yet probably only in the limited range of the crystal network, has been observed for [CoCl2(urotrop)2] (5). The overall magnetic behavior of the complexes is determined by subtle interactions mediated by the network of hydrogen bonds, in the presence of the Co(II) ion anisotropy and the considerable spin–orbit coupling, as in case of (5).

Supplementary data

CCDC 773830, CCDC 778784, CCDC 778383, CCDC 775309, CCDC 777557, and CCDC 804702 contain the supplementary crystallographic data for complexes [Co(SCN)2(β-pic)4], [Co(SCN)2(py(CH2)3OH)2], [Co(SCN)2(pyCH2OH)2], [Co(SCN)2(tzpyrim)2]·2CH3OH, [CoCl2(urotrop)2], and [Co(DMIM)3]Cl2·H2O. These data can be obtained free of charge from http://www.ccdc.cam.ac.uk/conts/retrieving.html, or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: (+44) 1223-336-033; or e-mail: deposit@ccdc.cam.ac.uk.