Introduction

The occurrence of polyhalogenated persistent organic pollutants (POPs), such as Cl/Br-substituted benzenes (CBz/BBz), biphenyls (PCBs/PBBs), diphenyl ethers (PCDEs/PBDEs), dibenzofurans (PCDFs/PBDFs), dibenzo-p-dioxins (PCDDs/PBDDs), and naphthalenes (PCNs/PBNs) in air, water, soil, and sediments has been identified as a serious environmental threat [1]. Large amounts of POPs come from various anthropogenic sources, including intentionally synthesized liquids utilized in transformers and capacitors, plasticisers, flame retardants, as well as thermal recycling of waste, domestic heating, etc. Substantial volumes of these compounds are released in effect of giant fires, as the most recent fire of the oil spill at the Deepwater Horizon platform in the Gulf of Mexico [2]. Regardless of their source, the exposure to POPs can cause a vast range of acute and chronic health effects, including mutagenic, carcinogenic, and metabolic ones. In addition, as persistent and liphophilic substances, POPs can be bioaccumulated in body and biomagnified in natural ecosystems [3].

Hence, there is an urgent need to determine physicochemical properties required to perform a comprehensive risk assessment for all POPs. Unfortunately, the number of all possible congeners (similar compounds based on the same carbon skeleton, but differ by a number of chlorine/bromine atoms and the substitution pattern) is extensive. In total, there are 1436 structurally different congeners of polychlorinated and polybrominated benzenes, biphenyls, dibenzo-p-dioxins, dibenzofurans, diphenyl ethers, and naphthalenes (Fig. 1). The number of possible mixed chloro- and bromo-substituted is at least one order of magnitude larger [4]. For such a large number of compounds, empirical measurement of the physicochemical properties is impossible, due to high costs and time limitations of the analytical procedures. Therefore, alternative methods for physicochemical characterization of POPs are required.

Fig. 1
figure 1

Chemical structures of parent molecules of benzenes, biphenyls, dibenzo-p-dioxins, dibenzofurans, diphenyl ethers, and naphthalenes used to construct chlorine-substituted congeners

Full size image

A very promising group of such methods is the quantitative structure–property relationships (QSPR) approach. QSPR is based on the assumption that each physicochemical property in a group of compounds can be expressed as a mathematical function of their chemical structure, represented by a set of so-called molecular descriptors. Thus, based on the experimental data, available only for some representatives of the group, it is possible to interpolate the lacking data for compounds, for which such data are missing, from the calculated molecular descriptors and a suitable mathematical model [5–7]. Two possible QSPR modeling strategies have been described in the literature, namely: local and global models. Local models are restricted only to one specific class of chemically related compounds (e.g., PCBs), whereas global models are developed for a large number of structurally similar groups of compounds (e.g., PCBs, PCNs, PCDDs, PCDFs, etc.). It is widely accepted that the local models have better predictive ability in comparison with the global models [8]. However, the global models seem to be very attractive from an economic point of view, because such a modeling strategy enables to additionally save resources by predicting new data for a larger number of compounds at a time. The argument against the global modeling is that this strategy may lead to mechanistic oversimplifications and/or higher errors in the predicted data [9]. Therefore, there are two fundamental questions related to the topic. First: How significant are the differences in the results obtained using local and global QSPRs? Second, consequently: Is the reduction of the model’s domain (to only one group of POPs) really necessary to improve the predictive power of a QSPR model? Our study was aimed to answer both questions.

Materials and methods

Global and local QSPRs

To find the answers, we initially selected one phys/chem property and one congeneric group of POPs, namely: water solubility in 25 °C and polychlorinated naphthalenes. Then, we performed a detailed comparison between the predictions with local and global QSPRs for this group. The solubility has been selected, because it is a property, important in estimating both environmental transport and toxicokinetics after entering the body [3]. The group of PCNs (containing 75 congeners) has been selected for the case study, since the parent molecule (naphthalene) is structurally the simplest polycyclic aromatic hydrocarbon. Moreover, polychlorinated naphthalenes were, historically, the first ever intentionally synthesized POPs (between 1910s and 1980s) [10]. The global model has been developed together for 11 other groups of halogenated POPs, namely: CBzs, BBzs, PCBs, PBBs, PCDDs, PBDDs, PCDFs, PBDFs, PCDEs, PBDEs, PBNs, and PCNs (1,436 compounds in total).

We hypothesized that water solubility obtained from a local QSPR model should not substantially differ from those predicted with a global QSPR model for POPs, due to the similarity of carbon skeletons, the level of halogenation and the substitution patterns of the studied compounds. To verify, whether the hypothesis and conclusions can be extended to the other phys/chem properties and groups of POPs, we additionally performed a cross comparison between few local and global QSPRs, collected from the literature.

Development of the global QSPR model

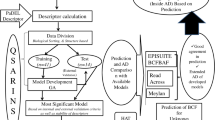
Development of a high-quality QSPR model with good predictive ability requires reliable experimental data, on one hand, and appropriate molecular descriptors on the other one. The procedure we followed when constructing the global model included five steps:

Step 1: Experimental data collection and splitting the compounds, for which the data are available, into a training set (T) and a validation set (V)

The crucial condition that must be met to obtain a plausible QSPR model is homogeneity and high-quality of the experimental data. It is because the quality of the data significantly influences the modeling results. Thus, no one can expect from the data predicted with the model to be better than the original data utilized to developing the model. In practice, this means that the experimental data should be obtained in a systematic way, according to the same standardized protocol [11]. This stage minimizes the risk of obtaining highly uncertain, extrapolated results from the QSPR modeling.

For the purpose of developing a global QSPR model, which quantitatively describes the relationship between the molecular structure of the halogenated POPs and water solubility (log S), we collected the experimental data on water solubility originally determined at 25 °C. The values of solubility for polychlorinated biphenyls (PCBs) were taken from [12, 13], for polychlorinated dibenzo-p-dioxins (PCDDs) from [14], for polychlorinated dibenzofuran (PCDFs) from [14], for polychlorinated/polybrominated diphenyl ethers (PCDEs/PBDEs) from [15, 16], for polychlorinated naphthalenes (PCNs) from [17], and for polychlorinated benzenes (CBz) from [18]. The experimental data have been available for 121 halogenated congeners of POPs in total. Logarithmic values of the solubility varied between −2.58 and −10.83 [mol/dm3] (for more details, please refer to the electronic Supplementary material).

Next, the 121 congeners were sorted along with the decreasing values of water solubility. Then, every fourth compound was moved to the so-called validation set (an additional set for further external validation of the model), while the remaining compounds formed the training set (for developing the model). The application of this “three-to-one” splitting algorithm ensured that the both training and validation sets were contain the compounds evenly distributed within the range of the water solubility [19]. The splitting procedure led to a training and a validation set consisted of 91 (75%) and 30 (25%) compounds, respectively.

Step 2: Calculating molecular descriptors

Simultaneously, we combinatorially generated molecular structures of all chloro- and bromo-substituted congeners (1436 compounds) with the ConGENER [20] software package, which is based on our earlier work on characterization of combinatorially generated libraries of tautomers [21]. We utilized those structures as inputs for quantum-mechanical calculations which included two stages: (i) optimization of the molecular geometry with respect to the energy gradient and (ii) calculation of the descriptors based on the optimized geometry. The calculations have been performed at the semi-empirical level of the theory with use of PM6 method [22] in MOPAC 2009 software package [23]. We calculated the following 26 molecular descriptors: the number of atoms in the molecule (nAT), the number of chlorine substituents (nX), the molecular weight (MW), the standard heat of formation (HOF), the electronic energy (EE), the core–core repulsion energy (Core), the total energy (TE), the total energy of the corresponding cation (TE+), the standard heat of formation in a solution represented by the Conductor-like Screening Model, COSMO (HOFc), the total energy in a solution represented by COMSO (TEc), the vertical ionization potential (IP), the energy of the highest occupied molecular orbital (HOMO), the energy of the lowest unoccupied molecular orbital (LUMO), the X vector of the dipole moment (D x ), the Y vector of the dipole moment (D y ), the Z vector of the dipole moment (D z ), the total dipole moment (D tot), the solvent accessible surface (SAS), the molecular volume (MV), the lowest negative Mulliken’s partial charge on the molecule (Q −), the highest positive partial charge on the molecule (Q +), the average polarizability derived from the heat of formation (A hof), the average polarizability derived from the dipole moment (A d), Mulliken’s electronegativity (EN), Parr and Pople’s absolute hardness (Hard), and Schuurmann MO shift alpha (Shift).

Step III: Calibrating and internal validation of the QSPR model

Having both, high-quality experimental data and molecular descriptors, we developed QSPR model following the golden standards and recommendations of the Organization for Economic Cooperation and Development (OECD) [24]. Regarding to the five OECD recommendations, an ideal QSPR model should be associated with:

  1. (i)

    a defined endpoint;

  2. (ii)

    an unambiguous algorithm;

  3. (iii)

    a defined applicability domain;

  4. (iv)

    appropriate measures of goodness-of-fit, robustness and predictivity;

  5. (v)

    a mechanistic interpretation, if possible.

We employed the Partial Least Squares regression combined with a genetic algorithm (GA-PLS) as the chemometric method of modeling. PLS is based on a linear transition from a large number of original descriptors to a small number of new orthogonal variables so-called “latent vectors” (LVs), being linear combinations of the original descriptors [25]. In order to select the optimal combination of the molecular descriptors to be utilized in the final QSPR model, we employed the Holland’s genetic algorithm (GA) [26]. The algorithm minimizes the prediction error by searching for the most optimal combination of the descriptors. The name “genetic” came from fact that this mathematical procedure uses the rules of Darwinian theory of evolution. However, in this case, the rules are applied to “populations” and “generations” of mathematical solutions (i.e., combinations of the descriptors), not to populations and generations of living organisms. The algorithm is controlled by a set of steering parameters. In our studies, we have specified the following ones: the size of a population: 124, the percentage of the initial terms: 40%, the maximum number of generations: 100, the percentage of convergence: 50%, the mutation rate: 0.005, double cross-over: the number of repetitions: 7. GA-PLS calculations were performed with MATLAB 7.6 [27] and PLS Toolbox 5.2 [28].

An integral part of QSPR modeling is to appropriately describe the borders of the optimum prediction space of the model. The space, so-called applicability domain (AD), is defined by the nature of the compounds included in the training set. We verified the applicability domain by use of the Williams plot, which is the plot of the leverage values versus cross-validated standardized residuals [29, 30]. The leverage value h i for every ith compound is calculated as follows: [31] (Eq. 1):

$$ h_{i} = {\mathbf{x}}_{i}^{{\mathbf{T}}} \left( {{\mathbf{X}}^{{\mathbf{T}}} {\mathbf{X}}} \right)^{ - 1} {\mathbf{x}}_{i} $$
(1)

where x i is the vector of descriptors calculated for the considered ith compound and X is the matrix of descriptors calculated for the whole training set.

The value of h i greater than the critical one (h*) means that the structure of a compound differs from the training set significantly and, in consequence, the compound falls outside the optimum prediction space of the model [32]. The warning value h* is calculated according to the formula (Eq. 2):

$$ h^{*} = {\frac{3(p + 1)}{n}} $$
(2)

where p is the number of variables used in the model and n is the number of training compounds.

However, fact that h i  > h* does not always indicate that the ith training compound is an outlier. It has been shown that training compounds with high leverages and small residuals (differences between the observed and predicted values) stabilize the model and make it more precise. Such points are so-called “good leverages.” Only the compounds with high leverages and residuals higher than ±3 standard deviations units (so-called “bad leverages”) destabilize the model [33].

In order to prove robustness of the model and reduce probability of the model’s overfitting, we performed an internal validation [29, 34]. For this purpose, we employed the leave-one-out cross-validation (CV-LOO) algorithm, in which the same compounds were used alternating for the training and validation [30].

Goodness-of-fit (i.e., how well the model fits the data) was measured by the determination coefficient in the training set (R 2) and the root mean square error of calibration (RMSEc) (Eqs. 3 and 4). Whereas the quantitative assessment of the robustness was expressed by the CV-LOO determination coefficient (Q 2CV ), the absolute average relative deviation (AARD), and root mean square error of cross-validation (RMSECV) (Eqs. 3–7) [30].

$$ R^{2} = 1 - {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i}^{\text{obs}} - y_{i}^{\text{pred}} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i}^{\text{obs}} - \bar{y}^{\text{obs}} } \right)^{2} } }}} $$
(3)
$$ {\text{RMSE}}_{\text{C}} = \sqrt {{\frac{{\sum\nolimits_{n = 1}^{n} {\left( {y_{i}^{\text{obs}} - y_{i}^{\text{pred}} } \right)^{2} } }}{n}}} $$
(4)
$$ Q_{\text{CV}}^{2} = 1 - {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i}^{\text{obs}} - y_{i}^{\text{predcv}} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {y_{i}^{\text{obs}} - \bar{y}^{\text{obs}} } \right)^{2} } }}} $$
(5)
$$ {\text{AARD}} = \frac{100}{n}\sum\limits_{i = 1}^{n} {{\frac{{\left| {y_{i}^{\text{obs}} - y_{i}^{\text{pred}} } \right|}}{{y_{i}^{\text{obs}} }}}} $$
(6)
$$ {\text{RMSE}}_{\text{CV}} = \sqrt {{\frac{{\sum\nolimits_{n = 1}^{n} {\left( {y_{i}^{\text{obs}} - y_{i}^{\text{predcv}} } \right)^{2} } }}{n}}} $$
(7)

where y obs i is the experimental (observed) value of the property for the ith compound, y pred i the predicted value for the ith compound, y predcv i the predicted value for the temporary excluded (cross-validated) ith compound, \( \bar{y}^{\text{obs}} \) the mean experimental value of the property in the training set, n the number of compounds in the training set.

Step IV: External validation of the developed QSPR model

To confirm the model’s predictive power, we carried out the external validation based on the compounds that were not previously engaged in the model’s optimization and/or calibration [30]. We utilized the external validation coefficient (Q 2Ext ) and the root mean square error of prediction (RMSEP) (Eqs. 8 and 9) as measures of the external predictivity.

$$ Q_{\text{Ext}}^{2} = 1 - {\frac{{\sum\nolimits_{j = 1}^{k} {\left( {y_{j}^{\text{obs}} - y_{j}^{\text{pred}} } \right)^{2} } }}{{\sum\nolimits_{j = 1}^{k} {\left( {y_{j}^{\text{obs}} - \bar{y}^{\text{obs}} } \right)^{2} } }}} $$
(8)
$$ {\text{RMSE}}_{\text{P}} = \sqrt {{\frac{{\sum\nolimits_{j = 1}^{k} {\left( {y_{j}^{\text{obs}} - y_{j}^{\text{pred}} } \right)^{2} } }}{k}}} $$
(9)

where y obs j is the experimental (observed) value of the property for the jth compound, y pred j the predicted value for jth compound, \( \bar{y}^{\text{obs}} \) the mean experimental value of the property in the validation set, and k the number of compounds in the validation set.

Step V: Applying the model to predict the endpoint values for new compounds

When the QSPR model fulfills all the validation criteria, it can be applied to predict the property (i.e., water solubility) of those new compounds, for which the experimental data have not been available.

Methodology of comparing local and global QSPR models

Particular local and global models were compared each other taking into account two aspects: economy and quality of each. The number of training compounds and applicability domain of the model represented the economic aspect, whereas the measures of goodness-of-fit, robustness, and predictivity—the qualitative aspect. In addition, we employed Student’s t test to verify, whether the average residuals from the predictions with local and global QSPR models differ significantly (p < 0.05).

Results and discussion

Comparing global and local QSPR models of water solubility

As mentioned, at first we performed a comparison between two QSPR models of water solubility (log S) developed by our group. The first model was developed within this study, whereas the second QSPR was taken from one of our previous contributions.

Global QSPR model of water solubility

When applied the five-step procedure of QSPR, including GA-PLS method, we obtained a statistically significant (p < 0.05) global model, capable to successfully predict the values of log S for 1436 halogenated POPs. The model utilized three latent vectors (LVs) explaining together 95% (57% + 17% + 21%) of the total variance in the molecular descriptors and 93% (90% + 2% + 1%) of the variance in the modeled endpoint (log S). Although the GA-PLS method uses orthogonal latent vectors for regression, it is also possible to derive “quasi-regression” coefficients for original descriptors (Eq. 10), keeping in mind that these coefficients cannot be individually interpreted, because they are not independent [25].

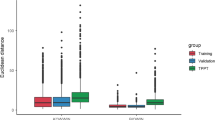
$$ \log S = - 0.287nAT - 0.293nX + 0.191{\text{LUMO}} - 0.320{\text{SAS}} + 0.085Q_{ + } + 0.126{\text{Shift}} $$
(10)

The global QSPR was characterized by the satisfactory goodness-of-fit, the robustness, and the external predictive performance (the statistical measures are summarized in Table 1). A visual correlation between the experimental and predicted values of log S is presented in Fig. 2a.

Table 1 Comparison of statistical parameters between local and global GA-PLS models of log S
Full size table
Fig. 2
figure 2

The experimentally determined values of log S versus the values of log S predicted by global (a) and local (b) QSPR models

Full size image

The model can be intuitively interpreted, according to the physicochemical theory of dissolvation. The theory divides the whole process into six stages, namely: (i) breaking up solute–solute intermolecular bonds; (ii) breaking up solvent–solvent intermolecular bonds; (iii) formation of a cavity in the solvent phase large enough to accommodate solute molecule; (iv) vaporization of solute into the cavity; (v) forming solute–solvent intermolecular bonds; and (vi) reforming solvent–solvent bonds with solvent restructuring. Thus, since formation of the cavity appropriate for highly halogenated, large molecules requires more energy, the solubility of larger congeners is lower, when comparing with less halogenated and smaller congeners. This factor is represented in the model equation (Eq. 10) by three descriptors: SAS, nAT, and nX that have a negative contribution to the solubility (i.e., the solubility increases when the solvent accessible surface, the number of atoms, and the number of halogen substituents decreases). Similarly, the descriptors that are related to electrostatic interactions (e.g., forming hydrogen bonds) between the solvent and solute and chemical reactivity, namely: LUMO, Q+, Shift, positively contribute the solubility. It is because the process of forming solute–solvent intermolecular bonds facilitates dissolvation.

Local QSPR model of water solubility

The local model, originally calibrated only for a group of 75 polychlorinated naphthalenes, has been adapted from our previous paper [35]. It was based on eight theoretical molecular descriptors, calculated exclusively from the chemical structures at the Density Functional Theory (DFT) level with the B3LYP functional and 6-311++G(d, p) basis set. A combination of those eight descriptors formed one latent vector, utilized then as an independent variable to construct a one-variable GA-PLS model. The model explained 93% of the structural variance (variance in the descriptors) and 96% of the variance in log S. This one-variable model can be alternatively expressed in the quasi-regression form (Eq. 11):

$$ \log S = - 0.109nClp1 + 0.123HOMO-0.131{\text{Hard}} + 0.129E_{t} -0.131{\text{SAS}}_{\text{w}} -0.132{\text{SAV}}_{\text{w}} + 0.131{\text{DE}}_{\text{w}} - \, 0.129{\text{TNE}}_{\text{w}} $$
(11)

where nClp1 is the number of chlorine atoms in the first aromatic ring, HOMO the energy of the highest occupied molecular orbital, Hard the molecular hardness, E t the total energy of the molecule, SASw the solvent accessible molecular surface area in the water, SAVw the solvent accessible molecular volume in the water, DEw the dispersion energy in the water, and TNEw the total non-electrostatic energy of solvation.

High values of R 2, Q 2CV , and Q 2Ext , as well as low values of the squared errors: RMSEC, RMSECV, and RMSEP (Table 1) confirmed that the model was well-fitted, robust, and demonstrated its good predictive ability. The existence of a strong linear correlation between the observed and predicted values of log S has been graphically proved (Fig. 2b). Details on the local QSPR’s development can be found in the original paper [35]. It should be mentioned, however, that the interpretation of the used descriptors is very similar to those for the global model. According to our previous contribution [35], the descriptors refer to the cavitation process (SASw and E t ) as well as to the dispersive (DEw and TNEw) and electrostatic (nClp1, HOMO, and Hard) interactions.

Results of the comparison

Whenever someone wants to compare two QSPR models, one usually starts from evaluating their statistical characteristics. Without doubts, the measures of goodness-of-fit, robustness, and predictivity (Table 1) favor the local QSPR. Higher correlation coefficients (R 2, Q 2CV , and Q 2Ext ) and up to two times lower values of the root mean square errors for both the training and the validation sets in comparison to the global model proved that local model was more accurate and had better performance of exploring relationships between the structure and water solubility of POPs.

This conclusion is also supported by analysis of two plots (Fig. 3) presenting residuals calculated for chloronaphthalenes based on the predictions with global and local QSPRs. Note, the residuals were calculated only for 15 PCNs, for which the experimentally determined data on water solubility have been available. In case of the local model that covered a narrow calibration domain (consisted of very similar chloronaphthalene congeners only), the prediction errors were considerably lower than the prediction errors of the global model with a wider domain (all POPs). By employing Student’s t test, we confirmed that the average residuals (for 15 PCNs) for both models differed significantly (t = 4.40, p = 0.0006).

Fig. 3
figure 3

Residual values (in log units) calculated for 15 chloronaphnthalene congeners based on the predictions with global (a) and local (b) QSPR models

Full size image

Therefore, from the qualitative point of view, an application of the local model should be recommended as being more accurate and precise. However, the performance of the evaluated global model for POPs was still fairly good in comparison with other, more general QSPRs. For instance, Delaney [36] put together statistics of 10 recently published QSPR models of water solubility, calibrated on training sets containing between 150 and 2874 compounds. Then, the models’ predictivity was tested on the same 21 compounds having a common chemical structure. The author found the standard errors of prediction for those 21 chemicals varied between 0.55 and 0.91 logarithmic units. Regarding that the higher residual observed for our “worse” global model for POPs was about one logarithmic unit, it may be concluded our global model predicts water solubility up to three times better than the general models reviewed by Delaney.

From the economical point of view, an optimal QSPR model should characterize by two features: (i) it should be based on possibly small number of training/validation compounds, without necessity to perform extensive experimental work and, simultaneously, (ii) it should ensure making predictions within a possibly wide applicability domain.

The minimal number of compounds required for developing a QSPR model is defined by the ratio between the number of descriptors and training compounds. According to the criterion proposed by Toppliss and Costello [37], this ratio should be at least 5:1. The local model that utilized one variable (latent vector) has been calibrated on 10 training compounds, whereas the global model that utilized three latent vectors has been calibrated on 91 training compounds. Thus, both studied models met the criterion, since the ratios were 10:1 for the local model and 30:1 for the global model, respectively.

There are no formal requirements related to the number of validation compounds, but different authors give some recommendations, based on their experience. For instance, Gramatica [30] recommends having at least five compounds to perform an appropriate external validation. Both models fulfilled this recommendation, since the number of validation compounds was 5 for the local and 30 for the global QSPR. However, according to our experience, when the validation set is small (of about 10 compounds and less), the results of external validation could be less reliable. It is because, in such a case, the validation statistics (Q 2Ext and RMSEP) strongly depend on the splitting algorithm. Indeed, they can significantly change, when one validation compound is replaced with another one [38]. Therefore, the external validation of our global model of log S seems to be more reliable in comparison to the external validation of the local one.

Applicability domains of both models were verified by using the Williams plots (Fig. 4). The global model has been calibrated and validated on congeners of CBzs (10 training and 2 validation compounds), PCDEs (25 training and 6 validation compounds), PBDEs (6 training and 3 validation compounds), PCBs (24 training and 10 validation compounds), PCDDs (11 training and 4 validation compounds), PCDFs (6 training and 2 validation compounds), and PCNs (9 training and 2 validation compounds). Water solubility of all validation compounds was predicted with the residuals lower than the critical threshold values (0 ± 3 standard deviations). This means the model can be successfully applied for predicting the values of log S for all seven groups of POPs listed above. Interestingly, three compounds from the training set (Fig. 4a) had the leverage values higher than the critical one (h* = 0.14). The compounds are perchlorinated benzene (CBz-12), perchlorinated naphalene (PCN-75), and perchlorinated biphenyl (PCB-209). But, simultaneously, their residuals were low. This suggests the model is well stabilized by the existence of so-called “good leverage points.” In addition, the model is probably capable to perform reliable predictions for the compounds not differing substantially from the training set, but formally situated outside of the applicability domain. The last conclusion, however, should be confirmed by an additional testing with an additional validation set of compounds that have high leverage values. In a similar way, low residuals and leverage values for all 10 training and 5 validation compounds (Fig. 4b) confirmed that the local model can be applied to make satisfying predictions of water solubility within the group of chloronaphthalenes.

Fig. 4
figure 4

Williams plot describing applicability domains of global (a) and local (b) QSPR models. Dotted lines represent the residual threshold (0 ± 3 standard deviation units), and the critical leverage value (h*), respectively

Full size image

The last aspect that should be taken into account when comparing both models is the selection of molecular descriptors employed in each case. One can be surprised that we compared two models utilizing the descriptors calculated at different levels of theory (i.e., the global model has been developed based on molecular descriptors from semiempirical PM6 calculations, whereas the local model used DFT descriptors). However, we previously demonstrated [39] that eventual differences in the numerical values of molecular descriptors for POPs calculated with both methods could be neglected. We proved that QSPR models employing the descriptors calculated at the level of novel semiempirical methods (PM6 and RM1) were of similar accuracy that the models utilizing descriptors from DFT (B3LYP functional with 6-311++G(d, p) basis set). This level of accuracy was out of reach for the models employing earlier semiempirical methods (e.g., PM3 and AM1).

Moreover, it may be unclear why, when putting together both model equations (Eqs. 10 and 11) for the same property (log S), the selected descriptors are different (e.g., LUMO in Eq. 10 and HOMO in Eq. 11)? To clarify these apparent contradictions, one needs to refer to the theory of dissolvation (described in section “Global QSPR model of water solubility”) and to keep in mind three following important issues.

First, the quantum–mechanical descriptors that we used are internally correlated. Thus, they form groups of descriptors related to the same “global” property (latent vectors) and, because of that, having very similar meaning. In consequence, one descriptor from the particular group (latent vector) can be replaced with another one from the same group without changing of the global interpretation of the model. For instance, in a group of chlorinated congeners, both total energy and the solvent accessible surface area mainly depend on the number of chlorine substituents present in molecules with the same carbon skeleton. Therefore, in this context, both descriptors have very similar meaning. For that reason, we decided to use PLS method of modeling instead of much simpler and more intuitively interpretative multiple linear regression (MLR).

Second, molecular descriptors for both local and global models were selected with use of the genetic algorithm. The algorithm is, in fact, an automatic probability-based procedure, blind on the mechanistic interpretation. In effect, when the algorithm has a choice between two strongly correlated descriptors related to the same “global” property (see above), it might select the first or the second descriptor only by chance.

Third, when considering a local model, developed for only one congeneric group (i.e., polychlorinated naphthalenes), the model is much more sensitive on the number of substituents (chlorine atoms) and the substitution pattern than the global model calibrated for more groups, in which the main differences between particular compounds are related to their carbon skeletons (i.e., the number of aromatic rings, presence of heteroatoms, etc.).

Hence, no one should expect exactly the same model equations for the global and local models being compared in our study. In the context of the dissolution mechanism, three structural features (“global” properties) of POPs’ congeners seem to be very important. They are: (i) the size of the parent molecule (carbon skeleton), (ii) the type and the number of substituents present in the molecule, and (iii) the substitution pattern. The first “global” property is obviously related to the cavitation process. We observed that the solubility decreases with the increasing size of the molecule. The type and the number of substituents are, of course, also strongly related to the size, and consequently, to the cavitation stage. Generally, molecules based on the same skeleton and substituted with the same number of bromine atoms are less soluble than their chlorinated analogues, due to larger radius of bromine substituents in comparison to chlorine atoms. Similarly, the solubility increases with the increasing number of halogen substituents (e.g., monochloronaphthalenes are more soluble than dichloronaphthalenes). The descriptors related to the factors influencing the cavitation process, namely: the size of a molecule, the type and number of substituents are nAT, nX, and SAS in Eq. 10, as well as E t , SASw, SAVw, DEw, and TNEw in Eq. 11.

The substitution pattern is the main factor deciding on differences in solubility between congeners containing the same number of substituents of the same type. Differences in the distribution of the substituents (over the same carbon skeleton) decide on differences in polarity of particular congeners. For example, 1,2,3,4-tetrachloronaphthalene is more polar than 2,3,6,7-tetrachloronaphthalene. Subsequently, electrostatic interactions with water as a solvent are stronger in the second case. Thus, the second congener in this pair is more soluble. Interestingly, as we demonstrated in many previous contributions [35, 40–42] such descriptors as HOMO and LUMO are strongly dependent on the substitution pattern. Thus, in study they should not be interpreted as those describing redox properties of the molecules (according to the well-known Koopman’s theorem), but rather their substitution patterns. Another descriptors related to the substitution pattern are Q + and Shift in Eq. 10, as well as nClp1 and Hard in Eq. 11. Therefore, the mechanistic interpretation of both global and local QSPR models would be very similar.

In summary, from the economical point of view, both models are acceptable, since they require a relatively small number of experimental data. In fact, both are based on the data taken from the literature, thus performing of any extensive empirical work was unnecessary. However, the use of the global QSPR would be more profitable, because it enables to make predictions for those groups of POPs, for which the number of experimental data is insufficient to develop appropriate local models. For example, the experimentally determined data on water solubility are available only for eight congeners of PCDFs, which is evidently too small for calibrating and validating a local model. Moreover, time and, in consequence, costs of obtaining the predicted values of log S can be significantly reduced by employing the global modeling scheme.

Comparing other global and local QSPR models

In addition, to extend the investigations on the other phys/chem properties, we performed similar pairwise comparisons for the other, previously published QSPR models. We used two of our previous global models developed for predicting n-octanol/water partition coefficient (log K OW) [40] and subcooled liquid vapor pressure (log P L) [42], respectively, for a group of 1436 POPs, including chloro- and bromo-analogues of dibenzo-p-dioxins, dibenzofurans, biphenyls, naphthalenes, diphenyl ethers, and benzenes. The models were compared with two corresponding local models published by other groups. The first one was designed to predict log K OW for 209 PCBs [43], whereas the second one the values of log P L for 210 congeners of PCDDs and PCDFs [44].

Interestingly, the conclusions from both comparisons (based on predicting log K OW and log P L) are even more optimistic than that for log S. The statistical measures of goodness-of-fit and robustness were very similar in pairs for corresponding global and local models (Table 2). Moreover, the observed differences between the experimentally measured and predicted values of by both methods of modeling (i.e., local and global) were not statistically significant (p > 0.05) (Table 3), which was consistent with our assumption. Regarding that (i) both global models have been developed for a much wider applicability domain (covering of about 85% more compounds) and (ii) they practically did not differ from their local counterparts in quality, we concluded that the employment of global QSPRs would be much more efficient then the development of particular local ones.

Table 2 Statistical parameters of local and global models of log P L and log K OW
Full size table
Table 3 Comparison between the residuals derived from the predictions of log P L and log K OW with local and global GA-PLS models by the Student t test
Full size table

Conclusions

We have verified the efficiency of two modeling strategies. The first one assumes the reduction of the model’s domain and the development of QSPR based on a small number of structurally similar compounds (local QSPR). According to the second one, the model is calibrated with use of the wider and more structurally diversified training set (global QSPR), even if this leads to a small decrease of the model’s predictivity.

Based on the obtained results, we recommend that whenever global models fulfill all quality criteria proposed by the Organization for Economic Cooperation and Development (OECD), they should be applied in practice without necessity of developing a series of local QSPRs. Such a recommendation is reasonable, because of three reasons. First, the global models allow for simultaneous predictions of physicochemical properties for even many hundreds of compounds. This feature is very important from the economic point of view, regarding that the number of new chemicals synthesized and/or identified in the environmental compartments is growing exponentially. Second, the global modeling approach may be the only possibility of modeling, when the number of chemicals from one specific class of the chemically related compounds is insufficient to calibrate and appropriately validate a local QSPR model. Third, as demonstrated, the performance (predictive ability) of global models is not always worse than these of local ones.