1 Introduction

The emergence of high-dimensional time series observed in matrix form gives birth to new modeling challenges in economics, finance, and related fields. The existing approaches to dimension reduction in high-dimensional multivariate time series analysis can be organized in two major classes: (a) factor models (Bai and Ng 2002; Forni et al. 2005; Lam et al. 2011), and (b) modeling with frequentist regularization or Bayesian methods (Rothman et al. 2010; Song and Bickel 2011; Kock and Callot 2015; Park and Casella 2008; Bańbura et al. 2010; Gefang 2014; Ahelegbey et al. 2016; Korobilis 2021).

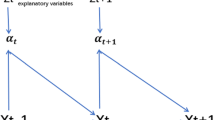
While most of the extant modelling paradigms are designed to encourage parsimony by treating observations as time series vectors, in economics, finance and other fields, observations in matrix or tensor form are often generated over time. For instance, the collection of panel data forms matrix-valued time series observations, whose rows might represent indicators and columns countries—see Fig. 1. In this context, univariate time series analysis focuses on one element of the matrix at a time. Vector and panel time series analysis deal with the co-movement of one row in the matrix. Modeling each dimension separately annihilates the multidimensional structure of data, and can therefore lead to a significant loss of information or efficiency.

A strand of literature has therefore developed and studied multidimensional time series models, including matrix-valued ones (Hoff 2015, 2011; Chen and Yang 2021; Wang et al. 2019; Billio et al. 2022). However, when the matrix observation has large dimensions, the matrix autoregressive (MAR) model involves a large number of parameters, which requires further dimension reduction techniques to produce accurate estimation. So far, this has been primarily tackled through the introduction of factor autoregressive models for multidimensional time series (Wang et al. 2019; Chen and Fan 2021; Gao and Tsay 2021; Chen et al. 2022). Although factor approaches can cope well with the dimensionality problem, the resulting parameters lack a clear interpretation. As in the vector case, the factor approach in a matrix-valued dataset involves replacing the original matrix of dependent variables with an estimated matrix of factors, featuring a sensibly lower number of rows and/or columns. Nevertheless, each coefficient refers to a factor, and not to an observed variable, thus hampering interpretation. In addition, factor models require choosing the number of factors, which is not a parameter that can be estimated. In light of this, dimensionality problems that preserve the original problem structure, such as the one performing variable selection and regularization, are preferred.

Fig. 1
figure 1

Time series of three economic indicators: GDP growth, Consumer Price Index, and Short-term Interest Rate for five countries

Full size image

In parallel, research on high-dimensional statistics has widely studied sparse recovery in the context of normal linear regression models (George and McCulloch 1993; Barrett and Gray 1994; George and McCulloch 1997; Chen and Huang 2016; Wang et al. 2018; Samanta et al. 2022). In the Bayesian literature, the treatment of high-dimensional linear regression models mostly stems from the seminal papers on variable selection via Gibbs sampling (George and McCulloch 1993, 1997), hereafter identified as stochastic search variable selection (SSVS). More recently, a deterministic alternative to stochastic search was proposed based on an EM variable selection (EMVS) algorithm to find maximum a posteriori probability (MAP) estimates (Ročková and George 2014). As in SSVS, the EMVS method combines a spike-and-slab regularization procedure for the discovery of active predictor sets with subsequent evaluation of posterior model probabilities. However, EMVS provides an appealing alternative to SVSS in terms of computational efficiency.

Fully Bayesian variable selection has attracted attention in the multivariate time series context, starting from a stochastic search approach to selecting restrictions for vector autoregressive (VAR) models (George et al. 2008). However, the EMVS framework has yet to be exploited in multivariate time series. Moreover, variable selection has only been considered in vector-valued time series models to date, highlighting the need of identifying restrictions in multidimensional autoregressive models. The absence of restrictions on the regression coefficients results in a potentially large number of parameters relative to the available data and with a limited number of observations, over-parameterization can affect the precision of inference.

We propose a novel matrix autoregressive model where sparsity is induced naturally. By deriving a compact form for MAR models borrowed from the tensor linear regression framework, we design an estimation strategy using MCMC, which allows a full range of Bayesian inference, and a Bayesian EMVS procedure, which allows for fast posterior mode identification. That is, the latter substantially reduces the computational time required for the MCMC procedure, making it feasible when dealing with large-scale multidimensional time series.

The properties of the proposed model are demonstrated through simulations and examples in an application to macroeconomic data. The simulation experiments show: (a) the gain in small sample efficiency of the proposed estimators relative to maximum likelihood (ML) in high-dimensional sparse settings; and (b) that the proposed estimators perform generally better than standard VARs and several competing alternatives suited for longitudinal data, while limiting computational intensity in the EMVS formulation. The empirical application to macroeconomic data confirms that the model is able to: (a) handle high-dimensional longitudinal data; (b) outperform competing alternatives in high-dimensional settings; and (c) yield enhanced interpretability given by the autoregressive model in matrix form.

The proposed model can be readily extended to the tensor autoregressive (TAR) framework. In contrast to other work (e.g. Billio et al. 2022), it encompasses a Tucker structure in the matrix coefficient rather than a PARAFAC decomposition. The PARAFAC decomposition arises in the general context of tensor decomposition and is applicable to matrices in the bi-dimensional case. In particular, it achieves dimension reduction by factorizing a tensor in the outer (element-wise) product of vectors. The resulting tensor is of rank one, featuring a large reduction in the number of coefficients.Footnote 1 Thus, the PARAFAC decomposition has the advantage of being highly parsimonious but it can be restrictive for empirical purposes. This is magnified in economic and financial applications where the relationship among variables exhibits complex and highly interconnected behaviors. Conversely, the Tucker structure admits an arbitrary number of factor components in each mode. This allows modeling dimension asymmetric tensors and benefits from enhanced interpretability of mode-specific interrelationships.

The remainder proceeds as follows. Section 2 outlines the proposed sparse MAR model, while Sect. 3 discusses the shrinkage priors and Sect. 4 describes the MCMC and EMVS estimation procedures. Section 5 describes the dynamic analysis via Kronecker generalized forecast error variance decomposition (GFEVD). Section 6 evaluates the model performance and computational times, compared to some key competitors, through a simulation study. Section 7 considers an empirical application to macroeconomic data. Section 8 contains some concluding remarks.

2 Model and prior structure

2.1 The matrix autoregressive model

The MAR model takes advantage of the original structure of the data by modeling matrix autoregressive dynamics in a bilinear form. This is of paramount importance, for instance, in panel data applications where each observation at time t can be conceived as a matrix and whose rows represent indicators and columns represent countries.

We introduce a well-known formulation of the MAR model (Chen and Yang 2021) and then propose a parsimonious alternative model. The alternative can be useful in the estimation required for a model with several lag orders relative to the number of time series observations. Then, given the multidimensional structure, we cast the model into the tensor linear regression framework which will allow easier estimation. Finally, we consider the estimation of high-dimensional MAR models via variable selection in a Bayesian framework.

we observe \(g=1,...,G\) indicators for a number of countries \(g=1,...,G\), across \(t=1,...,T\), \(t=1\ldots , T\) time points. Let \(\varvec{y}_{n,t}\) be the, G dimensional vector that collects the domestic indicators for each country. \(n=1,\ldots ,N\) Moreover, we define \({\textbf {Y}}_t=[{\textbf {y}}_{1,t},...,{\textbf {y}}_{N,t}]\) to be the \([G \times N]\) matrix of endogenous variables, obtained by horizontally stacking all the country specific vectors. The conditional mean of the matrix observation is expressed as the product of P lagged observations, each one multiplied by two left and right autoregressive coefficient matrices \({\textbf {A}}_1,...,{\textbf {A}}_P\) and \({\textbf {B}}_1,...,{\textbf {B}}_P\), of dimension \([G \times G]\) and \([N \times N]\), repsectively. Specifically, t (Chen and Yang 2021, Section 2)

$$\begin{aligned} \begin{aligned} \textbf{Y}_t&=\sum _{i=1}^P\textbf{A}_i\textbf{Y}_{t-i}\textbf{B}_i^{'}+\textbf{E}_t,\\ \textbf{E}_t&\sim {\mathcal {M}}{\mathcal {N}}(\textbf{0},\Sigma _1,\Sigma _2), \end{aligned} \end{aligned}$$
(1)

where \(\textbf{E}_t \in {\mathbb {R}}^{G \times N}\) is a white noise matrix of the same dimension as \(\textbf{Y}_t\) with two symmetric positive definite covariance matrices \(\Sigma _1\) and \(\Sigma _2\) of dimensions \(G \times G\) and \(N \times N\), respectively. We use \({\mathcal {M}}{\mathcal {N}}\) to denote the multilinear normal distribution (Gupta and N 1999; Ohlson et al. 2013).

Let \(\text{ vec }(\cdot )\) be the usual vectorization of a matrix by stacking its columns and \(\otimes \) the usual Kronecker product. Let \(\textbf{y}_{t-i}=\text{ vec }(\textbf{Y}_{t-i})\) for \(i=0,\ldots ,P\) and \(\textbf{e}_t=\text{ vec }(\textbf{E}_t)\). The vectorized form of the MAR model in Eq. (1) is

$$\begin{aligned} \begin{aligned} \textbf{y}_t&=\sum _{i=1}^P(\textbf{B}_i\otimes \textbf{A}_i)\textbf{y}_{t-i}+\textbf{e}_t,\\ \textbf{e}_t&\sim {\mathcal {N}}(\textbf{0},\Sigma _2\otimes \Sigma _1). \end{aligned} \end{aligned}$$
(2)

The representation in Eq. (2) shows that the MAR(P) model can be regarded as a special case of a VAR(P) model, with an autoregressive coefficient matrix given by a Kronecker product of the two mode-specific matrices. As a direct consequence of the equivalence, the MAR(P) in Eq. (1) is stationary if all the roots of \(|\textbf{I}_{GN}-(\textbf{B}_1\otimes \textbf{A}_1)z+\cdots +(\textbf{B}_P\otimes \textbf{A}_P)z^P|=0\) fall outside the unit circle. Under this assumption, the model in Eq. (1) can be rewritten as the infinite moving average representation

$$\begin{aligned} \textbf{y}_t=\textbf{e}_t+\varvec{\Psi }_1\textbf{e}_{t-1}+\cdots +\varvec{\Psi }_{\infty }\textbf{e}_{t-\infty }, \end{aligned}$$

where the \(GN\times GN\) coefficient matrices \(\varvec{\Psi }_k\) can be obtained via the following recursion

$$\begin{aligned} \varvec{\Psi }_k=(\textbf{B}_1\otimes \textbf{A}_1)\varvec{\Psi }_{k-1}+\cdots +(\textbf{B}_P\otimes \textbf{A}_P)\varvec{\Psi }_{k-P}, \,\,k=1,2,\ldots \end{aligned}$$

the model is thenwhere \(\varvec{\Psi }_k=\textbf{0}\) for \(k<0\) and \(\varvec{\Psi }_0=\textbf{I}_{GN}\).

2.2 Model interpretation

To ease the exposition, consider the case \(P=1.\) In order to interpret the model parameters, it is helpful to highlight that, if \(\textbf{Y}_{t}\) follows a MAR(1), then for a specific pair \(g=1,\ldots ,G\) and \(n=1,\ldots ,N\), the conditional expected value of each entry \(y_{gn,t}\) of \(\textbf{Y}_{t}\) is

$$\begin{aligned} E(y_{gn,t}|\textbf{y}_{t-1})=\sum _{i=1}^G\sum _{j=1}^Na_{g,i}b_{n,j}y_{ij,t-1}, \end{aligned}$$

where \(a_{g,i}\in \textbf{A}\) and \(a_{n,j}\in \textbf{B}\). Roughly speaking, \(a_{g,i}\) embeds the impact of the rows of \(\textbf{Y}_{t-1}\) on the gth row of \(\textbf{Y}_t\). Analogously, \(b_{n,j}\) describes the influence of the columns of \(\textbf{Y}_{t-1}\) on the nth column of \(\textbf{Y}_t\). This model could be referred to as a bilinear multiplicative model, given that the temporal effect on each observation is weighted by the product of two coefficients. Such restriction holds as long as the structure of the matrix dataset embeds two distinct dynamics, one for each dimension, which can be separately identified.

Consider the example shown in Fig. 1, where columns represent countries and rows macroeconomic indicators. Conceiving the model as a hierarchical structure, the conditional expectation of an economic indicator of one country is a linear combination of all the indicators of the other countries (globally adjusted combination):

$$\begin{aligned} {\tilde{\textbf{y}}}_{n,t}=[b_{n,1}y_{ij,t-1},\ldots ,b_{n,N}y_{iN,t-1}]^{'}, \end{aligned}$$

each one weighted for indicator-specific coefficients:

$$\begin{aligned} E(y_{gn,t}|\textbf{y}_{t-1})=[a_{g,1},\ldots ,a_{g,G}]\times {\tilde{\textbf{y}}}_{n,t}. \end{aligned}$$

This hierarchical structure, naturally induced by the matrix structure, is coherent with several restriction approaches proposed in the literature for Panel data in the vectorized framework (Pesaran et al. 2004; Canova and Ciccarelli 2009; Korobilis 2016; Camehl 2022). Analogous interpretations follow for the contemporaneous relationship captured by the left and right coefficient matrices \(\Sigma _1\) and \(\Sigma _2\). For a more detailed explanation of the model interpretation see Chen and Yang (2021).

The model can be made more parsimonious, if more restrictive, by assuming that the row and column effects matrices are time invariant (\(\textbf{A}_i=\textbf{A}\), \(\textbf{B}_i=\textbf{B}\)), while embedding the effects of lagged observations in a row vector \(\textbf{c}\in {\mathbb {R}}^{1 \times P}\). The conditional mean of \(\textbf{Y}_t\) is a linear combination of its P lagged values, pre and post multiplied by \(\textbf{A}\) and \(\textbf{B}\) as in a MAR(1). If \(c_i\in \textbf{c}\), the model is then

$$\begin{aligned} \begin{aligned} \textbf{Y}_t=\textbf{A}\bigg (\sum _{i=1}^{P}c_i\textbf{Y}_{t-i}\bigg )\textbf{B}^{'}+\textbf{E}_t\\ \end{aligned} \end{aligned}$$
(3)

Although it can be expressed as a MAR, the model arises naturally as a special case of tensor autoregression (TAR), as will be shown in the following subsection. We therefore denote the model in Eq. (3) as MAR\(^{*}\)(P).

It is clear that the MAR\(^{*}\) formulation is quite restrictive and might not be a feasible specification for several types of applications, given that the dependence is expressed by the sole \(c_i\) coefficients, while \({\textbf {A}}\) and \({\textbf {B}}\) remain fixed. However, this formulation might be seen as a parsimonious alternative in particularly high-dimensional contexts. It is not uncommon to find empirical applications to macroeconomic data where the length of the time series requires the use of dimension reduction techniques to estimate model parameters. Despite being restrictive, the fixed-parameter formulation can be useful in modeling the impacts of a large number of lags relative to the available number of time series observations.

An unrestricted VAR(P) estimates \((GN)^2P \in {\mathcal {O}}(n^5)\) parameters, but due to the Kronecker structure imposed on its coefficient matrices, the MAR(P) model estimates only \((G^2+N^2)P\in {\mathcal {O}}(n^3)\) parameters, where \({\mathcal {O}}(\cdot )\) denotes the order of parameter complexity. The further restriction imposed that yields the MAR\(^{*}\)(P) results in \(G^2+N^2+P\in {\mathcal {O}}(n^2)\) parameters to estimate. As a result, the number of parameters grows as a linear function of the lag order. This is clear from Fig. 2, in which a graphical comparison of the three models is depicted.

Fig. 2
figure 2

Logarithm of the number of parameters in a Panel VAR (a), MAR (b) and MAR\(^{*}\) (c) with \(G=5, N=2,\ldots ,10\) (y axis) and lags \(P=1,\ldots ,5\) (x axis). The MAR is much less sensitive than the VAR to the increase in G, but it suffers from over-parameterization compared to the MAR\(^{*}\), for which this effect is negligible

Full size image

2.3 Compact form

Vector and matrix operations can be readily generalized to the tensor case, but notions of tensor algebra are necessary to proceed. See Appendix A.1 for some basics of tensor notation and calculus and Cichocki (2018) and Kolda and Bader (2009) for more details.

Although an estimation procedure for the MAR(1) model is readily available (Chen and Yang 2021), a compact form of the model is instrumental for developing a more general and coherent estimation procedure for the MAR(P). We therefore derive a comprehensive compact form for any general K-dimensional TAR(P), which admits the MAR(P) and MAR\(^{*}\)(P) as special cases, by establishing a connection with the general Tensor Linear Regression (TLR) model. Indeed, as the VAR emerges as a multivariate linear regression (MLR) model in its compact form, the analogous counterpart for the MAR is a TLR model.

The compact form of the VAR can be easily derived via the matrix of dependent variables \(\textbf{Y}\) obtained by horizontally stacking each \(\textbf{y}_t\) for \(t=1,\ldots ,T\). However, for each point in time, the variables in a MAR are already matrix shaped, so that its related compact form consists of a third order tensor.

Let us consider a K way (order) tensor \({\mathcal {Y}}\in {\mathbb {R}}^{J_1,\ldots ,J_K}\) which is a K-dimensional array with entries \({\mathcal {Y}}_{j_1,\ldots ,j_K}\) with \(j_k=1,\ldots ,J_k\) for \(k=1,\ldots ,K\). We define the response and explanatory tensor for the MAR in Eq. (1). Let \({\mathcal {Y}}\) be a \(K=3\) way response tensor of dimension \([G\times N\times T-P]\) with \({\mathcal {Y}}_{:,:,t}=\textbf{Y}_t\). Then, define the explanatory tensor \({\mathcal {X}}\) to be of dimension \([GP\times NP\times T-P]\). When fixing the third dimension \(j_3=t=1,\ldots ,T-P\), we obtain tensor slices of dimensions \([GP\times NP]\), which we fill with the lagged values of \(\textbf{Y}_t\) and zeros otherwise:

$$\begin{aligned} {\mathcal {X}}_{:,:,t}=\left[ \begin{array}{cccc} \textbf{Y}_{t-1} &{} \textbf{0}&{} \cdots &{} \textbf{0}\\ \textbf{0}&{} \textbf{Y}_{t-2} &{} \cdots &{} \textbf{0}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \textbf{0}&{} \textbf{0}&{} \cdots &{} \textbf{Y}_{t-P} \end{array}\right] . \end{aligned}$$

In the case of the the MAR\(^{*}\)(P) in (3), the response and explanatory objects of interest need to be slightly modified. We define \({\mathcal {X}}\) to be a \(K=4\) order tensor of dimensions \([G\times N\times P\times T-P]\) such that \({\mathcal {X}}_{:,:,i,t}=\textbf{Y}_{t-i}\) and, for the sake of coherence, we modify \({\mathcal {Y}}\) to be a four-dimensional tensor \({\mathcal {Y}}\in {\mathbb {R}}^{G\times N\times 1\times T-P}\) as well.

We may now write a unique compact form which encompasses both MAR(P) and MAR\(^{*}\)(P). Let \({\mathcal {B}}=\{[\textbf{A}_1,\ldots ,\textbf{A}_P],[\textbf{B}_1,\ldots ,\textbf{B}_P],\textbf{I}_{T-P}\}\) and \(\varvec{\Sigma }=\{\Sigma _1,\Sigma _2,\textbf{I}_{T-P}\}\) in case of MAR(P), \({\mathcal {B}}=\{\textbf{A},\textbf{B},\textbf{c},\textbf{I}_{T-P}\}\) and \(\varvec{\Sigma }=\{\Sigma _1,\Sigma _2,\Sigma _3,\textbf{I}_{T-P}\}\)Footnote 2 in case of MAR\(^{*}\)(P). Denoting \({\bar{\times }}\) as the Tucker product and \({\mathcal {U}}\) the tensor white noise, then we have

$$\begin{aligned} \begin{aligned} {\mathcal {Y}}&={\mathcal {X}}{\bar{\times }}{\mathcal {B}}+{\mathcal {E}}\\ {\mathcal {E}}&={\mathcal {U}}{\bar{\times }}\varvec{\Sigma }^{1/2}\\ {\mathcal {U}}&\sim {\mathcal {M}}{\mathcal {N}}(\textbf{0},\textbf{I}_{J_1},\ldots ,\textbf{I}_{J_K}). \end{aligned} \end{aligned}$$
(4)

Notice that Eq. (4) can be seen as the multilinear generalization of the compact form of VAR models—see Lütkepohl (2005). We refer the reader to Appendix A.1 which describes the matricization and the Tucker product, the fundamental operators that are used to create and then manipulate \({\mathcal {B}}\) and \(\mathcal {\Sigma }\), and Kolda and Bader (2009); Bader and Kolda (2006) for further reference.Footnote 3

It is convenient to derive the MLR representation of the models. To simplify the notation, let \(\varvec{\Phi }_1=[\textbf{A}_1,\ldots ,\textbf{A}_P]\) and \(\varvec{\Phi }_2=[\textbf{B}_1,\ldots ,\textbf{B}_P]\) for the MAR(P), \(\varvec{\Phi }_1=\textbf{A}\), \(\varvec{\Phi }_2=\textbf{B}\) and \(\varvec{\Phi }_3=\textbf{c}\) for the MAR\(^{*}\)(P). Then, let \({\tilde{\textbf{Y}}}^k=\text{ mat}_k({\mathcal {Y}})\Sigma _{-k}\), \({\tilde{\textbf{X}}}^k=\text{ mat}_k({\mathcal {X}})\Sigma _{-k}\) and \({\tilde{\textbf{E}}}^k=\text{ mat}_k({\mathcal {E}})\Sigma _{-k}\), where \(\Sigma _{-k}=\Sigma _K\otimes \cdots \otimes \Sigma _{k+1}\otimes \Sigma _{k-1},\ldots ,\Sigma _1\), where \(\text{ mat}_k(\cdot )\) denotes the k-mode matricization operator as defined in Appendix A.1. By matricizing both sides of Eq. (4) for each k, one can easily derive a MLR model which highlights the kth way conditional mean and variance matrices \(\{\varvec{\Phi }_k,\Sigma _k\}\):

$$\begin{aligned} \begin{aligned} {\tilde{\textbf{Y}}}^k&=\varvec{\Phi }_k{\tilde{\textbf{X}}}^k+{\tilde{\textbf{E}}}^k \\ {\tilde{\textbf{E}}}^k&\sim {\mathcal {M}}{\mathcal {N}}(\textbf{0},\Sigma _k,\textbf{I}_{J_{-k}}). \end{aligned} \end{aligned}$$
(5)

The latter formulation allows the estimation to be carried out for each of the K modes separately. Notice that in the case of vector-valued time series, the compact form in Eq. (4) reduces to the formulation in Eq. (5).

3 Shrinkage priors

Consider the compact form in Eq. (4). Let \(J_{-k}=\prod _{l\ne k}J_l\) so that the likelihood can be written as:

$$\begin{aligned}{} & {} {\mathcal {L}}({\mathcal {Y}}|{\mathcal {B}},\varvec{\Sigma })\propto \prod _{k=1}^K|\Sigma _k|^{-\frac{J_{-k}}{2}}\nonumber \\ {}{} & {} \quad \exp \left( -\frac{1}{2}||({\mathcal {Y}}-{\mathcal {X}}{\bar{\times }}{\mathcal {B}}){\bar{\times }}\varvec{\Sigma }^{-\frac{1}{2}}||_2^2\right) . \end{aligned}$$
(6)

Also, notice that the likelihood for the MAR model in terms of \(\{\varvec{\Phi }_k,\Sigma _k\}\), given the other parameters, is proportional to the likelihood in Eq. (6):

$$\begin{aligned} {\mathcal {L}}({\mathcal {Y}}|\varvec{\Phi }_k,\Sigma _k)\propto {\mathcal {L}}({\mathcal {Y}}|\varvec{\Phi },\Sigma ). \end{aligned}$$

This implies that both ML and Bayesian estimation can be carried for each dimension separately (see, e.g., Hoff 2015). As a consequence, sparsity can be induced in the two modes independently, easing the introduction of regularization methods for MAR models.

We will consider a spike-and-slab framework for the prior to induce sparsity in the two mode-specific coefficients of the MAR; a related approach is available for VAR models (George et al. 2008).

The proposed model is a multi-dimensional generalization of the uni-dimensional linear regression framework. Therefore, the variable selection for the MAR has much in common with the variable selection for the VAR in the bi-dimensional setting (George et al. 2008). The key feature of the variable selection approach is to construct a hierarchical prior for each lagged coefficient \(\phi _{i,k}\in \varvec{\phi }_k=\text { vec }(\varvec{\Phi }_k)\). Each coefficient is endowed with a prior in the form of a mixture of two normal distributions, whose mixing coefficient is a latent variable \(\gamma _{i,k}=\{0,1\}\). The two normal distributions share the same mean, but have different variances. One has a large variance so that it mimics a uniform prior, whereas the other is tightly spiked around the shared mean. When \(\gamma _{i,k}=1\) (with probability \(\theta _{i,k}\)), the coefficient is said to be active, and governed by the normal distribution with large variance. When \(\gamma _{i,k}=0\) (with probability \(\gamma _{i,k}=1-\theta _{i,k}\)), the coefficient is said to be inactive, and thus drawn from the spiked normal. In this framework, variable selection can be performed through MCMC integration by evaluating the posterior of each \(\gamma _{i,k}\). The indices i, k such that the posterior median of \(\text{ P }(\gamma _{i,k}=1)>0.5\) indicate the selected variables, that is, the relevant subset of the predictors.

For each coefficient \(\phi _{i,k}\in \varvec{\phi }_k=\text { vec }(\varvec{\Phi }_k)\), we have a binary indicator \(\gamma _{i,k}\in \{0,1\}\), which encodes the state of \(\phi _{i,k}\) (the “spike” inactive state for \(\gamma _{i,k}=0\) and the “slab” active state for \(\gamma _{i,k}=1\)). Given \(\gamma _{i,k}\), the conditional mixture prior for each \(\phi _{i,k}\) can be expressed as

$$\begin{aligned} \phi _{i,k}|\gamma _{i,k}\sim (1-\gamma _{i,k}){\mathcal {N}}(0,\tau _0)+\gamma _{i,k}{\mathcal {N}}(0,\tau _1), \end{aligned}$$

which is controlled by the two hyperparameters \(\tau _0\) and \(\tau _1\). By selecting the two such that former approaches 0 whereas the latter is arbitrarily large, \(\gamma _{i,k}\) is able to identify restrictions on \(\phi _{i,k}\). The prior for the kth mode conditional mean parameters can be rewritten compactly as

$$\begin{aligned} \varvec{\phi }_k|\varvec{\gamma }_k\sim {\mathcal {N}}(\textbf{0},{\mathcal {V}}_k), \end{aligned}$$

where \({\mathcal {V}}_k=\text{ diag }(v_{1,k},\ldots ,v_{n_k,k})\) and \(v_{i,k}=(1-\gamma _{i,k})\tau _0+\gamma _{i,k}\tau _1\), being \(n_k\) the cardinality of \(\varvec{\phi }_k\). We assume each \(\gamma _{i,k} \) is independent Bernoulli, i.e.:

$$\begin{aligned} \gamma _{i,k}|\theta _k\sim {\mathcal {B}}\text{ er }(\theta _k). \end{aligned}$$

With a priori information on the level of sparsity in the coefficients, one can set \(\theta _k\) accordingly. Therefore, we endow each indicator with a Beta-Bernoulli hierarchical prior:

$$\begin{aligned} \begin{aligned} \pi (\varvec{\gamma }_k|\theta _k)&=\theta _k^{|\gamma _k|}(1-\theta _k)^{n_k-|\gamma _k|}\\ \theta _k&\sim {\mathcal {B}}\text{ eta }(\alpha _k,\beta _k), \end{aligned} \end{aligned}$$

where \(|\gamma _k|=\sum _i\gamma _{i,k}\).

Notice that the two covariance matrices of the MAR enter the likelihood in a multiplicative way, meaning their scales are not separately identifiable. Without imposing restrictions, such quantities would be determined completely by the prior covariance matrices. Further restrictions on the scales are therefore required without any additional a priori information.

As in Hoff (2011, 2015), we introduce dependence between the Inverse Wishart prior distribution of each \(\Sigma _k\) by adding a level of hierarchy through a hyperparameter \(\xi \)

$$\begin{aligned} \begin{aligned} \xi&\sim {\mathcal {G}}a(\eta _1,\eta _2)\\ \Sigma _k|\xi&\sim {\mathcal {W}}^{-1}(\xi \Omega _k,\nu _k), \end{aligned} \end{aligned}$$

where \({\mathcal {G}}a(\eta _1,\eta _2)\) is the Gamma distribution with shape and scale parameters \(\eta _1,\eta _2\) respectively. By setting \(\Omega _k=\textbf{I}_{J_k}/J_k\) and \(\nu _k=J_k+2\) the total variance is controlled only by a Kth power of \(\xi \):

$$\begin{aligned} \text{ E }\Big [\prod _k\text{ tr }(\Sigma _k)\Big ]=\xi ^K. \end{aligned}$$

Thus, if we let \(\mathbf {\Delta }_k\) be the collection of all the kth mode parameters except for \(\varvec{\gamma }_k\), the joint prior distribution takes the form

$$\begin{aligned} \begin{aligned}{}&{} \pi (\mathbf {\Delta }_1,\ldots ,\mathbf {\Delta }_K,\varvec{\gamma }_1,\ldots ,\varvec{\gamma }_K)\\{}&{} \qquad =\prod _k\pi (\varvec{\phi }_k|\varvec{\gamma }_k)\pi (\varvec{\gamma }_k|\theta _k)\pi (\theta _k)\pi (\Sigma _k|\xi )\pi (\xi ). \end{aligned} \end{aligned}$$

4 Bayesian estimation

We develop two computational methods for fitting the proposed Bayesian model (i) a Gibbs sampler and (ii) a maximum a posteriori (MAP) estimation procedure via EMVS. The Gibbs sampling algorithm will produce more accurate estimates and allow estimation of the full posterior. However, it is expected to be slower than the EMVS procedure, which aims only at identification of posterior modes by iteratively maximizing the conditional expectation of the log posterior.

An outline of the proposed Gibbs sampling procedure is given in Algorithm 1 in Appendix B along with the details on the full conditional posterior distributions. Notice that while we defer the description of how we obtain the MAP estimates, these are the ones we propose to use as starting values for the Gibbs sampler. As a matter of fact, posterior modes are often good starting values to use in MCMC simulation experiments (Geyer 2010; Jones and Qin 2022; Vats et al. 2021).

4.1 MAP estimation

A global optimization procedure to find the posterior mode can be set separately for each dimension K. However, given the mixture of prior for each \(\varvec{\phi }_k\), the direct optimization of the log conditional posterior \(\log \pi (\mathbf {\Delta }_k|{\mathcal {Y}})\) has no analytical solution. The presence of the sum prevents the logarithm from acting directly on the joint conditional posterior, which results in complicated expressions for the MAP solution.

We employ an Expectation Conditional Maximization (ECM) algorithm (Meng and Rubin 1993), which indirectly maximizes \(\log \pi (\mathbf {\Delta }_k,\varvec{\gamma }_k|{\mathcal {Y}})\) by iteratively maximizing its expected value under the posterior distribution of the latent variable. At iteration j, this expectation, denoted by \({\mathcal {Q}}(\mathbf {\Delta }_k|\mathbf {\Delta }^{[j-1]}_k)\), is given by

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(\mathbf {\Delta }^{[j]}_k|\mathbf {\Delta }^{[j-1]}_k)=\text { E}_{\varvec{\gamma }_k|\mathbf {\Delta }^{[j-1]}_k}\big [\log \pi (\mathbf {\Delta }_k,\varvec{\gamma }_k|{\mathcal {Y}})|\mathbf {\Delta }_k^{[j-1]}\big ], \end{aligned} \end{aligned}$$
(7)

which constitutes the E-step of the algorithm. In the M-step, we derive the revised estimate of all the other parameters by maximizing the function:

$$\begin{aligned} \mathbf {\Delta }_k^{[j]}=\underset{\mathbf {\Delta }_k}{\textrm{argmax}} \hspace{2mm} {\mathcal {Q}}(\mathbf {\Delta }_k|\mathbf {\Delta }^{[j-1]}_k) \end{aligned}$$

where \({\mathcal {Q}}(\mathbf {\Delta }_k|\mathbf {\Delta }^{[j-1]}_k)\) can be decomposed as:

$$\begin{aligned} \begin{aligned} \begin{aligned} {\mathcal {Q}}_{1,k}(\varvec{\phi }_k^{[j]}|-)&=-\frac{1}{2}\Big [(\varvec{\phi }_k-\hat{\varvec{\phi }_k})^{'}({\tilde{{\textbf {X}}}}^{k'}{\tilde{{\textbf {X}}}}^{k}\\ {}&\quad \otimes \Sigma _k^{-1})(\varvec{\phi }_k-{\hat{\varvec{\phi }}}_k)+\varvec{\phi }_k^{'}{\mathcal {V}}_k^{-1}\varvec{\phi }_k^{'}\Big ]\\ {\mathcal {Q}}_{2,k}(\Sigma _k^{[j]}|-)&=-(J_k+J_{-k}+\nu _k+1)\log |\Sigma _k|\\ {}&\quad -\text { tr }\Big \{\Sigma _k^{-1}\Big [\xi \Omega _k+({\tilde{{\textbf {Y}}}}^{k}\\ {}&\quad -\varvec{\Phi }_k{\tilde{{\textbf {X}}}}^{k})({\tilde{{\textbf {Y}}}}^{k}-\varvec{\Phi }_k{\tilde{{\textbf {X}}}}^{k})^{'}\Big ]\Big \}\\ {\mathcal {Q}}_{3,k}(\theta _k^{[j]}|-)&=(|\varvec{\gamma }_k|+\alpha _k-1)\log (\theta _k)\\ {}&\quad +(n_k-|\varvec{\gamma }_k|+\beta _k-1)\log (1-\theta _k)\\ {\mathcal {Q}}_4(\xi ^{[j]}|-)&=\frac{1}{2}\sum _k J_k\nu _k\log (\xi )\\ {}&\quad -\frac{1}{2}\sum _k\text { tr }(\Omega _k\Sigma _k^{-1})\xi +(\eta _1-1)\\ {}&\quad \log (\xi )-\eta _2\xi \end{aligned} \end{aligned} \end{aligned}$$

Notice that there is an identifiability issue arising from the structure of the MAR. Given the properties of the Kronecker product, if \(\varvec{\Phi }_1,\ldots ,\varvec{\Phi }_K\) are a solution of the problem, so are \(f_1\varvec{\Phi }_1,\ldots ,f_K\varvec{\Phi }_K\), with the condition \(\prod _k f_k=1\). To keep iterations of both the Gibbs and the EMVS stable, we choose \(f_k\) such that the magnitude between the various parameter matrices remains as stable as possible in the following way (see Hoff 2015):

$$\begin{aligned} f_k=\frac{\prod _{l\ne k}||\varvec{\Phi }_l||^{\frac{1}{K}}}{||\varvec{\Phi }_k||^{\frac{K-1}{K}}} \end{aligned}$$
(8)

The same applies for the covariance matrices. We illustrate the complete EMVS estimation procedure in Algorithm 2 in Appendix C.

5 Kronecker GFEVD

Dynamic analysis via Generalized Impulse Response Functions (GIRF) and Generalized Forecast Error Variance Decomposition (GFEVD) can be carried out easily on a variable-by-variable basis. In this context, a modification of the GFEVD (Lanne and Nyberg 2016) obtained from a GIRF (Koop et al. 1996) is appealing, as it has the desired property of unit row sum. Let \(\Lambda =\text{ diag }(\Sigma ^{-1})\), where \(\Sigma =\sigma _3\otimes \Sigma _2\otimes \Sigma _1\). The GFEVD for the vectorized MAR*(P) has the standard form

$$\begin{aligned} \theta _H^{ij}= \frac{\sum _{h=0}^H\textbf{e}_i^{'}\varvec{\Psi }_h\Sigma \Lambda _{jj}^{1/2}\textbf{e}_j}{\sum _{h=0}^H\textbf{e}_j^{'}\varvec{\Psi }_h\Sigma \Lambda \Sigma \varvec{\Psi }_h^{'}\textbf{e}_j}, \end{aligned}$$
(9)

where \(\textbf{e}_i\) is a selection vector. The collection of \(\theta _H^{ij} \in \varvec{\Theta }_H\) is referred to the GFEVD matrix.

Although the MAR estimates interpretable lower dimensional coefficients via the Tucker product, dynamic analysis can be performed through the vectorized form of the model (Chen and Yang 2021). Nevertheless, this leads to a significant loss of information on mode-specific interactions that is masked via the computation of the Kronecker product of the objects of interest. Rather than studying solely variable-by-variable impacts, it is convenient to exploit the enhanced interpretability given by the bi-dimensional structure of the model and decompose the GFEVD into two lower-dimensional matrices representing the K-mode specific GFEVD. Among all possible decompositions of a GFEVD matrix into its mode-specific counterparts, the most reasonable approach given the form of the model is via a Kronecker decomposition

$$\begin{aligned} \varvec{\Theta }_H^C\otimes \varvec{\Theta }_H^I\approx \varvec{\Theta }_H, \end{aligned}$$

where \(\varvec{\Theta }_H^I\in {\mathbb {R}}^{G\times G}\) and \(\varvec{\Theta }_H^C\in {\mathbb {R}}^{N\times N}\) will be, respectively, the country and indicator GFEVD.

We now describe the Kronecker decomposition problem for the GFEVD derived from the MAR model. Recall that, for each forecast horizon, \(\varvec{\Theta }_H\) is a stochastic matrix, having \(\varvec{\Theta }_H\ge \textbf{0}\) and \(\varvec{\Theta }_H{\varvec{1}}_{GN}={\varvec{1}}_{GN}\), where \({\varvec{1}}_{J}\) is a J-dimensional vector of ones. A simple approach to decompose \(\varvec{\Theta }_H\) into \(\varvec{\Theta }_H^C\otimes \varvec{\Theta }_H^I\), so to reflect the indicator and country GFEVD structure is to project \(\varvec{\Theta }_H\) onto the space of Kronecker products under the squared Frobenius norm

$$\begin{aligned} \min _{\varvec{\Theta }_H^{V}, \varvec{\Theta }_H^C} \quad ||\varvec{\Theta }_H- \varvec{\Theta }_H^{C}\otimes \varvec{\Theta }_H^I||^2_F, \end{aligned}$$

which represents a Nearest Kronecker Product (NKP) problem in matrix computation (Van Loan and Pitsianis 1993; Van Loan 2000). This approach is also at the basis of the projection method for MAR estimation (Chen and Yang 2021), which can be used to find the starting values of the ML procedure given a VAR estimate.

However, the two resulting matrices minimizing this problem are not guaranteed to be stochastic as well, a necessary condition to constitute GFEVD. Thus, in order to get the best stochastic Kronecker Product (SKP) approximation \(\varvec{\Theta }_H^{C}\) and \(\varvec{\Theta }_H^I\), the following constrained nonlinear least squares must be solved:

$$\begin{aligned} \begin{aligned} \min _{\varvec{\Theta }_H^I, \varvec{\Theta }_H^C} \quad&||\varvec{\Theta }_H- \varvec{\Theta }_H^{C}\otimes \varvec{\Theta }_H^I||^2_F\\ \text {s.t.} \quad&\varvec{\Theta }_H^I\ge \textbf{0}, \hspace{2mm} \varvec{\Theta }_H^I{\varvec{1}}_G={\varvec{1}}_G \\&\varvec{\Theta }_H^{C}\ge \textbf{0}, \hspace{2mm} \varvec{\Theta }_H^{C}{\varvec{1}}_N={\varvec{1}}_N.\\ \end{aligned} \end{aligned}$$
(10)

Notice that all the entries in \(\varvec{\Theta }_H^{C}\otimes \varvec{\Theta }_H^I\) are the same as all the entries in \(\varvec{\theta }_H^I\varvec{\theta }_H^{C'}\), where \(\varvec{\theta }_H^I=\text{ vec }(\varvec{\Theta }_H^I)\) and \(\varvec{\theta }_H^{C}=\text{ vec }(\varvec{\Theta }_H^{C})\), i.e. the matrices have the same set of elements, which only differ in their positions. By employing a rearrangement operator \({\mathcal {G}}(\cdot )\) such that \({\mathcal {G}}(\textbf{X}\otimes \textbf{Y})=\text{ vec }(\textbf{Y})\text{ vec }(\textbf{X})^{'}\), we can rewrite Eq. (10) as:

$$\begin{aligned} \begin{aligned} \min _{\varvec{\theta }_H^I, \varvec{\theta }_H^{C}} \quad&||{\mathcal {G}}(\varvec{\Theta }_H)- \varvec{\theta }_H^I\varvec{\theta }_H^{C'}||^2_F\\ \text {s.t.} \quad&\varvec{\theta }_H^I\ge \textbf{0}, \hspace{2mm} \textbf{R}_I\varvec{\theta }_H^I={\varvec{1}}_G \\&\varvec{\theta }_H^{C}\ge \textbf{0}, \hspace{2mm} \textbf{R}_C\varvec{\theta }_H^{C}={\varvec{1}}_N\\ \end{aligned} \end{aligned}$$
(11)

where \(\textbf{R}_I=[\textbf{I}_G,\ldots ,\textbf{I}_G]\) and \(\textbf{R}_C=[\textbf{I}_N,\ldots ,\textbf{I}_N]\) are linear equality constraint matrices of dimension \([G\times G^2]\) and \([N\times N^2]\). As it is expressed, the problem in Eq. (11) can be solved for \(\varvec{\theta }_H^I\) and \(\varvec{\theta }_H^{C}\) iteratively via standard constrained minimization routines.

6 Simulations

We design two simulation experiments. The first one is aimed at studying the small sample efficiency of the proposed method. The second one evaluates the estimation error, forecasting performance, and computational time of our proposed approach, relative to multiple existing estimation methods for longitudinal data. We further perform a comparative convergence analysis of the MCMC in Sect. 6.3.

We set our hyperparameters as follows:

  • \(\tau _0=0.01\), \(\tau _1=4\). This choice is motivated by the fact that all the parameters we consider in our specifications are strictly lower than 1 in terms of magnitude. Thus, it is reasonable to consider a variance of 0.01 as “small”, and a variance of 4 as “big”.

  • \(\Omega _k=\textbf{I}_{J_k}/J_k\), \(\nu _k=J_k+2\). This is standard in the VAR literature (Bańbura et al. 2010), being a combination that ensures minimal assumptions, but at the same time the existence of the expected value of the Inverse Wishart.

  • \(\alpha _k=1\), \(\beta _k=J_k-1\), \(\nu _1=1\). This choice has been recommended to obtain optimal posterior concentration rates in sparse settings (Ročková and George 2014; Castillo and van der Vaart 2012).

In the second experiment, we run all the Gibbs samplers for 1000 iterations. Given a confidence level of 0.05, this number is bigger than the minimum effective sample size (mESS) at a tolerance of 0.05, in the largest scenario, i.e. the one where \((G,N)=(8,10)\) (Vats et al. 2019). Details on the convergence of the sampler of our proposed model can be found in Appendix D.4.

6.1 Small sample efficiency

We compare the small sample efficiency of ML and MAP estimators by letting the length of the time series T and the level of sparsity in the autoregressive coefficients vary. The main purpose of this experiment is to obtain qualitative understanding of the small sample covariances of the two estimators under different sparsity settings. We compare the MAP against the ML estimator for two main reasons, other than its computational convenience. Firstly, given that the MAP can be also seen as s frequentist regularized procedure, it is allegedly a fair competitor to the ML estimator. Secondly, in the comparison we focus on point estimates. In this setting, MAP and median or mean of the posterior distribution of the Gibbs sampler would give pretty similar results.

To this aim, we simulate our synthetic data as follows. We generate matrix-valued time series observations from a MAR(1) with dimensions \(G,N=8\), with different lengths of the time series \(T=50,\ldots ,1000\). We place true nonzero loadings in the left and right model coefficient matrices according to four different settings. For each setting \(i=1,\ldots ,4\), we place \(SP_i\) non-zero coefficients for each row of \(\textbf{A}\) and \(\textbf{B}\), respectively. In particular, we consider \(SP_1=1, SP_2=2, SP_3=4\), and \(SP_4=8\). Our data generating process (DGP) is such that the main diagonal blocks of \(\textbf{A}\) and \(\textbf{B}\) are \([SP_i \times SP_i]\) matrices whose elements are drawn from a \({\mathcal {N}}(0,1)\), and zero otherwise. Notice that when \(i=1\) and \(i=4\) the two coefficient matrices are diagonal (1 out of 8 nonzero coefficient in each row) and full (8 out of 8 nonzero coefficient in each row), respectively. In the two intermediate cases, we have, respectively, 2 out of 8 (for \(i=2\)) and 4 out of 8 (for \(i=3\)) non-zero coefficient in each town of the coefficient matrices. The covariance matrices are set to \(\Sigma _1=\textbf{I}_G\) and \(\Sigma _2=\textbf{I}_N\). In setting our priors, we fix \(\alpha _k=1\), and choose \(\beta _k=J_k-1\) so to reflect a prior belief of a sparse DGP as the one in setting 1. Estimation errors are measured by the mean squared error (MSE):

$$\begin{aligned} MSE({\hat{\varvec{\Phi }}})=\frac{\text{ tr }\big [(\varvec{\Phi }-{\hat{\varvec{\Phi }}})^{'}(\varvec{\Phi }-{\hat{\varvec{\Phi }}})\big ]}{G\times N} \end{aligned}$$
(12)

where for the MAR model \(\varvec{\Phi }=\textbf{B}\otimes \textbf{A}\) and \({\hat{\varvec{\Phi }}}={\hat{\textbf{B}}} \otimes {\hat{\textbf{A}}}\).

Figure 3 illustrates a comparison of the small sample efficiencies of the ML and MAP estimators, as measured by the average estimation errors over 50 repetitions of \(MSE({\hat{\varvec{\Phi }}})\). The figure shows a decreasing trend of the average error of both estimators as T grows. As expected, given the imposed prior beliefs, the more sparse the DGP, the more the MAP estimator results in a higher efficiency in small samples. This is magnified in setting 1 (DGP with diagonal coefficient matrices), while the difference in efficiency between the two estimators gradually vanishes as the number of non-zero coefficients grow. Notice however that, even in setting 4 (DGP with full coefficient matrices) the efficiency of the two estimators is still comparable.

Fig. 3
figure 3

Comparison of the efficiencies of ML (red) and MAP (blue) estimators over 50 repetitions for \(T=50,\ldots ,1000\) under four sparsity settings. The figure shows the logarithm of the \(MSFE({\hat{\varvec{\Phi }}})\) (y axis) over different T (x axis). Gray shaded areas represent the 1 standard deviation confidence bounds

Full size image
Fig. 4
figure 4

The figure shows the median posterior of \(\theta _1\) (red lines), \(\theta _2\) (blue lines), and the true proportion of non-zero coefficients (black lines) over 50 repetitions for \(T=50,\ldots ,1000\) (x axis) under four sparsity settings

Full size image

The efficiency of the MAP estimator depicted in Fig. 3 proves the capacity of our model to retrieve the true DGP across different sparsity settings. The gain is evident in small T and sparse scenarios, where the model outperforms the plain vanilla ML, bearing in mind that the latter is a special case of our model with an apriori fixed \(\gamma _{i,k}=1\). This, in turn, implies that the superior performance depends on the capacity of the model to shrink towards the true zero coefficients, as expected. Another way to look at this evidence is via \(\theta _1\) and \(\theta _2\), whose posterior distributions provide information on the level of sparsity predicted by the model, as a function of the prior and the data.

As for the efficiency factor, we now represent in Fig. 4 the posterior median of \(\theta _1\) and \(\theta _2\), under four different settings. Results are averaged over the 50 replications. The black lines represent the true proportion of nonzero coefficients in \(\textbf{A}\) and \(\textbf{B}\), whereas the blue and red ones are the median of the posterior distribution of \(\theta _1\) and \(\theta _2\), respectively. In all of the four cases, the two coefficients are increasing for the lowest values of T, and then tend to stabilize. This is in line with the fact that with small T, the noise is high, and thus the signal-to-noise ratio drops, inducing the model to consider as non-significant more coefficients. What emerges is that two coefficients lie above the true value in the first two settings. However, such deviation is relatively small in terms of magnitude, being lower than 5%. The third setting is the best captured by the model, which very well replicates the features of the DGP. In the last case, all the coefficients are nonzero, and the model slightly underestimates the real sparsity pattern. However, this is not a matter of concern.

A possible explanation is that the higher the number of nonzero parameters, the lower is their overall magnitude, imposed to ensure stationarity. Thus, it is reasonable that the model might underestimate the true sparsity pattern in this fully dense specification. It might tend to assign zeros where a real 0 is not present, but the overall magnitude of these coefficients is still minimal. This is confirmed by the forecast performance presented above, which is in line with the ML. Recall that the more rigid ML always implies \(\theta _1=\theta _2=1\), even in highly sparse settings. Our model scales pretty well with different levels of sparsity, thus emerging as a valid alternative model to large MAR.

6.2 Comparative estimation, forecasting and computational performances

We aim to compare the estimation error, forecasting performance, and computation time of the illustrated estimators with other relevant competing alternatives for panel data. This is done for different choices of the matrix dimensions \((G,N)=(2,3),(4,6),(8,10)\), so setup a “small”, a “medium” and a “large” setting, relative to a reference sample size \(T=100\). We consider the three MAR estimators: ML, MCMC (Bayes), and MAP. The alternatives considered are the stacked VAR estimator (VAR), the country-block panel VAR (CB), the cross-sectional Shrinkage (CC) approach of Canova and Ciccarelli (2009, 2013), and the Stochastic Search Specification Selection (SSSS) of Koop and Korobilis (2016). In particular, the stacked VAR and the country-block PVAR are estimated with frequentist techniques, whereas the others with a Bayesian approach. We briefly describe the competing alternative models in Appendix D.1 along with the hyperparameter specification for the Bayesian ones in Appendix D.2.

We simulate a sparse VAR(1) able to reflect recurrent patterns in multi-country and multi-variable applications. Let \(\mathbf {\Xi }\) be the \([GN\times GN]\) matrix of autoregressive coefficients and \(\mathbf {\Xi }_{i,j}\in \Xi \) be the \([G\times G]\) country j block of parameters in the country i equations, and consider its entries related to the indicators k, l:

$$\begin{aligned} \mathbf {\Xi }_{i,j}^{k,l}= {\left\{ \begin{array}{ll} \lambda \lambda _n^{|i-j|}\lambda _g^{|k-l|} \hspace{4mm} \text{ if } \hspace{2mm} |i-j|\le r, |k-l|\le r \\ 0 \hspace{23mm} \text{ otherwise }, \end{array}\right. } \end{aligned}$$

where \(\lambda =0.95\) is an overall constant term, \(\lambda _n\) and \(\lambda _g\) are a country and an indicator penalty term, respectively, such that \(\lambda _n=0.5+{\mathcal {U}}_{[-0.1,0.1]}\) and \(\lambda _g=0.5+{\mathcal {U}}_{[-0.1,0.1]}\), and \(r=2\). The DGP is able to reflect heterogeneities in both dimensions such that coefficients are affected by a country penalty \(\lambda _n\), an indicator penalty \(\lambda _g\) and both of them combined. Such penalties act when the row and column distances \(|i-j|\) and \(|k-l|\) of the elements of the matrix \(\mathbf {\Xi }_{i,j}^{k,l}\) do not exceed the threshold level r.

Estimation errors of the models are measured by the MSE as in Eq. (12), whereas the forecasting performance for any fixed forecast horizon H is assessed by means of the Mean Squared Forecast Error (MSFE):

$$\begin{aligned} MSFE(H)=\frac{1}{G\times N\times H}\\\sum _{h=1}^{ H}({\hat{\textbf{y}}}_{T+h|T}-\textbf{y}_{T+h})^{'}({\hat{\textbf{y}}}_{T+h|T}-\textbf{y}_{T+h}), \end{aligned}$$

where \({\hat{\textbf{y}}}_{T+h|T}\) is the H-step forecast obtained with information up to the last sample size T.

We illustrate in Fig. 5 numerical results on the model MSE and MSFE related to \(H=1\). When the estimation of some competitor model was infeasible, corresponding results are omitted. We report results related to repeated experiments with \(T=500\) and a sparsity setting generated by \(r=3\) in Appendix D.3.

The proposed estimators, along with ML, tend to overperform all competing alternatives, both in terms of estimation and forecasting performances. The difference in performances becomes more substantial when considering the “large” dimensional setting. Results with \(T=500\) and \(r=3\) are consistent with the expectations that as T grows and true coefficient matrices are less sparse, performance gains compared to a standard VAR diminish in the “small” dimensional setting.

Fig. 5
figure 5

Average estimation error (MSE) (a–c) and 1 step ahead forecasting peformance (MSFE) (d–f) over 50 repetitions of each model for \((G,N)=(2,3),(4,6),(8,10)\) with \(T=100\)

Full size image

We now report the average computational time over 50 repetitions for the three different combination of G and N and \(T=100\) in Table 1. Being the estimators of VAR and CB closed form, their related execution times are naturally the lowest.

As expected, the computational times of MAP are much more favorable than those of the MCMC. The difference between the two lies in the fact that while the MCMC requires thousands of iterations to approximate the joint posterior distribution, the EMVS algorithm reaches convergence fairly quickly, usually in fewer than 100 iterations. Despite this difference, the two have exhibited comparable performances in estimating the autoregressive coefficient and forecasting performances.

Table 1 Average computational times (in seconds) over 50 repetitions for \((G,N)=(2,3), (4,6)\) and (8, 10), with \(T=100\)
Full size table

In our settings, the MCMC is also generally slower than CC, which exploits factors to reduce dimensionality, but is much faster than SSSS in “medium” and “large” settings. Further, given the dimensionality reduction achieved by the MAR, computation times of the MCMC grow slower with increasing model parameters than those related to the CC and SSSS estimators. Notice that the computational times of MAP are distinctly lower, not only than those of its full Bayesian counterpart, but also than those related to the CC and SSSS estimators. Notwithstanding this, estimation and forecasting performances of MAP (and, in general, of the two proposed computational methods) are generally superior in high-dimensional settings.

6.3 MCMC output analysis

Here we assess and compare the competing models’ MCMC algorithms based on effective sample size criteria (Vats et al. 2019; Gong and Flegal 2016). This criteria allows us to determine when should sampling stop in order to get reliable parameter estimates. Given a level of confidence \(\alpha \) and tolerance \(\epsilon \), one simple strategy is to run the Markov Chain at least for a number of iterations larger than the minimum Effective Sample Size (mESS) (Vats et al. 2019). The multivariate mESS satisfies

$$\begin{aligned} mESS \ge \frac{2^{2/p}\pi }{[p\Gamma (p/2)]^{2/p}} \frac{\chi ^2_{1-\alpha ,p}}{\epsilon ^2}, \end{aligned}$$
(13)

where p is the number of parameters to be estimated. It should be noticed that mESS is a function of p, \(\alpha \) and \(\epsilon \) and is therefore independent of the Markov chain or the underneath process. This paves the way for model comparison in terms of this quantity.

Notice that the three Gibbs samplers employed are characterized by a different number of parameters p. In particular, for each combination of [G, N] of the simulation study, the Gibbs sampler for the MAR produces, respectively, two chains of dimensions \([G^2 \times MC]\) ( MAR(B1) ) and \([N^2 \times MC]\) ( MAR(B2) ), where MC is the number of clean post burn-in draws. The samplers for the CC and the SSSS procedures produce two chains of dimensions \([GNF \times MC]\) (with \(F<GN\)) and \([G^2N^2 \times MC]\). Moreover, the CC is a factor model, for which the number of factors can differ among datasets, and is sensitive to the statistical method employed to extract the relevant factors. As a consequence, it is not possible to choose a common number of simulations such that the tolerance \(\epsilon \) is kept constant among all settings and models.

However, a possible strategy to overcome this issue is to use Eq. (13) in another way. Instead of choosing a different value of MC for each model and setting, one can set an arbitrarily large level so that it is guaranteed that in all settings at least a minimum pre-determined \(\epsilon \) is reached, and then compare the samplers in terms of tolerance levels. We can determine a model specific estimated ESS, calculated after running the MCMC, and then get the corresponding tolerance level \(\epsilon \) via Eq. (13). Given MC iterations in a Markov chain, the ESS measures the size of an i.i.d. sample with the same standard error. In a multivariate setting, the ESS is given by

$$\begin{aligned} ESS=MC\Bigg (\frac{|\Lambda |}{|\Sigma |}\Bigg )^{1/p}, \end{aligned}$$

where \(\Lambda \) is the sample covariance matrix and \(\Sigma \) is an estimate of the variance of the asymptotic normal distribution. Replacing mESS in Eq. (13) with ESS, we can express the former in terms of the tolerance \(\epsilon \), which can be viewed as a comparison in terms of convergence of the Gibbs sampler. The smaller the minimum effective samples, the larger the tolerance, and hence the smaller the number of simulations required.

A visual comparison of the tolerance level \(\epsilon \) for the three models under the different setting is depicted in Fig. 6. The figure shows that our sampler achieves generally greater tolerance than the analyzed competing alternatives, particularly in high-dimensional settings.

Fig. 6
figure 6

Tolerance \(\epsilon \) over 50 repetitions of each model for \((G,N)=(2,3),(4,6),(8,10)\) with \(T=100\)

Full size image

7 Application: panel of country economic indicators

We now conduct an empirical application of the proposed model to a panel of \(G=9\) world countries, which currently represent approximately the 64% of the world total Gross Domestic Product (GDP): Canada (CA), China (CH), France (FR), Germany (GE), India (IN), Italy (IT), Japan (JP), United Kingdom (UK) and United States (US). We consider quarterly observations of \(N=3\) economic indicators: GDP, Consumer Price Index (CPI) and Short-term Interest Rates (S-IR), all expressed in log differences. The sample ranges from 1980Q1 to 2019Q4 (\(T=162\)). The data is inherently multidimensional, as observations are generated in matrix form, where rows represent indicators and columns countries.

We estimate a fully Bayesian MAR*(3), which yields the full conditional posterior distribution of the parameters of interest. It is a standard procedure to fix an arbitrarily large lag length and then let the algorithm shrink the coefficients (George et al. 2008; Bańbura et al. 2010). By running the model with with several lag specifications (from 1 to 10 lags), we observed a progressively diminishing impact of lagged variables. In particular, three is the shortest number of lags such that the 95% credible interval for the lowest magnitude coefficient (\(\hat{c}_3\) in our case) does not contain zero. Figure 7 displays the posterior distribution of the lag order coefficients \(\hat{c}\) and shows a diminishing pattern of lag impacts over time, albeit still preserving a non negligible impact even for lag three. It is clear how values of the posterior distribution of \(\hat{c}\) decrease with the lag order itself, as one could expect. In Fig. 17 in Appendix D.4 we illustrate the posterior distribution of the mixing proportion parameters \({\hat{\theta }}\).

Fig. 7
figure 7

Posterior distribution of \(\hat{c}_1\) (red), \(\hat{c}_2\) (blue), \(\hat{c}_3\) (green)

Full size image

We illustrate in Fig. 8 the posterior median of the left (\({\hat{\textbf{A}}}\)) and right (\({\hat{\textbf{B}}}\)) coefficient matrices, along with the reconstructed coefficient matrix \({\hat{\textbf{B}}}\otimes {\hat{\textbf{A}}}\). Note that, given that only the Kronecker product \({\hat{\textbf{B}}}\otimes {\hat{\textbf{A}}}\) is uniquely identified, only magnitudes related to the left and right coefficient matrices can be meaningfully interpreted, rather than signs.

The figure shows that, as intuition suggests, the diagonal elements of the parameter matrices concur to a large portion of the system’s autoregressive dynamics. This is more evident from the left coefficient matrix, indicating a strong autocorrelation in the variable dimension. From the first order right coefficient matrix estimate notice that the two largest impacts are those of China on itself and US on Canada. The former can be explained through the relatively low impact of other countries on the Chinese economy as a whole and the latter seems reasonable given the geographical proximity and large trade activity between the two.

Fig. 8
figure 8

Median of the posterior entries of the first order left coefficient matrix \({\hat{\textbf{A}}}\) (a), of the right one \({\hat{\textbf{B}}}\) (b), and of \({\hat{\textbf{B}}}\otimes {\hat{\textbf{A}}}\) (c)

Full size image

We evaluate out-of-sample rolling forecasting performances and computational times of the proposed methods against the same competing models analyzed in Sect. 6.2. In particular, starting from 1995Q1 (T = 60) to 2019Q2 (T = 120), we fit the corresponding models by means of all available data at time \(t-1\) and compute the one step ahead MSFE. Results are summarized in Table 2. Further results related to the full set of estimations as well as the mixing of the Gibbs sampler of our proposed model are in Appendix D.4.

Table 2 Average Logarithm of the MSFE and average computational time (in seconds) over 50 repeated estimations of three different MAR estimators (ML, Bayes, MAP) against competing alternatives
Full size table

Notice that, on average, the MCMC outperforms all competing alternatives in the forecasting exercise, closely followed by the MAP and ML estimators. We then find the SSSS, CB and CC estimators which perform better than the stacked VAR. Despite its superior forecast accuracy, the MCMC method is more than 140 times slower than the EMVS. This might render the latter preferable in high-dimensional empirical applications, given the relatively little differences between the two in terms of performance.

A key advantage of the EMVS procedure relative to standard MCMC is that its lower computational intensiveness allows for dynamic posterior exploration (Ročková and George 2018). This consists of holding fixed at a high value the slab hyperparameter, while letting the spike hyperparameter gradually rise along a ladder of increasing values. In our case, dynamic posterior exploration can also be conducted on the “sparsity” parameters \(\theta _k\).

We therefore perform cross validation on a grid of ten values between 0.005 and 0.05 with a step of 0.005 for the spike parameter \(\tau _0\). Additionally, we let \(\beta _k=J_k^{\zeta }\) vary on a grid of ten values of \(\zeta \) from 0.1 to 1 with step 0.1. By performing dynamic posterior exploration, the average MSFE of the MAP estimator drops to \(2.89 \times 10^{-5}\) (std: \(1.69\times 10^{-5}\)), while preserving a reasonable amount of computation time of 16.81 s (std: 5.86).

We now illustrate the resulting Kronecker decomposition of the estimated GFEVD in Fig. 9. We refer the reader to Appendix D.4 for a graphical representation of the spectrum of the companion matrix. For what concerns \({\hat{\varvec{\Theta }}}_H^I\), a contribution of CPI and GDP to the GFEVD of S-IR is detected. Moreover, the figure shows that a portion of GFEVD in GDP is due to shocks in CPI and S-IR. Notice, however, that overall magnitudes of such cross-variance shares are small if compared to the country and full GFEVD matrices, meaning a weak dependence structure within the indicator dimension.

Fig. 9
figure 9

Kronecker decomposition of the estimated GFEVD: indicator GFEVD \({\hat{\varvec{\Theta }}}_H^I\) (a), country GFEVD \({\hat{\varvec{\Theta }}}_H^{C}\) (b) and full GFEVD \({\hat{\varvec{\Theta }}}_H\) (c). Diagonal elements are omitted

Full size image

Conversely, we find stronger cross-variance shares in the country dimension, as reflected by \({\hat{\varvec{\Theta }}}_H^{C}\). The largest pairwise contributions are those to Canada arising from shocks in the US economy, and vice versa, though with lower magnitude in the latter case. While both China and US are prone to transmit large portions of GFEVD to the rest of the countries, the former is generally more resilient to shocks in other countries. This with the exception of India, which is one of the largest exporters of China. Results also highlight noticeable cross variance shares across the EU countries, i.e. France, Germany and Italy. The full GFEVD matrix \({\hat{\varvec{\Theta }}}_H\) reflects instead variable by variable interactions, which seem consistent with the ones obtained through the Kronecker decomposition problem.

8 Concluding remarks

We developed a Bayesian method for variable selection in high-dimensional matrix autoregressive models which reflects and exploits the original matrix structure of data to reduce dimensionality and foster interpretability of multidimensional dependency structures. We firstly derived a compact form of the model stemming from the tensor linear regression framework, which facilitates the model estimation. We then outlined two computational methods: a fully Bayesian MCMC algorithm and an EMVS estimation procedure, which foresees the forthcoming need of modeling matrix-valued time series at large scales, while allowing for fast dynamic posterior exploration.

We have numerically investigated the small sample efficiency of the proposed estimators, showing the gain with respect to ML in sparse, high-dimensional settings. We have also numerically explored the comparative estimation, forecasting and computational performances of the proposed estimators relative to key competing alternative models for longitudinal data. The experiment has shown that the estimation and forecasting performances of the Bayesian and MAP estimators are generally superior in sparse high-dimensional settings, with the latter drastically reducing computational intensiveness. The proposed methodology has been applied to a panel of nine world countries’ economic indicators, for which we derived a method to decompose the GFEVD into its row and column dimensions, leading to country and indicator GFEVDs.

Our proposed method can be extended in several directions. The model can be easily generalized to a tensor autoregressive framework. Simultaneous sparsity both in the autoregressive coefficients and innovation covariance matrices can be introduced. Otherwise, the model can be equipped with different types of priors, e.g. those belonging to the class of global–local priors (Polson et al. 2011).

Furthermore, time variation can be embedded into the model. This also paves the way to the introduction of time varying parameter matrix autoregression with stochastic volatility (see Nakajima 2011), dynamic sparse factor matrix autoregressions (Rockova and McAlinn 2021), and dynamic covariance matrix estimation and prediction (Bucci et al. 2022).