Extreme value modeling with errors-in-variables in detection and attribution of changes in climate extremes

Abstract

The generalized extreme value (GEV) regression provides a framework for modeling extreme events across various fields by incorporating covariates into the location parameter of GEV distributions. When the covariates are subject to errors-in-variables (EIV) or measurement error, ignoring the EIVs leads to biased estimation and degraded inferences. This problem arises in detection and attribution analyses of changes in climate extremes because the covariates are estimated with uncertainty. It has not been studied even for the case of independent EIVs, let alone the case of dependent EIVs, due to the complex structure of GEV. Here we propose a general Monte Carlo corrected score method and extend it to address temporally correlated EIVs in GEV modeling with application to the detection and attribution analyses for climate extremes. Through extensive simulation studies, the proposed method provides an unbiased estimator and valid inference. In the application to the detection and attribution analyses of temperature extremes in central regions of China, with the proposed method, the combined anthropogenic and natural signal is detected in the change in the annual minimum of daily maximum and the annual minimum of daily minimum.

1 Introduction

Extreme events arise in many fields and often have catastrophic impacts. Examples include extreme weather (Field et al. 2012), natural hazards (Hamdi et al. 2021), and market crashes (Nolde and Zhou 2021). Statistical methods for prediction and inference in analyzing extreme events need to account for their unique distributional characteristics. The generalized extreme value (GEV) distribution is the natural choice as the limiting distribution of sample maximum (Fisher and Tippett 1928). Covariates can be incorporated into the location parameter to predict extreme events or understand the behavior of extreme observations (Coles et al. 2001). Such GEV regression models have been widely used in an enormous variety of applications (Smith 1989; Wang et al. 2004; Huerta and Sansó 2007; Hyun et al. 2019).

The validity of GEV regression analyses depends on a critical assumption that there is no errors-in-variables (EIV) or measurement error in the data. This assumption may be violated in many applications, such as the detection and attribution analyses in the context of climate extremes (see Sect. 3). One major tool for the detection and attribution analyses is fingerprinting, which was first introduced to study changes in mean climate conditions (e.g., mean temperature) (Hasselmann 1993; Hegerl et al. 1996; Allen and Stott 2003), and later extended to extreme climate conditions (Zwiers et al. 2011; Wang et al. 2017, 2021). The fingerprinting method fits a GEV distribution to the observed extremes and takes the fingerprints of external forcings of interest as covariates in the location parameters. The fingerprint, or signal, of a particular external forcing, is not observed but estimated from climate-model-simulated extremes, which introduces errors (i.e., EIV) and causes bias in the resulting estimator of the coefficients of the fingerprints (Wang et al. 2021).

Despite the voluminous literature on EIV issues in other regression settings, it has been rarely studied in GEV regressions even for independent data, let alone for time series or spatiotemporal data. The main challenge owes to the complex structure of GEV distribution, which prevents a straightforward extension of many methods. In the context of the fingerprinting, for example, though the EIV issue has been solved in the mean climate models under a linear regression setting by total least squares (Allen and Stott 2003), integrated likelihood (Hannart 2016), and Bayesian model averaging (Katzfuss et al. 2017), none of these approaches can be applied to the extremes setting in a relatively straightforward manner. In fact, the bias issue in GEV modeling has been explicitly raised but left unsolved (Wang et al. 2021). Additionally, the correlation in the measurement errors further complicates the problem. Among a wide range of applications of GEV modeling of spatiotemporal data, the EIVs are likely dependent. One example is again the fingerprinting with time series, where the signals are most likely to be temporally dependent as the parameters in the signals are often shared over time.

A promising approach to GEV regression with EIV is the corrected-score method (Nakamura 1990). In principle, this method constructs a corrected score equation whose expectation conditional on the contaminated covariates is the same as the original score equations evaluated at the true covariates. It is attractive because, as a functional approach, it does not require any distributional specification of the covariates as some approaches do. Given the complex expressions of the score functions under the GEV regression, which can be derived from the score functions of GEV distribution (Prescott and Walden 1980) using the chain rule, such construction is challenging because the expectations of the score functions in terms of the contaminated covariates have no closed forms, which prohibits closed-form corrections. The Monte Carlo corrected scores (MCCS) method, however, is well suited for the situation. It approximates the expectations of the score functions in terms of the contaminated covariates by Monte Carlo integration, which facilitates corrected scores (Novick and Stefanski 2002).

Our contributions are two-fold. First, as the first attempt to address the EIV issue in GEV modeling using a functional approach, we propose an MCCS-based approach and extend it to the settings where the EIVs are temporally dependent as in fingerprinting applications. We further develop a small-sample correction to the sandwich variance estimator. This is practically important because the record lengths of extremes are usually insufficient for the variance estimator to work well. Simulation studies show that the proposed method corrects the bias in estimating all the model parameters, especially the regression coefficients in the location parameter. The coverage rates of the confidence intervals based on our corrected sandwich variance estimator are acceptable. Our second contribution is an application of the methods to the detection and attribution analyses of changes in temperature extremes. The method accounts for the fact the unobserved signals are estimated from climate model simulations under the corresponding forcings. In applications we demonstrate the validity of the method via simulation studies that mimic the fingerprinting setting and real data.

The rest of the paper is organized as follows. Section 2 provides the MCCS framework under the GEV setting for both independent and temporally dependent EIVs. Section 3 adapts the method to the specific setting of fingerprinting for climate extremes in detection and attribution analyses. The methods are validated in simulation studies with both independent extremes and fingerprinting settings in Sect. 4. Section 5 reports an application to detection and attribution analyses of changes in temperature extremes in central China. A discussion concludes in Sect. 6.

2 Methodology

2.1 Statistical model

Consider GEV modeling with a regression setting for the location parameter. Let $F(\cdot \mid \mu , \sigma , \xi )$ denote a GEV distribution function with location $\mu$, scale $\sigma$, and shape $\xi$, and $Y_t$ be observed extreme with p-dimensional error-prone covariates $X_t$ and q-dimensional accurate covariates $Z_t$ for $t = 1, \ldots , n$. Suppose that $Y_t$ follows a GEV distribution with a location parameter that incorporates covariate effects. In particular,

$$\begin{aligned} Y_t \sim F(\cdot \mid \mu _t, \sigma , \xi ), \qquad \mu _t = Z_t^\top \alpha + X_t ^\top \beta , \end{aligned}$$

(1)

where $\alpha$ and $\beta$ are q- and p-dimensional regression coefficients, respectively. An intercept term is included in $\alpha$ by including a one in $Z_{t}$. The parameters of interest are $\theta = (\alpha , \beta , \sigma , \xi )$.

Assumption 1

When $X_t$ is observed, there exists an unbiased estimating function $\psi (Y_t, X_t, Z_t, \theta )$ with parameters $\theta$ such that

$$\begin{aligned} E\{\psi (Y_t, X_t, Z_t, \theta ) \mid X_t, Z_t\} = 0, \ \ t = 1,\ldots ,n. \end{aligned}$$

Then, the parameter $\theta$ can be estimated consistently by solving

$$\begin{aligned} \sum _{t=1}^n \psi (Y_t, X_t, Z_t, \theta ) = 0. \end{aligned}$$

By fulfilling Assumption 1, the score function $\psi (Y_t, X_t, Z_t, \theta )$ of GEV loglikelihood is an unbiased estimating function, where

$$\begin{aligned} \psi (Y_t, X_t, Z_t, \theta ) = \begin{pmatrix} Z_t f_1(Y_t; \mu _t, \sigma , \xi )\\ X_t f_1(Y_t; \mu _t, \sigma , \xi )\\ f_2(Y_t; \mu _t, \sigma , \xi )\\ f_3(Y_t; \mu _t, \sigma , \xi )\\ \end{pmatrix}, \end{aligned}$$

(2)

and $f_1$, $f_2$, and $f_3$ are the partial derivatives of the log density of $F(\cdot \mid \mu , \sigma , \xi )$ with respect to $\mu$, $\sigma$, and $\xi$, respectively, with specific expressions given in Appendix A (Prescott and Walden 1980). The maximum likelihood estimator (MLE) for $\theta$ can be obtained by solving the score equation $\sum _{t = 1}^n \psi (Y_t, X_t, Z_t, \theta ) = 0$. For $\xi > -0.5$, $\psi (Y_t, X_t, Z_t, \theta )$ has expectation zero and finite second moments (Smith 1985; Bücher and Segers 2017).

In situations where instead of $X_t$, a surrogate version $W_t$ is observed, substituting $X_t$’s directly with $W_t$ in estimating function (2) leads to a biased estimator of $\theta$. The magnitude of the bias depends on the measurement error specification. Assume that

$$\begin{aligned} W_t = X_t + e_t, \quad t = 1, \ldots , n, \end{aligned}$$

(3)

where the p-dimensional measurement error $e_t$, independent of $X_t$ and $Y_t$, is normally distributed with mean zero and covariance matrix $\Sigma _t$.

Assumption 2

When $X_t$ is not observed, there exists a corrected score function of the observed data such that for $t = 1, \dots , n$,

$$\begin{aligned} E\{\tilde{\psi }(Y_t, W_t, Z_t, \theta ) \mid (Y_t, X_t, Z_t)\} = \psi (Y_t, X_t, Z_t, \theta ). \end{aligned}$$

(4)

Based on Assumptions 1–2, we seek a corrected score function $\tilde{\psi }(Y_t, W_t, Z_t, \theta )$, which is conditionally unbiased given the observed quantities and results in estimating equations

$$\begin{aligned} \sum _{t=1}^n\tilde{\psi }(Y_t, W_t, Z_t, \theta ) = 0. \end{aligned}$$

While the corrected scores for some common families like normal and Poisson are available in a closed-form (Nakamura 1990), it is hard to obtain that of the GEV distribution because of its nonlinear and complicated structure. Therefore, we resort to the MCCS method developed by Novick and Stefanski (2002), where the conditional expectation in (4) is approximated by Monte Carlo integration. This method is relatively robust and can yield satisfying results in certain settings even when the normality assumption of $e_t$ is violated.

A further complication in practice, however, is that the measurement errors $e_t$’s in GEV could be correlated in various ways. For instance, in fingerprinting applications, the fingerprint or signal of an external forcing cannot be observed but is generally estimated from climate model simulations. The measurement errors $e_t$’s could be temporally correlated over time and we denote the covariance matrix for $e^\top =(e_1^\top ,\ldots ,e^\top _n)^\top$ as $\Sigma$. This brings an additional complexity compared to the classical MCCS approach in Novick and Stefanski (2002). In the sequel, we address this issue after dealing with independent EIVs.

2.2 MCCS for GEV regression with independent EIV

First, we illustrate the MCCS method for GEV regression under the assumption that measurement error $e_t$’s are mutually independent for $t = 1,\ldots ,n$. Let $\epsilon _{b,t}$ be the bth Monte Carlo copy generated from $N(0, \Sigma _t)$, where $\Sigma _t$ is the variance matrix for $e_t$, $t = 1,\ldots ,n$. The complex variates are constructed as $\widetilde{W}_{b,t} = W_t+ \iota \epsilon _{b,t}$ for $b = 1, \ldots , B$, where B is a large integer and $\iota = \sqrt{-1}$. Then, the following Lemma was established by Novick and Stefanski (2002).

Lemma 1

(Novick and Stefanski 2002) When the measurement error $e_t$’s are mutually independent, under integrability conditions and the assumption that $\psi (Y_t, X_t, Z_t, \theta )$ is an entire function of $X_t$ in the complex plane,

$$\begin{aligned}&E\{\psi (Y_t, \widetilde{W}_{b,t}, Z_t, \theta ) \mid (Y_t, X_t, Z_t)\}\\&\quad = E[\Re \{\psi (Y_t, \widetilde{W}_{b, t}, Z_t, \theta ) \} \\&\qquad \mid (Y_t, X_t, Z_t)] \\&\quad = \psi (Y_t, X_t, Z_t, \theta ), \end{aligned}$$

where $\Re (\cdot )$ is the real part of a complex number.

Consequently, $\Re \{\psi (Y_t, \widetilde{W}_{b, t}, Z_t, \theta ) \}$ is a corrected score based on a randomly generated random vector $\epsilon _{b,t}$. Then, we use Monte Carlo integration to approximate the conditional expectation as

$$\begin{aligned} \tilde{\psi }_B (Y_t, W_t, Z_t, \theta , \Sigma _t) = \frac{1}{B} \sum ^B_{b = 1} \Re [\psi (Y_t, \widetilde{W}_{b, t}, Z_t, \theta )], \end{aligned}$$

(5)

with its specific form in GEV provided in Appendix A. As $B \rightarrow \infty$, the MCCS converges to the exact conditional expectation (Novick and Stefanski 2002). The MCCS estimator $\tilde{\theta }_{n,B}$ solves the estimating equations

$$\begin{aligned} \sum _{t = 1}^n \tilde{\psi }_B (Y_t, W_t, Z_t, \theta , \Sigma _t) = 0. \end{aligned}$$

In practice, $\Sigma _t$ is unknown and needs to be replaced with a consistent estimator in the above derivation. We provide more details on estimating $\Sigma _t$ in Sect. 3. Let $\theta _0$ be the true value of $\theta$. When ($Y_t$, $W_t$) are mutually independent for $t = 1, \dots , n$, and $\tilde{\psi }_B(Y_t, W_t, Z_t, \theta , \Sigma _t)$ and $\psi (Y_t, W_t, Z_t, \theta ,\Sigma _t)$ are differentiable, there exists a consistent estimator for $\theta$ by solving $\sum _{t = 1}^n \tilde{\psi }_B (Y_t, W_t, Z_t, \theta , \Sigma _t) = 0$ (Nakamura 1990). The solution can be obtained via nleqslv (Hasselman 2018), a nonlinear equation solver package in R.

Proposition 1

Under certain regularity conditions, with $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n}(\tilde{\theta }_{n,B} - \theta _0)\rightarrow N(0, V_{\widetilde{\psi }}), \end{aligned}$$

where $V_{\widetilde{\psi }} = D^{-1}C(D^{-1})^\top$, $C = E[\tilde{\psi }_B(Y_t, W_t, Z_t, \theta , \Sigma ) \tilde{\psi }_B^\top (Y_t, W_t, Z_t, \theta , \Sigma _t)]$ and $D =E[(\partial / \partial \theta ^\top ) \tilde{\psi }_B(Y_t, W_t, Z_t, \theta , \Sigma _t)].$ The asymptotic variance $V_{\widetilde{\psi }}$ is consistently estimated by a sandwich formula estimator $\widetilde{V}_{n, \widetilde{\psi }} = \widetilde{D}_{n, \widetilde{\psi }}^{-1} \widetilde{C}_{n, \widetilde{\psi }} (\widetilde{D}_{n, \widetilde{\psi }}^{-1})^\top$, where

$$\begin{aligned} \widetilde{D}_{n, \widetilde{\psi }} = \frac{1}{n}\sum _{t=1}^n \frac{\widetilde{\psi }_B (Y_t, W_t, Z_t, \theta , \Sigma _t)}{\partial \theta ^\top } \Big \vert _{\theta = \tilde{\theta }_{n,B}}\end{aligned}$$

and

$$\begin{aligned} \widetilde{C}_{n, \widetilde{\psi }} = \frac{1}{n}\sum _{t=1}^n\widetilde{\psi }_B (Y_t, W_t, Z_t, \tilde{\theta }_{n,B}, \Sigma _t) \widetilde{\psi }_B^\top (Y_t, W_t, Z_t, \tilde{\theta }_{n,B}, \Sigma _t). \end{aligned}$$

The proof based on standard estimating equation theory is outlined in Appendix B.1.

2.3 MCCS for GEV regression with temporally dependent EIV

In many GEV applications, such as the fingerprinting set-up, measurement error $e_t$’s could be temporally correlated (Wang et al. 2021). Here we explain how to adapt the aforementioned MCCS approach to time-dependent EIV. To construct Monte Carlo replicates $\widetilde{W}^*_{b,t} = W_t+\iota \epsilon _{b,t}^*$, we propose to generate $\epsilon ^*_{b, t}$ as part of $\epsilon ^{*\top } _b= (\epsilon _{b,1}^{*\top },\ldots ,\epsilon _{b,n}^{*\top })^\top$ from $N\left( 0, \Sigma \right)$. Ideally, one would expect to construct corrected scores based on $Y^\top = \left( Y_1^\top ,\ldots ,Y_n^\top \right) ^\top$, $W^\top = \left( W_1^\top ,\ldots ,W_n^\top \right) ^\top$ and $Z^\top = \left( Z_1^\top ,\ldots ,Z_n^\top \right) ^\top$ to incorporate the temporal correlations. Such practice can be difficult or undesired for GEV modeling as the temporal dependence may be hard to specify. As $\theta$ is assumed to be shared across n years, we again consider the corrected score based on each year t as in Eq. (5) and obtain the unbiased estimator $\tilde{\theta }_{n,B}$. Though the estimating equation is constructed at each time point, the validity of the approach is stated in Proposition 1.

Lemma 2

Assume that $\psi (Y_t, X_t, Z_t, \theta )$ is an entire function of $X_t$ in the complex plane, and that measurement error $e^\top = (e_1^\top ,\ldots ,e_n^\top )^\top$ are temporally correlated with covariance matrix $\Sigma$. With $\epsilon ^{*\top } _b\sim N(0,\Sigma )$, the following equations still hold:

$$\begin{aligned}&E\{\psi (Y_t, \widetilde{W}_{b,t}^*, Z_t, \theta ) \mid (Y_t, X_t, Z_t)\} \\&= E[\Re \{\psi (Y_t, \widetilde{W}^*_{b, t}, Z_t, \theta ) \} \\&\mid (Y_t, X_t, Z_t)]= \psi (Y_t, X_t, Z_t, \theta ). \end{aligned}$$

This Lemma is based on representing $\psi$ as a multivariate power series and then applying Lemma 4 from Stefanski and Cook (1995). More details can be found in the Appendix B.3.

Then, we define

$$\begin{aligned} \tilde{\psi }^*_B (Y_t, W_t, Z_t, \theta , \Sigma ) = \frac{1}{B} \sum ^B_{b = 1} \Re [\psi (Y_t, \widetilde{W}^*_{b, t}, Z_t, \theta )], \end{aligned}$$

(6)

and the MCCS estimator $\tilde{\theta }^*_{n,B}$ solves the estimating equations

$$\begin{aligned} \sum _{t = 1}^n \tilde{\psi }^*_B (Y_t, W_t, Z_t, \theta , \Sigma ) = 0. \end{aligned}$$

(7)

Again, the R package nleqslv can be used to solve Equation (7).

Proposition 2

Under certain regularity conditions, with $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n}(\tilde{\theta }^*_{n,B} - \theta _0)\rightarrow N(0, V_{\widetilde{\psi }^*}), \end{aligned}$$

where $V_{\widetilde{\psi }^*} = D^{*-1}C^*(D^{*-1})^\top$, $C^* = \textrm{Var}\{n^{-1/2}\sum _{t=1}^n\tilde{\psi }_B^*(Y_t, W_t, Z_t, \theta , \Sigma )\}$. and $D^* =E[(\partial / \partial \theta ^\top ) \tilde{\psi }^*_B(Y_t, W_t, Z_t, \theta , \Sigma )].$ The asymptotic variance $V_{\widetilde{\psi }^*}$ can be estimated consistently as $\widehat{V}_{n, \widetilde{\psi }^*} = \widehat{D}_{n, \widetilde{\psi }^*}^{-1} \widehat{C}_{n, \widetilde{\psi }^*} (\widehat{D}_{n, \widetilde{\psi }^*}^{-1})^\top$, where

$$\begin{aligned} \widehat{D}_{n, \widetilde{\psi }^*} = n^{-1}\sum _{t=1}^n \frac{\widetilde{\psi }_B^* (Y_t, W_t, Z_t, \theta , \Sigma _t)}{\partial \theta ^\top } \Big \vert _{\theta = \tilde{\theta }^*_{n,B}} \end{aligned}$$

and

$$\begin{aligned} \widehat{C}_{n, \widetilde{\psi }^*} = \frac{1}{nB} \left[ \sum _{t, t^\prime =1}^n\sum _{b=1}^B \Re \left\{ \psi (Y_t, \widetilde{W}_{b,t}^*, \theta ^*_{n,B})\psi ^\top (Y_{t^\prime }, \widetilde{W}_{b,t^\prime }^*, \theta ^*_{n,B} )\right\} \right] , \end{aligned}$$

for $t = 1,\ldots ,n$.

The detailed proof is provided in Appendix B.2.

Remark 1

Our work is built upon standard estimating equation theory. There are some sufficient but not necessary conditions for our asymptotic theory to hold as below.

• 1. The parameter space is compact, and there is a unique $\theta$ in the parameter space satisfying $E\{ \tilde{\psi }_B^*(Y_t, W_t, Z_t, \theta ,\Sigma )\} = 0$ for all $t=1,\ldots ,n$.

• 2. The estimating equation (7) has a unique solution.

• 3. The matrix $D^*$ is of full rank within a neighborhood of the true value $\theta _0$. For sufficiently large n, $\widehat{D}_{n, \widetilde{\psi }^*}$ is of full rank with eigenvalues bounded away from 0 and $\pm \infty$ within a neighborhood of the true value $\theta _0$.

Sandwich variance estimators are known to under-estimate the variance for small samples (Mancl and DeRouen 2001; Westgate 2012). A major reason is that the middle matrix $C^*$ is under-estimated. To mitigate the potential underestimation of $\widehat{C}_{n, \widetilde{\psi }^*}$ when the sample size is small, and deal with the time dependency in extreme observations if that exists in the data, we propose a block bootstrap to account for the time dependency in $\widetilde{\psi }_B^*$, rendering an estimate for the variance matrix of $\widetilde{\psi }_B^*$. To create M bootstrap samples, we use the following bootstrap procedure for each $m = 1, \ldots , M$ and $t = 1, \dots , n$:

• 1. Calculate residuals by subtracting $Z_t ^\top \alpha + W_t^\top \beta$ from $Y_t$.

• 2. Group residuals into non-overlapping blocks of samples in specified length with replacement.

• 3. Obtain bootstrapped data $\mathcal {Y}_{m, t}$ by adding the grouped residuals to the $Z_t ^\top \alpha + W_t^\top \beta$.

• 4. Calculate the $\overline{\widetilde{\psi }}_{m, B} = n^{-1}\sum ^n_{t = 1} B^{-1} \sum ^B_{b = 1} \Re [\psi (\mathcal {Y}_{m, t}, \widetilde{W}_{m, b, t}^*, Z_t, \tilde{\theta }_{n, B})]$ for $m = 1, \dots , M$, where $\widetilde{W}^*_{m, b, t}$ is generated for the mth bootstrap sample.

• 5. Determine the covariance matrix of $\overline{\widetilde{\psi }}_{m, B}$ using M samples and multiplying the covariance matrix with n to get $\widehat{C}_{n, \widetilde{\psi }^*}$.

This bootstrap procedure is computationally efficient as it only requires evaluating the outer-products of individual estimating functions instead of solving any estimating equations. Of note, the bootstrap is only used for estimating the middle part of the sandwich estimator. As it does not bootstrap extremes directly, this procedure also avoids some potential issues in sampling extremes (Gilleland 2020), and the confidence intervals of the estimates are still built based on the asymptotic normality.

3 Application in fingerprinting with time series

Fingerprinting in the context of extremes is a direct application of the proposed method. Fingerprinting aims to quantify the impact of external forcings on the climate variable of interest, in which the expected responses of the climate system to external forcings, also called fingerprints, are treated as predictors (Li et al. 2021, 2023). These external forcings can be classified into two types: anthropogenic and natural, which are factors that impact the climate system while not being part of the climate system itself, such as greenhouse gas emissions and volcanic eruptions. The fingerprints are not observable but can be inferred from numerical climate model outputs. Climate models typically contain multiple initial condition ensembles, which, most of the time, can be treated as random independent and identically distributed samples from one multivariate spatial-temporal process due to their sensitivity to the initial conditions (Stein 2020). The estimated signals from these outputs are naturally temporally dependent. Here we limit our scope to a setting with time series data instead of spatiotemporal data; handling spatiotemporal EIVs requires a separate investigation. We investigate this application setting as follows.

Suppose the observed climate extremes $Y_t$ specified in Sect. 2 are available at a particular grid box for year $t = 1, \dots , n$. The climate extremes of interest can be station annual maximum of daily maximum (TXx) and minimum (TNx) temperatures or the annual minimum of daily maximum (TXn) and minimum (TNn) temperatures. The error-prone covariates $X_t$ in Equation (1) are signals of external forcings, and $\beta$ are the corresponding coefficients of the signals. We also assume a constant shape and scale parameters throughout the year at the site, and an intercept is included in the location parameter, which makes $Z_t$ a constant of 1 and $\alpha$ a scalar (Wang et al. 2021; Zwiers et al. 2011).

Since the signal vector $X_{t}$ is unknown, it needs to be estimated from the climate models simulations. Following Zwiers et al. (2011) and Wang et al. (2021), we assume another GEV model for the simulated climate extremes. Let $L_j$ denote the total number of available ensemble runs under the jth forcing from the climate models, and $U_{tj}^{(l)}$ extreme observations for the lth ensemble run under the jth forcing in year t, where $j = 1, \dots , p$, $t= 1, \dots , n$, and $l= 1, \dots , L_j$. The annual extremes $U_{tj}^{(l)}$ can be modeled as follows,

$$\begin{aligned} U_{tj}^{(l)} \sim F(\cdot \mid X_{tj}, \sigma ^\prime _j, \xi ^\prime _j), \qquad X_{tj} = \mu ( t; \gamma _{j}), \end{aligned}$$

(8)

where $\sigma ^\prime _j$ and $\xi ^\prime _j$ are forcing-specific scale and shape parameters, respectively, and $X_{tj}$ is the fingerprint or the signal of forcing j characterized by function $\mu$ with parameter vector $\gamma _j$. To account for the temporal dynamics, a flexible formulation for $\mu$ with B-splines is

$$\begin{aligned} \mu ( t; \gamma _{j}) = S_t^\top \gamma _j\end{aligned}$$

where $S_t = (S_1(t), \dots , S_D(t))^\top$, $S_d(t)$’s are a set of B-splines basis with D degree of freedom, and $\gamma _{j} = (\gamma _{j, 1}, \dots , \gamma _{j, D})^\top$ is the coefficient vector for the basis. The B-spline representation is assumed to be flexible enough to approximate the temporal pattern in signals. With all the ensemble runs under forcing j as independent replicates, we can obtain the MLE $\hat{\gamma }_{j}$ of $\gamma _{j}$ and its covariance matrix $\Sigma _{\gamma _j}$. Therefore, $W_{tj} = \sum _{d = 1}^D \hat{\gamma }_{j, d} S_d(t)$ is an MLE of $X_{tj}$ with covariance matrix $S_t^\top \Sigma _{\gamma _j} S_t$.

Given the B-spline model is correctly specified, using $W_t = (W_{t1}, \dots , W_{tp})^\top$ rather than the true $X_{t}$ introduces additional variability to Equation (1), resulting bias when estimating $\beta$. It has the same effect as EIV and needs to be recognized. This is exactly the unsolved issue raised by Wang et al. (2021), which results in biased estimation. Here the relationship between $X_t$ and $W_t$ is the same as in Equation (3), that is, $W_t = X_t + e_t$. In general, $e_{t}$ and $e_{t^\prime }$ for any $t \ne t^\prime$ are not independent as the variance of $e_{tj}$ and $e_{t^\prime j}$ both depend on $\hat{\gamma }_j$. The covariance of $e_j = (e_{1j}^\top , \dots , e_{nj}^\top )^\top$, can be estimated by $S^\top \Sigma _{\gamma _j}S$ with $S = (S_1^\top , \dots , S_n^\top )^\top$. This fits the situation in Sect. 2.3. For each $j = 1, \ldots , p$, we can generate $\widetilde{W}_{b, j}^\top = (\widetilde{W}_{b, 1j}^\top , \dots , \widetilde{W}_{b, nj}^\top )^\top$ from a multivariate normal distribution with mean $W^\top = (W_{1j}^\top , \dots , W_{nj}^\top )^\top$ and covariance matrix $S^\top \Sigma _{\gamma _j}S$. Since the runs under different forcings are independent, we can generate the Monte Carlo copies separately for each j. Then, $\widetilde{W}_{b, tj}$ for any $t = 1, \dots , n$ and $j = 1, \dots , p$ can be used to construct the corrected score in Equation (6), yielding the unbiased estimates of $\theta$ as explained in Sect. 2.

The coefficients of the fingerprints $\beta$, also known as scaling factors, are the primary target of the inference. To account for the time dependency in the measurement error, we rely on the block bootstrap method with 5-year blocks detailed in Sect. 2.3 to construct the 90% confidence interval for $\beta$, which is frequently used in attribution and detection analyses. If the 90% corresponding confidence interval of a scaling factor is above zero, then the fingerprint is claimed to be detected. Additionally, given that a fingerprint is detected, a 90% confidence interval covering one is the necessary evidence that the observed changes can be attributed to the corresponding external forcing.

4 Simulation studies

4.1 Independence setting

We first considered the case with independent measurement errors. For simplicity, $X_t$ is a univariate normal random variable with mean 0 and standard deviation 2, and $Z_t = 1$. The observed extremes $Y_t$ was subsequently generated from a generalized extreme value distribution with $\theta = (1, 1, 4, -0.2)$ by using the R package evd (Stephenson 2002). The observed surrogate $W_t$ was then generated from Equation (3) where $\Sigma$ reduces to $\sigma _e^2 I$ with $\sigma _e^2=1$. To carry out the MCCS method, $\widetilde{W}_{b, t}$ was obtained by adding $\iota \epsilon _{b,t}$ to $W_t$, where $\epsilon _{b,t}$ is also a normal variable with mean 0 and variance $\sigma _e^2 = 1$, and $b = 1, \dots , B$. Here we treat $\sigma _e$ as known and focus on estimating $\theta$. In the simulation, we consider the Monte Carlo sampling $B\in \{200, 400\}$ and the sample size $n\in \{100, 200\}$. For each configuration, 1000 data sets have been generated. Also, for each dataset, we obtained MLE for $\theta$ without correcting for $W_t$ and $\tilde{\theta }$ by implementing MCCS with $\widetilde{W}_{b, t}$. The MLE estimation was carried out by the package ismev (Heffernan and Stephenson 2018), and the MCCS was solved by using nleqslv.

Table 1 Summary of simulation results based on 1000 replications

Table 1 summarizes the results in estimating $\theta$. The MLEs of $\theta$ are the naive estimates with measurement error ignored. The naive estimates of $\alpha$, $\sigma$, and $\xi$ are unbiased under all configurations. The naive estimate of parameter $\beta$, however, is severely biased, and the coverage rate is low across different sample sizes. On the other hand, the proposed method provides an unbiased estimate of $\beta$, and the coverage rate is close to the nominal level 90% for all the settings, including the case that $B = 200$. The other parameters are consistently estimated, and their coverage rates are close to the nominal level as well. In general, as n increases, the convergence rate improves, and the bias, RMSE, ESE, and ASE decreases as n increases. Regarding the performance of the algorithm, the percentage of successfully finding a root using nleqslv is around 95% when n = 100 and improves to 99.5% when n increases to 200 in our simulation. Given a fixed n, however, the performance of MCCS estimators is very similar across different Bs in our setting. Nonetheless, the proposed method works well in correcting bias in $\beta$.

4.2 Fingerprinting setting

We also carried out simulation studies with fingerprinting setting described in Sect. 3 with one forcing ($p = 1$). In order to mimic the real detection and attribution process, we first simulated the climate model extremes $U_{t}^{(l)}$ from a generalized extreme model with $\sigma ^\prime = 2$ and $\xi ^\prime = -\,0.2$. The location parameter $X_t$ is determined by a cubic spline where $\gamma$ is uniformly distributed in (38, 40). The number of ensemble runs L is assumed to be 50, and for each run, we have 100 years of data. Then the observed extreme $Y_t$ was generated from a generalized extreme value distribution with $\{\alpha , \beta , \sigma , \xi \} = \{40, 1, 1, -\,0.2\}.$ Again, two levels of the Monte Carlo sampling size, $\{200, 400\}$ are considered here.

Table 2 summarizes the results in estimating $\theta$ in the fingerprinting setup. Both methods provide unbiased estimates to $\sigma$ and $\xi$. Unlike the previous results, the bias is observed in both $\alpha$ and $\beta$ in the naive estimates, resulting in extremely poor coverage rates. This could lead to misleading conclusions in the detection and attribution analysis which mainly relies on the statistical inferences of $\beta$. In contrast, MCCS estimates of $\alpha$ and $\beta$ are nearly unbiased. Even though the bias of $\hat{\alpha }$ estimated by MCCS is around $-1.2$ in Table 2, it is relatively unbiased given that the true value of $\alpha$ is 40. More importantly, the coverage rate of the scaling factor $\beta$ in MCCS is much closer to 90%, which implies a more reliable decision on the detection and attribution of a signal. Even though the coverage rates of $\sigma$ and $\xi$ are lower than the nominal level using the MCCS method, they are still around 85%, and their MCCS point estimates are also unbiased. In simulations, the convergence rate of the MCCS method is around 99%, indicating high success in finding a root.

5 Temperature extremes in central China

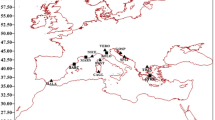
The observed annual temperature extremes in the East Asia region over the period of 1951–2010 were extracted from the HadEX2 data (Donat et al. 2013). For each temperature extreme described in Sect. 3, grid boxes of resolution $5^\circ \times 5^\circ$ (latitude $\times$ longitude) are available. After excluding the grid boxes with missing values, we have 47, 48, 41, and 43 grid boxes for TXx, TXn, TNx, and TNn, respectively. The longitude value covered by these grid boxes ranges from 100E to 150E, and latitude value ranges from 25N to 50N. Since observations on land are more reliable than those in the ocean, we focused on twelve land grid boxes with latitude ranging from 30N to 40N and longitude covering from 100E to 115E, which covers a large part of inland China (Fig. 1).

Table 2 Summary of simulation results based on 1000 replications

Fig. 1

Twelve grid boxes in central China were selected for analysis

The ALL (combination of anthropogenic and natural external) forcing is the single external forcing being considered. To avoid making any assumptions about the exchangeability of different climate models, we only used the second-generation Canadian Earth System Model (CanESM2) (Chylek et al. 2011) to estimate signals, which contains 50 runs under the ALL forcing. In order to match the spatial resolution of the HadEx2 data, the CanESM2 data also has been regridded to $5^\circ \times 5^\circ$ grid boxes. The 50 runs are independent replicates simulated under both anthropogenic factors (greenhouse gas and aerosol emissions) and natural-only factors (solar radiation and volcano eruptions). The signals under the ALL forcing at each grid box were estimated by fitting (8) to the 50 runs. A cubic spline with a 5-year knots was used to estimate the ALL signal. In regional detection and attribution analyses, it is often assumed that the scaling factors across all the grid boxes are the same (Zwiers et al. 2011; Wang et al. 2017, 2021), in which case, the spatial dependence among the grid boxes needs to be addressed. Since a spatial extension of the MCCS method needs a full investigation, here we apply the method to each grid box separately.

At each grid box, the fingerprinting method in Sect. 3 was applied to each of the four temperature extremes. The minimum extremes TXn and TNn were negated before the analyses. The size of Monte Carlo sampling was fixed at $B = 1,000$ for each analysis. For comparison, we also included the naive estimators, which ignored the measurement errors in the estimated fingerprint and fitted the data using the MLE method. To ensure $\xi > -0.5$, we use a Beta(9, 6) prior to constraint $\xi$ within a range of $(-0.5, 0.5)$ (Martins and Stedinger 2000) in both methods as done by Wang et al. (2021).

Fig. 2

The top and bottom graphs present the scaling factor estimation for all the temperature extremes and the corresponding 90% bootstrap confidence intervals for the selected grid boxes

Figure 2 displays the 90% confidence intervals of the scaling factor for each temperature extreme in each of the 12 grid boxes. Additional figures of other parameters are presented in the Appendix 1. The estimates of $\xi$ are negative in most grid boxes, which is consistent with the findings in Huang et al. (2016). The influence of the ALL forcing is detected for all the temperature extremes in most of the 12 grid boxes. In particular, the most detectable influence is on TNx, the annual maximum of daily minimum temperature, and the least detectable influence is on TXx, the annual maximum of daily maximum. In most cases, both naive and proposed methods reach consistent conclusions, although the point estimates of the scaling factor can be quite distinct from both methods in temperature minimums. For the maximums TNx and TXx, for example, the estimates of $\beta$ are quite close except for the (115E, 30N) case. The analysis on the minimums, especially on the TXn, displays a much larger discrepancy in the $\hat{\beta }$. In the (110E, 40N) case, for instance, the difference in the $\hat{\beta }$s bring about different conclusions in the attribution decision. Moreover, the proposed method tends to produce a larger standard error in most cases, which might lead to different conclusions even though the estimated values of $\beta$ are close for both approaches. For example, both methods produce similar values in $\hat{\beta }$ in the (105E, 40N) grid box, but the lower bound of the 90% confidence interval is much closer to 1 using the proposed method while the counterpart for the naive method is way above 1. Overall, both methods agree on the detection and attribution results on TNx and TXx for all the grid boxes. ALL forcings are always detected on TNx using both methods, but its evidence of attribution is obvious in the grid boxes with latitude 40N. Different from the results on TNx, the influence of ALL forcings are not detected in grid boxes (110E, 30N), (115E, 30N), (110E, 35N), and (115E, 35N). There is also no evidence that the change in TXx is attributable to ALL forcings. For TNn and TXn, there are a few cases that the ALL forcings are not detectable. For the (115E, 30N) grid box, the influence of the ALL forcing is not detectable using the proposed method, while the naive method reach a different decision. In terms of attribution, only the (115E, 30N) and (115E, 40N) grid boxes show necessary evidence of attributing the ALL influence to the change in TNn. Similar to the results of TNn, the change in TXn can only be attributed to ALL forcings in two grid boxes. Interestingly, both methods agree on the attribution results for the (100E, 30N) grid box, but disagree on the attribution results for (110E, 40N) grid box.

Table 3 Summaries of estimated parameters of the ALL signals for four temperature extremes in grid box indexed by longitude 110E and latitude 40N

For illustration purposes, we choose the (110E, 40N) grid box and report the point estimates (Est), the corresponding standard errors (SE), and the 90% confidence intervals (CI) of $\theta$ for each temperature extreme based on the two methods (Table 3). The estimates of $\xi$ and $\sigma$ between the two methods are quite similar, which is consistent with the simulation results in Sect. 4. On the other hand, the location parameters $\alpha$ and $\beta$ can be very different between the naive estimates and the MCCS estimates in some cases. For instance, the estimates of $\alpha$ and $\beta$ are very different between the two methods on TXn, directly resulting in a different conclusion. The naive method detects the ALL signal at all on TXn, but there is no evidence that the change on TXn is attributable to the influence of ALL forcings. On the opposite side, ALL forcings are not only detected by the proposed method but also demonstrate necessary evidence of attribution on TXn, with the corresponding 90% confidence interval being significantly greater than zero. For extremes other than TXn, both methods detect the ALL signal to the temperature change.

6 Discussion

Relatively little attention has been paid to understanding and correcting for the EIVs in the location parameters of GEV regressions. Motivated by the optimal fingerprinting method in the detection and attribution analysis of changes in climate extremes, we investigated the impact of measurement error in both the independent and time-correlated measurement error settings through simulation studies. The bias caused by the measurement error can be severe. Our MCCS method takes advantage of the existing score functions of the GEV distribution and the flexibility of Monte Carlo copies to correct for the bias of estimators. For inferences, the confidence intervals based on our block bootstrap approach appear to give acceptable coverage rates. Though our method was applied to single grid boxes, it is able to correct the bias and provide valid inference effectively. Given the fact that the signals at each grid box are much lower than those on a bigger spatial scale, our results are encouraging, indicating that our method can be served as a building block for further research on pooling boxes together to estimate $\beta$ (Wang et al. 2021). The corrected score functions also allow further extension of the fingerprinting by incorporating covariates in the scale parameter to account for non-stationarity and other possible influencing factors (Huang et al. 2016). Overall, the MCCS approach can be applied to GEV regressions with independent and temporally dependent EIVs that arise in many fields.

A few future directions are worth pursuing. Computationally, one concern is the numerical instability in estimation when the sample size is small. As many GEV regressions have a limited amount of observations, it would be useful to develop regularized estimation along the line of Firth (1993). For sandwich variance estimation, the “bread” part, or the inverse of the derivative of the corrected scores with respect to the parameters, could be poorly conditioned when the sample size is small. The regularized estimation might be helpful with this issue as well. Due to these computational issues, in our application to central China temperature extremes, we performed only one-signal analysis with the ALL signal. It is desirable to do two-signal analyses with both anthropogenic forcing and natural forcing at the same time. One possibility is to use a longer record of data, such as HadEX3 (Dunn et al. 2020) and CanESM5 (Swart et al. 2019). Methodologically, however, it would be interesting to extend the MCCS method to the spatial setting and restrict the scaling factors across grid boxes to be the same in one regional analysis (Zwiers et al. 2011). Incorporating spatial dependency to improve the efficiency of the MCCS method similar to the combined score equations (Wang et al. 2021) merits a full investigation.

Appendices

Appendix A Derivation of MCCS for GEV

The derivatives of the log density of $F(\cdot \mid \mu , \sigma , \xi )$ with respect to the parameter are (Prescott and Walden 1980)

$$\begin{aligned} f_1(Y; \mu , \sigma , \xi )&= \frac{1+\xi -\nu }{\sigma w},\\ f_2(Y; \mu , \sigma , \xi )&= \frac{1}{\sigma }\left\{ -1+\frac{(1+\xi -\nu )(Y -\mu )}{\sigma w}\right\} ,\\ f_3(Y; \mu , \sigma , \xi )&= {\left\{ \begin{array}{ll} \frac{\log (w)(1-\nu )}{\xi ^2}-\frac{(1+\xi -\nu )(Y-\mu )}{\xi \sigma w} &{} \xi \ne 0\\ \frac{1}{2}\left( 1 - \exp (\frac{Y - \mu }{ \sigma })\right) \left( \frac{Y - \mu }{ \sigma }\right) ^2 - \frac{Y - \mu }{\sigma w} &{} \xi = 0 \end{array}\right. }, \end{aligned}$$

where $w = 1+\xi (Y-\mu )/\sigma , \nu = w^{-1/\xi }\mathbbm {1}(\xi \ne 0) + e^{-(Y-\mu )/\sigma }\mathbbm {1}(\xi = 0)$, $\mu = Z^\top \alpha +X^\top \beta$, and $\mathbbm {1}(\cdot )$ is the indicator function.

To derive the real part of the $\tilde{\psi }_B$, we first replace X with $\widetilde{W}_{b, t}$ in $f_1(\cdot )$, $f_2(\cdot )$, and $f_3(\cdot )$. Then we can rewrite $Y - \mu$ as following,

$$\begin{aligned} Y - \mu = Y-W^\top \beta - Z^\top \alpha - \iota \epsilon _{b, t}^\top \beta = u - \iota v, \end{aligned}$$

(A1)

where $u = Y-W^\top \beta - Z^\top \alpha$ and $v = \epsilon _{b, t}^\top \beta$. In addition, using polar representation, we have

$$\begin{aligned} \sigma + \xi (u - \iota v) = re^{\iota \omega }, \end{aligned}$$

(A2)

where $r = \sqrt{(u\xi +\sigma )^2+(v\xi )^2}$ and $\omega = \textrm{atan2}\{-u\xi , (v\xi +\sigma )\}$. Note that $\textrm{atan2}\{-u\xi , (v\xi +\sigma )\}$ returns a single value $\omega$ such that $-\pi < \theta \le \pi$ and, for some $r >0$, $(a\xi +\sigma ) = r\cos \omega$ and $-b\xi = r\sin \omega$. From Euler’s formula, we can also write $re^{\iota \omega }$ as

$$\begin{aligned} re^{\iota \omega } = r\cos \omega + \iota r\sin \omega , \end{aligned}$$

(A3)

or equivalently, $re^{-\iota \omega } = r\cos \omega - \iota r\sin \omega$. Given these expressions, we can first start to rewrite $f_1(\cdot )$ in the following way,

$$\begin{aligned}&f_1(Y; \mu , \sigma , \xi )\\&\quad = \frac{1+\xi -\nu }{\sigma w}\\&\quad = \frac{1+\xi -w^{-1/\xi }}{\sigma \{1+\xi (Y-\mu )/\sigma \}}\\&\quad = \frac{1+\xi -\{1+\xi (Y-\mu )/\sigma \}^{-1/\xi }}{\sigma \{1+\xi (Y-\mu )/\sigma \}}\\&\quad = \frac{1+\xi -\{1+\xi (u-\iota v)/\sigma \}^{-1/\xi }}{\sigma \{1+\xi (u-\iota v)/\sigma \}} (\text { use }(A1))\\&\quad = (re^{\iota \omega })^{-1}\left\{ 1+\xi -(re^{\iota \omega }/\sigma )^{-1/\xi }\right\} (\text { use } (A2))\\&\quad = \frac{\cos \omega - \iota \sin \omega }{r}\\&\qquad \left[ 1+\xi -\frac{r^{-1/\xi } \{\cos (\omega /\xi ) - \iota \sin (\omega /\xi )\}}{\sigma ^{-1/\xi }}\right] (\text { use } (A3))\\&\quad = c + \iota d, \end{aligned}$$

where

$$\begin{aligned} c&= \frac{\cos \omega }{r}\left\{ 1+\xi -\left( \sigma /r\right) ^{1/\xi } \cos \left( \omega /\xi \right) \right\} \\&\qquad + \frac{\sin \omega }{r}(\sigma /r)^{1/\xi }\sin (\omega /\xi ),\\ d&\quad = \frac{\cos \omega }{r}(\sigma /r)^{1/\xi }\sin (\omega /\xi )\\&\qquad - \frac{\sin \omega }{r} \left\{ 1+\xi -(\sigma /r)^{1/\xi }\cos (\omega /\xi )\right\} . \end{aligned}$$

In a similar way, we can also rearrange $f_2(\cdot )$ such that,

$$\begin{aligned} f_2(Y; \mu , \sigma , \xi )&= \frac{1}{\sigma }\left\{ -1+f_1\cdot (u - \iota v)\right\} \\&= \frac{-1+(c+\iota d)(u - \iota v)}{\sigma }\\&= \frac{-1+cu+dv}{\sigma }+\iota \frac{du-cv}{\sigma }. \end{aligned}$$

We then focus on the case when $\xi \ne 0$ to separate the real and imaginary part of $f_3(\cdot )$, and we have,

$$\begin{aligned}&f_3(Y; \mu , \sigma , \xi )\\&= \frac{\log (w)(1-\nu )}{\xi ^2}-\frac{(\sigma f_2+1)}{\xi }\\&= \frac{1}{\xi ^{2}}\log \left\{ \frac{\sigma +\xi (u-\iota v)}{\sigma }\right\} \left[ 1-\left\{ \frac{\sigma +\xi (u-\iota v)}{\sigma }\right\} ^{-1/\xi }\right] \\&\quad -\frac{(\sigma f_2+1)}{\xi }\\&= \frac{1}{\xi ^{2}}\log \left( \frac{re^{\iota \omega }}{\sigma }\right) \left( 1-\frac{(re^{\iota \omega })^{-1/\xi }}{\sigma ^{-1/\xi }}\right) -\frac{(\sigma f_2+1)}{\xi } \qquad (\text { use } ())\\&= \frac{\log r - \log \sigma + \iota \omega }{\xi ^2} \times \left[ 1-(\sigma /r)^{1/\xi } \left\{ \cos (\omega /\xi )-\iota \sin (\omega /\xi )\right\} \right] \\&\quad -\frac{(\sigma f_2+1)}{\xi }\\&= \frac{\log (r /\sigma ) \left\{ 1-(\sigma /r)^{1/\xi } \cos (\omega /\xi )\right\} }{\xi }-\frac{\omega (\sigma /r)^{1/\xi } \sin (\omega /\xi )}{\xi ^2}\\&\quad -\frac{(cu+dv)}{\xi }\\&\quad + \iota \frac{\omega \left\{ 1-(\sigma /r)^{1/\xi }\cos (\omega /\xi )\right\} }{\xi ^2} - \iota \frac{\log (r /\sigma )\sin (\omega /\xi ) }{\xi ^2}\\&\quad - \iota \frac{(du-cv)}{\xi }. \end{aligned}$$

The real part of the three functions can be readily obtained by,

$$\begin{aligned} \Re (f_1(Y; \mu , \sigma , \xi ))&= c,\\ \Re (f_2(Y; \mu , \sigma , \xi ))&= \frac{-1+cu+dv}{\sigma },\\ \Re (f_3(Y; \mu , \sigma , \xi ))&= \frac{\log (r /\sigma )\left\{ 1-(\sigma /r)^{1/\xi }\cos (\omega /\xi )\right\} }{\xi ^2}\\&\quad -\frac{\omega (\sigma /r)^{1/\xi }\sin (\omega /\xi )}{\xi ^2} -\frac{(cu+dv)}{\xi }. \end{aligned}$$

Furthermore, $\Re (W f_1) = \Re ((W+\iota \epsilon _{b, t})(c+\iota d)) = cW-d\epsilon _{b, t}$, and $\Re (Z f_1) = Z c$. The derivation of the case when $\xi = 0$ can be done in a similar way.

Appendix B Sketch of technical arguments

1.1 B.1 Argument for Proposition 1

Denote $\tilde{\psi }_{B,t} (\theta )= \tilde{\psi }_B(Y_t, W_t, Z_t, \theta , \Sigma _t)$. By Taylor series,

$$\begin{aligned}{} & {} n^{-1/2}\sum _{t=1}^n \left\{ \tilde{\psi }_{B,t} (\tilde{\theta }_{n,B})-\tilde{\psi }_{B,t} (\theta _0)\right\} \\{} & {} \qquad =n^{-1/2}\sum _{t=1}^n \left\{ \frac{\partial \tilde{\psi }_{B,t}(\theta _0)}{\partial \theta _0^\top } (\tilde{\theta }_{n,B}-\theta _0)+o_p\Vert \tilde{\theta }_{n,B}-\theta _0\Vert \right\} \\{} & {} \qquad = \left\{ n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }_{B,t}(\theta _0)}{\partial \theta _0^\top } \right\} \sqrt{n}(\tilde{\theta }_{n,B}-\theta _0) + o_p(1). \end{aligned}$$

Thus,

$$\begin{aligned}{} & {} \sqrt{n}(\tilde{\theta }_{n,B}-\theta _0) = -\left\{ n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }_{B,t}(\theta _0)}{\partial \theta _0^\top } \right\} ^{-1} \\{} & {} \quad n^{-1/2}\sum _{t=1}^n \left\{ \tilde{\psi }_{B,t} (\tilde{\theta }_{n,B})-\tilde{\psi }_{B,t} (\theta _0)\right\} +o_p(1). \end{aligned}$$

Subsequently, we have

$$\begin{aligned} n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }_{B,t}(\theta _0)}{\partial \theta _0^\top } = D + o_p(1), \end{aligned}$$

and

$$\begin{aligned} \sqrt{n}(\tilde{\theta }_{n,B}-\theta _0) \rightarrow N(0, C), \end{aligned}$$

where D and C are defined as in Proposition 1.

1.2 B.2 Argument for Proposition 2

Denote $\tilde{\psi }_{B,t}^* (\theta )= \tilde{\psi }_B^*(Y_t, W_t, Z_t, \theta , \Sigma )$. By Taylor series,

$$\begin{aligned}{} & {} n^{-1/2}\sum _{t=1}^n \left\{ \tilde{\psi }_{B,t}^* (\tilde{\theta }^*_{n,B})-\tilde{\psi }_{B,t}^* (\theta _0)\right\} \\{} & {} \qquad =n^{-1/2}\sum _{t=1}^n \left\{ \frac{\partial \tilde{\psi }^*_{B,t}(\theta _0)}{\partial \theta _0^\top } (\tilde{\theta }^*_{n,B}-\theta _0)+o_p\Vert \tilde{\theta }^*_{n,B}-\theta _0\Vert \right\} \\{} & {} \qquad = \left\{ n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }^*_{B,t}(\theta _0)}{\partial \theta _0^\top } \right\} \sqrt{n}(\tilde{\theta }^*_{n,B}-\theta _0) + o_p(1). \end{aligned}$$

Thus,

$$\begin{aligned}{} & {} \sqrt{n}(\tilde{\theta }^*_{n,B}-\theta _0) = -\left\{ n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }^*_{B,t}(\theta _0)}{\partial \theta _0^\top } \right\} ^{-1}\\{} & {} \quad n^{-1/2}\sum _{t=1}^n \left\{ \tilde{\psi }_{B,t}^* (\tilde{\theta }_{n,B}^*)-\tilde{\psi }^*_{B,t} (\theta _0)\right\} +o_p(1). \end{aligned}$$

Let $D^*= E\left\{ \frac{\partial \tilde{\psi }_B(Y_t, W_t, Z_t, \theta )}{\partial \theta ^\top }\right\}$, then we have

$$\begin{aligned} D^*= & {} E\left\{ \frac{\partial \tilde{\psi }^*_B(Y_t, W_t, Z_t, \theta )}{\partial \theta ^\top }\right\} \\= & {} \frac{\partial E\{\tilde{\psi }^*_B(Y_t, W_t, Z_t, \theta )\}}{\partial \theta ^\top }\\= & {} \frac{\partial E[E\{\tilde{\psi }^*_B(Y_t, W_t, Z_t, \theta ) \mid (Y_t, X_t, Z_t)\}]}{\partial \theta ^\top }\\= & {} \frac{\partial E\{\psi ^*(Y_t, X_t, Z_t, \theta )\}}{\partial \theta ^\top }\\= & {} E\left\{ \frac{\partial \psi ^*(Y_t, X_t, Z_t,\theta )}{\partial \theta ^\top }\right\} \\= & {} E\left[ E\left\{ \frac{\partial \psi ^*(Y_t, X_t, Z_t, \theta )}{\partial \theta ^\top }\bigm \vert X_t \right\} \right] \\= & {} E\left( \textrm{Re}\left[ E\left\{ \frac{\partial \psi ^*(Y_t, \widetilde{W}^*_{t,b}, Z_t, \theta )}{\partial \theta ^\top }\bigm \vert X_t\right\} \right] \right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} n^{-1}\sum _{t=1}^n \frac{\partial \tilde{\psi }^*_{B,t}(\theta _0)}{\partial \theta _0^\top } = D^* + o_p(1), \end{aligned}$$

and

$$\begin{aligned} \sqrt{n}(\tilde{\theta }_{n,B}^*-\theta _0) \rightarrow N(0, C^*), \end{aligned}$$

where $C^* = \textrm{Var}\{n^{-1/2}\sum _{t=1}^n\tilde{\psi }_B^*(Y_t, W_t, Z_t, \theta , \Sigma )\}$. Considering the correlations among $\tilde{\psi }_{B,t}^*$’s caused by correlated measurement errors, $C^*$ can be decomposed as $\textrm{Var}\left\{ \tilde{\psi }_{B,t}^*(\theta )\right\}$ and $\textrm{Cov}\left\{ \tilde{\psi }_{B,t}^*(\theta )\tilde{\psi }_{B,t'}^*(\theta )\right\}$.

For the bth Monte Carlo copy of year t, we generate $\tilde{Z}_{b1}$ and ${\tilde{Z}}_{b2}$ independently from $N(0, I_{np\times np})$ and construct $\widetilde{W}^*_{b,t} = W_t+\iota \Delta _t {\tilde{Z}}_{b1}$ and $\widetilde{W}^*_{b,t'} = W_{t'}+\iota \Delta _{t'} {\tilde{Z}}_{b2}$, where $\Delta = \Sigma ^{1/2}$ and $\{\Delta _t\}_{p\times np}$ is the top tth chunk of $\Delta$. We have

$$\begin{aligned}{} & {} E \left[ \textrm{Re}\left\{ \psi (Y_t, \widetilde{W}_{b,t}^*, Z_t, \theta ) \psi ^\top (Y_t, \widetilde{W}_{b,t}^*, Z_t, \theta )\right\} \bigm \vert (Y_t, X_t, Z_t)\right] \\{} & {} = E \left[ \textrm{Re}\left\{ \psi (Y_t, X_{t}+e_t+\iota \Delta _t \tilde{Z}_{b1}, Z_t, \theta )\right. \right. \\ {}{} & {} \left. \left. \psi ^\top (Y_t, X_{t}+e_t+\iota \Delta _t {\tilde{Z}}_{b1}, Z_t, \theta )\bigm \vert (Y_t, X_t, Z_t)\right\} \right] \\{} & {} \text {(Expand around }X_t) \approx \psi (Y_t, X_{t}, Z_t,\theta )\psi ^\top (Y_{t}, X_{t}, Z_t, \theta ), \end{aligned}$$

and similarly,

$$\begin{aligned}&E \left[ \textrm{Re}\left\{ \psi (Y_t, \widetilde{W}_{b,t}^*, Z_t, \theta ) \psi ^\top (Y_{t'}, \widetilde{W}_{b,t'}^*, Z_{t'}, \theta )\right\} \right. \\&\left. \bigm \vert (Y_t, Y_{t'}, X_t, X_{t'}, Z_t, Z_{t'})\right] \\&\approx \psi (Y_t, X_{t}, Z_t,\theta )\psi ^\top (Y_{t'}, X_{t'}, Z_{t'}, \theta ). \end{aligned}$$

Fig. 3

The top and bottom graphs present the location parameter $\alpha$ estimation for all the temperature extremes and the corresponding 90% bootstrap confidence intervals for the selected grid boxes

Fig. 4

The top and bottom graphs present the scale parameter $\sigma$ estimation for all the temperature extremes and the corresponding 90% bootstrap confidence intervals for the selected grid boxes

Fig. 5

The top and bottom graphs present the scale parameter $\xi$ estimation for all the temperature extremes and the corresponding 90% bootstrap confidence intervals for the selected grid boxes

Thus, for $t = 1,\ldots ,n$ and $t' = 1,\ldots ,n$, a consistent estimator for $C^*$ can be constructed as below,

$$\begin{aligned} \widehat{C}_{\widetilde{\psi }^*}&= \frac{1}{nB} \left[ \sum _{t, t'=1}^n\sum _{b=1}^B \Re \left\{ \psi (Y_t, \widetilde{W}_{b,t}^*, Z_t, \theta ^*_{n,B})\right. \right. \\&\left. \left. \psi ^\top (Y_{t'}, \widetilde{W}_{b,t'}^*, Z_{t'}, \theta ^*_{n,B} )\right\} \right] . \end{aligned}$$

1.3 B.3 Argument for Lemma 2

We denote ${\tilde{Z}}_{b}^\top = ({\tilde{Z}}_{b,1}^\top ,\ldots ,\tilde{Z}_{b,t}^\top ,\ldots ,{\tilde{Z}}_{b,n}^\top )^\top$ from $N(0, I_{np\times np})$ and generate $\widetilde{W}^*_{b} = W+\iota \Sigma ^{1/2} \tilde{Z}_{b}$ for the bth Monte Carlo copy. The first equality is based on Lemma 1–2 in Stefanski and Cook (1995). Then, we denote $\{\Delta _t\}_{p\times np}$ be the top tth chunk of $\Sigma ^{1/2}$ and have

$$\begin{aligned}&E \left[ \textrm{Re}\left\{ \psi (Y_t, \widetilde{W}^*_{b,t}, \theta )\right\} \bigm \vert (Y_t, X_t)\right] = E \left[ \textrm{Re}\left\{ \psi (Y_t, X_{t}+e_t \right. \right. \\&\quad \left. \left. +\iota \Delta _t {\tilde{Z}}_{b,t}, \theta )\right\} \right] =\psi (Y_t, X_{t}, \theta ). \end{aligned}$$

As the measurement error $e_t$ and $\Delta _t {\tilde{Z}}_{b,t}$ are independent and identically distributed random vectors generated from $N(0, \Sigma )$, the last equality is a result of Lemma 4 in Stefanski and Cook (1995). Hence, we finish the proof for Proposition 2.

Appendix C Additional figures

This section contains plots for parameters, $\alpha$, $\sigma$, and $\xi$, in the application of modeling temperature extremes in central China. See Figs. 3, 4, and 5, respectively. Each plot includes the point estimates and corresponding 90% bootstrap confidence intervals. In most grid boxes, the estimates of shape parameter $\xi$ are negative, which aligns with the findings in Huang et al. (2016).